Thermoelastic Response of Closed Cylindrical Shells in a Supersonic Gas Flow

Abstract

The work is devoted to the investigation of flutter oscillations and the stability of the closed cylindrical shell in supersonic gas flow in an inhomogeneous temperature field. It is assumed that supersonic gas flows on the outside of the shell with an unperturbed velocity U, directed parallel to the cylinder generatrix. Under the action of an inhomogeneous temperature field the shell bulges out, this deformed state is accepted as unperturbed, and the stability of this state is studied. The main nonlinear equations and relationships describing the behavior of the examined system are derived. The formulated boundary value problem is solved using the Galerkin method. The joint influence of the flow and the temperature field on the relationship between the amplitude of nonlinear oscillations of a cylindrical shell and the speed of the flowing stream is studied. The critical velocity values are calculated from the corresponding linear system and are given in tables. The numerical results show that: (a) the surrounding flow significantly affects the nature of the investigated relationship; (b) a certain interval of supersonic velocity exists where it is impossible to excite steady-state flutter oscillations (the silence zone); (c) the dependence of amplitude on the supersonic velocity can be either multivalued or single-valued.

1. Introduction

The problem of the interaction of different media and physical fields is the center of attention for researchers in mechanics of continuous deformable media. In particular, the issues of mechanics of shells and plates interacting with a supersonic gas flow and temperature fields are of particular importance. These problems relate to the modern and rapidly developing field—mechanics of a deformable body, they are very relevant and cover a wide class of general theoretical and applied problems that arise when considering a physical experiment, creating measuring equipment, designing aviation and space structures, building engineering structures, shipbuilding, etc. Ensuring the dynamic strength of engineering structures and the thin-walled elements of aircraft during their interaction with gas flow is one of the most complex problems that arise during the development of new structures and their operation. Reliability is the main indicator of quality and an important design goal is to improve this indicator.

The interaction of a structure with a supersonic flow can lead to undamped elastic oscillations, called flutter, which are very dangerous; in particular, dynamic stresses in the structure can quickly reach destructive values. Therefore, investigation of the flutter phenomenon is very relevant; a rigorous formulation of the problem and its study in the case of plates and shells made of new structural materials is required.

A fundamental contribution to studies on this topic is due to the introduction of piston theory by Ashley and Zartarian in 1956 [1]. In many interesting works, the stability of a shell in supersonic flow was studied using a linear shell model, including the works of Dowell [2], Olson and Fung [3], as well as Ganapati et al. [4] predicted the onset of flutter instability. Experiments [3,5] showed that the amplitude of flutter oscillations is commensurable to the thickness of the shell; therefore, for the accurate prediction of the amplitude of flutter, the nonlinear theory of shells should be used.

The solution method in studies [6,7,8,9], devoted to nonlinear flutter, is based on the Galerkin method, paying attention to a number of retained terms in the Fourier series. Similar problems were considered in detail in [10,11] taking into account the way the shell’s edges were fixed. In the study of flutter in both linear and nonlinear formulations, a significant contribution was made by the representatives of the Armenian scientific school [12,13,14,15,16,17].

Until now, many significant aspects of flutter phenomenon have not been sufficiently studied. There are a large number of works devoted to flutter, but few experimental works have been published, since it is both expensive and difficult to implement. Therefore, the construction of a mathematical model of the phenomenon of panel flutter and the numerical solution of the obtained equations is relevant. Based on the theory of plane sections of an Ilyushin [6], it is possible to construct a fairly simple mathematical model of the studied phenomenon.

This work is devoted to the investigation of flutter oscillations of a closed cylindrical shell in supersonic gas flow in the presence of an inhomogeneous temperature field. Let us present here some results and the novelty of this work. It is shown that under the action of a nonuniform thermal field a thin-walled body (cylindrical shell) bends with deflection and thermal stresses as well as surface pressure occurring in the body. Therefore, a new static deformed state occurs in the body, which is strongly different from the initial (undeformed) state. Issues of stability and nonlinear vibrations of the noted bent state (which is accepted as undisturbed) are investigated in this work. The nonhomogeneous boundary value problem, describing the undisturbed state, is formulated and solved. Stresses and displacements of the undisturbed state are determined, depending on the thermal field and speed of the flowing stream. Using the already found formulas for stresses and displacements of undisturbed state and based on the theory of elastic stability of flexible plates, the governing equations and boundary conditions of the disturbed state are derived. As a result, the dynamic nonlinear boundary value problem, characterizing the disturbed state, is formulated. In this problem the coefficients contain terms, describing stresses and displacements of the undisturbed state. These two very important issues are related to the mathematical modeling and formulation of the problem. We cannot find these results in any published worldwide scientific work. Investigation of stability and vibrations via the Galerkin method is usually reduced to a study of the existence of nontrivial solutions for nonlinear ordinary differential equations. This system of ordinary differential equations is solved exactly using the harmonic balance method. One of the main and basic novelties of this work is the solution methodology and representation (13) is taken as a solution for the system of nonlinear ordinary differential equations. The presence of free terms in this representation gives an opportunity to take into account the effect of quadratic nonlinearity on the process of vibrations which brings relationships of a new type between the amplitude of limit-cycle oscillations and the flowing speed. The next new result of this paper is the multivalued relationship between the amplitude and the frequency of nonlinear oscillations. The graphs of these relationships consist of two branches, one of them, where the amplitude has comparatively small values, is probably unstable. In the case of disturbances smaller than those lying on the unstable branch, the system returns to the undisturbed state, otherwise, vibrations with a greater amplitude are characterized by the stable branch. This phenomenon is due to quadratic aerodynamic nonlinearity and is one of our main important results. Let us note that such a type of relationship takes place in the case of nonlinear natural vibrations of shells. The comparisons between the known in the literature results and ours are brought in the paper. These comparisons have a qualitative nature. To do quantitative comparison in more detail is almost impossible, because there are no analytical investigations for the solutions of the system of ordinary differential equations, obtained and presented in this paper, and we could not find any information about the methodology of the numerical calculations. On the other hand, the work is multifunctional and the detailed numerical investigation is done with respect to the main parameters (which describe the flowing stream, thermal field, geometry) to explore the effect of this influence.

2. The Problem Statement

In this paper a thin isotropic closed cylindrical shell of length $a$ and constant thickness $h$ in a stationary temperature field $T$ is considered. The coordinate lines $x$ and $\mathsf{\phi }$ of the cylindrical coordinates system $\left(r,\mathsf{\phi },x\right)$ coincide with the lines of curvature of the shell’s middle surface ($\mathsf{\phi }$–along the arc of the cross section, $x$–along the generatrix). A supersonic gas stream flows along one side of the shell, it has an unperturbed velocity $U$ directed along the axis $0x$. We investigate the issues of the axisymmetric stability of this aero-thermo-elastic system and the influence of the temperature field on the amplitude−frequency relationship of nonlinear flutter oscillations of the system. The following well-known assumptions are taken as the basis of the study:

(a)

the Kirchhoff–Love hypothesis of nondeformable normal [18];

$$\begin{array}{l}{u}_x=u-\left(r-R\right)\frac{\partial w}{\partial x},\\ u_{\mathsf{\phi }}=\left(1+\frac{r-R}{R}\right)v-\left(r-R\right)\frac{\partial w}{\partial \mathsf{\phi }},\\ u_r=w\left(x,\mathsf{\phi },t\right),\end{array}$$

(1)

(b)

the basic assumptions of the theory of flexible plates taking into account that normal displacements are comparable with the thickness of the plate [19];

(c)

the “law of plane sections” to find the aerodynamic pressure [1,6];

$$p=p_{\infty }{\left(1+\frac{\mathsf{\gamma }-1}{2}\frac{v_3}{a_{\infty }}\right)}^{\frac{2\mathsf{\gamma }}{\mathsf{\gamma }-1}}$$

(2)

where $p$ is the gas pressure on the surface of the shell, $p_{\infty }$ and ${\mathsf{\rho }}_{\infty }$ are the gas pressure and density in the unperturbed state, $a_{\infty }$ is the speed of sound in the unperturbed gas $\left(a_{\infty }^2=\mathsf{\gamma }{p}_{\infty }{\mathsf{\rho }}_{\infty }^{-1}\right)$, $v_3$ is the normal component of the speed of the shell’s surface points, $\mathsf{\gamma }$ is the polytropic exponent;

(d)

the linear law of temperature change over the thickness of the shell [20]

$$T=T_0(x,\mathsf{\phi })+(R-r)\Theta (x,\mathsf{\phi }),$$

(3)

where $T_0=\frac{T^{+}+T^{-}}{2},\Theta =\frac{k\left(T^{+}-T^{-}\right)}{kh-2\lambda }$, $k$ is the heat transfer coefficient, $\lambda$ is the thermal conductivity of the shell material;

(e)

the Neumann hypothesis on the absence of displacements from the temperature changes [21].

For clarity we assume that the heat exchange from the front surfaces of the shell $\left(r=R\pm h/2\right)$ to the medium obeys the Newton−Richmann law (the surfaces maintain the constant temperatures T⁺ and T⁻), and the side surfaces ($x=0$ and $x=a$) are heat-insulated.

The stationary temperature field $T$ which is inhomogeneous over the thickness of the shell $\Theta \ne 0$, leads to the shell buckling (with a deflection $w_T(x)$ and a longitudinal displacement $u_T(x)$) and, as a result, an additional aeroelastic pressure appears. We accept this buckled state as unperturbed [16] and study its stability under the influence of the temperature field and the pressure of the gas flow.

In this paper we consider the axisymmetric problem. In [16] the characteristics of the unperturbed state are determined, which have the following form:

The thermoelastic stresses and displacements $u_T$ and $w_T$ are determined from the following equations:

$$\frac{d^2{u}_T}{d{x}^2}+\frac{\mathsf{\mu }}{R}\frac{d{w}_T}{dx}=0$$

(4)

$$D\left[\frac{d^4{w}_T}{d{x}^4}+\frac{12}{R{h}^2}\left(\mathsf{\mu }\frac{d{u}_T}{dx}+\frac{w_T}{R}\right)\right]+\mathsf{\gamma }{p}_{\infty }M\frac{d{w}_T}{dx}=0,$$

(5)

the internal forces are obtained from the formulas

$$\begin{array}{l}{T}_{11}^0={\displaystyle \underset{R-h/2}{\overset{R+h/2}{\int }}{\mathsf{\sigma }}_{11}^{0}dr}=\frac{Eh}{1-{\mathsf{\mu }}^2}\left[\frac{d{u}_T}{dx}+\mathsf{\mu }\frac{w_T}{R}-\mathsf{\alpha }\left(1+\mathsf{\mu }\right)T_0\right],\\ T_{22}^0={\displaystyle \underset{R-h/2}{\overset{R+h/2}{\int }}{\mathsf{\sigma }}_{22}^{0}dr}=\frac{Eh}{1-{\mathsf{\mu }}^2}\left[\mathsf{\mu }\frac{\partial u_T}{\partial x}+\frac{w_T}{R}-\mathsf{\alpha }(1+\mathsf{\mu })T_0\right].\end{array}$$

(6)

Here $D=E{h}^3/12(1-{\mathsf{\mu }}^2)$, $E$ is the elastic modulus, $M=U{a}_{\infty }^{-1}$ is the Mach number for the unperturbed flow, $\mathsf{\alpha }$ is the coefficient of linear thermal expansion of the shell material, $\mathsf{\mu }$ is the Poisson’s ratio.

Let the edges of the shell be hinge supported and fixed in plane. Then the boundary conditions take the form:

$$w_T=0,\hspace{1em}\frac{d^2{w}_T}{d{x}^2}+\mathsf{\alpha }\left(1+\mathsf{\mu }\right)\Theta =0\hspace{1em}\mathrm{at}\hspace{1em}x=0,x=a$$

(7)

$$u_T=0\hspace{1em}\mathrm{at}\hspace{1em}x=0,x=a.$$

(8)

Then, using the boundary conditions (7) (8), we obtain the following expression for determining the deflection $u_T$

$$u_T=-\frac{\mathsf{\mu }}{R}{\displaystyle \underset{0}{\overset{x}{\int }}{w}_T(\xi )}d\xi +\frac{\mathsf{\mu }x}{Ra}{\displaystyle \underset{0}{\overset{a}{\int }}{w}_T(x)}dx,$$

(9)

and the transverse deflection $w_T$ is determined from the equation

$$D\frac{d^4{w}_T}{d{x}^4}+\frac{12}{R{h}^2}\left(\frac{1-{\mathsf{\mu }}^2}{R}{w}_T+\frac{{\mathsf{\mu }}^2}{Ra}{\displaystyle \underset{0}{\overset{a}{\int }}{w}_T(x)dx}\right)+\mathsf{\gamma }{p}_{\infty }M\frac{d{w}_T}{dx}=0$$

(10)

Substituting the obtained expressions into (6) we have:

$$\begin{array}{l}{T}_{11}^0=\frac{E\mathsf{\mu }}{1-{\mathsf{\mu }}^2}\frac{h}{a}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{w_T(x)}{R}}dx-\frac{Eh\mathsf{\alpha }}{1-\mathsf{\mu }}{T}_0,\\ T_{22}^0=Eh\left[\frac{w_T}{R}+\frac{{\mathsf{\mu }}^2}{1-{\mathsf{\mu }}^2}\frac{1}{Ra}{\displaystyle \underset{0}{\overset{a}{\int }}{w}_T(x)dx}-\frac{\mathsf{\alpha }{T}_0}{1-\mathsf{\mu }}\right]\end{array}$$

(11)

Using the obtained characteristics of the unperturbed state, similarly to [16] we obtain the following nonlinear equation with respect to the displacement $w\left(x,t\right)$ of the shell points

$$\begin{array}{l}D\left(\frac{{\partial }^{4}w}{\partial x^4}+\frac{12}{R{h}^2}\left(\frac{w}{R}+\mathsf{\mu }\frac{d{w}_T}{dx}\frac{\partial w}{\partial x}+\frac{{\mathsf{\mu }}^2}{a}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{w}{R}dx}+\frac{\mathsf{\mu }}{a}{\displaystyle \underset{0}{\overset{a}{\int }}\frac{d{w}_T}{dx}\frac{\partial w}{\partial x}dx}\right)\right)+\mathsf{\rho }h\frac{{\partial }^{2}w}{\partial t^2}+\frac{Eh}{1-\mathsf{\mu }}\mathsf{\alpha }{T}_0\frac{{\partial }^{2}w}{\partial x^2}+\\ +\frac{Eh}{2a\left(1-{\mathsf{\mu }}^2\right)}\left\{\frac{d^2{w}_T}{d{x}^2}{\displaystyle \underset{0}{\overset{a}{\int }}{\left(\frac{\partial w}{\partial x}\right)}^{2}d{x}_1}+\frac{{\partial }^{2}w}{\partial x^2}{\displaystyle \underset{0}{\overset{a}{\int }}\left[2\frac{d{w}_T}{dx}\frac{\partial w}{\partial x}+{\left(\frac{\partial w}{\partial x}\right)}^2\right]d{x}_1}\right\}+\\ +\left(\mathsf{\rho }h\epsilon +\frac{\mathsf{\gamma }{p}_{\infty }}{a_{\infty }}\right)\frac{\partial w}{\partial t}+\mathsf{\gamma }{p}_{\infty }M\frac{\partial w}{\partial x}+\frac{\mathsf{\gamma }\left(\mathsf{\gamma }+1\right)}{4}{p}_{\infty }{M}^2\left[2\frac{d{w}_T}{dx}+\frac{\partial w}{\partial x}\right]\frac{\partial w}{\partial x}+\\ +\frac{\mathsf{\gamma }\left(\mathsf{\gamma }+1\right)}{12}{p}_{\infty }{M}^3\left[3\frac{d{w}_T}{dx}+\frac{\partial w}{\partial x}\right]{\left(\frac{\partial w}{\partial x}\right)}^2=0\end{array}$$

(12)

The solutions of Equation (12) must satisfy the following condition of hinge support:

$$w=0,\hspace{1em}\frac{{\partial }^{2}w}{\partial x^2}=0\hspace{1em}\mathrm{at}\hspace{1em}x=0,\hspace{1em}x=a .$$

(13)

The obtained nonlinear problem (12) (13) is solved approximately by representing its solution in the Galerkin form

$$w\left(x,t\right)={\displaystyle \sum _{i=1}^n{f}_i(t)\sin {\lambda }_{i}x},\hspace{1em}\left({\lambda }_i=i\mathsf{\pi }/a\right).$$

(14)

Representation (14) satisfies the boundary conditions (13). Substituting solution (14) into equation (12) we obtain a nonlinear system of ordinary differential equations with respect to the unknown dimensionless functions $x_i=f_i(t)/h$. Thus, we reduce the stability problem of the investigated hydroelastic system to the study of behavior of solutions of a system of nonlinear ordinary differential equations depending on the value of the velocity of the gas flow (the parameter $\mathsf{\nu }$) and temperature (the values $T, \Theta$).

3. Solution of the Linear Problem

Before proceeding to the solution of the nonlinear problem the corresponding linear problem should be analyzed first. In the case of two-mode approximation the linear system which corresponds to the obtained nonlinear system has the form

$$\begin{array}{l}\frac{d^2{x}_1}{d{\mathsf{\tau }}^2}+\chi \frac{d{x}_1}{d\mathsf{\tau }}-K\mathsf{\nu }\left(\frac{2}{3}+\overline{\Theta }{\mathsf{\alpha }}_{12}^{\Theta }\right)x_2+\left({\mathsf{\alpha }}_{11}+{\overline{T}}_0{\mathsf{\alpha }}_{11}^T+\overline{\Theta }{\mathsf{\alpha }}_{11}^{\Theta }\right)x_1=0 ,\\ \frac{d^2{x}_2}{d{\mathsf{\tau }}^2}+\chi \frac{d{x}_2}{d\mathsf{\tau }}+K\mathsf{\nu }\left[\frac{2}{3}+\overline{\Theta }{\mathsf{\alpha }}_{21}^{\Theta }\right]x_1+\left(4{\mathsf{\alpha }}_{22}+4{\overline{T}}_0{\mathsf{\alpha }}_{22}^T+\overline{\Theta }{\mathsf{\alpha }}_{22}^{\Theta }\right)x_2=0,\end{array}$$

(15)

where

$$\begin{array}{l}{\overline{T}}_0=12T_0\mathsf{\alpha }\left(1+\mathsf{\mu }\right),\hspace{1em}\overline{\Theta }=\frac{1}{16}\Theta \mathsf{\alpha }\left(1+\mathsf{\mu }\right)\frac{a^2}{h},\\ \mathsf{\phi }=\frac{{\left(1+{\mathsf{\pi }}^2{\left(\frac{R}{a}\right)}^2\right)}^2}{12{\mathsf{\pi }}^4\left(1-{\mathsf{\mu }}^2\right){\left(\frac{R}{a}\right)}^6+{\left(\frac{h}{a}\right)}^2{\left(1+{\mathsf{\pi }}^2{\left(\frac{R}{a}\right)}^2\right)}^4},\\ {\mathsf{\delta }}_1=3\left(1-{\mathsf{\mu }}^2\right)+4{\mathsf{\pi }}^4\frac{R^2{h}^2}{a^4},\hspace{1em}{\mathsf{\delta }}_2=96{\mathsf{\mu }}^2+12{\mathsf{\pi }}^2\left(1-{\mathsf{\mu }}^2\right)+{\mathsf{\pi }}^6\frac{R^2{h}^2}{a^4},\\ {\mathsf{\delta }}_3=96\left(4-7{\mathsf{\mu }}^2\right)-4{\mathsf{\pi }}^2\left(9-17{\mathsf{\mu }}^2\right)-3{\mathsf{\pi }}^6\frac{R^2{h}^2}{a^4},\hspace{1em}{\mathsf{\delta }}_4=96\mathsf{\mu }-\left(1+\mathsf{\gamma }\right)\frac{a^4}{R^{3}h}{\left(\frac{1}{\mathsf{\phi }}\right)}^{2}K{\mathsf{\nu }}^2,\\ \mathsf{\Delta }=9{\mathsf{\delta }}_1{\mathsf{\delta }}_2+K^2{\mathsf{\nu }}^2{\mathsf{\pi }}^2{\left(\frac{1}{\mathsf{\phi }}\right)}^2{\left(\frac{a}{R}\right)}^4,\\ {\mathsf{\alpha }}_{11}={\mathsf{\delta }}_2{\left(\frac{R}{a}\right)}^2\mathsf{\phi },\hspace{1em}{\mathsf{\alpha }}_{22}={\mathsf{\delta }}_1{\left(\frac{R}{a}\right)}^2\mathsf{\phi },\\ {\mathsf{\alpha }}_{11}^T=-{\mathsf{\pi }}^2{\left(\frac{R}{a}\right)}^4\mathsf{\phi },\hspace{1em}{\mathsf{\alpha }}_{22}^T={\mathsf{\alpha }}_{11}^T,\\ {\mathsf{\alpha }}_{11}^{\Theta }=[\left(1+\mathsf{\gamma }\right)K{\mathsf{\nu }}^2-96\mathsf{\mu }{\left(\frac{R}{a}\right)}^3\frac{h}{a}\mathsf{\phi }+\frac{1}{{\mathsf{\pi }}^2\mathsf{\Delta }}{\left(\frac{R}{a}\right)}^3\mathsf{\phi }\{4608\mathsf{\mu }\frac{h}{a}{\mathsf{\delta }}_1(24{\mathsf{\pi }}^2\left(1-{\mathsf{\mu }}^2\right)+\\ +\left(288-{\mathsf{\pi }}^4\right){\mathsf{\mu }}^2+3{\mathsf{\pi }}^6\frac{R^2{h}^2}{a^4})-K{\mathsf{\nu }}^2{\left(\frac{a}{R}\right)}^7{\mathsf{\pi }}^2\frac{1}{\mathsf{\phi }}[96\left(1+\mathsf{\gamma }\right)\left(12\left(1-{\mathsf{\mu }}^2\right)+{\mathsf{\pi }}^2{\mathsf{\mu }}^2\right){\mathsf{\delta }}_1{\left(\frac{R}{a}\right)}^4+\\ +K{\left(\frac{1}{\mathsf{\phi }}\right)}^2\left(48\mathsf{\mu }\left(32-{\mathsf{\pi }}^2\right)\frac{R^{3}h}{a^4}\mathsf{\phi }-K{\mathsf{\nu }}^2\left(1+\mathsf{\gamma }\right){\mathsf{\pi }}^2\right)]\}],\\ {\mathsf{\alpha }}_{22}^{\Theta }=\left(1+\mathsf{\gamma }\right)K{\mathsf{\nu }}^2+\frac{4}{5\mathsf{\Delta }}{\left(\frac{R}{a}\right)}^3\frac{h}{a}\mathsf{\phi }{\mathsf{\delta }}_4\left[96\left(12\left(1-{\mathsf{\mu }}^2\right)+{\mathsf{\pi }}^2{\mathsf{\mu }}^2\right){\mathsf{\delta }}_1+K^2{\mathsf{\nu }}^2{\mathsf{\pi }}^2{\left(\frac{a}{R}\right)}^4{\left(\frac{1}{\mathsf{\phi }}\right)}^2\right],\\ {\mathsf{\alpha }}_{12}^{\Theta }=-\frac{2}{5\mathsf{\Delta }}\frac{Rh}{a^2}{\mathsf{\delta }}_3\left({\mathsf{\delta }}_4-15\left(1+\mathsf{\gamma }\right)\frac{a^4}{R^{3}h}{\left(\frac{1}{\mathsf{\phi }}\right)}^{2}K{\mathsf{\nu }}^2\right),\\ {\mathsf{\alpha }}_{21}^{\Theta }=-\frac{4}{5\mathsf{\Delta }}\frac{Rh}{a^2}{\mathsf{\delta }}_3{\mathsf{\delta }}_4,\end{array}$$

(16)

We represent the solution of the system (16) in the form

$$x_1=y_1{e}^{\mathsf{\beta }\mathsf{\tau }},\hspace{1em}{x}_2=y_2{e}^{\mathsf{\beta }\mathsf{\tau }},$$

(17)

Substituting (17) into (16) we obtain the characteristic equation (with respect to $\mathsf{\beta }$); its coefficients depend on the velocity parameter. The value of the parameter $\mathsf{\nu }={\mathsf{\nu }}_{cr}$ at which two of the characteristic indicators become purely imaginary, and the rest still lie in the left half-plane, is critical, it corresponds to the critical velocity of the panel flutter in the linear formulation of this problem. Taking $\mathsf{\nu }={\mathsf{\nu }}_{cr}$, we can find the shell’s oscillations frequency value ${\mathsf{\theta }}_{cr}$ from the characteristic equation. On the basis of the characteristic equation we obtain the following values of the flutter critical velocity for different parameters of thermal field.

Table 1. The critical velocity values in the case of a constant temperature field.

	${\mathit{T}}_0$	−500	−300	−100	−50	0	5
$\frac{\mathit{h}}{\mathit{a}}$
1/70		8.2821	4.9792	1.6764	0.8506	0.0249	0.0577
1/100		3.9496	2.3312	0.7128	0.3082	0.0964	0.1369
1/200		0.9678	0.5632	0.1586	0.0575	0.0437	0.0538
1/500		0.1540	0.0892	0.0245	0.0083	0.0079	0.0095

;

Table 2. The critical velocity values in the case of an inhomogeneous temperature field.

	$\mathsf{\Theta }$	−1000	−500	−100	100	500	1000
$\frac{\mathit{h}}{\mathit{a}}$
1/70		0.0354	0.0302	0.0260	0.0238	0.0196	0.0143
1/100		0.0919	0.0942	0.0960	0.0968	0.0986	0.1008
1/200		0.0426	0.0432	0.0436	0.0438	0.0442	0.0447
1/500		0.0077	0.0078	0.0078	0.0079	0.0080	0.0081

show that: (a) when the temperature is constant, the thinner the shell, the lower the critical velocity of the flow, (b) for a certain thickness, the critical velocity of the flow as a function of the temperature field has a minimum point.

4. Solution of the Nonlinear Problem

The obtained nonlinear system in the case of the two-term approximation is solved by the harmonic balance method, i.e., an approximate periodic solution of the obtained system of ordinary differential equations is sought in the form [12]

$$\begin{array}{l}{x}_1=A_1\cos \mathsf{\theta }\mathsf{\tau }+B_1\sin \mathsf{\theta }\mathsf{\tau }+C_1+\dots ,\\ x_2=A_2\cos \mathsf{\theta }\mathsf{\tau }+B_2\sin \mathsf{\theta }\mathsf{\tau }+C_2+\dots \end{array}$$

(18)

where $A_i,\hspace{1em}{B}_i,\hspace{1em}{C}_i$ and $\mathsf{\theta }\hspace{1em}(i=1,2)$ are the unknown constants; the dots denote the terms with high harmonics. We substitute solution (18) into the nonlinear system, then equate to zero the coefficients of the free term, $\cos \mathsf{\theta }\mathsf{\tau }$ and $\sin \mathsf{\theta }\mathsf{\tau }$ (neglecting the terms with high harmonics). We do not bring the resulting system of nonlinear algebraic equations into this paper as it is quite cumbersome to study.

The system of nonlinear algebraic equations is solved numerically for the following initial parameters: $E=7.3\cdot {10}^{10}{\mathrm{N}/\mathrm{m}}^2;\hspace{1em}\mathsf{\mu }=0.34;\hspace{1em}{\mathsf{\rho }}_0=2.79\cdot {10}^3{\mathrm{kg}/\mathrm{m}}^3$ (Duralumin), $\mathsf{\gamma }=1.4; {\mathsf{\rho }}_{\infty }=1.29 \mathrm{kg}/{\mathrm{m}}^3; a_{\infty }=340.29 \mathrm{m}/\mathrm{s}$ (air). The dependence of the amplitude $A$ of steady-state flutter oscillations on the parameters $\mathsf{\theta }$ and $\mathsf{\nu }$ for the different values of the parameters $h/a$ and $R/a$ is investigated.

5. The Case of Sufficiently Thick Shells. The Effect of a Constant Temperature Field

Numerical calculations based on the nonlinear system show that the constant component of the temperature field has both a qualitative and a quantitative effect on the nature of flutter oscillations of the aero-thermo-elastic system under consideration. We give here the most significant results, in our opinion.

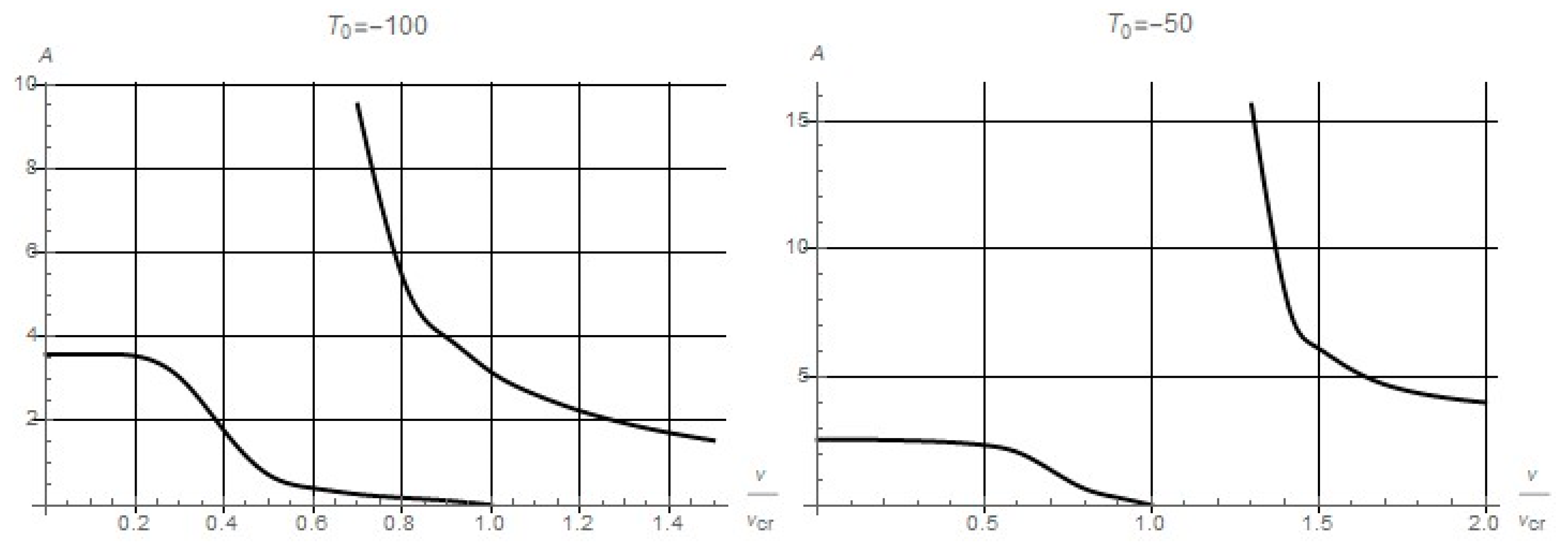
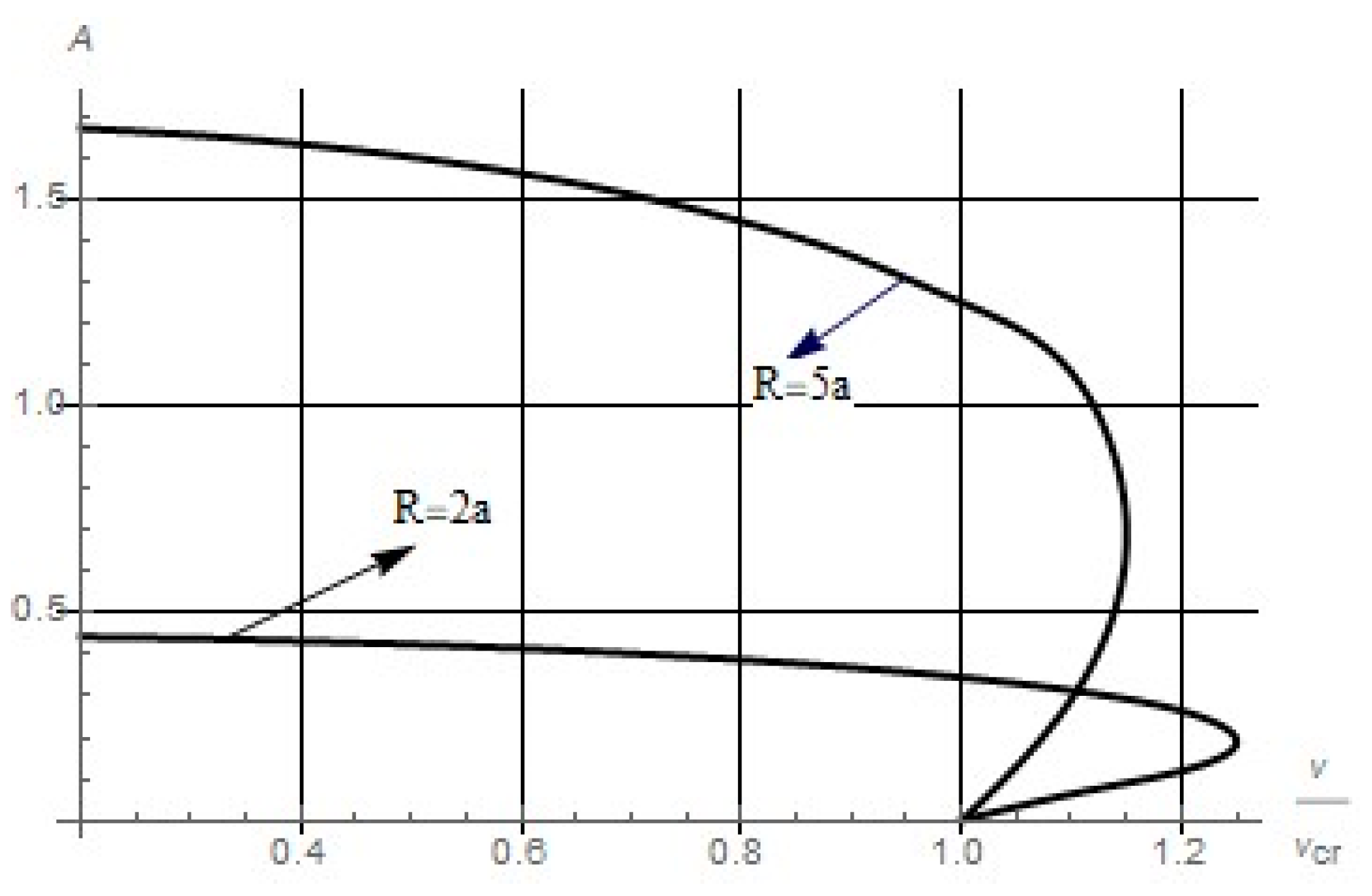
For $T_0<0$ and sufficiently large values of $\left|T_0\right|$, the dependence of the amplitude of flutter oscillations on the velocity of the flowing stream is a monotonously decreasing function, which is shown in Figure 1. Namely, there exist such values of the flow velocity ${\mathsf{\nu }}_{*}$ and ${\mathsf{\nu }}^{*}$ that for $0<\mathsf{\nu }<{\mathsf{\nu }}_{*}$ and $\mathsf{\nu }>{\mathsf{\nu }}^{*}$ the function $A\left(\mathsf{\nu }\right)$ is a single-valued and monotonically decreasing function, and for ${\mathsf{\nu }}_{*}<\mathsf{\nu }<{\mathsf{\nu }}^{*}$ it is two-valued, and the lower branch is unstable

Figure 1 and calculations also show that, depending on the geometric parameters of the system, there is a certain temperature value ${\overline{T}}_0$ such that with $T_0>{\overline{T}}_0$ the monotonous nature of $A(\mathsf{\nu })$ function remains and a silence zone appears, i.e., there is an interval of velocity values where it is impossible to excite flutter oscillations. With a further increase in temperature, the picture of the dependence of the oscillations amplitude on the flow velocity changes substantially and takes the form shown in Figure 2, where the critical temperature is indicated as $T_{cr}$ at which the system under consideration loses stability in the absence of the flowing stream.

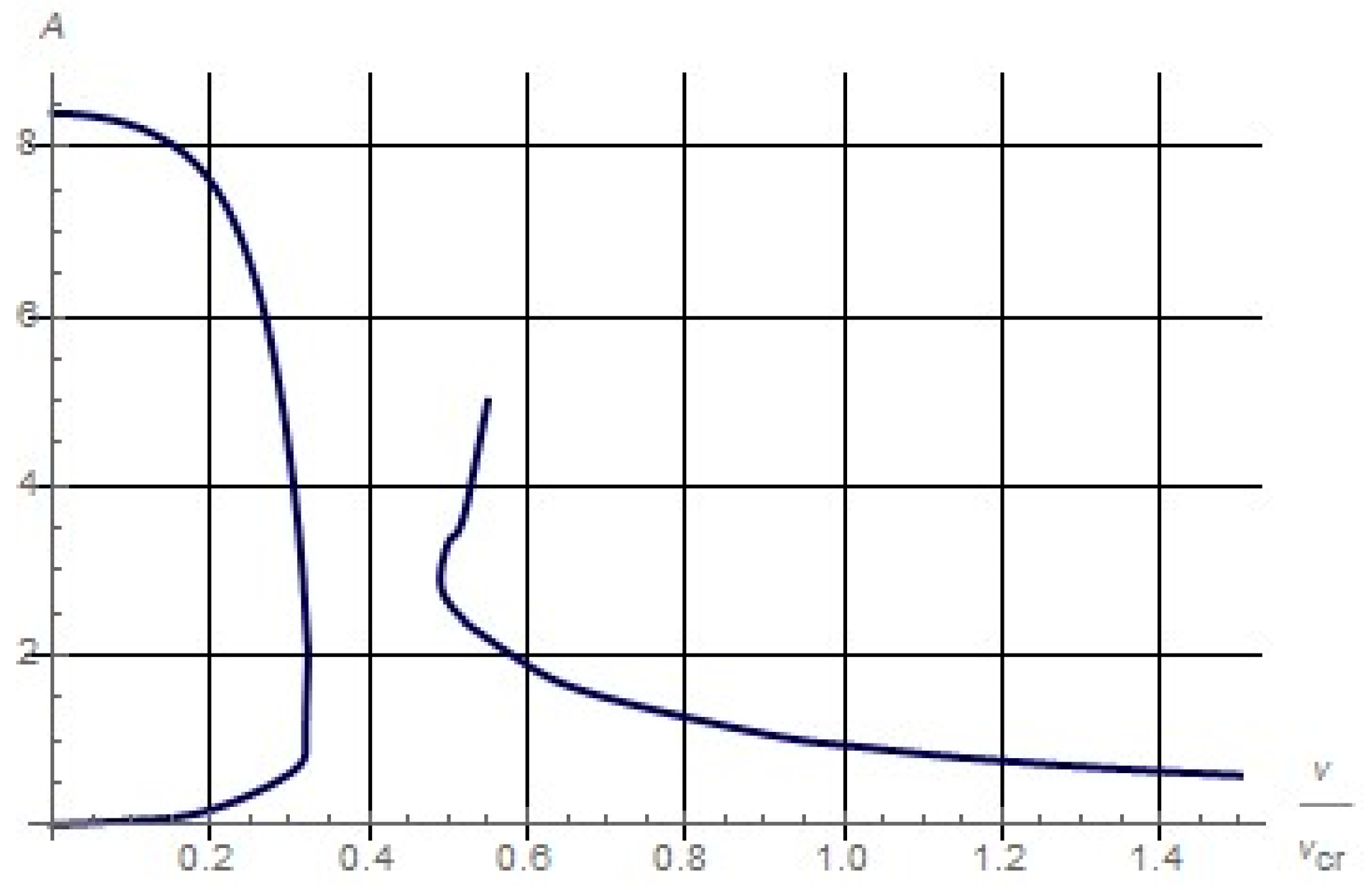
Figure 2 shows that if the flow velocity is gradually increased, the flutter oscillation mode is maintained up to a certain value of the flow velocity, where the oscillations “break” and the unperturbed state of the shell is restored. With a decrease in speed, the unperturbed state is stable as long as $\mathsf{\nu }>{\mathsf{\nu }}_{*}$, where ${\mathsf{\nu }}_{*}<{\mathsf{\nu }}^{cr}$. When $\mathsf{\nu }={\mathsf{\nu }}_{*}$ the amplitude of flutter oscillations jumps up to a certain value. With further decrease in speed, the amplitude increases. Calculations also show that the value ${\mathsf{\nu }}^{cr}$—at which the amplitude of flutter oscillations jumps to a certain value and the second branch of function $A(\mathsf{\nu })$ occurs—increases with temperature.

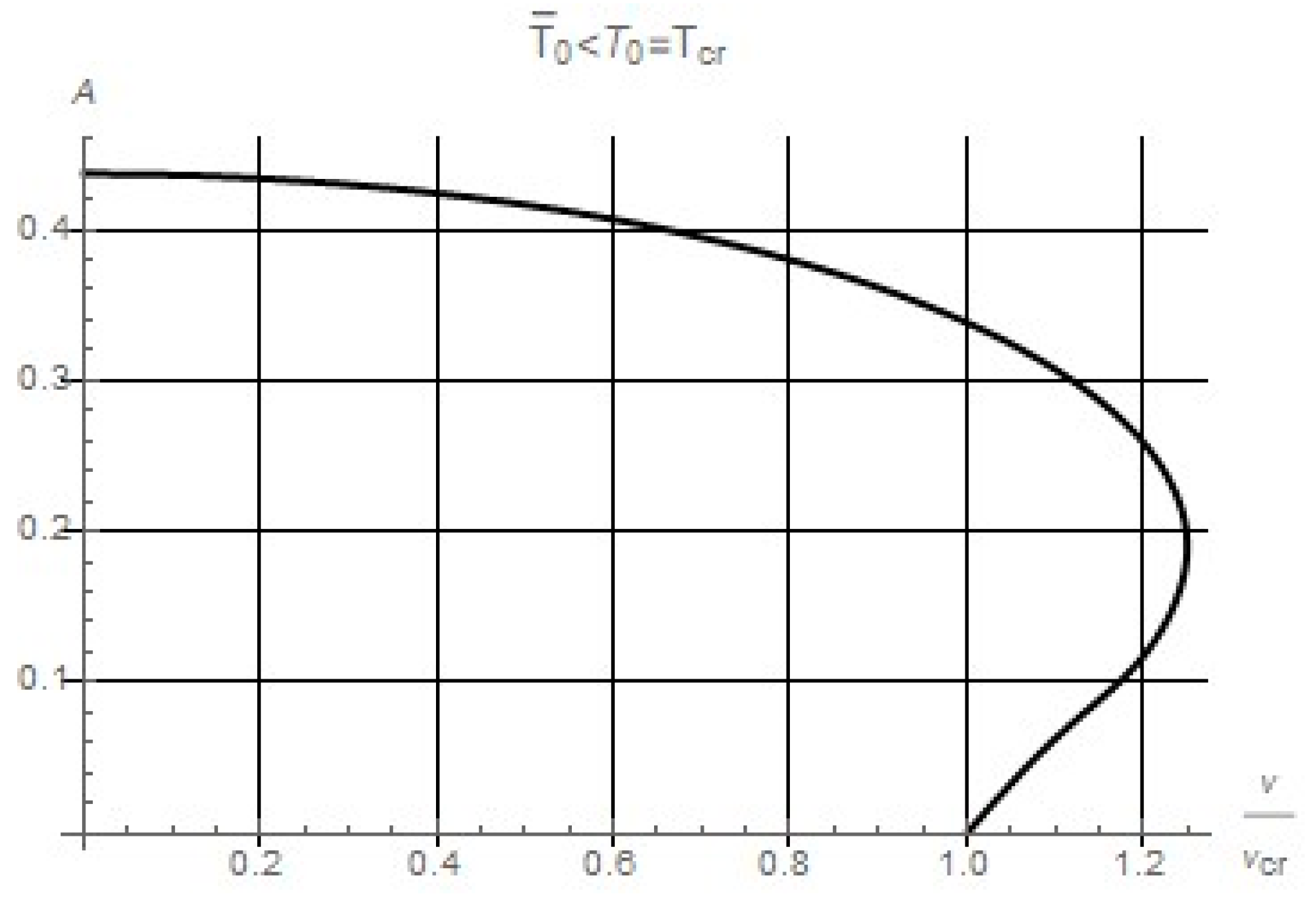
When $\mathsf{\theta }={\mathsf{\theta }}_{cr}$ we have ${\mathsf{\nu }}_{*}={\mathsf{\nu }}_{cr}$. As the value $\mathsf{\theta }$ changes, the value ${\mathsf{\nu }}_{*}$ also changes.

If $T_0>0$, then the following picture is observed (Figure 3).

.

The function $A(\mathsf{\nu })$ is defined on the interval $[0,{\mathsf{\nu }}_{*}]$ and has a maximum point on that interval, which depends on the geometric parameters of the aero-thermo-elastic system.

A change in the geometric parameters of the system leads to both quantitative and qualitative changes in the investigated relationship, i.e., a transition from one of the above pictures to another is possible.

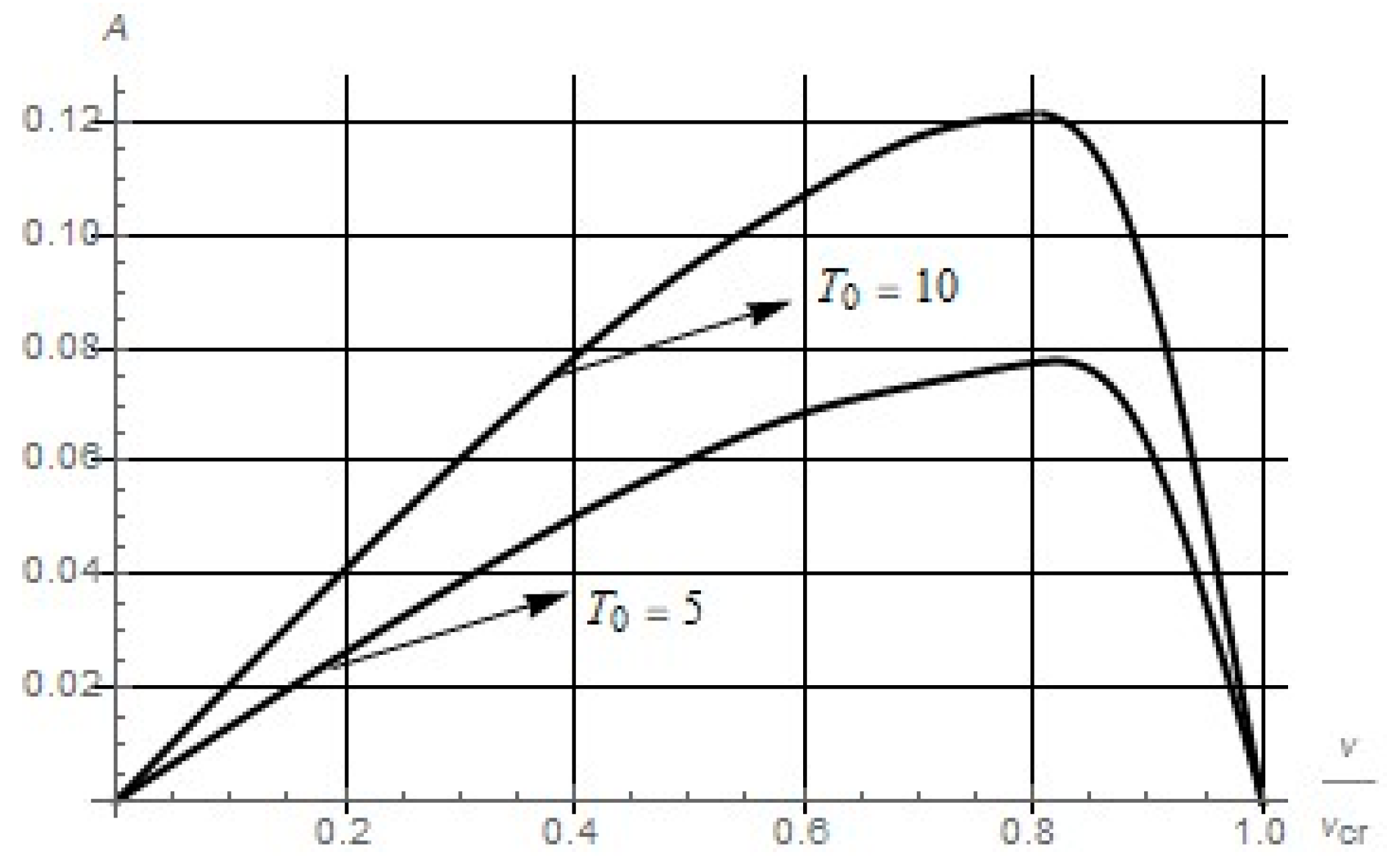
Changing the value of the oscillation frequency also affects the indicated relationship. At $\mathsf{\theta }<{\mathsf{\theta }}_{cr}$ and negative temperatures, there is a value of the flow velocity ${\mathsf{\nu }}_{*}$ such that (a) the region $\mathsf{\nu }<{\mathsf{\nu }}_{*}$ is a zone of silence; (b) when $\mathsf{\nu }>{\mathsf{\nu }}_{*}$ the relationship “amplitude−velocity” is a monotonously decreasing function; (c) with an increase in the parameter $R/a$, the value ${\mathsf{\nu }}_{*}$ decreases (Figure 4). Note that for relatively large $R/a$ the case ${\mathsf{\nu }}^{*}<{\mathsf{\nu }}_{cr}$ is possible;

Calculations show that a decrease in the frequency (while the other parameters of the system are fixed) leads to (a) a decrease in ${\mathsf{\nu }}^{*}$ and in the amplitude, (b) the appearance of the second branch of the function $A\left(\mathsf{\nu }\right)$ in the interval $\left(0,{\mathsf{\nu }}_{*}\right)$, and as a result, to a decrease, and moreover, to the disappearance of the silence zone, (c) a decrease in temperature leads to an increase in the amplitude of the oscillations.

At $\mathsf{\theta }>{\mathsf{\theta }}_{cr}$ the character of the dependence of the amplitude of flutter oscillations on the velocity of the flowing stream has the picture shown in Figure 5.

Figure 5 shows that (a) the function $A\left(\mathsf{\nu }\right)$ can be both two-valued and single-valued, (b) there is a silence zone.

6. Influence of an Inhomogeneous Temperature Field

Variable temperature leads to the following picture.

The function $A\left(\mathsf{\nu }\right)$ has the form, shown in Figure 6 and similar to Figure 2

Figure 6 shows that an increase in the parameter leads to an increase in the amplitude and to a decrease in the value of the upper critical velocity.

7. Joint Influence of the Temperature Field Characteristics, General Case

Numerous calculations show that the combined influence of the characteristics of the temperature field is mainly quantitative and all the above options are possible here. The case shown in Figure 7 is also possible.

The graph shows that the new characteristic feature of function $A\left(\mathsf{\nu }\right)$ is that it can be two-valued also in the interval $\mathsf{\nu }>{\mathsf{\nu }}^{*}$.

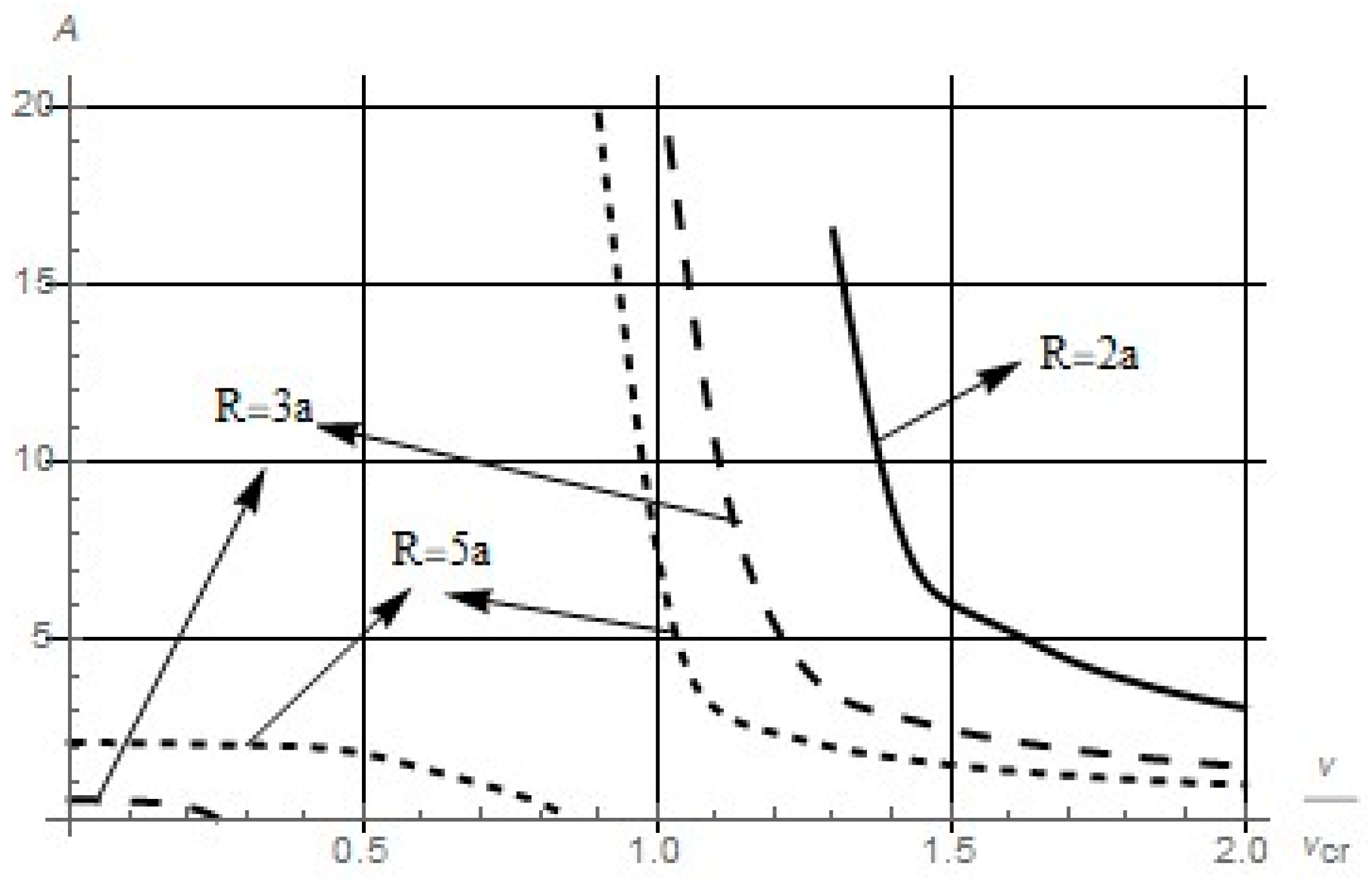
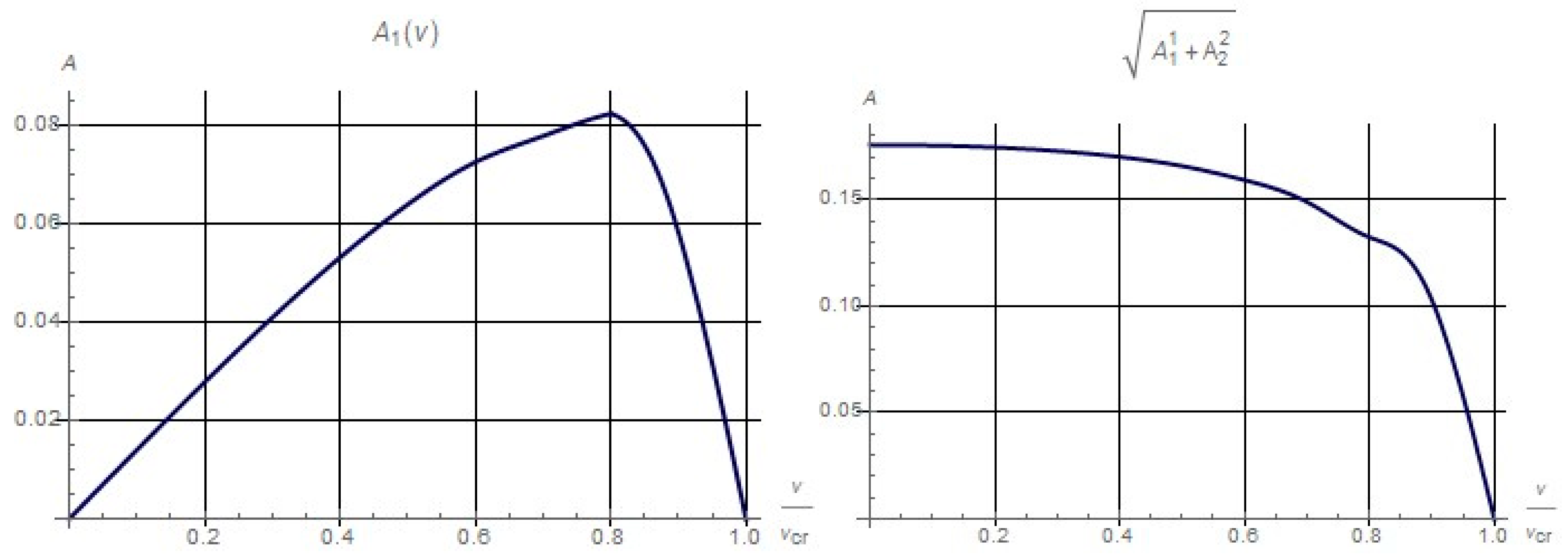
8. The Case of Sufficiently Thin Shells and Shells of Medium Thickness

A decrease in the shell thickness leads to a quantitative change in the investigated dependence of the amplitude of flutter oscillations on the flow velocity. For this reason, in this part it should be noted that the functional dependence $A_1\left(\mathsf{\nu }\right)$ determined from formula (5) has so far been presented in the graphs. It should be noted that for certain parameters of the problem, the nature of the dependence $\sqrt{A_1^2+A_2^2}$ differs significantly from $A_1\left(\mathsf{\nu }\right)$, but is within the cases described above in this article. This means that the second amplitude can also have an effect on the investigated dependence. As a proof of this fact, in the Figure 8 we give one example of this difference.

9. The Main Results

The numerical solutions, the tables and graphs show that (a) the flowing stream significantly affects the nature of the investigated dependence, (b) the certain interval of supersonic velocity exists, where it is impossible to excite steady-state flutter oscillations (the silence zone), (c) the amplitude dependence on the supersonic velocity can be single-valued or multi-valued, (e) the value of the critical velocity is a monotonously decreasing function of the relative thickness of the shell and has a minimum point depending on the value of the temperature field.