2.1. Eigen-Value Problem
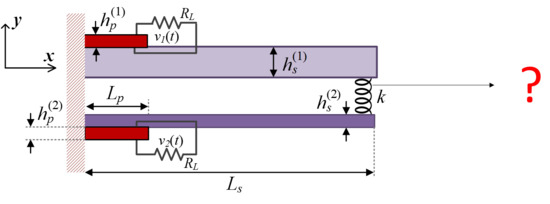
Figure 1 shows that the lengths of both piezoelectric patches are very small compared to the length of the beams. As a result, they have negligible effects on the mode shapes. Therefore, in the upcoming derivations (which aim to find the mode shapes of the coupled system) the effects of the piezoelectric patches are ignored.
By utilizing Hamilton’s principal, the normalized free vibration equations of the system and the corresponding kinematic and natural boundary conditions are derived as [
21].
Kinematic boundary conditions:
Natural boundary conditions:
In these equations
, is the length of the beams,
is the Young’s modulus of the beams material,
,
represents the second area moment of inertia of the
th beam’s cross section around its neutral axis,
is the area cross section of the
th beam and
is the elastic constant of the connecting linear spring. Moreover, the normalized variables
,
and
are defined by
where
is the deflection of the
th beam and
in which
is the material density.
The dynamic response of a linear continuous system can be expressed as a linear combination of its mode shapes [
21]. Therefore, an essential first step in the dynamic modelling of a continuous structure, either single or multi-body, is to find the mode shapes of that system. A mode shape of a system is a state of motion of that system in which all of its elements move with the same frequency and phase, but not necessarily with the same amplitude.
Appendix A presents the derivation of the exact natural frequencies and the mode shapes of the system. To verify the accuracy of the proposed analytical technique, a system with physical and geometrical parameters given in
Table 1 is considered.
Using the numerical values reported in
Table 1, the first three normalized natural frequencies of the system are obtained as given in
Table 2. In this table, the analytical results are compared with those of finite element (FE) simulations using the commercial software Abaqus. The numerical and analytical results are in excellent agreement.
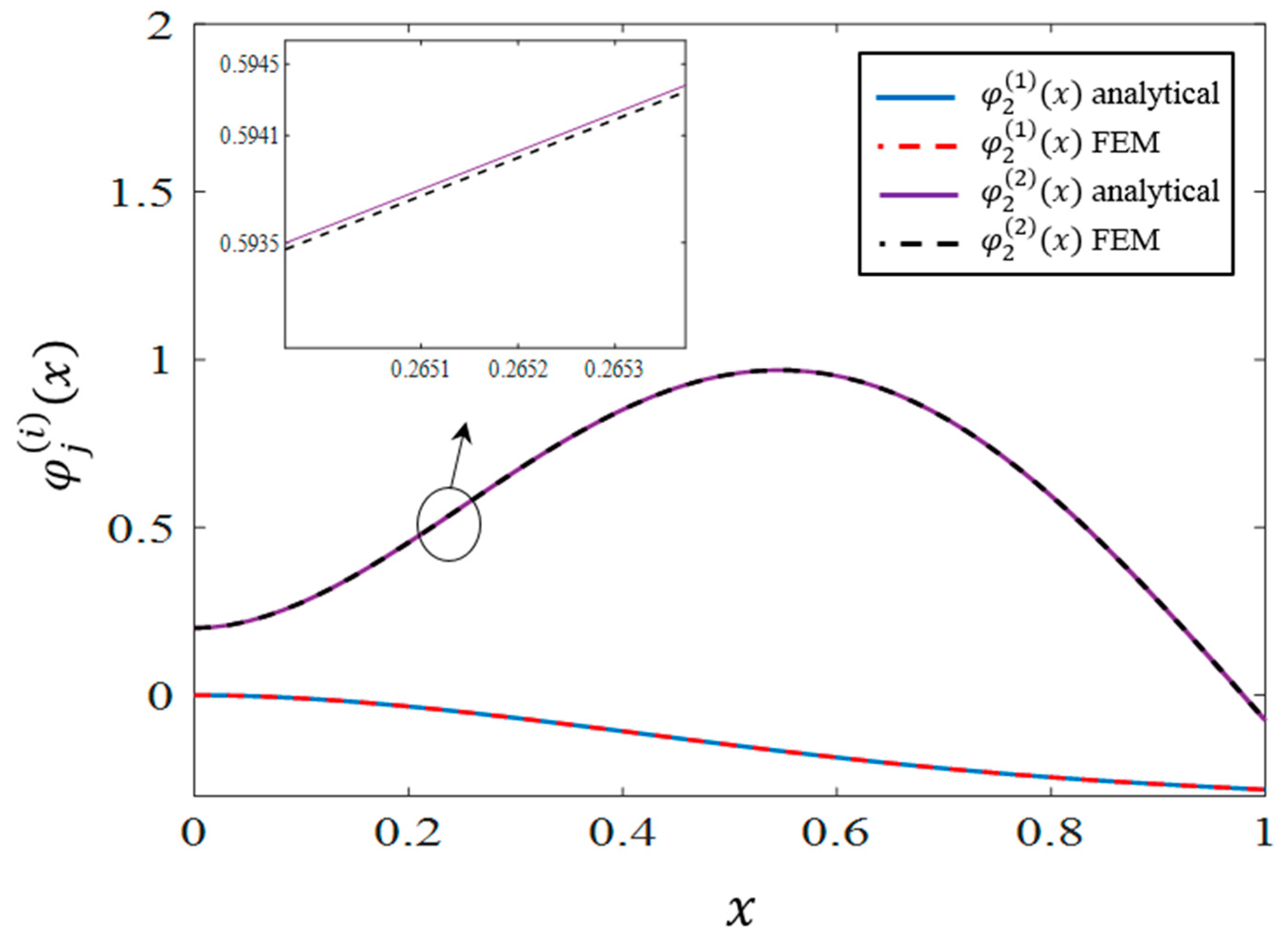
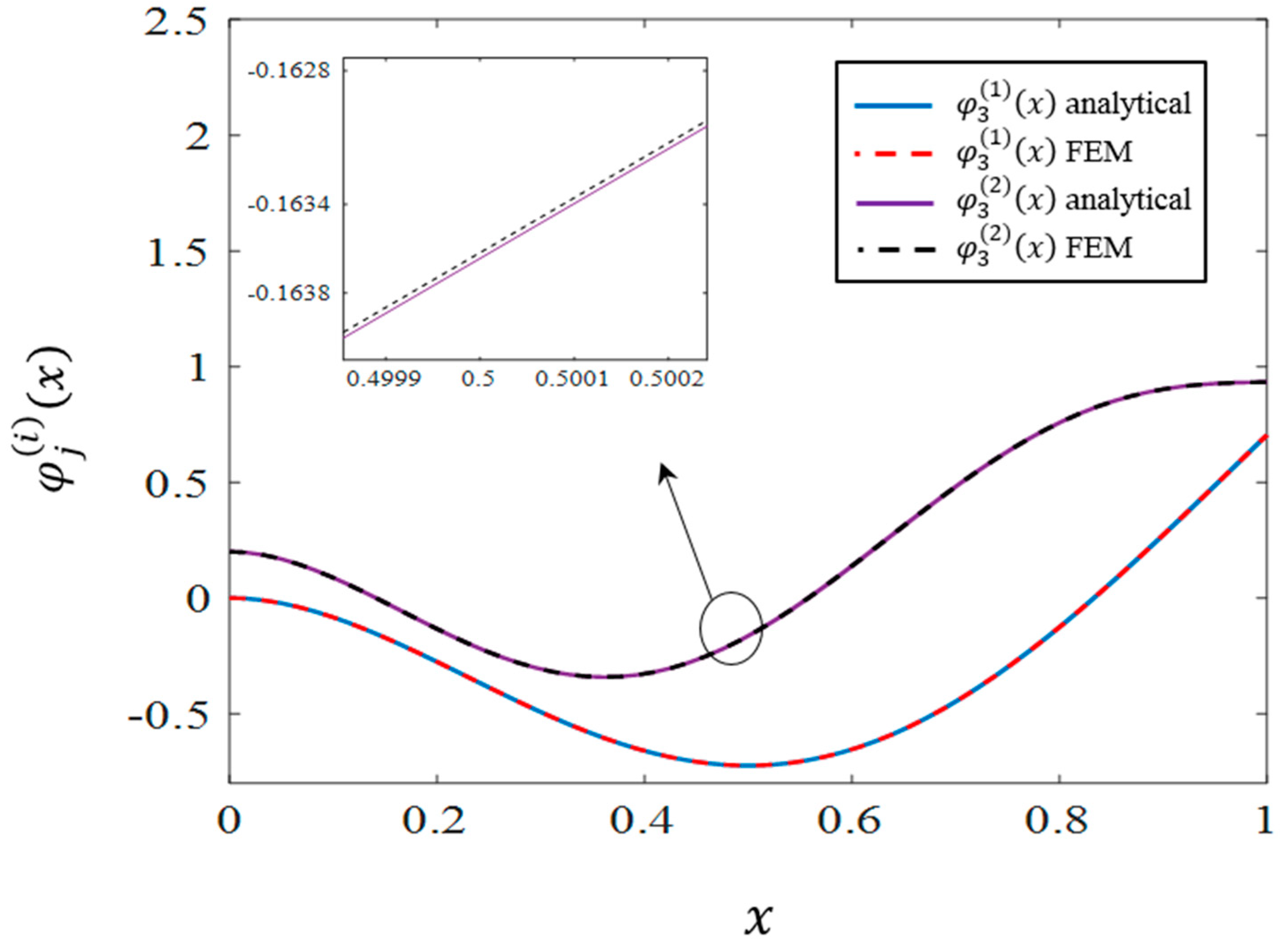
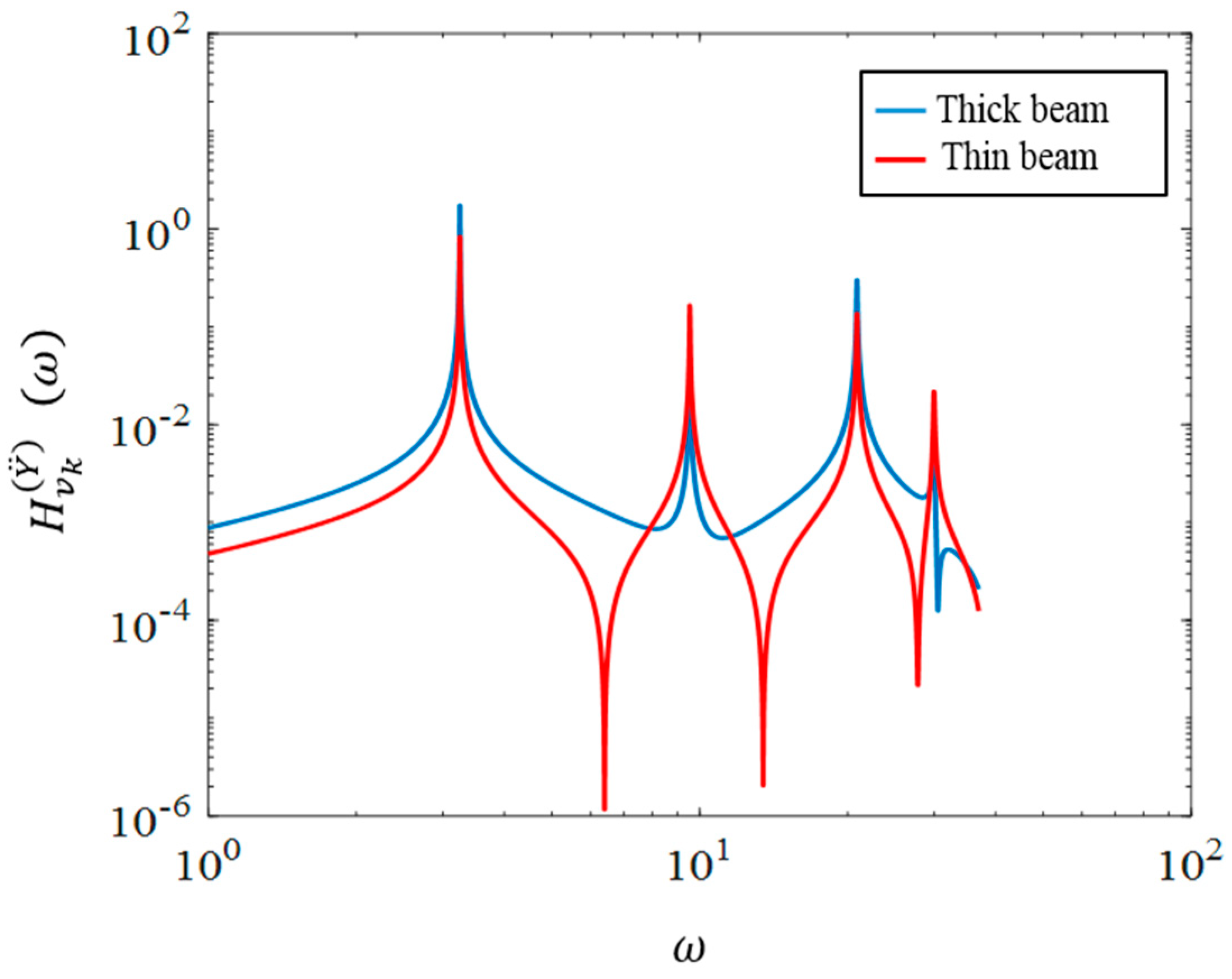
In order to investigate the accuracy of the analytical mode shapes,
Figure 2,
Figure 3 and
Figure 4 are provided. In these figures, the first three analytical and FE modes are compared, and acceptable agreement is observed. To make the numerical and analytic modes comparable, they have both been normalized such that
.
2.2. Dynamic Analysis
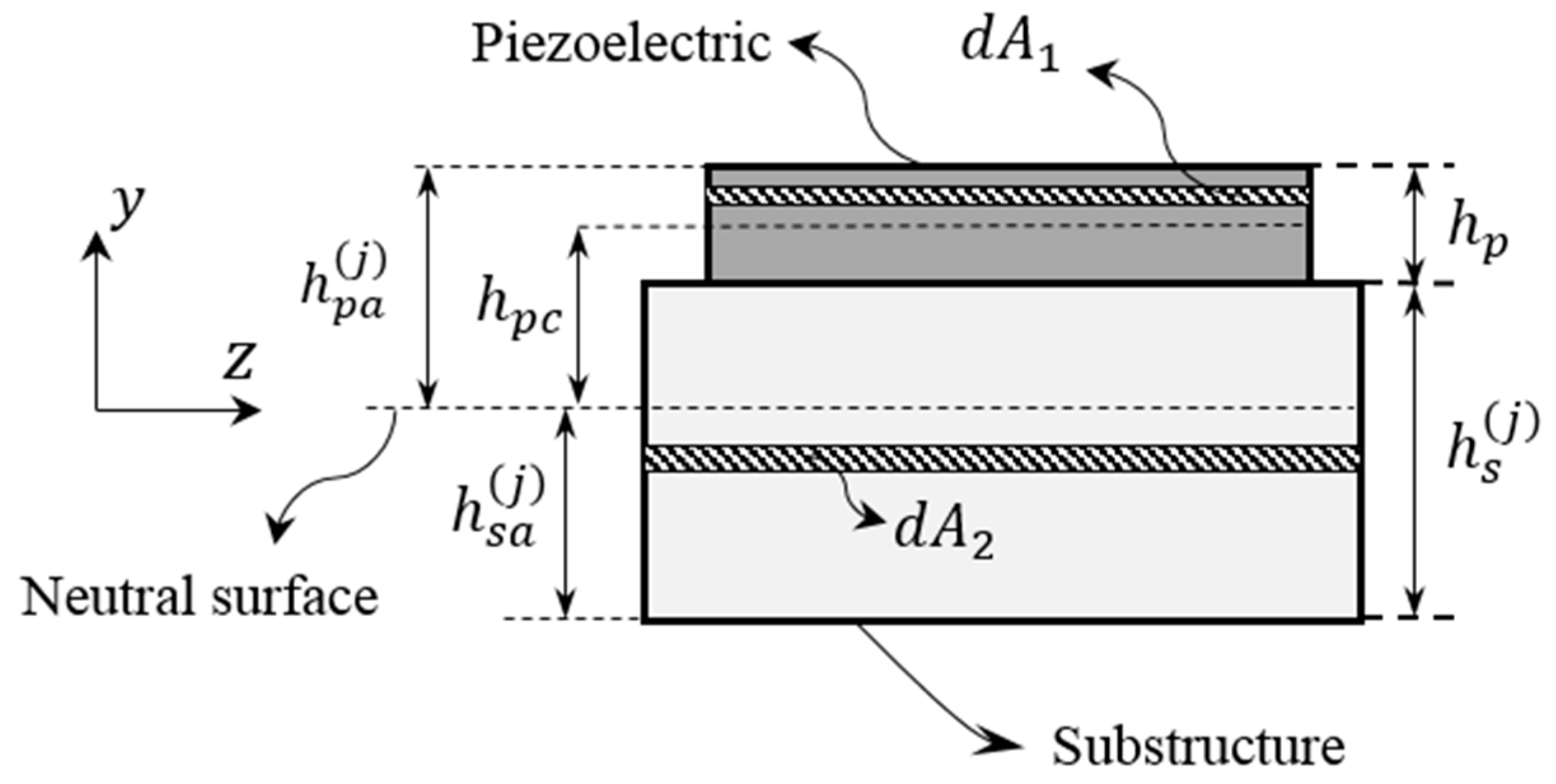
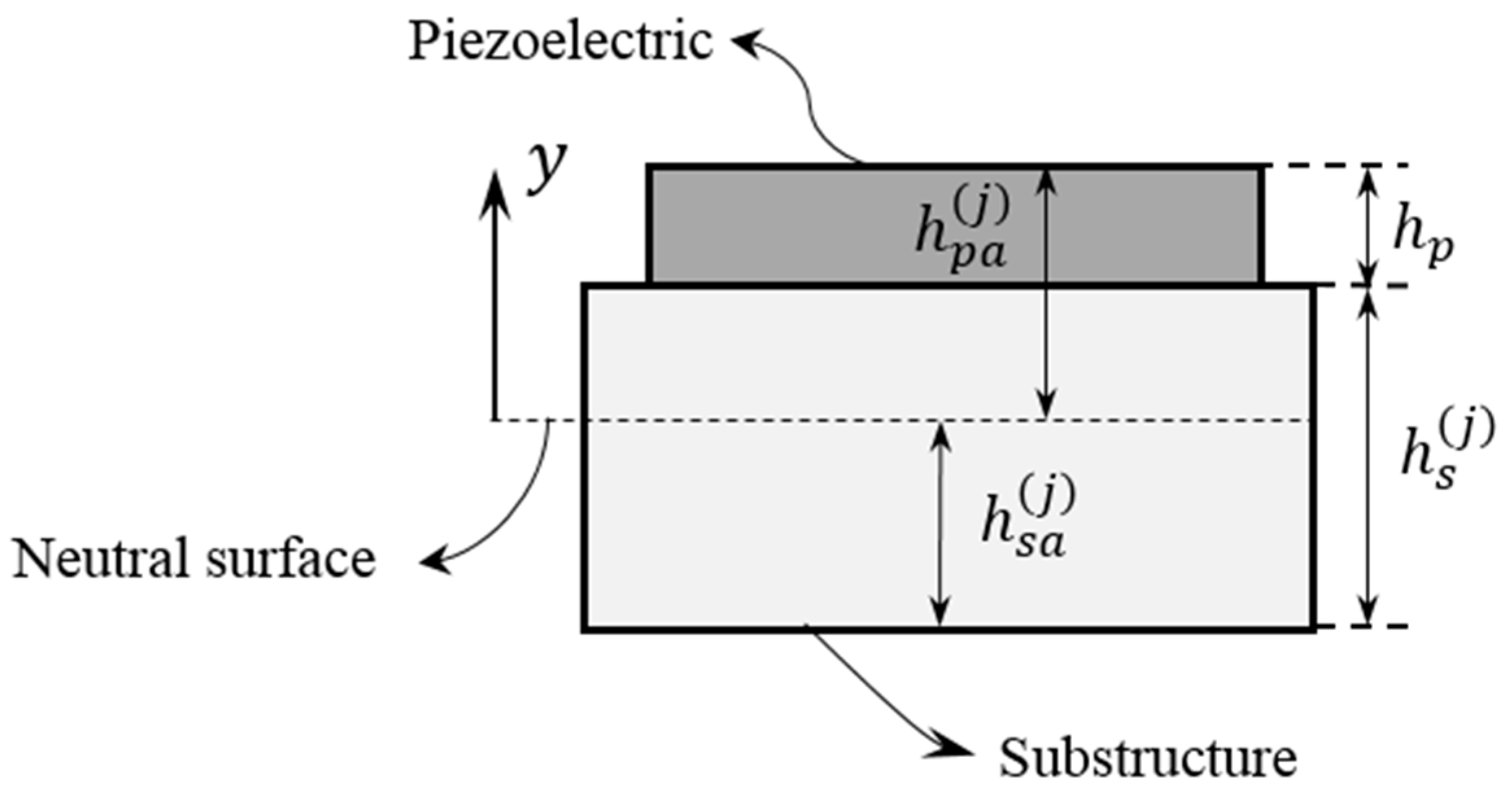
Lagrange’s equations are employed here to derive the differential equations governing the dynamic behavior of the system. This requires the analytical expressions for the potential and kinetic energies, as well as the virtual work done on the system. The potential energy of the system shown in
Figure 1 is composed of three parts: (1) strain energy of the substructure,
, (2) potential energy of the piezoelectric material,
, and (3) strain energy of the spring,
.
• Strain Energy of the Substructure
Assuming linear elastic material for the beams, the strain energy of the harvester can be written as
where
the length of the piezoelectric patches (see
Appendix B) and
• Potential Energy of the Piezoelectric Layers
The potential energy of the piezoelectric material,
, is composed of a strain energy
and a potential electrical component
. The strain energy of the piezoelectric layers in the system shown in
Figure 1 can be expressed as [
22]
where
and
are respectively the normal stress components of the piezoelectric layers attached to the thick and thin beams, while
and
are their strain counterparts. Moreover,
is the volume of the
kth piezoelectric layer. The following constitutive equations show the relation between the stress and strain in the piezoelectric layers [
23]:
In Equations (11) and (12), and denote the vector of electrical displacement and the electric field of the ith piezoelectric material in direction, represents the piezoelectric stress coefficient, and is the dielectric constant of the piezoelectric material. In addition, as explained earlier, is the elastic modulus of the piezoelectric layer.
Substituting Equation (11) into (10), assuming
[
24] (where
is the generated voltage in the
kth piezo layer) and employing the stress–strain relationships, one may simplify the
expression as
where
and
are defined as
The internal electrical energy generated in the piezoelectric layers,
, can be expressed as [
23]
By substituting
from Equation (12), considering
and employing the strain-displacement relation
, Equation (16) can be simplified in terms of
and
as
in which
Thus, the total potential energy of piezoelectric layers is obtained as
• Strain Energy of the Connecting Spring
The elastic strain energy of the linear connecting spring,
, is simply
Assuming that the mass of the spring is negligible, the kinetic energy of the system can be derived by adding the kinetic energies of the constitutive beams and the piezoelectric layers as
where
is the base displacement.
To account for the modal damping, it is assumed that the system is vibrating in a linearly damped viscous media. The damping coefficient for both beams is assumed to be
per unit length. In such a condition, the virtual work done on the system due to this damping will be as
In addition, as the electrical charge is
,
, in the load circuit with resistance
, the virtual work is
Hence, the effective virtual work done to the system can be summarized as
The dynamic response of linear systems can be effectively approximated as a linear combination of their mode shapes. This theory has been examined and verified in many published studies [
5,
25]. Hence, for the system under study,
where
represents the contribution of the
th mode in the dynamic response. Now,
, as well as
and
, can be considered as the generalized coordinates. By substituting Equation (26) into (7), (20), (21), (22), and (25), while employing Lagrange’s equation, after some simple manipulations, the governing equations are derived. For notational simplicity, the following normalized variable is defined
where
is defined as
. Further, the parameter
is the distance between the center of the piezoelectric layer and the neutral axis and
and
are piezoelectric constants whose typical values are given in
Table 3. Using the normalized variable
, the dimensionless governing equations are reduced to
In Equation (29),
and
are defined as
In these equations,
represents differentiation with respect to normalized time
. Moreover, the elements of the matrices
,
,
and vectors
and
are functions of the mode shapes as well as the physical and geometrical parameters of the system, and are given by
where
in Equation (35) is calculated as
In addition,
in Equation (36) is
In the next step, the dynamic Equations (28) and (29) are transformed into state space. To do so, the state vector
is defined as
where the superscript
denotes the transpose operator. The state space equations governing the dynamic behavior of the system are then
In Equation (39), the matrices
and
are defined as
The matrix
in Equation (40) is defined as
where
and
.
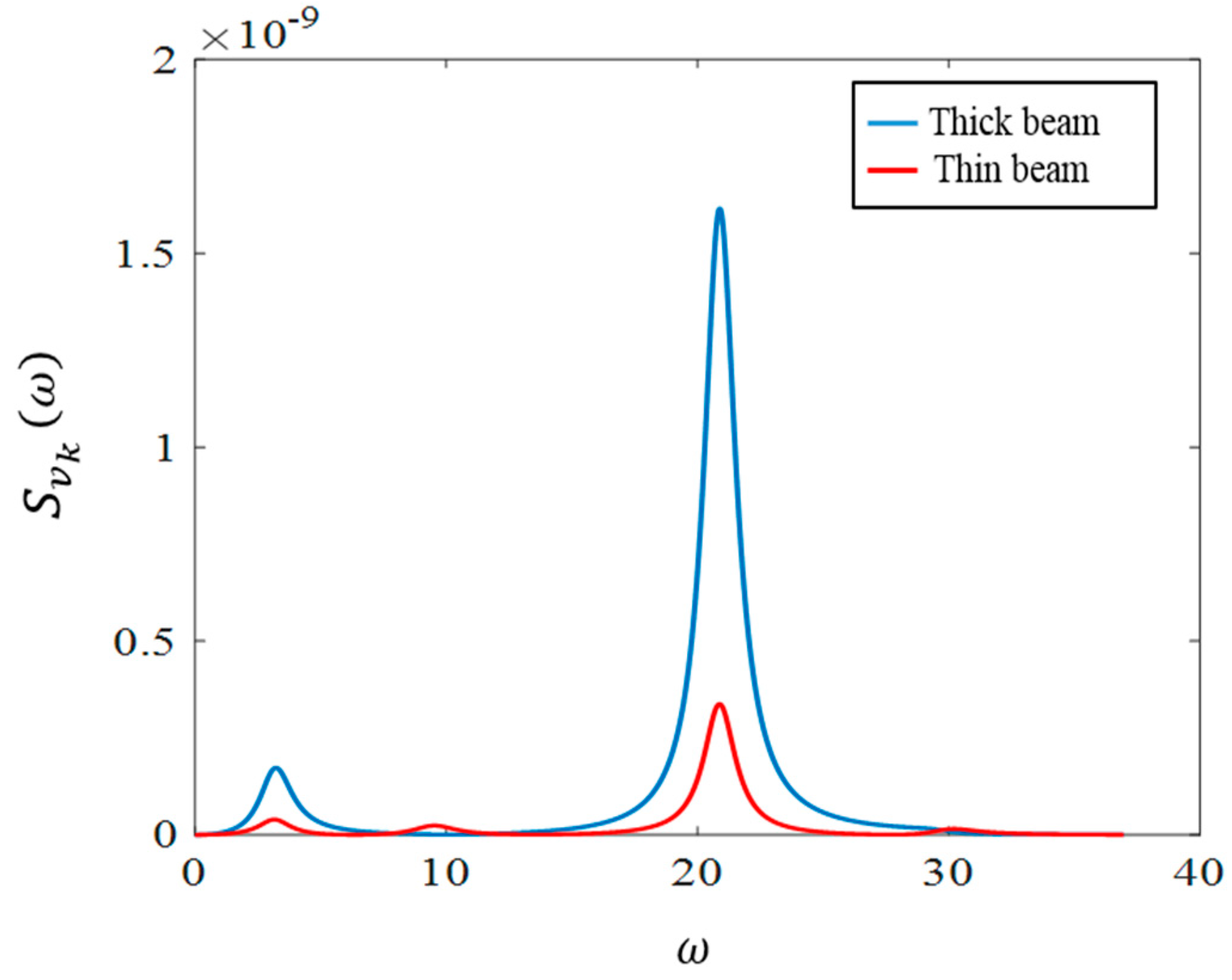
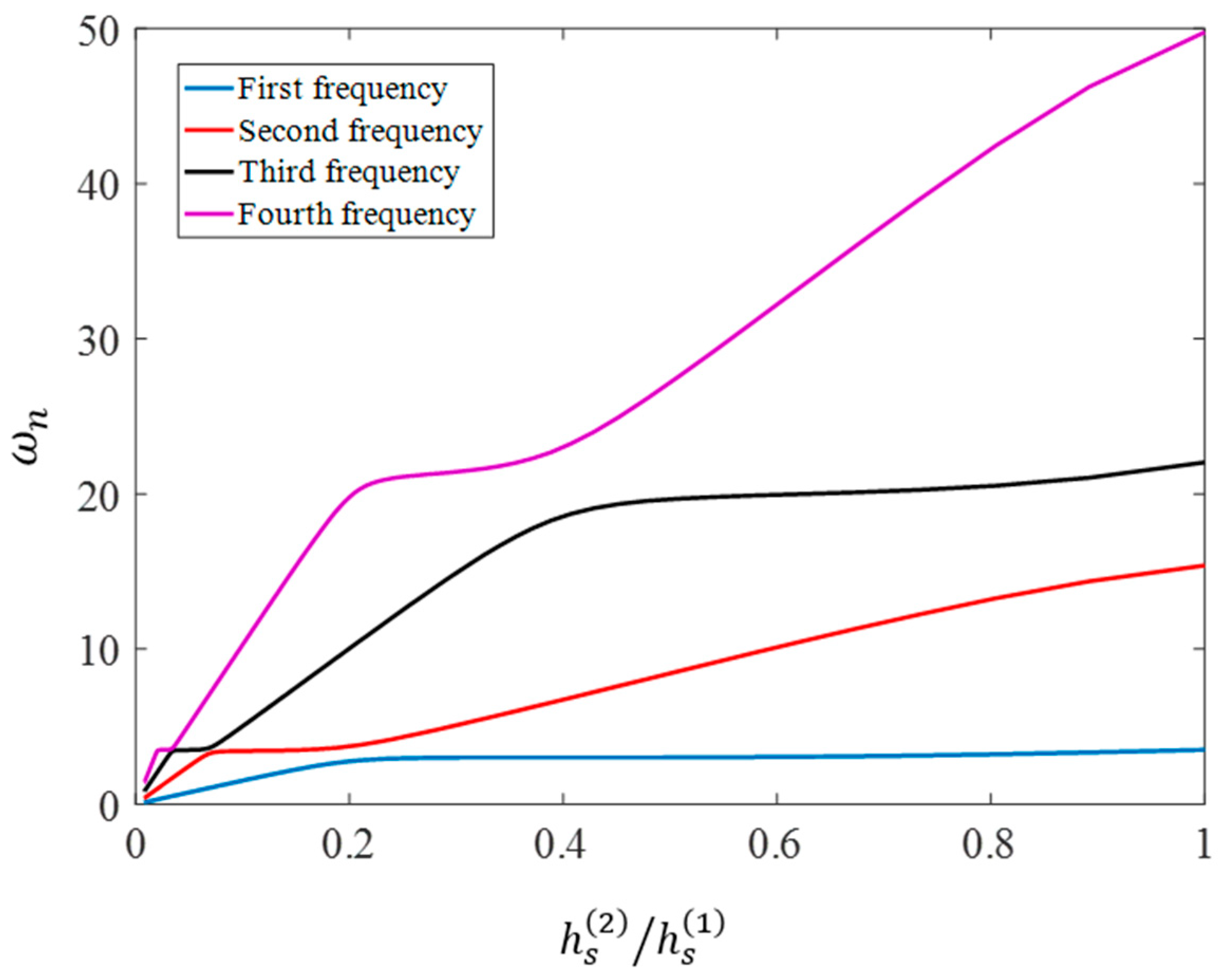
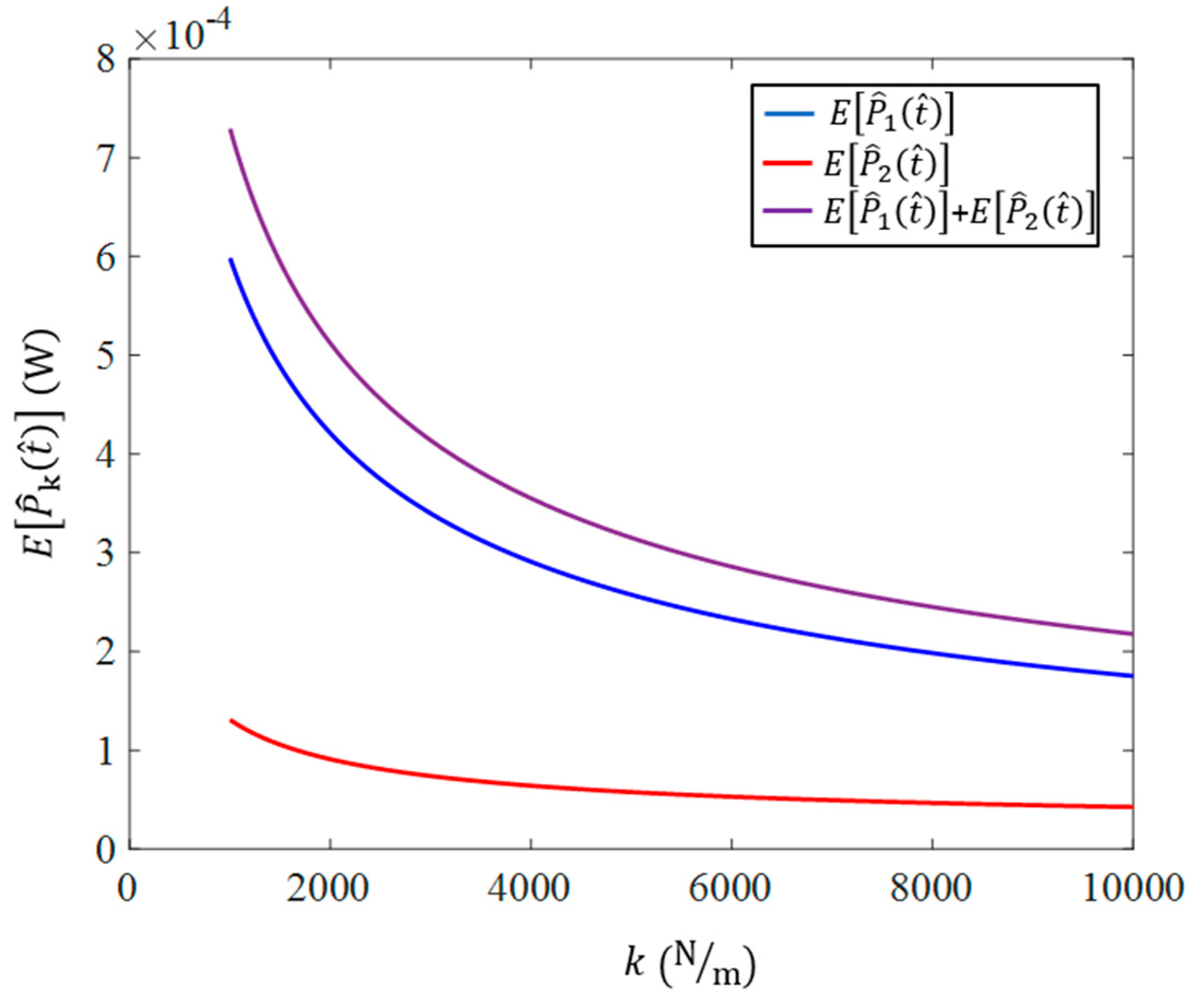
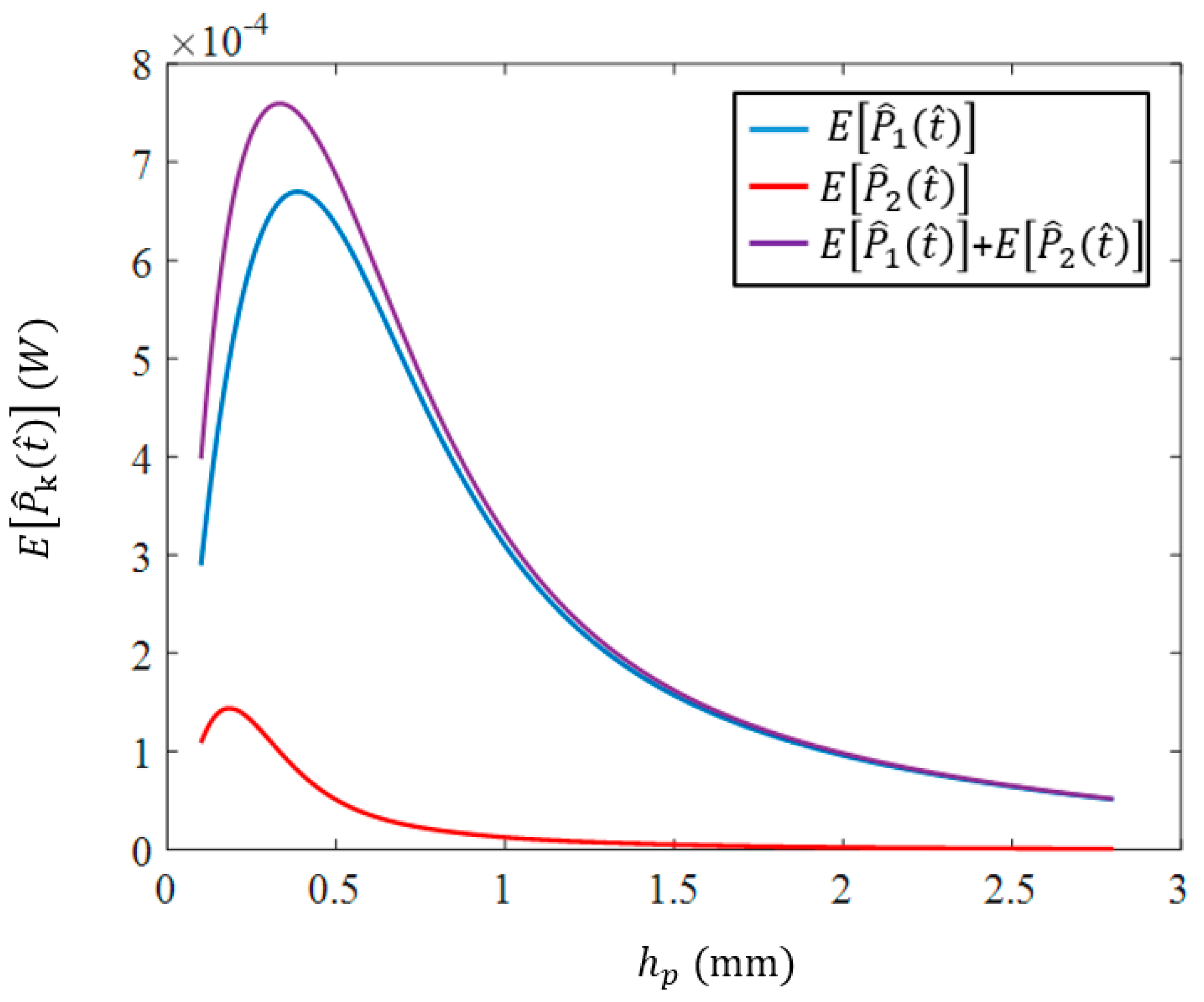
To investigate the number of modes that contribute significantly to the dynamic response, a physical system with the specifications given in
Table 1 (for the substructure) and
Table 3 (for the piezoelectric materials) is considered. Moreover, here and in the rest of this paper, unless otherwise stated, the damping
is selected such that the modal damping of the first mode becomes a nominal value of 0.01.