Drone Launched Short Range Rockets
Abstract
:1. Introduction
2. Artillery Rockets and Warheads
2.1. Artillery Rockets
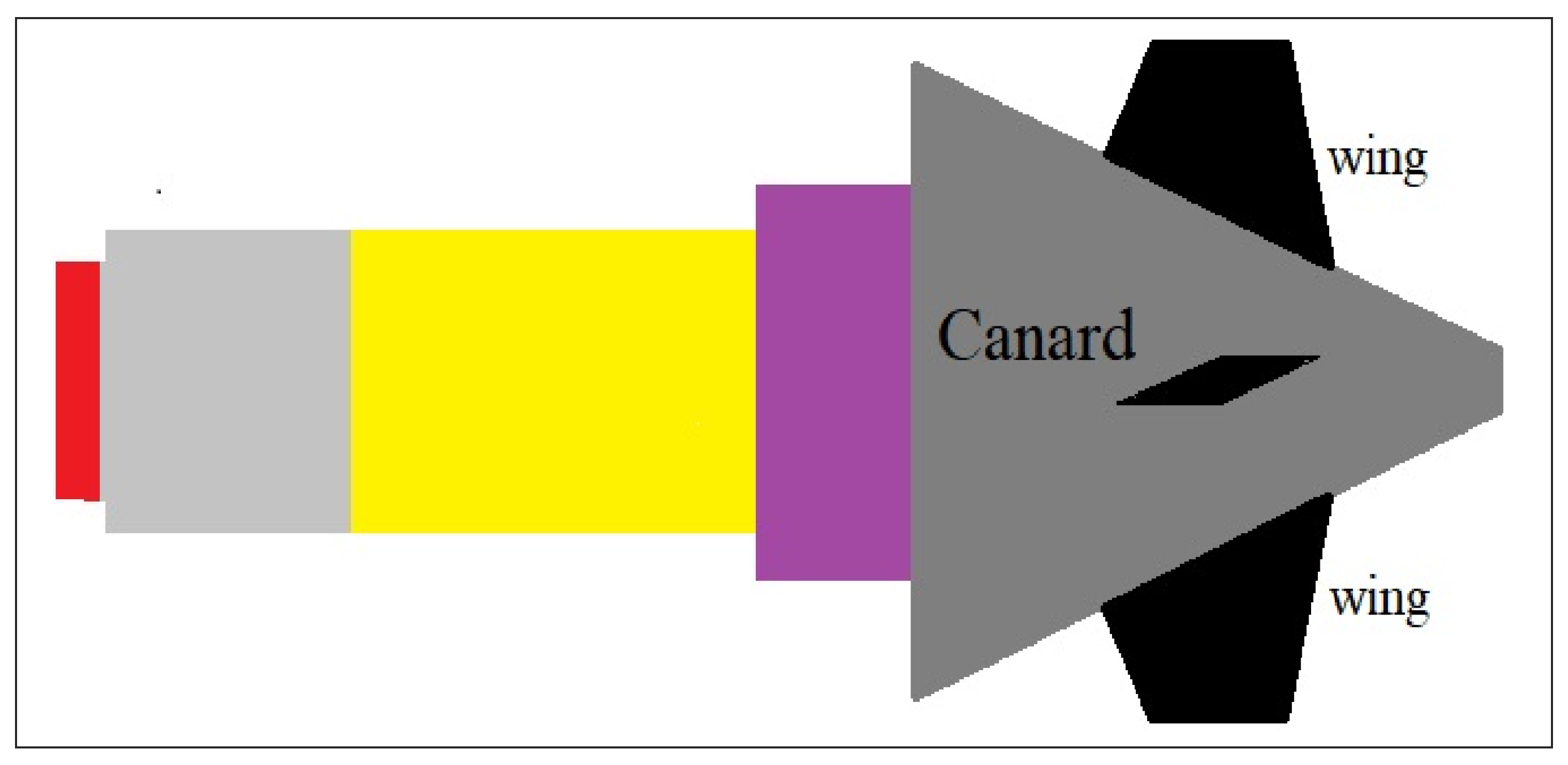
2.2. Guided Munitions
2.3. Anti-Aircraft Missiles
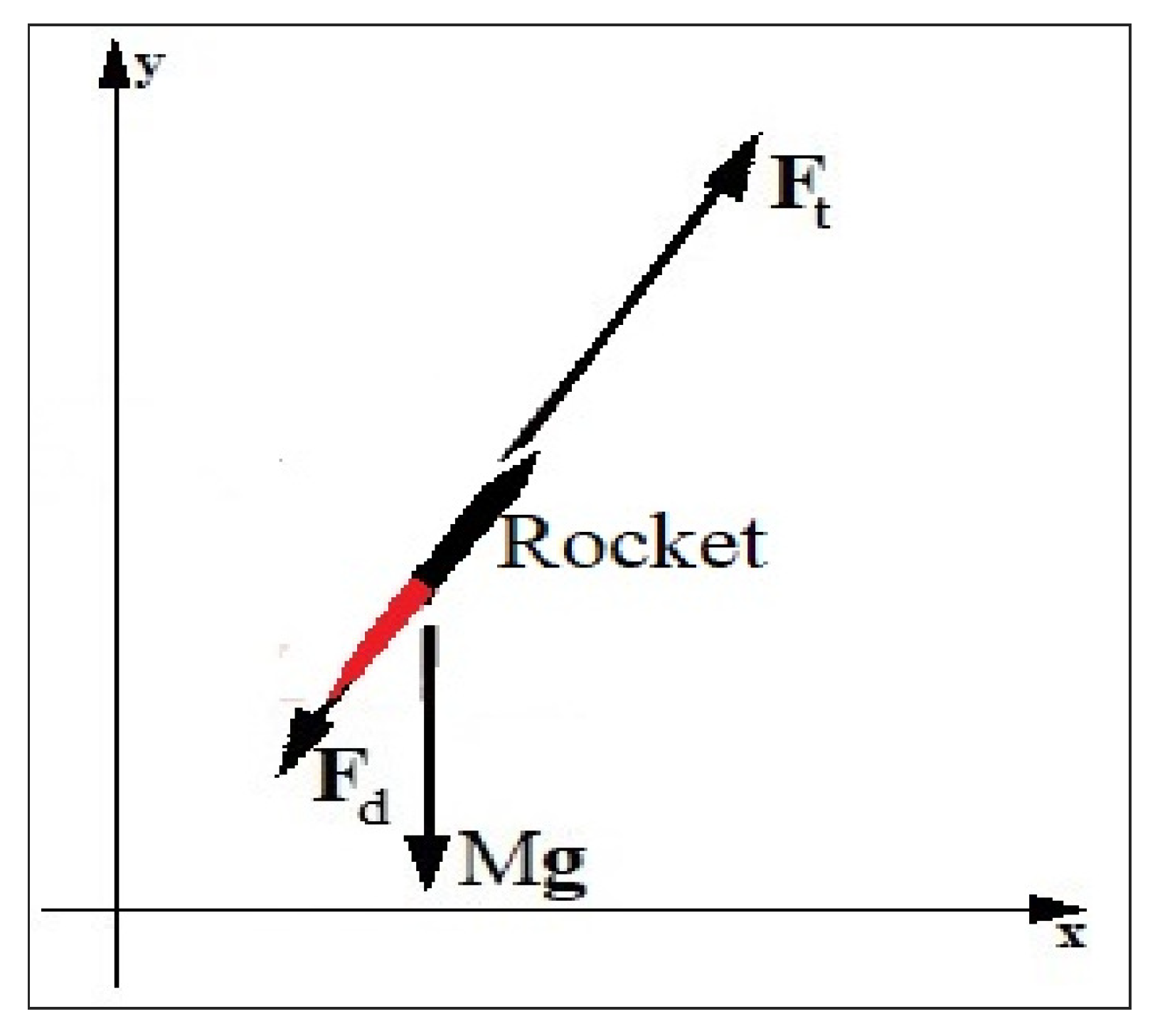
3. The Physics of Rocket Flight
4. DLSRR Engines
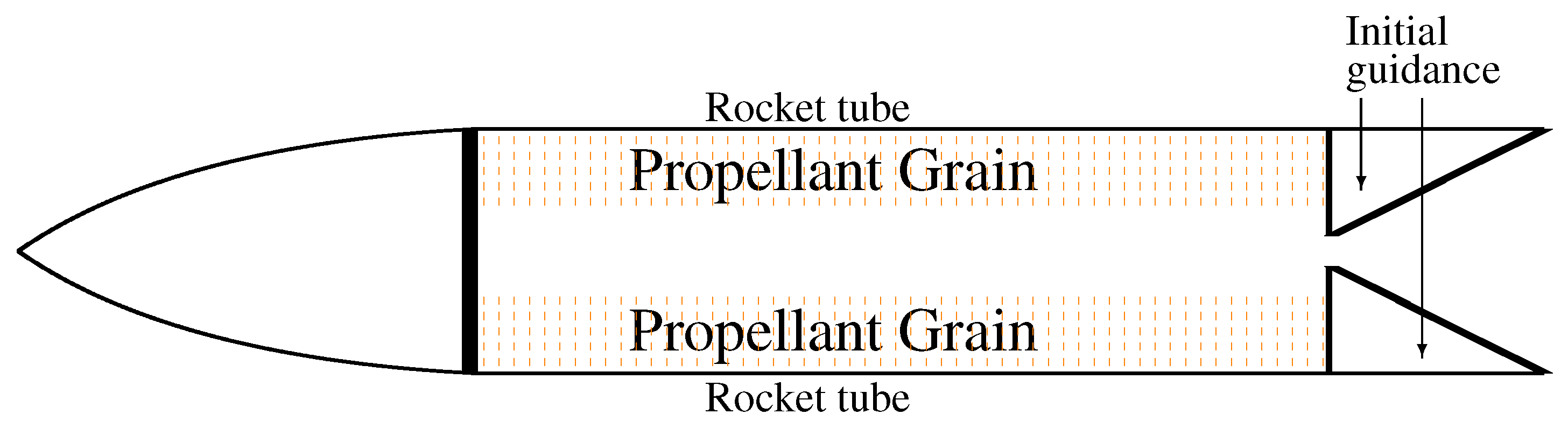
4.1. Solid Propellant Rockets
4.2. Propellant Composition
4.3. Grain Shape
5. Rocket and Warhead Performance
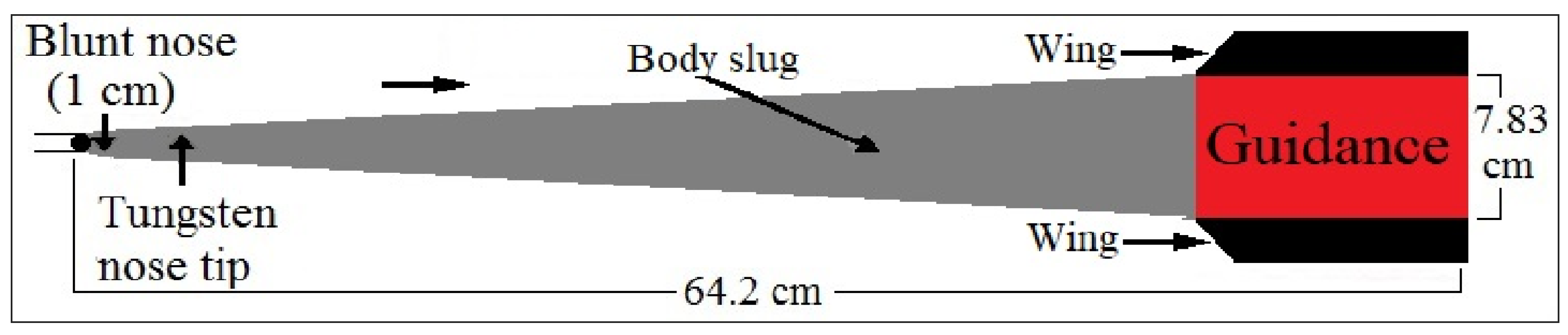
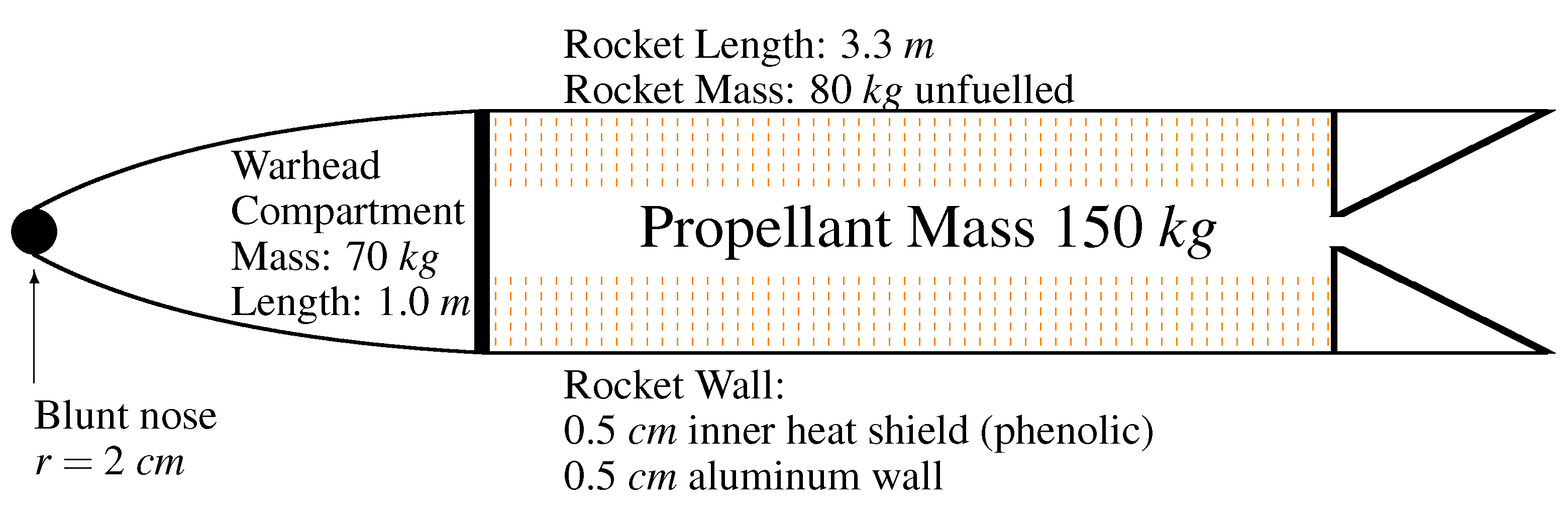
5.1. Performance of 30 cm Drone Launched Short Range Rockets (DLSRR)
5.2. Impact Velocity Calculation
5.2.1. Hypervelocity Projectile
5.2.2. European Hypersonic Projectile
6. Aerodynamic Heating and Thermal Protection
6.1. General Expressions for Heat Flux
6.1.1. Stagnation Point Heat Flux
6.1.2. General Turbulent Flow Heat Flux
6.1.3. Rocket Cylinder
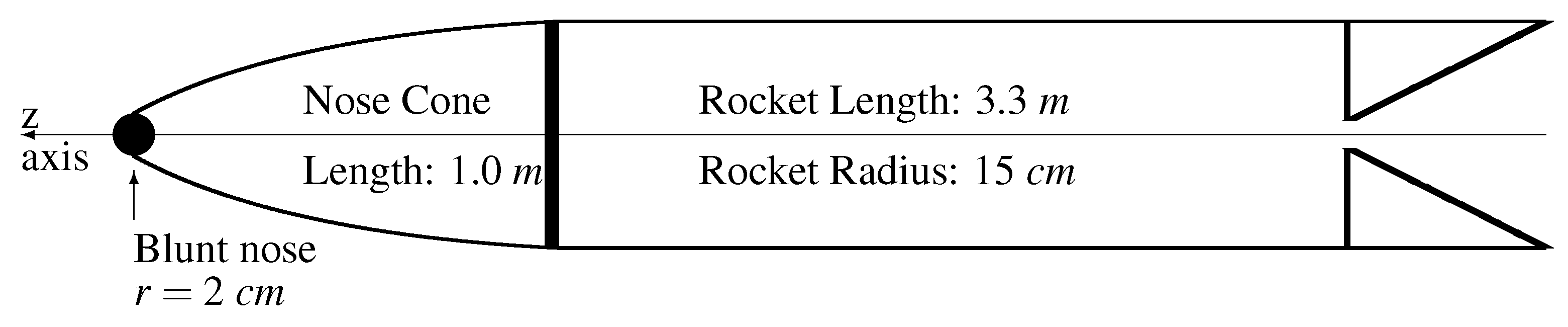
6.1.4. Nose Cone
6.2. Thermal Protection Systems
6.2.1. Radiative Heat Shields
Outermost Layer—Oxidation Resistant Metals
Second Layer—High Temperature Thermal Insulation
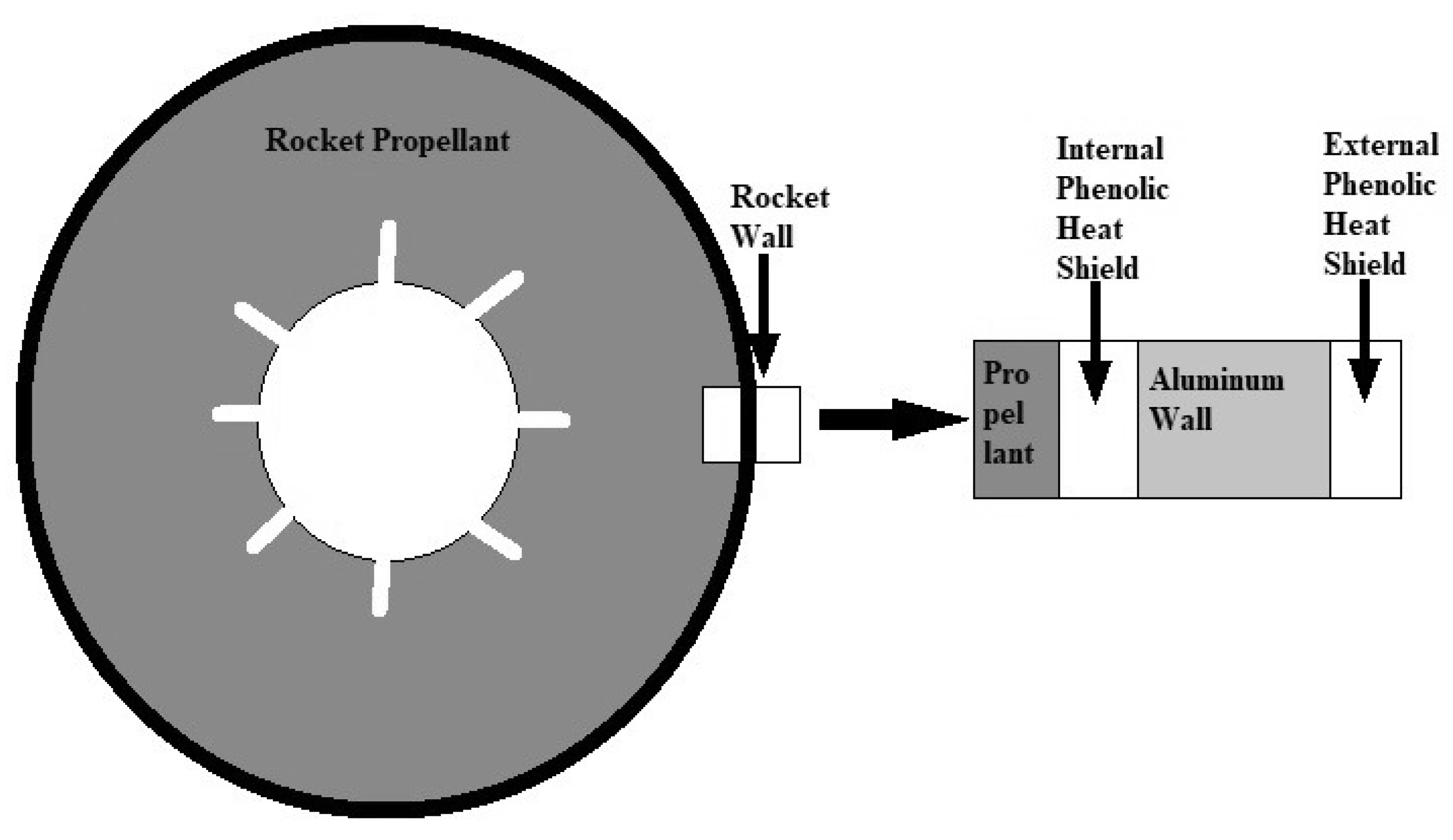
DLSRR Thermal Insulation
6.2.2. Heat Sink Shields
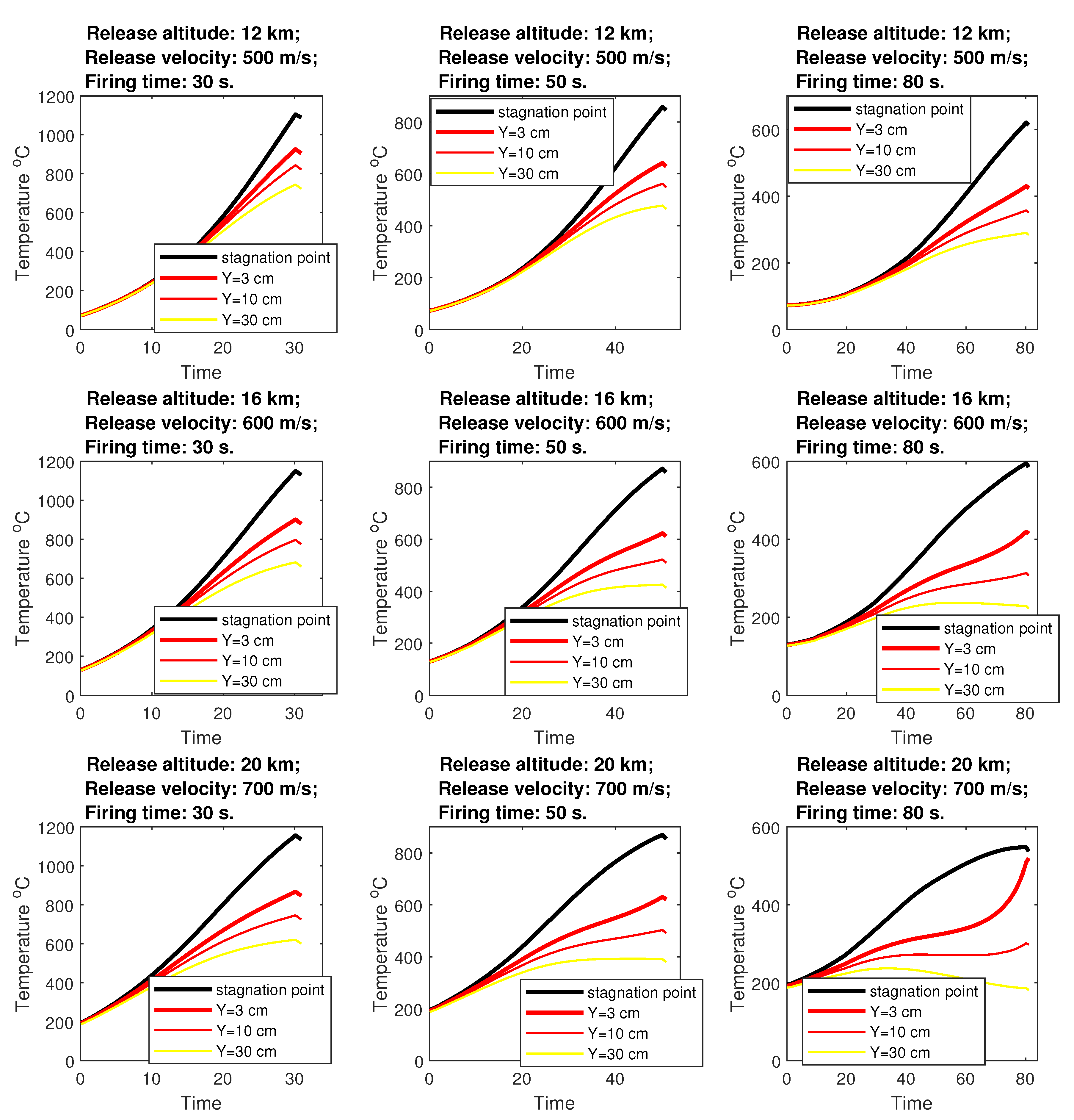
6.3. DLSRR Heating
6.3.1. DLSRR Stagnation Point
6.3.2. DLSRR Nose Cone
6.3.3. DLSRR Cylinder
7. Conclusions
Funding
Conflicts of Interest
Abbreviations
| General |
| ATACMS—army tactical missile system (USA) |
| CEP—circular error probability |
| DF—Dong–Feng ballistic missiles (China) |
| DLSRR—drone launched short range rockets |
| GMLRS—guided multiple launch rocket system (USA) |
| HPV—hypervelocity projectile |
| JDAM—joint direct attack munition (guidance kit for any bomb) |
| LORA—long range attack missile (Israel) |
| MKV—multiple kill vehicle |
| MLRS—multiple launch rocket system |
| PGK—precision guidance kit |
| RASAero—aerodynamic analysis and flight simulation software |
| RLA—rocket launcher aircraft |
| RPA—rocket propulsion analysis |
| SAM—surface to air missile |
| SRBM —short range ballistic missiles |
| TBM—theatre ballistic missile |
| Chemicals |
| AP—ammonium perchlorate |
| AN—ammonium nitrate |
| HTPB—hydroxyl-terminated polybutadiene |
Appendix A. Programs Used
References
- National Research Council (U.S.). Reusable Booster System: Review and Assessment; National Academies Press: Washington, DC, USA, 2012. [Google Scholar]
- Becker, J. Militarizing Musk, War on The Rocks. 2016. Available online: https://warontherocks.com/2016/05/militarizing-musk/ (accessed on 19 April 2020).
- Perrimond, G. 1944–2001: The Threat of Theatre Ballistic Missiles; Supplément à TTU Europe: Paris, France, 2002. [Google Scholar]
- Wood, J. Russia, the Asymmetric Threat to the United States: A Potent Mixture of Energy and Missiles; Praeger Security International: Santa Barbara, CA, USA, 2009. [Google Scholar]
- Parker, S.; Pang, A. The M270 Multiple Rocket Launcher; Capstone Press: Mankato, MN, USA, 2008. [Google Scholar]
- Office of the Under Secretary of Defense (Comptroller). Procurement Programs, Department of Defense Budget Fiscal Year 2016; Office of the Under Secretary of Defense: Washington, DC, USA, 2015. [Google Scholar]
- Eshel, T. Israel Tests Sea-Launched LORA Missile, Defense Update. 20 June 2017. Available online: http://defense-update.com/20170620_lora-2.html (accessed on 7 March 2018).
- Heginbotham, E. The US-China Military Scorecard: Forces, Geography, and the Evolving Balance of Power, 1996-2017; RAND: Santa Monica, CA, USA, 2015. [Google Scholar]
- US Department of Defense (DoD). Annual Report to Congress: Military and Security Developments Involving the People’s Republic of China; US Department of Defense: Washington, DC, USA, 2017.
- Wunderle, W.D. US Army Weapons Systems 2009; Skyhorse Pub: New York, NY, USA, 2008. [Google Scholar]
- Prenatt, J.; Hook, A. Katyusha: Russian Multiple Rocket Launchers 1941-Present; Bloomsbury Publishing Place: London, UK, 2016. [Google Scholar]
- AR3 Multiple Launch Rocket System. Available online: http://www.military-today.com/artillery/ar3.htm (accessed on 14 January 2018).
- Turner, P.E. New and Evolving Armaments and Subsystems for Future Conflicts; Precision Fires Rocket and Missile Systems: Huntsville, AL, USA, 2016. [Google Scholar]
- Merkley, J.A. Trident II Missiles: Capability, Costs, and Alternatives; Congress of the U.S., Congressional Budget Office: Washington, DC, USA, 1986.
- Gormley, D.M. Dealing with the Threat of Cruise Missiles; Routledge: Abingdon, UK, 2017. [Google Scholar]
- Technical tune to Agni test before talks. In Telegraph; Telegraph Media Group: London, UK, 2004.
- Watts, B.D. Six Decades of Guided Munitions and Battle Networks: Progress and Prospects; Center for Strategic and Budgetary Assessments: Washington, DC, USA, 2007. [Google Scholar]
- Bogan, J. Boeing boosts production of precision-guided bomb kits made in St. Charles to fight ongoing wars by air. Saint Louis Today, 27 January 2017. [Google Scholar]
- Fresconi, F.; Celmins, I.; Silton, S.; Costello, M. High Maneuverability Projectile Flight Using Low Cost Components. Aerosp. Sci. Technol. 2015, 41, 175–188. [Google Scholar] [CrossRef]
- Biass, E.H. Compendium Artillery. Armada Int. 2015, 39, 1–54. [Google Scholar]
- Foss, C. Smart ammo: Precision-guided munitions for field artillery. Jane’S Def. Wkly. 2015, 6, 1–14. [Google Scholar]
- ATK’s Precision Guidance Kit for artillery projectiles now approved for production. In Army Recognition; 2015; Available online: https://www.armyrecognition.com/february_2015_global_defense_security_news_uk/atk_s_precision_guidance_kit_for_artillery_projectiles_now_approved_for_production.html (accessed on 5 June 2020).
- Burke, P.G.; Pergolizzi, A. XM1156 Precision Guidance Kit (PGK) Overview. In Proceedings of the 2010 Fuze Conference, Kansas City, MO, USA, 11–13 May 2010. [Google Scholar]
- Forrester, A. Orbital ATK Reaches Milestone in M1156 Precision Guidance Kit Production. Govconwire. 2018. Available online: https://www.govconwire.com/2018/05/orbital-atk-reaches-milestone-in-m1156-precision-guidance-kit-production (accessed on 9 June 2019).
- Wang, B. Israel Converts Artillery into a Precision Guided Weapons. In Next, Big Future. 2017. Available online: https://www.nextbigfuture.com/2017/10/israel-converts-artillery-into-a-precision-guided-weapons.html (accessed on 5 June 2020).
- O’Rourke, R. Navy Lasers, Railgun, and Hypervelocity Projectile: Background and Issues for Congress; Congressional Research Service 7-5700: Washington, DC, USA, 2015. [Google Scholar]
- Nemets, A. Conflict with Russia: Part I &, Part 2; Xlibris Corporation: Bloomington, IN, USA, 2015. [Google Scholar]
- O’Rourke, R. Sea-Based Ballistic Missile Defense: Background and Issues for Congress; Congressional Research Service, Library of Congress: Washington, DC, USA, 2009. [Google Scholar]
- O’Rourke, R. Navy Aegis Ballistic Missile Defense (bmd) Program: Background and Issues for Congress; Congressional Research Service: Washington, DC, USA, 2014. [Google Scholar]
- Silverstone, P.H. The Navy of the Nuclear Age, 1947-2007; Routledge: New York, NY, USA, 2009; p. xxvi. [Google Scholar]
- Tsiolkovski, K.; Tikhonravov, M.K. Works on Rocket Technology; National Aeronautics and Space Administration: Washington, DC, USA, 1965.
- Cohen, N.S.; Flanigan, D.A. Mechanisms and Models of Solid-Propellant Burn Rate Temperature Sensitivity—A Review. AIAA J. 1985, 23, 1538–1547. [Google Scholar] [CrossRef]
- Biblarz, O.; Sutton, G.P. Rocket Propulsion Elements, 8th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Jain, S.R.; Oommen, C. Ammonium nitrate: A promising rocket propellant oxidizer. J. Hazard. Mater. 1999, 67, 253–281. [Google Scholar]
- Caveny, L.H.; Felsheim, C.R.; Summerfield, M. Burning Rate Measurement of Thin Sheets of Double Base Prpopellant; Princeton University: Princeton, NJ, USA, 1975. [Google Scholar]
- Ponomarenko, I.A. Rocket Propulsion Analysis. V 1.2.6, Lite Edition 2011, Cologne, Germany. 2011. Available online: http://www.propulsion-analysis.com (accessed on 5 June 2014).
- Brewster, Q.; Ishihara, A.; Sheridan, T. Ammonium nitrate-magnesium propellant combustion and heat transfer mechanisms. J. Propuls. Power 1992, 2, 760–769. [Google Scholar] [CrossRef]
- Azuma, Y.; Murata, H.; Simoda, M.; Tohara, T. Effect of magnalium (Mg-Al alloy) on combustion characteristics of ammonium nitrate-based solid propellant. Sci. Technol. Energ. Mater. 2000, 61, 58–66. [Google Scholar]
- Northam, G.B. Effects of Propellant Composition Variables on Acceleration-Induced Burning-Rate Augmentation of Solid Propellants; NASA Langley Research Center: Hampton, VA, USA, 1972. [Google Scholar]
- Lengellé, G.; Duterque, J.; Trubert, J.F. Combustion of Solid Propellants; Research Scientists, Energetics Department Office National Détudes et de Recherches Aérospatiales (ONERA): Bordeaux, France, 2004.
- Kubota, N. Propellants and Explosives; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2007. [Google Scholar]
- OnlineMetals.com, Web. Available online: https://www.onlinemetals.com/ (accessed on 14 May 2019).
- Aluminum 6061-T6; 6061-T651, MatWeb, Your Source for Materials Information. Available online: http://www.matweb.com/SpecificMaterial.asp?bassnum=MA6061t6> (accessed on 4 September 2019).
- Innovation in Composite CNG Cylinders. In JEC Asia 2009 Automotive & Mass Transport Forum; Owens Corning: Toledo, OH, USA, 2009.
- Rogers, C.E.; Cooper, D. RASAero II, Rocket Aerodynamic Analysis and Flight Simulation Software; V 1.0.1; Rogers Aeroscience: Lancaster, CA, USA, 2016. [Google Scholar]
- Hundertmark, S.; Lancelle, D. A Scenario for a Future European Shipboard Railgun. In Proceedings of the 17th International Symposium on Electromag, Launch Tech. (EML), San Diego, CA, USA, 7–11 July 2014. [Google Scholar]
- Crowell, G.A. The Descriptive Geometry of Nose Cone, Scribd. 1996. Available online: http://www.scribd.com/doc/60921375/ (accessed on 5 June 2019).
- McNab, I.R.; Fish, S.; Stefani, F. Parameters for an Electromagnetic Naval Railgun. IEEE Trans. Magn. 2001, 37, 223–228. [Google Scholar] [CrossRef]
- Kulfan, R.M. Historic Background on Flat Plate Turbulent Flow Skin Friction and Boundary Layer Growth; HSR Airframe Technical Review: Los Angeles, CA, USA, 1998. [Google Scholar]
- Woodward, D. Space Launch Vehicle Design. Master’s Thesis, Department of Mechanical and Aerospace Engineering, University of Texas at Arlington, Arlington, TX, USA, 2017. [Google Scholar]
- Tauber, M.E. A Review of High-Speed, Convective, Heat-Transfer Computation Methods; NASA Technical Paper 2914; Ames Research Center: Mountain View, CA, USA, 1989. [Google Scholar]
- Fleeman, E.L. Tactical Missile Design; Educational Series; AIAA: Reston, VA, USA, 2001. [Google Scholar]
- Clancy, L.J. Aerodynamics; Pitman Publ. Lim.: London, UK, 1975. [Google Scholar]
- Sutton, K.; Graves, R.A. A General Stagnation Point Convective Heating Equation for Arbitrary Gas Mixtures; NASA TR-R-376; NASA: Washington, DC, USA, 1971. [Google Scholar]
- Chapman, G.T. Theoretical Laminar Convective Heat Transfer & Boundary Layer Characteristics on Cones at Speeds to 24 km/s; NASA TN D-2463; NASA: Washington, DC, USA, 1964. [Google Scholar]
- Detra, R.W.; Hidalgo, H. Generalized heat transfer formulas and graphs for nose cone re-entry into the atmosphere. ARS J. 1961, 31, 318–321. [Google Scholar] [CrossRef]
- Trinh, K.T.; Tuoc, K. On The Critical Reynolds Number For Transition From Laminar to Turbulent Flow. arXiv 2010, arXiv:1007.0810. [Google Scholar]
- Lienhard, J., IV; Lienhard, J.V. A Heat Transfer Textbook, 3rd ed.; Phlogiston Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Higgins, K. Comparison of Engineering Correlations for Predicting Heat Transfer in Zero-pressure-gradient Compressible Boundary Layers with CFD and Experimental Data. Defence Science and Technology Organisation. 2008. Available online: http://www.dsto.defence.gov.au/corporate/reports/DSTO-TR-2159.pdf (accessed on 11 September 2019).
- Gottlieb, J.J.; Ritzel, D.V. A Semi-Empirical Equation for the Viscosity of Air; Suffield Technical Note No. 454; Defence Research Establishment: Suffield, AB, Canada, 1979. [Google Scholar]
- Crabtree, L.F.; Dommett, R.L.; Woodley, J.G. Estimation of Heat Transfer to Flat Plates, Cones and Blunt Bodies; Aeronautical Research Council Reports and Memoranda, R. & M. No. 3637; Her Mmjesty’s Stationery Office: London, UK, 1970. [Google Scholar]
- Akin, D.L. Entry Aerothermodynamics, Slides from. 2012 NASA Thermal and Fluids Analysis Workshop. Available online: https://tfaws.nasa.gov/TFAWS12/Proceedings/Aerothermodynamics%20Course.pdf (accessed on 15 August 2019).
- Lide, D.R. (Ed.) CRC Handbook of Chemistry and Physics, 84th ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Johnson, R.; Killpatrick, D.H. Evaluation of Dispersion Strengthened Nickel—Base Alloy Heat Shields for Space Shuttle Application; National Aeronautics and Space Adminstration: Washington, DC, USA, 1976.
- Haugsrud, R. On the high-temperature oxidation of nickel. Corros. Sci. 2003, 45, 211–235. [Google Scholar] [CrossRef]
- Finfrock, C.C.; Greene, G.A. Oxidation of Inconel 718 in Air at Temperatures from 973 K to 1620 K; Energy Sciences and Technology Department, Brookhaven National Laboratory: Upton, NY, USA, 2000. [Google Scholar]
- Astle, M.J.; Weast, R.C. CRC Handbook of Chemistry and Physics, 63rd ed.; CRC Press: Boca Raton, FL, USA, 1982. [Google Scholar]
- “0.02” Nickel 625 Sheet. OnlineMetals.com. 2019. Available online: https://www.onlinemetals.com (accessed on 19 September 2019).
- Scruggs, D.M. Modified Chromium for Unprotected Structures. ARS J. 1961, 31, 1527–1533. [Google Scholar] [CrossRef]
- Hallström, S.; Halvarsson, M.; Höglund, L.; Jonsson, T.; Ågren, J. High temperature oxidation of chromium: Kinetic modeling and microstructural investigation. Solid State Ionics 2013, 240, 41–50. [Google Scholar] [CrossRef]
- Dickinson, C.D.; Seigle, L.L. Experimental Study of Factors Controlling the Effectiveness of High-Temperature Protective Coatings for Tungsten; Technical Documentary Report No. ASD-TDR-63-774; Defense Documentation Center for Scientific and Technical Information Cameron Station: Alexandria, VA, USA, 1964. [Google Scholar]
- Ceramfiber, Ceramic Fiber Blanket by Ceramafiber. Amazon. 2019. Available online: https://www.amazon.com/ceramafiber-Ceramic-Fiber-Blanket-Insulation/dp/B0771QNP3G/ (accessed on 19 September 2019).
- Product Data Book, Thermal Ceramics Is a Business of Morgan Advanced Materials. 2018. Available online: http://www.morganthermalceramics.com/ (accessed on 6 September 2019).
- CeramicFiberOnline, Ceramic Fiber Paper Zirconia Grade, CeramicFiberOnline. 2019. Available online: https://www.ceramicfiberonline.com/product/ceramic-fiber-paper-552-108240125/ (accessed on 1 September 2019).
- Jenkins, D.R.; Launius, R.D. Coming Home: Reentry and Recovery from Space; US Government Printing Office: Washington, DC, USA, 2011.

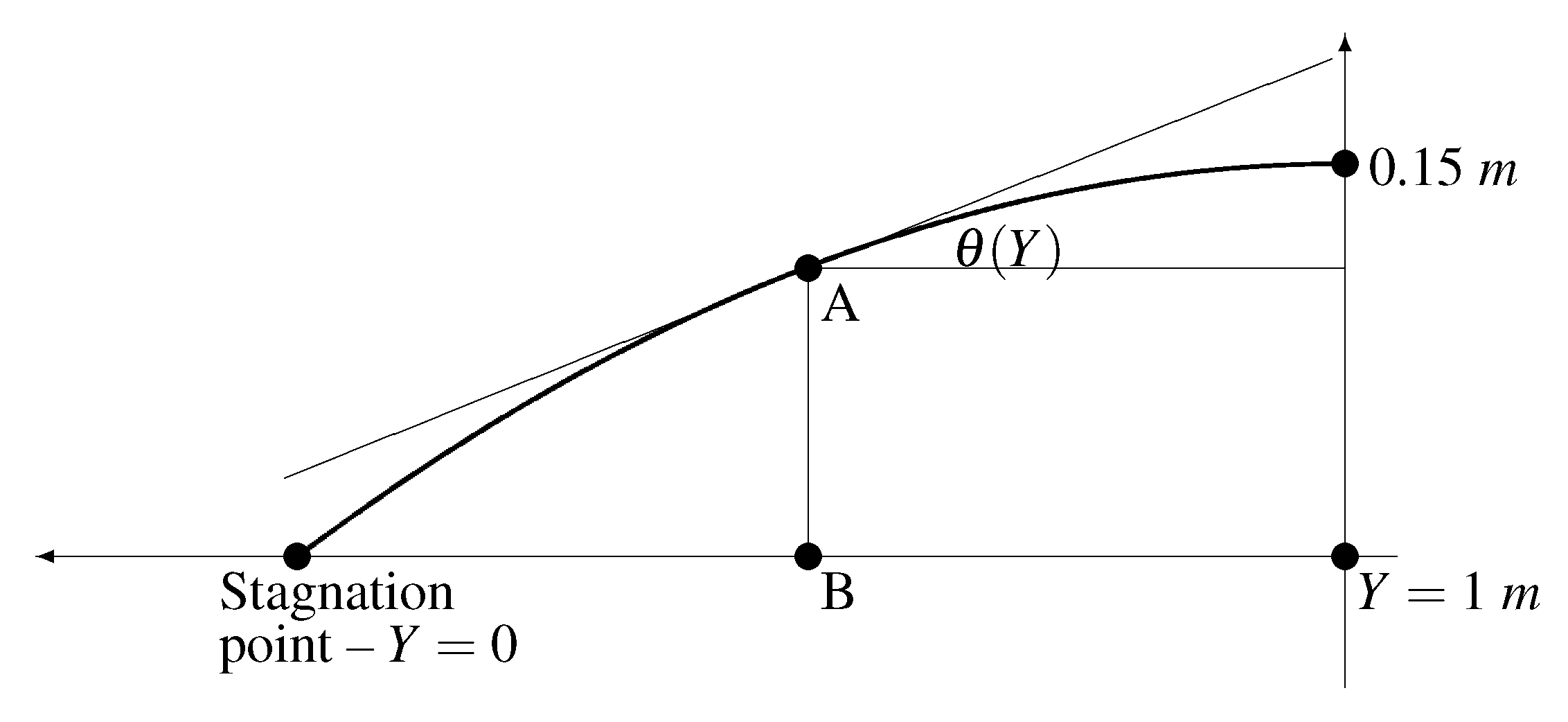
| Missile | Range | Throw Weight | Unit Cost | Cost per kg Delivered |
|---|---|---|---|---|
| GMLRS | 84 km | 90 kg | $136,000 | $1500 |
| ATACMS | 165 km | 560 kg | $1,500,000 | $2700 |
| ATACMS | 300 km | 230 kg | $1,500,000 | $6500 |
| Trident II [14] | 7840 km | 2800 kg | $37,300,000 | $13,300 |
| Missile | Range | Throw Weight | Unit Cost | Cost per kg Delivered |
|---|---|---|---|---|
| Dong-Feng 15 | 500 km | 600 kg | $4,000,000 | $6700 |
| Scud C | 600 km | 600 kg | $2,000,000 | $3300 |
| Agni II [16] | 2000 km | 1000 kg | $5,100,000 | $5100 |
| Propellant | Temperature | at 40 atm, | Burning | n Coefficient |
|---|---|---|---|---|
| Composition | at 40 atm | Exp 15 | Rate | at 40 atm |
| Vacuum | ||||
| 20% Binder, 72% AN, 8% MgAl [37] | 1280 °C | 2140 m/s | 2.0 mm/s | 0.5 |
| 20% Binder, 68% AN, 12% MgAl | 1450 °C | 2240 m/s | NA | NA |
| 20% Binder, 64% AN, 16% MgAl [37] | 1700 °C | 2320 m/s | 3.0 mm/s | 0.5 |
| 25% Binder, 60% AN, 15% MgAl [37] | 1410 °C | 2170 m/s | 1.6 mm/s | 0.7 |
| 17.8% HTPB, 64% AN, | 1660 °C | 2270 m/s | 2.0 mm/s | 0.05 |
| 14.6% Mg, 3.6% AC [38] | ||||
| Nitrocellulose 9% N | 1060 °C | 1990 m/s | NA | NA |
| Nitrocellulose 10% N | 1350 °C | 2090 m/s | NA | NA |
| Nitrocellulose 11% N | 1680 °C | 2200 m/s | NA | NA |
| Nitrocellulose 12% N | 2030 °C | 2290 m/s | NA | NA |
| Nitrocellulose 13% N | 2380 °C | 2420 m/s | NA | NA |
| Nitrocellulose 14% N | 2690 °C | 2530 m/s | NA | NA |
| 90% Nitrocellulose 7.5% N, 10% Mg | 1290 °C | 2080 m/s | NA | NA |
| 90% Nitrocellulose 8% N, 10% Mg | 1410 °C | 2130 m/s | NA | NA |
| 90% Nitrocellulose 8.5% N, 10% Mg | 1540 °C | 2200 m/s | NA | NA |
| 70% AP, 15% Al, 15% HTPB | 2880 °C | 2610 m/s | 6.5 mm/s | 0.35 |
| Standard Propellant [39] | ||||
| 56% NG, 44% Cellulose | 1340 °C | 2090 m/s | NA | NA |
| 59% NG, 41% Cellulose | 1510 °C | 2150 m/s | NA | NA |
| 66% NG, 34% Cellulose [40] (pp. 4–5) | 1950 °C | 2300 m/s | 4.0 mm/s | 0.7 |
| 77% NG, 23% Cellulose [40] (pp. 4–5) | 2560 °C | 2530 m/s | 7.0 mm/s | 0.7 |
| 82.5% NG, 17.5% Cellulose [40] (pp. 4–5) | 2790 °C | 2630 m/s | 10 mm/s | 0.7 |
| 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | 3.00 | |
| 0.265 | 0.260 | 0.261 | 0.380 | 0.432 | 0.404 | 0.381 | 0.352 | 0.328 | 0.308 | 0.289 | 0.273 | |
| 3.25 | 3.50 | 3.75 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.25 | 5.50 | 5.75 | 6.00 | |
| 0.259 | 0.246 | 0.235 | 0.225 | 0.216 | 0.208 | 0.200 | 0.193 | 0.187 | 0.181 | 0.175 | 0.168 | |
| 6.25 | 6.50 | 6.75 | 7.00 | 7.25 | 7.50 | 7.75 | 8.00 | 8.25 | 8.50 | 8.75 | 9.00 | |
| 0.163 | 0.159 | 0.154 | 0.150 | 0.147 | 0.144 | 0.141 | 0.139 | 0.137 | 0.135 | 0.133 | 0.131 |
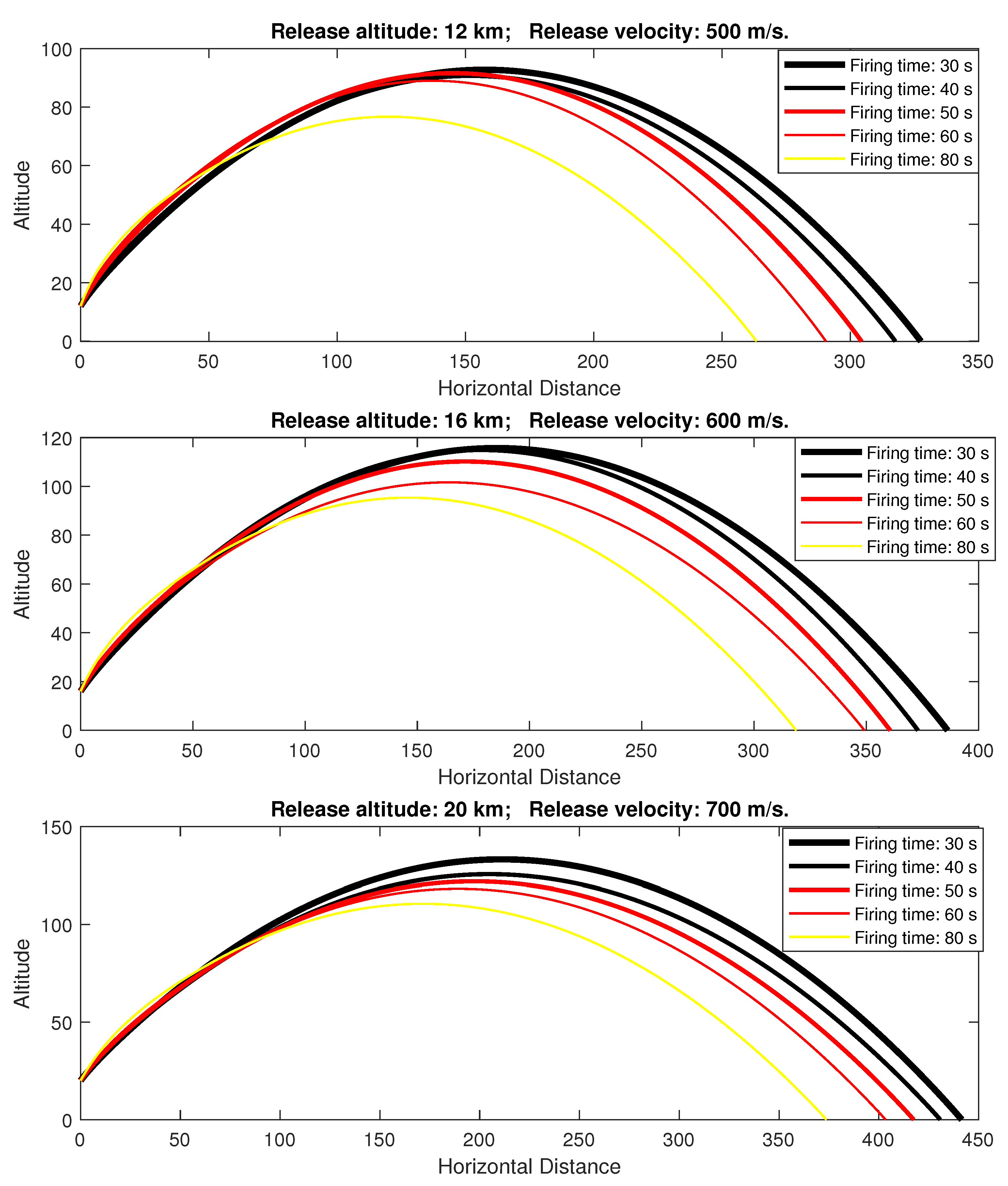
| Release altitude: 12 km. Release velocity: 500 m/s. | |||||
|---|---|---|---|---|---|
| Firing time, s | 30 | 40 | 50 | 60 | 80 |
| Optimal firing angle, ° | 54 | 57 | 61 | 64 | 68 |
| Flight time, s | 282 | 288 | 289 | 289 | 277 |
| Drag loss, m/s | 98 | 84 | 76 | 69 | 62 |
| Gravity loss, m/s | 93 | 131 | 169 | 209 | 285 |
| Rocket Velocity Gain, m/s | 1457 | 1457 | 1457 | 1456 | 1459 |
| Flight apogee, km | 93 | 94 | 92 | 89 | 77 |
| Range, km | 327 | 317 | 304 | 291 | 263 |
| Release altitude: 16 km. Release velocity: 600 m/s. | |||||
| Firing time, s | 30 | 40 | 50 | 60 | 80 |
| Optimal firing angle, ° | 54 | 57 | 59 | 60 | 65 |
| Flight time, s | 311 | 314 | 311 | 303 | 300 |
| Drag loss, m/s | 51 | 45 | 42 | 40 | 35 |
| Gravity loss, m/s | 90 | 124 | 158 | 188 | 263 |
| Rocket Velocity Gain, m/s | 1457 | 1457 | 1457 | 1456 | 1456 |
| Flight apogee, km | 116 | 115 | 110 | 102 | 95 |
| Range, km | 386 | 373 | 361 | 349 | 318 |
| Release altitude: 20 km. Release velocity: 700 m/s. | |||||
| Firing time, s | 30 | 40 | 50 | 60 | 80 |
| Optimal firing angle, ° | 53 | 54 | 56 | 58 | 62 |
| Flight time, s | 320 | 325 | 323 | 322 | 318 |
| Drag loss, m/s | 29 | 26 | 24 | 22 | 20 |
| Gravity loss, m/s | 82 | 113 | 144 | 176 | 242 |
| Rocket Velocity Gain, m/s | 1457 | 1457 | 1457 | 1456 | 1459 |
| Flight apogee, km | 125 | 126 | 122 | 118 | 111 |
| Range, km | 444 | 431 | 417 | 403 | 374 |
| 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 | |
| 0.208 | 0.203 | 0.202 | 0.289 | 0.336 | 0.325 | 0.292 | 0.265 | 0.243 | 0.225 | 0.208 | |
| 3.00 | 3.25 | 3.50 | 3.75 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.25 | 5.50 | |
| 0.194 | 0.181 | 0.171 | 0.161 | 0.152 | 0.145 | 0.139 | 0.133 | 0.127 | 0.122 | 0.117 | |
| 5.75 | 6.00 | 6.25 | 6.50 | 6.75 | 7.00 | 7.25 | 7.50 | 7.75 | 8.00 | ||
| 0.112 | 0.106 | 0.103 | 0.099 | 0.095 | 0.091 | 0.089 | 0.087 | 0.085 | 0.083 |
| DLSRR , m/s | 500 | 600 | 700 | 500 | 600 | 700 | 500 | 600 | 700 |
| DLSRR , km | 12 | 16 | 20 | 12 | 16 | 20 | 12 | 16 | 20 |
| DLSRR , s | 30 | 30 | 30 | 50 | 50 | 50 | 80 | 80 | 80 |
| Apogee h, km | 93 | 116 | 133 | 92 | 110 | 122 | 77 | 95 | 111 |
| Apogee v, m/s | 1239 | 1310 | 1399 | 1170 | 1265 | 1398 | 1151 | 1241 | 1349 |
| Range, km | 328 | 386 | 442 | 305 | 360 | 418 | 264 | 319 | 374 |
| Impact v, m/s | 1252 | 1422 | 1567 | 1215 | 1372 | 1501 | 1110 | 1269 | 1409 |
| , m/s | 580 | 574 | 571 | 565 | 568 | 584 | 573 | 579 | 589 |
| M | 0.25 | 0.50 | 0.75 | 1.00 | 1.25 | 1.50 | 1.75 | 2.00 | 2.25 | 2.50 | 2.75 |
| 0.184 | 0.182 | 0.181 | 0.264 | 0.297 | 0.268 | 0.242 | 0.219 | 0.200 | 0.184 | 0.169 | |
| M | 3.00 | 3.25 | 3.50 | 3.75 | 4.00 | 4.25 | 4.50 | 4.75 | 5.00 | 5.25 | 5.50 |
| 0.156 | 0.145 | 0.135 | 0.126 | 0.119 | 0.112 | 0.106 | 0.100 | 0.095 | 0.091 | 0.086 | |
| M | 5.75 | 6.00 | 6.25 | 6.50 | 6.75 | 7.00 | 7.25 | 7.05 | 7.75 | 8.00 | |
| 0.081 | 0.076 | 0.072 | 0.069 | 0.066 | 0.062 | 0.060 | 0.058 | 0.056 | 0.055 |
| DLSRR , m/s | 500 | 600 | 700 | 500 | 600 | 700 | 500 | 600 | 700 |
| DLSRR , km | 12 | 16 | 20 | 12 | 16 | 20 | 12 | 16 | 20 |
| DLSRR , s | 30 | 30 | 30 | 50 | 50 | 50 | 80 | 80 | 80 |
| Apogee h, km | 93 | 116 | 133 | 92 | 110 | 122 | 77 | 95 | 111 |
| Apogee v, m/s | 1239 | 1310 | 1399 | 1170 | 1265 | 1398 | 1151 | 1241 | 1349 |
| Range, km | 328 | 386 | 442 | 305 | 361 | 418 | 264 | 319 | 374 |
| Impact v, m/s | 1555 | 1730 | 1879 | 1507 | 1675 | 1817 | 1400 | 1573 | 1726 |
| , m/s | 277 | 266 | 260 | 272 | 265 | 268 | 282 | 274 | 272 |
| Firing Time | 30 s | 40 s | 50 s | 60 s | 80 s |
|---|---|---|---|---|---|
| km, m/s | 94 °C | 81 °C | 68 °C | 58 °C | 47 °C |
| km, m/s | 75 °C | 66 °C | 59 °C | 55 °C | 46 °C |
| km, m/s | 61 °C | 56 °C | 52 °C | 48 °C | 43 °C |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shubov, M.V. Drone Launched Short Range Rockets. Aerospace 2020, 7, 76. https://doi.org/10.3390/aerospace7060076
Shubov MV. Drone Launched Short Range Rockets. Aerospace. 2020; 7(6):76. https://doi.org/10.3390/aerospace7060076
Chicago/Turabian StyleShubov, Mikhail V. 2020. "Drone Launched Short Range Rockets" Aerospace 7, no. 6: 76. https://doi.org/10.3390/aerospace7060076
APA StyleShubov, M. V. (2020). Drone Launched Short Range Rockets. Aerospace, 7(6), 76. https://doi.org/10.3390/aerospace7060076





