Sequential Low-Thrust Orbit-Raising of All-Electric Satellites
Abstract
1. Introduction
2. Problem Formulation
2.1. Spacecraft Dynamics
2.2. Sequential Orbit-Raising
2.3. Solar Array Degradation
3. Methodology
3.1. Fast and Slow Variable Considerations
3.2. Direct Transcription and Collocation
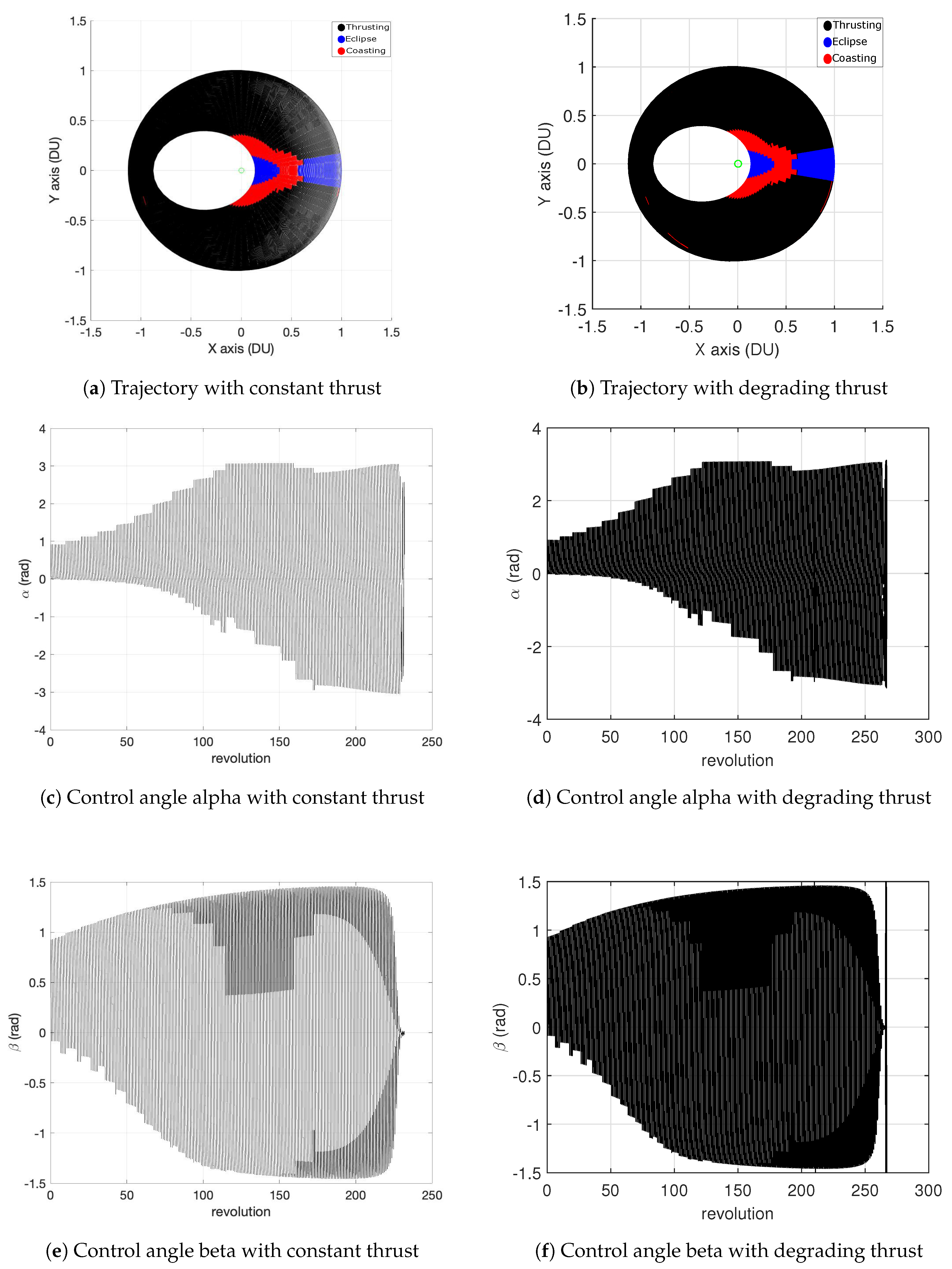
3.3. Trajectory Segments in Eclipses
3.4. Relative Thrust Efficiency
3.5. Optimization Sub-Problem
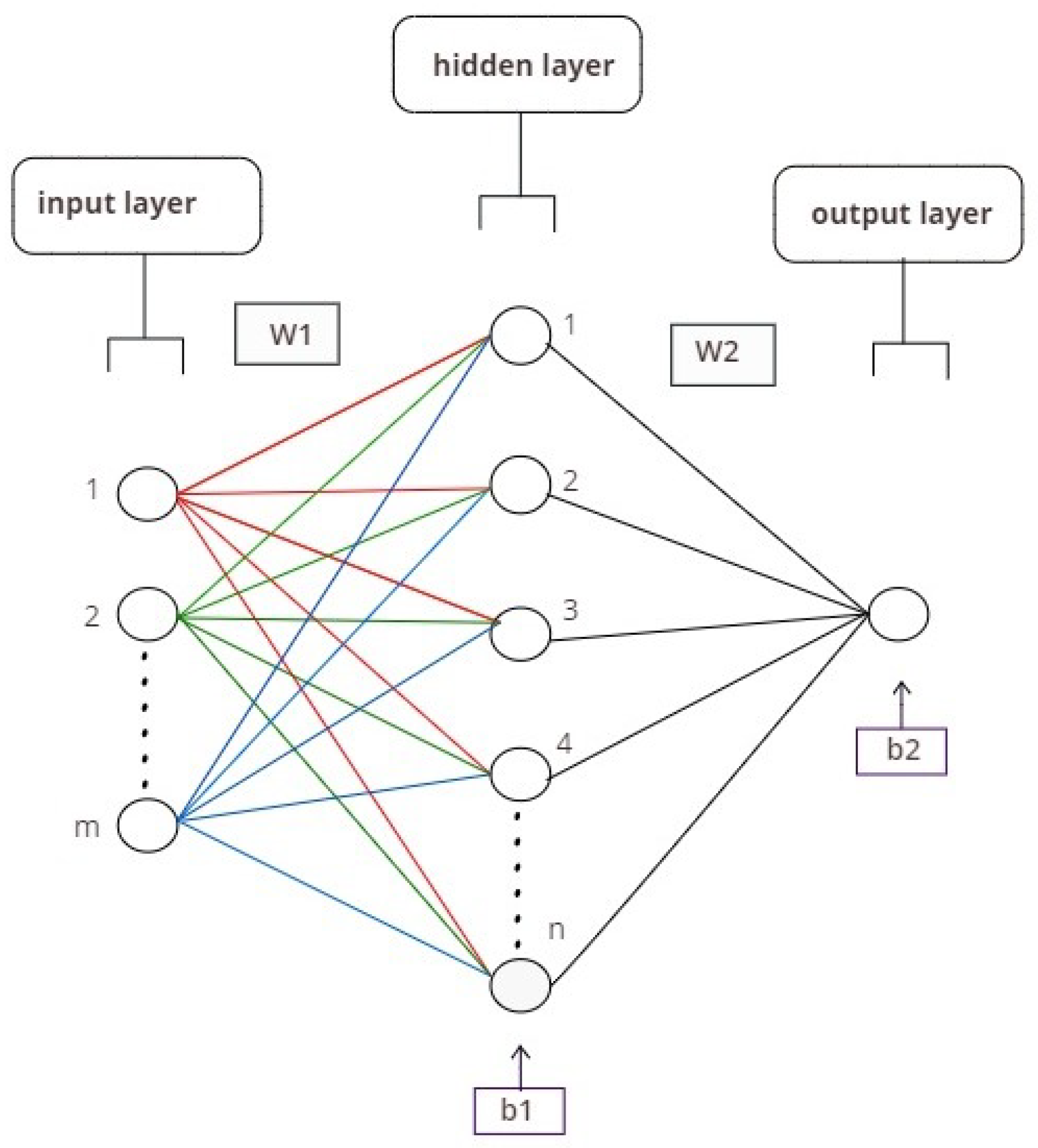
3.6. Neural Network for Predicting Power Loss
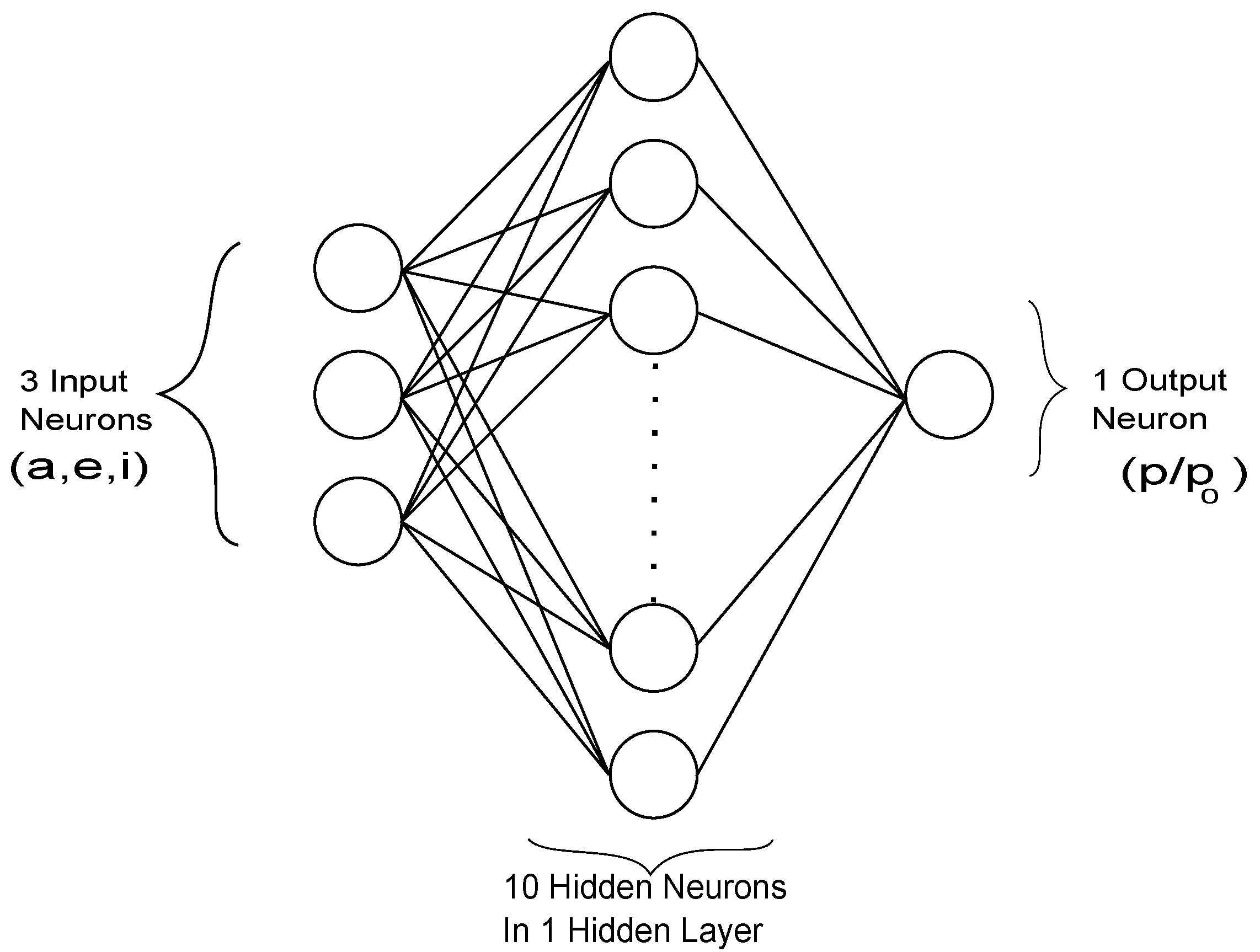
3.7. Neural Network Training of Radiation Data
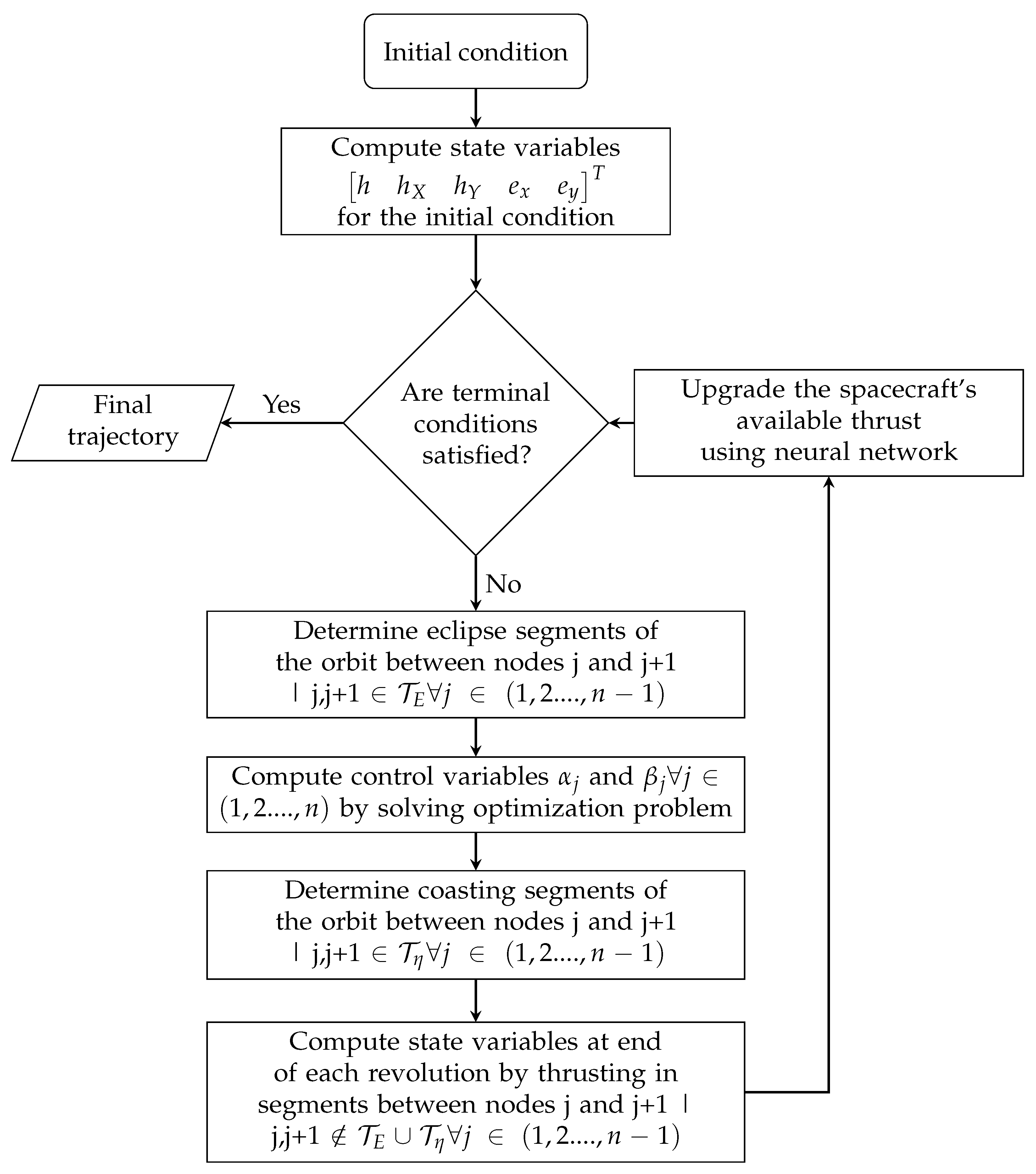
3.8. Optimization Tool Flow Chart
4. Numerical Results
4.1. Transfer from GT0 to GEO
4.2. Transfer from Sub-GT0 to GEO
4.3. Transfer from Super-GTO to GEO
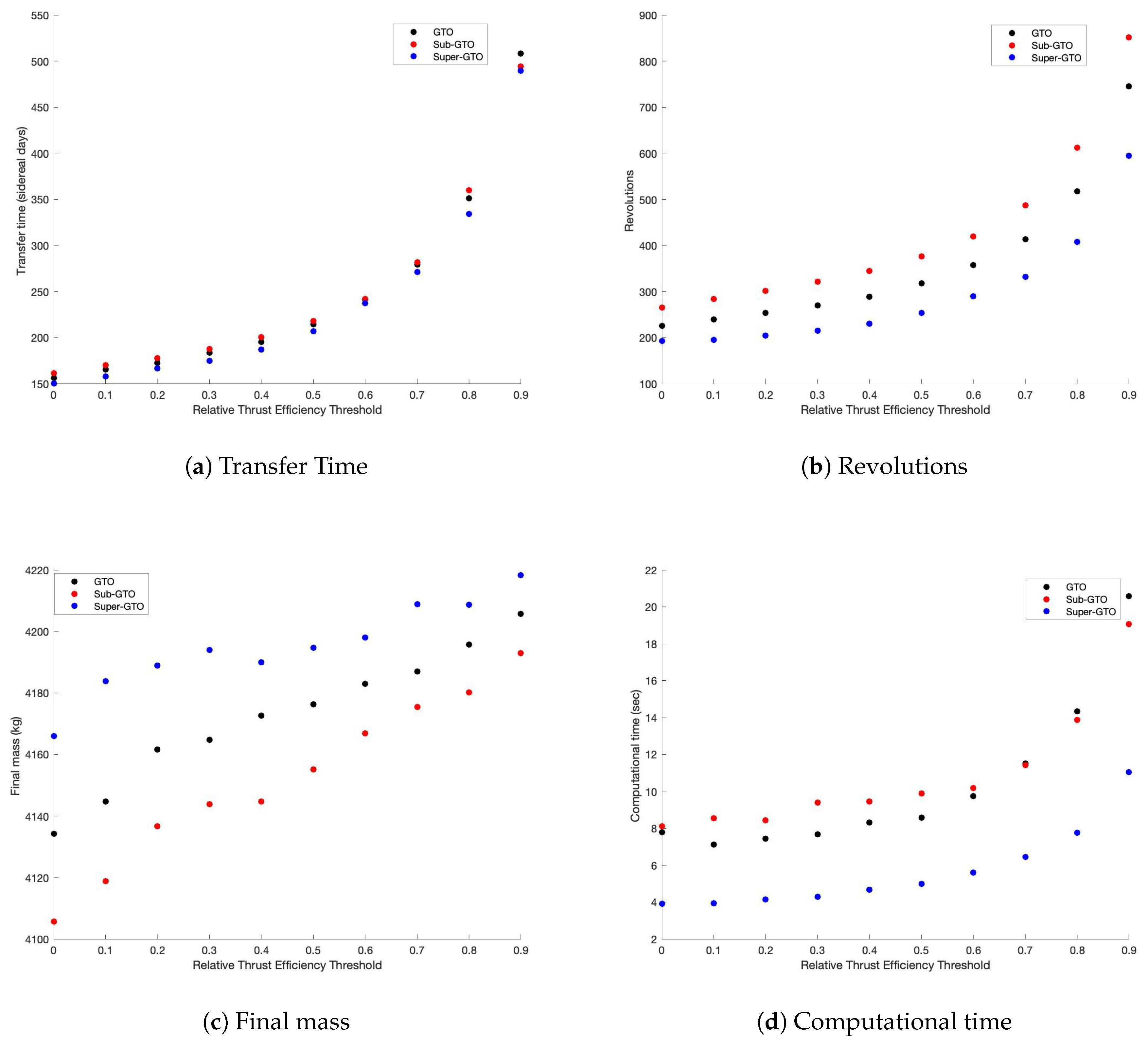
4.4. Variations with Respect to the Thrust Efficiency Threshold
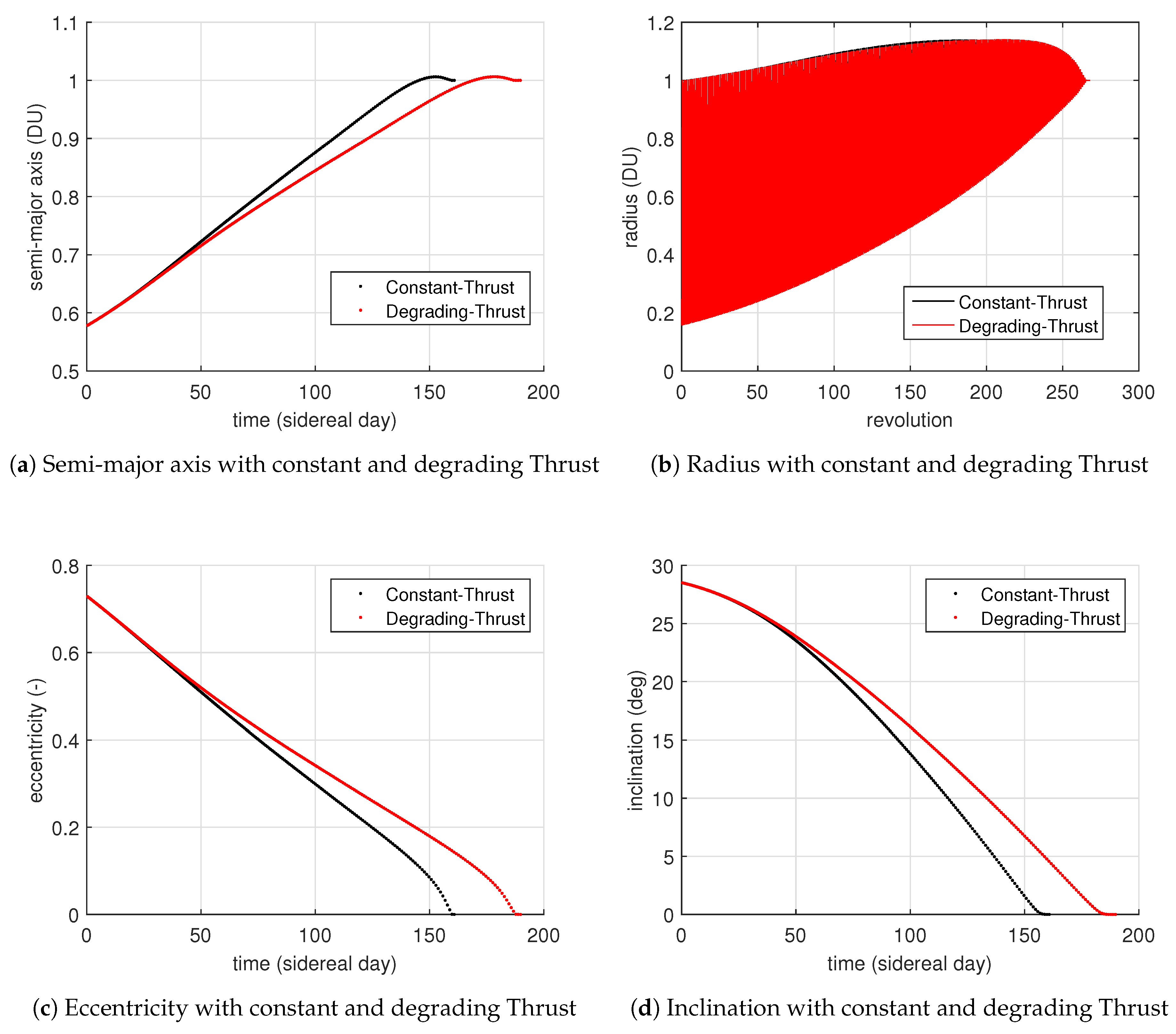
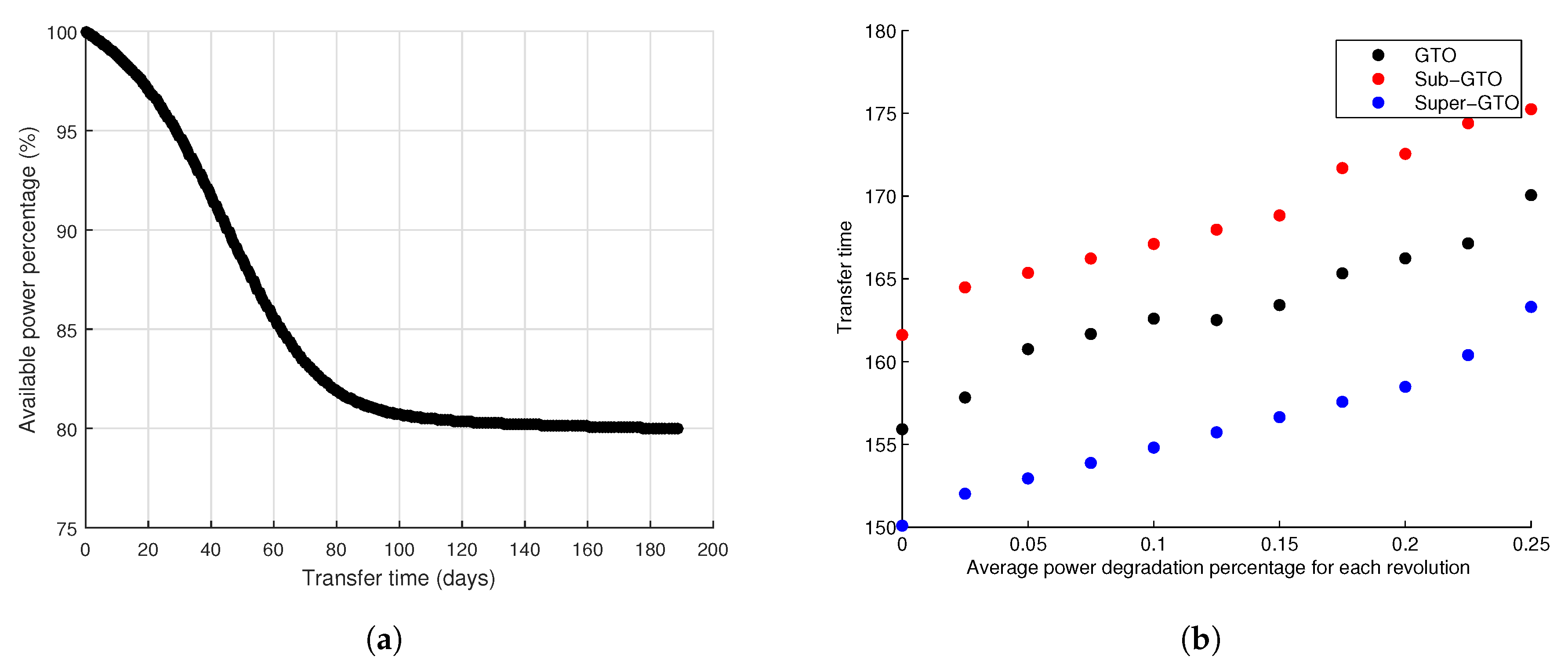
4.5. Power Degradation Due to Radiation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mazouffre, S. Electric propulsion for satellites and spacecraft: Established technologies and novel approaches. Plasma Sources Sci. Technol. 2016, 25, 033002. [Google Scholar] [CrossRef]
- Levchenko, I.; Bazaka, K.; Mazouffre, S.; Xu, S. Prospects and physical mechanisms for photonic space propulsion. Nat. Photonics 2018, 12, 649–657. [Google Scholar] [CrossRef]
- Van Loef, E.; Dorenbos, P.; Van Eijk, C.; Krämer, K.; Güdel, H.U. High-energy-resolution scintillator: Ce 3+ activated LaBr 3. Appl. Phys. Lett. 2001, 79, 1573–1575. [Google Scholar] [CrossRef]
- Levchenko, I.; Keidar, M.; Cantrell, J.; Wu, Y.L.; Kuninaka, H.; Bazaka, K.; Xu, S. Explore space using swarms of tiny satellites. Nature 2018, 562, 185–187. [Google Scholar] [CrossRef] [PubMed]
- Boeuf, J.P. Tutorial: Physics and modeling of Hall thrusters. J. Appl. Phys. 2017, 121, 011101. [Google Scholar] [CrossRef]
- Lemmer, K. Propulsion for cubesats. Acta Astronaut. 2017, 134, 231–243. [Google Scholar] [CrossRef]
- Lev, D.R.; Herscovitz, J.; Kariv, D.; Mizrachi, I. Heated gas propulsion system conceptual design for the Samson nano-satellite (propulsion). J. Small Satell. 2017, 6, 551–564. [Google Scholar]
- Feuerborn, S.A.; Perkins, J.; Neary, D.A. Finding a way: Boeing’s all electric propulsion satellite. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint PropulsionConference, San Jose, CA, USA, 14–17 July 2013. [Google Scholar]
- Sembély, X.; Wartelski, M.; Doubrère, P.; Deltour, B.; Cau, P.; Rochard, F. Design and Development of an Electric Propulsion Deployable Arm for Airbus Eurostar E3000 ComSat Platform. In Proceedings of the 35th International Electric Propulsion Conference Georgia Institute of Technology, Atlanta, GA, USA, 8–12 October 2017. [Google Scholar]
- Huifeng, X. Space Development with Chinese Characteristics and its Practical Significance. Aerosp. China 2019, 19, 39–45. [Google Scholar]
- Lawden, D. Optimal Trajectories for Space Navigation; Butterworths: London, UK, 1963. [Google Scholar]
- Marasch, M.W.; Hall, C.D. Application of Energy Storage to Solar Electric Propulsion Orbital Transfer. J. Spacecr. Rockets 2000, 37, 645–652. [Google Scholar] [CrossRef][Green Version]
- Ferrier, C.H.; Epenoy, R. Optimal Control for Engines with Electro-Ionic Propulsion under Constraint of Eclipse. Acta Astronaut. 2001, 48, 181–192. [Google Scholar] [CrossRef]
- Kluever, C.A. Geostationary Orbit Transfers Using Solar Electric Propulsion with Specific Impulse Modulation. J. Spacecr. Rockets 2004, 41, 461–466. [Google Scholar] [CrossRef]
- Kiforenko, B.N. Optimal low-thrust orbital transfers in a central gravity field. Int. Appl. Mech. 2005, 41, 1211–1238. [Google Scholar] [CrossRef]
- Russell, R. Primer Vector Theory Applied to Global Low-Thrust Trade Space Studies. J. Guid. Control Dyn. 2007, 30, 2. [Google Scholar] [CrossRef]
- Kluever, C.A.; Oleson, S.R. Direct approach for computing near-optimal low-thrust earth-orbit transfers. J. Spacecr. Rockets 1998, 35, 509–515. [Google Scholar] [CrossRef]
- Falck, R.; Dankanich, J. Optimization of Low-Thrust Spiral Trajectories by Collocation. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Guidance, Navigation, and Control and Co-located Conferences, Minneapolis, MI, USA, 13–16 August 2012. [Google Scholar]
- Dutta, A.; Libraro, P.; Kasdin, N.J.; Choueiri, E. A Direct Optimization Based Tool to Determine Orbit-Raising Trajectories to GEO for All-Electric Telecommunication Satellites. In Proceedings of the AAS Astrodynamics Specialist Conference, Minneapolis, MI, USA, 13–16 August 2012. [Google Scholar]
- Graham, K.F.; Rao, A.V. Minimum-Time Trajectory Optimization of Low-Thrust Earth-Orbit Transfers with Eclipsing. J. Spacecr. Rockets 2016, 53, 289–303. [Google Scholar] [CrossRef]
- Betts, J.T.; Campbell, S.L.; Thompson, K.C. Solving optimal control problems with control delays using direct transcription. Appl. Numer. Math. 2016, 108, 185–203. [Google Scholar] [CrossRef]
- Betts, J.T.; Campbell, S.L.; Digirolamo, C. Initial guess sensitivity in computational optimal control problems. Numer. Algebra Control Optim. 2020, 10, 31. [Google Scholar] [CrossRef]
- Edelbaum, T.N. Propulsion requirements for controllable satellites. ARS J. 1961, 31, 1079–1089. [Google Scholar] [CrossRef]
- Flandro, G.A. Asymptotic Solution for Solar Electric Low-Thrust Orbit Raising with Eclipse Penalty. In Proceedings of the AIAA Mechanics and Control of Flight Conference, Anaheim, CA, USA, 5–9 August 1974. [Google Scholar]
- Wiesel, W.; Alfano, S. Optimal Many-Revolution Orbit Transfer. J. Guid. Control Dyn. 1985, 8, 155–157. [Google Scholar] [CrossRef]
- Kechichian, J.A. Low-Thrust Eccentricity-Constrained Orbit Raising. J. Spacecr. Rockets 1998, 35, 327–335. [Google Scholar] [CrossRef]
- Kechichian, J.A. Orbit Raising with Low-Thrust Tangential Acceleration in Presence of Earth Shadow. J. Spacecr. Rockets 1998, 35, 516–525. [Google Scholar] [CrossRef]
- Kechichian, J.A. Low-Thrust Inclination Control in Presence of Earth Shadow. J. Spacecr. Rockets 1998, 35, 526–532. [Google Scholar] [CrossRef]
- Kluever, C. Simple Guidance Scheme for Low-Thrust Orbit Transfers. J. Guid. Control Dyn. 1998, 21, 1015–1017. [Google Scholar] [CrossRef]
- Petropoulos, A.E. Simple Control Laws for Low-thrust Orbit Transfers. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Big Sky Resort, Big Sky, MT, USA, 3–7 August 2003. [Google Scholar]
- Colasurdo, G.; Casalino, L. Optimal Low-Thrust Maneuvers in Presence of Earth Shadow. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Wall, B.; Conway, B. Shape-Based Approach to Low-Thrust Rendezvous Trajectory Design. J. Guid. Control Dyn. 2009, 32, 95–101. [Google Scholar] [CrossRef]
- Kluever, C. Using Edelbaum’s Method to Compute Low-Thrust Transfers with Earth-Shadow Eclipses. J. Guid. Control Dyn. 2011, 34, 300–303. [Google Scholar] [CrossRef]
- Taheri, E.; Abdelkhalik, O. Shape-Based Approximation of Constrained Low-Thrust Space Trajectories Using Fourier Series. J. Spacecr. Rockets 2012, 49, 535–545. [Google Scholar]
- Falck, R.D.; Sjauw, W.K.; Smith, D.A. Comparison of Low-Thrust Control Laws for Applications in Planetocentric Space. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. [Google Scholar]
- Betts, J.T. Optimal low–thrust orbit transfers with eclipsing. Opt. Control Appl. Methods 2015, 36, 218–240. [Google Scholar] [CrossRef]
- Kelchner, M.J.; Kluever, C.A. Rapid Evaluation of Low-Thrust Transfers from Elliptical Orbits to Geostationary Orbit. J. Spacecr. Rockets 2020. to appear, published online as Article in Advance. [Google Scholar] [CrossRef]
- Junkins, J.L.; Taheri, E. Exploration of Alternative State Vector Choices for Low-Thrust Trajectory Optimization. J. Guid. Control Dyn. 2019, 42, 47–64. [Google Scholar] [CrossRef]
- Sreesawet, S.; Dutta, A. Fast and Robust Computation of Low-Thrust Orbit-Raising Trajectories. AIAA J. Guid. Control Dyn. 2018, 41, 1888–1905. [Google Scholar] [CrossRef]
- Sreesawet, S.; Dutta, A. Receding Horizon Control for Spacecraft with Low-Thrust Propulsion. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018. [Google Scholar]
- Dutta, A.; Vijayan, S.; Olson, T. Deployment of High Power Class All-Electric Satellites in the Geosynchronous Equatorial Orbit. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference (AIAA SPACE Forum), Long Beach, CA, USA, 13–16 September 2016. [Google Scholar]
- Sreesawet, S.; Pappu, V.; Dutta, A.; Steck, J. Neural Networks Based Adaptive Controller for Attitude Control of All-Electric Satellites. In Advances in the Astronautical Sciences; Number AAS 15-754; Univelt: Vail, CO, USA, 2015. [Google Scholar]
- Chadalavada, P.S.; Dutta, A. Relative Equations of Motion using a New Set of Orbital Elements. Adv. Astronaut. Sci. 2018, 167, 565–581. [Google Scholar]
- Dutta, A.; Arora, L. Objective Function Weight Selection for Sequential Low-Thrust Orbit-Raising Optimization Problem. In Proceedings of the AIAA/AAS Space Flight Mechanics Meeting, Ka’anapali, Maui, HI, USA, 13–17 January 2019. [Google Scholar]
- Arora, L.; Dutta, A. Reinforcement Learning for Sequential Low-Thrust Orbit Raising Problem. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Petropoulos, A.E. Low-thrust Orbit Transfers Using Candidate Lyapunov Functions with a Mechanism for Coasting. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Providence, RI, USA, 16–19 August 2004. [Google Scholar]
- Dutta, A.; Libraro, P.; Kasdin, N.J.; Choueiri, E.; Francken, P. Minimum-fuel electric orbit-raising of telecommunication satellites subject to time and radiation damage constraints. In Proceedings of the 2014 American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 2942–2947. [Google Scholar]
- Kluever, C.A.; Messenger, S.R. Solar-Cell Degradation Model for Trajectory Optimization Methods. J. Spacecr. Rockets 2019, 56, 844–853. [Google Scholar] [CrossRef]
- Messenger, S.; Jackson, E.; Warner, J.; Walters, R. Scream: A new code for solar cell degradation prediction using the displacement damage dose approach. In Proceedings of the 35th IEEE Photovoltaic Specialists Conference, Honolulu, HI, USA, 20–25 June 2010; pp. 001106–001111. [Google Scholar]
- Dutta, A.; Kasdin, N.J.; Choueiri, E.; Francken, P. Minimizing proton displacement damage dose during electric orbit raising of satellites. J. Guid. Control Dyn. 2016, 39, 963–969. [Google Scholar] [CrossRef]
- Levchenko, I.; Bazaka, K.; Belmonte, T.; Keidar, M.; Xu, S. Advanced Materials for Next,-Generation Spacecraft. Adv. Mater. 2018, 30, 1802201. [Google Scholar] [CrossRef] [PubMed]
- Levchenko, I.; Xu, S.; Teel, G.; Mariotti, D.; Walker, M.; Keidar, M. Recent progress and perspectives of space electric propulsion systems based on smart nanomaterials. Nat. Commun. 2018, 9, 879. [Google Scholar] [CrossRef] [PubMed]
- Lozinski, A.R.; Horne, R.B.; Glauert, S.A.; Del Zanna, G.; Heynderickx, D.; Evans, H.D. Solar Cell Degradation Due to Proton Belt Enhancements During Electric Orbit Raising to GEO. Space Weather 2019, 17, 1059–1072. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]


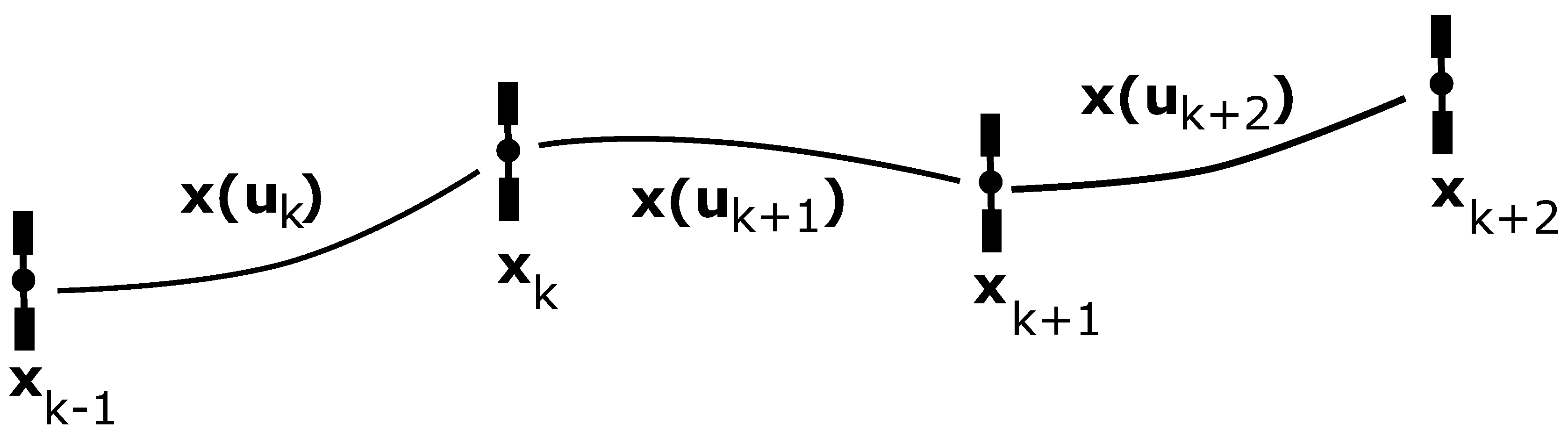
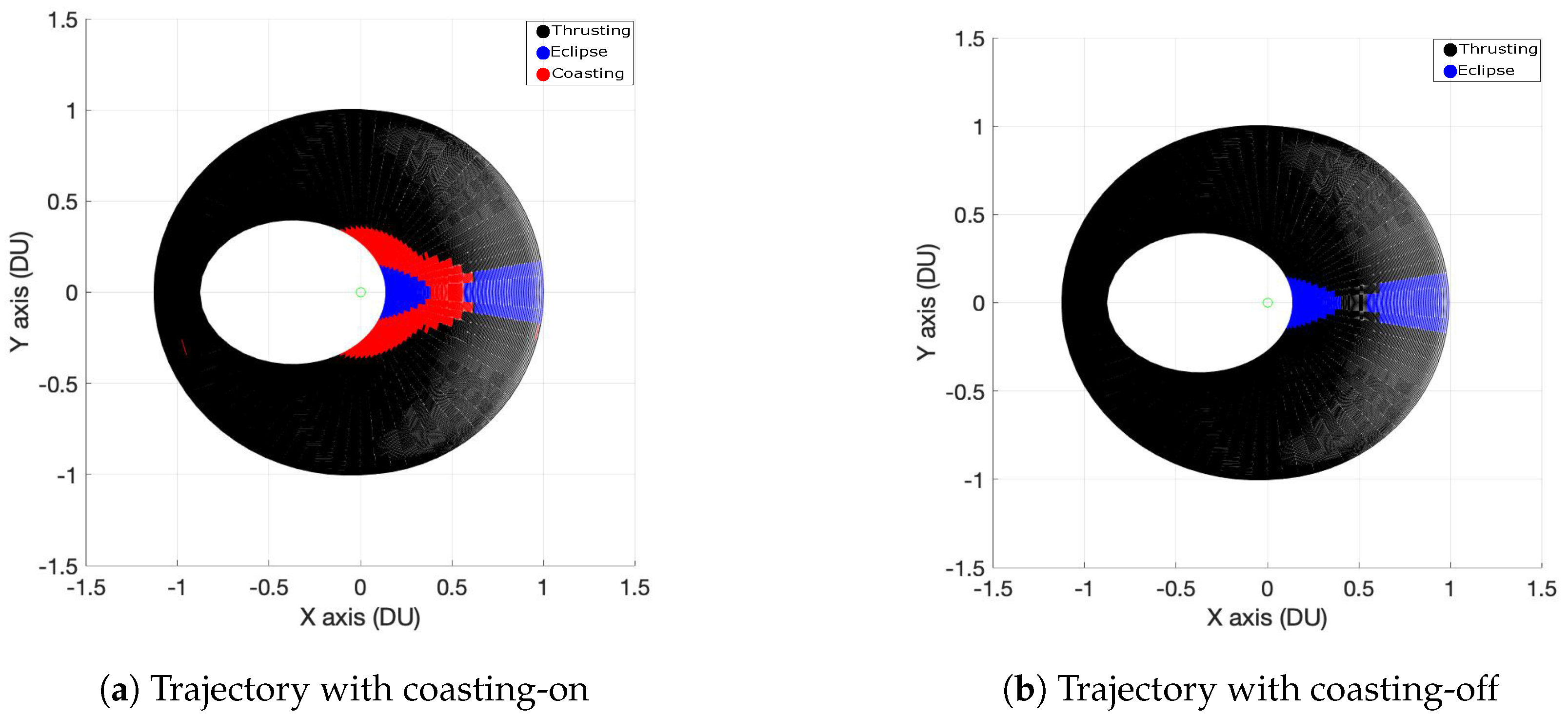
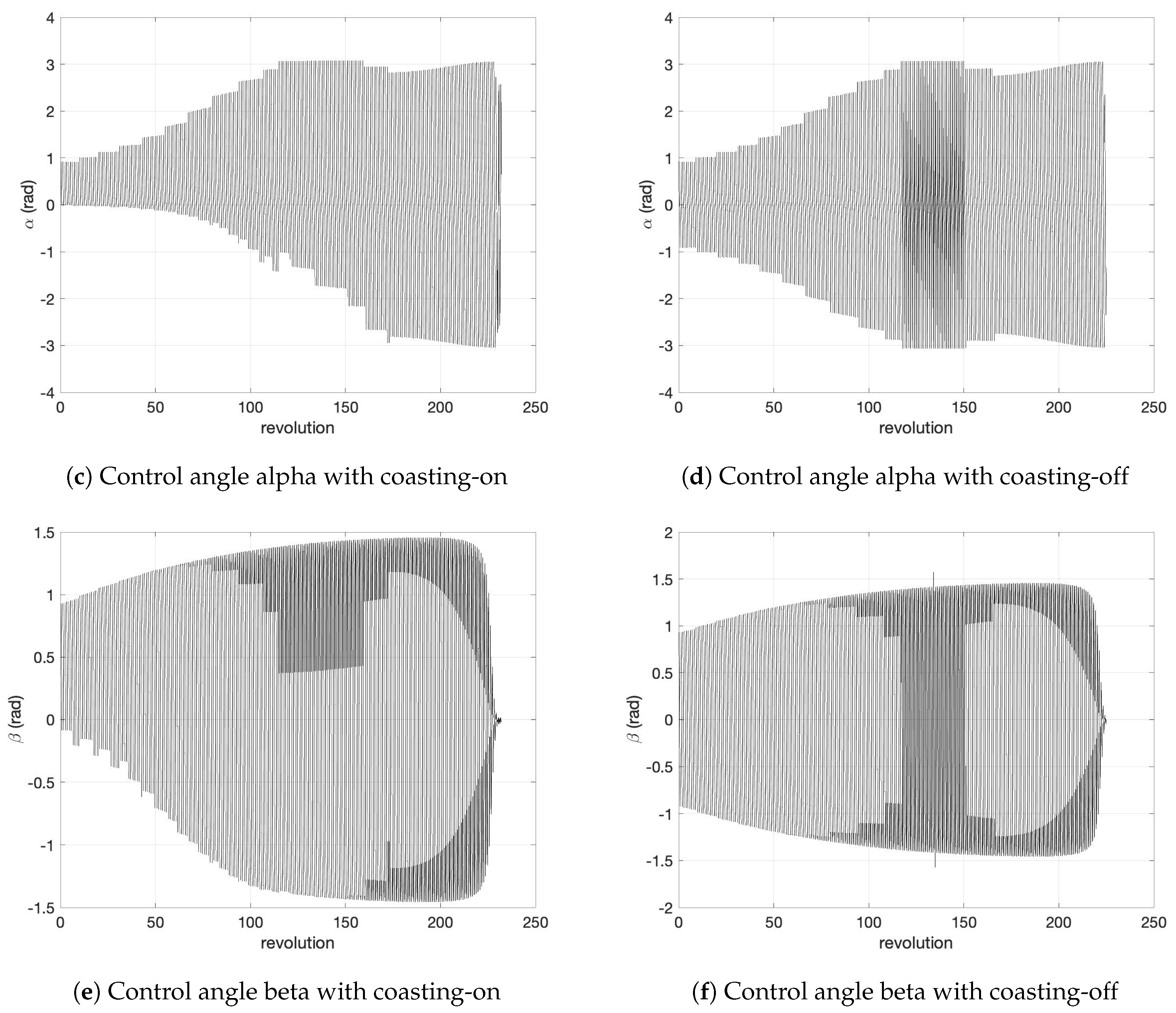
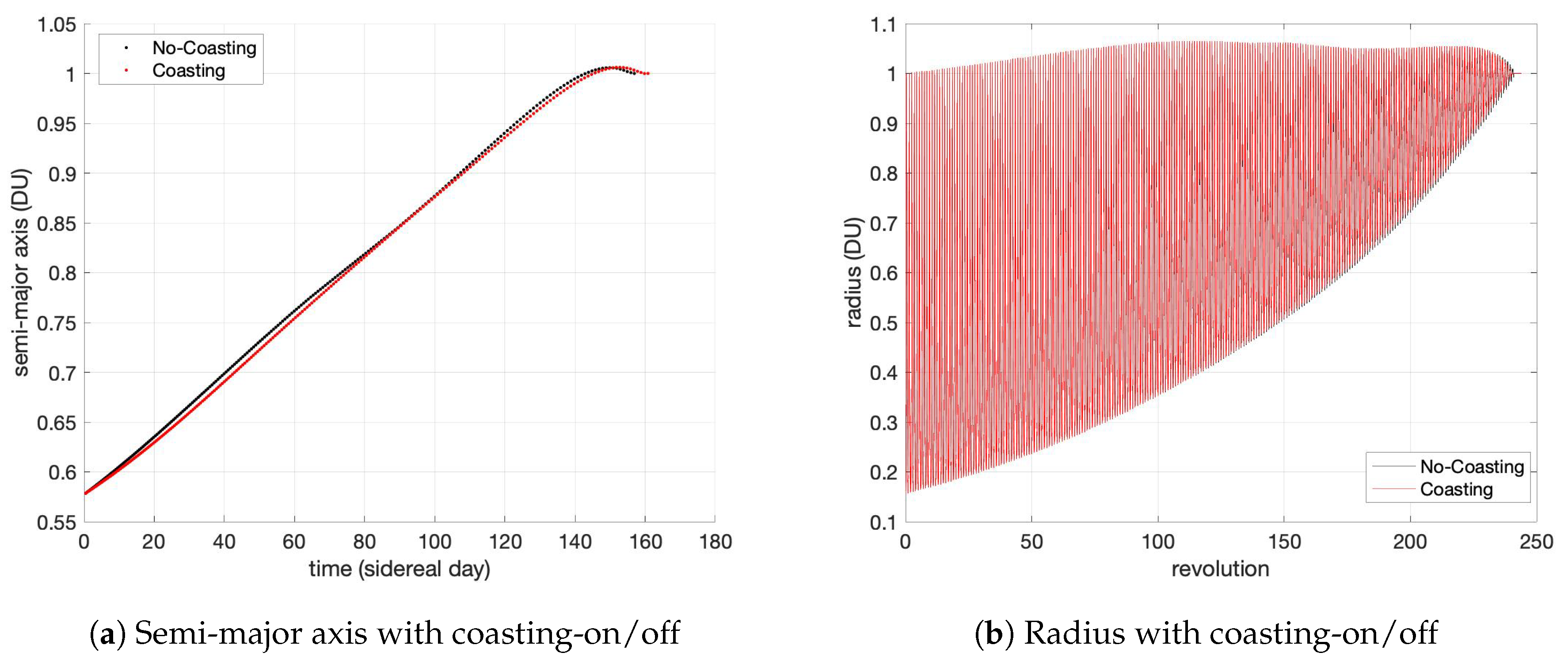
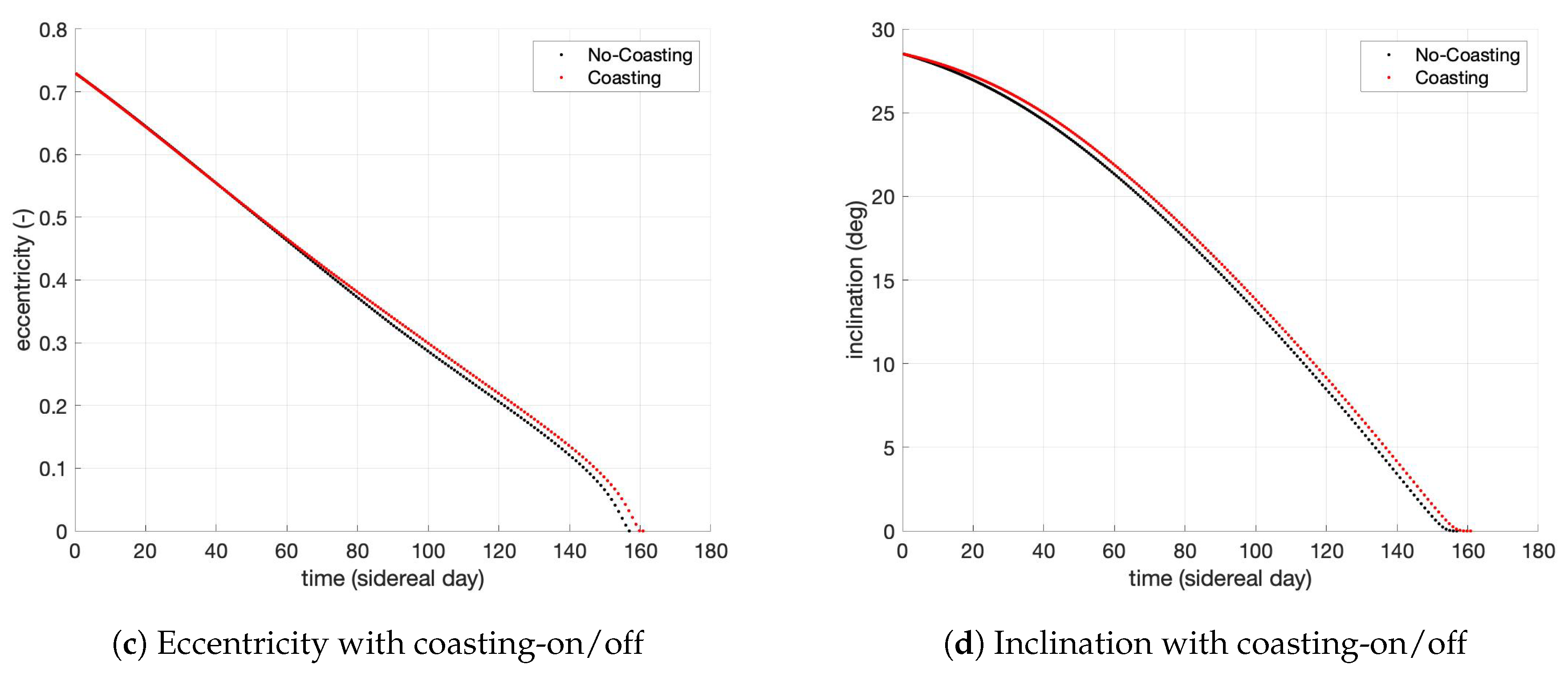

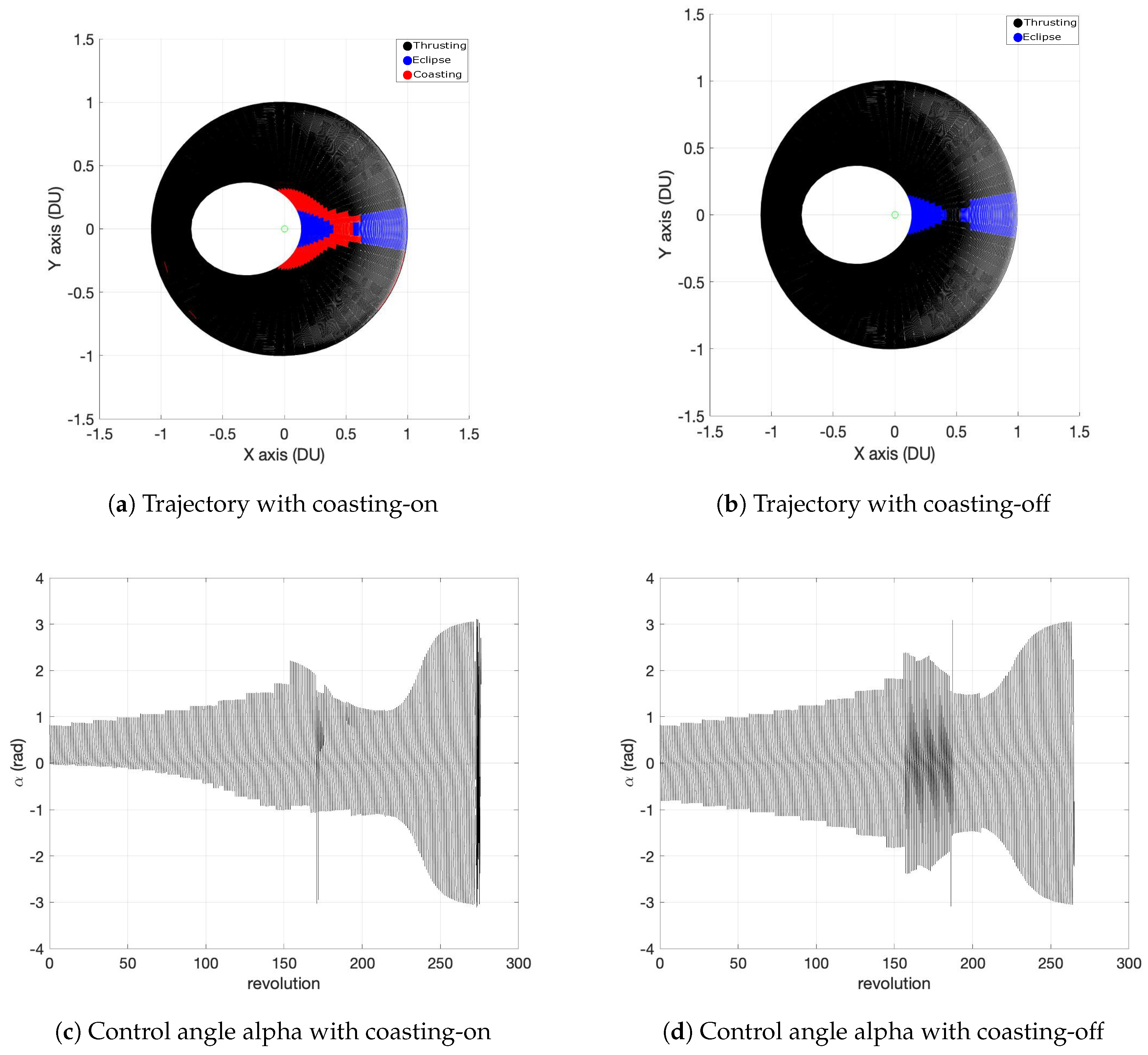

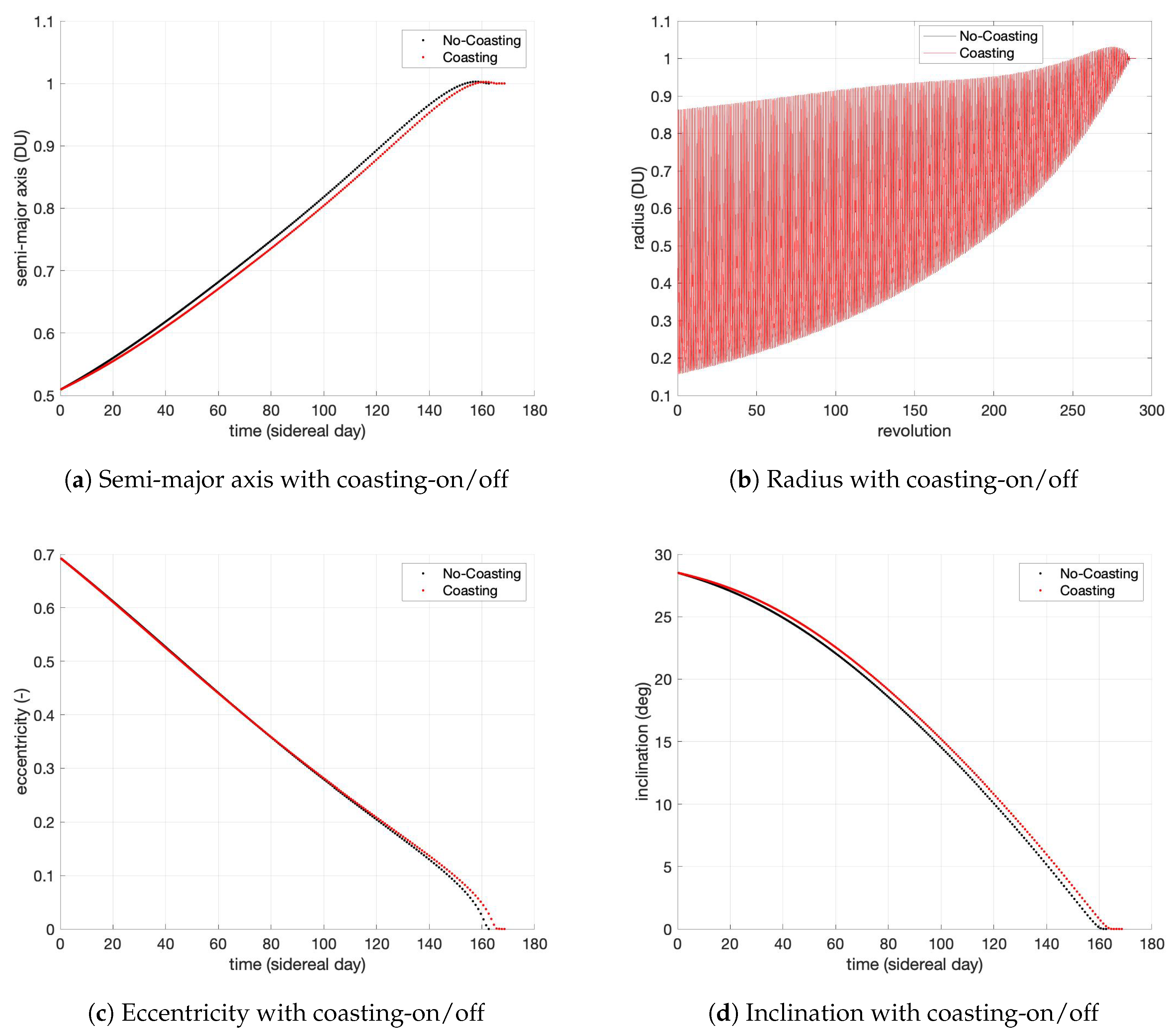
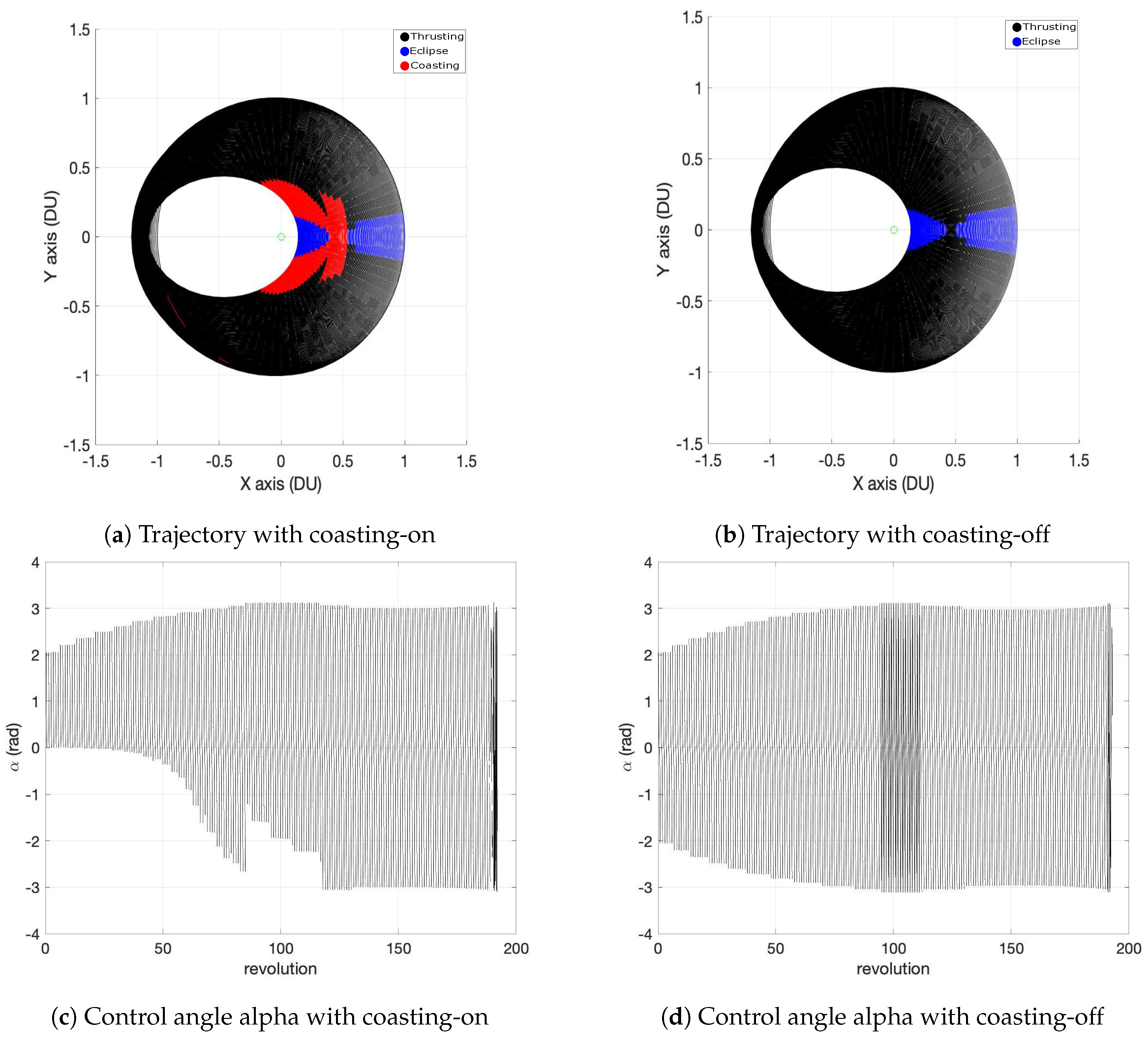
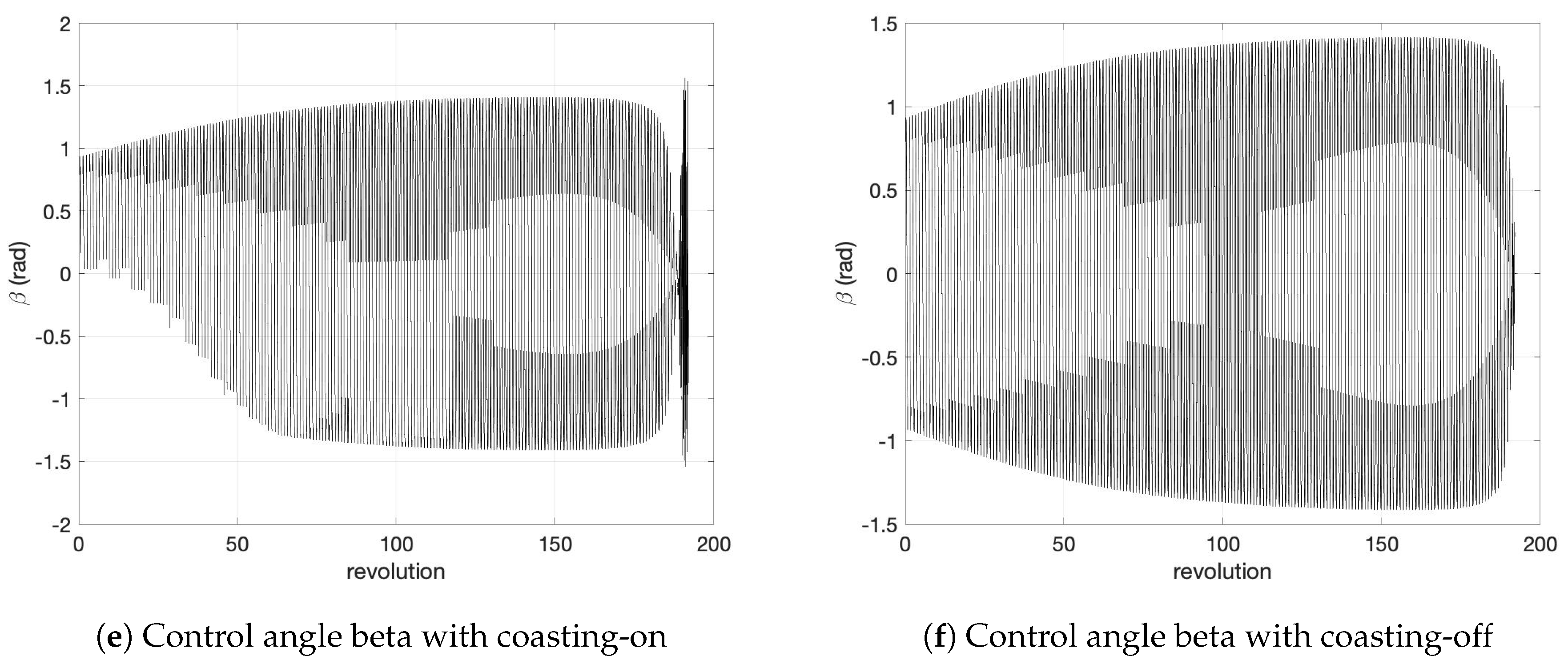
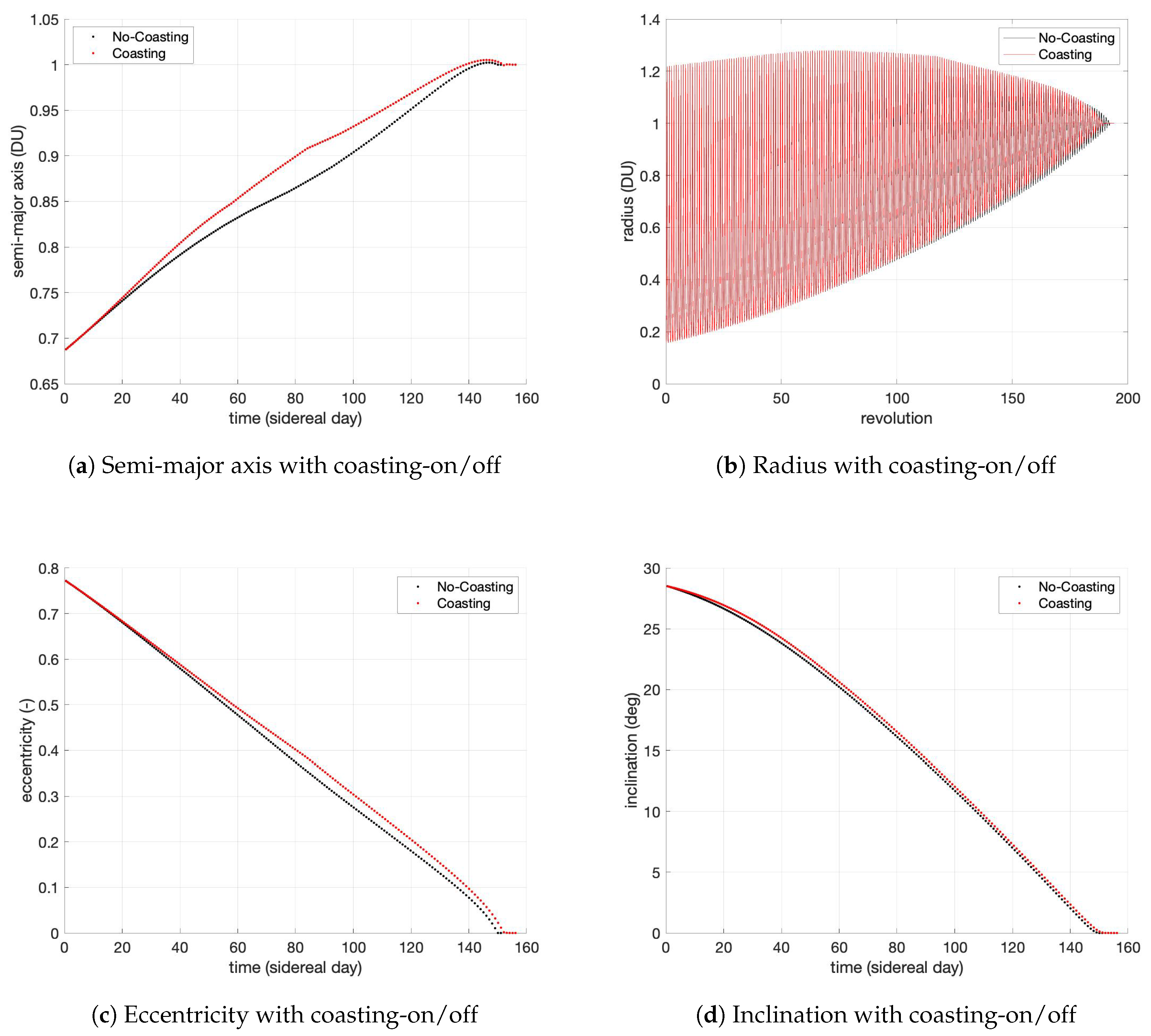
| Parameter | Coasting-ON | Coasting-OFF |
|---|---|---|
| Final Mass | 4140.35 kg | 4134.28 kg |
| Transfer Time | 160.81 days | 155.91 days |
| Revolutions | 232 | 225 |
| Computational Time | 7.87 s | 7.81 s |
| Parameter | Coasting-ON | Coasting-OFF |
|---|---|---|
| Final Mass | 4104.83 kg | 4105.74 kg |
| Transfer Time | 167.55 days | 161.60 days |
| Revolutions | 276 | 265 |
| Computational Time | 10.39 s | 9.30 s |
| Parameter | Coasting-ON | Coasting-OFF |
|---|---|---|
| Final Mass | 4175.53 kg | 4165.99 kg |
| Transfer Time | 154.15 days | 150.08 days |
| Revolutions | 192 | 193 |
| Computational Time | 5.6 s | 5.23 s |
| Parameter | Constant Thrust | Degrading Thrust |
|---|---|---|
| Final Mass | 4140.35 kg | 4131.91 kg |
| Transfer Time | 160.81 days | 188.72 days |
| Revolutions | 232 | 267 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chadalavada, P.; Farabi, T.; Dutta, A. Sequential Low-Thrust Orbit-Raising of All-Electric Satellites. Aerospace 2020, 7, 74. https://doi.org/10.3390/aerospace7060074
Chadalavada P, Farabi T, Dutta A. Sequential Low-Thrust Orbit-Raising of All-Electric Satellites. Aerospace. 2020; 7(6):74. https://doi.org/10.3390/aerospace7060074
Chicago/Turabian StyleChadalavada, Pardhasai, Tanzimul Farabi, and Atri Dutta. 2020. "Sequential Low-Thrust Orbit-Raising of All-Electric Satellites" Aerospace 7, no. 6: 74. https://doi.org/10.3390/aerospace7060074
APA StyleChadalavada, P., Farabi, T., & Dutta, A. (2020). Sequential Low-Thrust Orbit-Raising of All-Electric Satellites. Aerospace, 7(6), 74. https://doi.org/10.3390/aerospace7060074





