Abstract
Zero-dimensional models based on the description of the thermo-gas-dynamic process are widely used in the design of engines and their control and diagnostic systems. The models are subjected to an identification procedure to bring their outputs as close as possible to experimental data and assess engine health. This paper aims to improve the stability of engine model identification when the number of measured parameters is small, and their measurement error is not negligible. The proposed method for the estimation of engine components’ parameters, based on multi-criteria identification, provides stable estimations and their confidence intervals within known measurement errors. A priori information about the engine, its parameters and performance is used directly in the regularized identification procedure. The mathematical basis for this approach is the fuzzy sets theory. Synthesis of objective functions and subsequent scalar convolutions of these functions are used to estimate gas-path components’ parameters. A comparison with traditional methods showed that the main advantage of the proposed approach is the high stability of estimation in the parametric uncertainty conditions. Regularization reduces scattering, excludes incorrect solutions that do not correspond to a priori assumptions and also helps to implement the gas path analysis with a limited number of measured parameters. The method can be used for matching thermodynamic models to experimental data, gas path analysis and adapting dynamic models to the needs of the engine control system.
1. Introduction
Aircraft gas turbine engines are the most expensive and vital components of the aircraft. Their maintenance and operating costs depend on the engine performance, which is mainly determined by a condition of the engine gas path components such as the compressor, turbine, combustor, ducts, etc. For this reason, engine maintenance is usually supported by a prognostics and health management system (PHM), which usually implements a diagnostic procedure known as gas path analysis (GPA).
Nowadays, different approaches are used for processing flight and test-cell data to estimate component performance and detect faults [1]. These methods can be divided into two groups [2]:
- Model-based methods which use thermodynamic models to relate failures to measured parameters of the gas path [3]
- Artificial intelligence (AI) methods which belong to expert systems [4]
Model-based and hybrid systems [5] are effective only if a validated engine model is available.
The non-linear thermo-gas-dynamic models of turbine engines [6] and identification procedures have been applied in diagnostics for more than 40 years. Identification adjusts the model to make its output parameters as close as possible to the experimental data [7,8,9,10,11,12,13,14]. Besides the significant improvement in the gas path simulation, the estimated parameters contain information about the health of each component. Model identification involves the minimization of a functional which is a sum of squared deviations, calculated as differences of calculated and measured values. This is the Least Squares Method (LSM) which is usually implemented in non-linear GPA solvers using iterative Newton–Raphson algorithm.
Matching the engine model to experimental data is characterized by the presence of multiple parameters, which can be used for the model correction. These parameters can be strongly correlated. At the same time, a quantity of measured parameters is strongly limited. These reasons decrease the stability of the correction procedure, which is based on LSM, and forced researchers to look for methods to improve the stability. Hence, matching engine models needs regularization.
For more stable solutions, V. Borovick and Ye. Taran applied the least modulus method [15], which is more robust to outliers. S. Yepifanov implemented the Levenberg–Marquardt method [16] as well as Singular Value Decomposition and ε-structuration [17,18]. A. Volponi et al. applied the Kalman filter [19], and this approach is followed and developed in many papers [20,21,22,23,24], whose authors improved stability of the algorithm and its applicability to a non-linear engine model. X. Chang et al. applied an alternative method based on the non-linear filtration (sliding mode observer) [25,26,27].
Stability of identification procedures can be improved by regularization. This tool has been long known and used in statistical parameter estimation but was not common in system identification until recently [28]. T. Breikin et al. presented a regularization-based approach to the estimation of engine model coefficients [29]. It was based on the regularity of the frequency response pattern over the operation range of the engine, but that method is not universal. This paper is based on the Levenberg–Marquardt algorithm and Tikhonov regularization which were also used by S. Guseynov et al. [30,31]. These papers did not analyse the bias nor consider how the regularization coefficient influences the bias and the noise, which could impede practical applications.
It is well-known that regularization reduces the modification of the LSM functional by adding the regularizing component to it. This causes biased estimates of the model coefficients. B. Roth, D. Doel et al. demonstrated this clearly [32]. The biased estimates cause errors in GPA diagnosing solutions. The errors of the estimated parameters caused by the bias need to be monitored, but the traditional methods of regularization essentially prevent this. There is no universal recommendation on a choice of the weight coefficient for the added regularizing component.
This paper presents a new method for the regularized identification of gas-turbine models based on a priori information (Figure 1). First, the traditional Tikhonov regularisation is applied to simulated engine data to analyse the impact of regularization on a non-linear least squares solution and select the optimal value of the regularisation coefficient (Section 2.3). Next, membership function is used to implement a priori information into non-linear identification procedure, which is based on a generic algorithm (Section 2.4). Finally, the proposed method is tested with a turboshaft model and test-cell data and compared with traditional approaches.
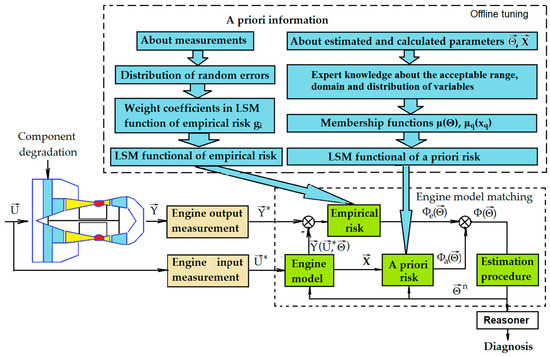
Figure 1.
Regularized multi-criteria identification of gas-turbine model.
The proposed approach is a significant modification of the standard model-based procedure for estimation of the performance parameters of engine components. The ability to implement prior knowledge in different forms to stabilize the solution is the main contribution of the paper. Regularized multi-criteria identification enables engine users to implement Non-Linear GPA [1,2] in ill-conditioned configurations with a limited number of measured parameters.
2. Materials and Methods
2.1. Basic Identification Procedure
The model calculates parameters of the engine gas path at steady-state modes depending on an operating point, external conditions and component performance . Hence, in the general case, it is presented as:
The linear model may be formulated as
which relates small deviations of the gas path parameters and parameters of components’ performances at a single operating point. H is an influence coefficient matrix (ICM). The linear model (2) is a component of the identification algorithm for the non-linear model.
Identification of the non-linear model (1) by measuring results and requires determining estimations , which are solutions of the following optimization task:
where is the Euclidean norm of the vector, Φ–least squares functional to be minimized.
The precision of estimation will improve if the amount of a priori information is higher than the number of unknown parameters. Therefore, the identification can be provided by a set of measurements that are done at N different operating points. For this purpose, the generalized vector of residuals is minimized:
Model (1) which is included in (4) is numerical. Therefore, the minimization of residuals (4) is a numerical iterative procedure, which in each iteration determines the solution as a sum of the previous solution and current correction:
and iterations continue until corrections become negligible.
The correction is determined as a solution of the overdetermined system of linear algebraic equations:
where
is a generalized matrix of influence coefficients, which is composed of elementary matrixes determined for each operating point. In accordance with Equation (6), for each iteration, such correction of required parameters is found, which minimizes residuals (4).
The known solution of the linear system (6) by the least squares method takes the form:
where –Fisher information matrix, G–weight diagonal matrix, whose elements are inverse to variations of measuring errors .
Unfortunately, the least squares method is sensitive to outliers in the right part of the system (6), which can be related to faults in experimental data. Therefore, practical applications of the classic LSM suffer from the instability of estimations and poor convergence of the identification algorithm as a whole. In some cases, the estimations are far from the expected values. The reasons for such results may be the lack of empirical information, an excessive number of estimated parameters or correlation between two or more state parameters. This causes ill-conditioning of the Fisher Matrix and excessive deviations of estimations. These estimations lose a physical sense (are out of range of possible components’ performances parameters variation—for example, efficiency is more than one) and can cause the model calculation program to crash.
Hence, the LSM identification procedure needs modification to provide its stability and physically adequate estimations.
2.2. Regularized Identification Procedure
In the known regularization procedure named for Tikhonov, the generalized functional is minimized, which besides the residuals of measured parameters includes a norm of the finding parameter vector with a weighting factor α. The identification task takes the following form:
where gi is the weight coefficient that describes measurement error (), yi is a component of vector and is a component of vector .
The regularized identification is based on the least squares method described above. As it is shown in Equation (9), the minimized functional is extended by elements which are related to parameters to be found. Thus, the main changes in the identification procedure are the generalized vector of residuals and generalized matrix of influence coefficients . The modified terms have the following structure:
where I is an identity matrix.
This identification procedure will deliver the non-regularized solution if the regularization coefficient is zero. Otherwise, the influence of coefficient α depends on the proportion between components: and of the generalized functional . Therefore, the effect of regularization is determined by the conditions of identification such as the number of measured parameters m, number of operating points N, measuring errors G and number of estimated parameters r.
2.3. Numerical Simulation
To assess the impact of the regularization coefficient α, the identification procedure was tested with the zero-dimensional thermodynamic model of a turboshaft engine [17] (Figure 2), based on experimental component maps. Performed numerical experiments involved calculation of N = 12 operating points for two scenarios:
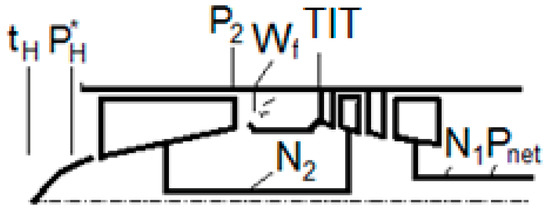
Figure 2.
Scheme and measured parameters of the engine.
- (1)
- Without measuring noise, for a wide range of α values;
- (2)
- With measuring noise, for selected α values.
Five gas path parameters were used for model identification:
- (1)
- Compressor discharge pressure p2;
- (2)
- Turbine inlet temperature TIT;
- (3)
- Power turbine discharge temperature;
- (4)
- Rotational speeds of rotors N2 and N1.
Initial deviations of two compressor performance parameters were assumed as follows:
- Deviation of mass flow rate: = ΔWC = −0.03;
- Deviation of compressor efficiency: = ΔηC = −0.04.
Four estimated parameters included:
- Deviation of flow rate: = ΔWC;
- Deviation of compressor efficiency: = ΔηC;
- Deviation of HPT mass flow: = ΔWHPT;
- Deviation of HPT efficiency: = ΔηHPT.
Figure 3 presents estimations and simulation results for different values of α, which varied in a range from 0 to 1. ΔYav is the average deviation between initial and estimated models:
and is the average deviation between measurements and estimated model:
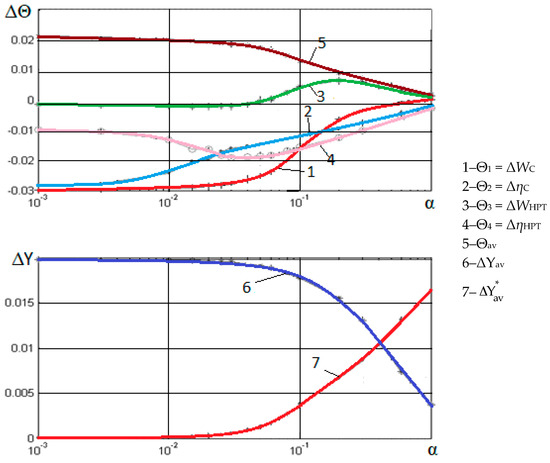
Figure 3.
Influence of the regularization coefficient on estimations when noise is absent.
Figure 3 shows that despite the initial growth of and absolute values, the average value decreases monotonically, whereas the residual between measurements and the corrected model increases. This corresponds to theoretical predictions of the influence of regularization on the identification process.
The simulation results help to choose the value of the regularization coefficient α. If the deviation of parameters is to be lower than 5 % and the deviation of parameters lower than 1%, then the value of α cannot exceed 0.03.
To obtain precise values of variance and to analyse the distributions of estimations , a sequence of data sets with random measuring errors with variance was generated and identified 1000 times. This provided the average precision of about 1% of initial residuals for parameters Y and about 0.5 % of simulated deviation 0.03 for the estimated parameters .
Figure 4 presents histograms for calculations with two estimated parameters at α = 0 and α = 0.04. Both non-regularized and regularized estimations have distributions close to normal ones. Total scatter of estimations is also similar, but centres of regularized estimations moved from their true values by 0.008 and 0.005, respectively.
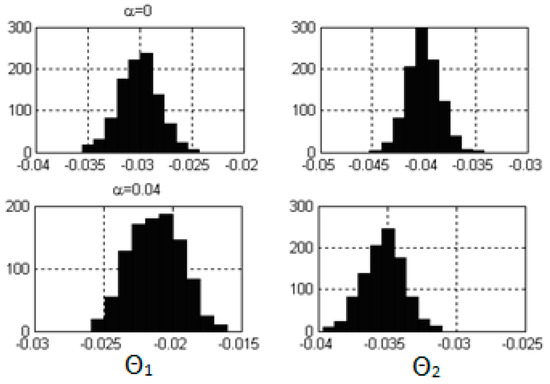
Figure 4.
Distributions of estimations when two parameters are estimated.
When four parameters were estimated (Figure 5), estimations and preserved their distributions while estimations and had significant differences. Such abnormal behaviour of parameters and is explained by their correlation.
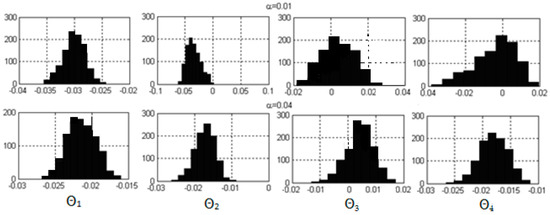
Figure 5.
Distributions of estimations when four parameters are estimated.
At low values of the regularization coefficient α, centres of distributions are close to their true values, but scatter is high, and distributions are strongly asymmetrical. When α increases, then mean values move, but scatter decreases, and its distribution approaches the normal one.
As shown above, the value of the regularization coefficient α has to be set appropriately to provide meaningful results of regularized least squares. This procedure is useful in ill-conditioned engine model fitting but needs preliminary adjustment and sensitivity analysis.
2.4. Regularized Identification Procedure Development Using a Priori Information
This paper demonstrates an idea to implement engine heuristics involving component parameters and performances to improve the precision and stability of model identification. The main difficulty is in the diversity of this information, which is presented in one of the following forms:
- Exact statement (for example, a part-load performance in a determined area is smooth);
- Statement in the form of limitations of the area of acceptable solutions (for example, the efficiency of the individual compressor cannot differ more than 3% from the efficiency of an “average” compressor, the performance of which is used in the initial model);
- Statement in the form of fuzzy information (for example, the gas temperature in the turbine will grow with the engine’s life);
- Statistical form (for example, probability density functions of parameters).
The next difficulty is in the formalization of parameters that characterize the model quality. These parameters are set on the basis of subjective preferences of decision makers (DM). The same difficulties appear in the ranking of partial criteria and limitations according to their significance for estimation of the model quality. The analysis showed that the main problem is that theoretical-probabilistic methods are difficult to apply in the presence of uncertainties, which are related to subjective preferences whose nature is not statistical. Actually, the choice of the model’s structure is the DM procedure, which in multi-criteria case is inevitably highly subjective. If the complexity of the task increases, the role of quality factors will grow. Therefore, it is possible to take into account all criteria using the proper mathematical tool.
We propose to use the fuzzy set theory [33] as this tool. This theory makes the uniform base to describe the information given in all the forms listed above, thus providing the correct mathematical definition of the identification task.
An example of applying fuzzy sets in the GPA and engine model matching is given by M. Zwingenberg et al. [34]. They used fuzzy logic for the evaluation of sensor failures. In contrast, we introduce a priori information about engine performance and experimental data directly into the stabilizing functional through the fuzzy logic approach.
Generalization of the functional (9) gives:
where is the least squares functional (3), which minimizes measurement error, so it is called the empirical risk functional and is the stabilizing functional, which is considered as the functional of a priori risk.
The determined a priori information is set as a limitation, which may take the form of an equality or inequality. The more general form of setting a priori information is its representation as a fuzzy set. The fuzzy set of parameter x is represented as a definition domain and a membership function in this domain. For the considered task, the parameters x may be the model parameters or the output (calculated) variables .
Next, we will use limited normal fuzzy sets with limited definition domain (xmin, xmax) and . We will express each a priori information as a particular functional of a priori risk and will determine the general functional of a priori risk as a linear composition of particular functionals:
where are weight coefficients.
Let us consider some types of a priori information and its expression in view of fuzzy sets:
Case 1. Limitations of some parameters are known. For example, it is known that 0 < η < 1 and 0 < σ < 1, etc. Using experience and calculation results, these limits can be significantly reduced; for example, 0.5 < η < 0.9 and 0.9 < σ < 0.99 (Figure 6).
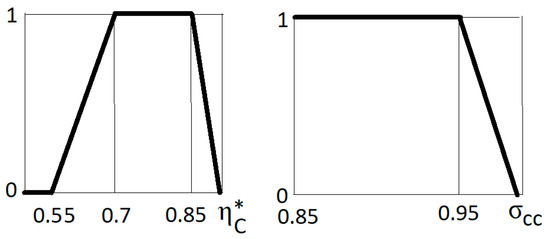
Figure 6.
Examples of membership functions.
Case 2. The a priori mathematical model is known. This can be the model with design maps of components or the model of the average engine, which is matched with previous testing results.
This information may be expressed as a relationship between μa or Φa and the difference between parameters that correspond to the matched and a priori models. These parameters may be the model parameters as measured (for example fuel flow) or non-measured calculated parameters (for example thrust). The membership function, in this case, can be of symmetrical triangular shape and the functional of a priori risk that characterizes the similarity between values of the parameter of matched and a priori models can be formed as
where xq is a calculated parameter of the engine; is the value calculated by the model to be matched; —the value calculated by the a priori model; are the parameters of the a priori model.
Case 3. Information about the confidence in different sets of experimental data obtained in different conditions with different precision.
Case 4. Confidence in the available maps of the engine components. For example, we know that the compressor map used in the model corresponds to the old version of the engine and is far from the actual map. Thus, we can express this knowledge in view of the confidence functions that are in this case the membership functions.
The empirical risk functional in Equation (3) may be considered as a square of Euclidian distance between two sets, one of which contains experimental data, and the other is composed of simulation results:
By analogy, the stabilizing functional can be formed as a second power of a distance from estimated parameter (or function x() that is determined using the estimated parameters).
The main problem in this analogy is that the fuzzy set that contains a priori information is infinite, so the sum in the above equation must be replaced with integral. For example, the second power of the distance from the engine map parameter θ = x to the fuzzy set with a given membership function μ(θ) equals:
In the iteration process of the task solution, each integral must be calculated numerically. This requires a lot of time and high computational capacity. A numerical solution can be found for certain types of the membership function. We considered the trapezoidal function, the particular cases of which are the rectangle, triangle and isosceles trapezium (Figure 7).

Figure 7.
Considered membership functions.
The functional derived for the trapezium:
The proposed modifications of the objective functional cause the non-linearity of the estimation problem, so traditional solution methods are not applicable. This problem is overcome by adapting genetic optimization algorithm to the specifics of the engine model matching [35]. Genetic algorithms are increasingly used in gas turbines to solve complex optimization problems [4,10,36,37].
3. Results
The designed methods were implemented using experimental data obtained during the test-cell testing of the helicopter turboshaft engine. Table 1 contains the values of measured parameters. The last row presents mean squared measurement errors σi, which were used to form the diagonal weight matrix G (Equation (8)).

Table 1.
Parameters acquired during bench testing.
The model parameters to be corrected:
πC*(c)—Scaling factor of CPR (Compressor Pressure Ratio);
πC*(a)—Factor of rotation in CPR-WCcor plane of the compressor pressure map;
πC*(b)—Factor of rotation in CPR-Ncor plane;
WHPT(c)—HPT flow coefficient;
WPT(c)—Power turbine flow coefficient;
ηC*(a)—Factor of rotation in the ηC*–WCcor plane of the compressor efficiency map;
ηC*(c)—Scaling factor of the compressor efficiency map;
ηCC—Scaling factor of combustion efficiency;
3.1. Least Squares Identification
The initial values of model parameters that correspond to the average engine (a priori information) are shown in Table 2.

Table 2.
Initial values of the model parameters.
In the first step of the iteration procedure, the following corrections to component maps were determined:
Such large corrections make it impossible to calculate part-load performance and influence coefficient matrices for the next iteration. Therefore, the calculation procedure was modified: Corrections to the component maps were limited. At corrections as high as 7%, the procedure slowly becomes convergent (by 7–9 iterations). The solution corresponds to small (less than 1%) corrections to the component maps.
The results of the standard least squares (the Newton–Raphson method) show that this method has low stability due to a weak conditionality of the engine model. Therefore, practical application requires improvement of the method’s stability.
3.2. Regularized Identification
The same experimental data were processed by the regularized method based on Equation (9). Parameter α was set at 0.01. Table 3 shows corrections for the first three iterations while Table 4 presents the parameters calculated by the corrected model.

Table 3.
Corrections for three first iterations.

Table 4.
Values of measured parameters determined by the corrected model.
Table 3 shows the high stability of the procedure: Estimations change slowly, without significant oscillations. The changes become smaller from iteration to iteration (this is a sign of stability). Comparison of Table 1 and Table 4 shows that parameters determined by the corrected model are well correlated with the measured parameters. Thus, the developed procedure of component performance estimation and the engine model matching can be implemented in practice.
3.3. Regularized Multi-Criteria Identification
Finally, the above task of multi-mode diagnostics was considered with a priori information about the model of the average engine, the parameters of which were estimated by previous testing data (Table 2). It is also known that a scatter of measured parameters of different engines at Pnet = const, N1 = const follows the normal distribution with the following mean squared error (Table 5).

Table 5.
Mean squared error of performance parameters in the engine population.
This information was then transformed into the functional Φa (Equation (13)), and taking into account that in this case, the functionals Φe and Φa are homogeneous as they contain residuals by parameters of the same names. This facilitated the setting of weight coefficients in Equation (14). They had to relate to a scatter of measurements and a scatter of the engine parameters by series. This provided the composition of the functionals:
In the considered example ≈ 8.
Table 6 shows the estimated parameters of the model in subsequent iterations. The final results of the corrected model are presented in Table 7. The comparison of Table 1, Table 4 and Table 7 confirms that the proposed procedure is stable. For the corrected model, deviations of output parameters from experimental data are within the measurement error. The introduction of a priori information results in a smaller deviation of results compared to the conventional regularization method.

Table 6.
Corrections for three first iterations.

Table 7.
Values of measured parameters determined by the corrected model.
Figure 8 presents the experimental data and modelling results for part-load performance. As the initial model is far enough from the field data, the diagnostic algorithm needs a preliminary adjustment to make the model closer to the average engine and to improve the precision of GPA. The visible lines correspond to the initial model before the correction, the average engine model and corrected model of the analyzed engine. The deviations of performance parameters from the reference indicate the engine’s health status.
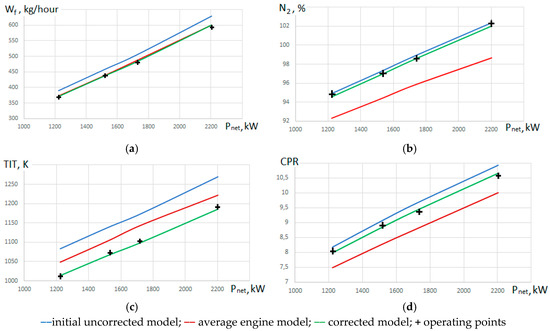
Figure 8.
Experimental data vs models. (a) fuel flow; (b) high pressure rotor rotation speed; (c) turbine inlet temperature; (d) compressor pressure ratio.
Figure 9 illustrates the correction of compressor maps and confirms that the procedure was effective even though the initial model was inaccurate.
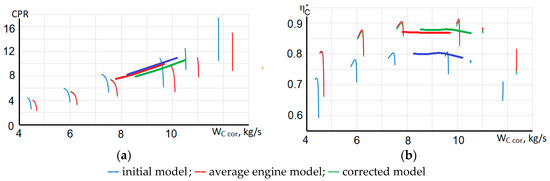
Figure 9.
Compressor maps with the operating lines.
4. Discussion
Matching turbine engine models to experimental data is an inverse problem of mathematical modelling which is often characterized by parametric uncertainty. This results from the fact that the number of measured parameters is significantly lower than the number of components’ performance parameters needed to describe the real engine. It was shown that in such conditions, even small measurement errors resulted in a high variation of results, hence the obtained efficiency, loss factors, etc., exceeded physically feasible ranges.
It was confirmed that extending the least squares functional by regularizing term improved stability of estimation but caused significant bias, which could lead to incorrect diagnoses. Stable operation of the algorithm and tolerant bias of the estimates in wide range of engine operation conditions are difficult to achieve as only selected values of the regularization coefficient α can ensure that. Finding its optimal solution is complicated because the regularizing term is not related to the physical properties of the object.
The new regularization procedure of multi-criteria identification, introduced in Section 2.4, uses a priori information about the engine, its measurement system, mathematical model and expected performance (Figure 1). This information is heterogeneous: Partially, it is presented in the form of statistic parameters and partially in the form of heuristic expert representations. Some other methods, e.g., Extended Kalman Filter can also use a priori information [22]. Undoubtedly, the quality of implemented expert knowledge should be carefully checked in advance.
The framework that supported the formalization of the regularization problem used fuzzy sets theory [33,37]. Similarly to the solution of Tanaka et al. [38], membership functions were introduced directly into the minimized functional, which contained a priori information about an acceptable range of estimated parameters. However, fuzzy logic is not used here for the non-linear mapping of parameters like in AI-based diagnostics [39]. In this work, inputs and outputs are measured variables with Gaussian noise.
The integral form of the stabilization functional was proposed which operates with continuous membership functions. To accelerate numerical calculations, the trapezoidal membership function was recommended. The analytical equation was derived for the stabilization functional with this function, which was used in place of numerical integration, thus decreasing the computing capacity required for the estimation procedure.
In the example presented in Section 3.3, available component maps were significantly different from the actual maps of the tested engine. Nevertheless, the estimation algorithm worked stable and provided a perfect matching of the model to the experimental data. Thanks to regularizing terms implemented in the estimation procedure, intermediate estimations did not exceed their limits when the computational algorithm was unstable.
Further studies and more field data are needed to quantify the accuracy and the stability of the procedure in relation to the number of estimated parameters. However, when a large number of engine parameters is measured, measurement uncertainty is low, and the number of coefficients of the model to be found is significantly less than the number of measured parameters, the estimates will not exceed the acceptable range, stability is not a problem, and the regularization does not have a positive effect and is not required. Hence, the proposed method is efficient when the number of measured parameters is small, and errors of measurement are significant. This is often the case in real applications.
5. Conclusions
A new method for the stable estimation of engine performance parameters is proposed. It uses a priori information about the engine and data acquisition system, i.e., the expected performance and acceptable variations of parameters. The method improves the accuracy of gas-turbine performance models in off-design conditions. A priori information is introduced in the model identification procedure in the form of membership functions, which are transformed into additional stabilization terms of the functional to be minimized.
The proposed approach was used to process test-cell data from a helicopter engine. The comparison with the conventional least squares and Tikhonov regularization proved the following:
- (1)
- LSM has low stability that can cause the engine simulation software to crash.
- (2)
- Conventional regularization improves the stability, but the intensive bias of the estimates needs to be excluded in advance.
- (3)
- A priori information has a physical sense, so it improves the stability and precision of the estimation. The introduced identification method is effective in ill-conditioned configurations and provides small bias of estimates.
Author Contributions
Conceptualization, O.K. and R.Z.; methodology, O.K.; software, R.Z.; validation, R.P. and S.Y.; formal analysis, S.Y. and R.Z.; investigation, O.K.; writing—original draft preparation, S.Y.; writing—review and editing, R.P.; visualization, S.Y., R.Z. and R.P. All authors have read and agreed to the published version of the manuscript.
Funding
This publication was prepared within the framework of the AERO-UA project, which has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 724034, and with the support of the Ministry of Education and Science of Ukraine (research project No. D203-3/2019-П).
Acknowledgments
The authors would like to acknowledge the constructive comments, and suggestions provided by the anonymous reviewers that greatly improved the quality of the article. We are also grateful to Michail Ugryumov and Anatolyi Mazurkov for their help in the application of the genetic optimization procedure and Kacper Grzędziński for his comments on an earlier version of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
The following abbreviations and symbols are used in this manuscript:
| AI | Artificial intelligence |
| av | Average value |
| C | Generalized matrix of influence coefficients compressor |
| CC | Combustion Chamber |
| CPR | Compressor Pressure Ratio |
| G | Weight diagonal matrix |
| GPA | Gas Path Analysis |
| H | Influence coefficient matrix |
| HPC | High Pressure Compressor |
| HPT | High Pressure Turbine |
| I | Identity matrix |
| ICM | Influence coefficient matrix |
| N | Number of operating points, rotational speed |
| LPT | Low Pressure Turbine |
| LSM | Least Squares Method |
| m | Number of measured parameters |
| OP | Operating Point |
| P | Pressure |
| Pnet | Net thrust |
| r | Number of estimated parameters |
| sim | Simulated value |
| TIT | Turbine Inlet Temperature |
| U | Parameters that determine the engine operating conditions |
| W | Mass flow rate of air/gas |
| Wf | Fuel flow |
| Y | Measured parameters |
| Z | Generalized vector of measured parameters |
| α | Regularization (weighting) factor |
| Δ | Parameter’s correction |
| δ | Relative deviation |
| η | Efficiency |
| σ2 | Variance |
| π | Pressure ratio |
| σ | Pressure loss coefficient |
| θ | Component’s map parameter |
| → | Vector |
| ^ | Estimated parameter |
| * | Measured value |
References
- Simon, D.L.; Borguet, S.; Léonard, O.; Zhang, X.F. Aircraft Engine Gas Path Diagnostic Methods: Public Benchmarking Results. In Proceedings of the ASME Turbo Expo 2013: Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; GT2013-95077. p. 13. [Google Scholar] [CrossRef]
- Fentaye, A.D.; Baheta, A.T.; Gilani, S.I.; Kyprianidis, K.G. A Review on Gas Turbine Gas-Path Diagnostics: State-of-the-Art Methods, Challenges and Opportunities. Aerospace 2019, 6, 83. [Google Scholar] [CrossRef]
- Stamatis, A.; Mathioudakis, K.; Papailiou, K.D. Adaptive Simulation of Gas Turbine Performance. J. Eng. Gas Turbines Power 1990, 112, 168–175. [Google Scholar] [CrossRef]
- Sampath, S.; Singh, R. An Integrated Fault Diagnostics Model Using Gen10etic Algorithm and Neural Networks. J. Eng. Gas Turbines Power 2008, 130, 49–56. [Google Scholar] [CrossRef]
- Lu, F.; Chunyu, J.; Huang, J.; Wang, J.; You, C. A Novel Data Hierarchical Fusion Method for Gas Turbine Engine Performance Fault Diagnosis. Energies 2016, 9, 828. [Google Scholar] [CrossRef]
- Bayona-Roa, C.; Solís-Chaves, J.; Bonilla, J.; Rodriguez-Melendez, A.; Castellanos, D. Computational Simulation of PT6A Gas Turbine Engine Operating with Different Blends of Biodiesel—A Transient-Response Analysis. Energies 2019, 12, 4258. [Google Scholar] [CrossRef]
- Lambiris, B.; Mathioudakis, K.; Stamatis, A.; Papailiou, K. Adaptive Modeling of Jet Engine Performance with Application to Condition Monitoring. J. Propuls. Power 1994, 10, 890–896. [Google Scholar] [CrossRef]
- Kong, C.; Ki, J.; Kang, M. A New Scaling Method for Component Maps of Gas Turbine Using System Identification. J. Eng. Gas Turbines Power 2003, 125, 979–985. [Google Scholar] [CrossRef]
- Li, Y.G.; Pilidis, P.; Newby, M.A. An Adaptation Approach for Gas Turbine Design-point Performance Simulation. J. Eng. Gas Turbines Power 2006, 128, 789–795. [Google Scholar] [CrossRef]
- Li, Y.G.; Ghafir, M.F.A.; Wang, L.; Singh, R.; Huang, K.; Feng, X. Nonlinear Multiple Points Gas Turbine Off-design Performance Adaptation Using a Genetic Algorithm. J. Eng. Gas Turbines Power 2011, 133, 071701. [Google Scholar] [CrossRef]
- Roth, B.A.; Doel, D.L.; Cissell, J.J. Probabilistic Matching of Turbofan Engine Performance Models to Test Data. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea and Air, Reno-Tahoe, NV, USA, 6–9 June 2005; GT2005-68201. pp. 541–548. [Google Scholar] [CrossRef]
- Tsoutsanis, E.; Li, Y.G.; Pilidis, P.; Newby, M. Non-linear Model Calibration for Off-design Performance Prediction of Gas Turbines with Experimental Data. Aeronaut. J. 2017. [Google Scholar] [CrossRef]
- Ramadhan, E.; Li, Y.-G.; Maherdianta, D. Application of Adaptive GPA to an Industrial Gas Turbine Using Field Data. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; GT2019-90686. p. 11. [Google Scholar] [CrossRef]
- Zaccaria, V.; Stenfelt, M.; Sjunnesson, A.; Hansson, A.; Kyprianidis, K.G. A Model-Based Solution for Gas Turbine Diagnostics: Simulations and Experimental Verification. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; GT2019-90858. p. 11. [Google Scholar] [CrossRef]
- Litvinov, Y.; Borovick, V. Performances and Maintenance Properties of Aircraft Turbine Engines; Mechanical Engineering Publishing: Moscow, Russia, 1979; p. 288. [Google Scholar]
- Yepifanov, S. Turbine Engine Parameters Optimum Estimation on Experimental Data. In Proceedings of the Scientific Conference Gas Turbine and Combined Power Plants, Moscow, Russia, 17–19 November 1983; p. 14. [Google Scholar]
- Yepifanov, S.; Kuznetsov, B.; Bogayenko, I. Synthesis of Turbine Engine Control and Diagnosing Systems; Technical Publishing: Kiev, Ukraine, 1998; p. 312. [Google Scholar]
- Vapnik, V. Dependences Reconstruction by Empirical Data; Science Publishing: Moscow, Russia, 1979; p. 447. [Google Scholar]
- Volponi, A.J.; DePold, H.; Ganguli, R.; Daguang, C. The Use of Kalman Filter and Neural Network Methodologies in Gas Turbine Performance Diagnostics: A Comparative Study. J. Eng. Gas Turbines Power 2003, 125, 917–924. [Google Scholar] [CrossRef]
- Simon, D. A Comparison of Filtering Approaches for Aircraft Engine Health Estimation. Aerosp. Sci. Technol. 2008, 12, 276–284. [Google Scholar] [CrossRef]
- Bourguet, S.; Leonard, O. Comparison of Adaptive Filters for Gas Turbine Performance Monitoring. J. Comput. Appl. Math. 2010, 204, 2202–2212. [Google Scholar] [CrossRef]
- Lu, F.; Ju, H.; Huang, J. An Improved Extended Kalman Filter with Inequality Constraints for Gas Turbine Engine Health Monitoring. Aerosp. Sci. Technol. 2016, 58, 36–47. [Google Scholar] [CrossRef]
- Pourbabaee, B.; Meskin, N.; Khorasani, K. Sensor Fault Detection, Isolation, and Identification Using Multiple-model-based Hybrid Kalman Filter for Gas Turbine Engines. IEEE Trans. Control Syst. Technol. 2016, 24, 1184–1200. [Google Scholar] [CrossRef]
- Yang, Q.; Li, S.; Cao, Y.; Gu, F.; Smith, A. A Gas Path Fault Contribution Matrix for Marine Gas Turbine Diagnosis Based on a Multiple Model Fault Detection and Isolation Approach. Energies 2018, 11, 3316. [Google Scholar] [CrossRef]
- Chang, X.; Huang, J.; Lu, F.; Sun, H. Gas-path Health Estimation for an Aircraft Engine Based on a Sliding mode observer. Energies 2016, 9, 15. [Google Scholar] [CrossRef]
- Chang, X.; Huang, J.; Lu, F. Robust In-flight Sensor Fault Diagnostics for Aircraft Engine Based on Sliding Mode Oobservers. Sensors 2017, 17, 835. [Google Scholar] [CrossRef]
- Chang, X.; Huang, J.; Lu, F. Health Parameter Estimation with Second-order Sliding Mode Observer for a Turbofan Engine. Energies 2017, 10, 1040. [Google Scholar] [CrossRef]
- Ljung, L.; Singh, R.; Chen, T. Regularization Features in the System Identification Toolbox. IFAC-PapersOnLine 2015, 48, 745–750. [Google Scholar] [CrossRef]
- Breikin, T.V.; Arkov, V.Y.; Kulikov, G.G. Regularization Approach for Real-time Modelling of Aero Gas Turbines. Control Eng. Pract. 2004, 12, 401–407. [Google Scholar] [CrossRef]
- Guseynov, S.E.; Aleksejeva, J.V.; Andreyev, S.A. On one Regularizing Algorithm for Comprehensive Diagnosing of Apparatus, Engines and Machinery. Adv. Mater. Res. 2015, 1117, 254–257. [Google Scholar] [CrossRef]
- Guseynov, S.E.; Yunusov, S.M. New Regularizing Approach to Determining the Influence Coefficient Matrix for Gas-turbine Engines. Discret. Contin. Dyn. Syst. Ser. A 2011, 614–623. [Google Scholar] [CrossRef]
- Roth, B.; Doel, D.L.; Mavris, D.; Beeson, D. High-Accuracy Matching of Engine Performance Models to Test Data. In Proceedings of the ASME Turbo Expo 2003: Power for Land, Sea and Air, Atlanta, GA, USA, 16–19 June 2003; GT2003-38784. p. 9. [Google Scholar] [CrossRef]
- Zadeh, L.A. The Linguistic Approach and its Application to Decision Analysis. In Advances in Fuzzy Systems—Applications and Theory, Fuzzy Sets, Fuzzy Logic, and Fuzzy Systems; Directions in large-scale systems; World Scientific: Singapore, 1996; pp. 260–282. [Google Scholar] [CrossRef]
- Zwingenberg, M.; Benra, F.-K.; Werner, K.; Dobrzynski, B. Generation of Turbine Maps Using a Fusion of Validated Operational Data and Streamline Curvature Method. In Proceedings of the ASME Turbo Expo 2010: Power for Land, Sea, and Air, Volume 7: Turbomachinery, Parts A, B, and C, Glasgow, UK, 14–18 June 2010; pp. 2757–2768. [Google Scholar] [CrossRef]
- Meniailov, I.; Khustochka, O.; Ugryumova, K.; Chernysh, S.; Yepifanov, S.; Ugryumov, M. Mathematical Models and Methods of Effective Estimation in Multi-objective Optimization Problems Under Uncertainties. In Advances in Structural and Multidisciplinary Optimization; Springer: Cham, Switzerland, 2018; pp. 411–427. [Google Scholar] [CrossRef]
- Zhang, Y.; Martínez-García, M.; Kalawsky, R.S.; Latimer, A. Grey-box modelling of the swirl characteristics in gas turbine combustion system. Measurement 2020, 151, 107266. [Google Scholar] [CrossRef]
- Zhang, Y.; Martinez-Garcia, M.; Serrano-Cruz, J.R.; Latimer, A. Multi-region System Modelling by using Genetic Programming to Extract Rule Consequent Functions in a TSK Fuzzy System. In Proceedings of the 4th IEEE International Conference on Advanced Robotics and Mechatronics, ICARM 2019, Toyonaka, Japan, 3–5 July 2019; pp. 987–992. [Google Scholar] [CrossRef]
- Tanaka, H.; Uejima, S.; Asai, K. Linear Regression Analysis with Fuzzy Model. IEEE Trans. Syst. Man Cybern. 1982, 12, 903–907. [Google Scholar] [CrossRef]
- Cao, Y.; Hu, P.; Yang, Q.; He, Y.; Li, S.; Yu, F.; Du, J. Fuzzy Analytic Hierarchy Process Evaluation Method of Gas Turbine Based on Health Degree. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition. Volume 6: Ceramics; Controls, Diagnostics, and Instrumentation; Education; Manufacturing Materials and Metallurgy, Oslo, Norway, 11–15 June 2018. V006T05A012. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).