Accurate 2-D Modelling of Transonic Compressor Cascade Aerodynamics
Abstract
1. Introduction
2. Numerical Model and Validation
2.1. Cascade Performance Parameters
2.2. Computational Domain and Mesh
2.3. Test Cases Data
2.4. Boundary Conditions, Operating Conditions and Solver Setup
2.5. Specification of the Inlet Flow Conditions
2.6. Calculation of the Exit Variables
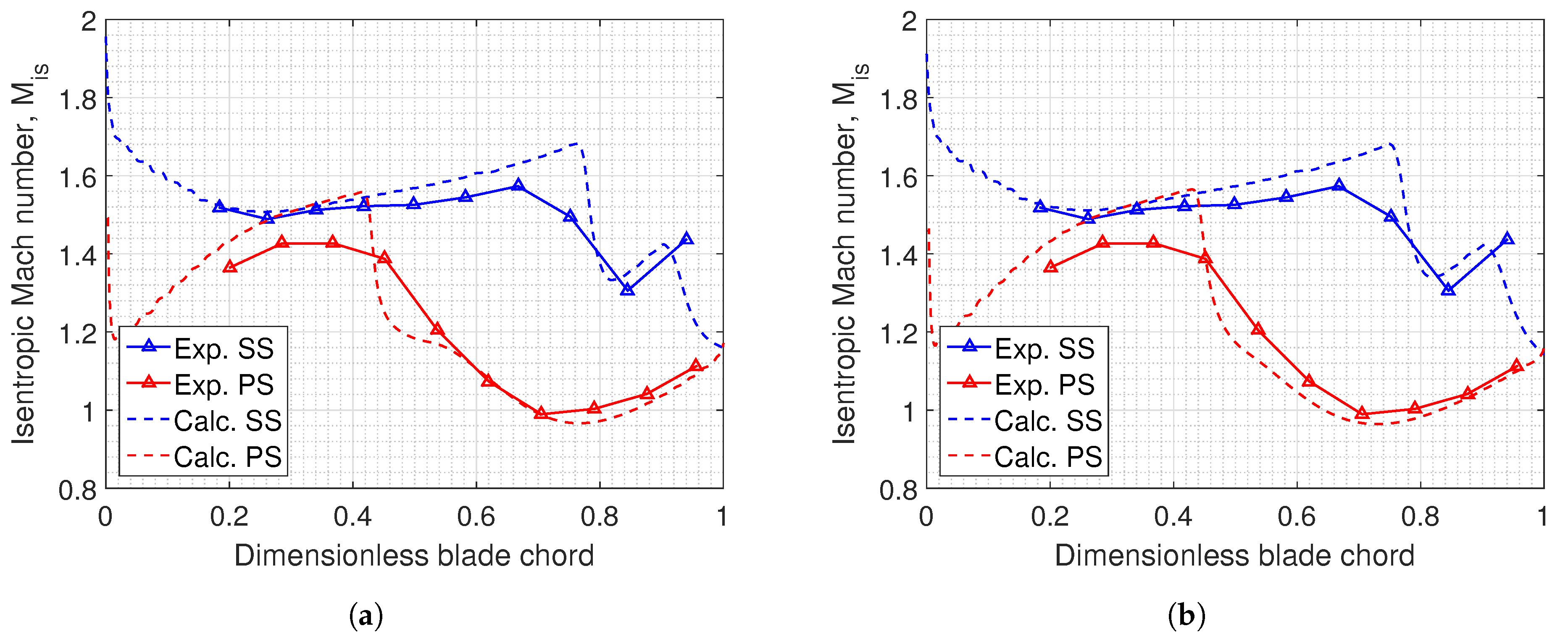
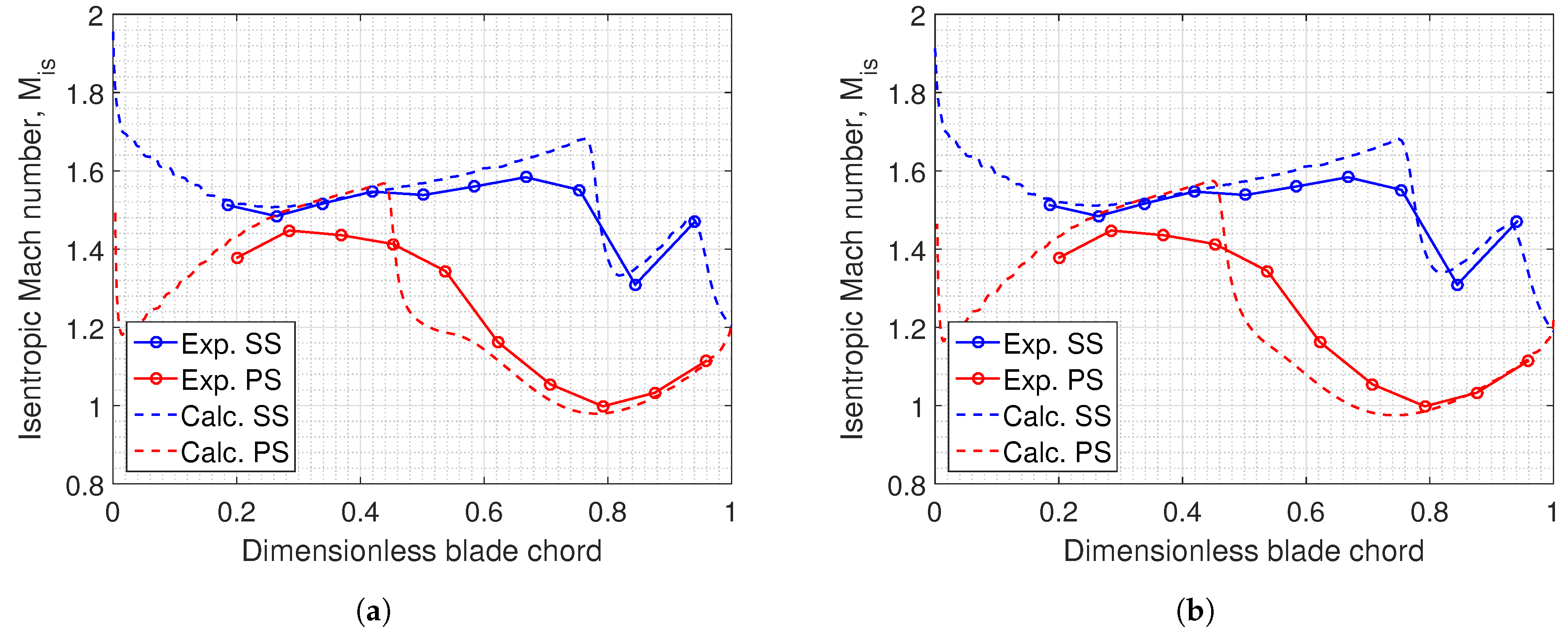
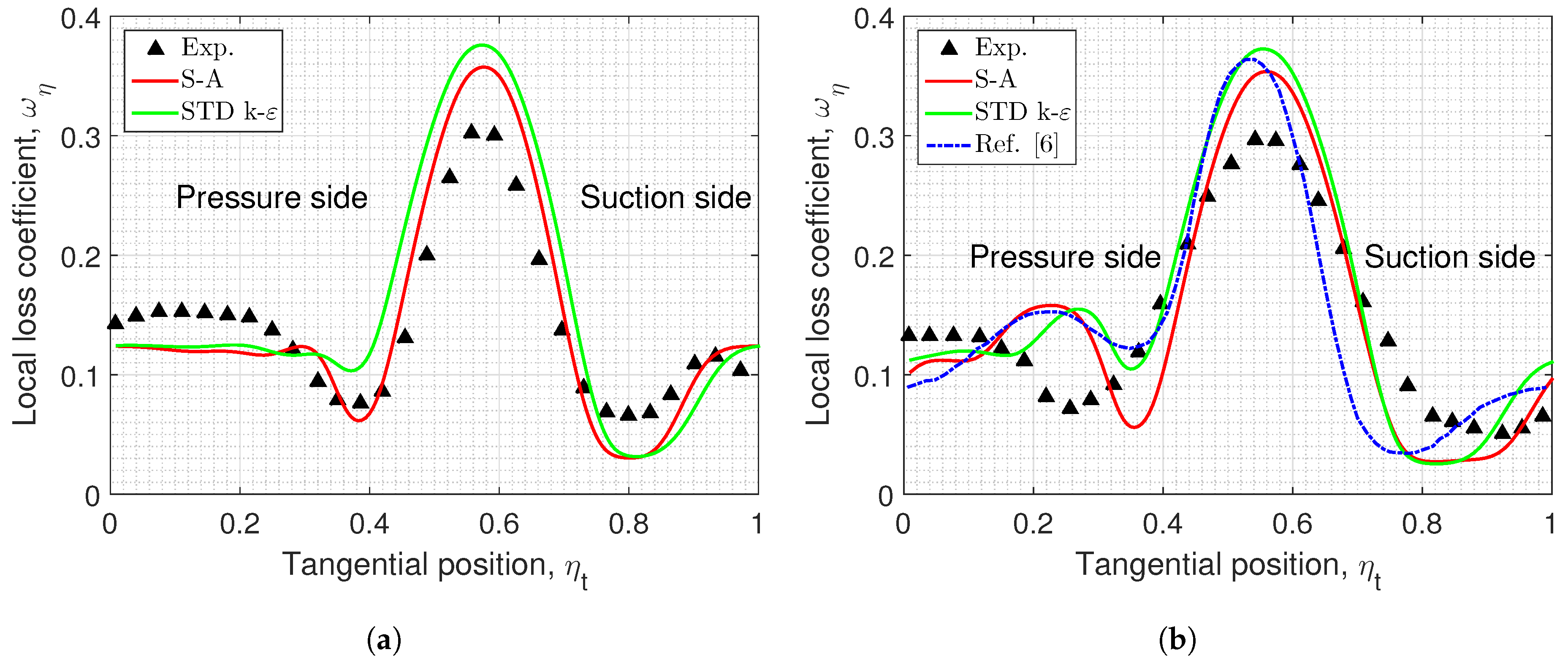
2.7. Results of Validation and Grid Sensitivity Analysis
3. Parametric Study of the ARL-SL19 Supersonic Cascade
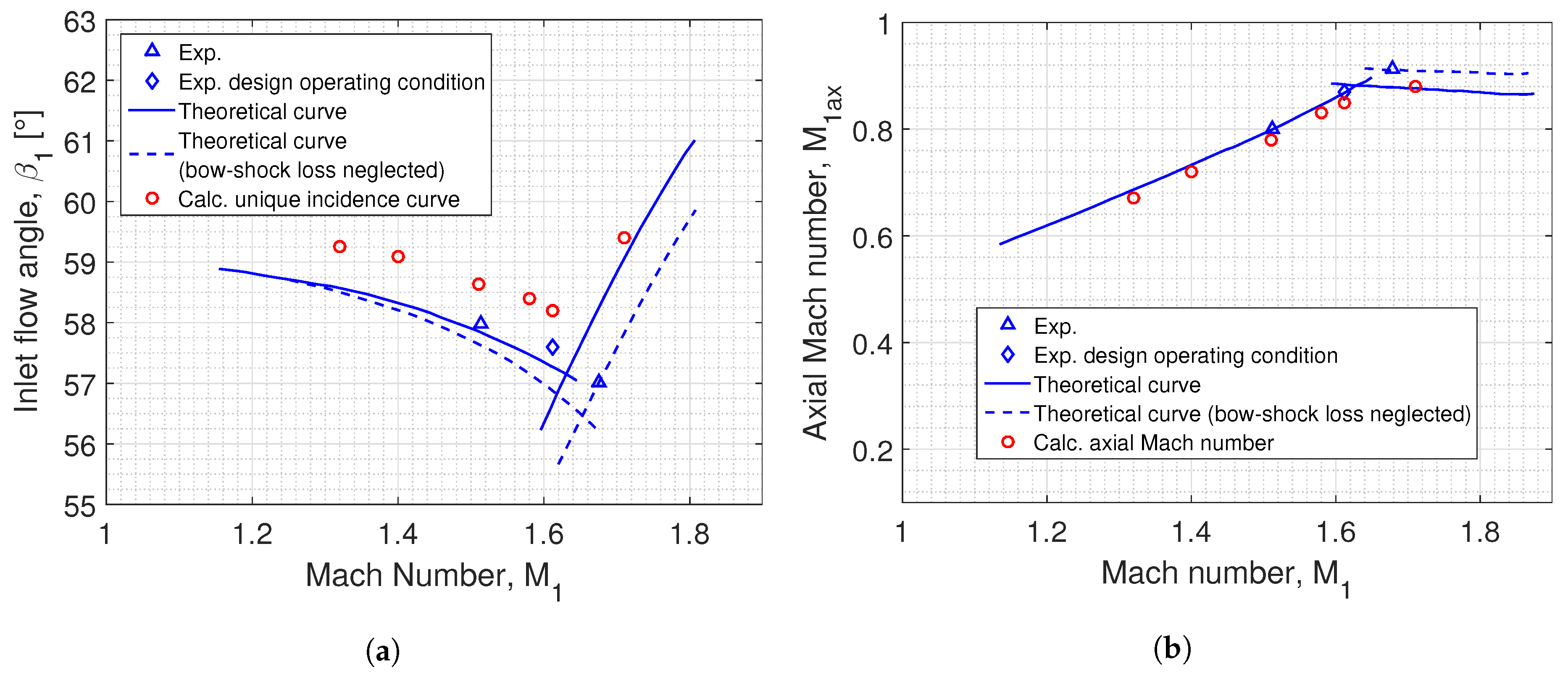
3.1. Numerical Determination of the Unique Incidence Curve
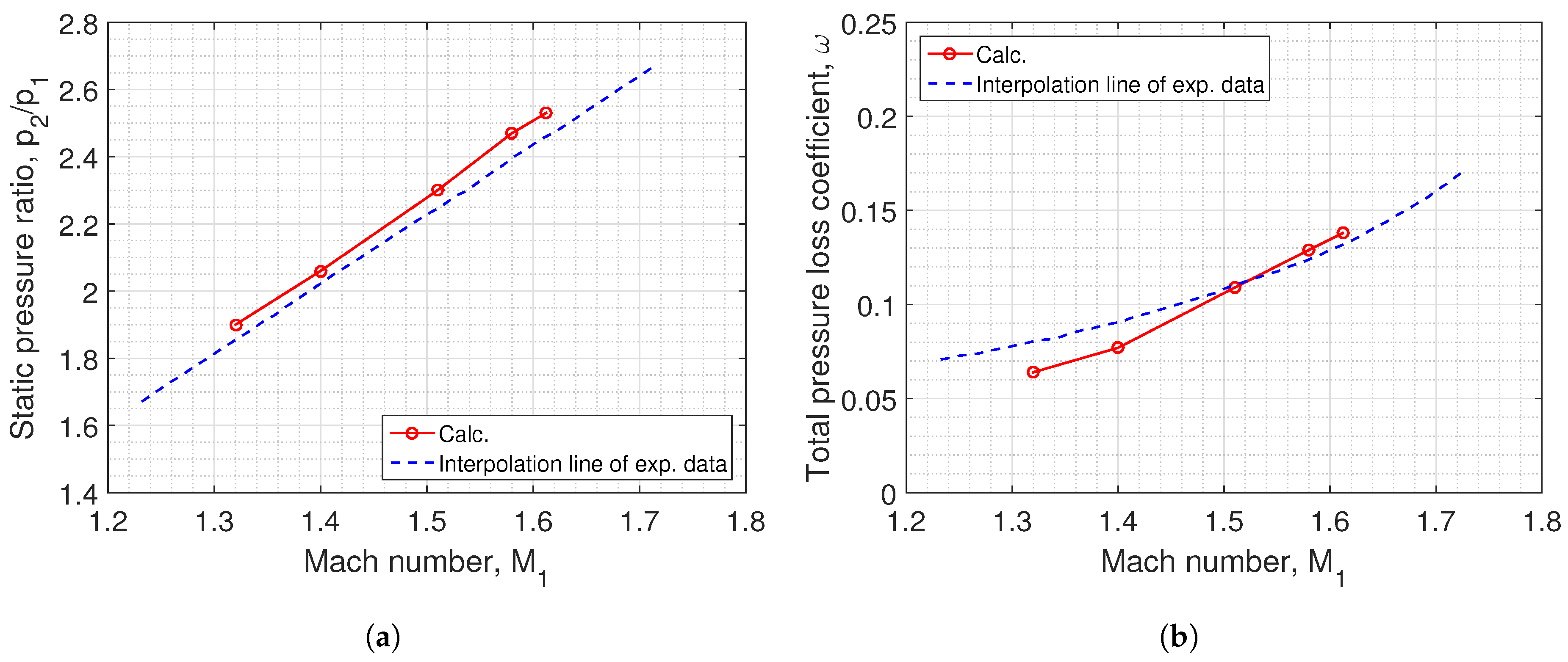
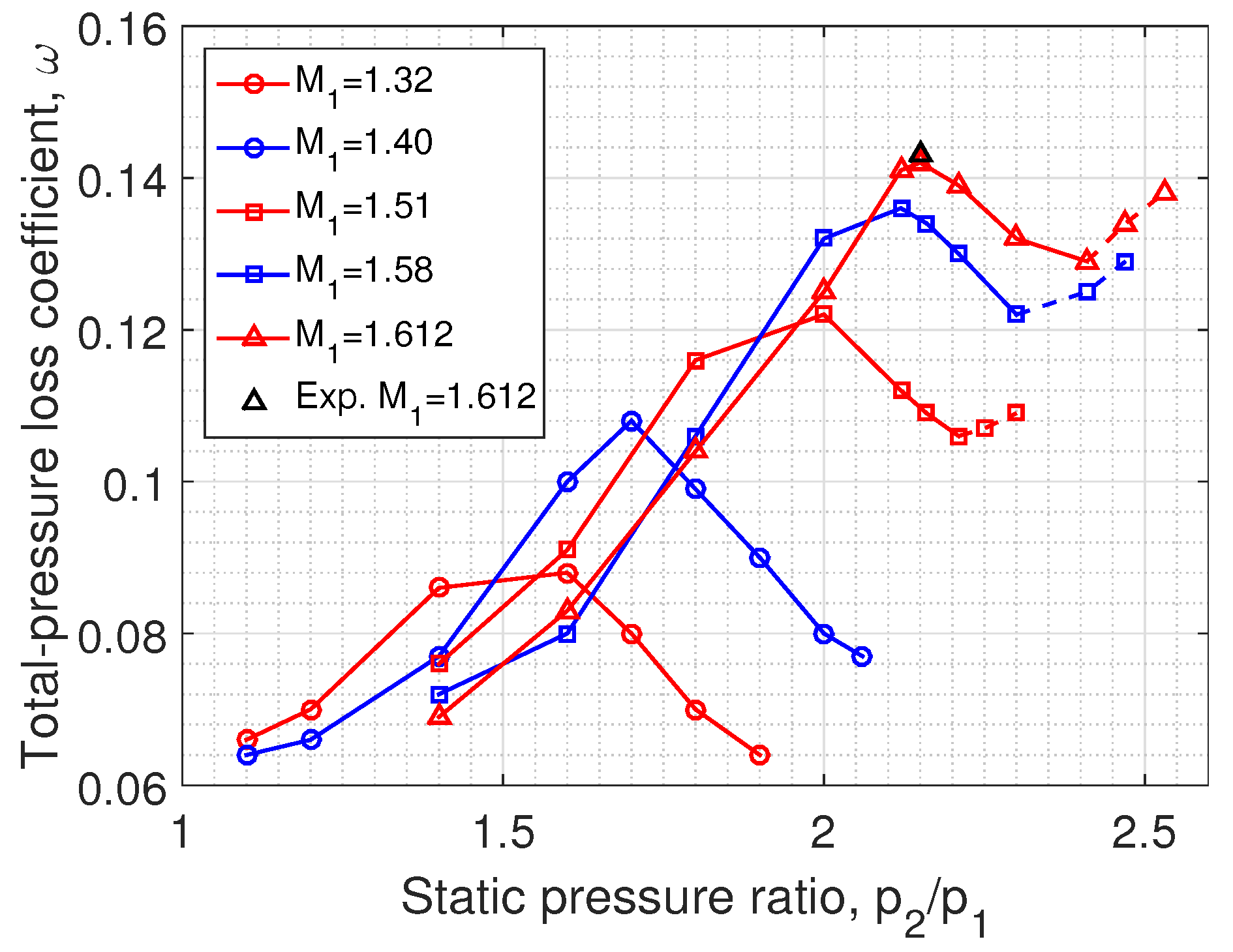
3.2. Influence of Inlet Mach Number
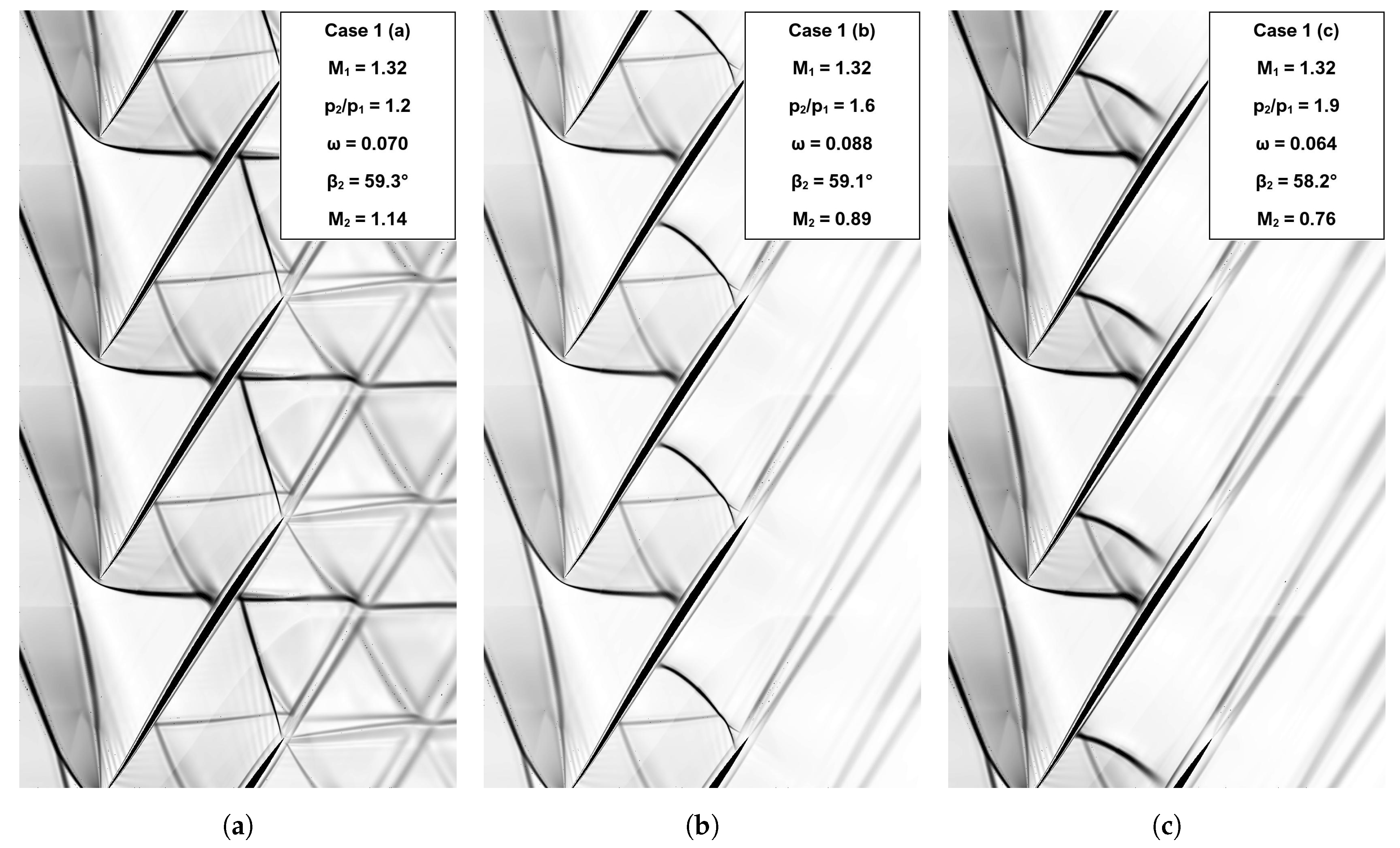
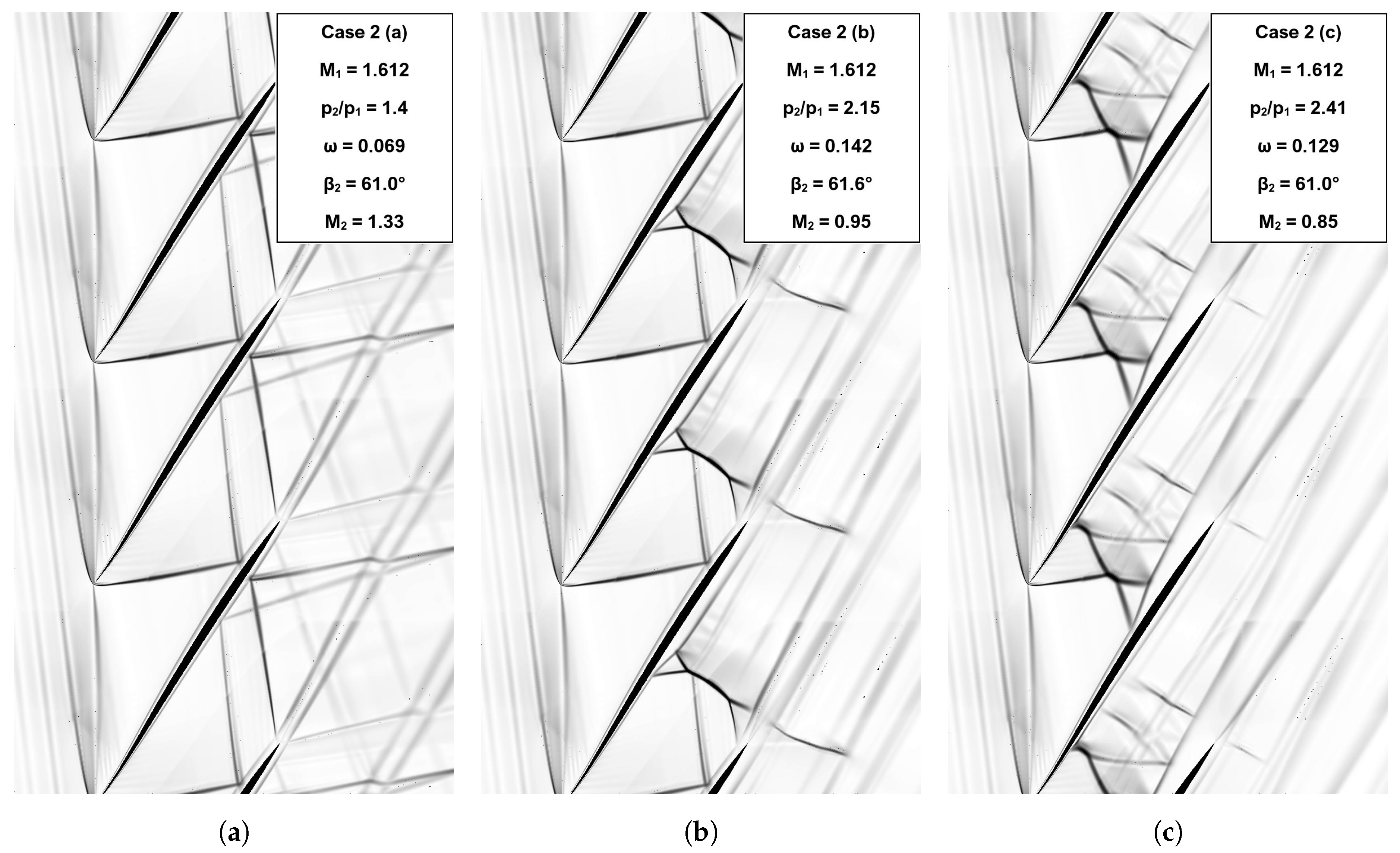
3.3. Influence of the Static Pressure Ratio
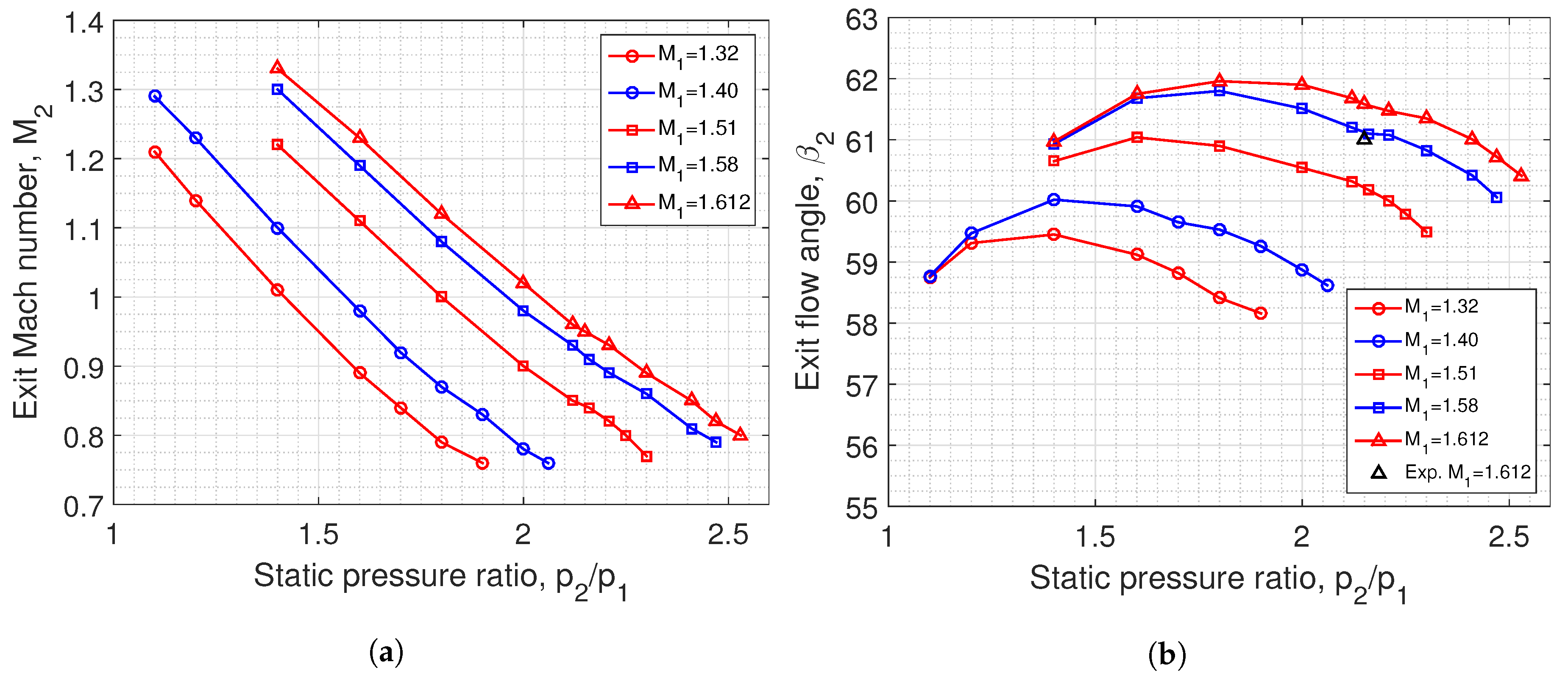
3.3.1. Exit Mach Number and Flow Angle
3.3.2. Total-Pressure Loss Coefficient
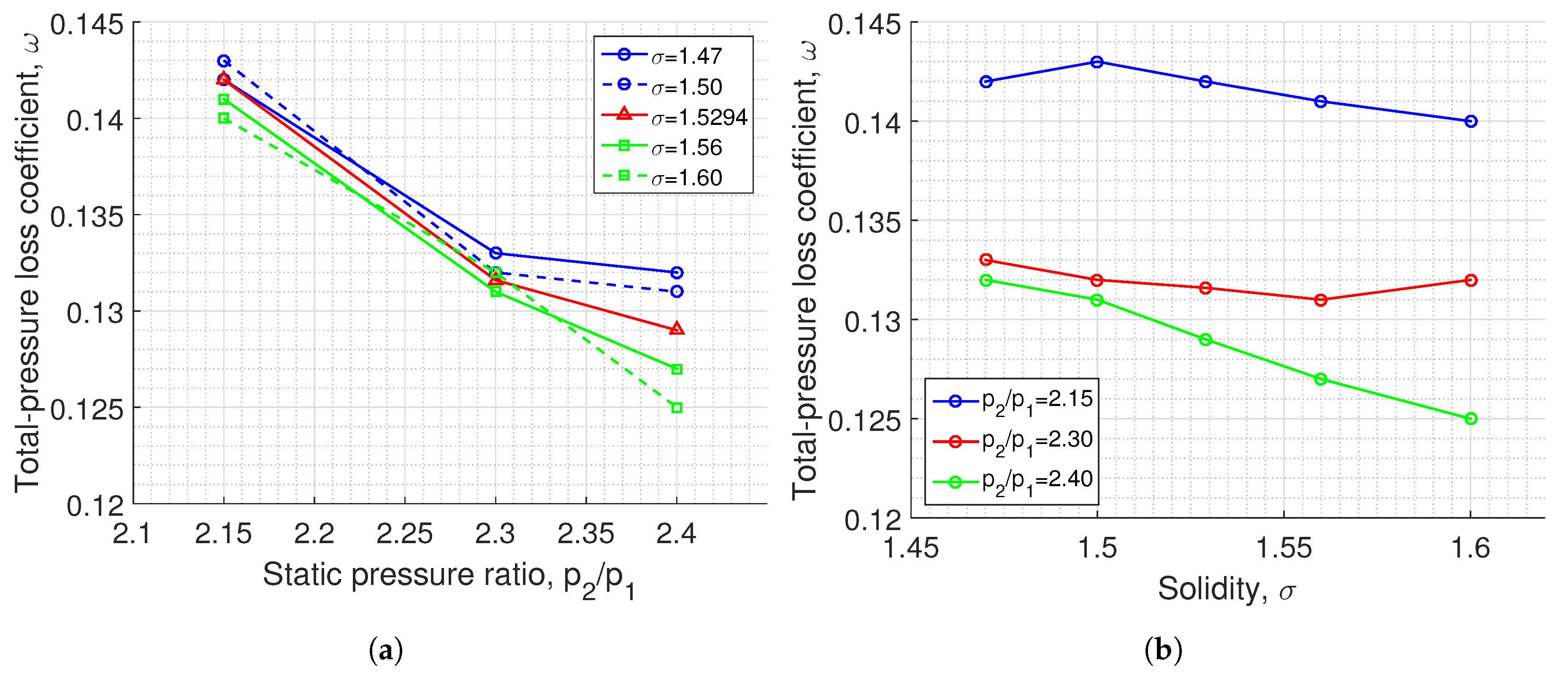
3.4. Influence of Solidity
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AVDR | Axial Velocity-Density Ratio |
| CFD | Computational Fluid Dynamics |
| DDA | Detroit Diesel Allison |
| DFVLR | Deutsche Forschungs- und Versuchsanstalt für Luft- und Raumfahrt |
| DLR | Deutsches Zentrum für Luft- und Raumfahrt e.V. |
| MCA | Multiple Circular Arc |
| ONERA | Office National d’Etudes et de Recherches Aérospatiales |
| RANS | Reynolds-Averaged Navier-Stokes equations |
| RNG | Re-Normalisation Group |
| STD | Standard |
| SWBLI | Shock wave-boundary layer interaction |
| Axial chord length | |
| Inlet Mach number | |
| Exit Mach number | |
| Axial inlet Mach number | |
| Isentropic Mach number | |
| Inlet static pressure | |
| Outlet static pressure | |
| Inlet total pressure | |
| Outlet total pressure | |
| Inlet axial velocity | |
| Outlet axial velocity | |
| Inlet flow angle | |
| Exit flow angle | |
| Ratio of specifc heats | |
| Flow turning | |
| Prandtl-Meyer function | |
| Cascade solidity | |
| Inlet density | |
| Outlet density | |
| Total-pressure loss coefficient |
References
- Biollo, R.; Benini, E. Recent Advances in Transonic Axial Compressor Aerodynamics. Prog. Aerosp. Sci. 2013, 56, 1–18. [Google Scholar] [CrossRef]
- Calvert, W.J.; Ginder, R.B. Transonic Fan and Compressor Design. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 1999, 213, 419–436. [Google Scholar] [CrossRef]
- Kusters, B.; Schreiber, H.A. Compressor cascade flow with strong shock-wave/boundary-layer interaction. AIAA J. 1998, 36, 2072–2078. [Google Scholar] [CrossRef]
- Cui, C.; Zhenggui, Z.; Jinhuan, Z.; Sheng, T. Influence of Key Geometric Parameters on the Aerodynamic Performance of a Supersonic Compressor Cascade. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2018, 12, 2338–2348. [Google Scholar] [CrossRef]
- Song, D.J.; Hwang, H.C.; Kim, Y.I. A Numerical Study of Shock Wave/Boundary Layer Interaction in a Supersonic Compressor Cascade. KSME Int. J. 2001, 15, 366–373. [Google Scholar] [CrossRef]
- Liu, B.; Shi, H.; Yu, X. A New Method for Rapid Shock Loss Evaluation and Reduction for the Optimization Design of a Supersonic Compressor Cascade. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 232, 2458–2476. [Google Scholar] [CrossRef]
- Venturelli, G.; Benini, E. Kriging-assisted Design Optimization of S-shape Supersonic Compressor Cascades. Aerosp. Sci. Technol. 2016, 58, 275–297. [Google Scholar]
- Benini, E. Three-Dimensional Multi-Objective Design Optimization of a Transonic Compressor Rotor. J. Propuls. Power 2004, 20, 559–565. [Google Scholar] [CrossRef]
- Mohsen, M.; Owis, F.M.; Hashim, A.A. The Impact of Tandem Rotor Blades on the Performance of Transonic Axial Compressors. Aerosp. Sci. Technol. 2017, 67, 237–248. [Google Scholar] [CrossRef]
- Yue, S.; Yangang, W.; Haitong, W. Design and Optimization of Tandem Arranged Cascade in a Transonic Compressor. J. Therm. Sci. 2018, 27, 349–358. [Google Scholar] [CrossRef]
- Epsipha, P.; Zuber, M.; Kamarul, A.A. CFD Investigation of Transonic Axial Compressor Rotor Blade at Various Off-design Conditions. Pertanika J. Sci. Technol. 2016, 24, 451–463. [Google Scholar]
- Tweedt, D.L.; Schreiber, H.A.; Starken, H. Experimental Investigation of the Performance of a Supersonic Compressor Cascade. ASME J. Turbomach. 1988, 110, 456–466. [Google Scholar] [CrossRef]
- Wennestrom, A.J. The Design and Evaluation of a High-Through-Flow Transonic Axial Compressor. In Proceedings of the 6th International Symposium on Air Breathing Engines, Paris, France, 6–10 June 1983. [Google Scholar]
- Wennerstrom, A.J.; Frost, G.R. Design of a 1500ft/sec Transonic High-Through-Flow Single-Stage Axial Compressor with Low Hub-Tip Ratio; AFAPL-TR-76-59; Air Force Aero-Propulsion Lab/TB: Wright-Patterson AFB, OH, USA, 1976. [Google Scholar]
- Fleeter, S.; Holtmann, R.L.; McClure, R.B.; Sinnet, G.T. Experimental Investigation of a Supersonic Compressor Cascade; ARL TR 75-0208; Aerospace Research Laboratories: Wright-Patterson AFB, OH, USA, 1975. [Google Scholar]
- Fourmaux, A.; Gaillard, R.; Losfeld, G.; Meauzè, G. Test Results on the ARL 19 Supersonic Blade Cascade. ASME J. Turbomach. 1988, 110, 450–455. [Google Scholar] [CrossRef]
- Serovy, G.K.; Okiishi, T.H. Performance of a Compressor Cascade Configuration with Supersonic Entrance Flow—A Review and Comparison of Experiments in Three Installations. ASME J. Turbomach. 1988, 110, 441–449. [Google Scholar] [CrossRef]
- ANSYS Fluent. Fluent 16.2 User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2015. [Google Scholar]
- Levine, P. The Two Dimensional Inflow Conditions for a Supersonic Compressor with Curved Blades. ASME J. Appl. Mech 1957, 24, 165–169. [Google Scholar]
- Lichtfuss, H.J.; Starken, H. Supersonic Cascade Flow. Prog. Aerosp. 1974, 15, 37–149. [Google Scholar] [CrossRef]
- Cumpsty, N.A. Compressor Aerodynamics; Longman Group: London, UK, 1984. [Google Scholar]
- Spalart, P.; Allmaras, S. A One-Equation Turbulence Model for Aerodynamic Flows. AIAA J. 1992, 439. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The Numerical Computation of Turbulent Flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Yakhot, V.; Orszag, S.A. Renormalization Group Analysis of Turbulence. I. Basic Theory. J. Sci. Comput. 1986, 1, 3–51. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New κ-ϵ Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- Menter, F. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Schreiber, H.A.; Starken, H. Experimental Cascade Analysis of a Transonic Compressor Rotor Blade Section. J. Eng. Gas Turbines Power 1984, 106, 288–294. [Google Scholar] [CrossRef]
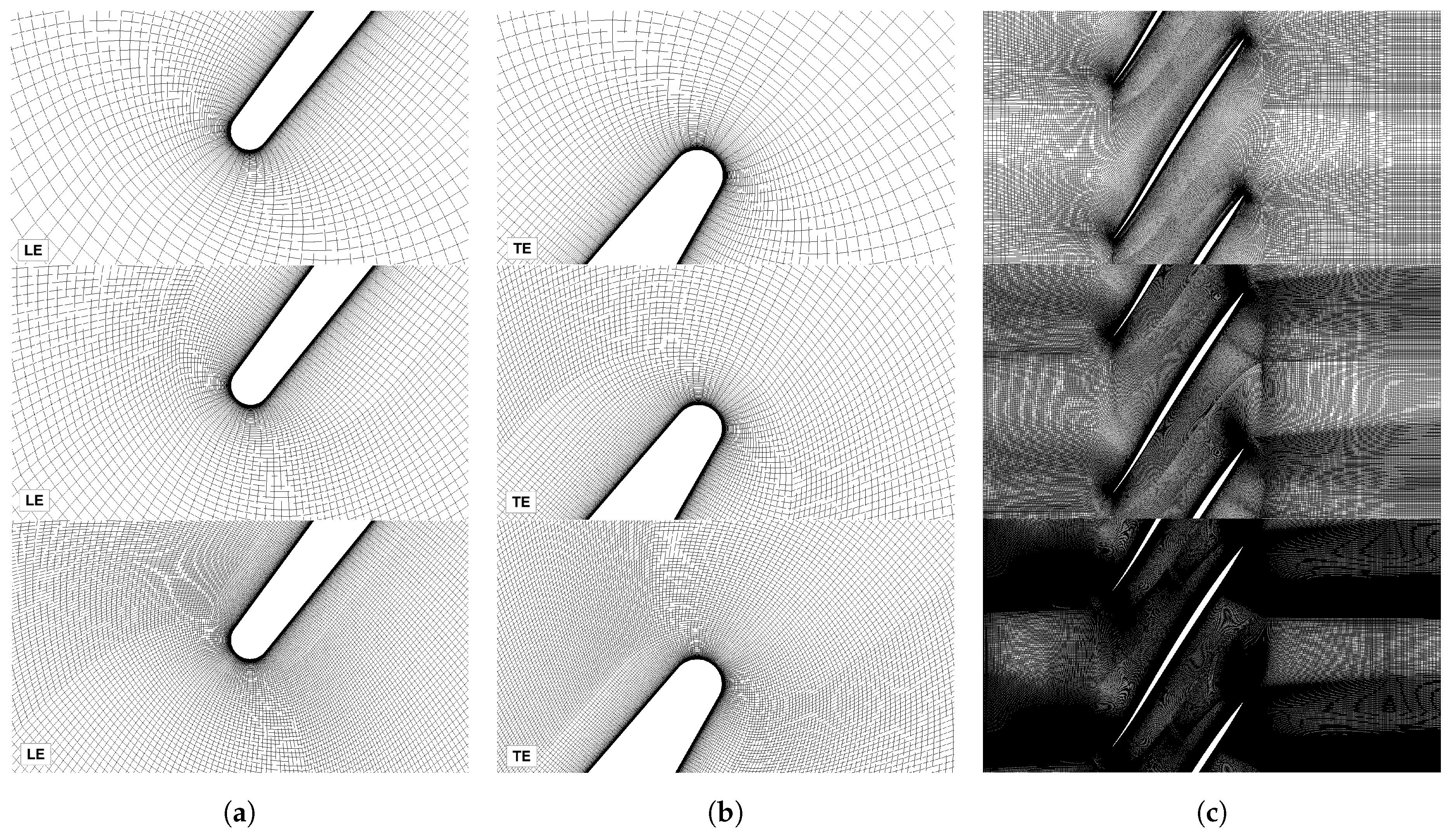
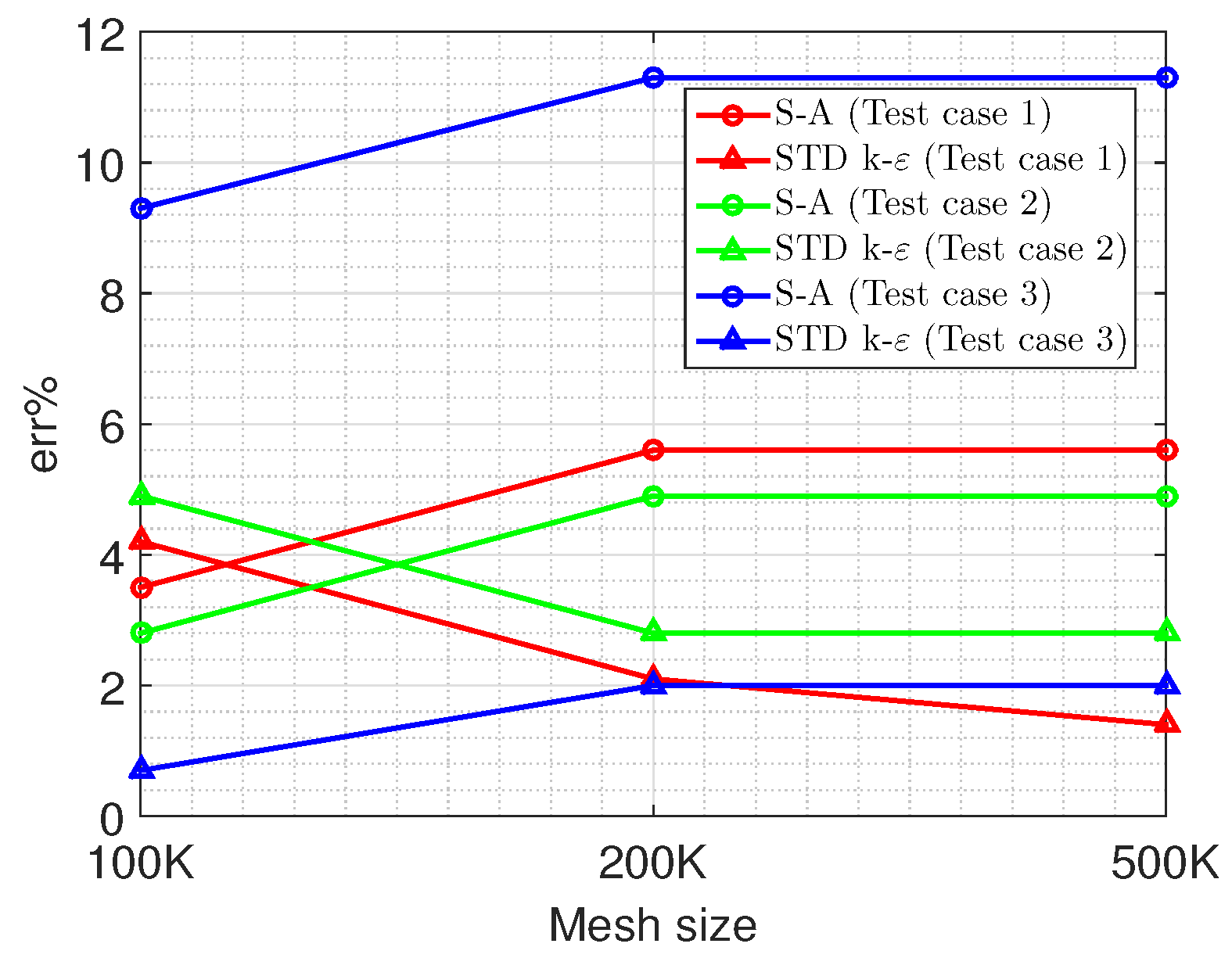

| Parameter | Coarse Mesh | Medium Mesh | Fine Mesh |
|---|---|---|---|
| Total elements | 100k | 200k | 500k |
| Minimum Orthogonal Quality | 0.79 | 0.78 | 0.77 |
| Maximum Ortho Skew | 0.21 | 0.22 | 0.23 |
| Parameter | Test Case 1 | Test Case 2 | Test Case 3 | |
|---|---|---|---|---|
| Input | ||||
| inlet Mach number | 1.58 | 1.58 | 1.59 | |
| inlet flow angle | 57.9° | 57.9° | 57.9° | |
| static pressure ratio | 2.16 | 2.12 | 2.21 | |
| axial velocity-density ratio | AVDR | 1.00 | 0.99 | 1.02 |
| Output | ||||
| exit Mach number | 0.91 | 0.93 | - | |
| exit flow angle | 60.8° | 61.2° | 60.2° | |
| total-pressure loss coefficient | 0.143 | 0.144 | 0.150 |
| Input | Output | ||
|---|---|---|---|
| 1.612 | 0.87 | ||
| / | 2.15 | 0.143 | |
| 57.6° | 61.0° | ||
| AVDR | 1.00 | −3.4° | |
| AVDR = 1.00 | ||||||||||
| Mesh Coarse 100k | Mesh Medium 200k | Mesh Fine 500k | ||||||||
| Exp. | S-A | STD - | SST - | S-A | STD - | SST - | S-A | STD - | SST - | |
| 57.9 | 58.4 | 58.6 | 58.3 | 58.4 | 58.6 | 58.3 | 58.4 | 58.6 | 58.3 | |
| 0.91 | 0.91 | 0.90 | 0.91 | 0.91 | 0.90 | 0.92 | 0.91 | 0.90 | 0.92 | |
| 60.8 | 61.1 | 60.9 | 61.3 | 61.1 | 60.8 | 61.3 | 61.1 | 60.8 | 61.3 | |
| 0.143 | 0.138 | 0.149 | 0.128 | 0.135 | 0.146 | 0.123 | 0.135 | 0.145 | 0.123 | |
| AVDR = 0.99 | ||||||||||
| Mesh Coarse 100k | Mesh Medium 200k | Mesh Fine 500k | ||||||||
| Exp. | S-A | STD - | SST - | S-A | STD - | SST - | S-A | STD - | SST - | |
| 57.9 | 58.4 | 58.6 | 58.3 | 58.4 | 58.6 | 58.3 | 58.4 | 58.6 | 58.3 | |
| 0.93 | 0.92 | 0.91 | 0.93 | 0.92 | 0.91 | 0.93 | 0.92 | 0.91 | 0.93 | |
| 61.2 | 61.2 | 60.9 | 61.3 | 61.2 | 60.9 | 61.3 | 61.2 | 60.9 | 61.3 | |
| 0.144 | 0.140 | 0.151 | 0.132 | 0.137 | 0.148 | 0.128 | 0.137 | 0.148 | 0.128 | |
| AVDR = 1.02 | ||||||||||
| Mesh Coarse 100k | Mesh Medium 200k | Mesh Fine 500k | ||||||||
| Exp. | S-A | STD - | SST - | S-A | STD - | SST - | S-A | STD - | SST - | |
| 57.9 | 58.3 | 58.5 | 58.2 | 58.3 | 58.5 | 58.3 | 58.3 | 58.5 | 58.3 | |
| - | 0.90 | 0.89 | 0.91 | 0.90 | 0.89 | 0.91 | 0.90 | 0.89 | 0.91 | |
| 60.2 | 61.2 | 60.9 | 61.3 | 61.2 | 60.9 | 61.3 | 61.2 | 60.9 | 61.3 | |
| 0.150 | 0.136 | 0.149 | 0.124 | 0.133 | 0.147 | 0.120 | 0.133 | 0.147 | 0.120 | |
| Parameter | Exp. | Calculation |
|---|---|---|
| 57.6° | 58.2° | |
| 61.0° | 61.6° | |
| −3.4° | −3.4° | |
| 0.143 | 0.142 | |
| 0.87 | 0.85 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Piovesan, T.; Magrini, A.; Benini, E. Accurate 2-D Modelling of Transonic Compressor Cascade Aerodynamics. Aerospace 2019, 6, 57. https://doi.org/10.3390/aerospace6050057
Piovesan T, Magrini A, Benini E. Accurate 2-D Modelling of Transonic Compressor Cascade Aerodynamics. Aerospace. 2019; 6(5):57. https://doi.org/10.3390/aerospace6050057
Chicago/Turabian StylePiovesan, Tommaso, Andrea Magrini, and Ernesto Benini. 2019. "Accurate 2-D Modelling of Transonic Compressor Cascade Aerodynamics" Aerospace 6, no. 5: 57. https://doi.org/10.3390/aerospace6050057
APA StylePiovesan, T., Magrini, A., & Benini, E. (2019). Accurate 2-D Modelling of Transonic Compressor Cascade Aerodynamics. Aerospace, 6(5), 57. https://doi.org/10.3390/aerospace6050057







