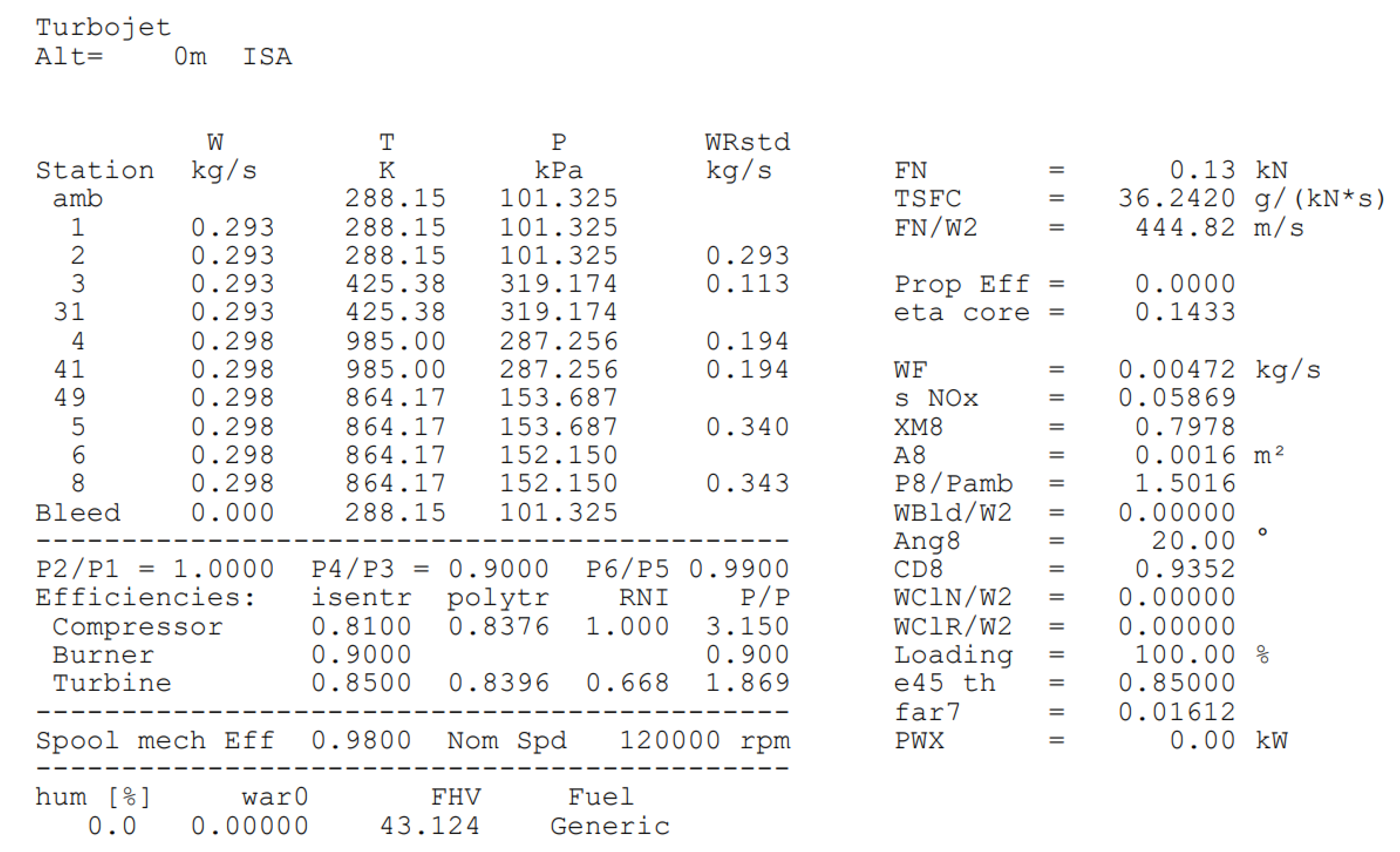
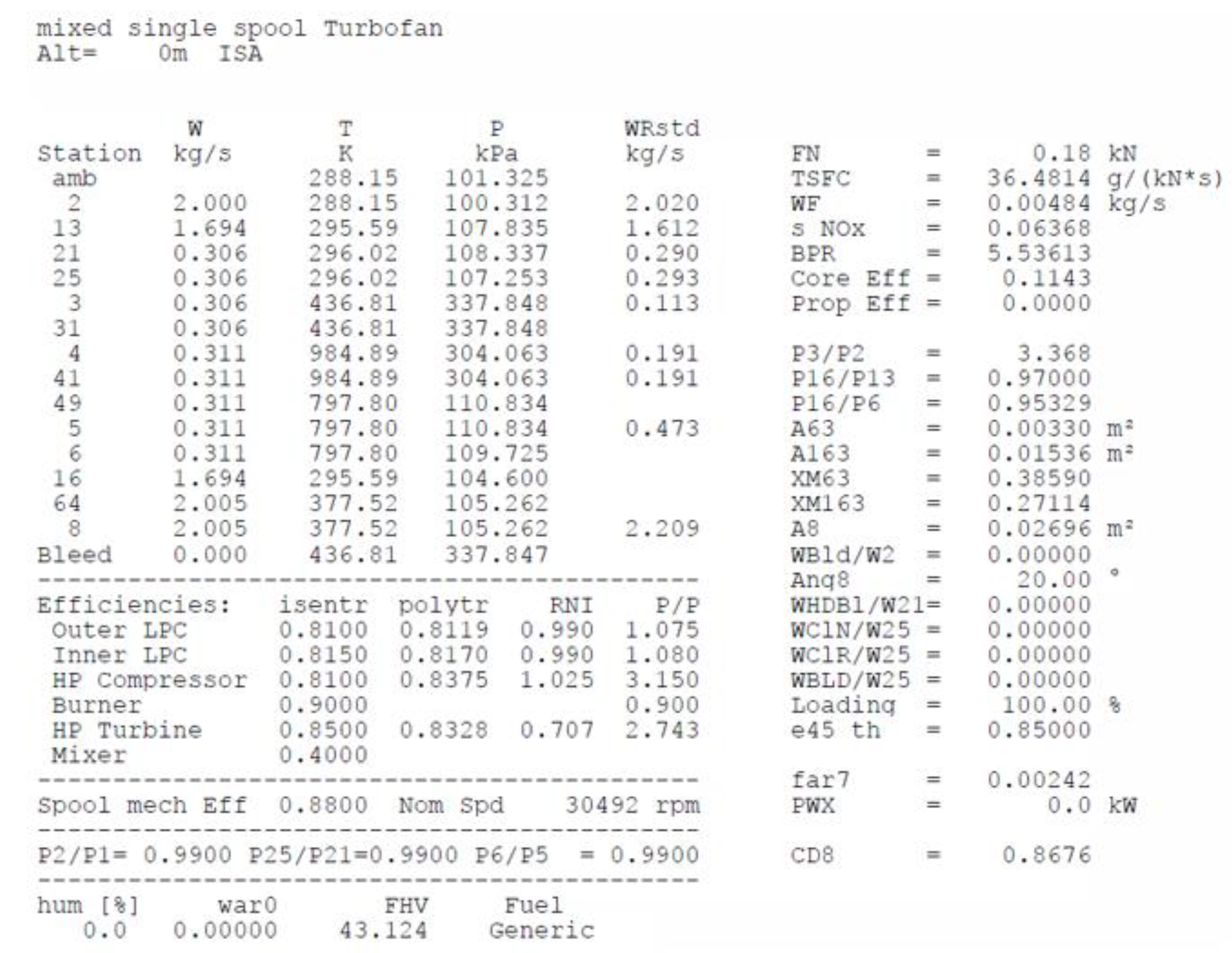
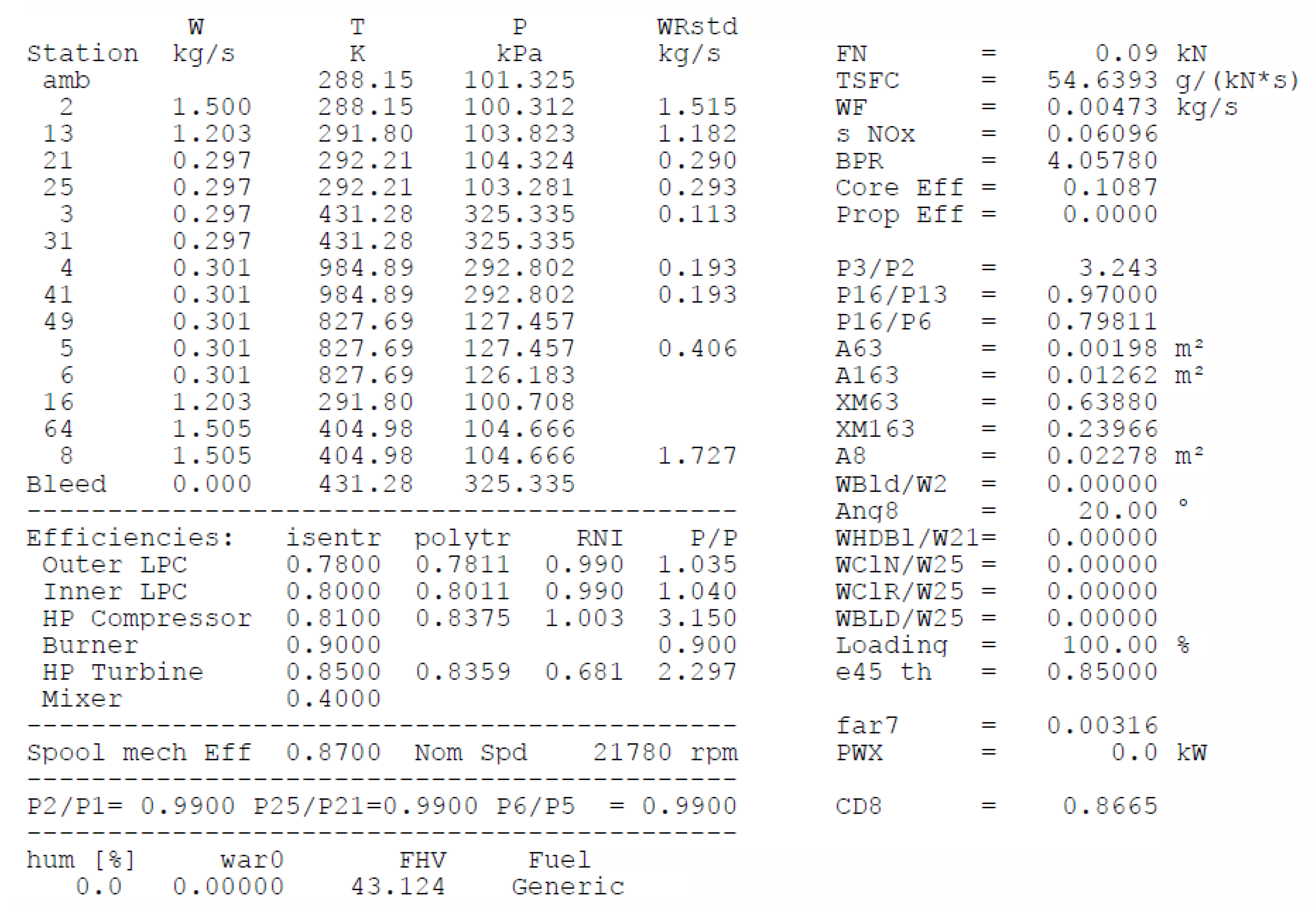
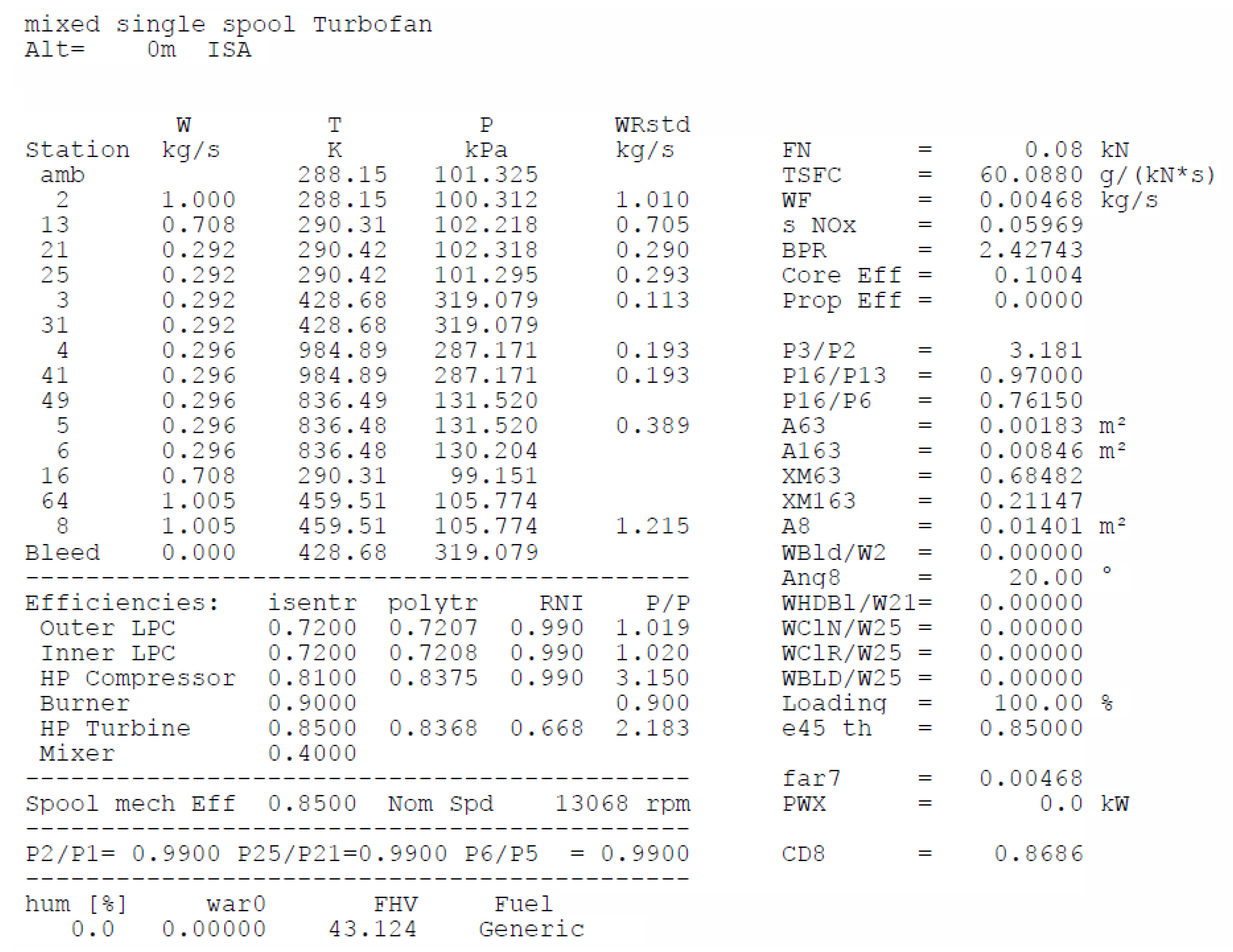
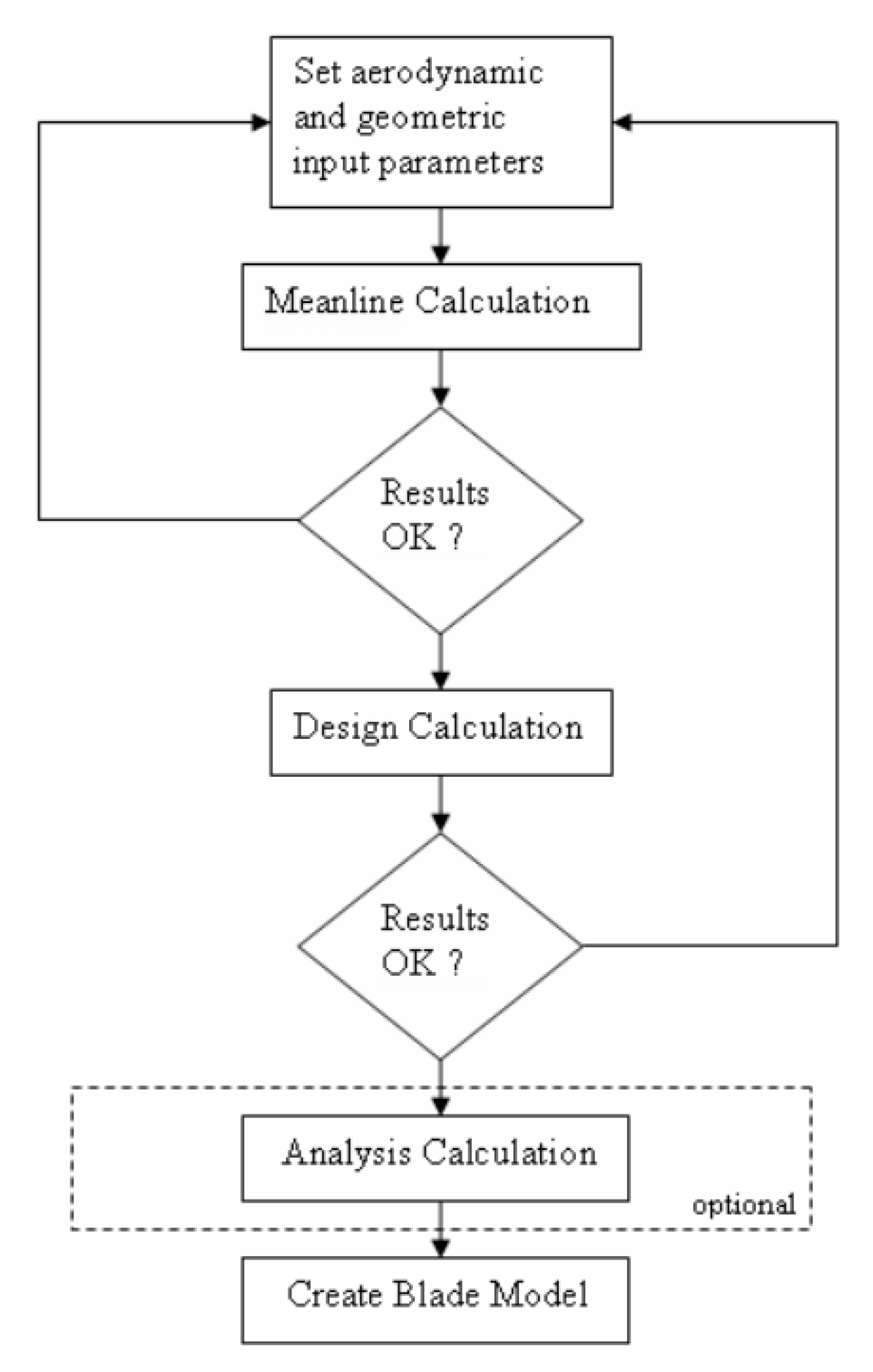
3.3.1. One Dimensional Meanline Calculation
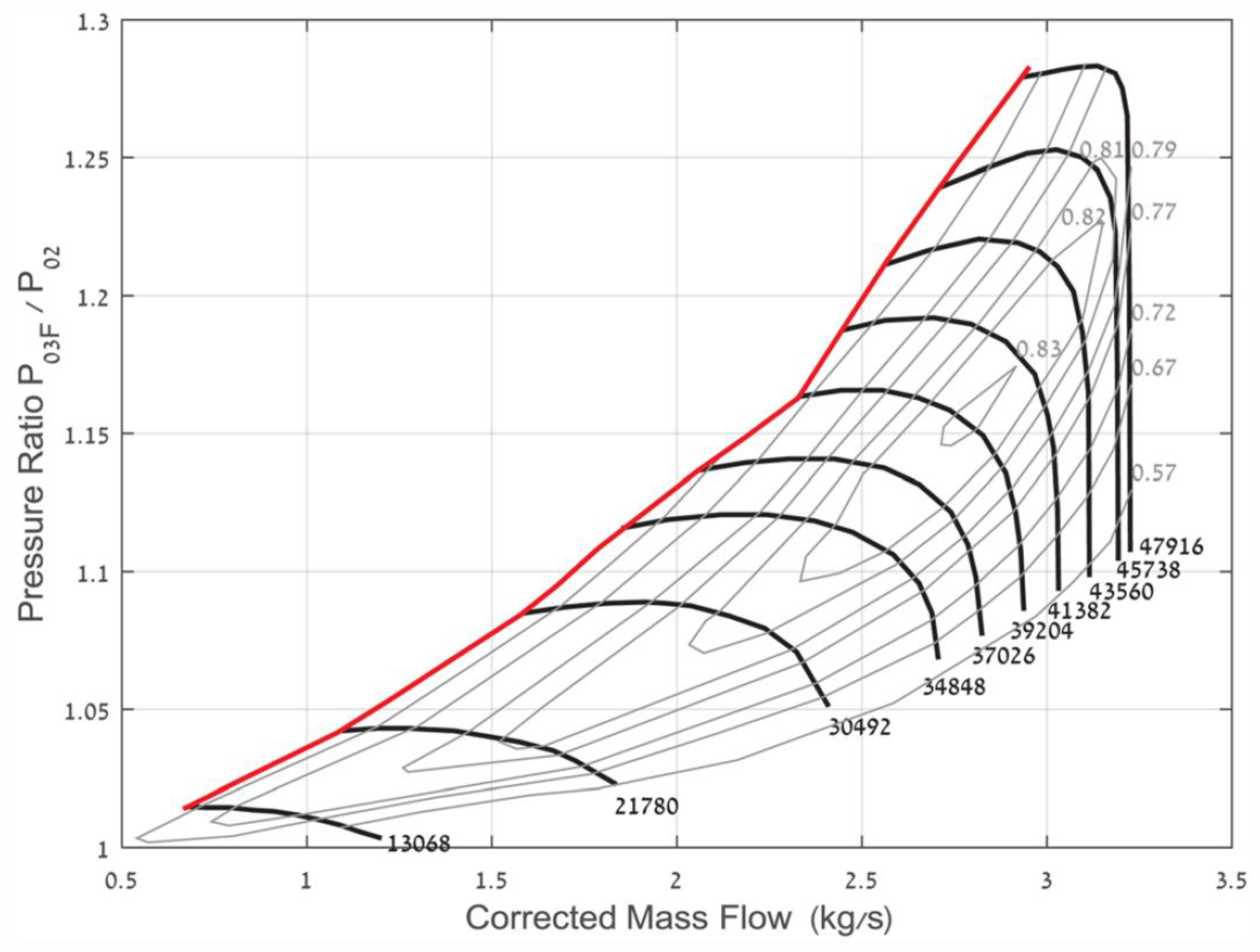
The LPC design point for the varying speeds was identified through the iteration of performance values taken from a scaled fan map and simulated with the GasTurb engine performance software. The first step of the design procedure is to make the appropriate assumptions and calculations for the LPC efficiency, tip speed, axial velocity and related parameters. First, a constraint of the fan tip relative Mach number ≤ 1 (LPC tip speed = 330 m/s) is imposed, thereby avoiding associated wave drag from the supersonic flow. The inlet Mach number is fixed at 0.5 (≈160 m/s) for the design point of cruise conditions. The design parameters already identified from the engine simulation are as follows:
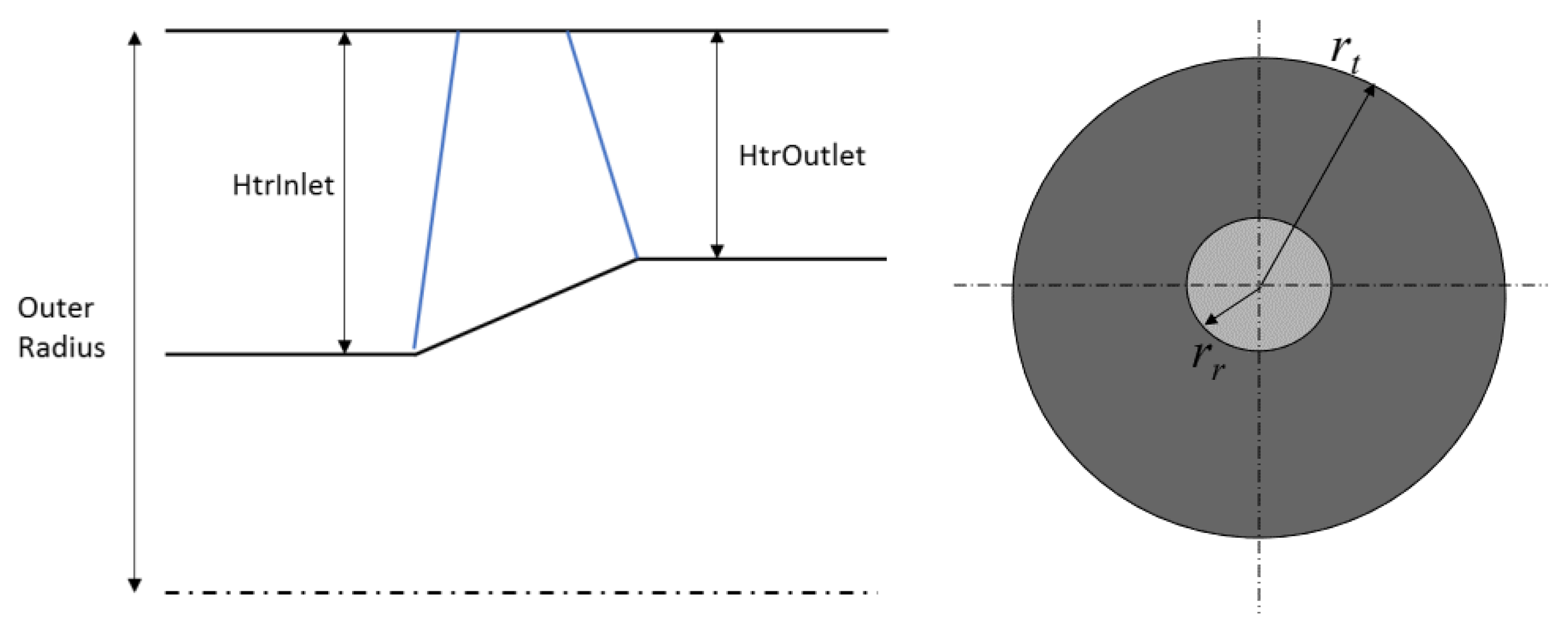
Next, the overall annulus dimensions, inlet and outlet of the compressor (hub-to-tip ratio—
rh = hub radius,
rt = tip radius) are sized (see
Figure 11):
From the lessons learned in [
2], no IGV is employed, as it is assumed in the design of this LPC that similar drops in efficiency can be expected due blading and increased shock losses. Therefore, no whirl velocity component is assumed in the calculation. From the isentropic flow equations: (Cp = 1.005 KJ/kg, R = 287 J/kg):
From the continuity equation:
The tip speed, tip radius and nominal spool speed are related by:
Thus, with the use of a simple spreadsheet and the above equations, the tip radius and spool speed can be evaluated over a range of different hub to tip ratios. The purpose of the evaluation is to iterate the variables of the hub-tip ratio and blade tip speed, in order to reach a target nominal speed as close to 30,492 RPM as possible, thus keeping the design parameters close to the results from the engine simulation.
Table 5 presents the results of the study. The initial selection of the tip speed at 330 m/s is chosen as an upper limit, and in order to reach a satisfactory solution the tip speed is reduced to 225 m/s. At a hub-tip ratio of 0.51, the speed is equal to 30,498 RPM, which is sufficient to match the required parameters. The hub to tip ratio of 0.51 is selected as an arbitrary starting point, and the study is conducted from 0.4–0.6. A high hub-tip ratio results in an increased annulus diameter and increases the overall weight of the system; it may be seen that the blades would be approximately 70 mm for an annulus dimension of 150 mm. Conversely, a practical limit of the blade size must be realized, and an overly small hub-tip ratio results in a blade of around 66 mm. The hub-tip ratio will be later studied and adjusted in more detail through a numerical analysis. The relative Mach number at the rotor tip is calculated in order to validate the results. From the velocity triangle:
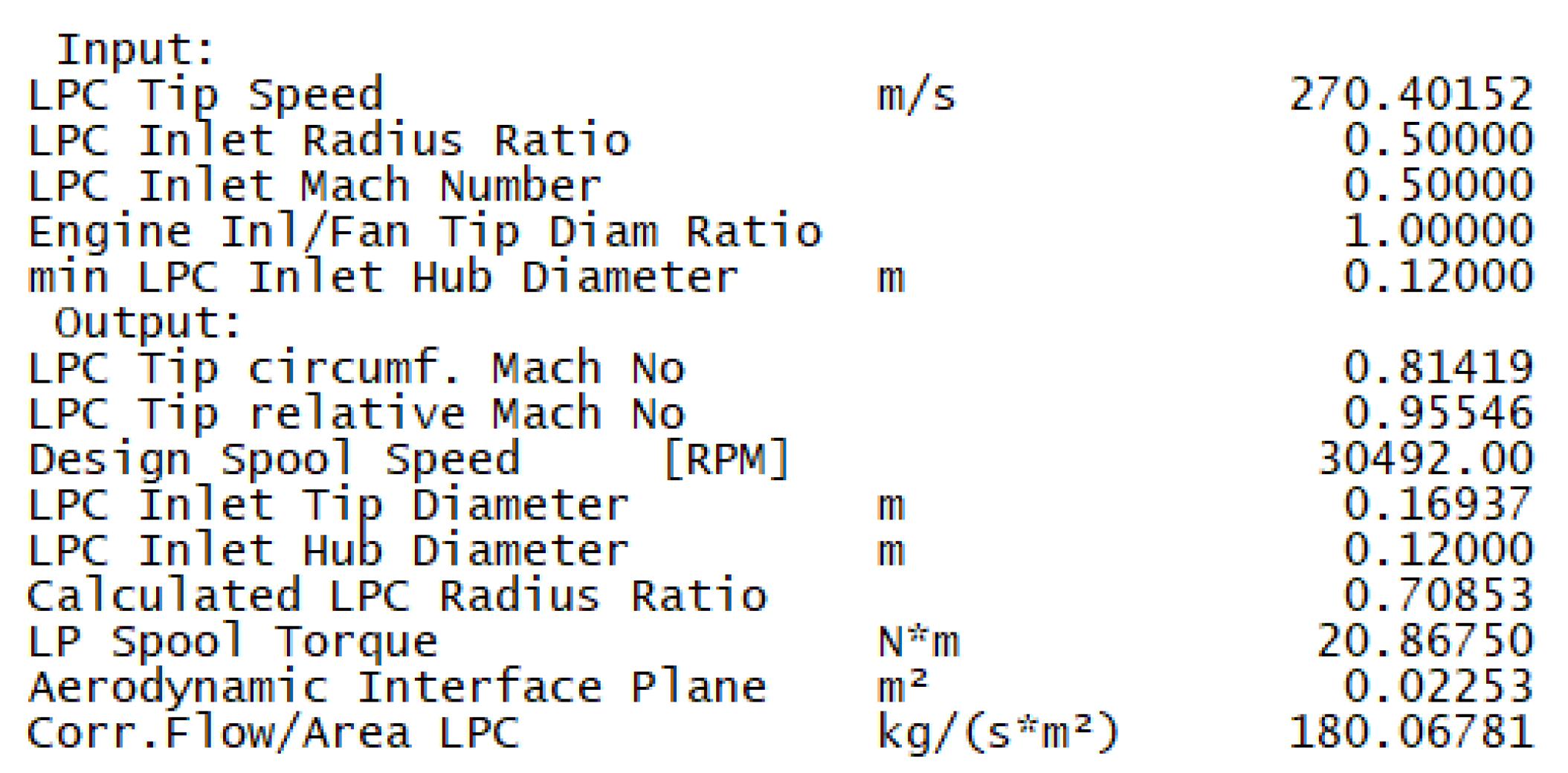
Therefore, an acceptable subsonic relative Mach number at the rotor tip of 0.83 is calculated. The LPC inlet parameters are validated using the GasTurb software. For the chosen design point along the 30,492 RPM speed line, the LPC design parameters are input. The iteration variables, such as the LPC inlet radius ratio, design bypass ratio and LPC outer pressure ratio, are set, and the target design spool speed is set as the studied fan map speed line. Upon simulation, GasTurb iterates between variables and converges on an acceptable solution with independent variables, LPC Inlet Radius Ratio and Design Spool Speed, which are the criteria for the fan preliminary design.
Figure A5 in
Appendix A summarises the results for the LPC preliminary design reached after numerous iterations. A design spool speed of 30,494 RPM is achieved, which matches the scaled performance curve by an acceptable degree for this stage. At this spool speed, a minimum 4:1 reduction gearbox is required to separate the fan from the core spool speed of 120,000 RPM. It may also be seen that the LPC diameter is calculated at 140 mm, which, considering the 110 mm inlet of the BMT 120 KS, is an acceptable solution for a low bypass solution.
The aerodynamic inlet operating conditions determined previously are used as the initial design parameters in the meanline analysis, as seen below in
Table 6. The total pressure rises through the rotor after any downstream pressure losses, neglecting the swirl component. Downstream mixing losses specifies the proportion of axial dynamic pressure at the rotor exit that is assumed to be lost due to the aerodynamic mixing process, which, left as the default value of 25%, offers a robust solution. The hub velocity deficit factor is used to adjust the meanline calculation to take into account the influence of the boundary layer at the hub.
With the aerodynamic inputs defined, for one dimensional meanline calculations the remaining parameters affecting the results are the outer diameter, hub/tip ratio inlet and hub/tip outlet (see
Figure 11). The initial LPC annulus/rotor geometries, calculated from the GasTurb engine model simulation, are used as the starting point for the flow through analysis of the geometry inputs. The inlet tip diameter, calculated at 0.14092 m, provides a first good estimate for the annulus outer dimensions. At a hub-tip ratio of 0.53, the resulting blade height estimate is 66.27 mm; thus, the tip clearance is 4.19 mm or s/h = 0.05, which for this stage is sufficient. The clearance has a strong effect on the efficiency, but it is not modelled in the meanline calculation and will be taken into consideration at a later design phase.
The evaluation of the initial meanline calculation results for an annulus outer diameter of 0.141 m and hub-tip ratio of 0.53 produces unsatisfactory results. It is found that the hub is overly loaded with the minimum stage loading calculated at 0.95 for a hub-tip ratio equal to 0.53, in addition to the flow coefficient exceeding the <0.8 criterion for both the meanline and hub. The study is expanded to allow for slight modification of the annulus dimensions, and the considerations include the fact that an outer diameter that is too large for the duty will suffer from increased swirl and associated pressure losses. Equally, a diameter that is too small will lead to higher loadings and a reduced DeHaller (DH) number (where a light aerodynamic loading is the key here, i.e., a low rate of diffusion with DH = W2/W1 > 0.72).
To achieve acceptable solutions for the meanline calculation, the annulus outer diameter must be increased. From further sizing of the LPC inlet and with reference to
Table 5, it is calculated that the maximum obtainable annulus size, limited by the relative tip Mach number, whilst maintaining the initial input aerodynamic parameters (mass flow/spool speed/pressure ratio), is 0.17 m; this is validated in GasTurb, and the results are summarized in
Figure A6 in
Appendix A.
Different values for the annulus diameter, up to 0.17 m, are analyzed.
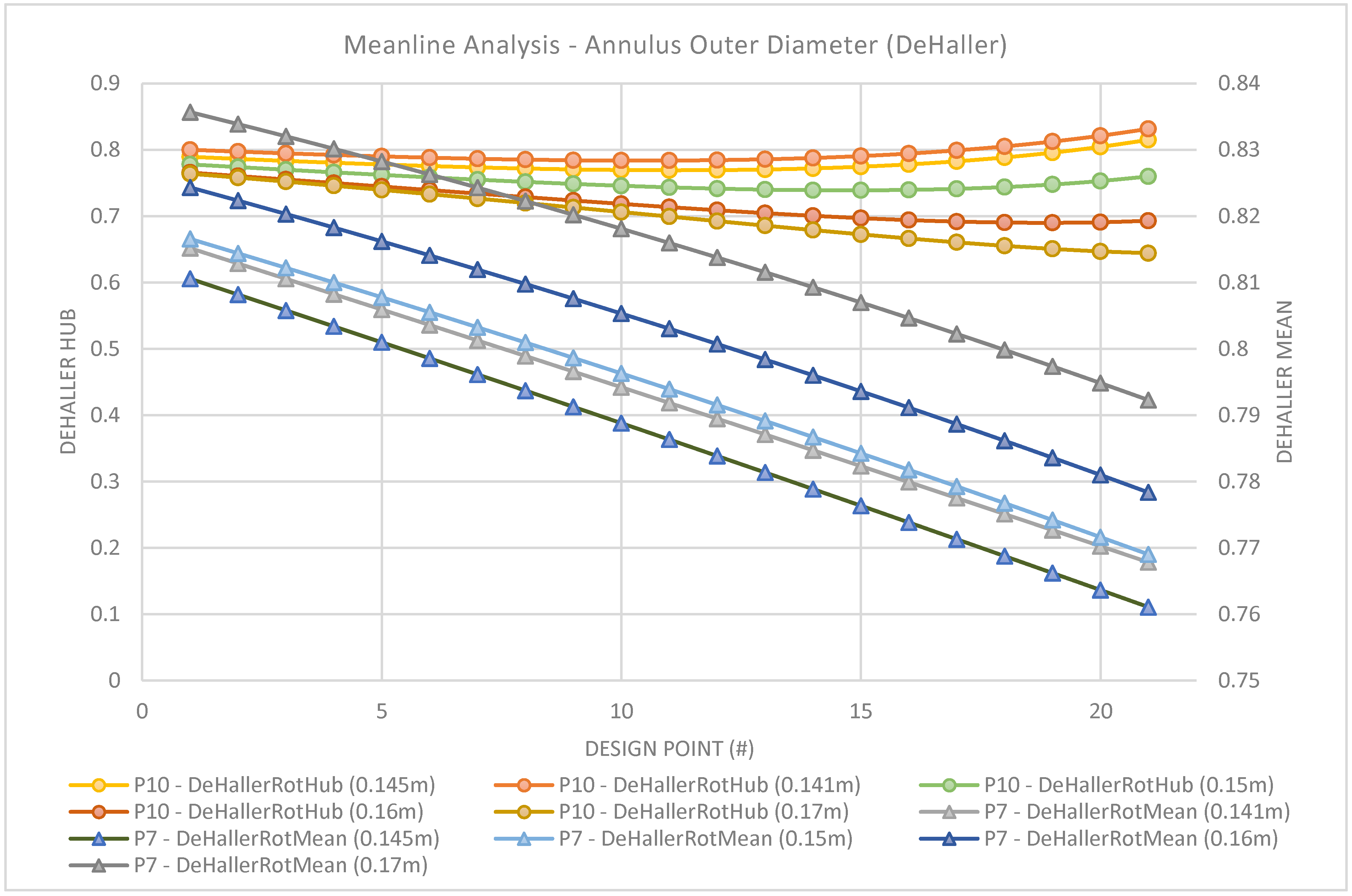
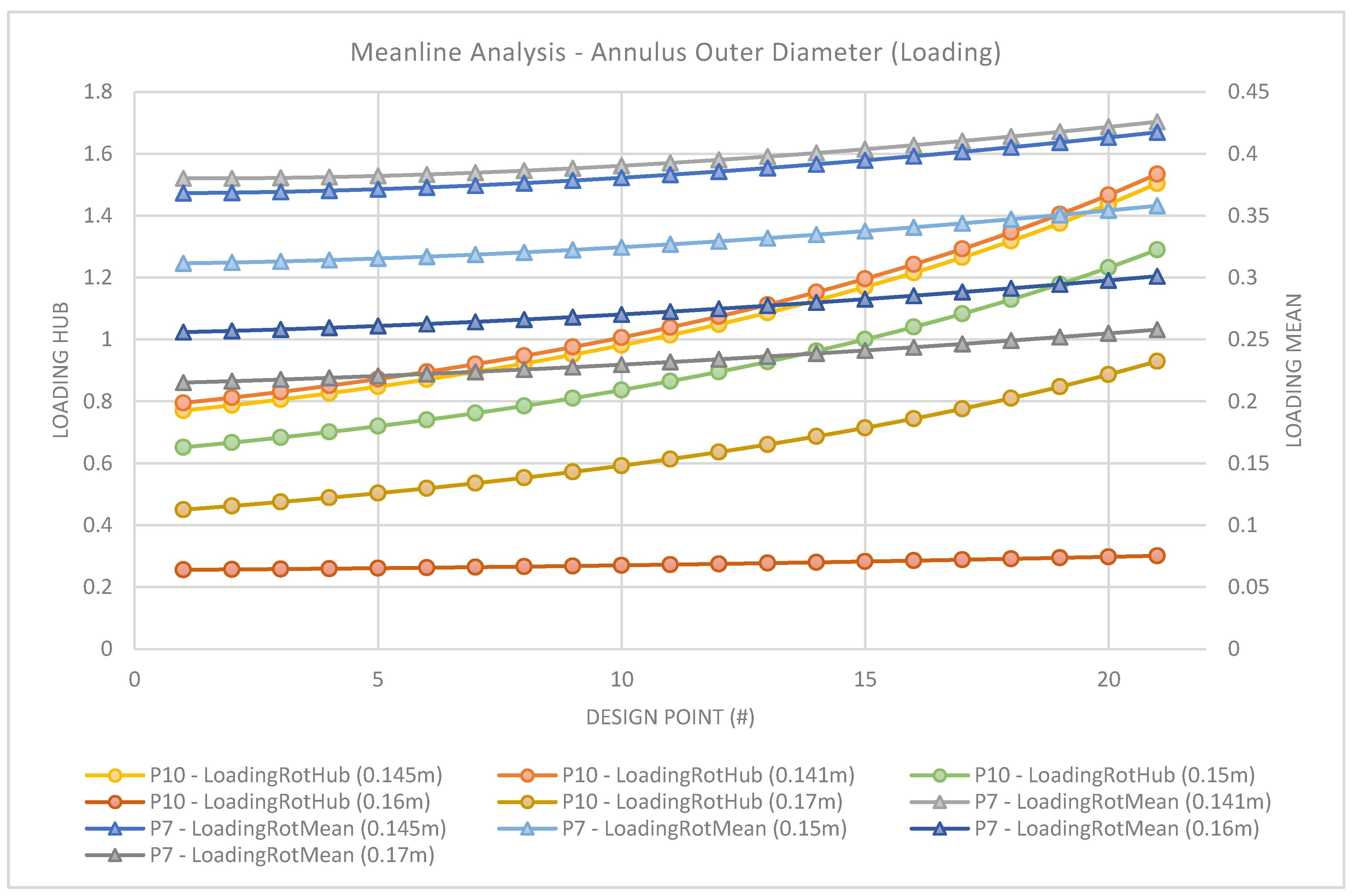
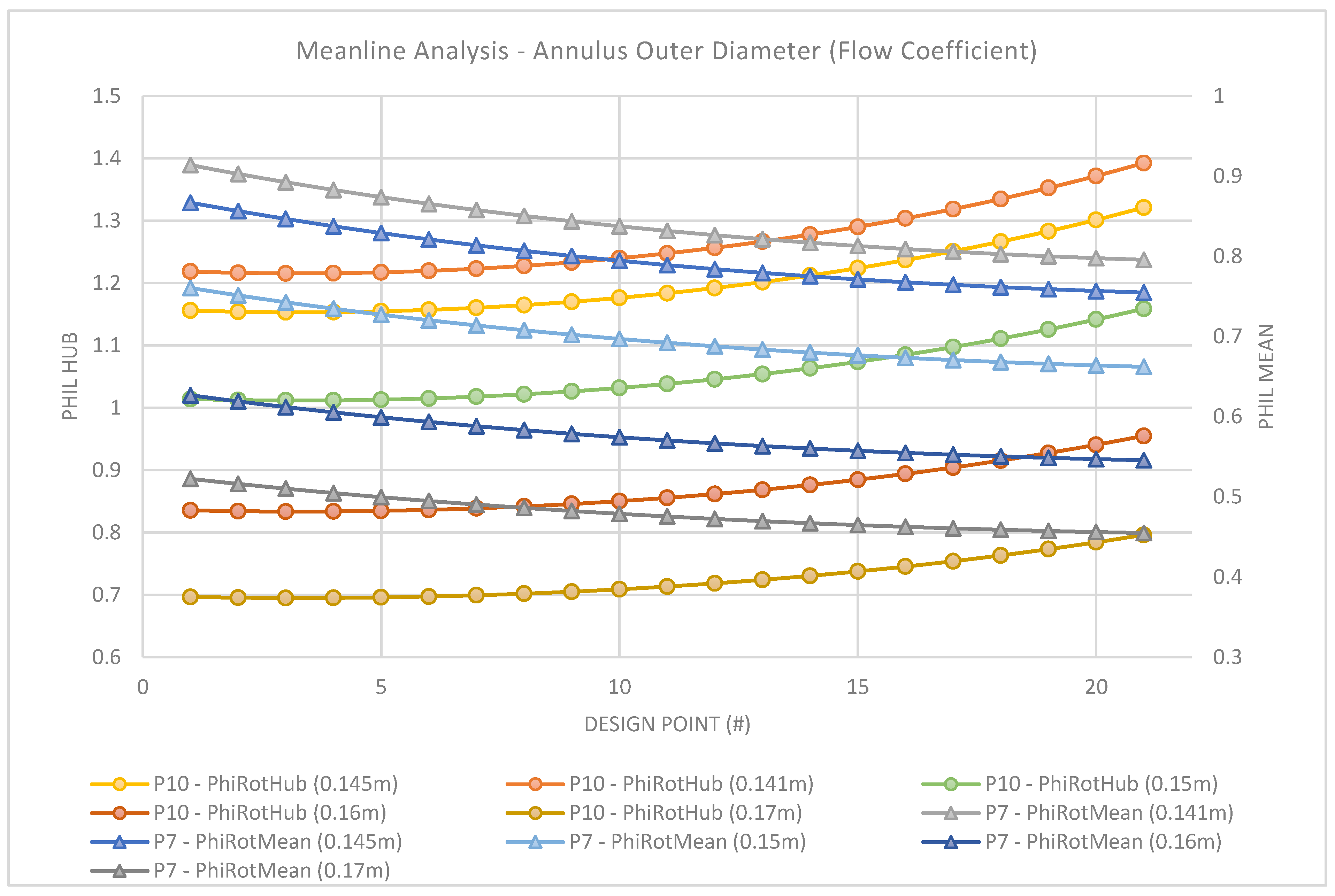
Figure 12,
Figure 13 and
Figure 14 shows the graphical results of the meanline calculation for the study of the annulus outer diameter. The design point is associated with the hub-tip inlet, which is varied at +0.01 from 0.4–0.6 for the study.
Studying
Figure 12,
Figure 13 and
Figure 14, it may be seen that the meanline and hub for all annulus diameters satisfies the criteria of DeHaller >0.72. Additonally, a smaller annulus diameter produces more favorable results in terms of the meanline DeHaller, especially approaching higher hub-tip ratios of more than 0.55 (DP 15). However, as a consequence, the hub becomes highly loaded, which significantly impacts the efficiency. Moreover, from the evaluation of the loading coefficient (ψ), it is apparent that for all annulus dimensions but 0.17 m, a suitable design would not be achievable as hub ψ exceeds 1. Finally, the flow coefficient, which is given by the axial velocity over the rotational speed of the rotor, is thus dependent only on the inlet hub to tip ratio. An acceptable solution for the flow coefficient should be below 0.8, which again leaves the 0.17 outer diameter as the more suitable value.
With the outer annulus diameter determined, the hub/tip ratio input and output parameters are then varied during an iteration study to determine the optimum values for the 1D meanline analysis (
Table 7). It is advantageous to increase the outer hub/tip over the inlet in order to accelerate the axial flow, increasing the overall pressure rise of the stage and assisting in the prevention of stall. For the first set of data, the hub/tip inlet and outlet values are constant (i.e., HtrInlet = 0.53 and HtrOutlet = 0.53). After the baseline evaluation is complete, the values are iterated at +0.01 intervals from 0.4–0.6 to estimate the performance for given aerodynamic and geometric input parameters. A table displaying the meanline analysis iteration process may be seen below.
Figure 15,
Figure 16 and
Figure 17 present the results of the study for evaluating the hub to tip ratio for the rotor at an annulus outer diameter of 0.17 m. In this study, the objective is to find the optimum annulus geometry and size before further studying and optimization is conducted with a through-flow calculation.
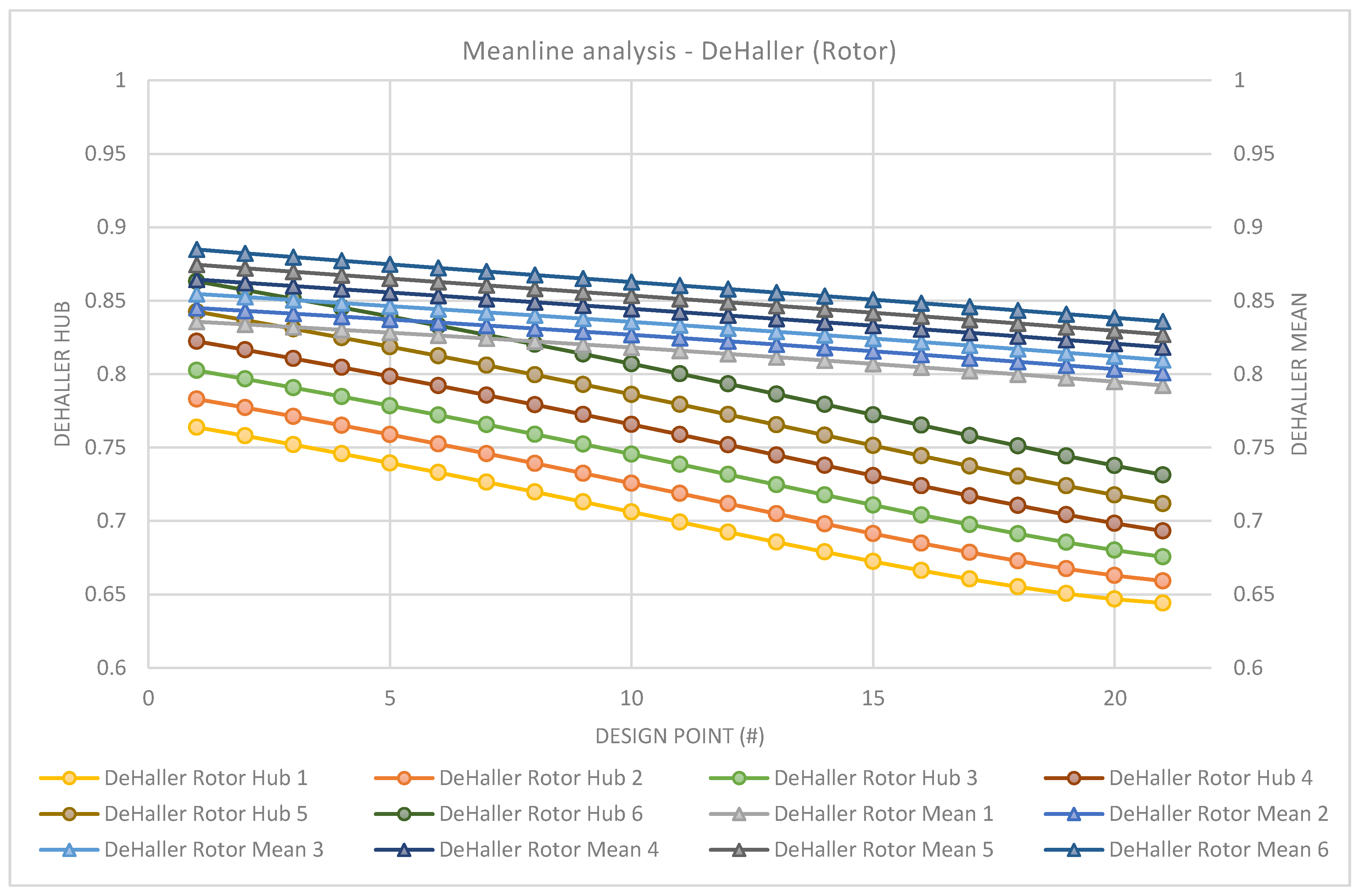
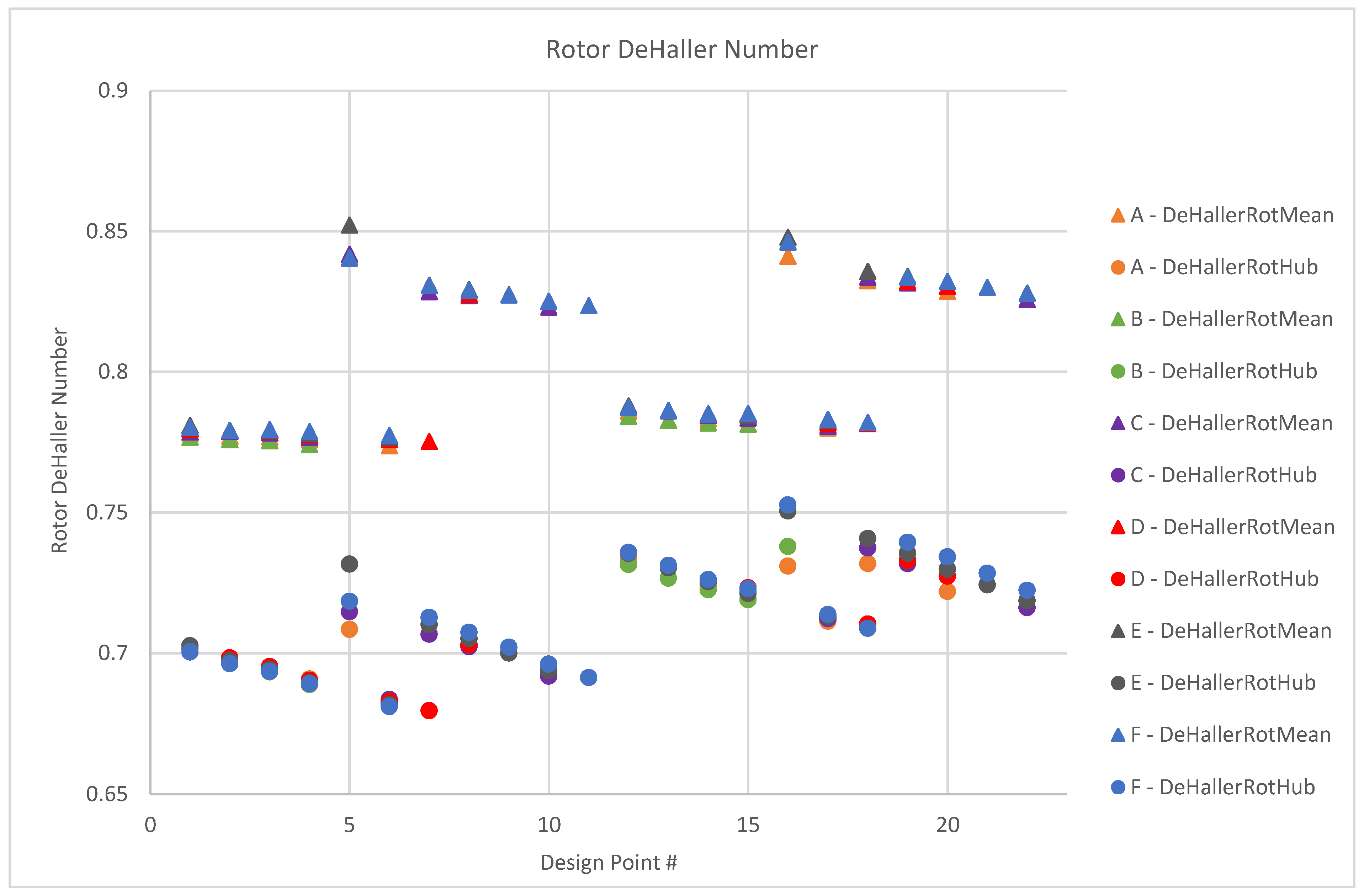
Figure 15 shows the meanline flow analysis DeHaller number results graphically. The graph is used in conjunction with numerical data to determine the geometry for producing preferable results in terms of the DeHaller number (ratio of relative velocities, W
2/W
1 > 0.72). It is clearly observed that increasing the hub-tip ratio at the outlet over the inlet increases the axial velocity: for example, design point 6 (HtrInlet 0.54, HtrOutlet 0.54) with hub DeHaller 0.72 and meanline 0.82, compared to the last iteration (HtrInlet 0.54, HtrOutlet 0.59) with an equivalent hub DeHaller 0.82 and meanline 0.86. The iterations 1 to 3 for the design points 1 to 10 proved to be geometries with a preferable hub DeHaller; the meanline DeHaller remains high for all of the evaluated geometries, indicating light aerodynamic loading, i.e., a low rate of diffusion. The loading coefficient for the study is seen in
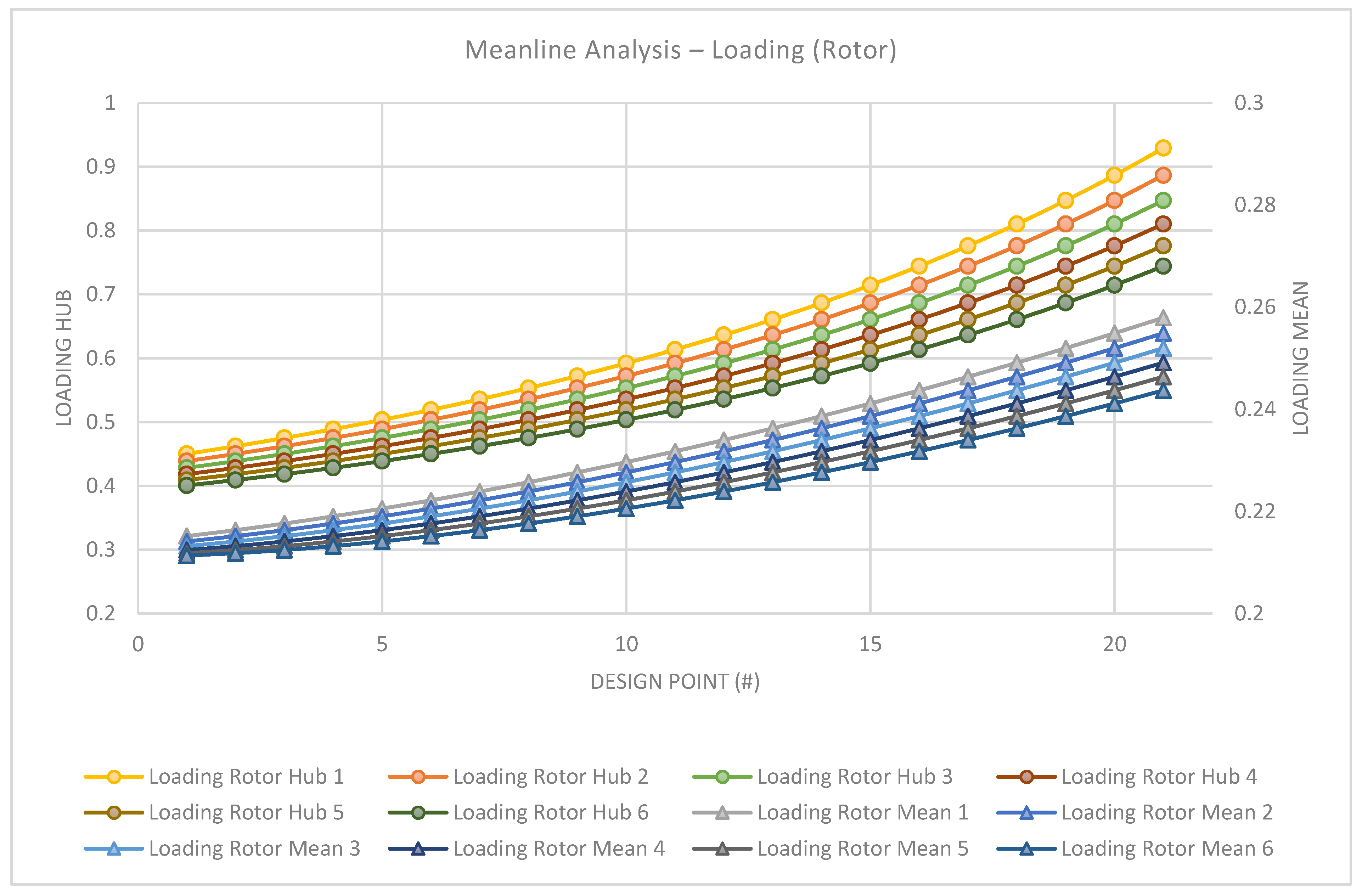
Figure 16. As stated in the background section, studies show that the peak efficiency of the compressors peaks around a loading coefficient of 0.35–0.42. From the evaluation of the loading coefficient, the design points 1–10 present geometries with a slightly increased aerodynamic loading for a peak efficiency with a low loaded meanline. Increasing the hub-tip ratio above 0.5 results in an excessively loaded hub.
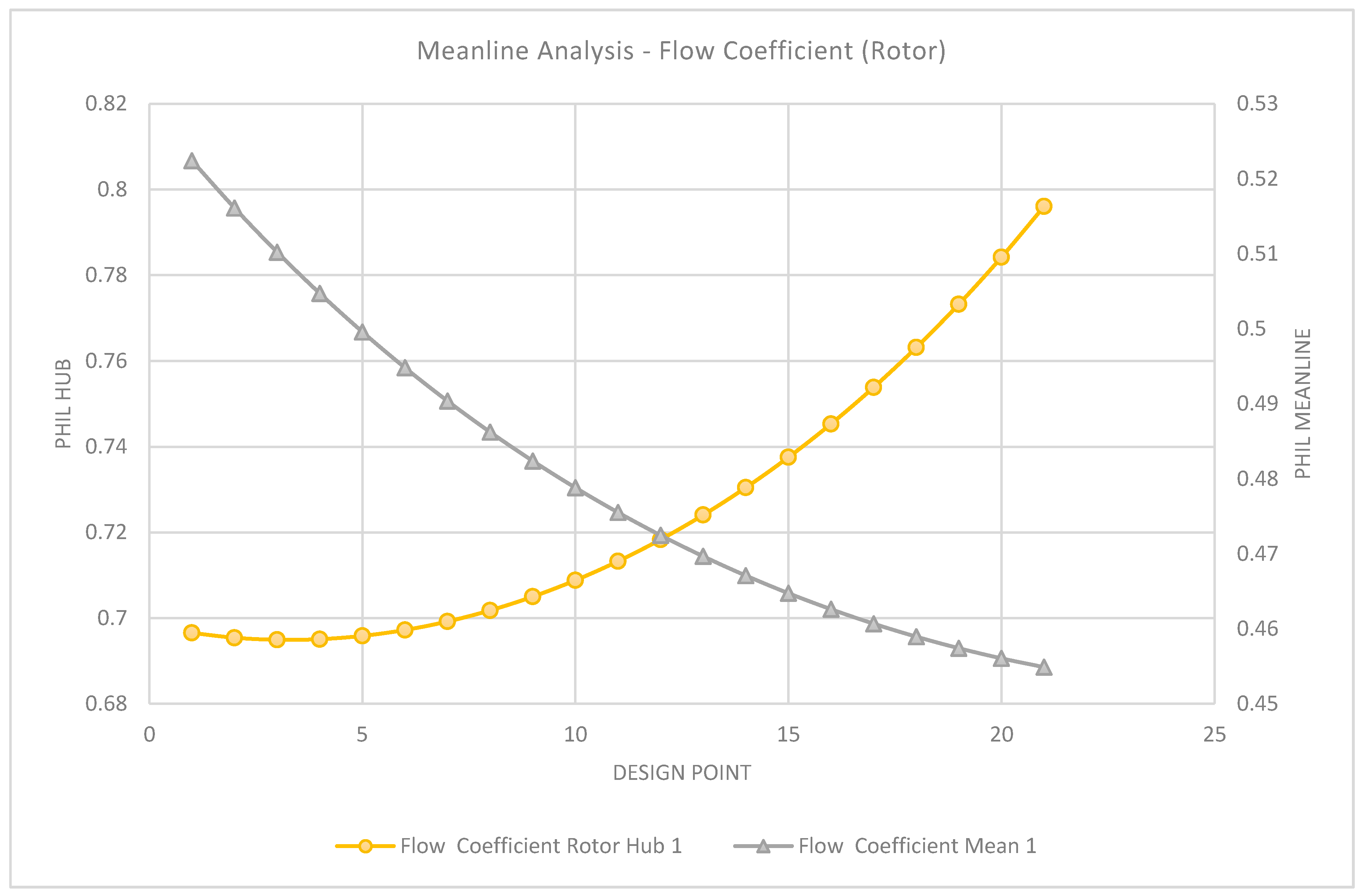
Figure 17 shows the flow coefficient for the meanline calculation, where all design points meet the criteria of <0.8. The hub flow coefficient is preferable in the region of design points 1–12.
3.3.3. Two-Dimensional Streamline Through-Flow Analysis
With satisfactory results from the meanline calculation for a selection of hub tip ratios, the performance study is expanded to include additional aerodynamic dependent input/output parameters. The additional input parameters include the rotor vane aspect ratio, number of vanes and profile trim. The aspect ratio is defined as the blade height/hub chord. From the works of [
2] and individual experimentation yielding unacceptable results, it is found that for this application common aspect ratios of 3 to 5 cannot be achieved. Thus, the vanes are restricted to aspect ratios around unity, with wide streamwise hub chords ensuring a reasonable thickness to maximise the low Reynolds numbers in micro turbomachinery. The profile trim is defined as the chord at the tip chord/hub chord; for the rotor, this value is commonly <1, reducing the chord with as the span increases. In a similar procedure to the meanline calculation, a set of iteration parameters (as seen below) are defined, and the variables are iterated for different values. The design points and iterative setup may be seen in
Table 10 and
Table 11 as well as in
Figure A7 and
Figure A8 in
Appendix A. The results of this study are summarised in
Appendix A (
Figure A9 and
Figure A10).
The figures from
Figure 18,
Figure 19 and
Figure 20 present the results of the 2D streamline through-flow study for variations in the rotor blade parameters. The iteration study (see
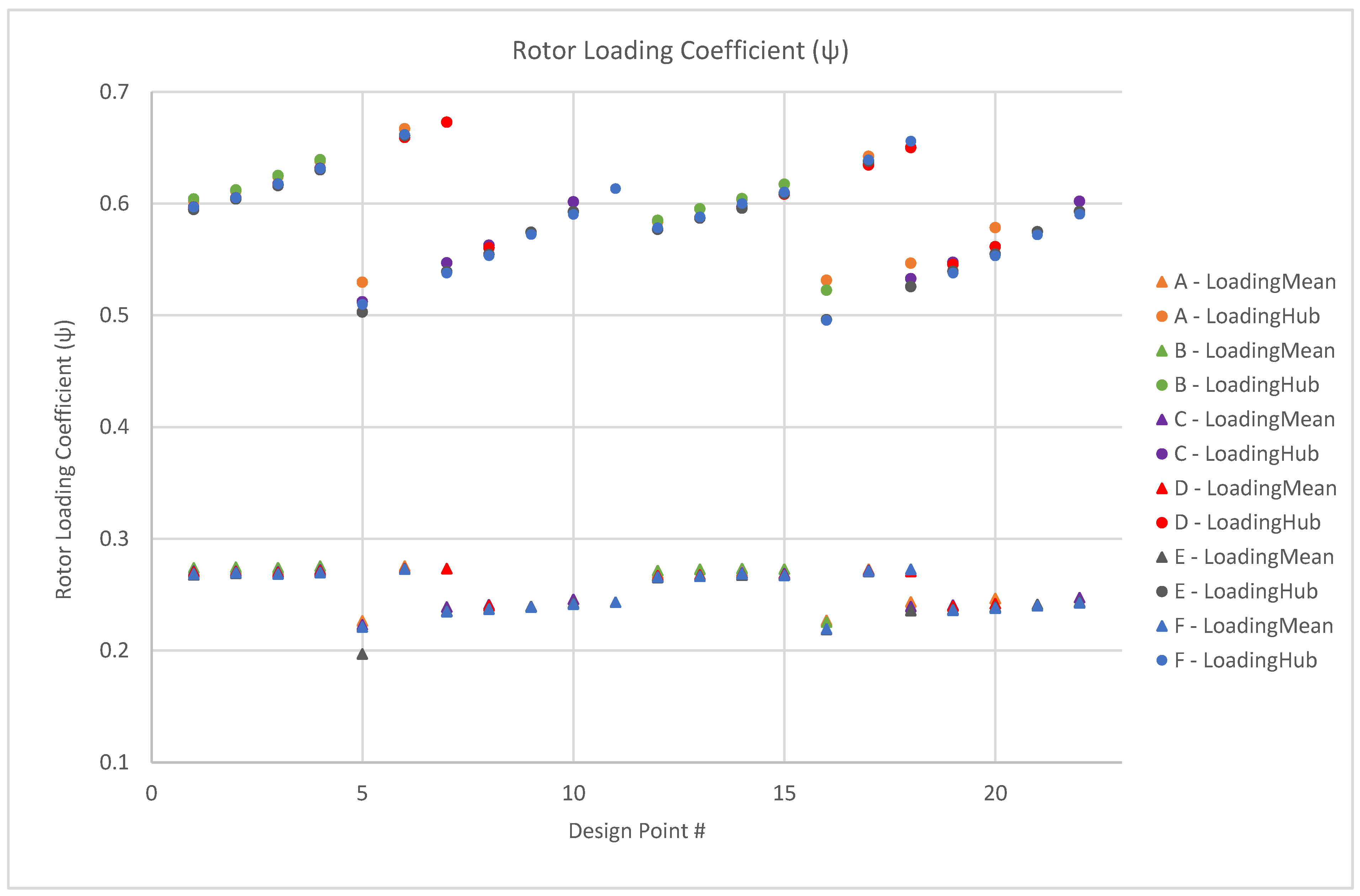
Table 11) is performed for varying rotor blade parameters; note that a blade aspect ratio greater than 1.2 produces failed results, and in addition the blades acquire unsuitable dimensions for manufacture. As with the 1D analysis, the rotor loading at the hub increases as the hub-tip ratio decreases (
Figure 18), i.e., for a fixed annulus the hub dimensions are reduced and thus become more loaded with an increased mass flux. The slight increase in the hub-tip outlet ratio also follows the same trend of reducing the hub loading. The meanline loading in both cases remains light. Similarly, the DeHaller number follows the same trend as with the 1D analysis (
Figure 19), whereby W
2/W
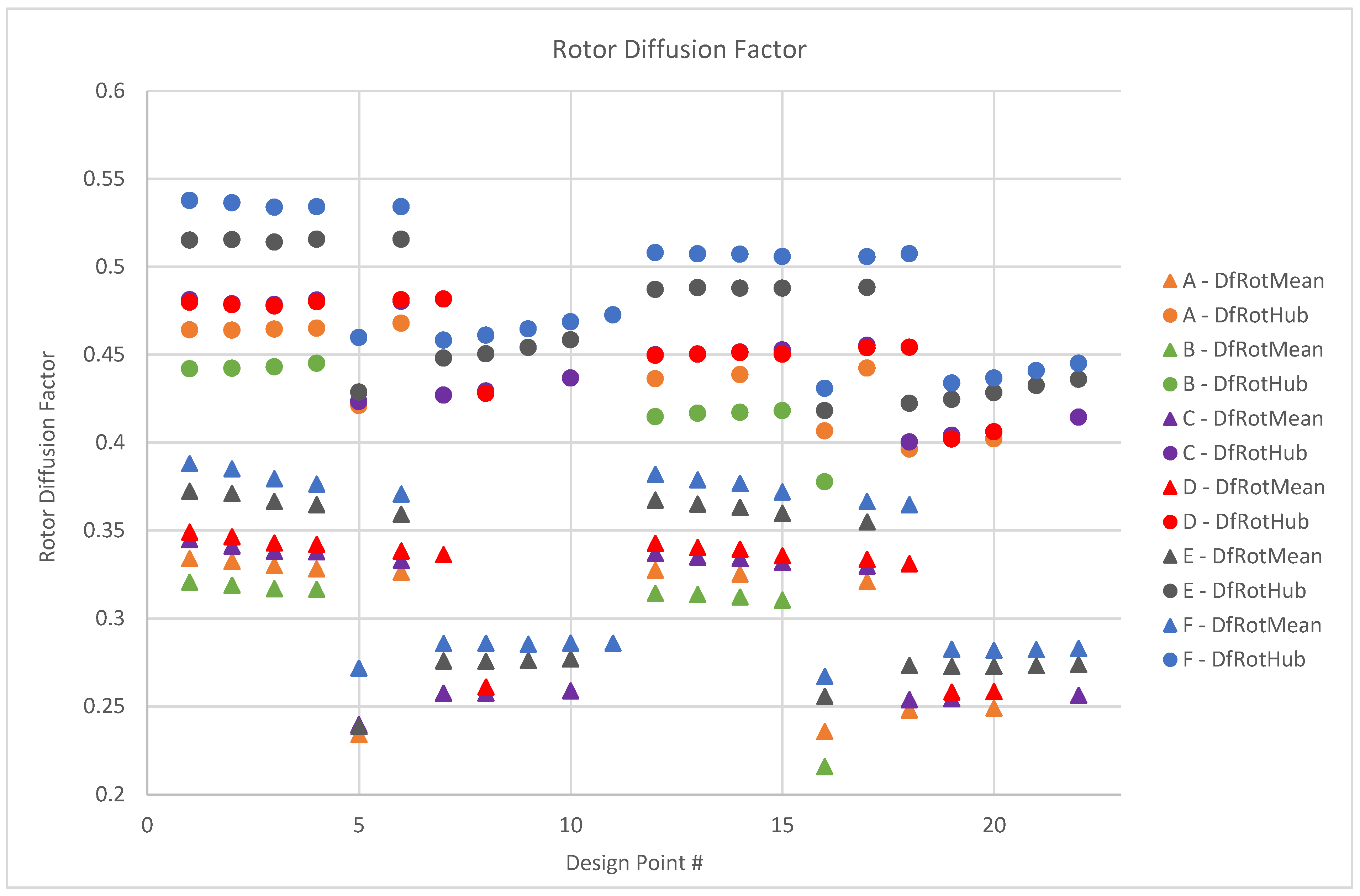
1 expectedly decreases with the reduced hub-tip ratio. The diffusion factor describes the tendencies for the boundary layer to separate under the influence of the pressure rise in the blade passage and is a good indicator for the blade spacing or pitch to chord ratio s/c. For a high efficiency, an upper limit of 0.6 for the hub and 0.4–0.45 for the meanline is applied; above 0.5, the associated blading losses rise exponentially. From
Figure 20, it is clearly seen that designs with an increased trailing edge blade pitch (s), i.e., with fewer blades, have higher diffusion factors and thus increased blade losses. At the calculated diffusion factors, however, the increased losses are potentially negligible against the benefits of a reduced weight and complexity of the design.
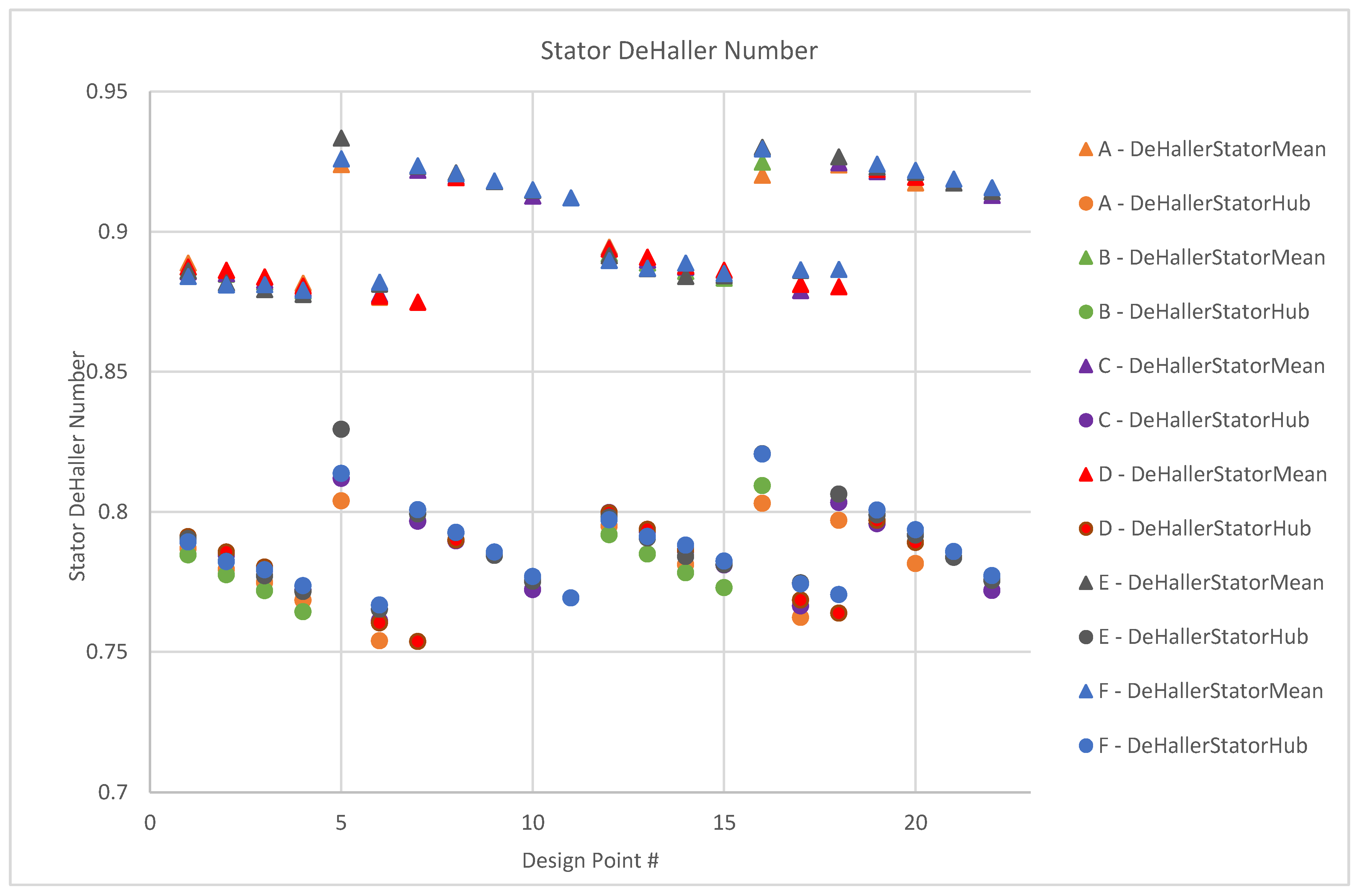
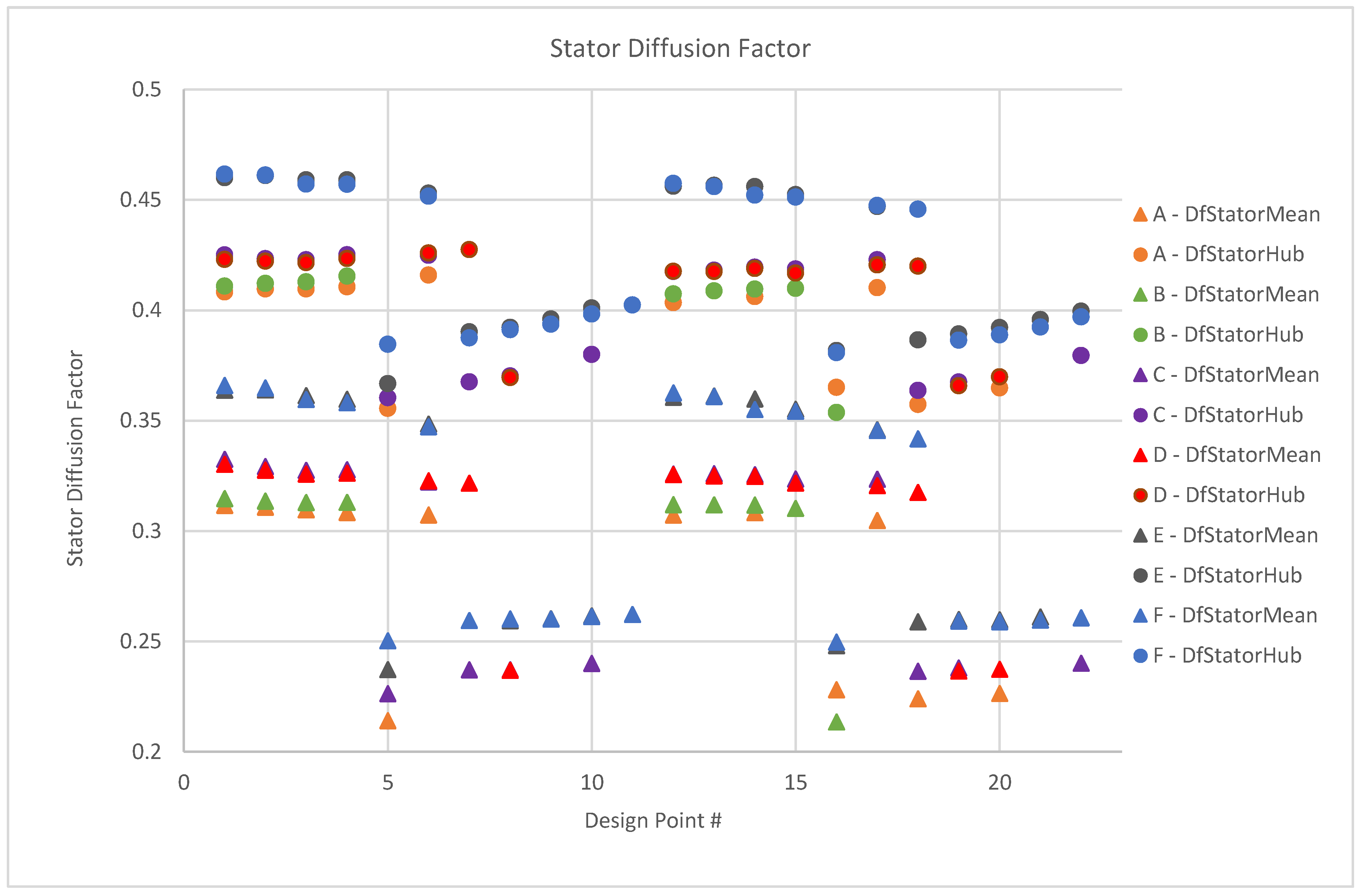
Figure 21 and
Figure 22 present the results for the stator through-flow streamline calculation. Based on the DeHaller number, the stator is highly loaded, both on the meanline and hub, due to the high axial velocities with an increased rotor swirl and an introduced ramp on the rotor flow path which expectedly increases the velocity and the loading further downstream in the stator. Higher diffusion factors are satisfactory for the stator, with a constraint of <0.6; all of the design points satisfy the criteria.
Design points 5 and 16 (DP5 = HtrInlet = HtrOutlet = 0.56–DP16 = HtrInlet = 0.56, HtrOutlet = 0.57, respectively) present anomalies in the data pattern for both rotor and stator through-flow analysis. For the rotor, both design points at iteration E and F are calculated with reduced hub loading and more favourably diffusion factors. The associated stator design for these points is highly loaded at both hub and on meanline, however, investigation into the use of IGV’s to reduce stator loading can be conducted in future works. In conclusion of the through-flow analysis, input parameters associated with design points 5 and 6 for iteration E and F are chosen for further design evaluation (see
Table 12). Preliminary blade geometry for further analysis may also be seen in
Table 13 and
Figure 23.