Uncertainty Quantification of the Effects of Small Manufacturing Deviations on Film Cooling: A Fan-Shaped Hole
Abstract
:1. Introduction
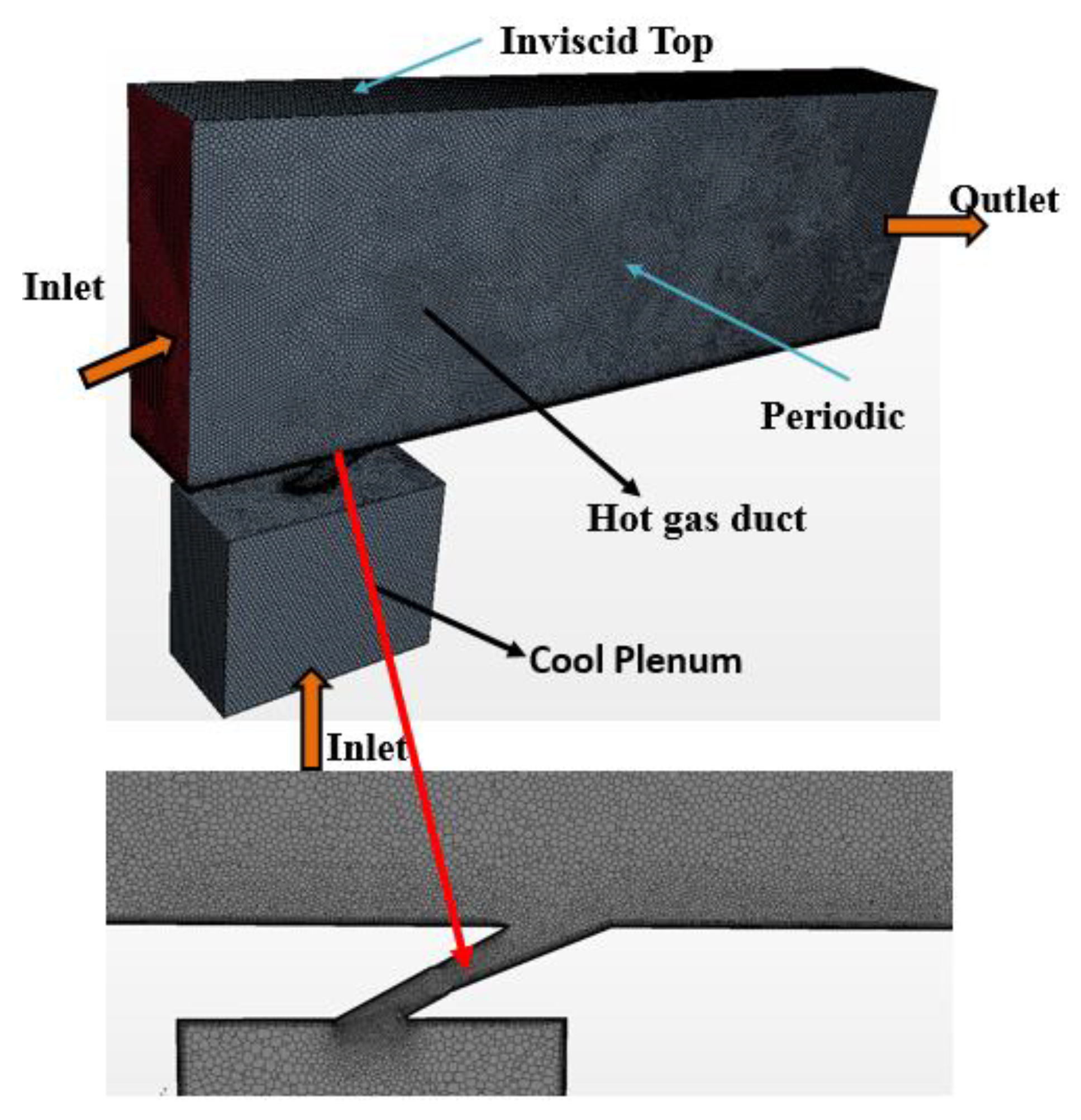
2. Computational Setup and Validation
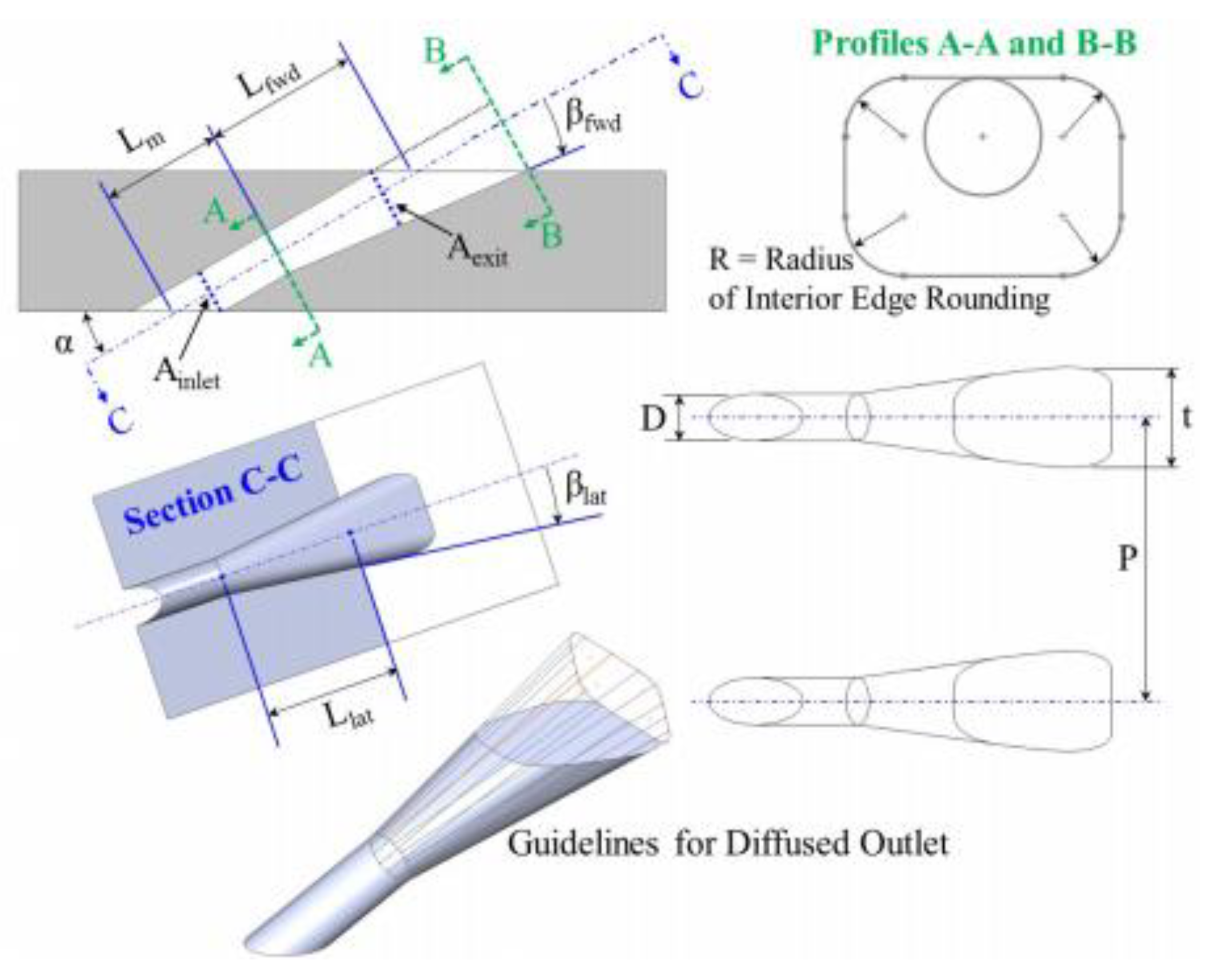
2.1. Geometry Models
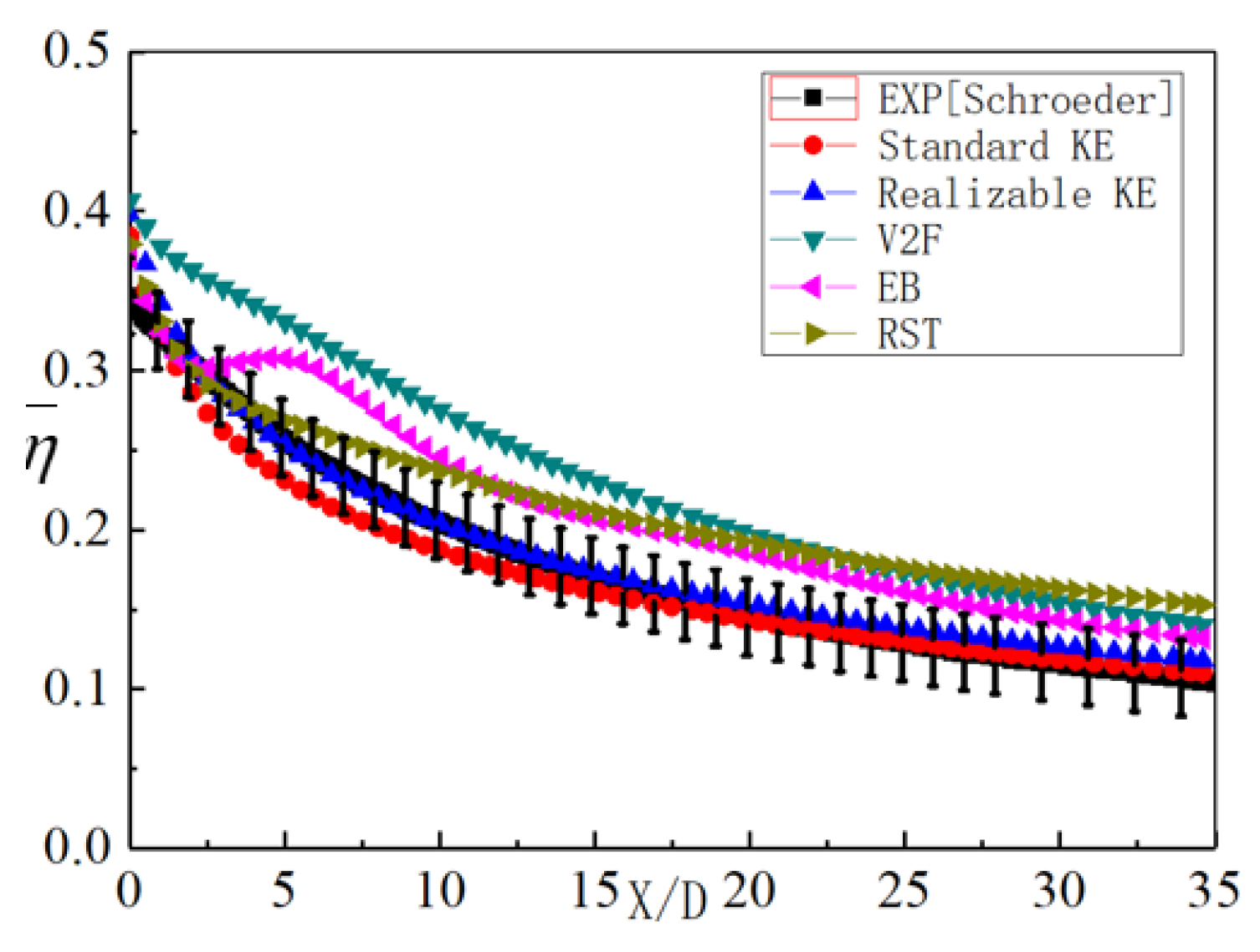
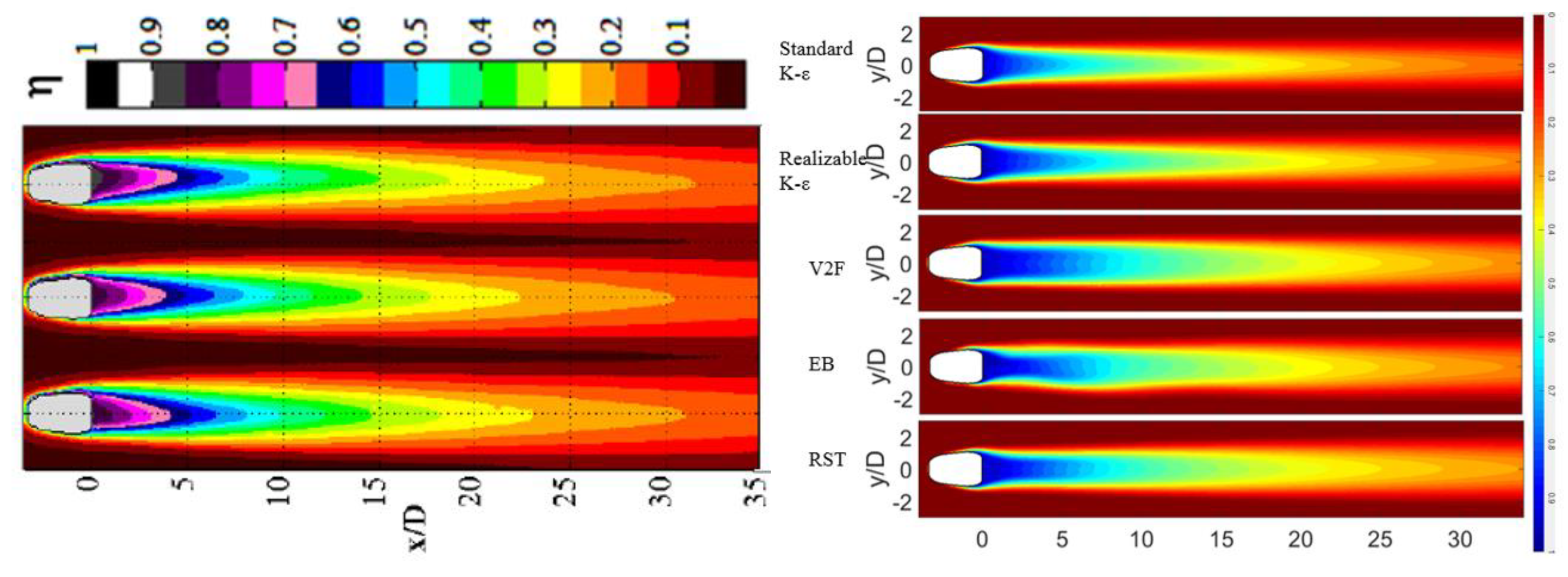
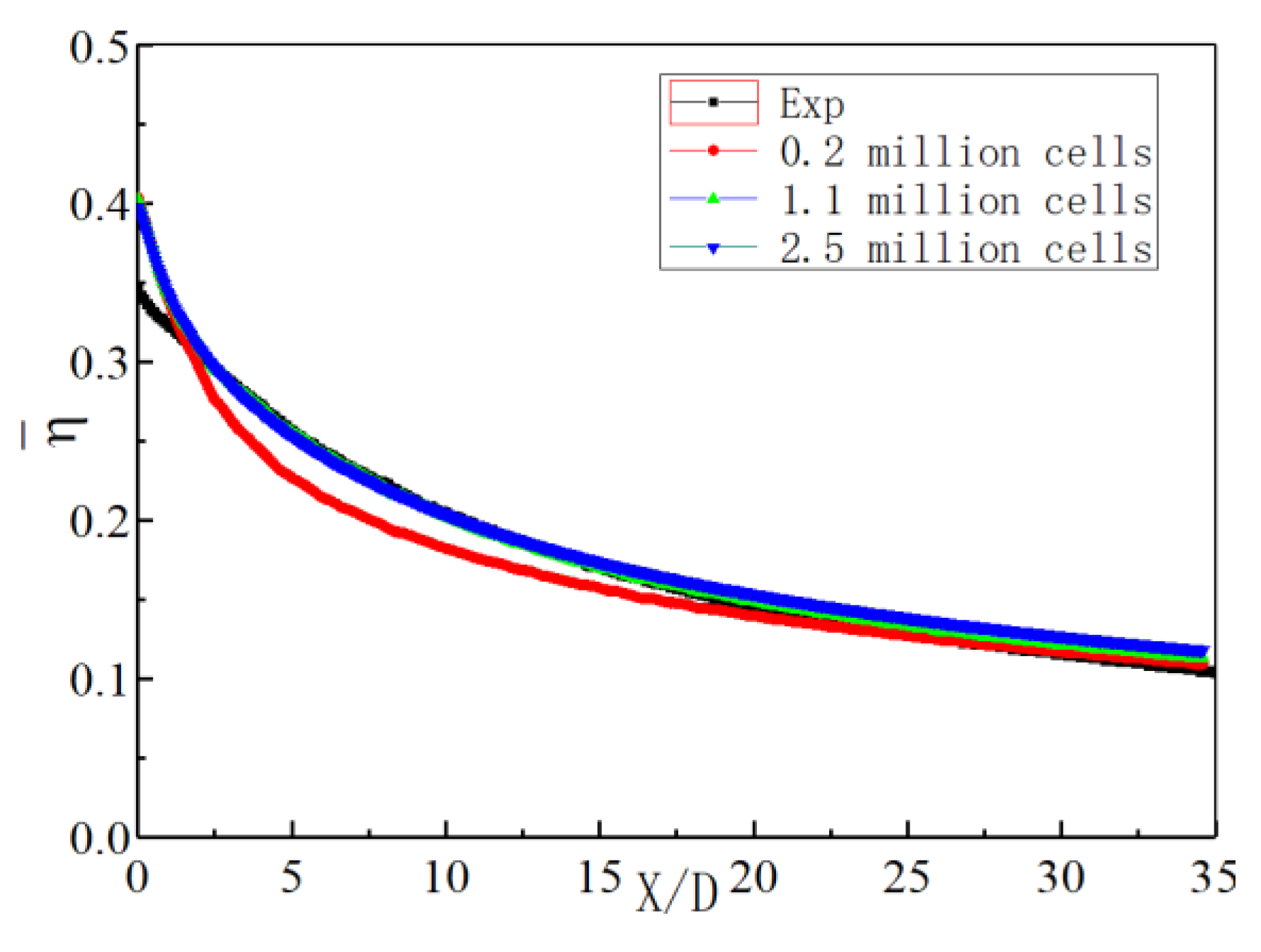
2.2. Numerical Method and Validation
3. Uncertainty Quantification Methodology
4. Results and Discussion
4.1. Film Cooling Effectiveness
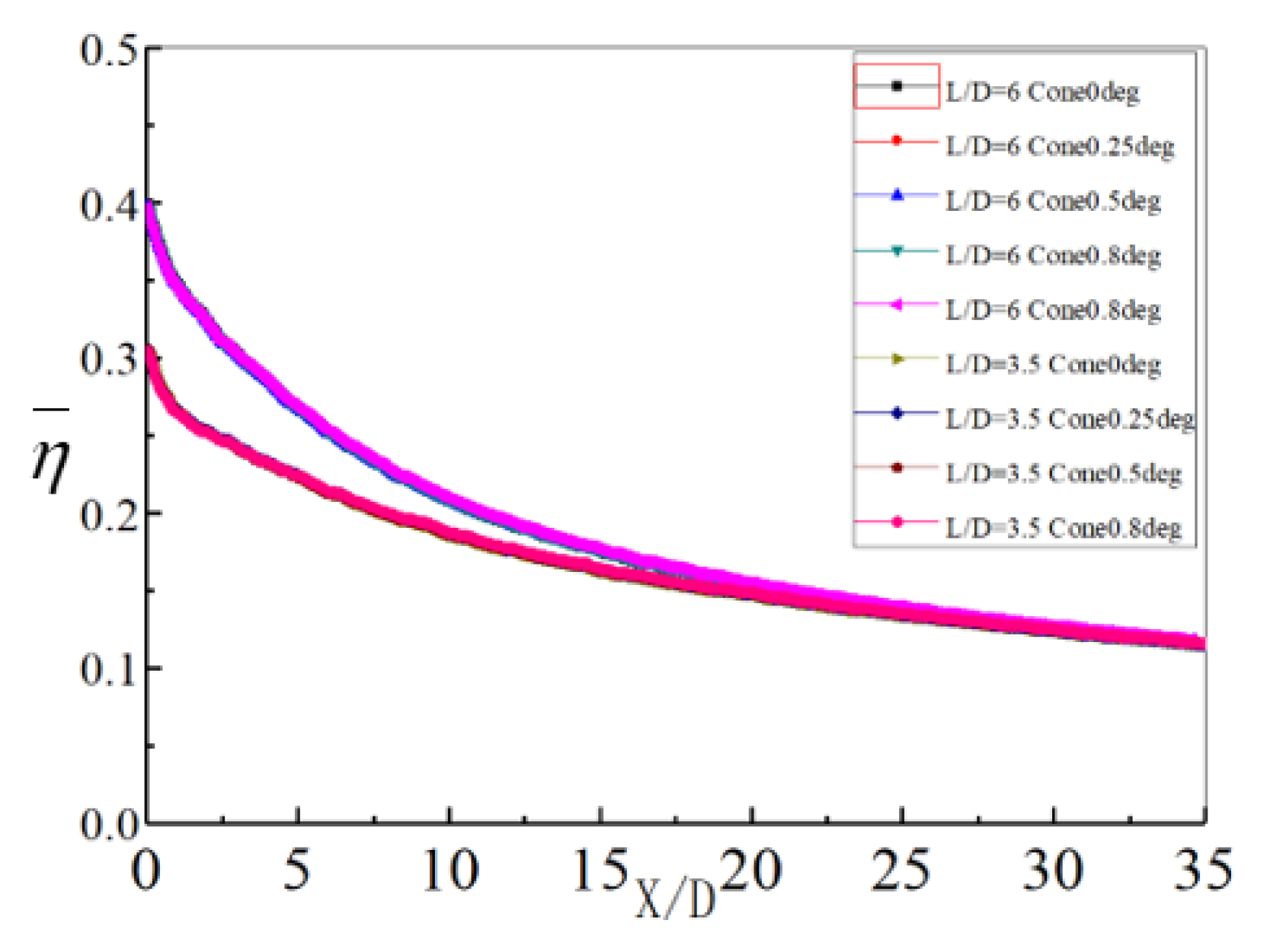
4.1.1. Effect of the Conical Angle Deviation on Film Cooling Effectiveness
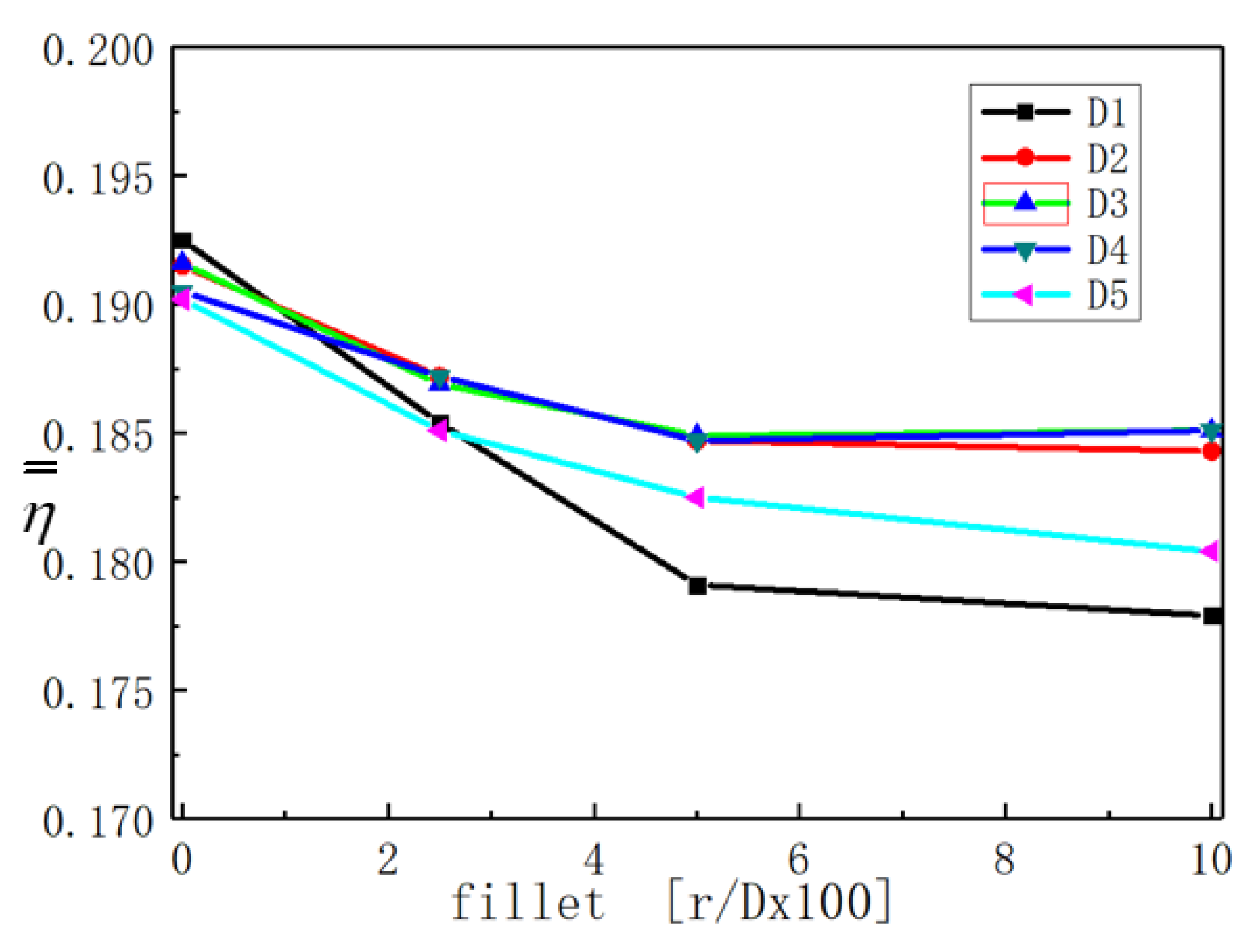
4.1.2. Effect of the Diameter and Filleted Edge Deviations on Film Cooling Effectiveness
4.2. Discharge Coefficient
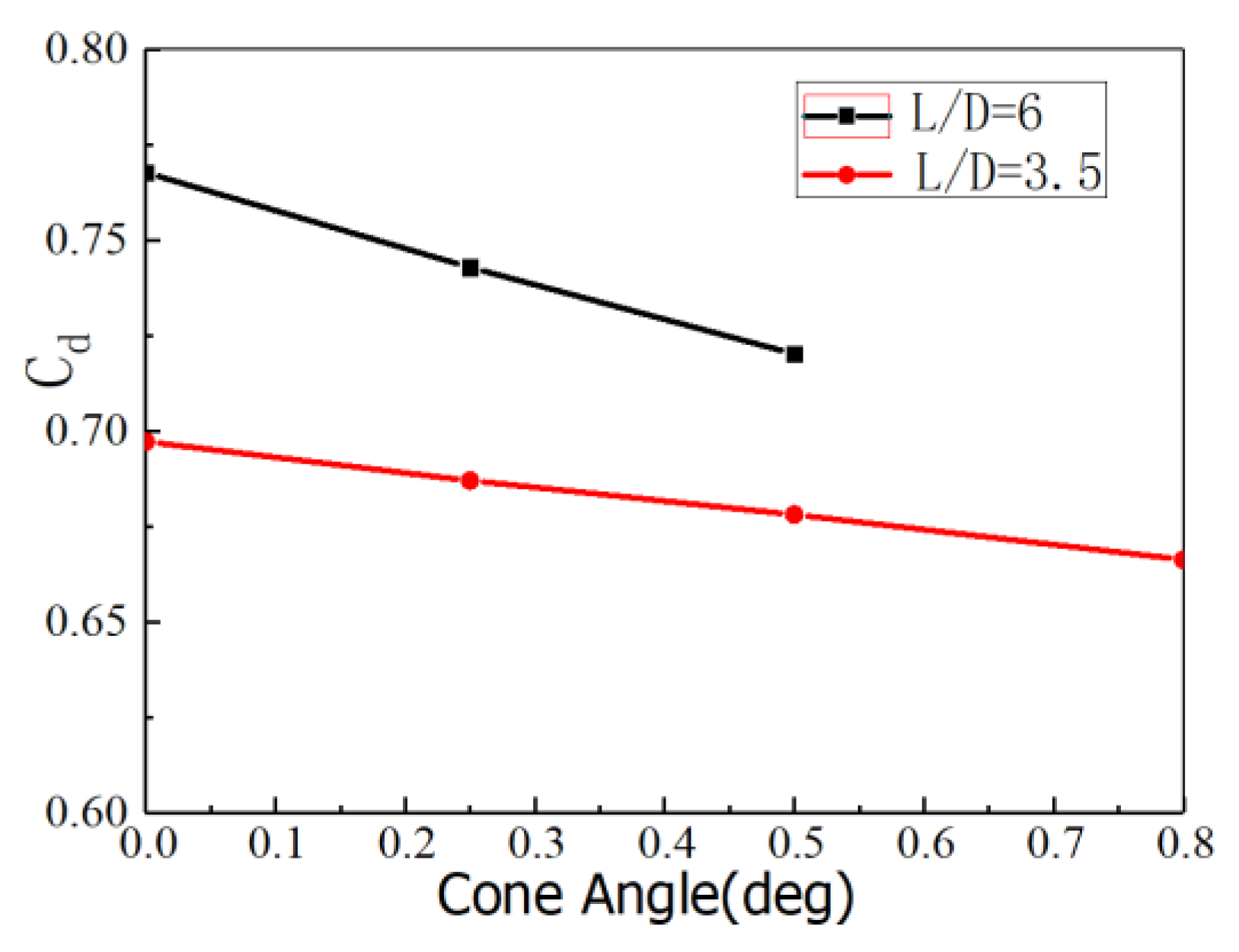
4.2.1. Effect of the Conical Angles on the Discharge Coefficient
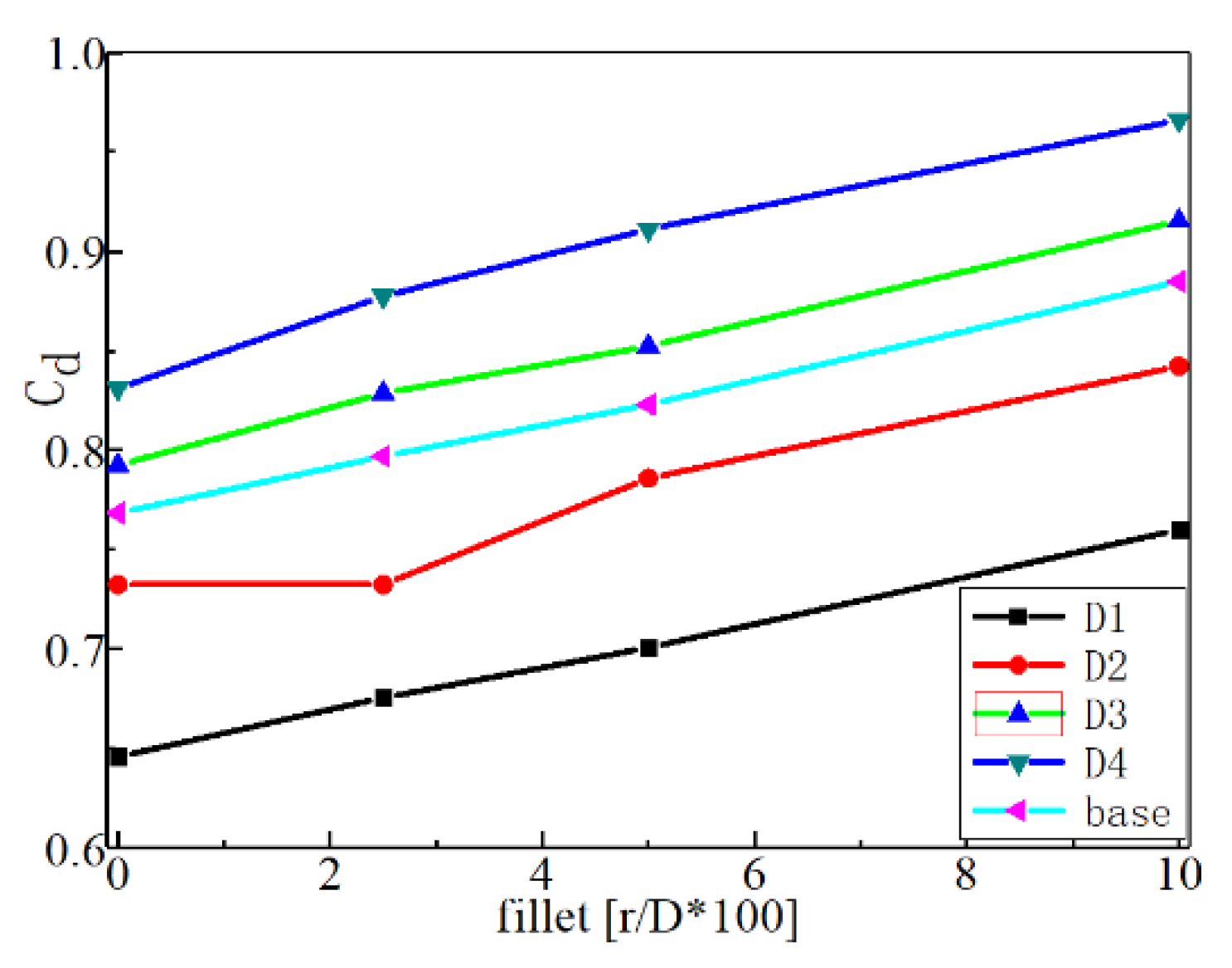
4.2.2. Effect of the Diameter and Filleted Edge Deviations on the Discharge Coefficient
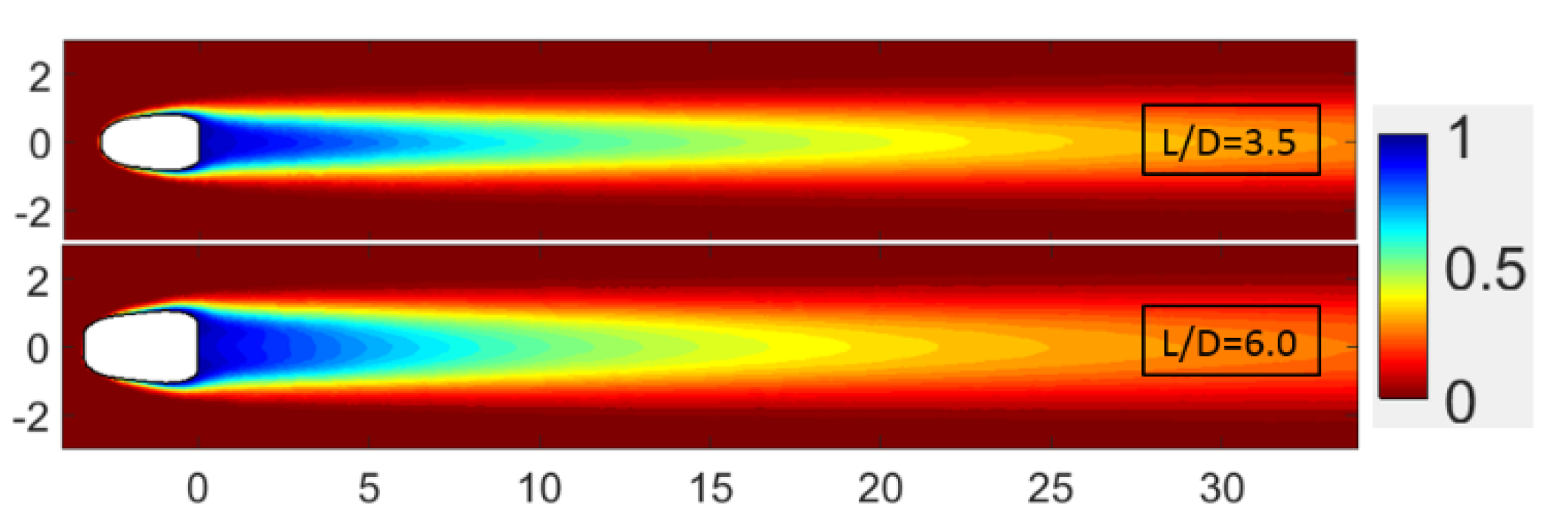
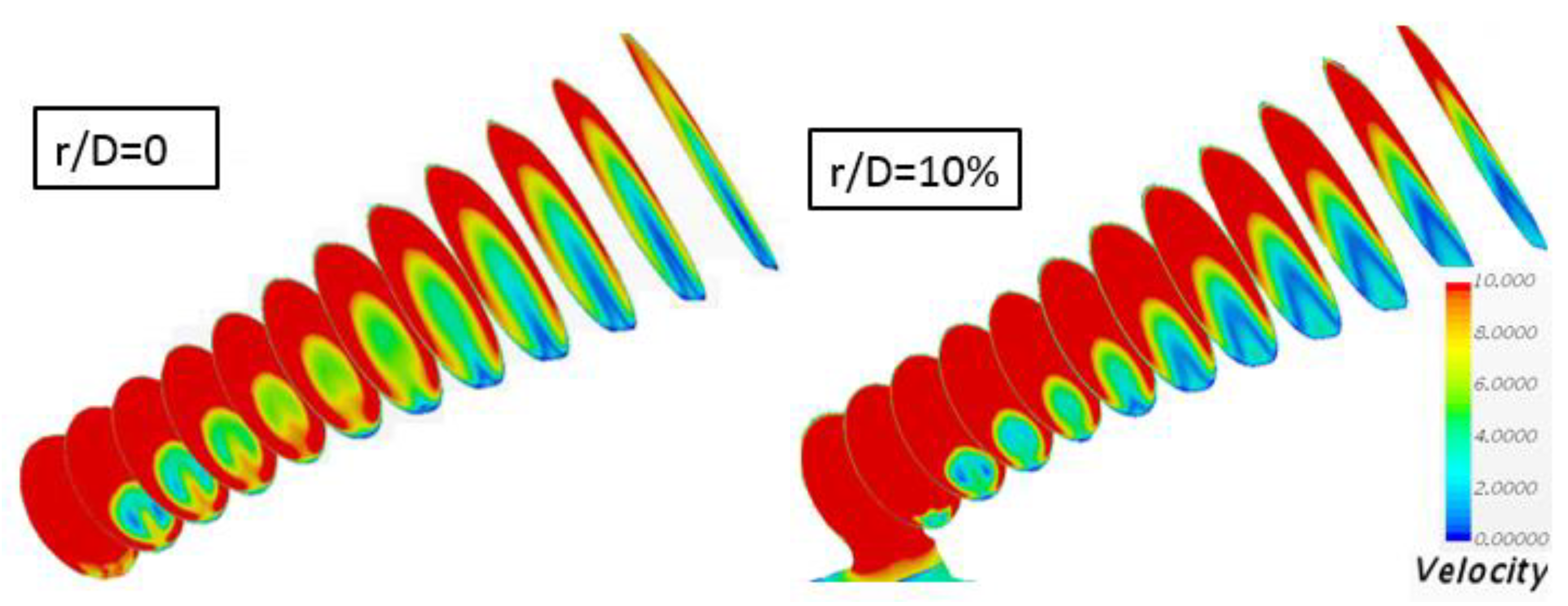
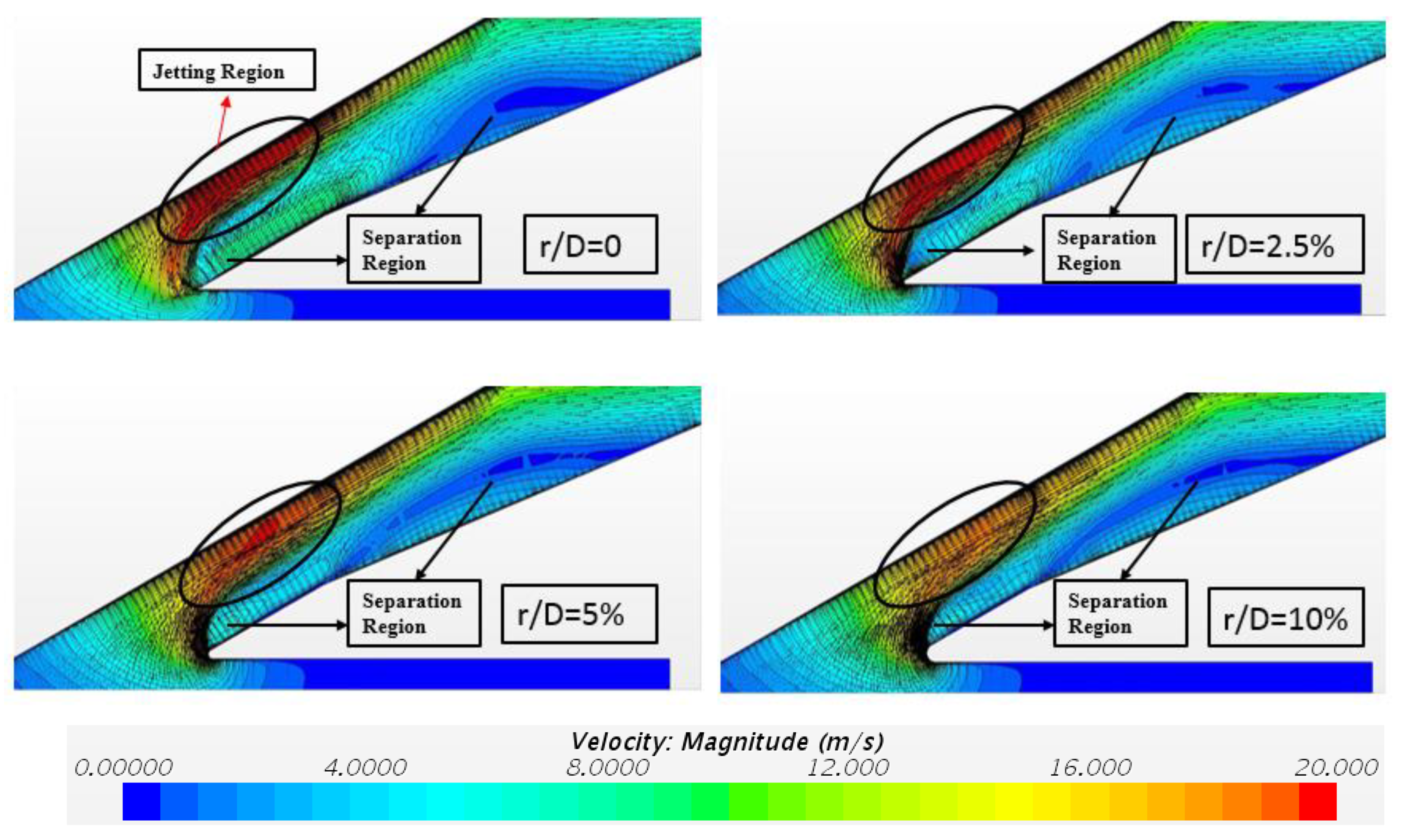
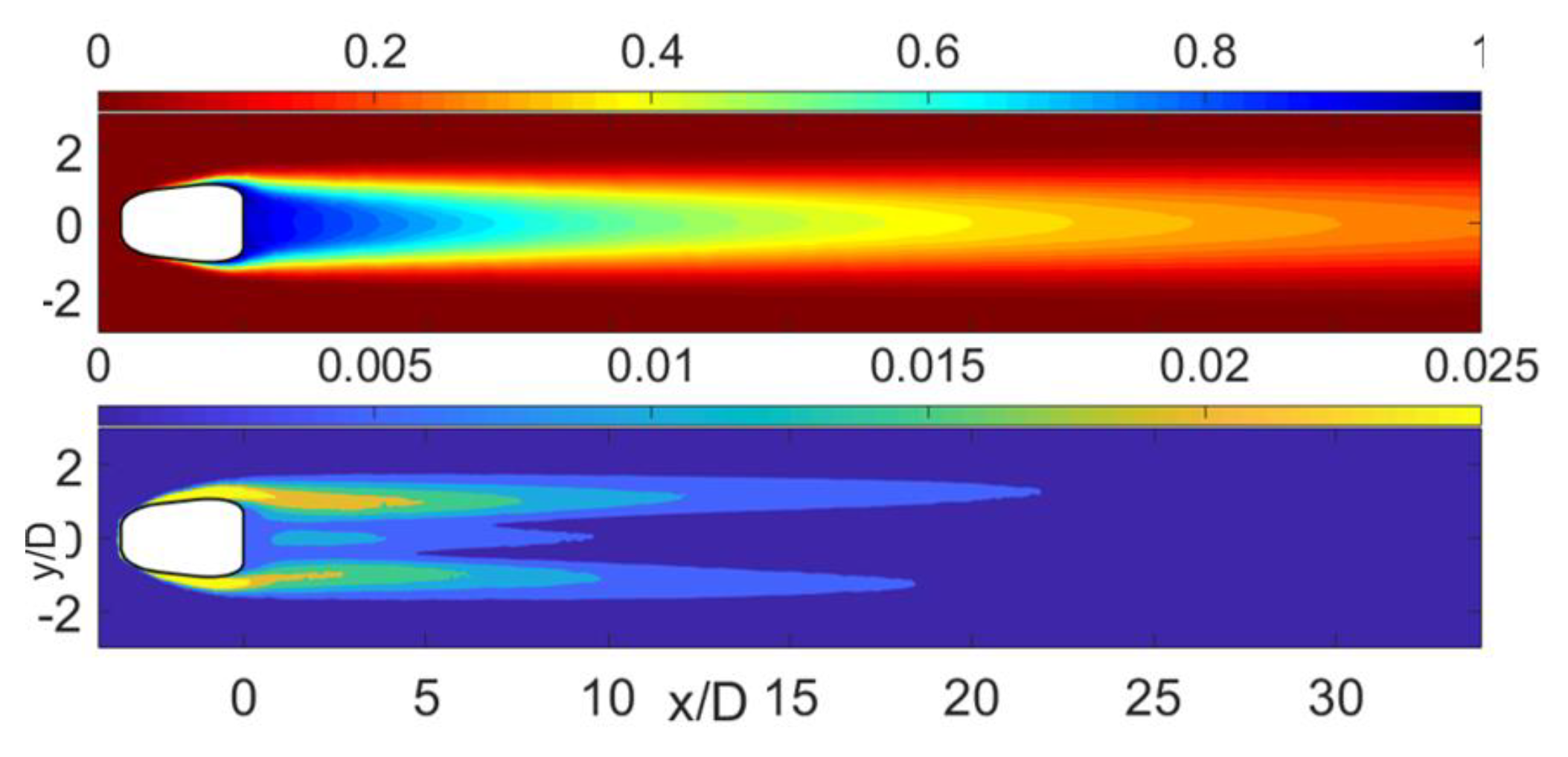
4.3. In-Hole Flow Field with Filleted Edge
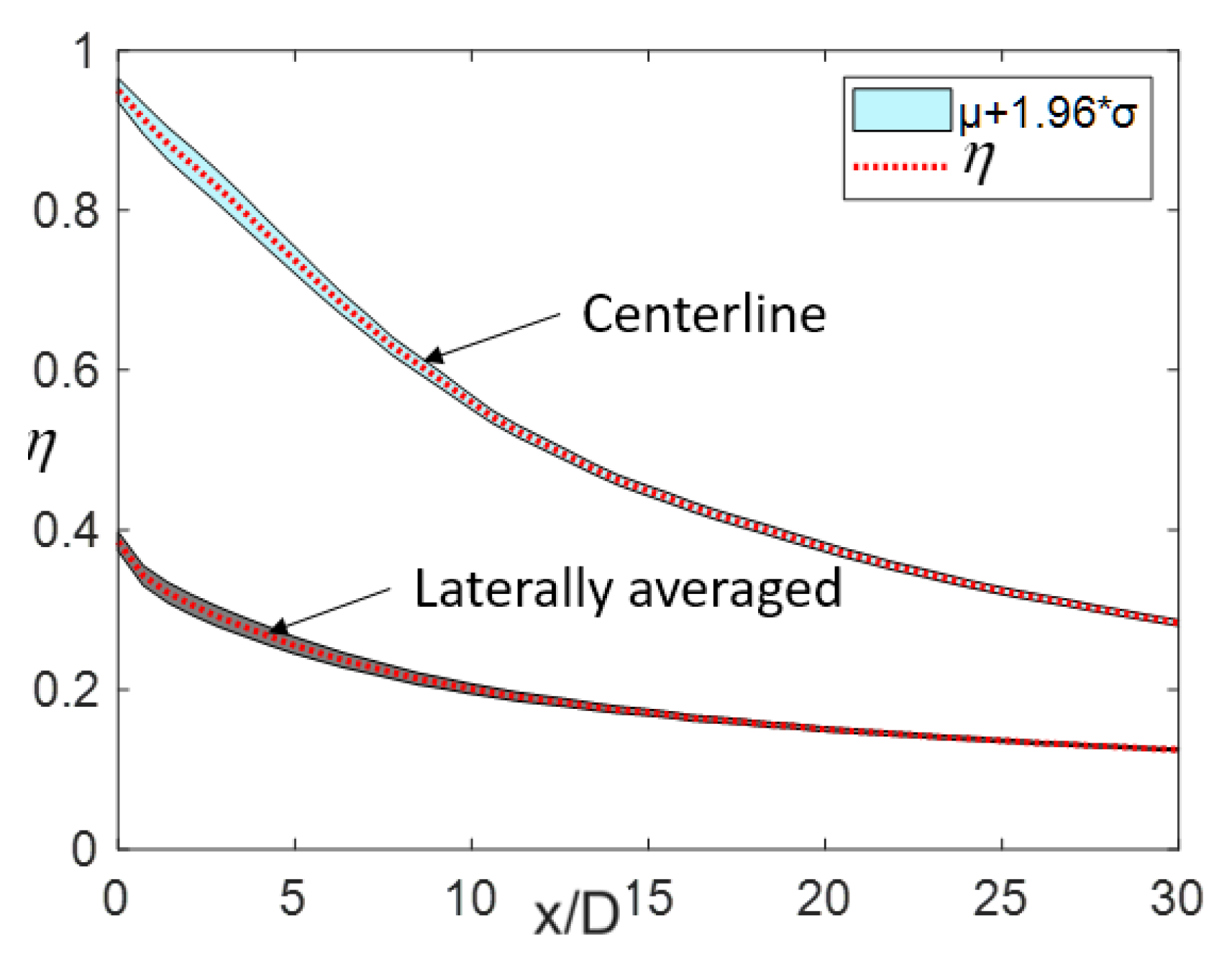
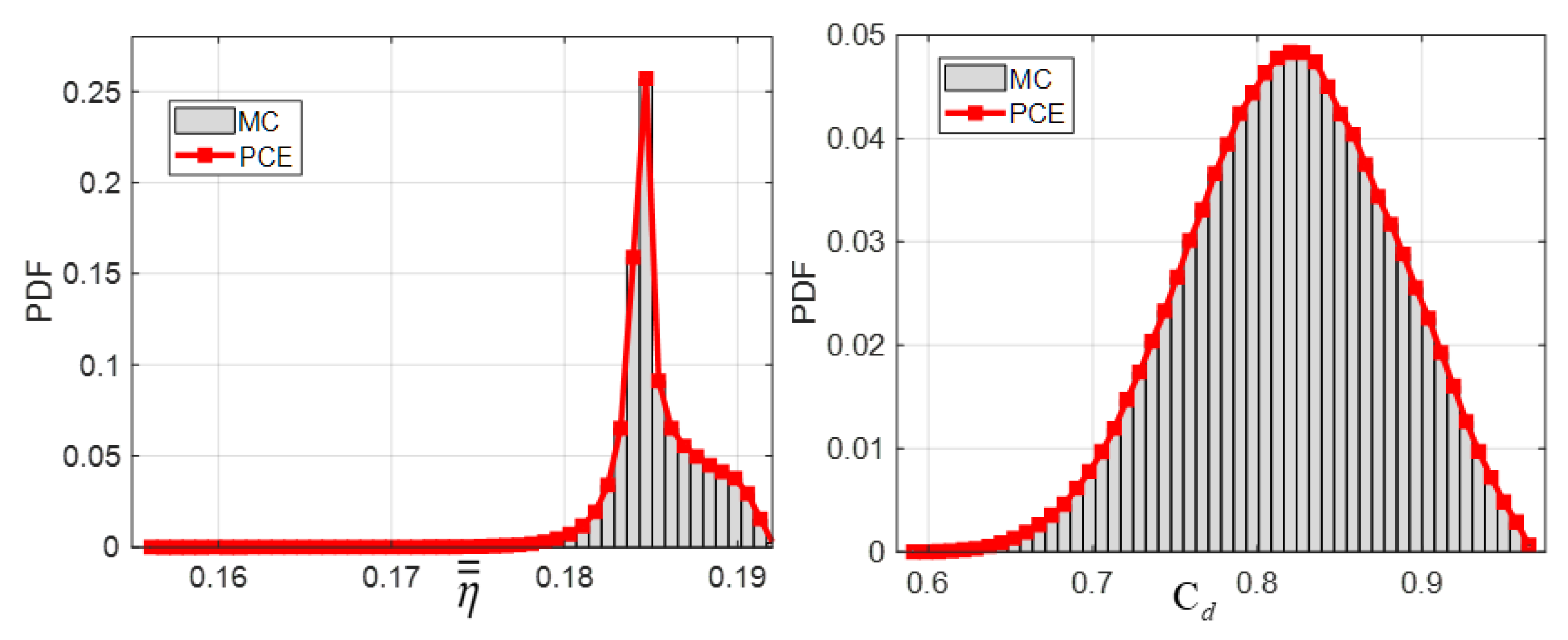
4.4. UQ Analysis
5. Conclusions
- Conical angle deviation exerts no obvious effect on η. However, Cd decreases by 6.2% when the conical angle deviation is 0.5° and increases to 12.9 when the angle is 1.0°.
- The presence of diameter and fillet deviations produces a superposition effect. The area average η decreases by 3.4%, and Cd increases to 15.2% with the fillet deviation existing alone. However, the values are 7.6% and 25.7% when the two deviations exist.
- The decrease in Cd is mainly caused by the weakened streamwise vorticity of in-tube and the blockage effect when the hole possesses a fillet. The velocity distribution of the hole exit exerts an important impact on the change in η.
- The UQ analysis shows that the 95% confidence interval of the centerline and laterally-averaged η both are relatively small. The effects of cylindrical section deviations on η is limited, and the fillet radii mainly affects the flow field in-hole. The result also shows that the PDF of area average η does not satisfy the regular distribution, while the PDF of Cd basically still satisfies the Gaussian distribution.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| EDM | Electrical Discharge Machining |
| AM | Additive Manufacturing |
| Cd | discharge coefficient |
| UQ | Uncertainty quantification |
| PCE | Polynomial Chaos Expansion |
| Std | Standard deviation |
| Probability Density Function | |
| SRSM | Stochastic Response Surface Method |
| MC | Monte Carlo |
| L | Hole Length |
| D | Hole Diameter |
| TIT | Turbine Inlet Temperature |
| BR | Blowing ratio |
| DR | Density Ratio |
| r | Fillet radius |
| EB | Elliptic Blending model |
| Pm | mainstream pressure |
| Ptc | total pressure of the coolant |
| LE | Leading Edge of hole |
| TE | Trailing Edge of hole |
| CRVP | Counter Rotating Vortex Pair |
| RST | Reynolds Stress Turbulence |
| Greek symbols | |
| Film cooling effectiveness | |
| Conical angle | |
| Subscripts | |
| w | wall |
| mainstream flow | |
| c | inlet of coolant duct |
| aw | adiabatic wall |
| entrance | |
| exit | |
References
- Bunker, R.S. Gas Turbine Cooling: Moving from Macro to Micro Cooling. ASME Conf. Proc. 2013, 2013, 94277. [Google Scholar]
- Bunker, R.S. The Effects of Manufacturing Tolerances on Gas Turbine Cooling. J. Turbomach. 2009, 131, 041018. [Google Scholar] [CrossRef]
- PRIMA North America, Inc. Laser Drilling of Cylindrical and Shaped Holes. Available online: https://slideplayer.com/slide/6880655/ (accessed on 20 September 2017).
- Wen, Z.; Pei, H.; Zhang, C.; Wang, B. Analysis of Surface Quality of Multi-film Cooling Holes in Nickel-based Single Crystal Superalloy. Mater. Sci. Technol. 2016, 32, 1845–1854. [Google Scholar] [CrossRef]
- Maina, M.R. Modeling and Control of Nd: YAG Laser Percussion Drilling of Nickel-Based Super Alloys. Master’s Thesis, Jomo Kenyatta University of Agriculture and Technology, Juja, Kenya, 2015. [Google Scholar]
- Ramesh, S.; Ramirez, D.G.; Ekkad, S.V.; Alvin, M.A. Analysis of film cooling performance of advanced tripod hole geometries with and without manufacturing features. J. Heat Mass Transf. 2016, 94, 9–19. [Google Scholar] [CrossRef]
- Montomoli, F.; Massini, M.; Salvadori, S.; Martelli, F. Geometrical Uncertainty and Film Cooling: Fillet radii. J. Turbomach. 2012, 134, 011019. [Google Scholar] [CrossRef]
- Cerantola, D.J.; Birk, A.M. Quantifying Blowing Ratio for Shaped Cooling Holes. J. Turbomach. 2018, 140, 021008. [Google Scholar] [CrossRef]
- Johnson, P.L.; Ricklick, M.; Kapat, J.S.; Zuniga, H.; Brown, G. The Impact of Manufacturing Techniques on Film Cooling Effectiveness. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 15–17 July 2013. [Google Scholar]
- Haydt, S.; Lynch, S.; Lewis, S. The Effect of a Meter-Diffuser Offset on Shaped Film Cooling Hole Adiabatic Effectiveness. J. Turbomach. 2017, 139, 091012. [Google Scholar] [CrossRef]
- Montomoli, F.; Carnevale, M.; D’Ammaro, A.; Massini, M.; Salvadori, S. Uncertainty Quantification in Computational Fluid Dynamics and Aircraft Engines, 2nd ed.; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Seshadri, P.; Shahpar, S.; Parks, G. Aggressive Design in Turbomachinery. In Proceedings of the 7th Dresdner Probabilistic Workshop, Dresden, Germany, 9 October 2014. [Google Scholar]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA/CR-2014-218178; NASA Langley Research Center: Hampton, VA, USA, 2014.
- Schroeder, R.P.; Thole, K.A. Adiabatic Effectiveness Measurements for a Baseline Shaped Film Cooling Hole. In Proceedings of the ASME Turbo Expo 2014: Turbine Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 July 2014. GT2014-25992. [Google Scholar]
- Schroeder, R.P.; Thole, K.A. Effect of high freestream turbulence on flowfields of shaped film cooling holes. J. Turbomach. 2016, 138, 091001. [Google Scholar] [CrossRef]
- Wiener, N. The homogeneous chaos. Am. J. Math. 1938, 60, 897–936. [Google Scholar] [CrossRef]
- Xiu, D.; Karniadakis, G.E. The Wiener—Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Xiong, F.; Yang, S. Engineering Probability Uncertainty Analysis Method; Science Press: Beijing, China, 2015. [Google Scholar]
- Isukapalli, S.S. Uncertainty Analysis of Transport-Transformation Models. Ph.D. Thesis, The State University of New Jersey, New Brunswick, NJ, USA, 1999. [Google Scholar]
- Isukapalli, S.S.; Roy, A.; Georgopoulos, P.G. Efficient sensitivity/uncertainty analysis using the combined stochastic response surface method and automated differentiation: Application to environmental and biological systems. Risk Anal. 2000, 20, 591–602. [Google Scholar] [CrossRef] [PubMed]
- Haydt, S.; Lynch, S.; Lewis, S. The Effect of Area Ratio Change via Increased Hole Length for Shaped Film Cooling Holes With Constant Expansion Angles. J. Turbomach. 2018, 140, 051002. [Google Scholar] [CrossRef]
- Adami, P.; Martelli, F.; Montomoli, F.; Saumweber, C. Numerical Investigation of Internal Crossflow Film Cooling. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; pp. 51–63. [Google Scholar]
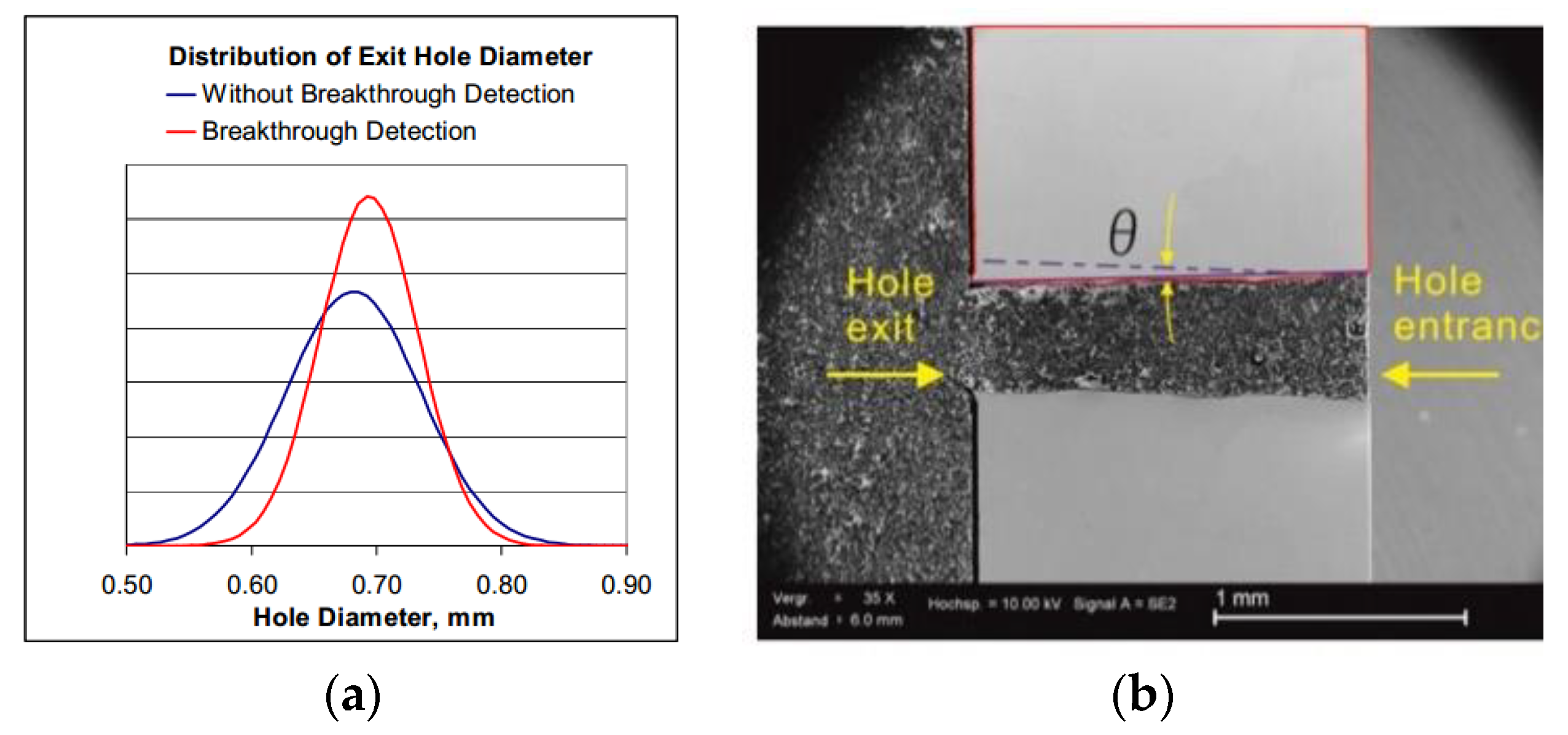
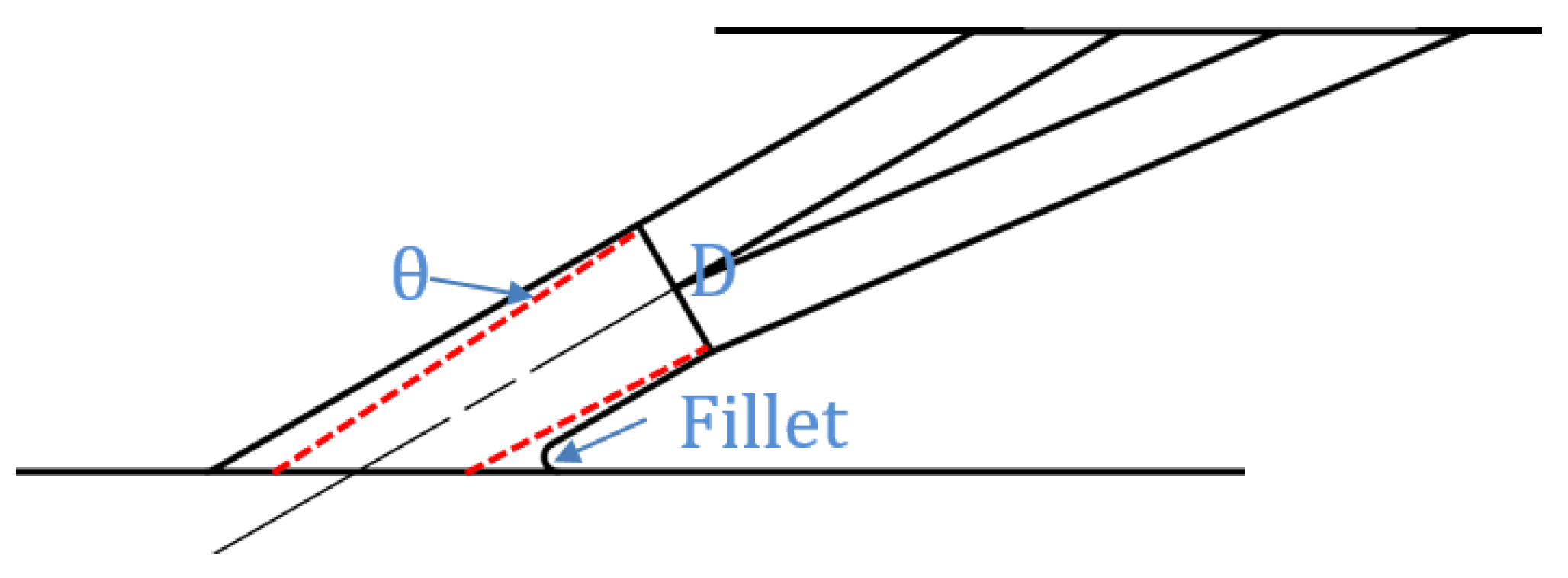
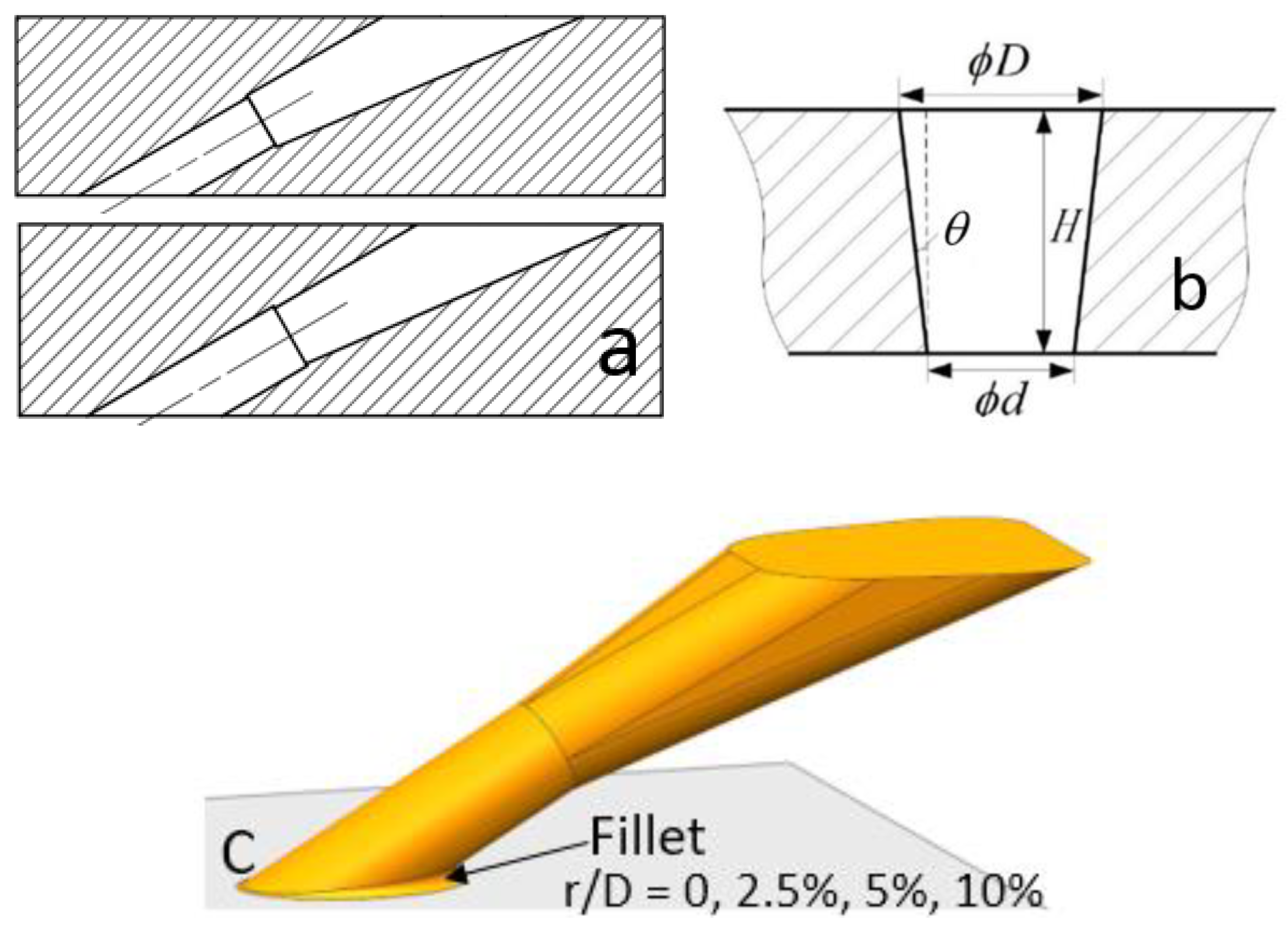
| Parameter | Range |
|---|---|
| Mainstream inlet velocity, U | 20 m/s |
| Mainstream inlet temperature, T∞ | 450 K |
| Mainstream Re (based on hole diameter) | 5190 |
| Turbulent intensity of mainstream, Tu∞ | 5.4% |
| Turbulent intensity of coolant, Tuc | 5% |
| Coolant inlet temperature, Tc | 300 K |
| Blowing ratio, M | 1.0 |
| Density ratio, DR | 1.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Chen, P.; Li, X.; Ren, J.; Jiang, H. Uncertainty Quantification of the Effects of Small Manufacturing Deviations on Film Cooling: A Fan-Shaped Hole. Aerospace 2019, 6, 46. https://doi.org/10.3390/aerospace6040046
Shi W, Chen P, Li X, Ren J, Jiang H. Uncertainty Quantification of the Effects of Small Manufacturing Deviations on Film Cooling: A Fan-Shaped Hole. Aerospace. 2019; 6(4):46. https://doi.org/10.3390/aerospace6040046
Chicago/Turabian StyleShi, Wei, Pingting Chen, Xueying Li, Jing Ren, and Hongde Jiang. 2019. "Uncertainty Quantification of the Effects of Small Manufacturing Deviations on Film Cooling: A Fan-Shaped Hole" Aerospace 6, no. 4: 46. https://doi.org/10.3390/aerospace6040046
APA StyleShi, W., Chen, P., Li, X., Ren, J., & Jiang, H. (2019). Uncertainty Quantification of the Effects of Small Manufacturing Deviations on Film Cooling: A Fan-Shaped Hole. Aerospace, 6(4), 46. https://doi.org/10.3390/aerospace6040046