A Simple Model to Assess the Role of Dust Composition and Size on Deposition in Rotorcraft Engines
Abstract
1. Introduction
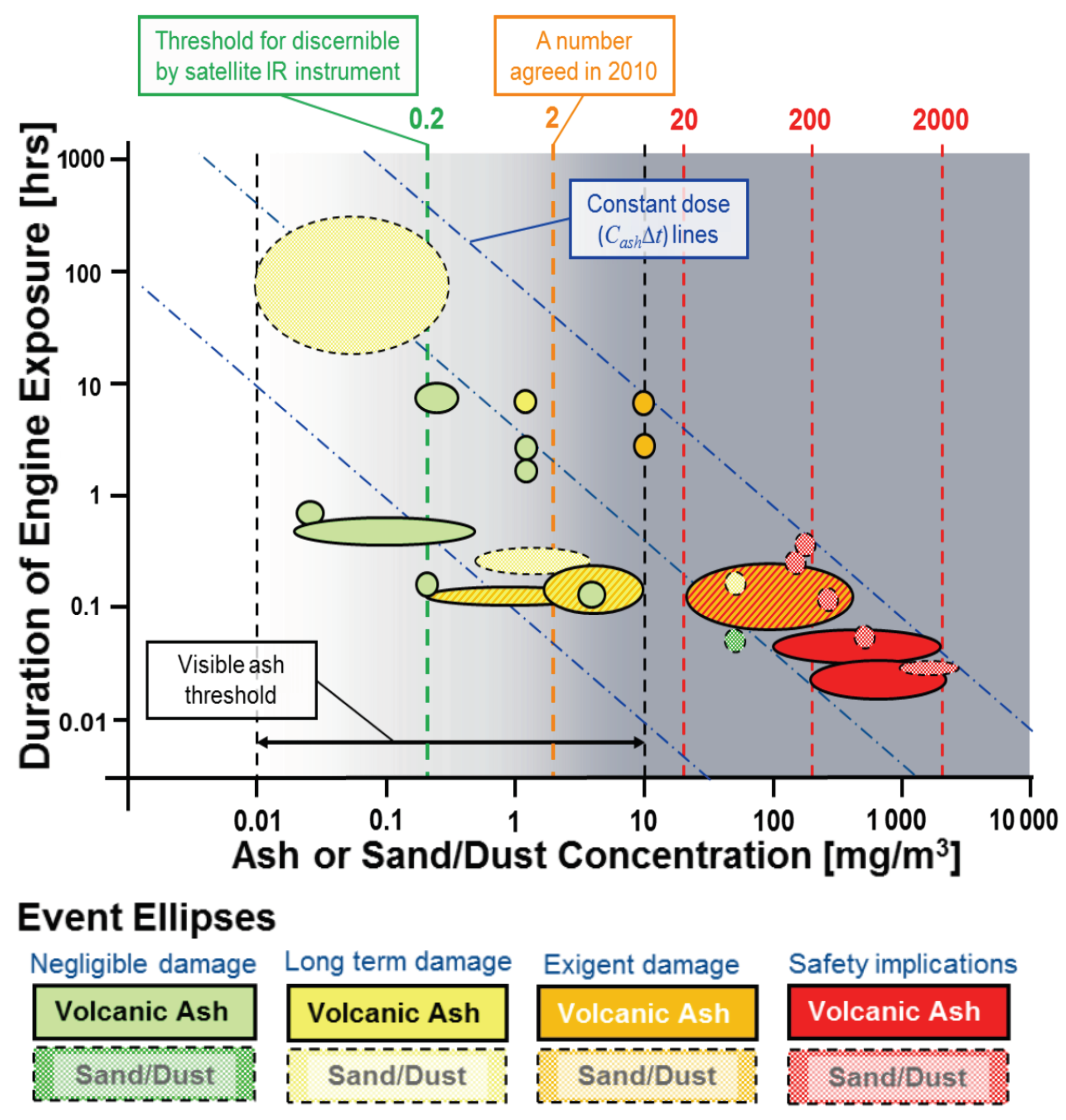
1.1. Dose
1.2. Composition
1.3. Scope
2. Materials and Methods
2.1. Theory
2.1.1. Dust Dose Model
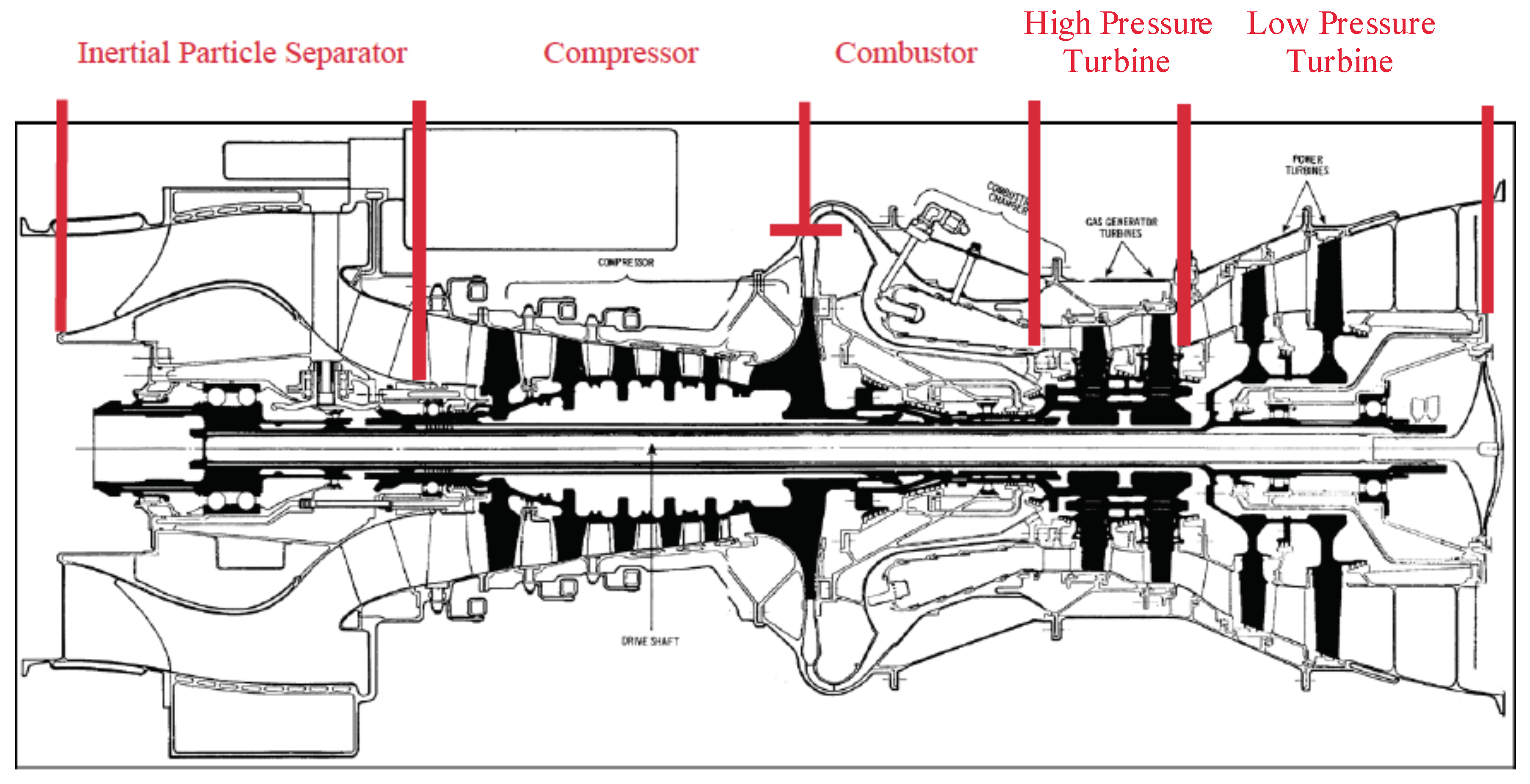
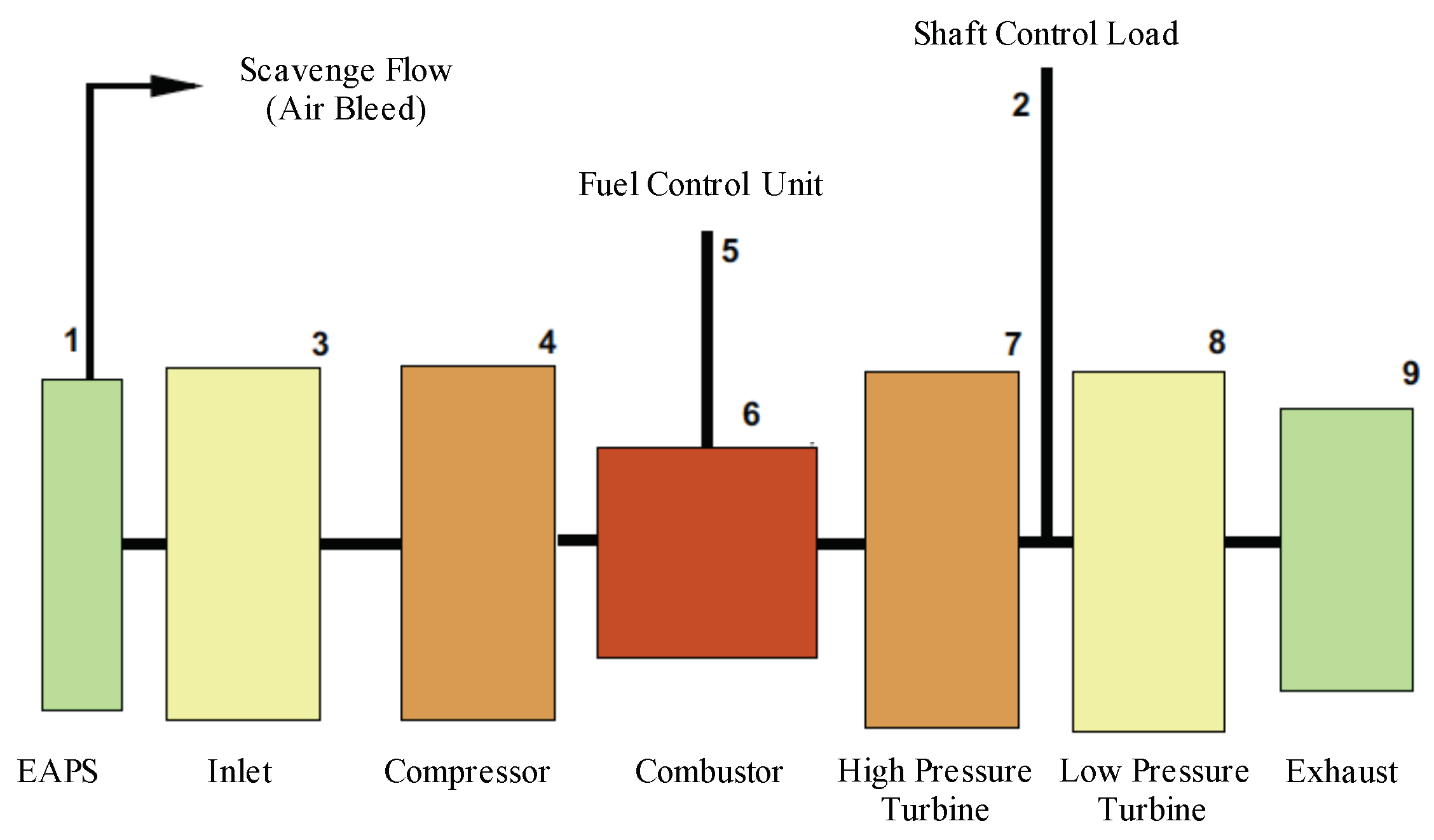
2.1.2. Integrated Inertial Particle Separator
2.1.3. Compressor
2.1.4. Combustor
2.1.5. Turbine
2.2. NGV Capture Efficiency
2.2.1. Sticking Probability Models
2.2.2. Reduced Order Sticking Model
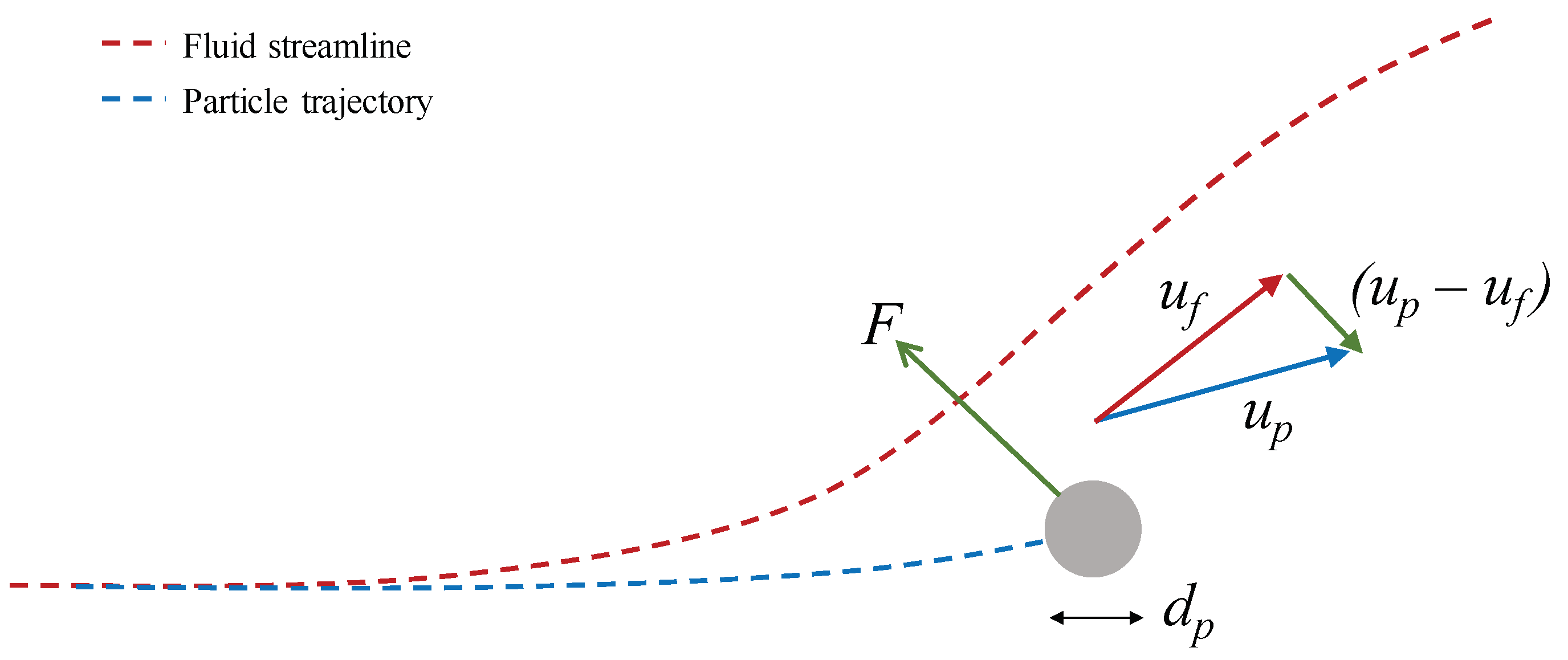
2.2.3. Particle Acceleration
2.2.4. Thermal Stokes Number
2.2.5. Particle Heating
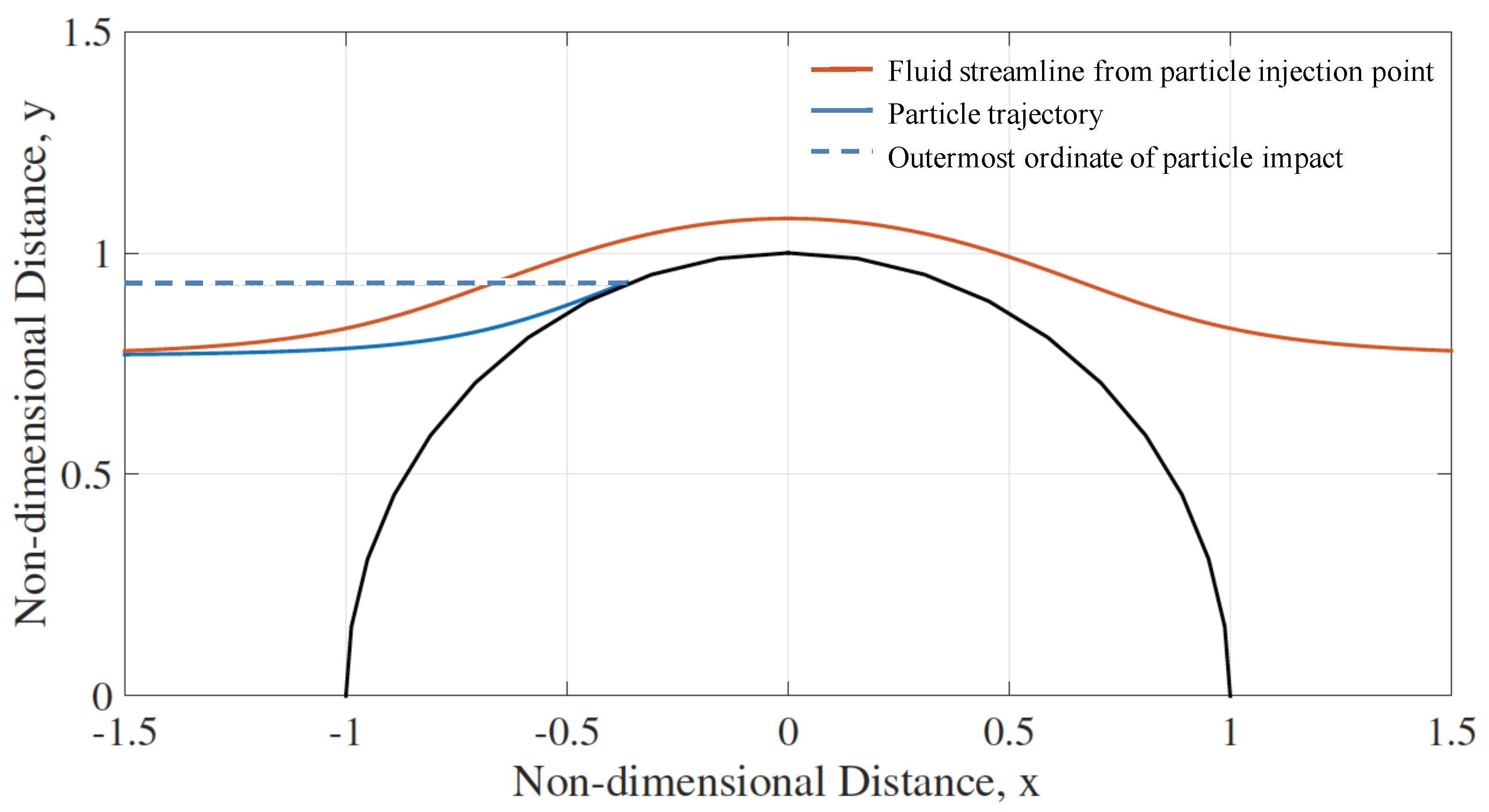
2.2.6. Potential Flow over a 2D Right Cylinder
2.2.7. Accumulation Factor
2.3. Model Inputs
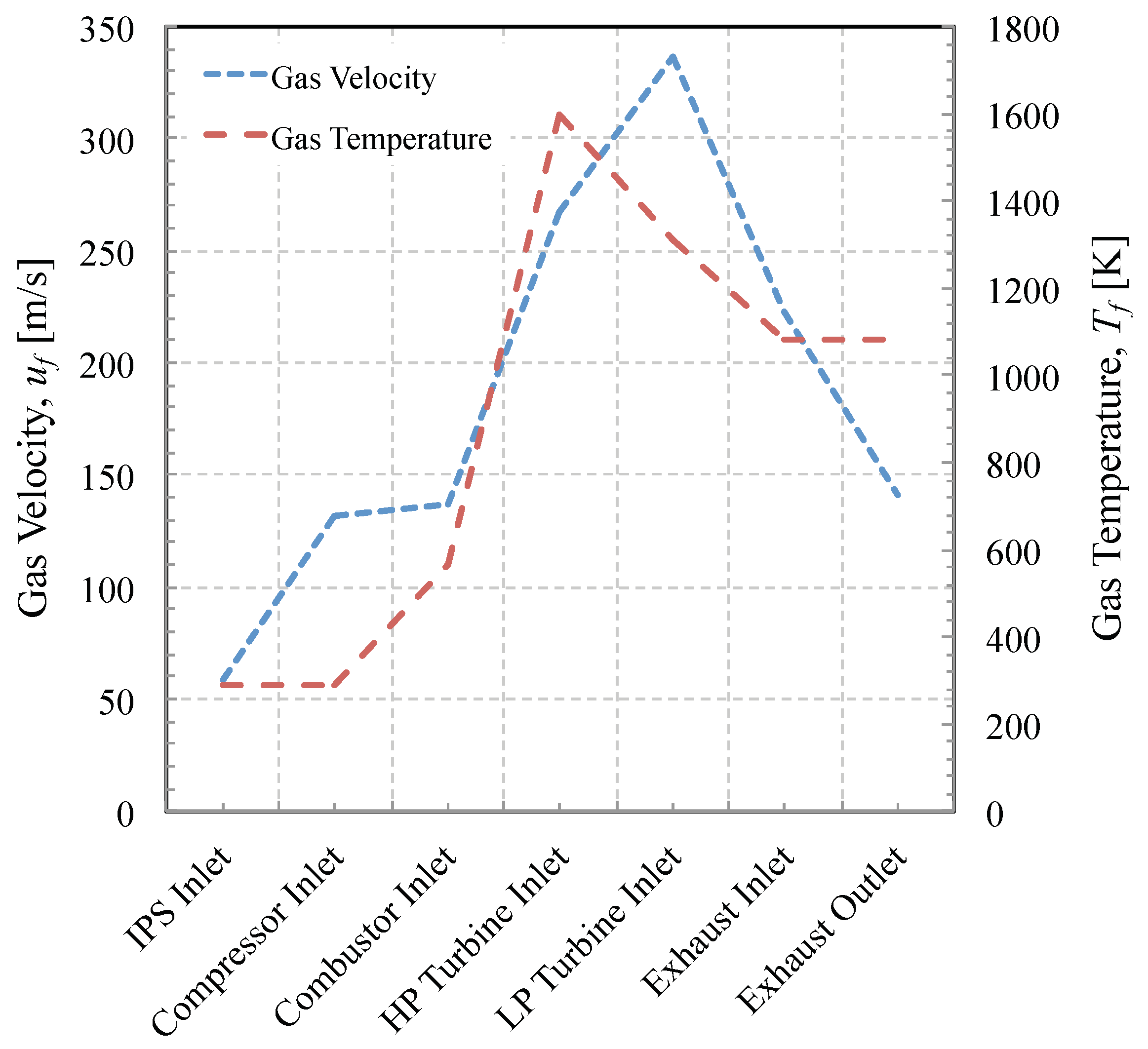
2.3.1. Engine Operating Condition
2.3.2. Dust Exposure Event
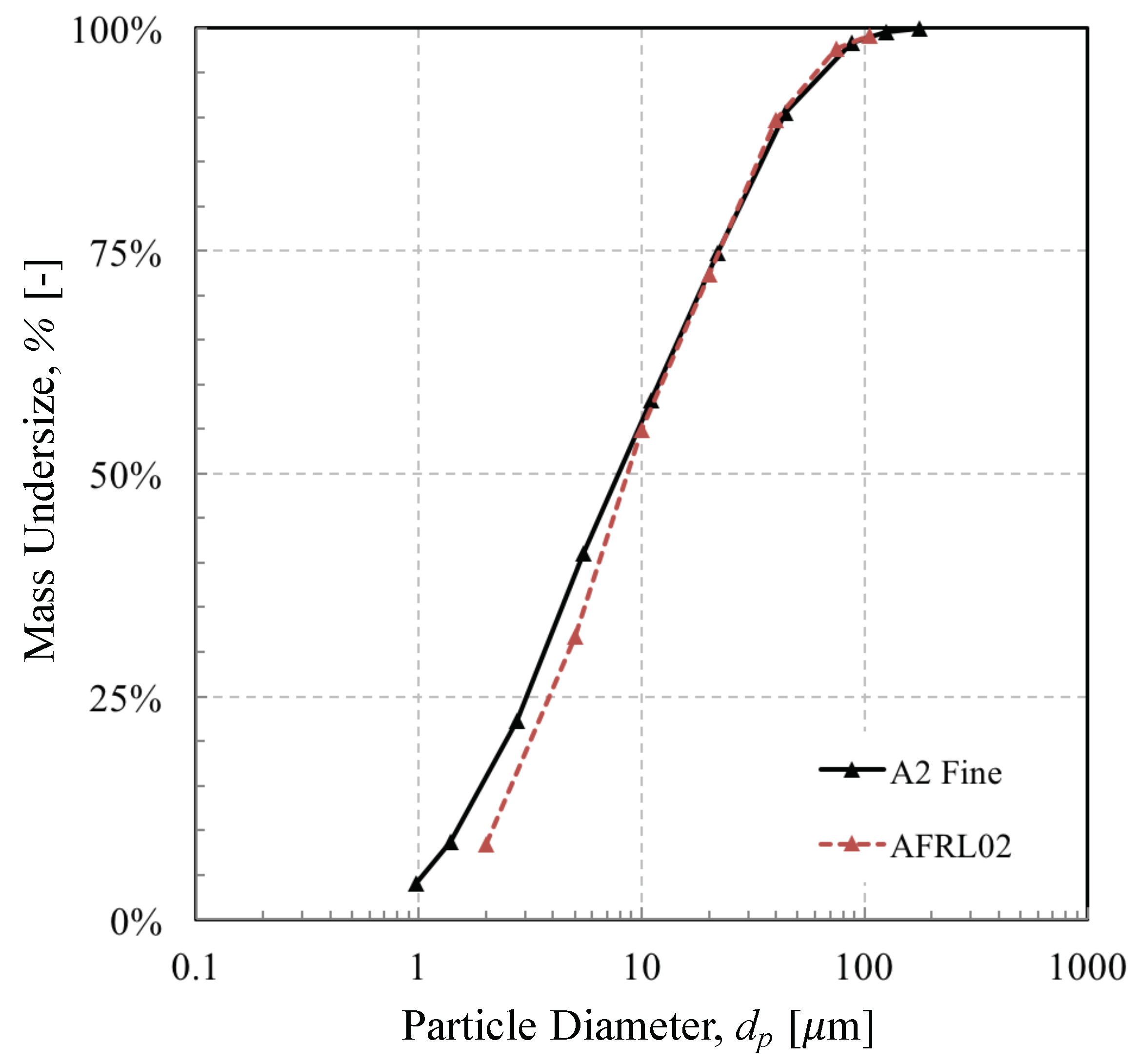
- Arizona A2 Fine, a commonly-used test dust for certification of particle separators.
- AFRL02, a commercially available blend developed by Krisak et al. [5] at the U.S. Air Force Research Laboratories (AFRL) for sand ingestion testing to mimic the chemistry of CMAS-forming natural dusts.
3. Results and Discussion
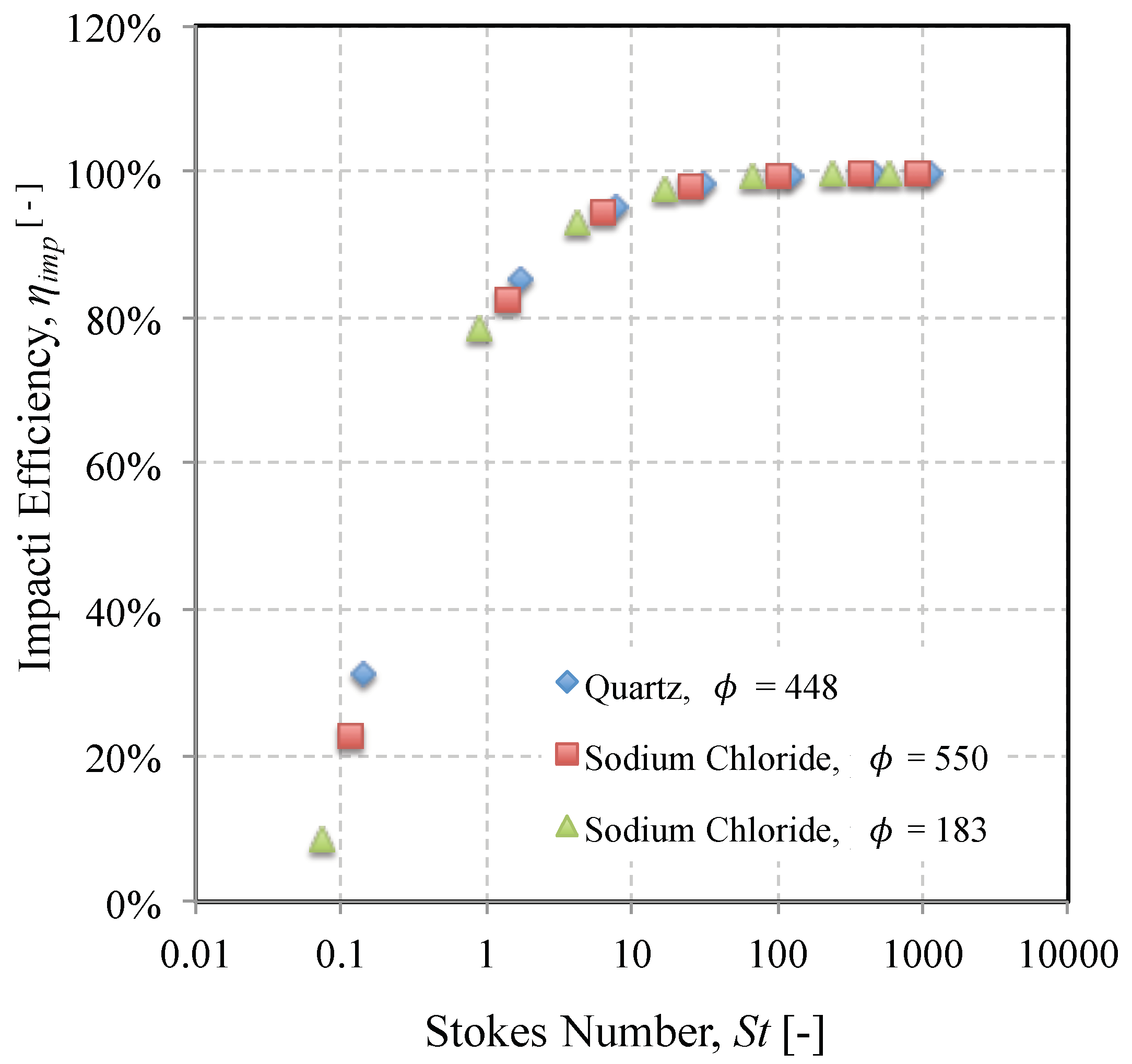
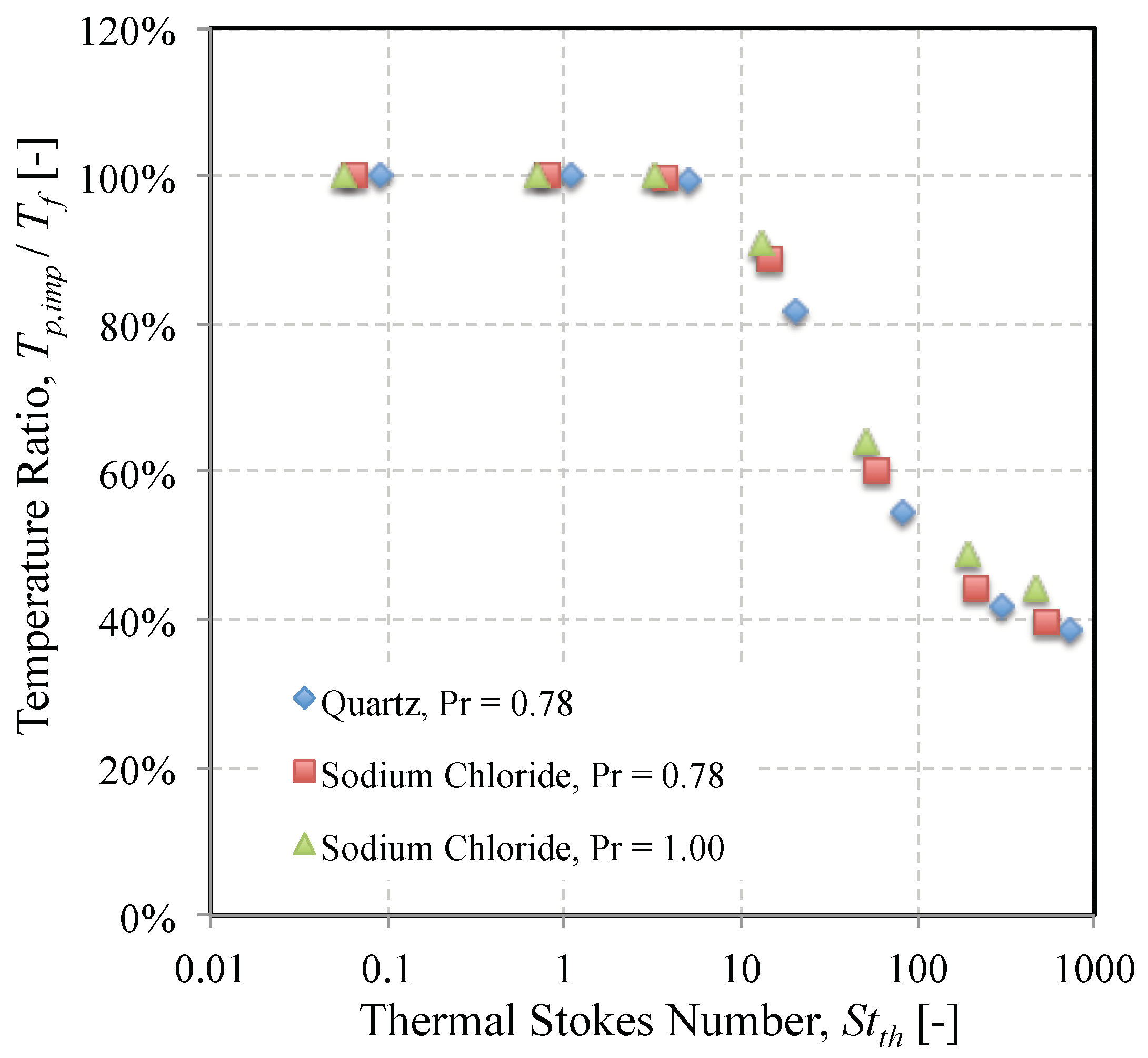
3.1. Impact Efficiency of Mineral Dusts on an Isolated Cylinder
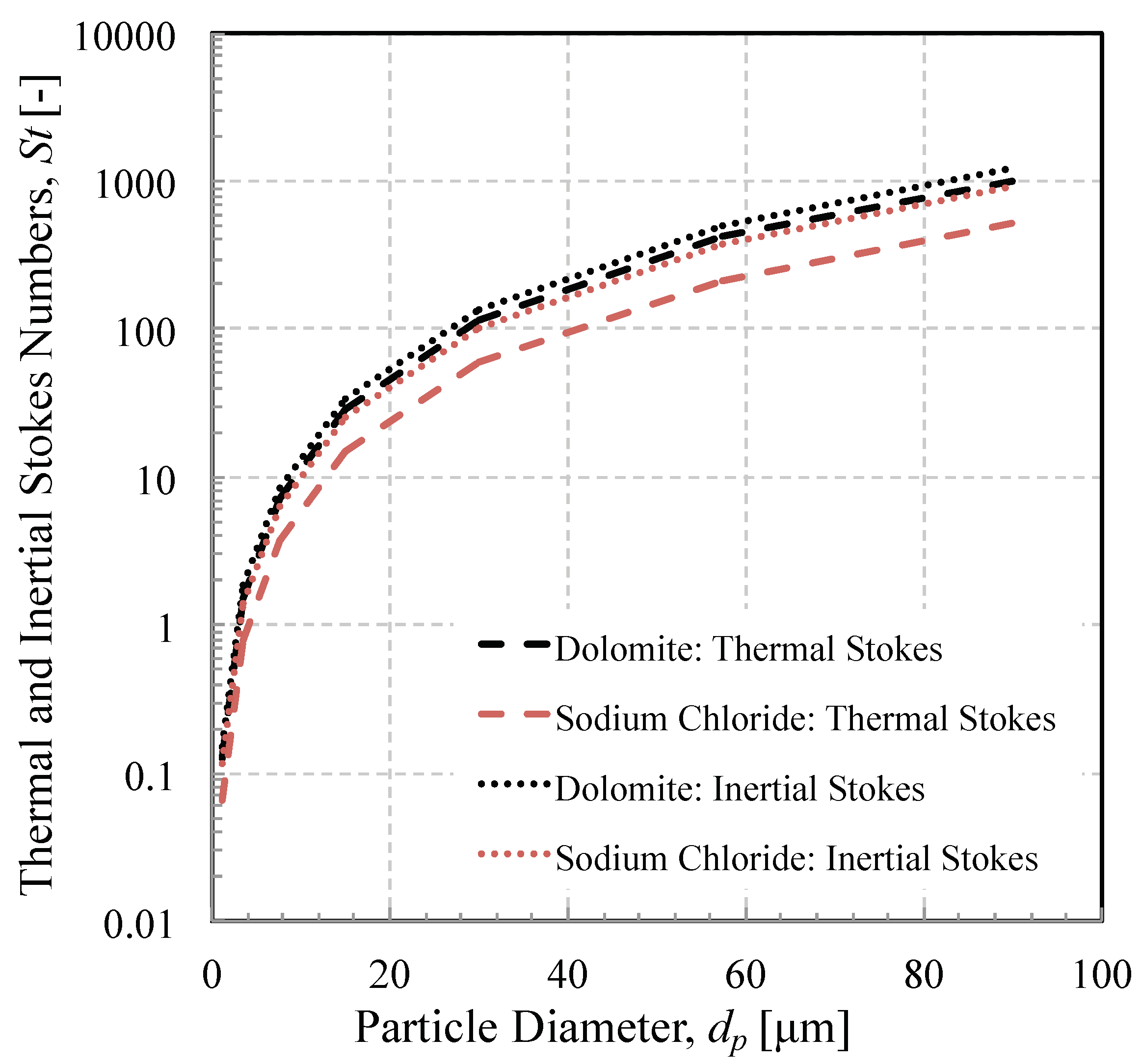
3.2. Influence of Mineralogy on Stokes Number
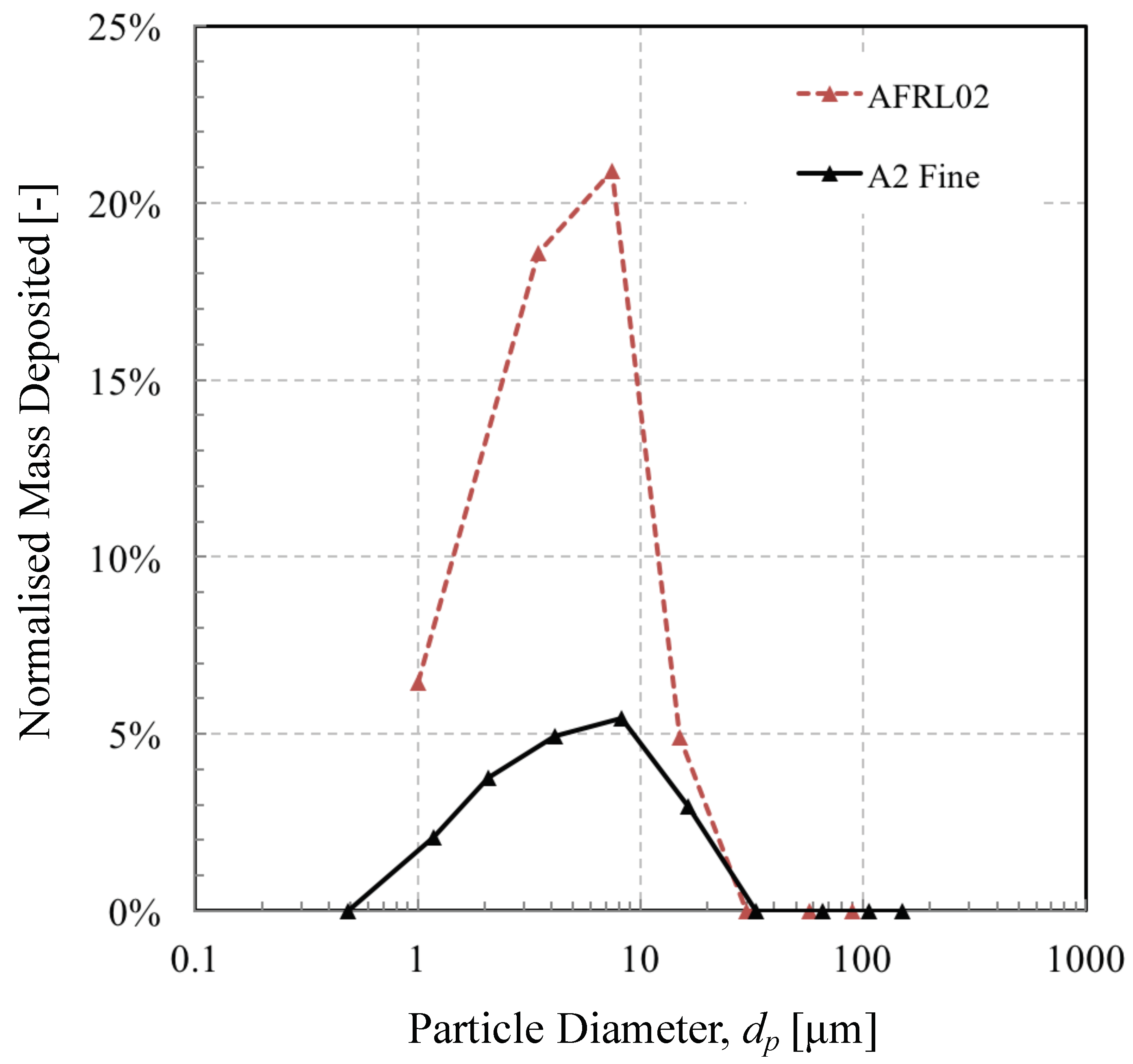
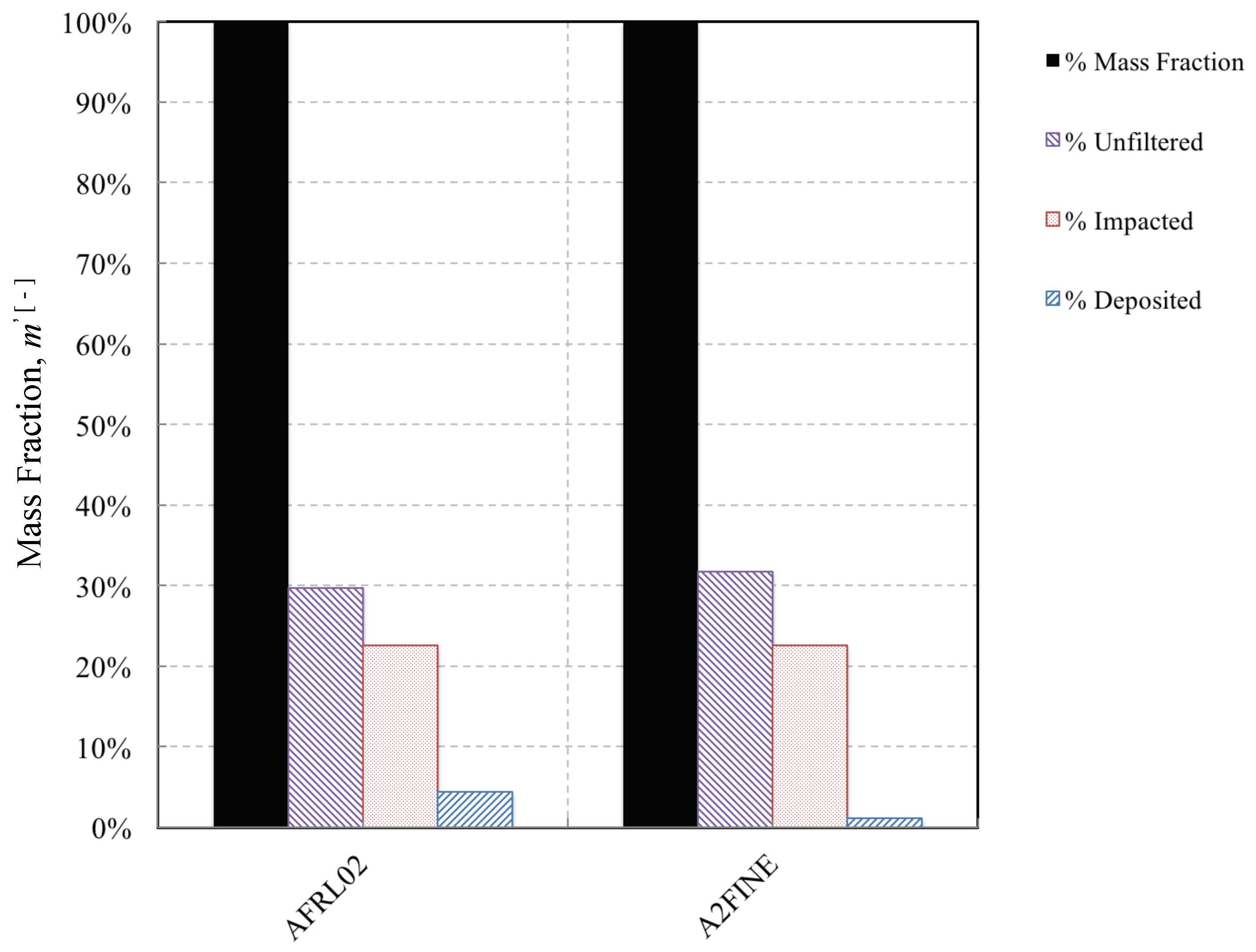
3.3. Effect of Particle Mineralogy on Impact and Accumulation Efficiency
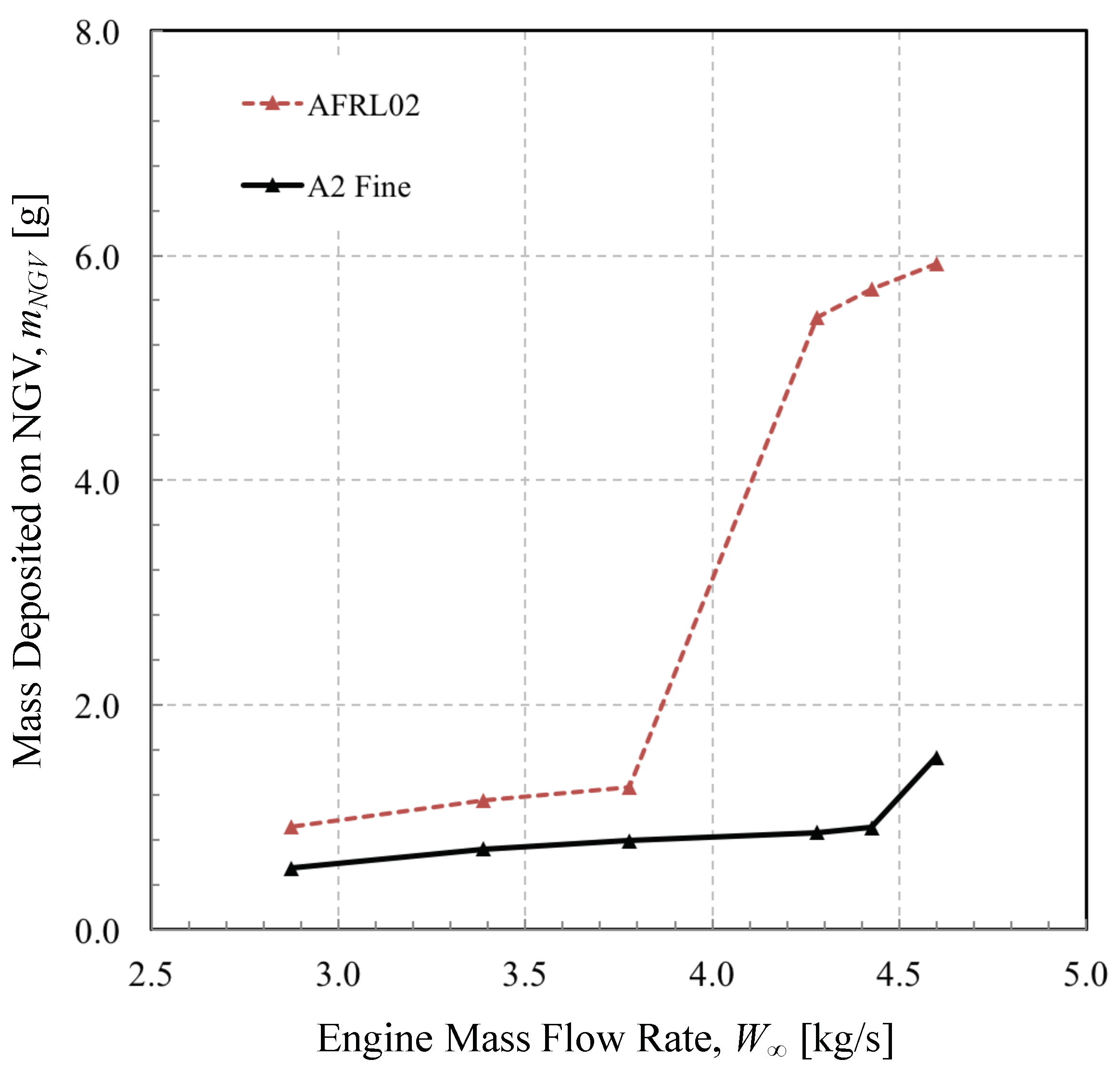
3.4. Mass Collected during Brownout Landing of an HH-60 Helicopter
4. Conclusions
- Chemical properties of ingested dust should have equal prominence in the development of test dusts for engine durability tests, owing to the variation in heating rates and melting points of the constituents of real dusts. This may lead to an underprediction of the mass of material deposited in the field in comparison with the test bed.
- Particle size has a big influence on the likelihood of deposition in the external gas path. Generally, the smaller particles do not possess the inertia to deviate from flow streamlines and interact with surfaces in the core gas path, unless small enough to be transported by turbulent eddies or thermophoresis (not modelled here). The largest particles that do interact cannot reach their melting point in the short transit time. This effectively leads to an “inertial” and “thermal” sorting, which leads to a difference between the initial test dust and the constituents of the surface deposit. Predictions of this sorting effect could be used to create test dusts that more closely resemble the material deposited on engine components.
- The thermal Stokes number is likely to exhibit a greater variance than the momentum Stokes number, over a range of identical particle sizes for a given real-world dust. The significance of this is that there is likely to be more of a difference in the sticking efficiency than the impact efficiency for a dust of several constituent minerals.
- The Stokes numbers are both heavily influenced by particle size. An inertial particle separator removes a significant proportion of the ingested dust. The dust that evades removal, however, has a much narrower size distribution and a much smaller mass mean diameter. The mean Stokes numbers of the dust decrease. While this reduces the impact efficiency, this means that particles on average take less time to reach the melting point, thereby increasing their likelihood of capture.
- Due to the fact that the accumulation efficiency increases with momentum Stokes number, but decreases with thermal Stokes number, both of which increase with the square of particle diameter, there may exist a level of engine mass flow rate for which deposition rates remain low. Conversely, as the engine mass flow rate increases, the build up of molten dust may be non-linear, due to the discontinuous way crystalline material decomposes and changes phase.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AFB | Air Force Base |
| AFRL | Air Force Research Laboratory |
| CMAS | Calcium-Magnesium Aluminosilicate |
| HP | High Pressure |
| IPS | Inertial Particle Separator |
| ISO | International Organisation for Standardization |
| RANS | Reynolds-Averaged Navier–Stokes |
| RPM | Revolutions per Minute |
| NGV | Nozzle Guide Vane |
References
- Milluzzo, J.; Leishman, J.G. Assessment of Rotorcraft Brownout Severity in Terms of Rotor Design Parameters. J. Am. Helicopter Soc. 2010, 55, 32009–320099. [Google Scholar] [CrossRef]
- Syal, M.; Martin, M.; Leishman, J.G. Development of a Lagrangian-Lagrangian Methodology to Predict Brownout Dust Clouds. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2012. [Google Scholar]
- Bojdo, N. Rotorcraft Engine Air Particle Separation. Ph.D. Thesis, University of Manchester, Manchester, UK, 2012. [Google Scholar]
- Dunn, M.G.; Padova, C.; Moller, J.E.; Adams, R.M. Performance Deterioration of a Turbofan and a Turbojet Engine Upon Exposure to a Dust Environment. J. Eng. Gas Turbines Power 1987, 109, 336. [Google Scholar] [CrossRef]
- Krisak, M. Environmental Degradation of Nickel-Based Superalloys Due to Gypsiferous Desert Dusts. Ph.D. Thesis, Air Force Institute of Technology, WPAFB, OH, USA, 2015. [Google Scholar]
- Smialek, J.; Archer, F.; Garlick, R. Turbine Airfoil Degradation in the Persian Gulf War. JOM 1994, 46, 39–41. [Google Scholar] [CrossRef]
- Barone, D.; Loth, E.; Snyder, P. Efficiency of an Inertial Particle Separator. J. Propuls. Power 2015, 31, 997–1002. [Google Scholar] [CrossRef]
- Singh, S.; Tafti, D. Particle deposition model for particulate flows at high temperatures in gas turbine components. Int. J. Heat Fluid Flow 2015, 52, 72–83. [Google Scholar] [CrossRef]
- Drew, J. Fatal MV-22 crash in Hawaii linked to excessive debris ingestion. FlightGlobal. 25 November 2015. Available online: https://www.flightglobal.com/news/articles/fatal-mv-22-crash-in-hawaii-linked-to-excessive-debr-419484/ (accessed on 6 December 2018).
- Clarkson, R.J.; Majewicz, E.J.; Mack, P. A re-evaluation of the 2010 quantitative understanding of the effects volcanic ash has on gas turbine engines. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2016, 230, 2274–2291. [Google Scholar] [CrossRef]
- Clarkson, R.; Simpson, H. Maximising Airspace Use During Volcanic Eruptions: Matching Engine Durability against Ash Cloud Occurrence. In Proceedings of the Science and Technology Organisation Meeting STO-MP-AVT-272, Vilnius, Lithuania, 15–17 May 2017; pp. 1–20. [Google Scholar] [CrossRef]
- Cowherd, C. Sandblaster 2: Support of See-Through Technologies for Particulate Brownout; Technical Report 110565; Defence Advanced Research Projects Agency (DARPA): Arlington County, VA, USA, 2007.
- Boulanger, A.; Patel, H.; Hutchinson, J.; DeShong, W.; Xu, W.; Ng, W.; Ekkad, S. Preliminary Experimental Investigation of Initial Onset of Sand Deposition in the Turbine Section of Gas Turbines. In ASME Turbo Expo 2016, Volume 1: Aircraft Engine; Fans and Blowers; Marine; ASME: New York, NY, USA, 2016; p. V001T01A003. [Google Scholar] [CrossRef]
- Bojdo, N.; Filippone, A. Performance Prediction of Inlet Barrier Filters for Rotorcraft Engines. J. Aircr. 2011, 48, 1903–1912. [Google Scholar] [CrossRef]
- Barone, D.; Loth, E.; Snyder, P. Influence of particle size on inertial particle separator efficiency. Powder Technol. 2017, 318, 177–185. [Google Scholar] [CrossRef]
- Dunn, M.G. Operation of Gas Turbine Engines in an Environment Contaminated With Volcanic Ash. J. Turbomach. 2012, 134, 051001. [Google Scholar] [CrossRef]
- Venti, M.; Lekki, J.; Loy-Kraft, G. Vehicle Integrated Propulsion Research (VIPR) III Volcanic Ash Environment (VAE) Preliminary Visual and Teardown Observations; Technical Report; NASA: Washington, DC, USA, 2016.
- Hamed, A.; Tabakoff, W.C.; Wenglarz, R. Erosion and Deposition in Turbomachinery. J. Propuls. Power 2006, 22, 350–360. [Google Scholar] [CrossRef]
- Kim, J.; Dunn, M.G.; Baran, A.J.; Wade, D.P.; Tremba, E.L. Deposition of Volcanic Materials in the Hot Sections of Two Gas Turbine Engines. J. Eng. Gas Turbines Power 1993, 115, 641. [Google Scholar] [CrossRef]
- Kleinhans, U.; Wieland, C.; Babat, S.; Scheffknecht, G.; Spliethoff, H. Ash particle sticking and rebound behavior: A mechanistic explanation and modeling approach. Proc. Combust. Inst. 2017, 36, 2341–2350. [Google Scholar] [CrossRef]
- Suman, A.; Casari, N.; Fabbri, E.; Pinelli, M.; di Mare, L.; Montomoli, F. Gas Turbine Fouling Tests: Review, Critical Analysis, and Particle Impact Behavior Map. J. Eng. Gas Turbines Power 2018, 141, 032601. [Google Scholar] [CrossRef]
- Patel, H. Experimental Investigation of Initial Onset of Sand Deposition in the Turbine Section of Gas Turbines. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 2015. [Google Scholar]
- Bons, J.P.; Crosby, J.; Wammack, J.E.; Bentley, B.I.; Fletcher, T.H. High-Pressure Turbine Deposition in Land-Based Gas Turbines From Various Synfuels. J. Eng. Gas Turbines Power 2007, 129, 135. [Google Scholar] [CrossRef]
- Dean, J.; Taltavull, C.; Clyne, T. Influence of the composition and viscosity of volcanic ashes on their adhesion within gas turbine aeroengines. Acta Mater. 2016, 109, 8–16. [Google Scholar] [CrossRef]
- Giehl, C.; Brooker, R.A.; Marxer, H.; Nowak, M. An experimental simulation of volcanic ash deposition in gas turbines and implications for jet engine safety. Chem. Geol. 2017, 461, 160–170. [Google Scholar] [CrossRef]
- Brach, R.M.; Dunn, P.F. A Mathematical Model of the Impact and Adhesion of Microsphers. Aerosol Sci. Technol. 1992, 16, 51–64. [Google Scholar] [CrossRef]
- El-Batsh, H.; Haselbacher, H. Numerical Investigation of the Effect of Ash Particle Deposition on the Flow Field Through Turbine Cascades. In ASME Turbo Expo 2002, Volume 5: Parts A and B; ASME: New York, NY, USA, 2002; pp. 1035–1043. [Google Scholar] [CrossRef]
- Ai, W.; Fletcher, T.H. Computational Analysis of Conjugate Heat Transfer and Particulate Deposition on a High Pressure Turbine Vane. J. Turbomach. 2012, 134, 041020. [Google Scholar] [CrossRef]
- Singh, S.; Tafti, D. Predicting the Coefficient of Restitution for Particle Wall Collisions in Gas Turbine Components. In ASME Turbo Expo 2013, Volume 6B: Turbomachinery; ASME: New York, NY, USA, 2013; p. V06BT37A041. [Google Scholar] [CrossRef]
- Yu, K.; Tafti, D. Size and Temperature Dependent Deposition Model of Micro-Sized Sand Particles. In ASME Turbo Expo 2017, Volume 2D: Turbomachinery; ASME: New York, NY, USA, 2017; p. V02DT48A008. [Google Scholar] [CrossRef]
- Agati, G.; Borello, D.; Rispoli, F.; Venturini, P. An Innovative Approach to Model Temperature Influence on Particle Deposition in Gas Turbines. In ASME Turbo Expo 2016, Volume 5C: Heat Transfer; ASME: New York, NY, USA, 2016; p. V05CT12A012. [Google Scholar] [CrossRef]
- Bons, J.; Prenter, R.; Whitaker, S. A Simple Physics-Based Model for Particle Rebound and Deposition in Turbomachinery. J. Turbomach. 2017, 139, 081009. [Google Scholar] [CrossRef]
- Mills, K.; Sridhar, S. Viscosities of ironmaking and steelmaking slags. Ironmak. Steelmak. 1999, 26, 262–268. [Google Scholar] [CrossRef]
- Giordano, D.; Russell, J.K.; Dingwell, D.B. Viscosity of magmatic liquids: A model. Earth Planet. Sci. Lett. 2008, 271, 123–134. [Google Scholar] [CrossRef]
- Crowe, C.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Particles and Droplets; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Shinozaki, M.; Roberts, K.A.; van de Goor, B.; Clyne, T.W. Deposition of Ingested Volcanic Ash on Surfaces in the Turbine of a Small Jet Engine. Adv. Eng. Mater. 2013, 15, 986–994. [Google Scholar] [CrossRef]
- Israel, R.; Rosner, D.E. Use of a Generalized Stokes Number to Determine the Aerodynamic Capture Efficiency of Non-Stokesian Particles from a Compressible Gas Flow. Aerosol Sci. Technol. 1982, 2, 45–51. [Google Scholar] [CrossRef]
- Wood, C.A.; Slater, S.L.; Zonneveldt, M.; Thornton, J.; Armstrong, N.; Antoniou, R.A. Characterisation of Dirt, Dust and Volcanic Ash: A Study on the Potential for Gas Turbine Engine Degradation; Technical Report; Australian Government Department of Defence Science and Technology: Victoria, Australia, 2017.
- Cengel, Y.; Turner, R.; Cimbala, J.; Kanoglu, M. Fundamentals of Thermal-Fluid Sciences; McGraw-Hill Education: New York, NY, USA, 2008. [Google Scholar]
- Waples, D. A review and evaluation of specific heat capacities of rocks, minerals, and subsurface fluids. Part 1: Minerals and nonporous rocks. Nat. Resour. Res. 2004, 13, 97–122. [Google Scholar] [CrossRef]
- Haynes, W. CRC Handbook of Chemistry and Physics; Taylor and Francis Group: Abingdon, UK, 2014. [Google Scholar]
- Lewis, R.; Hawley, G. Hawley’s Condensed Chemical Dictionary, 6th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Chase, M.W. NIST-JANAF Themochemical Tables, 4th ed.; National Institute of Standards and Technology: Gaithersburg, MD, USA, 1998.
- Qu, Y.; Yang, Y.; Zou, Z.; Zeilstra, C.; Meijer, K.; Boom, R. Melting and Reduction Behaviour of Individual Fine Hematite Ore Particles. ISIJ Int. 2015, 55, 149–157. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem 2019 update: improved access to chemical data. Nucleic Acids Res. 2019, 47, D1102–D1109. [Google Scholar] [CrossRef]
- Zumdahl, S.S.; DeCoste, D.J. Chemical Principals; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Brun, R.; Lewis, W.; Perkins, P.; Serafini, J. Impingement of Cloud Droplets on a Cylinder and Procedure for Measuring Liquid-Water Content and Droplet Sizes in Supercooled Clouds by Rotating Multicylinder; Technical Report; NACA: Cleveland, OH, USA, 1955. [Google Scholar]
| Description | Symbol | A2 Fine | AFRL02 | Units |
|---|---|---|---|---|
| Landing Duration | 20 | 20 | s | |
| Dust Concentration | 1.80 | 1.80 | g/m | |
| Mass-weighted Mean Particle Diameter | 17.6 | 16.4 | m | |
| Mass-weighted Mean Density | 2709 | 2551 | kg/m | |
| Mass-weighted Specific Heat Capacity | 756 | 863 | J/kg·K | |
| Bulk Melting Temperature [5] | 1433 | 1423 | K |
| Mineral Name | Mass Fraction % | Chemical Formula | Mean Density kg/m | Specific Heat J/kg·K | Melting Point K | |
|---|---|---|---|---|---|---|
| A2 Fine | AFRL02 | |||||
| Quartz | 72.0 | 34.0 | SiO | 2650 [40] | 740 [40] | 1983 [38] |
| Gypsum | 0.0 | 30.0 | CaSO2HO | 2320 [40] | 1070 [40] | 2873 [38] |
| Albite | 0.0 | 17.0 | NaAlSiO | 2620 [40] | 730 [40] | 1388 [38] |
| Dolomite | 0.0 | 14.0 | CaMg(CO) | 2840 [40] | 870 [40] | 2973 [38] |
| Salt (Sodium Chloride) | 0.0 | 5.0 | NaCl | 2170 [41] | 864 [41] | 1074 [41] |
| Aluminium Oxide | 12.5 | 0.0 | AlO | 3700 [42] | 499 [43] | 2303 [42] |
| Hematite | 4.0 | 0.0 | FeO | 5150 [40] | 620 [40] | 1838 [44] |
| Calcium Oxide | 3.5 | 0.0 | CaO | 3340 [41] | 681 [43] | 2613 [41] |
| Potassium Oxide | 3.0 | 0.0 | KO | 2130 [41] | 878 [43] | 1010 [41] |
| Sodium Oxide | 2.7 | 0.0 | NaO | 2300 [45] | 1211 [43] | 1548 [45] |
| Periclase | 1.5 | 0.0 | MgO | 3550 [40] | 970 [40] | 3073 [38] |
| Titanium Dioxide | 0.8 | 0.0 | TiO | 4050 [45] | 626 [46] | 2128 [45] |
| TOTAL | 100.0 | 100.0 | ||||
| Size Band (m) | Mid-Size (m) | Mass Fraction | Quartz | Gypsum | Albite | Dolomite | Sodium Chloride | TOTAL |
|---|---|---|---|---|---|---|---|---|
| 0–105 (All) | 16.4 (Mean) | Initial % | 34.0 | 30.0 | 17.0 | 14.0 | 5.0 | 100 |
| Impacted % | 30.1 | 26.1 | 15.0 | 12.4 | 4.3 | 88.0 | ||
| Deposited % | 0.0 | 0.0 | 7.6 | 0.0 | 3.0 | 10.6 | ||
| 0–2 | 1 | Initial % | 2.9 | 2.5 | 1.4 | 1.2 | 0.4 | 8.4 |
| Impacted % | 0.9 | 0.6 | 0.4 | 0.4 | 0.1 | 2.5 | ||
| Deposited % | 0.0 | 0.0 | 0.4 | 0.0 | 0.1 | 0.5 | ||
| 2–5 | 3.5 | Initial % | 7.9 | 7.0 | 4.0 | 3.3 | 1.2 | 23.3 |
| Impacted % | 6.8 | 5.8 | 3.4 | 2.8 | 1.0 | 19.7 | ||
| Deposited % | 0.0 | 0.0 | 3.4 | 0.0 | 1.0 | 4.3 | ||
| 5–10 | 7.5 | Initial % | 7.9 | 6.9 | 3.9 | 3.2 | 1.2 | 23.1 |
| Impacted % | 7.5 | 6.5 | 3.7 | 3.1 | 1.1 | 22.0 | ||
| Deposited % | 0.0 | 0.0 | 3.7 | 0.0 | 1.1 | 4.8 | ||
| 10–20 | 15 | Initial % | 5.9 | 5.2 | 3.0 | 2.4 | 0.9 | 17.5 |
| Impacted % | 5.8 | 5.1 | 2.9 | 2.4 | 0.9 | 17.2 | ||
| Deposited % | 0.0 | 0.0 | 0.0 | 0.0 | 0.9 | 0.9 | ||
| 20–40 | 30 | Initial % | 5.9 | 5.2 | 3.0 | 2.4 | 0.9 | 17.4 |
| Impacted % | 5.9 | 5.2 | 2.9 | 2.4 | 0.9 | 17.3 | ||
| Deposited % | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 40–75 | 57.5 | Initial % | 2.7 | 2.4 | 1.4 | 1.1 | 0.4 | 8.0 |
| Impacted % | 2.7 | 2.4 | 1.4 | 1.1 | 0.4 | 8.0 | ||
| Deposited % | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | ||
| 75–105 | 90 | Initial % | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 1.5 |
| Impacted % | 0.5 | 0.4 | 0.3 | 0.2 | 0.1 | 1.5 | ||
| Deposited % | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bojdo, N.; Filippone, A. A Simple Model to Assess the Role of Dust Composition and Size on Deposition in Rotorcraft Engines. Aerospace 2019, 6, 44. https://doi.org/10.3390/aerospace6040044
Bojdo N, Filippone A. A Simple Model to Assess the Role of Dust Composition and Size on Deposition in Rotorcraft Engines. Aerospace. 2019; 6(4):44. https://doi.org/10.3390/aerospace6040044
Chicago/Turabian StyleBojdo, Nicholas, and Antonio Filippone. 2019. "A Simple Model to Assess the Role of Dust Composition and Size on Deposition in Rotorcraft Engines" Aerospace 6, no. 4: 44. https://doi.org/10.3390/aerospace6040044
APA StyleBojdo, N., & Filippone, A. (2019). A Simple Model to Assess the Role of Dust Composition and Size on Deposition in Rotorcraft Engines. Aerospace, 6(4), 44. https://doi.org/10.3390/aerospace6040044





