Comparison of Constrained Parameterisation Strategies for Aerodynamic Optimisation of Morphing Leading Edge Airfoil
Abstract
1. Introduction
2. Optimisation Framework
2.1. Problem Formulation and Objectives Evaluation
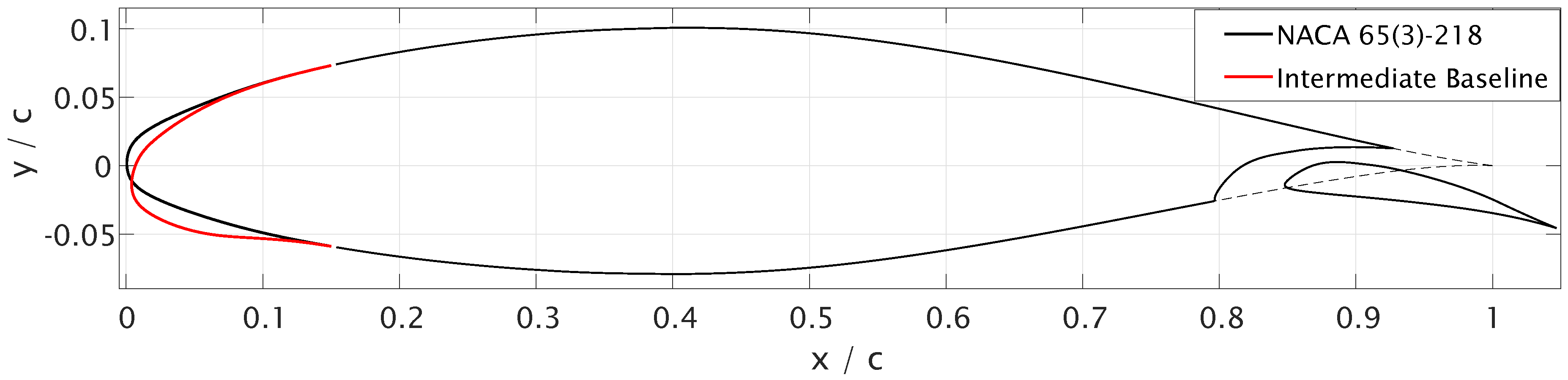
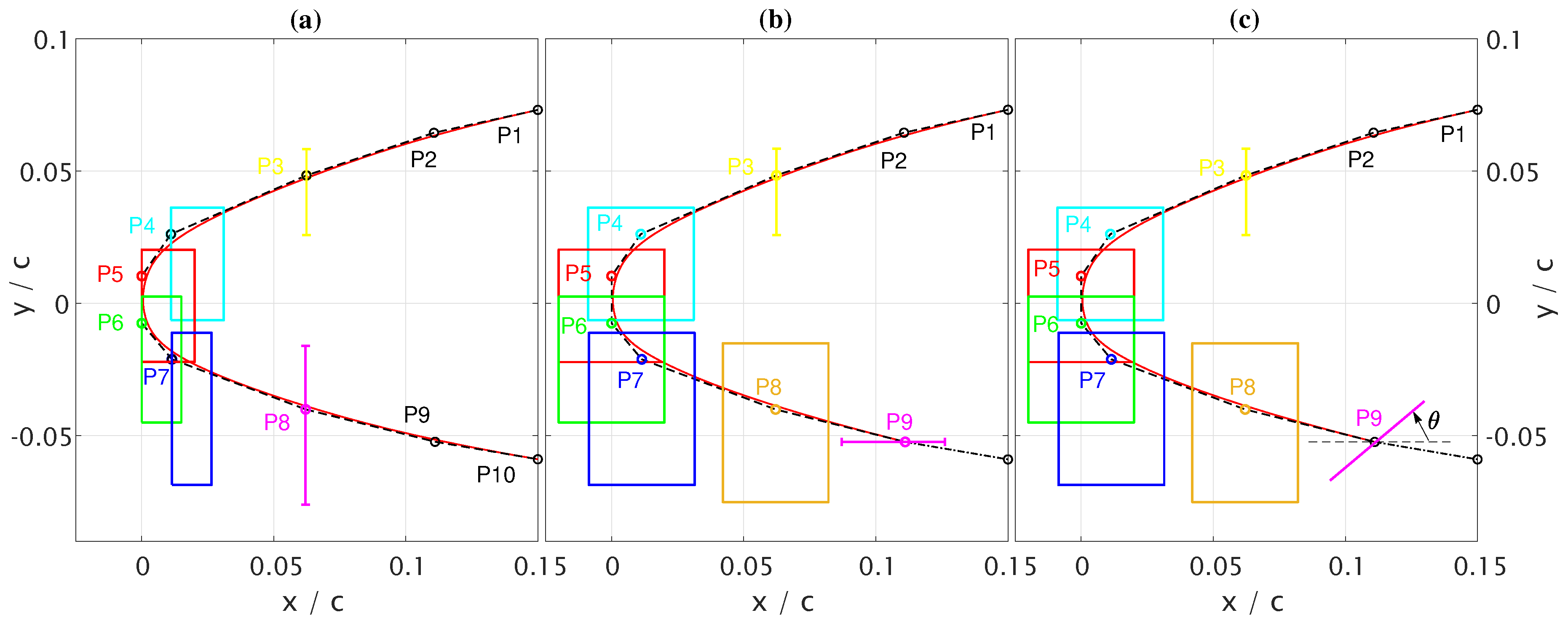
2.2. Parameterisation Strategy
3. Results and Discussion
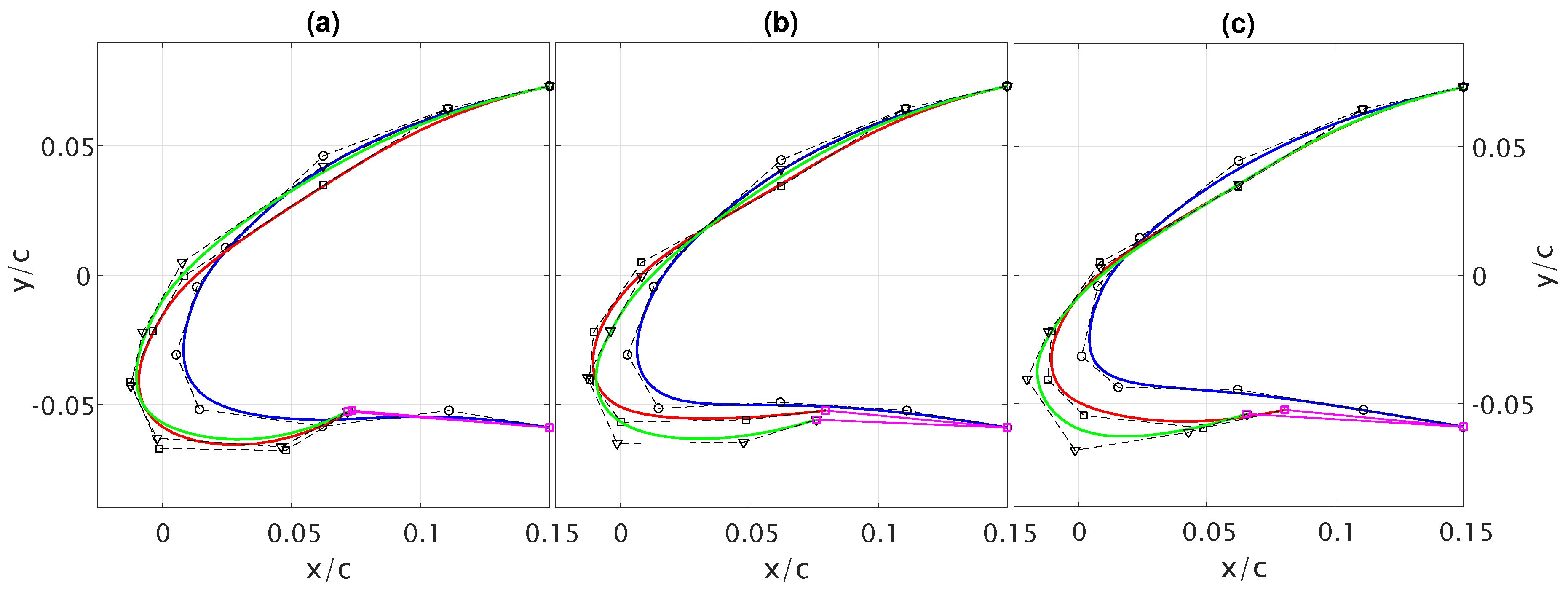
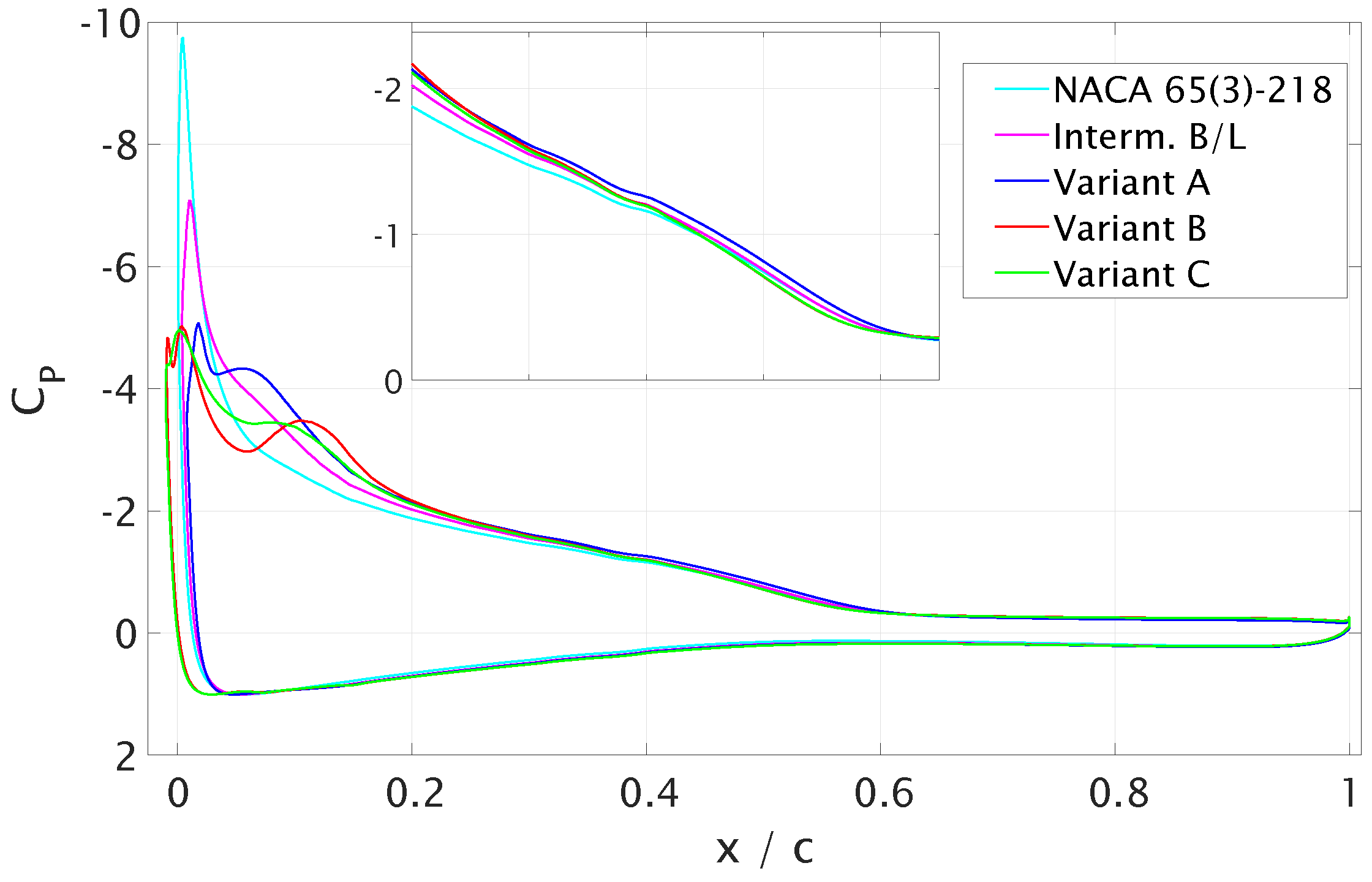
3.1. Optimisation without Flap
3.2. Optimisation with Flap
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CAL | Constant Arc Length |
| CFD | Computational Fluid Dynamics |
| CP | Control Point |
| DP | Design Point |
| DV | Design Variable |
| FRP | Fiber-reinforced Plastic |
| MDO | Multi-Disciplinary Optimisation |
| Angle of attack | |
| c | Airfoil chord |
| Drag coefficient | |
| Lift coefficient | |
| Pressure coefficient | |
| Curvature | |
| L | Arc length |
| Lift to drag ratio | |
| Displacement direction |
References
- ACARE. Flightpath 2050. Europe’s Vision for Aviation; Technical Report; European Commission, Directorate-General for Research and Innovation: Brussels, Belgium, 2011. [Google Scholar] [CrossRef]
- IATA. IATA Vision 2050 Report; Technical Report; International Air Transport Association: Montreal, QC, Canada, 2011. [Google Scholar]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Ronch, A.D.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Chow, L.; Mau, K.; Remy, H. Landing Gears and High Lift Devices Airframe Noise Research. In Proceedings of the 8th AIAA/CEAS Aeroacoustics Conference and Exhibit, Breckenridge, CO, USA, 17–19 June 2002. [Google Scholar] [CrossRef]
- Kintscher, M.; Wiedemann, M.; Monner, H.P.; Heintze, O.; Kühn, T. Design of a smart leading edge device for low speed wind tunnel tests in the European project SADE. Int. J. Struct. Integr. 2011, 2, 383–405. [Google Scholar] [CrossRef]
- Wild, J. Recent research topics in high-lift aerodynamics. CEAS Aeronaut. J. 2016, 7, 345–355. [Google Scholar] [CrossRef]
- Ameduri, S. Chapter 16—Morphing of the Leading Edge. In Morphing Wing Technologies; Concilio, A., Dimino, I., Lecce, L., Pecora, R., Eds.; Butterworth-Heinemann: Oxford, UK, 2018; pp. 491–515. [Google Scholar] [CrossRef]
- Kintscher, M.; Monner, P.; Kühn, T.; Wild, J.; Wiedemann, M. Low Speed Wind Tunnel Test of a Morphing Leading Edge. In Proceedings of the Italian Association of Aeronautics and Astronautics XXII Conference, Naples, Italy, 9–12 September 2013. [Google Scholar]
- Monner, H.P. SADE Project Final Report; Technical Report; DLR: Köln, Germany, 2012. [Google Scholar]
- Kirn, J.; Storm, S. Kinematic solution for a highly adaptive droop nose. In Proceedings of the ICAST 2014, Hague, The Netherlands, 6–8 October 2014. [Google Scholar]
- De Gaspari, A. Design, Manufacturing and Wind Tunnel Validation of an Active Camber Morphing Wing Based on Compliant Structures. In Proceedings of the ICAST 2014, Hague, The Netherlands, 6–8 October 2014. [Google Scholar]
- Sodja, J.; Martinez, M.; Simpson, J.; De Breuker, R. Experimental evaluation of the morphing leading edge concept. In Proceedings of the AIAA SciTech, 23nd AIAA/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Contell Asins, C.; Landersheim, V.; Schwarzhaupt, O. Development and Demonstration of a Multifunctional Morphing Leading Edge for a Regional A/C. In Proceedings of the Advanced Aircraft Efficiency in a Global Air Transport System AEGATS ’18 Conference, Toulouse, France, 23–25 October 2018. [Google Scholar]
- Ajaj, R.M.; Beaverstock, C.S.; Friswell, M.I. Morphing aircraft: The need for a new design philosophy. Aerosp. Sci. Technol. 2016, 49, 154–166. [Google Scholar] [CrossRef]
- Fincham, J.; Friswell, M. Aerodynamic optimisation of a camber morphing aerofoil. Aerosp. Sci. Technol. 2015, 43, 245–255. [Google Scholar] [CrossRef]
- De Gaspari, A.; Ricci, S. Knowledge-Based Shape Optimization of Morphing Wing for More Efficient Aircraft. Int. J. Aerosp. Eng. 2015, 2015, 325724. [Google Scholar] [CrossRef]
- Molinari, G.; Quack, M.; Dmitriev, V.; Morari, M.; Jenny, P.; Ermanni, P. Aero-Structural Optimization of Morphing Airfoils for Adaptive Wings. J. Intell. Mater. Syst. Struct. 2011, 22, 1075–1089. [Google Scholar] [CrossRef]
- Burdette, D.A.; Martins, J.R. Design of a transonic wing with an adaptive morphing trailing edge via aerostructural optimization. Aerosp. Sci. Technol. 2018, 81, 192–203. [Google Scholar] [CrossRef]
- Woods, B.K.; Friswell, M.I. Multi-objective geometry optimization of the Fish Bone Active Camber morphing airfoil. J. Intell. Mater. Syst. Struct. 2016, 27, 808–819. [Google Scholar] [CrossRef]
- Abbott, I.; Von Doenhoff, A. Theory of Wing Sections, Including a Summary of Airfoil Data; Dover Books on Aeronautical Engineering Series; Dover Publications: New York, NY, USA, 1959. [Google Scholar]
- Sun, R.; Chen, G.; Zhou, C.; Zhou, L.; Jiang, J. Multidisciplinary design optimization of adaptive wing leading edge. Sci. China Technol. Sci. 2013, 56, 1790–1797. [Google Scholar] [CrossRef]
- Lyu, Z.; Martins, J.R.R.A. Aerodynamic Shape Optimization of an Adaptive Morphing Trailing Edge Wing. J. Aircr. 2015, 52, 1951–1970. [Google Scholar] [CrossRef]
- Secanell, M.; Suleman, A.; Gamboa, P. Design of a Morphing Airfoil Using Aerodynamic Shape Optimization. AIAA J. 2006, 44, 1550–1562. [Google Scholar] [CrossRef]
- Sugar Gabor, O.; Koreanschi, A.; Botez, R.M. Optimization of an Unmanned Aerial System’ Wing Using a Flexible Skin Morphing Wing. SAE Int. J. Aerosp. 2013, 6, 115–121. [Google Scholar] [CrossRef]
- De Gaspari, A.; Gilardelli, A.; Ricci, S.; Airoldi, A.; Moens, F. Design of a Leading Edge Morphing Based on Compliant Structures in the Framework of the CS2-AIRGREEN2 Project. In Proceedings of the ASME 2018 Conference on Smart Materials, Adaptive Structures and Intelligent Systems, San Antonio, TX, USA, 10–12 September 2018; 2018. [Google Scholar] [CrossRef]
- Allmaras, S.R.; Johnson, F.T. Modifications and Clarifications for the Implementation of the Spalart-Allmaras Turbulence Model. In Proceedings of the Seventh International Conference on Computational Fluid Dynamics (ICCFD7), Big Island, HI, USA, 9–13 July 2012. [Google Scholar]
- Menter, F. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R.; Smirnov, P.E.; Liu, T.; Avancha, R. A One-Equation Local Correlation-Based Transition Model. Flow Turbul. Combust. 2015, 95, 583–619. [Google Scholar] [CrossRef]
- Menter, F.; Langtry, R.; Völker, S. Transition Modelling for General Purpose CFD Codes. Flow Turbul. Combust. 2006, 77, 277–303. [Google Scholar] [CrossRef]
- Drela, M. XFOIL: An Analysis and Design System for Low Reynolds Number Airfoils. In Low Reynolds Number Airfoil Aerodynamics; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Comis Da Ronco, C.; Benini, E. A Simplex Crossover based evolutionary algorithm including the genetic diversity as objective. Appl. Soft Comput. 2013, 13, 2104–2123. [Google Scholar] [CrossRef]
- Benini, E.; Venturelli, G.; Łaniewski, W. Comparison between pure and surrogate assisted evolutionary algorithms for multiobjective optimization. Front. Artif. Intell. Appl. 2016, 281, 229–242. [Google Scholar] [CrossRef]
- Samareh, J.A. A Survey of Shape Parametrisation Techniques. In CEAS/AIAA/ICASE/NASA Langley International Forum on Aeroelasticity and Structural Dynamics 1999; National Aeronautics and Space Administration: Hampton, VA, USA, 1999. [Google Scholar]
- Suzuki, H.; Rinoie, K.; Tezuka, A. Laminar Airfoil Modification Attaining Optimum Drag Reduction by Use of Airfoil Morphing. J. Aircr. 2010, 47, 1126–1132. [Google Scholar] [CrossRef]
- Du, S.; Ang, H. Design and Feasibility Analyses of Morphing Airfoil Used to Control Flight Attitude. Strojniški Vestnik J. Mech. Eng. 2012, 58, 46–55. [Google Scholar] [CrossRef]
- Kulfan, B.M. CST Universal Parametric Geometry Representation Method with Application to Supersonic Aircraft. In Proceedings of the Fourth International Conference on Flow Dynamics, Sendai, Japan, 26–28 September 2007. [Google Scholar]
- Magrini, A.; Benini, E. Aerodynamic Optimization of a Morphing Leading Edge Airfoil with a Constant Arc Length Parameterization. J. Aerosp. Eng. 2018, 31, 04017093. [Google Scholar] [CrossRef]
- Bettadapura, R.; Mashburn, T.; Crawford, R. Length-Constrained Bezier Curve Smoothing. Available online: https://pdfs.semanticscholar.org/b96a/4066a532713d31fcd4e54cfd4e0c1511a0aa.pdf (accessed on 21 January 2019).



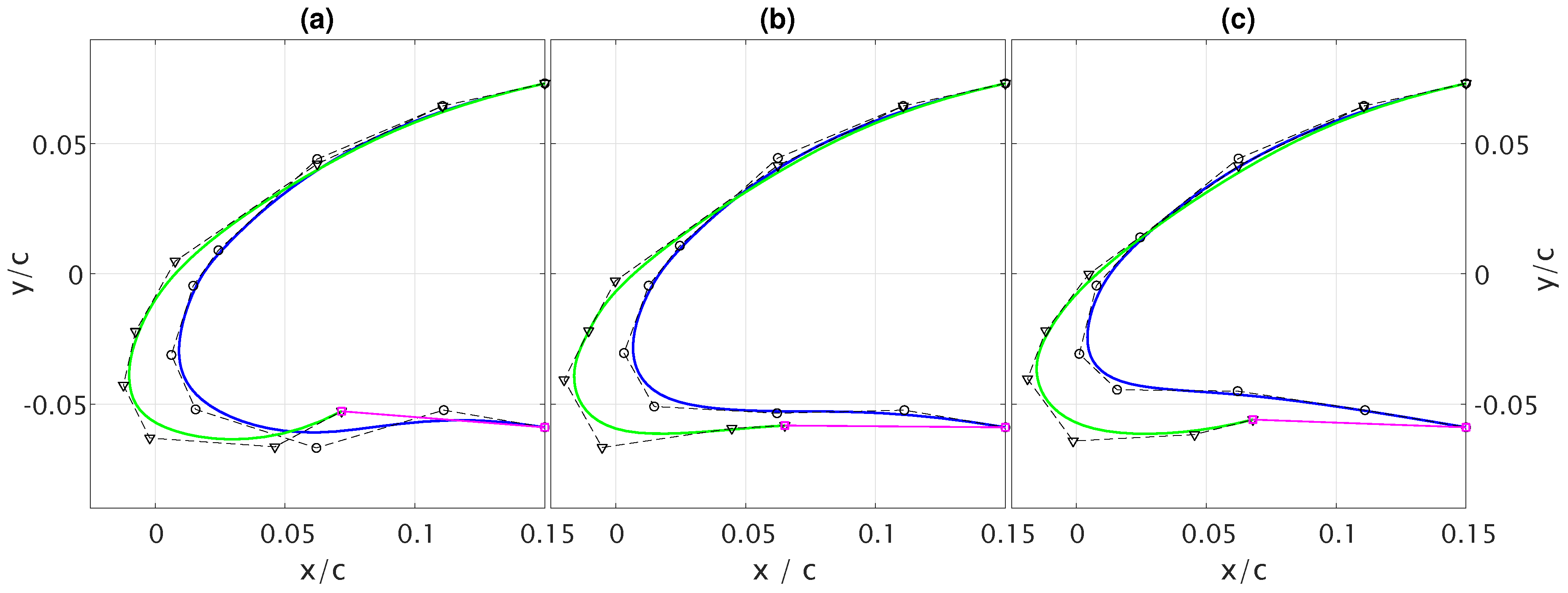
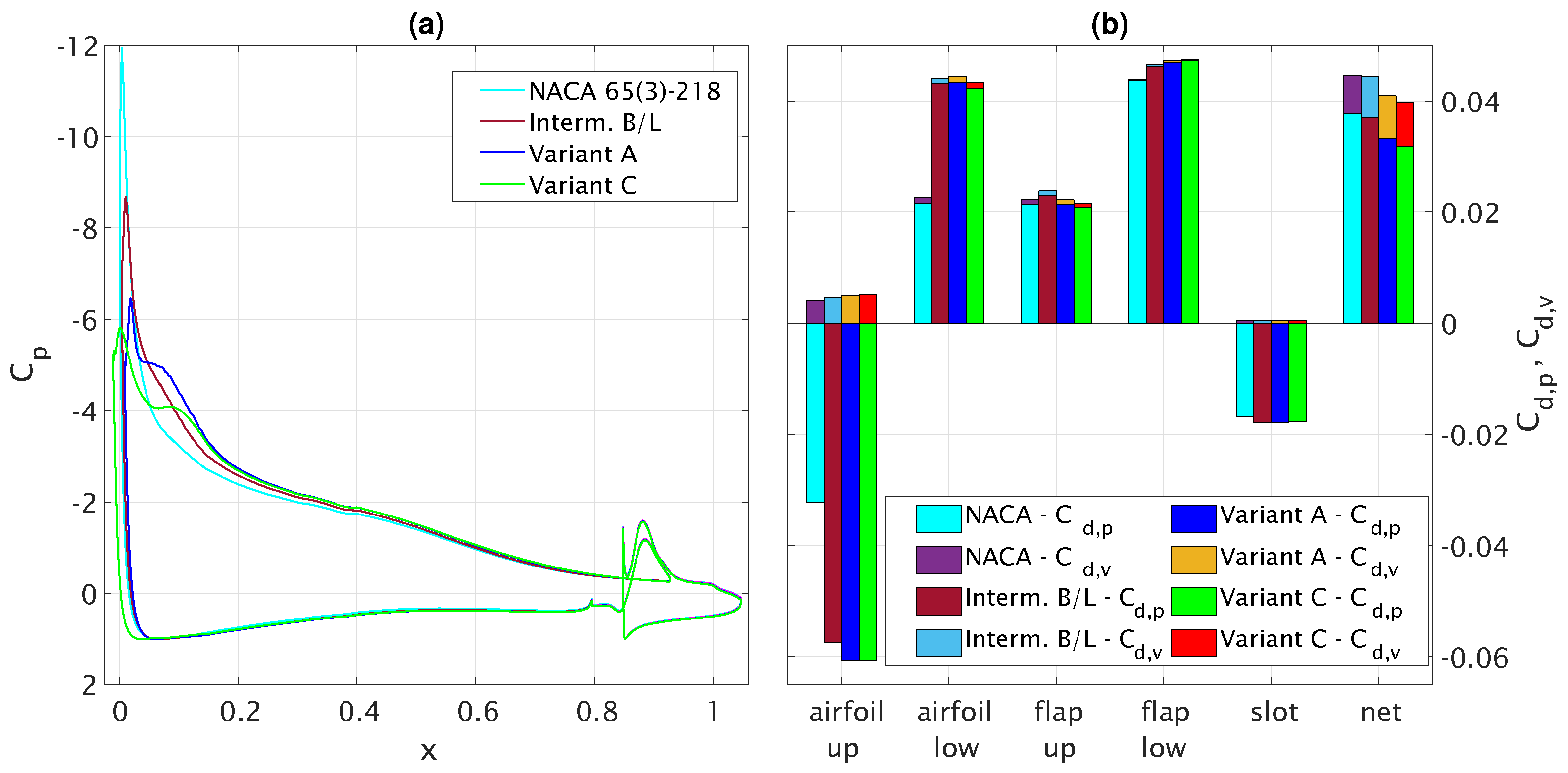
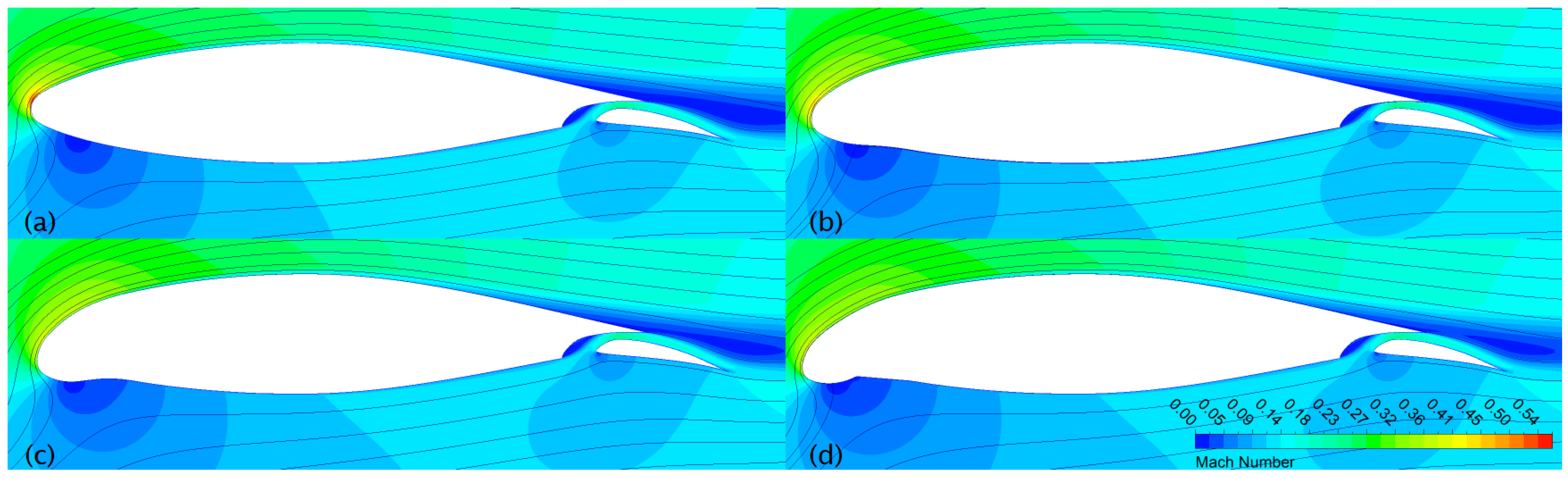
| DP1 | DP2 | |||
|---|---|---|---|---|
| Airfoil | (rel. var. %) | (rel. var. %) | (rel. var. %) | |
| NACA 65(3)-218 | 0.04766 (−2.22) | 1.571 (−5.07) | 17.00 | 80.42 (−2.37) |
| Interm. Baseline | 0.04874 | 1.655 | 18.00 | 82.37 |
| Best L/D—var. A | 0.04722 (−3.11) | 1.669 (+0.82) | 18.00 | 83.17 (+0.97) |
| Best L/D—var. B | 0.04663 (−4.33) | 1.687 (+1.95) | 18.00 | 83.74 (+1.66) |
| Best L/D—var. C | 0.05400 (+10.80) | 1.705 (+3.00) | 19.00 | 83.85 (+1.79) |
| Best Cl—var. A | 0.05390 (+10.58) | 1.685 (+1.82) | 19.00 | 82.65 (+0.33) |
| Best Cl—var. B | 0.05280 (+8.33) | 1.712 (+3.43) | 19.00 | 83.32 (+1.15) |
| Best Cl—var. C | 0.05252 (+7.75) | 1.722 (+4.07) | 19.00 | 83.52 (+1.39) |
| DP1 | DP2 | |||
|---|---|---|---|---|
| Airfoil | (rel. var. %) | (rel. var. %) | (rel. var. %) | |
| NACA 65(3)-218 | 0.04461 (0.51) | 2.250 (−4.64) | 14.00 | 82.30 (−1.79) |
| Interm. Baseline | 0.04438 | 2.359 | 15.00 | 83.80 |
| Best L/D—var. A | 0.04253 (−4.17) | 2.379 (+0.85) | 15.00 | 84.40 (+0.72) |
| Best L/D—var. C | 0.04047 (−8.80) | 2.432 (+3.07) | 15.00 | 85.23 (+1.71) |
| Best Cl—var. A | 0.04092 (−7.80) | 2.397 (+1.62) | 15.00 | 84.04 (+0.29) |
| Best Cl—var. C | 0.03978(−10.36) | 2.438 (+3.36) | 15.00 | 84.99 (+1.42) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Magrini, A.; Benini, E.; Ponza, R.; Wang, C.; Khodaparast, H.H.; Friswell, M.I.; Landersheim, V.; Laveuve, D.; Contell Asins, C. Comparison of Constrained Parameterisation Strategies for Aerodynamic Optimisation of Morphing Leading Edge Airfoil. Aerospace 2019, 6, 31. https://doi.org/10.3390/aerospace6030031
Magrini A, Benini E, Ponza R, Wang C, Khodaparast HH, Friswell MI, Landersheim V, Laveuve D, Contell Asins C. Comparison of Constrained Parameterisation Strategies for Aerodynamic Optimisation of Morphing Leading Edge Airfoil. Aerospace. 2019; 6(3):31. https://doi.org/10.3390/aerospace6030031
Chicago/Turabian StyleMagrini, Andrea, Ernesto Benini, Rita Ponza, Chen Wang, Hamed Haddad Khodaparast, Michael I. Friswell, Volker Landersheim, Dominik Laveuve, and Conchin Contell Asins. 2019. "Comparison of Constrained Parameterisation Strategies for Aerodynamic Optimisation of Morphing Leading Edge Airfoil" Aerospace 6, no. 3: 31. https://doi.org/10.3390/aerospace6030031
APA StyleMagrini, A., Benini, E., Ponza, R., Wang, C., Khodaparast, H. H., Friswell, M. I., Landersheim, V., Laveuve, D., & Contell Asins, C. (2019). Comparison of Constrained Parameterisation Strategies for Aerodynamic Optimisation of Morphing Leading Edge Airfoil. Aerospace, 6(3), 31. https://doi.org/10.3390/aerospace6030031











