Effects of Nozzle Pressure Ratio and Nozzle-to-Plate Distance to Flowfield Characteristics of an Under-Expanded Jet Impinging on a Flat Surface
Abstract
1. Introduction
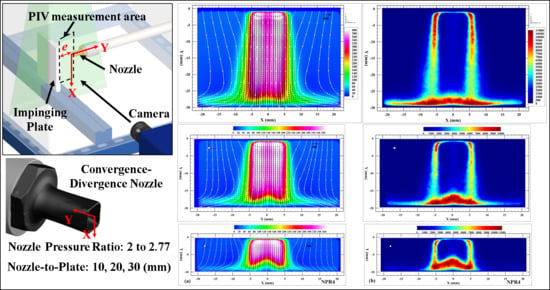
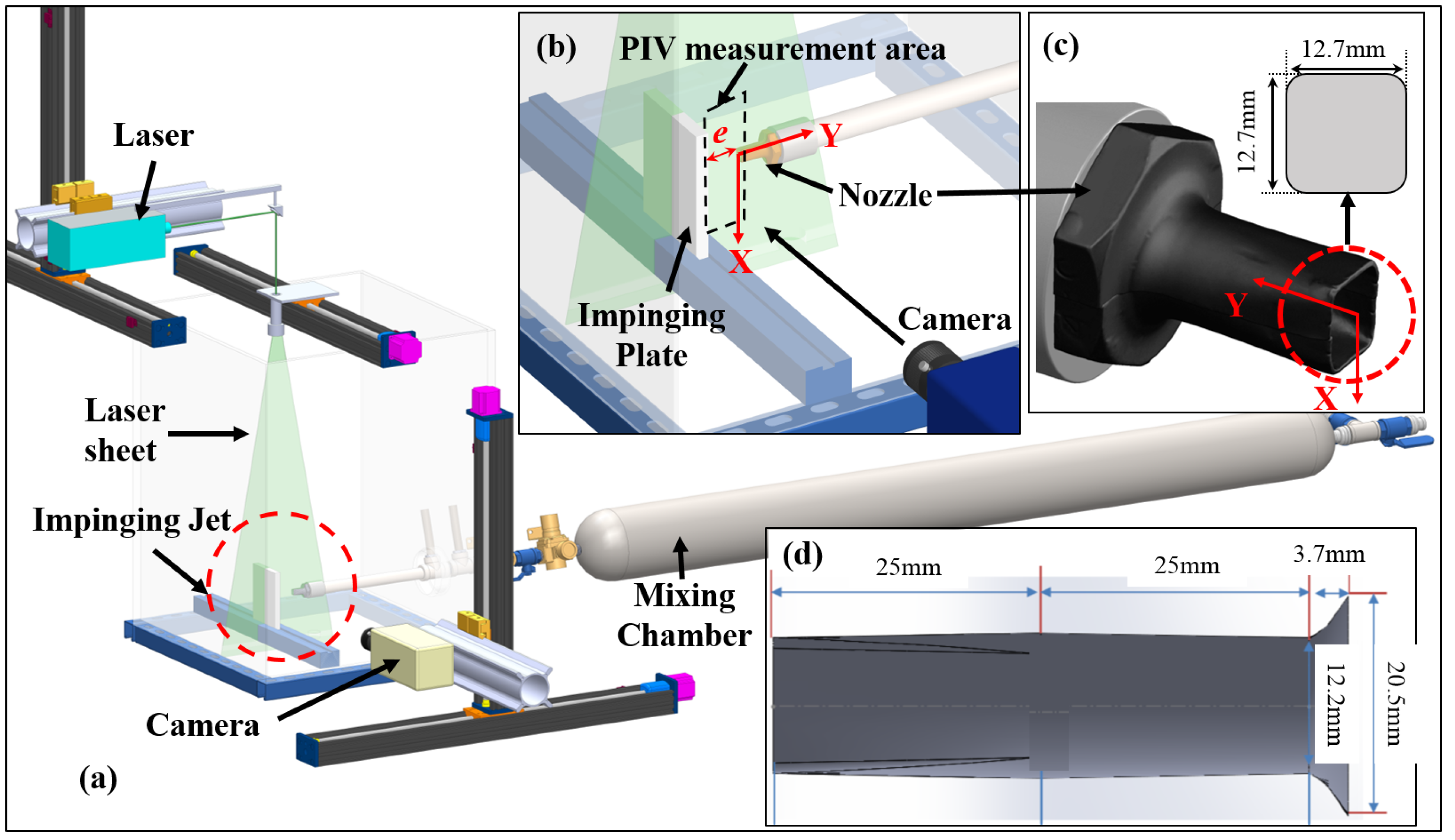
2. Experimental Facility and Particle Image Velocimetry (PIV) Experimental Setup
2.1. Experimental Facility of Impinging Jet
2.2. PIV Experimental Setup
3. Results from PIV Measurements of Under-Expanded Free Jets and Impinging Jets
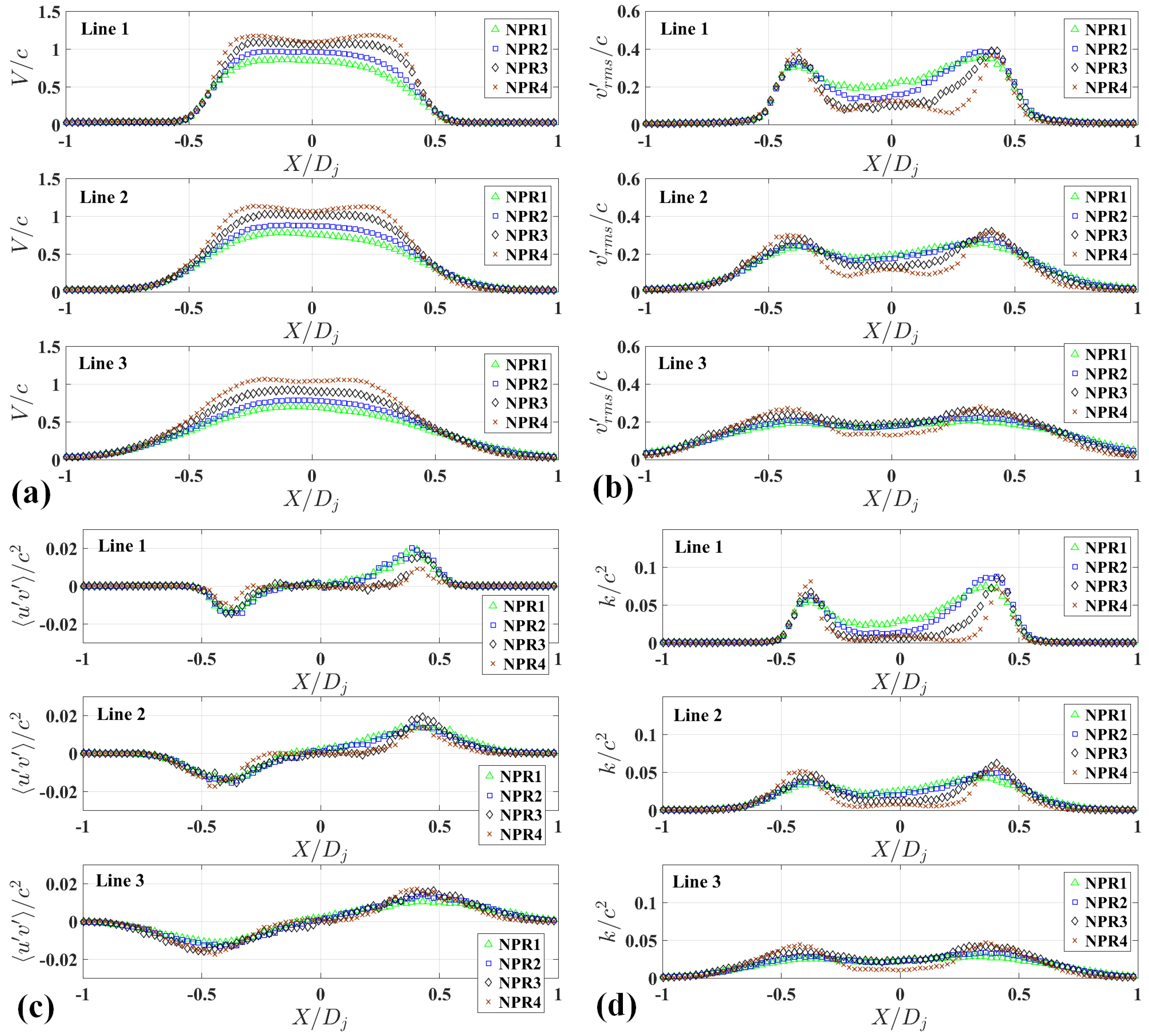
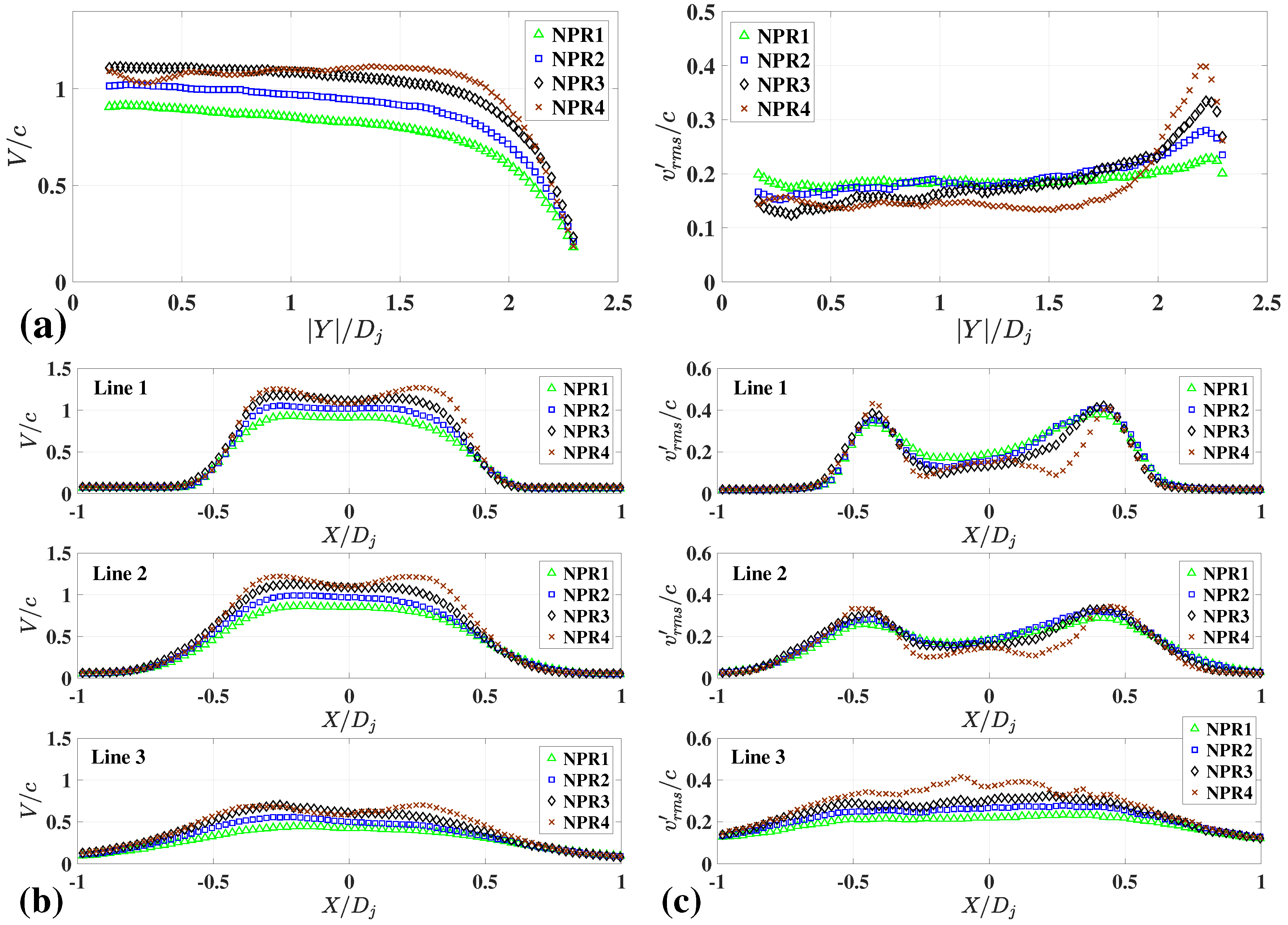
3.1. Experimental Results of Under-Expanded Free Jets for Various Values of NPRs
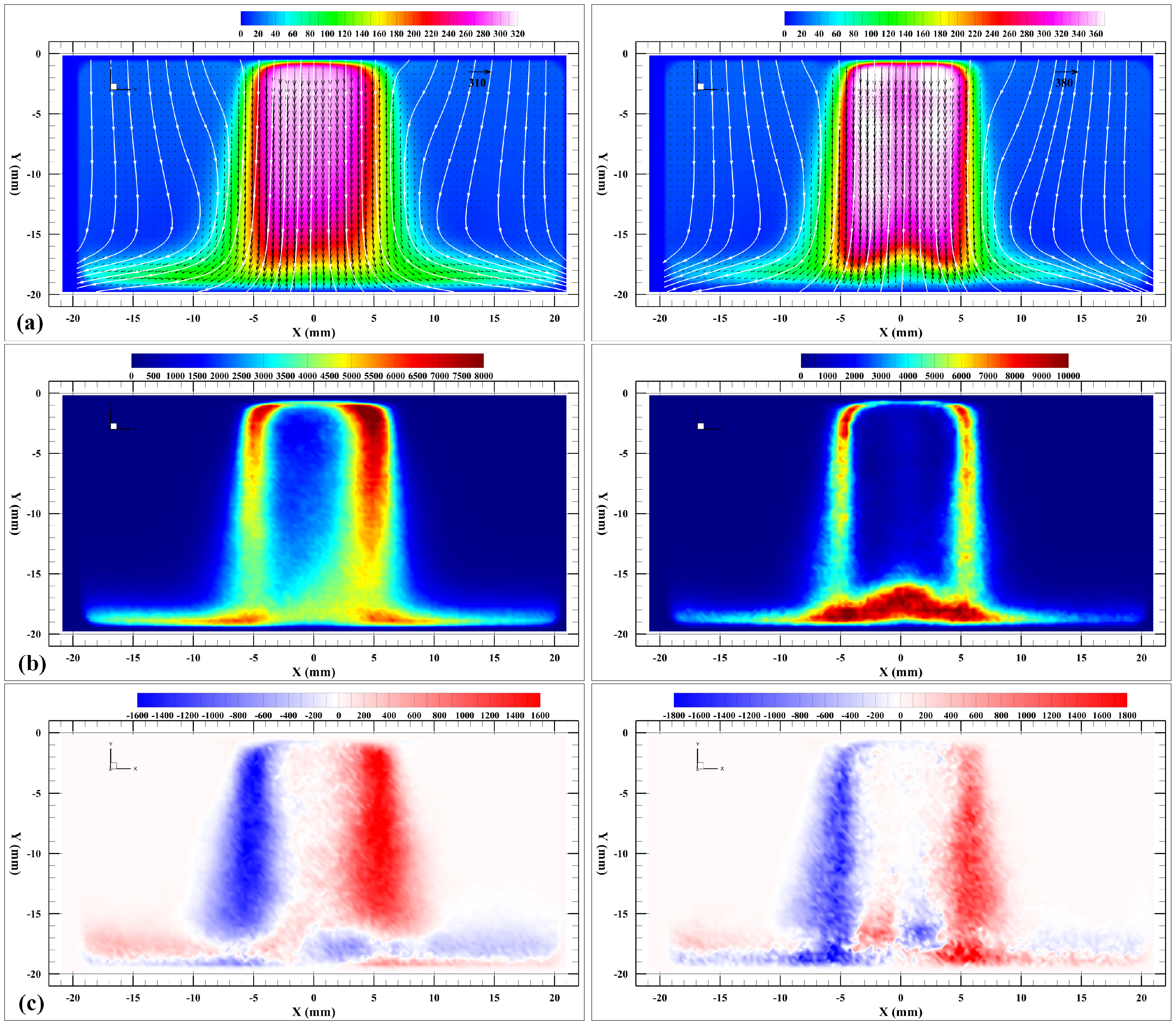
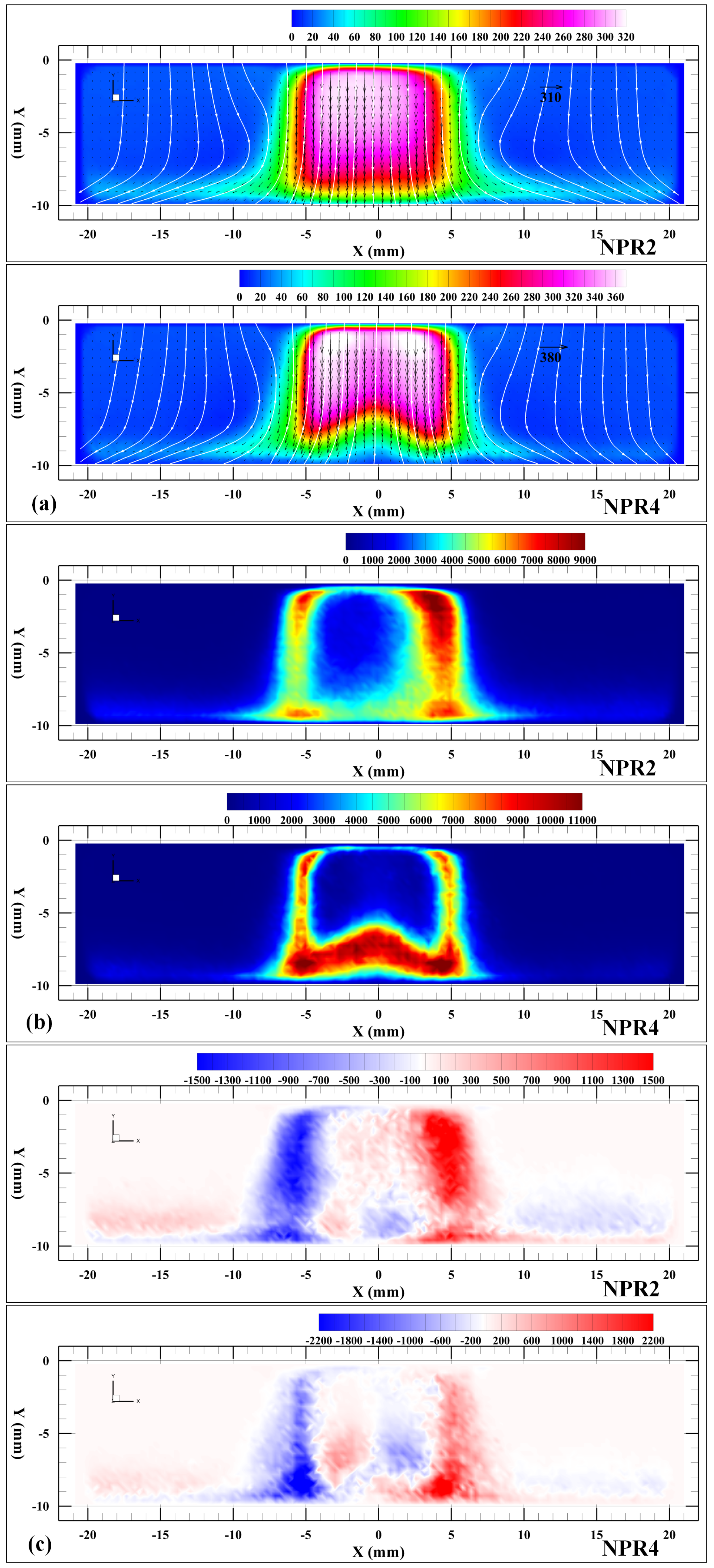
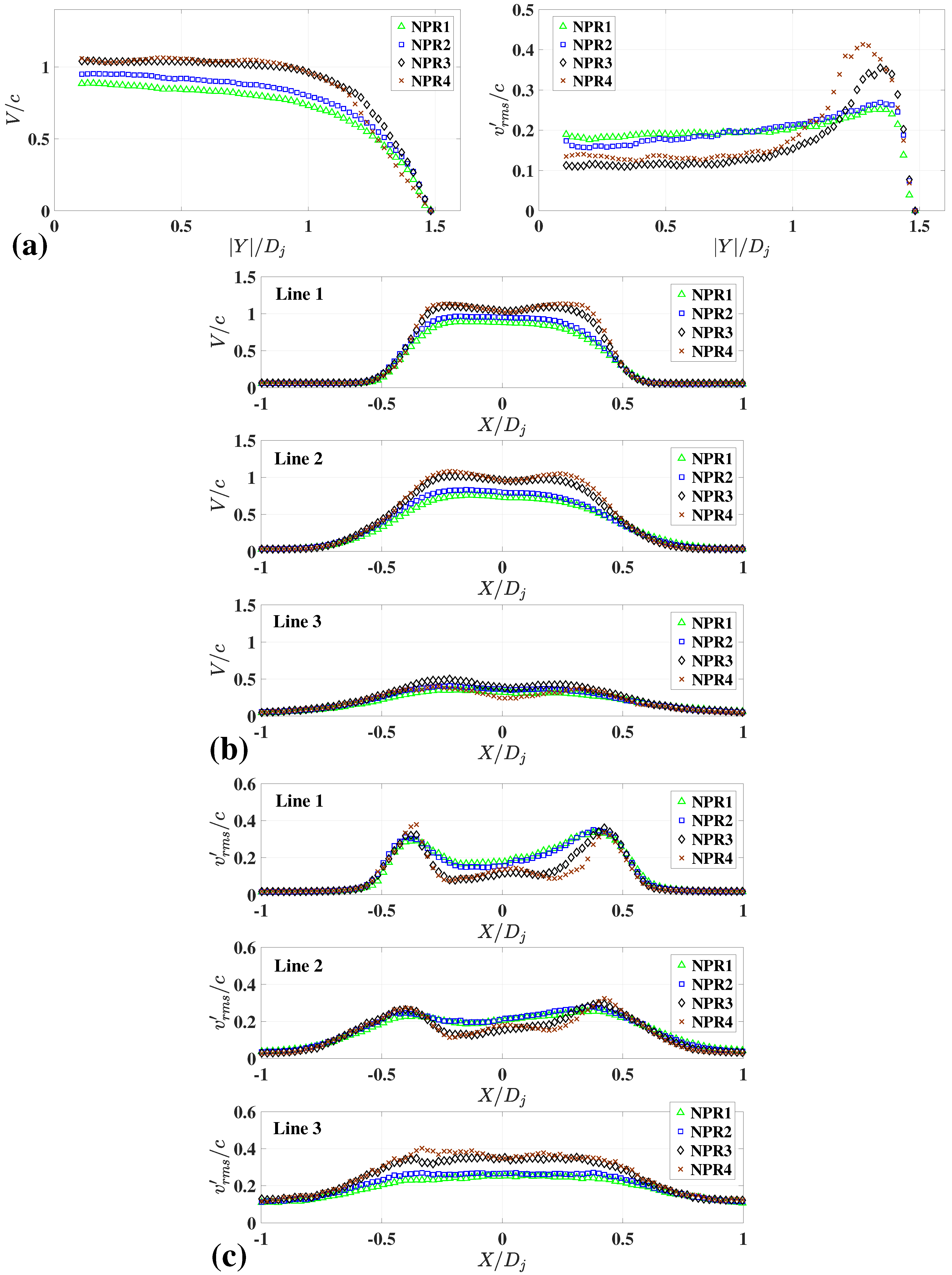
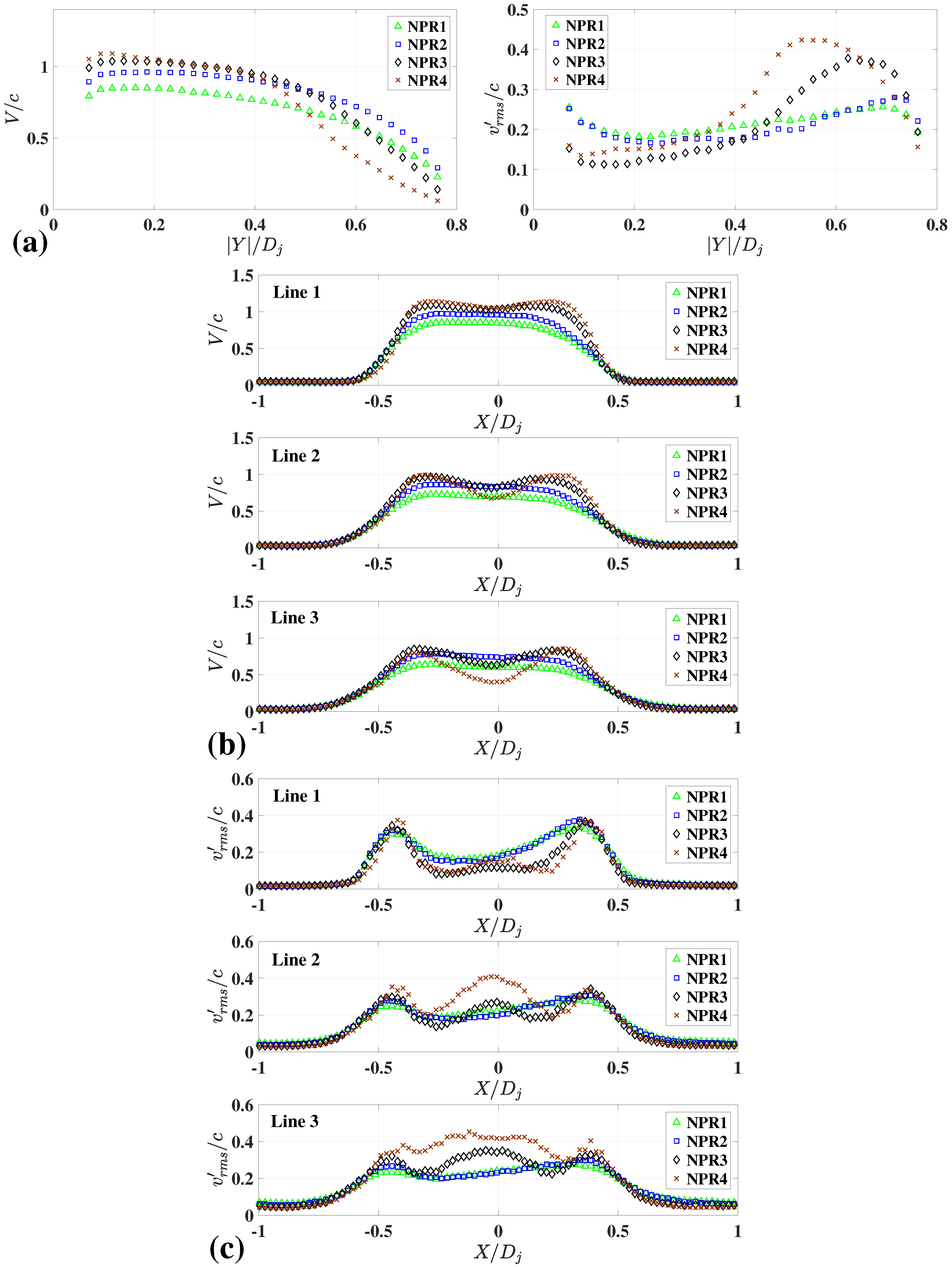
3.2. Experimental Results of Under-Expanded Impinging Jets for Various Nozzle-to-Plate Gaps and NPRs
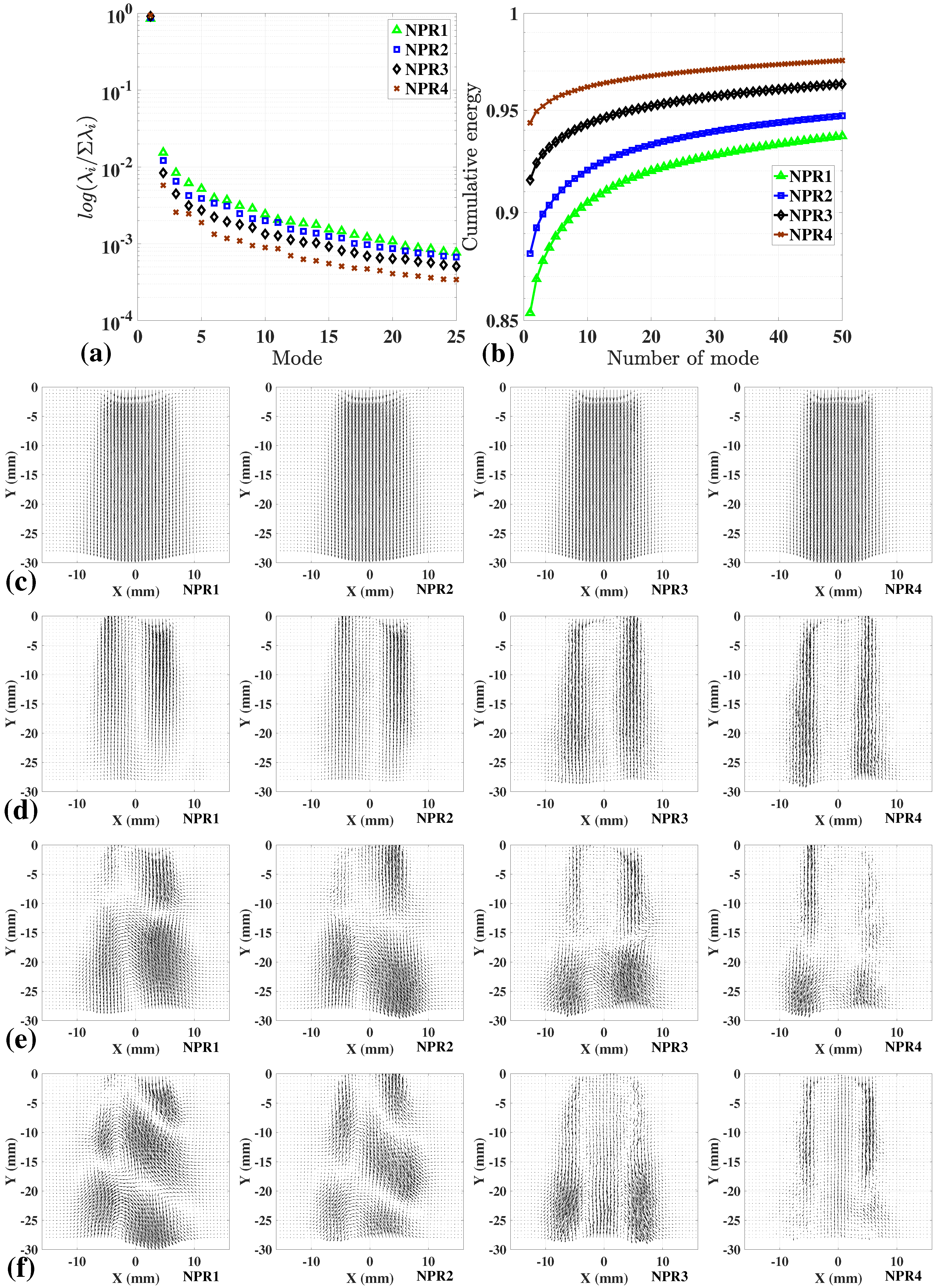
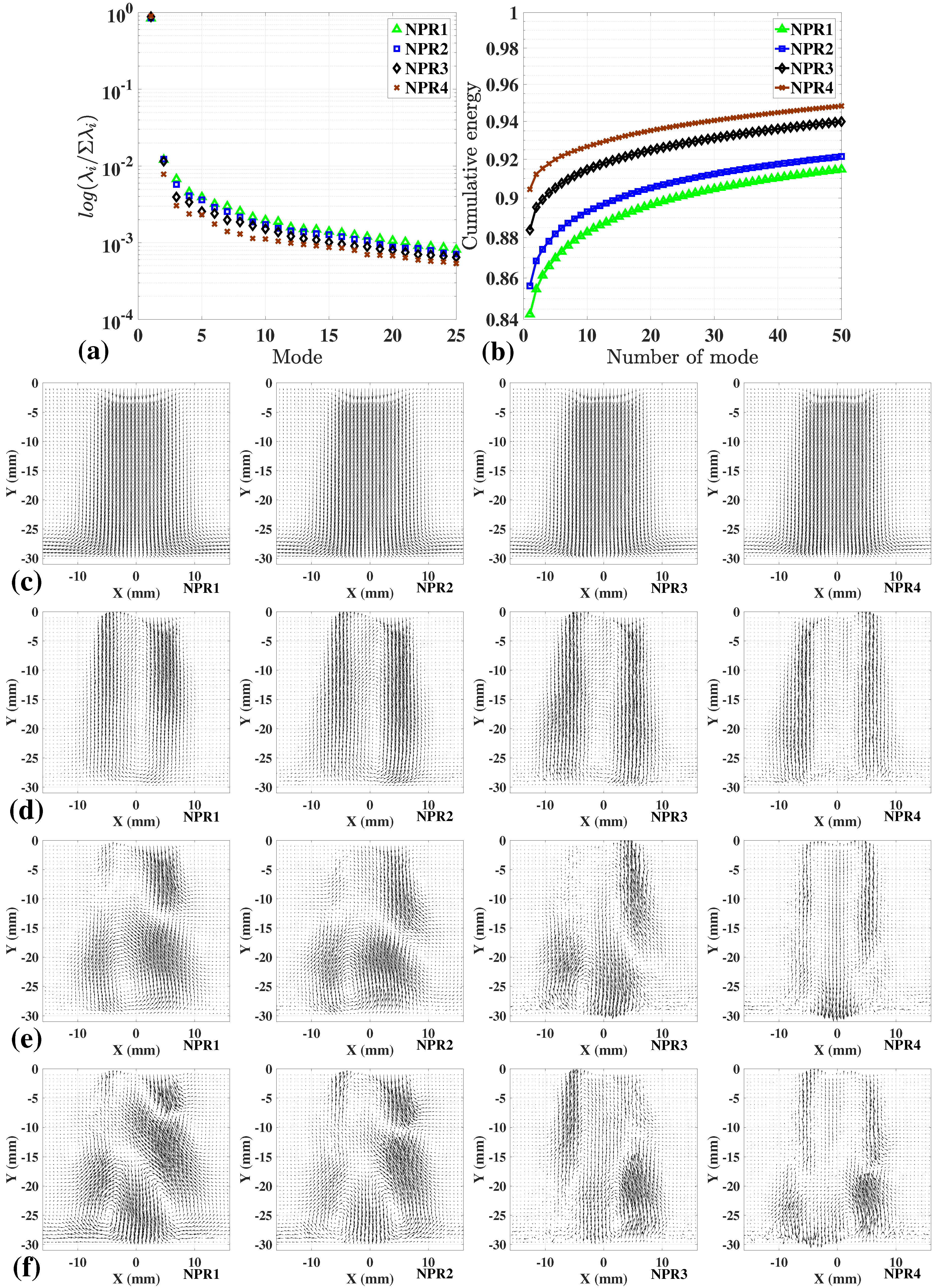
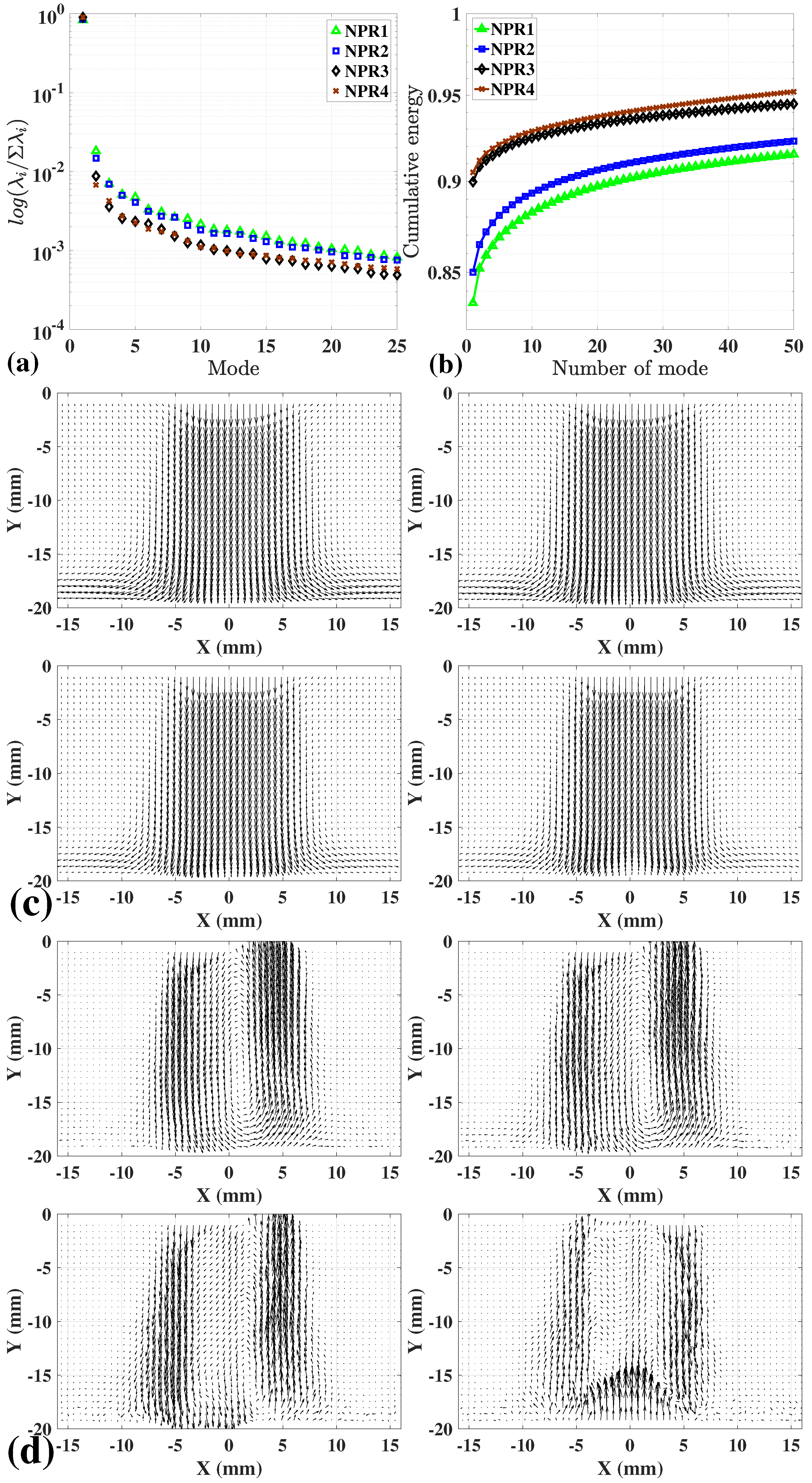
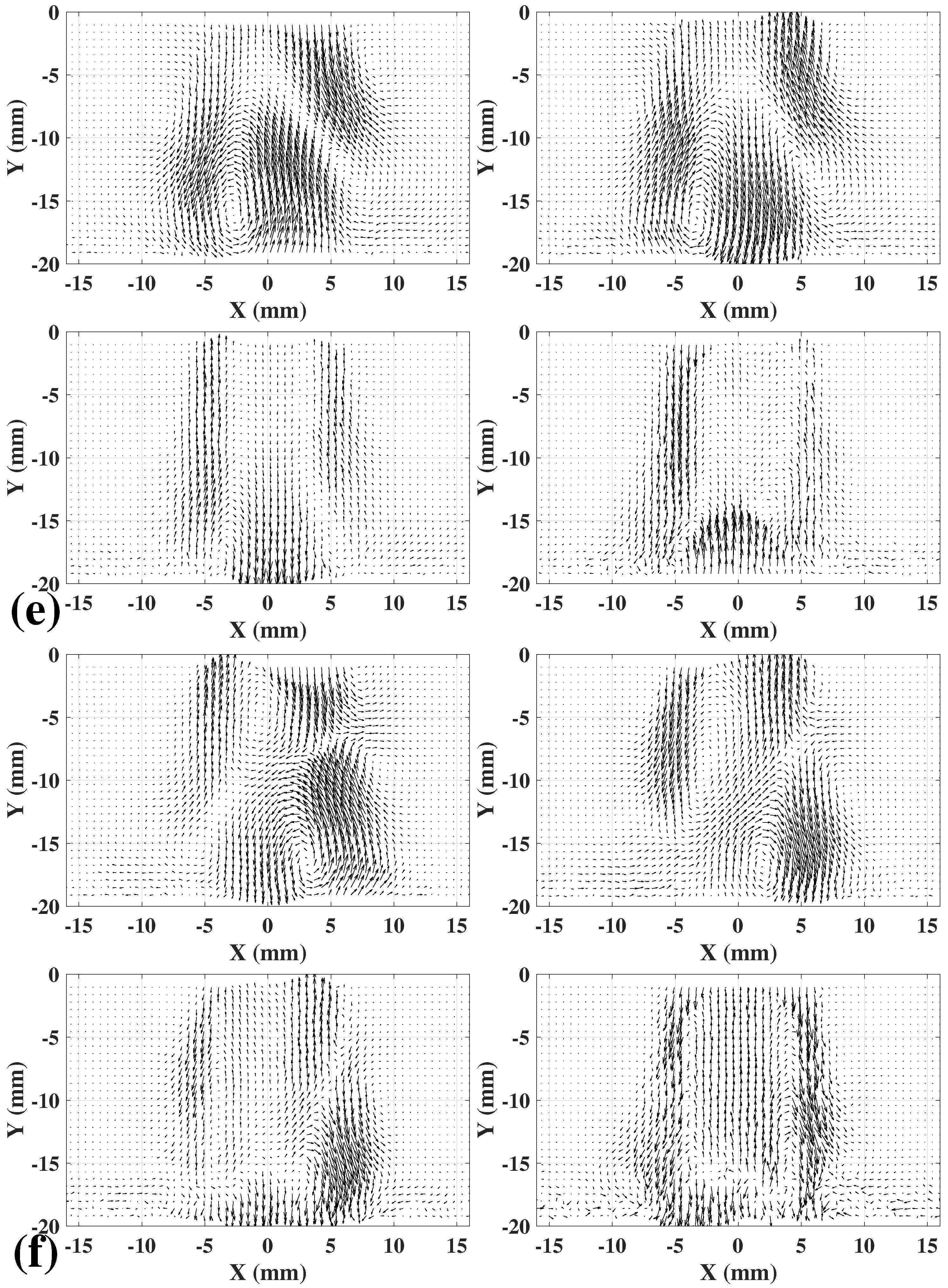
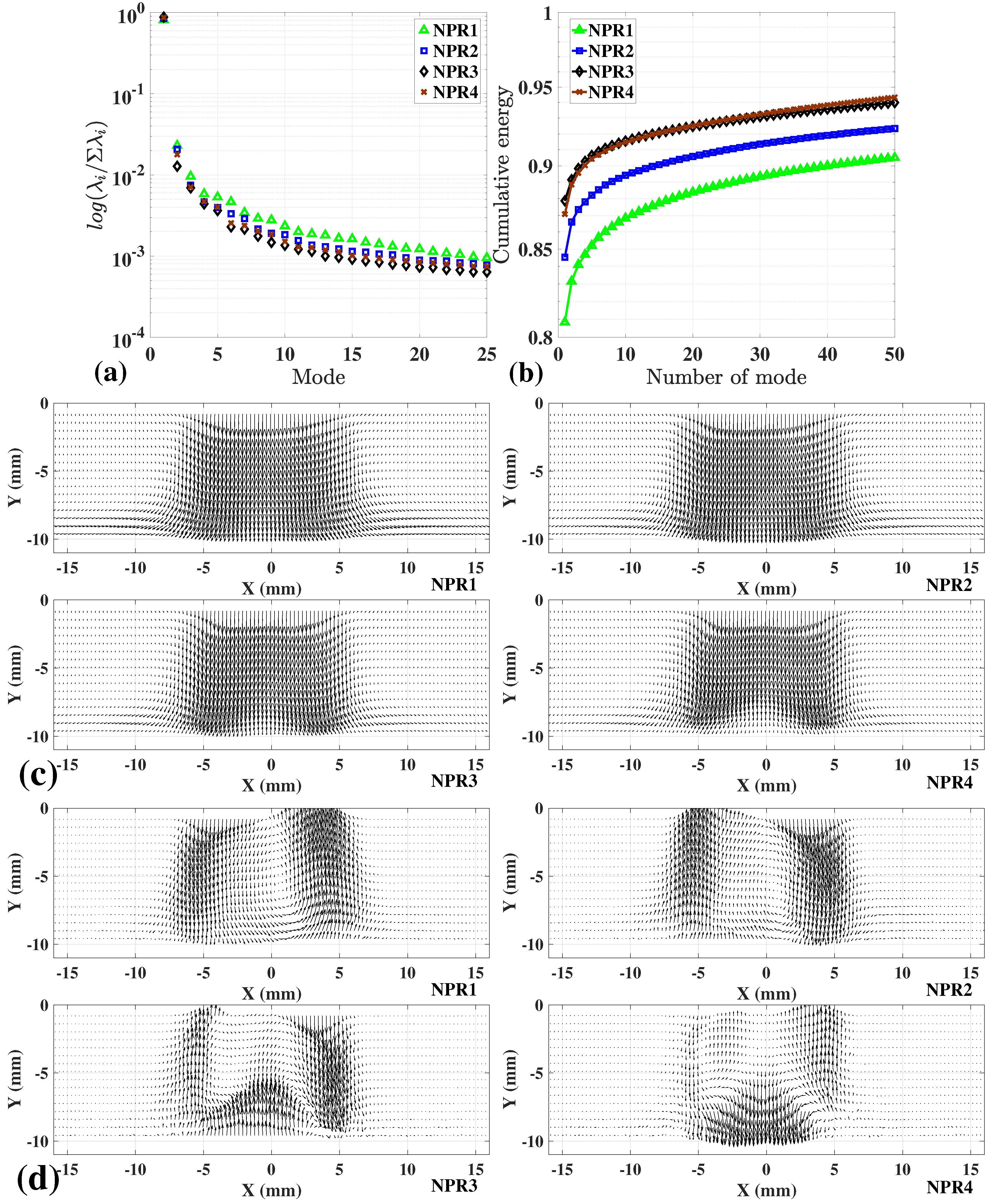
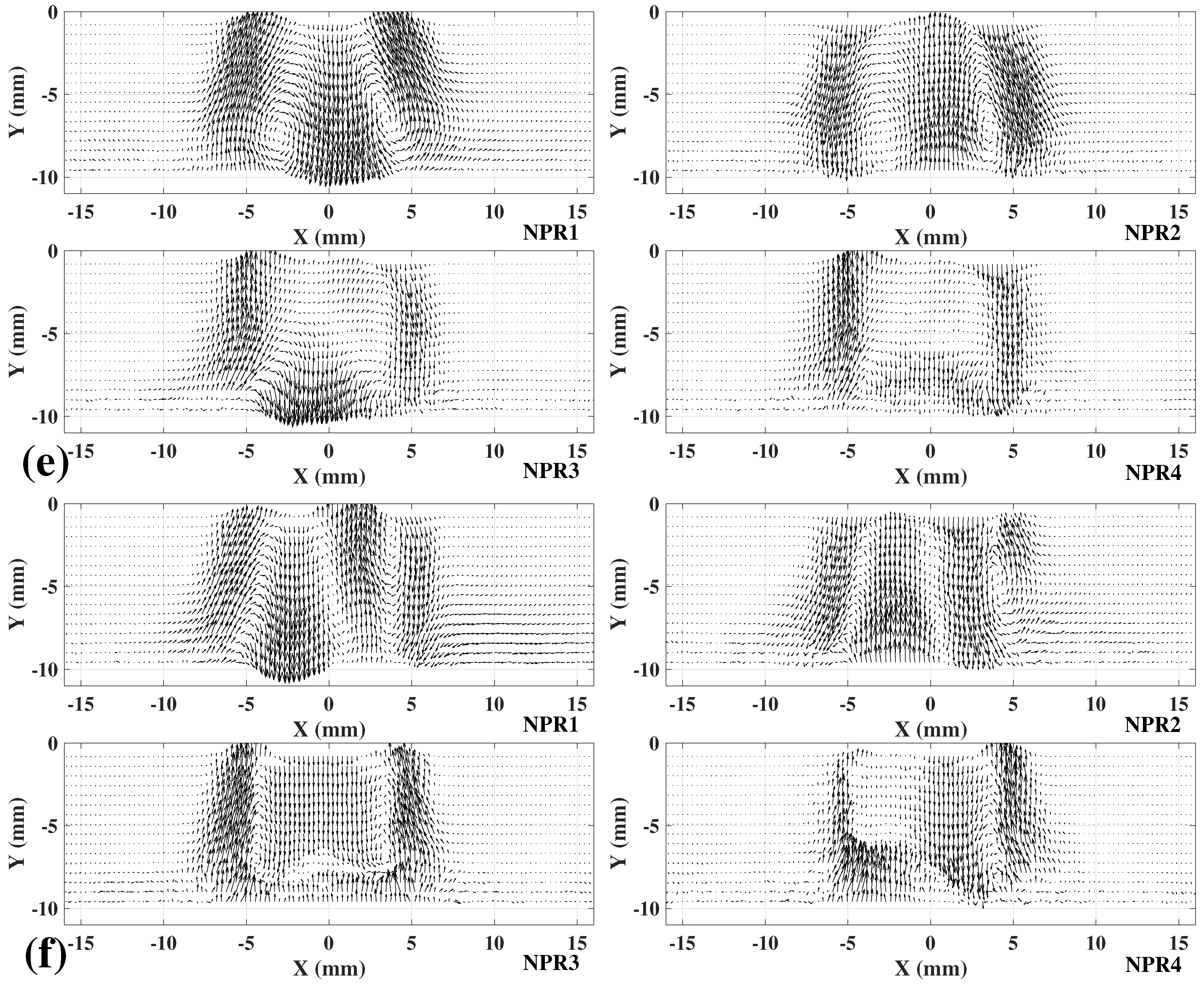
4. Proper Orthogonal Decomposition Analysis to the Free Jet and Impinging Jet Flows
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Saddington, A.J.; Lawson, N.; Knowles, K. An experimental and numerical investigation of under-expanded turbulent jets. Aeronaut. J. 2004, 108, 145–152. [Google Scholar] [CrossRef]
- Hadžiabdić, M.; Hanjalić, K. Vortical structures and heat transfer in a round impinging jet. J. Fluid Mech. 2008, 596, 221–260. [Google Scholar] [CrossRef]
- Krothapalli, A.; Rajkuperan, E.; Alvi, F.; Lourenco, L. Flow field and noise characteristics of a supersonic impinging jet. J. Fluid Mech. 1999, 392, 155–181. [Google Scholar] [CrossRef]
- Cabrita, P.; Saddington, A.; Knowles, K. PIV measurements in a twin-jet STOVL fountain flow. Aeronaut. J. 2005, 109, 439–449. [Google Scholar] [CrossRef]
- Saddington, A.; Knowles, K.; Cabrita, P. Flow measurements in a short takeoff, vertical landing fountain: Parallel jets. J. Aircr. 2008, 45, 1736–1743. [Google Scholar] [CrossRef]
- Saddington, A.; Knowles, K.; Cabrita, P. Flow Measurements in a Short Takeoff, Vertical Landing Fountain: Splayed Jets. J. Aircr. 2009, 46, 874–882. [Google Scholar] [CrossRef]
- Wilke, R.; Sesterhenn, J. Statistics of fully turbulent impinging jets. J. Fluid Mech. 2017, 825, 795–824. [Google Scholar] [CrossRef]
- Franquet, E.; Perrier, V.; Gibout, S.; Bruel, P. Free underexpanded jets in a quiescent medium: A review. Prog. Aerosp. Sci. 2015, 77, 25–53. [Google Scholar] [CrossRef]
- Henderson, L. Experiments on the impingement of a supersonic jet on a flat plate. Z. Angew. Math. Phys. ZAMP 1966, 17, 553–569. [Google Scholar] [CrossRef]
- Weightman, J.L.; Amili, O.; Honnery, D.; Soria, J.; Edgington-Mitchell, D. An explanation for the phase lag in supersonic jet impingement. J. Fluid Mech. 2017, 815. [Google Scholar] [CrossRef]
- Uzun, A.; Kumar, R.; Hussaini, M.Y.; Alvi, F.S. Simulation of tonal noise generation by supersonic impinging jets. AIAA J. 2013, 51, 1593–1611. [Google Scholar] [CrossRef]
- Akamine, M.; Okamoto, K.; Gee, K.L.; Neilsen, T.B.; Teramoto, S.; Okunuki, T.; Tsutsumi, S. Effect of Nozzle–Plate Distance on Acoustic Phenomena from Supersonic Impinging Jet. AIAA J. 2018, 56, 1943–1952. [Google Scholar] [CrossRef]
- Brown, G.L.; Roshko, A. On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 1974, 64, 775–816. [Google Scholar] [CrossRef]
- Tam, C.K.; Ahuja, K. Theoretical model of discrete tone generation by impinging jets. J. Fluid Mech. 1990, 214, 67–87. [Google Scholar] [CrossRef]
- Henderson, B.; Powell, A. Experiments concerning tones produced by an axisymmetric choked jet impinging on flat plates. J. Sound Vib. 1993, 168, 307–326. [Google Scholar] [CrossRef]
- Henderson, B. The connection between sound production and jet structure of the supersonic impinging jet. J. Acoust. Soc. Am. 2002, 111, 735–747. [Google Scholar] [CrossRef] [PubMed]
- Henderson, B.; Bridges, J.; Wernet, M. An experimental study of the oscillatory flow structure of tone-producing supersonic impinging jets. J. Fluid Mech. 2005, 542, 115–137. [Google Scholar] [CrossRef]
- Sinibaldi, G.; Marino, L.; Romano, G.P. Sound source mechanisms in under-expanded impinging jets. Exp. Fluids 2015, 56, 105. [Google Scholar] [CrossRef]
- Gojon, R.; Bogey, C.; Marsden, O. Investigation of tone generation in ideally expanded supersonic planar impinging jets using large-eddy simulation. J. Fluid Mech. 2016, 808, 90–115. [Google Scholar] [CrossRef]
- Ho, C.M.; Nosseir, N.S. Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 1981, 105, 119–142. [Google Scholar] [CrossRef]
- Nosseir, N.S.; Ho, C.M. Dynamics of an impinging jet. Part 2. The noise generation. J. Fluid Mech. 1982, 116, 379–391. [Google Scholar] [CrossRef]
- Kays, W.M. Convective Heat and Mass Transfer; Tata McGraw-Hill Education: New York, NY, USA, 2012. [Google Scholar]
- Solovitz, S.A.; Mastin, L.G.; Saffaraval, F. Experimental study of near-field entrainment of moderately overpressured jets. J. Fluids Eng. 2011, 133, 051304. [Google Scholar] [CrossRef]
- Nguyen, T.; Pellé, J.; Harmand, S.; Poncet, S. PIV measurements of an air jet impinging on an open rotor-stator system. Exp. Fluids 2012, 53, 401–412. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Souad, H. PIV measurements in a turbulent wall jet over a backward-facing step in a three-dimensional, non-confined channel. Flow Meas. Instrum. 2015, 42, 26–39. [Google Scholar] [CrossRef]
- Raffel, M.; Willert, C.E.; Wereley, S.; Kompenhans, J. Particle Image Velocimetry: A Practical Guide; Springer: Berlin, Germany, 2013. [Google Scholar]
- Scarano, F. Overview of PIV in supersonic flows. In Particle Image Velocimetry; Springer: Berlin, Germany, 2007; pp. 445–463. [Google Scholar]
- Alvi, F.; Ladd, J.; Bower, W. Experimental and computational investigation of supersonic impinging jets. AIAA J. 2002, 40, 599–609. [Google Scholar] [CrossRef]
- Mitchell, D.; Honnery, D.; Soria, J. Particle relaxation and its influence on the particle image velocimetry cross-correlation function. Exp. Fluids 2011, 51, 933. [Google Scholar] [CrossRef]
- Samimy, M.; Lele, S. Motion of particles with inertia in a compressible free shear layer. Phys. Fluids A Fluid Dyn. 1991, 3, 1915–1923. [Google Scholar] [CrossRef]
- Erdem, E.; Saravanan, S.; Lin, J.; Kontis, K. Experimental Investigation of Transverse Injection Flowfield at March 5 and the Influence of Impinging Shock Wave. In Proceedings of the 18th AIAA/3AF International Space Planes and Hypersonic Systems and Technologies Conference, Tours, France, 24–28 September 2012; p. 5800. [Google Scholar]
- Ragni, D.; Schrijer, F.; Van Oudheusden, B.; Scarano, F. Particle tracer response across shocks measured by PIV. Exp. Fluids 2011, 50, 53–64. [Google Scholar] [CrossRef]
- Eckstein, A.C.; Charonko, J.; Vlachos, P. Phase correlation processing for DPIV measurements. Exp. Fluids 2008, 45, 485–500. [Google Scholar] [CrossRef]
- Eckstein, A.; Vlachos, P.P. Digital particle image velocimetry (DPIV) robust phase correlation. Meas. Sci. Technol. 2009, 20, 055401. [Google Scholar] [CrossRef]
- Westerweel, J. Efficient detection of spurious vectors in particle image velocimetry data. Exp. Fluids 1994, 16, 236–247. [Google Scholar] [CrossRef]
- Timmins, B.H.; Wilson, B.W.; Smith, B.L.; Vlachos, P.P. A method for automatic estimation of instantaneous local uncertainty in particle image velocimetry measurements. Exp. Fluids 2012, 53, 1133–1147. [Google Scholar] [CrossRef]
- Wilson, B.M.; Smith, B.L. Uncertainty on PIV mean and fluctuating velocity due to bias and random errors. Meas. Sci. Technol. 2013, 24, 035302. [Google Scholar] [CrossRef]
- Charonko, J.J.; Vlachos, P.P. Estimation of uncertainty bounds for individual particle image velocimetry measurements from cross-correlation peak ratio. Meas. Sci. Technol. 2013, 24, 065301. [Google Scholar] [CrossRef]
- Boomsma, A.; Bhattacharya, S.; Troolin, D.; Pothos, S.; Vlachos, P. A comparative experimental evaluation of uncertainty estimation methods for two-component PIV. Meas. Sci. Technol. 2016, 27, 094006. [Google Scholar] [CrossRef]
- Saffaraval, F.; Solovitz, S.A. Near-exit flow physics of a moderately overpressured jet. Phys. Fluids 2012, 24, 086101. [Google Scholar] [CrossRef]
- Snedeker, R.S.; Donaldson, C.D. A study of free jet impingement. Part 1. Mean properties of free and impinging jets. J. Fluid Mech. 1971, 45, 281–319. [Google Scholar]
- Donaldson, C.D.; Snedeker, R.S.; Margolis, D.P. A study of free jet impingement. Part 2. Free jet turbulent structure and impingement heat transfer. J. Fluid Mech. 1971, 45, 477–512. [Google Scholar] [CrossRef]
- Alvi, F.; Iyer, K. Mean and unsteady flowfield properties of supersonic impinging jets with lift plates. In Proceedings of the 5th AIAA/CEAS Aeroacoustics Conference and Exhibit, Bellevue, WA, USA, 10–12 May 1999; p. 1829. [Google Scholar]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Wave Propagation; Yaglom, A.M., Tatarski, V.I., Eds.; Nauka: Moscow, Russia, 1967; pp. 166–178. [Google Scholar]
- Nguyen, T.D.; Wells, J.C.; Mokhasi, P.; Rempfer, D. Proper orthogonal decomposition-based estimations of the flow field from particle image velocimetry wall-gradient measurements in the backward-facing step flow. Meas. Sci. Technol. 2010, 21, 115406. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Holmes, P.; Lumley, J.L.; Berkooz, G. Turbulence, Coherent Structures, Dynamical Systems And Symmetry; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Nguyen, T.; Kappes, E.; King, S.; Hassan, Y.; Ugaz, V. Time-resolved PIV measurements in a low-aspect ratio facility of randomly packed spheres and flow analysis using modal decomposition. Exp. Fluids 2018, 59, 127. [Google Scholar] [CrossRef]
- Sirovich, L.; Kirby, M. Low-dimensional procedure for the characterization of human faces. J. Opt. Soc. Am. 1987, 4, 519–524. [Google Scholar] [CrossRef]
- Palacios, A.; Gunaratne, G.H.; Gorman, M.; Robbins, K.A. Cellular pattern formation in circular domains. Chaos Interdiscip. J. Nonlinear Sci. 1997, 7, 463–475. [Google Scholar] [CrossRef] [PubMed]
- Moreno, D.; Krothapalli, A.; Alkislar, M.; Lourenco, L. Low-dimensional model of a supersonic rectangular jet. Phys. Rev. E 2004, 69, 026304. [Google Scholar] [CrossRef] [PubMed]
- Wilke, R.; Sesterhenn, J. Numerical simulation of subsonic and supersonic impinging jets. In High Performance Computing in Science and Engineering’15; Springer: Berlin, Germany, 2016; pp. 349–369. [Google Scholar]
- Wilke, R.; Sesterhenn, J. On the origin of impinging tones at low supersonic flow. arXiv, 2016; arXiv:1604.05624. [Google Scholar]
- Berry, M.G.; Stack, C.M.; Magstadt, A.S.; Ali, M.Y.; Gaitonde, D.V.; Glauser, M.N. Low-dimensional and data fusion techniques applied to a supersonic multistream single expansion ramp nozzle. Phys. Rev. Fluids 2017, 2, 100504. [Google Scholar] [CrossRef]
- Guariglia, D.; Rubio Carpio, A.; Schram, C. Design of a facility for studying shock-cell noise on single and coaxial jets. Aerospace 2018, 5, 25. [Google Scholar] [CrossRef]
- Berry, M.G.; Ali, M.Y.; Magstadt, A.S.; Glauser, M.N. DMD and POD of time-resolved schlieren on a multi-stream single expansion ramp nozzle. Int. J. Heat Fluid Flow 2017, 66, 60–69. [Google Scholar] [CrossRef]
- Nair, U.S.; Goparaju, K.; Gaitonde, D. Energy-Dynamics Resulting in Turbulent and Acoustic Phenomena in an Underexpanded Jet. Aerospace 2018, 5, 49. [Google Scholar] [CrossRef]
- Berry, M.; Magstadt, A.; Glauser, M. Application of POD on time-resolved schlieren in supersonic multi-stream rectangular jets. Phys. Fluids 2017, 29, 020706. [Google Scholar] [CrossRef]
- Weightman, J.L.; Amili, O.; Honnery, D.; Soria, J.; Edgington-Mitchell, D. Signatures of shear-layer unsteadiness in proper orthogonal decomposition. Exp. Fluids 2018, 59, 180. [Google Scholar] [CrossRef]
- Karami, S.; Soria, J. Analysis of Coherent Structures in an Under-Expanded Supersonic Impinging Jet Using Spectral Proper Orthogonal Decomposition (SPOD). Aerospace 2018, 5, 73. [Google Scholar] [CrossRef]


| NPR | 2 | 2.2 | 2.5 | 2.77 | |
| Nozzle Outlet Temperature (K) | 287.1 | 287.0 | 286.5 | 274.1 | |
| Exit Air Density (kg/m) | 2.46 | 2.73 | 3.08 | 3.42 | |
| Exit Air Viscosity (Pa/s) | |||||
| Ambient Sound Speed (m/s) | 339 | 339 | 339 | 339 | |
| Free Jet | Exit Centerline Velocity (m/s) | 273.4 | 309.1 | 343.1 | 353.1 |
| Reynolds number | 458,037.3 | 574,651.6 | 720,724.8 | 824,301.7 | |
| Impinging Jet | Exit Centerline Velocity (m/s) | 291.9 | 326.6 | 351.1 | 354.7 |
| Reynolds number | 489,031.1 | 607,186.1 | 737,529.8 | 828,036.9 | |
| Impinging Jet | Exit Centerline Velocity (m/s) | 285.4 | 306.8 | 335.5 | 336.3 |
| Reynolds number | 478,141.4 | 570,375.7 | 700,558.8 | 785,082.6 | |
| Impinging Jet | Exit Centerline Velocity (m/s) | 273.1 | 308.5 | 334.7 | 348.1 |
| Reynolds number | 457,534.7 | 573,536.2 | 703,079.6 | 812,629.4 |
| Free Jets | Impinging Jet ( mm) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| NPRs | (%) | (%) | (%) | (%) | NPRs | (%) | (%) | (%) | (%) |
| 2 | 85.65 | 1.5 | 0.85 | 0.65 | 2 | 84.48 | 1.39 | 0.66 | 0.45 |
| 2.2 | 88.8 | 1.12 | 0.59 | 0.44 | 2.2 | 86.03 | 1.18 | 0.60 | 0.44 |
| 2.5 | 91.8 | 0.80 | 0.42 | 0.33 | 2.5 | 88.43 | 1.13 | 0.42 | 0.34 |
| 2.77 | 94.37 | 0.58 | 0.26 | 0.25 | 2.77 | 90.44 | 0.78 | 0.30 | 0.24 |
| Impinging Jet (mm) | Impinging Jet (mm) | ||||||||
| NPRs | (%) | (%) | (%) | (%) | NPRs | (%) | (%) | (%) | (%) |
| 2 | 84.07 | 1.81 | 0.72 | 0.48 | 2 | 81.72 | 2.37 | 0.85 | 0.59 |
| 2.2 | 86.21 | 1.29 | 0.62 | 0.46 | 2.2 | 85.67 | 1.84 | 0.73 | 0.44 |
| 2.5 | 90.28 | 0.8 | 0.42 | 0.29 | 2.5 | 88.10 | 1.21 | 0.70 | 0.46 |
| 2.77 | 90.51 | 0.68 | 0.43 | 0.27 | 2.77 | 87.07 | 1.78 | 0.71 | 0.47 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nguyen, D.T.; Maher, B.; Hassan, Y. Effects of Nozzle Pressure Ratio and Nozzle-to-Plate Distance to Flowfield Characteristics of an Under-Expanded Jet Impinging on a Flat Surface. Aerospace 2019, 6, 4. https://doi.org/10.3390/aerospace6010004
Nguyen DT, Maher B, Hassan Y. Effects of Nozzle Pressure Ratio and Nozzle-to-Plate Distance to Flowfield Characteristics of an Under-Expanded Jet Impinging on a Flat Surface. Aerospace. 2019; 6(1):4. https://doi.org/10.3390/aerospace6010004
Chicago/Turabian StyleNguyen, Duy Thien, Blake Maher, and Yassin Hassan. 2019. "Effects of Nozzle Pressure Ratio and Nozzle-to-Plate Distance to Flowfield Characteristics of an Under-Expanded Jet Impinging on a Flat Surface" Aerospace 6, no. 1: 4. https://doi.org/10.3390/aerospace6010004
APA StyleNguyen, D. T., Maher, B., & Hassan, Y. (2019). Effects of Nozzle Pressure Ratio and Nozzle-to-Plate Distance to Flowfield Characteristics of an Under-Expanded Jet Impinging on a Flat Surface. Aerospace, 6(1), 4. https://doi.org/10.3390/aerospace6010004