Transducer Placement Option of Lamb Wave SHM System for Hotspot Damage Monitoring
Abstract
1. Introduction
2. Lamb Wave Propagation
3. Sensor Positioning Approach for Hotspot SHM
3.1. Crack Growth in Damage Tolerance Structure
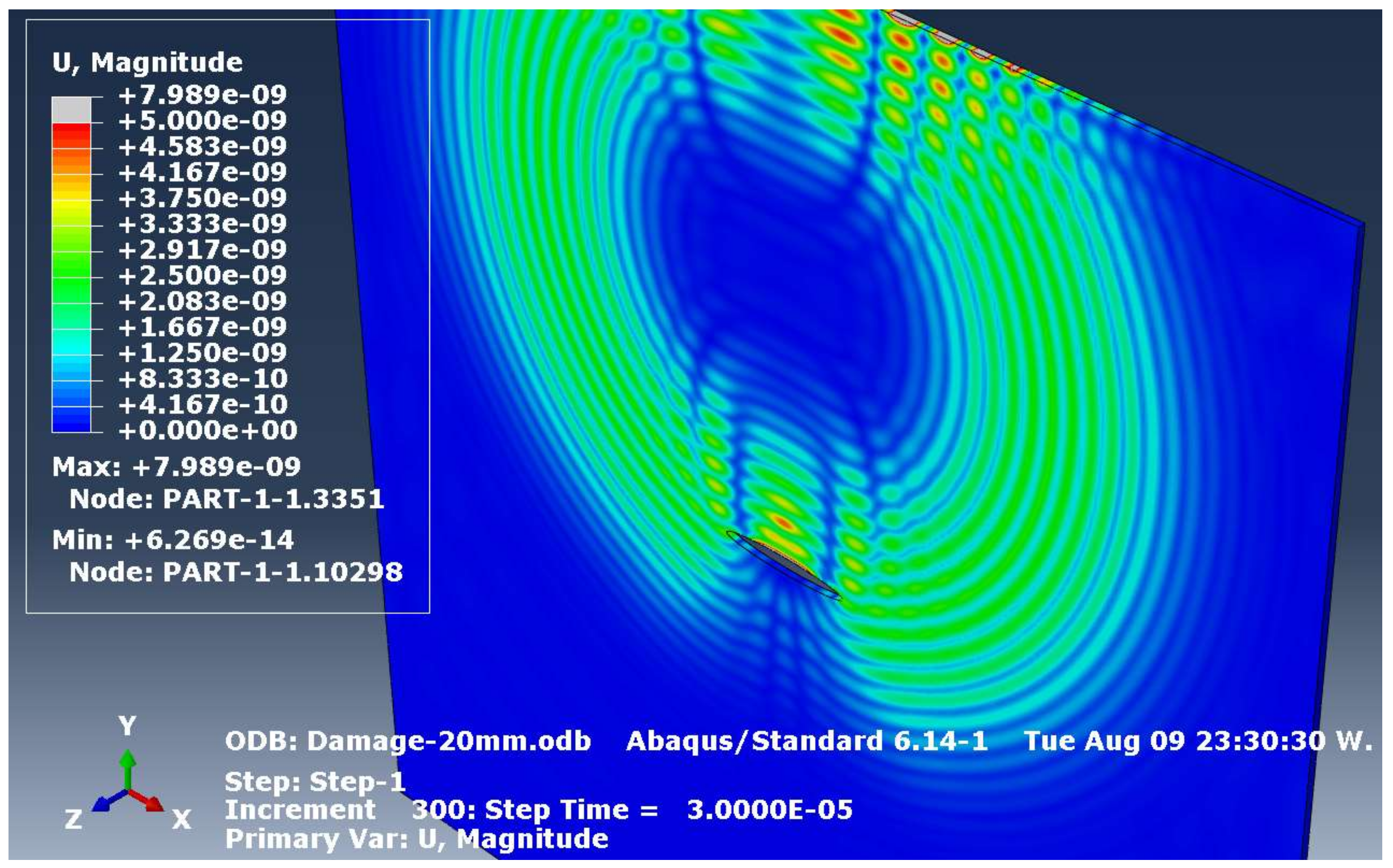
3.2. Simulation of Lamb Wave Propagation
3.3. Additive Color Model
4. Results and Discussion
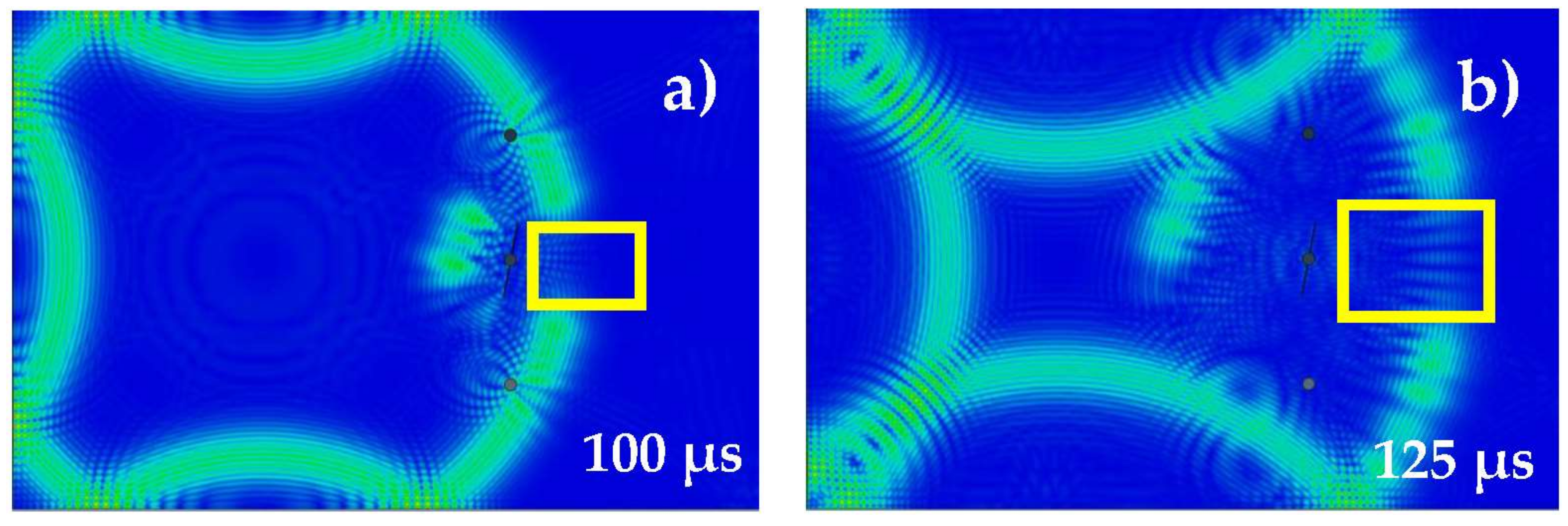
4.1. Simulation
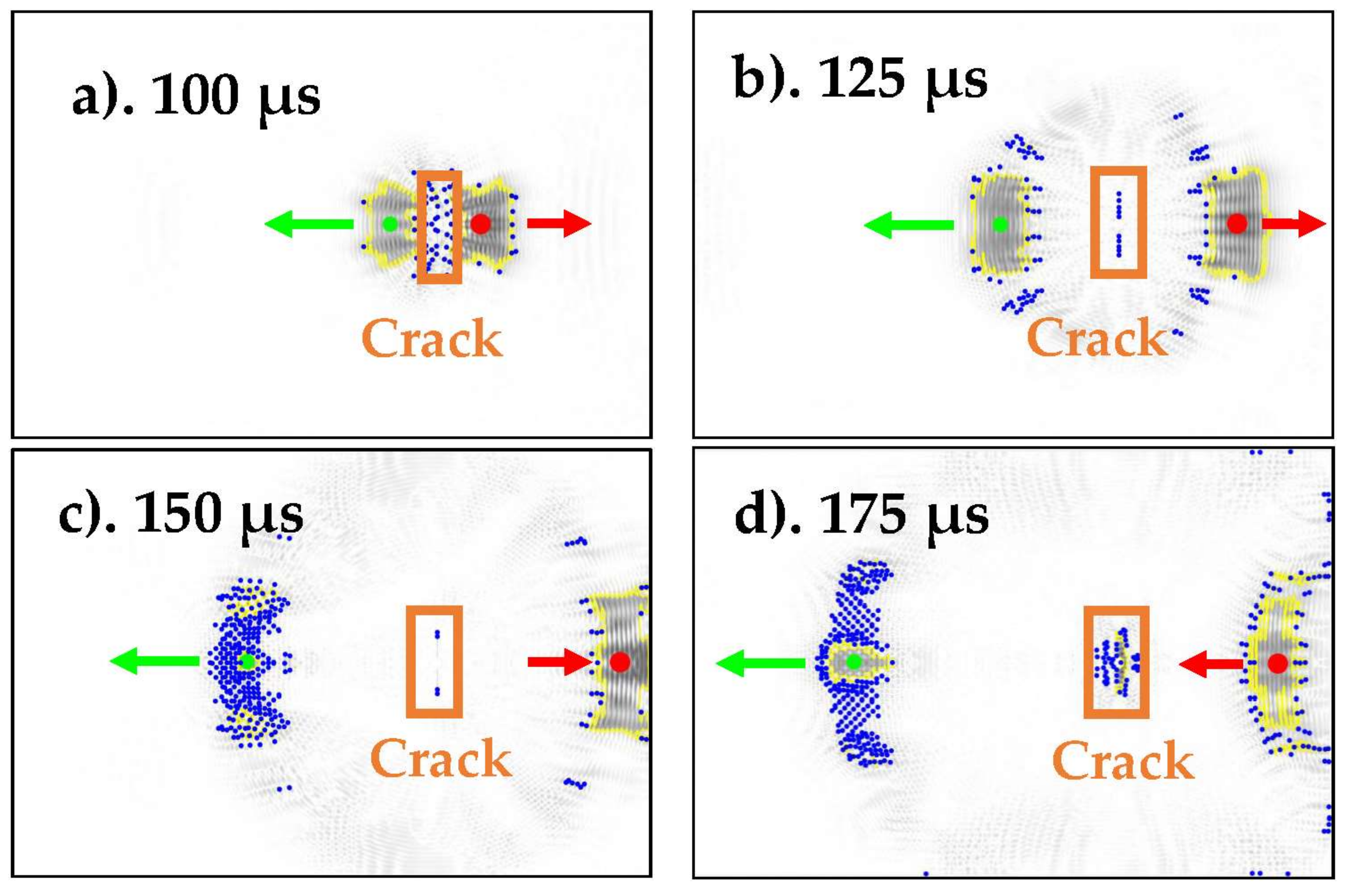
4.2. Data Extraction
4.3. Differential Images
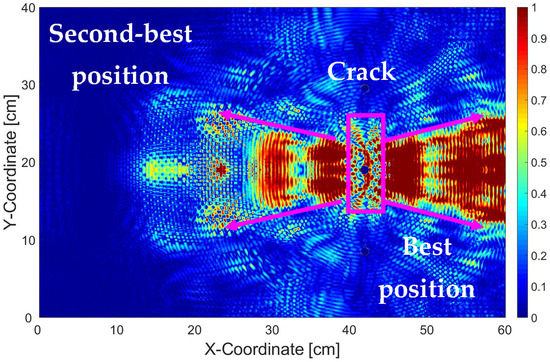
4.4. Sensor Placement
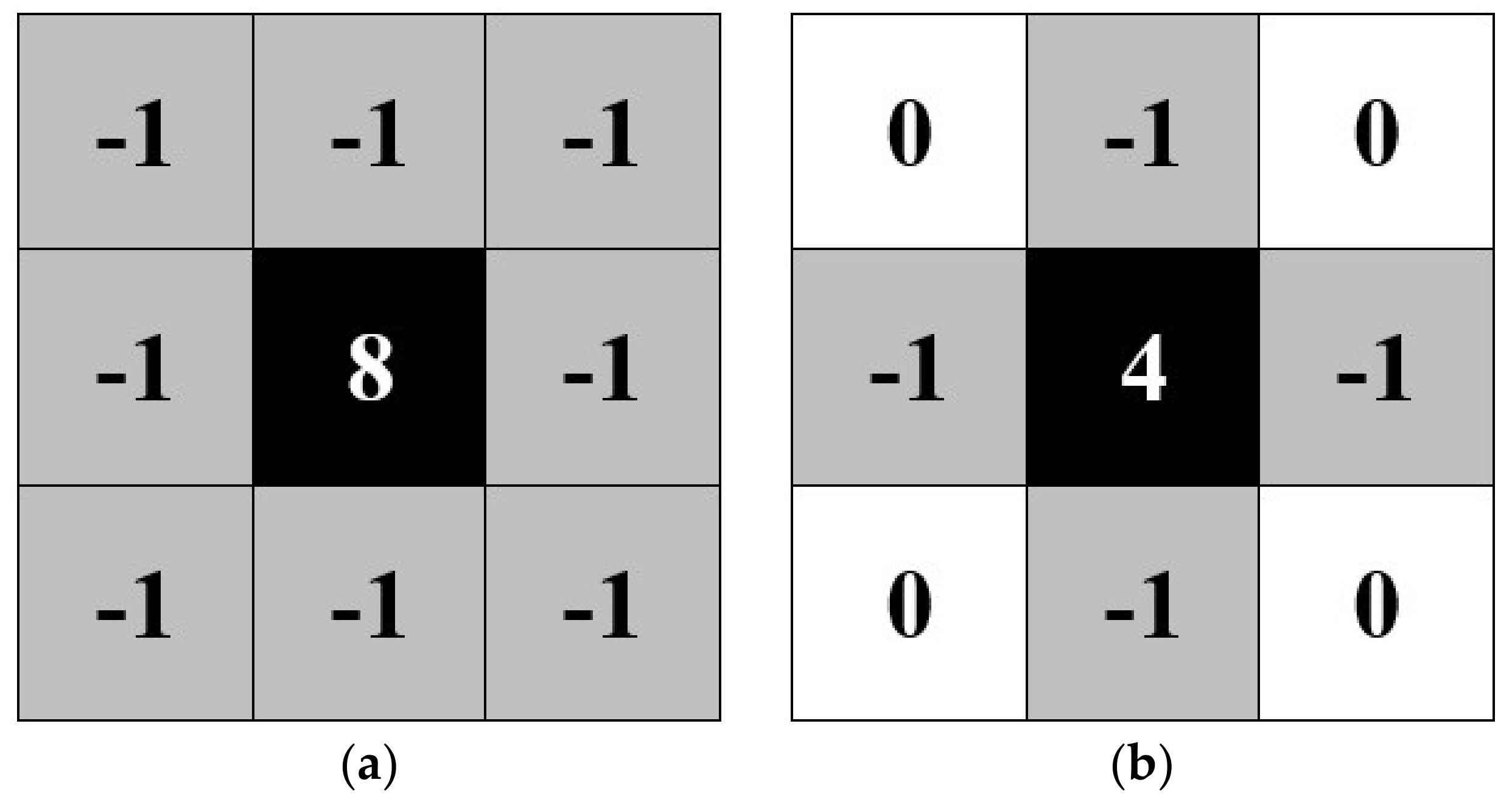
| Algorithm 1: Algorithm for blob detection and centroids calculation | Meaning: | |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | j ← number of available image files for i ← 1:j img[i] ← imread(image[i]) I[i] ← mat2gray(rgb2gray(img[])) BW[i] ← I[i] < threshold B{i} ← boundaries(BW,8) s(i) ← regionprops(BW end n ← number of detected blobs for m ← 1:n S[m] ← s[m].Area [val ind] ← sort(S,‘descend’) boundary{m} ← B{ind(m)} centroids[m] ← mean(boundary{m}) X ← [X centroids(2)] Y ← [Y centroids(1)] end | Assign j as the number of available images Loop over images from 1 to j: Store the image in matrix ‘img’ Convert the RGB array into greyscale Set the pixel intensity threshold Trace region with 8-pixel connectivity Open the region properties End the loop Assign n as the number of detected blobs Loop over all traced region from 1 to n: Store the area information in matrix ‘S’ Sort from the largest to smallest blob Store the blob boundaries Calculate blob centroids Assign X-coordinate from the centroid Assign Y-coordinate from the centroid End the loop |
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hellier, C. Handbook of Nondestructive Evaluation, 2nd ed.; McGraw Hill Professional: New York, NY, USA; Chicago, IL, USA; London, UK; Madrid, Spain, 2003. [Google Scholar]
- Gopalakrishnan, S.; Ruzzene, M.; Hanagud, S. Computational Techniques for Structural Health Monitoring; Springer: London, UK; Dordrecht, The Netherlands; Heidelberg, Germany; New York, NY, USA, 2011. [Google Scholar]
- Haldar, A. Health Assessment of Engineered Structures—Bridges, Buildings and Other Infrastructures; World Scientific Publishing Co. Pte. Ltd.: Singapore, Singapore, 2013. [Google Scholar]
- Rajabzadeh, A.; Hendriks, R.C.; Heusdens, R.; Groves, R.M. Classification of Composite Damage from FBG Load Monitoring Signals. In Proceedings of the SPIE Conference Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Denver, CO, USA, 25–29 March 2017. [Google Scholar]
- Kahandawa, G.C.; Epaarachchi, J.; Wang, H.; Lau, K.T. Use of FBG Sensors for SHM in Aerospace Structures. J. Photonic Sens. 2012, 2, 203–214. [Google Scholar] [CrossRef]
- Wilcox, P.D.; Lowe, M.; Cawley, P. Long Range Lamb Wave Inspection: The Effect of Dispersion and Modal Selectivity. Rev. Prog. Quant. Nondestruct. Eval. 1999, 18, 151–158. [Google Scholar]
- Edalati, K.; Kermani, A.; Naderi, B.; Panahi, B. Defects Evaluation in Lamb Wave Testing of Thin Plates. In Proceedings of the 3rd Middle East Non-Destructive Testing Conference & Exhibition (MENDT), Manama, Bahrain, 27–30 November 2005. [Google Scholar]
- Kuznetsov, S.; Ozolinsh, E.; Ozolinsh, I.; Pavelko, I.; Pavelko, V.; Wevers, M.; Pfeiffer, H. Lamb Wave Interaction with a Fatigue Crack in a Thin Sheet of Al2024-T3. In Proceedings of the EU Project Meeting on AISHA, Leuven, Belgium, June 2007. [Google Scholar]
- Wilcox, P.D.; Lowe, M.; Cawley, P. Mode and Transducer Selection for Long Range Lamb Wave Inspection. J. Intell. Mater. Syst. Struct. 2001, 12, 553–565. [Google Scholar] [CrossRef]
- Cobb, R.G.; Liebst, B.S. Sensor Placement and Structural Damage Identification from Minimal Sensor Information. AIAA J. 1997, 35, 369–374. [Google Scholar] [CrossRef]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Optimum Sensor Placement for Structural Damage Detection. J. Eng. Mech. 2000, 126, 1173–1179. [Google Scholar] [CrossRef]
- Kripakaran, P.; Saitta, S.; Ravibndran, S.; Smith, I.F.C. Optimal Sensor Placement for Damage Detection. In Proceedings of the 18th International Workshop on Database and Expert System Applications, Regensburg, Germany, 3–7 September 2007. [Google Scholar]
- Li, B.; Wang, D.; Wang, F.; Ni, Y.Q. High Quality Sensor Placement for SHM Systems: Refocusing on Application Demands. In Proceedings of the INFOCOM IEEE Conference on Computer Communications, San Diego, CA, USA, 14–19 March 2010. [Google Scholar]
- Fendzi, C.; Morel, J.; Rébillat, M.; Guskov, M.; Mechbal, N.; Coffignal, G. Optimal Sensor Placement to Enhance Damage Detection in Composite Plates. In Proceedings of the 7th European Workshop on Structural Health Monitoring (EWSHM), Nantes, France, 8–11 July 2014. [Google Scholar]
- Haynes, C. Effective Health Monitoring Strategies for Complex Structures. Ph.D. Thesis, University of California San Diego (UCSD), San Diego, CA, USA, 2014. [Google Scholar]
- Flynn, E.B.; Todd, M. A Bayesian Approach to Optimal Sensor Placement for Structural Health Monitoring with Application to Active Sensing. Mech. Syst. Signal Process. 2010, 24, 891–903. [Google Scholar] [CrossRef]
- Sun, H.; Büyüköztürk, O. Optimal Sensor Placement in Structural Health Monitoring Using Discrete Optimization. Smart Mater. Struct. 2015, 25, 125034. [Google Scholar] [CrossRef]
- Yi, T.H.; Li, H.N.; Gu, M. Optimal Sensor Placement for Structural Health Monitoring Based on Multiple Optimization Strategies. J. Struct. Des. Tall Spec. Build. 2011, 20, 881–900. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, X.; Sun, Q.; Zhang, L. Optimal Sensor Placement for a Truss Structure Using Particle Swarm Optimisation Algorithm. Int. J. Acoust. Vib. 2017, 22, 439–447. [Google Scholar] [CrossRef]
- Shan, D.; Wan, Z.; Qiao, L. Optimal Sensor Placement for Long-span Railway Steel Truss Cable-stayed Bridge. In Proceedings of the 3rd International Conference on Measuring Technology and Mechatronics Automation (ICMTMA), Shanghai, China, 6–7 January 2011. [Google Scholar]
- Capellari, G.; Chatzi, E.; Mariani, S. Optimal Sensor Placement through Bayesian Experimental Design: Effect of Measurement Noise and Number of Sensors. In Proceedings of the 3rd International Electronic Conference on Sensors and Applications, 15–30 November 2016. [Google Scholar]
- Thiene, M.; Sharif Khodaei, Z.; Aliabadi, M.H. Optimal Sensor Placement for Maximum Area Coverage for Damage Localization in Composite Structures. Smart Mater. Struct. 2016, 25, 095037. [Google Scholar] [CrossRef]
- Venkat, R.S.; Boller, C.; Qiu, L.; Ravi, N.B.; Mahapatra, D.R.; Chakraborty, N. Integrated Approach to Demonstrate Optimum Sensor Positions in a Guided Wave Based SHM System Using Numerical Simulation. In Proceedings of the 8th International Symposium on NDT in Aerospace, Bangalore, India, 3–5 November 2016. [Google Scholar]
- Lamb, H. On Waves in an Elastic Plate. R. Soc. Lond. Ser. A 1917, 93, 114–128. [Google Scholar] [CrossRef]
- Döring, D. Luftgekoppelter Ultraschall und Geführte Wellen für die Anwendung in der Zerstörungsfreien Werkstoffprüfung. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 2011. [Google Scholar]
- Pant, S. Lamb Wave Propagation and Material Characterization of Metallic and Composite Aerospace Structures for Improved Structural Health Monitoring (SHM). Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2014. [Google Scholar]
- Hosseini, S.M.H.; Gabbert, U. Analysis of Guided Lamb Wave Propagation (GW) in Honeycomb Sandwich Panels. Proc. Appl. Math. Mech. 2010, 10, 11–14. [Google Scholar] [CrossRef]
- Gomez, P.; Fernández, J.P.; Garcia, P.D. Lamb Waves and Dispersion Curves in Plates and its Applications in NDE Experiences Using COMSOL Multiphysics Pablo Gómez. In Proceedings of the COMSOL Conference, Stuttgart, Germany, 26–28 October 2011. [Google Scholar]
- Harris, C.E.; Starnes, J.H., Jr.; Shuart, M.J. Advanced Durability and Damage Tolerance Design and Analysis Methods for Composite Structures—Lesson Learned from NASA Technology Development Programs; NASA Langley Research Center: Hampton, VA, USA, 2003. [Google Scholar]
- Pugno, N.; Ciavarella, M.; Cornetti, P.; Carpinteri, A. A Generalized Paris’ Law for Fatigue Crack Growth. J. Mech. Phys. Solids 2006, 54, 1333–1349. [Google Scholar] [CrossRef]
- Schors, J.; Harbich, K.W.; Hentschel, M.P.; Lange, A. Non-Destructive Micro Crack Detection in Modern Materials. In Proceedings of the 9th European Conference of Non-Destructive Testing (ECNDT), Berlin, Germany, 25–29 September 2006. [Google Scholar]
- Wang, X.S.; Wua, B.S.; Wang, Q.Y. Online SEM Investigation of Microcrack Characteristics of Concretes at Various Temperatures. Cem. Concr. Res. 2005, 35, 1385–1390. [Google Scholar] [CrossRef]
- Milella, PP. Fatigue and Corrosion in Metals; Springer: Milan, Italy; Heidelberg, Germany; New York, NY, USA; Dordrecht, The Netherlands; London, UK, 2013. [Google Scholar]
- McMaster, R.C. Nondestructive Testing Handbook, 3rd ed.; Visual Testing (VT); American Society for Nondestructive Testing: Columbus, OH, USA, 2010; Volume 9. [Google Scholar]
- Gilchrist, M.D. Attenuation of Ultrasonic Rayleigh-Lamb Waves by a Symmetrical Embedded Crack in an Elastic Plate. J. Appl. Math. Mech. 1999, 79, 497–498. [Google Scholar]
- Wang, Q.; Su, Z. Crack Diagnosis and Monitoring Method Using Linear-Phased PZT Sensor Array. In Proceedings of the 2nd International Conference of Structural Health Monitoring and Integrity Management (ICSHMIM), Nanjing, China, 24–26 September 2014. [Google Scholar]
- Iesulauro, E.; Ingraffea, A.R.; Arwade, S.; Wawrzynek, P.A. Simulation of Grain Boundary Decohesion and Crack Initiation in Aluminum Microstructure Models. ASTM J. Fatigue Fract. Mech. 2003, 33, 715–728. [Google Scholar]
- Richard, H.A.; Sander, M. Technische Mechanik: Festigkeitslehre (2. Auflage); Vieweg+Teubner: Wiesbaden, Germany, 2008. [Google Scholar]
- Taltavull, A.; Qiu, L.; Venkat, R.S.; Dürager, C.; Boller, C.; Ren, Y.Q.; Yuan, S. Simulation, Realization and Validation of Guided Wave SHM System Solutions for Aircraft Metallic Structural Repairs. In Proceedings of the 11th International Workshop on Structural Health Monitoring (IWSHM), Stanford, CA, USA, 12–14 September 2017. [Google Scholar]
- Duczek, S.; Joulaian, M.; Düster, A.; Gabbert, U. Numerical Analysis of Lamb Waves Using the Finite and Spectral Cell Methods. Int. J. Numer. Methods Eng. 2014, 99, 26–53. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. Finite Element Method—Its Basis and Fundamentals, 6th ed.; Elsevier Butterworth-Heinemann: Oxford, UK; Burlington, NJ, USA, 2005. [Google Scholar]
- Wriggers, P. Nonlinear Finite Element Methods; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Ewald, V. Post-Design Damage Tolerance Enhancement of Primary Aircraft Structures by Ultrasonic Lamb Wave Based Structural Health Monitoring (SHM) System. Master’s Thesis, Universität des Saarlandes, Saarbrücken, Germany, 2015. [Google Scholar]
- Cerniglia, D.; Pantano, A.; Montinaro, N. 3D Simulations and Experiments of Guided Wave Propagation in Adhesively Bonded Multi-Layered Structures. J. NDT E Int. 2010, 43, 527–535. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; Chakraborty, A.; Mahapatra, D.R. Spectral Finite Element Method—Wave Propagation, Diagnostics and Control in Anisotropic and Inhomogeneous Structures; Springer: London, UK, 2008. [Google Scholar]
- Elert, G. Color; The Physics Hypertextbook. Available online: https://physics.info/color/ (accessed on 3 February 2018).
- Lightshot Program. Available online: https://app.prntscr.com/en/index.html (accessed on 3 February 2018).
- MATLAB IPT Documentation. Available online: https://de.mathworks.com/help/images/ (accessed on 3 February 2018).
- Kong, H.; Akakin, H.C.; Sarma, S.E. A Generalized Laplacian of Gaussian Filter for Blob Detection and Its Applications. IEEE Trans. Cybern. 2013, 43, 1719–1733. [Google Scholar] [CrossRef] [PubMed]
- Lindeberg, T. Feature Detection with Automatic Scale Selection; Technical Report ISRN KTH/NA/P–96/18–SE; Kungliga Tekniska Högskolan (KTH): Stockholm, Sweden, 1998. [Google Scholar]
- Heinze, C.; Sinapius, M.; Wierach, P. Lamb Wave Propagation in Complex Geometries—Model Reduction with Approximated Stiffeners. In Proceedings of the 7th European Workshop on Structural Health Monitoring (EWSHM), Nantes, France, 8–11 July 2014. [Google Scholar]
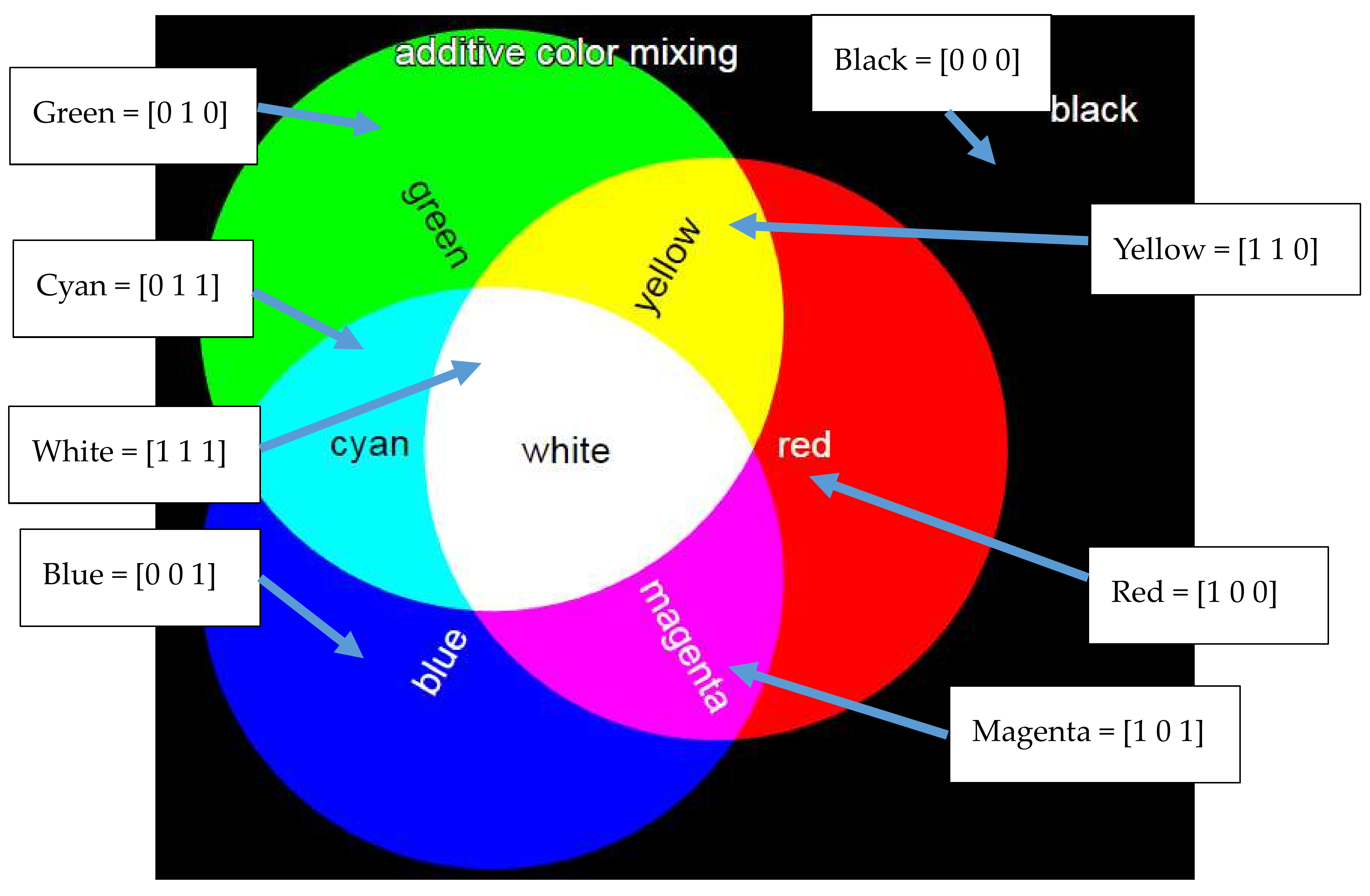
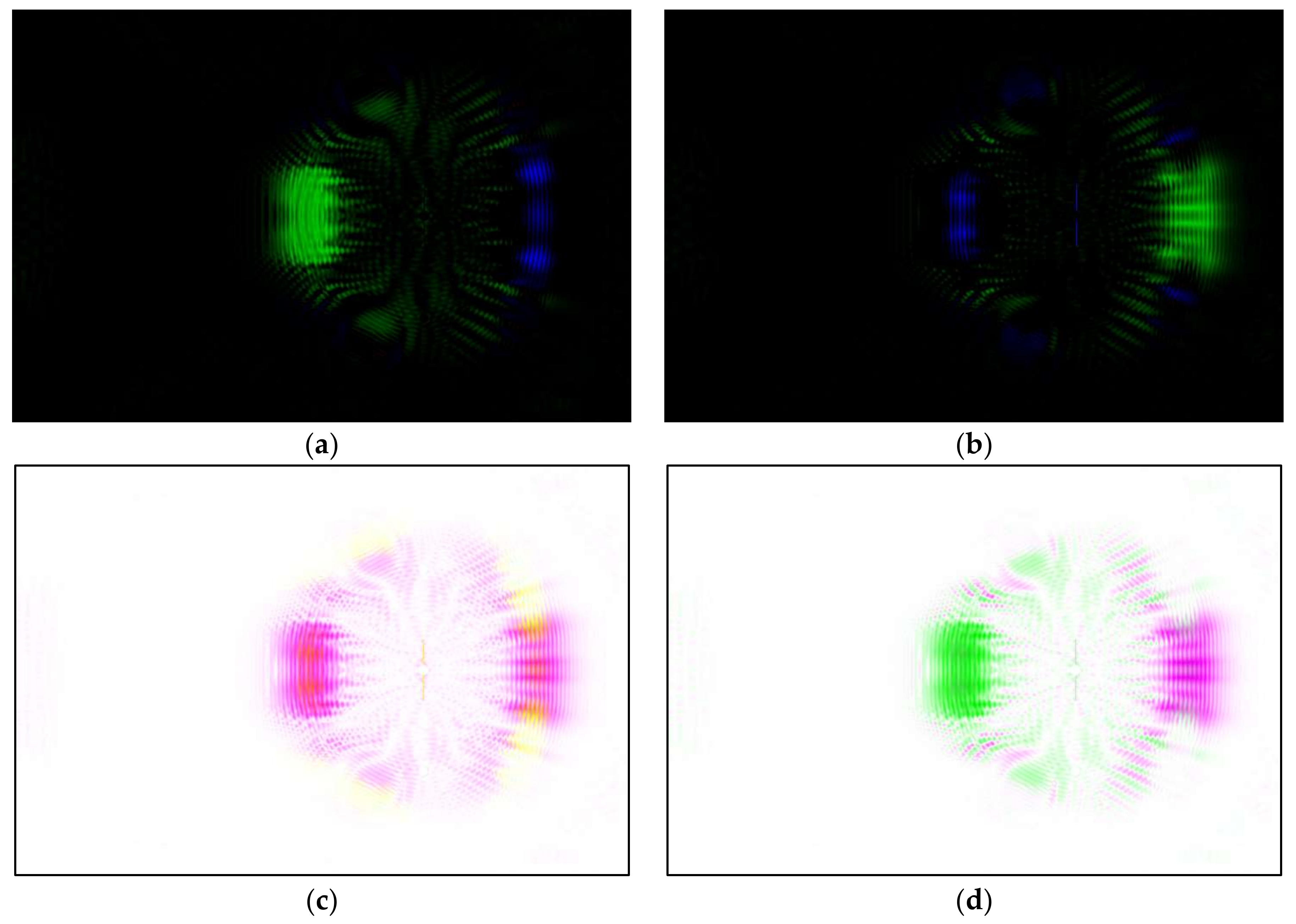
| y–x | R | G | B | C | M | Y | K |
| R | K | R | R | R | K | K | R |
| G | G | K | G | K | G | K | G |
| B | B | B | K | K | K | B | B |
| C | C | B | G | K | G | B | C |
| M | B | M | R | R | K | B | M |
| Y | G | R | Y | R | G | K | Y |
| K | K | K | K | K | K | K | K |
| Time Frame | Largest Centroid | Second-Largest Centroid | ||||
|---|---|---|---|---|---|---|
| (pixel) | (mm) | Area (pixel) | (pixel) | (mm) | Area (pixel) | |
| 100 μs | 888,403 | 440,200 | 15,910 | 716,403 | 355,200 | 12,917 |
| 125 μs | 1,031,402 | 511,199 | 29,535 | 582,404 | 289,200 | 18,794 |
| 150 μs | 1,154,402 | 572,199 | 27,067 | 445,401 | 221,200 | 8808 |
| 175 μs | 1,111,405 | 551,201 | 24,214 | 304,402 | 151,199 | 7949 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ewald, V.; Groves, R.M.; Benedictus, R. Transducer Placement Option of Lamb Wave SHM System for Hotspot Damage Monitoring. Aerospace 2018, 5, 39. https://doi.org/10.3390/aerospace5020039
Ewald V, Groves RM, Benedictus R. Transducer Placement Option of Lamb Wave SHM System for Hotspot Damage Monitoring. Aerospace. 2018; 5(2):39. https://doi.org/10.3390/aerospace5020039
Chicago/Turabian StyleEwald, Vincentius, Roger M. Groves, and Rinze Benedictus. 2018. "Transducer Placement Option of Lamb Wave SHM System for Hotspot Damage Monitoring" Aerospace 5, no. 2: 39. https://doi.org/10.3390/aerospace5020039
APA StyleEwald, V., Groves, R. M., & Benedictus, R. (2018). Transducer Placement Option of Lamb Wave SHM System for Hotspot Damage Monitoring. Aerospace, 5(2), 39. https://doi.org/10.3390/aerospace5020039