Experimental and Numerical Investigation of the Outer Ring Cooling Concept in a Hybrid and in an All-Steel Ball Bearing Used in Aero-Engines by the Introduction of a Helical Duct

Abstract

Rolling element bearings for aero engine applications have to withstand very challenging operating conditions because of the high thermal impact due to elevated rotational speeds and loads. The high rate of heat generation in the bearing has to be sustained by the materials, and in the absence of lubrication these will fail within seconds. For this reason, aero engine bearings have to be lubricated and cooled by a continuous oil stream. When the oil has reached the outer ring it has already been heated up, thus its capability to remove extra heat from the outer ring is considerably reduced. Increasing the mass flow of oil to the bearing is not a solution since excess oil quantity would cause high parasitic losses (churning) in the bearing chamber and also increase the demands in the oil system for oil storage, scavenging, cooling, hardware weight, etc. A method has been developed for actively cooling the outer ring of the bearing. The idea behind the outer ring cooling concept was adopted from fins that are used for cooling electronic devices. A spiral groove engraved in the outer ring material of the bearing would function as a fin body with oil instead of air as the cooling medium. The method was first evaluated in an all steel ball bearing and the results were a 50% reduction in the lubricating oil flow with an additional reduction in heat generation by more than 25%. It was then applied on a Hybrid ball bearing of the same size and the former results were reconfirmed. Hybrid bearings are a combination of steel made parts, like the outer ring, the inner ring, and the cage and of ceramic rolling elements. This paper describes the work done to-date as a follow up of the work described in, and demonstrates the potential of the outer ring cooling for a bearing. Friction loss coefficient, Nusselt number, and efficiency correlations have been developed on the basis of the test results and have been compared to correlations from other authors. Computational Fluid Dynamics (CFD) analysis with ANSYS CFX has been used to verify test results and also for parametric studies.

1. Introduction

Ceramics are widely used in the aviation industry not only because they are lighter, but also because they can withstand much higher loads at a much higher endurance when compared to steel [1]. Particularly in the case of bearings, the benefit of ceramics is also in the reduction of the friction losses between the mating parts.

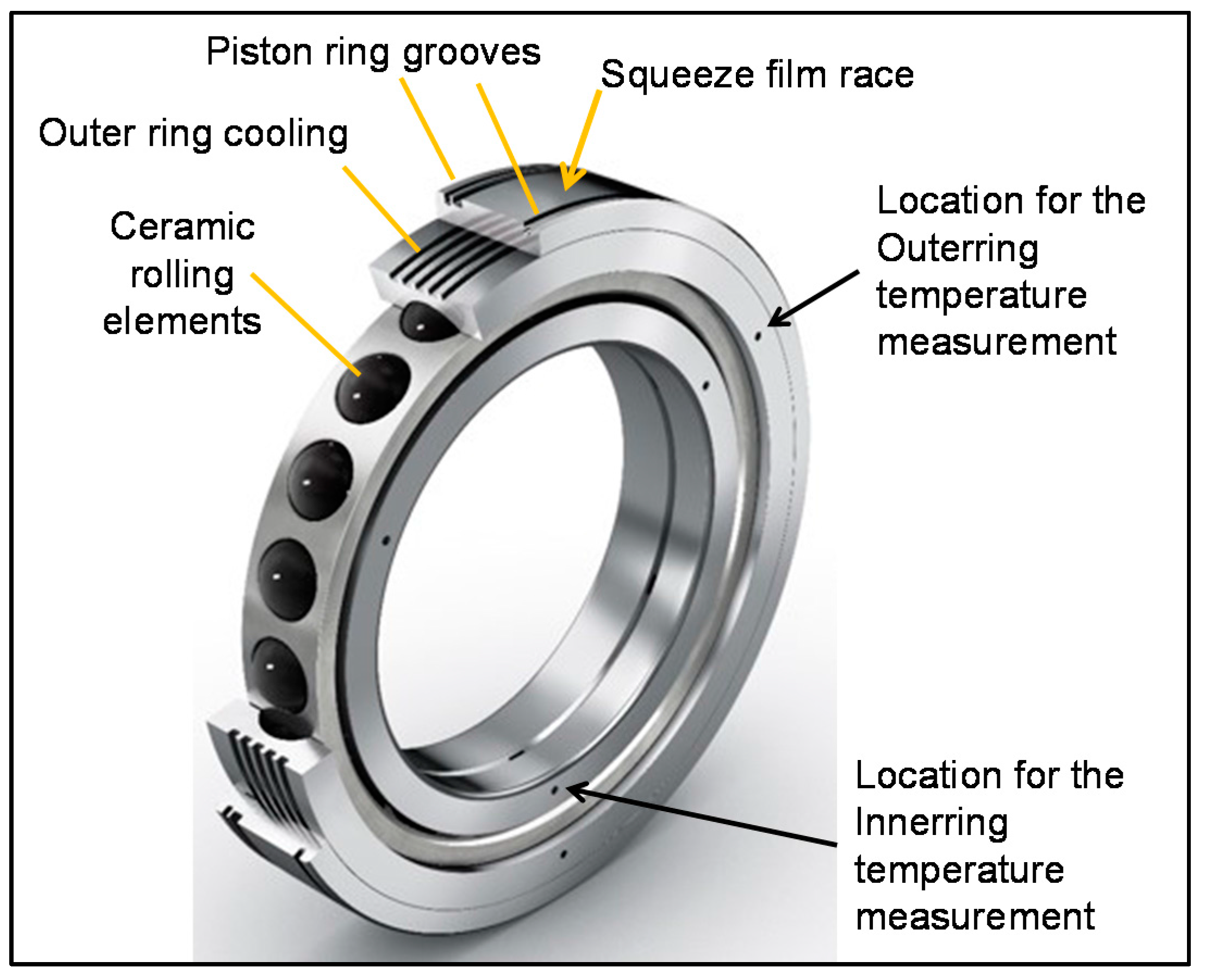
When compared to the all-steel version, the hybrid bearing was equipped with a squeeze film damper in order to damp vibrations [1]. Additionally, the bearing races were duplex hardened since higher stresses are induced by the ceramic rolling elements [1]. The combination of the four technologies (outer ring cooling, ceramics, duplex hardening, and squeeze film damper) in one product has led to a significant achievement, which was reported in the international press. For the first time an engine bearing had broken the 4 million speed parameter barrier [2]. Detailed mechanical aspects of the hybrid bearing were presented in [1].

In order to lubricate and remove the heat that is generated in the bearings through friction, oil brands, especially certified for aviation are used. Nevertheless, oil itself has not unlimited capabilities and can only remove heat as long as its temperature does not reach critical limits. When critical limits are reached or even exceeded, the oil will suffer chemical decomposition (coking) with severe deterioration of its properties. This would subsequently cause damage to the bearing components. In order to extend the bearing’s life, an operating temperature of not more than 150 °C is the design intend. Above this temperature a penalty in the bearing’s life can be expected. Oil is normally transferred into the bearings through holes in the inner ring using the centrifugal forces due to the rotation. In its way through the bearing, the oil continuously removes heat from the inner ring, the rolling elements, and the bearing cage until it reaches the outer ring.

Figure 1 shows on the left hand side the schematic of the bearing with the outer ring cooling duct and on the right hand side the cooling duct with the inflow, the outflow, and also the flow direction [1,3,4]. The lubrication oil is transferred centrifugally into the bearing through the slots in the inner ring. In its way through the bearing the lubrication oil continuously removes heat from the inner ring, the rolling elements and the bearing cage until it reaches the outer ring. Since the oil has not unlimited capability to remove heat, therefore heat removal from the outer ring is limited. This has problem has initiated the idea of the active outer ring cooling.

During the first research campaign (2007–2010) an all steel bearing was successfully tested [3,4]. Due to the very good results further investigations between 2012 and 2015, this time on a hybrid bearing followed.

Figure 2 shows the all steel bearing on the left hand side and the hybrid bearing on the right hand side. The hybrid bearing version is equipped with a squeeze film damper, as this is shown in Figure 3. This enabled damping of possible vibrations during testing. Geometrical and material details of the two bearing configurations are displayed in

Table 1. Design details of the bearings.

Geometry/Materials	All-Steel Bearing	Hybrid Bearing Including SQF
Outer ring material	M50NiL (AMS6278)	M50NiL, duplex-hardened
Ball material	M50 (AMS6491)	Si3N4
Inner ring material	M50 (AMS6491)	M50NiL, duplex-hardened
Cage material	SAE 4340 (AMS6414)	SAE 4340 (AMS6414)
Bearing ID/OD (mm)	133/202	133/219
Pitch diameter (mm)	167.5	167.5
Number of balls	20	20

.

2. Operating Fluids

The tests with the all steel bearing were carried out using the Aeroshell 500 oil [5], whereas the tests with the hybrid bearing were performed using the Mobil Jet II oil (Moncton, NB, Canada). Both brands are certified aviation oils of MIL-PRF-23699 standard and have a kinetic viscosity of 5cSt (5.0 × 10⁻⁶ m²/s) at 100 °C. They can be mixed at any portion for engine operation. Therefore, differences in their thermal behavior are disclosed. For detailed information on aviation turbine lubricants the authors recommend [5,6,7].

3. Test Facility

Testing of the bearings was performed at the facility located at FAG Aerospace in an extra modified rig. Figure 4 shows the cross sections of the rig [1,3,4]. The rig could perform up to 24,000 rpm and could enable axial loads up to 80 kN. The oil supply to the test bearing was individual for damping, lubrication, or outer ring cooling purposes. The outer ring temperature of the test bearing was recorded using static thermocouples, whereas telemetric temperature measurement was applied to the inner ring. The oil supply flow to the bearing for lubrication could be adjusted up to 12 L/min (720 L/h) and up to 10 L/min (600 L/h) for the outer ring cooling. Additionally, thermocouples were placed adjacent to the test bearing from both sides and were for measuring the oil exit temperatures from the bearing. Therefore, a very accurate calculation of the heat to oil could be performed. Scavenge oil flow measurements on both sides of the bearing have confirmed the pumping action of the bearing [4,8]. The accuracy of the pressure measurements was ±0.15%. For fluid and material temperatures, NiCrNi thermocouples at an accuracy of ±1.0 K were used.

4. Results

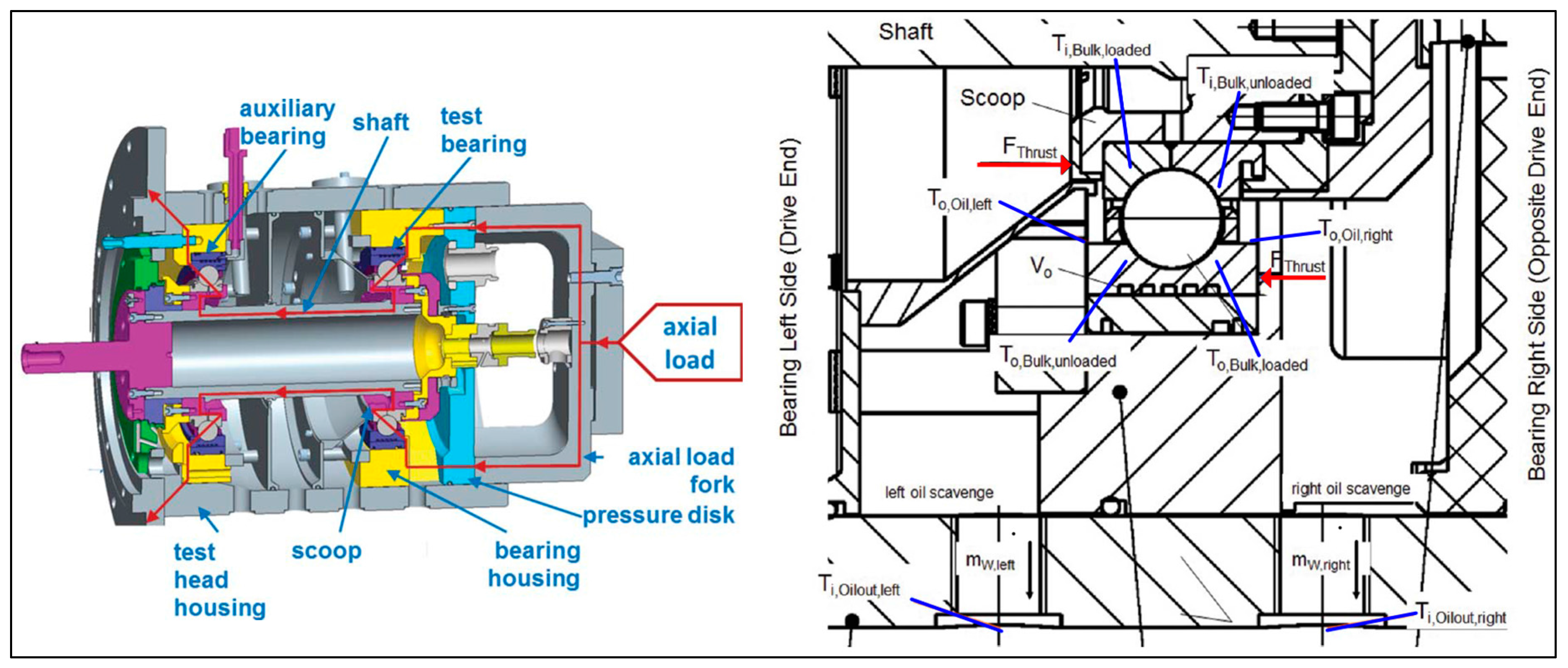
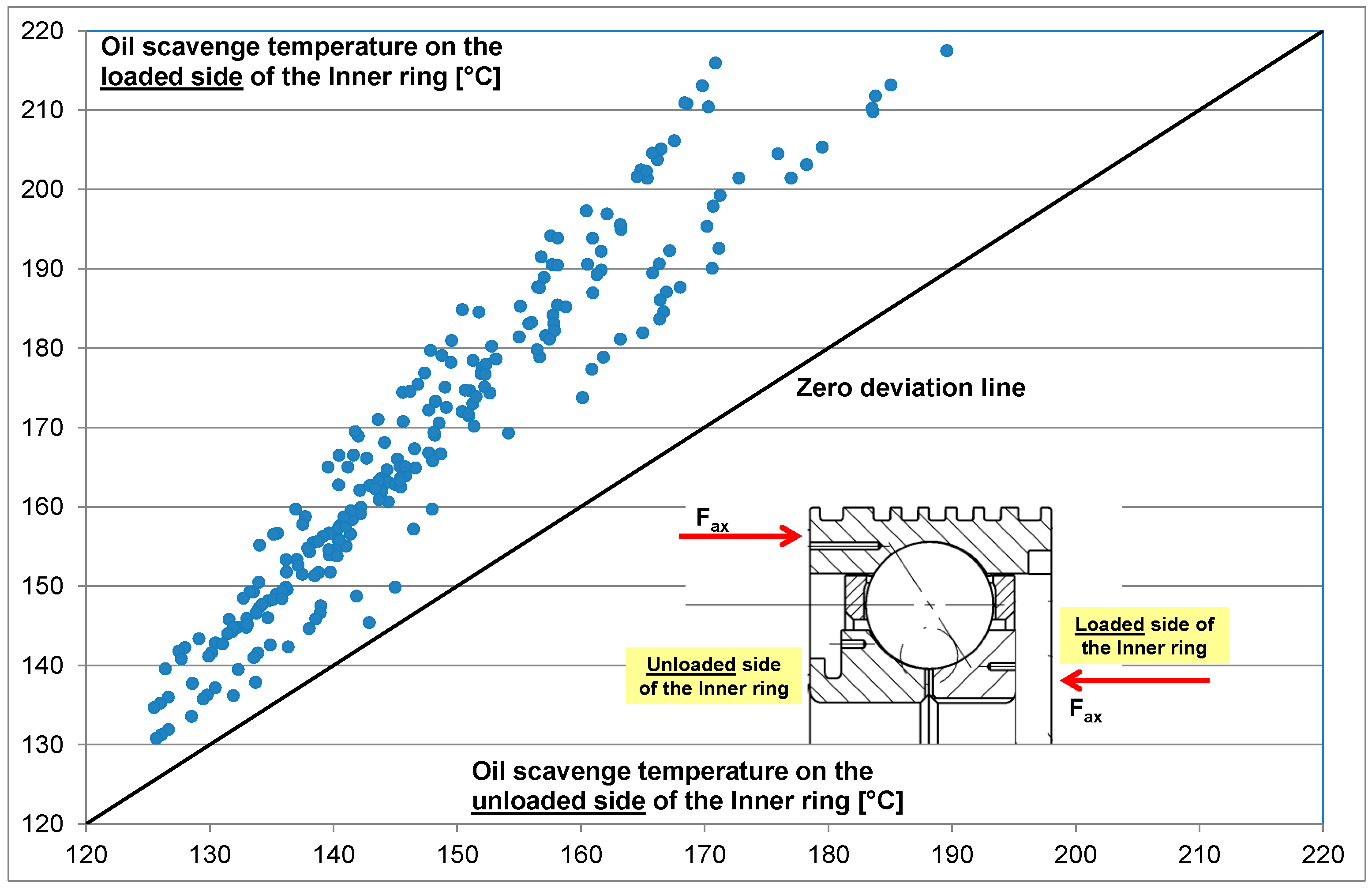
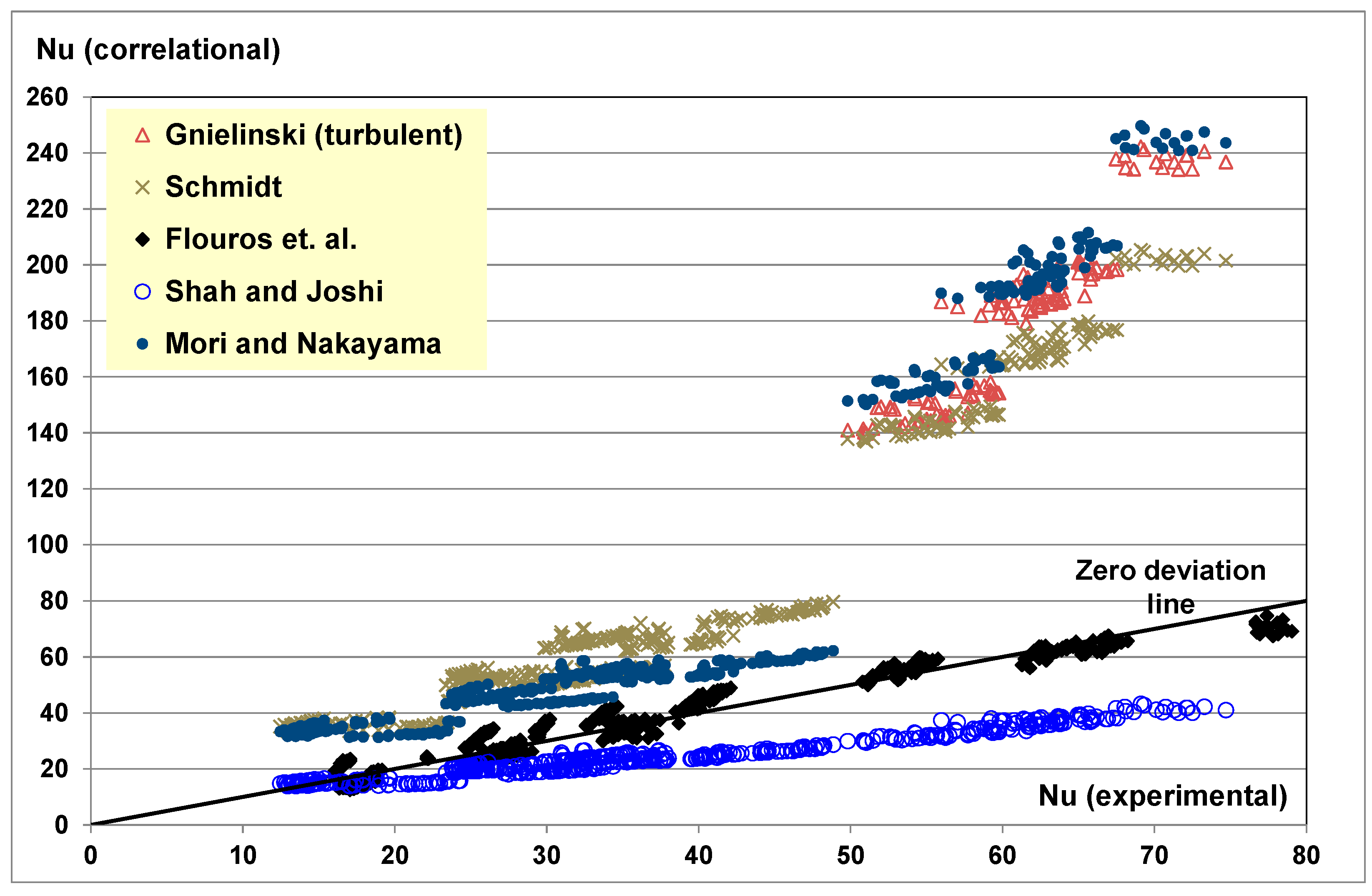
Oil scavenge temperature measurements on both sides of the test bearing are depicted in Figure 5. Their distance to the zero deviation line indicates that the values on both sides of the bearing are much different. This is a phenomenon that has been observed in ball bearings and has to do with the pumping action induced by the axial load [4,8].

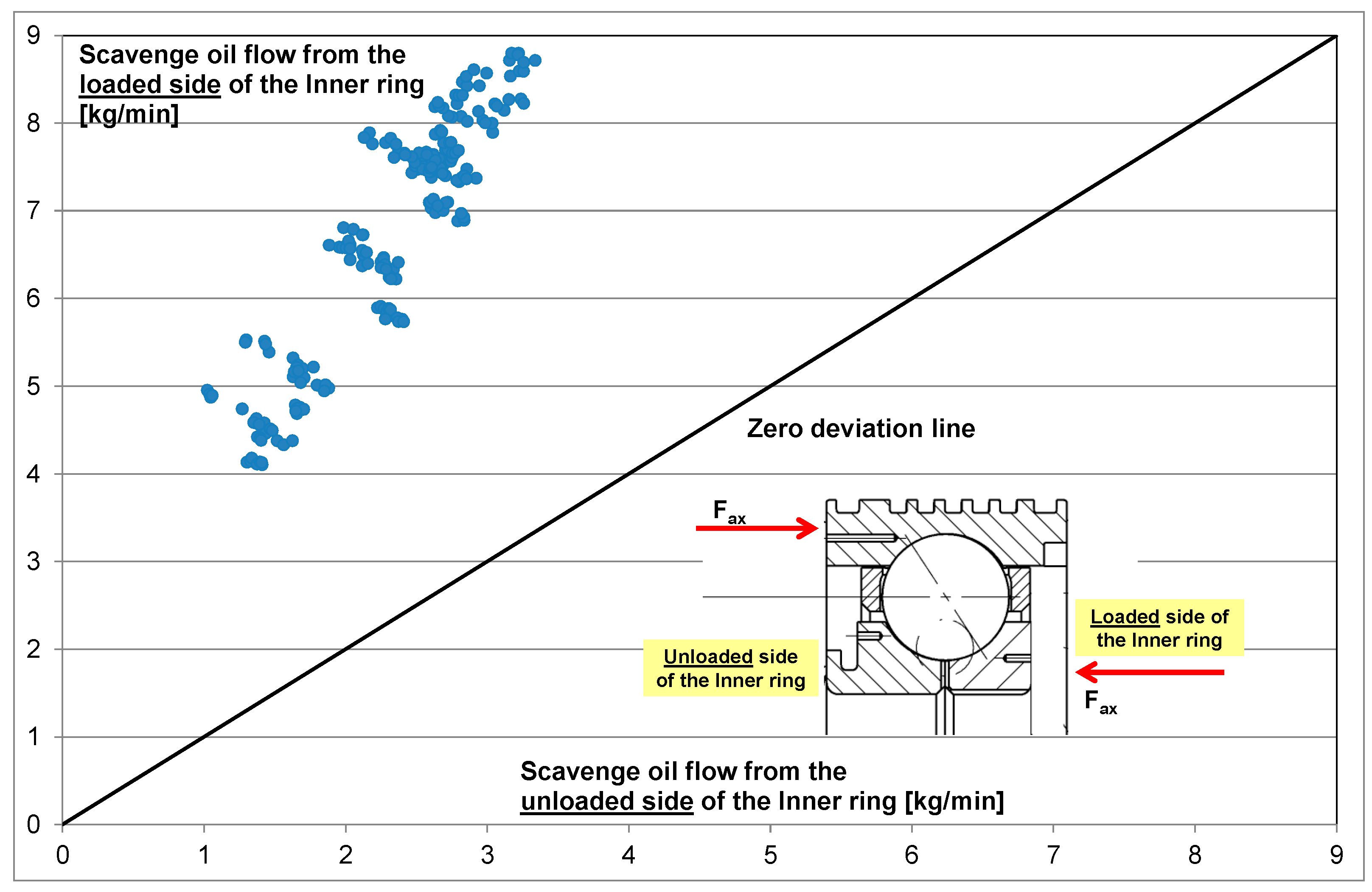
Scavenge flow measurements from both sides of the bearing showed that the highest oil scavenge flow and also the highest oil temperature is on the side of the bearing that is against the direction of the axial load on the inner ring (Figure 5 and Figure 6). The distance of the points to the zero deviation line is an indication of the difference in the measured values on both sides of the bearing. During the first part of the testing campaign on the basis of the all-steel bearing, a correlation for heat to oil prediction was created [3,4]. This correlation was then used during the testing of the hybrid bearing for verification. 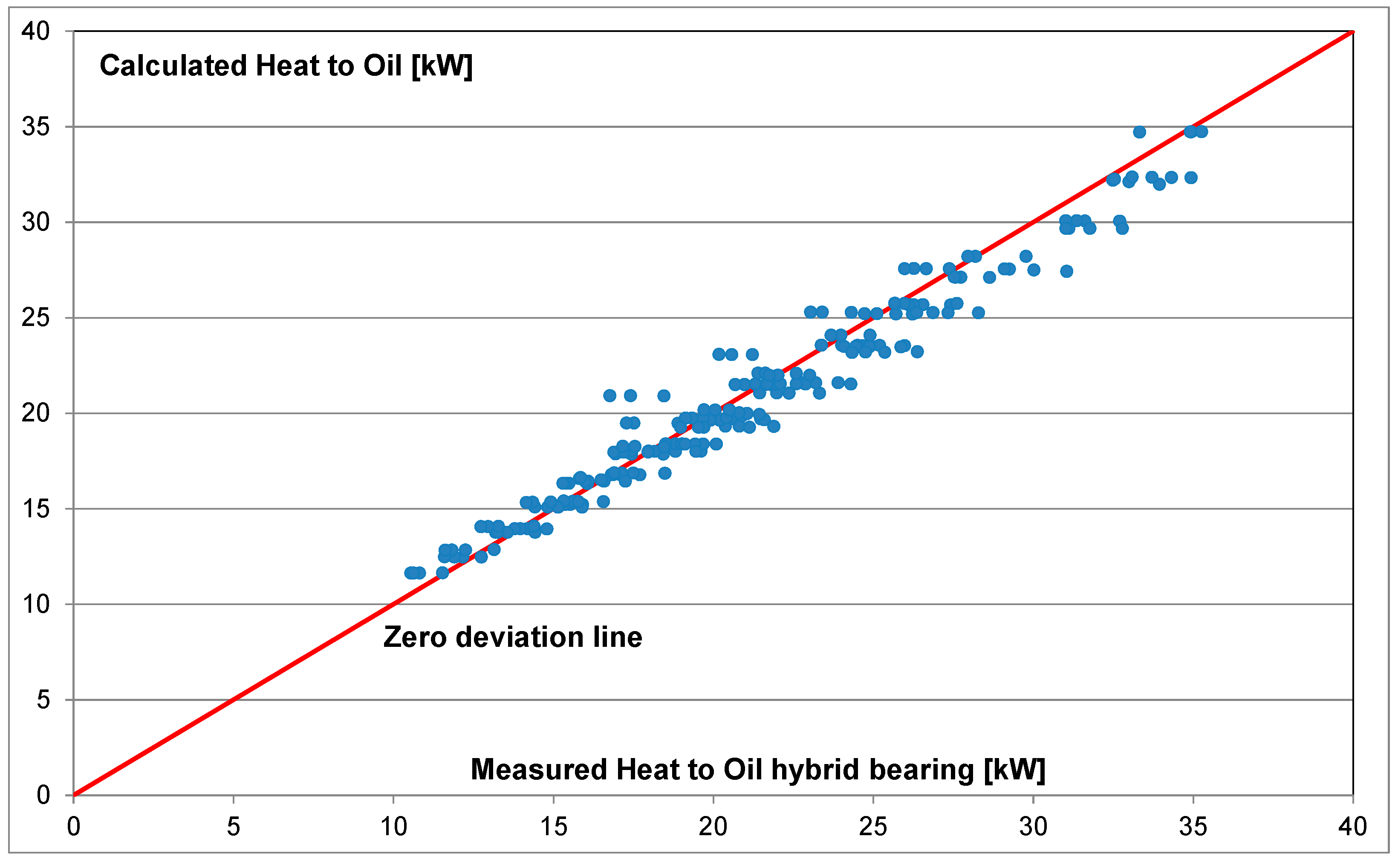Figure 7 shows a comparison of results between the correlation and the measurements from the hybrid bearing. The vast majority of the points are along the zero deviation line, thus very good accuracy between measurement and prediction is achieved.

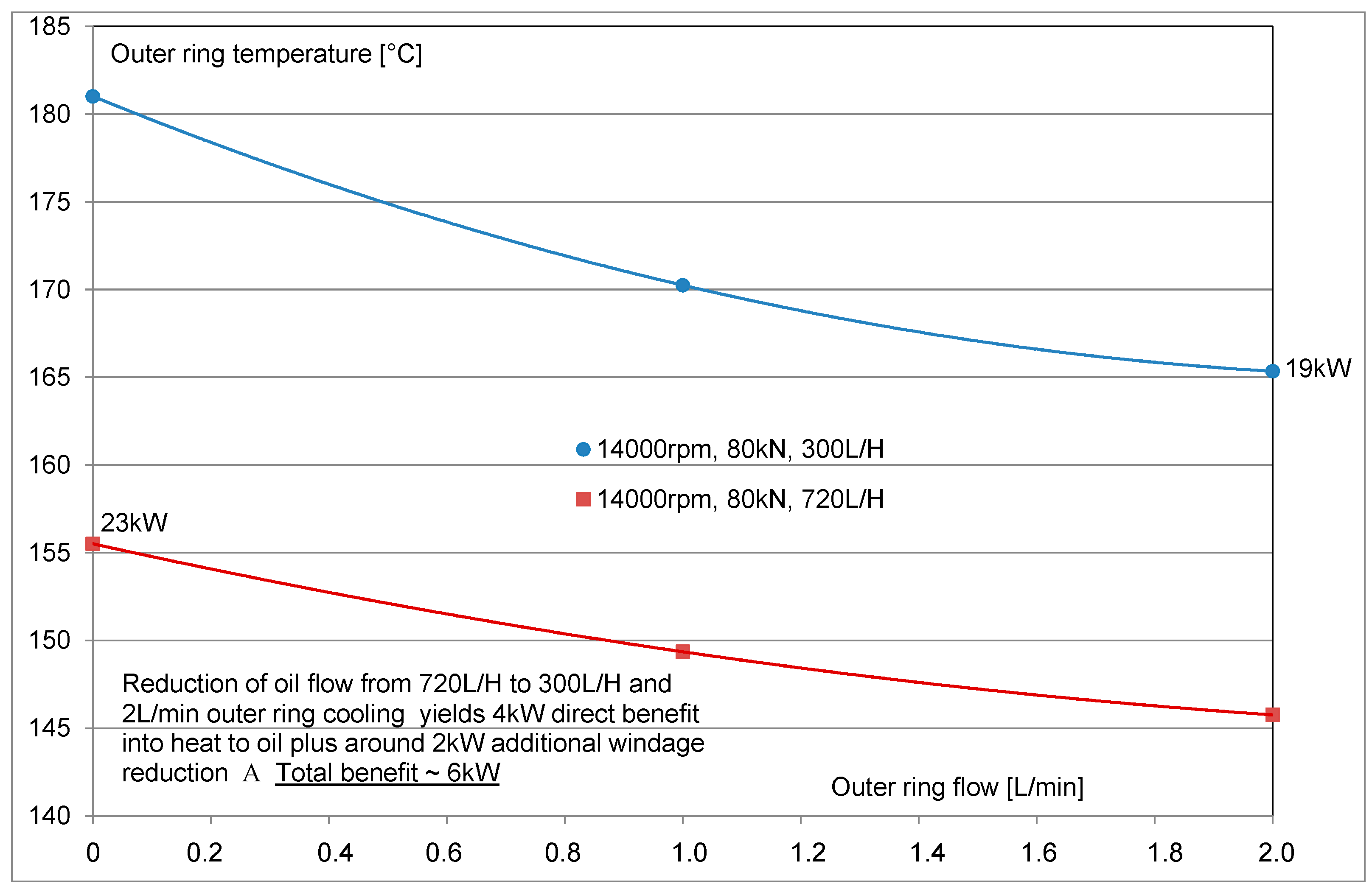
The benefits of the outer ring cooling were demonstrated during the all-steel bearing testing in the first part of the program and were again confirmed in the second part during the hybrid bearing testing. Figure 8 shows at 14,000 rpm the benefit of the lubricant flow reduction from 720 to 300 L/h. Using only 120 L/h outer ring cooling flow, the total heat to oil reduction is in the order of 6 kW (25%). Further information on the heat to oil reduction as a result of the outer ring cooling is given in [3,4].

Proper design of the cooling concept is an important issue. For this reason, very good knowledge of the pressure losses and of the heat transfer is important. In order to assess pressure drop and heat transfer in the outer ring channel a number of more than 500 test results were evaluated and were compared to the work performed by other authors.

5. Pressure Drop

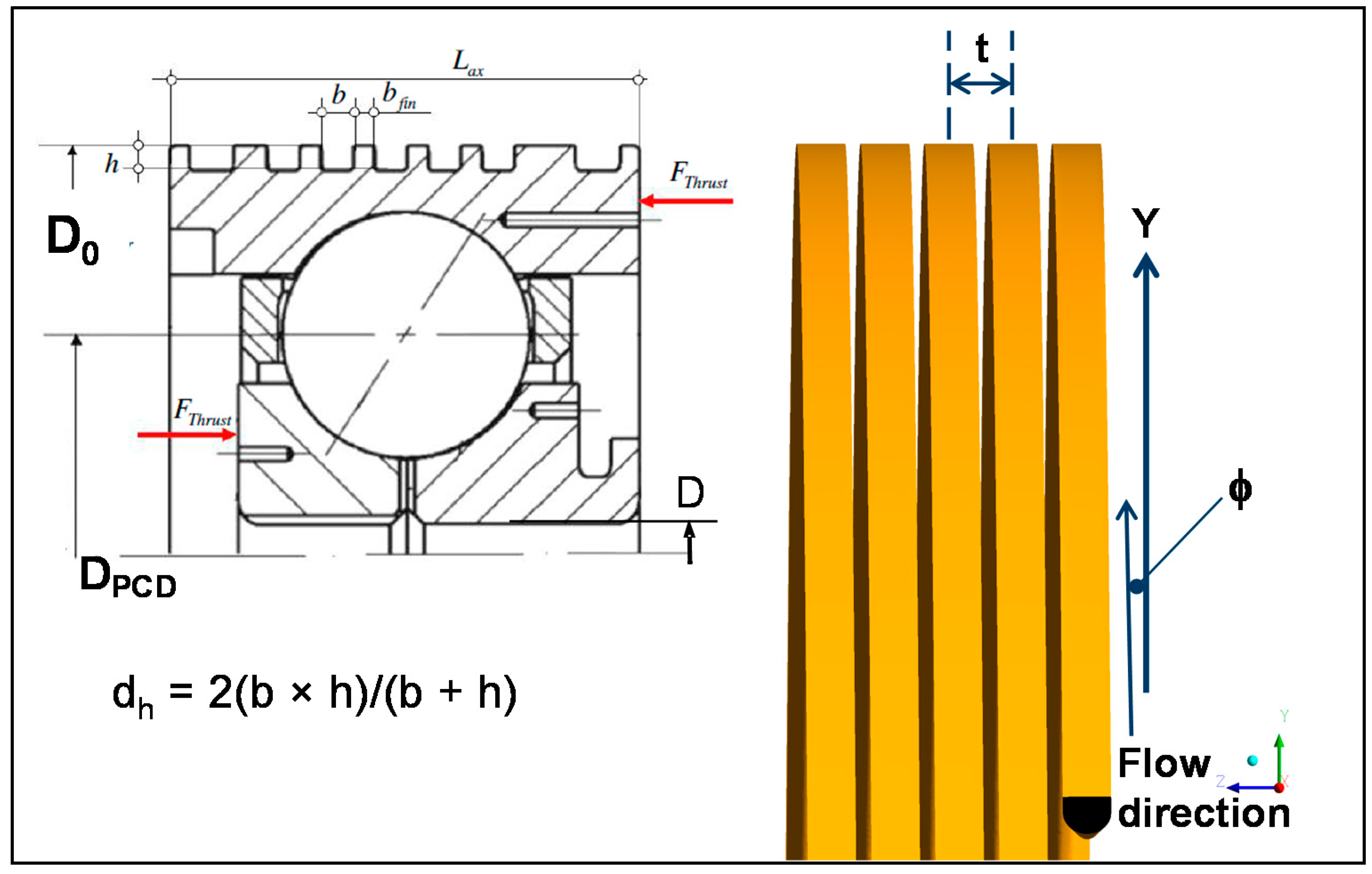
The pressure drop in the outer ring channel can be expressed as Δp = ½ ρ f u² ($\frac{L}{d_{\mathrm{h}}}$) = f (Re, geometry) with f the friction loss coefficient, ρ, and u the average density and velocity of the fluid and d_h the hydraulic diameter of the duct (Figure 9). L is the length of the outer ring channel. Since the channel is a spiral groove the flow direction is never perpendicular to the channel’s area. The inclination of the groove (pitch angle φ) can be given as φ = $\arctan \left[\frac{\left(t +b\right)}{\left(\pi D_0\right)}\right]$ with t the pitch, b the width of the groove and D₀ the bearing outer diameter (Figure 9). Thus the corrected width can be calculated as b_cor = b/cosφ and the corrected flow area is given A = h × b_cor. The corrected hydraulic diameter can be expressed as a function of b_cor:

$$d_{\mathit{hcor}}=\frac{2h{b}_{\mathit{cor}}}{\left(h+b_{\mathit{cor}}\right)}$$

The number of threads can be estimated using

$$\mathrm{N}=\frac{\left(L_{ax}-z1-z2+b_{fin}\right)}{\left(b_{fin}+b_{\mathit{cor}}\right)}$$

with L_ax, z₁, z₂, b_fin from Figure 9.

The outer ring diameter (coil diameter) is given by D_w = (D₀ − h) and represents the mean thread diameter. Due to the pitch angle φ the real coil diameter (diameter of the coil curvature D_cor) is not vertical, but oblique. According to [9], the corrected diameter can be calculated using the following relation,

$$D_{cor}=D_w{\left[1+{\left[\frac{t}{\mathsf{\pi }{D}_w}\right]}^2\right]}^{0.5}$$

In 1928, Dean [10] showed on a purely theoretical basis that a secondary flow is induced as a result of the centrifugal pressure gradient and the difference in the centrifugal forces that are caused by the fluid elements moving with different axial velocities in the main flow [11,12,13]. The secondary flow apparently has a stabilizing effect on the laminar flow and any disturbances are apparently damped by it [14]. For this reason, the critical Reynolds number increases as compared to the critical Reynolds number, which is valid for straight pipes. For the latter, the transition point from laminar to turbulent flow is at Re = 2300.

According to Schmidt [15], the critical Re number for coiled tubes can be determined using the following correlation: Re_coil = 2300 [1 + 8.6${\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.45}$].

Similarly, Ito [16] has developed an empirical relation for the critical Re number:

Re_coil = 20,000${\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.32}$, valid for ratios of d_h/D_cor between 1/15 and 1/860 on the basis of a circular cross section (1/860 < $\left(\frac{d_{hcor}}{D_{cor}}\right)$ < 1/15). In the case of the hybrid bearing the cross section of the duct is quadratic and the ratio is 0.013 (1/76.7), a number that is within Ito’s validity range. For values less than 1/860 (=0.00116), the critical Re number should be taken as that for the straight tube.

Srinivasan et al. [17] have documented in their work the critical Re number approximations from other authors:

Kubair and Varrier [18],	Recoil = $\mathrm{12,730}{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.2}$	for 0.0005 < $\left(\frac{d_{hcor}}{D_{cor}}\right)$ < 0.103
Kutateladze and Borishanskii [19],	Recoil = 2300 + 12,930 ${\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.3}$	for 0.0417 < $\left(\frac{d_{hcor}}{D_{cor}}\right)$ < 0.1667
Srinivasan et al. [17],	Recoil = 2100 [1 + 12${\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}$]	for 0.04 < $\left(\frac{d_{hcor}}{D_{cor}}\right)$ < 0.1

Table 2. Critical Reynold numbers for helical ducts from different authors.

Author	Recoil
Schmidt [15]	5108
Ito [16]	4990
Kubair and Varrier [18]	5346
Kutateladze and Borishanskii [19]	5819
Srinivasan [17]	4980

shows critical Re_coil numbers originated by different authors:

In [14], Schmidt’s correlation is preferred and this will be the selection in this work as well.

The friction loss coefficient can be expressed as:

$$\mathrm{f} =\frac{2 \Delta p}{\varrho u^2}·\frac{d_{hcor}}{L}$$

In 1932, White [20] had developed a correlation for smooth pipes (turbulent conditions). This correlation is a useful approximation for the design of coiled tubes:

for 15,000 < Re < 10⁵,

$$\mathrm{f}=0.32R{e}^{-0.25}+0.048{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}$$

(1)

Ito [16] has developed the correlation:

$\mathrm{for}300>Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^2>0.034,$

$$\mathrm{f}=\left[0.029+0.304{\left(Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^2\right)}^{-0.25}\right]{\left(\frac{D_{cor}}{d_{hcor}}\right)}^{-0.5}$$

(2)

Schmidt [15] has published correlations valid for laminar, transitional and turbulent flow of water or oil:

For laminar flow in the range 100 < Re < Re_coil,

$$\mathrm{f}=\left[1+0.14{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.97}R{e}^{\left(1-0.644{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.312}\right)}\right]\left(\frac{64}{Re}\right)$$

(3)

for Re_coil < Re < 22,000 (transitional flow),

$$\mathrm{f}=\left[1+\frac{\mathrm{28,800}}{Re}{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.62}\right]\left(\frac{0.3164}{R{e}^{0.25}}\right)$$

(4)

and for the fully turbulent flow and 20,000 < Re < 1.5 × 10⁵

$$\mathrm{f}=\left[1+0.0823\left(1+\frac{d_{hcor}}{D_{cor}}\right){\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.58}{\mathit{Re}}^{0.25}\right]\left(\frac{0.3164}{{\mathit{Re}}^{0.25}}\right)$$

(5)

Mishra and Gupta [21] have tested 60 helical coils in a wide range of diameters and pitch and have developed correlations valid in the laminar and in the turbulent flow region. The correlations are valid within the geometrical ranges 0.003 < $\left(\frac{d_{hcor}}{D_{cor}}\right)$ < 0.15 and 0 < $\left(\frac{t}{D_{cor}}\right)$ < 25.4 with t the pitch of the coil (Figure 9).

For the laminar flow and Re < Re_cor,

$$\mathrm{f}=\left(\frac{64}{Re}\right)\left[1+0.033{\left(Lo{g}_{10}\left(Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}\right)\right)}^4\right]$$

(6)

and for the turbulent flow within 4500 < Re < 10⁵,

$$\mathrm{f}=\left(\frac{0.3164}{R{e}^{0.25}}\right)\left[1+0.095{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}R{e}^{0.25}\right]$$

(7)

Shah and Joshi [22] have developed for the fully developed laminar flow and $\frac{D_w}{d_{hcor}}$ > 3 the following correlations:

for $Re{\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}\le 30$,

$$\mathrm{f}=\left(\frac{64}{Re}\right)$$

(8)

for 30 ≤ Re ${\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}$ ≤ 300,

$$\mathrm{f}=\left(\frac{27}{R{e}^{-0.725}}\right){\left(\frac{d_{hcor}}{D_w}\right)}^{0.1375}$$

(9)

and for $300\le Re{\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}$,

$$\mathrm{f}=\left(\frac{7.2}{R{e}^{-0.5}}\right){\left(\frac{d_{hcor}}{D_w}\right)}^{0.25}$$

(10)

Gnielinski [14] has developed friction loss correlations applying on coiled tubes of circular cross-section. He has extended his correlations with introduction of near wall phenomena like the ratio of the dynamic viscosities between wall and core stream:

for laminar flow:

$$\mathrm{f}=\left(\frac{64}{Re}\right)\left(1+0.33{\left(Lo{g}_{10}\left[Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}\right]\right)}^4\right){\left(\frac{{\eta }_{\mathrm{w}}}{\eta }\right)}^{0.27}$$

(11)

for turbulent flow:

$$\mathrm{f}=\left(\frac{0.3164}{R{e}^{0.25}}\right)\left[1+0.03{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}\right]{\left(\frac{{\eta }_{\mathrm{w}}}{\eta }\right)}^{0.27}$$

(12)

One of the most recent works is from Ju et al. [23]. They introduced between the laminar and the turbulent flow region an intermediate region, which they called laminar flow with a large vortex. Additionally, they also distinguish in the turbulent flow region between smooth and rough pipe wall:

for $Re{\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}\le 11.6$ and laminar flow,

$$\mathrm{f}=\left(\frac{64}{Re}\right)$$

(13)

for $Re{\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}\ge 11.6$ and Re < Re_coil, laminar flow with large vortex,

$$\mathrm{f}=\left(\frac{64}{Re}\right)\left(1+0.015R{e}^{0.75}{\left(\frac{d_{hcor}}{D_w}\right)}^{0.4}\right)$$

(14)

for $Re{\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}\ge 11.6$ and Re > Re_coil, turbulent, smooth pipe,

$$\mathrm{f}=\left(\frac{0.316}{R{e}^{0.25}}\right)$$

(15)

and for $Re{\left[\frac{d_{hcor}}{D_w}\right]}^{0.5}\ge 11.6$ and Re > Re_coil, turbulent, rough pipe with δ the roughness of the pipe,

$$\mathrm{f}=0.1{\left[1.46\left(\frac{\mathsf{\delta }}{D_w}\right)+100/Re\right]}^{0.25}\left[1+0.11R{e}^{0.23}{\left[\frac{d_{\mathit{hcor}}}{D_w}\right]}^{0.14}\right]$$

(16)

Based on the experimental results, the authors have developed their own correlation. They have assumed that the critical Re number for the transition from laminar to turbulent flow is the one according to Schmidt [15], Re_coil = 2300 [1 + 8.6 ($\frac{d_{hcor}}{D_{cor}}$)^0.45].

The author’s correlation is:

$$\mathrm{f}=1.35R{e}^{-0.43}$$

(17)

and is valid for 1000 < Re < 12,000.

The deviation of the experimental data around the friction loss coefficient from Equation (17), is as follows: 84% of the data within the ±5% and 99% of data within the ±10% range. This is a very good accuracy.

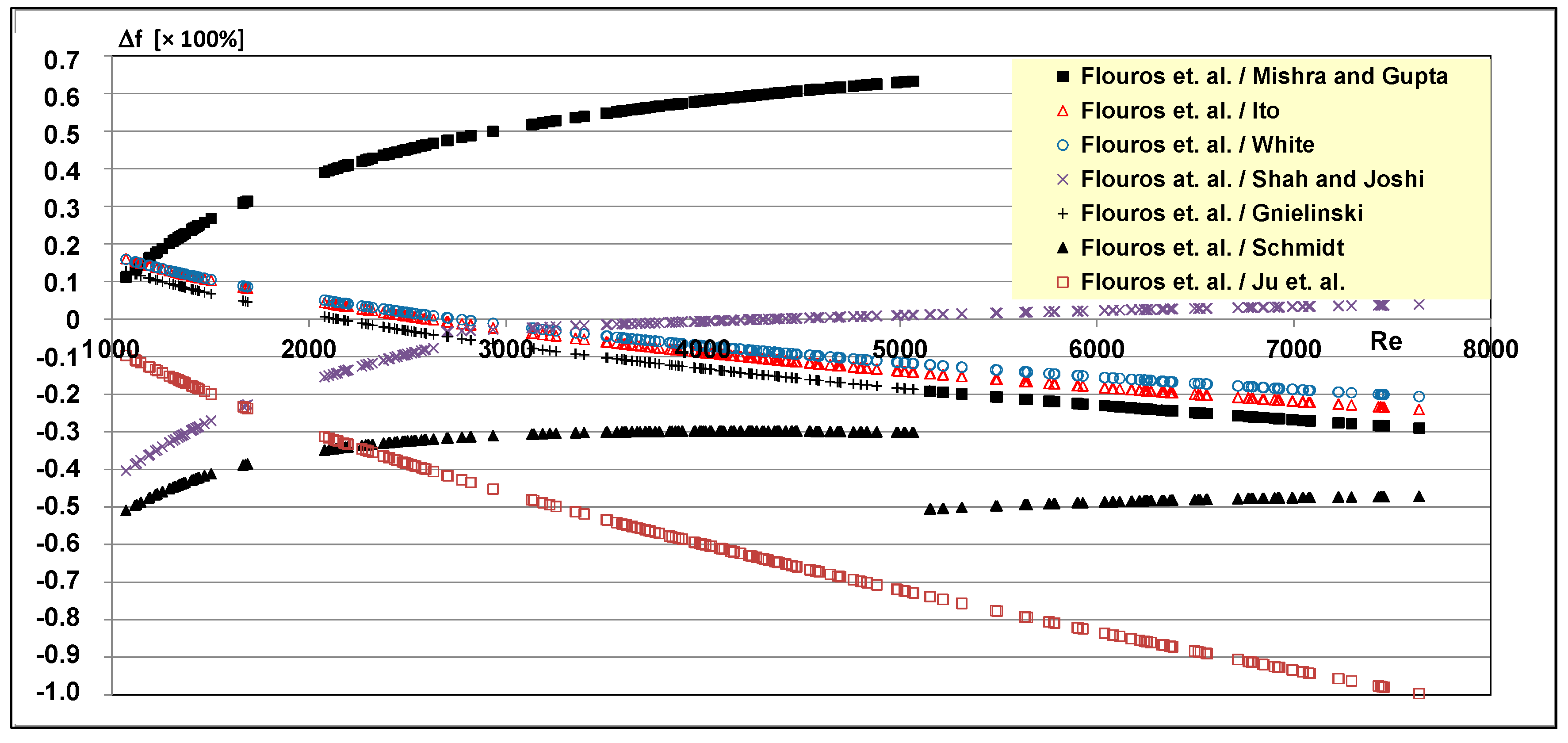
Figure 10 shows the accuracy between the author’s correlation (Equation (17)) and the correlations by White, Ito, Schmidt, Mishra/Gupta, Shah/Joshi, Gnielinski and Ju as a function of the Re number up to a Re number of 7600. This Re number would correspond to a pressure of about 36 bar at the outer ring duct inlet. Over the Reynold’s number range, the average accuracy is 26% for Mishra/Gupta, 7% for Ito, 6% for White, 3% for Shah/Joshi, 11% for Gnielinski, 27% for Schmidt and −62% for Ju, respectively (Figure 10).

6. Heat Transfer

For the derivation of a relation for the heat transfer in the helical duct temperature measurements of the fluid and of the material were used. It has been assumed that the physical problem is that of a flow through a duct having a constant heat flux through its walls. For the quantification of the flow in laminar or turbulent, the estimation of the critical Re number was based on the correlation given by Schmidt [15], Re_coil = 2300 [1 + 8.6 (d_hcor/D_cor)^0.45] and has been reported already in the previous chapter. Before processing with the derivation of the own correlation an extensive survey on correlations existing in the technical literature was carried out. The following authors have contributed Nusselt number correlations for helical coils or ducts:

Schmidt [15] has developed his correlations by distinguishing among laminar, transitional, and turbulent flow regimes. For the laminar flow Re < Re_coil,

$$Nu=3.65+0.08\left[1+0.8{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.9}\right]R{e}^{\left(0.5+0.2903{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.194}\right)}P{r}^{1/3}$$

(18)

for the transitional flow with Re_coil < Re < 22,000,

$$Nu=0.023\left[1+14.8\left(1+\frac{d_{hcor}}{D_{cor}}\right){\left(\frac{d_{hcor}}{D_{cor}}\right)}^{1/3}\right]R{e}^{\left(0.8-0.22{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.1}\right)}{Pr}^{1/3}$$

(19)

and in the fully turbulent region for 22,000 < Re < 150,000

$$Nu=0.023\left[1+3.6\left(1-\frac{d_{hcor}}{D_{cor}}\right){\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.8}\right]R{e}^{0.8}P{r}^{1/3}$$

(20)

Gnielinski [14] has adopted for laminar coil flows the correlation by Schmidt (Equation (18)) and has recommended for turbulent flows the following relation:

$$Nu=\left(\frac{f}{8}\right)RePr{\left[1+12.7{\left(\frac{f}{8}\right)}^{0.5}\right]}^{0.8}\left(P{r}^{2/3}-1\right)$$

(21)

$$f=\frac{0.3164}{R{e}^{0.25}+0.03{\left(\frac{d_{\mathit{hcor}}}{D_{\mathit{cor}}}\right)}^{0.5}}{\left[\frac{\left({\nu }_w{\rho }_w\right)}{\nu \rho }\right]}^{0.27}$$

Shah and Joshi [22] have developed a correlation, which is valid for 0.005 < Pr < 1600 and for 1.0 < Re${(\frac{d_{hcor}}{D_{cor}})}^{0.5}$ < 1000,

$$Nu={\left[{\left(3.66+\frac{4.343}{a}\right)}^3+1.158{\left(Re\frac{{\left(\frac{d_{\mathit{hcor}}}{D_{\mathit{cor}}}\right)}^{0.5}}{b}\right)}^{3/2}\right]}^{1/3}{\left(\frac{\eta }{{\eta }_w}\right)}^{0.14}$$

(22)

where, a $=\frac{\left(1+927\left(\frac{d_{\mathit{hcor}}}{D_{\mathit{cor}}}\right)\right)}{R{e}^{2}Pr}$ and b = 1 + $\frac{0.477}{Pr}$.

Mori and Nakayama [24,25] have investigated heat transfer in curved circular ducts for constant heat flux and constant wall temperature conditions and laminar air flow. Surprisingly, the Nusselt numbers were found to be the same for both wall boundary conditions. They also extended their work on turbulent air flows. Their correlations are as follows:

For laminar flow:

$$Nu=\left(\frac{0.864}{\zeta }\right){\left[Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}\right]}^{0.5}\left[1+2.35{\left(Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.5}\right)}^{-0.5}\right]$$

(23)

with

$$\begin{gathered} \mathsf{\zeta }=\left(\frac{2}{11}\right)\left[1+{\left(1+\left(\frac{77}{4}\right)P{r}^{-2}\right)}^{0.5}\right]\mathrm{for}Pr>1 \\ \mathsf{\zeta }=\left(\frac{1}{5}\right)[2+\left(1+{\left(\frac{10}{P{r}^{-2}}-1\right)}^{0.5}\right]\mathrm{for}Pr<1 \end{gathered}$$

For the turbulent flow:

$$Nu=\left(\frac{1}{41}\right)R{e}^{\left(5/6\right)}P{r}^{0.4} {\left(\frac{d_{hcor}}{D_{cor}}\right)}^{1/12}\left[1+0.061\frac{1}{{\left(Re{\left(\frac{d_{hcor}}{D_{cor}}\right)}^{2.5}\right)}^{1/6}}\right]$$

(24)

Seban and McLaughlin [26] experimentally studied heat transfer in coiled tubes for laminar and turbulent water flows. They investigated coils with ($\frac{d_{hcor}}{D_{cor}}$) ratios between 1/17 (0.0588) and 1/104 (0.0096) and Re numbers ranging from 12 to 5600 for the laminar region and up to 65,000 for the turbulent region. The Pr-numbers were between 2.9 and 657. The curvature ratio ($\frac{d_{hcor}}{D_{cor}}$) of the outer ring cooling duct herein is 1/77 (0.013), which is in the range from [26]. Seban and McLaughlin derived the following correlation, which is valid for both laminar and turbulent flows:

$$Nu=\left(0.023\right)R{e}^{0.85}P{r}^{0.4} {\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.1}$$

(25)

Another widely used method is that of Sieder and Tate [27], who recommended the following correlation for applications with large property variations initiated by the temperature difference between the bulk flow and the wall.

$$Nu=\left(0.027\right)R{e}^{0.8}P{r}^{\left(\frac{1}{3}\right)} {\left(\frac{{\eta }_{bulk}}{{\eta }_w}\right)}^{0.14}$$

(26)

Rogers and Mayhew [28] have investigated heat transfer in steam heated helically coiled tubes. They proposed the following relation for Re numbers up to 50,000:

$$Nu=\left(0.021\right)R{e}^{0.85}P{r}^{0.4} {\left(\frac{d_{hcor}}{D_{cor}}\right)}^{0.1}$$

(27)

Based on the test results the authors of this paper have derived their own correlation. For the range between 1000 < Re < 12,000 and 48 < Pr < 107, the authors propose the following relation:

$$Nu=3.7+\left(0.0016\right)R{e}^{0.7632}P{r}^{0.3909} {\left(\frac{L}{d_{hcor}}\right)}^{0.2736}$$

(28)

with L being the length of the spiral groove. When the experimentally derived Nu numbers were plotted against the Re number [Nu = f(Re)] a curve was the result. This curve was extrapolated for Re → 0 in order to get the limiting Nu number value. The derived limiting value was about 3.68, thus the authors decided to set to 3.7. The limiting Nu number is the one that is for a laminar, thermally, and hydro-dynamically fully developed flow. The distance that is necessary for the laminar flow to become thermally and hydro-dynamically fully developed is called the combined entry length and can be determined by using the relation given by Incropera et al. [29]:

$$\left(\frac{x}{d_h}\right)=0.05Re·Pr$$

(29)

with x the combined entry length. Assuming the lowest Re number from the test (~1000), also the lowest Pr number of around 50 and a hydraulic diameter of about 2.6 mm, Equation (29) yields for the combined entry length x, 2500 mm. This means that the heat transfer problem at laminar flows is dominated by entrance region phenomena.

In [29] on page 519, a table with Nu numbers for fully developed laminar flow in tubes is depicted. For a rectangular cross section with a ratio of width to depth of 1.43 and a constant flux over the wall the laminar fully developed value of the Nu number is 3.73, which is very close to the derived value of 3.7, which is proposed by the authors.

Figure 11 and Figure 12 show comparisons between values of the Nusselt number derived by using Equations (18)–(28) and the test results. Equations (18)–(21), (23)–(27) are in the vicinity of the zero deviation line when the flow is laminar and move considerably away when the flow turns turbulent. Only Equation (22) by Joshi and Shah shows a smooth transition from the laminar into the turbulent region and has least deviation to the test results.

7. Efficiency of the Outer Ring Cooling

As already mentioned, the idea behind the outer ring cooling concept was adopted from fins that are used for cooling electronic devices. The authors believe that the system is a combination between a finned body and a heat exchanger. In this sense the physics behind the system were accordingly treated. It has been assumed that the efficiency is a function of the oil heat pickup ratio from the fins and the maximum possible heat, which is dictated by the maximum temperature difference between wall and oil.

$${\mathsf{\epsilon }}_{\mathrm{HX}}=\left(\mathrm{heat}\mathrm{extracted}\mathrm{from}\mathrm{the}\mathrm{fins}\right)/\left(\max \mathrm{power}\mathrm{extracted}\mathrm{by}\mathrm{the}\mathrm{fluid}\right)=\frac{\left(c_{poil1} {\mathsf{\Delta }\mathrm{T}}_{ORC}\right)}{c_{poil2} \left(TOR-T_{ORCin}\right)}$$

where c_poil is the average specific heat capacity of the oil, ΔT_ORC the oil temperature increase in the outer ring duct, TOR the bearing material outer ring temperature in average and T_ORCin the oil inlet temperature into the outer ring duct. An additional variable, which is known from heat exchangers was introduced as well. 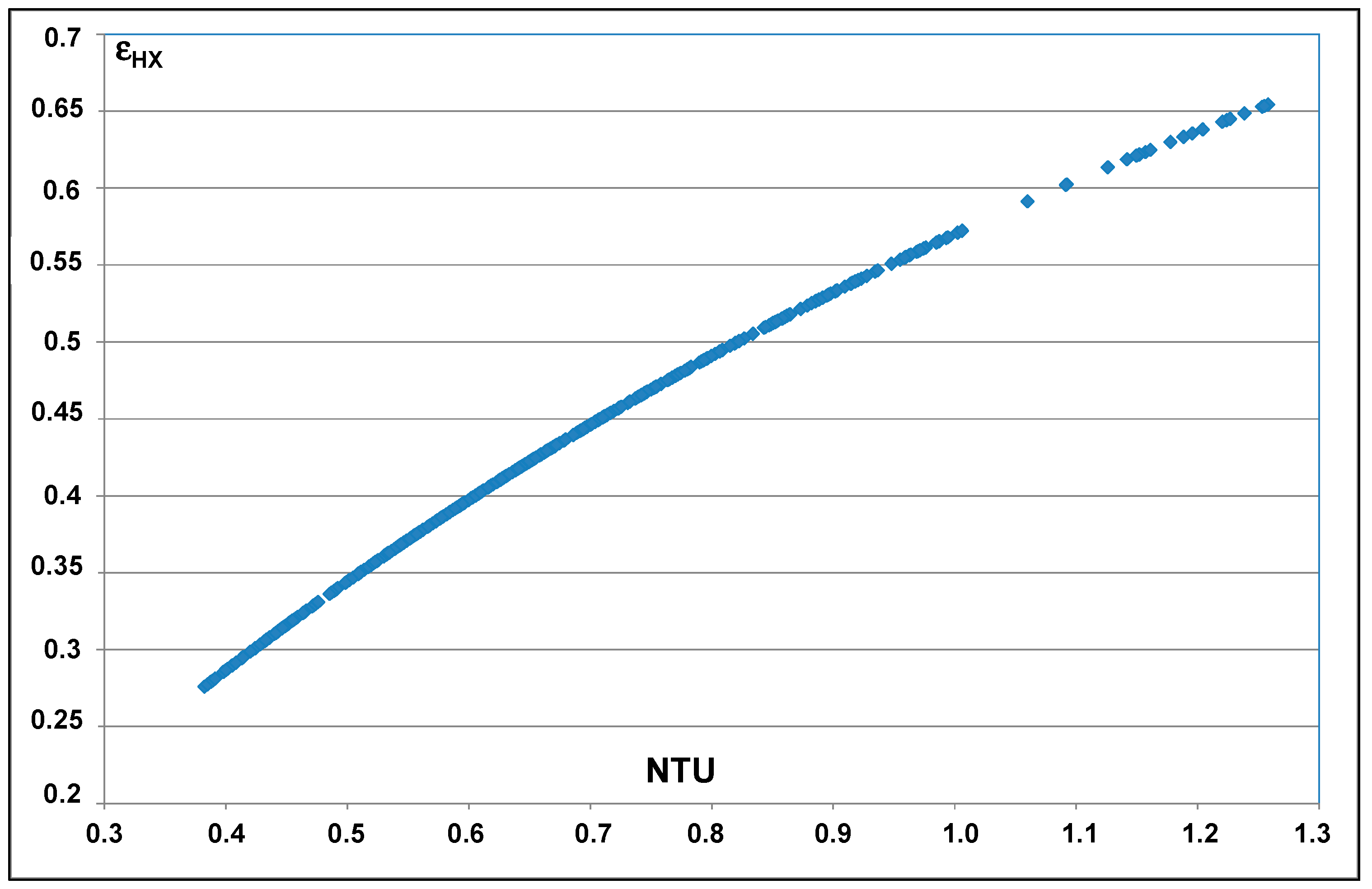This is the Number of (heat) Transfer Units (NTU) with NTU = $\frac{\alpha A_K}{m_{oil}{c}_{poil}}$, where α the heat transfer coefficient in the outer ring duct, A_K the heat transfer area (duct internal area) and m_oil the oil mass flow. The relation between the efficiency and the NTU was determined on the basis of the test results leading to

$${\mathsf{\epsilon }}_{\mathrm{HX}}=1-{\mathrm{e}}^{\left(-0.8438\mathrm{NTU}\right)}$$

(30)

with e the exponential function. If the test results are plotted against efficiency the curve, which is depicted in Figure 13 is created. The highest efficiency is achieved with least fluid flow at highest temperature increase and highest heat transfer coefficient for the fluid. For best efficiency an iterative process is necessary, so that good performance at an acceptable pressure loss is achieved.

8. Numerical Analysis

8.1. Numerical Analysis—Thermal and Pressure Drop Assessment

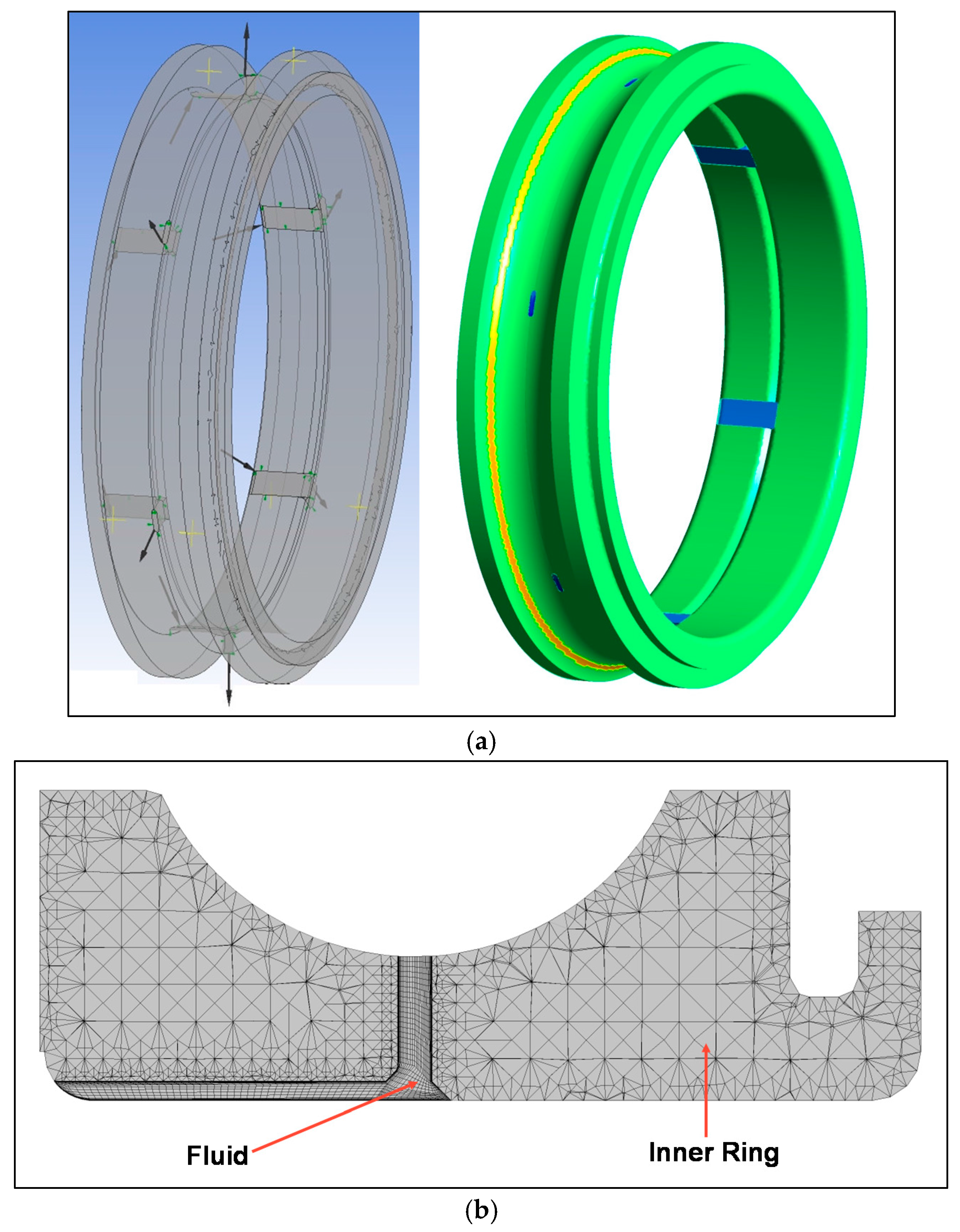
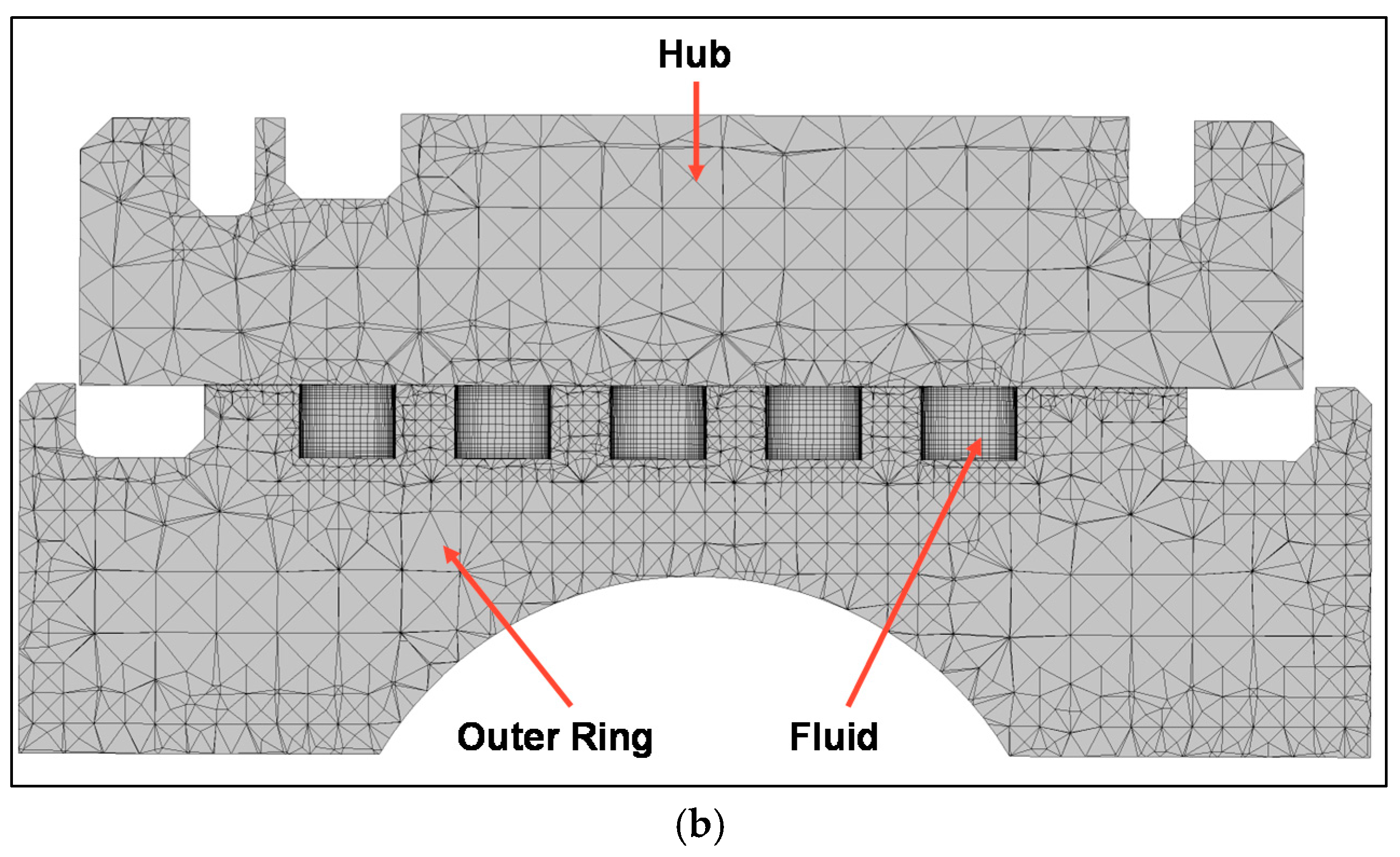
For the numerical analysis ANSYS CFX version 17 was used. Both rings of the bearing were modeled. Figure 14a shows the inner ring and Figure 15a shows the outer ring domain. The yellow stripes are for the heat flux, which is ingested into the material by the contact with the rolling elements. The “contact” heat flux was introduced into the model by means of a step function. It was calculated by using company owned functions. Additional churn losses were also calculated and introduced into the ring tracks as heat sources.

The inner ring was modeled using a fluid and a solid domain. For the fluid domain 408,000 hexahedral elements were used, whereas 1.9 million tetrahedral elements were used for the solid. Figure 14b shows a cut through the inner ring mesh. The outer ring was modeled using 1.7 million hexahedral elements for the fluid and 5.3 million tetrahedral elements for simulating the solid domain. Figure 15b shows the mesh in a plane cut through the outer ring.

The non-dimensional wall distance y⁺ for a wall-bounded flow adjacent to the duct’s internal and external walls was evaluated. y⁺ is commonly used in the boundary layer theory and is defined as the ratio of the product of the friction velocity u* at the nearest wall node and of the distance y to this node divided by the local kinematic viscosity ν of the fluid, y⁺ = u* $\frac{y}{\nu }$ with u* = $\frac{{\tau }_w}{{\rho }^{0.5}}$ and τ_w as the wall shear stress.

For y⁺ values over 11 scalable wall functions are used. This approach is not suitable for accurate heat transfer predictions. Therefore, a fine mesh was created for which y⁺ was kept below 6. For this mesh a general dominant low Reynolds near wall formulation was used. This is more suitable for heat transfer computations. It is recommended that the value of y⁺ is not higher than 11 (11.06 is the intersection between the logarithmic and the linear near wall profile). The following average values were calculated:

$${y^{+}}_{InnerRing}=0.76\mathrm{and} {y^{+}}_{OuterRing} =3.4$$

At inner ring fluid inlet a mass flow rate and a temperature were set as the boundary conditions, whereas at its outlet a static pressure was set. The SST (Shear Stress Transport) turbulence model was used. The inner ring solid domain was modelled as rotating with the angular velocity being the input.

At the outer ring fluid inlet the oil mass flow and the oil temperature were set as the boundary conditions. At outlet, a static pressure boundary condition was set. The SST turbulence model was used here as well. On the interface between the outer ring and the squeeze film damper (SQF) a heat transfer coefficient was set. The flow in the SQF cavity is laminar at very low Re numbers and the flow is also hydraulically and thermally fully developed. The heat pick up due to the oil flow in the SQF is about 2% of the heat generation in the bearing. Therefore, SQF systems are not suitable for heat removal purposes, but only for rotor dynamics purposes.

The calculation of the heat conduction in the solid material and the standard CFD calculation are done in one single solver using the CHT (Conjugate Heat Transfer) method. This is a full coupled method to exchange heat flux and temperature between the solid and the fluid.

Solid and fluid representing times (Timescale) are quite different. However, as we are only interested in a steady state solution, the time discretization has been chosen nearly 1000 time bigger for the material than for the fluid, thus large computation time could be avoided.

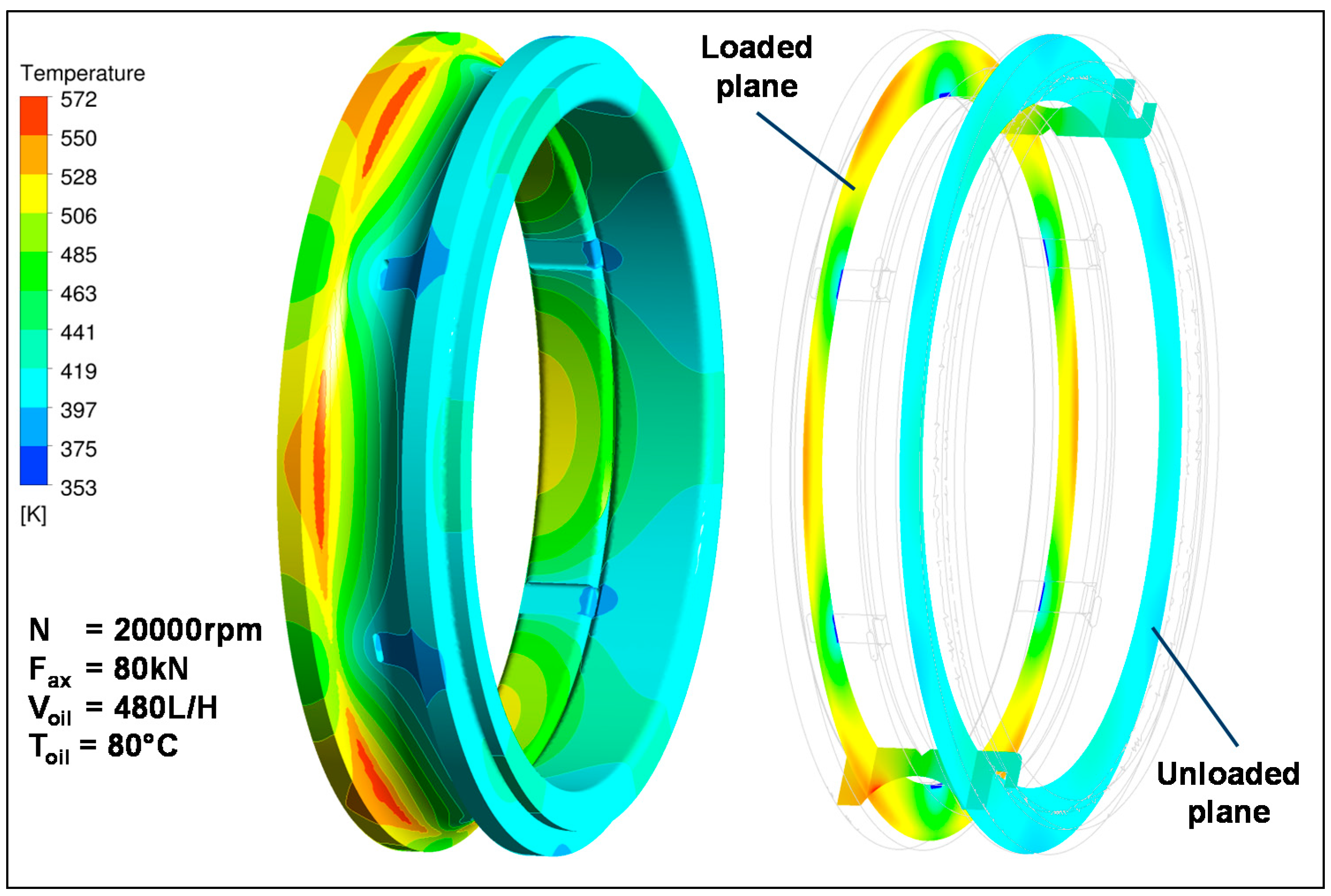
Figure 16 shows the results of the temperature distribution in the inner ring at 20,000 rpm, 80 kN of thrust, and at 480 L/h of oil flow at 80 °C. On the LHS, the surface temperature distribution is depicted. On the RHS, the two planes are shown where temperatures by means of telemetry thermocouples were recorded. The average measured temperatures in the loaded and in the unloaded planes of the inner ring are given in

Table 3. Comparison between the measured and the calculated temperatures for the Inner ring at the operating conditions mentioned above.

Measured Temperatures Material Loaded/Unloaded Side (°C)	Calculated Temperatures Material Loaded/Unloaded Side (°C)
231/137	228/139

and are also compared to the calculated values. The accuracy of the calculation is very good.

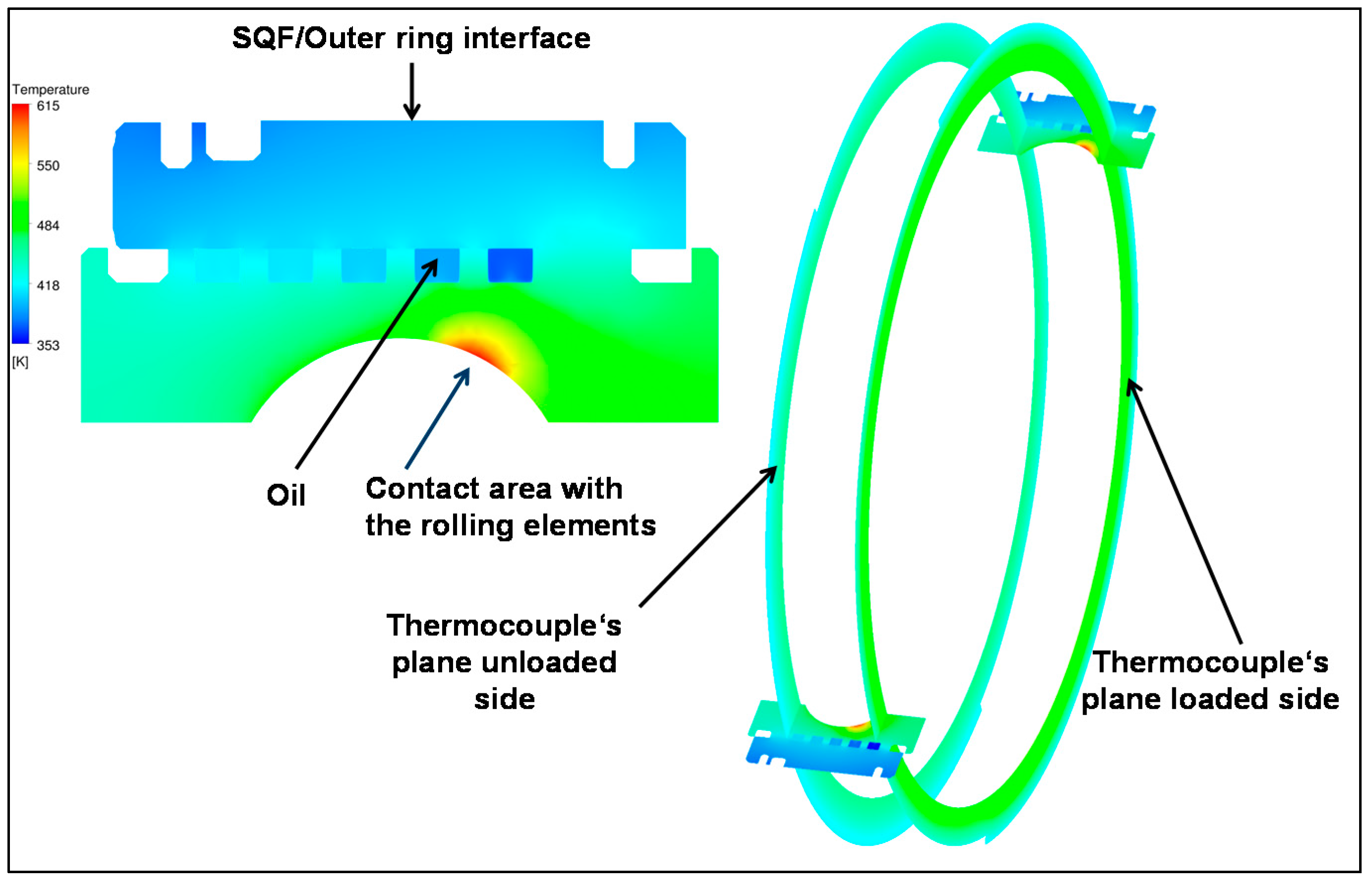
Figure 17 shows a plane cut through the outer ring. At the same operating conditions as for the inner ring the average material temperatures in the planes, where thermocouples were placed on both sides are depicted. The accuracy between the measured and the calculated material temperatures is very good, as is shown in

Table 4. Comparison between the measured and the calculated average temperatures for the Outer ring at the operating conditions mentioned above.

Measured Material and Oil Temperatures Loaded/Unloaded Side (°C)	Calculated Material and Oil Temperatures loaded/unloaded side (°C)
Material: 201/175	Material: 202/174
Oil: 141 (exit)	Oil: 140 (exit)

. Also, in Table 4, the oil outlet temperatures from the outer ring are compared and show that the accuracy of the computation is very good.

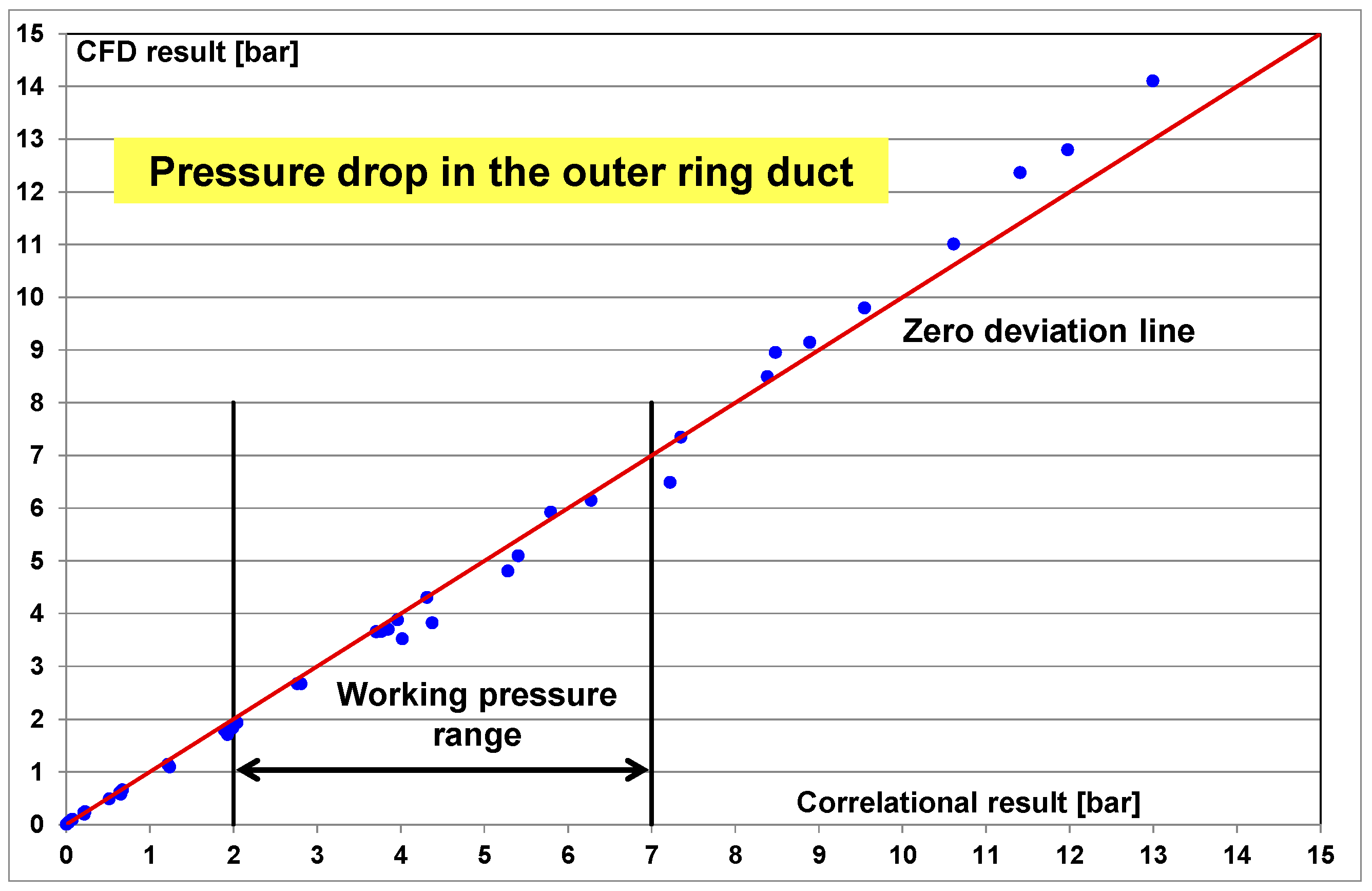
For the hydraulic assessment a series of computations took place with flows ranging between 3 and 415 L/h. The pressure drop in the outer ring duct was evaluated and results were compared to results derived by the correlation, Δp = $0.5\rho u^2\frac{L}{d_{\mathit{hcor}}}f$, with the friction loss coefficient f from Equation (17).

Figure 18 depicts pressure drop result comparison. The scatter around the zero deviation line is small indicating towards a good accuracy between the numerical and the analytical results. Particularly within the working pressure drop range between 2 and 7 bar, the quality of the analytical results using Equation (17) is very well. For aviation oils of MIL-PRF-23699 standard at 80 °C this pressure drop range would correspond to flows between 60 and 130 L/h.

8.2. Numerical Analysis—Flow Details

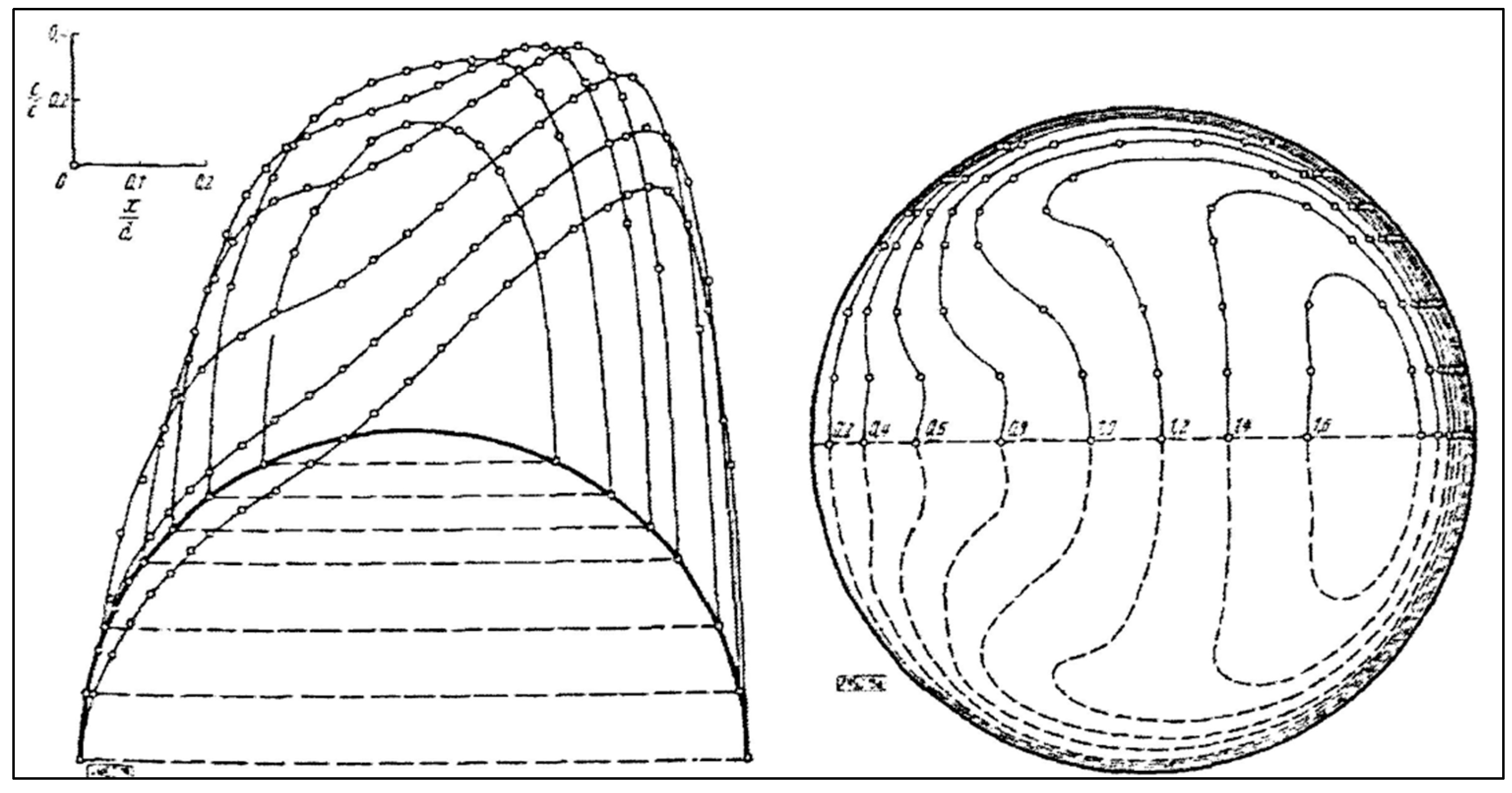
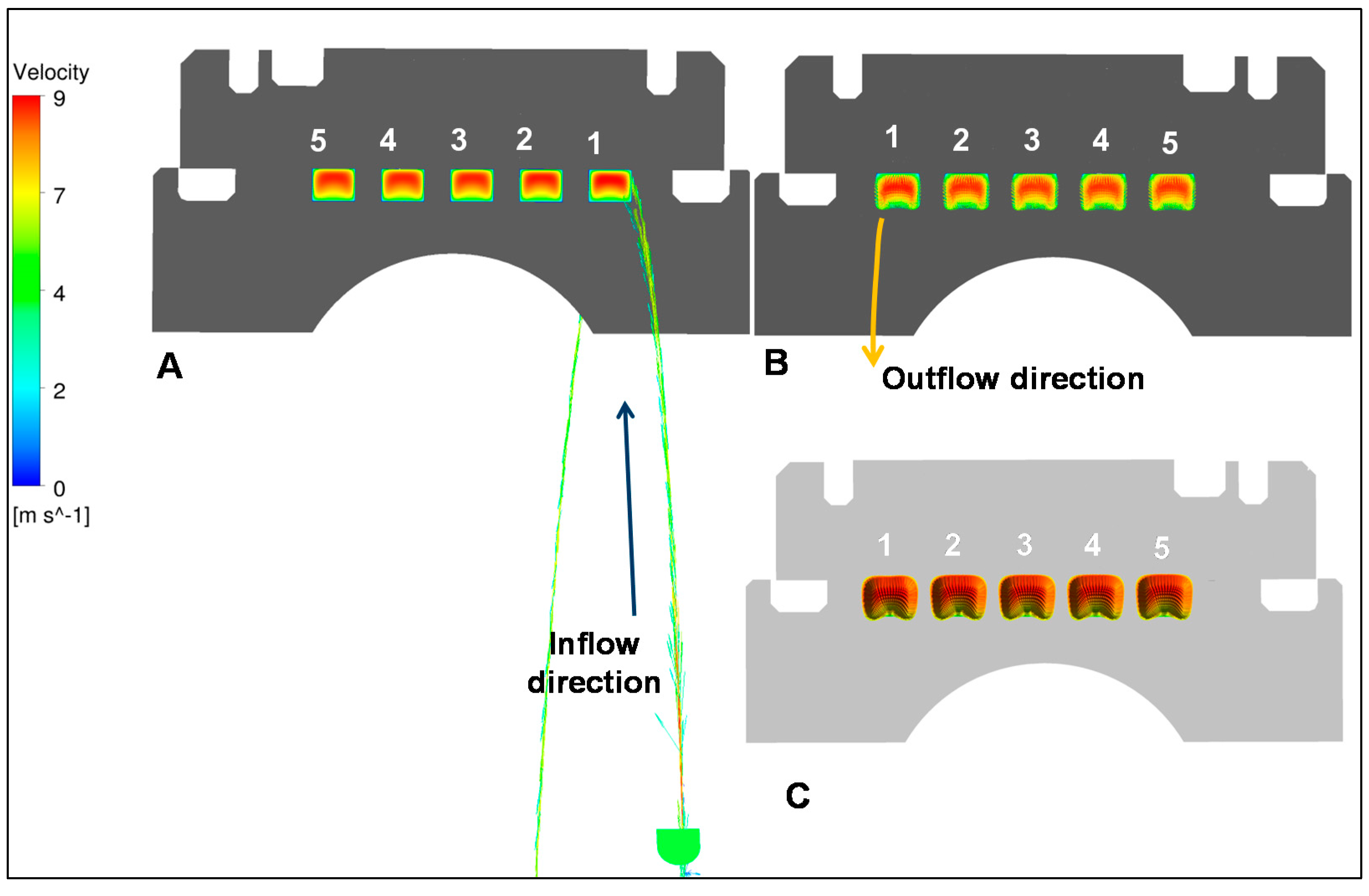
In 1934, Adler [30] has investigated flow patterns by measuring in helically coiled tubes with circular cross section. Figure 19 shows the flow pattern as a velocity distribution (LHS) or as isotachs (RHS). In the case of the outer ring duct, the cross section is not circular, but is rectangular. Very similar to Adler’s velocity profiles, Figure 20 shows the velocity distribution profiles and the typical “kidney” like isotachs.

8.3. Numerical Analysis—Helical Duct Cross Section Modification

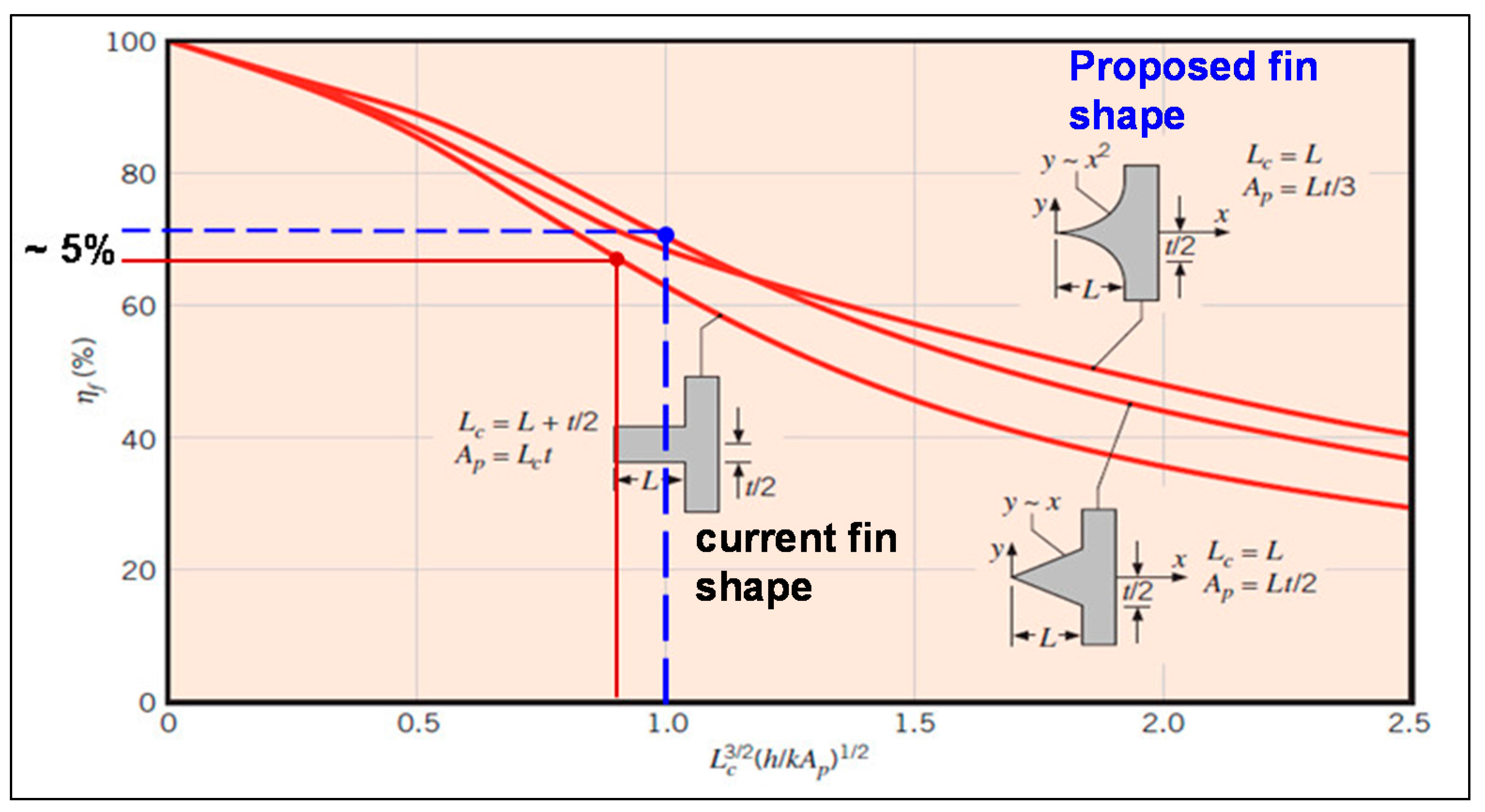
As already mentioned, the outer rings with the helical cooling duct were assumed to be a finned body heat exchanger. In the course of improving the efficiency, the authors came up with an idea which has its origin in the fin theory. It is known that tapered fins are better in performance than constant cross section fins [29]. Figure 21 compares efficiency of fins with different shapes. If the current rectangular shape is replaced by a tapered shape fin the expected performance efficiency could increase by up to 5%. 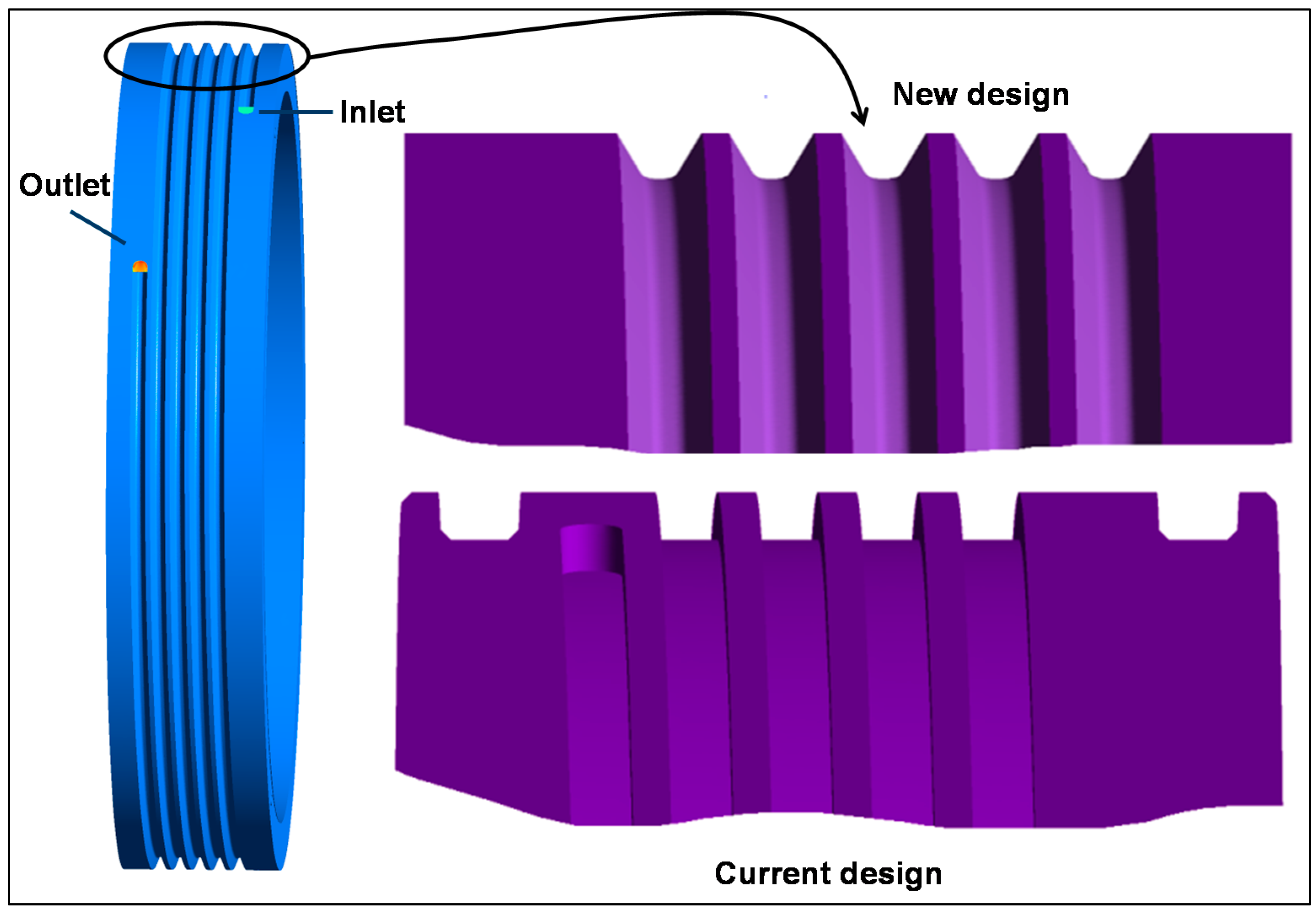Figure 22 shows the proposed design. The difference to the conventional design is in the shape of the fins. Length, depth, and hydraulic diameter of the duct were kept the same in order make comparisons easier. For this reason, no deterioration in terms of pressure drop is expected. The simulations were performed using CFX. 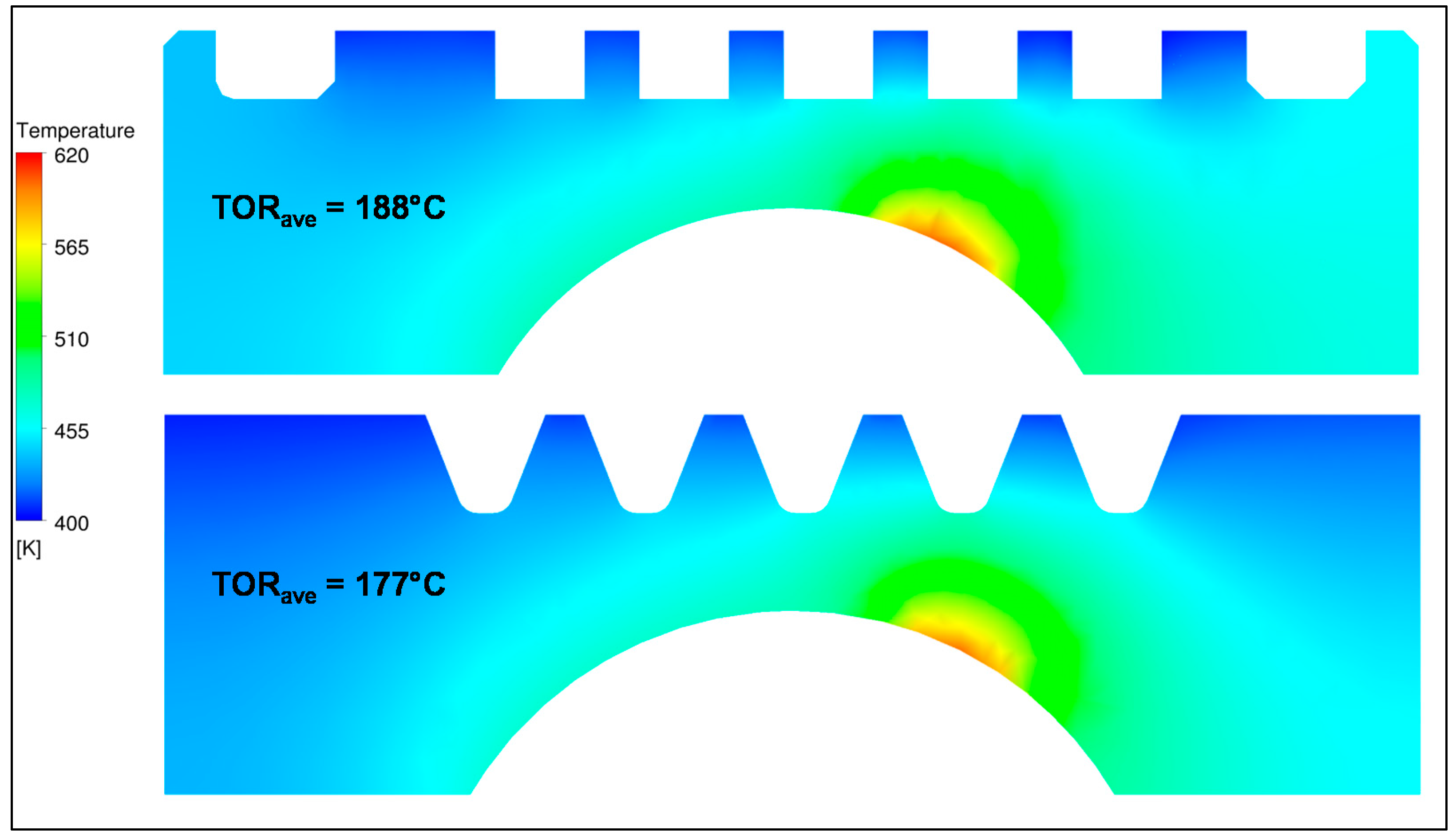Figure 23 shows a comparison of the two designs at the same operating conditions. The new design leads to a lower average temperature in the material (177 °C/450 K vs. 188 °C/461 K) and consequently to a higher ΔT in the fins (54 K for the new design vs. 46 K).

Both helical duct configurations are capable of removing considerable amounts of heat from the material. In the absence of a helical duct, hence full solid outer ring, the calculated average temperature in the material would reach 254 °C (527 K). This temperature is 66 K higher than with outer ring cooling and a rectangular duct or 77 K higher than with outer ring cooling and a V-type duct.

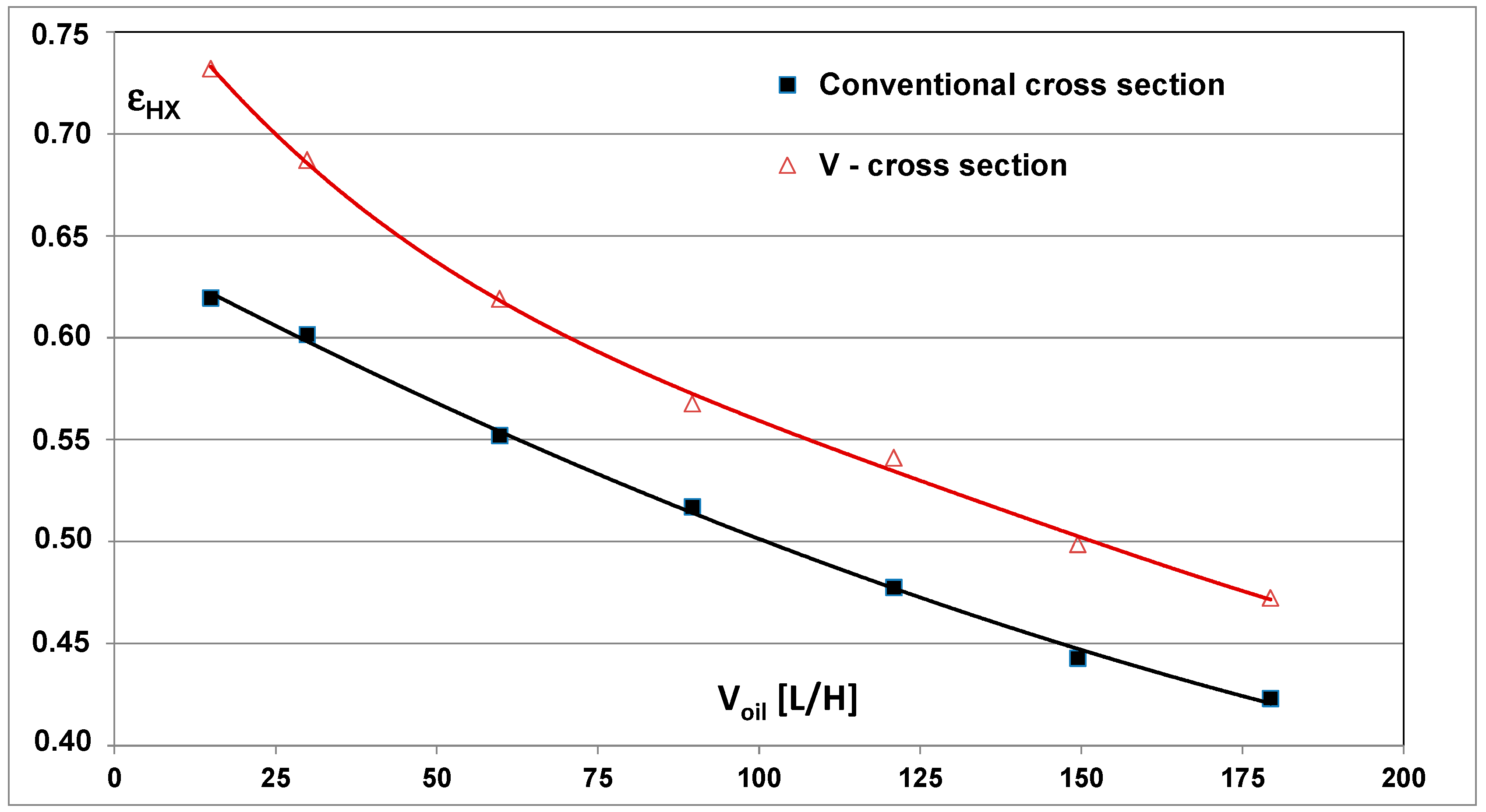
Figure 24 depicts an efficiency comparison between the conventional and the new V-type groove. As a result of the tapered shape, this duct can demonstrate throughout the range of oil flows an average performance/efficiency increase of 16%.

The current bearing has achieved a technological leap since for the first time an engine bearing has broken the 4 million rpm × mm speed parameter barrier [2]. It is expected that the new configuration could contribute towards increasing this number by additional 5%, thus even allow higher rotational speeds.

8.4. Numerical Analysis—Helical Duct Length

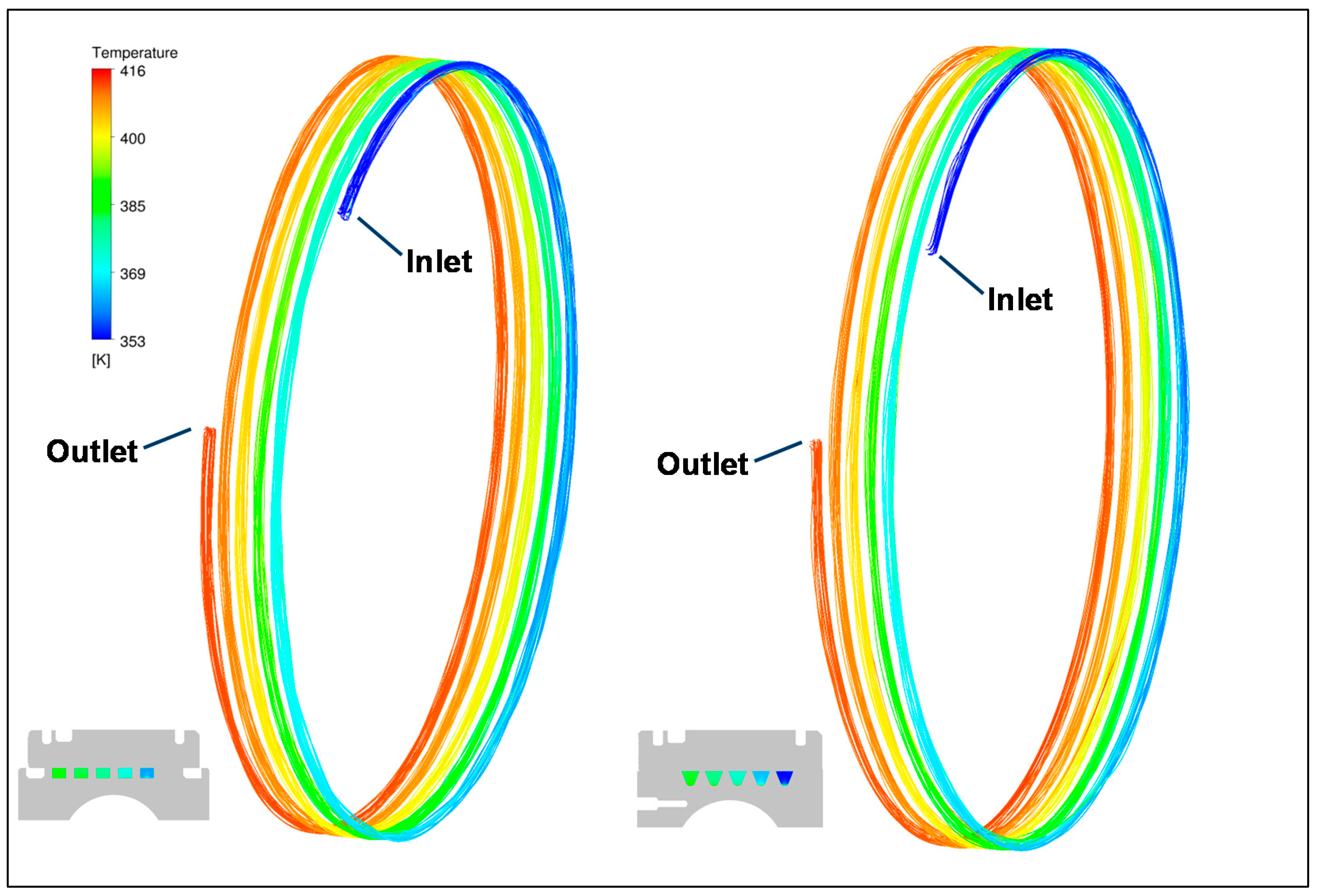
The total length of the helical duct is around 3.1 m and is stretched around the outer ring, forming approximately five threads. The rate of change in oil temperature diminishes from the first to the fifth convolution. Most of the heat pickup takes place already in the first three threads. Figure 25 shows this relation for the conventional helical duct with rectangular cross section (LHS) and with the V-cross section (RHS). Apparently, there is a very good potential in terms of optimization in terms of the helical duct length. This will be part of future work.

9. Summary and Outlook

A 167.5 mm PCD hybrid bearing equipped with a helical cut around its outer ring for active cooling purposes and also equipped with a squeeze film damper was successfully tested. The combination of four technologies (ceramics, duplex hardening of the races, outer ring cooling, and combined squeeze film damping and outer ring cooling) has led to a significant achievement that was reported in the international press in 2015. For the first time an engine bearing had broken the 4 million speed parameter barrier with 3 million being the threshold. The physics behind the outer ring cooling were investigated experimentally and a numerical and analytical evaluation followed. It has been assumed that the physical model is a combination between a heat exchanger and a finned body. Correlations for the pressure drop, heat exchange, and efficiency were created and have been compared with correlations from other authors. Up to a 50% reduction in lubricant flow and 25% reduction in heat generation were achieved. The current outer ring cooling duct geometry (rectangular cross-section) can be further improved so even higher efficiency can be achieved. A modified cross-section with V-type (tapered) fins was investigated numerically and has shown further efficiency improvement potential in the order of 16%.

The length of the current duct can further be optimized. Also, the helical duct could be placed only in that half of the outer ring which experiences the highest temperature impact, i.e., the side of the outer ring which is loaded. All these issues will be part of the oncoming future work.