Winglet Geometry Impact on DLR-F4 Aerodynamics and an Analysis of a Hyperbolic Winglet Concept
Abstract
:1. Introduction
2. Materials and Methods
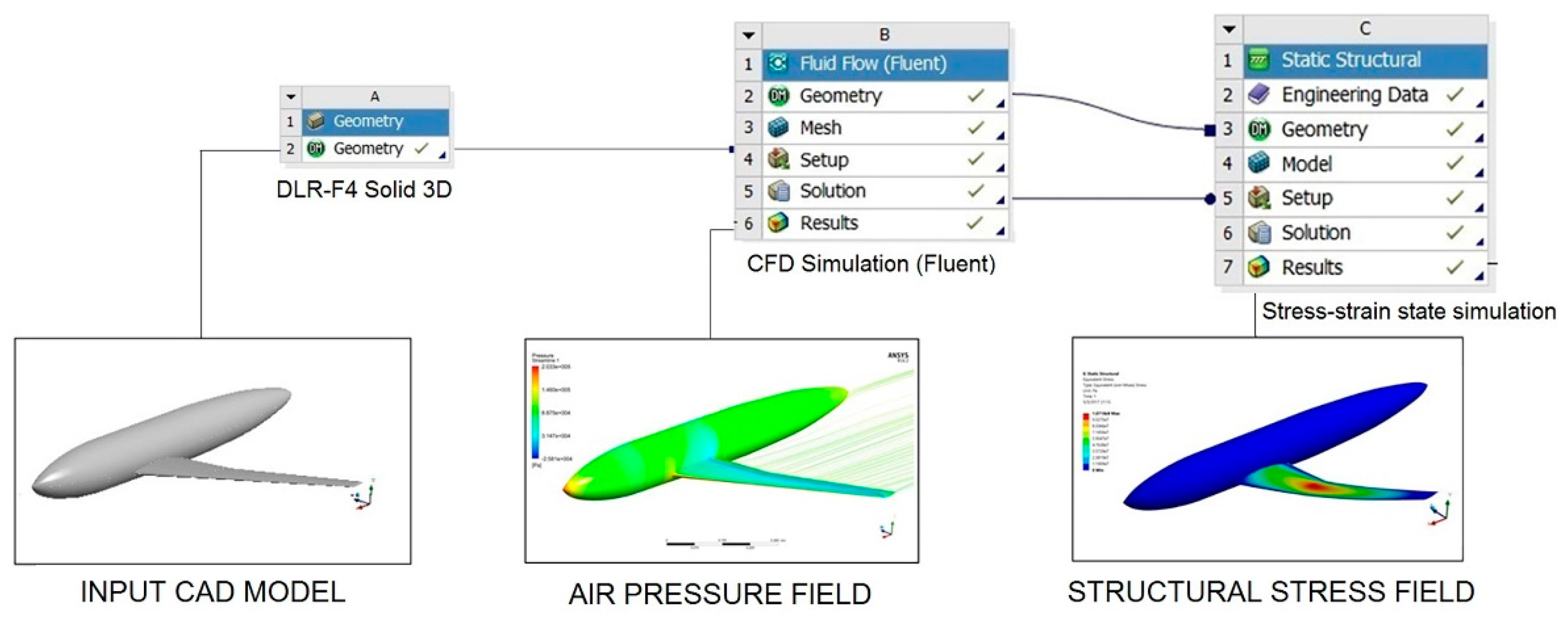
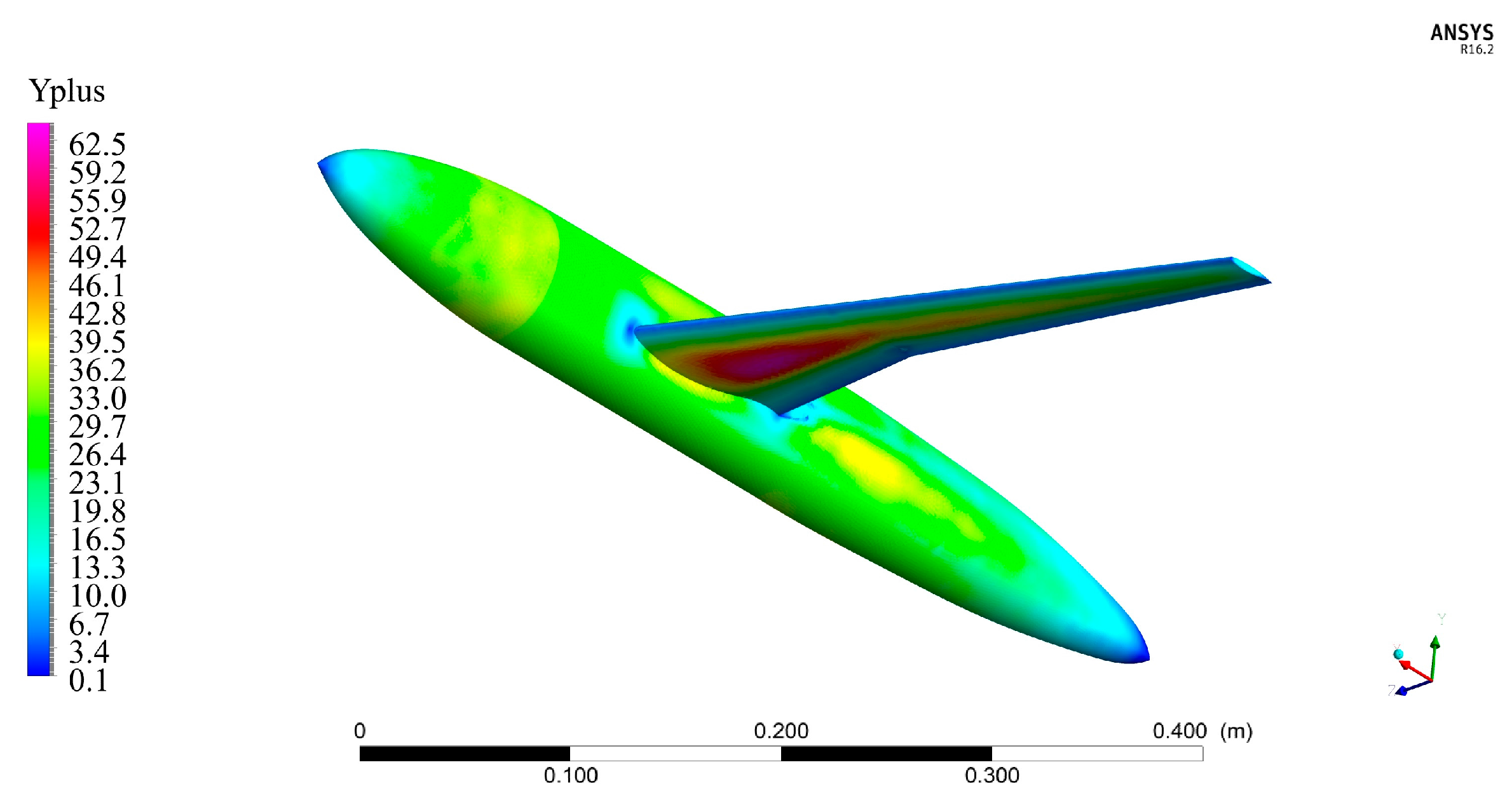
2.1. Methodology and Tools for CFD and Structural Stress Simulation
Governing Equations
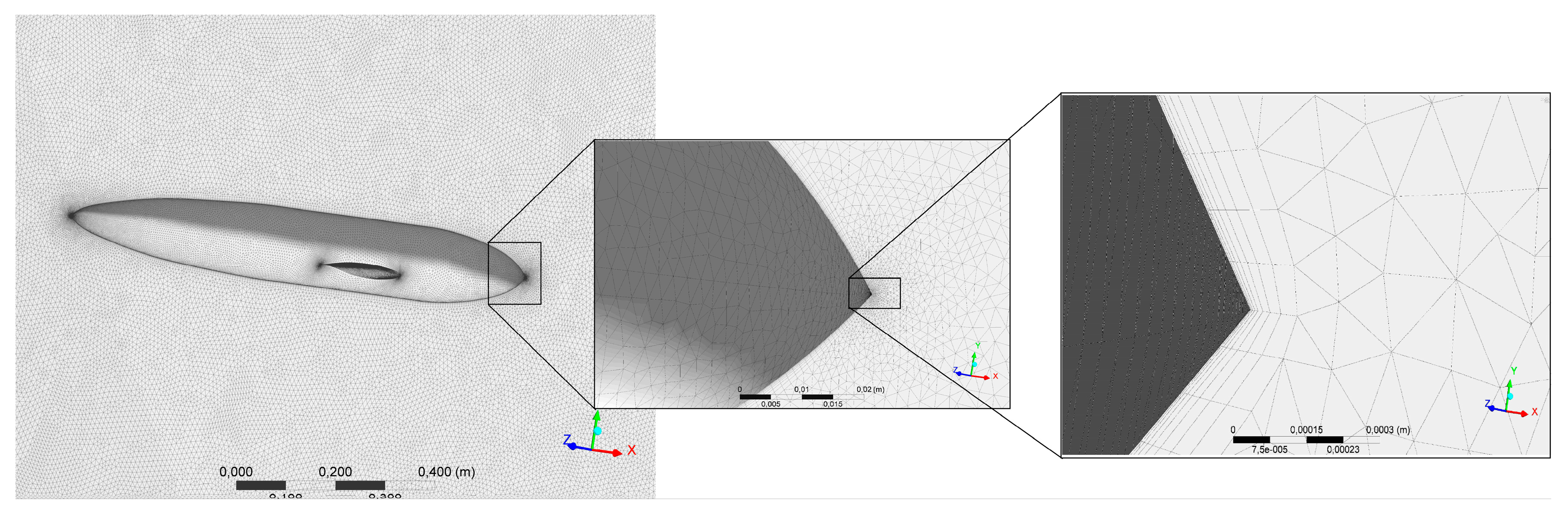
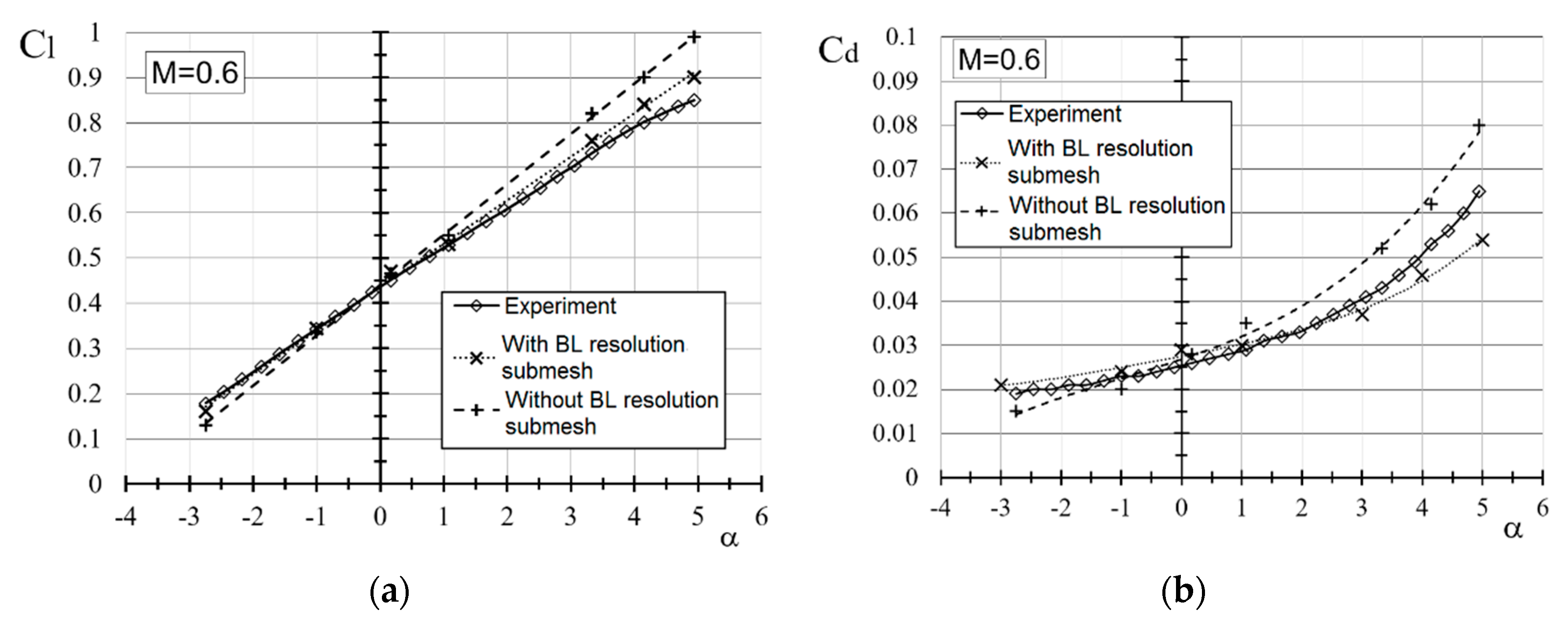
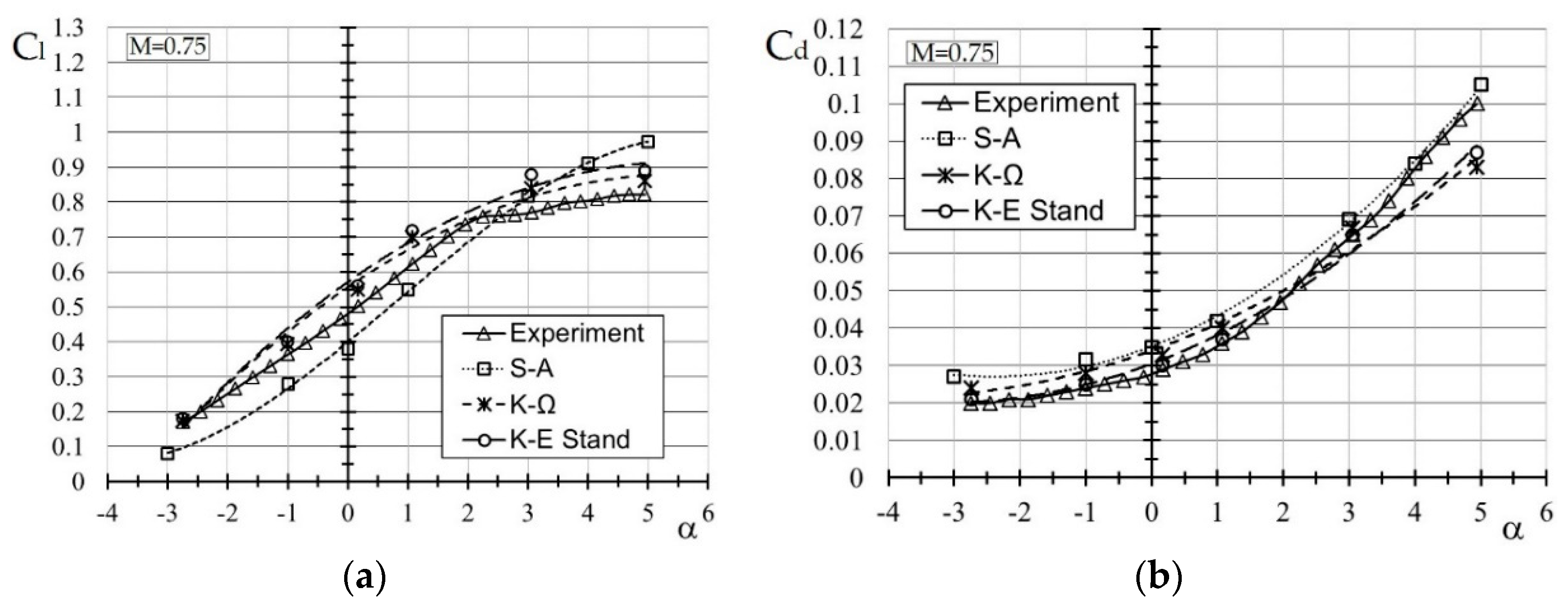
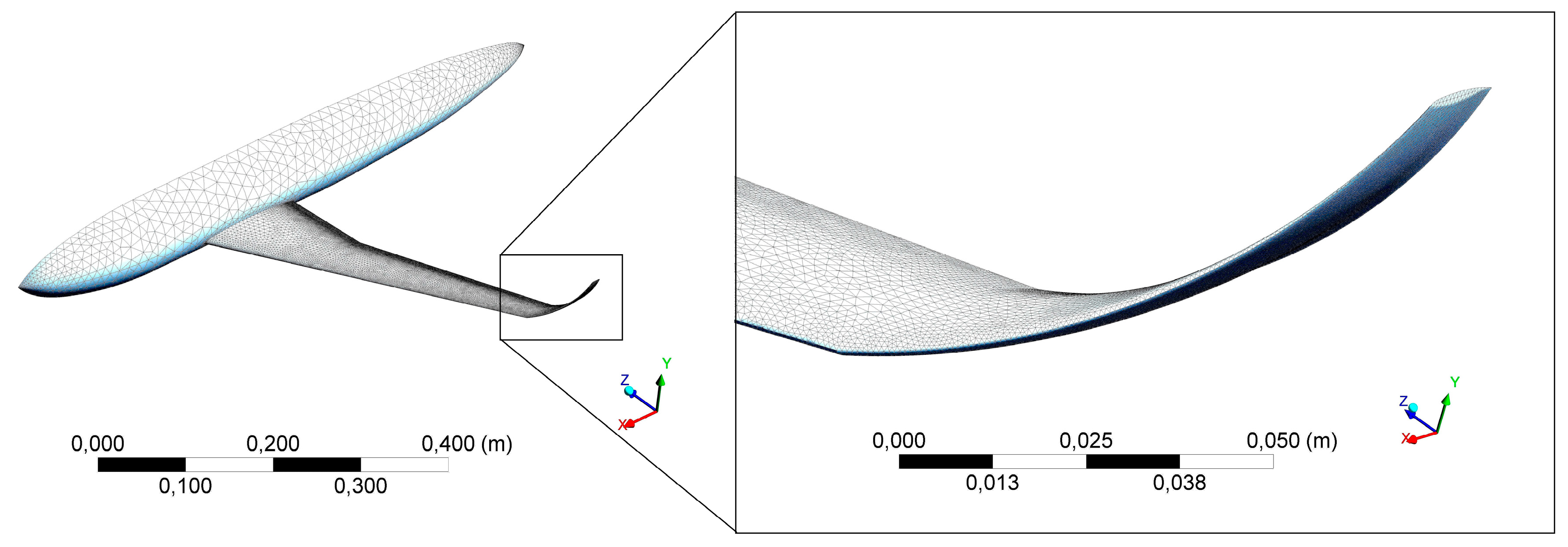
2.2. General Description of DLR-F4 Simulated Model and Mesh Convergence Study
2.3. Design Space Exploration for Different Wingtip Device Geometries
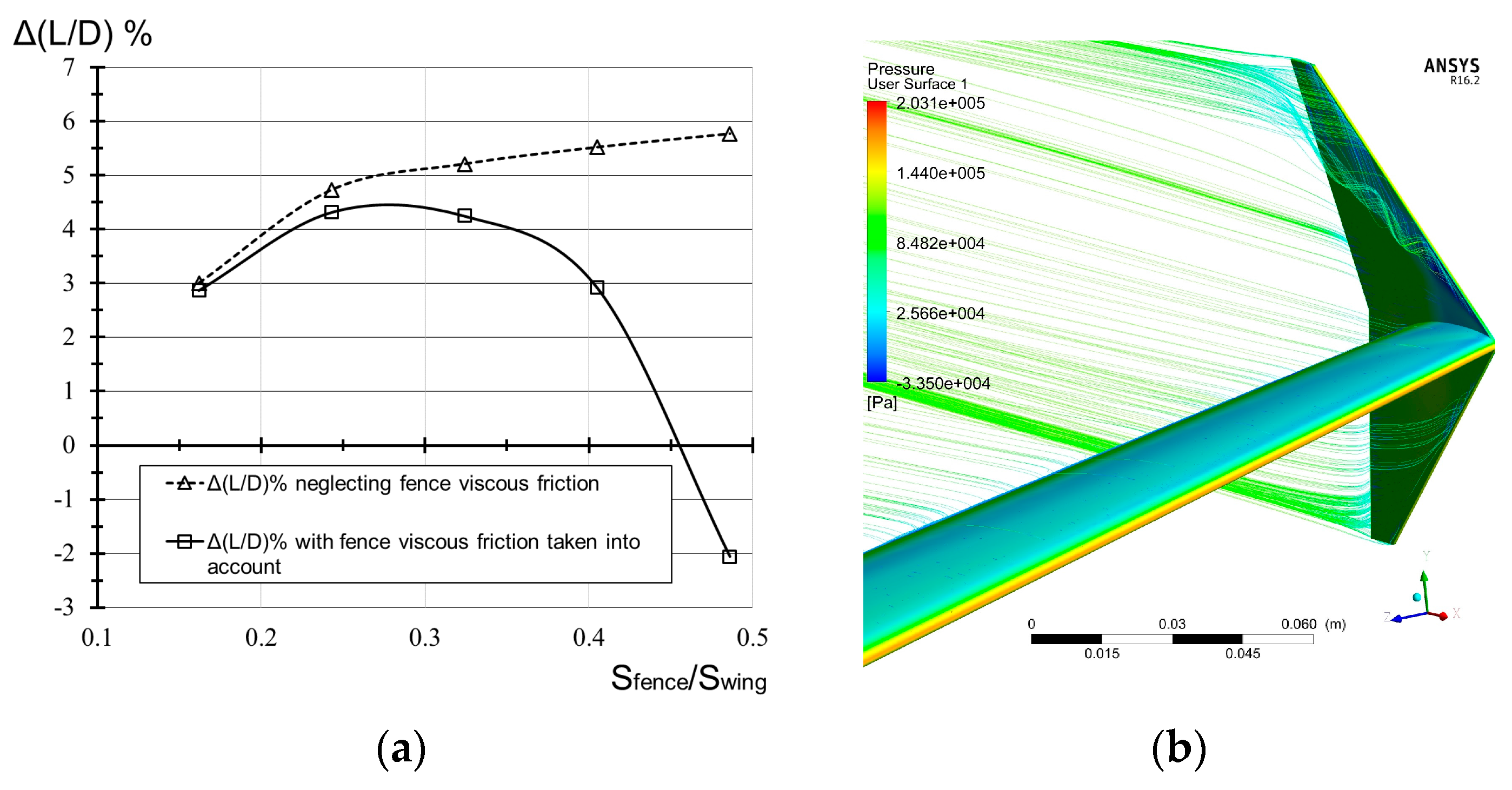
2.3.1. Wingtip Fence Design Space
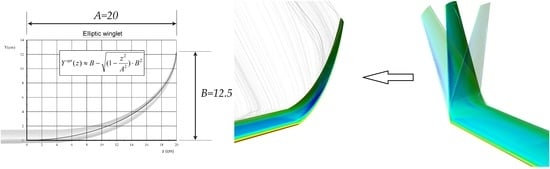
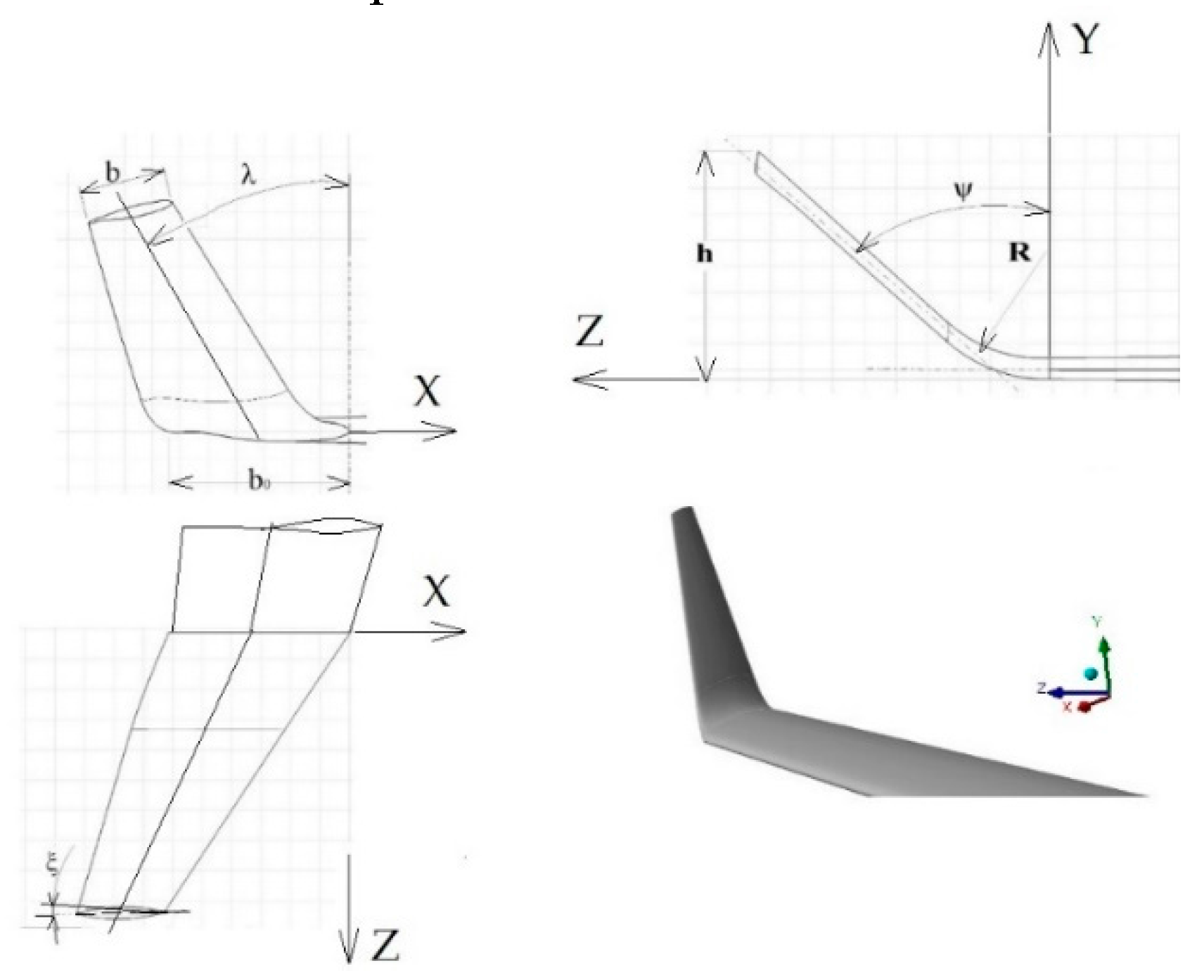
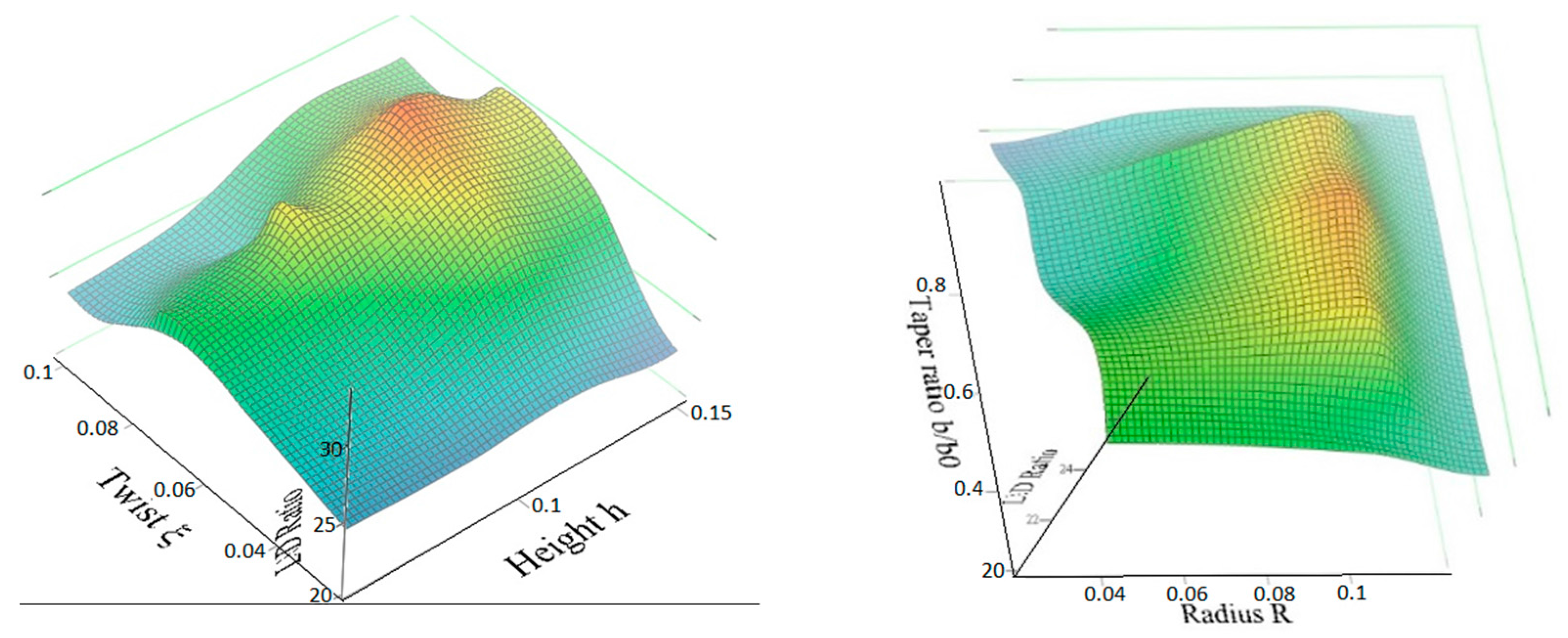
2.3.2. Winglet Design Space
2.3.3. Mathematical Modeling of the Winglet Local Flow Field
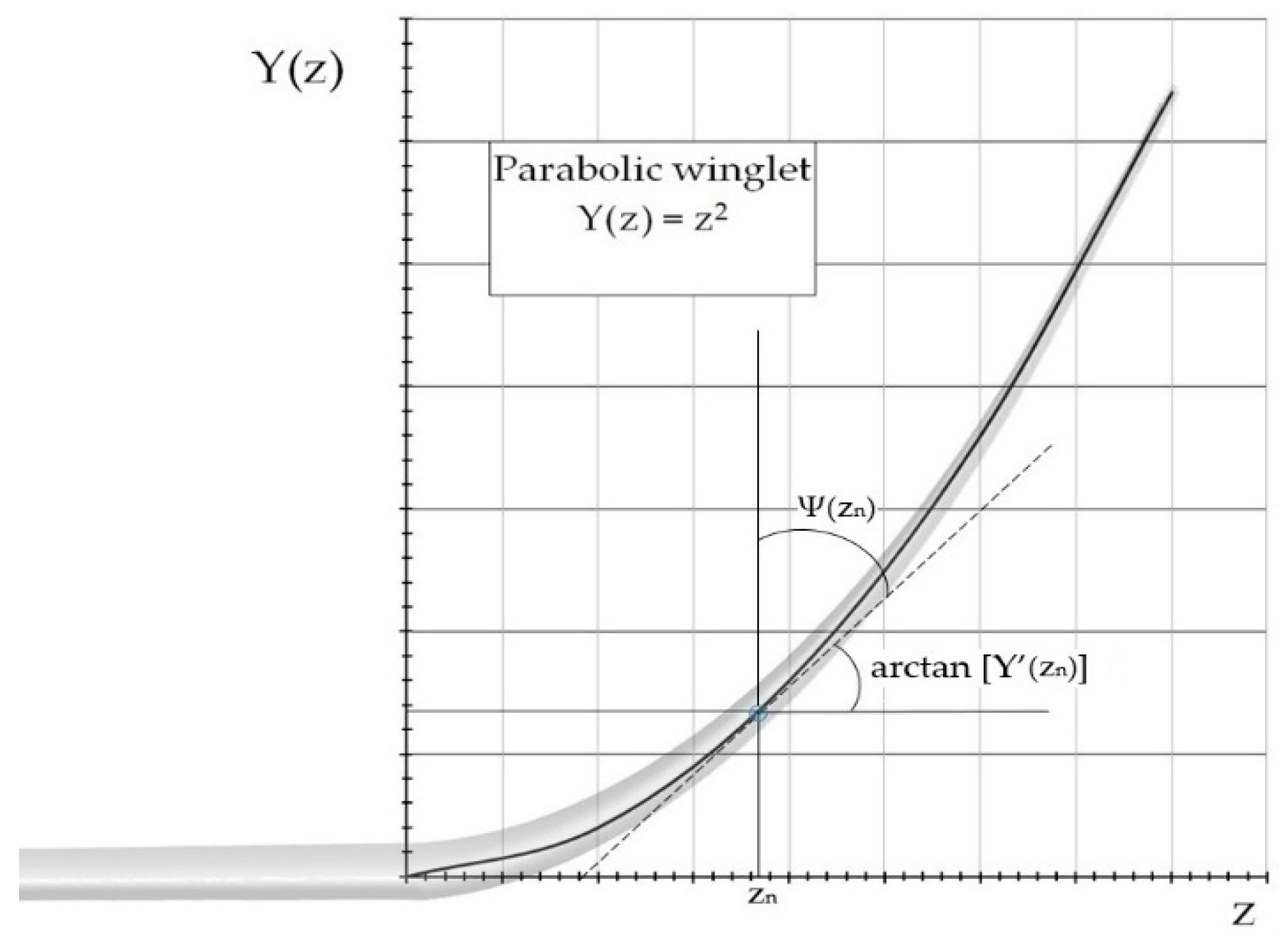
- : the winglet twist, a function of z coordinate (changes spanwise): means no twist at the winglet root. By convention, an outward twist at some zn coordinate, which leads to an increased local , is considered positive: .
- : Cant coefficient accounting for the winglet angle of attack sensitivity to changing the general angle of attack of the model (or the wing) , which is linked to the cant ψ as follows: omitting both and (definition below), can be found from (1) and the assumption that increasing the angle of attack of a wing equipped with a vertical winglet (, see Figure 9) does not increase the angle of attack of the winglet itself (as a vertical winglet would be rotating over z axis in its own plane, experiencing a greater slip instead). From (1): . While for a horizontal winglet (, the winglet angle of attack is directly equal to the wing angle of attack (a horizontal winglet is just an extension of the wing itself), from (1) this means . Solving the system of equations:
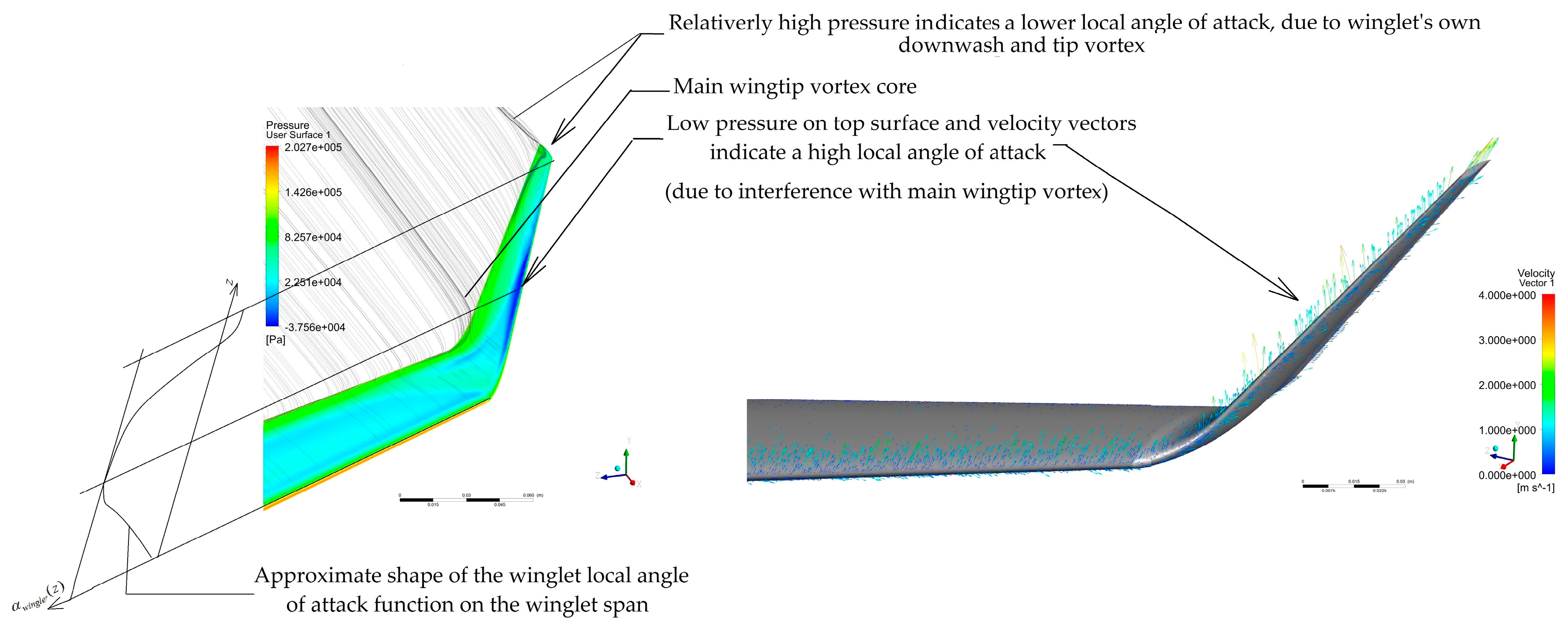
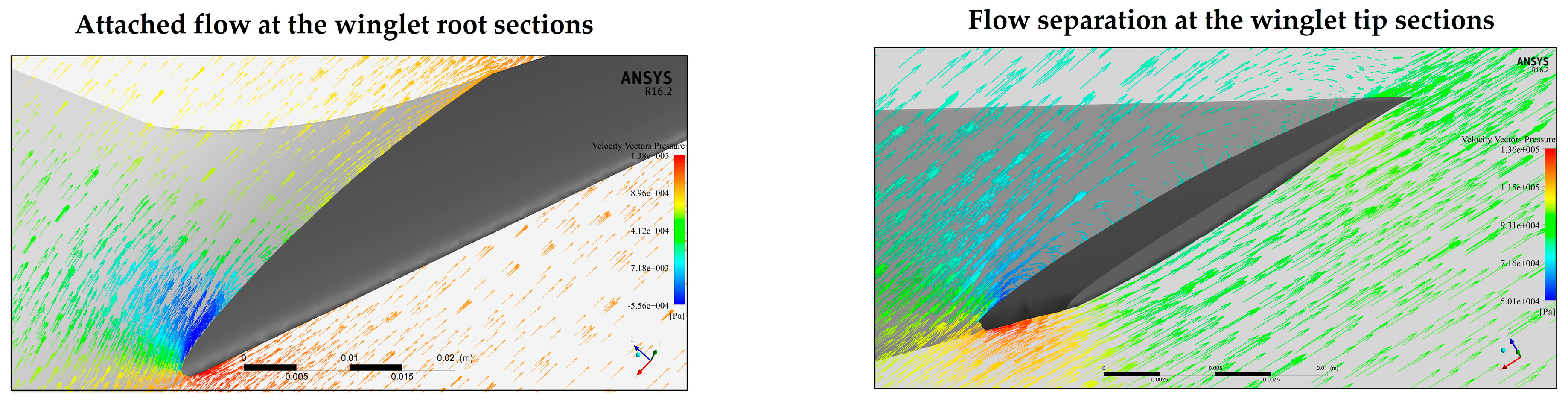
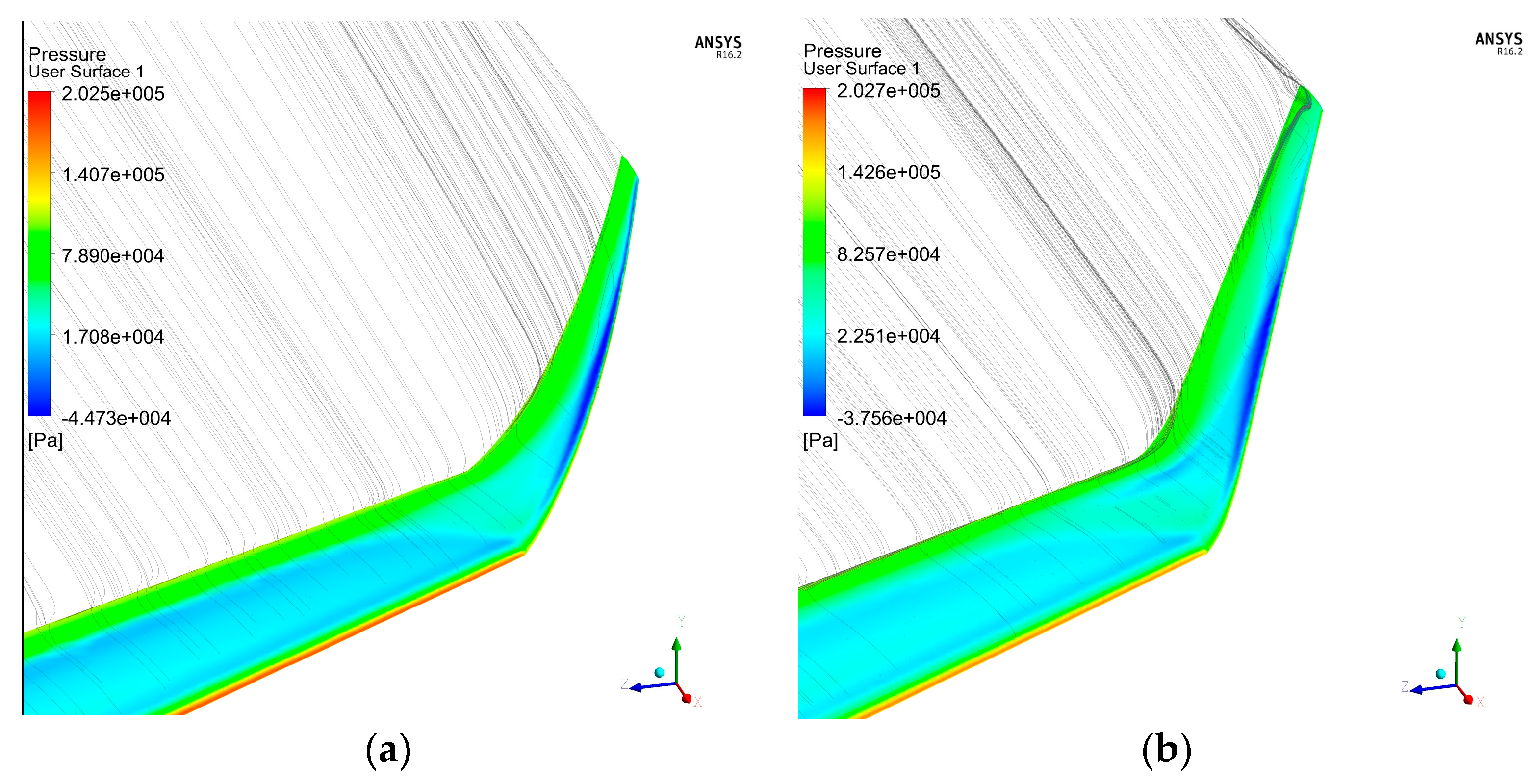
- accounts for three-dimensional flow field near the winglet, involving a strong interference with the main wingtip vortex, which tends to increase local at the winglet root sections (this can be clearly seen in Figure 11, where a substantially lower pressure on top winglet surface near the leading edge close to the wing junction). On the other hand, the winglet’s own ‘downwash’ and its smaller own tip vortex, lead to a slight decrease in local at the winglet tip sections. The interaction between the tip vortex and angle of attack has been studied in [37,38], and a method for predicting local root and tip variations, using local induced velocities is given in [39]. For a fixed winglet geometry at a fixed , is a function of the location on the winglet span (z coordinate):
3. Results
3.1. CFD Simulation Results of the Winglet-Equipped DLR-F4 Model
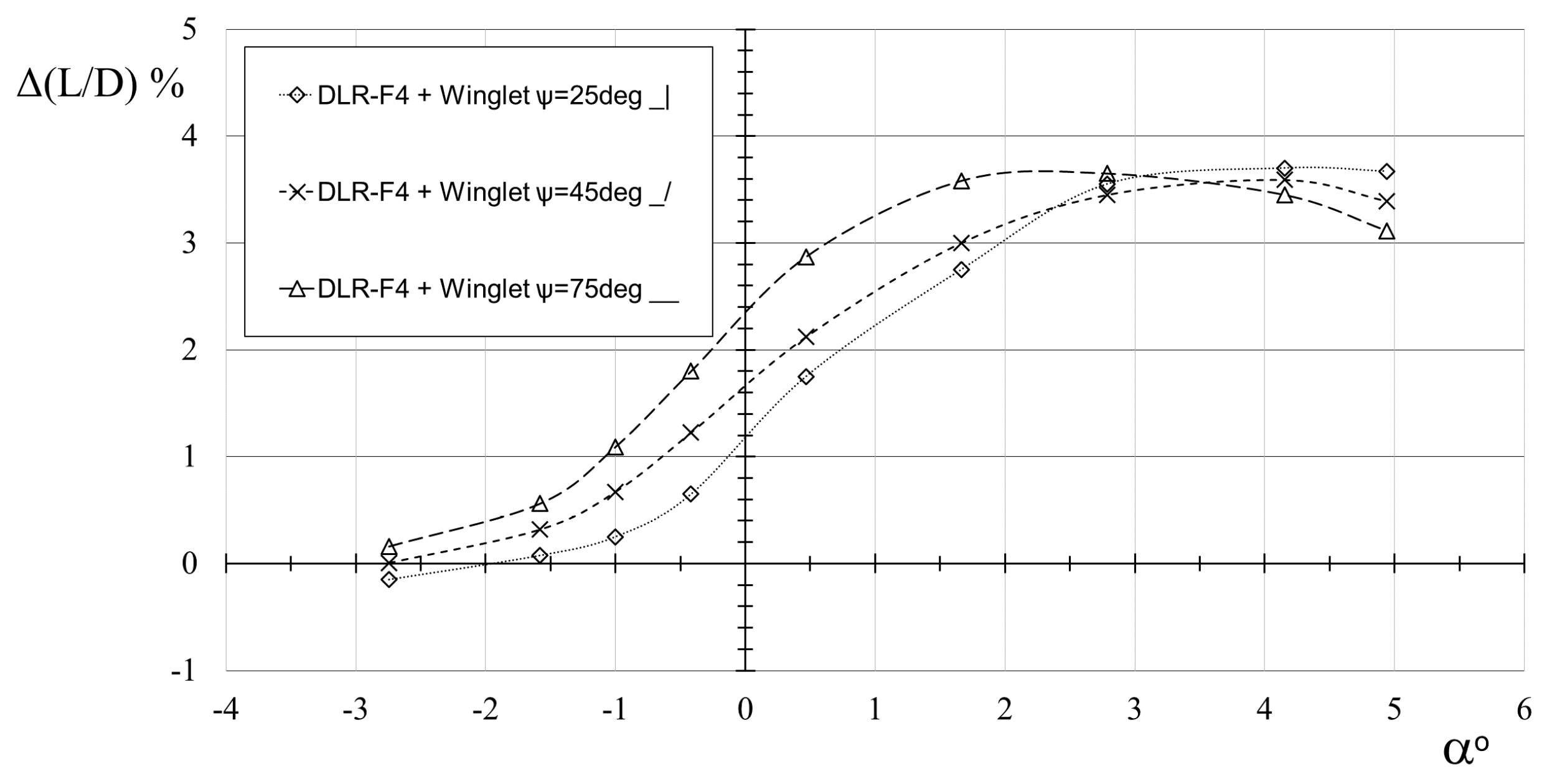
3.1.1. Impact of the Winglet Cant Angle on DLR-F4 Lift-to-Drag Ratio
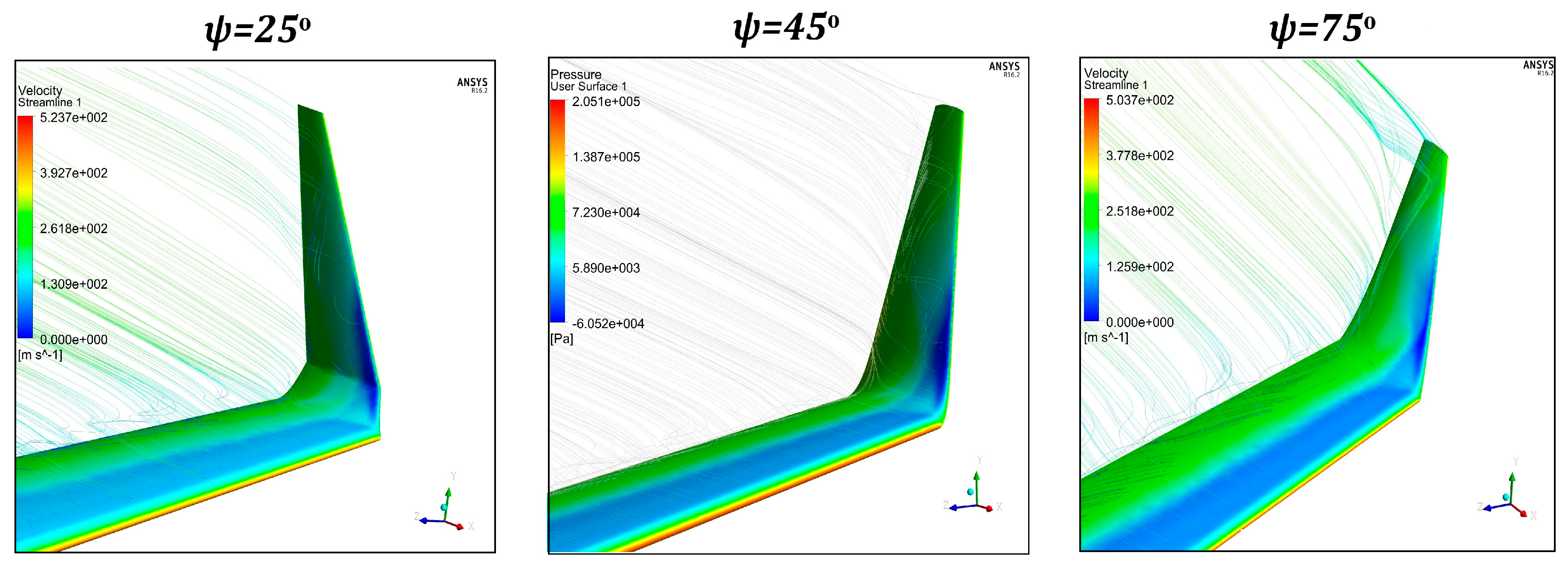
3.1.2. Winglet Cant Optimization for a Sustainable Efficiency along α Range Using a Curved Span
3.1.3. Optimal Cant Function
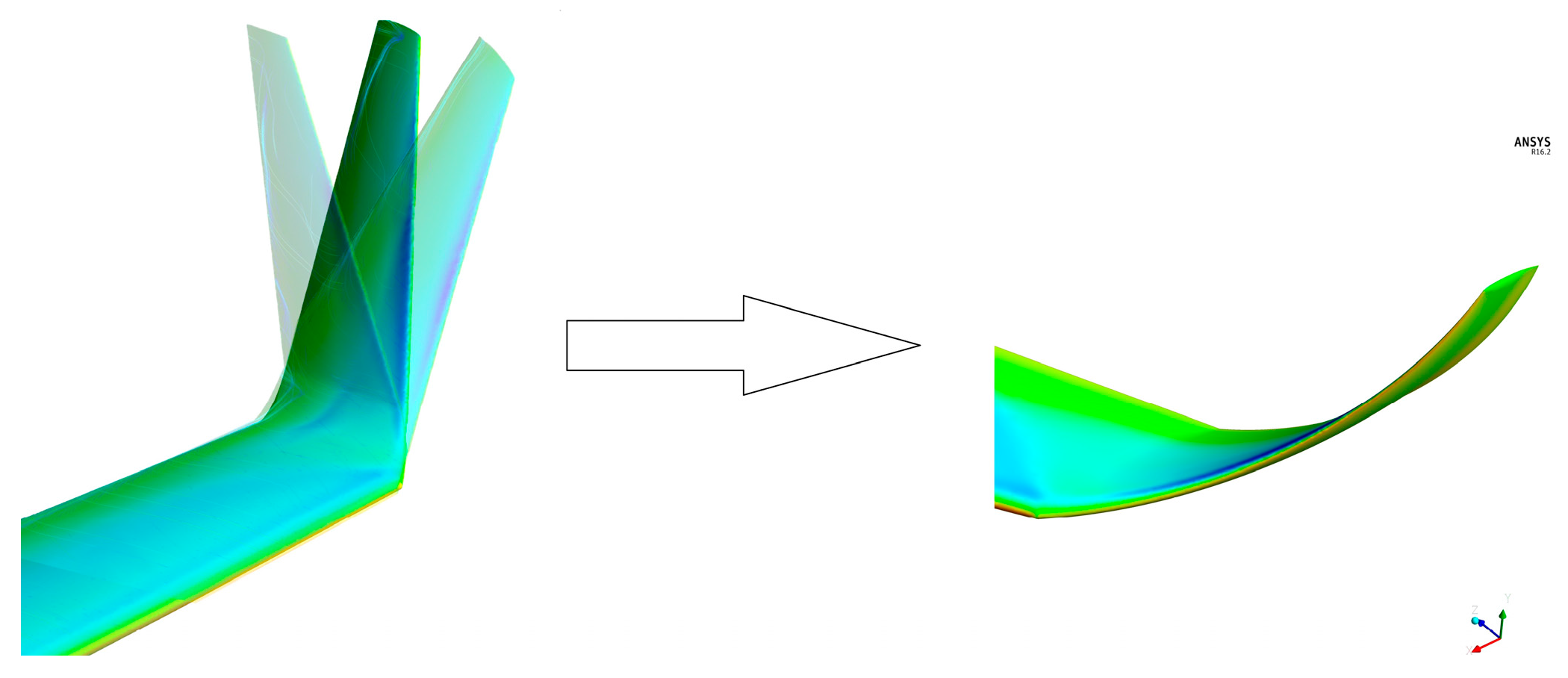
- Ensuring the highest possible, yet under critical, local angle of attack of the winglet: for a curved winglet design, this is interpreted as the highest cant possible at root, in order to best harness the main wingtip vortex energy (see Figure 11) and use it to increase local . Also, in order to get the highest possible local increase, should the wing angle of attack increases (see Section 2.3.2, Equation (2)). This highest cant is achieved through a tangent connection to the wing at zroot = 0: . Substituting in (6):
- Ensuring the smallest possible pressure difference between upper and lower surfaces at the winglet tip, thus keeping the winglet tip vortex and its own downwash at the lowest possible intensity. This can be achieved by making the tip vertical (with zero cant), in order to prevent its angle of attack from increasing (and the pressure difference from rising), should the general angle of attack increases: (see Section 2.3.2). Hence , Substituting in (6):(10) means an infinite slope (vertical) tangent line to Y(z)optim. graph at the at the winglet tip.
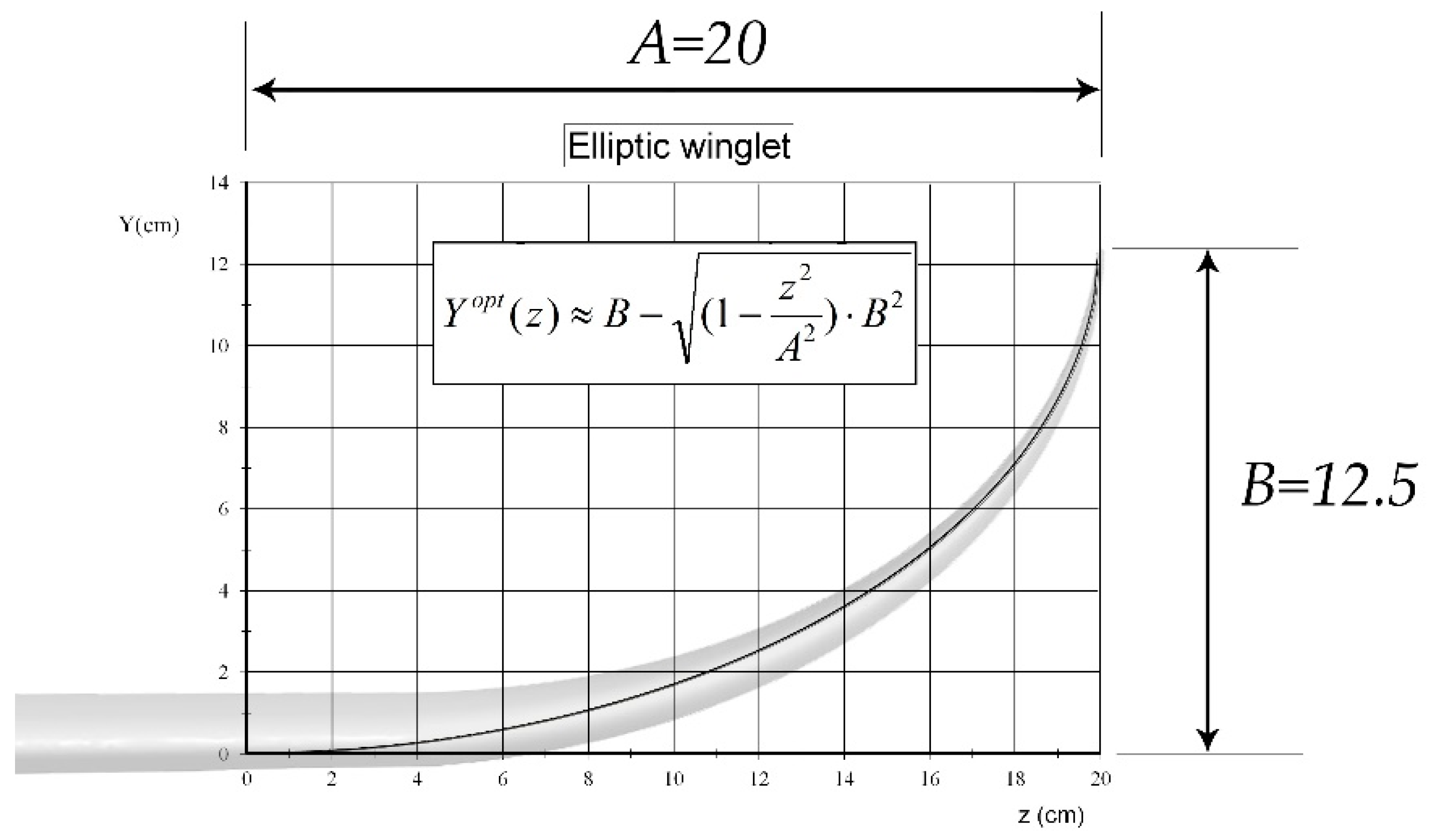
- Ensuring the most advantageous transition from to . From (8), this requires a well-known flow field dependency ; defining it is beyond the scope of this paper, see [37,39]. We can only notice that itself depends on the winglet geometry, meaning that the optimization process is iterative, starting from an arbitrary second order parametrization function, defining for it (either mathematically or experimentally), identifying an improvement direction, and then gradually adapting the parametrization function up until the point where L/D ratio does not grow anymore. It is well-known, however, that optimal spanwise circulation distribution of a lifting surface with the minimum induced drag is elliptical. Therefore, we may assume that a similar elliptic cant parametrization which easily complies with (9) and (10), would result in the highest L/D ratio of the winglet.
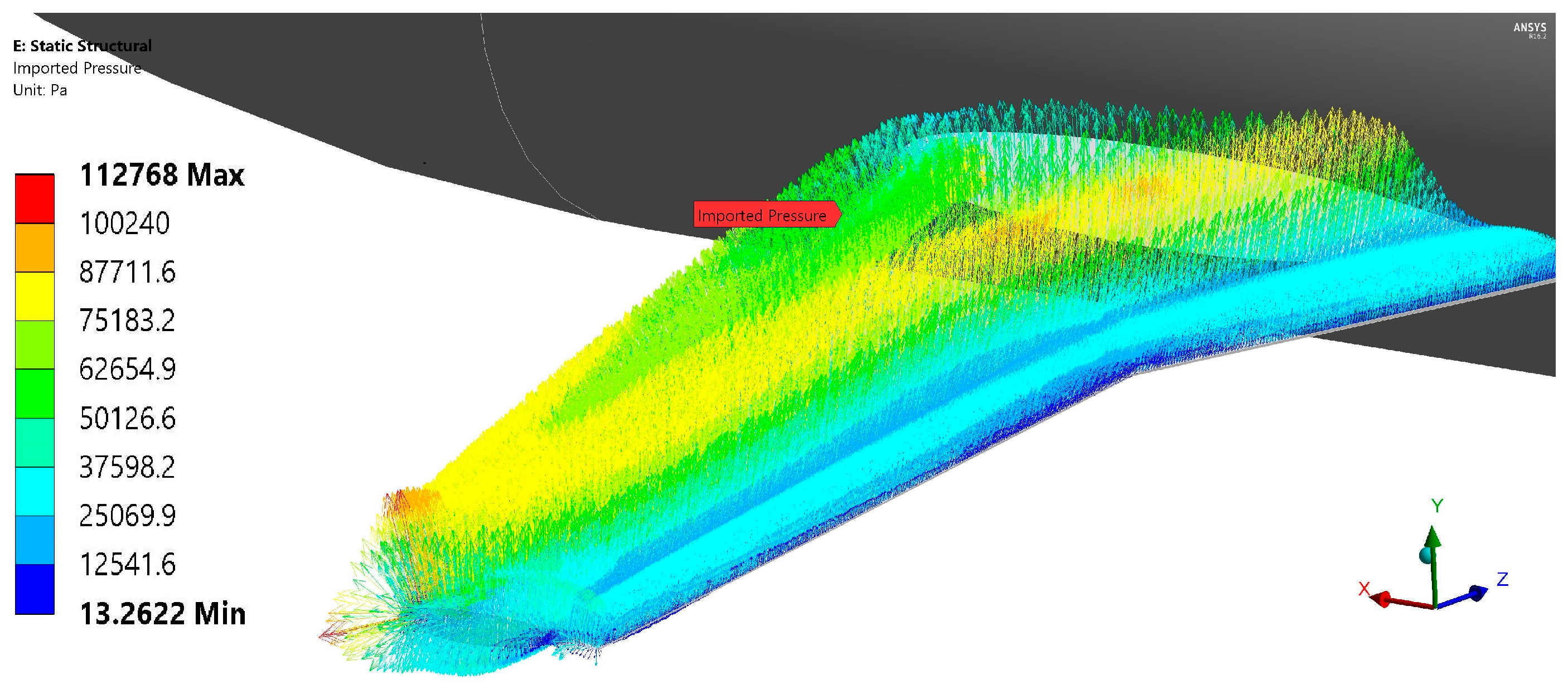
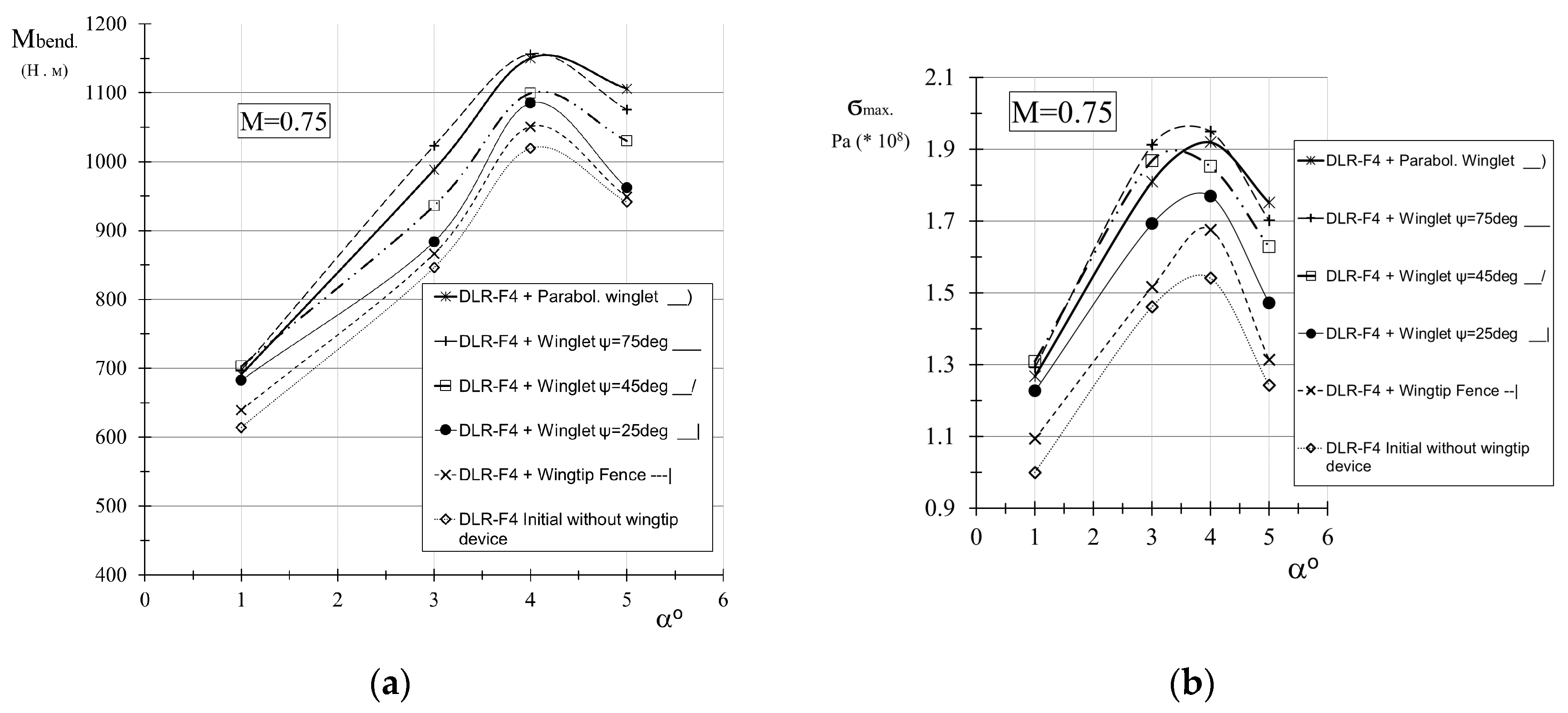
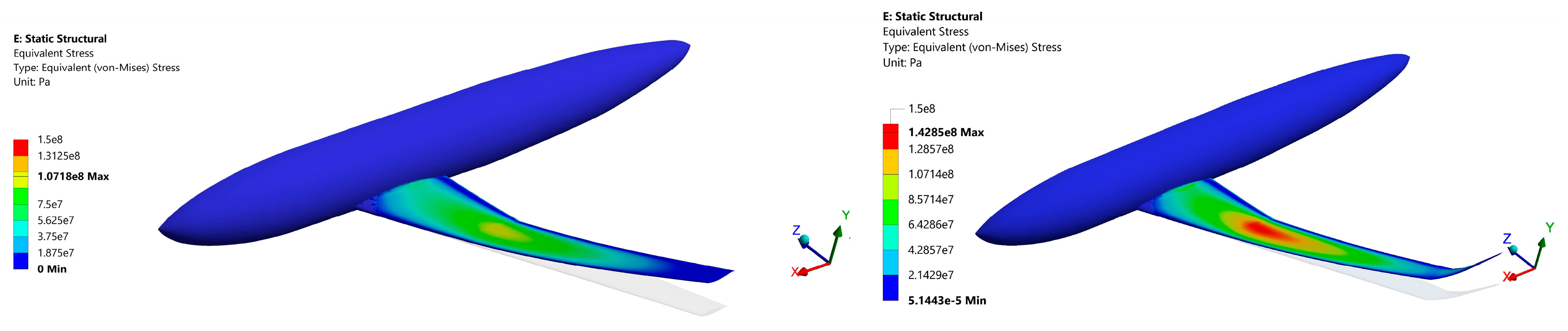
3.2. Stress-Strain State Simulation Results of Winglet-Equipped DLR-F4
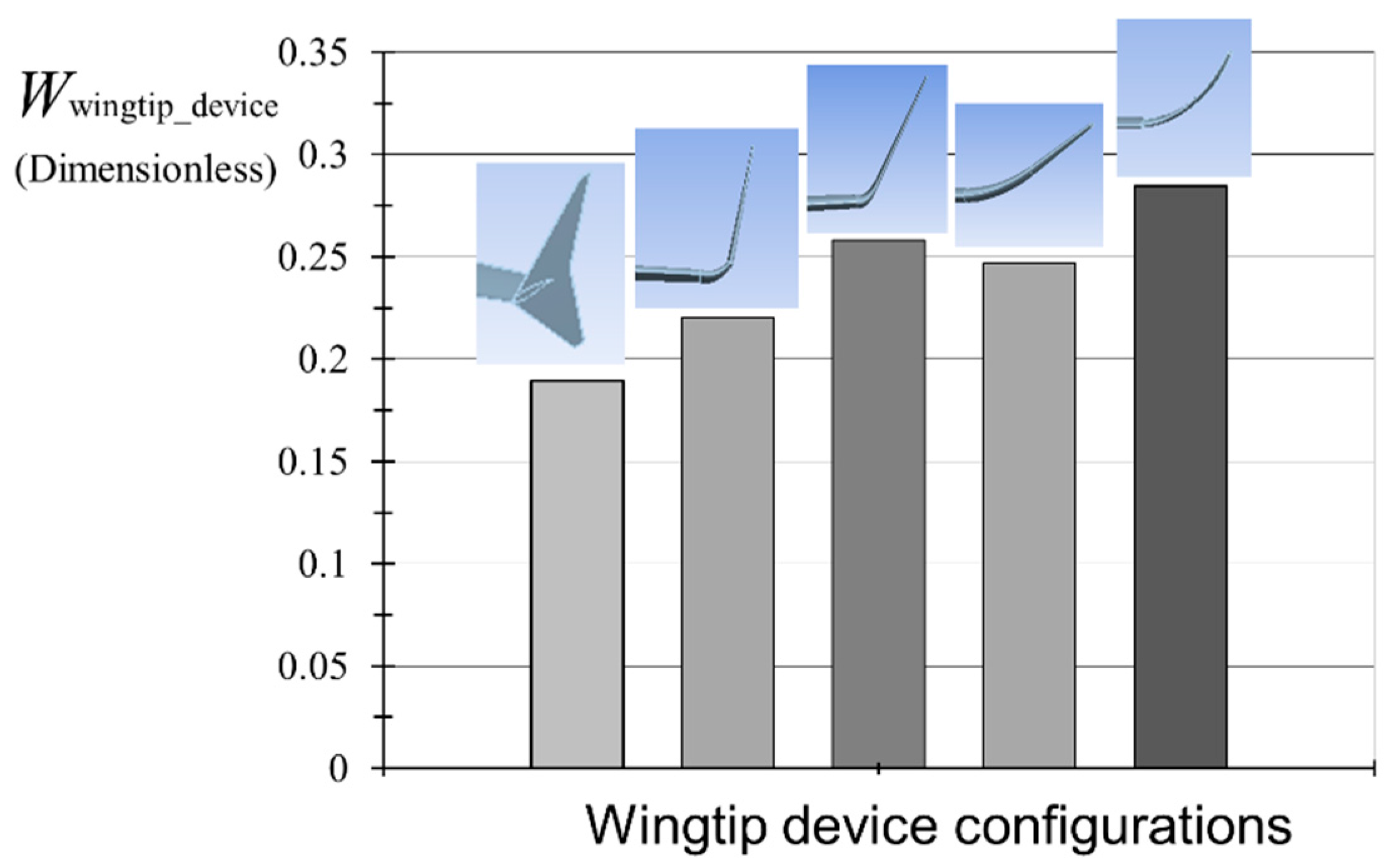
3.3. Developing a Multidisciplinary Criterion for Wingtip Device Aerodyamic Efficiency Assessment Regarding Structural Weight Penalty
4. Discussion of Results and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Glossary
| Re | Reynolds number |
| M | Mach number |
| Density | |
| Velocity vector | |
| P | Static pressure |
| Stress tensor | |
| E | Total energy |
| Energy transfer due to conduction | |
| Energy transfer due to species diffusion | |
| Energy transfer due to viscous dissipation | |
| Effective conductivity ( where is the turbulent thermal conductivity, defined according to the turbulence model being used) | |
| T | Temperature |
| Sensible enthalpy for species j | |
| Diffusion flux of species j | |
| Effective stress tensor | |
| Absolute pressure | |
| R | Universal gas constant |
| Molecular weight | |
| Dynamic viscosity | |
| Reference molecular viscosity | |
| Reference temperature, usually 273.0 K | |
| Sutherland constant, a characteristic of the gas | |
| n | Temperature exponent, usually set to 1.5 for most gases |
| k | Turbulence Kinetic energy |
| u | Velocity magnitude |
| Effective diffusivity of k | |
| Generation of turbulence kinetic energy due to mean velocity gradients | |
| Dissipation of k due to turbulence | |
| ϖ | Specific dissipation rate |
| Effective diffusivity of ϖ | |
| Generation of ϖ due to mean velocity gradients | |
| Dissipation of ϖ due to turbulence | |
| DLR-F4 geometric angle of attack (AOA) | |
| L/D | Lift-to-Drag ratio, Cl/Cd |
| Sfence | Wingtip fence plan area |
| Swing | DLR-F4 wing plan area, including its ventral non-wetted part |
| [Sfence/Swing]optim | Optimal wingtip fence relative area, yielding maximum L/D ratio of (LR-F4 + fence) system |
| λ | Winglet sweep angle |
| ψ | Winglet cant angle |
| ξ | Winglet twist angle |
| h | Winglet height |
| R | Winglet fillet radius |
| b/b0 | Winglet taper ratio |
| b0 | Winglet root chord length |
| b | Winglet tip chord length |
| DLR-F4 wing geometric AOA, equal to | |
| Winglet effective AOA, including its geometric angle of attack and | |
| Winglet AOA increment due to three-dimensional flow field over the winglet span | |
| z | Wing-spanwise coordinate |
| zroot | z-coordinate at the winglet root |
| ztip | z-coordinate at the winglet tip |
| Winglet twist function on z coordinate | |
| Winglet cant coefficient, equal to | |
| Local AOA at the winglet root | |
| Local AOA at the winglet tip | |
| Y(z) | Winglet centerline front projection parametrization function |
| Y(z)optim. | Winglet optimal parametrization function, yielding maximum L/D ratio of (DLR-F4 + winglet) system |
| Winglet cant function, depicting local cant angle at each z coordinate spanwise | |
| Winglet optimal cant function, depicting local ψ in the case of an optimal winglet shape, parametrized through Y(z)optim. | |
| A | Semi-major axis of an elliptic winglet span curve |
| B | Semi-minor axis of an elliptic winglet span curve |
| Dimensionless wingtip device overall efficiency criterion | |
| DLR-F4 L/D ratio growth at cruise conditions, due to the wingtip device | |
| Maximum structural stress growth on DLR-F4 wing due to wingtip device | |
| Required thrust for level flight | |
| Aircraft take-off weight |
References
- Whitcomb, R.T. A Design Approach and Selected Wind-Tunnel Results at High Subsonic Speeds for Wing-Tip Mounted Winglets; NASA TN D-8260; NASA: Washington, DC, USA, 1976; pp. 1–33. [Google Scholar]
- Flechner, S.G.; Jacobs, P.F.; Whitcomb, R.T. A High Subsonic Speed Wind-Tunnel Investigation of Winglets on a Representative Second-Generation Jet Transport Wing; NASA TN D-8264; NASA: Washington, DC, USA, 1976; pp. 1–71. [Google Scholar]
- Keizo, T.; Keita, H. Multidisciplinary Design Exploration for a Winglet. AIAA J. Aircr. 2008, 45. [Google Scholar] [CrossRef]
- Himisch, J. Winglet Shape and Load Optimization with a numerically supported Lifting Line Method. In Proceedings of the 12th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Victoria, BC, Canada, 10–12 September 2008. [Google Scholar] [CrossRef]
- Ning, A.S.; Kroo, I. Multidisciplinary Considerations in the Design of Wings and Wing Tip Devices. J. Aircr. 2010, 47. [Google Scholar] [CrossRef]
- Streit, T.; Himisch, J.; Heinrich, R.; Nagel, B.; Horstmann, K.H.; Liersch, C. Design of a Retrofit Winglet for a Transport Aircraft with Assessment of Cruise and Ultimate Structural Loads. In New Results in Numerical and Experimental Fluid Mechanics VI; Springer: Berlin/Heidelberg, Germany, 2006; pp. 61–69. [Google Scholar]
- Mann, A.; Elsholz, E. The M-DAW Project Investigations in Novel Wing Tip Device Design. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar] [CrossRef]
- Hesham, S.M.; Essam, E.K.; Osama, E.A.; Gamal, E. Effect of Raked Winglet on Aircraft Performance. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Hesham, S.M.; Essam, E.K.; Osama, E.A.; Gamal, M.E. Aircraft-Blended Winglet Performance Analyses. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Pfeifferm, N.J. Numerical Winglet Optimization. In Proceedings of the 42nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 5–8 January 2004. [Google Scholar] [CrossRef]
- Mills, J.; Ajaj, R. Flight Dynamics and Control Using Folding Wingtips: An Experimental Study. Aerospace 2017, 14, 19. [Google Scholar] [CrossRef]
- Gomes, A.A.; Falcao, L. Study of an Articulated Winglet Mechanism. In Proceedings of the 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Boston, MA, USA, 8–11 April 2013. [Google Scholar] [CrossRef]
- Afonso, F.; Vale, J.; Lau, F.; Suleman, A. Multidisciplinary Performance Based Optimization of Morphing Aircraft. In Proceedings of the AIAA SciTech 22nd AIAA/ASME/AHS Adaptive Structures Conference, National Harbor, ML, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Hornschemeyer, R.; Rixen, C.; Kauertz, S.; Neuwerth, G.; Henke, R. Active Manipulation of a Rectangular Wing Vortex Wake with Oscillating Ailerons and Winglet-Integrated Rudders. In New Results in Numerical and Experimental Fluid Mechanics VI; Springer: Berlin/Heidelberg, Germany, 2006; pp. 44–51. [Google Scholar]
- Allen, A.; Breitsamter, C. Transport Aircraft Wake Influenced by a Large Winglet and Winglet Flaps. J. Aircr. 2008, 45. [Google Scholar] [CrossRef]
- Tamarack Aerospace Group. Active Winglets: FAA Certified Disruptive Technology. Available online: http://tamarackaero.com/technology (accessed on 20 November 2017).
- Guha, T.K.; Kumar, R. Characteristics of a wingtip vortex from an oscillating winglet. Exp. Fluids 2017, 58. [Google Scholar] [CrossRef]
- Guha, T.K.; Kumar, R. Active Control of Wingtip Vortices using Piezoelectric Actuated Winglets. In Proceedings of the AIAA SciTech, 54th AIAA Aerospace Science Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Popov, S.A.; Gueraiche, D.; Kuznetsov, A.V. Experimental study of the aerodynamics of a wing with various configurations of wingtip triangular extension. Russ. Aeronaut. 2016, 59, 1934–7901. [Google Scholar] [CrossRef]
- La Roche, U.; La Roche, H.L. Induced Drag Reduction Using Multiple Winglets, Looking beyond the Prandtl-Munk Linear Model. In Proceedings of the 2nd AIAA Flow Control Conference, Portland, OR, USA, 28 June–1 July 2004. [Google Scholar] [CrossRef]
- Krebs, T.; Bramesfeld, G. An Optimization Approach to Split-Winglet Design for Sailplanes. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. [Google Scholar] [CrossRef]
- Aviation Partners, Inc. Aircraft Winglets: Types of Blended Winglets. Available online: http://www.aviationpartners.com/aircraft-winglets/types-blended-winglets/#blended (accessed on 20 November 2017).
- Airbus Group. A 350 XWB MS1 Winglet Close Up: Shaping Efficiency with the A350 XWB. Available online: http://www.airbus.com/newsroom/search.image.html?q=Winglet&lang=en#media-image-image-all-20 (accessed on 20 November 2017).
- Airbus Group. Winglets: A Tip-Top Solution for More Efficient Aircraft. Available online: http://www.airbus.com/newsroom/news/en/2017/02/winglets-a-tip-top-solution-for-more-efficient-aircraft.html (accessed on 20 November 2017).
- Han, X.; Zingg, D.W. An Evolutionary Geometry Parametrization for Aerodynamic Shape Optimization. In Proceedings of the 20th AIAA Computational Fluid Dynamics Conference, Honolulu, HI, USA, 27–30 June 2011. [Google Scholar] [CrossRef]
- Zhang, M.; Nangia, R.; Rizzi, A. Design and Shape Optimization of Morphing Winglet for Regional Jetliner. In Proceedings of the 2013 Aviation Technology, Integration, and Operations Conference, Los Angeles, CA, USA, 12–14 August 2013. [Google Scholar] [CrossRef]
- Luciano, D.; Antonio, D.; Giovanni, M.; Rauno, C. An Invariant Formulation for the Minimum Induced Drag Conditions of Non-planar Wing Systems. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, ML, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- ANSYS Fluent Documentation: ANSYS Fluent Theory Guide. Available online: www.ansys.com (accessed on 20 November 2017).
- Anderson, J.; Hughes, W. Fundamentals of Aerodynamics, 5th ed.; McGraw-Hill Series in Aeronautical and Aerospace Engineering; McGraw-Hill: New York, NY, USA, 2011; ISBN 10: 0073398101. [Google Scholar]
- Vassberg, J.; Lee-Rausch, B. Drag Prediction Workshops IV and V. J. Aircr. 2014, 51. [Google Scholar] [CrossRef]
- Tinoco, E.N. Summary of Data from the Sixth AIAA CFD Drag Prediction Workshop: CRM Cases 2 to 5. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Wilox, D.C. Multiscale model for turbulent flows. AIAA J. 1988, 26, 1311–1320. [Google Scholar] [CrossRef]
- Redeker, G. DLR-F4 Wing Body Configuration/A Selection of Experimental Test Cases for the Validation of CFD Codes. In AGARD-AR-303; Advisory Group for Aerospace Research and Development: Neuilly-Sur-Seine, France, 1994; Volume II, pp. 1–24. [Google Scholar]
- McDonald, M.A. AGARD-AR-303; Advisory Group for Aerospace Research and Development: Neuilly-Sur-Seine, France, 1994; Volume 1B. [Google Scholar]
- Hemke, P.E. Drag of Wings with End Plates; NACA-TR-267; NASA: Washington, DC, USA, 1927; pp. 1–13. [Google Scholar]
- Donald, R.R. Wind Tunnel Investigation and Analysis of the Effects of end Plates on the Aerodynamic Characteristics of an Unswept Wing; NACA-TN-2440; NASA: Washington, DC, USA, 1951; pp. 1–56. [Google Scholar]
- May, D.H.; Vatistas, G.H. Tip Vortex Dependence with Angle of Attack. J. Aircr. 2006, 43. [Google Scholar] [CrossRef]
- Kianoosh, Y.; Reza, S. Three-dimensional suction flow control and suction jet length optimization of NACA 0012 wing. Meccanica 2015, 50, 1481–1494. [Google Scholar] [CrossRef]
- Guntur, S.; Sorensen, N. An evaluation of several methods of determining the local angle of attack on wind turbine blades. J. Phys. 2014. [Google Scholar] [CrossRef]
- Kushner, L.K.; Drain, B.A.; Schairer, E.T.; Heineck, J.T.; Bell, J.H. Model Deformation and Optical Angle of Attack Measurement System in the NASA Ames Unitary Pan Wind Tunnel. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar] [CrossRef]
- Boeing 787. Available online: http://www.boeing.com/commercial/787/ (accessed on 12 December 2017).
- Zotov, A.A.; Moscow Aviation Institute, Moscow, Russia. Personal communication, 2013.
- Efremov, A.; Zakharchenko, V.; Ovcharenko, V. Flight Dynamics (Russian: Dinamika Poleta); Mashinostroenie: Moscow, Russia, 2011; p. 135. ISBN 978-5-9500368-0-4. [Google Scholar]



© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gueraiche, D.; Popov, S. Winglet Geometry Impact on DLR-F4 Aerodynamics and an Analysis of a Hyperbolic Winglet Concept. Aerospace 2017, 4, 60. https://doi.org/10.3390/aerospace4040060
Gueraiche D, Popov S. Winglet Geometry Impact on DLR-F4 Aerodynamics and an Analysis of a Hyperbolic Winglet Concept. Aerospace. 2017; 4(4):60. https://doi.org/10.3390/aerospace4040060
Chicago/Turabian StyleGueraiche, Djahid, and Sergey Popov. 2017. "Winglet Geometry Impact on DLR-F4 Aerodynamics and an Analysis of a Hyperbolic Winglet Concept" Aerospace 4, no. 4: 60. https://doi.org/10.3390/aerospace4040060
APA StyleGueraiche, D., & Popov, S. (2017). Winglet Geometry Impact on DLR-F4 Aerodynamics and an Analysis of a Hyperbolic Winglet Concept. Aerospace, 4(4), 60. https://doi.org/10.3390/aerospace4040060