Efficient Algorithm for a k-out-of-N System Reliability Modeling-Case Study: Pitot Sensors System for Aircraft Velocity

Abstract

The k-out-of-N system is widely applied in several industrial systems. This structure is a part of fault-tolerant systems for which both parallel and series systems are special cases. Because of the importance of industrial systems reliability determination for production and maintenance management purposes, a number of techniques and methods are incorporated to formulate and estimate its analytic expression. In this paper, an algorithm is put forward for a k-out-of-N system with identical components under information about the influence factors that affect the system efficiency. The developed approach is applied in the case of the Pitot sensors system. However, the algorithm application could be generalized for any device which during a mission is subject to environmental and operational factors that affect its degradation process.

1. Introduction

The Pitot sensor (Henri Pitot, 1732) is widely used to measure the velocity and flow rate of an air mass. Many studies describe the functional properties of the Pitot sensor. In the case of aeronautic application and to reduce accidents and critical situations, the Pitot sensor measurement returned must be very accurate. It is therefore fundamental to study the functional aspect of the sensor in order to ensure its efficiency. The first description of an instrument for air flow pressure measurement was introduced by Pitot [1], whose Pitot tubes owe him their names. Darcy [2] proposed improvements in the Pitot tube functional aspect by optimizing the performance of its mechanical properties. Bouhy [3] provides an overview of the Pitot sensor evolution and describes the key standards that have been developed for Pitot sensors’ designs and use.

For all types of manometers, the measured dynamic pressure depends not only on the flow characteristics surrounding the measurement instrument such as the density and the flow turbulence, but also on the geometry of the used instrument itself. It is obviously desirable that the geometry affects the readings precision, as little as possible. Erdem and Kontis [4] provide experimental investigations for the impact of the air flow characteristics on pressure ratio measurement. The authors affirm that the described methods and investigations could generally apply to other gases’ and even liquids’ flow with modifications regarding flow physical properties in the established equations. A specific case of a three-dimensional experiment at hypersonic flows is also discussed. Ower and Pankhurst [5] applied established properties for the case of a Pitot static sensor. Miller [6] provides a flow measurement engineers with a single reference in which the reader is introduced to fluid properties, measurement accuracy increasing techniques, and the most commonly used industrial flowmeters. The handbook introduces the engineering equations, physical property data, accuracy estimation, and installation requirements for the studied flowmeters.

The current maintenance policies are mainly based on basic models to estimate the reliability of the machine. These models can be classified into two groups: models developed for the study of non-repairable systems and those for repairable systems. Generally, the standard models are part of the first group, while the stochastic models are the second.

Failure modes and risk analysis is a management tool which is widely implemented by companies. Dhillon [7] detailed the history of this tool since the 1950s, when it was used to design aircraft control systems. This technique has been extensively  used in the defense industry and in aviation.

Reliability theory is detailed in [8,9,10]. The key models of reliability modeling are the stochastic and regression models. Stochastic models are mainly based on the Poisson processes and Markov chains and semi Markov. These models were discussed by [11], while regression models are mainly based on standard distributions where the exponential distributions, Weibull, and log normal are the most used.

In some cases, the reliability model considers only operational conditions effect. Other models consider only the effect of maintenance actions. Proportional hazard model is one of the most common models introducing the above factors into the component’s reliability model. Regression models for survival data have traditionally been based on the Cox regression model. Cox’s proportional hazard model, proposed by David Cox [12], is widely used in the analysis of time-to-event data. Cox assumed a semi-parametric form for the hazard function of the distribution of the failure time.

Many studies have investigated the determination of the reliability of multi-unit systems. The k-out-of-N system was a point of interest of many proposals focusing on the computation of their reliability function. A k-out-of-N system is a system with N  components which functions if and only if k or more of the components function.

Eryilmaz [13] proposed a model to determine system reliability, equipped with a single warm standby unit. Thanks to the model, the author obtains an explicit expression of the reliability function for arbitrary lifetime distributions. Proschan and Boland [14] studied the reliability function properties for the case of a k-out-of-N system.

This work is mainly motivated by aeronautical accidents linked to a malfunctioning of the Pitot system. The current research work is derived by a practical need to control Pitot sensors’ system functioning for aeronautic applications. The main contribution of the current study is to develop an algorithm for modeling, firstly, the reliability function for a single Pitot sensor. Secondly, the algorithm is extended to determine the reliability expression for the whole Pitot sensors system, considered as a k-out-of-N system. Since the application case of this study is the Pitot sensors system for aircraft velocity measurement, the next section describes the operating mechanism of a sensor during a mission.

Section 2 aims to condense information about the use of the Pitot tube in the air flow velocity measurement. The endpoint of this part is to describe the Pitot sensor functional and software aspects.

Section 3 describes the proposed algorithm for Pitot sensor reliability determination. The algorithm consists of five steps, where the first four aim to model the reliability expression for a single Pitot sensor. The fifth step permits the reliability to be computed for the whole system, considered as a k-out-of-N one. Our algorithm improves the application of proportional hazard models to the study of the Pitot sensor functioning, as these models conventionally help to highlight effects of a set of defined factors on the studied equipment life duration.

Section 4 provides a numerical application of the proposed algorithm to give the analytic reliability expression for the Pitot sensor system as a  function of parameters that affect the system measurements accuracy during a flight.

2. Technical Review of Pitot Sensors

The Pitot sensor is used in several industrial applications. The instrument indicates the fluid flow velocity by measuring the difference between the dynamic and static pressure.

The Pitot sensor has two co-axial tubes. the inner tube measures the total pressure, while the outer one provides the static pressure. The dynamic pressure expresses the difference between the total pressure and the static one.

2.1. Functional Aspect

In this section, techniques of total and static pressures measurement are described.

2.1.1. Total Pressure Measurement Technique

When a fluid is considered incompressible, the velocity measurement is directly deduced from the difference between the static pressure and the total pressure. The total pressure setting mechanism is simple. Indeed, on the surface of any solid immersed  in a fluid, there exists a point where the fluid stagnates: point of stagnation. The pressure measured at this point expresses the flow total pressure.

As illustrated in Figure 1, the Pitot sensor is immersed in the fluid so that the inner tube is connected to the leading edge of the object (stagnation point in which the velocity is practically zero).

Let g be the gravity acceleration, z the height, U and $P_O$ are, respectively, the velocity and the pressure of the uniform flow (flow undisturbed by the presence of the sensor). Based on the hypothesis of a stationary fluid (speed independent of time) which is perfect and incompressible  (density $\rho$ constant), and has current lines with approximately the same altitude, by applying the conservation law of the “Enthalpy of the mass of the fluid” we obtain the following expression for the current lines for points A and O (Figure 1):

$$P_O+\rho g{z}_O+\frac{1}{2}\rho v_O^2=P_A+\rho g{z}_A+\frac{1}{2}\rho v_A^2$$

(1)

where $z_O=z_A;V_O=U;V_A=0$.

The expression of the stagnation pressure (total pressure) becomes:

$$P_A=P_O+\frac{1}{2}\rho U^2$$

(2)

2.1.2. Static Pressure Measurement Technique

The Pitot sensor used for aircraft has one or more openings for detection of the static pressure.

The static pressure is measured on a hole drilled in the sensor surface where the nearest power lines are parallel to the speed vector of the surrounding flow. The principle of static pressure measurement is illustrated in Figure 2.

The pressure coefficient permits the best opening position for the static pressure measurement to be determined.

The pressure coefficient, denoted $C_p$, is expressed as:

$$C_p=\frac{\left(P-P_{\inf }\right)}{Q_{\inf }}$$

(3)

where:

• P is the pressure of the flow surrounding the probe
• $P_{\inf }$ is the static pressure of the flow at points remote from the probe
• $Q_{\inf }$ is the dynamic pressure of the flow at points remote from the probe

2.2. Software Aspect

In the current study, the pitot probe working cycle on the software side can be described as follows:

• The probe is connected to an electronic module which interprets the total pressure and the static pressure measurements to deduce the dynamic pressure, and thus the relative flow velocity. This module is equipped with a differential pressure sensor whose electrical signal is interpreted by a micro-controller that will convert the speeds into values which are  recognized and exploitable.
• In the case of this study, a Pitot sensor is considered as a failing equipment when it returns inaccurate measurements.
• During the system’s good working time (K out of N sensors give correct measurements), the sensor measurement quality degrades continuously.
• The degradation process is a function of operational and environmental factors in which the Pitot probe operates during the mission.

3. Algorithm for Pitot Sensor System Reliability Estimation

Degradation models are generally classified into two main groups: deterministic models based on regression and stochastic models based on random processes.

Stochastic models are mainly based on the Poisson process and the Markovian and semi-Markovian processes. For more details about these approaches, the reader can refer to the study of Cocozza-Thivent [11]. In addition to modeling the degradation process, deterministic models provide information about factors that affect the equipment degradation process. These models include several approaches, including regression approaches (traditional approaches). Regression methods are used to determine the reliability function of a system based on $NC$ failure dates $t_i$ $(i=1...N)$ corresponding to $NC$ components. The endpoint of interest of these methods remains to estimate the reliability expression parameters as a function of influencing factors’ values. Proportional hazard models (PHMs) are the most commonly used regression models. Dale [15] demonstrated the benefits of using the proportional hazards model in failure rate analysis, and recommended its use for industrial systems’ reliability estimation. Hosmer [16] provided a presentation of commonly used modeling techniques, and illustrated concrete examples for real case studies.

PHMs consider that the failure rate is expressed by the product of a nominal failure rate ${\lambda }_0(t)$ and a positive term $\psi (X,\beta )$, integrating influencing factors such as temperature, pressure, design changes, etc. Thus, the failure rate—based on time and influencing factors—is defined as follows:

$$\lambda (t,X)={\lambda }_0(t)\psi (X,\beta )$$

(4)

X is the vector of the influence factors associated to the equipment and $\beta$ is the regression coefficients vector. The nominal failure rate is identical to the total failure rate when influencing factors have no effect on the occurrence of failures. Influencing factors can affect the failure rate so that it is higher or lower than the nominal failure rate. Cox’s model [12] represents the basic model of PHM. The choice of the nominal failure rate function is arbitrary. In this work, we will retain an exponential form for $\psi (X,\beta )$, as it is the most commonly used one for PHM models. The failure rate is expressed as:

$$\lambda (t,X)={\lambda }_0(t)e^{\beta X}$$

(5)

For the basic failure rate function, we adopt a two-parameter Weibull modeling. Thus, the analytic expression of the nominal failure rate is given by the following relation:

$${\lambda }_0(t)=\frac{\alpha }{\eta }(\frac{t}{\eta }{)}^{\alpha -1}$$

(6)

where $\alpha$ is the shape parameter and $\eta$ the scale parameter in units of time. To determine the failure rate analytic expression, we propose the following algorithm:

3.1. Step 1: Choice and Coding of Influencing Factors

In this step, variables that have an impact on the degradation process of the studied equipment are determined. Once defined, influencing factors should be coded to facilitate their integration into the Cox model. Factors coding is based on the following basic principles:

• When the influence factor is quantitative (e.g., air density, described in Section 4), the measurement values can be integrated directly into the model.
• When the variable is qualitative (e.g., weather conditions, described in Section 4), it is recommended to use discrete values to quantify it. These values are associated with a scale defined by the modeller [12].
• To facilitate the data evaluation and the model results analysis, it is recommended to split influencing factors’ values into different levels.

3.2. Step 2: Data Acquisition

Data acquisition consists of collecting the necessary information for the failure rate modeling. For each component of the study sample, the following data is required:

• The failure date
• The values of the corresponding influencing factors.

3.3. Step 3: Determination of Regression Parameters

Estimation of the best combination of regression parameters is based on the component failure date and the associated influencing factors’ values. David Cox [12] was able to recast his method of estimation through what he called “partial likelihood”. The partial likelihood, $L(\beta ,X)$, is expressed by the following relation [17]:

$$L(\beta ,X)=\prod _{i=1}^{NC}\frac{e^{{\beta }_i{X}_i}}{{\sum }_{j\in SR}{e}^{{\beta }_j{X}_j}}$$

(7)

$NC$ expresses the number of components under investigation (sample size).

$\lambda (t_i,X_i)$ expresses the component i  failure rate.

SR is the indices set corresponding to components that still operate at time $t_i$.

To obtain the maximum likelihood estimator, it is necessary to solve the following maximum likelihood $NC$ equations system:

$$\frac{\partial }{\partial {\beta }_{j\in 1..NC}}ln(L({\beta }_1,{\beta }_2,..,{\beta }_{NC},X)$$

(8)

Unlike linear regression, an exact analytical solution does not exist. It is therefore necessary to use an iterative algorithm. There are several algorithms to maximize the likelihood and thus determine the $\beta$ vector. Among these methods, the Newton–Raphson algorithm is frequently used. When estimating parameters that affect lifetime, the interaction between influencing factors must also be verified. The interaction of two or more variables can be modeled by introducing a new influence factor which corresponds to the product of the influencing factors in question. On the other hand, if there is an interaction between the influencing factors, the estimation of the regression parameter for this new influence factor must be significant. Bendell [18] obtained interesting results using the interaction of influencing factors. If the influencing factors are estimated in groups formed by different data, a statistical analysis test is carried out to determine whether the influencing factors have the same effect in the different data groups.

The basic failure rate is the risk that an equipment fails when the influence factor values are NULL. The baseline failure rate ${\lambda }_0(t)$ can be modeled from a previously chosen parametric distribution. Nevertheless, the PHM model can be used without providing an expression of ${\lambda }_0(t)$. However, to predict the number of failures in a given time interval, the hypothesis of having a parametric distribution for the form of ${\lambda }_0(t)$ yields better results.

Once the vector $\beta$ is determined, we try to express the baseline failure rate ${\lambda }_0(t)$. $\alpha$ and $\eta$ values are determined from the following expressions, deduced from the maximum likelihood function expression [19]:

$$\frac{NC}{\alpha }+\sum _{i=1}^{NC}ln(t_i{(e^{{\beta }_i{X}_i})}^{\frac{1}{\alpha }})-\frac{NC{\sum }_{i=1}^{NC}(t_i{(e^{{\beta }_i{X}_i})}^{\frac{1}{\alpha }}{)}^{\alpha }ln(t_i{(e^{{\beta }_i{X}_i})}^{\frac{1}{\alpha }})}{{\sum }_{i=1}^{NC}{{(t_i(e^{{\beta }_i{X}_i})}^{\frac{1}{\alpha }})}^{\alpha }}=0$$

(9)

$$\eta =(\frac{{\sum }_{i=1}^{NC}{(t_i{(e^{{\beta }_i{X}_i})}^{\frac{1}{\alpha }})}^{\alpha }}{NC}{)}^{\frac{1}{\alpha }}$$

(10)

For more details about the procedure for determining the failure rate and estimating the reliability function, the reader may refer to the work of [20].

The significance of failure rate estimation from proportional hazard models is a function of several parameters. The time dependence of certain influencing factors is a determining factor in the accuracy of the estimated model. If it exists, the extension of the proportional hazards model is recommended in order to increase the performance of the model.

After adding an interaction between a time function and an influence factor included in the initial model, the significance of the model must be verified. If the integrated influence factor is significant, the proportionality hypothesis is violated for the given influence factor and its effect varies over time. The basic model of Cox does not take into account the interaction of influencing factors over time. However, there is evidence in the literature that time dependence can be consistent with this model and that it can be applied to estimate the effect of the interaction of  factors of influence over time [21].

3.4. Step 4: Synthesis and Results Analysis

At this stage, the key requirements are available to express the failure rate and conclude the reliability function. From this data, the effect of each factor of influence on the failure and duration of the component can thus be determined and discussed. The described procedure is then applied in the case of the Pitot probe during a flight mission.

The reliability function is then deduced from the failure rate function and expressed as follows:

$$R(t,X)=(e^{-{\int }_0^t{\lambda }_0(u)\mathrm{d}u}{)}^{e^{\beta X}}=(e^{-{(\frac{t}{\eta })}^{\alpha }}{)}^{e^{\beta X}}$$

(11)

3.5. Step 5: Reliability of the Whole System

In the current study, the following assumptions are considered:

• Components have two states: either good or bad.
• The N components of the system function independently (statistically independent).
• The system is good if and only if at least k of its components are good.

The system reliability model is based on the following notations:

• $R=(R_1,R_2,...,R_N)$ is the vector of components reliabilities.
• $s=(s_1,s_2,\dots ,s_N)$ represents any vector with binary values.

Mathematical Formulation

The probability that k or more of the components is functioning is expressed by:

$$H_k(R)=H_k(R_1,R_2,...,R_N)=\sum _{s/s_1+···+s_N\ge k}{R}_1^{s_1}...R_N^{s_N}{(1-R_1)}^{1-s_1}...{(1-R_N)}^{1-s_N}$$

(12)

$$H_k:{[0,1]}^N->[0,1]$$

This function is called the reliability function for a k-out-of-N system with N independent components.

For more details about this function and its properties, the reader is invited to refer to [14].

Theorem 1.

In the case where the reliability function is nearly the same for the N system components. The probability that k or more of the components is functioning is expressed as follows:

$$H_k(R)=H_k(R_1,R_2,...,R_N)=\sum _{i=k}^N\left(\genfrac{}{}{0pt}{}{N}{i}\right)R^i{(1-R)}^{N-i}$$

(13)

where

$$R_1=...=R_N$$

$$\left(\genfrac{}{}{0pt}{}{N}{i}\right)=\frac{N!}{i!(N-i)!}$$

Proof. 

Consider $R_1=...=R_N$

$$H_k(R)={\sum }_{s/s_1+···+s_N\ge k}{R}^{s_1}...R^{s_N}{(1-R)}^{1-s_1}...{(1-R)}^{1-s_N}={\sum }_{s_1+···+s_N\ge k}{R}^{s_1...+s_N}{(1-R)}^{N-(s_1+...+s_N)}$$

(14)

Consider $i=s_1+s_2+\dots .+s_N$

$$H_k(R)=\sum _{i\ge k}{R}^i{(1-R)}^{N-i}$$

(15)

For each $i\ge k$, i combination can be formed for the set s which is a subset of i distinct elements. The set s has N elements, the number of i-combinations is equal to the binomial coefficient. The number of possible vectors for each i is then:

$$\left(\genfrac{}{}{0pt}{}{N}{i}\right)=\frac{N!}{i!(N-i)!}$$

In addition, the reliability function can be expressed as mentioned in Theorem 1. ☐

The proposed approach for the Pitot sensors system reliability evaluation—when the components are considered identical—is introduced in detail. The current study is applied in the case of the Pitot sensor system in aeronautic application. Once the analytic expression for a Pitot sensor reliability is determined, one can determine the reliability function for the whole system, considered as a k-out-of-N system.

4. Application of the Reliability Determination Algorithm for the Case of a Pitot Sensor System

In the following section, the algorithm described in Section 3 will be applied in the case of a Pitot sensors system during a flight.

4.1. Step 1: Application

The following three influencing factors will be retained as the main influencing factors on the degradation process of the Pitot sensor. This choice is based on the analysis carried out in [22].

• Air density
• Air flow nature
• weather conditions

The objective is to model the failure rate as a function of the defined factors of influence. The event of interest is the Pitot sensor failure during a finite time horizon. A Pitot sensor is considered to be failing when it returns inaccurate measurements.

Influence factors are defined as follows:

• $X_1$: The nature of the flow will be modeled by the Mach number (M), which is a dimensionless quantity representing the ratio of the flow velocity to the local velocity of the sound. The Mach number is expressed as: M = U / S, where U is the speed of the object ans S is the sound velocity. We split the Mach value into two levels:

  -

  The subsonic level when $X_1$ < 0.85

  -

  The transonic level when $X_1$ ≈ 1

• $X_2$: Air density is a function of altitude, temperature, and humidity variations. We assume that the air density has three levels:

  -

  Low if $X_2$ < 1.1

  -

  High if $X_2$ > 1.3

  -

  Normal otherwise

• $X_3$: Weather conditions. Unlike the first two factors of influence, the variable modeling weather is a qualitative variable. To integrate this variable into the model, it is necessary to convert it into a quantitative variable. Thus, $X_3$ is evaluated as 1 when weather conditions favor the formation of ice crystals, and 0 otherwise. The non-optimal conditions that do not result in the formation of ice crystals also assume the value 0).

4.2. Step 2: Application

In the numerical application, $NC$ Pitot probes are considered for which the data of the form ($t_i$, $X_i$), (i = 1 ... $NC$) is collected, $t_i$ corresponds to the failure date and $X_i$ represents the influence factors vector associated to the $i^{th}$ sensor. For database collection, the following assumptions will be used:

• Time horizon: 24 hours.
• Study sample ($NC$): 200 Pitot sensors.
• Failure dates are randomly generated according to a Weibull distribution.

In the present study, the database for influence factors values is based on the data available in [23,24]. These references provide studies on the calibration of air flow measurement tools. The data discussed in these references has been reviewed and approved by the National Aeronautics and Space Administration (NASA).

4.3. Step 3: Application

The following R program is developed for regression parameters estimation:

DataPitotSensor <-read.csv
Library (survival)
Library (splines)
MODELResults <-coxph (formula = Surv (Failure-Date,
    Failure) ~ X_1 + X_2 + X_3, data = DataPitotSensor)
		

Running this program, the following expression for the failure rate is obtained:

$\lambda (t,X)={\lambda }_0(t)e^{0.65X_1-0.6X_2+0.69X_3}$

At this stage, the best combination of influencing factors, different information on the dates of the failure of the studied sensors, the influence factor values, and the values of the parameters of the regression vector $\beta$ are available. The parameters $\alpha$ and $\eta$ are thus computed via the equations given in Section 3.3.

$\alpha$ = 1.45

$\eta$ = 11.4 h

4.4. Step 4: Application

The expression of the reliability function—as a function of the influencing factors—can be deduced from the failure rate function as computed in Section 3.4:

$$R(t,X)={(e^{-{(\frac{t}{\eta })}^{\alpha }})}^{e^{\beta X}}={(e^{-{(\frac{t}{11.4})}^{1.45}})}^{e^{0.65X_1-0.6X_2+0.69X_3}}$$

(16)

4.5. Step 5: Application

Considering the case of a Pitot sensors system that consists of three Pitot sensors (N = 3) and k = 2 which is interpreted to mean that the system is functional if and only if at least two of the three sensors are functional. In this case, the system reliability is:

$$R_{[2-out-of-3-system]}=\sum _{i\ge k}\left(\genfrac{}{}{0pt}{}{N}{i}\right)R^i{(1-R)}^{N-i}=\sum _{i=2}^3\left(\genfrac{}{}{0pt}{}{i}{3}\right)R^i{(1-R)}^{3-i}=3R^2-2R^3$$

(17)

4.6. Results Analysis

The failure rate expression established in the third step is a function of the factors of influence on the efficiency of the Pitot sensor during the flight. The proportional hazard model helps to analyze these factors’ effects on the regression parameters, computed in the third step and listed in the

Table 1. Simulation results for regression parameters estimation (Step 3).

Factor	Coefficient
Air speed	0.65611
Air density	−0.6
Weather conditions	0.69747

:

In order to analyze the marginal effect of a factor, one should compute the exponential of the corresponding estimated parameter in the $\beta$ vector. For example, referring to results shown in Table 1, for the “air-speed” factor, $e^{0.65}=1.9$ leads to the conclusion that going from a subsonic environment to a transonic one would multiply chances of failure risk by 1.9.

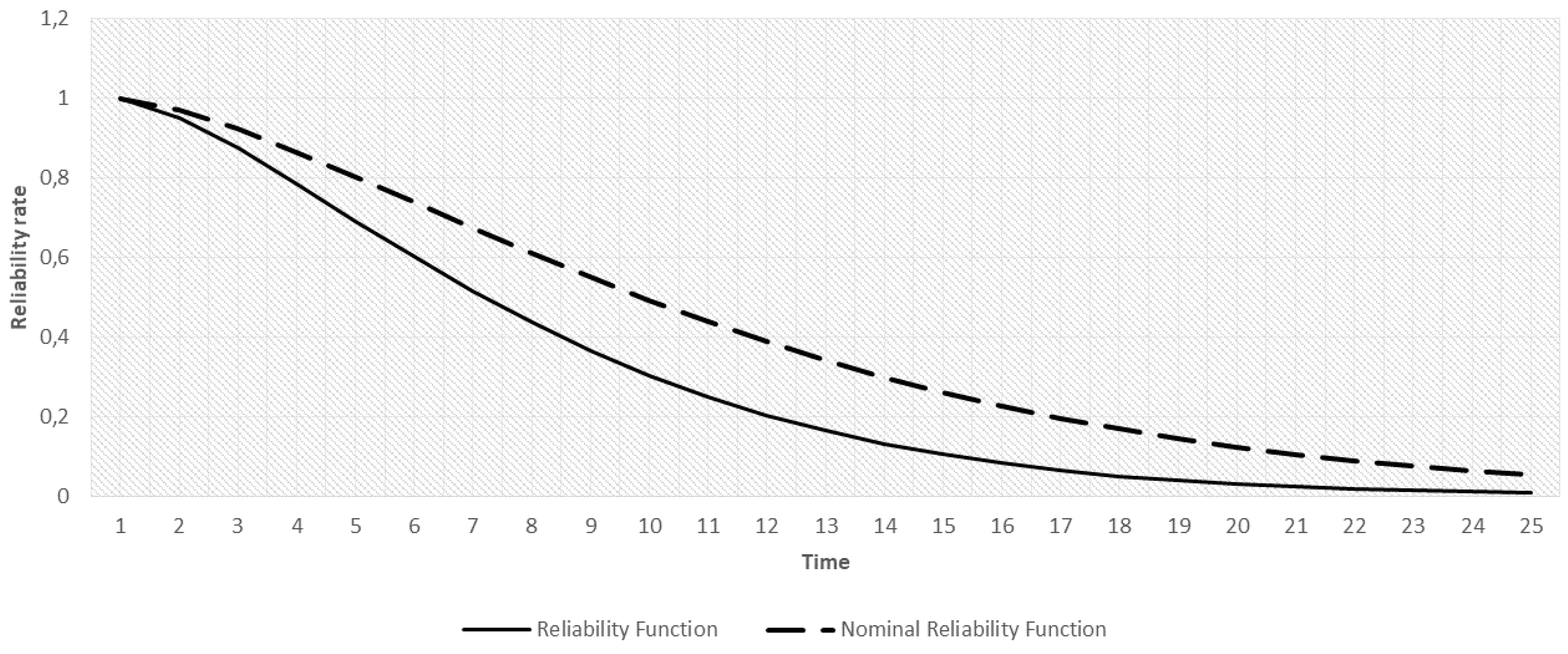
Thanks to the failure rate expression, the reliability expression for one component is computed in the forth step of the algorithm. Figure 3 illustrates this function in the case where data values for the mission are as follows:

• $X_1$ = 0.98 (Transonic environment)
• $X_2$ = 1.2 (Normal density)
• $X_3$ = 1 (Bad weather conditions)

The results of the example application in Figure 3 show significant differences between the Reliability Function and the nominal one (the nominal function corresponds to the reliability function when the effect of influence factors is not considered—i.e., $X_1=X_2=X_3=0$). The differences observed are due to the effect of the factors on the Pitot sensor efficiency during the mission. The established expression in the Equation (16) assumes that each factor reduces the component reliability continuously.

In this paper, when the reliability expression for one component is available, the analytic expression for reliability of a k-out-of-N system with identical components is obtained. The Pitot sensor system reliability is expressed as a function of time (Equation (17)). This expression is then in good agreement with real conditions and properties where reliability and other performance measures of any system are functions of time. The established reliability function is a decreasing function of time since it is impossible to repair the Pitot sensors system until its mission is complete.

5. Conclusions

This study deals with a Pitot sensor for aircraft which during a mission is subject to internal and external conditions that impact measurement accuracy. The primary motivation of this paper stems from the empirical evidence that there is a practical need to reduce accidents and flight problems linked to Pitot sensor malfunctioning. In this paper, an algorithm is derived for estimating a k-out-of-N system based on regression models. This study is proposed for a Pitot sensor which during its mission is assumed to be subject to external conditions which impact its degradation process. The first part of the paper gives a technical review of the Pitot sensor for aircraft velocity. In the second part, an efficient algorithm for the computation of the reliability function parameters is established. A numerical application is given in the last part in order to illustrate the algorithm steps. The developed method is applied for modeling Pitot sensors’ system reliability. However, the algorithm key steps could be generalized to be applied to any device which during a mission is subject to environmental and operational factors that affect its degradation process. The extension of the algorithm in order to update the reliability estimation during the flight as a function of influence factors’ fluctuation is also interesting.

In this study, we concentrate on a technique for the reliability evaluation of a k-out-of-N system with identical components. As a perspective for this work, the developed algorithm could be extended for system reliability determination when the components are not necessarily identical.