An Efficiently Parallelized High-Order Aeroacoustics Solver Using a Characteristic-Based Multi-Block Interface Treatment and Optimized Compact Finite Differencing
Abstract
:1. Introduction
2. Fourth-Order Solver
2.1. Governing Equations
2.2. Turbulence Modelling
2.3. Spatial Discretization
2.4. Temporal Discretization
2.5. Filtering Scheme
2.6. Characteristic Equations
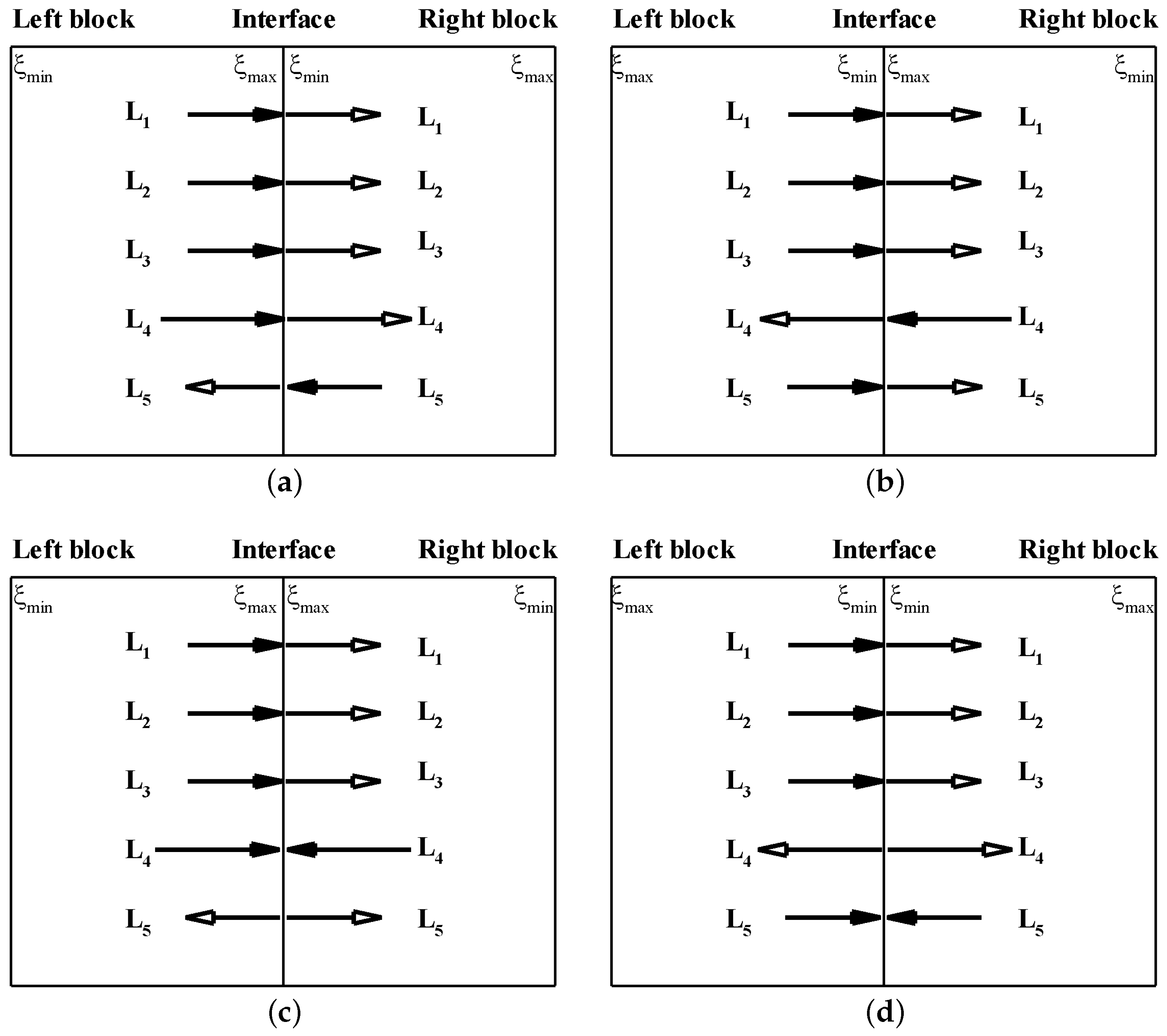
2.7. Interface Matching
2.8. Interface Matching of Turbulence Quantities
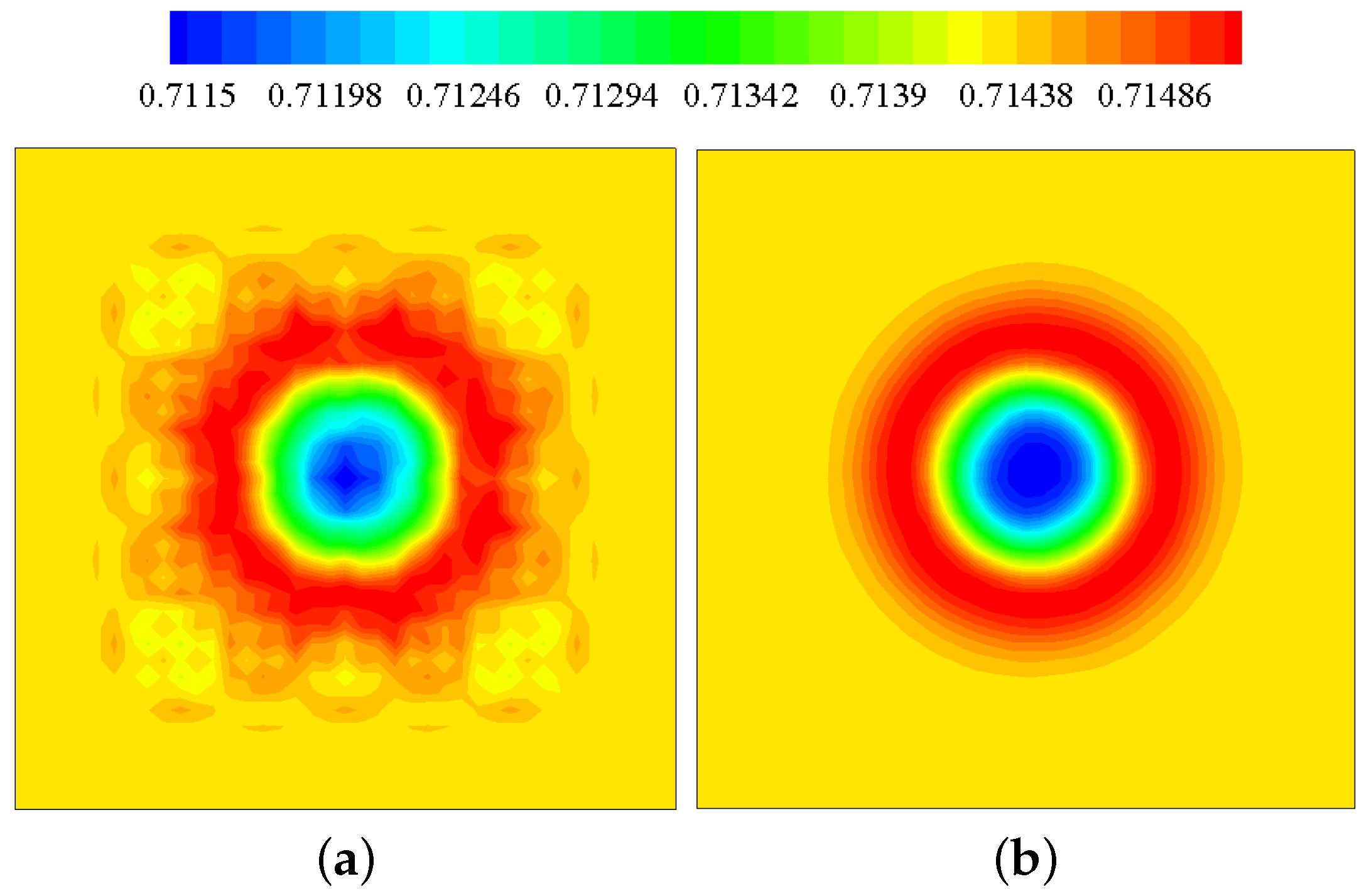
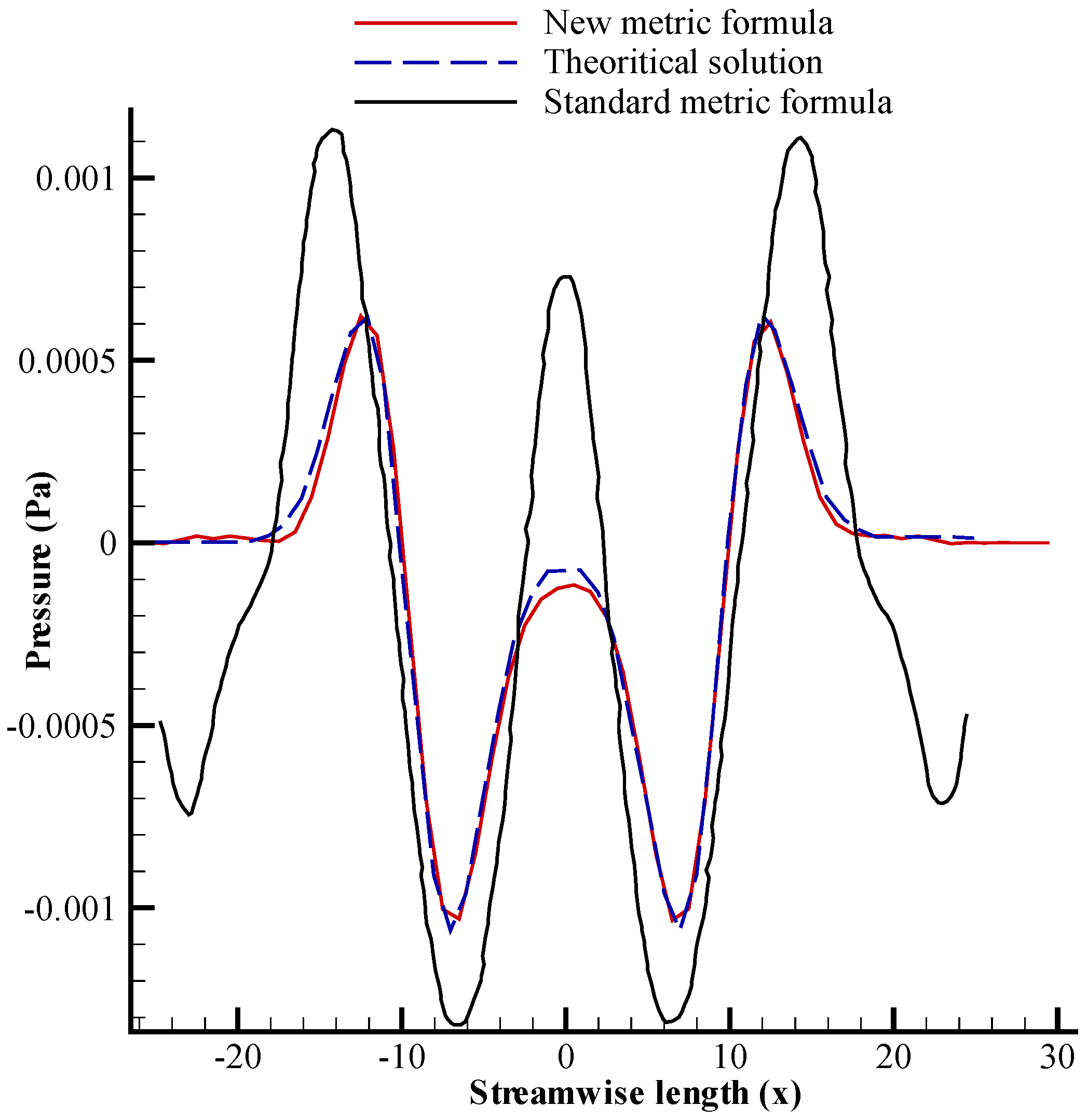
2.9. Metric Cancellation Errors
3. Validation
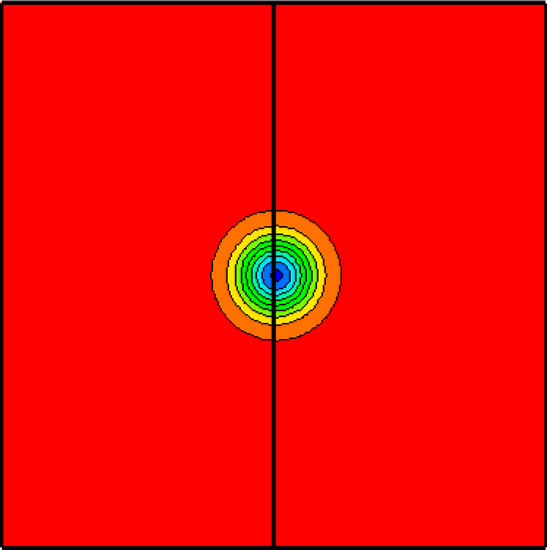
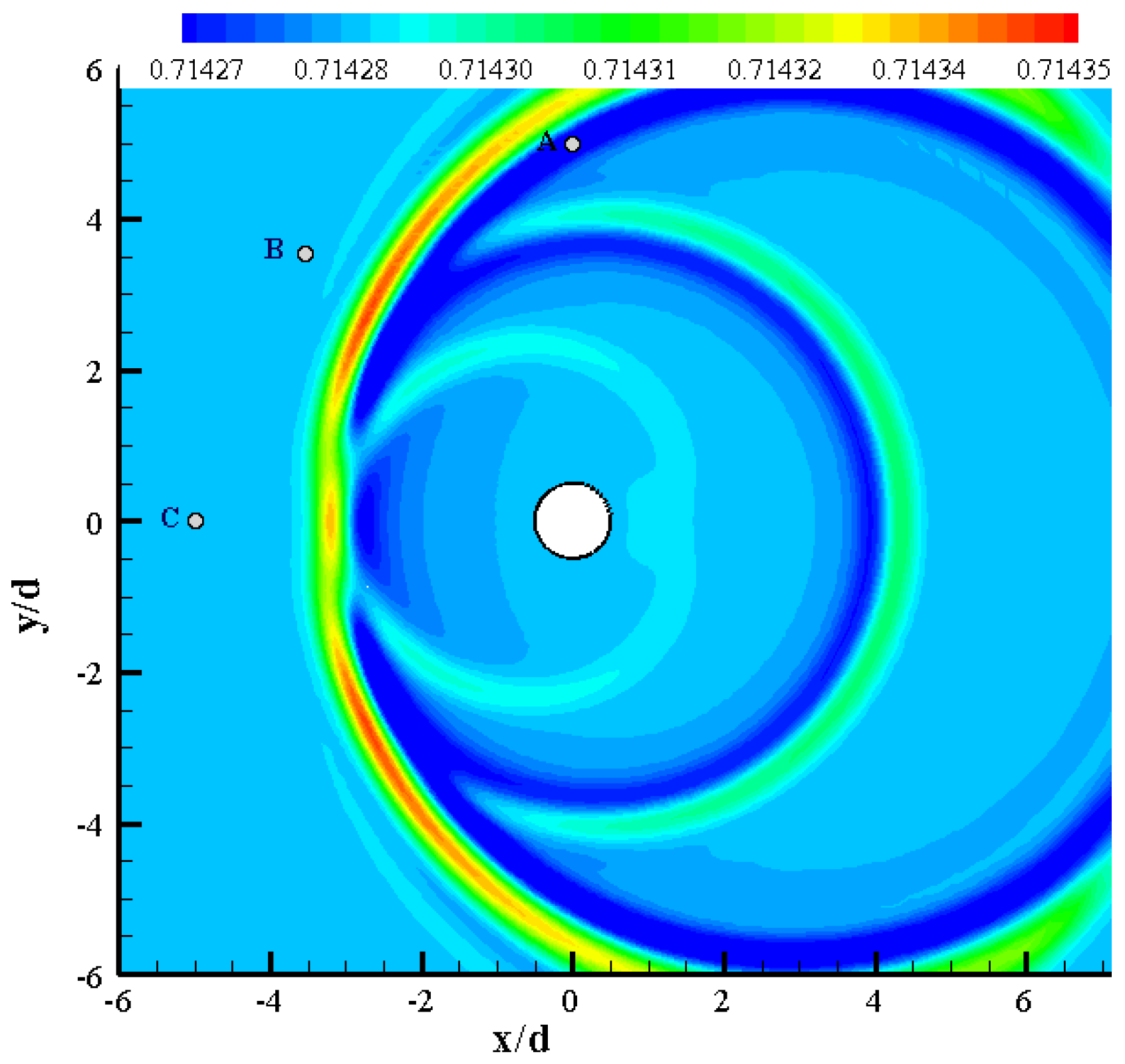
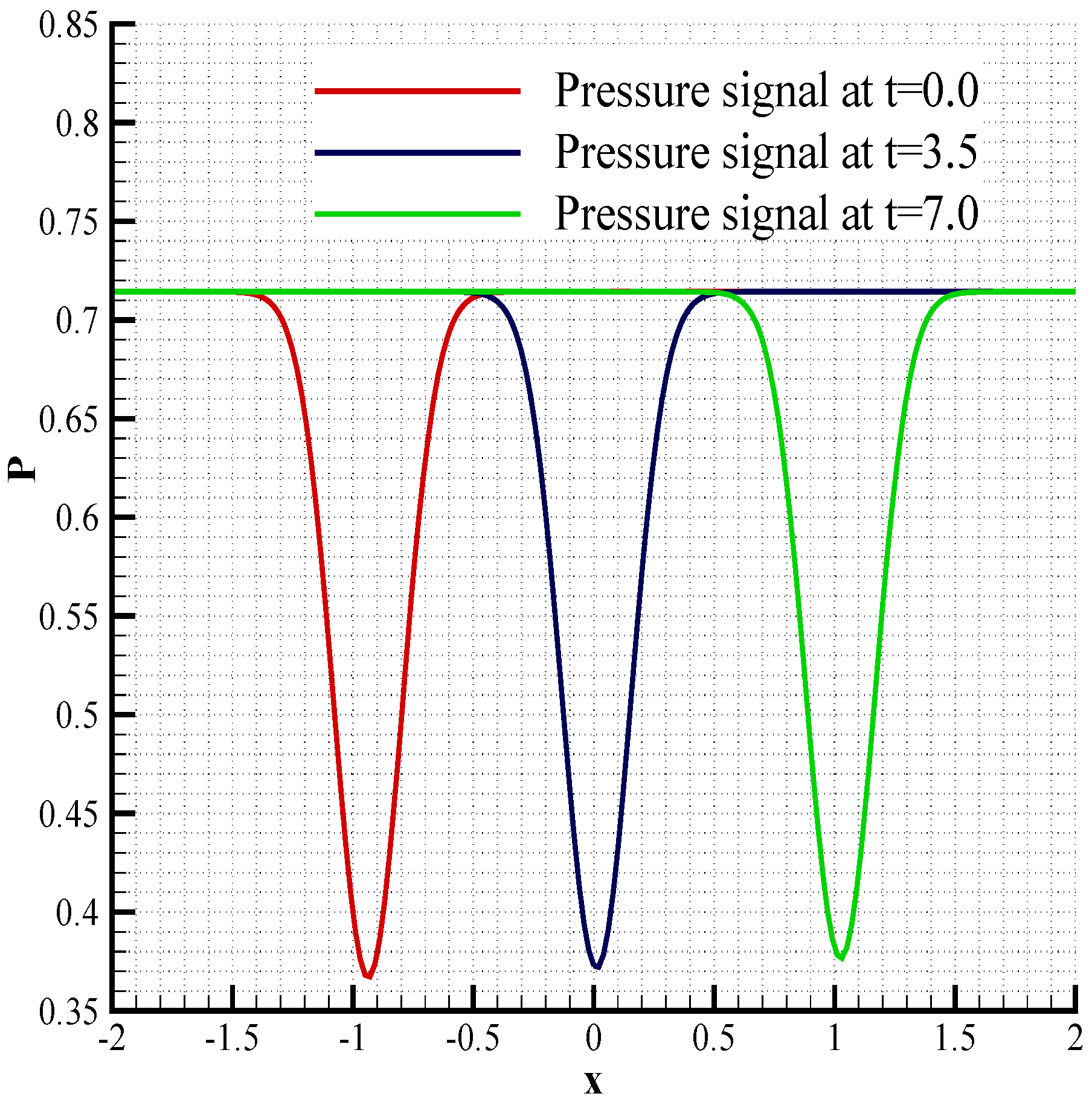
3.1. Two-Dimensional Acoustic Scattering
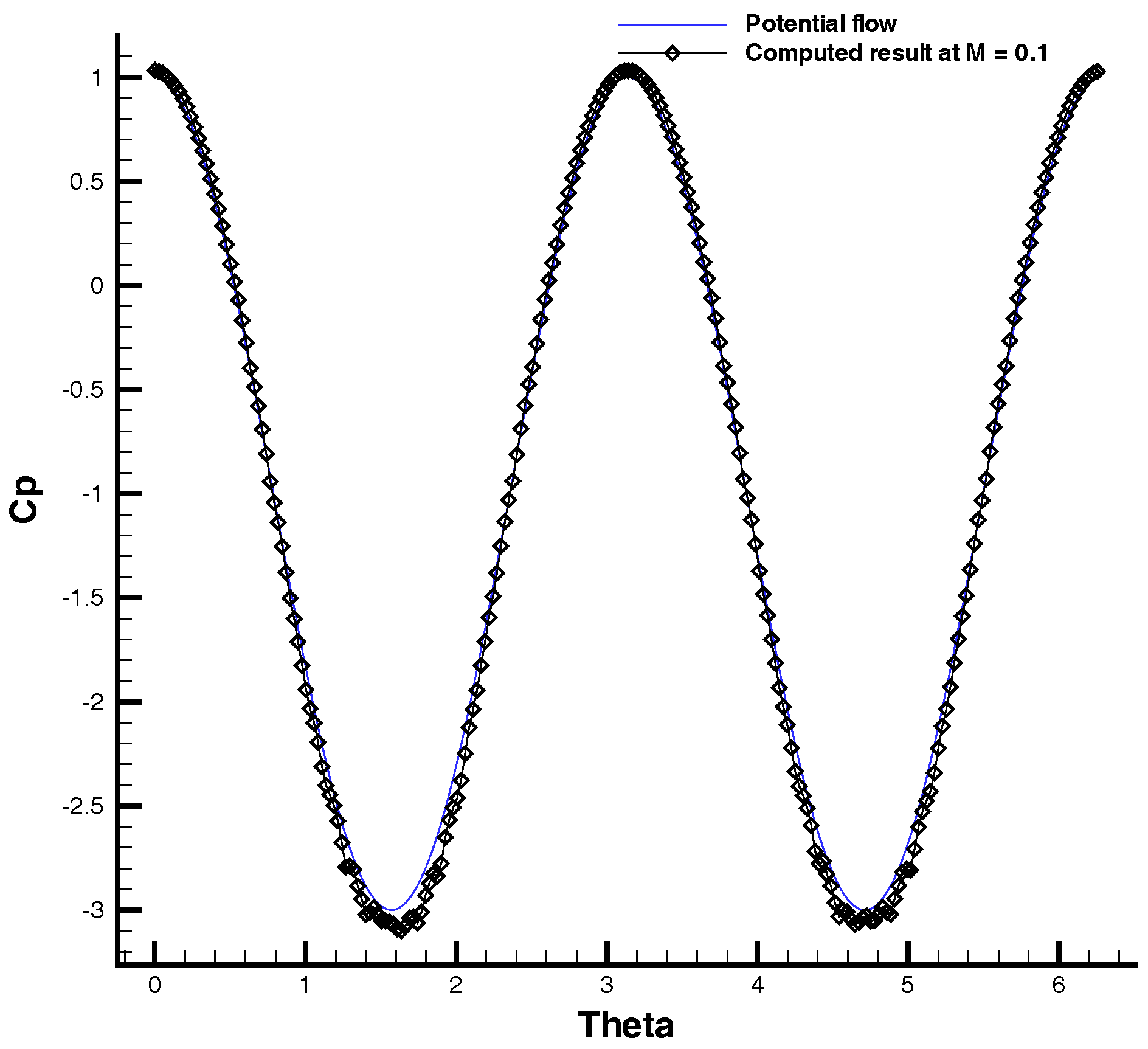
3.2. Inviscid Flow Past a 2D Cylinder
3.3. Sound Propagation in 3D Curvilinear Meshes
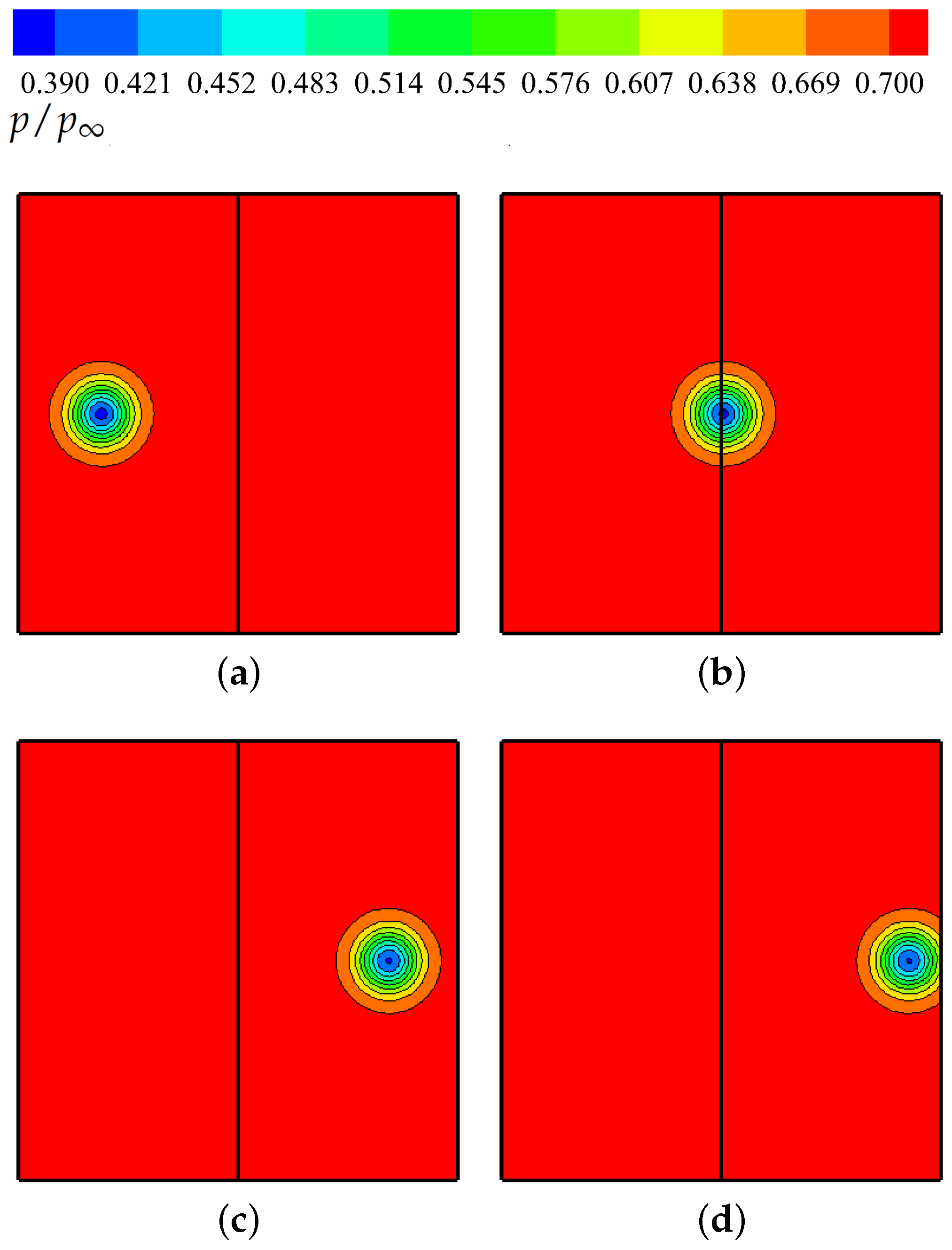
3.4. Vortex Propagation across a Block Interface
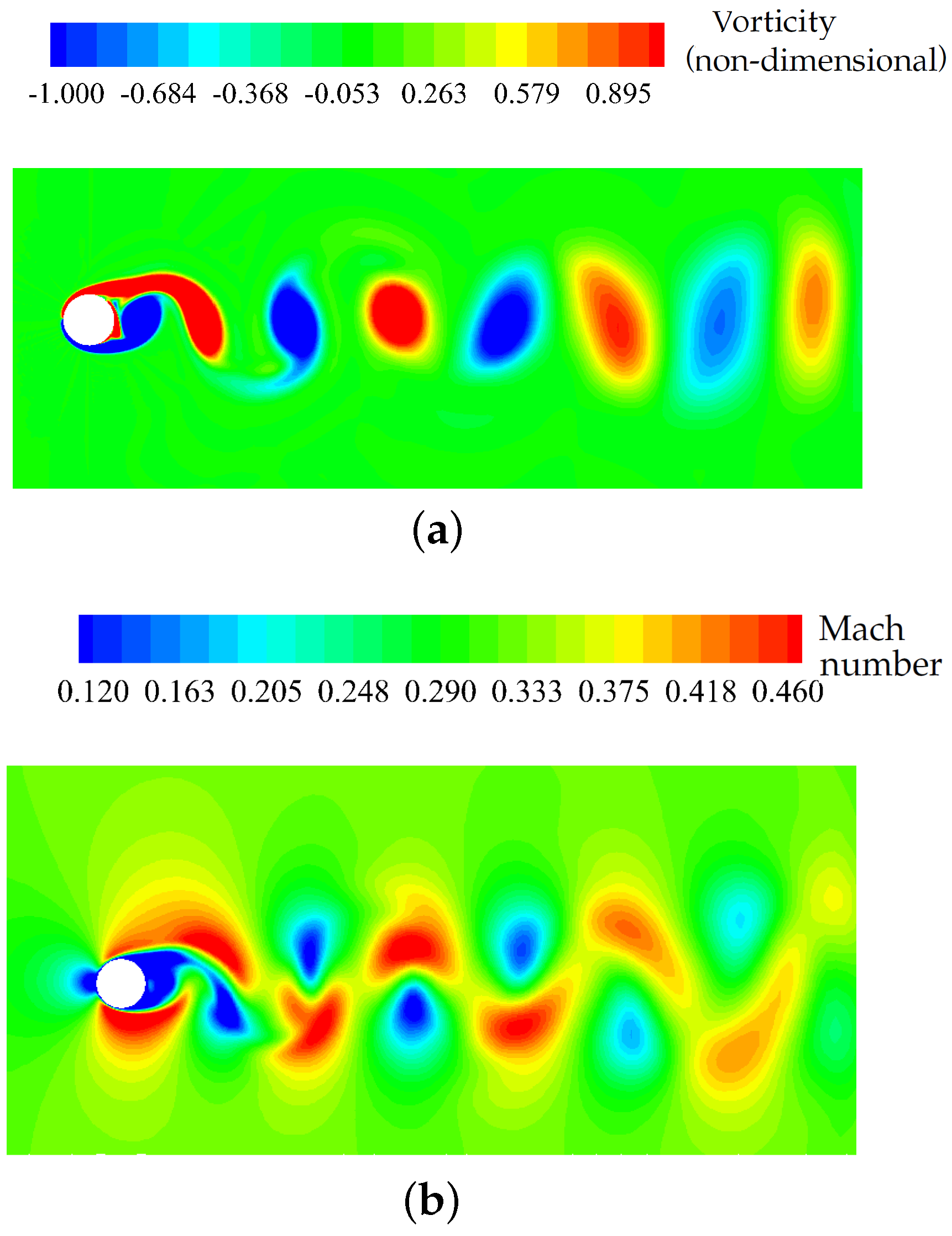
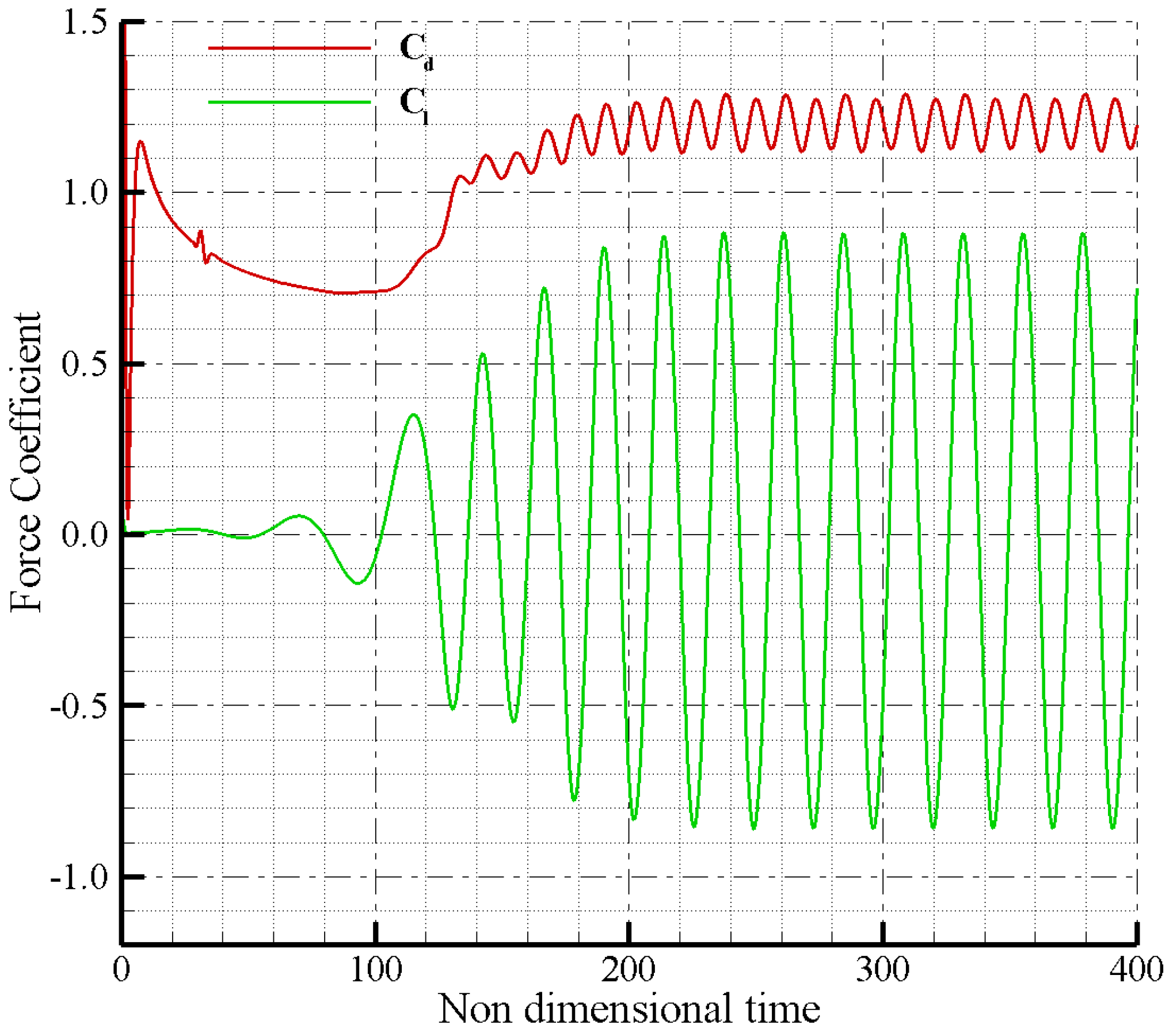
3.5. Laminar Flow Past a 2D Cylinder
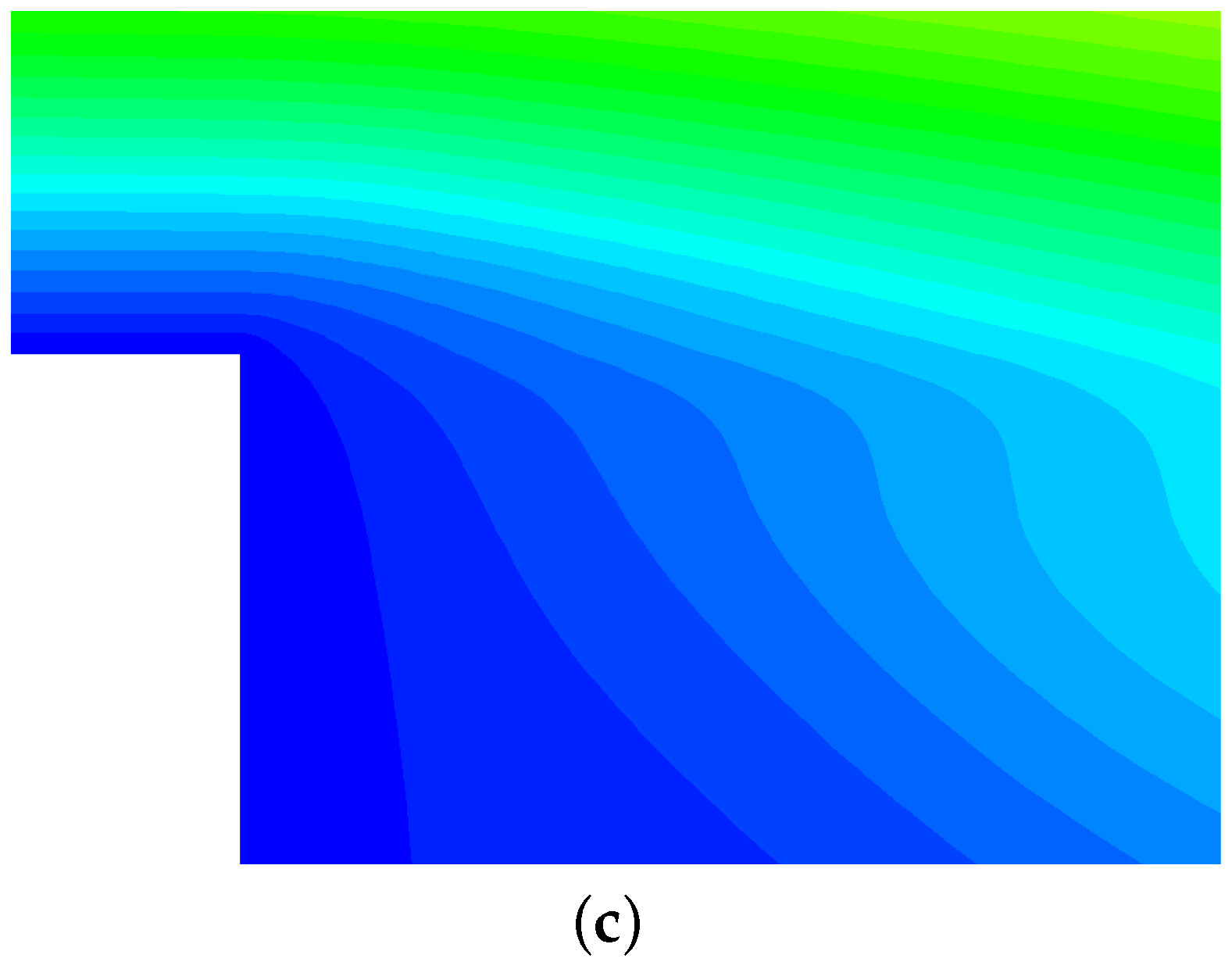
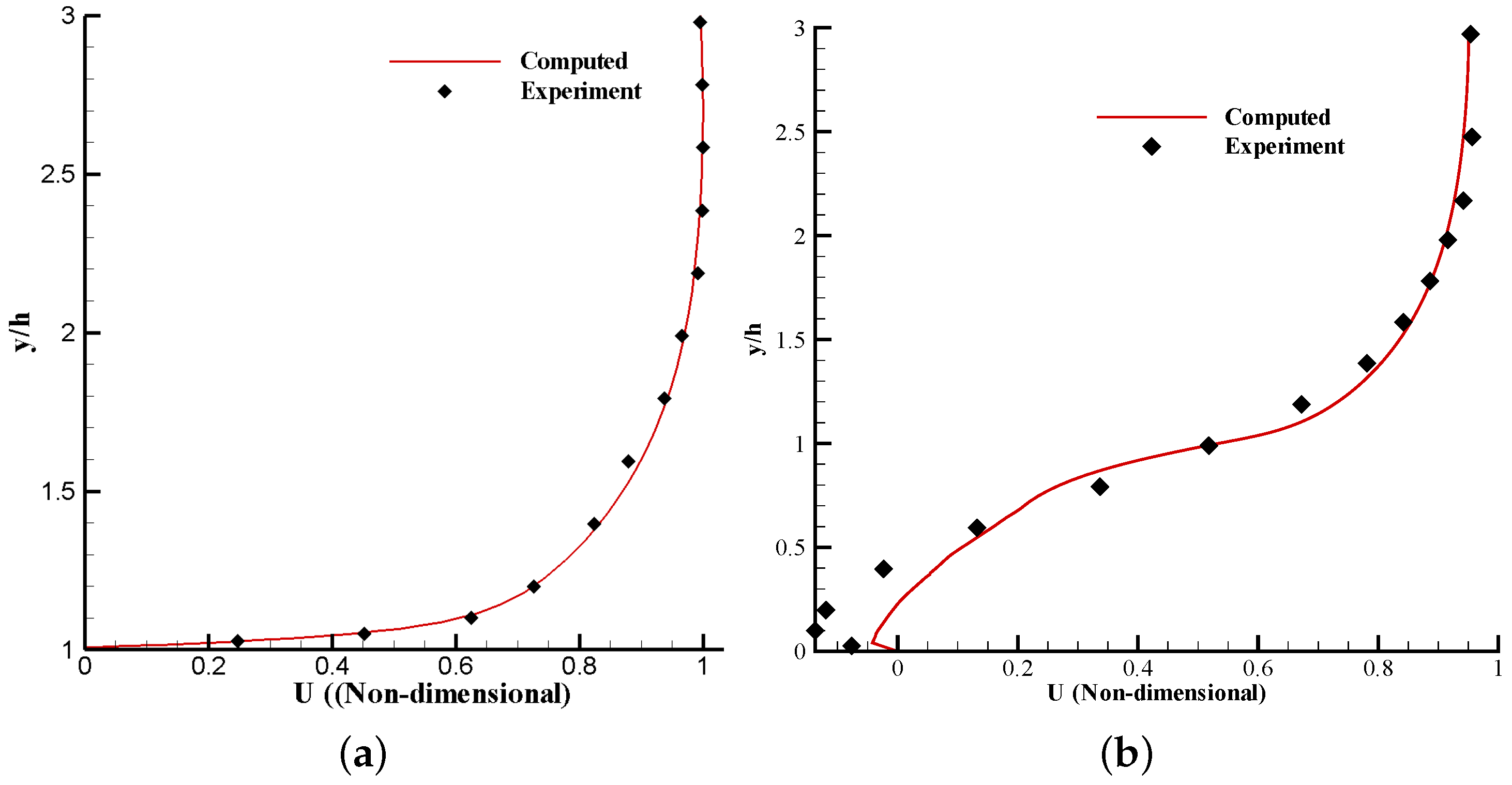
3.6. Turbulent Flow Past a Backward-Facing Step
4. Conclusions
Author Contributions
Conflicts of Interest
Nomenclature
| CAA | computational aeroacoustics. |
| CFD | computational fluid dynamics. |
| CFL | Courant-Friedrichs-Lewy. |
| DES | detached-eddy simulation. |
| DDES | delayed detached-eddy simulation. |
| GCL | geometric conservation law. |
| LES | large eddy simulation. |
| MPI | message passing interface. |
| NSCBC | Navier–Stokes characteristic boundary conditions. |
| RANS | Reynolds-averages Navier–Stokes. |
| R-K | Runge-Kutta. |
| SA | Spalart-Allmaras. |
| a | speed of sound. |
| two-dimensional drag coefficient. | |
| two-dimensional lift coefficient. | |
| specific heat at constant pressure. | |
| pressure coefficient . | |
| specific heat at constant volume. | |
| d | diameter, turbulent length scale. |
| detached-eddy simulation turbulent length scale. | |
| specific internal energy. | |
| f | frequency. |
| viscous damping term. | |
| production term of turbulent viscosity. | |
| h | height. |
| J | Jacobian. |
| k | thermal conductivity. |
| l | characteristic length. |
| M | Mach number. |
| p | static pressure. |
| Pr | Prandtl number . |
| q | heat flux. |
| r | radius. |
| Re | Reynolds number . |
| St | Strouhal number . |
| t | time. |
| T | temperature. |
| U | general velocity. |
| velocity vector components in Cartesian coordinates . | |
| Cartesian coordinates. | |
| destruction term of turbulent viscosity. | |
| ratio of specific heats, . | |
| general angle. | |
| von Karman constant. | |
| molecular dynamic viscosity. | |
| effective dynamic viscosity, . | |
| turbulent dynamic viscosity. | |
| kinematic viscosity. | |
| turbulent transport variable. | |
| turbulent kinematic viscosity. | |
| generalised coordinate system. | |
| density. | |
| viscous stress. | |
| perturbation value. | |
| reference value. | |
| freestream value. | |
| non-dimensional value. | |
| root mean square value. |
Appendix A. Integrability Conditions for Partial Differential Equations
Appendix B. Characteristic Transformation Matrices
References
- Singer, B.A.; Guo, Y. Development of computational aeroacoustic tools for airframe noise calculations. Int. J. Comput. Fluid D. 2004, 18, 455–469. [Google Scholar] [CrossRef]
- Tam, C.K.W. Computational acoustics: Issues and methods. AIAA J. 1995, 33, 1788–1796. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Webb, J.C. Dispersion-Relation-Perserving finite difference schemes for computational acoustics. J. Comput. Phys. 1993, 107, 262–281. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, D.J. Optimised compact finite difference schemes with maximum resolution. AIAA J. 1996, 34, 887–893. [Google Scholar] [CrossRef]
- Hixon, R. Prefactored small-stencil compact schemes. J. Comput. Phys. 2000, 165, 522–541. [Google Scholar] [CrossRef]
- Thompson, K.W. Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 1987, 68, 1–24. [Google Scholar] [CrossRef]
- Thompson, K.W. Time dependent boundary conditions for hyperbolic systems II. J. Comput. Phys. 1990, 89, 439–461. [Google Scholar] [CrossRef]
- Lele, S.K. Compact finite difference schemes with spectral-like resolution. J. Comput. Phys. 1992, 103, 16–42. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, D.J. Generalized characteristic boundary conditions for computational aeroacoustics. AIAA J. 2000, 38, 2040–2049. [Google Scholar] [CrossRef]
- Kim, J.W.; Lee, D.J. Generalized characteristic boundary conditions for computational aeroacoustics, Part 2. AIAA J. 2004, 42, 47–55. [Google Scholar] [CrossRef]
- Sunderland, J.C.; Kennedy, C.A. Improved boundary conditions for viscous, reacting, compressible flows. J. Comput. Phys. 2003, 191, 502–524. [Google Scholar] [CrossRef]
- Yoo, C.S.; Wang, Y.; Trouve, A.; Im, H.G. Characteristic boundary conditions for direct simulations of turbulent counterflow flames. Combust. Theor. Model. 2005, 9, 617–646. [Google Scholar] [CrossRef]
- Yoo, C.S.; Im, H.G. Characteristic boundary conditions for simulations of compressible reacting flows with multi-dimensional, viscous and reaction effects. Combust. Theor. Model. 2007, 11, 259–286. [Google Scholar] [CrossRef]
- Sumi, T.; Kurotaki, T. Generalized characteristic interface conditions for accurate multi-block computations. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. Number AIAA-2006-1272. [Google Scholar]
- Kim, J.W.; Lee, D.J. Characteristic interface conditions for multiblock high-order computation on singular structured grid. AIAA J. 2003, 41, 2341–2348. [Google Scholar] [CrossRef]
- Sumi, T.; Kurotaki, T.; Hiyama, J. Practical multi-block computations with generalized characteristic interface conditions around complex geometry. In Proceedings of the 18th AIAA Computational Fluid Dynamics Conference, Miami, FL, USA, 25–28 June 2007. Number AIAA-2007-4471. [Google Scholar]
- Chen, X.; Zha, G.C. Implicit application of non-reflective boundary conditions for Navier-Stokes equations in generalized coordinates. Int. J. Numer. Methods Fluids 2006, 50, 767–793. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A one-equation turbulence model for aerodynamic flows. In Proceedings of the 30th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. Number AIAA-1992-0439. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. Comments on the feasibility of LES for wings and on a hybrid RANS/LES approach. Proceedings of First AFOSR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997. [Google Scholar]
- Spalart, P.R.; Deck, S.; Shur, M.L.; Squires, K.D.; Strelets, M.K.; Travin, A. A new version of detached-eddy simulation, resistant to ambiguous grid densities. Theor. Comp. Fluid Dyn. 2006, 20, 181–195. [Google Scholar] [CrossRef]
- Kim, J.W. Optimised boundary compact finite difference schemes for computational aeroacoustics. J. Comput. Phys. 2007, 225, 995–1019. [Google Scholar] [CrossRef]
- Hu, F.Q.; Hussaini, M.Y.; Manthey, J. Low-dissipation and -dispersion Runge-Kutta schemes for computational acoustics. J. Comput. Phys. 1996, 124, 177–191. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V. On the use of higher-order finite-difference schemes on curvilinear and deforming meshes. J. Comput. Phys. 2002, 181, 155–185. [Google Scholar] [CrossRef]
- Khanal, B. Numerical Modelling of Cavity Flow and Noise. Ph.D. Thesis, Cranfield University, Shrivenham, Swindon, UK, 2010. [Google Scholar]
- Pulliam, T.H.; Steger, J.L. Implicit finite difference simulation of three dimensional compressible flows. AIAA J. 1980, 18, 159–167. [Google Scholar] [CrossRef]
- Thomas, P.D.; Lombard, C.K. Geometric conservation law and its application to flow computations on moving grids. AIAA J. 1979, 17, 1030–1058. [Google Scholar] [CrossRef]
- Chung, Y.M.; Tucker, P.G. Accuracy of higher-order finite difference schemes on non-uniform grids. AIAA J. 2003, 41, 1609–1611. [Google Scholar] [CrossRef]
- Visbal, M.R.; Gaitonde, D.V. Very high-order spatially implicit schemes for computational acoustics on curvilinear meshes. J. Comput. Acoust. 2001, 9, 1259–1286. [Google Scholar] [CrossRef]
- Khanal, B.; Knowles, K.; Saddington, A.J. Study of cavity unsteady flowfield. In Proceedings of the 4th International Symposium on Integrating CFD and Experiments in Aerodynamics, Sint-Genesius-Rode, Belgium, 14–16 September 2009. [Google Scholar]
- Tam, C.K.W.; Hardin, J.C. Second Computational Aeroacoustics Workshop on Benchmark Problems; Technical Report CP-1997-3352; NASA Langley Research Center: Hampton, VA, USA, 1997.
- Schlichting, H. Boundary-Layer Theory, 7th ed.; McGraw Hill: New York, NY, USA, 1979. [Google Scholar]
- Jovic, S.; Driver, D.M. Backward-Facing Step Measurements at Low Reynolds Number, Reh = 5000; Technical Report TM-1994-108807; NASA Ames Research Center: Mountain View, CA, USA, 1994.
- Wilcox, D.C. Turbulence Modelling for CFD, 3rd ed.; DCW Industries: La Cañada Flintridge, CA, USA, 2006. [Google Scholar]
- Forsyth, A.R. A Treatise on Differential Equations, 3rd ed.; Macmillan and Co. Ltd.: London, UK, 1903. [Google Scholar]







| Cases | Strouhal Number (St) | Drag Coefficient () | rms Lift Coefficient |
|---|---|---|---|
| Experiment | |||
| Computed | 0.212 | 1.202 | 0.612 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khanal, B.; Saddington, A.; Knowles, K. An Efficiently Parallelized High-Order Aeroacoustics Solver Using a Characteristic-Based Multi-Block Interface Treatment and Optimized Compact Finite Differencing. Aerospace 2017, 4, 29. https://doi.org/10.3390/aerospace4020029
Khanal B, Saddington A, Knowles K. An Efficiently Parallelized High-Order Aeroacoustics Solver Using a Characteristic-Based Multi-Block Interface Treatment and Optimized Compact Finite Differencing. Aerospace. 2017; 4(2):29. https://doi.org/10.3390/aerospace4020029
Chicago/Turabian StyleKhanal, Bidur, Alistair Saddington, and Kevin Knowles. 2017. "An Efficiently Parallelized High-Order Aeroacoustics Solver Using a Characteristic-Based Multi-Block Interface Treatment and Optimized Compact Finite Differencing" Aerospace 4, no. 2: 29. https://doi.org/10.3390/aerospace4020029
APA StyleKhanal, B., Saddington, A., & Knowles, K. (2017). An Efficiently Parallelized High-Order Aeroacoustics Solver Using a Characteristic-Based Multi-Block Interface Treatment and Optimized Compact Finite Differencing. Aerospace, 4(2), 29. https://doi.org/10.3390/aerospace4020029