Fixed-Wing UAV Attitude Estimation Using Single Antenna GPS Signal Strength Measurements
Abstract
:1. Introduction
2. Methodology
2.1. Satellite Elevation Angle with Respect to Antenna Bore-Sight, α
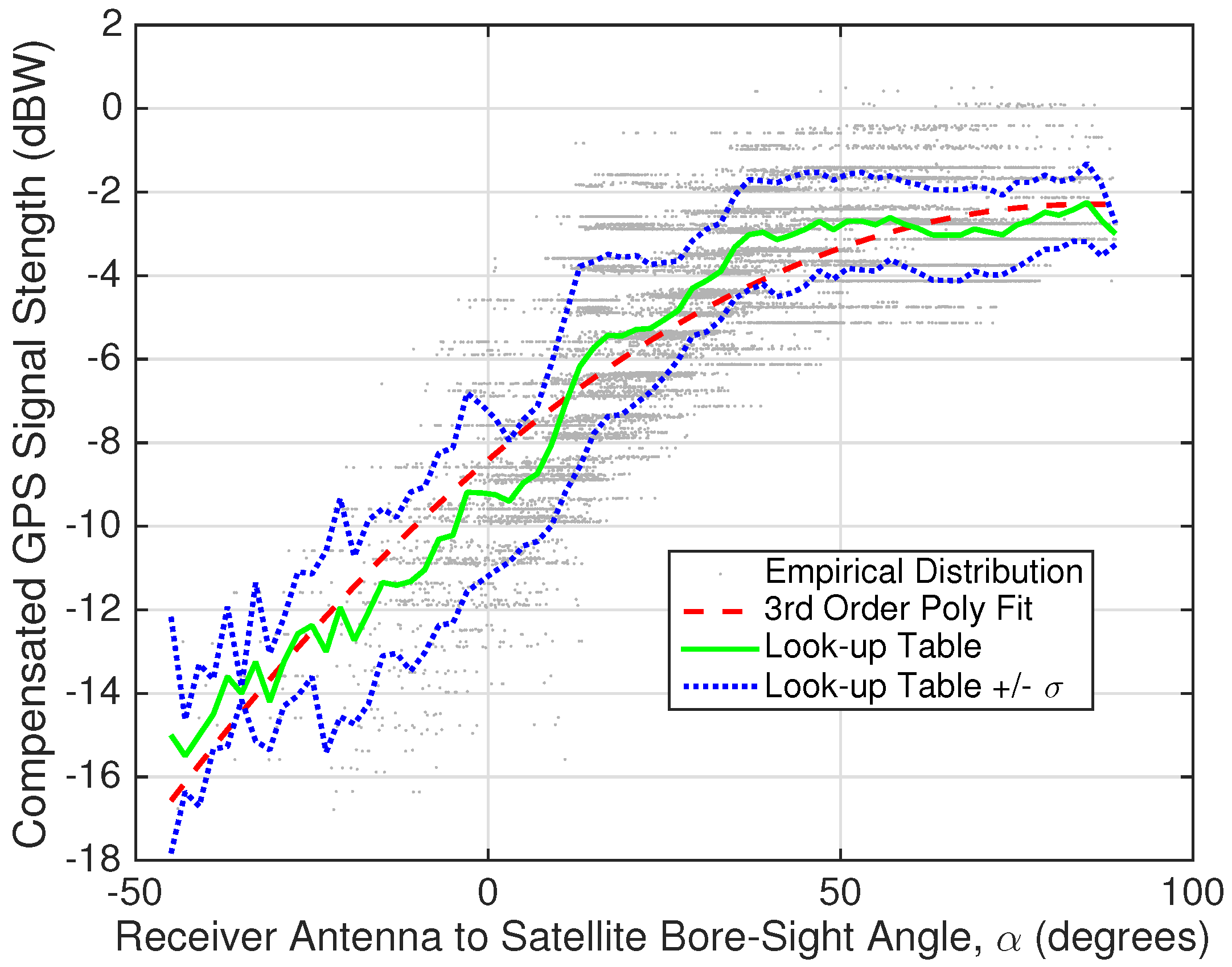
2.2. GPS Signal Strength to α Mapping
2.3. Compensating GPS Signal Strength Measurements for Known Effects
2.4. Look-up Table Calibration
2.5. Polynomial Fit Calibration
2.6. Elevation Dependent Weighting of Signal Strength Observations
2.7. Process Model for UAV Attitude and GPS Heading
2.8. Nonlinear Kalman Filter
3. Experimental Set-up
4. Results
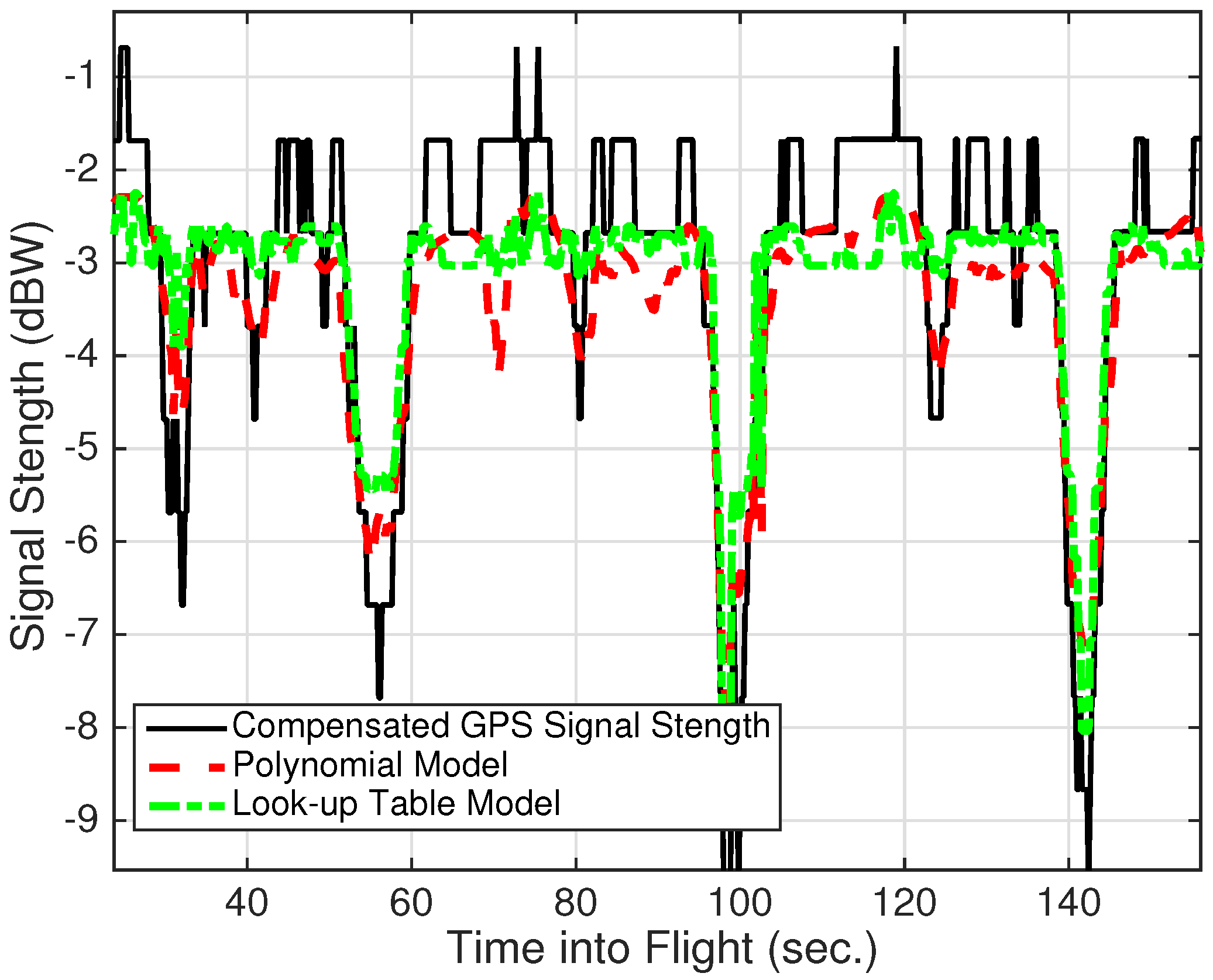
4.1. Calibration Model
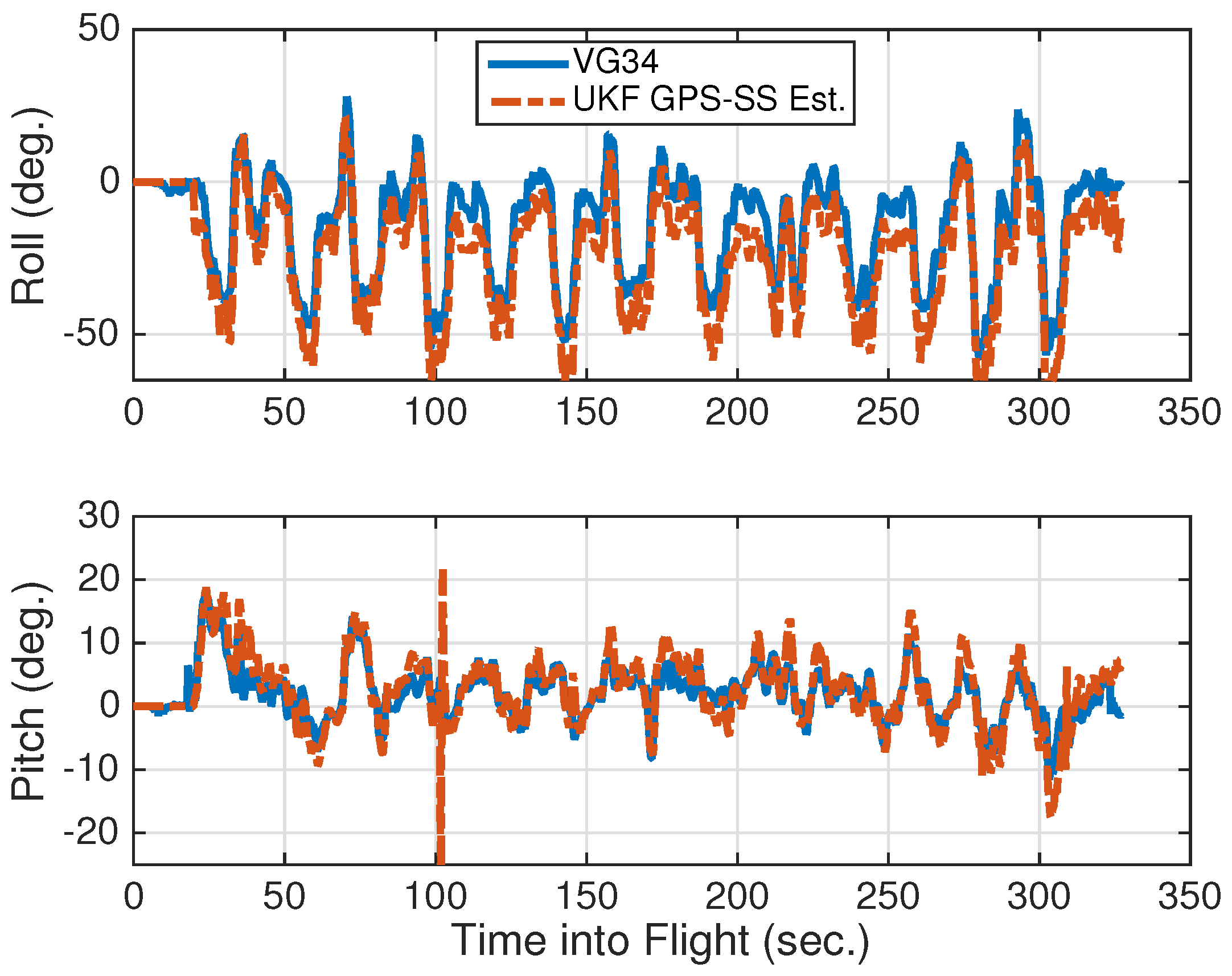
4.2. Attitude Estimation
- Poly-Flat: Using the polynomial model without elevation dependent weighting.
- Poly-ElvDep: Using the polynomial model with elevation dependent weighting.
- LUT-Flat: Using the look-up table model without elevation dependent weighting.
- LUT-ElvDep: Using the look-up table model with elevation dependent weighting.
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| ECEF | Earth Centered Earth Fixed |
| GLONASS | Globalnaya Navigazionnaya Sputnikovaya Sistema |
| GPS | Global Positioning System |
| GPS-MET | GPS Metrology Mission |
| IMU | Inertial Measurement Unit |
| PPS | Pulse Per Second |
| PVA | Position, Velocity, Attitude |
| SNR | Signal to Noise Ration |
| UAV | Unmanned Aerial Vehicle |
| UKF | Unscented Kalman Filter |
| VG34 | Vertical Gyro Model Number 34 |
| WVU | West Virginia University |
References
- Kerns, A.J.; Shepard, D.P.; Bhatti, J.A.; Humphreys, T.E. Unmanned aircraft capture and control via GPS spoofing. J. Field Robot. 2014, 31, 617–636. [Google Scholar] [CrossRef]
- Petritoli, E.; Giagnacovo, T.; Leccese, F. Lightweight GNSS/IRS integrated navigation system for UAV vehicles. In Metrology for Aerospace (MetroAeroSpace); IEEE: Benevento, Italy, 2014; pp. 56–61. [Google Scholar]
- Gross, J.N.; Gu, Y.; Rhudy, M.B.; Gururajan, S.; Napolitano, M.R. Flight-test evaluation of sensor fusion algorithms for attitude estimation. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 2128–2139. [Google Scholar] [CrossRef]
- Petritoli, E.; Leccese, F. Improvement of altitude precision in indoor and urban canyon navigation for small flying vehicles. In Metrology for Aerospace (MetroAeroSpace); IEEE: Rome, Italy, 2015; pp. 56–60. [Google Scholar]
- Gu, Y.; Gross, J.N.; Rhudy, M.B.; Lassak, K. A Fault-Tolerant Multiple Sensor Fusion Approach Applied to UAV Attitude Estimation. Int. J. Aerosp. Eng. 2016, 2016, 6217428. [Google Scholar] [CrossRef]
- Axelrad, P.; Behre, C.P. Satellite attitude determination based on GPS signal-to-noise ratio. Proc. IEEE 1999, 87, 133–144. [Google Scholar] [CrossRef]
- Wang, C.; Walker, R.A.; Moody, M.P. An Improved Single Antenna Attitude System Based on GPS Signal Strength. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, San Francisco, CA, USA, 15–18 August 2005.
- Lightsey, E.G.; Madsen, J. Three-axis attitude determination using global positioning system signal strength measurements. J. Guid. Control Dyn. 2003, 26, 304–310. [Google Scholar] [CrossRef]
- Ang, P.; Roth, N.; Bonin, G.; Zee, R.E. Global Navigation Satellite System Based Coarse Attitude Determination on Small Satellites. In Proceedings of the 29th Annual AIAA/USU Conference on Small Satellites, Technical Session X: Advanced Technologies II, SSC15-X-5, Logan, UT, USA, 8–13 August 2015.
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements and Performance Second Edition; Ganga-Jamuna Press: Lincoln, MA, USA, 2006. [Google Scholar]
- Stevens, B.L.; Lewis, F.L. Aircraft Control and Simulation; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Joseph, A. GNSS Solutions: Measuring GNSS Signal Strength. Inside GNSS Eng. Solut. Glob. Navig. Satell. Syst. Community 2010, 5, 20–25. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. Proc. SPIE 1997, 3068. [Google Scholar] [CrossRef]
- Wan, E.A.; van der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the Adaptive Systems for Signal Processing, Communications, and Control Symposium 2000. AS-SPCC. The IEEE 2000, 1–4 October 2000; Lake Louise, AB, Canada; pp. 153–158.
- Simon, D. Optimal State Estimation: Kalman, H Infinity, and Nonlinear Approaches; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Crassidis, J.L.; Junkins, J.L. Optimal Estimation of Dynamic Systems; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Rhudy, M.B.; Gu, Y.; Chao, H.; Gross, J.N. Unmanned Aerial Vehicle Navigation Using Wide-Field Optical Flow and Inertial Sensors. J. Robot. 2015, 501, 251379. [Google Scholar] [CrossRef]
- Rhudy, M.; Gross, J.; Gu, Y.; Napolitano, M.R. Fusion of GPS and redundant IMU data for attitude estimation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012.
- Gross, J.N. Sensor Fusion Based Fault-Tolerant Attitude Estimation Solutions for Small Unmanned Aerial Vehicles. Ph.D. Thesis, West Virginia University, 2011. [Google Scholar]
- Gu, Y.; Gross, J.; Barchesky, F.; Chao, H.; Napolitano, M. Avionic Design for a Sub-Scale Fault Tolerant Flight Control Test-Bed. In Recent Advances in Aircraft Technology; Agarwal, R., Ed.; InTech: Rijeka, Croatia, 2012; pp. 499–522. [Google Scholar]

| Strategy | Roll | Pitch | ||
|---|---|---|---|---|
| (°) | (°) | (°) | σ (°) | |
| Poly-Flat | –10.4 | 5.6 | 2.6 | 4.1 |
| Poly-ElvDep | –9.3 | 4.3 | 0.5 | 3.0 |
| LUT-Flat | –8.2 | 7.6 | –0.3 | 3.2 |
| LUT-ElvDep | –7.0 | 7.3 | –1.1 | 2.7 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gross, J.; Gu, Y.; Rhudy, M. Fixed-Wing UAV Attitude Estimation Using Single Antenna GPS Signal Strength Measurements. Aerospace 2016, 3, 14. https://doi.org/10.3390/aerospace3020014
Gross J, Gu Y, Rhudy M. Fixed-Wing UAV Attitude Estimation Using Single Antenna GPS Signal Strength Measurements. Aerospace. 2016; 3(2):14. https://doi.org/10.3390/aerospace3020014
Chicago/Turabian StyleGross, Jason, Yu Gu, and Matthew Rhudy. 2016. "Fixed-Wing UAV Attitude Estimation Using Single Antenna GPS Signal Strength Measurements" Aerospace 3, no. 2: 14. https://doi.org/10.3390/aerospace3020014
APA StyleGross, J., Gu, Y., & Rhudy, M. (2016). Fixed-Wing UAV Attitude Estimation Using Single Antenna GPS Signal Strength Measurements. Aerospace, 3(2), 14. https://doi.org/10.3390/aerospace3020014







