Vertical Wind Tunnel for Prediction of Rocket Flight Dynamics
Abstract
:1. Introduction
2. Methodology—Wind Tunnel
2.1. Concept and Design
- The flow conditioner was a cylindrical section at the inlet of the tunnel with an internal diameter of 1.4 m and a 9 mm wall thickness. The flow conditioner holds the honeycomb and a mesh screen.
- The reducer took the flow from the 1.4 m internal diameter flow conditioner to the 0.6 m internal diameter test section. This contraction before the test section can also reduce velocity fluctuations and form a more uniform flow. The reducer walls were fabricated from 6 mm bendy ply so that it would fit into the smaller internal diameter of the test section.
- The test section was 2 m long, had an internal diameter of 0.6 m and was formed with 6 mm bendy ply. Due to the length and thin walls of the test section a 77 × 38 mm length of pine was run down each side. The door for the test section was then framed using 75 × 38 mm pine and 17 mm plywood. The frame was then removed and the door cut from the test section. At the bottom of the test section, a metal grille recessed into a plywood ring was placed to protect the fan.
- The diffuser transitioned the flow from the 0.6 m internal diameter test section to the 1 m internal diameter fan housing. The diffuser was also made from 6 mm bendy ply.
- The fan was 1 m diameter and had up to 15 kW available in power. The blade angle was at 23° so was left unchanged. The fan was on wheels, and could be adjusted to meet flush with the diffuser.
2.2. Construction
2.2.1. General Methods
2.2.2. Flow Conditioner and Fan Grille
3. Methodology—Rocket Systems and Modelling
3.1. Improvements to Airframe and Avionics Stack
3.2. Testing Rocket Stability
- Assemble the rocket with a dummy mass motor.
- Measure the center of mass by balancing the rocket on a beam less than 20 mm wide. Mark the center of mass.
- Fix a pipe clamp, with string tied securely to both ends of the pipe clamp to the rocket, at the measured center of mass.
- Feed the string from both sides of the clamp through the two 4 mm holes on the sides of the wind tunnel. Tie the string around the back of the wind tunnel, and tension the ropes to lift the center of mass of the rocket as close as possible to the holes in the side of the wind tunnel.
- Attach the nose tip of the rocket to the vertical string. The purpose of this string is to prevent an unstable rocket from damaging the walls, or prevent the rocket from falling should the clamps slip. The vertical string should be taut only when the nose of the rocket is close to the wind tunnel walls.
- Start the wind tunnel, and check the rocket straightens at 15, 20 and 30 m/s.
3.3. Rocket Roll Dynamics Modelling
3.3.1. Minimal Model
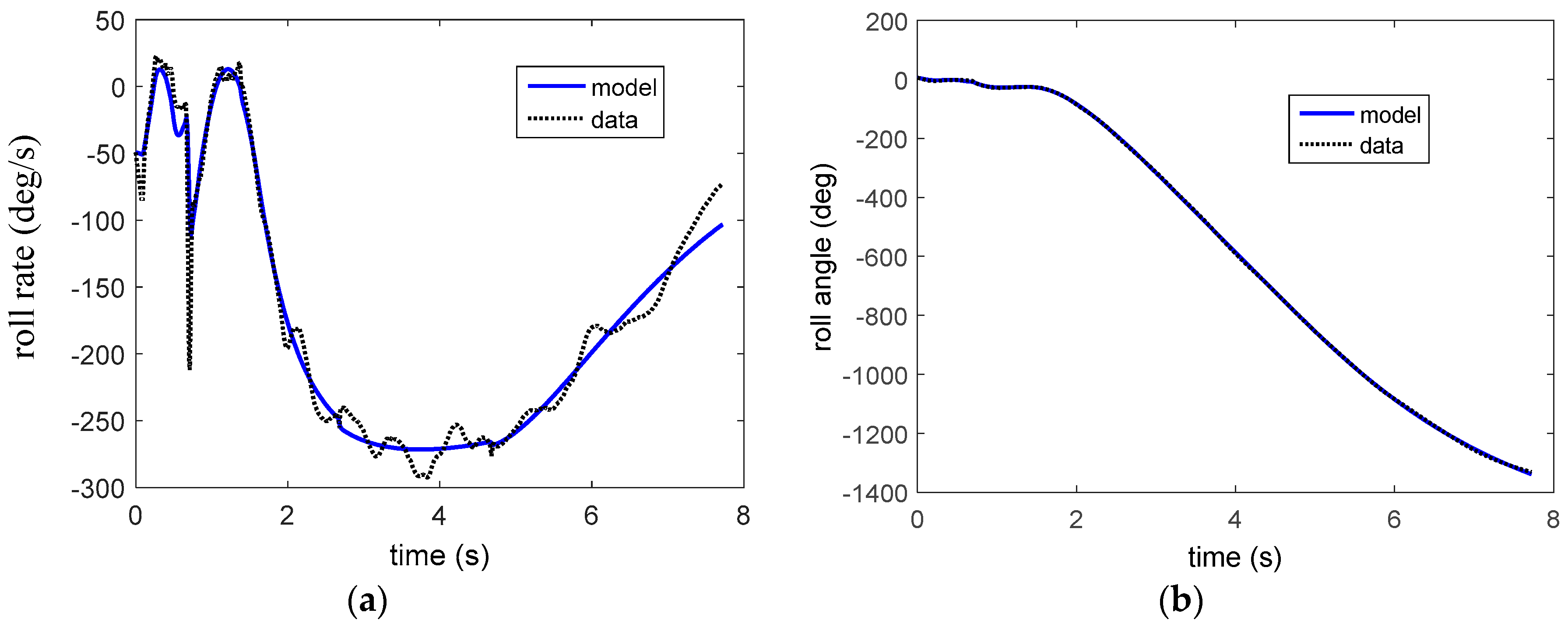
3.3.2. Parameter Identification
4. Results and Discussion
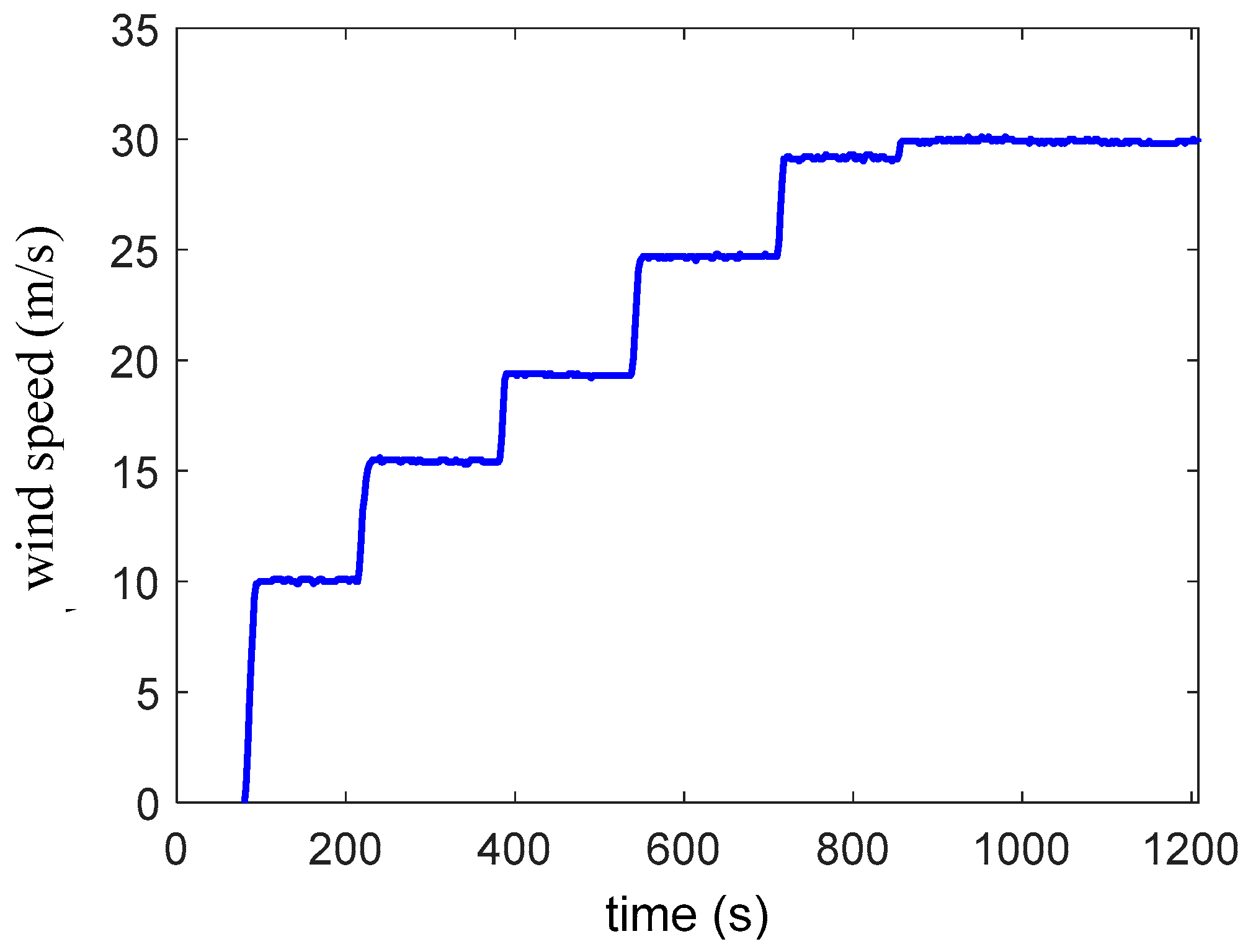
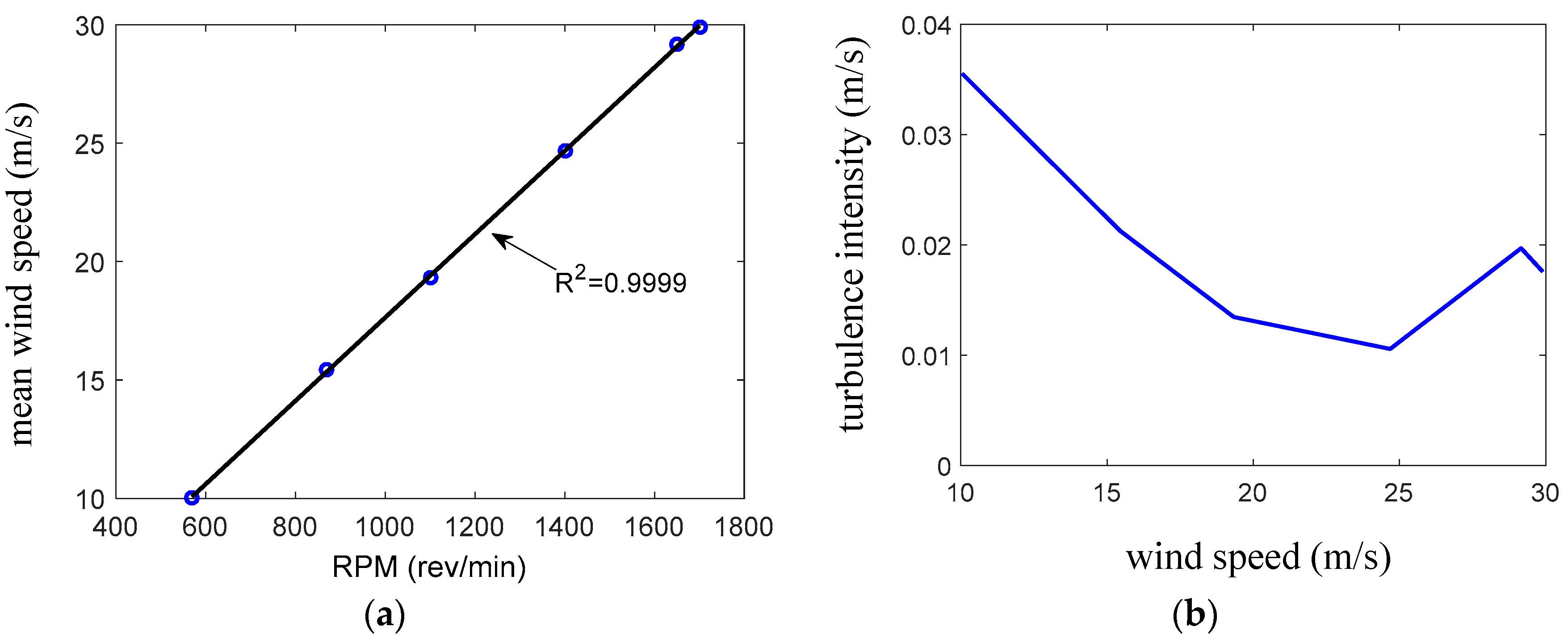
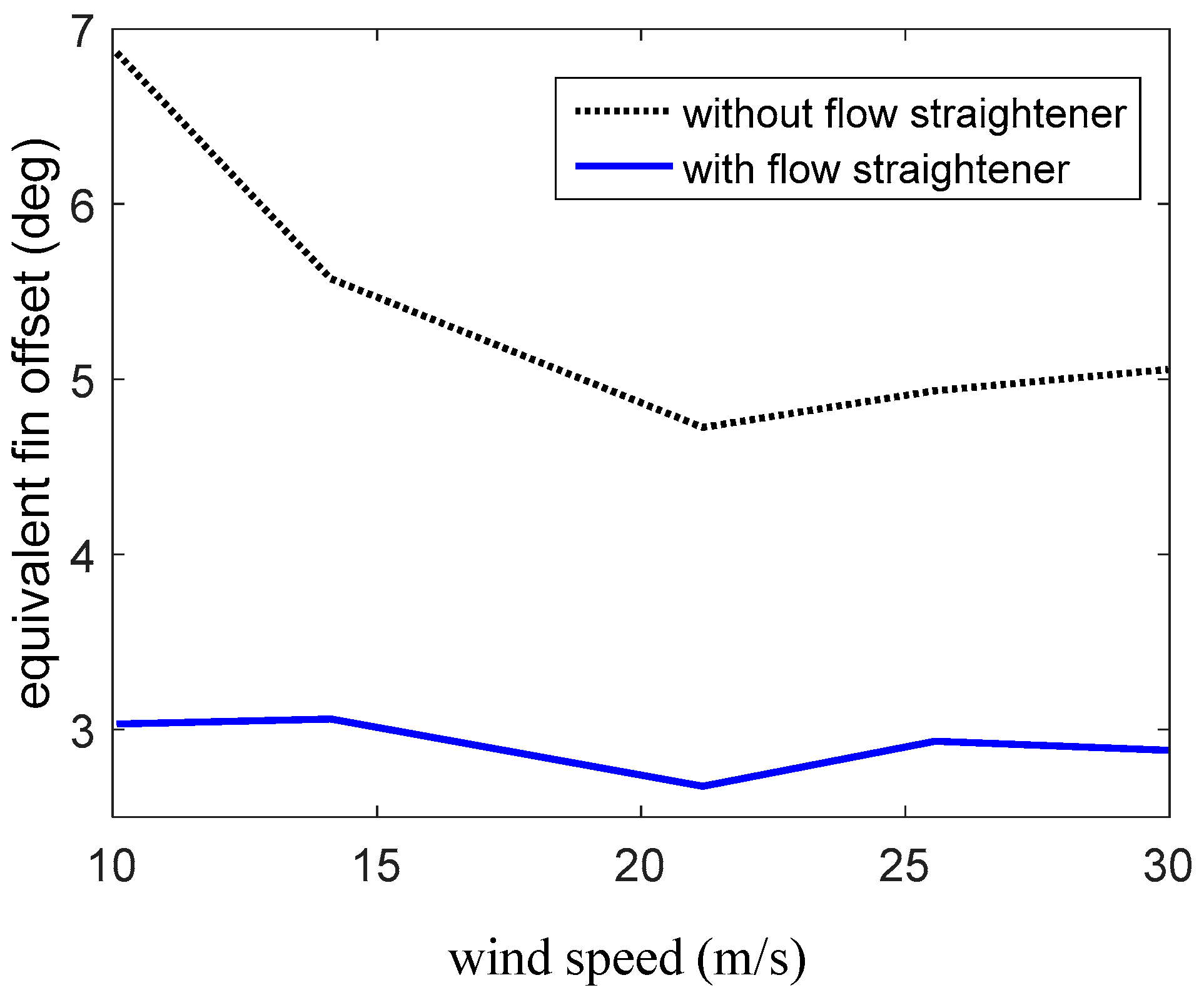
4.1. Wind Tunnel Flow Quality
4.1.1. Turbulence Intensity
4.1.2. Swirl
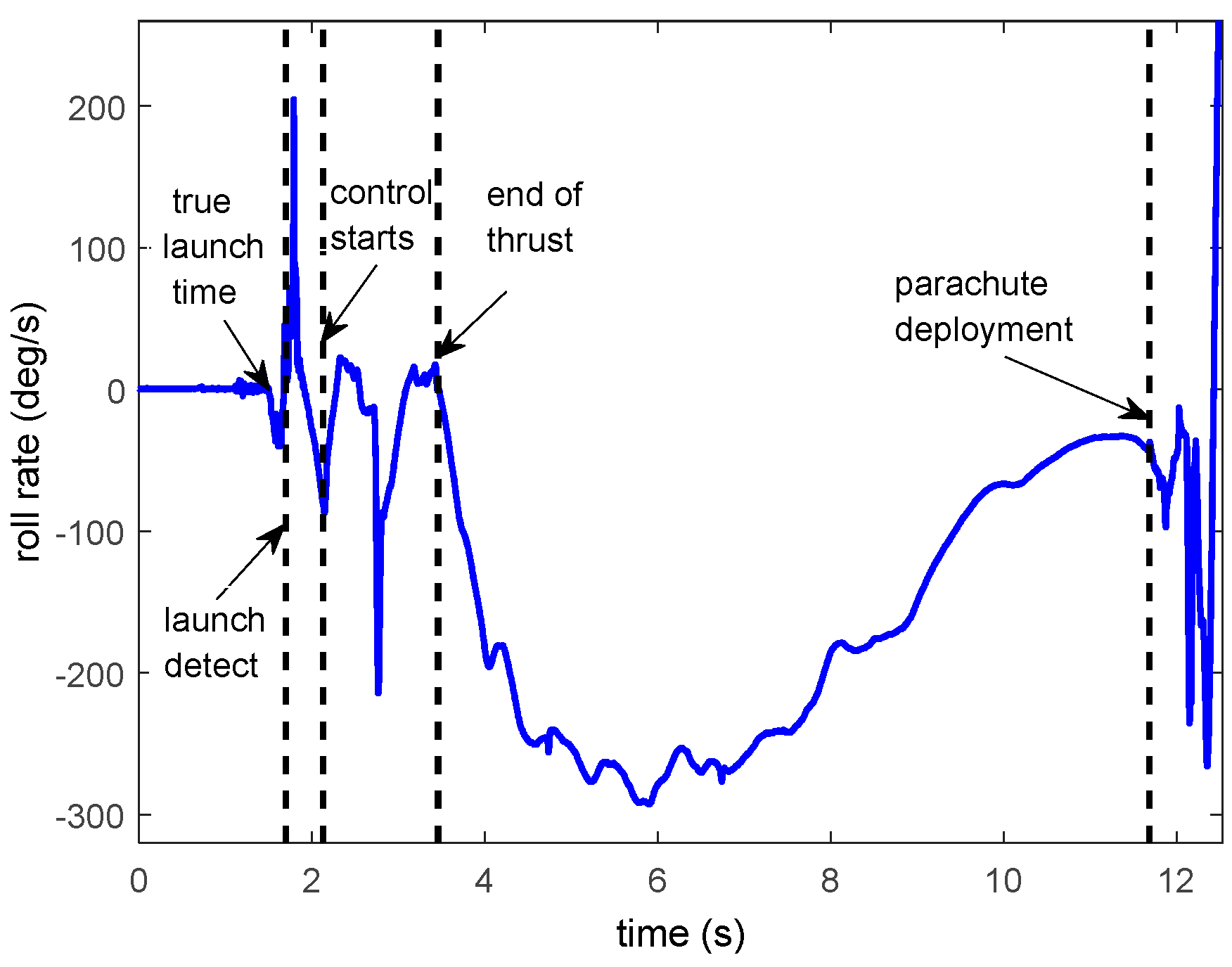
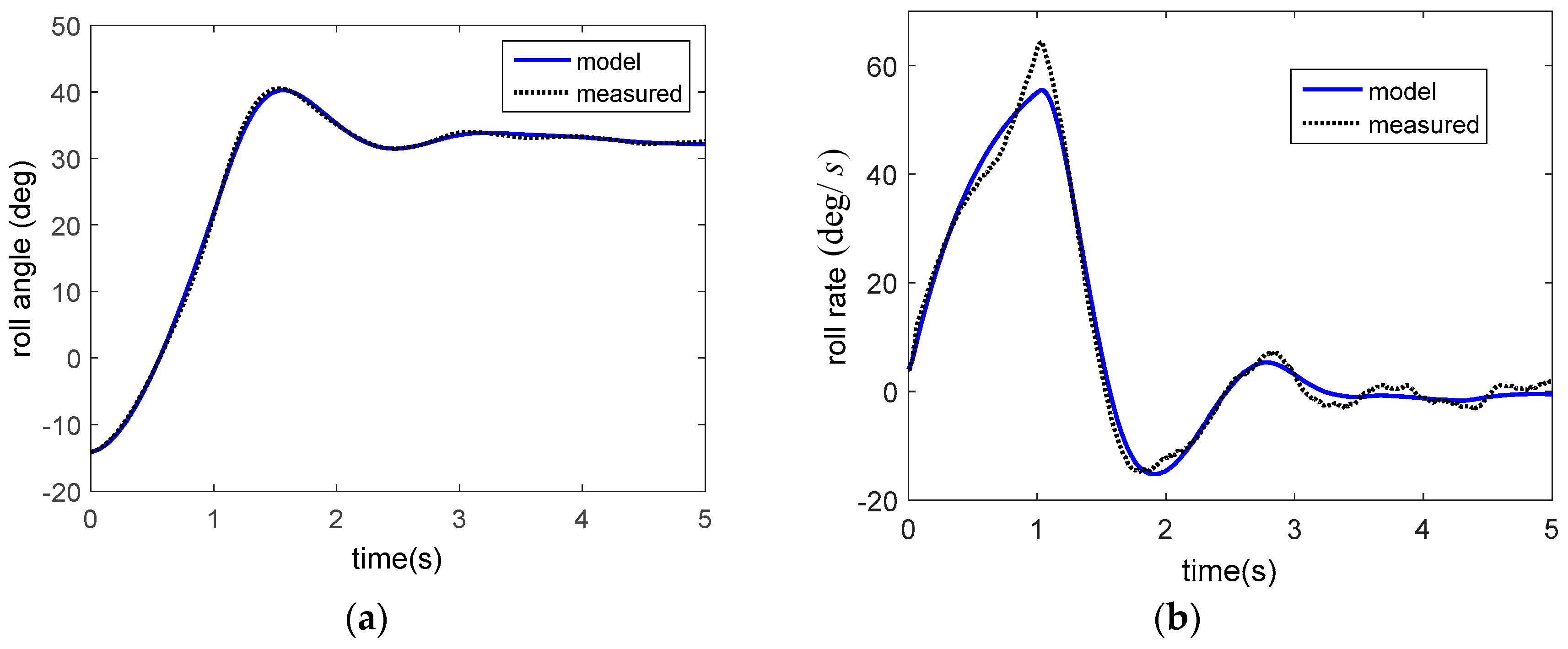
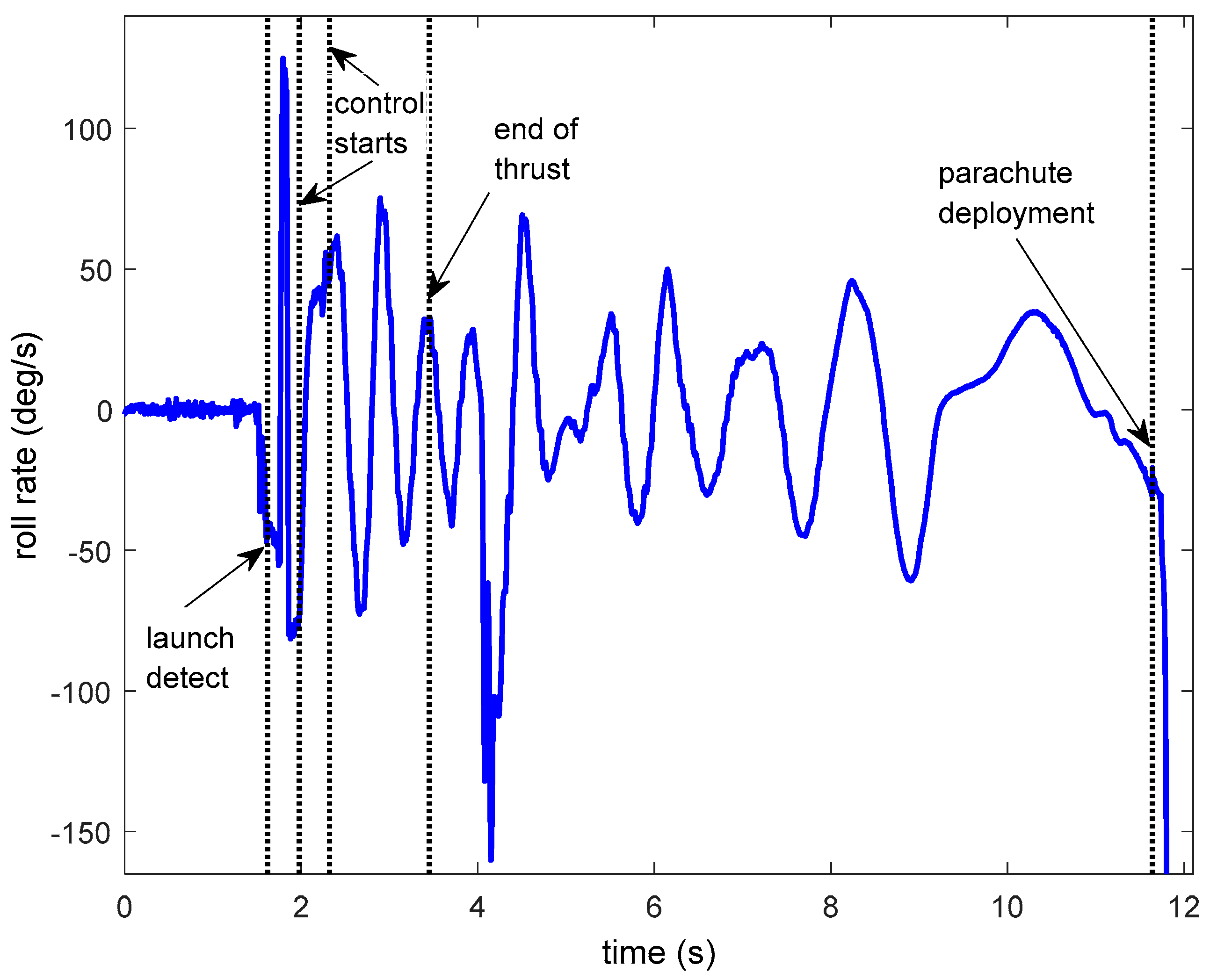
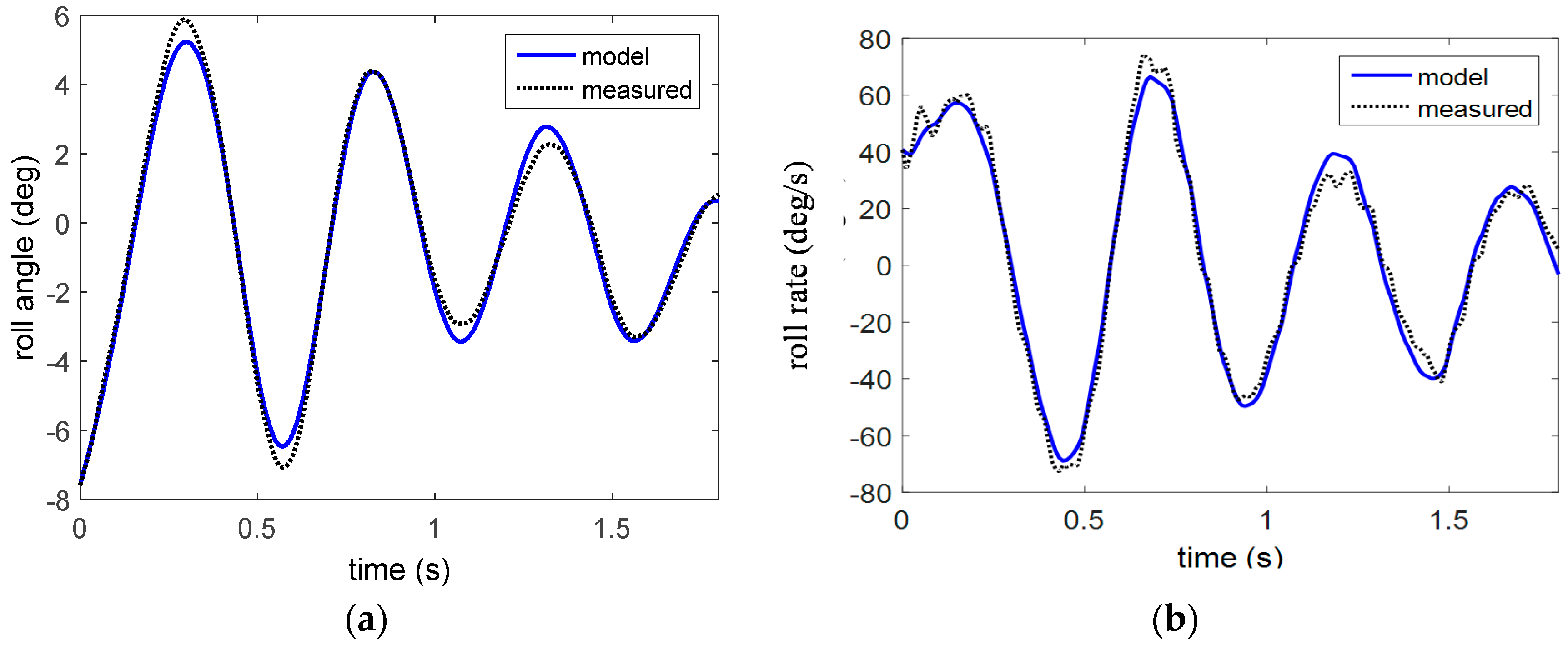
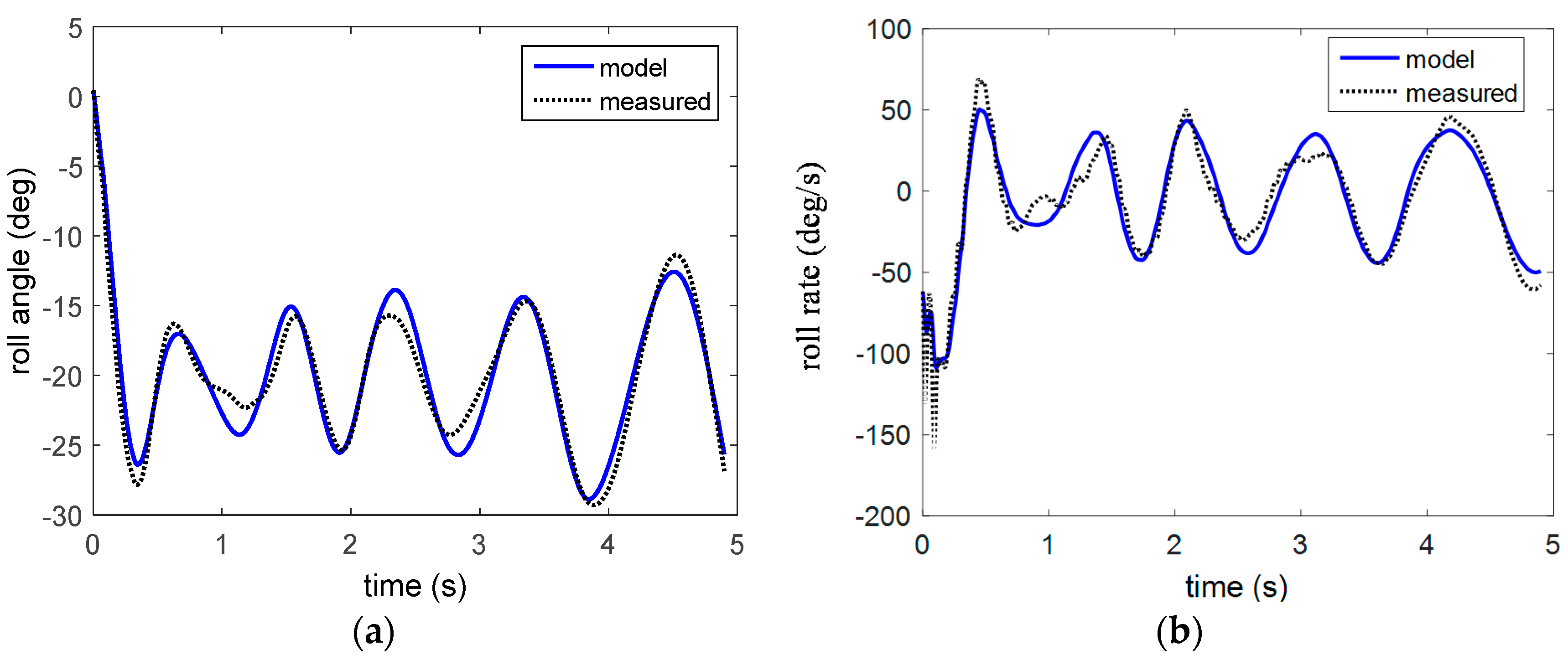
4.2. Tasha III—Launch 1
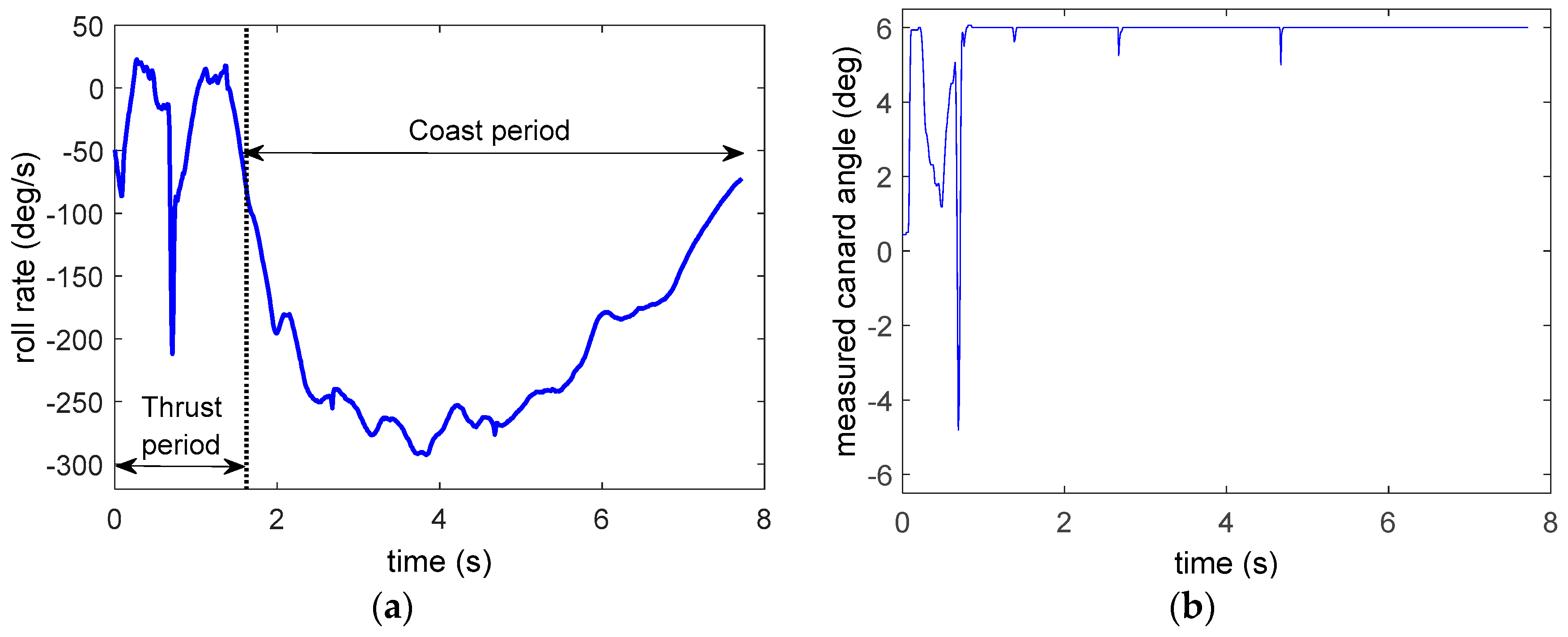
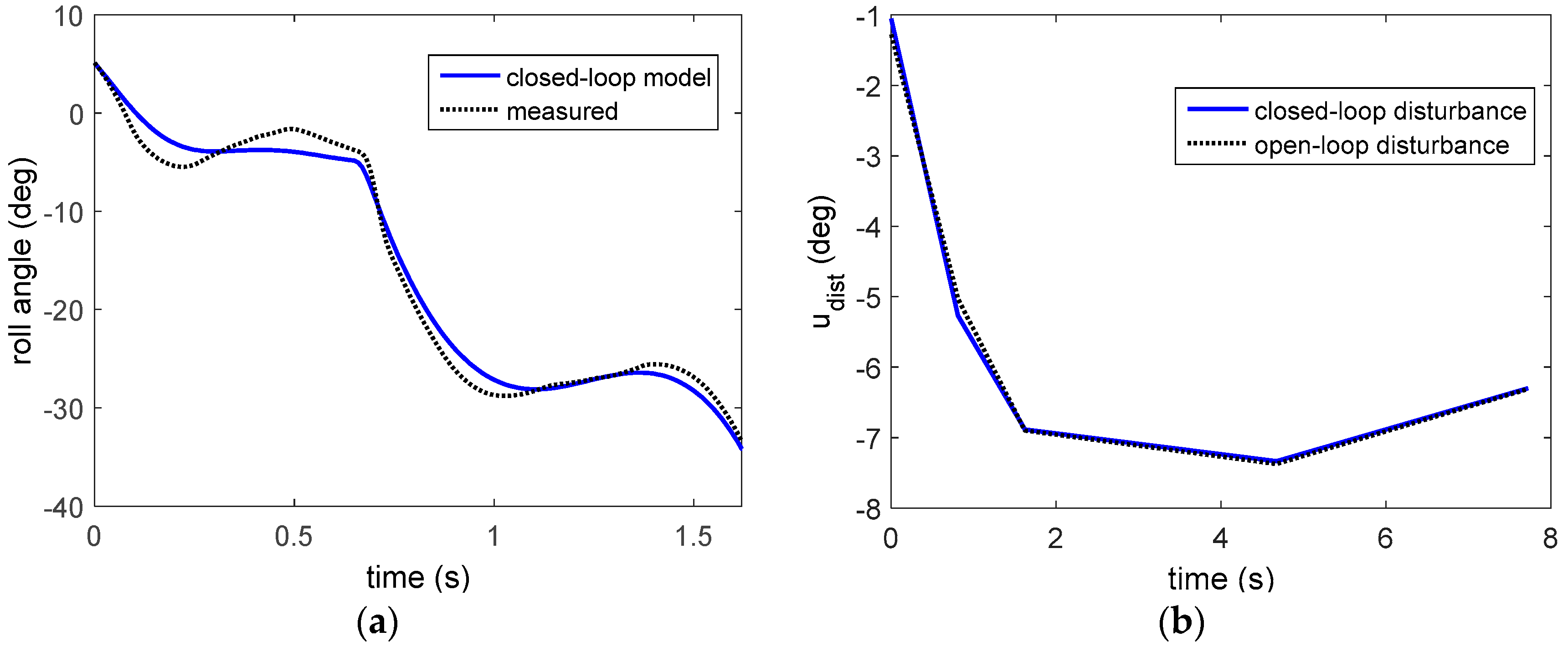
4.3. Tasha III—Launch 2
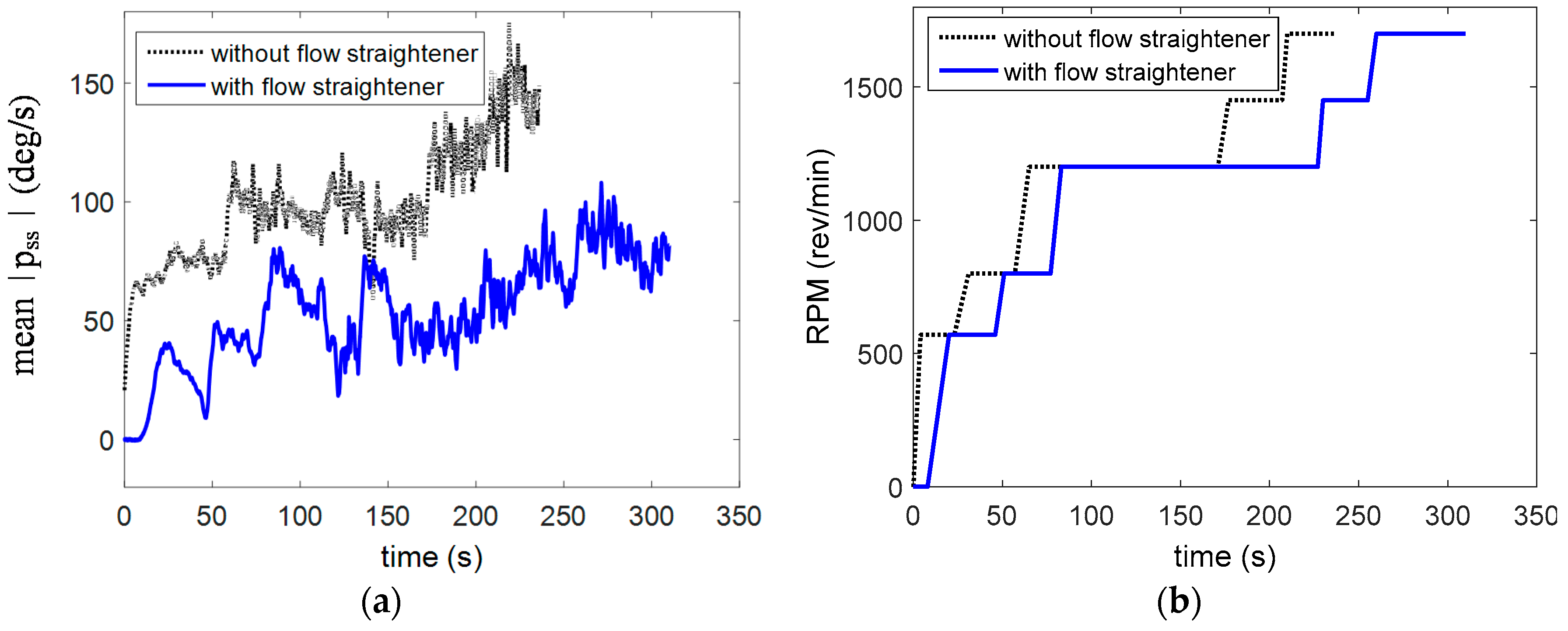
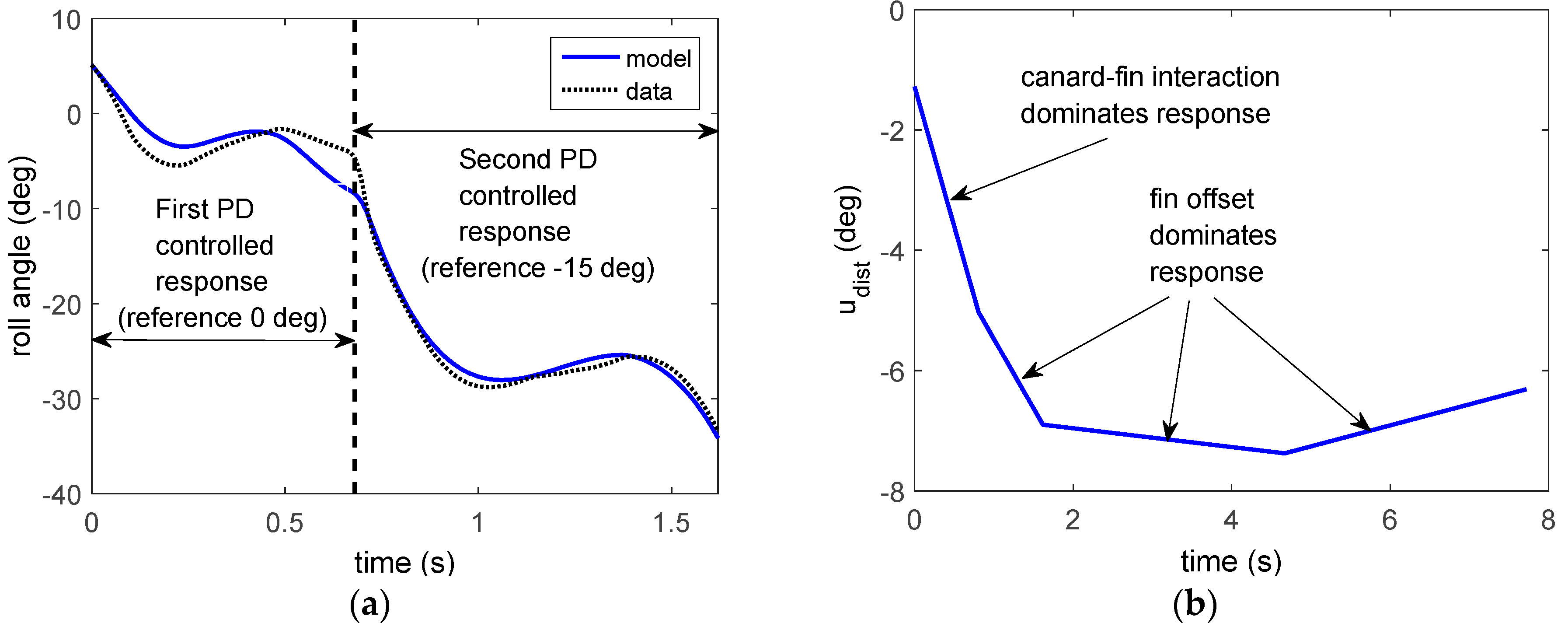
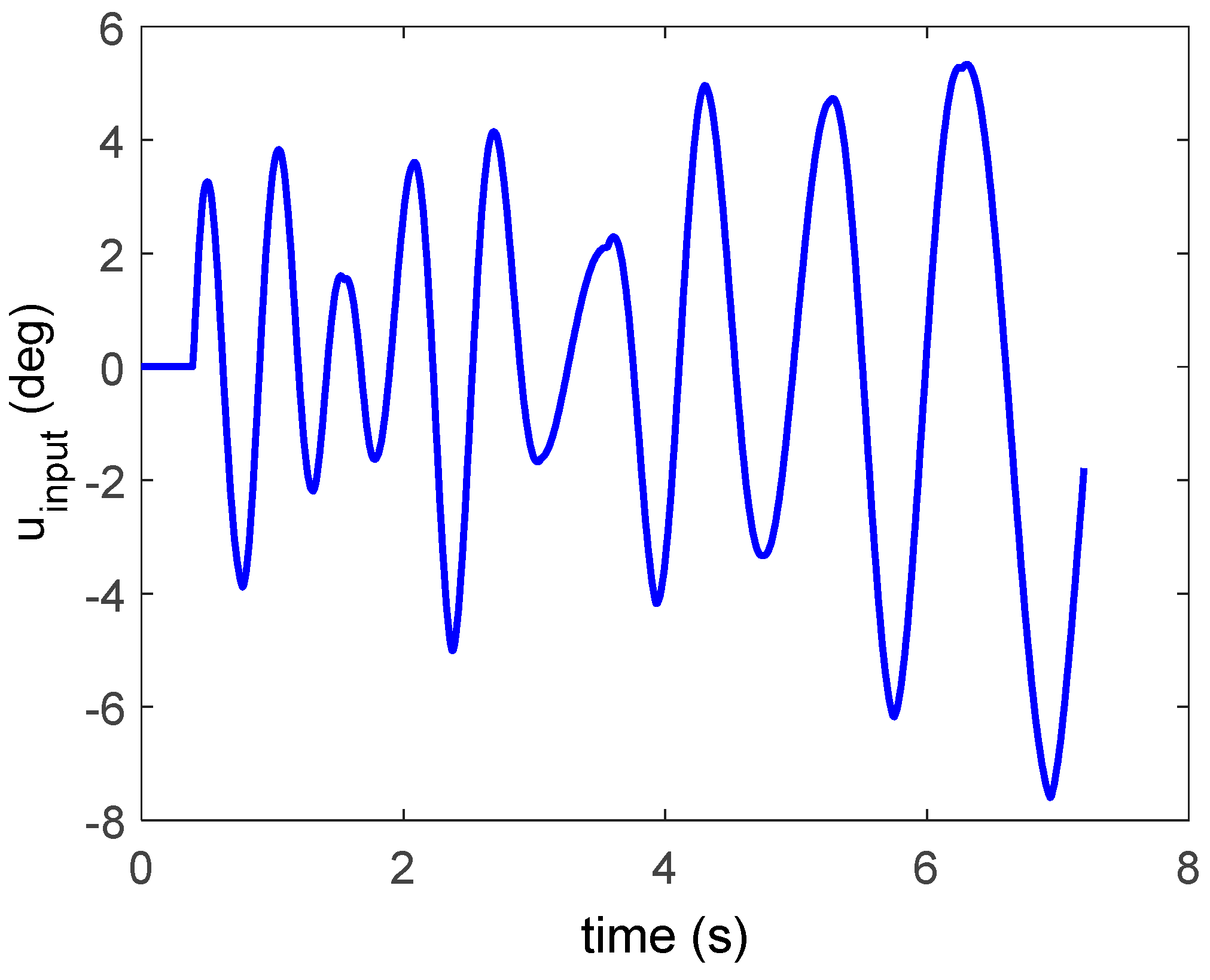
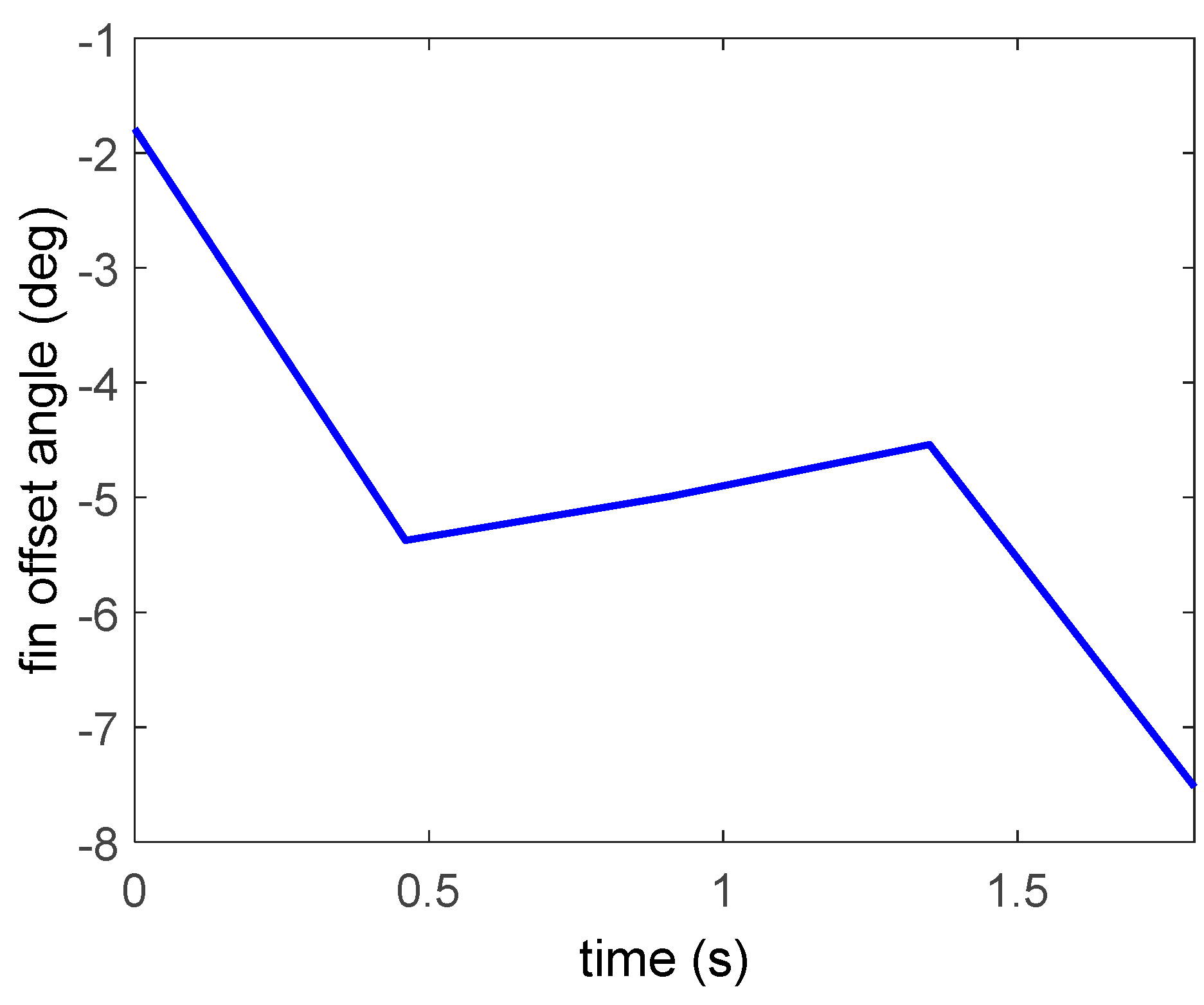
4.3.1. Wind Tunnel Step Responses
4.3.2. Flight Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
Inertia in roll axis (kg/m2) | |
Air density (kg/m3) | |
Damping constant (m2) | |
Torque constant (m) | |
Roll fin angle (rad) | |
Cross sectional area (m2) | |
Roll rate (rad/s) | |
velocity (m/s) | |
Proportional and derivative gains | |
Reference angle (rad) | |
Time-varying disturbance offset angle parameters (rad) | |
Measured roll angle (rad) | |
Open and closed loop numerical solutions to roll equations (rad) | |
Ranges for α, β in the grid search for parameter identification | |
Turbulence intensity (m/s) | |
Standard deviation of wind speed (m/s) | |
Commanded canard angle (rad) | |
Measured canard angle by encoder (rad) | |
Individual canard commands (rad) | |
Individually measured encoders (rad) | |
Minimum and maximum canard limits for actuation (rad) | |
Mean absolute roll rate for open loop and closed loop controllers | |
Mean absolute roll angle for open loop and closed loop controllers | |
Open loop input signal into PD controller |
Abbreviations
| PD | Proportional-derivative |
| NASA | The National Aeronautics and Space Administration |
| UC | University of Canterbury |
| CFD | Computational Fluid Dynamics |
| RPM | Revolutions per minute |
| OL | Open loop |
| CL | Closed loop |
References
- UC Rocketry Project. Available online: http://ucrocketry.org/ (accessed on 1 March 2016).
- Schrijer, F.; Bannink, W. Description and Flow Assessment of the Delft Hypersonic Ludwieg Tube. J. Spacecr. Rocket. 2010, 47, 125–133. [Google Scholar] [CrossRef]
- Spirito, J.D.; Vaughn, M.E., Jr.; Washington, W.D. Numerical Investigation of Canard-Controlled Missile with Planar and Grid fins. J. Spacecr. Rocket. 2003, 40, 363–370. [Google Scholar] [CrossRef]
- Silton, S.I.; Fresconi, F. Effect of Canard Interactions on Aerodynamic Performance of a Fin-Stabilized Projectile. J. Spacecr. Rocket. 2015, 52, 1430–1442. [Google Scholar] [CrossRef]
- Curfman, H.J.; Grisby, C.E. Longitudinal Stability and Control Characteristics of a Canard Missile Configuration for Mach Numbers from 1.1 to 1.93 as Determined from Free-Flight and Wind-Tunnel Investigations; Technical Report for NASA Langley Aeronautical Laboratory: Hampton, VA, USA, 1952. Available online: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19930087105.pdf (accessed on 1 March 2016).
- Dollyhigh, S.M. Subsonic and Supersonic Longitudinal Stability and Control Characteristics of an Aft-Tail Fighter Configuration with Cambered and Uncambered Wings and Cambered Fuselage; Technical Report for NASA Langley Research Center: Hampton, VA, USA, 1977. Available online: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770024149.pdf (accessed on 1 March 2016).
- Blair, A.B., Jr.; Hernandez, G. Effect of Tail-Fin Span on Stability and Control Characteristics of a Canard-Controlled Missile at Supersonic Mach Numbers; Technical Report for NASA Langley Research Center: Hampton, VA, USA, 1983. Available online: http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19830019688.pdf (accessed on 1 March 2016).
- Dillenius, M.F.E.; Lesieutre, D.J.; Hegedus, M.C.; Perkins, S.C., Jr.; Love, J.F.; Lesieutre, T.O. Engineering-Intermediate- and High-Level Aerodynamic Prediction Methods and Applications. J. Spacecr. Rocket. 1999, 36, 609–620. [Google Scholar] [CrossRef]
- Lesieutre, D.J.; Love, J.F.; Dillenius, M.F.E. Prediction of the Nonlinear Aerodynamic Characteristics of Tandem-Control and Rolling-Tail Missiles. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, AIAA 2002-4511, Monterey, CA, USA, 6 August 2002.
- Beresh, S.J.; Smith, J.A.; Henfling, J.F.; Grasser, T.W.; Spillers, R.W. Interaction of a Fin Trailing Vortex with a Downstream Control Surface. J. Spacecr. Rocket. 2009, 46, 318–328. [Google Scholar] [CrossRef]
- Lesieutre, D.J.; Quijano, O. Studies of Vortex Interference Associated with Missile Configurations. In Proceedings of the 52nd Aerospace Sciences Meeting, AIAA SciTech (AIAA 2014-0213), National Harbor, MD, USA, 13–17 January 2014.
- Buchanan, G.; Wright, D.; Hann, C.E.; Bryson, H.; Snowdon, M.; Rao, A.; Slee, A.; Sültrop, H.P.; Jochle-Rings, B.; Barker, Z.; et al. The Development of Rocketry Capability in New Zealand—World Record Rocket and First of its Kind Rocketry Course. Aerospace 2015, 2, 91–117. [Google Scholar] [CrossRef]
- Hann, C.E.; Snowdon, M.; Rao, A.; Winn, O.; Wongvanich, N.; Chen, X.Q. Minimal Modelling Approach to Describe Turbulent Rocket Roll Dynamics in a Vertical Wind Tunnel. Proc. Inst. Mech. Eng. G J. Aerosp. Eng. 2012, 226, 1042–1060. [Google Scholar] [CrossRef]
- Assato, M.; Moraes, L.F.; Chisaki, M. Investigation of a Boundary-Layer Control System by Air Blowing in a Closed-Circuit Subsonic Wind Tunnel. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Aerospace Sciences Meetings, Reno, NV, USA, 8–11 January 2007.
- Seo, Y. Effect of hydraulic diameter of flow straighteners on turbulence intensity in square wind tunnel. HVAC R Res. 2013, 19, 141–147. [Google Scholar]
- Wind Tunnel Design. Available online: http://www-htgl.stanford.edu/bradshaw/tunnel/index.html (accessed on 1 March 2016).
- BBS Timbers Ltd. Available online: http://bbstimbers.co.nz/flexible-plywood-bendy-plywood/ (accessed on 1 March 2016).
- Kestrel AU Pocket Weather Instruments. Available online: http://kestrelmeters.com.au/ (accessed on 1 March 2016).
- Sioruis, G.M. Missile Guidance and Control Systems; Springer-Verlag Inc.: New York, NY, USA, 2004. [Google Scholar]
















| Property | Smokey | Tasha III Launch 1 | Tasha III Launch 2 |
|---|---|---|---|
| Mass | 3.0 kg | 3.47 kg | 3.99 kg |
| Length | 1.52 m | 1.51 m | 1.51 m |
| Z-axis Inertia | 0.00311 kg·m2 | 0.00361 kg·m2 | 0.00393 kg·m2 |
| Fin material | 3D printed ABS | 3D printed PLA with fibreglass lamination | 3D printed PLA with fibre glass lamination |
| Canards | 3D printed ABS | 3D printed ABS | Fibre glass moulded |
| Avionics | Subsonic capable | Subsonic capable with spot tracker | Supersonic capable with spot tracker |
| Step Response | ||||
|---|---|---|---|---|
| 1 | 13 | 10.5 | [−5.59,−7.71] | [1.64,6.23] |
| 2 | 15 | 6.5 | [−5.82,−6.10] | [0.70,2.38] |
| 3 | 22 | 10.5 | [−6.04,−6.35] | [1.13,4.40] |
| 4 | 15 | 6.0 | [−4.18,−7.16] | [0.42,2.08] |
| 5 | 25 | 12.5 | [−5.90,−6.51] | [0.82,2.92] |
| 6 | 23 | 10.5 | [−5.12,−6.25] | [0.26,1.66] |
| 7 | 15 | 10.5 | [−6.11,7.41] | [1.43,5.84] |
| 8 | 27 | 10.0 | [−5.47,−5.44] | [0.60,2.66] |
| Mean | 19.4 | 9.6 | [−5.47,6.62] | [0.88,3.52] |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bryson, H.; Sültrop, H.P.; Buchanan, G.; Hann, C.; Snowdon, M.; Rao, A.; Slee, A.; Fanning, K.; Wright, D.; McVicar, J.; et al. Vertical Wind Tunnel for Prediction of Rocket Flight Dynamics. Aerospace 2016, 3, 10. https://doi.org/10.3390/aerospace3020010
Bryson H, Sültrop HP, Buchanan G, Hann C, Snowdon M, Rao A, Slee A, Fanning K, Wright D, McVicar J, et al. Vertical Wind Tunnel for Prediction of Rocket Flight Dynamics. Aerospace. 2016; 3(2):10. https://doi.org/10.3390/aerospace3020010
Chicago/Turabian StyleBryson, Hoani, Hans Philipp Sültrop, George Buchanan, Christopher Hann, Malcolm Snowdon, Avinash Rao, Adam Slee, Kieran Fanning, David Wright, Jason McVicar, and et al. 2016. "Vertical Wind Tunnel for Prediction of Rocket Flight Dynamics" Aerospace 3, no. 2: 10. https://doi.org/10.3390/aerospace3020010
APA StyleBryson, H., Sültrop, H. P., Buchanan, G., Hann, C., Snowdon, M., Rao, A., Slee, A., Fanning, K., Wright, D., McVicar, J., Clark, B., Harris, G., & Chen, X. Q. (2016). Vertical Wind Tunnel for Prediction of Rocket Flight Dynamics. Aerospace, 3(2), 10. https://doi.org/10.3390/aerospace3020010







