Path Planning Using Concatenated Analytically-Defined Trajectories for Quadrotor UAVs †
Abstract
:1. Introduction
2. Quadrotor Dynamics and Kinematics
3. Trajectory Planning
3.1. Sub-Riemannian Curves for Quadrotor Trajectory Planning
3.2. Trajectory Repositioning and Reorientation
4. Obstacle Detection
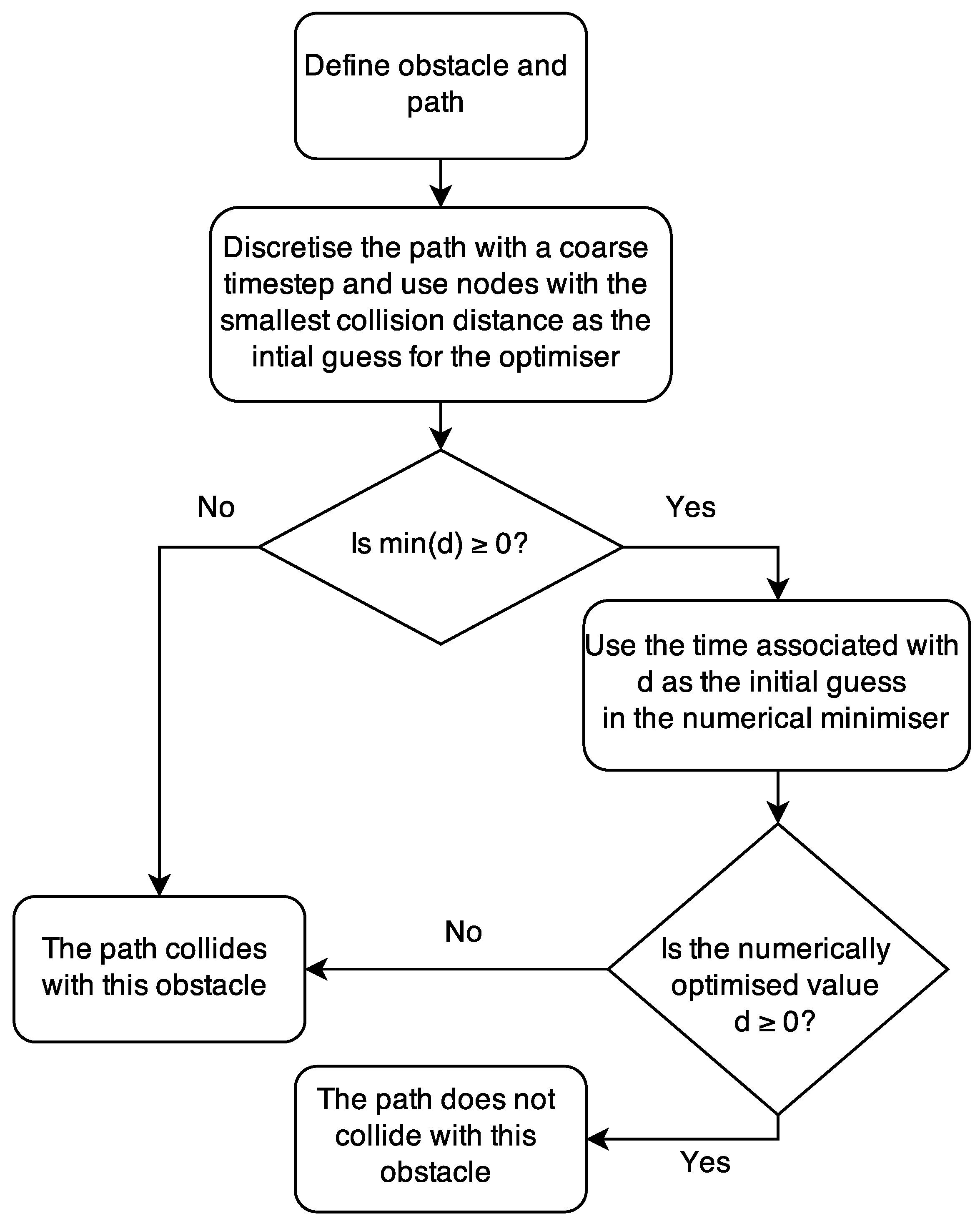
5. Simulations
5.1. Tracking Controller
5.2. Waypoints
| Waypoint | |||
|---|---|---|---|
| 1 | 3 | 4 | 5 |
| 2 | −2 | 7 | 3 |
| 3 | −2 | 0 | 6 |
| 4 | 3 | −4 | 6 |
| 5 | 2 | 0 | 0 |
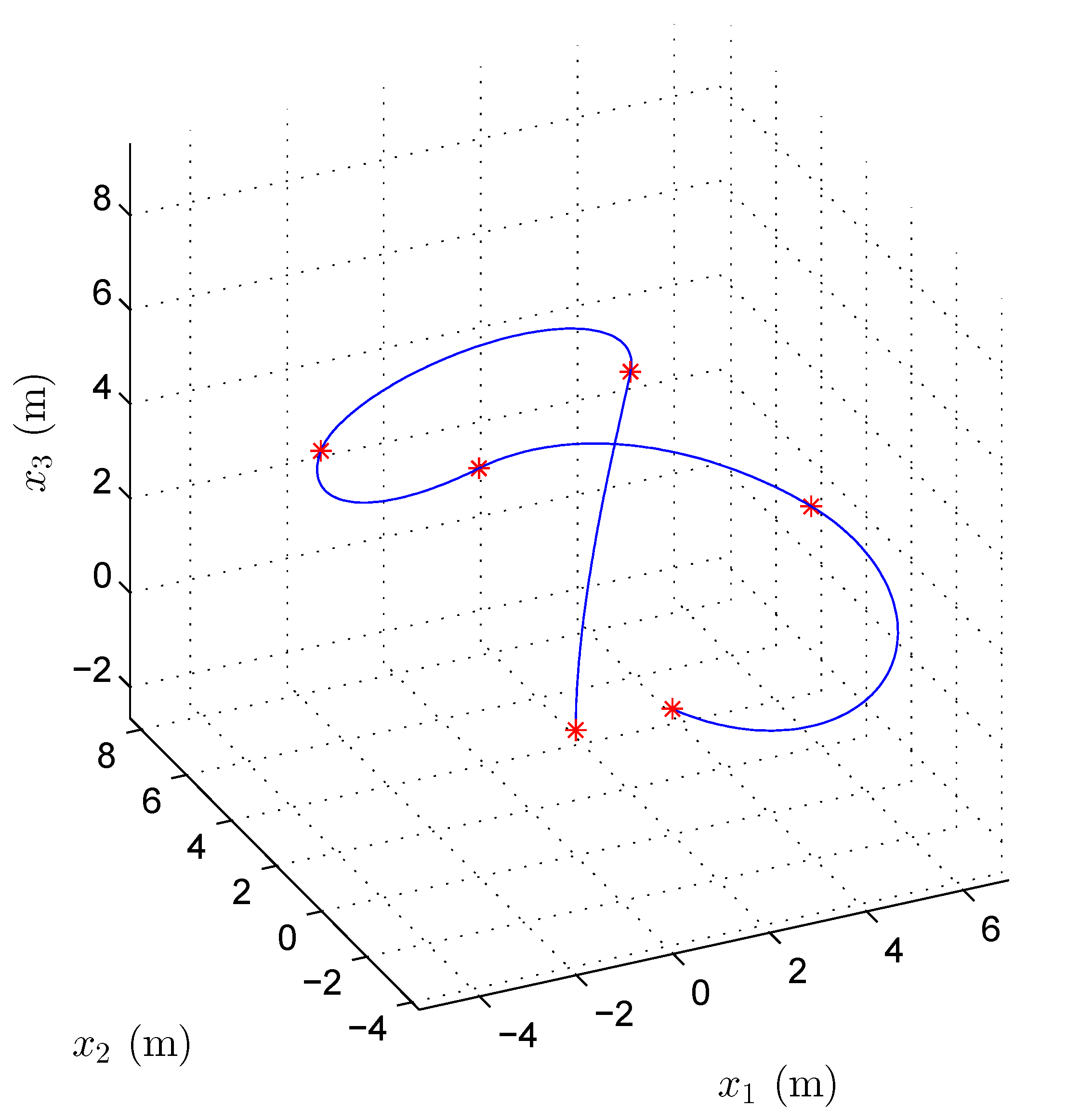
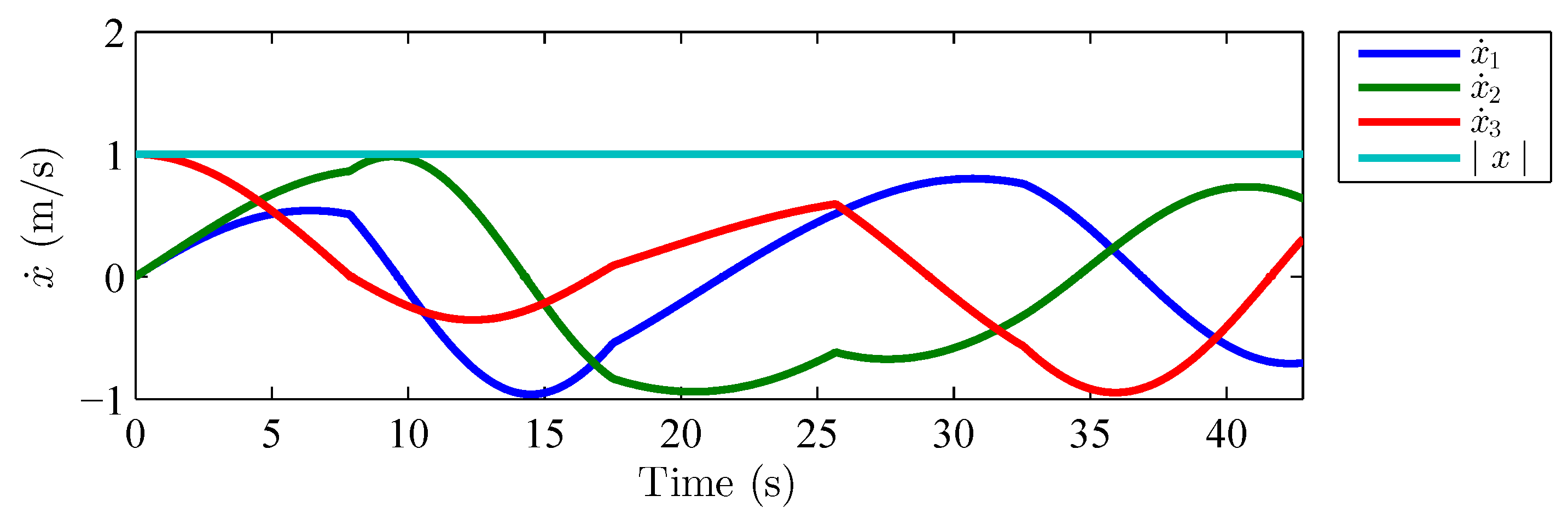
| Segment | T | Solution Time (ms) | |||
|---|---|---|---|---|---|
| 1 | −14.136 | 14.281 | 2.773 | 7.858 | 526 |
| 2 | −28.675 | −15.967 | −9.2926 | 9.656 | 183 |
| 3 | −11.621 | −10.550 | 3.025 | 8.161 | 108 |
| 4 | −15.955 | 10.789 | 2.482 | 6.898 | 194 |
| 5 | −23.425 | 13.467 | 4.527 | 10.224 | 130 |

5.3. Obstacle Collision Detection

6. Conclusions
Author Contributions
Conflicts of Interest
Appendix: Analytical Curves Proof
References
- Matsumoto, T.; Kita, K.; Suzuki, R.; Oosedo, A.; Go, K.; Hoshino, Y.; Konno, A.; Uchiyama, M. A hovering control strategy for a Tail-Sitter VTOL UAV that increases stability against large Disturbance. In Proceedings of the 2010 IEEE International Conference on Robotics and Automation (ICRA 2010), Anchorage, AK, USA, 3–8 May 2010; pp. 54–59.
- Mueller, M.W.; Hehn, M.; D’Andrea, R. A computationally efficient algorithm for state-to-state quadrocopter trajectory generation and feasibility verification. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2013), Tokyo, Japan, 3–7 November 2013; pp. 3480–3486.
- Bouktir, Y.; Haddad, M.; Chettibi, T. Trajectory planning for a quadrotor helicopter. In Proceedings of the 2008 16th Mediterranean Conference on Control and Automation, Ajaccio Corsica, France, 25–27 June 2008; pp. 1258–1263.
- Babel, L. Three-dimensional route planning for unmanned aerial vehicles in a risk environment. J. Intell. Robot. Syst. 2013, 71, 255–269. [Google Scholar] [CrossRef]
- Lizarraga, M.; Elkaim, G. Spatially deconflicted path generation for multiple UAVs in a bounded airspace. In Proceedings of the 2008 IEEE/ION Position, Location and Navigation Symposium, Monterey, CA, USA, 5–8 May 2008; pp. 1213–1218.
- Lewis, L.R.; Ross, I.M.; Gong, Q. Pseudospectral motion planning techniques for autonomous obstacle avoidance. In Proceedings of the 2007 46th IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 5997–6002.
- Lewis, L.P.R. Rapid Motion Planning and Autonomous Obstacle Avoidance for Unmanned Vehicles. Ph.D. Thesis, Naval Postgraduate School, Monterey, CA, USA, 2006. [Google Scholar]
- Lin, Y.; Saripalli, S. Path planning using 3D dubins curve for unmanned aerial vehicles. In Proceedings of the 2014 IEEE International Conference on Unmanned Aircraft Systems (ICUAS 2014), Orlando, FL, USA, 27–30 May 2014; pp. 296–304.
- Van den Berg, J.; Lin, M.; Manocha, D. Reciprocal velocity obstacles for real-time multi-agent navigation. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA 2008), Pasadena, CA, USA, 19–23 May 2008; pp. 1928–1935.
- Shim, D.H.; Sastry, S. An evasive maneuvering algorithm for UAVs in see-and-avoid situations. In Proceedings of the 2007 IEEE American Control Conference (ACC 2007), New York, NY, USA, 9–13 July 2007; pp. 3886–3891.
- Jamieson, J.; Biggs, J. Trajectory generation using sub-riemannian curves for quadrotor UAVs. In Proceedings of the 2015 European Control Conference (ECC 2015), Linz, Austria, 15–17 July 2015.
- Bouabdallah, S. Design and Control of Quadrotors with Application to Autonomous Flying. Ph.D. Thesis, Swiss Federal Institute of Technology in Lausanne, Lausanne, Switzerland, 2007. [Google Scholar]
- Martinez, V. Modelling of the Flight Dynamics of a Quadrotor Helicopter. M.Sc. Thesis, Cranfield University, Bedford, UK, 2007. [Google Scholar]
- Amir, M.; Abbass, V. Modeling of quadrotor helicopter dynamics. In Proceedings of the 2008 International Conference on Smart Manufacturing Application (ICSMA 2008), Goyang-si, Korea, 9–11 April 2008; pp. 100–105.
- Lee, T.; Leoky, M.; McClamroch, N. Geometric tRacking control of a quadrotor UAV on SE(3). In Proceedings of the 2010 49th IEEE Conference on Decision and Control (CDC 2010), Atlanta, GA, USA, 15–17 December 2010; pp. 5420–5425.
- Biggs, J.; Holderbaum, W.; Jurdjevic, V. Singularities of optimal control problems on some 6-D Lie groups. IEEE Trans. Autom. Control 2007, 52, 1027–1038. [Google Scholar] [CrossRef] [Green Version]
- Biggs, J.; Holderbaum, W. Optimal kinematic control of an autonomous underwater vehicle. IEEE Trans. Autom. Control 2009, 54, 1623–1626. [Google Scholar] [CrossRef]
- Walsh, G.; Montgomery, R.; Sastry, S. Optimal path planning on matrix Lie groups. In Proceedings of the 33rd IEEE Conference Decision and Control, Lake Buena Vista, FL, USA, 14–16 December 1994; Volume 2, pp. 1258–1263.
- Jurdjevic, V. Geometric Control Theory; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Pounds, P.; Mahony, R.; Corke, P. Modelling and control of a large quadrotor robot. Control Eng. Pract. 2010, 18, 691–699. [Google Scholar] [CrossRef] [Green Version]
- Pounds, P.; Mahony, R.; Gresham, J.; Corke, P.; Roberts, J.M. Towards dynamically-favourable quad-rotor aerial robots. In Proceedings of the 2004 Australasian Conference on Robotics & Automation, Canberra, Australia, 26 April–1 May 2004.
- Sussmann, H.J. An introduction to the coordinate-free maximum principle. In Geometry of Feedback and Optimal Control; Jakubczyk, B., Respondek, W., Eds.; Marcel Dekker, Inc.: New York, NY, USA, 1997; pp. 463–557. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jamieson, J.; Biggs, J. Path Planning Using Concatenated Analytically-Defined Trajectories for Quadrotor UAVs. Aerospace 2015, 2, 155-170. https://doi.org/10.3390/aerospace2020155
Jamieson J, Biggs J. Path Planning Using Concatenated Analytically-Defined Trajectories for Quadrotor UAVs. Aerospace. 2015; 2(2):155-170. https://doi.org/10.3390/aerospace2020155
Chicago/Turabian StyleJamieson, Jonathan, and James Biggs. 2015. "Path Planning Using Concatenated Analytically-Defined Trajectories for Quadrotor UAVs" Aerospace 2, no. 2: 155-170. https://doi.org/10.3390/aerospace2020155
APA StyleJamieson, J., & Biggs, J. (2015). Path Planning Using Concatenated Analytically-Defined Trajectories for Quadrotor UAVs. Aerospace, 2(2), 155-170. https://doi.org/10.3390/aerospace2020155






