Operator Dynamics Approach to Short-Arc Orbital Prediction Based on the Wigner Distribution

Abstract

We propose an uncertainty propagation framework based on phase space that treats the error distribution as the marginal of a Wigner quasi-probability distribution and defines an effective uncertainty constant quantifying the minimal resolvable phase-space cell. Recognizing that observational updates systematically reduce uncertainty, we adopt a generalized Koopman–von Neumann equation grounded in operator dynamical modeling to propagate the density operator corresponding to the error distribution. The scaling parameter $\kappa$ quantifies the reduction in uncertainty following each filter update. Although the potential is presently retained only to second order—so that both propagation and update preserve Gaussian form and permit direct Kalman recursion—the framework itself lays the analytical foundation for a future treatment of non-Gaussian features. Validated on 1215 orbits (semi-major axis: 9600 km to 42,164 km), the method shows that within a 3 min fit/10 min forecast window, observational noise contributes 350 m while unmodeled dynamics adds only 0.6 m. Kruskal–Wallis rank-sum tests and the accompanying scatter-plot trend rank the semi-major axis as the dominant sensitive parameter. The proposed model outperforms Chebyshev and high-fidelity propagators in real time, offering a physically interpretable route for short-arc orbit prediction.

1. Introduction

Accurate and timely orbit prediction is essential for space situational awareness, collision avoidance, and satellite operations. As the population of space objects continues to grow, initial acquisition typically yields fewer than three minutes of short-arc data. These observations suffer from low signal-to-noise ratios, incomplete angular coverage, and insufficient arc length, rendering initial orbit determination (IOD) and subsequent propagation highly sensitive to both observational noise and dynamical model errors [1,2]. Moreover, critical missions such as planetary entry and precision airdrop depend heavily on rigorous quantification of state uncertainty for robust autonomous decision-making. Consequently, developing efficient and reliable uncertainty quantification methods that can accurately characterize the probabilistic evolution of orbital states is a fundamental requirement.

In the pursuit of balancing computational efficiency with accuracy, uncertainty propagation research has evolved beyond the classical Monte Carlo method, which, despite its intuitive sampling principle, incurs prohibitive costs for high-fidelity applications. To address this, modern techniques have largely branched into two sophisticated directions: Liouville-based PDF propagation and operator-theoretic approaches. Liouville-based methods focus on solving the conservation equation of probability flow. A prominent example is the Orthogonal Probability Approximation (OPA) method [3,4]. Rooted in Liouville theorem, OPA approximates the full PDF with high fidelity using values sampled at specific nodal points combined with a Chebyshev polynomial basis. These schemes have been validated with real satellite data and achieve significantly higher computational efficiency compared to conventional Monte Carlo simulations [5,6].

Parallel to this, the Koopman operator framework has emerged as an active area for astrodynamics, shifting the focus from state-space trajectories to the evolution of observables [7,8]. This operator-theoretic approach transforms the nonlinear system dynamics into a linear propagation problem in a lifted space. Recent advancements in this domain include Koopman-based uncertainty evolution, analytical solvers, and full Koopman-operator filters that propagate moments or PDFs before performing updates [9,10]. By avoiding the explicit integration of trajectory ensembles, this framework offers a powerful paradigm for analyzing nonlinear systems under parametric uncertainty [11]. While these approaches are structurally close to the goals of this study, this paper introduces a distinct uncertainty quantification framework based on the Wigner distribution function and the generalized Koopman–von Neumann (KvN) equation. Unlike pure PDF propagation or observable-based evolution, the proposed method operates on a quasi-probability distribution in phase space, naturally handling the coupling between position and momentum uncertainties through generalized commutation relations.

Phase-space methods offer a natural framework for describing the joint distribution of position and velocity errors. The Wigner quasi-probability distribution $W(\mathit{x},\mathit{p};\mathrm{t})$, originally introduced in quantum mechanics [12,13,14], provides a real-valued function on classical phase space that encodes both marginal uncertainties and their correlations in a single framework. Applications of the Wigner distribution beyond quantum mechanics include time-frequency analysis in signal processing and stochastic control (see Refs. [15,16,17,18,19]). The evolution of the Wigner distribution under Hamiltonian dynamics is governed by the von Neumann equation through the corresponding density operator. However, these formulations describe systems with fixed uncertainty structure, whereas successive filter updates systematically compress the error distribution and refine orbital knowledge. Recently, a generalized KvN equation has been derived within the Operational Dynamic Modeling framework [20], which establishes a unified quantum-classical mechanics by introducing a generalized algebra of observables. This formalism yields a continuously parametrized family of evolution equations, bridging the gap between diffusive, high-uncertainty dynamics and sharp, near-deterministic propagation. The generalized KvN equation, with its embedded scaling parameter $\kappa$, provides a single propagator that automatically adapts to varying uncertainty levels during orbit determination.

In this paper, we propose a Wigner-based Kalman filtering framework in which the observed position and velocity error distributions are treated as marginals of a Wigner quasi-probability distribution $W(\mathit{x},\mathit{p};\mathrm{t})$ over classical phase space. Because successive observations systematically compress the error distribution, refining orbital state knowledge, a propagator capable of accommodating continuously varying levels of uncertainty is required. To this end, we adopt the generalized KvN equation that governs the temporal evolution of the density operator $\widehat{\rho }$ associated with the error distribution. We define an effective uncertainty constant $\kappa {\hslash }_{\mathrm{eff}}$ that quantifies the minimal resolvable phase-space cell at each filter cycle. The parameter $\kappa \in [0,1]$ parametrizes this transition: when observations are sparse, $\kappa \approx 1$ enforces a diffusive propagator consistent with high uncertainty; as measurements accumulate and posterior covariance contracts, $\kappa$ asymptotically approaches zero and the propagator recovers the deterministic Liouville limit. At each prediction step, the current density operator is propagated forward under this $\kappa$-scaled generalized KvN equation; the evolved density operator is then mapped back to its Wigner representation, which directly enters the filter update as the predicted error distribution. This formulation evolves the full phase-space density according to a global evolution equation rather than linearizing dynamics at successive state estimates, thereby retaining position-velocity correlations that arise from the coupled phase-space flow over the entire prediction horizon. The parameter $\kappa$ is continuously adjusted based on the filter’s posterior covariance, enabling the propagator to transition smoothly from diffusive behavior under sparse observations to near-deterministic evolution as measurements accumulate.

To validate the method’s generality and quantify error sources, we design a comprehensive simulation campaign spanning 1215 test cases. The parameter space covers three orbital regimes (the simulations were carried out for three representative semi-major axes: 9600 km, 24,382 km, and 42,164 km), two levels of dynamical fidelity, and two observational noise levels. Each case simulates a 3 min observational arc followed by a 10 min forecast horizon. In the present implementation, the gravitational potential is approximated to second order to intuitively validate the feasibility of the method through a simplified model. It maintains the Gaussian form throughout the prediction-update cycle and simplifies the scheme to an analytic Kalman recursion. The theoretical framework nevertheless admits higher-order potentials and non-Gaussian error distributions, offering a natural pathway toward models that capture nonlinear perturbations. Statistics show that within a 10 min forecast horizon the error is dominated by observational noise, whose contribution is two orders of magnitude larger than dynamical model error (500 m vs. 1.75 m). Under identical 3 min arcs the $\kappa$-calibrated ODM consistently outperforms both Chebyshev-polynomial extrapolation and a high-fidelity dynamical propagator.

The remainder of this paper is organized as follows. In Section 2, we establish the theoretical foundation of our Wigner–Kalman filtering framework, introducing the Wigner quasi-probability distribution, the KvN equation, the generalized KvN equation derived via the operator-dynamic model, and the resulting evolution equation for the Wigner distribution in phase space. Section 3 specifies the physical realization of this framework for gravitational orbit dynamics, detailing the concrete form of the Wigner distribution appropriate for orbital states, the generalized KvN evolution under gravitational potentials and perturbative forces, the quantification of orbital uncertainty, and the calibration of the uncertainty parameter $\kappa$. Section 4 presents a comprehensive numerical validation through 1215 simulated orbital scenarios, analyzing prediction accuracy across varying orbital regimes, observational noise levels, and filtering time windows. Section 5 summarizes the principal findings, discusses current limitations, and outlines prospective extensions to multi-object tracking, non-Keplerian dynamics, and operational space situational awareness systems.

2. Wigner-Based Filtering Framework: Theoretical Foundation

This section establishes the mathematical foundation of our Wigner-based filtering approach by developing the operator-theoretic machinery necessary to represent and propagate probability distributions in phase space. Classical Kalman filtering characterizes uncertainty via covariance matrices which is a representation that implicitly assumes Gaussian statistics and discards higher-order correlations. In contrast, our framework operates directly on the phase-space probability density $\rho (\mathit{x},\mathit{p};t)$, retaining the full structure of position-momentum correlations essential for accurate nonlinear orbit propagation.

We proceed in four stages. First, we introduce the Wigner quasi-probability distribution to characterize the error distribution in phase space, whose marginal distributions correspond to the experimentally measured position or velocity error distributions. We further define an effective uncertainty parameter based on the minimal resolvable volume element in phase space. Then, we review the Koopman–von Neumann formalism, which recasts classical Hamiltonian dynamics as unitary evolution on a Hilbert space of observables, providing a natural bridge between Liouvillian flow and operator-algebraic methods. The KvN formalism has gained renewed attention in recent years for data-driven modeling of complex dynamical systems, particularly in fluid dynamics and nonlinear control [21,22], and has been extended to non-Hamiltonian and dissipative systems through generalized formulations [23,24]. We further introduce the generalized KvN equation from operator-dynamic modeling, which features a continuous parameter $\kappa$ that interpolates between broad (high-uncertainty) and sharply localized (low-uncertainty) phase-space distributions, and reformulate it to encode the filtering process as a geometric contraction in phase space. Finally, we present the concrete evolution scheme for the error Wigner quasi-probability distribution, wherein the Wigner function is propagated by evolving its associated density operator via the generalized KvN equation.

Taken together, this section constitutes a closed mathematical framework in which orbital filtering is realized through the continuous deformation of the Wigner distribution in phase space, driven by generalized Koopman–von Neumann dynamics and regulated by the $\kappa$-parameter that controls the transition from diffuse to localized probability densities. The physical realization of this framework for gravitational systems is deferred to Section 3.

2.1. The Wigner Quasi-Probability Distribution

Classical mechanics represents the state of a deterministic system as a point $(\mathit{x},\mathit{p})$ in phase space, where $\mathit{x}\in {\mathbb{R}}^3$ denotes position and $\mathit{p}\in {\mathbb{R}}^3$ denotes momentum. When uncertainty enters through imperfect initial knowledge or observational noise, the natural generalization is a probability density $\rho (\mathit{x},\mathit{p})$ satisfying $\rho \ge 0$ and $\int \int \rho (\mathit{x},\mathit{p}){\mathrm{d}}^3\mathit{x}{\mathrm{d}}^3\mathit{p}=1$. However, such classical phase-space distributions do not naturally accommodate the operator structure required for systematic uncertainty propagation via the Koopman–von Neumann formalism. The Wigner distribution, introduced by Wigner [25] in 1932, provides a phase-space representation that bridges classical probability densities and operator-algebraic methods [26,27,28,29]. Originally developed for quantum mechanics, the Wigner formalism has found broad applications in theoretical physics, signal processing, time-frequency analysis, and quantum information theory [15,17,30,31,32,33,34].

Consider a quantum-mechanical system with density operator $\widehat{\rho }$ on a Hilbert space $\mathcal{H}$. In the position representation, the Wigner function is defined via the Wigner–Weyl transform as

$$W(\mathit{x},\mathit{p})={\displaystyle \frac{1}{{(2\pi \hslash )}^3}}{\mathit{\int }}_{{\mathbb{R}}^3}\langle \mathit{x}-\frac{1}{2}\mathit{s}|\widehat{\rho }|\mathit{x}+\frac{1}{2}\mathit{s}\rangle e^{i\mathit{p}·\mathit{s}/\hslash }{\mathrm{d}}^3\mathit{s},$$

(1)

where $\langle \mathit{x}\left|\widehat{\rho }\right|{\mathit{x}}^{\prime }\rangle$ denotes the position-space matrix element of the density operator. For a pure state $\widehat{\rho }=|\psi \rangle \langle \psi |$, this reduces to

$$W(\mathit{x},\mathit{p})={\displaystyle \frac{1}{{(2\pi \hslash )}^3}}{\int }_{{\mathbb{R}}^3}{\psi }^{*}\left(\mathit{x}-\frac{1}{2}\mathit{s}\right)\psi \left(\mathit{x}+\frac{1}{2}\mathit{s}\right)e^{i\mathit{p}·\mathit{s}/\hslash }{\mathrm{d}}^3\mathit{s}.$$

(2)

The Wigner formalism, though originally formulated for quantum systems, applies directly to classical phase-space dynamics. In the classical orbital setting, Equation (1) remains formally unchanged, but ℏ is reinterpreted as an effective parameter ${\hslash }_{\mathrm{eff}}$ that quantifies the minimum resolvable phase-space volume element dictated by measurement errors rather than quantum indeterminacy. Here, ${\hslash }_{\mathrm{eff}}$ serves as a phenomenological parameter encoding both observational precision and dynamical time scales relevant to the filtering problem. The Wigner distribution thereby captures the central orbital estimate via its peak location and the uncertainty spread via its width, analogous to a covariance matrix but retaining the full functional structure necessary for nonlinear dynamical evolution.

A defining property of the Wigner distribution is that its marginals recover the correct position and momentum probability densities:

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^3}W(\mathit{x},\mathit{p}){\mathrm{d}}^3\mathit{p}& ={\rho }_x\left(\mathit{x}\right)={\left|\psi \left(\mathit{x}\right)\right|}^2,\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill {\int }_{{\mathbb{R}}^3}W(\mathit{x},\mathit{p}){\mathrm{d}}^3\mathit{x}& ={\rho }_p\left(\mathit{p}\right)={\left|\tilde{\psi }\left(\mathit{p}\right)\right|}^2,\hfill \end{array}$$

(4)

where $\tilde{\psi }\left(\mathit{p}\right)={(2\pi \hslash )}^{-3/2}\int \psi \left(\mathit{x}\right)e^{-i\mathit{p}·\mathit{x}/\hslash }{\mathrm{d}}^3\mathit{x}$ is the momentum-space wavefunction. Integrating out either variable yields the correct one-dimensional probability distribution, which is essential for filtering applications where observations typically measure only position (e.g., radar ranging) while velocity must be inferred through dynamical evolution. The full phase-space structure $W(\mathit{x},\mathit{p})$ retains both observed and unobserved information consistently. A critical distinction between the Wigner distribution and classical probability densities is that $W(\mathit{x},\mathit{p})$ can assume negative values in certain regions of phase space. This negativity does not violate physical principles because W is not directly observable; only its marginals and appropriately weighted integrals correspond to measurable quantities.

We now adapt this framework to orbital filtering. Two considerations motivate this choice. First, real tracking systems produce position estimates ${\mathit{x}}_{\mathrm{obs}}$ and velocity estimates ${\mathit{v}}_{\mathrm{obs}}$ with independent uncertainties whereas they evolve together through the equations of motion. A classical covariance matrix ${\Sigma }_{xp}$ describes second-order statistics and linear correlations, but provides an incomplete representation when nonlinear dynamics induce non-Gaussian features or significant higher-order correlations. The Wigner distribution retains the full functional structure of the joint state, allowing more accurate propagation through nonlinear dynamics. Second, Equations (3) and (4) provide a direct link: given measured error distributions ${\rho }_x\left(\mathit{x}\right)$ for position and ${\rho }_p\left(\mathit{p}\right)$ for momentum, we can construct a Wigner function $W(\mathit{x},\mathit{p})$ whose marginals exactly match the observations. The phase-space structure of W then captures how position and momentum uncertainties become correlated during propagation, even though the measurements themselves treat them separately.

In practice, orbital tracking systems deliver measurements whose errors are approximately Gaussian under typical conditions. The measured position distribution has the form

$$P\left(\mathit{x}\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}{\left|{\Sigma }_x\right|}^{1/2}}}exp\left\{-{\displaystyle \frac{1}{2}}{(\mathit{x}-{\mathit{\mu }}_x)}^T{\Sigma }_x^{-1}(\mathit{x}-{\mathit{\mu }}_x)\right\},$$

(5)

where ${\mathit{\mu }}_x$ denotes the estimated position and ${\Sigma }_x$ is the $3\times 3$ covariance matrix describing uncertainties along each spatial axis. For a diagonal ${\Sigma }_x$, the determinant $|{\Sigma }_x|$ gives the overall error volume. The momentum distribution has a similar structure:

$$P\left(\mathit{p}\right)={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}{\left|{\Sigma }_p\right|}^{1/2}}}exp\left\{-{\displaystyle \frac{1}{2}}{(\mathit{p}-{\mathit{\mu }}_p)}^T{\Sigma }_p^{-1}(\mathit{p}-{\mathit{\mu }}_p)\right\},$$

(6)

where ${\mathit{\mu }}_p=m{\mathit{v}}_{\mathrm{obs}}$ is the estimated momentum (satellite mass m multiplied by observed velocity) and ${\Sigma }_p$ is the momentum covariance matrix with determinant $|{\Sigma }_p|$. These Gaussian profiles arise from a combination of measurement noise, signal propagation effects, and receiver electronics.

To bridge these observed distributions with the Wigner formalism, we introduce an effective action parameter ${\hslash }_{\mathrm{eff}}$ that quantifies the smallest phase-space volume resolvable given the measurement precision. The idea of defining an effective action from minimal phase-space cells also appears in Ref. [35] in a different physical context, though the explicit construction differs. We define characteristic uncertainties by taking geometric means:

$$\Delta x=|{\Sigma }_x{|}^{1/6},\Delta p={\left|{\Sigma }_p\right|}^{1/6},$$

(7)

which represent average widths of the error ellipsoids. We then set

$${\hslash }_{\mathrm{eff}}=2\Delta x\Delta p.$$

(8)

This definition plays a dual role. On one hand, it ties the scale ${\hslash }_{\mathrm{eff}}$ in the Wigner transform (Equation (1)) directly to measurable quantities $\Delta x$ and $\Delta p$, removing any ambiguity about how to choose it. On the other hand, it identifies ${\hslash }_{\mathrm{eff}}$ with the elementary phase-space cell volume ${(\Delta x)}^3{(\Delta p)}^3\sim {\hslash }_{\mathrm{eff}}^3$, below which distinctions become meaningless given the available precision and relevant time scales.

With the observed Gaussian marginals (Equations (5) and (6)) in hand, we can write down the Wigner function of uncertainty distribution that reproduces them:

$$W(\mathit{x},\mathit{p})={\displaystyle \frac{1}{{\left(\pi {\hslash }_{\mathrm{eff}}\right)}^3}}exp\left\{-{\displaystyle \frac{1}{2}}{(\mathit{x}-{\mathit{\mu }}_x)}^T{\Sigma }_x^{-1}(\mathit{x}-{\mathit{\mu }}_x)-{\displaystyle \frac{1}{2}}{(\mathit{p}-{\mathit{\mu }}_p)}^T{\Sigma }_p^{-1}(\mathit{p}-{\mathit{\mu }}_p)\right\}.$$

(9)

This function is positive everywhere, normalizes to unity when integrated over all of phase space, and by construction reproduces Equations (5) and (6) when marginalized over $\mathit{p}$ or $\mathit{x}$, respectively. Note that the prefactor $1/{\left(\pi {\hslash }_{\mathrm{eff}}\right)}^3$ arises from substituting the minimum uncertainty relation $\sqrt{det(\Sigma )}={({\hslash }_{\mathrm{eff}}/2)}^3$ into the standard Gaussian normalization constant. This ensures that $\int Wd\mathbf{x}d\mathbf{p}=1$ and preserves the correct probabilistic interpretation of the marginals. The factorized exponential reflects our assumption that position and momentum errors are uncorrelated at the moment of measurement. However, as $W(\mathit{x},\mathit{p})$ evolves under the orbital dynamics, this factorization typically breaks down and correlations emerge.

The key point is this: even though position ${\mathit{x}}_{\mathrm{obs}}$ and velocity ${\mathit{v}}_{\mathrm{obs}}$ are measured separately at any given time, their errors do not evolve independently between measurements. A straightforward classical approach that treats $P\left(\mathit{x}\right)$ and $P\left(\mathit{p}\right)$ as unrelated quantities will miss the correlations induced by the dynamics. The Wigner function $W(\mathit{x},\mathit{p})$ encodes this coupling through its joint phase-space structure. Under the generalized KvN equation (Section 2.4), W evolves according to the Hamiltonian flow, maintaining phase-space volume while letting correlations develop in a nonlinear fashion. Even when we start with a simple product state, evolution through nonlinear forces generally introduces cross-correlations that cannot be captured by propagating $P\left(\mathit{x}\right)$ and $P\left(\mathit{p}\right)$ separately.

It is instructive to note that Equation (9), though derived from observed error statistics, is fully compatible with the standard Wigner formalism based on density operators. The phase-space function $W(\mathbf{x},\mathbf{p})$ can be inverted via Fourier transform,

$$\rho (\mathbf{u},\mathbf{v})={\int }_{{\mathbb{R}}^3}{d}^{3}pW\left({\displaystyle \frac{\mathbf{u}+\mathbf{v}}{2}},\mathbf{p}\right)exp\left\{{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}}}\mathbf{p}(\mathbf{v}-\mathbf{u})\right\},$$

(10)

to yield the density operator in position representation. Introducing two position coordinates $\mathbf{u},\mathbf{v}\in {\mathbb{R}}^3$, we obtain

$$\begin{array}{cc}\hfill \rho (\mathbf{u},\mathbf{v})={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}{\left|{\Sigma }_x\right|}^{1/2}}}exp\{& -{\displaystyle \frac{1}{4}}\left[{(\mathbf{u}-{\mathit{\mu }}_x)}^T{\Sigma }_x^{-1}(\mathbf{u}-{\mathit{\mu }}_x)+{(\mathbf{v}-{\mathit{\mu }}_x)}^T{\Sigma }_x^{-1}(\mathbf{v}-{\mathit{\mu }}_x)\right]\hfill \\ \hfill & +{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}}}{\mathit{\mu }}_p(\mathbf{v}-\mathbf{u})\}.\hfill \end{array}$$

(11)

Here, $\mathbf{v}$ and $\mathbf{u}$ represent two independent position coordinates in the density operator representation, related to the phase-space coordinate $\mathbf{x}$ and integration variable $\xi$ through $\mathbf{u}=\mathbf{x}-\mathit{\xi }/2$ and $\mathbf{v}=\mathbf{x}+\mathit{\xi }/2$. Conversely, one can verify the consistency of this formalism by applying the forward Wigner transform to the density operator:

$$W(\mathbf{x},\mathbf{p})={\displaystyle \frac{1}{{\left(2\pi {\hslash }_{\mathrm{eff}}\right)}^3}}{\int }_{{\mathbb{R}}^3}\rho \left(\mathbf{x}-{\displaystyle \frac{\mathit{\xi }}{2}},\mathbf{x}+{\displaystyle \frac{\mathit{\xi }}{2}}\right)e^{-i\mathbf{p}·\xi /{\hslash }_{\mathrm{eff}}}{d}^3\xi ,$$

(12)

which recovers precisely the error distribution in Wigner form given by Equation (9). This closed-loop transformation confirms that our empirically motivated phase-space description is mathematically equivalent to a proper density operator, with ${\hslash }_{\mathrm{eff}}=2\Delta x\Delta p$ serving as the effective quantization scale that bridges classical error statistics and phase-space distribution formalism.

Gaussian Wigner functions like Equation (9) provide natural initial conditions for orbital filtering and stay nearly Gaussian as long as nonlinearities remain weak. When nonlinear effects become significant, the Wigner approach offers a theoretical framework that can systematically handle these nonlinear influences, providing a potential pathway beyond linearized covariance methods. Overall, the Wigner quasi-probability distribution provides a phase-space representation that reproduces the classical position and momentum marginals to directly match the observed error statistics. It captures position–momentum correlations through its joint structure and a finite resolution scale ${\hslash }_{\mathrm{eff}}$ determined from observations. Furthermore, it fits naturally into the Koopman–von Neumann operator framework, enabling a more systematic treatment of uncertainty propagation in nonlinear dynamics. The advantage of this framework lies in providing a systematic theoretical platform for handling coupled position–momentum uncertainties under nonlinear evolution.

2.2. The Koopman–von Neumann Formalism

The Koopman–von Neumann theory [36,37,38] provides an operator-algebraic formulation of classical mechanics that parallels the structure of quantum mechanics. Unlike the standard Hamiltonian formulation, which describes the trajectory of a point in phase space, the KvN formalism describes the evolution of a complex-valued wave function $|\Psi (t)\rangle$ residing in a Hilbert space. This section reviews the essential elements of this formalism, which serves as the foundation for the generalized framework discussed later. Further details and applications of KvN theory can be found in Refs. [39,40,41,42].

Consider a one-dimensional classical system with position x and momentum p. The KvN formalism introduces four fundamental operators: $\widehat{x}$, $\widehat{p}$, ${\widehat{\lambda }}_x$, and ${\widehat{\lambda }}_p$, satisfying the commutation relations:

$$[\widehat{x},\widehat{p}]=0,$$

(13)

$$[\widehat{x},{\widehat{\lambda }}_x]=i,[\widehat{p},{\widehat{\lambda }}_p]=i,$$

(14)

$$[\widehat{x},{\widehat{\lambda }}_p]=[\widehat{p},{\widehat{\lambda }}_x]=[{\widehat{\lambda }}_x,{\widehat{\lambda }}_p]=0.$$

(15)

The key distinction from quantum mechanics is Equation (13): position and momentum commute, reflecting the classical nature of the underlying system. This ensures that position and momentum can be simultaneously measured with arbitrary precision, consistent with classical mechanics. The operators ${\widehat{\lambda }}_x$ and ${\widehat{\lambda }}_p$ are conjugate to $\widehat{x}$ and $\widehat{p}$, respectively, and act as generators for translations in phase space.

According to Stone’s theorem on one-parameter unitary groups, the time evolution of the state vector $|\Psi (t)\rangle$ is governed by a self-adjoint generator called the Liouvillian operator $\widehat{L}$:

$$i{\displaystyle \frac{d}{dt}}|\Psi \left(t\right)\rangle =\widehat{L}|\Psi \left(t\right)\rangle$$

(16)

For a classical Hamiltonian system with Hamiltonian $H(x,p)=p^2/\left(2m\right)+U\left(x\right)$, the Liouvillian operator is constructed to reproduce the classical equations of motion. Following Ref. [20], a general form of the Liouvillian is:

$$\widehat{L}={\displaystyle \frac{\widehat{p}}{m}}{\widehat{\lambda }}_x-U^{\prime }\left(\widehat{x}\right){\widehat{\lambda }}_p+f(\widehat{x},\widehat{p}),$$

(17)

where $U^{\prime }\left(\widehat{x}\right)$ denotes the derivative of the potential and $f(\widehat{x},\widehat{p})$ is an arbitrary real-valued function representing a gauge freedom. The first two terms generate the classical Hamiltonian flow in phase space. By computing the commutators $[\widehat{x},\widehat{L}]$ and $[\widehat{p},\widehat{L}]$ using the commutation relations (14) and (15), one can verify that the expectation values satisfy the Ehrenfest equations:

$$\begin{array}{cc}\hfill {\displaystyle \frac{d\langle \widehat{x}\rangle }{dt}}& ={\displaystyle \frac{\langle \widehat{p}\rangle }{m}},\hfill \\ \hfill {\displaystyle \frac{d\langle \widehat{p}\rangle }{dt}}& =-\langle U^{\prime }\left(\widehat{x}\right)\rangle ,\hfill \end{array}$$

(18)

which have the form of classical Hamilton’s equations. Notably, the arbitrary function $f(\widehat{x},\widehat{p})$ does not contribute to these equations, confirming its gauge nature.

To connect this framework with familiar classical descriptions, we project the formalism onto the $xp$-representation using the eigenstates $|x,p\rangle$. In this representation, the conjugate operators act as differential operators:

$${\widehat{\lambda }}_x=-i{\displaystyle \frac{\partial }{\partial x}},{\widehat{\lambda }}_p=-i{\displaystyle \frac{\partial }{\partial p}}$$

(19)

The wave function is given by $\Psi (x,p;t)=\langle x,p|\Psi (t)\rangle$, and substituting Equation (19) into the evolution Equation (16) yields:

$$\left[{\displaystyle \frac{\partial }{\partial t}}+i\left({\displaystyle \frac{p}{m}}{\displaystyle \frac{\partial }{\partial x}}-U^{\prime }\left(x\right){\displaystyle \frac{\partial }{\partial p}}-f(x,p)\right)\right]\Psi (x,p;t)=0$$

(20)

The physically measurable quantity is the probability density in phase space:

$$\rho (x,p;t)={|\Psi (x,p;t)|}^2$$

(21)

Taking the time derivative of $\rho$ and using Equation (20), the contribution from the gauge function f cancels, yielding the classical Liouville equation:

$${\displaystyle \frac{\partial \rho }{\partial t}}=-{\displaystyle \frac{p}{m}}{\displaystyle \frac{\partial \rho }{\partial x}}+U^{\prime }\left(x\right){\displaystyle \frac{\partial \rho }{\partial p}}=-{\{\rho ,H\}}_{PB}$$

(22)

where ${\{·,·\}}_{PB}$ denotes the Poisson bracket. Thus, the KvN theory elegantly subsumes classical statistical mechanics as a natural consequence of operator dynamics in Hilbert space, providing the foundation for the $\kappa$-dependent generalization discussed next.

2.3. The Operator Dynamic Model and Generalized KvN Equation

Building upon the KvN formalism, Bondar et al. [12,20] developed a remarkable generalization that interpolates between classical and quantum mechanics through a continuous parameter $\kappa \in [0,1]$. This section presents the mathematical structure of this framework, including the modified commutation relations, the unified Hamiltonian, and the limiting cases.

The generalization is achieved by replacing the commutation relation (13) with a $\kappa$-dependent version. Specifically, the operators ${\widehat{x}}_k$ and ${\widehat{p}}_k$ (where the subscript k indicates that these belong to the $\kappa$-dependent algebra) satisfy:

$$[{\widehat{x}}_k,{\widehat{p}}_k]=i\hslash \kappa$$

(23)

while the conjugate operators maintain their canonical commutation relations:

$$[{\widehat{x}}_k,{\widehat{\lambda }}_x]=i,[{\widehat{p}}_k,{\widehat{\lambda }}_p]=i$$

(24)

where ${\widehat{\lambda }}_x$ and ${\widehat{\lambda }}_p$ are the same operators as those in the KvN formalism.

The parameter $\kappa \in [0,1]$ continuously varies the fundamental uncertainty structure of the theory: when $\kappa =0$, Equation (23) recovers the classical commutation relation $[{\widehat{x}}_{k=0},{\widehat{p}}_{k=0}]=0$; when $\kappa =1$, we obtain the canonical quantum commutation relation $[{\widehat{x}}_{k=1},{\widehat{p}}_{k=1}]=i\hslash$; for $0<\kappa <1$, the system exhibits intermediate behavior with partial non-commutativity. This interpolation provides a one-parameter family of theories that smoothly connects classical and quantum descriptions. Based on the properties discussed above, one can derive the following two fundamental transformation formulas among these operators:

$${\widehat{x}}_k=\widehat{x}-\hslash \kappa {\widehat{\lambda }}_p/2,{\widehat{p}}_k=\widehat{p}+\hslash \kappa {\widehat{\lambda }}_x/2.$$

(25)

These transformation relations explicitly describe how the $\kappa$ parameter mediates the coupling between the original operators $(\widehat{x},\widehat{p})$ and their modified counterparts $({\widehat{x}}_k,{\widehat{p}}_k)$ through the conjugate momentum variables $({\widehat{\lambda }}_x,{\widehat{\lambda }}_p)$.

Following Ref. [20], the unified Hamiltonian operator for the $\kappa$-dependent system is constructed through consistency requirements known as the Ehrenfest conditions. These conditions demand that the time derivatives of the expectation values of position and momentum satisfy equations of the appropriate form. For a system with kinetic energy $p^2/\left(2m\right)$ and potential energy $U\left(x\right)$, the unified Hamiltonian takes the form:

$${\widehat{\mathcal{H}}}_k={\displaystyle \frac{1}{\kappa }}\left[{\displaystyle \frac{{\widehat{p}}_k^2}{2m}}+U\left({\widehat{x}}_k\right)\right]-{\displaystyle \frac{1}{2m\kappa }}{\left({\widehat{p}}_k-\hslash \kappa {\widehat{\lambda }}_x\right)}^2-{\displaystyle \frac{1}{\kappa }}U\left({\widehat{x}}_k+\hslash \kappa {\widehat{\lambda }}_p\right)$$

(26)

and the equation of motion is:

$$i\hslash {\displaystyle \frac{\mathrm{d}}{\mathrm{d}t}}|{\Psi }_{\kappa }\left(t\right)\rangle ={\widehat{\mathcal{H}}}_k|{\Psi }_{\kappa }\left(t\right)\rangle .$$

(27)

Under the $\widehat{x}\widehat{p}$-transformation, the Hamiltonian can be written equivalently as:

$${\widehat{\mathcal{H}}}_k={\displaystyle \frac{\hslash }{m}}\widehat{p}{\widehat{\lambda }}_x+{\displaystyle \frac{1}{\kappa }}U\left(\widehat{x}-{\displaystyle \frac{\hslash \kappa }{2}}{\widehat{\lambda }}_p\right)-{\displaystyle \frac{1}{\kappa }}U\left(\widehat{x}+{\displaystyle \frac{\hslash \kappa }{2}}{\widehat{\lambda }}_p\right).$$

(28)

To understand the structure of this Hamiltonian, consider the Taylor expansion of the potential terms for small $\kappa$:

$$U\left(\widehat{x}\pm {\displaystyle \frac{\hslash \kappa }{2}}{\widehat{\lambda }}_p\right)=U\left(\widehat{x}\right)\pm {\displaystyle \frac{\hslash \kappa }{2}}{U}^{\prime }\left(\widehat{x}\right){\widehat{\lambda }}_p+O\left({\kappa }^2\right).$$

(29)

Substituting into Equation (28) and keeping the leading terms, this reduces to:

$${\widehat{\mathcal{H}}}_k\approx {\displaystyle \frac{\hslash }{m}}\widehat{p}{\widehat{\lambda }}_x-\hslash U^{\prime }\left(\widehat{x}\right){\widehat{\lambda }}_p(\kappa \to 0),$$

(30)

which is precisely the classical Liouvillian (up to a factor of ℏ) discussed in Section 2.2.

Conversely, when $\kappa =1$, the commutation relation becomes the standard quantum relation $[{\widehat{x}}_1,{\widehat{p}}_1]=i\hslash$. Substituting $\kappa =1$ into Equation (26) and evaluating in the position representation yields:

$${\widehat{\mathcal{H}}}_1={\displaystyle \frac{{\widehat{p}}_1^2}{2m}}+U\left({\widehat{x}}_1\right)+F\left({\widehat{p}}_1-\hslash {\widehat{\lambda }}_x,{\widehat{x}}_1+\hslash {\widehat{\lambda }}_p\right).$$

(31)

This is the standard quantum Hamiltonian operator where the function F is experimentally undetectable, confirming that the $\kappa =1$ case reproduces quantum mechanics exactly.

For $0<\kappa <1$, the Hamiltonian defines a continuum of theories with partial non-commutativity. This intermediate regime is characterized by a generalized uncertainty relation that interpolates between the deterministic classical limit and the Heisenberg uncertainty principle. The physical interpretation of this regime and its application to orbital uncertainty propagation will be developed in Section 3. In the context of orbital mechanics, intermediate values of $\kappa$ naturally describe systems with continuously decreasing uncertainty, providing a unified framework that smoothly connects deterministic trajectory propagation ($\kappa \to 0$) with probabilistic descriptions ($\kappa \sim 1$).

Moreover, the complexity of the Hamiltonian’s functional form depends strongly on the nature of the potential. An important simplification occurs for quadratic potentials: the Hamiltonian (28) reduces to the simple form ${\widehat{\mathcal{H}}}_k=\hslash \widehat{L}$, where $\widehat{L}$ is the Liouvillian operator with a straightforward structure [20].

2.4. Evolution for the Wigner Quasi-Probability Distribution

The time evolution of the Wigner distribution can be approached in two distinct ways. The first is to evolve W directly via the Moyal equation, a nonlocal integro-differential equation in phase space. The second is to evolve the underlying density operator ${\widehat{\rho }}_{\kappa }\left(t\right)$ according to the generalized Koopman–von Neumann dynamics and then reconstruct $W_{\kappa }(x,p;t)$ via the Wigner transform at each time step. The present work adopts the latter approach.

This choice is motivated by the specific requirements of orbital filtering. In our framework, the effective uncertainty ${\hslash }_{\mathrm{eff}}$ is initially determined from the measurement covariance and represents an intrinsic property of the observational system. However, each filtering cycle refines the state estimate and reduces the uncertainty in the error distribution. This manifests as a progressive narrowing of the distribution in phase space. In the ideal limit where all uncertainty is eliminated, the distribution would collapse to a delta function on phase space, corresponding to a state with simultaneously well-defined position and velocity. At that point, the evolution equation must reduce to the classical Liouville equation.

To accommodate this reduction in uncertainty at each filtering step, we introduce the parameter $\kappa$ to quantify the degree of uncertainty present after each update. Correspondingly, the evolution equation itself must be adjusted to reflect the current level of uncertainty. This is precisely the role of the generalized Koopman–von Neumann framework: it interpolates continuously between the quantum-like regime (when $\kappa =1$ and uncertainty matches ${\hslash }_{\mathrm{eff}}$) and the classical limit (as $\kappa \to 0$). Within this framework, evolving the density operator and then extracting the Wigner distribution is a natural and consistent procedure. It is worth noting that both approaches, direct Moyal evolution and density operator evolution, are theoretically equivalent, but the latter provides greater flexibility for handling the adaptive uncertainty parameter $\kappa$ in the filtering context.

To extract the density operator elements from the generalized KvN equation and construct the evolution equation for the density operator, we transform the equation

$$i{\hslash }_{eff}{\displaystyle \frac{\partial {\Psi }_{\kappa }}{\partial t}}={\displaystyle \frac{{\hslash }_{eff}}{m}}{\displaystyle \frac{{\partial }^2{\Psi }_{\kappa }}{\partial {\lambda }_p\partial x}}+{\displaystyle \frac{1}{\kappa }}\left[U\left(x-\frac{{\hslash }_{eff}\kappa {\lambda }_p}{2}\right)-U\left(x+\frac{{\hslash }_{eff}\kappa {\lambda }_p}{2}\right)\right]{\Psi }_{\kappa }$$

(32)

in the $x{\lambda }_p$-representation to the $uv$-representation, where new variables are introduced from

$$u=x-{\displaystyle \frac{{\hslash }_{eff}\kappa {\lambda }_p}{2}},v=x+{\displaystyle \frac{{\hslash }_{eff}\kappa {\lambda }_p}{2}}.$$

(33)

Under this transformation, the generalized KvN equation becomes

$$\left[i{\hslash }_{eff}\kappa {\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{{\left({\hslash }_{eff}\kappa \right)}^2}{2m}}\left({\displaystyle \frac{{\partial }^2}{\partial v^2}}-{\displaystyle \frac{{\partial }^2}{\partial u^2}}\right)-U\left(u\right)+U\left(v\right)\right]{\rho }_{\kappa }(u,v,t)=0,$$

(34)

with the relation between functions in different representations given by

$${\Psi }_{\kappa }(x,{\lambda }_p,t)=\sqrt{{\hslash }_{eff}\kappa }{\rho }_{\kappa }(u,v,t).$$

(35)

In operator form, this correspondence can be expressed as

$$\langle x{\lambda }_p|{\Psi }_{\kappa }\left(t\right)\rangle =\sqrt{{\hslash }_{eff}\kappa }\langle u|{\widehat{\rho }}_{\kappa }\left(t\right)|v\rangle ,$$

(36)

where $|u\rangle$ and $|v\rangle$ denote position eigenstates in the extended Hilbert space, and ${\widehat{\rho }}_{\kappa }\left(t\right)$ represents the density operator. We introduce the modified position and momentum operators defined by

$${\widehat{x}}_k=\widehat{x}-{\displaystyle \frac{{\hslash }_{eff}\kappa {\widehat{\lambda }}_p}{2}},{\widehat{p}}_k=\widehat{p}+{\displaystyle \frac{{\hslash }_{eff}\kappa {\widehat{\lambda }}_x}{2}},$$

(37)

which act on the position eigenstates as multiplication and differentiation operators:

$${\widehat{x}}_k|u\rangle =u|u\rangle ,{\widehat{p}}_k|u\rangle =-i{\hslash }_{eff}\kappa {\displaystyle \frac{\partial }{\partial u}}|u\rangle .$$

(38)

These operators form a canonical pair with the effective Planck constant ${\hslash }_{eff}\kappa$, satisfying the commutation relation $[{\widehat{x}}_k,{\widehat{p}}_k]=i{\hslash }_{eff}\kappa$. The structure of Equation (34) can now be interpreted in terms of the commutator $[{\widehat{H}}_{eff},{\widehat{\rho }}_{\kappa }]$, where the effective Hamiltonian is given by

$${\widehat{H}}_{eff}={\displaystyle \frac{{\widehat{p}}_k^2}{2m}}+U\left({\widehat{x}}_k\right).$$

(39)

To establish this connection, we evaluate the matrix elements of the commutator in the position representation. The kinetic term yields

$$\langle u|\left[{\displaystyle \frac{{\widehat{p}}_k^2}{2m}},{\widehat{\rho }}_{\kappa }\right]|v\rangle ={\displaystyle \frac{{\left({\hslash }_{eff}\kappa \right)}^2}{2m}}\left({\displaystyle \frac{{\partial }^2}{\partial v^2}}-{\displaystyle \frac{{\partial }^2}{\partial u^2}}\right){\rho }_{\kappa }(u,v,t),$$

(40)

and the potential term gives

$$\langle u|[U\left({\widehat{x}}_k\right),{\widehat{\rho }}_{\kappa }]|v\rangle =[U\left(u\right)-U\left(v\right)]{\rho }_{\kappa }(u,v,t),$$

(41)

reflecting the difference in potential energy evaluated at the two positions. Combining these results, Equation (34) can be expressed in the compact operator form

$$i{\hslash }_{eff}\kappa {\displaystyle \frac{\partial {\widehat{\rho }}_{\kappa }}{\partial t}}=[{\widehat{H}}_{eff},{\widehat{\rho }}_{\kappa }],$$

(42)

which is recognized as the generalized von Neumann equation for the density operator evolution. This equation governs the dynamics of the $\kappa$-deformed density operator with ${\hslash }_{eff}\kappa$ serving as the effective uncertainty.

The formal solution over a time interval $\tau$ is

$${\widehat{\rho }}_{\kappa }(t+\tau )=e^{-i{\widehat{H}}_{eff}\tau /{\hslash }_{eff}\kappa }{\widehat{\rho }}_{\kappa }\left(t\right)e^{i{\widehat{H}}_{eff}\tau /{\hslash }_{eff}\kappa }.$$

(43)

The numerical implementation of this evolution equation can be achieved through various computational approaches. In this work, we employ the split-step Fourier method, which provides an efficient and accurate scheme for time propagation of the density operator. Once the evolved density operator ${\widehat{\rho }}_{\kappa }(t+\tau )$ is obtained, we extract the corresponding Wigner distribution $W_{\kappa }(x,p;t+\tau )$ through the inverse transformation from the $uv$-representation. This allows us to compute the marginal distributions in position and momentum, which are then used in the filtering process to incorporate new measurement data.

At this stage, we have established a complete theoretical framework for the filtering procedure. It is worth emphasizing that our filtering approach is capable of handling arbitrary forms of error distributions and is not restricted to Gaussian cases, thus constituting a generalized Bayesian filtering method. However, for practical considerations and computational efficiency, we make a quadratic approximation to the gravitational potential experienced by the satellite orbit in subsequent numerical experiments. This approximation ensures that error distributions maintain their Gaussian character throughout the evolution process. Consequently, under the quadratic potential approximation, our filtering scheme reduces to a Kalman filter, which combines the computational advantages of linear-Gaussian systems with the theoretical generality of the extended phase-space formalism.

3. Physical Realization for Gravitational Orbit Dynamics

We now turn to the central question of this work: how to apply this framework to practical satellite orbit prediction. In this chapter, we address the implementation details within the specific context of short-arc satellite orbit prediction. The discussion encompasses several key aspects: first, we establish the procedure for selecting the covariance parameters and determining the effective uncertainty scale ${\hslash }_{eff}\kappa$ that characterizes the system; second, we specify the form of the Wigner distribution representing measurement errors in satellite state observations, taking into account the typical error characteristics in real tracking data; third, we derive the evolution equations appropriate for orbital motion under the extended phase-space formalism and describe the numerical methods employed for their solution; finally, we present the complete filtering algorithm that integrates measurement updates with dynamical propagation and the parameter $\kappa$ which is determined adaptively through the filtering process based on the observed measurement uncertainties and state estimation errors, thereby enabling sequential state estimation for operational orbit determination scenarios.

3.1. Wigner Distribution for Orbital States

We begin by specifying the phase-space representation of satellite states appropriate for optical tracking observations. In our experimental setup, ground-based optical stations measure the instantaneous range r and two angular coordinates (azimuth and elevation) that locate the satellite relative to the observation site. Through standard coordinate transformations from spherical to Cartesian coordinates, accounting for the station’s geodetic position and Earth’s rotation, these measurements yield the satellite’s three-dimensional position vector $\mathit{x}=(x,y,z)$ in an Earth-centred inertial frame. The measurement process involves multiple error sources, including photon shot noise, atmospheric turbulence, timing uncertainties, and instrument calibration errors. A rigorous treatment of these contributions leads to an estimated position covariance matrix that characterizes the uncertainty in the reconstructed position.

For the velocity determination, we adopt a simplified model suitable for short-arc predictions where orbital perturbations remain small. Specifically, we assume the satellite follows a circular Keplerian orbit, for which the orbital speed satisfies

$$v=\sqrt{{\displaystyle \frac{GM}{r}}},$$

(44)

where G is the gravitational constant, M is the Earth’s mass, and R is the geocentric distance derived from the position measurement. The velocity vector $\mathit{p}/m$ (with m being the satellite mass) is then determined by imposing that it lies tangent to the instantaneous orbital plane and perpendicular to the position vector. The uncertainty in velocity propagates from the position measurement error through this relation. Specifically, the initial state estimate is constructed under the assumption of a minimum-inclination circular orbit at the first observation epoch. However, our simulation scenarios are explicitly designed to exclude circular trajectories. Consequently, the initial velocity uncertainty is not arbitrary noise, but physically stems from the discrepancy between this circular assumption and the actual elliptical dynamics. This approach ensures that our performance evaluation naturally encompasses a wide and realistic spectrum of initial error conditions.

In realistic orbital tracking, measurement uncertainties are rarely isotropic due to the geometry of ground stations, atmospheric effects, and instrumental biases. We therefore characterize the errors by covariance matrices ${\Sigma }_x$ and ${\Sigma }_p$ for position and momentum, which encode the magnitude and correlation structure of uncertainties. Under the assumption that errors follow Gaussian statistics, the Wigner function describing the satellite’s phase-space distribution is given by

$$W(\mathit{x},\mathit{p})={\displaystyle \frac{1}{{\left(\pi {\hslash }_{\mathrm{eff}}\right)}^3}}exp\left(-{\displaystyle \frac{1}{2}}{(\mathit{x}-{\mathit{x}}_0)}^T{\Sigma }_x^{-1}(\mathit{x}-{\mathit{x}}_0)-{\displaystyle \frac{1}{2}}{(\mathit{p}-{\mathit{p}}_0)}^T{\Sigma }_p^{-1}(\mathit{p}-{\mathit{p}}_0)\right),$$

(45)

where ${\mathit{x}}_0$ and ${\mathit{p}}_0$ denote the mean position and momentum vectors derived from observations and dynamical models. The covariance matrices are typically obtained from orbit determination procedures that account for measurement noise and model uncertainties. This Gaussian form remains positive definite and represents the uncertainty compatible with the given error structure.

A crucial parameter in the extended phase-space formalism developed in the previous chapter is the effective uncertainty scale ${\hslash }_{\mathrm{eff}}$, which plays the role of an effective Planck constant in the generalized quantum-like description. Following the convention established for Gaussian phase-space distributions, we take the definition ${\hslash }_{\mathrm{eff}}=2\Delta x\Delta p=2{\left|{\Sigma }_x\right|}^{1/6}{\left|{\Sigma }_p\right|}^{1/6}$, which quantity quantifies the minimal resolvable volume element in phase-space induced by measurement errors. It represents the fundamental cell size within which the satellite’s state cannot be further localized given the observational uncertainties. In other words, ${\hslash }_{\mathrm{eff}}$ characterizes the coarse-graining scale of the phase-space distribution imposed by the finite precision of tracking data, rather than arising from any fundamental quantum uncertainty relation. For typical low Earth orbit satellites with optical tracking precision on the order of meters to tens of meters and velocity uncertainties of millimeters per second (after accounting for the satellite mass), ${\hslash }_{\mathrm{eff}}$ assumes values many orders of magnitude larger than Planck’s constant, reflecting the macroscopic nature of the system.

The Wigner distribution in Equation (45) can be mapped to the density operator representation in the $(u,v)$ phase-space coordinates. Applying the inverse transformation from Wigner to density operator form yields

$$\begin{array}{cc}\hfill \rho (u,v)={\displaystyle \frac{1}{{\left(2\pi \right)}^{3/2}{\left|{\Sigma }_x\right|}^{1/2}}}exp[& -{\displaystyle \frac{1}{4}}{(u-{\mathit{x}}_0)}^T{\Sigma }_x^{-1}(u-{\mathit{x}}_0)\hfill \\ \hfill & -{\displaystyle \frac{1}{4}}{(v-{\mathit{x}}_0)}^T{\Sigma }_x^{-1}(v-{\mathit{x}}_0)+{\displaystyle \frac{i{\mathit{p}}_0^T(v-u)}{{\hslash }_{eff}}}].\hfill \end{array}$$

(46)

This representation serves as the initial state for the subsequent dynamical evolution and filtering procedure. The density operator in Equation (46) encodes both the mean orbital state and its associated uncertainty, providing the complete probabilistic description required for Bayesian inference in the orbit determination problem.

3.2. Generalized KvN Evolution Under Gravitational Forces

In practical applications, we expand the potential energy around a reference point using a Taylor series. For the satellite orbit prediction problem considering Earth’s oblateness, the gravitational potential takes the form

$$U\left(\mathbf{x}\right)=-{\displaystyle \frac{GM}{r}}\left[1-J_2{\left({\displaystyle \frac{R_E}{r}}\right)}^2{P}_2(sin\varphi )\right],$$

(47)

where $r=\left|\mathbf{x}\right|=\sqrt{x^2+y^2+z^2}$ is the distance from Earth’s centre, G denotes the gravitational constant, M represents the Earth’s mass, $J_2\approx 1.08263\times {10}^{-3}$ is the second zonal harmonic coefficient, $R_E\approx 6378$ km is the Earth’s equatorial radius, $\varphi$ is the geocentric latitude with $sin\varphi =z/r$, and $P_2(sin\varphi )={\displaystyle \frac{1}{2}}(3{sin}^2\varphi -1)$ is the second-order Legendre polynomial.

We perform a second-order Taylor expansion about the reference position ${\mathbf{x}}_0$, which yields

$$U\left(\mathbf{x}\right)\approx U\left({\mathbf{x}}_0\right)+\nabla U\left({\mathbf{x}}_0\right)·(\mathbf{x}-{\mathbf{x}}_0)+{\displaystyle \frac{1}{2}}{(\mathbf{x}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{x}-{\mathbf{x}}_0),$$

(48)

where $r_0=\left|{\mathbf{x}}_0\right|$ and $H\left(U\right)$ is the Hessian matrix. This approximation remains valid when $|\mathbf{x}-{\mathbf{x}}_0|\ll r_0$, making it suitable for short-arc orbit prediction scenarios.

Under the quadratic approximation of the potential, the generalized Hamiltonian simplifies to

$${\widehat{\mathcal{H}}}_k={\displaystyle \frac{{\hslash }_{\mathrm{eff}}}{m}}\widehat{p}{\widehat{\lambda }}_x-{\hslash }_{\mathrm{eff}}{U}^{\prime }\left(\widehat{x}\right){\widehat{\lambda }}_p,$$

(49)

where $U^{\prime }\left(\widehat{x}\right)$ denotes the gradient of the potential function. In the $x{\lambda }_p$ representation, the evolution equation becomes

$$i{\hslash }_{\mathrm{eff}}{\displaystyle \frac{\partial {\Psi }_{\kappa }}{\partial t}}={\displaystyle \frac{{\hslash }_{\mathrm{eff}}}{m}}{\displaystyle \frac{{\partial }^2{\Psi }_{\kappa }}{\partial {\lambda }_p\partial x}}-{\hslash }_{\mathrm{eff}}{U}^{\prime }\left(x\right){\lambda }_p{\Psi }_{\kappa }.$$

(50)

Transforming to the $(u,v)$ representation through the relations

$$u=x-{\displaystyle \frac{{\hslash }_{\mathrm{eff}}\kappa {\lambda }_p}{2}},v=x+{\displaystyle \frac{{\hslash }_{\mathrm{eff}}\kappa {\lambda }_p}{2}},$$

(51)

the one-dimensional evolution equation takes the form

$$i{\displaystyle \frac{\partial {\rho }_{\kappa }}{\partial t}}={\displaystyle \frac{{\hslash }_{\mathrm{eff}}\kappa }{2m}}\left({\displaystyle \frac{{\partial }^2{\rho }_{\kappa }}{\partial v^2}}-{\displaystyle \frac{{\partial }^2{\rho }_{\kappa }}{\partial u^2}}\right)-{\displaystyle \frac{1}{{\hslash }_{\mathrm{eff}}\kappa }}{U}^{\prime }\left({\displaystyle \frac{u+v}{2}}\right)(v-u){\rho }_{\kappa }.$$

(52)

For three-dimensional systems with $\mathbf{x}=(x,y,z)$, this generalizes to

$$i{\displaystyle \frac{\partial {\rho }_{\kappa }(\mathbf{u},\mathbf{v},t)}{\partial t}}={\displaystyle \frac{{\hslash }_{\mathrm{eff}}\kappa }{2m}}\left({\nabla }_{\mathbf{v}}^2-{\nabla }_{\mathbf{u}}^2\right){\rho }_{\kappa }-{\displaystyle \frac{1}{{\hslash }_{\mathrm{eff}}\kappa }}{\mathbf{U}}^{\prime }\left({\displaystyle \frac{\mathbf{u}+\mathbf{v}}{2}}\right)·(\mathbf{v}-\mathbf{u}){\rho }_{\kappa }.$$

(53)

The potential gradient required in the evolution equation is obtained by differentiating the second-order expansion:

$$\nabla U\left(\mathbf{x}\right)=\nabla U\left({\mathbf{x}}_0\right)+H\left(U\right)(\mathbf{x}-{\mathbf{x}}_0).$$

(54)

Evaluating this at the positions $\mathbf{u}$ and $\mathbf{v}$, and noting that the constant term $U\left({\mathbf{x}}_0\right)$ drops out in the difference $U\left(\mathbf{v}\right)-U\left(\mathbf{u}\right)$, the evolution equation becomes

$$\begin{array}{cc}\hfill i{\hslash }_{\mathrm{eff}}\kappa {\displaystyle \frac{\partial {\rho }_{\kappa }(\mathbf{u},\mathbf{v},t)}{\partial t}}=& {\displaystyle \frac{{\left({\hslash }_{\mathrm{eff}}\kappa \right)}^2}{2m}}\left({\nabla }_{\mathbf{v}}^2-{\nabla }_{\mathbf{u}}^2\right){\rho }_{\kappa }-\nabla U\left({\mathbf{x}}_0\right)·(\mathbf{v}-\mathbf{u})\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{(\mathbf{v}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{v}-{\mathbf{x}}_0)-{\displaystyle \frac{1}{2}}{(\mathbf{u}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{u}-{\mathbf{x}}_0){\rho }_{\kappa }.\hfill \end{array}$$

(55)

The linear term in $\nabla U\left({\mathbf{x}}_0\right)$ drives the center-of-mass motion of the wave packet, while the Hessian terms encode the local curvature of the gravitational field and govern the wave packet deformation.

To solve this evolution equation numerically, we employ the split-step Fourier method, which exploits the natural separation between kinetic and potential terms. The evolution equation can be recast in operator form as

$$i{\hslash }_{\mathrm{eff}}\kappa {\displaystyle \frac{\partial {\rho }_{\kappa }}{\partial t}}=\widehat{H}{\rho }_{\kappa }=(\widehat{T}+\widehat{V}){\rho }_{\kappa },$$

(56)

where the kinetic operator is given by

$$\widehat{T}={\displaystyle \frac{{\left({\hslash }_{\mathrm{eff}}\kappa \right)}^2}{2m}}\left({\nabla }_{\mathbf{v}}^2-{\nabla }_{\mathbf{u}}^2\right),$$

(57)

and the potential operator takes the form

$$\widehat{V}=-\left[\nabla U\left({\mathbf{x}}_0\right)·(\mathbf{v}-\mathbf{u})+{\displaystyle \frac{1}{2}}{(\mathbf{v}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{v}-{\mathbf{x}}_0)-{\displaystyle \frac{1}{2}}{(\mathbf{u}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{u}-{\mathbf{x}}_0)\right].$$

(58)

The formal solution over a time step $\tau$ is expressed as

$${\rho }_{\kappa }(t+\tau )=exp\left(-{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}\kappa }}\widehat{H}\tau \right){\rho }_{\kappa }\left(t\right).$$

(59)

Since the kinetic and potential operators do not commute, we apply a symmetric Trotter splitting to second-order accuracy:

$$exp\left(-{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}\kappa }}\widehat{H}\tau \right)\approx exp\left(-{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}\kappa }}\widehat{V}{\displaystyle \frac{\tau }{2}}\right)exp\left(-{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}\kappa }}\widehat{T}\tau \right)exp\left(-{\displaystyle \frac{i}{{\hslash }_{\mathrm{eff}}\kappa }}\widehat{V}{\displaystyle \frac{\tau }{2}}\right)+O\left({\tau }^3\right).$$

(60)

The numerical implementation proceeds in five stages. First, we evolve the density operator by a half-step under the potential operator in real space:

$${\rho }_{\kappa }^{\left(1\right)}(\mathbf{u},\mathbf{v})=exp\left[-{\displaystyle \frac{i\tau }{2{\hslash }_{\mathrm{eff}}\kappa }}{V}_{\mathrm{eff}}(\mathbf{u},\mathbf{v})\right]{\rho }_{\kappa }(\mathbf{u},\mathbf{v},t),$$

(61)

where the effective potential is defined as

$$\begin{array}{cc}\hfill V_{\mathrm{eff}}(\mathbf{u},\mathbf{v})=& -\left[\nabla U\left({\mathbf{x}}_0\right)·(\mathbf{v}-\mathbf{u})+{\displaystyle \frac{1}{2}}{(\mathbf{v}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{v}-{\mathbf{x}}_0)\right.\hfill \\ & \left.-{\displaystyle \frac{1}{2}}{(\mathbf{u}-{\mathbf{x}}_0)}^{T}H\left(U\right)(\mathbf{u}-{\mathbf{x}}_0)\right].\hfill \end{array}$$

(62)

Second, we transform to momentum space via a six-dimensional Fourier transform:

$${\tilde{\rho }}_{\kappa }^{\left(1\right)}({\mathbf{k}}_u,{\mathbf{k}}_v)=\int \int {\rho }_{\kappa }^{\left(1\right)}(\mathbf{u},\mathbf{v})e^{-i{\mathbf{k}}_u·\mathbf{u}}{e}^{-i{\mathbf{k}}_v·\mathbf{v}}{d}^3\mathbf{u}{d}^3\mathbf{v}.$$

(63)

Third, in momentum space, the Laplacian operators become multiplicative, allowing us to apply a full kinetic evolution step:

$${\tilde{\rho }}_{\kappa }^{\left(2\right)}({\mathbf{k}}_u,{\mathbf{k}}_v)=exp\left[-{\displaystyle \frac{i\tau \hslash \kappa }{2m}}\left(|{\mathbf{k}}_u{|}^2-{\left|{\mathbf{k}}_v\right|}^2\right)\right]{\tilde{\rho }}_{\kappa }^{\left(1\right)}({\mathbf{k}}_u,{\mathbf{k}}_v).$$

(64)

Fourth, we return to real space through an inverse Fourier transform:

$${\rho }_{\kappa }^{\left(2\right)}(\mathbf{u},\mathbf{v})={\displaystyle \frac{1}{{\left(2\pi \right)}^6}}\int \int {\tilde{\rho }}_{\kappa }^{\left(2\right)}({\mathbf{k}}_u,{\mathbf{k}}_v)e^{i{\mathbf{k}}_u·\mathbf{u}}{e}^{i{\mathbf{k}}_v·\mathbf{v}}{d}^3{\mathbf{k}}_u{d}^3{\mathbf{k}}_v.$$

(65)

Finally, we complete the evolution with a second half-step under the potential operator:

$${\rho }_{\kappa }(\mathbf{u},\mathbf{v},t+\tau )=exp\left[-{\displaystyle \frac{i\tau }{2{\hslash }_{\mathrm{eff}}\kappa }}{V}_{\mathrm{eff}}(\mathbf{u},\mathbf{v})\right]{\rho }_{\kappa }^{\left(2\right)}(\mathbf{u},\mathbf{v}).$$

(66)

The complete propagation scheme can be compactly written as

$${\rho }_{\kappa }(t+\tau )=e^{-{\displaystyle \frac{i\tau }{2{\hslash }_{\mathrm{eff}}\kappa }}\widehat{V}}·{\mathcal{F}}^{-1}\left[e^{-{\displaystyle \frac{i\tau {\hslash }_{\mathrm{eff}}\kappa }{2m}}\left(\right|{\mathbf{k}}_u{|}^2-|{\mathbf{k}}_v{|}^2)}·\mathcal{F}\left[e^{-{\displaystyle \frac{i\tau }{2{\hslash }_{\mathrm{eff}}\kappa }}\widehat{V}}{\rho }_{\kappa }\left(t\right)\right]\right],$$

(67)

where $\mathcal{F}$ and ${\mathcal{F}}^{-1}$ denote the forward and inverse Fourier transforms, respectively. This method preserves unitarity and maintains the trace of the density operator throughout the evolution, ensuring physically consistent results.

3.3. Filtering Procedure

After propagating the density operator ${\widehat{\rho }}_{\kappa }(t+\tau )$ over the time interval $\tau$, the corresponding Wigner function $W(\mathit{x},\mathit{p};t+\tau )$ is obtained through the Weyl transformation, from which the position marginal distribution follows by integration over momentum coordinates. Because the potential energy in our dynamical model retains only second-order terms in its Taylor expansion, the evolved Wigner distribution remains Gaussian in form, and consequently the position marginal distribution also preserves its Gaussian character. At the end of each propagation interval, a new observation of the satellite’s position becomes available. This fresh measurement, together with its associated covariance matrix, is then incorporated into the predicted position distribution via standard Kalman update equations. The filtering step combines the prior distribution (propagated density operator) with the observation likelihood, yielding a posterior distribution (filtered density operator) whose uncertainty is necessarily reduced relative to the prior. This updated distribution after propagation serves as the prior distribution for the next propagation interval, and this process is repeated each time a new observation is received.

Each Kalman update refines the state estimate by narrowing the error distribution, thereby progressively reducing the overall uncertainty of the error distribution. Since the posterior distribution at any given instant retains Gaussian form, it is fully characterized by the covariance matrices $|{\Sigma }_x{|}_{pos}$ and $|{\Sigma }_p{|}_{pos}$. The variables $\delta x$ and $\delta p$ are defined by the following equations:

$$\delta x=|{\Sigma }_x{|}_{pos}^{1/6},\delta p={\left|{\Sigma }_p\right|}_{pos}^{1/6},$$

(68)

To explicitly quantify the reduction in uncertainty throughout the filtering process, we introduce the scaling parameter $\kappa$. Contrary to being a passive derived variable, $\kappa$ serves as a governing parameter in the generalized Koopman–Von Neumann evolution equation, directly determining the regime of the dynamics as the system determines its state. We define $\kappa$ as the ratio of the phase-space uncertainty volume at the current estimation step ($\delta x·\delta p$) to the initial macroscopic uncertainty ($\Delta x·\Delta p$):

$$\kappa ={\displaystyle \frac{\delta x·\delta p}{\Delta x·\Delta p}}.$$

(69)

Physically, $\kappa$ represents the degree of “squeezing” of the error distribution. As measurement updates reduce the estimation error, $\kappa$ decreases, thereby dynamically adjusting the coefficients in the evolution equation. This explicit mathematical formulation provides a concrete realization of the interpolation concept discussed in the original reference [20], allowing the model to adaptively transition between different uncertainty scales during the orbital determination process.

To make the filtering procedure explicit, we introduce discrete observation epochs $t_{i-1}$, $t_i$, and $t_{i+1}$ separated by time intervals $\tau$. Suppose the Kalman update at epoch $t_{i-1}$ has produced a filtered density operator ${\widehat{\rho }}_{i-1}$ and that posterior distribution is characterized by ${\delta }_{i-1}x$ and ${\delta }_{i-1}p$. The rescaling parameter at this epoch is then

$${\kappa }_{i-1}={\displaystyle \frac{{\delta }_{i-1}x·{\delta }_{i-1}p}{\Delta x·\Delta p}}.$$

(70)

Over the interval $[t_{i-1},t_i]$, the density operator (corresponds with posterior distribution) evolves according to

$$i{\hslash }_{\mathrm{eff}}{\kappa }_{i-1}{\displaystyle \frac{\partial {\widehat{\rho }}_{i-1}}{\partial t}}=[{\widehat{H}}_{\mathrm{eff}},{\widehat{\rho }}_{i-1}].$$

(71)

Integration over the interval $\tau$ yields the propagated density operator ${\widehat{\rho }}_{i-1}^{\tau }$ as well as the priori distribution just before the next measurement. At epoch $t_i$, the new observation provides position and momentum data $(x_i,p_i)$ together with their covariance matrix. A standard Kalman update then combines this measurement with ${\widehat{\rho }}_{i-1}^{\tau }$ to produce the filtered density operator ${\widehat{\rho }}_i$ and the associated characters ${\delta }_{i}x$ and ${\delta }_{i}p$ of the posterior distribution. The updated rescaling parameter

$${\kappa }_i={\displaystyle \frac{{\delta }_{i}x·{\delta }_{i}p}{\Delta x·\Delta p}}$$

(72)

governs propagation from $t_i$ to $t_{i+1}$ through the analogous equation

$$i{\hslash }_{\mathrm{eff}}{\kappa }_i{\displaystyle \frac{\partial {\widehat{\rho }}_i}{\partial t}}=[{\widehat{H}}_{\mathrm{eff}},{\widehat{\rho }}_i].$$

(73)

Repeating this propagation-update cycle for successive observations constitutes the complete filtering algorithm, wherein dynamical evolution and measurement assimilation alternate to maintain a statistically consistent representation of the satellite’s state under continuous observational input. The next section presents numerical results obtained with this procedure.

4. Experimental Results

4.1. Experimental Design and Data Generation

4.1.1. Orbit-Parameter Combinations and Simulation Setup

To comprehensively evaluate the proposed model, we simulate 405 satellite orbits by an almost exhaustive enumeration. The first five Keplerian elements are combined according to

Table 1. Orbital parameter values.

Parameter	Symbol	Values	Unit
Semi-major axis	a	9600, 24,382, 42,164	km
Eccentricity	e	0.001, 0.01, 0.1	–
Inclination	i	5, 15, 25, 35, 45
Right ascension of node	$\Omega$	0, 120, 240
Argument of perigee	$\omega$	0, 120, 240

, and the mean anomaly is sampled at 30° intervals to guarantee full coverage of the station-visible orbital arcs.

4.1.2. Perturbation Modeling and Error-Source Characterization

The true trajectory is propagated for 13 min by Euler integration.

• Self-consistent run: only two-body plus J₂ perturbation, identical to the force model used in the estimator.
• Biased run: additionally includes solar-radiation pressure and atmospheric drag to assess performance under small systematic errors.

Atmospheric-drag model:

$$\mathbf{F}=-\frac{1}{2}\rho C_{D}A\left|\mathbf{v}\right|\mathbf{v},$$

(74)

where $\rho$ is the atmospheric density, $C_D$ the drag coefficient, A the cross-sectional area, and $\mathbf{v}$ the velocity of the satellite relative to the atmosphere.

The perturbations are calculated according to

Table 2. Perturbation factors.

Perturbation	Symbol	$\mathit{\eta }={\mathit{f}}_{\mathit{i}}/{\mathit{f}}_{\oplus }$
Earth oblateness	${\eta }_E$	$2.79\times {10}^{-3}$
Atmospheric drag	${\eta }_D$	$6.8763\times {10}^{-7}$
Solar radiation pressure	${\eta }_{\odot }$	$4.651\times {10}^{-9}$

, which gives their magnitudes relative to the Earth’s central two-body attraction.

In the experiment, we set the constant acceleration due to solar-radiation pressure to $1.023\times {10}^{-9}\mathrm{m}{\mathrm{s}}^{-2}$, the drag coefficient to $C_D=2.2$, the atmospheric density to a fixed value of $\rho =4.19\times {10}^{-13}\mathrm{kg}{\mathrm{m}}^{-3}$, and the area-to-mass ratio to $A=0.02{\mathrm{m}}^2{\mathrm{kg}}^{-1}$.

4.1.3. Construction and Grouping Strategy of Observation Data

Each arc is split into an observation window (first 3 min) and a prediction window (subsequent 10 min). Three datasets are generated to quantify different error sources:

• Clean (no-bias set): contains only machine-precision truncation errors; serves as the theoretical lower bound for filter consistency checks.
• SysBias (small-bias set): adds un-modeled atmospheric drag and solar-radiation pressure (Table 2) to the true trajectory, yielding long-term drift at the level of $\sim {10}^{-6}{f}_{\oplus }$; used to test robustness under mild model mismatch.
• ObsNoise (random-error set): further superimposes zero-mean Gaussian white noise on the SysBias truth, with standard deviations taken from current optical and laser ranging accuracies (radial $\approx$$5 \mathrm{arcsec}$, along/cross $\approx 10 \mathrm{m}$); dominant in short-term scatter and used to evaluate the benefit of improving observation precision versus refining dynamical models.
  In the current trajectory generator, only Earth oblateness, constant drag, and constant solar-radiation pressure are included; the fixed drag coefficient and fixed SRP area-to-mass ratio cannot capture the large, seasonally varying eclipse fraction and polar-density enhancement that dominate polar-orbit evolution.

4.2. Statistical Analysis of Prediction Errors

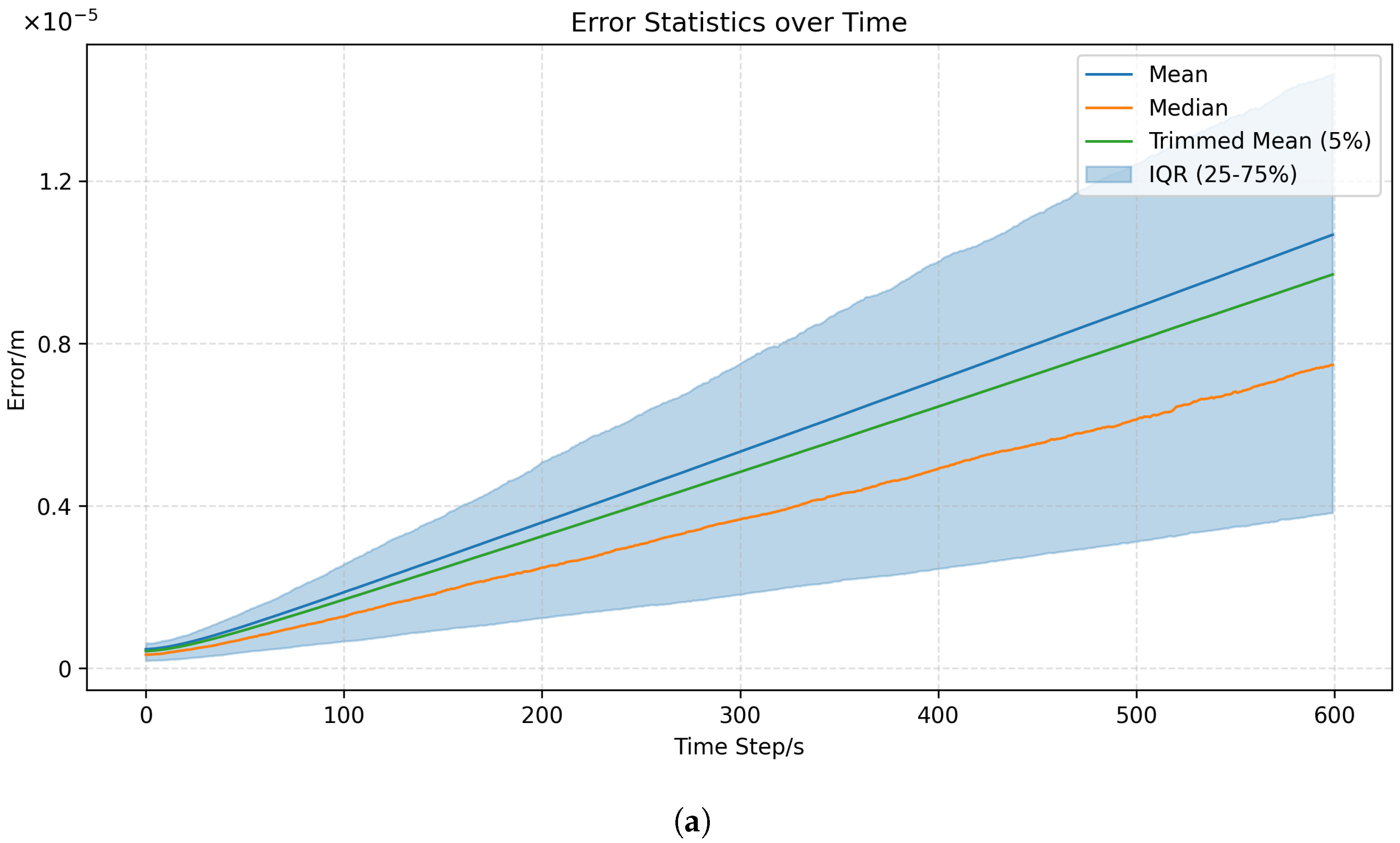
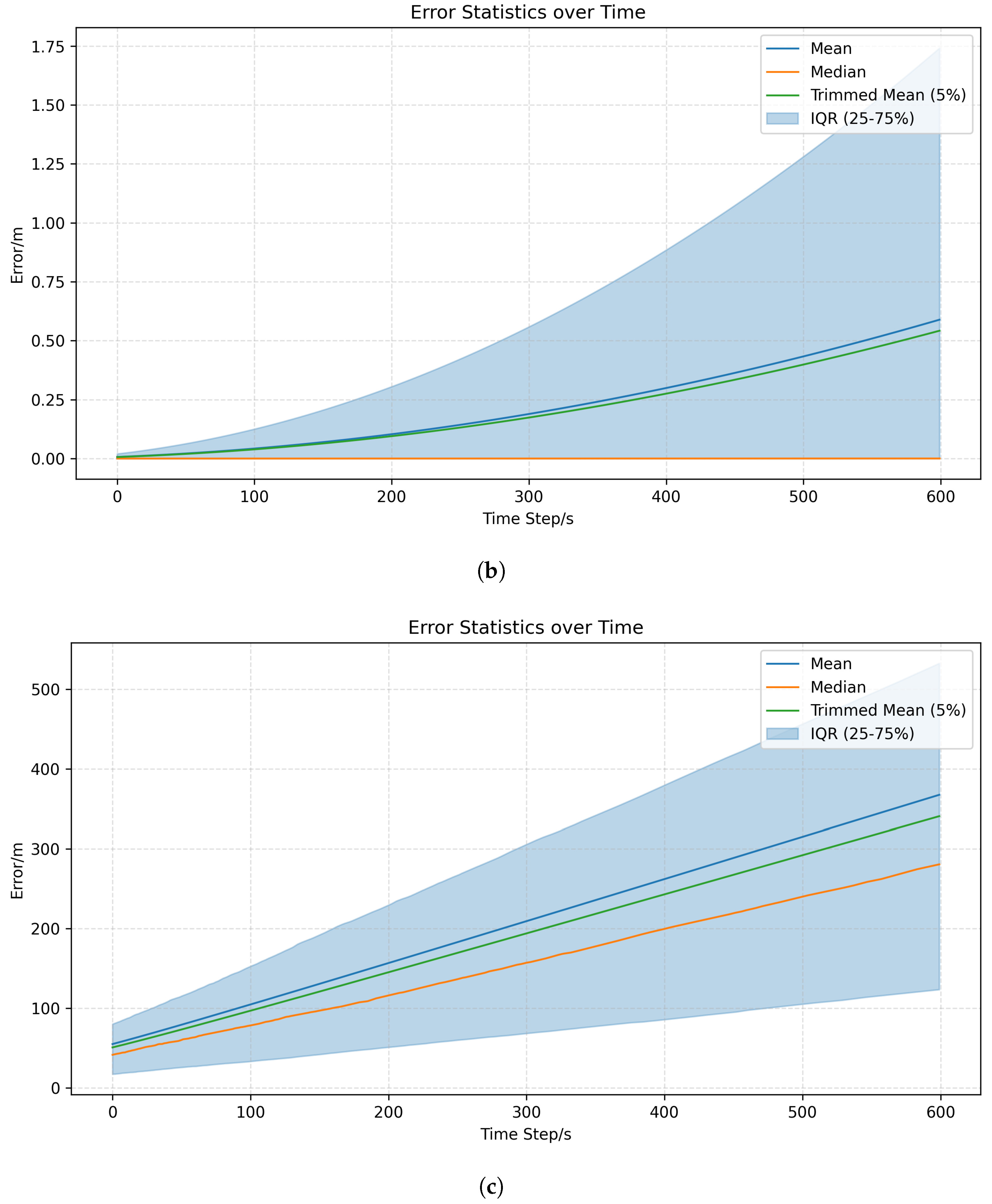
4.2.1. Ten-Minute Prediction-Error Distribution

Figure 1 presents the 10 min position-error statistics (mean, median, $5\%$ trimmed mean, and 1/4–3/4 quartile envelopes) for the three sample groups. The Clean group exhibits the smallest errors; the SysBias group shows a pronounced right tail; the ObsNoise group displays a distribution similar to that of the Clean group, indicating that observation precision is currently the dominant limiting factor.

4.2.2. Comparison Among Clean, SysBias, and ObsNoise Groups

• Clean: errors grow linearly and slowly with time, confirming model self-consistency.
• SysBias: mean deviates from median, indicating systematic outliers.
• ObsNoise: envelope width increases markedly, yet without skewness; random errors dominate.

4.3. Parameter-Sensitivity Analysis

To further analyse the effects of bias and random errors on the prediction, we computed error distributions as functions of inclination, semi-major axis, and eccentricity (Figure 2, Figure 3 and Figure 4) and identified inclination as an irrelevant variable. In the figures, “abs” denotes the absolute error, while R, T, and N indicate the radial, transverse, and normal components of the error, respectively.

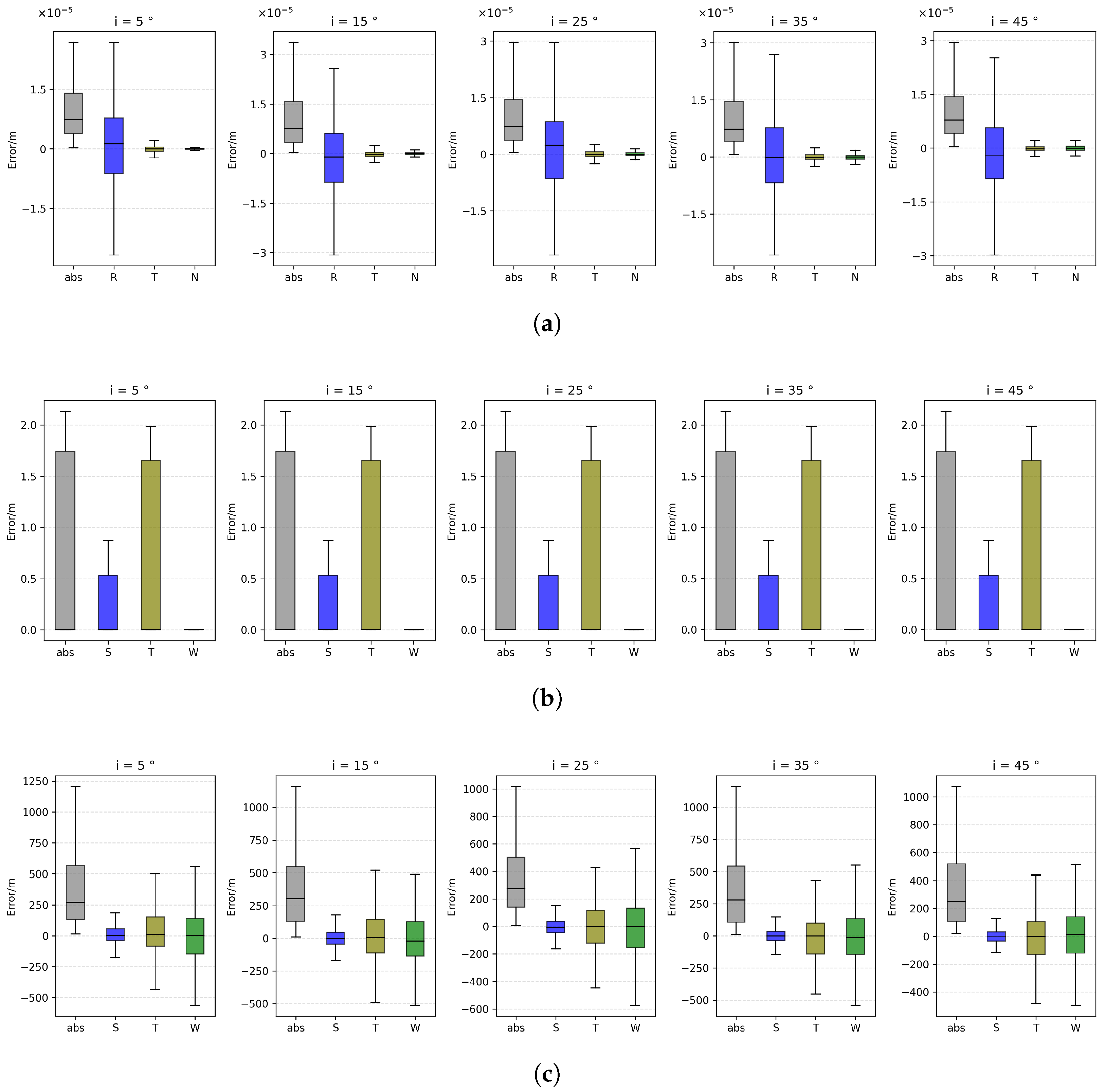
4.3.1. Effect of Inclination (Verification of Irrelevance)

Figure 2 presents the error statistics grouped by inclination. Within each subset the distributions are virtually identical for all inclination values, confirming that inclination has no significant influence on prediction accuracy; this variable is therefore excluded from further analysis.

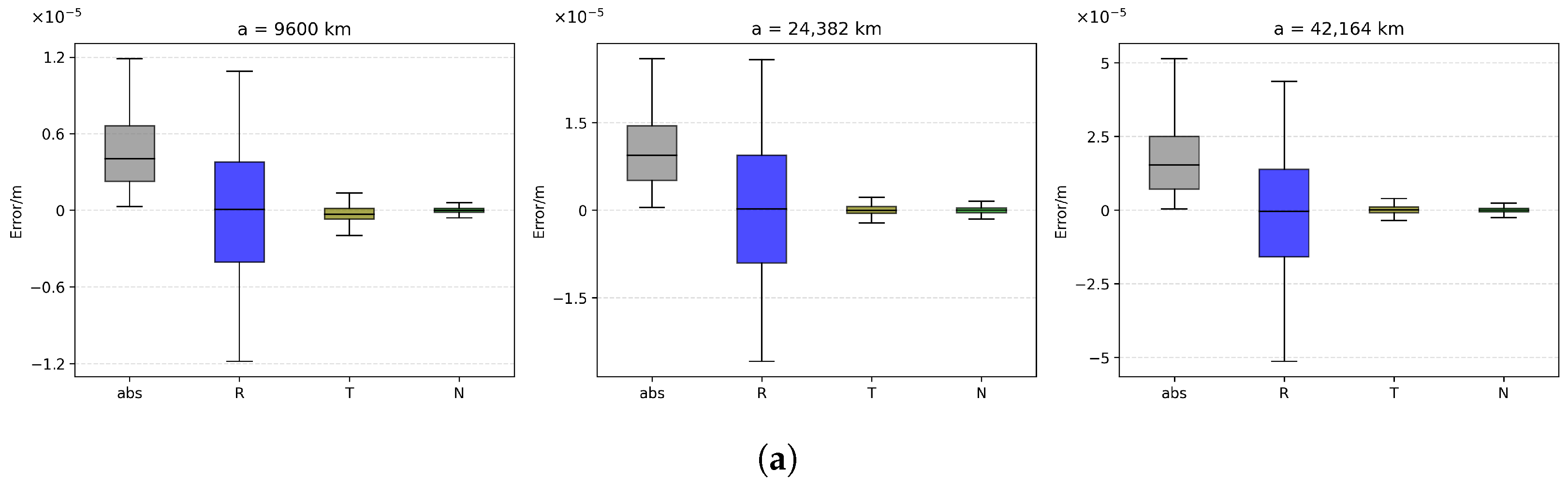
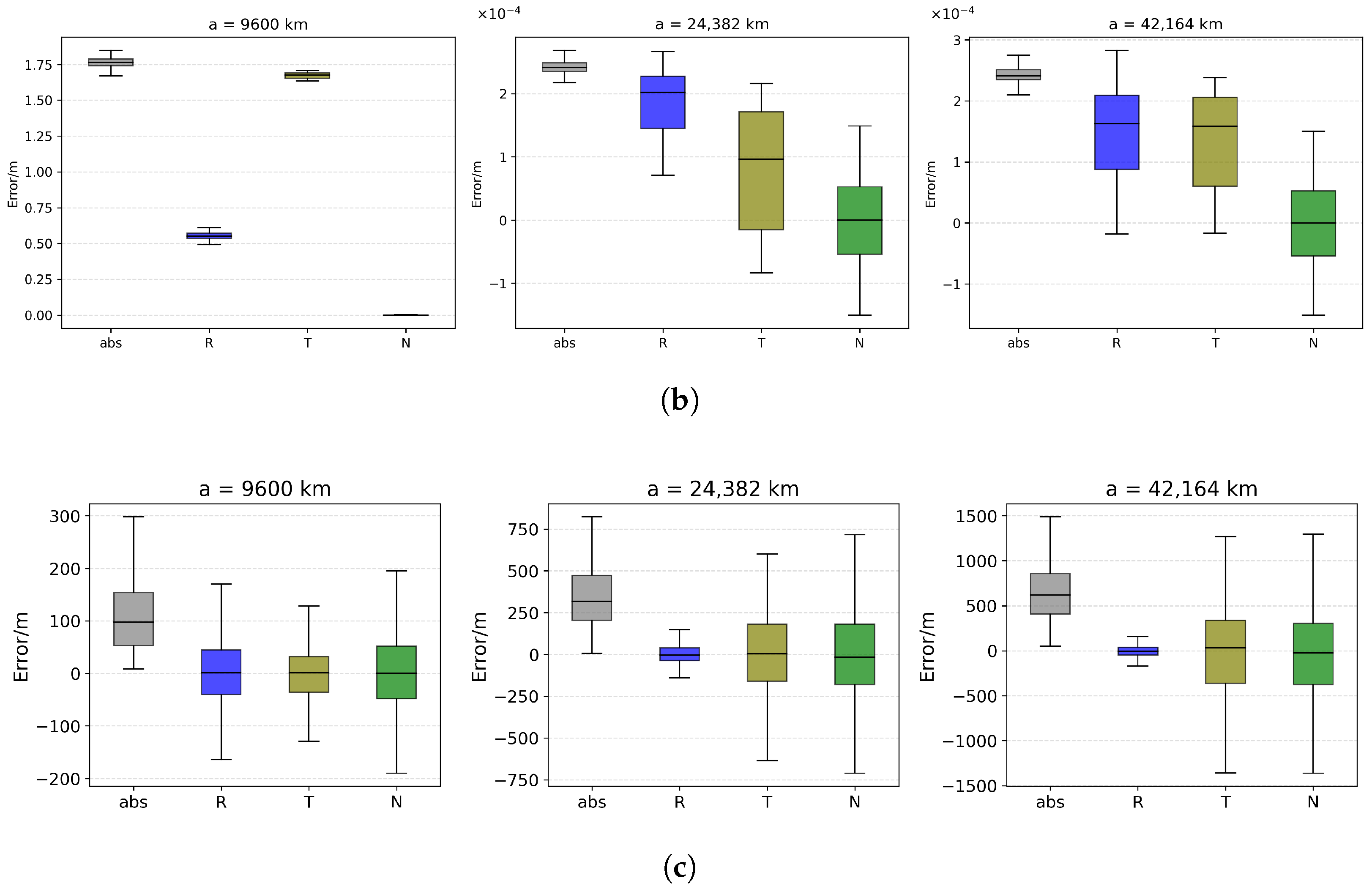
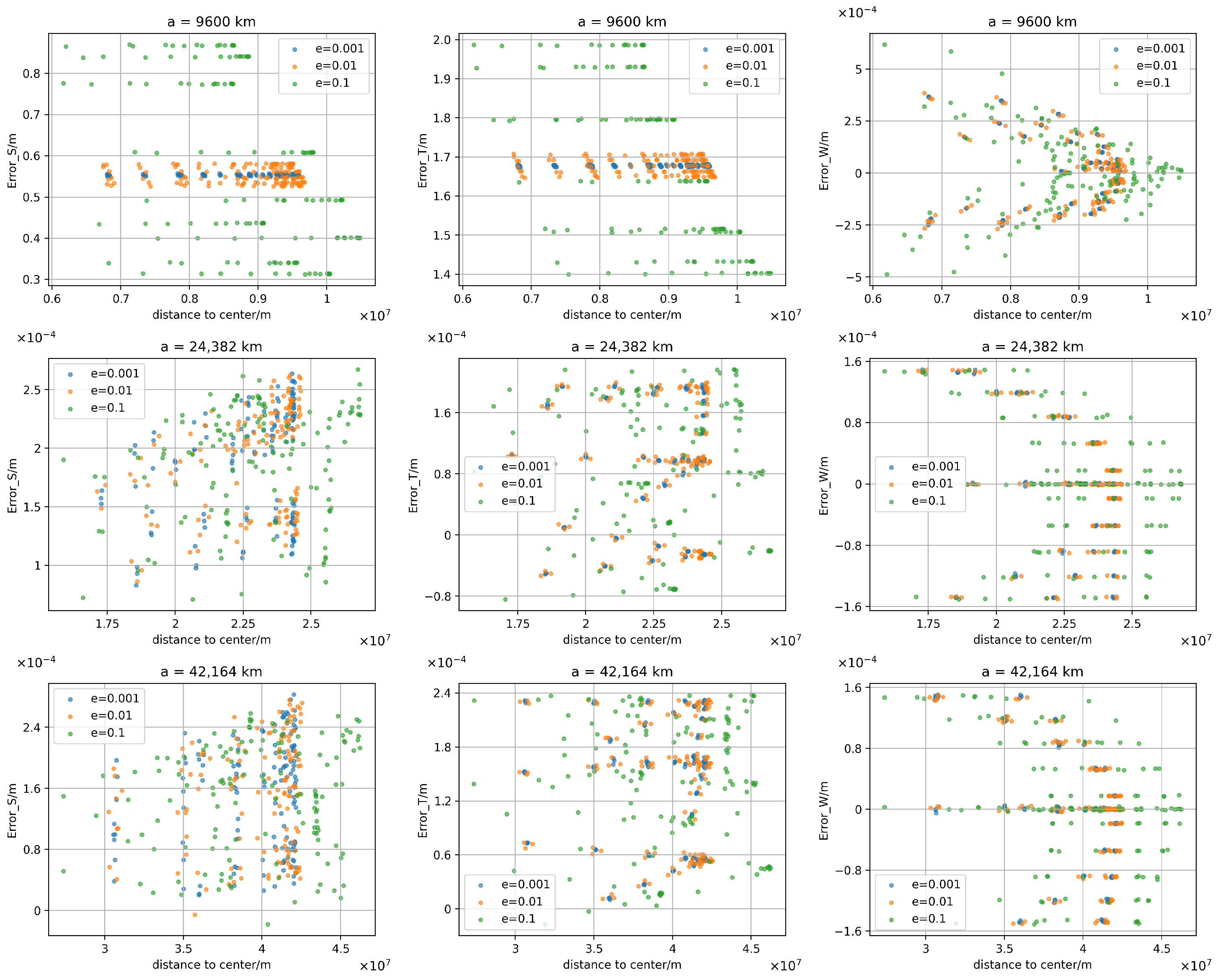
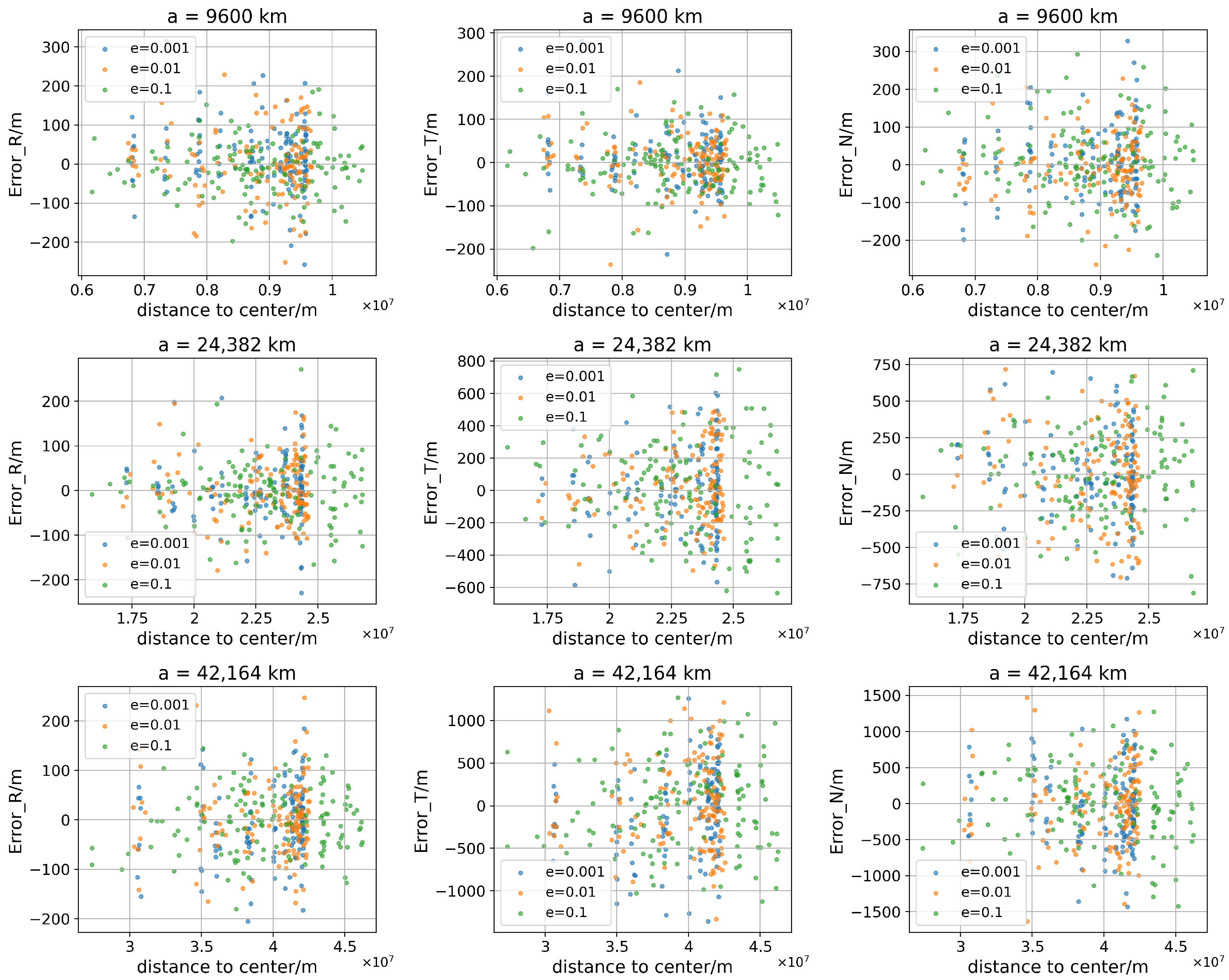
4.3.2. Coupled Effect of Semi-Major Axis and Perturbations

Figure 3 shows that for both the Clean and ObsNoise sets, the error increases monotonically with the semi-major axis. In the SysBias set, however, a distinct peak appears at the smallest semi-major axis, corresponding to the maximum atmospheric-drag acceleration; at the largest semi-major axis, the relative contribution of solar-radiation pressure rises, so the error induced by this perturbation also grows as the semi-major axis increases.

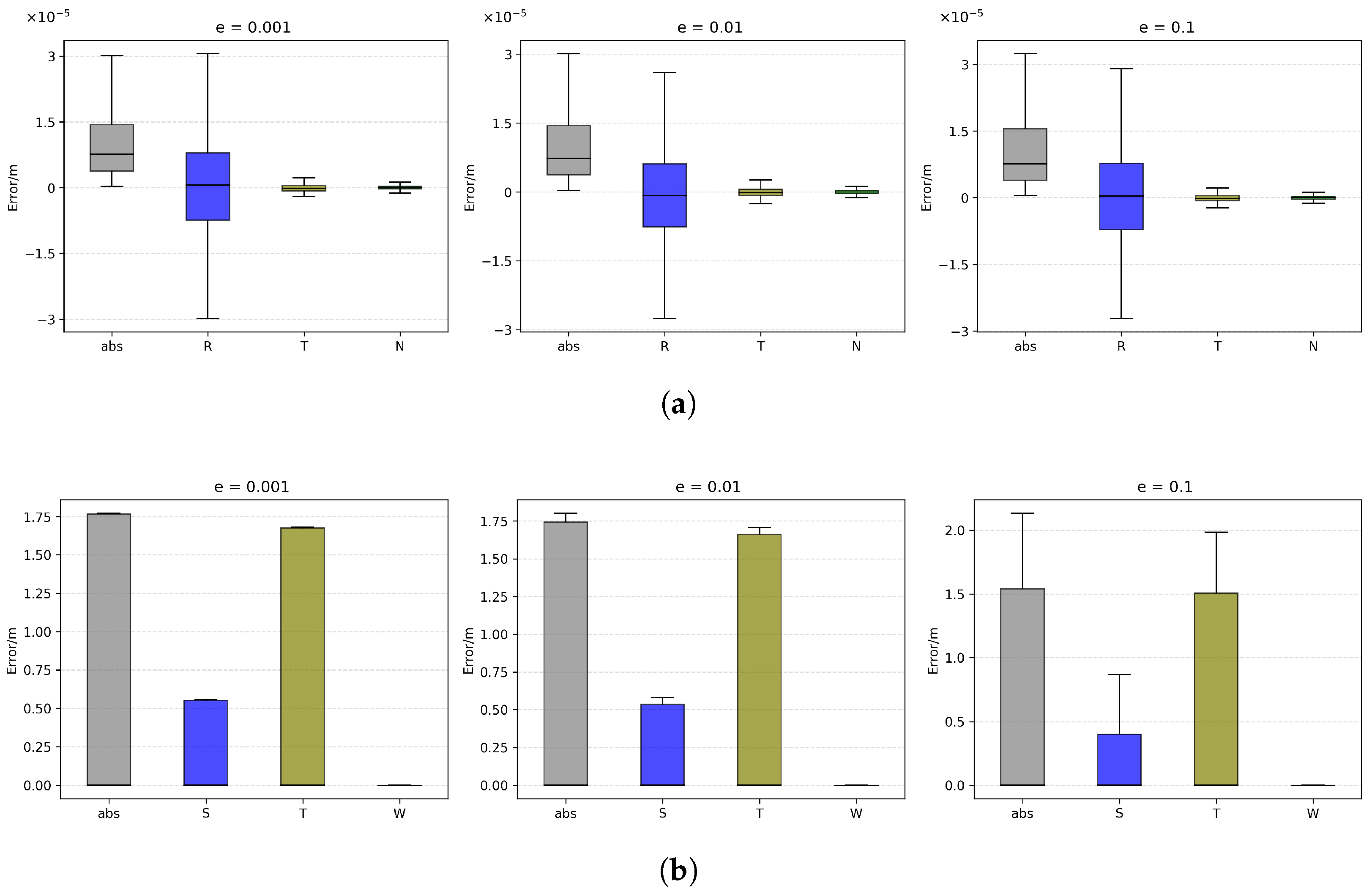
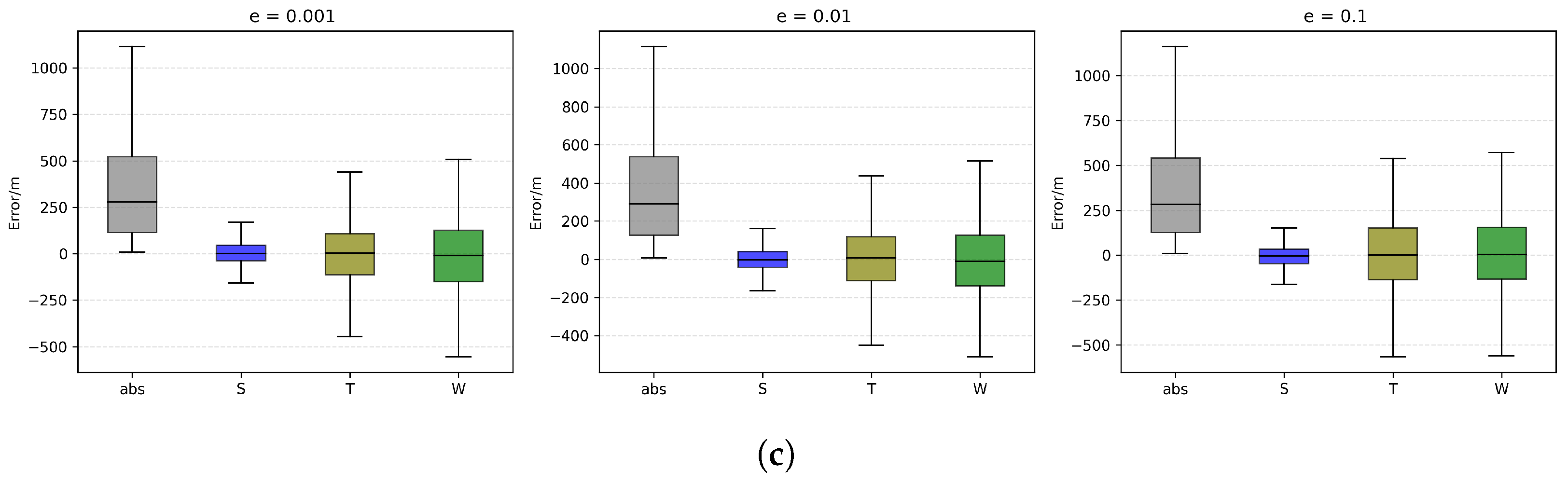
4.3.3. Modulation of Error Distribution by Eccentricity

Figure 4 indicates that only the SysBias set exhibits an increasingly pronounced outlier trend as eccentricity grows, whereas the distributions of the other two sets remain virtually unchanged with eccentricity.

4.3.4. Rank-Sum Sensitivity Test

To quantify, in a statistical sense, the influence of orbital parameters on forecast error, we applied the Kruskal–Wallis rank-sum test separately to inclination, semi-major axis, and eccentricity. The null hypothesis is that the error rankings are identical across all factor levels; the method is a one-way non-parametric ANOVA that requires neither normality nor homoscedasticity, making it suitable for the highly non-Gaussian errors typical of short-arc orbit determination.

The test statistic is defined as

$$H={\displaystyle \frac{12}{N(N+1)}}\sum _{i=1}^k{\displaystyle \frac{R_i^2}{n_i}}-3(N+1),$$

where k is the number of groups, $n_i$ is the sample size of group i, $R_i$ is the rank sum of group i, and $N=\sum n_i$ is the total number of observations. Under the null hypothesis, H is approximately ${\chi }^2$-distributed with $\mathrm{df}=k-1$ degrees of freedom; the confidence (p-value) is obtained from $p=P({\chi }_{k-1}^2>H)$, and $p<0.05$ is considered significant.

Table 3. Rank-sum sensitivity test results.

Scene	Factor	Error	H	p
Clean	Inclination	abs	0.929	0.9203
Clean	Inclination	R	9.511	0.0495
Clean	Inclination	T	8.021	0.0908
Clean	Inclination	N	5.047	0.2825
Clean	Semi-Major Axis	abs	370.698	0.0000
Clean	Semi-Major Axis	R	0.569	0.7523
Clean	Semi-Major Axis	T	26.254	0.0000
Clean	Semi-Major Axis	N	0.543	0.7624
Clean	Eccentricity	abs	0.493	0.7814
Clean	Eccentricity	R	1.799	0.4067
Clean	Eccentricity	T	0.344	0.8418
Clean	Eccentricity	N	0.088	0.9568
SysBias	Inclination	abs	0.323	0.9883
SysBias	Inclination	R	7.676	0.1042
SysBias	Inclination	T	2.105	0.7165
SysBias	Inclination	N	0.239	0.9934
SysBias	Semi-Major Axis	abs	809.385	0.0000
SysBias	Semi-Major Axis	R	832.716	0.0000
SysBias	Semi-Major Axis	T	843.947	0.0000
SysBias	Semi-Major Axis	N	0.006	0.9972
SysBias	Eccentricity	abs	0.467	0.7916
SysBias	Eccentricity	R	0.317	0.1042
SysBias	Eccentricity	T	0.158	0.7165
SysBias	Eccentricity	N	0.101	0.9934
ObsNoise	Inclination	abs	2.352	0.6713
ObsNoise	Inclination	R	3.728	0.4441
ObsNoise	Inclination	T	2.426	0.6580
ObsNoise	Inclination	N	1.934	0.7478
ObsNoise	Semi-Major Axis	abs	713.261	0.0000
ObsNoise	Semi-Major Axis	R	1.254	0.5343
ObsNoise	Semi-Major Axis	T	0.227	0.8928
ObsNoise	Semi-Major Axis	N	1.675	0.4329
ObsNoise	Eccentricity	abs	0.431	0.8059
ObsNoise	Eccentricity	R	2.518	0.2840
ObsNoise	Eccentricity	T	0.048	0.9761
ObsNoise	Eccentricity	N	2.892	0.2355

summarizes the H statistics and corresponding p-values for the four error components (abs, R, T, N) under the Clean, SysBias, and ObsNoise scenarios. The main findings are as follows:

• Semi-major axis is highly significant for the abs error in all scenes ($p<0.001$, H 350–840), confirming orbital altitude as the most sensitive parameter. The R component is also significant under SysBias ($p<0.001$), while T is significant only in SysBias and N is never significant, indicating that altitude amplifies errors mainly within the orbital plane.
• Inclination shows only marginal significance for the R component in the Clean scene ($p=0.0495$); all other components and scenes yield $p>0.05$ with $H<4.0$, verifying that inclination has no statistically significant influence on 10 min forecast error.
• Eccentricity gives $p>0.05$ and H values 0.05–2.9 (far below ${\chi }_{2,0.05}^2=5.99$) in every scene and component, demonstrating that within the commonly used eccentricity range the short-term error is not significantly affected by this parameter.

Based on the rank-sum statistics, the parameter sensitivity ranking is: semi-major axis ≫ inclination ≈ eccentricity (non-significant).

4.4. Visualization of Combined Bias and Error Effects

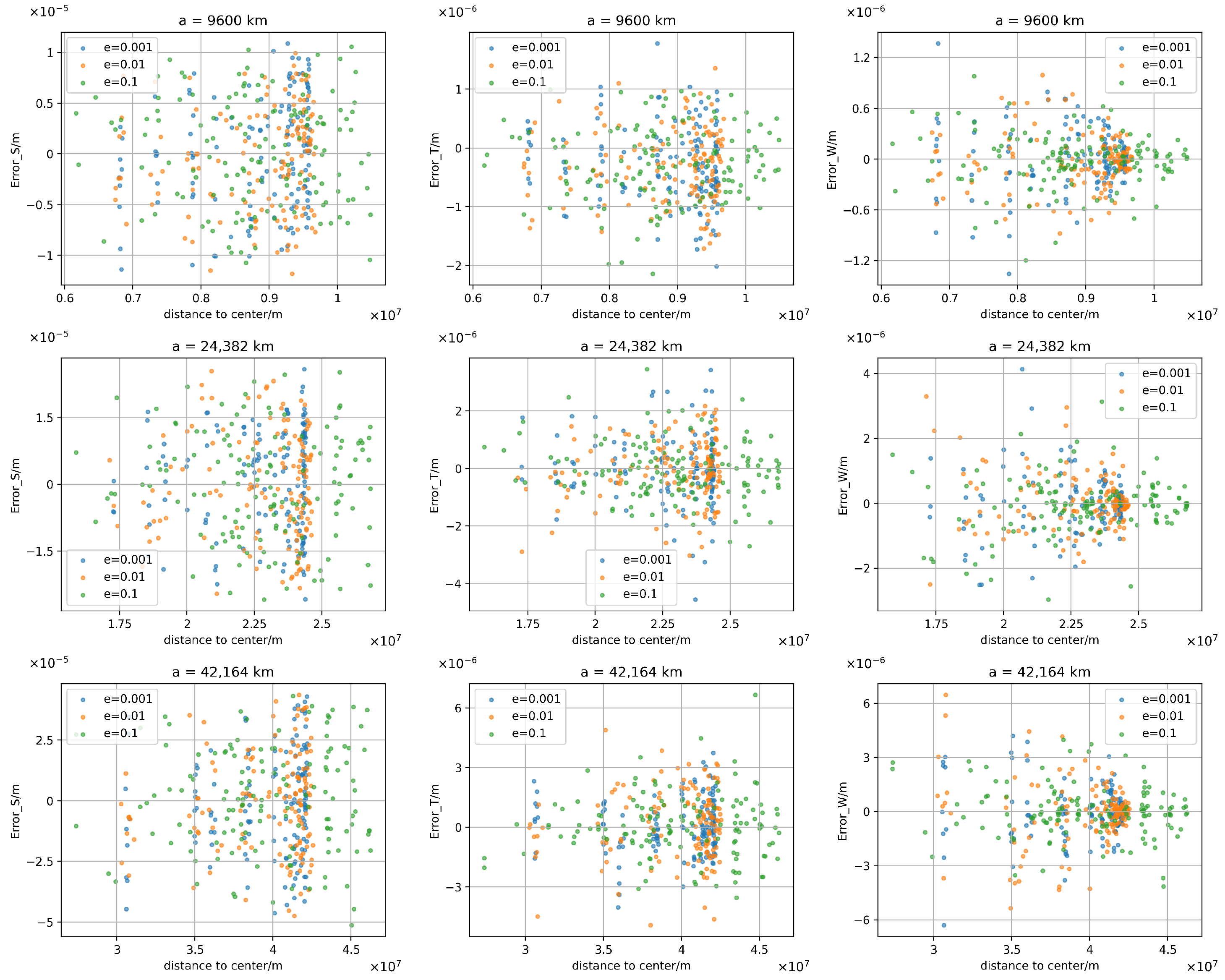
4.4.1. Scatter Plots of Radial/Along-Track/Cross-Track Errors

Figure 5 shows that the Clean-set scatter cloud is isotropic with the smallest spread. Figure 6 reveals that, under the action of systematic perturbations, the entire cloud of the SysBias set is shifted markedly in the radial and along-track directions; the combined effect of atmospheric-drag bias and large eccentricity further enlarges the cloud, while its spread in the cross-track direction increases as the actual orbital altitude decreases. Figure 7 displays a random, isotropic expansion of the scatter cloud for the ObsNoise set, with no directional offset.

4.4.2. Dominant-Factor Discrimination Between Bias and Noise

Comparing Figure 6 and Figure 7, the spread and directionality of the scatter clouds show that under the tested 3 min-fit/10 min-forecast window, observational error enlarges the distribution range in all directions by at least a factor of 100. Consequently, for this specific short-term prediction tasks with the present model, improving observation accuracy should take priority over refining the perturbation model.

4.4.3. Summary of Experimental Findings

In the typical 3 min short-arc, 10 min forecast scenario, error decomposition shows that observation noise contributes approximately 350 m, while unmodeled dynamical biases account for only 0.6 m—a three-order-of-magnitude difference. This indicates that the proposed model is sufficiently accurate for short-term prediction and demonstrates its robustness under information-deficient conditions: credible error bounds can still be obtained from observational data even when dynamical details are unknown. Statistical tests further show that inclination and eccentricity yield p > 0.05 almost globally, implying no significant effect on error medians; however, boxplots and scatter diagrams reveal an increasing number of outliers as eccentricity grows.

5. Discussion

5.1. Comparison with Current Practice Under SysBias

To benchmark our proposed model against current practice, we selected two widely used methods—Chebyshev fitting and dynamical fitting—for comparison. We consider that the model-versus-truth errors of both approaches likewise fall under the SysBias category; hence, we compare their results with those of the SysBias group in this paper.

Chebyshev polynomial extrapolation was tested with three fitting strategies [8,10], [10,18], and [14,30] (order, number of nodes).

Table 4. The forecast error of the Chebyshev method based on 3 min angle-and-range data (semi-major axis: 9600 km).

Time/s	4	8	12	16	20
error for Chebyshev [8,10]/m	14.61	48.11	113.53	228.20	419.18
error for Chebyshev [10,18]/m	2.45	8.32	21.29	48.87	99.81
error for Chebyshev [14,30]/m	4.67	24.41	80.77	215.76	510.60

shows that the best Chebyshev run ([10,18]) reaches 99.8 m at 20 s forecast, while the proposed model achieves a median error of 1.75 m at 10 min (Figure 3b).

Dynamical extrapolation was performed with the Shanghai Astronomical Observatory EODP full-perturbation propagator.

Table 5. The forecast error of the dynamical extrapolation method based on 3 min angle-and-range data.

Time/min	0	1	2	3	4	5	6	7	8	9	10
error (m) at semi-major axis: 9600 km	5.9	9.8	17.9	29.0	42.2	56.4	/	/	/	/	/
error (m) at semi-major axis: 42,164 km	56.5	56.6	56.4	56.2	56.6	56.3	56.3	56.5	56.3	56.3	56.5

gives 56.36 m (semi-major axes: 9600 km) at 5 min and 56.45 m (semi-major axes: 42,164 km) at 10 min; the corresponding 10 min median errors of the proposed model are 1.75 m (semi-major axes: 9600 km) and 0.00025 m (semi-major axes: 42,164 km) (Figure 3b), both substantially lower than the 5 min dynamical baseline.

Across the 3 min fit/10 min forecast window, the proposed model achieves median errors of 1.75 m (semi-major axes: 9600 km) and 0.00025 m (semi-major axes: 42,164 km), both substantially smaller than the 5 min baseline of the dynamical extrapolation tool and the 20 s best result of Chebyshev extrapolation, demonstrating clear accuracy gains under the same small-bias condition.

5.2. Future Improvements and Extensions

At present, the model incorporates only conservative forces; for non-conservative effects such as atmospheric drag and solar-radiation pressure, we have preliminarily introduced a forced-damped harmonic-oscillator equation. Initial experiments show that this correction reduces the 10 min forecast error of the small-bias group by one to two orders of magnitude, providing a viable path for future accuracy improvements. In addition, we will test the model with pure angle-only (two-dimensional) data to verify its ability to handle incomplete observations and the stability of $\kappa$ calibration under information-deficient conditions.

The proposed model presents an innovative approach to short-arc orbit prediction by integrating physical interpretability with real-time engineering feasibility. This approach not only enhances the accuracy and reliability of orbit predictions but also provides a robust framework for addressing the challenges associated with incomplete observations and uncertainties in dynamic environments. By effectively utilizing the principles of dynamics and leveraging observational data, this model demonstrates the potential to significantly advance the field of orbit prediction, ensuring improved performance in aerospace applications.

It is important to distinguish the fundamental mechanism of the proposed approach from standard Kalman filtering schemes, particularly regarding the propagation of uncertainty. Standard filters (like EKF) directly evolve the statistical moments (mean and covariance) of the state vector. In contrast, our approach treats the uncertainty as a Wigner distribution function defined over the full phase space. The evolution of this distribution is governed strictly by the generalized Koopman–von Neumann (KvN) equation.

In this study, we deliberately employ a quadratic approximation of the gravitational potential to validate the mathematical feasibility of the framework. It is a known property of Wigner dynamics that under a quadratic potential (linear dynamics), an initial Gaussian Wigner function naturally evolves into a Gaussian state without requiring external truncation or “forcing” approximations. Therefore, while the resulting evolution of the mean and covariance in this specific test case aligns with linear Kalman filtering, the underlying “engine”—the operator-theoretic evolution of the phase-space density—is fundamentally different. This setup serves as a validation benchmark; unlike standard filters, the KvN–Wigner framework is designed to naturally accommodate non-Gaussian features and higher-order dynamical couplings in future extensions where the quadratic restriction is lifted.

The feasibility of the proposed operator-theoretic model was established by comparing it with Chebyshev and dynamic fitting methods. This simplification served as a necessary benchmark to validate the mathematical consistency of the underlying KvN evolution machinery. Future work will extend this framework to the full gravitational potential, where the method is designed to naturally capture nonlinear effects and non-Gaussian phase-space features without artificial truncation. Furthermore, the accuracy and efficiency of the proposed framework will be rigorously evaluated against state-of-the-art nonlinear uncertainty propagation methods, specifically, Koopman-based uncertainty evolution techniques and Orthogonal Probability Approximation (OPA) schemes.