Abstract
The fuel electro-hydraulic servo valve is a core component of the aero-engine fuel control system, playing a crucial role in engine performance. Due to the operational characteristics of the aviation fuel supply and injection system, fuel is directly sprayed through the nozzle for combustion after passing through the pipeline. The working environment and medium are subject to a wide temperature range, and the medium lacks a circulating filtration process, making it difficult to effectively remove impurities. As a result, the fuel contains a high concentration of contaminant particles. Under high-temperature conditions, colloidal particles precipitated from the fuel medium collide and adhere to metallic and other contaminant particles carried by the fuel, subsequently attaching to the internal surfaces of the fuel servo valve, causing valve sticking. This study aims to establish an adhesion criterion suitable for colloidal particles in fuel systems based on a traditional particle collision model. The adhesion criterion incorporates the viscoelastic and surface energy characteristics of colloidal particles, providing a more accurate description of their deposition behavior under the conditions studied. A particle–particle and particle–wall collision test apparatus was designed, and experiments were conducted. A comparison between experimental results and theoretical calculations shows that the overall error for collisions between colloidal particles and walls is controlled within 10%, validating the feasibility of the adhesion criterion. The Young’s modulus, Poisson’s ratio, and surface free energy of the colloidal particles were measured as 688 MPa, 0.39, and 77 mJ/m2, respectively. These results provide theoretical and experimental foundations for particle migration and deposition processes in fuel systems. The analytical method clarifies the key mechanism of adhesion caused by colloidal particles, providing guidance for improving the reliability, safety, and maintenance of fuel servo valves in aero-engine applications.
1. Introduction
The reliability of hydraulic systems has long been one of the core concerns in the field of engineering, with hydraulic oil contamination being a primary cause of system failures. Studies indicate that over 75% of hydraulic system malfunctions originate from particulate contaminants in the oil. These contaminant particles mainly come from three sources: internal residues, external intrusion, and internal generation. Among them, colloidal particles, as typical internally generated contaminants, are primarily formed by the oxidative degradation of hydraulic oil under high-temperature conditions. Due to their unique adhesiveness and susceptibility to plastic deformation, colloidal particles can cause severe contamination-induced jamming issues in critical hydraulic components, such as servo valves. However, their specific mechanisms of influence remain insufficiently studied, leading to an underestimation of associated risks [1,2].
In studies on particle motion characteristics, Haoting Li et al. employed the CFD–DEM approach to investigate the separation behavior of mineral particles in porous rocks and their subsequent migration and deposition [3]. Cundall et al. examined the interparticle forces and motion behavior of solid particles through discrete numerical simulations [4]. Mittal proposed an immersed boundary method that can be applied to compute the motion of particles across multiple scales in flow fields [5]. Vito Tic et al. analyzed the motion characteristics of contaminant particles in hydraulic tanks based on an Euler–Lagrangian two-phase flow approach [6]. The forces and migration behavior of rigid spherical particles in viscous fluids near wall boundaries were studied using direct finite element simulations [7].
In aerospace fuel control systems, fuel serves as the working medium, where its contamination level is generally lower than that of conventional hydraulic systems, while the operating environment and fuel temperature exhibit a wider range of variation. Recent studies have indicated that when operating in fuel media, the precision flow passages between the jet pipe and the receiver in two-stage jet pipe servo valves are particularly sensitive to colloidal particles [8,9,10]. Excessive fuel temperature may cause partial precipitation of colloidal particles or even carbonization. Under wide temperature operating conditions, colloidal particles that precipitate from the fuel medium tend to adhere to metallic debris and other contaminants, which may subsequently result in spool sticking problems in fuel electro-hydraulic servo valves.
In hydraulic systems, spool sticking induced by contamination is usually mitigated by investigating the migration behavior of contaminant particles to prevent their accumulation. Terrell’s hybrid modeling approach has demonstrated that the trajectories of nanoscale particles in fluids exhibit kinetic characteristics similar to the migration of colloidal particles [11]. In recent years, increasing attention has been directed toward the anti-contamination performance of servo valves, and significant progress has been made in understanding contaminant characteristics in hydraulic oils. The sticking process of servo valve spools involves complex interactions among fluid dynamics, multiphase flow, heat transfer, and particle dynamics.
Many scholars have focused on particle collision theory and numerical simulation methods. Thornton proposed a more refined contact model [12,13], Walton simplified the formulation of viscoelastic models [14], Tykhoniuk et al. established a piecewise linear model [15], and Luding et al. further improved the relationship between unloading stiffness and loading history [16,17,18].
In studies concerning the influence of particle behavior on pump and valve system performance, Zhang Yuliang et al. conducted numerical simulations of solid–liquid two-phase flow in centrifugal pumps, and the results demonstrate that an increase in particle diameter or concentration leads to reduced pump efficiency [19]. Liu Xinqiang et al. investigated the impact of solid particles on spool valves without orifices and found that particles in the fluid are the primary cause of port corrosion damage [20]. In hydraulic servo valves, viscous heating during operation may induce spool deformation, which in turn results in hydraulic sticking phenomena.
With the continuous advancement of particle collision theory, Moreno et al. studied the effect of adhesion on the flowability of particle systems [21], while Hassanpour reported that discrepancies of up to 160% may exist between DEM simulations and experimental results [22]. These studies laid the foundation for advancing particle collision theory. Considering the unique adhesive and plastic deformation characteristics of colloidal particles, research on their behavior is of particular importance. Wang et al. revealed that both ionic concentration and pH value significantly influence the migration of petroleum colloids [23].
In studies on the characteristics of irregular particles, Daghooghi and Borazjani compared irregularly shaped particles with their equivalent spheres and found that the average shear particle stress of irregular particles can be 20–120% higher than the maximum value of their spherical counterparts [24]. Yohsuke Tanaka et al. employed a high-resolution PIV technique to record the trajectories of particles in a Kármán vortex street [25]. Ahmed Elrahmani proposed a CFD–DEM-based modeling framework and successfully simulated the migration and deposition of fine particles in porous media. Xianyu Yang simulated the suspension flow of nanoparticles in shale pores using CFD and DEM methods [26].
In research on aerospace fuel systems, it has been demonstrated that severe erosion of pilot-stage components caused by particulate contaminants gradually degrades the overall performance of jet-deflector servo valves. The maximum erosion rate occurs at the splitter wedge angle of the receiver port and increases with the contamination level [27]. Closed-loop constant differential pressure control valves are widely applied in fuel metering systems of aero-engines, and an integral constant differential pressure control valve has been shown to achieve servo tracking without steady-state errors through a robust LQR design method [28]. Investigations on pneumatic servo systems of auxiliary power units (APUs) have further revealed that the throttling area ratio exerts a significant influence on system linearity [29].
In studies on fuel electro-hydraulic servo valves, the retention of micron-sized particles within valve clearances can cause spool sticking due to the flammability of the fuel medium and the lack of effective recirculation filtration. It has been found that the release location of particles accounts for 63% of the influence on particle migration time, whereas the surface roughness of the valve contributes 37% [30]. The velocity distribution at the outlet of the jet deflector significantly affects the pressure characteristics of the pilot stage, with dynamic deflection velocity distribution models showing the best agreement with CFD results [31]. Research on contamination-induced friction indicates that the critical particle size for sticking lies between 0.7 and 0.9 times the clearance [32].
In studies on erosion and wear mechanisms, Alister Forder et al. proposed a CFD-based erosion model to investigate corrosion in petroleum control valves [33]. Although jet-deflector valves exhibit excellent anti-contamination performance, they are still subject to erosion and wear caused by solid particles in hydraulic oil. The main wear occurs at the splitter wedge angle, characterized by regular and fluctuating distribution patterns [34]. Investigations on direct-drive electro-hydraulic servo valves have indicated that erosion and wear are the primary physical failure modes, and predictive models established using exponential smoothing and ARIMA algorithms provide effective methods for forecasting valve performance [35].
Regarding experimental methods, Kandlikar et al. conducted simulations on the unidirectional flow characteristics of microsystems with 14% roughness [36]. Olivier Reinertz et al. designed an experimental setup to detect changes in hydraulic valve control characteristics after studying wear mechanisms [37]. William H. Mitchell and Saverio E. Spagnolie derived integral equations for the surface traction double layer of moving objects in low-Reynolds-number viscous flows [38].
However, most existing studies have focused on solid particles in conventional hydraulic oils, with limited attention to the unique behavior of colloidal contaminants in fuel systems. In particular, the collision and adhesion mechanisms between colloidal particles precipitated from fuel at high temperatures and metallic or other contaminant particles remain poorly understood. This knowledge gap hampers the development of precise contamination control strategies for aerospace servo valves operating over wide temperature ranges. To address this issue, the present study investigates the adhesion behavior of colloidal particles through a combined theoretical modeling and experimental validation approach, aiming to elucidate their role in contamination-induced sticking and to provide insights for the design and optimization of anti-contamination fuel hydraulic components.
2. Analysis of Viscoelastic Collisions in Colloidal Particles
2.1. Effect of Particles on Slide Valves
The structure of common fuel electro-hydraulic servo valves is shown in Figure 1. The electro-hydraulic servo valve is generally composed of three parts: a torque motor, hydraulic amplifier, and feedback mechanism. The aviation fuel control system uses fuel as its working medium. Compared with conventional hydraulic systems, it exhibits lower fluid contamination levels but operates under significantly wider ranges of environmental and working medium temperatures. When fuel temperatures become excessively high, certain fuel components may precipitate colloidal particles or even undergo carbonization.
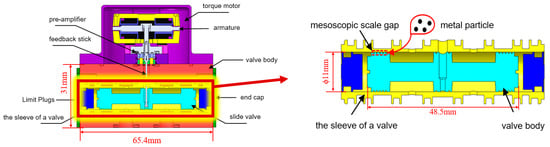
Figure 1.
Schematic diagram of internal structure of fuel electro-hydraulic servo valve.
In the event of an excess of particles being transported and accumulated within the specified gap, these particles, being of a sensitive nature, will inevitably lead to friction and wear on the surface of the slide valve spool during its movement within the hydraulic system. This, in turn, will have a direct effect on the performance and longevity of the hydraulic system as a whole and may even result in spool stagnation. Such an eventuality will in turn lead to failure of the hydraulic components, thus affecting the normal operation of the hydraulic system as a whole.
2.2. Analysis of Particle Collision Contact Forces and Adhesion Criteria
Considering the unique adhesive behavior and plastic deformation characteristics of colloidal particles, a theoretical framework was developed by referencing and integrating multiple classical collision theories. For particle collision analysis, the Hertzian contact theory was primarily selected as the theoretical foundation. This contact theory serves as the basis for solving elastic contact problems between curved particle surfaces, with the following fundamental assumptions: the contacting particle surfaces are smooth and homogeneous, the contact area is negligible compared to the particle size, only elastic deformation occurs within the contact zone, and the contact force acts normal to the contact surface.
Building upon this foundation, an extended investigation of the adhesion behavior of gel particles was conducted. Based on fundamental contact theory and considering the viscoelastic–plastic collision characteristics inherent to the gel particles under study (as illustrated in Figure 2), a schematic diagram of elastic collision between two gel particles is presented. In Figure 2, the dashed lines indicate the original particle surfaces without deformation, while the normal overlap is given by Equation (1).
In this equation,
- —Normal overlap displacement between colliding particles (m);
- —Radius of Particle 1 (m);
- —Radius of Particle 2 (m);
- —Position vector of Particle 1’s spherical center (m);
- —Position vector of Particle 2’s spherical center (m).
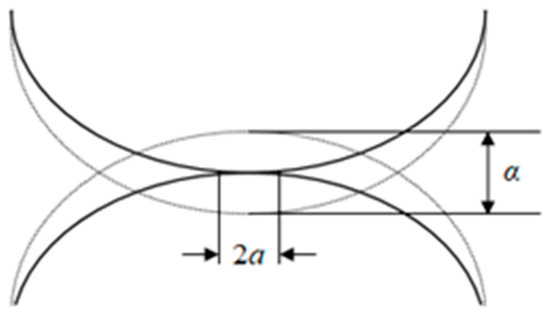
Figure 2.
Schematic diagram of contact deformation during collision between two spherical particles based on Hertzian contact theory.
Upon determination of the normal overlap displacement during collision contact deformation between two spherical particles, standardization of particle radii, elastic moduli, and masses was implemented due to identical overlap conditions. The effective radius (R), effective elastic modulus (E), and effective mass (m*) for the particle system are expressed by Equations (2)–(4), respectively:
In this equation,
- —Effective radius between particles (m);
- —Effective elastic modulus (Pa);
- —Effective mass (kg);
- —Elastic modulus of Particle 1 (Pa);
- —Poisson’s ratio of Particle 1;
- —Mass of Particle 1 (kg);
- —Elastic modulus of Particle 2 (Pa);
- —Poisson’s ratio of Particle 2;
- —Mass of Particle 2 (kg).
The normal contact force, P (N), acting during particle collision is determined by Equation (5).
- —Normal contact force (N).
The contact radius (a) can be derived from the normal contact force, as given by Equation (6):
The conversion relationship between a and α is derived from Equations (6) and (7) as follows:
The incremental normal contact force, ΔP, corresponding to an overlap increment, Δα, between two contacting particles is given by Equation (8):
The work performed by the normal contact force when the relative impact velocity, V, reaches sufficient magnitude to induce yielding in either sphere is given by Equation (9):
In this equation,
- —Yield velocity (m/s);
- —Contact radius at yield point (m).
The yield pressure, py, is determined by Equation (10) when the contact radius reaches its yield condition value, ay:
The yield velocity is then given by Equation (11):
However, the conventional Hertzian contact theory neglects the adhesive effects between particles and considers only their mechanical collisions. Therefore, the viscoelastic contact theory is introduced to incorporate the adhesive interactions between molecules/atoms at particle contact surfaces. This theory correlates the contact area with both the elastic material properties and surface interaction strength, while introducing the concept of particle surface energy. The modified Hertzian contact theory establishes the relationship between relative contact force and approach distance, with the corresponding relationship curve shown in Figure 3.
In this equation,
- —Surface energy of particles (mJ/m2);
- —Critical adhesive force (N);
- —Maximum adhesive overlap (m).
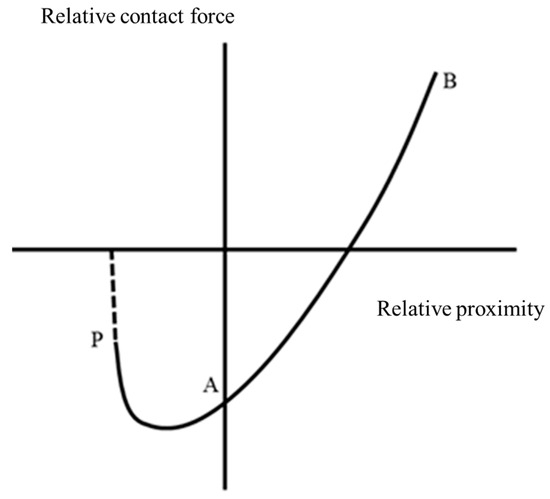
Figure 3.
Force–displacement relationship for viscoelastic adhesive spheres.
According to viscoelastic theory, when two particle surfaces come into contact, the normal force between them immediately drops to a specific value due to van der Waals forces (Point A in Figure 3). Assuming both particles undergo purely elastic deformation without reaching the yield limit, the particle velocity reduces to zero when the contact force peaks (Point B in Figure 3). During the entire loading phase, kinetic energy is converted to other forms of energy.
In the restitution phase, while the stored elastic energy is released, the particles remain adhered even at zero normal overlap (α = 0). The final separation occurs at Point P, with the required detachment work, Ws, (equal to the area under the curve) given by Equation (14):
Neglecting energy dissipation from particle collisions, the sole work required during the impact process is that needed to separate the adhesive surfaces. Consequently, the kinetic energy equation is given by Equation (15):
In this equation,
- —Relative impact velocity before collision (m/s);
- —Rebound velocity after collision (m/s).
The critical sticking velocity, Vs, emerges when particle collisions result in zero rebound velocity, establishing the threshold condition for permanent adhesion as defined by Equation (16).
Particle collisions may induce both elastic and plastic deformation, with the latter occurring at sufficiently high impact velocities. Figure 4 illustrates the normal contact force loading path when plastic deformation occurs. During collision, the normal contact force initially increases along the primary loading stiffness curve until reaching maximum overlap. As the particles begin recovery, the contact force follows an unloading stiffness curve due to yielding, eventually reaching zero at a residual overlap defined as the plastic overlap length, δp. In subsequent collisions, the contact force first increases along the previous unloading stiffness curve until reaching the historical maximum force, then transitions back to the primary loading curve. During unloading, when the normal overlap decreases below δp, adhesive forces develop up to a maximum value, fmin, before diminishing with further unloading.
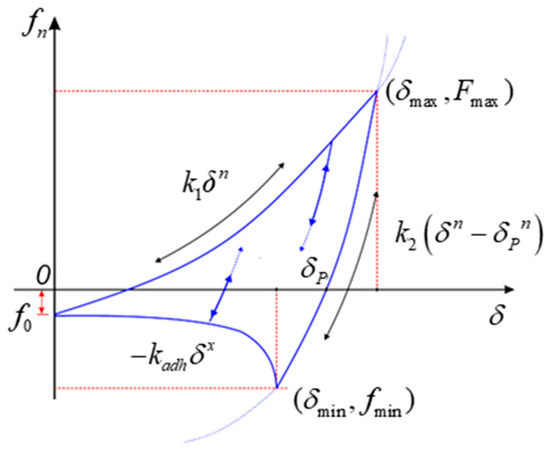
Figure 4.
Loading path model of contact force with plastic deformation.
The analysis reveals that plastic deformation produces non-unique unloading stiffness curves. The collision outcome can be determined by comparing the positive work (area above the force–displacement curve) to the negative work (area below the curve). Particle separation occurs when positive work exceeds negative work, while adhesion dominates in the opposite case. This energy-based criterion effectively captures the competition between plastic dissipation and adhesive bonding in particle collisions.
As evidenced by the loading path model in Figure 4, the normal contact force curve undergoes significant modifications with variations in the loading branch exponent, n. The model reduces to a linear formulation when n = 1, as demonstrated in Figure 5, which serves as the basis for calculating the work performed by normal contact forces.
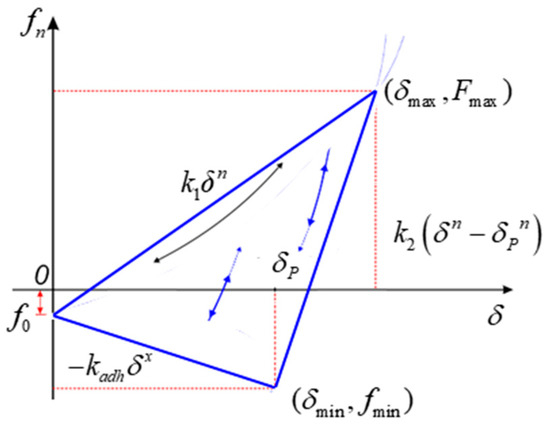
Figure 5.
Linear loading path model for plastic deformation contact forces.
The expression for the constant pull-off force, , is given by Equation (17):
The expression for the initial loading stiffness, , is given by Equation (18):
The coefficient of restitution, , during particle collision, which also determines the outcome of the collision, is given by Equation (19):
The relationship between the initial loading stiffness, , and the unloading stiffness, , is given by Equation (20):
Introducing the contact plasticity ratio, , between particles, which links the initial loading stiffness, , and the unloading stiffness, , is achieved by Equation (21):
is the maximum overlap. can be obtained from Equations (2)–(7) and Equations (2)–(9) and is given by Equation (22):
The plastic overlap, , is calculated from the contact plasticity ratio, , and the maximum overlap, . The plastic overlap, , is given by Equation (23):
fmin is the maximum adhesion force, given by Equation (24):
In this equation,
- —The adhesion index.
is the overlap corresponding to zero contact normal force during the loading phase, given by Equation (25):
First, calculate the work performed by the contact force in the positive direction, , given by Equation (26):
In this equation,
- —The normal contact force when the particle overlap is .
Next, calculate the work performed by the contact force in the reverse direction, , given by Equation (27):
Expanding and simplifying Equation (27) yields the final expression for , given by Equation (28):
The final comparison between the magnitudes of W1 and W2 determines the particle collision outcome.
Through the aforementioned analysis, both the yield velocity for plastic deformation and the critical adhesion velocity for elastic deformation of particles have been established. This reveals that during particle collisions, the relative impact velocity must first be analyzed to determine the deformation type: For elastic deformation, compare the velocity with the critical adhesion velocity. For plastic deformation, calculate the work performed by normal contact forces and compare the magnitudes of positive (W1) and negative (W2) work to obtain the collision result.
Analysis of the Collision Deformation Process of Colloidal particles under Two Working Conditions:
- (1)
- Condition 1: Yield Velocity Greater than Adhesion Velocity
When the relative collision velocity is less than the critical adhesion velocity, the collision velocity is also necessarily less than the yield velocity. The particle collision is thus determined to undergo elastic deformation, as shown in Figure 6a. Based on the aforementioned theory, the particles are deemed to adhere. When the relative collision velocity exceeds the critical adhesion velocity but remains below the yield velocity, the particle collision is still determined to undergo elastic deformation, as shown in Figure 6b. Consequently, the elastic energy generated by the collision is released, causing the particles to separate. When the relative collision velocity exceeds the yield velocity, the particles undergo plastic deformation. Part of the kinetic energy is converted into elastic energy, while another part is dissipated, resulting in irreversible plastic deformation, as shown in Figure 6c. This scenario requires separate discussion.
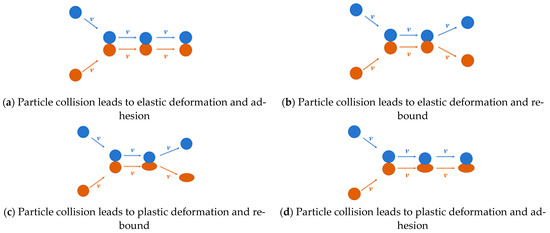
Figure 6.
Particle collision deformation process.
- (2)
- Condition 2: Yield Velocity Less than Adhesion Velocity
When the relative collision velocity is less than the yield velocity, it is also necessarily less than the critical adhesion velocity. As shown in Figure 6d, the particle collision is determined to undergo elastic deformation. Based on the aforementioned theory, the particles are deemed to adhere. When the relative collision velocity exceeds the yield velocity but remains below the critical adhesion velocity, part of the kinetic energy is converted into elastic energy, while another part is dissipated, resulting in irreversible plastic deformation. However, since the particles would still adhere under conditions where the energy is fully converted into elastic energy, the particles are determined to adhere in this case. When the relative collision velocity exceeds the adhesion velocity, the particles undergo plastic deformation. Part of the kinetic energy is converted into elastic energy, while another part is dissipated, resulting in irreversible plastic deformation. This scenario should be discussed together with the third case of Condition 1. It is necessary to calculate whether the total work performed by the contact normal force in the positive direction can exceed the total work performed when the contact normal force is in the reverse direction to determine whether adhesion occurs between the particles.
3. Viscoelastic Collision Model of Colloidal Particles
3.1. Colloidal Particle Properties
When fuel evaporates during heating, the residual substance is gum, which has adhesive properties. The formation of fuel gum is mainly due to the oxidation of fuel caused by a rise in temperature when it comes into contact with air, leading to the formation of gum deposits, which adversely affect performance. There are many factors that affect the formation of colloids, such as oil components (unstable components, hydrocarbons, and non-hydrocarbon substances), oil additives, processing technology, and storage conditions (temperature, oxygen content, storage time, light, etc.). On this basis, the fuel is heated by controlling the temperature, and the concentration of gum particles generated by the fuel is observed to determine the variation of gum concentration with temperature.
Firstly, take out the aviation fuel at room temperature and heat it to oxidize it, obtaining the results shown in Figure 7. The label on the beaker is in Chinese characters, “aviation kerosene”. The oxidation process resulted in aviation fuel transforming from a colorless transparent liquid into a yellow–brown oil. The particles had already self-aggregated inside the oil, forming a textured aggregation structure. From the flow state, aviation fuel becomes denser, with significantly increased viscosity.

Figure 7.
Comparison chart of fuel gum generation.
After exploring the conditions for the precipitation of aviation fuel gum, an experiment on fuel gum precipitation was conducted under segmented heating at 60 °C, 80 °C, 100 °C, and 120 °C and by conducting heating tests on the fuel separately. The results of observing the heating of aviation kerosene are shown in Figure 8, the labels consist of numbers and Chinese characters, representing a specific temperature in degrees Celsius.

Figure 8.
Fuel heating results.
The aviation fuel showed no significant changes after being heated at 60 °C and 80 °C for 8 h, maintaining a clear appearance with no noticeable variation in viscosity, as shown in Figure 8a,b. When heated at 100 °C for 8 h (Figure 8c), the aviation fuel exhibited slight coloration, developing a faint yellow tint. Based on the characteristics of colloidal particles observed in previous experiments, this confirms significant colloidal formation that altered the fuel’s color, though viscosity remained unchanged. At 120 °C for 8 h (Figure 8d), more pronounced color changes occurred, showing distinct yellow coloration that was markedly stronger than at 100 °C, indicating substantial colloidal generation while viscosity still showed no significant variation.
The heating results demonstrate that below certain temperatures, colloidal formation is undetectable. Beyond threshold temperatures, significant oxidation drives observable colloidal generation. The colloidal concentration reaches levels sufficient to alter fuel color. Higher concentrations promote particle aggregation and size growth. Prolonged high-temperature exposure ultimately affects viscosity.
3.2. Colloidal Particle Property Characterization
After heating, colloidal concentrations were measured using a rheometer across different temperature conditions. The fitted curve (Figure 9) shows that colloidal concentration increases continuously with temperature, and the rate of concentration increase accelerates at higher temperatures.
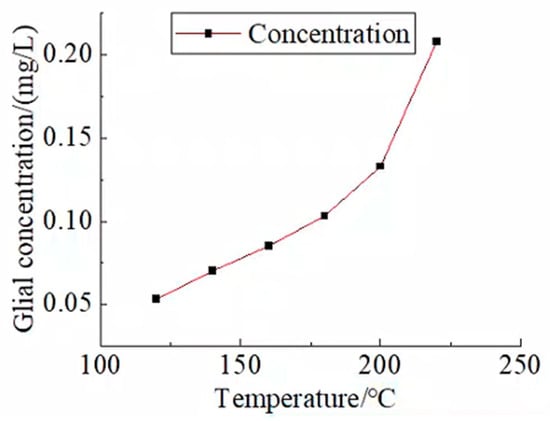
Figure 9.
Variation curve of colloidal concentration with temperature.
After the colloidal particles were extracted from heated aviation kerosene, their Young’s modulus and Poisson’s ratio were measured using a DMA (Dynamic Mechanical Analyzer). The test results show that the colloidal particles had a Young’s modulus of 688 MPa and a Poisson’s ratio of 0.39.
The surface free energy of the fuel-derived colloidal particles was measured using a DSA30 contact angle goniometer. The analysis determined that the colloidal particles had a surface free energy of 77 mJ/m2 (Figure 10).

Figure 10.
Deposition of colloidal particles.
The extracted fuel colloids were further tested for density using a B-012001 pycnometer. The pycnometer method involves measuring the mass difference between an empty pycnometer and a pycnometer filled with the sample at a known volume to calculate density. The measured density of the colloidal sample was 1.12 g/cm3.
The fuel colloids were then subjected to tribological testing using a coefficient-of-friction tester and impact testing machine. The test results show that the colloid particles had a restitution coefficient of 0.12 upon impact.
For the heated aviation kerosene samples, particle size distribution was analyzed using a particle size analyzer. The results are presented in Table 1, showing the detailed size distribution.

Table 1.
Particle size distribution of colloidal particles.
Upon completion of the aforementioned tests, the fundamental characteristics of the colloidal particles were essentially determined. Based on these results, the yield velocity and adhesion velocity during particle collisions could be calculated, thereby providing a theoretical foundation for subsequent particle collision experiments.
4. Particle–Particle and Particle–Wall Collision Experimental Validation
4.1. Design and Construction of Collision Test Apparatus
After discussing the theoretical formulas and collision laws governing particle–particle and particle–wall collisions, this study presents the design of a collision test apparatus based on the fundamental properties of colloidal particles obtained from the aforementioned characterization experiments. The apparatus will allow for conducting experiments on particle–particle and particle–wall collisions, enabling the experimental results to cross-verify the theoretical formulas and collision laws.
To control the pre-collision velocity of particles and the impact angle between particles and the metal wall, this experiment employed free-fall motion to facilitate collisions between particles and other particles or metal plates. A rotatable mechanism ensured adjustable impact angles. By precisely controlling the falling height of particles and the rotation angle of the metal plate, the 3D model of the collision test apparatus shown in Figure 11 was designed.
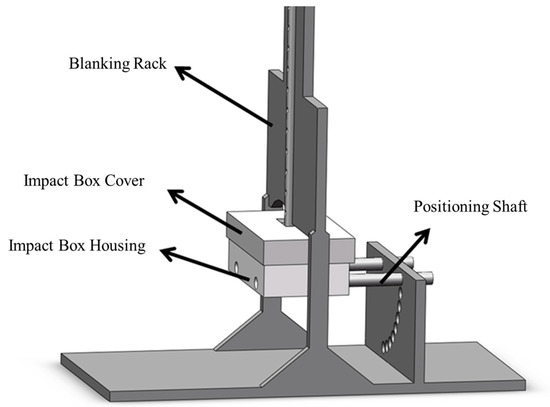
Figure 11.
Three-dimensional model of collision test apparatus.
For controlling particle falling heights, discrete height intervals were set at 1 cm increments. Regarding metal plate rotation angles, discrete angle intervals of 10° were established, resulting in 9 discrete angular positions.
As observed in Figure 11, the apparatus primarily comprises four components: a feeding frame, collision chamber cover, collision chamber body, and positioning shaft.
The vertical plate of the feeding frame features circular flow channels for particle descent and adjustable apertures for height control. A rotatable bore on the baseplate enables metal plate angle adjustments. The collision chamber body incorporates bottom apertures, while its cover includes guiding rails for precise particle positioning. This design ensures experimental accuracy for particle–particle collisions, with the positioning shaft securing the chamber assembly.
Following the apparatus design, transparent resin was utilized for its high light transmittance and optical clarity. The 3D-printed prototype (Figure 12) meets transparency requirements, enabling direct external observation of particle motion trajectories during free-fall experiments.

Figure 12.
Collision test apparatus.
The experiments were conducted using the metal plates and metal particles shown in Figure 13. The metal materials were iron and copper. The colloidal particles had diameters of 0.5 mm, 1.0 mm, and 1.5 mm.

Figure 13.
Metallic plates and particles.
This experimental validation was mainly divided into two parts. The first part was the collision and adhesion test between particles and metal walls, which used particles with diameters of 0.5 mm, 1.0 mm, and 1.5 mm. The second part was the collision and adhesion test between particles. For the materials used in the entire experiment, only iron was selected for the metal plates, while iron and copper were chosen for the metal particles.
4.2. Impact Angle-Dependent Collision Tests on Iron Plates
4.2.1. Experimental Results of Particle Collision at 0° Impact Angle
Prior to conducting the experiments, the yield velocity and adhesion velocity of particle collisions were first calculated for different gel particle sizes. By comparing their magnitudes, it was determined that particles yield before adhesion occurs. Therefore, the calculation of contact normal force work, as discussed above, was required to determine particle collision outcomes. The work performed by the contact normal force during collisions between gel particles and an iron metal plate was calculated for different particle sizes and drop heights.
The results are shown in Figure 14.
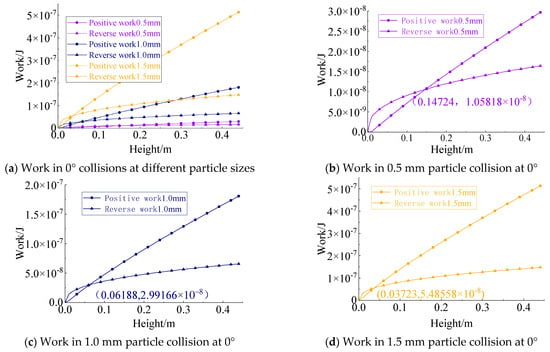
Figure 14.
Work performed by collisions between different-sized colloidal particles and an iron metal plate at 0°.
An analysis of Figure 14 demonstrates that at constant drop heights, the work performed by the contact normal force between colloidal particles and iron plates escalates dramatically with increasing particle diameters. Under low-height conditions, reverse-direction work dominates over forward-direction work, indicating adhesion as the collision outcome. As the drop height increases, forward-direction work exhibits linear growth, while the magnitude of reverse-direction work shows a near-quadratic relationship with height. This creates a mathematically defined single intersection point between the forward and reverse work curves. When the drop height exceeds this critical threshold, collision outcomes transition to rebound separation. Notably, larger particle diameters reduce the critical separation height while simultaneously increasing the magnitude of work at this transition point.
Following these calculations determining critical adhesion heights, collision experiments were initiated. Prior to testing, the iron plate was precisely positioned within the collision chamber according to Figure 15 specifications and rigidly secured to the feeding frame assembly.

Figure 15.
Installation of the metal iron plate.
Subsequently, colloidal particles of varying diameters were released from different heights, yielding the particle collision results depicted in Figure 16.

Figure 16.
Collision outcomes of colloidal particles with varying diameters impacting a steel plate.
Repeated experimentation yielded critical particle adhesion heights under varying diameters, with the results documented in Table 2.

Table 2.
Critical adhesion heights of colloidal particles on iron plates at a 0° impact angle for varying particle diameters.
The experimental results indicate that for smaller particle sizes, the critical adhesion height obtained from the tests is smaller than the theoretical value, whereas for larger particle sizes, the critical adhesion height obtained from the tests is greater than the theoretical value.
4.2.2. Experimental Results of Particle Collision at 20° Impact Angle
Continue rotating the collision box to change the impact angle between the particles and the metal plate from 0° to 20°. At this point, the tangential velocity of the particles upon collision further increases, while the normal velocity further decreases. The work performed by the contact normal force is calculated and compared to determine the critical adhesion height of the particles, with the results shown in Figure 17. The computational results indicate that after the angle is increased by 20°, the critical adhesion height of the particles continues to rise, and its growth rate also increases with larger particle sizes.
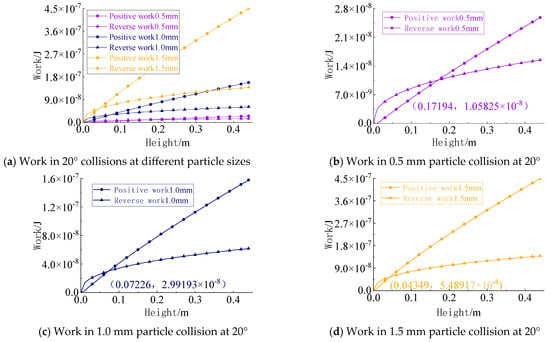
Figure 17.
Work performed by collisions between different-sized colloidal particles and an iron metal plate at 20°.
After completing the aforementioned calculations, the collision box was further rotated to alter the impact angle between the particles and the metal plate. Additional particle drop tests were then conducted under these adjusted conditions, ultimately yielding the collision results illustrated in Figure 18.

Figure 18.
Collision results between colloidal particles and an iron metal plate at 20°.
The aforementioned experiment was repeatedly conducted, and the results were recorded to obtain the critical adhesion heights of particles under different particle sizes, as shown in Table 3.

Table 3.
Critical adhesion heights of colloidal particles on iron plates at a 20° impact angle for varying particle diameters.
The experimental results indicate that as the size of the colloidal particles increases, the deviation between experimental and theoretical values becomes more pronounced. At this stage, the collision angle between the colloidal particles and the metal wall further increases, leading to a higher proportion of tangential velocity during impact. Consequently, the discrepancy between experimental and theoretical values continues to grow compared to scenarios with lower collision angles.
4.2.3. Experimental Results of Particle Collision at 40° Impact Angle
The collision box was further rotated to increase the impact angle between particles and the metal plate from 20° to 40°. Under this configuration, the tangential velocity of particles upon collision continued to rise, while the normal velocity further decreased. The work performed by the contact normal force was calculated and compared to determine the critical adhesion height of particles, with the results presented in Figure 19.
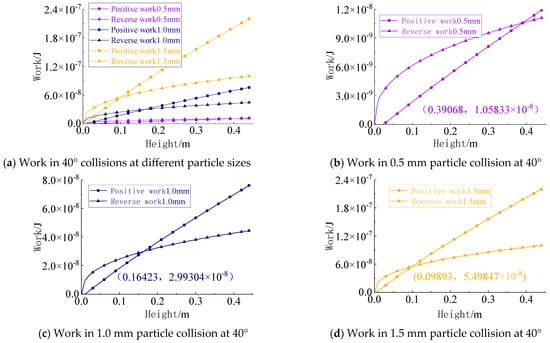
Figure 19.
Work performed by collisions between different-sized colloidal particles and an iron metal plate at 40°.
Following these calculations, the collision chamber of the experimental setup was rotated to modify the impact angle between particles and the metal plate. Subsequent tests were conducted by varying the release height of particles, ultimately yielding the collision results shown in Figure 20.

Figure 20.
Collision results between colloidal particles and an iron metal plate at 40°.
The experimental procedure was repeated, with recorded results demonstrating the critical adhesion heights for particles of different sizes, as summarized in Table 4.

Table 4.
Critical adhesion heights of colloidal particles on iron plates at a 40° impact angle for varying particle diameters.
From the experimental results, it was found that the critical adhesion heights obtained from the tests were consistently lower than the theoretical predictions. At this point, the collision angle between the colloidal particles and the metal surface reached 40°, and the tangential and normal velocities of the particles upon impact were nearly equal. It was observed that an increase in tangential velocity led to particle rebound, a behavior distinct from that observed in low-angle collisions.
Based on the experimental results at different collision angles, we conclude that the following: When the collision angle between colloidal particles and a metal surface is too small, the tangential velocity during collision promotes particle adhesion. Conversely, when the collision angle is too large, the tangential velocity inhibits adhesion. At a collision angle of 0°, the deviation between experimental results and theoretical predictions is less than 10%.
4.3. Particle Impact Tests on Different Metallic Materials
4.3.1. Collision Test Results Between Colloidal Particles and Iron Particles
Following the collision tests between colloidal particles and metal plates, we proceeded to conduct collision experiments between colloidal particles and metal particles. The initial tests employed iron particles with precisely controlled diameters of 0.5 mm, 1.0 mm, and 2.0 mm. The work performed by normal contact forces was calculated, with the computational results presented in Figure 21.
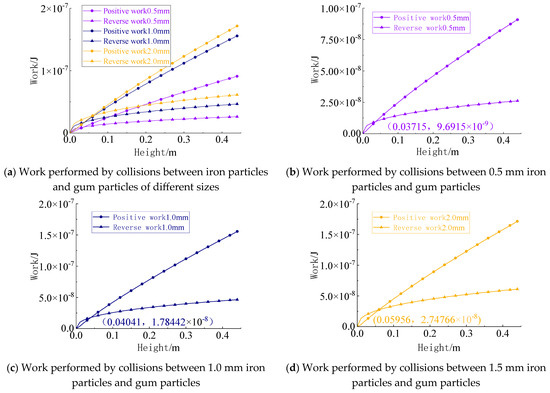
Figure 21.
Work performed by collisions between gel particles and iron particles of different sizes.
After completing the calculations of normal contact force work, we obtained the critical impact velocities between colloidal particles and iron particles of varying sizes. Subsequently, the prepared metal particles were carefully positioned within the circular apertures of the collision chamber, as illustrated in Figure 22.

Figure 22.
Installation of iron particles with different particle sizes.
Colloidal particles were then released from different heights, yielding the collision results shown in Figure 23.

Figure 23.
Collision results between gel particles and iron particles of different sizes.
The experiments revealed three distinct collision regimes:
At low impact velocities, colloidal particles exhibited complete adhesion with iron particles; at moderate velocities, colloidal particles adhered to iron particles but were jointly ejected from the discharge orifice; at high velocities, colloidal particles directly dislodged the iron particles from the orifice.
The experimental results are systematically recorded in Table 5, revealing several key findings:

Table 5.
Critical adhesion height of colloidal particles with iron particles of different sizes.
With a constant adhesive particle size, the theoretical critical adhesion height increased proportionally with the iron particle size; when the iron particle size was smaller than the adhesive particle size, all experimental values exceeded theoretical predictions; when the iron particle size exceeded the adhesive particle size, the experimental values remained higher than the theoretical values, though with relatively smaller deviations.
4.3.2. Collision Test Results Between Colloidal Particles and Copper Particles
A particle collision deformation assessment was conducted and the work performed by normal contact forces was calculated. The results are presented in Figure 24.
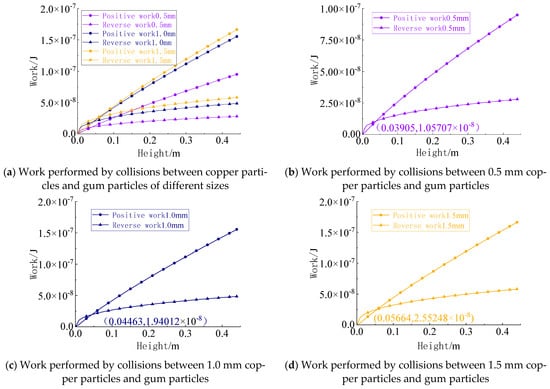
Figure 24.
Work performed by collisions between gel particles and copper particles of different sizes.
Calculated critical impact velocities between colloidal particles and copper particles of varying diameters. Prepared copper particles were positioned in the circular apertures of the collision chamber (Figure 25).

Figure 25.
Installation of copper particles with different particle sizes.
Colloidal particles were dropped from various heights. The obtained collision results are shown in Figure 26.

Figure 26.
Collision results between gel particles and copper particles of different sizes.
Repeated tests yielded critical adhesion heights between adhesive and copper particles (see Table 6).

Table 6.
Critical adhesion height of colloidal particles with copper particles of different sizes.
A comparative analysis with the iron particle tests revealed the following:
Both particle types exhibited similar trend patterns in their collision behavior. The copper particles demonstrated significantly larger fluctuation ranges compared to the iron particles under identical test conditions.
4.4. Particle Collision Tests Under Different Colloidal Particle Sizes
4.4.1. Collision Test Results Between Colloidal Particles and Iron Particles
After adjusting the particle size of the metal particles, the diameter of the metal particles was fixed at 1.0 mm. By varying the size of the colloidal particles, particle collision tests were conducted with different metal materials to study their impact behavior.
First, iron particles were used for the collision tests, with the colloidal particle sizes controlled at 0.5 mm, 1.0 mm, and 1.5 mm. The yield velocity and adhesion velocity under these three particle sizes were calculated, and particle collision deformation was assessed. The yield velocity remained significantly lower than the adhesion velocity, and the work performed by the normal contact force was calculated (Figure 27).
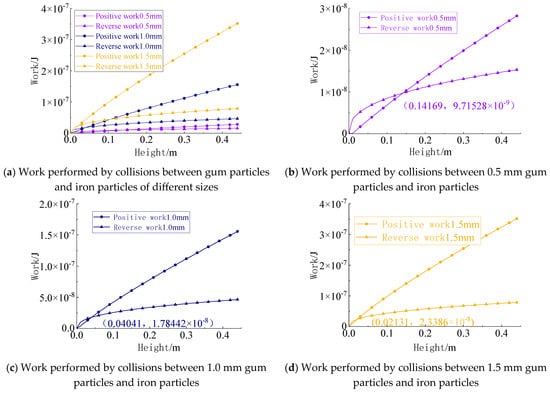
Figure 27.
Work performed by collisions between gel particles of different sizes and iron particles.
After computing the work performed by the normal contact force, the critical collision velocity between colloidal particles and iron particles of different sizes was determined. Subsequently, the prepared metal particles were placed in the circular holes of the collision chamber, and the colloidal particles were dropped from various heights. The collision results between the colloidal particles and iron particles are illustrated in Figure 28.


Figure 28.
Collision results between gel particles of different sizes and iron particles.
The experimental results were recorded, and the critical adhesion heights of iron particles under different particle size conditions are presented in Table 7.

Table 7.
Critical adhesion height of iron particles with colloidal particles of different sizes.
The findings reveal that when the size of the iron particles is constant, the theoretical critical adhesion height decreases as the colloidal particle size increases. When the colloidal particle size approaches that of the iron particles, the discrepancy between the theoretical and experimental values becomes smaller.
4.4.2. Collision Test Results Between Colloidal Particles and Copper Particles
The metal particles used in the collision tests were switched to copper particles, with the colloidal particle sizes controlled at 0.5 mm, 1.0 mm, and 1.5 mm. The yield velocity and adhesion velocity under these three particle size conditions were calculated to evaluate particle collision deformation (Figure 29).
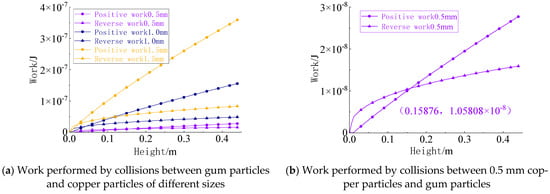
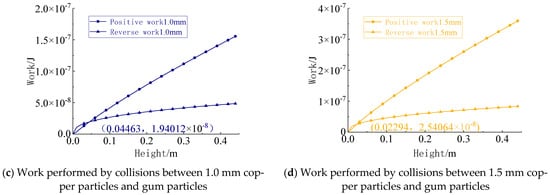
Figure 29.
Work performed by collisions between gel particles of different sizes and copper particles.
Collision tests were then conducted by dropping the colloidal particles from various heights, and the particle collision results are presented in Figure 30.

Figure 30.
Collision results between gel particles of different sizes and copper particles.
The experimental observations reveal that when colloidal particles of different sizes collide with copper particles, the copper particles may be displaced outside the discharge hole after impact. An analysis of the results shows the following:
When the copper particles remain within the discharge hole, the collision outcome between the colloidal and copper particles is always adhesion. When the copper particles are knocked outside the discharge hole, the final collision results exhibit both rebound and adhesion states.
As shown in Table 8. With a fixed copper particle size, the theoretical critical adhesion height decreases as the colloidal particle size increases. When comparing metal particles (iron vs. copper), the discrepancy between the experimental and theoretical values for copper particles remains similarly small.

Table 8.
Critical adhesion height of copper particles with colloidal particles of different sizes.
4.4.3. Collision Test Results Between Colloidal Particles
The particles used for collision tests were changed to colloidal particles, with their sizes controlled at 0.5 mm, 1.0 mm, and 1.5 mm. The yield velocity and adhesion velocity under these three particle size conditions were calculated to evaluate particle collision deformation. The results show that the yield velocity remained significantly lower than the adhesion velocity. Consequently, the work performed by the normal contact force was calculated, yielding the computational results presented in Figure 31.
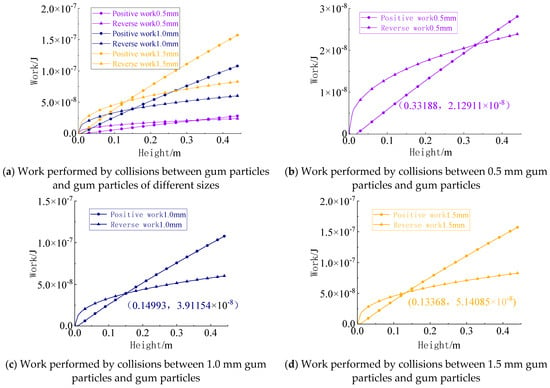
Figure 31.
Work performed by collisions between gel particles of different sizes.
The particles were then dropped from various heights, producing the collision results shown in Figure 32.

Figure 32.
Results of collisions between gel particles of different sizes.
The experimental data were recorded, and the critical adhesion heights between colloidal particles under different size conditions are summarized in Table 9.

Table 9.
Critical adhesion height between colloidal particles of different sizes.
The key findings of this table are as follows:
When the size of the colloidal particles was fixed, the theoretical critical adhesion height decreased as the particle size increased. When the metal particles were replaced with colloidal particles in the collisions, all experimental values were higher than the theoretical predictions. The discrepancy between the experimental and theoretical values increased with greater differences in size between the two colloidal particles.
5. Conclusions
This study establishes an adhesion criterion for colloidal particles in fuel servo valves and validates it experimentally, which has not been reported in previous works. The proposed methodology provides a deeper understanding of particle migration and deposition, offering guidance for improving the reliability and maintenance of fuel servo valves under wide temperature conditions. The main contributions and findings are summarized as follows:
1. Development of a Colloidal Particle Collision Model
Considering the propensity of colloidal particles to undergo plastic yield deformation and exhibit significant adhesion during collisions, the traditional particle collision model was extended. By comparing the work performed by normal contact forces in opposing directions during collision, an energy-based adhesion criterion specific to colloidal particles was established, providing an effective theoretical framework for analyzing colloidal particle adhesion behavior.
2. Experimental Investigation of Physical Properties and Temperature-Dependent Concentration of Colloidal Particles
Heating tests on aviation fuel revealed a nonlinear relationship between colloidal concentration and temperature, with the generation rate of colloids accelerating at higher temperatures. Fundamental physical properties of colloidal particles—including a Young’s modulus of 688 MPa, a Poisson’s ratio of 0.39, and a surface energy of 77 mJ/m2—were experimentally determined, supplying reliable parameters for the collision model. Particle size distribution analyses characterized the size distribution of colloidal particles within the fuel.
3. Design and Validation of Collision Test Apparatus
A dedicated experimental apparatus integrating both particle–particle and particle–wall collision tests was designed and fabricated. Systematic experiments were conducted under varying collision angles (0°, 20°, and 40°), material types (metallic iron plate, iron particles, and copper particles), and particle sizes (0.5 mm, 1.0 mm, and 1.5 mm). Experimental outcomes were compared with theoretical predictions for validation.
4. Correlation Analysis between Experimental and Theoretical Results
The results demonstrate that the deviation between theory and experiment for colloidal particle–metallic wall collisions was minimal, with errors within 10%, indicating the model’s accuracy for predicting particle–wall adhesion. Larger discrepancies were observed in particle–particle collisions, primarily due to differences in material properties and particle size affecting adhesion behavior.
5. Influence of Particle Size and Collision Angle on Adhesion Behavior
When the sizes of colloidal and metallic particles are similar, the difference between theoretical and experimental critical adhesion heights is reduced, indicating improved predictive accuracy with size matching. Increasing the collision angle results in higher tangential velocity components, which suppress adhesion and raise the critical collision energy threshold.
6. Practical Implications and Future Work
This work provides fundamental data on colloidal particle properties and establishes a robust adhesion criterion and collision model, laying a theoretical and experimental foundation for understanding particle migration and deposition in fuel systems. These findings offer valuable insights for contamination control and lifetime prediction of fuel components, which can inform the design, filtration strategies, and predictive maintenance of fuel servo valves in industrial applications. This includes, for example, installing cooling systems to reduce the formation of colloidal particles.
Future research may integrate multi-physics coupling simulations to explore colloidal particle dynamics under complex flow environments, long-term validation in real fuel systems, the influence of different fuel types, more complex particle geometries and mixtures, and predictive reliability models.
Author Contributions
Methodology, J.Z. and R.D.; investigation, H.W. and R.D.; validation, J.Z. and R.D.; data curation, J.N.; resources, Y.L.; formal analysis, R.D. and G.C.; writing—original draft preparation, R.D., J.N. and W.Y.; writing—review and editing, J.Z., R.D., J.N. and W.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China, grant number 52275068. This research was funded by the Open Foundation of the State Key Laboratory of Taihang Laboratory, grant number QTJLHT202404090002. This research was funded by the industry–university–research cooperation project of Aviation Engine Corporation of China, grant number HFZL2024CXY014.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Zhang, H.P.; Huang, W.; Zhang, Y.D.; Shen, Y.; Li, D.Q. Design of the microfluidic chip of oil detection. Appl. Mech. Mater. 2011, 117–119, 517–520. [Google Scholar] [CrossRef]
- Novak, N.; Trajkovski, A.; Kalin, M.; Majdič, F. Degradation of hydraulic system due to wear particles or medium test dust. Appl. Sci. 2023, 13, 7777. [Google Scholar] [CrossRef]
- Li, H.; Gao, G.; Hao, M.; Tian, R.; Lu, Z.; Zhao, Y. Simulation on detachment and migration behaviors of mineral particles induced by fluid flow in porous media based on CFD-DEM. Geoenergy Sci. Eng. 2025, 247, 213727. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Mittal, R.; Iaccarino, G. Immersed boundary methods. Annu. Rev. Fluid Mech. 2005, 37, 239–261. [Google Scholar] [CrossRef]
- Tic, V.; Lovrec, D. Trajectories of solid and gaseous particles in a hydraulic reservoir. In Proceedings of the 8th International Fluid Power Conference IFK, Dresden, Germany, 22–24 March 2010. [Google Scholar]
- Yazdi, A.A.; D’Avino, G. Sedimentation and migration dynamics of a spherical particle in an elastoviscoplastic fluid near a wall. J. Non-Newton. Fluid Mech. 2023, 314, 105004. [Google Scholar] [CrossRef]
- Kang, S.; Kong, X.; Zhang, J.; Du, R. Modeling of a Jet Pipe Servovalve Considering Nonlinear Flow Forces Acting on the Spool. Water 2024, 16, 683. [Google Scholar] [CrossRef]
- Kang, S.; Kong, X.; Zhang, J.; Du, R. Research on pressure-flow characteristics of pilot stage in jet pipe servo-valve. Sensors 2022, 23, 216. [Google Scholar] [CrossRef] [PubMed]
- Gao, Q.; Zhang, S.; Zhu, Y. Investigation of the dynamic characteristics of a two-stage high-speed on/off valve with adjustable maximum opening. Aerospace 2023, 10, 109. [Google Scholar] [CrossRef]
- Terrelle, J.; Higgs, C.F. A modeling approach for predicting the abrasive particle motion during chemical mechanical polishing. J. Tribol. 2007, 129, 933–941. [Google Scholar] [CrossRef]
- Thornton, C.; Ning, Z.M. Theoretical model for the stick/bounce behaviour of adhesive, Elastic-Plastic spheres. Powder Technol. 1998, 99, 154–162. [Google Scholar]
- Thornton, C. Coefficient of restitution for collinear collisions of elastic-perfectly plastic spheres. J. Appl. Mech. 1997, 64, 383–386. [Google Scholar] [CrossRef]
- Walton, O.R.; Johnson, S.M. Simulating the effects of interparticle cohesion in micron-scale powders. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2009; Volume 1145, pp. 897–900. [Google Scholar]
- Tykhoniuk, R.; Tomas, J.; Luding, S.; Kappl, M.; Heim, L.; Butt, H.-J. Ultrafine cohesive powders: From interparticle contacts to continuum behaviour. Chem. Eng. Sci. 2007, 62, 2843–2864. [Google Scholar] [CrossRef]
- Luding, S.; Tykhoniuk, R.; Tomas, J. Anisotropic material behavior in dense, cohesive-frictional powders. Chem. Eng. Technol. 2003, 26, 1229–1232. [Google Scholar] [CrossRef]
- Luding, S.; Manetsberger, K.; Mullers, J. A discrete model for long time sintering. J. Mech. Phys. Solids 2005, 53, 455–491. [Google Scholar] [CrossRef]
- Luding, S. Cohesive, frictional powders: Contact models for tension. Granul. Matter 2008, 10, 235–246. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, Y.; Cui, B.; Zhu, Z.; Dou, H. Numerical simulation and analysis of solid-liquid two-phase flow in centrifugal pump. Chin. J. Mech. Eng. 2013, 26, 53–60. [Google Scholar] [CrossRef]
- Xinqiang, L.; Hong, J.; Wei, M.; Zhi, Z.; Jinlin, W. Erosion behavior and influence of solid particles in hydraulic spool valve without notches. Eng. Fail. Anal. 2020, 108, 104262. [Google Scholar] [CrossRef]
- Moreno-Atanasio, R.; Antony, S.J.; Ghadiri, M. Analysis of flowability of cohesive powders using distinct element method. Powder Technol. 2005, 158, 51–57. [Google Scholar] [CrossRef]
- Hassanpour, A.; Ghadiri, M. Characterisation of flowability of loosely compacted cohesive powders by indentation. Part. Part. Syst. Charact. 2007, 24, 117–123. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, T.; Zhang, H.; Li, Y.; Song, Y.; Chen, J.; Fu, X.; Qi, Z.; Zhang, Q. Factors affecting the transport of petroleum colloids in sat-urated porous media. Colloids Surf. A Physicochem. Eng. Asp. 2020, 585, 124134. [Google Scholar] [CrossRef]
- Daghooghi, M.; Borazjani, I. The effects of irregular shape on the particle stress of dilute suspensions. J. Fluid Mech. 2018, 839, 663–692. [Google Scholar] [CrossRef]
- Tanaka, Y.; Oba, G.; Hagiwara, Y. Experimental study on the interaction between large scale vortices and particles in liquid–solid two-phase flow. Int. J. Multiph. Flow 2003, 29, 361–373. [Google Scholar] [CrossRef]
- Yang, X.; Chen, S.; Shi, Y.; Feng, R.; Cai, J.; Jiang, G. CFD and DEM modelling of particles plugging in shale pores. Energy 2019, 174, 1026–1038. [Google Scholar] [CrossRef]
- Liang, N.; Yuan, Z.; Zhang, F. Oil particle-induced erosion wear on the deflector jet servo valve prestage. Aerospace 2023, 10, 67. [Google Scholar] [CrossRef]
- Zhao, W.; Wang, X.; Long, Y.; Zhou, Z.; Tian, L. Robust LQR Design Method for the Aero-Engine Integral Constant Pressure Drop Control Valve with High Precision. Aerospace 2023, 10, 428. [Google Scholar] [CrossRef]
- Yang, F.; Wang, M.; Liu, Y.; Guo, Z.; Yue, L. Modelling and Transmission Characteristics Analysis of APU Pneumatic Servo System. Aerospace 2024, 11, 868. [Google Scholar] [CrossRef]
- Zhang, J.; Du, R.; Dong, P.; Zhang, K.; Wang, S.; Li, Y.; Zhang, K. Effect of Slide Valve Gap Surface Roughness on Particle Transport Properties. Aerospace 2025, 12, 608. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, W.; Zeng, L.; Wu, L. Pressure Characteristics Analysis of the Deflector Jet Pilot Stage Under Dynamic Skewed Velocity Distribution. Aerospace 2025, 12, 638. [Google Scholar] [CrossRef]
- Fan, S.; Xu, R.; Ji, H.; Yang, S.; Yuan, Q. Experimental investigation on contaminated friction of hydraulic spool valve. Appl. Sci. 2019, 9, 5230. [Google Scholar] [CrossRef]
- Forder, A.; Thew, M.; Harrison, D. A numerical investigation of solid particle erosion experienced within oilfield control valves. Wear 1998, 216, 184–193. [Google Scholar] [CrossRef]
- Yan, H.; Li, J.; Cai, C.; Ren, Y. Numerical investigation of erosion wear in the hydraulic amplifier of the deflector jet servo valve. Appl. Sci. 2020, 10, 1299. [Google Scholar] [CrossRef]
- Mi, J.; Huang, G. Dynamic prediction of performance degradation characteristics of direct-drive electro-hydraulic servo valves. Appl. Sci. 2023, 13, 7231. [Google Scholar] [CrossRef]
- Kandlikar, S.G.; Schmitt, D.; Carrano, A.L.; Taylor, J.B. Characterization of surface roughness effects on pressure drop in single-phase flow in minichannels. Phys. Fluids 2005, 17, 100606. [Google Scholar] [CrossRef]
- Reinertz, O.; Schlemmer, K.; Schumacher, J.T.; Murrenhoff, H. Development of an Accelerated Ageing Test for Hydraulic Spool and Poppet Valves. In Proceedings of the the 7th international Fluid Power Conference, Aachen, Germany, 22–24 March 2010. [Google Scholar]
- Mitchell, W.H.; Spagnolie, S.E. A generalized traction integral equation for Stokes flow, with applications to near-wall particle mobility and viscous erosion. J. Comput. Phys. 2017, 333, 462–482. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).