1. Introduction
Analysing the aeroelastic response in the development of new aircraft is becoming critical as design trends move towards lighter and more flexible structures to improve efficiency and reduce emissions. The interaction between aerodynamic forces, the structure flexibility, and its inertial forces needs to be assessed in order to analyse the dynamic response of the system and the aeroelastic instabilities as divergence and flutter [
1]. Due to their importance in aeroelastic design and the insights they provide into the system behaviour, this work focuses only on these instabilities, rather than on other responses such as control reversal or the response to gusts.
On the one hand, divergence is a static aeroelastic instability that causes structural failure as the lifting surface twist increases due to the aerodynamic forces overcoming the maximum restoring moment due to the structural stiffness [
2]. In modern aircraft, the divergence speed is usually higher than the flutter speed, but its study is still required as part of the certification process [
3,
4]. On the other hand, flutter is a dynamic aeroelastic instability caused by the positive feedback of the aerodynamic forces that produces self-oscillations of the system. Small disturbances on the system can lead to increasing amplitude oscillations that would be catastrophic. Regarding flutter, aircraft design must ensure that it is free of flutter conditions within the flight envelope with an adequate stability margin [
3,
4].
During the development of aerospace engineering, these aeroelastic instabilities have been extensively studied by means of experimental studies since the 1940s with the work of Theodorsen and Garrick [
5,
6]. In the early developments, airfoil models (or strip theory for wings) were considered to understand these phenomena [
7]. To study the aeroelasticity of wings, the concept of the typical section, introduced by Theodorsen and Garrick in 1940 [
5], was extensively used [
6,
8]. The typical section approach relies on the findings of Theodorsen and Garrick based on extensive wind tunnel tests, carried out mostly on straight wings. They concluded that the aeroelastic behaviour of a cantilever wing can be represented by the aeroelasticity of a two-dimensional problem with the properties of the most representative section, which lies close to the three-quarter semi-span location [
5].
Further developments in aeroelastic theory and the numerical methods allowed us to analyse the aeroelastic behaviour of wings in three-dimensional models, through the extended use of unsteady aerodynamic panels methods such as the Doublet-Lattice Method (DLM) [
9,
10,
11,
12,
13]. Thus, the concept of the typical section became mostly a useful concept for understanding aeroelastic phenomena, as extensively described in academic texts [
1,
14,
15].
Nevertheless, the concept of the typical section is still of interest as an approach for validation and simplification for the development of new methods [
16,
17,
18,
19,
20], the study of non-linear effects [
21,
22,
23], analysing the performance of control systems [
24], or application of optimisation techniques [
25,
26,
27]. Therefore, a systematic approach for determining the typical section is proposed in this work, considering also swept wings and a wide range of aspect ratios, unlike the classic definition of Theodorsen and Garrick for straight wings with a large aspect ratio.
Section 2 proposes a formal definition of the typical section from the flutter and divergence speeds that is applied to a set of cantilever wings with different geometries (
Section 3).
Section 4 presents the concept of the wing station model as the two-dimensional model for sections along the wing span. The corresponding numerical model as well as the three-dimensional model for the whole wing are presented in
Section 5.
Section 6 presents this work’s results, analysing the location of the typical section along the wing semi-span depending on different parameters, suhc as the aspect ratio, the sweep angle, or the ratio between the wing plunge and pitch eigenfrequencies. Finally,
Section 7 summarises the main conclusions of this work.
2. Methodology
The typical section as a reduced model of the three-dimensional wing is based on a two-dimensional model presenting the same aeroelastic behaviour as the wing. For this work, the aeroelastic behaviour of the three-dimensional wing is defined by the divergence and flutter speeds.
To determine the wing typical section, the following steps are carried out: First, a set of two-dimensional models are defined, each one with structural properties (chord, mass, inertia, bending stiffnes, etc) corresponding to different locations along the wing span, called stations. Then, for each of these models, the divergence and flutter speeds are determined considering two-dimensional unsteady aerodynamic theory.
Within this work, the typical section is defined as the station whose aeroelastic behaviour matches that of the three-dimensional wing. As will be shown in the result analysis, in general, one station (one location along the wing span) matches the wing divergence speed, and a different one matches the wing flutter speed. Therefore, in general, the typical section for divergence differs from the typical section for flutter, and only in some cases, a unique typical section can be defined.
3. Case Studies
To analyse the concept of the typical section, cantilever trapezoidal flat wings (null dihedral angle) are considered. Their geometry is defined by the parameters shown in
Figure 1.
To study their influence on the typical section (i.e., its assumed location in the wing), several parameters are varied within the set: the wing aspect ratio (
), which is
; the taper ratio (
); and the sweep angle (
). The values of these parameters considered in this work (
Table 1) were selected to represent typical values from aircraft wings to unmanned aerial vehicle wings, providing a set of 495 cases. For all cases, a chord at the root of
m and a thickness of 3 mm were considered.
As presented in
Section 2, two-dimensional models are used to analyse the aeroelastic behaviour of the wing stations. For this type of model, the flutter condition can arise due to the coupling between the plunge and pitch modes. To adequately represent the flutter behaviour of the wing (and its three-dimensional model), it is necessary that, if it happens due to modal coupling, the wing flutter is due to the coupling of the bending and torsion modes.
Within this work, this behaviour is ensured by including a stiffener in the wing structure located along the
line along the wing semi-span. A T-section is used to increase mainly the wing bending stiffness without noticeably modifying the torsion one. Theodorsen and Garrick [
5] modified instead the wing structure by means of chord-wise cuts. The T cross-section considered has a height and width of 25 mm and a uniform thickness of 3 mm.
For both the wing surface and the stiffener, aluminium was considered as structural material, with Young’s modulus GPa, density kg/m3, and Poisson ratio .
4. Wing Station Model
For each station considered along the wing span, a two-degree-of-freedom airfoil model considering plunge and pitch with respect to the elastic axis is defined. The plunge of the elastic axis (EA)
is positive downwards, and the angle of attack
is measured from the upstream flow to the airfoil zero-lift line (ZLL). The structural model, shown in
Figure 2, is an airfoil of chord
c, mass
M, inertia
around the elastic axis, and equivalent plunge and pitch stiffnesses
and
, respectively. The elastic axis is located at a distance
from the leading edge, and the centre of mass is at a distance
d downstream from the elastic axis.
To define the wing station structural model, the location of the elastic axis, the location of the centre of mass, and the values of the model properties (M,,,) need to be determined from the three-dimensional wing model.
4.1. Elastic Axis
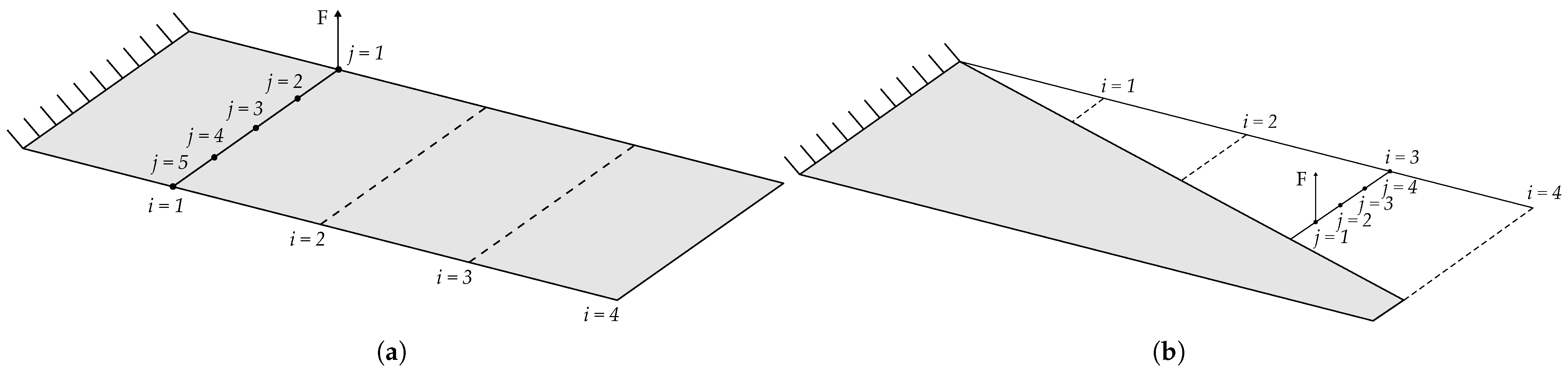
The plunge and pitch with respect to the elastic axis are used for the two-dimensional model so that they are uncoupled. This property is used for its determination. The three-dimensional model’s response to point loads is used to determine its location by determining the location where these loads produce bending but a null twist of the structure. To this end, point loads are applied in the station nodes from the leading to the trailing edge successively, calculating the static rotation of the wing tip.
Figure 3a depicts the procedure for a straight wing with four stations and five nodes along each of them. The distance of the elastic axis from the leading edge is determined from the rotation of the wing tip at the two adjacent nodes (with different rotation signs) through the regula falsi method. This procedure can be applied straightforwardly given that the elastic axis intersects the station within the wing area. If the elastic axis is outside the wing area (beyond the leading edge), a procedure based on the application of the point load at the end of an RBAR element, whose other end is connected to the corresponding node of the leading edge, is used, as shown in
Figure 3b. The location of the point load is varied until the wing rotation shift sign changes, and then the regula falsi method is carried out.
4.2. Structural Properties
Once the elastic axis of the wing is defined, the structural properties for each wing station can be determined.
The plunge stiffness
is determined from the station vertical displacement due to a unitary point load applied at the location of the elastic axis
. To take into account the actual section behaviour (which is not perfectly rigid in the wing model but is in the two-dimensional model), the average vertical displacement of the station (
) is considered. The plunge mass of the wing station is defined to match the first bending eigenfrequency of the wing
(obtained through the three-dimensional model):
Pitch parameters (
,
) are obtained in an analogous way by applying unitary torque in the direction perpendicular to the root chord at the location of the elastic axis in the station. The station pitch angle is determined from the vertical displacement of the leading and trailing edges (
). The pitch parameters
are defined to match the first torsion eigenfrequency of the wing
(obtained through the three-dimensional model).
Figure 4 shows the values of the station stiffness and mass parameters for a wing with
,
,
, and 3 mm thickness.
5. Aeroelastic Models
This section presents the aeroelastic models for both the wing and each of the stations considered along the semi-span, including the structure, aerodynamics, and fluid–structure interaction. All numerical models were developed in MSC.Nastran 2022 [
28].
5.1. Wing Model
For each wing analysed, a different numerical model is developed and analysed. The wing model is composed of a flate plate made up of a set of quadrilateral plate elements (CQUAD4) with shell properties according to the mechanical properties stated in
Section 3. The stiffener model is composed of a set of one-dimensional elements (CBEAM) with the mechanical properties stated in
Section 3 by means of a PBEAM entry. The CBEAM element nodes are coincident with the CQUAD4 ones. All displacements and rotations at the root chord are restricted to simulate the cantilever condition. No damping is included in the model.
The modelling of the aerodynamic is carried out by means of DLM for subsonic flow [
9], implemented in Nastran [
29].
The interaction between the aerodynamic boxes defined in the DLM and the structural elements is based on the theory of splines. An infinite plate spline is used between all aerodynamic boxes and all nodes in the structure.
5.2. Wing Station Model
For each wing studied, 20 different numerical models were developed and analysed, one for each of the stations considered along the semi-span. For each model, the structure is defined by means of a concentrated mass element (CONM2) for the inertia properties and two scalar spring elements (CELAS2) for the plunge and pitch stiffness, with null structural damping. The aerodynamic forces are calculated with strip theory [
29]. The fluid–structure interaction is considered by means of a beam spline.
5.3. Divergence and Flutter Analysis
The wing divergence and flutter speeds are determined through MSC.NASTRAN solution sequences 144 and 145, respectively. For divergence, the first divergence dynamic pressure is calculated for incompressible flow (
) at sea level (
kg/m
3). For flutter, the aerodynamic force matrix is calculated for mach number
in a range of reduced frequency between 0.05 and 6.0. The wing flutter is analysed by means of the p-k method [
29,
30], also at sea level considering the first seven modes.
Each wing station divergence and flutter speed are both determined by means of MSC.NASTRAN solution sequence 145 with the same parameters (aerodynamic force matrix for
and flight at sea level). The divergence speed is determined as the speed at which the damping changes its sign besides having zero frequency [
7,
16].
6. Results and Discussion
6.1. Characteristics of the Wings
The characteristics of the wing population studied are presented. First the flutter (
) and divergence (
) speeds are calculated by means of the three-dimensional model presented. The flutter mechanism was identified in all cases to be the coupling of the first plunge and pitch modes.
Figure 5 shows the value of the flutter and divergence speeds for some of the wings studied to show the trends with the wing platform geometry.
The results show that both flutter and divergence speeds increase for lower aspect ratios and that the sweep angle has a minor influence on the flutter speed and a major one on the divergence speed. Both speeds increase with the taper ratio. The wing population studied shows a ratio of velocities
between 1.15 and 2.35, and the maximum flutter and divergence Mach numbers are 0.15 and 0.31, respectively, considered adequate for the incompressible flow hypothesis [
31].
One of the main quantities known to influence the flutter is the ratio between the plunge and pitch eigenfrequencies (
).
Figure 6 shows this value for some of the wings studied to show the trends with the wing platform geometry.
In the wing population studied, varies from 0.27 to 0.85. It decreases with the aspect ratio, the sweep angle, and the taper ratio. The wing pitch eigenfrequencies range from 21.2 rad/s to 140.6 rad/s in the cases studied.
6.2. Flutter and Divergence Typical Section
As stated in
Section 2, for each wing, the flutter typical section (TS
f) is defined as the station that presents the same flutter speed as the wing, and the divergence typical section (TS
d) is defined equivalently. Within this study, twenty wing stations evenly distributed along the semi-span are considered. As
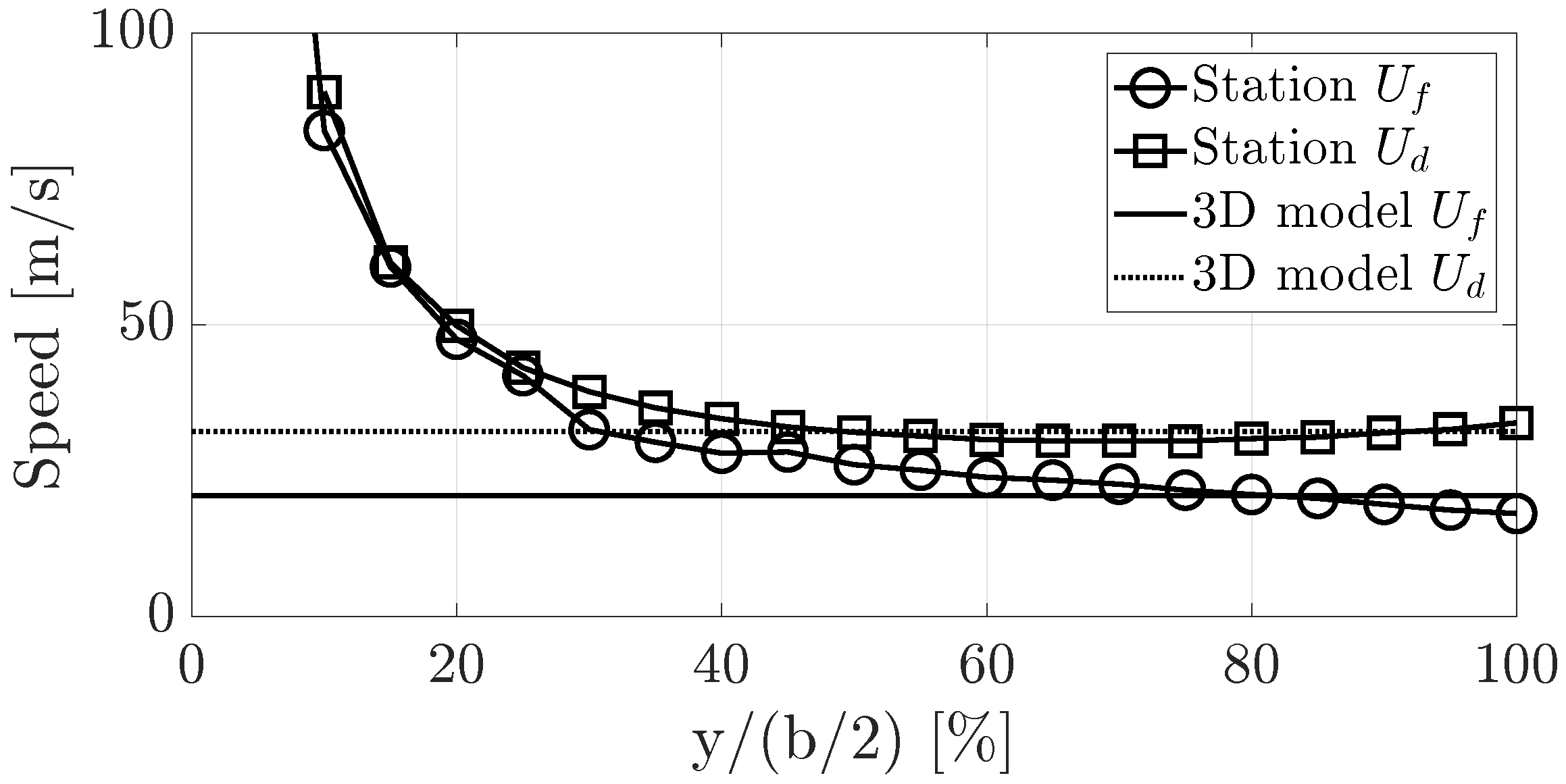
Figure 7 shows, the station speeds vary smoothly; therefore, interpolation is used to determine the exact span-wise location where the typical section is located. For the wing shown in
Figure 7, the flutter and divergence typical sections are located at 75% and 59% of the semi-span, respectively.
The location of the divergence typical section, TS
d, is shown in
Figure 8. The results show that it tends towards the wing tip with the aspect ratio and the taper ratio. Nevertheless, two particular scenarios are found: no typical section or several typical sections.
On one hand, for some of the wings studied, no divergence typical section can be defined as none of the stations show the same divergence speed as the wing, as is the case for the wing with
,
, and
, shown in
Figure 8.
On the other hand, for some of the wings studied, more than one of the stations show the same divergence speed as the wing. Among the cases depicted in
Figure 8, this is the case for two wings, both with
,
,
, and
. The comparison between the stations and the wing behaviours for
= 12,
, and
20° is shown in
Figure 9, which clearly shows that two different stations show the same divergence speed as the wing. These cases are included in
Figure 8 by duplicating the corresponding marker. Multiple TS
d are found for wings with
= 12 and a high sweep angle.
For the flutter typical section, TS
f, shown in
Figure 10, different trends can be identified depending on the wing aspect ratio. For a high aspect ratio, the sweep angle and the taper ratio have minor influence, unlike for low-aspect-ratio wings. For the lowest
value, again, cases of multiple flutter typical sections are found as more than one station shows the same flutter speed as the wing. This fact, represented with multiple markers in
Figure 10, is found for only wings with
= 4 and low sweep angles.
Figure 11 shows the location of both TS
f and TS
d for four values of the aspect ratio. Each group depicts the results for all the values of taper ratio and sweep angle analysed. For each wing, the data for the flutter and divergence TS are joined by a dotted line. Those cases with multiple TS
d or TS
f are represented with red markers and connected with red dotted lines to the other typical sections.
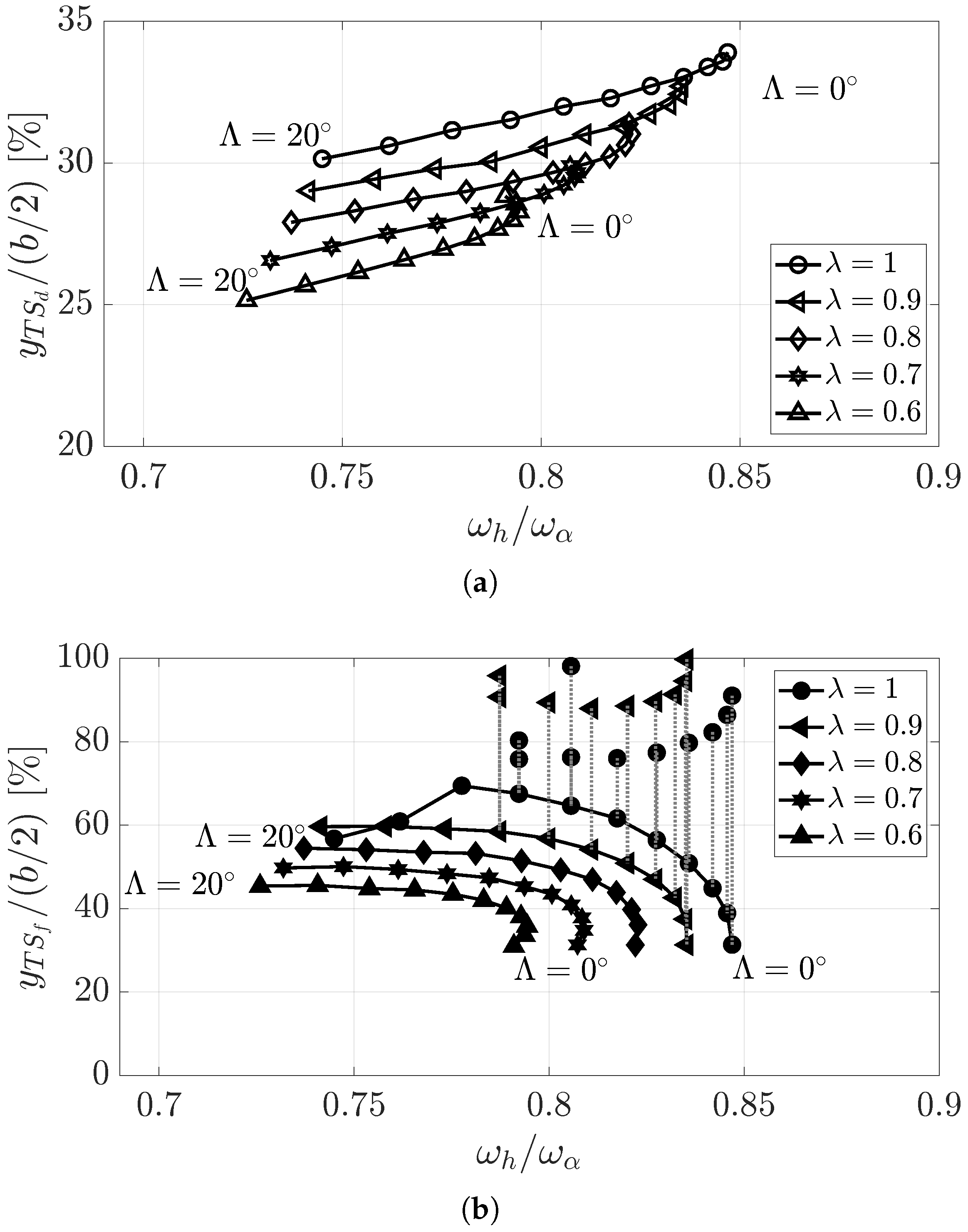
Figure 11 highlights that, in general, both TSs are not located in the same semi-span location. For the largest aspect ratio studied (
= 12) both typical sections tend to lie close for any taper ratio and sweep angle. Nevertheless, some wings (with a taper ratio between 0.6 and 0.8 and high sweep angle) show an additional TS
d closer to the wing root. For smaller values of the aspect ratio, both TSs are at distinct locations. The relationship between the location of the typical sections and
is also clear: both move towards the wing root as the magnitude increases.
Figure 12 shows the location of the TS
d and TS
f for wings with
, facilitating the identification of taper ratio and sweep angle trends. The distance between both is minimal for straight wings (
), and they separate with an increasing sweep angle (TS
d goes towards the wing root, and TS
f goes towards the wing tip). For wings with several TS
fs, multiple markers joined by a dotted line are depicted.
As shown by these results, for straight wings like those studied by Theodorsen and Garrick to conclude the classic definition of the typical section (three-quarter of the semi-span), both flutter and divergence sections are the closest, allowing it be considered a unique typical section. The three-quarter semi-span location is adequate for aspect ratios close to 9 and low
values. In general, for a given wing with a known aspect ratio and
, a first estimation of the typical section can be extracted from
Figure 11, although for large sweep angles, two should be considered: the divergence one closer to the root chord and the flutter one close to the wing tip.
7. Conclusions
The concept of the typical section of a lifting surface was originally proposed for applying two-dimensional unsteady aerodynamic theories to three-dimensional problems. More recently it has also been employed in analysing transient or non-linear phenomena or to make use of optimisation techniques.
This work proposes a formal definition of the typical section as a two-dimensional model that presents the same flutter/divergence speed as the wing considering the structure stiffness along the semi-span and with the same eigenfrequencies as the wing. This definition is applied to a set of cantilever trapezoidal wings with different geometries (aspect ratio, taper ratio, and sweep angle).
From this systematic study, it is concluded that as a general rule, there is a typical section for flutter and a different typical section for the wing divergence, with different locations along the wing semi-span. For large-aspect-ratio wings, close divergence and flutter typical sections can be found while the distance between them increases for a decreasing aspect ratio and increasing sweep angle. Their location tends toward the wing tip for high aspect ratios and low values of the ratio of the plunge to pitch eigenfrequencies. For low aspect ratios, their location differs greatly, except for with very low sweep angles. The results obtained allow us to adequately estimate the location of these sections for a given wing from its platform and first bending and torsion eigenfrequencies.
For certain configurations, particularly wings with high sweep angles or extreme aspect ratios, multiple typical sections exist as multiple stations match the wing flutter or divergence speed. In some cases, no typical section could be identified for divergence, indicating limitations in the simplified two-dimensional representation.
Although this work analyses the validity of the typical section concept based on the flutter and divergence speeds considering the original studies based on flutter, other aeroelastic studies should be considered in the future, such as on control reversal or the response to discrete gusts or continuous turbulence.
Author Contributions
Conceptualisation, M.C.M.; methodology, M.C.M.; software, M.N.G.; validation, M.N.G. and M.C.M.; formal analysis, M.N.G. and M.C.M.; investigation, M.N.G. and M.C.M.; resources, M.C.M.; data curation, M.N.G. and M.C.M.; writing—original draft preparation, M.C.M.; writing—review and editing, M.N.G. and M.C.M.; visualisation, M.C.M.; supervision, M.C.M. All authors have read and agreed to the published version of the manuscript.
Funding
The work was supported by the Ministry for Education of Spain, with the fellowship “Becas de colaboración en Departamentos universitarios para el curso académico 2023–2024”.
Data Availability Statement
No new data were created or analyzed in this study.
Acknowledgments
The authors would like to thank Pablo García-Fogeda Núñez and Keyvan Salehi Paniagua for their valuable discussions and insightful feedback, which contributed to the development of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bisplinghoff, R.; Ashley, H.; Halfman, R. Aeroelasticity; Dover Books on Aeronautical Engineering Series; Dover Publications: Mineola, NY, USA, 1996. [Google Scholar]
- Wright, J.; Cooper, J. Introduction to Aircraft Aeroelasticity and Loads; Aerospace Series; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- European Union Aviation Safety Agency (EASA). Certification Specifications for Large Aeroplanes (CS-25); European Union Aviation Safety Agency (EASA): Cologne, Germany, 2007.
- Federal Aviation Administration (FAA). Title 14 Code of Federal Regulations (CFR) Part 25—Airworthiness Standards: Transport Category Airplanes; Federal Aviation Administration (FAA): Washington, DC, USA, 1964.
- Theodorsen, T.; Garick, I. A Theoretical and Experimental Investigation of the Flutter Problem; Technical report; NACA: Boston, MA, USA, 1940. [Google Scholar]
- Theodorsen, T. General Theory of Aerodynamic Instability and the Mechanism of Flutter; Technical report; NACA: Boston, MA, USA, 1949. [Google Scholar]
- Rodden, W.; Stahl, B. A strip method for prediction of damping in subsonic wind tunnel andflight flutter tests. J. Aircr. 1969, 6, 9–17. [Google Scholar] [CrossRef]
- Scanlan, R.; Rosenbaum, R. Introduction to the Study of Aircraft Vibration and Flutter; The Macmillan Company: New York, NY, USA, 1951. [Google Scholar]
- Albano, E.D.; Rodden, W.P. A doublet-lattice method for calculating lift distributions on oscillating surfaces in subsonic flows. AIAA J. 1969, 7, 279–285. [Google Scholar] [CrossRef]
- Petrolo, M. Flutter analysis of composite lifting surfaces by the 1D Carrera Unified Formulation and the doublet lattice method. Compos. Struct. 2013, 95, 539–546. [Google Scholar] [CrossRef]
- Guimarães Neto, A.B.; da Silva, R.G.; Paglione, P. Control-point-placement method for the aerodynamic correction of the vortex and the doublet-lattice methods. Aerosp. Sci. Technol. 2014, 37, 117–129. [Google Scholar] [CrossRef]
- Dababneh, O.; Kipouros, T.; Whidborne, J.F. Multidisciplinary Design Optimization of the NASA Metallic and Composite Common Research Model Wingbox: Addressing Static Strength, Stiffness, Aeroelastic, and Manufacturing Constraints. Aerospace 2025, 12, 476. [Google Scholar] [CrossRef]
- Salehi Paniagua, K.; García-Fogeda Núñez, P.; Arévalo Lozano, F. A cost-efficient method to determine the dynamic stability of a missile/rocket configuration with grid fins. Aerosp. Sci. Technol. 2025, 159, 109948. [Google Scholar] [CrossRef]
- Hodges, D.H.; Pierce, G.A. Introduction to Structural Dynamics and Aeroelasticity, 2nd ed.; Cambridge Aerospace Series; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Dowell, E.; Clark, R.; Cox, D.; Curtiss, H.; Edwards, J.; Hall, K.; Peters, D.; Scanlan, R.; Simiu, E.; Sisto, F.; et al. A modern Course in Aeroelasticity; Solid Mechanics and its Applications; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1–766. [Google Scholar]
- Edwards, J.W.; Wieseman, C.D. Flutter and Divergence Analysis Using the Generalized Aeroelastic Analysis Method. J. Aircr. 2008, 45, 906–915. [Google Scholar] [CrossRef]
- Iannelli, A.; Marcos, A.; Lowenberg, M. Comparison of Aeroelastic Modeling and Robust Flutter Analysis of a Typical Section. IFAC-PapersOnLine 2016, 49, 409–414. [Google Scholar] [CrossRef]
- Marqui, C.R.; Bueno, D.D.; Goes, L.C.; Gonçalves, P.J. A reduced order state space model for aeroelastic analysis in time domain. J. Fluids Struct. 2017, 69, 428–440. [Google Scholar] [CrossRef]
- Berci, M. On Aerodynamic Models for Flutter Analysis: A Systematic Overview and Comparative Assessment. Appl. Mech. 2021, 2, 516–541. [Google Scholar] [CrossRef]
- Pilakkadan, J.S.; Ajaj, R.M.; Haider, Z.; Amoozgar, M. On the Aeroelasticity of a Cantilever Wing Equipped with the Spanwise Morphing Trailing Edge Concept. Aerospace 2023, 10, 809. [Google Scholar] [CrossRef]
- Padmanabhan, M.A.; Pasiliao, C.L.; Dowell, E.H. Simulation of Aeroelastic Limit-Cycle Oscillations of Aircraft Wings with Stores. AIAA J. 2014, 52, 2291–2299. [Google Scholar] [CrossRef]
- Sanches, L.; Guimarães, T.A.; Marques, F.D. Aeroelastic tailoring of nonlinear typical section using the method of multiple scales to predict post-flutter stable LCOs. Aerosp. Sci. Technol. 2019, 90, 157–168. [Google Scholar] [CrossRef]
- Darabseh, T.; Tarabulsi, A.; Mourad, A.H.I. Discrete-Time Model Predictive Controller Using Laguerre Functions for Active Flutter Suppression of a 2D wing with a Flap. Aerospace 2022, 9, 475. [Google Scholar] [CrossRef]
- Schildkamp, R.; Chang, J.; Sodja, J.; De Breuker, R.; Wang, X. Incremental Nonlinear Control for Aeroelastic Wing Load Alleviation and Flutter Suppression. Actuators 2023, 12, 280. [Google Scholar] [CrossRef]
- Jonsson, E.; Riso, C.; Lupp, C.A.; Cesnik, C.E.; Martins, J.R.; Epureanu, B.I. Flutter and post-flutter constraints in aircraft design optimization. Prog. Aerosp. Sci. 2019, 109, 100537. [Google Scholar] [CrossRef]
- Kaiser, C.; Quero, D. Effect of Aerodynamic Damping Approximations on Aeroelastic Eigensensitivities. Aerospace 2022, 9, 127. [Google Scholar] [CrossRef]
- Riso, C.; Cesnik, C.E.S.; Epureanu, B.I. Bifurcation-Diagram-Free Postflutter Response Constraint for Design Optimization. AIAA J. 2023, 61, 3449–3465. [Google Scholar] [CrossRef]
- MSC Software Corporation. MSC Nastran User’s Guide; MSC Software Corporation: Newport Beach, CA, USA, 2022. [Google Scholar]
- MSC Software Corporation. MSC Aeroelastic User’s Guide; MSC Software Corporation: Newport Beach, CA, USA, 2022. [Google Scholar]
- Hassig, H.J. An approximate true damping solution of the flutter equation by determinant iteration. J. Aircr. 1971, 8, 885–889. [Google Scholar] [CrossRef]
- Anderson, J. Fundamentals of Aerodynamics; McGraw-Hill series in aeronautical and aerospace engineering; McGraw-Hill: Columbus, OH, USA, 2017. [Google Scholar]
Figure 1.
Planform of cantilever wing: is the chord at the root, is the tip chord, is the half span, and is the sweep angle, between the line and the line perpendicular to the root chord.
Figure 1.
Planform of cantilever wing: is the chord at the root, is the tip chord, is the half span, and is the sweep angle, between the line and the line perpendicular to the root chord.
Figure 2.
Two-degree-of-freedom airfoil model considered for each wing station span-wise.
Figure 2.
Two-degree-of-freedom airfoil model considered for each wing station span-wise.
Figure 3.
Point load application scheme for determination of elastic axis if it is inside (a) or outside (b) the structure.
Figure 3.
Point load application scheme for determination of elastic axis if it is inside (a) or outside (b) the structure.
Figure 4.
Value of stiffness and mass parameters for the 20 stations along the semi-span for a wing with , , , and 3 mm thickness.
Figure 4.
Value of stiffness and mass parameters for the 20 stations along the semi-span for a wing with , , , and 3 mm thickness.
Figure 5.
Value of the three-dimensional model flutter speed (a) and divergence speed (b) as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle (straight wing and 20°).
Figure 5.
Value of the three-dimensional model flutter speed (a) and divergence speed (b) as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle (straight wing and 20°).
Figure 6.
Value of as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle (straight wing and 20° sweep angle).
Figure 6.
Value of as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle (straight wing and 20° sweep angle).
Figure 7.
Flutter and divergence speeds (,) for each wing station compared to the flutter and divergence speeds obtained through the three-dimensional model for a wing with = 9, , and 8°.
Figure 7.
Flutter and divergence speeds (,) for each wing station compared to the flutter and divergence speeds obtained through the three-dimensional model for a wing with = 9, , and 8°.
Figure 8.
Location of divergence typical section as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle ( 0°, 10°, and 20°). Additional markers are shown for wings with multiple typical sections.
Figure 8.
Location of divergence typical section as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle ( 0°, 10°, and 20°). Additional markers are shown for wings with multiple typical sections.
Figure 9.
Flutter and divergence speeds (,) for each wing station compared to the flutter and divergence speeds obtained through the three-dimensional model for a wing with = 12, , and 20°.
Figure 9.
Flutter and divergence speeds (,) for each wing station compared to the flutter and divergence speeds obtained through the three-dimensional model for a wing with = 12, , and 20°.
Figure 10.
Location of the flutter typical section as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle ( 0°, 10°, and 20°). Additional markers are shown for wings with multiple typical sections.
Figure 10.
Location of the flutter typical section as a function of the aspect ratio for three values of the taper ratio and the two values of the sweep angle ( 0°, 10°, and 20°). Additional markers are shown for wings with multiple typical sections.
Figure 11.
Location of the flutter and divergence typical section as a function of for four values of the aspect ratio with a different taper ratio and sweep angle. Each pair of data points joined by a dotted line represent the two sections for the same given wing. Additional red markers are shown for wings with multiple typical sections.
Figure 11.
Location of the flutter and divergence typical section as a function of for four values of the aspect ratio with a different taper ratio and sweep angle. Each pair of data points joined by a dotted line represent the two sections for the same given wing. Additional red markers are shown for wings with multiple typical sections.
Figure 12.
Location of divergence (a) and flutter (b) typical section for for different taper ratios and sweep angles. Multiple TSfs are depicted with additional markers joined by a dotted line.
Figure 12.
Location of divergence (a) and flutter (b) typical section for for different taper ratios and sweep angles. Multiple TSfs are depicted with additional markers joined by a dotted line.
Table 1.
Values of aspect ratio , sweep angle , and taper ratio considered.
Table 1.
Values of aspect ratio , sweep angle , and taper ratio considered.
| Parameter | Value |
|---|
| [-] | 12, 11, 10, 9, 8, 7, 6, 5, 4 |
| [-] | 1, 0.9, 0.8, 0.7, 0.6 |
| [°] | 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).