Precise Cruise Control for Fixed-Wing Aircraft Based on Proximal Policy Optimization with Nonlinear Attitude Constraints

Abstract

In response to the issues of severe pitch oscillation and unstable roll attitude present in existing reinforcement learning-based aircraft cruise control methods during dynamic maneuvers, this paper proposes a precise control method for aircraft cruising based on proximal policy optimization (PPO) with nonlinear attitude constraints. This method first introduces a combination of long short-term memory (LSTM) and a fully connected layer (FC) to form the policy network of the PPO method, improving the algorithm’s learning efficiency for sequential data while avoiding feature compression. Secondly, it transforms cruise control into tracking target heading, altitude, and speed, achieving a mapping from motion states to optimal control actions within the policy network, and designs nonlinear constraints as the maximum reward intervals for pitch and roll to mitigate abnormal attitudes during maneuvers. Finally, a JSBSim simulation platform is established to train the network parameters, obtaining the optimal strategy for cruise control and achieving precise end-to-end control of the aircraft. Experimental results show that, compared to the cruise control method without dynamic constraints, the improved method reduces heading deviation by approximately 1.6° during ascent and 4.4° during descent, provides smoother pitch control, decreases steady-state altitude error by more than 1.5 m, and achieves higher accuracy in overlapping with the target trajectory during hexagonal trajectory tracking.

1. Introduction

With the advantages of a large flight radius and strong load capacity, fixed-wing aircraft have important roles in remote sensing detection, material transportation, and cooperative operations [1]. The cruising process is the basis for fixed-wing aircraft to realize all the tasks, and it is also the longest duration flight activity, which consumes the pilot’s energy tremendously. Therefore, the unmanned modification of manned fixed-wing aircraft and the realization of a cruise control method with good performance and robustness to assist the pilot’s driving are of great significance in reducing the burden of the pilot and the flight cost.

In the existing research on cruising control methods, control approaches based on deep reinforcement learning have gained attention due to their ability to extract effective information from high-dimensional observations. They can utilize reward functions as incentives, autonomously explore through trial and error for iterative learning, and obtain optimal control strategies in complex scenarios. This makes them well-suited to address issues where control logic is complex and scene features are difficult to express explicitly, leading to widespread research and application.

Currently, the methods for aircraft cruise control based on deep reinforcement learning mainly utilize algorithms, such as PPO, SAC, and DDQN. The focus of improvements is primarily on enhancing the network structure and optimizing the reward function. In reference [2], David J. Richter and Ricardo A. Calix, from the United States, used DDQN to control the pitch and roll angles of an aircraft, achieving smooth control of the aircraft’s basic attitude. Meanwhile, Kai Deng and his team from the Harbin Institute of Technology implemented attitude control for fixed-wing aircraft using the DQN method by directly discretizing the action space [3]. This approach improved the system’s response speed compared to the incremental control method in reference [2], but sacrificed some smoothness. Based on the PPO method, Xunfei Yu and his team from Xi’an University adjusted the pitch angle of the aircraft under simulated stall conditions, quickly restoring stable flight [4]. The Beijing Complex System Control Laboratory [5], on the other hand, accomplished the adjustment of the aircraft pitch and roll by utilizing the PPO method to output the control quantities of the ailerons, elevator, and throttle valves, and realized the tracking of the target angle, demonstrating superior overall performance in terms of speed and oscillation characteristics compared to PID methods. Additionally, Yupeng Fu and his team from the Naval Engineering University improved the previous dual-channel PID control method by replacing the PID control loop with a PPO network, achieving control of a six-degree-of-freedom aircraft [6]. To accelerate the learning speed of the network, they also implemented a posture control method based on imitation learning in 2022 [7]. Due to the strong handling capability of recurrent neural networks for temporal control problems, Chowdhury and Keshmiri from the University of Kansas designed a new controller structure by combining LSTM with the PPO method. Experimental results show that this method not only performs better but exhibits greater robustness [8,9]. Building on this, researchers from Nankai University improved the success rate and stability of training using curriculum learning methods [10]. In order to speed up the convergence of the algorithm, the College of Air and Space Science of the National University of Defense Technology designed an improved trajectory tracking method for fixed-wing aircraft using the DDPG [11]. Zhang Sheng and others from the China Aerodynamics Research and Development Center implemented control for a six-degree-of-freedom aircraft using DDPG [12]. The Delft University of Technology in the Netherlands also developed an intelligent flight controller using DDPG for obstacle crossing actions of fixed-wing aircraft in the longitudinal plane [13]. To enhance the adaptability of the algorithm and its exploration capability for optimal solutions, the Technical University of Madrid implemented waypoint tracking using SAC [14]; Eivind Bøhn et al. from the Norwegian University of Science and Technology also proposed an efficient SAC-based drone control method, considering the differences between virtual environments and real displays, achieving stable control of the aircraft using three minutes of flight data, with strong robustness [15].

Current research has provided many end-to-end cruise control solutions based on reinforcement learning, achieving good trajectory tracking accuracy. However, due to factors such as coupling oscillations between channels and sudden changes in forces and moments, aircraft still experience slow convergence in trajectory tracking accuracy and sudden state anomalies during maneuvers. This can lead to a further decline in cruise control performance when facing meteorological disturbances, and even pose risks of instability and loss of control, which is insufficient to meet the requirements for control accuracy, stability, and safety in practical applications of aircraft.

In order to enhance the dynamic control stability of the end-to-end cruise control model, this paper proposes a precise control method for aircraft cruising based on proximal policy optimization under nonlinear attitude constraints. The method first combines long short-term memory networks with fully connected layers to form an FC–LSTM–FC policy network structure, achieving a mapping from state input to flight control action output. It utilizes recurrent neural networks to improve the algorithm’s learning efficiency for sequential data and to enhance its ability to estimate environmental disturbances. Next, using altitude and yaw angle as variables, nonlinear constraint functions for pitch and roll are designed, which strengthen the stability control of the attitude while implementing end-to-end control. Finally, a simulation platform is built for training to obtain the optimal weights of the policy network. Based on this, comparative experiments with different models are conducted to further validate the advantages of this model.

This paper is organized as follows. A literature review has been presented in Section 1. In Section 2, the reinforcement learning method is introduced briefly and the structure of the control model are discussed. In Section 3, the reward functions are designed, including the trajectory tracking reward and nonlinear constraint for attitude. The simulation environment and training strategy are expanded in Section 4. The experiments are carried out and the results are shown and analyzed in Section 5. Finally, A conclusion is presented in Section 6.

2. Cruise Control Method for Fixed-Wing Aircraft Based on PPO

2.1. Cruise Control Model Based on Deep Reinforcement Learning

Reinforcement learning methods are designed to create suitable reward functions based on input observations and target states, and to obtain optimal policies through training. In a trajectory of length $\mathit{T}$, the trajectory reward $\mathit{G}(\mathit{\tau })$ obtained by the agent is the total sum of the rewards received for taking action ${\mathit{a}}_{\mathit{t}}$ at each state ${\mathit{s}}_{\mathit{t}}$ in the trajectory, discounted by the factor $\gamma$. Under different policies, the agent will take different actions from the same initial state, resulting in different trajectories and trajectory rewards. The goal of reinforcement learning is to continuously adjust the parameters of the policy network through model training, allowing the agent to learn the optimal policy ${\pi }_{\vartheta }^{\ast }$, thereby maximizing the reward obtained from various initial states.

$$\mathit{G}(\mathit{\tau })={\displaystyle \sum _{\mathit{t}=0}^{\mathit{T}}{\gamma }^{\mathit{t}}\mathit{R}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})}$$

(1)

$${\pi }_{\vartheta }^{\ast }=\underset{\vartheta }{\arg \max }{\mathbb{E}}_{\tau \sim \mathrm{\Gamma }({\mathit{S}}_0,{\pi }_0)}[\mathit{G}(\mathit{\tau })]$$

(2)

Deep reinforcement learning methods are optimization techniques that introduce deep neural networks to describe the value function based on reinforcement learning [16]. Among the many deep reinforcement learning methods, the PPO method is a policy-based approach that uses the Actor–Critic (AC) framework. Proposed by OpenAI in 2017 [17], the core idea of this method is to optimize the policy to the greatest extent while introducing the clipping function in Equation (3) in the update of the policy function to ensure that new and old policies do not differ too much, which could lead to policy collapse. It has been widely applied and has demonstrated strong performance in complex control problems.

$${\mathit{L}}^{\mathit{C}\mathit{L}\mathit{I}\mathit{P}}(\theta )={\mathbb{E}}_{\mathit{t}}[\min ({\mathit{r}}_{\mathit{t}}(\theta ){\mathit{A}}_{\mathit{t}},\mathrm{clip}({\mathit{r}}_{\mathit{t}},1-\epsilon ,1+\epsilon ){\mathit{A}}_{\mathit{t}})]$$

(3)

In the formula, ${\mathit{r}}_{\mathit{t}}(\theta )={\displaystyle \frac{{\pi }_{\theta }({\mathit{a}}_{\mathit{t}}|{\mathit{s}}_{\mathit{t}})}{{\pi }_{{\theta }_{\mathit{o}\mathit{l}\mathit{d}}}({\mathit{a}}_{\mathit{t}}|{\mathit{s}}_{\mathit{t}})}}$ represents the difference in action selection between old and new policies in the same state, describing the degree of change between the old and new policies; $\epsilon$ is the clipping coefficient.

Using the PPO algorithm as the main controller, this paper models the cruise control of fixed-wing aircraft as a process that maps input states to control outputs, achieving the tracking of target heading, speed, and altitude to capture a specific trajectory. The small general aviation fixed-wing aircraft Cessna 172P is used as the reference controlled object, and the content of state inputs and control action outputs is determined, followed by the design of the network structure and reward function.

2.2. Cruise Control Model Policy Network Structure

The fixed-wing aircraft is a highly coupled and under-actuated model across various channels [18]. Due to the significant lag characteristics in control, this paper designs the policy network input, as shown in the Equation (4).

$${\mathit{s}}_{\mathit{t}}=[{\delta }_{\mathit{h},\mathit{t}},{\delta }_{\psi ,\mathit{t}},{\delta }_{\mathit{v},\mathit{t}},{\mathit{h}}_{\mathit{t}},{\varphi }_{\mathit{t}},{\theta }_{\mathit{t}},{\mathit{v}}_{\mathit{N},\mathit{t}},{\mathit{v}}_{\mathit{E},\mathit{t}},{\mathit{v}}_{\mathit{D},\mathit{t}},{\omega }_{\psi ,\mathit{t}},{\omega }_{\varphi ,\mathit{t}},{\omega }_{\theta ,\mathit{t}}]$$

(4)

In this context, $\mathit{t}$ represents time; ${\delta }_{\mathit{t}}=[{\delta }_{\mathit{h},\mathit{t}},{\delta }_{\psi ,\mathit{t}},{\delta }_{\mathit{v},\mathit{t}}]$ is the difference between the aircraft’s altitude, heading, and the speed of the aircraft’s nose direction and the target value, defined as positive when the state value is less than the target value; ${\mathit{h}}_{\mathit{t}}$ is the altitude of the aircraft relative to mean sea level; ${\varphi }_{\mathit{t}}$ and ${\theta }_{\mathit{t}}$ are the roll and pitch angles of the aircraft, respectively; $\mathit{v}=[{\mathit{v}}_{N,\mathit{t}},{\mathit{v}}_{\mathit{E},\mathit{t}},{\mathit{v}}_{D,\mathit{t}}]$ and $\omega =[{\omega }_{\psi ,\mathit{t}},{\omega }_{\varphi ,\mathit{t}},{\omega }_{\theta ,\mathit{t}}]$ are the speed and angular velocity of the aircraft. To avoid issues of gradient explosion or gradient vanishing during network training due to inconsistent scales of observation variables, this paper applies uniform scaling and clipping to each state variable based on their distribution before inputting them into the network.

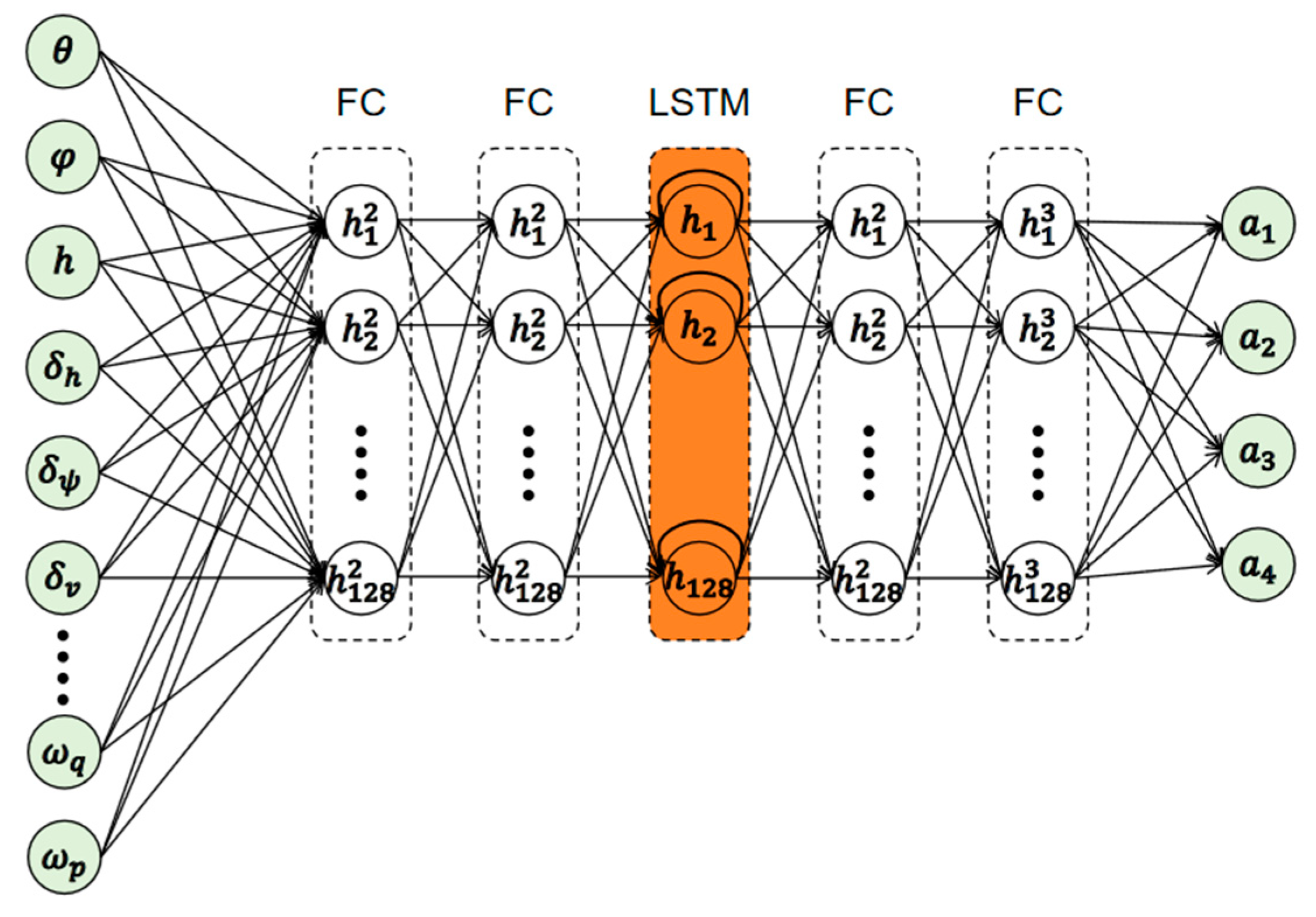
The cruise control of an aircraft is a partially sizable Markov problem because of the large amount of perturbations and noise in the environment. In order to strengthen the estimation ability of the control model for unobservable measurements in the environment, this paper introduces LSTM to learn the long-term dependencies in the time series data. Considering the complex coupling characteristics and control difficulty of the aircraft model, as well as the possible problems of feature compression and insufficient extraction of features in the LSTM network, this paper combines the fully-connected layer to design the network structure, as shown in Figure 1:

The first and second layers are 128-dimensional fully-connected layers, which are responsible for preprocessing the input states and providing richer feature information for the LSTM layer; the third layer is the LSTM layer, which contains 128 network cells, and is responsible for learning long-term dependencies in the state trajectories, and estimating perturbations and noises in the environment; the fourth and fifth layers are also 128-dimensional fully-connected layers, which are responsible for mapping the LSTM outputs to the control action output in Equation (5).

$$\mathit{a}=[{\mathit{a}}_{\mathit{r}\mathit{u}\mathit{d}\mathit{d}\mathit{e}\mathit{r}},{\mathit{a}}_{\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{r}\mathit{o}\mathit{n}},{\mathit{a}}_{\mathit{e}\mathit{l}\mathit{e}\mathit{v}\mathit{a}\mathit{t}\mathit{o}\mathit{r}},{\mathit{a}}_{\mathit{t}\mathit{h}\mathit{r}\mathit{o}\mathit{t}\mathit{t}\mathit{l}\mathit{e}}]$$

(5)

In the above equation, ${\mathit{a}}_{\mathit{a}\mathit{i}\mathit{l}\mathit{e}\mathit{r}\mathit{o}\mathit{n}}$ is the aileron control quantity; ${\mathit{a}}_{\mathit{r}\mathit{u}\mathit{d}\mathit{d}\mathit{e}\mathit{r}}$ is the rudder, which affects the yaw of the vehicle; ${\mathit{a}}_{\mathit{e}\mathit{l}\mathit{e}\mathit{v}\mathit{a}\mathit{t}\mathit{o}\mathit{r}}$ is the elevator control quantity of the vehicle, and ${\mathit{a}}_{\mathit{t}\mathit{h}\mathit{r}\mathit{o}\mathit{t}\mathit{t}\mathit{l}\mathit{e}}$ is the engine throttle control quantity.

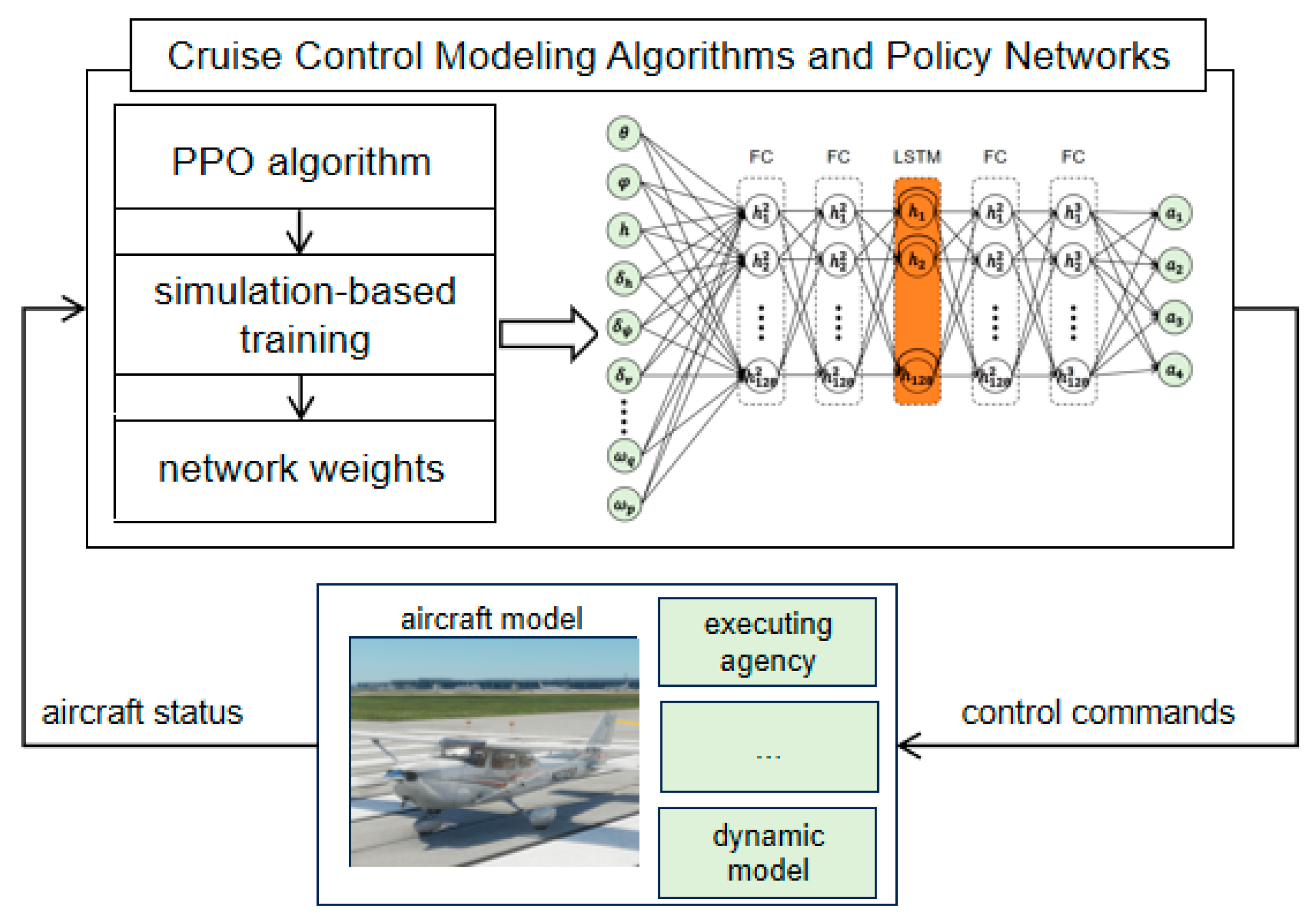
In summary, the control model structure shown in Figure 2 can be obtained to complete the design of fixed-wing aircraft cruise controller.

3. Cruise Control Model Reward Function Design

3.1. Trajectory Tracking Reward Function Design

The reward function is a calculation method composed of input state observations, where the agent receives rewards as the aircraft approaches the target state value. It is also key to guiding the model in learning the optimal strategy. Based on the modeling of the cruise control model, this paper first designs a dense shape reward function for trajectory tracking as follows:

$$\left\{\begin{array}{l}{\mathit{R}}^{\mathit{T}\mathit{T}}={\mathit{R}}^{\psi }({\delta }_{\psi ,\mathit{t}})\cdot {\mathit{R}}^{\mathit{h}}({\delta }_{\mathit{h},\mathit{t}})\cdot {\mathit{R}}^{\mathit{v}}({\delta }_{\mathit{v},\mathit{t}})\cdot {\mathit{R}}^{\mathit{r}}({\varphi }_{\mathit{t}})\hfill \\ {\mathit{R}}^{\psi }({\delta }_{\psi ,\mathit{t}})={\mathit{e}}^{-{[({\delta }_{\psi ,\mathit{t}})/{\mathit{B}}^{\psi }]}^2}\hfill \\ {\mathit{R}}^{\mathit{h}}({\delta }_{\mathit{h},\mathit{t}})={\mathit{e}}^{-{({\delta }_{\mathit{h},\mathit{t}}/{\mathit{B}}^{\mathit{h}})}^2}\hfill \\ {\mathit{R}}^{\mathit{v}}({\delta }_{\mathit{v},\mathit{t}})={\mathit{e}}^{-{({\delta }_{\mathit{v},\mathit{t}}/{\mathit{B}}^{\mathit{v}})}^2}\hfill \\ {\mathit{R}}^{\mathit{r}}({\varphi }_{\mathit{t}})={\mathit{e}}^{-{({\varphi }_{\mathit{t}}/{\mathit{B}}^{\varphi })}^2}\hfill \\ {\mathit{B}}^{\psi }=0.5°,{\mathit{B}}^{\mathit{h}}=5 \mathrm{m},{\mathit{B}}^{\mathit{v}}=3 \mathrm{m}/\mathrm{s},{\mathit{B}}^{\varphi }=20°\hfill \end{array}\right.$$

(6)

Among them, ${\mathit{R}}^{\mathit{T}\mathit{T}}$ is the total reward for trajectory tracking, while ${\mathit{R}}^{\psi }({\delta }_{\psi ,\mathit{t}})$, ${\mathit{R}}^{\mathit{v}}({\delta }_{\mathit{v},\mathit{t}})$, and ${\mathit{R}}^{\mathit{h}}({\delta }_{\mathit{h},\mathit{t}})$ are the rewards obtained from tracking the target states of heading angle, altitude, and speed, which are used to guide the aircraft in following the target states. ${\mathit{R}}^{\mathit{r}}({\varphi }_{\mathit{t}})$ is the reward related to the roll angle, which guides the aircraft to maintain roll stability while ensuring that it does not lose too much reward during the process of turning through rolling.

3.2. Nonlinear Constraint Design for Attitude

Due to the imbalance between the transient phase and the steady-state phase, in terms of time length, the control model is easy to fall into a locally optimal strategy that only focuses on the steady-state reward and ignores the control effect of the transient phase in the strategy training. Therefore, in this paper, on the basis of steady state tracking reward, for the deficiencies occurring in the cruise process, and using the altitude and yaw error as variables, a nonlinear reward function is set to constrain the pitch angle and roll angle to improve the dynamic control performance of the vehicle.

First, this paper designs the constraint reward Function (7) to map the altitude deviation to the target angle of the pitch through logarithmic and proportional functions, and optimizes the serial control method of altitude–pitch–rudder implemented under the original reward Function (6) to a parallel control method of altitude–rudder and pitch–rudder, to achieve the improvement of the response speed of the altitude and pitch channels, and to mitigate the steady state errors and overshoots of the altitude and pitch control.

$$\left\{\begin{array}{l}{\mathit{R}}^{\mathit{P}\mathit{S}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})={\mathit{e}}^{-{({\theta }_{\mathit{t}}-{\theta }_{\mathit{t}}^{*}/{\theta }_{\mathit{s}\mathit{c}\mathit{a}\mathit{l}\mathit{e}})}^2}\hfill \\ {\theta }_{\mathit{t}}^{*}=3{\log }_2(\left|{\delta }_{\mathit{h},\mathit{t}}\right|+1)+\frac{{\delta }_{\mathit{h},\mathit{t}}}{10} {\delta }_{\mathit{h},\mathit{t}}>0\hfill \\ {\theta }_{\mathit{t}}^{*}=-3{\log }_2(\left|{\delta }_{\mathit{h},\mathit{t}}\right|+1)+\frac{{\delta }_{\mathit{h},\mathit{t}}}{10} {\delta }_{\mathit{h},\mathit{t}}<0\hfill \end{array}\right.$$

(7)

With the logarithmic and proportional functions in the pitch smoothing function, the controller is able to maintain different frequency characteristics in different altitude error intervals, taking into account the speed of response to subtle altitude deviations and the wide range of altitude transfer, and also mitigating the mutual interference caused by the coupling of the two channels under parallel control.

The heading change of the fixed-wing vehicle is primarily driven by the lateral lift force generated by the roll angle, considering that the direct control of the roll angle for heading tracking is liable to lead to the instability of the heading correction due to inertia or external perturbation, this paper introduces the strategy of hierarchical control, designing a roll-channel control method that first maps the heading error to a target roll angle and then maps the roll angle error to a target roll rate, which forms a reward function, as shown in Equation (8). By replacing ${\mathit{R}}^{\mathit{r}}$ in Equation (6) with Equation (8), while incorporating angular rate feedback as a damping term into the mapping function and omitting the logarithmic component from the mapping function, the controller can ensure the accuracy of heading tracking through the outer loop roll angle control, can ensure the stability and response speed of the roll control through the inner loop angular rate control, and can also mitigate the overshoot of the heading adjustment due to the control of the high frequency, so as to realize a better heading control.

$$\left\{\begin{array}{l}{\mathit{R}}^{\mathit{R}\mathit{S}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})={\mathit{e}}^{-{({\omega }_{\varphi ,\mathit{t}}-{\omega }_{\varphi ,\mathit{t}}^{\ast }/{\omega }_{\varphi ,\mathit{t}\mathit{s}\mathit{c}\mathit{a}\mathit{l}\mathit{e}})}^2}\hfill \\ {\varphi }_{\mathit{t}}^{\ast }=0.35{\delta }_{\psi ,\mathit{t}}+0.1{\stackrel{·}{\delta }}_{\psi ,\mathit{t}}\hfill \\ {\omega }_{\varphi ,\mathit{t}}^{\ast }=0.15{\varphi }_{\mathit{t}}^{\ast }\hfill \\ \left|{\varphi }_{\mathit{t}}^{\ast }\right|<60° \left|{\omega }_{\varphi ,\mathit{t}}^{\ast }\right|<10°/\mathrm{s}\hfill \end{array}\right.$$

(8)

With the roll smoothing reward, the aircraft no longer uses zero roll as the maximum reward angle, but adjusts the target angle based on the yaw angle tracking error, which not only takes into account the stabilization of the heading angle, but avoids the anomaly of the roll angle due to the interference of other channels through the constraint.

To summarize, the vehicle cruise control model contains the trajectory tracking reward function ${\mathit{R}}^{\mathit{T}\mathit{T}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})$, and the constrained reward functions ${\mathit{R}}^{\mathit{P}\mathit{S}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})$ and ${\mathit{R}}^{\mathit{R}\mathit{S}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})$. The total reward function is established, as shown below:

$$\mathit{R}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})={\mathit{R}}^{\mathit{T}\mathit{T}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}}){\mathit{R}}^{\mathit{P}\mathit{S}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}}){\mathit{R}}^{\mathit{R}\mathit{S}}({\mathit{s}}_{\mathit{t}},{\mathit{a}}_{\mathit{t}})$$

(9)

With the reward function set in Equation (9), the control model will take into account the trajectory tracking accuracy as well as the constraints of pitch and roll angles in order to maximize the reward during training, it will avoid the loss of reward due to the drastic dynamics, and ultimately obtain a good weight of the policy network.

4. Simulation Training of Cruise Control Model Strategy Network

After completing the design of the control model structure and the strategy network reward function, it is necessary to obtain the strategy network weight parameters through simulation training. For this reason, this paper builds the JSBSim-based simulation conditions and models the Cessna 172P vehicle. JSBSim is a Flight Dynamics Model (FDM) simulation engine, featuring precise Earth and atmospheric environment models. It can precisely model aircraft through mathematical and physical models, and build motion models to simulate motion under various control mechanisms and natural forces.

According to the common operating range of the vehicle, this paper sets the parameters, as shown in

Table 1. Initial state sampling range of the aircraft.

Aircraft State	Sampling Range	Units of State
${\psi }_0$	[0, 180]	°
${\nu }_0$	[40, 50]	m/s
${\mathit{h}}_0$	[450, 1050]	m

, acquires the initial state of the vehicle by random sampling, and uses the initial state as the target state for simulation training of trajectory tracking. It should be added that the initial roll ${\varphi }_0$, pitch ${\theta }_0$, and angular velocity ${\omega }_0$ of the vehicle are set to zero, and the oil–mix ratio of the engine is set to 0.9.

During a cruise that can last up to 600 s, this paper checks whether the aircraft completes tracking the current target state at 30-s intervals. If the aircraft completes the tracking of the current state, the target is reset, as in Equation (10), for a new round of state tracking and reward accumulation; if the tracking fails, the state and target of the aircraft are re-initialized for a new round of tracking. With this design, the cruise control model is able to gradually learn the tracking ability of the attitude and the transition ability of the attitude.

$${\psi }_{\mathit{n}\mathit{e}\mathit{w}}={\eta }_{\psi }\ast \mathrm{\Delta }\psi , {\mathit{H}}_{\mathit{n}\mathit{e}\mathit{w}}={\eta }_{\mathit{H}}\ast \mathrm{\Delta }\mathit{H}, {\nu }_{\mathit{n}\mathit{e}\mathit{w}}={\eta }_{\nu }\ast \mathrm{\Delta }\nu$$

(10)

where ${\eta }_{\psi },{\eta }_{\mathit{h}},{\eta }_{\mathit{v}}\in [0,1]$ is the scaling factor randomly generated by the algorithm and $\mathrm{\Delta }\psi =180°,$ $\mathrm{\Delta }\mathit{H}=100 \mathrm{m},$ $\mathrm{\Delta }\nu =10 \mathrm{m}/\mathrm{s}$ is the maximum change value of the target state in the new round.

In order to accelerate model convergence, this paper utilizes a course learning approach to train the model in steps. Firstly, let ${\mathit{B}}^{\psi }=2°$ in Equation (6) to enhance the range of the model that can be explored to the reward, so that the model can quickly realize the end-to-end control strategy, thereby obtaining a pre-train model. Next, ${\mathit{B}}^{\psi }=0.5°$ in Equation (6) is made to perform a second training to improve the heading tracking accuracy. Finally, the rewards (7) and (8) are added to optimize the parameters of the strategy network to enhance the dynamic control performance of the vehicle, and finally the cruise control model of the vehicle based on the optimization of proximal strategy under nonlinear attitude constraints is obtained.

5. Experimental Results and Analysis

In order to verify the advantages of the model improvement, based on the JSBSim simulation conditions and the Cessna 172P vehicle model, this paper designs three sets of experiments for straight-line climb, descent, and hexagonal trajectory tracking, respectively, to validate the control model’s steady state result accuracy, dynamic control stability, and rapidity, respectively.

5.1. Straight Line Climb and Descent Experiments

In order to verify the stability of the attitude control of the algorithm in the process of altitude change, this paper sets up two groups of experiments for straight line climb and descent, respectively, and trains two groups of control models based on whether or not they contain the dynamic constraints rewarding ${\mathit{R}}^{\mathit{P}\mathit{S}}$ and ${\mathit{R}}^{\mathit{R}\mathit{S}}$ to compare the effectiveness of the attitude constraints.

The initial heading, pitch, and roll angles of the vehicle are all set to 0°, the speed is 50 m/s, the initial altitude is 600 m, and it climbs and descends several times in accordance with the altitude change of 30 m for every 30 s interval. The, we record the vehicle’s heading holding error, altitude, pitch, and roll status, and plot the cruise control results of the two models, as shown in Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13:

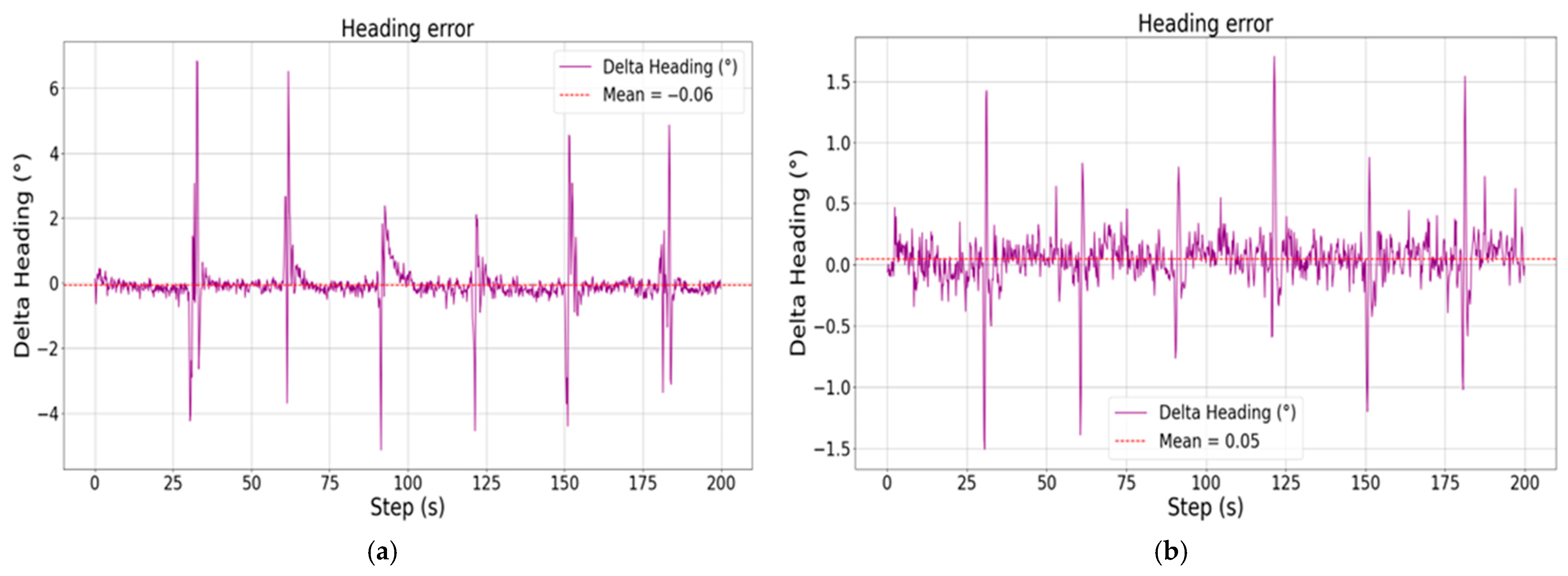
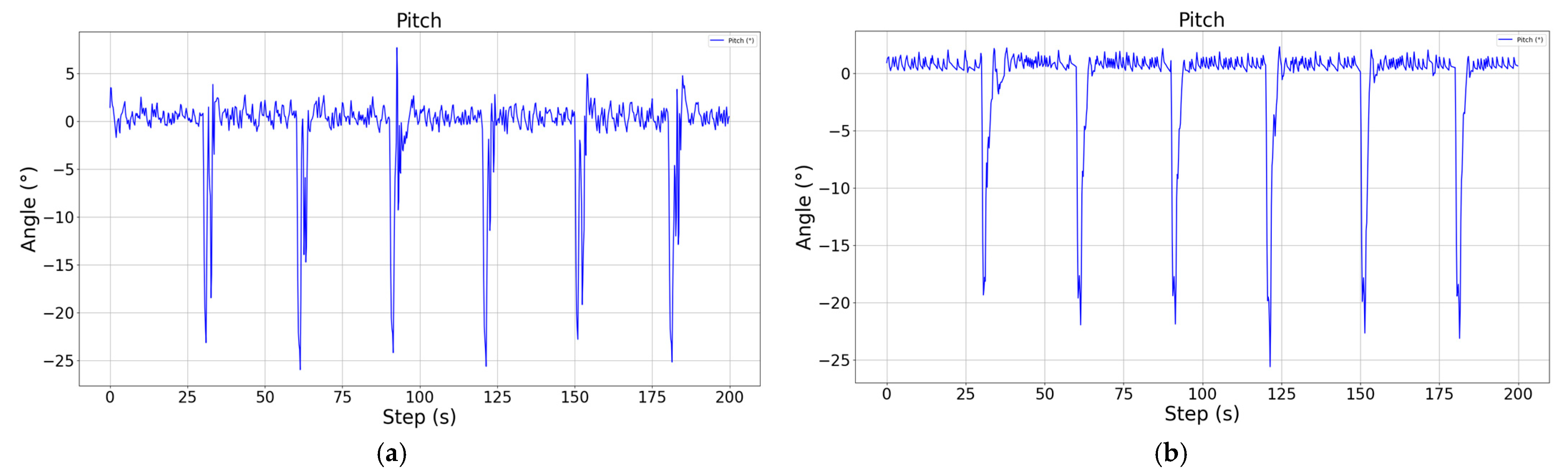
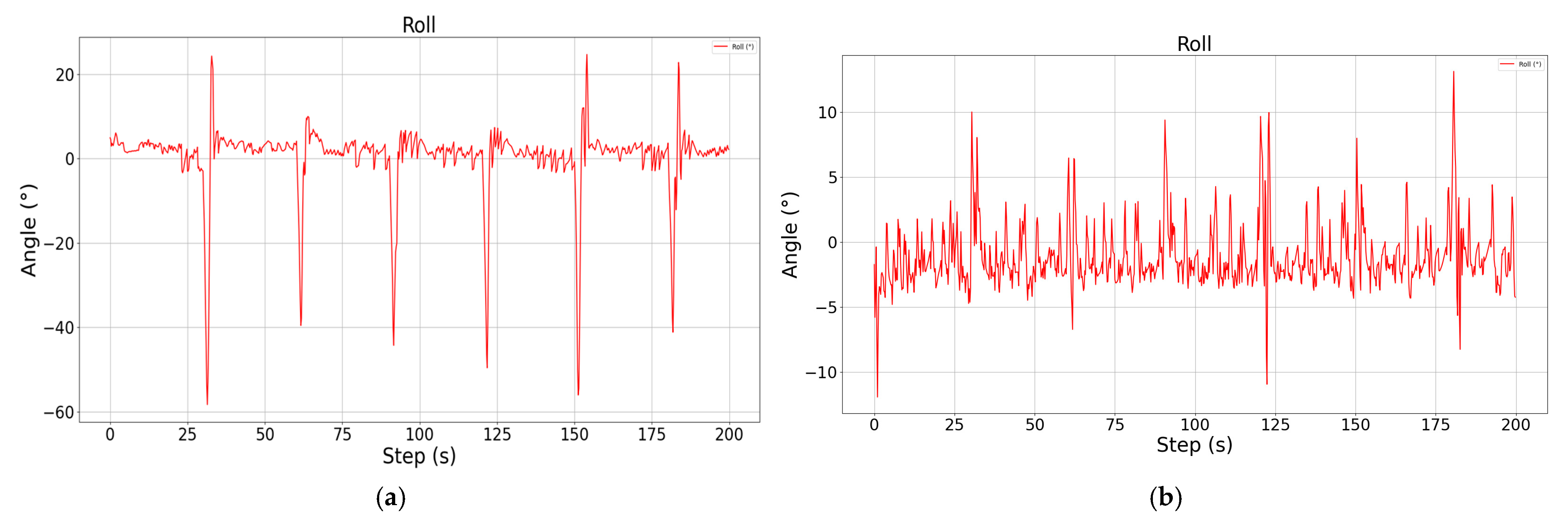
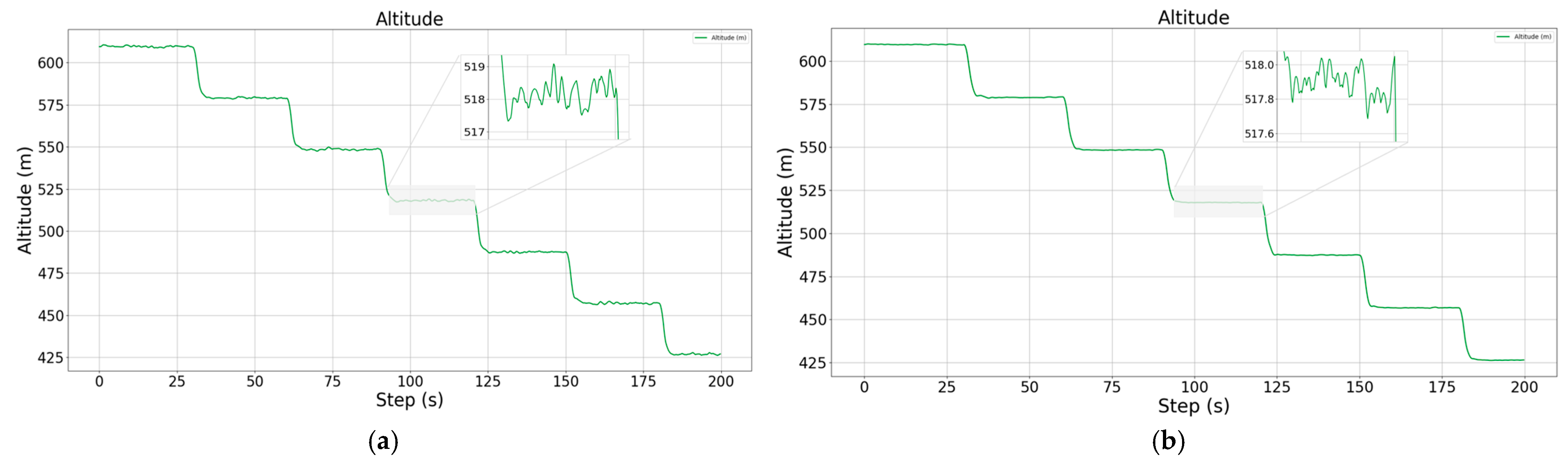
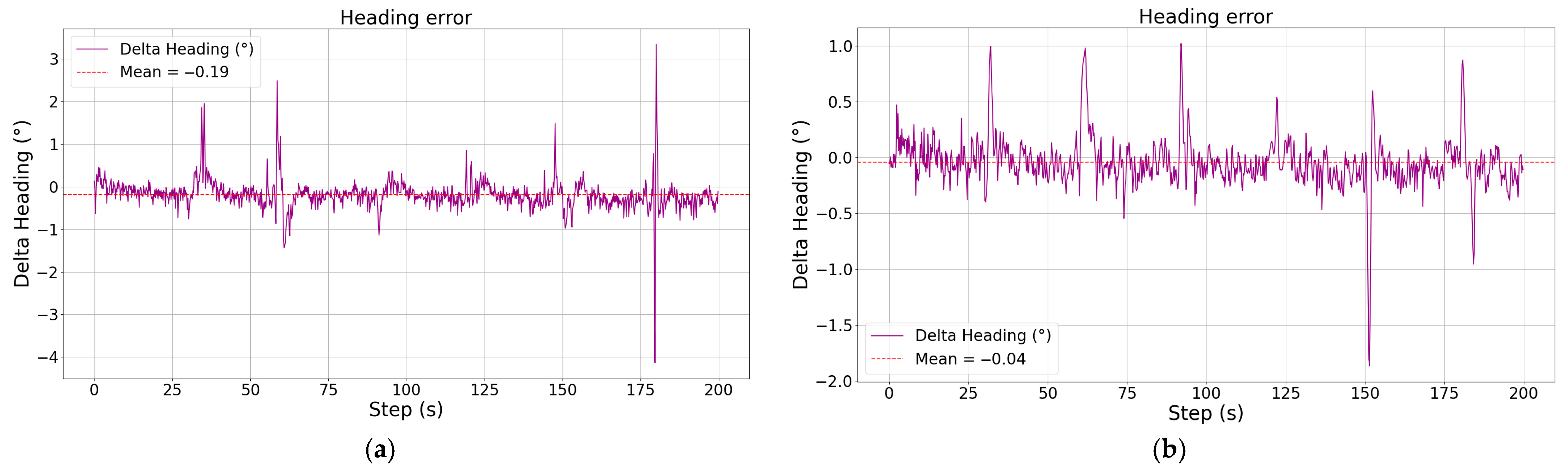
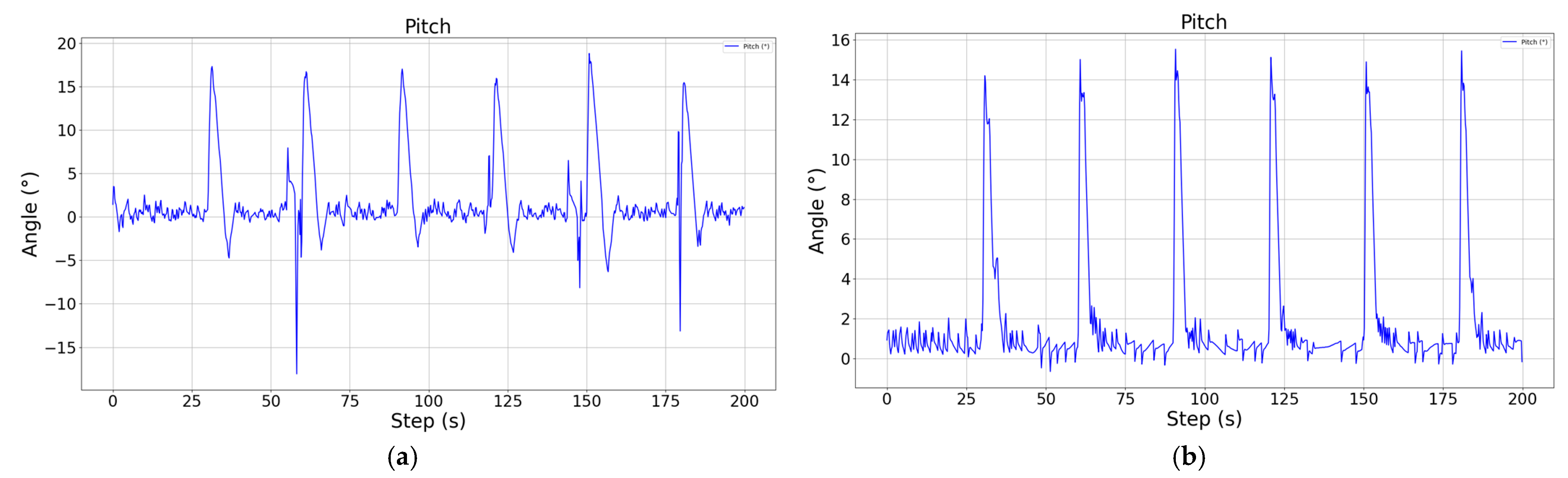
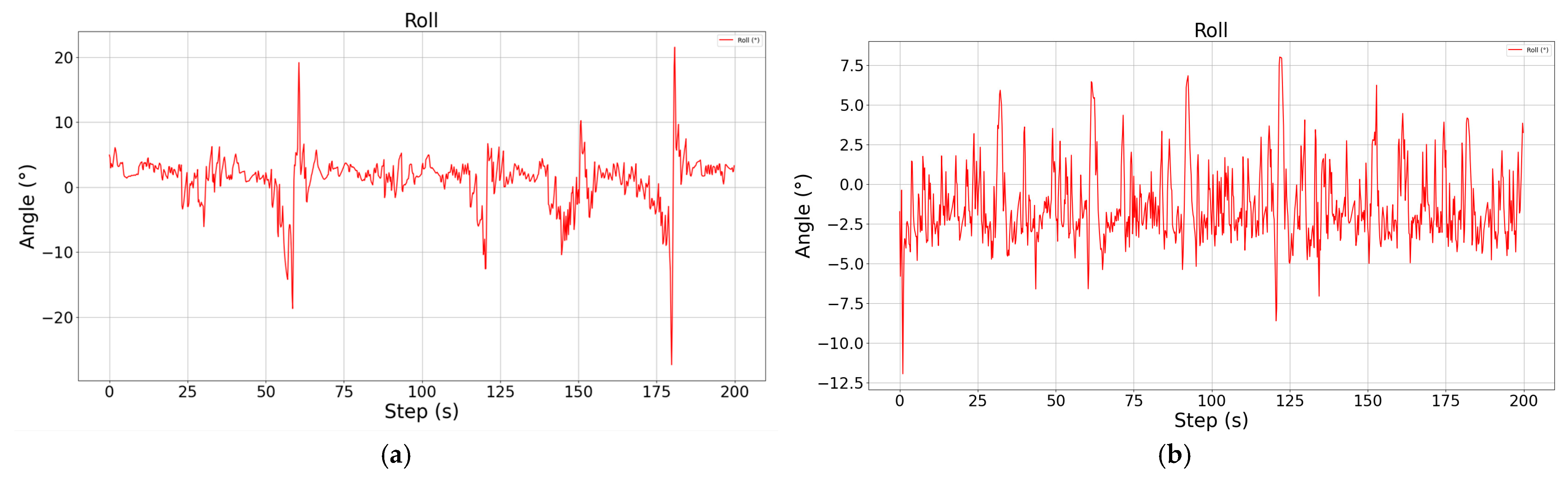
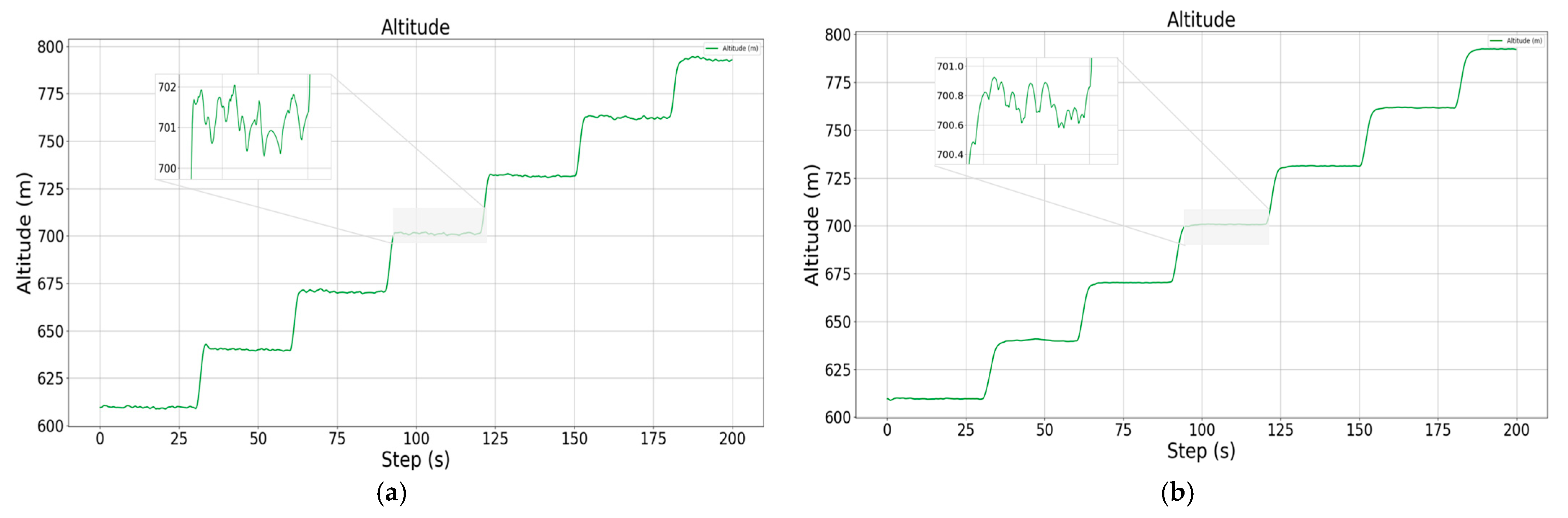
It can be found through comparison that the improved cruise control model significantly improves the adjustment speed of the altitude and pitch angle by means of parallel control, and not only realizes the smooth and stable control of the pitch angle, but reduces the steady state error of the altitude by nearly 1.5 m, reaching a steady state error level of less than 0.4 m. As for the roll channel with added constraints, although there are some irregular oscillations during the climbing and descending process, the offset of the heading angle can be basically controlled within 1.5° compared to the unconstrained case, and the trajectory tracking accuracy is higher.

Figure 7. Schematic diagram of heading deviation during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 7. Schematic diagram of heading deviation during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 8. Schematic diagram of pitch angle during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 8. Schematic diagram of pitch angle during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 9. Schematic diagram of roll angle during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 9. Schematic diagram of roll angle during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 10. Schematic diagram of altitude change during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 10. Schematic diagram of altitude change during descent, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

During the descent, the control of altitude is more accurate and smooth under the attitude constraint, and the steady state error is also within 0.4 m, while the roll angle constraint plays a greater role, and the yaw angle deviation is reduced by more than 4°. It should be noted that there is always a sudden and large change in the roll angle during the altitude change process, which is because the speed is greatly affected during the altitude change process, and the vehicle adjusts the engine power in order to maintain the speed stability, resulting in a sudden change in the propeller torque, and the vehicle is out of the leveling state, even though the vehicle is able to re-level quickly, it still has a certain effect on the yaw angle of the vehicle. Although the vehicle can be re-leveled quickly, the yaw angle of the vehicle is still affected to a certain extent.

5.2. Hexagonal Trajectory Tracking Experiment

In order to have a more intuitive verification of the performance and practicability of the cruise control algorithm, this paper designs a hexagonal trajectory tracking simulation experiment. The experiment uses an equirectangular projection map to plan the trajectory, and after initialization in accordance with the way in experiment A, first cruise along the north direction, and then turn right by 60° in turn to complete the tracking of the hexagonal trajectory. The side length of the hexagonal trajectory is set to 6 km, and waypoints are set at 3 km intervals. During the tracking process, this paper defines the target heading as the bearing of the line between the current position and the position of the next waypoint, and updates the next waypoint as the new target waypoint when it is 300 m away from the next waypoint, so as to capture the complete trajectory. The information, such as heading deviation and altitude of the vehicle during the recorded cruise, is plotted as follows:

Figure 11. Schematic diagram of the altitude change during the tracking of the hexagonal trajectory, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 11. Schematic diagram of the altitude change during the tracking of the hexagonal trajectory, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

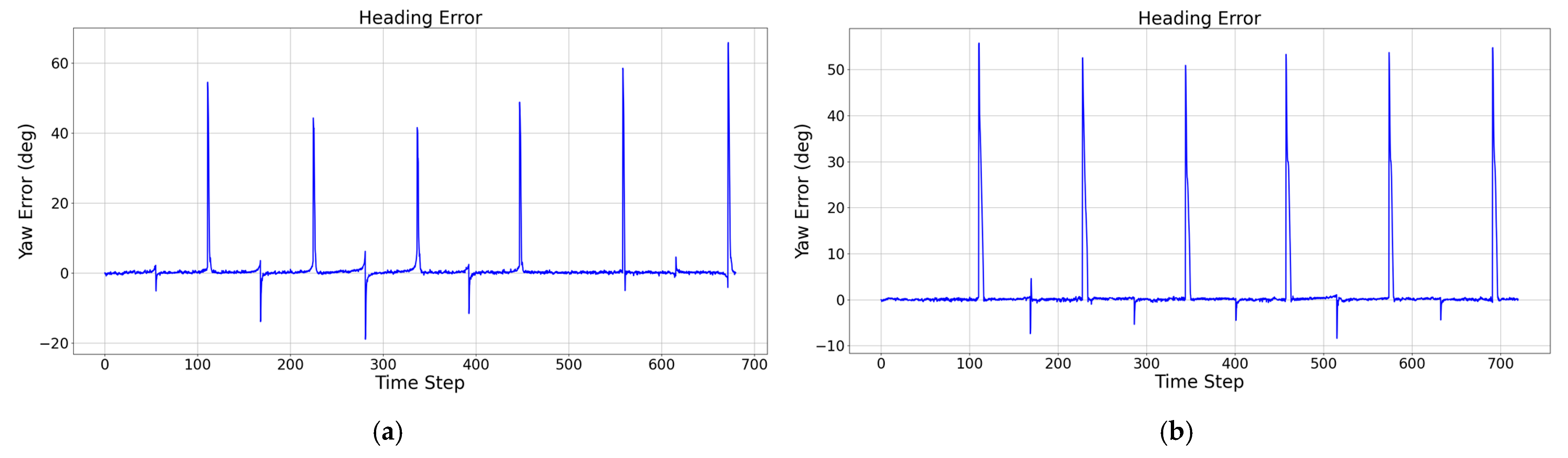
Figure 12. Schematic diagram of the yaw angle during the tracking of the hexagonal trajectory, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 12. Schematic diagram of the yaw angle during the tracking of the hexagonal trajectory, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

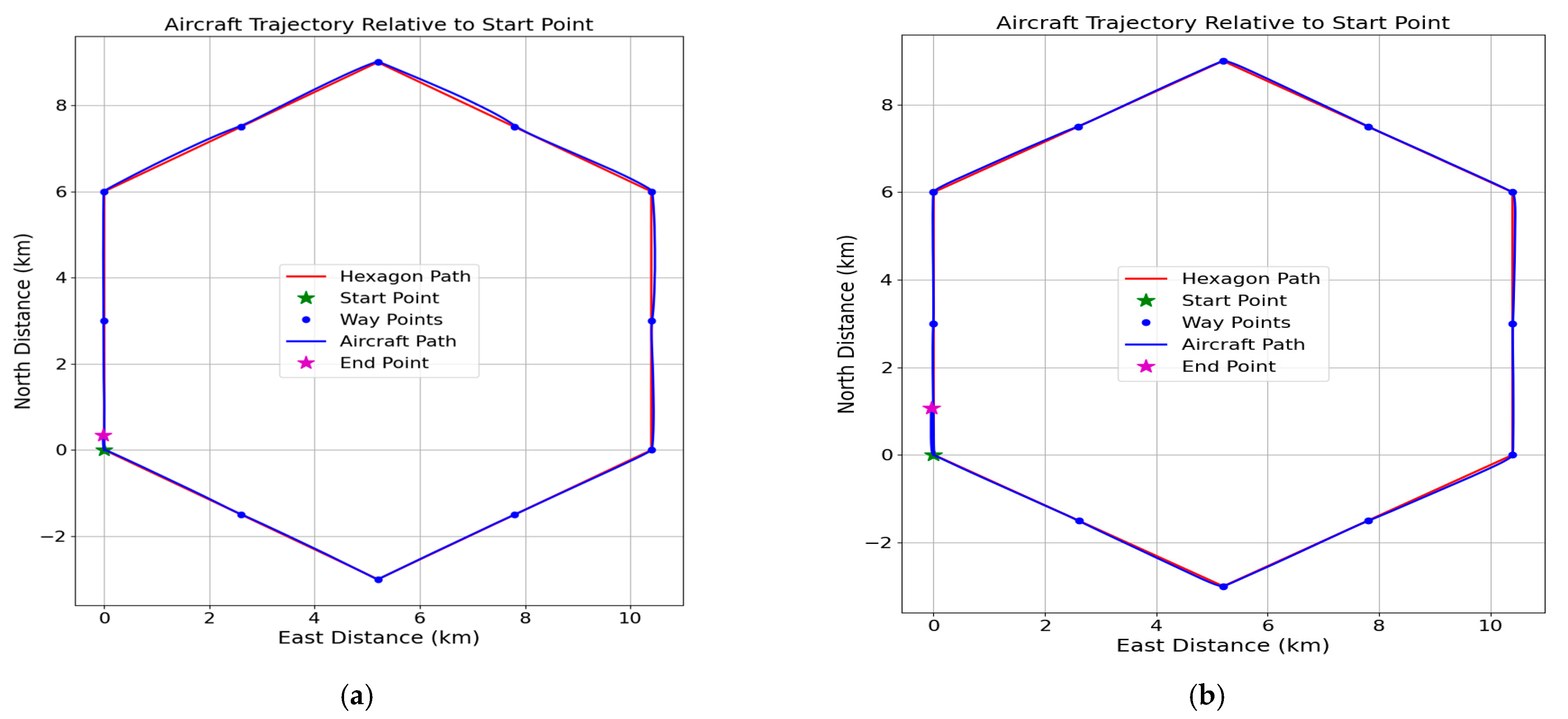
Figure 13. Schematic diagram of hexagonal trajectory tracking results, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

Figure 13. Schematic diagram of hexagonal trajectory tracking results, showing the control results without attitude constraints (a) and with attitude constraints (b), respectively.

When the target heading changes, because the aircraft generates a roll angle, the lift force decreases in the direction of gravity, and the aircraft makes a pull-up maneuver accordingly to increase the angle of attack and to overcome the decrease in altitude. Because the process is more complex and short in duration, it is difficult for the reinforcement learning algorithm to pay attention to and learn the control strategy with predictability during the training process, so the altitude channel of the aircraft will have a certain amplitude of shock response when the waypoint changes but, under pitch attitude constraints, the vehicle’s response to altitude changes and regulation speed is better, the altitude is maintained more stably, and the peak of deviation is more stable with respect to the deviation peak, which is reduced by nearly 3 m relative to the cruise control results under an unconstrained attitude.

In terms of trajectory tracking, the cruise control model under attitude constraints is more accurate than that without constraints, and can not only adjust to the target state at a stable speed during the course adjustment, but can maintain stable tracking, and the trajectory with the target trajectory can be better overlapped without deviation from the trajectory.

6. Conclusions

In this paper, the composite network structure is constructed based on the approximate strategy optimization method, the trajectory tracking reward function containing attitude constraints is designed, and the precise control method of vehicle cruise based on approximate strategy optimization under nonlinear attitude constraints is proposed, which improves the control stability in the transient phase of the vehicle control and achieves a smoother attitude control while guaranteeing the end-to-end cruise control accuracy. The experimental results show that the vehicle control method under attitude constraints is able to control the peak heading deviation within 1.5° by attitude constraints during straight-line climb and descent, and reduce the overshoot of the altitude channel to reduce the steady-state error of altitude control to within 0.4 m. Therefore, the precise control method of vehicle cruise based on approximate strategy optimization under nonlinear attitude constraints can autonomously adjust the actuator for maneuvering under various conditions, complete the rapid capture and stable tracking of cruise trajectory, and achieve smooth, safe, and precise trajectory tracking, which is of great significance for the practical application of reinforcement learning algorithms on large vehicles.