Visual Active SLAM Method Considering Measurement and State Uncertainty for Space Exploration
Abstract
1. Introduction
- The perception-aware planning method makes full use of Fisher Information Matrix (FIM) and the uncertainty quantification metric for measurement information selection and path planning to improve MAV localization performance.
- The Cramér–Rao Lower Bound (CRLB) of the pose uncertainty in the stereo SLAM system is derived to describe the boundary of the pose uncertainty.
- The visual odometry information selection method and local bundle adjustment information selection method considering measurement uncertainty are proposed to improve the computational efficiency in both the front-end and back-end of the system.
- The generalized unary node and generalized unary edge are defined to quantify local state uncertainty and to improve the computational efficiency in computing local state uncertainty. Further, the perception-aware active loop closing planning method considering local state uncertainty is proposed for MAV space exploration and decision-making, which is beneficial to improving MAV localization performance.
2. Related Work
3. Uncertainty in Visual SLAM
3.1. Graph Optimization Theory in Visual SLAM
3.2. Cramér–Rao Lower Bound and Fisher Information Matrix
3.3. Cramér–Rao Lower Bound of Uncertainty for Visual SLAM with Stereo Camera
3.4. Optimality Criteria
4. Method
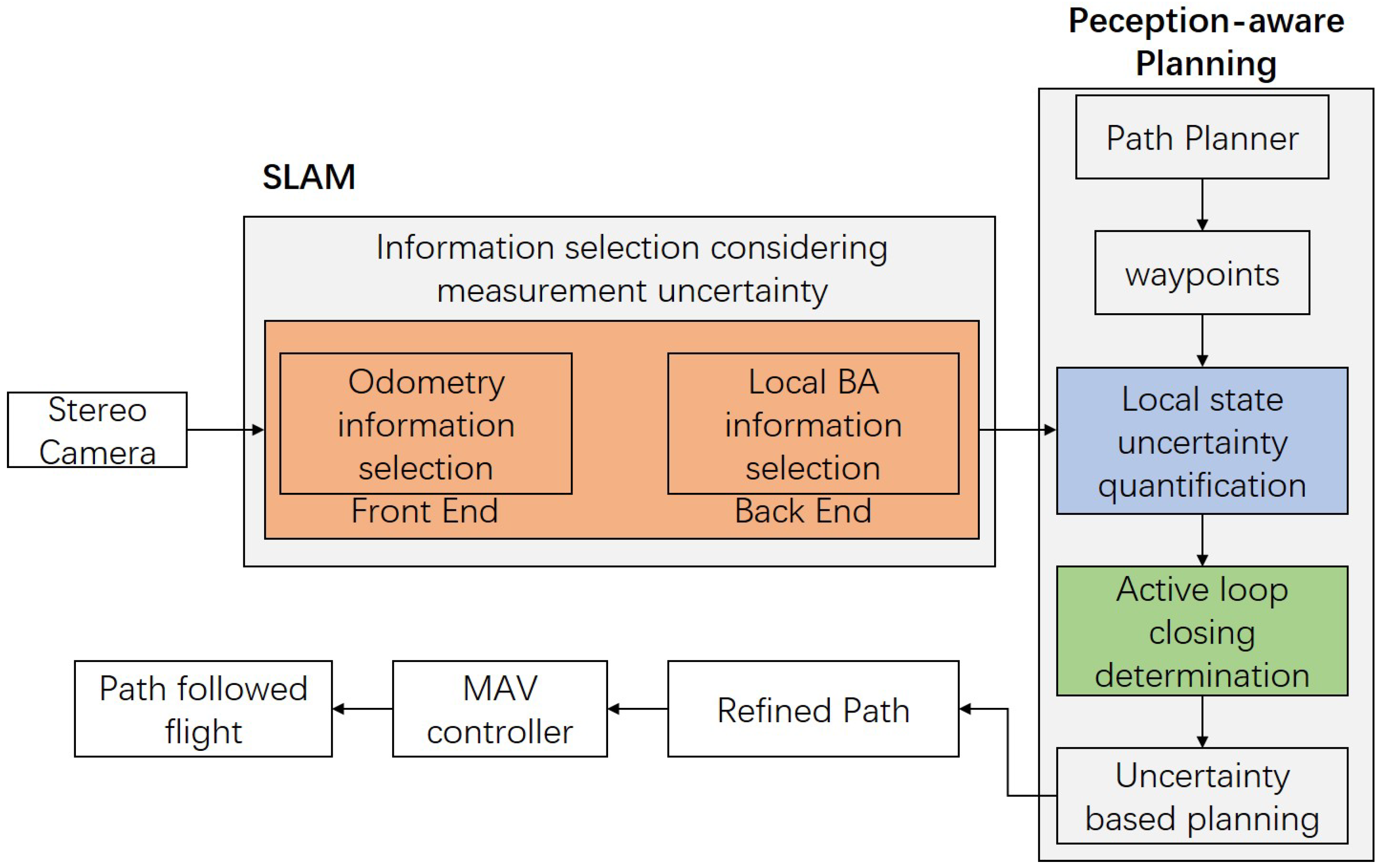
4.1. System Overview
4.2. Information Selection Considering Measurement Uncertainty
4.2.1. Odometry Information Selection Considering Measurement Uncertainty
| Algorithm 1 odometry information selection algorithm considering measurement uncertainty |
|
4.2.2. Local BA Information Selection Considering Measurement Uncertainty
| Algorithm 2 local BA information selection algorithm considering measurement uncertainty |
|
4.3. Perception-Aware Active Loop Closing Planning Considering Local State Uncertainty
4.3.1. Definition of Generalized Unary Node and Generalized Unary Edge in Local BA
4.3.2. Uncertainty Representation of Local States
4.3.3. Active Loop Closing Strategy Considering Local State Uncertainty
| Algorithm 3 Active loop closing planning algorithm considering local state uncertainty |
|
5. Results and Analysis
5.1. Experimental Settings and Sensors Configuration
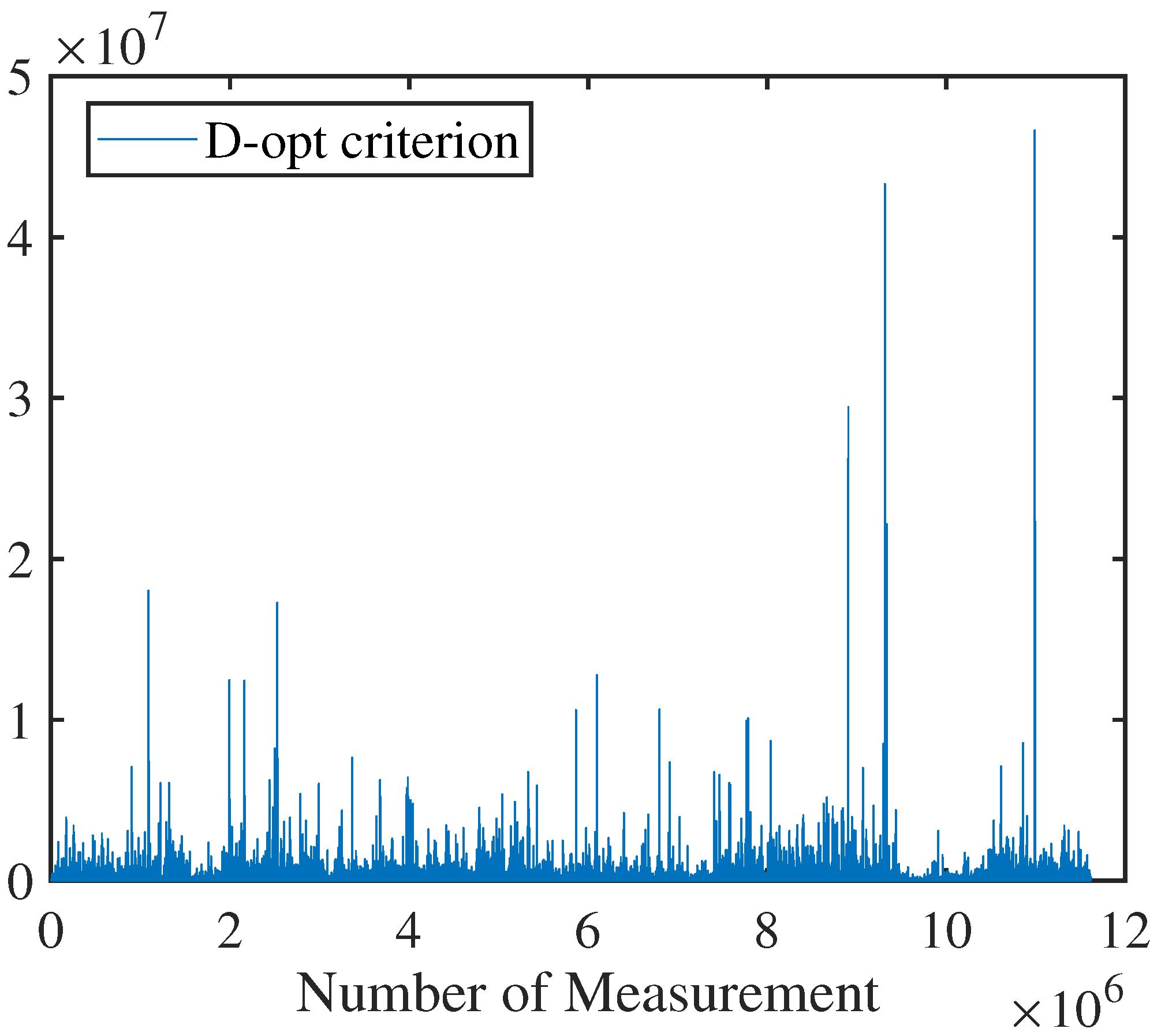
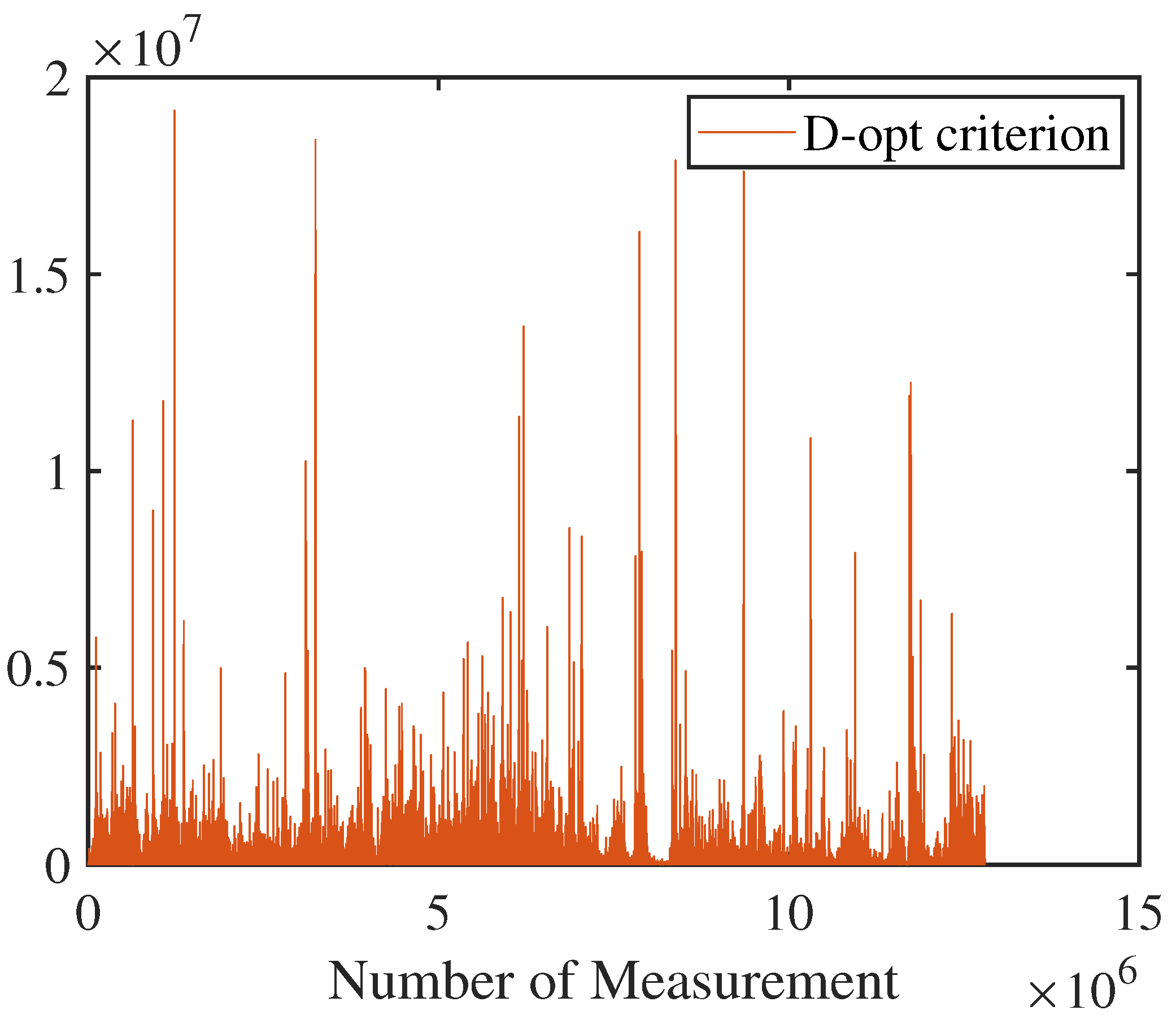
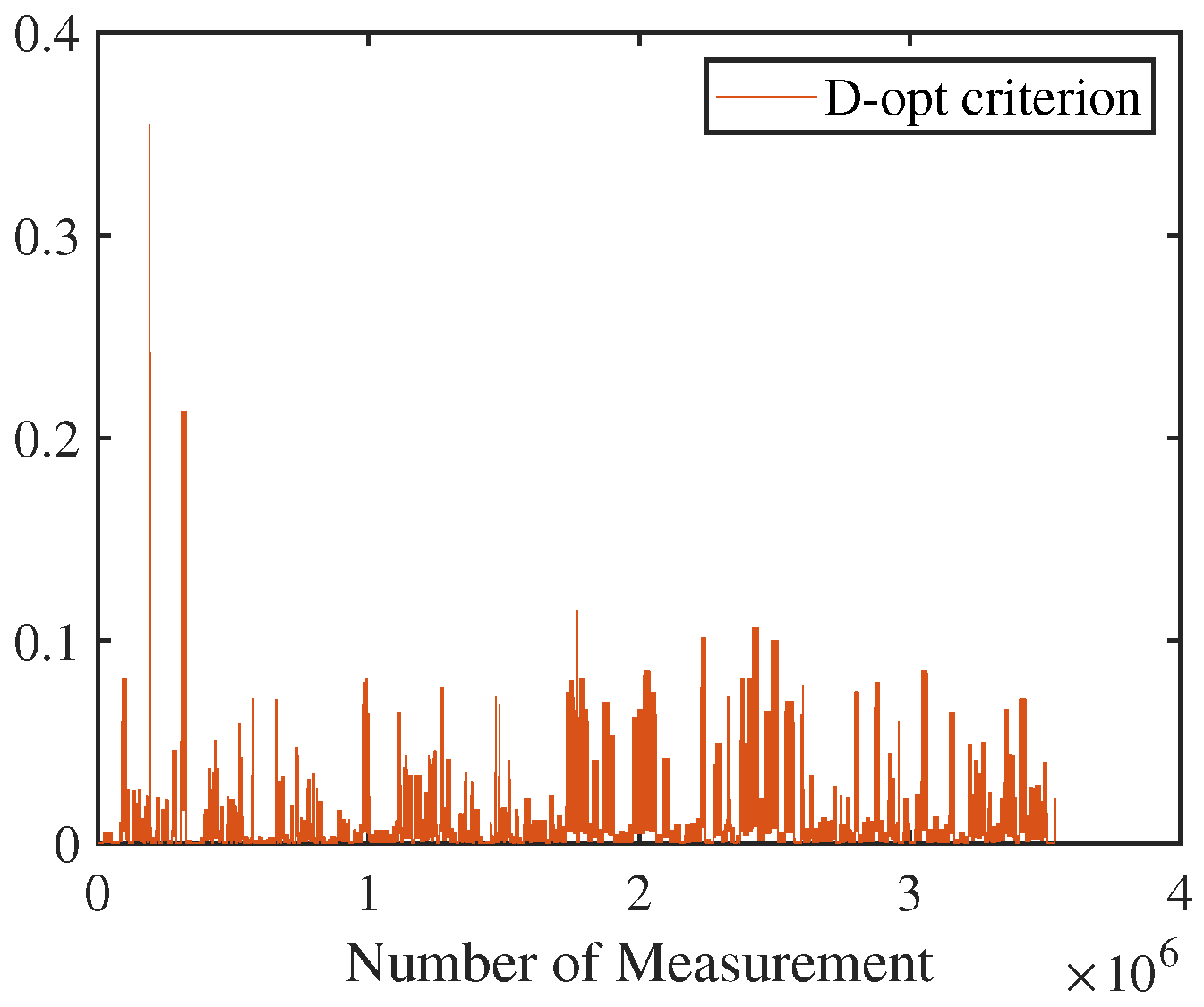
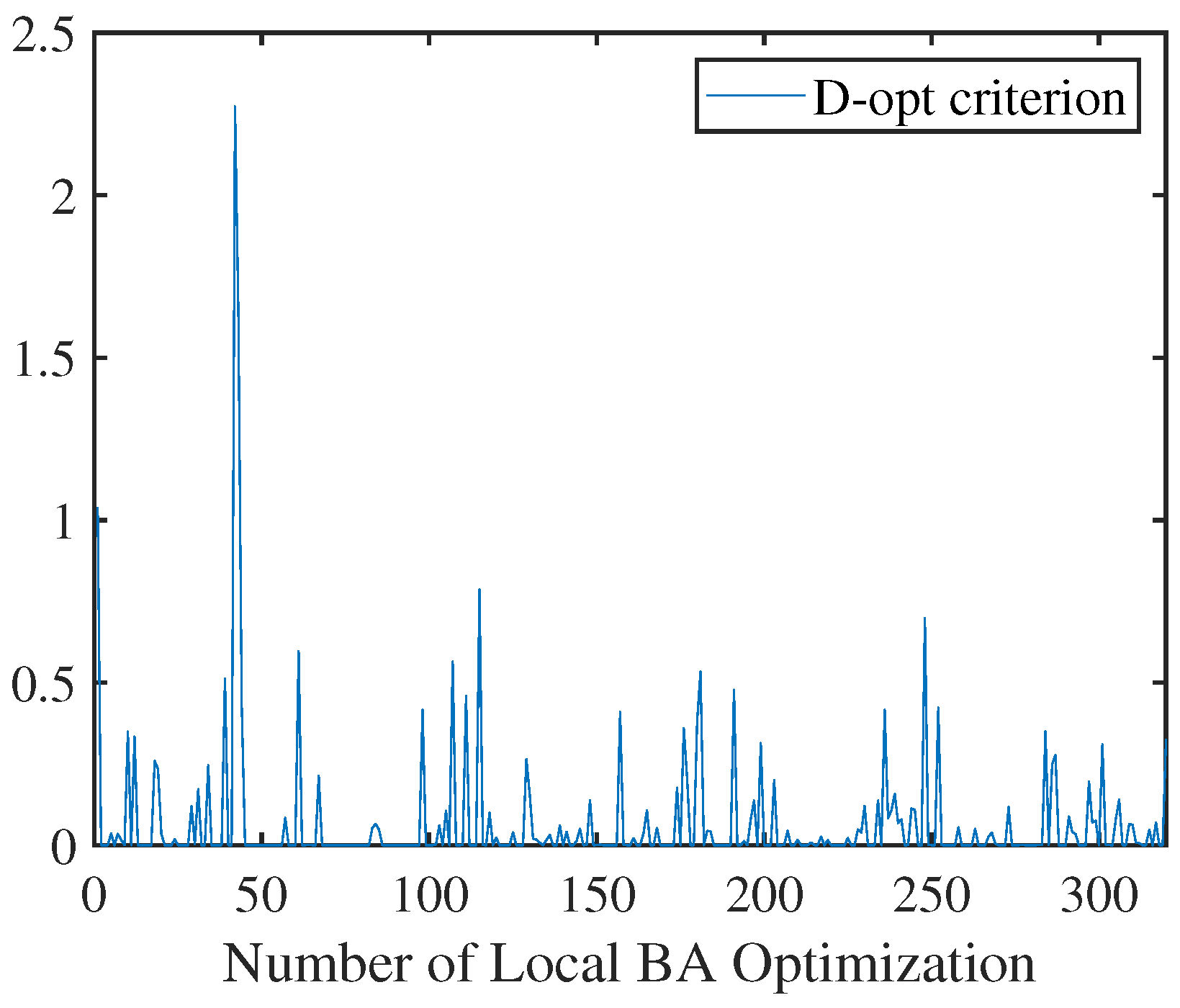
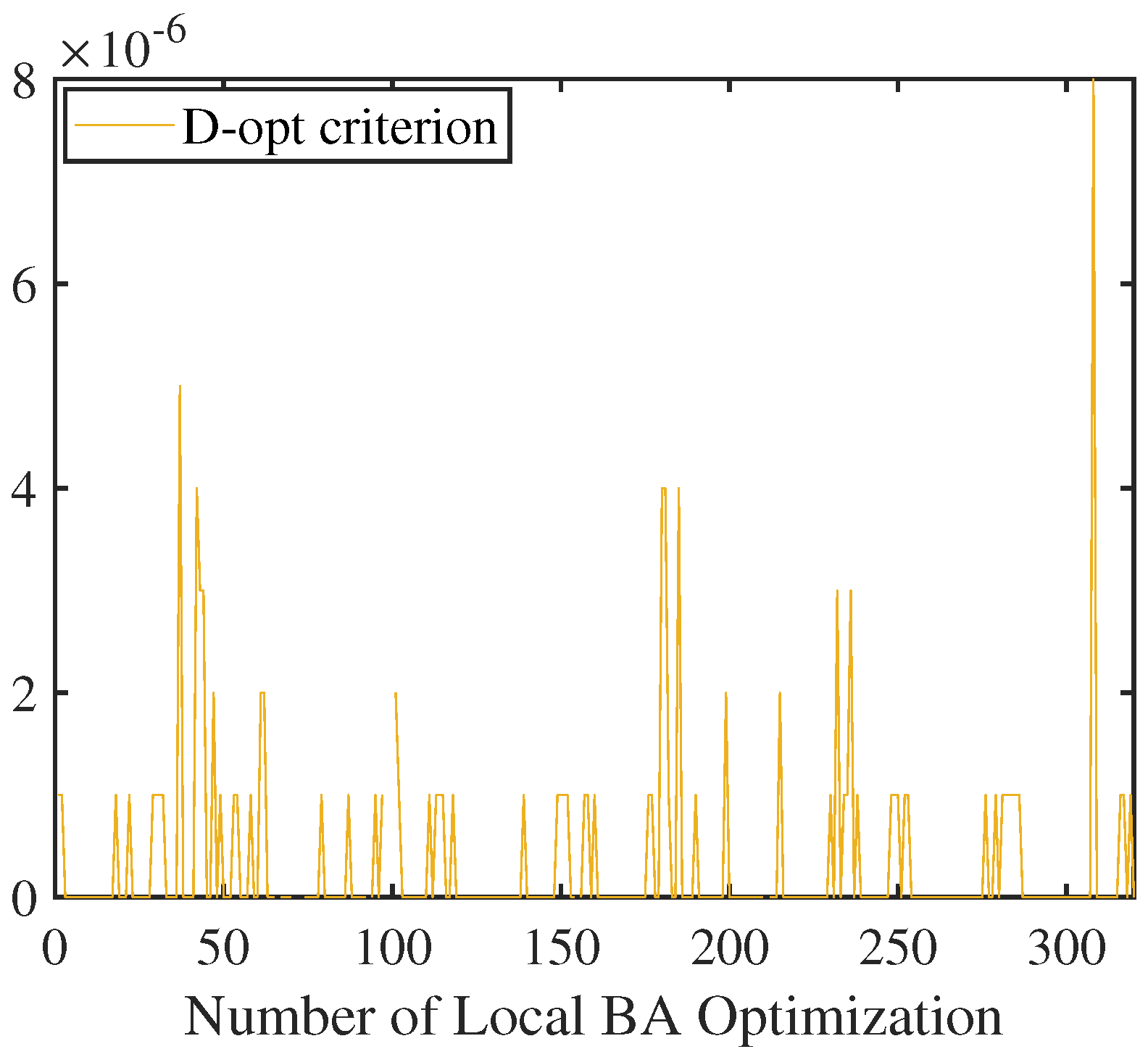
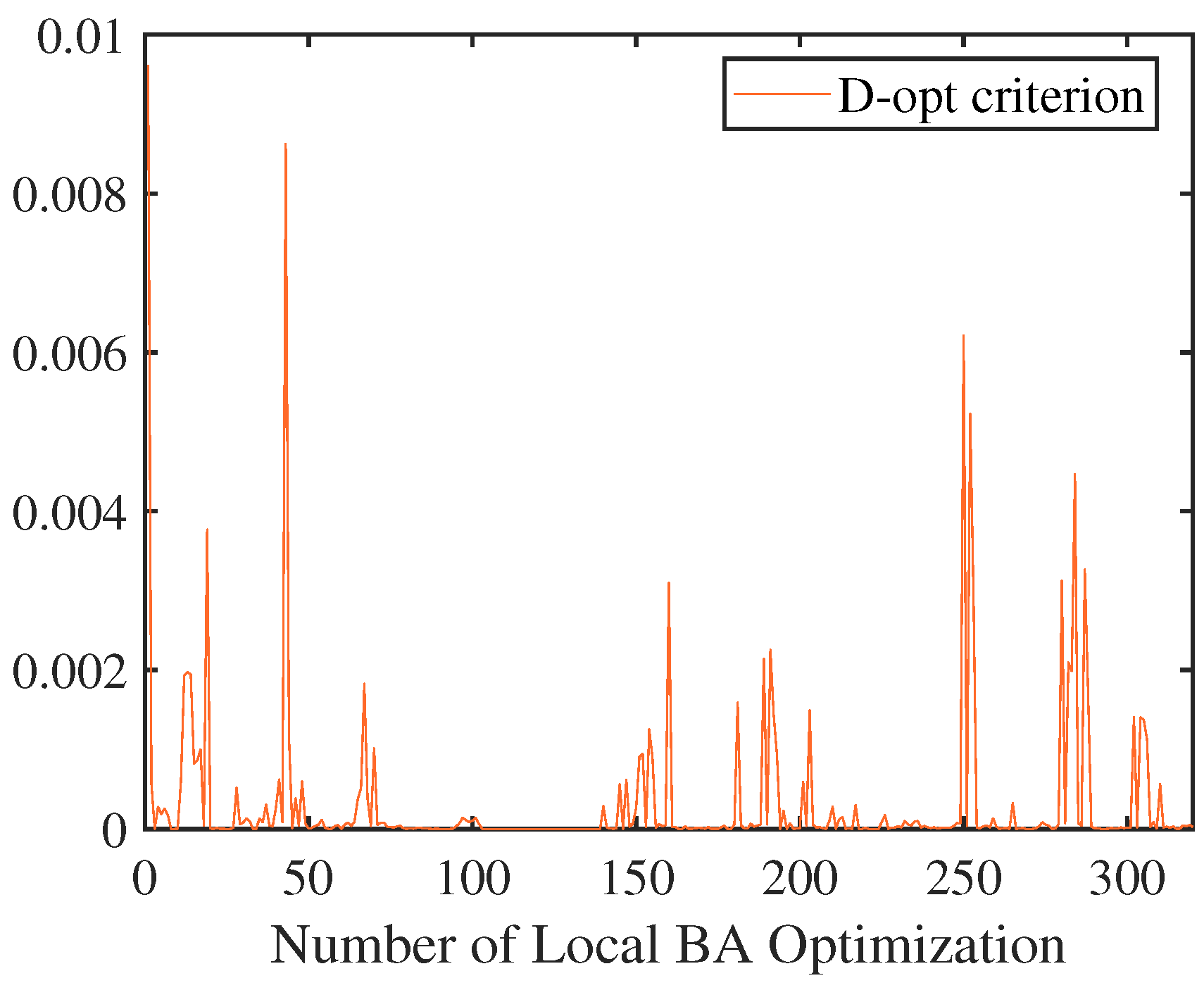
5.2. Results for Information Selection Considering Measurement Uncertainty
5.2.1. Visual Odometry Measurement Information Selection
5.2.2. Local BA Measurement Information Selection
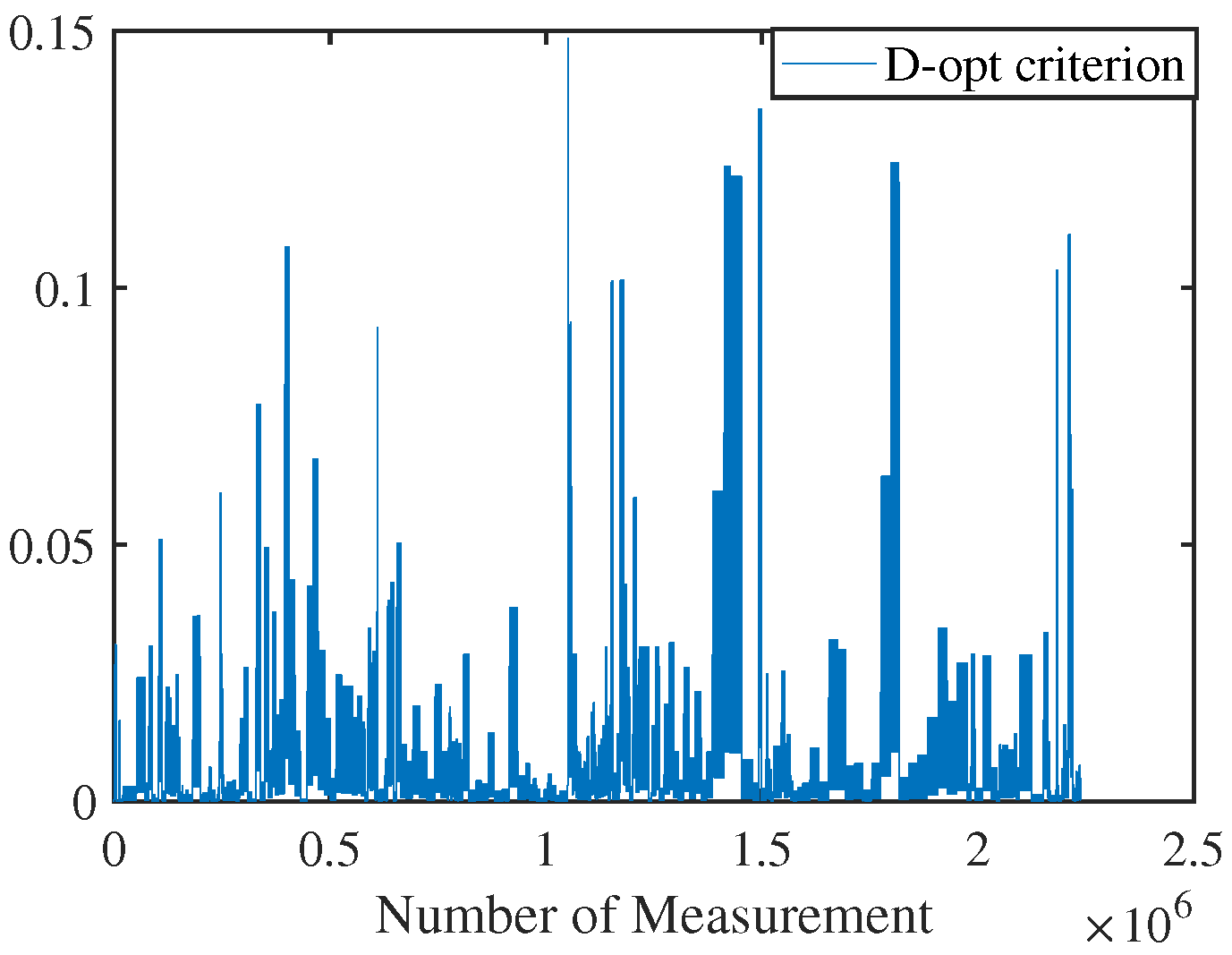
5.3. Results for Active Loop Closing Planning Considering Local State Uncertainty
5.4. Field Tests
5.5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Zheng, S.; Lin, X.; Zhu, F. Improving RGB-D SLAM accuracy in dynamic environments based on semantic and geometric constraints. Measurement 2023, 217, 113084. [Google Scholar] [CrossRef]
- Niroui, F.; Zhang, K.; Kashino, Z.; Nejat, G. Deep reinforcement learning robot for search and rescue applications: Exploration in unknown cluttered environments. IEEE Robot. Autom. Lett. 2019, 4, 610–617. [Google Scholar] [CrossRef]
- Xia, L.; Meng, D.; Zhang, J.; Zhang, D.; Hu, Z. Visual-Inertial Simultaneous Localization and Mapping: Dynamically Fused Point-Line Feature Extraction and Engineered Robotic Applications. IEEE Trans. Instrum. Meas. 2022, 71, 5019211. [Google Scholar] [CrossRef]
- Li, J.; Zhao, J.; Kang, Y.; He, X.; Ye, C.; Sun, L. Dl-slam: Direct 2.5 d lidar slam for autonomous driving. In Proceedings of the 2019 IEEE Intelligent Vehicles Symposium (IV), Paris, France, 9–12 June 2019; pp. 1205–1210. [Google Scholar]
- Cheng, J.; Zhang, L.; Chen, Q.; Hu, X.; Cai, J. Map aided visual-inertial fusion localization method for autonomous driving vehicles. Measurement 2023, 221, 113432. [Google Scholar] [CrossRef]
- Zhang, D.; Shen, Y.; Lu, J.; Jiang, Q.; Zhao, C.; Miao, Y. IPR-VINS: Real-time monocular visual-inertial SLAM with implicit plane optimization. Measurement 2024, 226, 114099. [Google Scholar] [CrossRef]
- Jacobson, A.; Zeng, F.; Smith, D.; Boswell, N.; Peynot, T.; Milford, M. Semi-supervised slam: Leveraging low-cost sensors on underground autonomous vehicles for position tracking. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 3970–3977. [Google Scholar]
- Chen, Y.; Huang, S.; Fitch, R. Active SLAM for mobile robots with area coverage and obstacle avoidance. IEEE/Asme Trans. Mechatronics 2020, 25, 1182–1192. [Google Scholar] [CrossRef]
- Norbelt, M.; Luo, X.; Sun, J.; Claude, U. UAV Localization in Urban Area Mobility Environment Based on Monocular VSLAM with Deep Learning. Drones 2025, 9, 171. [Google Scholar] [CrossRef]
- Zhou, B.; Li, C.; Chen, S.; Xie, D.; Yu, M.; Li, Q. ASL-SLAM: A LiDAR SLAM with Activity Semantics-Based Loop Closure. IEEE Sens. J. 2023, 23, 13499–13510. [Google Scholar] [CrossRef]
- Kim, D.; Lee, B.; Sung, S. Design and Verification of Observability-Driven Autonomous Vehicle Exploration Using LiDAR SLAM. Aerospace 2024, 11, 120. [Google Scholar] [CrossRef]
- Feder, H.J.S.; Leonard, J.J.; Smith, C.M. Adaptive mobile robot navigation and mapping. Int. J. Robot. Res. 1999, 18, 650–668. [Google Scholar] [CrossRef]
- Carrillo, H.; Reid, I.; Castellanos, J.A. On the comparison of uncertainty criteria for active SLAM. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St Paul, MN, USA, 14–18 May 2012; pp. 2080–2087. [Google Scholar]
- Bonetto, E.; Goldschmid, P.; Pabst, M.; Black, M.J.; Ahmad, A. iRotate: Active visual SLAM for omnidirectional robots. Robot. Auton. Syst. 2022, 154, 104102. [Google Scholar] [CrossRef]
- Rodríguez-Arévalo, M.L.; Neira, J.; Castellanos, J.A. On the importance of uncertainty representation in active SLAM. IEEE Trans. Robot. 2018, 34, 829–834. [Google Scholar] [CrossRef]
- Placed, J.A.; Castellanos, J.A. Fast Autonomous Robotic Exploration Using the Underlying Graph Structure. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 September–1 October 2021; pp. 6672–6679. [Google Scholar]
- Chen, Y.; Huang, S.; Zhao, L.; Dissanayake, G. Cramér–Rao bounds and optimal design metrics for pose-graph SLAM. IEEE Trans. Robot. 2021, 37, 627–641. [Google Scholar] [CrossRef]
- Carlone, L.; Du, J.; Kaouk Ng, M.; Bona, B.; Indri, M. Active SLAM and exploration with particle filters using Kullback-Leibler divergence. J. Intell. Robot. Syst. 2014, 75, 291–311. [Google Scholar] [CrossRef]
- Yuan, J.; Zhu, S.; Tang, K.; Sun, Q. ORB-TEDM: An RGB-D SLAM Approach Fusing ORB Triangulation Estimates and Depth Measurements. IEEE Trans. Instrum. Meas. 2022, 71, 5006315. [Google Scholar] [CrossRef]
- Carlone, L.; Karaman, S. Attention and anticipation in fast visual-inertial navigation. IEEE Trans. Robot. 2018, 35, 1–20. [Google Scholar] [CrossRef]
- Murali, V. Perception-Aware Planning for Differentially Flat Robots. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2024. [Google Scholar]
- Sun, G.; Zhang, X.; Liu, Y.; Wang, H.; Zhang, X.; Zhuang, Y. Topology-Guided Perception-Aware Receding Horizon Trajectory Generation for UAVs. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Detroit, MI, USA, 1–5 October 2023; pp. 3070–3076. [Google Scholar]
- Chen, X.; Zhang, Y.; Zhou, B.; Shen, S. APACE: Agile and Perception-Aware Trajectory Generation for Quadrotor Flights. arXiv 2024, arXiv:2403.08365. [Google Scholar]
- Sun, G.; Zhang, X.; Liu, Y.; Zhang, X.; Zhuang, Y. Safety-Driven and Localization Uncertainty-Driven Perception-Aware Trajectory Planning for Quadrotor Unmanned Aerial Vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8837–8848. [Google Scholar] [CrossRef]
- Takemura, R.; Ishigami, G. Perception-and-Energy-aware Motion Planning for UAV using Learning-based Model under Heteroscedastic Uncertainty. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 10103–10109. [Google Scholar]
- Mur-Artal, R.; Tardós, J.D. Orb-slam2: An open-source slam system for monocular, stereo, and rgb-d cameras. IEEE Trans. Robot. 2017, 33, 1255–1262. [Google Scholar] [CrossRef]
- Pázman, A. Foundations of Optimum Experimental Design; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Zhang, Z.; Scaramuzza, D. Beyond point clouds: Fisher information field for active visual localization. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 5986–5992. [Google Scholar]
- Kiefer, J. General equivalence theory for optimum designs (approximate theory). Ann. Stat. 1974, 2, 849–879. [Google Scholar] [CrossRef]
- Zhao, Y.; Xiong, Z.; Zhou, S.; Wang, J.; Zhang, L.; Campoy, P. Perception-Aware Planning for Active SLAM in Dynamic Environments. Remote Sens. 2022, 14, 2584. [Google Scholar] [CrossRef]
- Koenig, N.; Howard, A. Design and use paradigms for gazebo, an open-source multi-robot simulator. In Proceedings of the 2004 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (IEEE Cat. No. 04CH37566), Sendai, Japan, 28 September–2 October 2004; Volume 3, pp. 2149–2154. [Google Scholar]
- Furrer, F.; Burri, M.; Achtelik, M.; Siegwart, R. Rotors—A modular gazebo mav simulator framework. In Robot Operating System (ROS); Springer: Berlin/Heidelberg, Germany, 2016; pp. 595–625. [Google Scholar]
- Bircher, A.; Kamel, M.; Alexis, K.; Oleynikova, H.; Siegwart, R. Receding horizon “next-best-view” planner for 3d exploration. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 1462–1468. [Google Scholar]




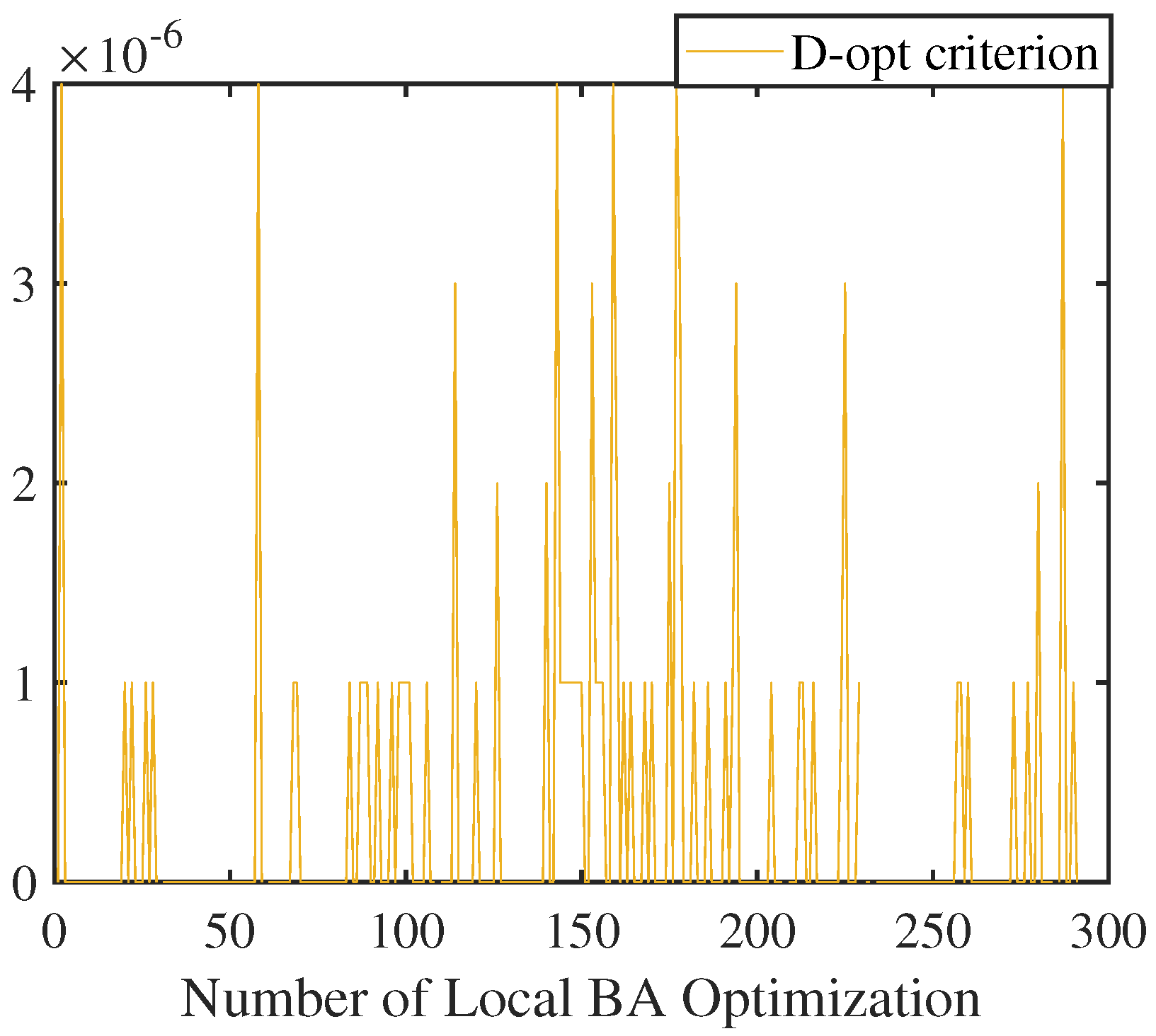
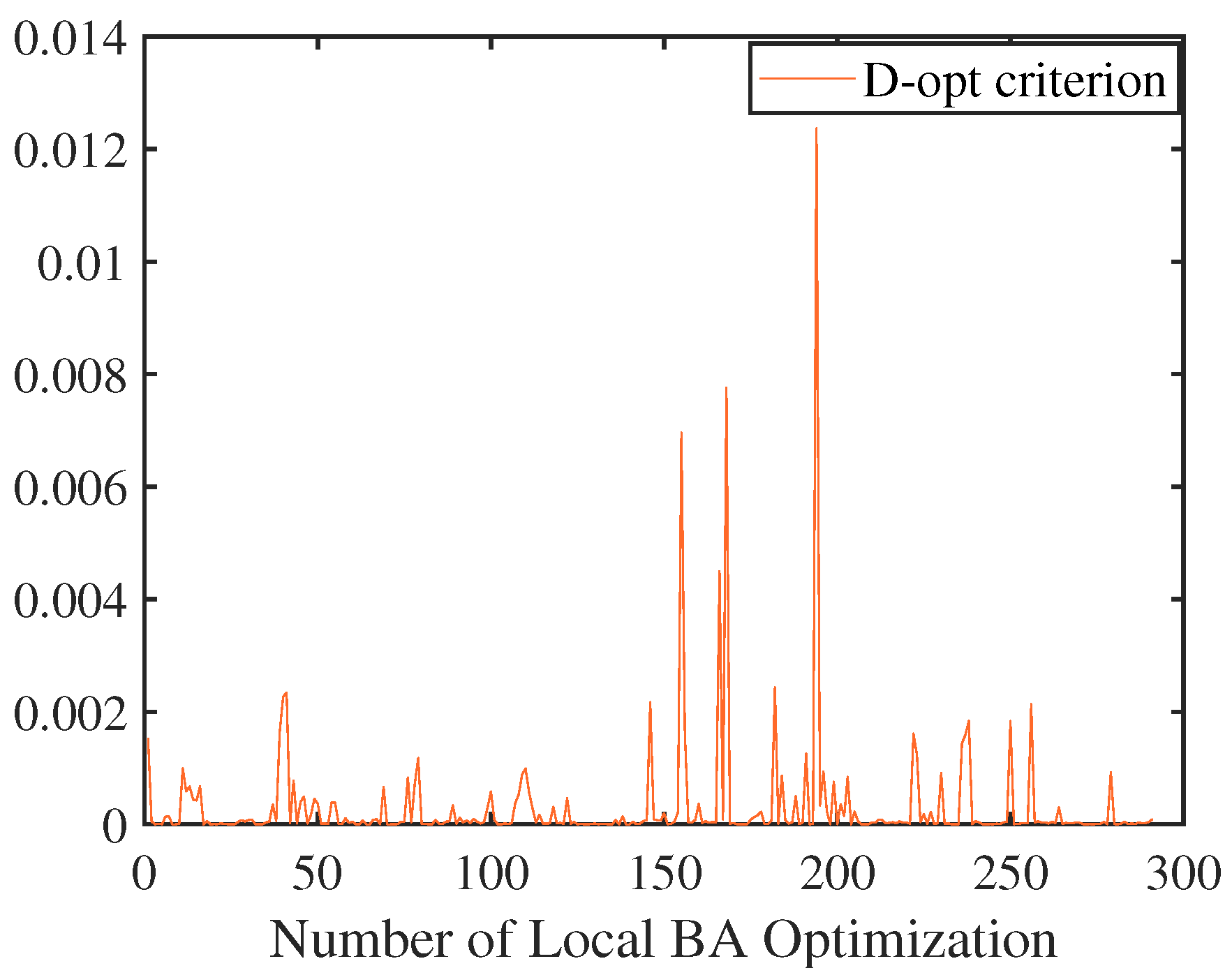

| Scenarios | U-NBVP | U-ALCP |
|---|---|---|
| Uncertainty Threshold | Uncertainty Threshold | |
| small-scale | ||
| middle-scale | ||
| large-scale |
| Scenarios | Method | Information Section | Median Tracking Time (ms) | Mean Tracking Time (ms) |
|---|---|---|---|---|
| small-scale | NBVP | × | 48.68 | 50.33 |
| U-NBVP(ours) | ✓ | 45.74 | 47.43 | |
| ALCP | × | 44.93 | 46.32 | |
| U-ALCP(ours) | ✓ | 44.08 | 45.72 | |
| medium-scale | NBVP | × | 50.72 | 53.79 |
| U-NBVP(ours) | ✓ | 48.80 | 50.90 | |
| ALCP | × | 49.34 | 52.15 | |
| U-ALCP(ours) | ✓ | 47.72 | 50.31 | |
| large-scale | NBVP | × | 53.21 | 56.13 |
| U-NBVP(ours) | ✓ | 50.76 | 54.01 | |
| ALCP | × | 52.28 | 55.83 | |
| U-ALCP(ours) | ✓ | 50.37 | 53.15 |
| Scenarios | Method | Information Selection | RMSE (m) | Mean (m) |
|---|---|---|---|---|
| small-scale | NBVP | × | 3.25 | 2.56 |
| U-NBVP(ours) | ✓ | 3.29 | 2.51 | |
| ALCP | × | 3.21 | 2.87 | |
| U-ALCP(ours) | ✓ | 3.21 | 2.88 | |
| medium-scale | NBVP | × | 2.32 | 1.78 |
| U-NBVP(ours) | ✓ | 2.35 | 1.76 | |
| ALCP | × | 1.00 | 0.91 | |
| U-ALCP(ours) | ✓ | 0.94 | 0.95 | |
| large-scale | NBVP | × | 4.89 | 3.66 |
| U-NBVP(ours) | ✓ | 4.86 | 3.70 | |
| ALCP | × | 3.45 | 3.49 | |
| U-ALCP(ours) | ✓ | 3.45 | 3.50 |
| Scenarios | U-NBVP | U-ALCP |
|---|---|---|
| Uncertainty Threshold | Uncertainty Threshold | |
| small-scale | 0.1 | 0.1 |
| middle-scale | 2 | 2 |
| large-scale | 4.5 | 4.5 |
| Scenarios | Method | Information Selection | Median Tracking Time (ms) | Mean Tracking Time (ms) |
|---|---|---|---|---|
| small-scale | NBVP | × | 105.78 | 157.65 |
| U-NBVP(ours) | ✓ | 99.26 | 148.23 | |
| ALCP | × | 91.56 | 139.59 | |
| U-ALCP(ours) | ✓ | 80.26 | 120.02 | |
| medium-scale | NBVP | × | 199.85 | 279.61 |
| U-NBVP(ours) | ✓ | 184.20 | 270.62 | |
| ALCP | × | 159.82 | 227.05 | |
| U-ALCP(ours) | ✓ | 123.97 | 175.09 | |
| large-scale | NBVP | × | 191.45 | 257.11 |
| U-NBVP(ours) | ✓ | 169.49 | 201.20 | |
| ALCP | × | 186.92 | 203.04 | |
| U-ALCP(ours) | ✓ | 163.28 | 190.77 |
| Scenarios | Method | Information Selection | RMSE (m) | Mean (m) |
|---|---|---|---|---|
| small-scale | NBVP | × | 3.25 | 2.56 |
| U-NBVP(ours) | ✓ | 3.26 | 2.56 | |
| ALCP | × | 3.21 | 2.87 | |
| U-ALCP(ours) | ✓ | 3.27 | 2.90 | |
| medium-scale | NBVP | × | 2.32 | 1.78 |
| U-NBVP(ours) | ✓ | 2.19 | 1.76 | |
| ALCP | × | 1.00 | 0.91 | |
| U-ALCP(ours) | ✓ | 0.79 | 0.85 | |
| large-scale | NBVP | × | 4.89 | 3.66 |
| U-NBVP(ours) | ✓ | 4.82 | 3.70 | |
| ALCP | × | 3.45 | 3.49 | |
| U-ALCP(ours) | ✓ | 3.43 | 3.55 |
| Scenarios | U-NBVP | U-ALCP |
|---|---|---|
| Uncertainty Threshold | Uncertainty Threshold | |
| small-scale | 0.005 | 0.004 |
| middle-scale | 0.015 | 0.01 |
| large-scale | 0.18 | 0.15 |
| Scenarios | Method | Active Loop Closing | Uncertainty Quantification | RMSE (m) | Mean (m) |
|---|---|---|---|---|---|
| small-scale | NBVP | × | × | 3.25 | 2.56 |
| U-NBVP(ours) | ✓ | ✓ | 3.23 | 2.51 | |
| ALCP | ✓ | × | 3.21 | 2.87 | |
| U-ALCP(ours) | ✓ | ✓ | 3.21 | 2.88 | |
| medium-scale | NBVP | × | × | 2.32 | 1.78 |
| U-NBVP(ours) | ✓ | ✓ | 2.19 | 1.67 | |
| ALCP | ✓ | × | 1.00 | 0.91 | |
| U-ALCP(ours) | ✓ | ✓ | 0.79 | 0.85 | |
| large-scale | NBVP | × | × | 4.89 | 3.66 |
| U-NBVP(ours) | ✓ | ✓ | 4.33 | 3.54 | |
| ALCP | ✓ | × | 3.45 | 3.49 | |
| U-ALCP(ours) | ✓ | ✓ | 3.18 | 3.36 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Xiong, Z.; Wang, J.; Zhang, L.; Campoy, P. Visual Active SLAM Method Considering Measurement and State Uncertainty for Space Exploration. Aerospace 2025, 12, 642. https://doi.org/10.3390/aerospace12070642
Zhao Y, Xiong Z, Wang J, Zhang L, Campoy P. Visual Active SLAM Method Considering Measurement and State Uncertainty for Space Exploration. Aerospace. 2025; 12(7):642. https://doi.org/10.3390/aerospace12070642
Chicago/Turabian StyleZhao, Yao, Zhi Xiong, Jingqi Wang, Lin Zhang, and Pascual Campoy. 2025. "Visual Active SLAM Method Considering Measurement and State Uncertainty for Space Exploration" Aerospace 12, no. 7: 642. https://doi.org/10.3390/aerospace12070642
APA StyleZhao, Y., Xiong, Z., Wang, J., Zhang, L., & Campoy, P. (2025). Visual Active SLAM Method Considering Measurement and State Uncertainty for Space Exploration. Aerospace, 12(7), 642. https://doi.org/10.3390/aerospace12070642







