Resolving Non-Proportional Frequency Components in Rotating Machinery Signals Using Local Entropy Selection Scaling–Reassigning Chirplet Transform
Abstract
1. Introduction
- (1)
- To accurately analyze signals containing multiple fundamental frequency components, particularly those exhibiting nonlinear and non-proportional characteristics;
- (2)
- To effectively resolve closely spaced IF components, thereby enhancing the interpretability and resolution of TFRs in complex signal scenarios.
- (1)
- Chirp Rate (CR) Scaling Mechanism: By modulating the chirp rate, the method generates a set of sub-time–frequency representations (sub-TFRs) corresponding to different frequency modulations.
- (2)
- Entropy-Based CR Selection: An entropy minimization criterion is utilized to select multiple CRs at the same time center, thereby preserving distinct IF ridges and improving component separability.
- (3)
- Local Reassignment Strategy: A localized reassignment scheme is incorporated to further sharpen the energy concentration in the TFR, enhancing both clarity and interpretability.
2. Conceptual Foundations and Motivation
2.1. Overview of SBCT
2.2. Limitations of SBCT
- (1)
- SBCT exhibits limited capability in analyzing non-stationary signals containing multiple fundamental frequency components that do not conform to a proportional relationship. As revealed by the mathematical formulation (e.g., Equation (8)), the core assumption of SBCT relies on the proportionality among IF trajectories. When the frequency components do not satisfy the proportional constraint, the matching capability of the method significantly degrades, as demonstrated by the example signals constructed earlier.
- (2)
- When non-stationary signals contain closely spaced IF components, the energy concentration capability of SBCT becomes insufficient. Specifically, when the frequency spacing between multiple IF components is small, the energy distribution obtained by SBCT tends to spread within the frequency support of the window function, resulting in blurred ridges and reduced resolution in the TFR, making it difficult to accurately distinguish adjacent components.
- (3)
- SBCT currently lacks a post-processing mechanism to enhance the energy concentration in the TFR. The time–frequency output of the existing SBCT algorithm is not subjected to energy reconstruction or optimization, which limits its potential for further improvement in energy concentration and time–frequency resolution. Introducing effective post-processing strategies, such as energy reassignment or enhancement operations, is anticipated to greatly enhance the readability and analytical accuracy of the TFR.
3. Local Entropy Selection Scaling–Reassigning Chirplet Transform Method
3.1. TFR Optimization Criterion Based on Rényi Entropy
3.2. Energy Reconstruction-Based Concentration Enhancement Mechanism
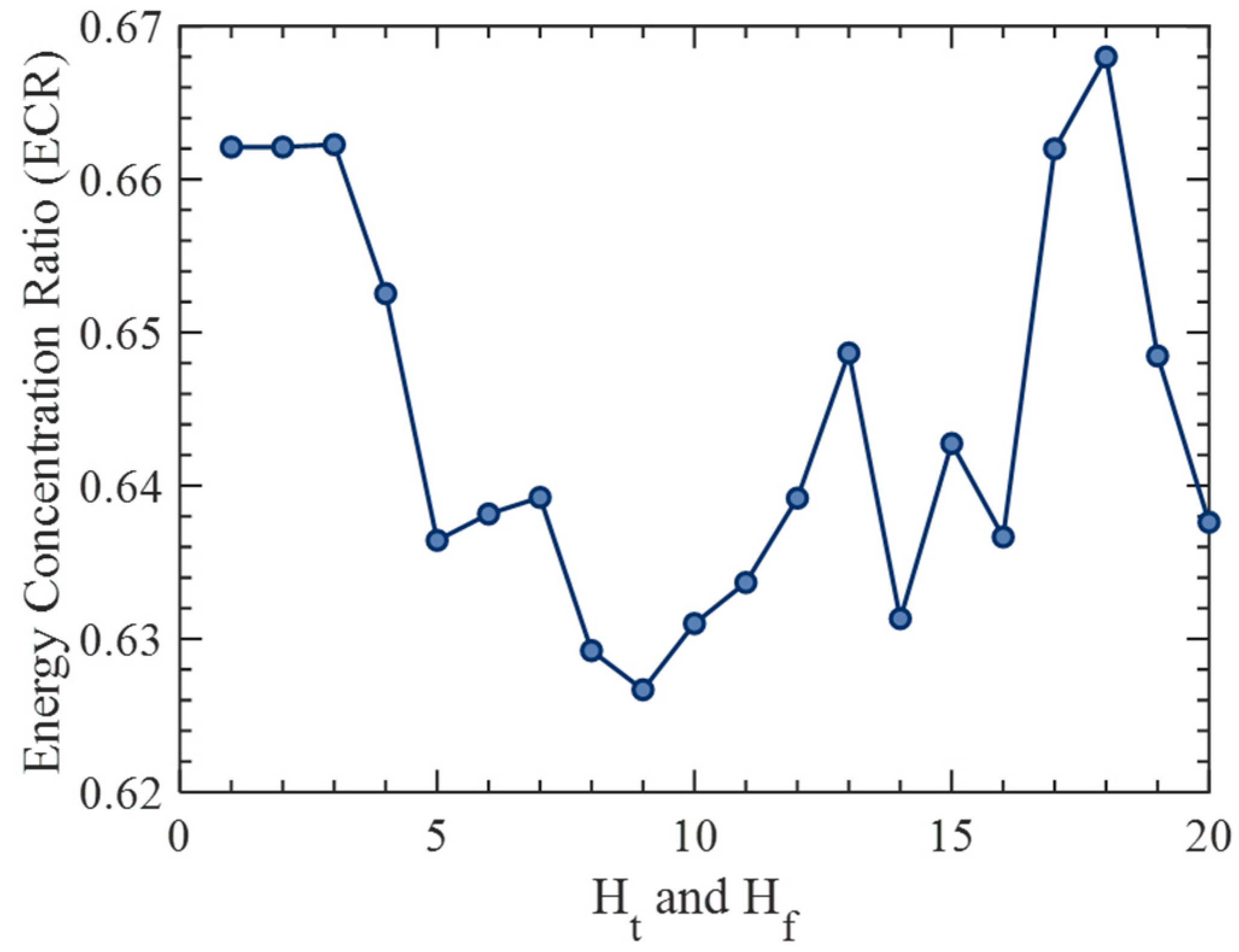
3.3. Implementation of the LESSRCT Method
| Algorithm 1: LESSRCT algorithm |
| Step 1: Initial Parameter Configuration (1) The signal s(t), the length of the window L, the sampling frequency Fs, and the count of Gaussian windows K, along with the values of delta and ε. (2) local-TFR ← zeros(NH, NL). Step 2: Computation of the local-TFR for i = 1: NH for j = 1: NH local-TFR(i, k) ← SBCT(t, f). local-TFRg(i, k) ← SBCTg′(t, f). end for end for Step 3: Localized Entropy Selection (3) Apply entropy to divide the local time–frequency segments. for i = 1: N E-SBCT(:, :) ← the minimum value (entropy (local-TFR (:, i))) E-SBCT (g)’(:, :) ← the minimum value (entropy (local-TFRg(:, i))) end for Step 4: Energy Reconstruction (4) Compute:E ← mean(s(t)). for i = 1: NL for j = 1: NL LESSRCT (i, j) ← LESSRCT (i, j) + sub-TFR (i, j) if abs(i-fr(i, j)) < ε δs(i, j) = 1 end for end for end if (5) LESSRCT(i, j) ← E-SBCT(i, j)·δs(i, j). |
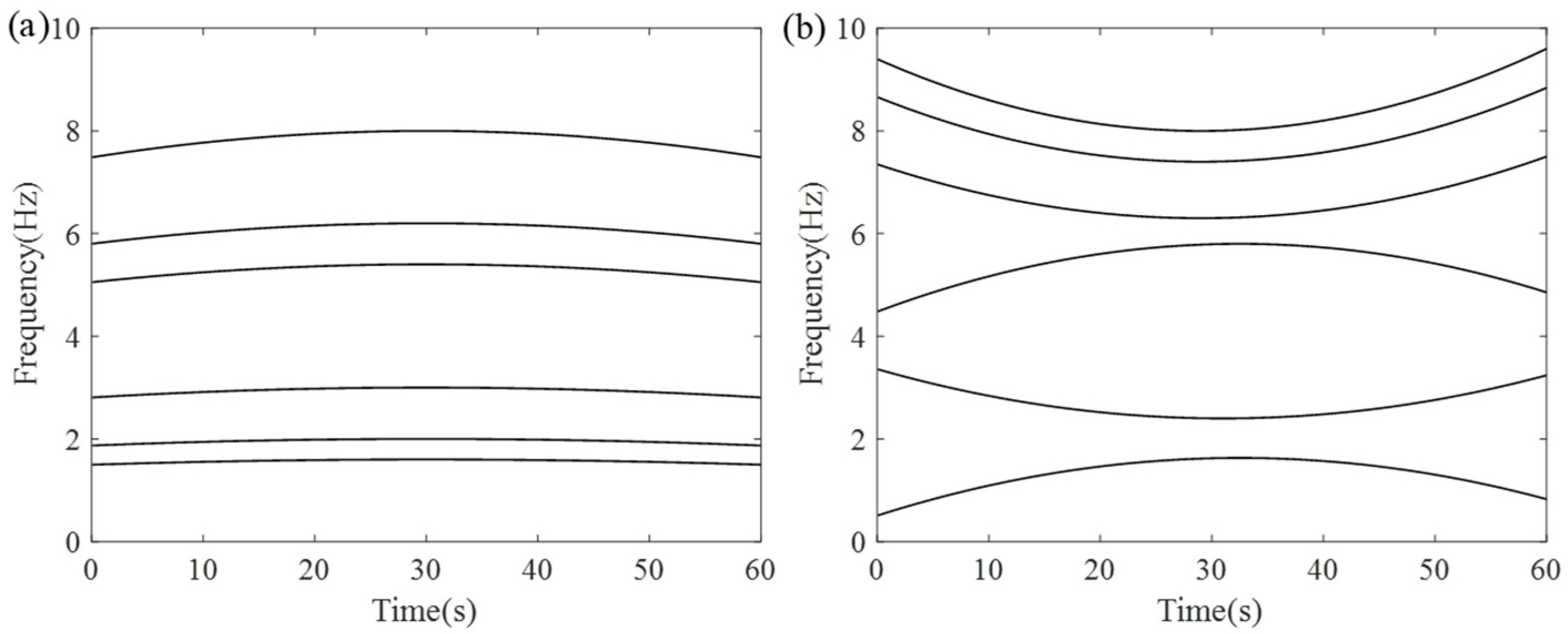
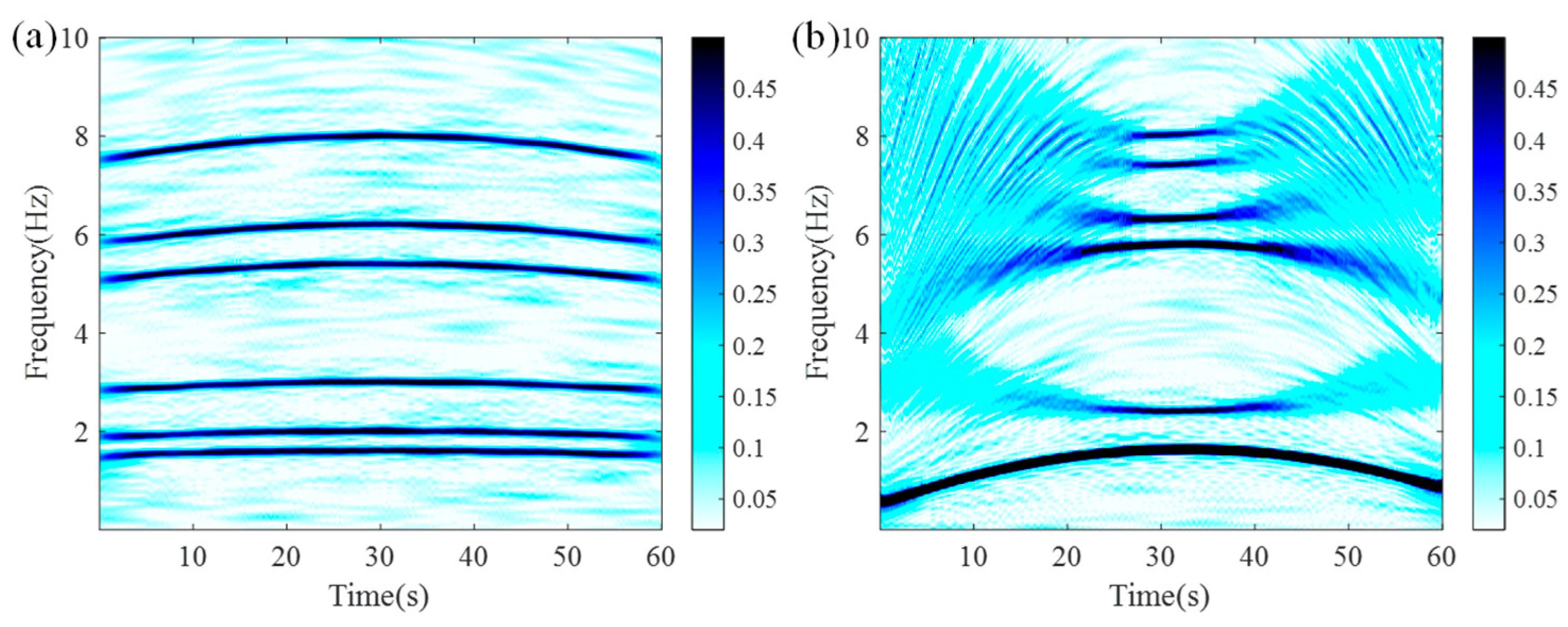
4. Numerical Experimentation
5. Validation in Practice
5.1. Evaluation of Bat Echolocation Calls
5.2. Inner Race Defect Testing in Rolling Bearings
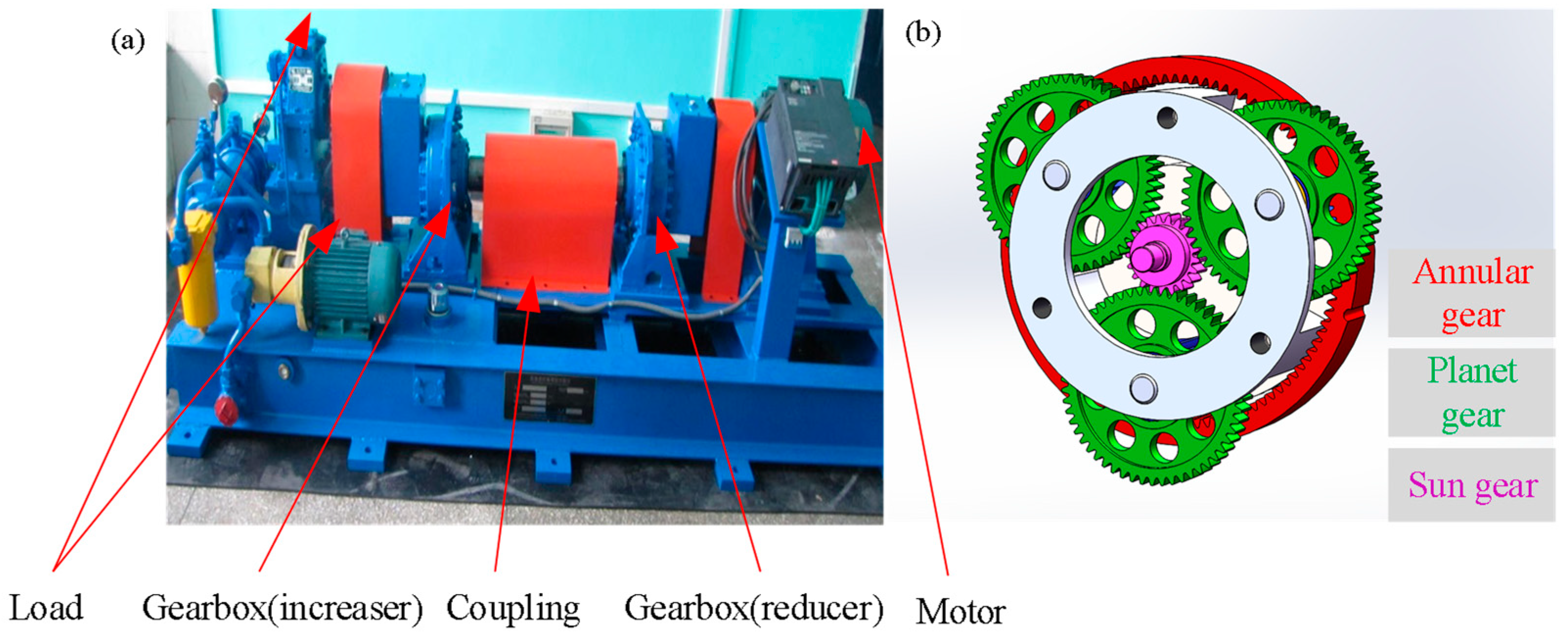
5.3. Evaluation of Gearbox Performance in Wind Turbine Power Transmission
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviation | Full Term |
| TFA | time–frequency analysis |
| TFR | time–frequency representation |
| STFT | Short-time Fourier transform |
| WVD | Wigner–Ville Distribution |
| CWT | continuous wavelet transform |
| IF | instantaneous frequency |
| CT | Chirplet transform |
| SBCT | scaling-basis Chirplet transform |
| PECT | Proportional Extraction Chirplet Transform |
| VSLCT | velocity synchronous linear Chirplet transform |
| SSCT | Slope-Synchronized Chirplet Transform |
| GLCT | General Linear Chirplet Transform |
| CMCT | Component-Matching Chirplet Transform |
| SSIM | Structural Similarity Index Measure |
| SST | synchro-squeezing transform |
| RM | reassignment method |
| SET | synchro-extracting transform |
| SRT | Synchronized Reassignment Transform |
| EMCT | Entropy Matching Chirplet Transform |
| GCBT | Generalized Chirplet Basis Transform |
| CR | chirp rate |
| TFD | time–frequency distribution |
| FT | Fourier transform |
| RO | reassignment operator |
| LESSRCT | Local Entropy Selection Scaling–Reassigning Chirplet Transform |
| RF | rotational frequency |
| FCF | fault characteristic frequencies |
References
- Liu, D.; Cui, L.; Wang, H. Rotating machinery fault diagnosis under time-varying speeds: A review. IEEE Sens. J. 2023, 23, 29969–29990. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.; Liu, T.; Li, S. Rotating machinery fault diagnosis based on typical resonance demodulation methods: A review. IEEE Sens. J. 2023, 23, 6439–6459. [Google Scholar] [CrossRef]
- Huang, P.; Yu, H.; Wang, T. A Study Using Optimized LSSVR for Real-Time Fault Detection of Liquid Rocket Engine. Processes 2022, 10, 1643. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, A.; Jiang, W.; Yue, Y.; Jing, L.; Zhou, J. Small-Sample Fault Diagnosis of Axial Piston Pumps across Working Conditions, Based on 1D-SENet Model Migration. J. Mar. Sci. Eng. 2024, 12, 1430. [Google Scholar] [CrossRef]
- Wang, Y.; Fan, Z.; Liu, H.; Gao, X. Planetary Gearbox Fault Diagnosis Based on ICEEMD-Time-Frequency Information Entropy and VPMCD. Appl. Sci. 2020, 10, 6376. [Google Scholar] [CrossRef]
- Li, W.; Yang, W.; Jin, G.; Chen, J.; Li, J.; Huang, R.; Chen, Z. Clustering Federated Learning for Bearing Fault Diagnosis in Aerospace Applications with a Self-Attention Mechanism. Aerospace 2022, 9, 516. [Google Scholar] [CrossRef]
- Marijančević, A.; Braut, S.; Žigulić, R.; Skoblar, A. Fatigue Assessment of Marine Propulsion Shafting Due to Cyclic Torsional and Bending Stresses. Machines 2025, 13, 384. [Google Scholar] [CrossRef]
- Long, M.; Zhu, H.; Zhang, G.; He, W. Aerospace Equipment Fault Diagnosis Method Based on Fuzzy Fault Tree Analysis and Interpretable Interval Belief Rule Base. Mathematics 2024, 12, 3693. [Google Scholar] [CrossRef]
- Wei, Y.; Li, Y.; Xu, M.; Huang, W. A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery. Entropy 2019, 21, 409. [Google Scholar] [CrossRef]
- Guo, Y.; Cheng, Z.; Zhang, J.; Sun, B.; Wang, Y. A review on adversarial–based deep transfer learning mechanical fault diagnosis. J. Big Data 2024, 11, 151. [Google Scholar] [CrossRef]
- Liu, T.; Yan, S.; Zhang, W. Time-Frequency Analysis of Nonstationary Vibration Signals for Deployable Structures by Using the Constant-Q Nonstationary Gabor Transform. Mech. Syst. Signal Process. 2016, 75, 228–244. [Google Scholar] [CrossRef]
- Yang, Y.; Peng, Z.; Zhang, W.; Meng, G. Parameterised Time-Frequency Analysis Methods and Their Engineering Applications: A Review of Recent Advances. Mech. Syst. Signal Process. 2019, 119, 182–221. [Google Scholar] [CrossRef]
- Bai, Y.; Cheng, W.; Wen, W.; Liu, Y. Application of time-frequency analysis in rotating machinery fault diagnosis. Shock. Vib. 2023, 2023, 9878228. [Google Scholar] [CrossRef]
- Zhao, H.; Niu, G. Enhanced order spectrum analysis based on iterative adaptive crucial mode decomposition for planetary gearbox fault diagnosis under large speed variations. Mech. Syst. Signal Process. 2023, 185, 109822. [Google Scholar] [CrossRef]
- Shi, G.; Qin, C.; Zhang, Z.; Tao, J.; Liu, C. Towards complex multi-component pulse signal with strong noise: Deconvolution and time–frequency assisted mode decomposition. Mech. Syst. Signal Process. 2024, 212, 111274. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Portnoff, M. Time-Frequency Representation of Digital Signals and Systems Based on Short-Time Fourier Analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 55–69. [Google Scholar] [CrossRef]
- Boashash, B.; Black, P. An Efficient Real-Time Implementation of the Wigner-Ville Distribution. IEEE Trans. Acoust. Speech Signal Process. 1987, 35, 1611–1618. [Google Scholar] [CrossRef]
- Daubechies, I. The Wavelet Transform, Time-Frequency Localization and Signal Analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Mann, S.; Haykin, S. The Chirplet Transform: Physical Considerations. IEEE Trans. Signal Process. 1995, 43, 2745–2761. [Google Scholar] [CrossRef]
- Li, M.; Wang, T.; Chu, F.; Han, Q.; Qin, Z.; Zhou, J.M. Scaling-Basis Chirplet Transform. IEEE Trans. Ind. Electron. 2020, 68, 8777–8788. [Google Scholar] [CrossRef]
- Zhang, D.; Feng, Z. Proportion-Extracting Chirplet Transform for Nonstationary Signal Analysis of Rotating Machinery. IEEE Trans. Ind. Inform. 2022, 19, 2674–2683. [Google Scholar] [CrossRef]
- Guan, Y.; Liang, M.; Necsulescu, D.S. Velocity Synchronous Linear Chirplet Transform. IEEE Trans. Ind. Electron. 2018, 66, 6270–6280. [Google Scholar] [CrossRef]
- Miao, Y.; Sun, H.; Qi, J. Synchro-Compensating Chirplet Transform. IEEE Signal Process. Lett. 2018, 25, 1413–1417. [Google Scholar] [CrossRef]
- Yu, G.; Zhou, Y. General Linear Chirplet Transform. Mech. Syst. Signal Process. 2016, 70–71, 958–973. [Google Scholar] [CrossRef]
- Li, M.; Wang, T.; Chu, F.; Feng, Z. Component Matching Chirplet Transform via Frequency-Dependent Chirp Rate for Wind Turbine Planetary Gearbox Fault Diagnostics under Variable Speed Condition. Mech. Syst. Signal Process. 2021, 161, 107997. [Google Scholar] [CrossRef]
- Daubechies, I.; Lu, J.; Wu, H.T. Synchrosqueezed Wavelet Transforms: An Empirical Mode Decomposition-Like Tool. Appl. Comput. Harmonic Anal. 2011, 30, 243–261. [Google Scholar] [CrossRef]
- Auger, F.; Flandrin, P. Improving the Readability of Time-Frequency and Time-Scale Representations by the Reassignment Method. IEEE Trans. Signal Process. 1995, 43, 1068–1089. [Google Scholar] [CrossRef]
- Yu, G.; Yu, M.; Xu, C. Synchroextracting Transform. IEEE Trans. Ind. Electron. 2017, 64, 8042–8054. [Google Scholar] [CrossRef]
- Li, M.; Wang, T.; Kong, Y.; Chu, F. Synchro-Reassigning Transform for Instantaneous Frequency Estimation and Signal Reconstruction. IEEE Trans. Ind. Electron. 2021, 69, 7263–7274. [Google Scholar] [CrossRef]
- He, Y.; Hu, M.; Jiang, Z.; Feng, K.; Ming, X. Local Maximum Synchrosqueezes from Entropy Matching Chirplet Transform. Mech. Syst. Signal Process. 2022, 181, 109476. [Google Scholar] [CrossRef]
- Han, Q.; Wang, T.; Ding, Z.; Xu, X.; Chu, F. Magnetic Equivalent Modeling of Stator Currents for Localized Fault Detection of Planetary Gearboxes Coupled to Electric Motors. IEEE Trans. Ind. Electron. 2020, 68, 2575–2586. [Google Scholar] [CrossRef]
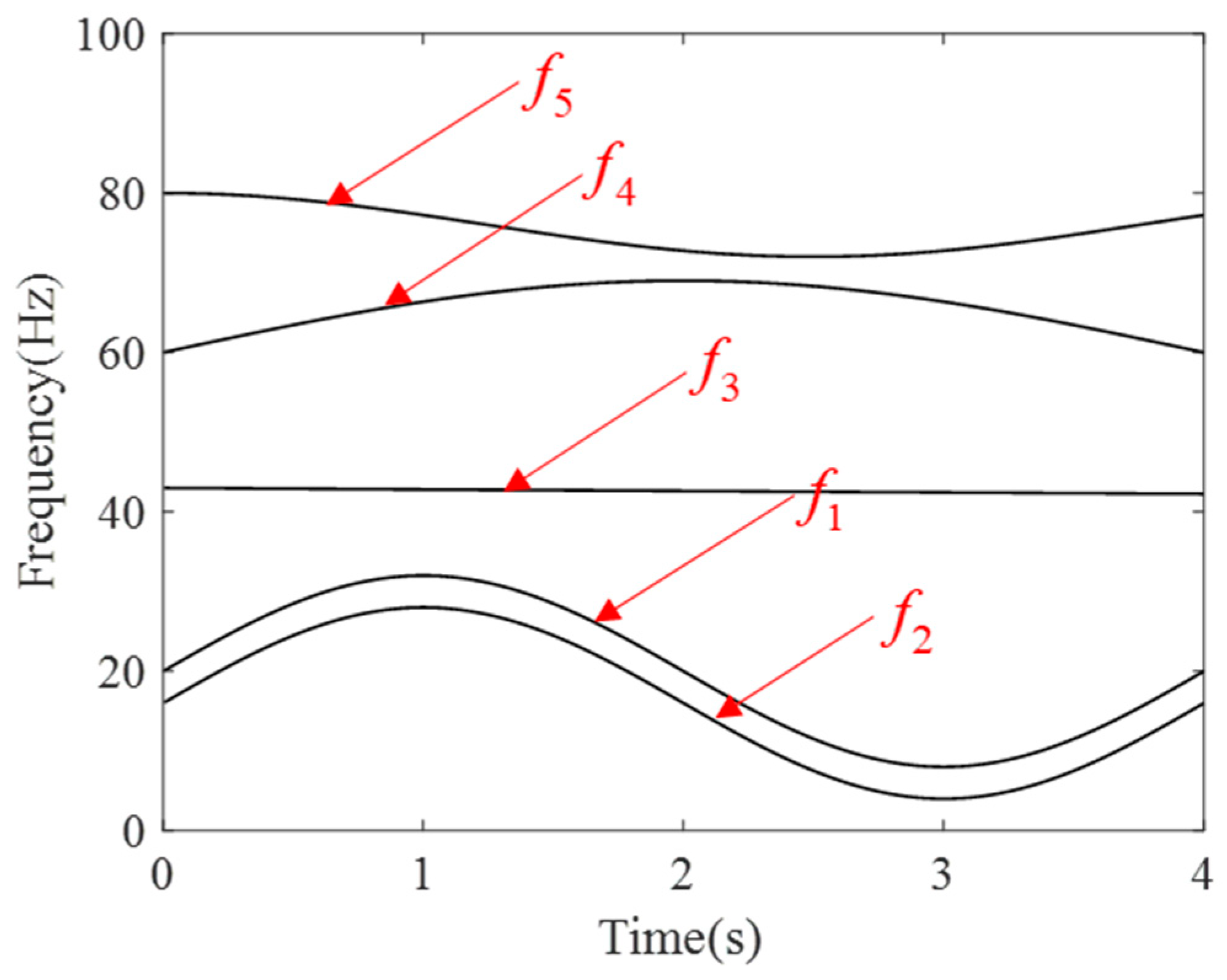
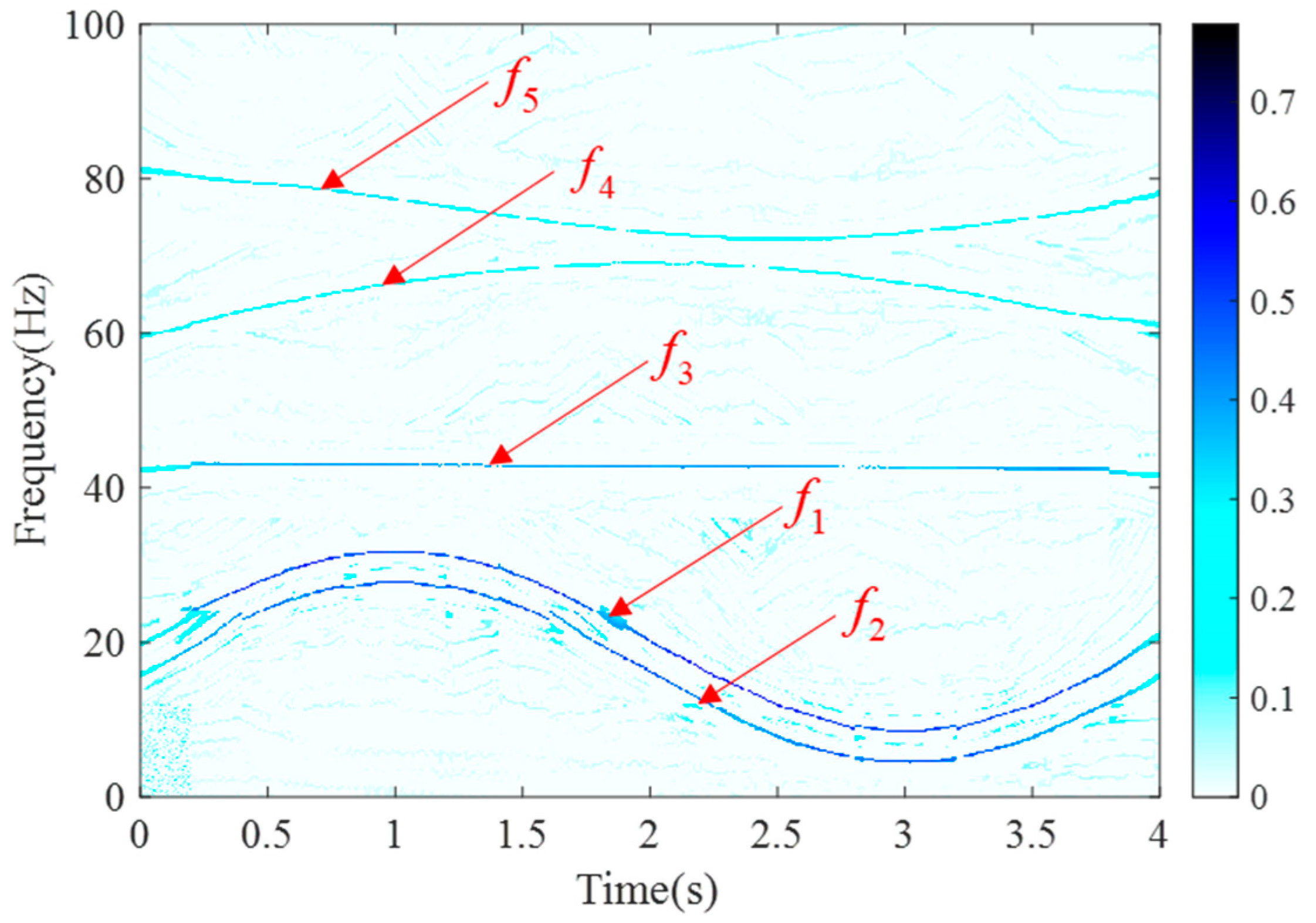


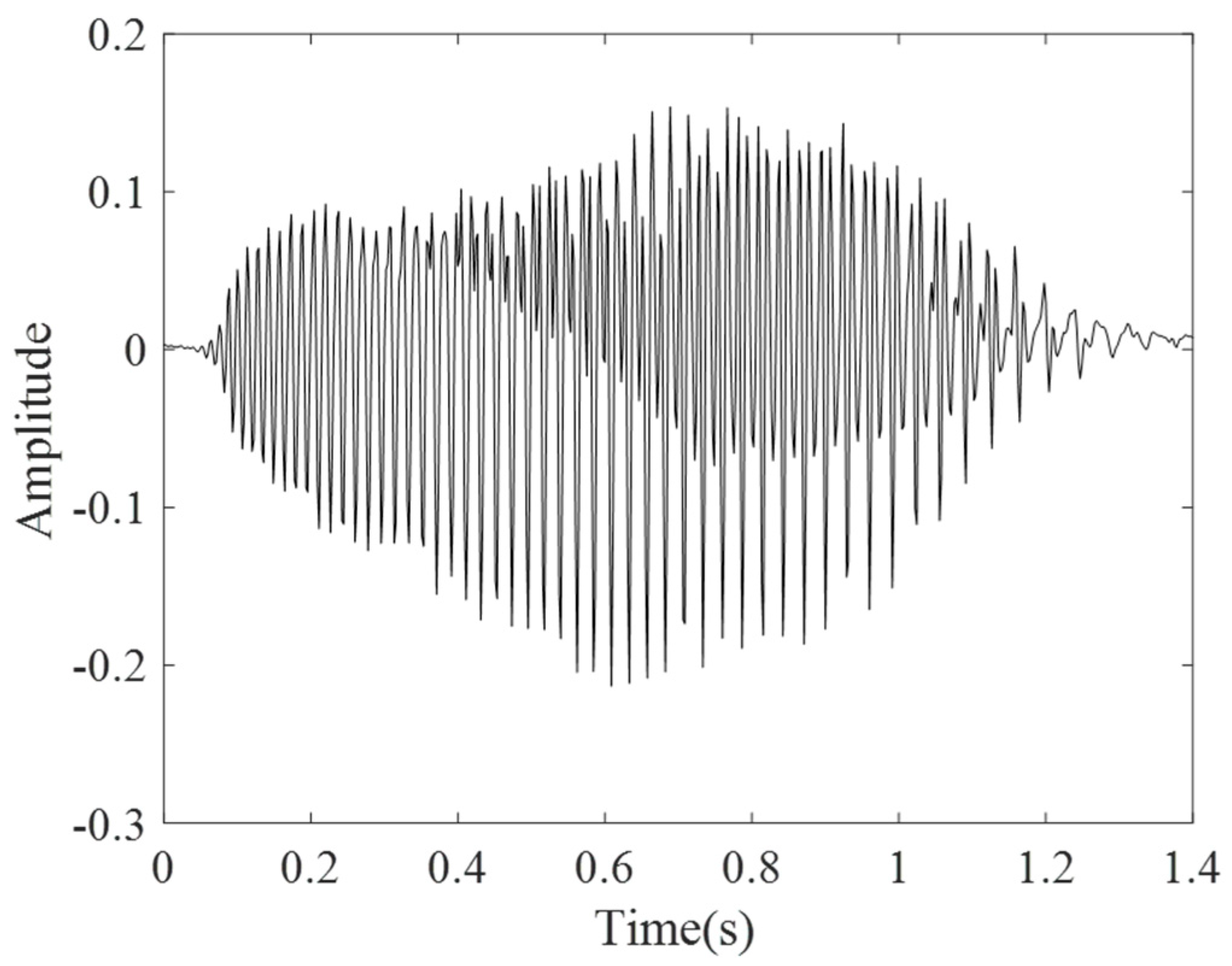
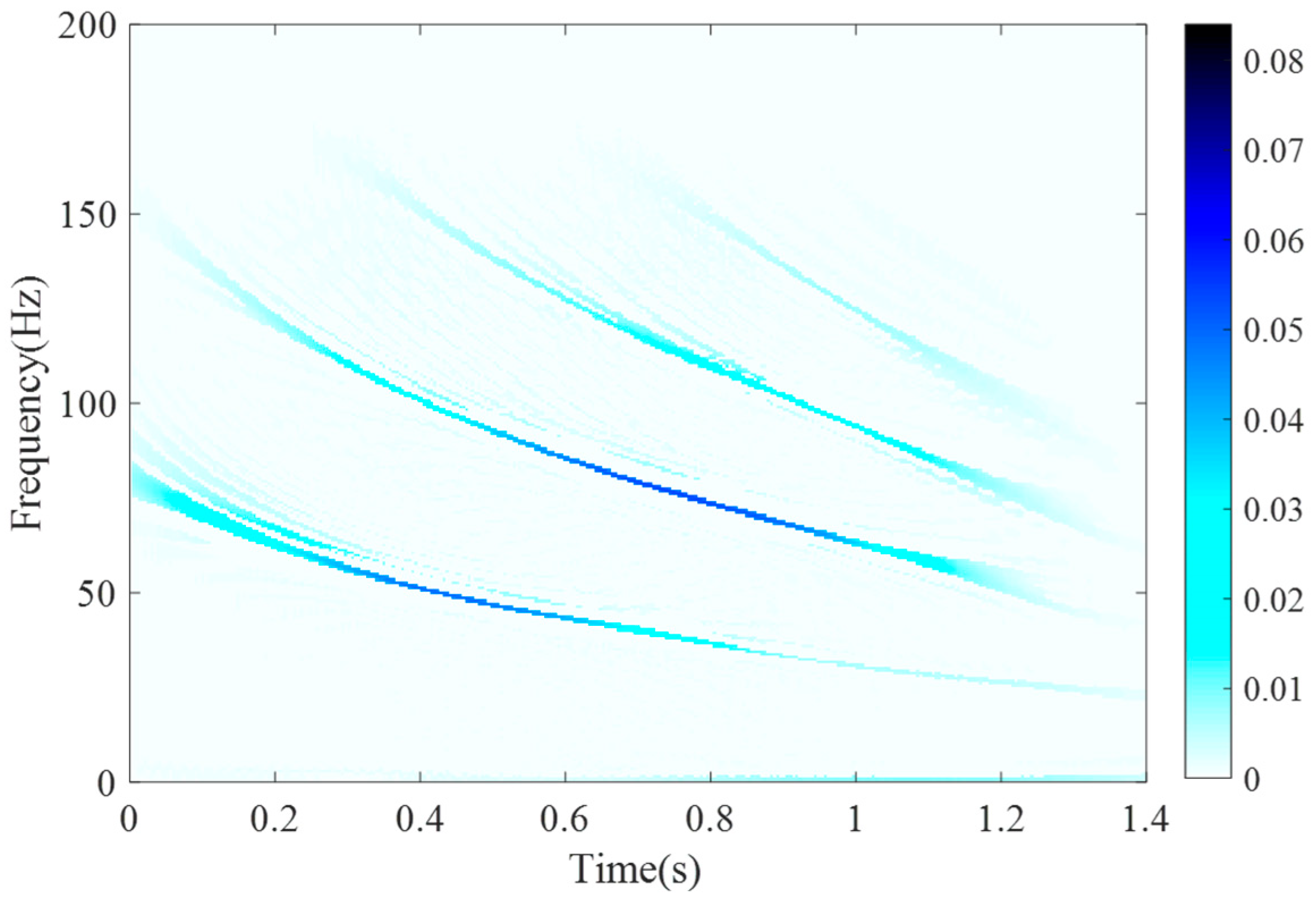
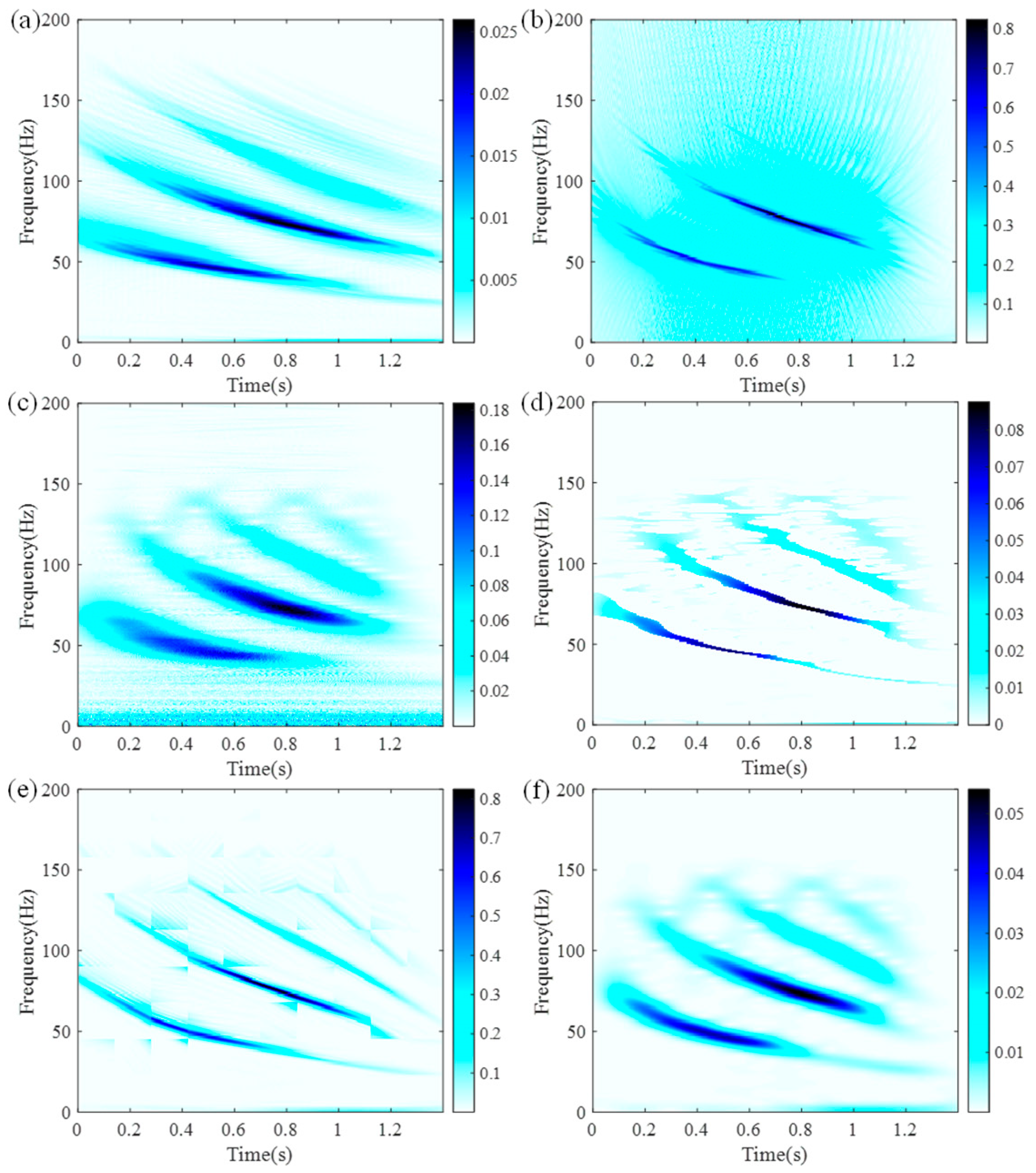


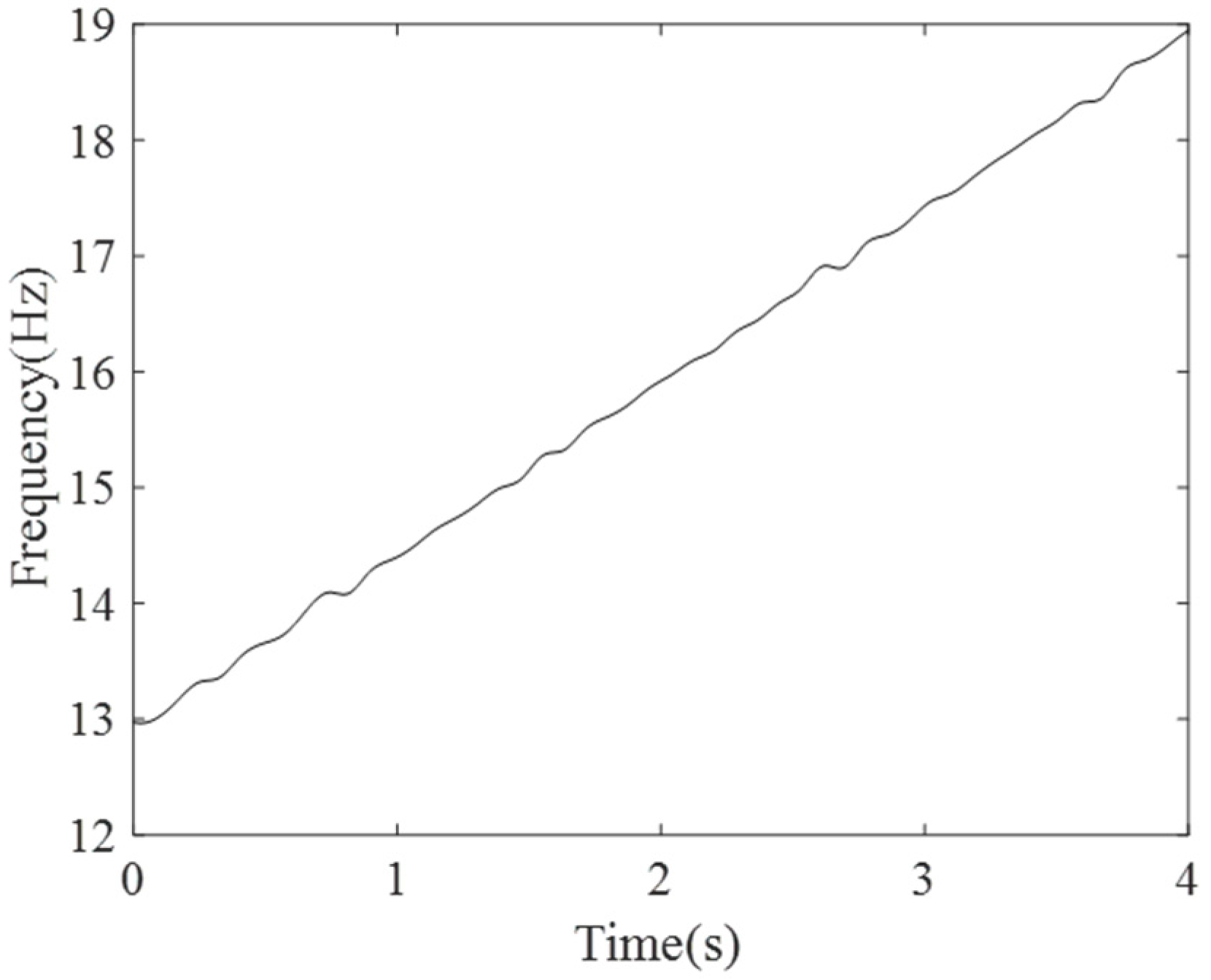

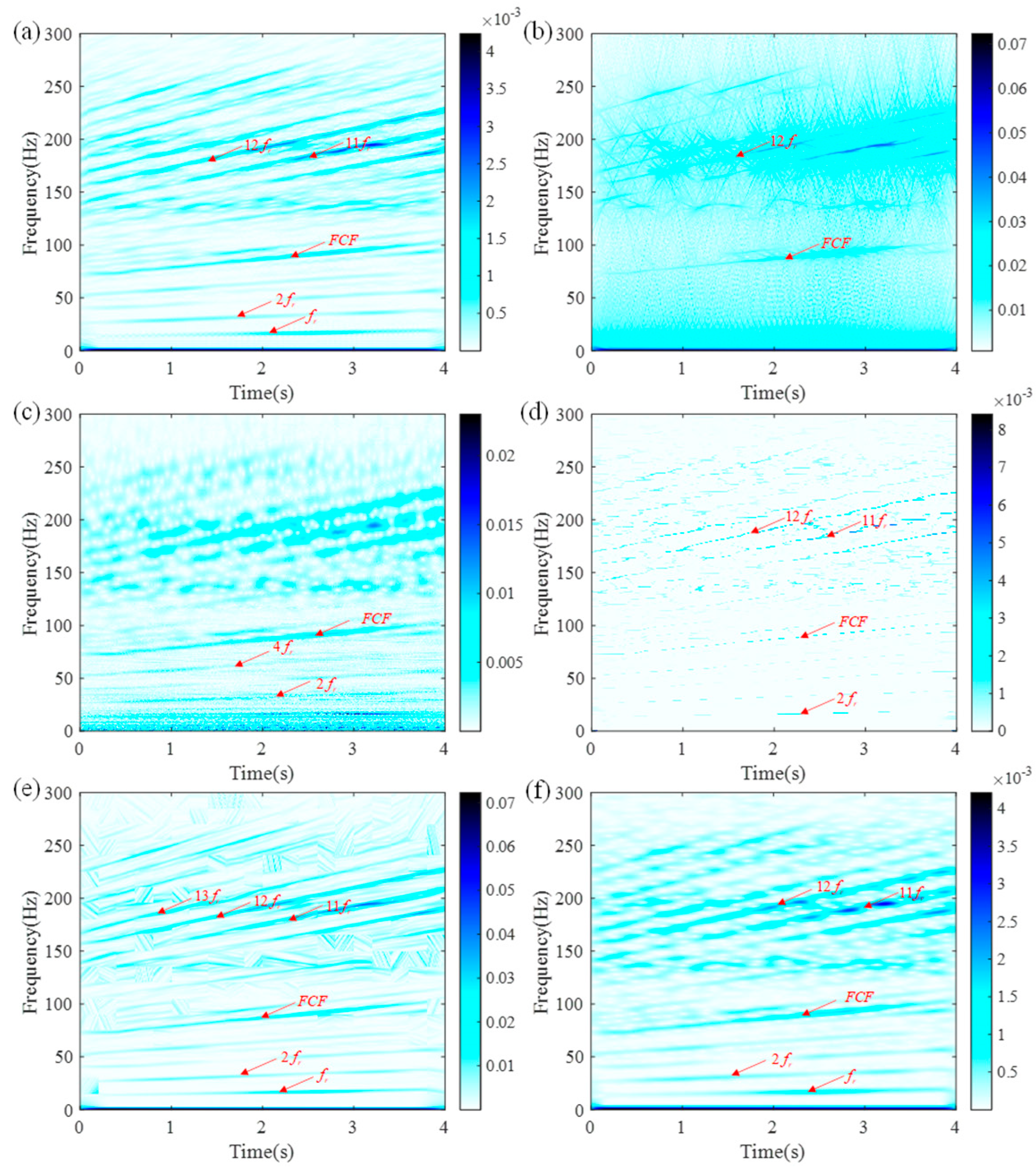
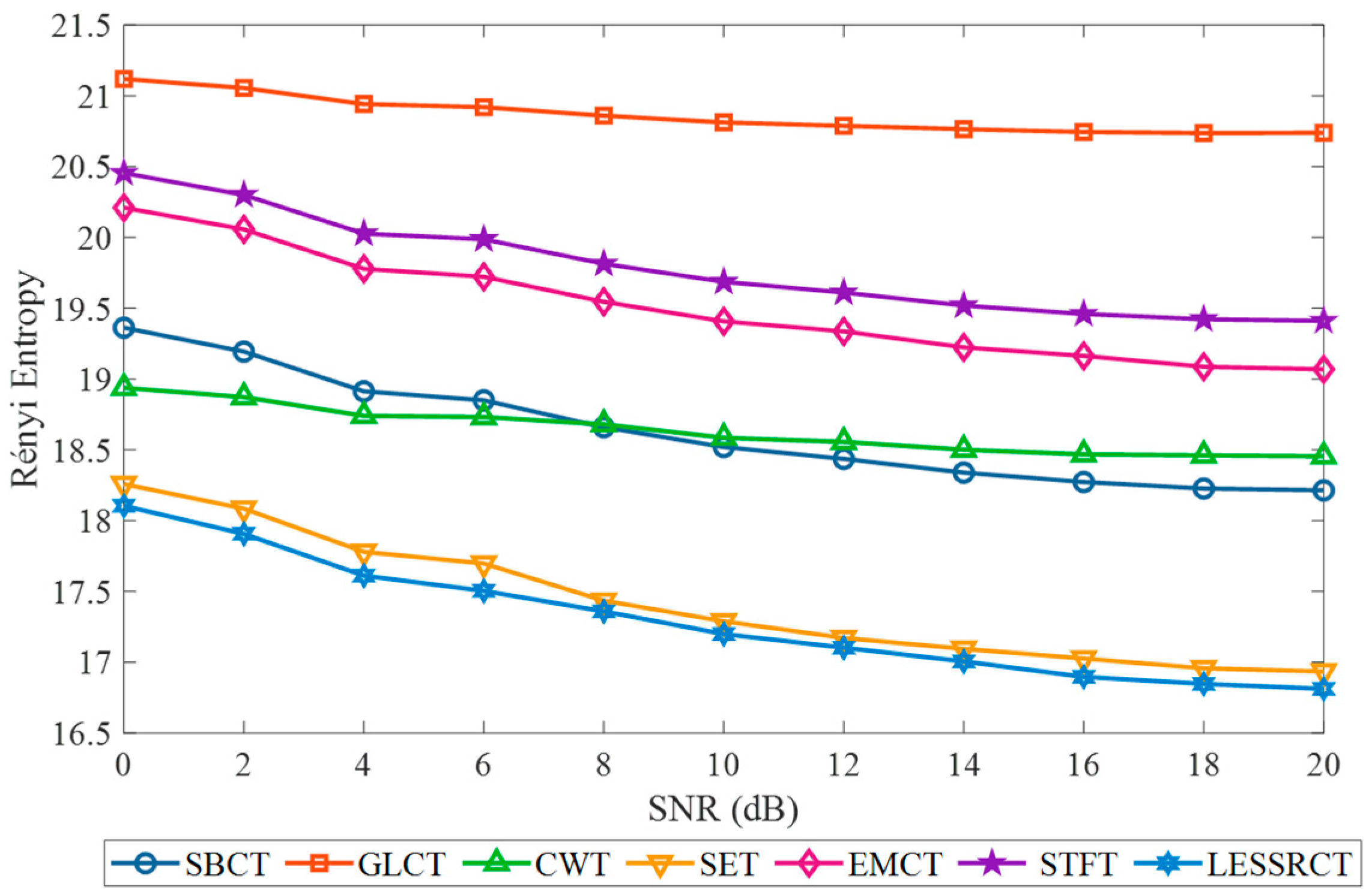

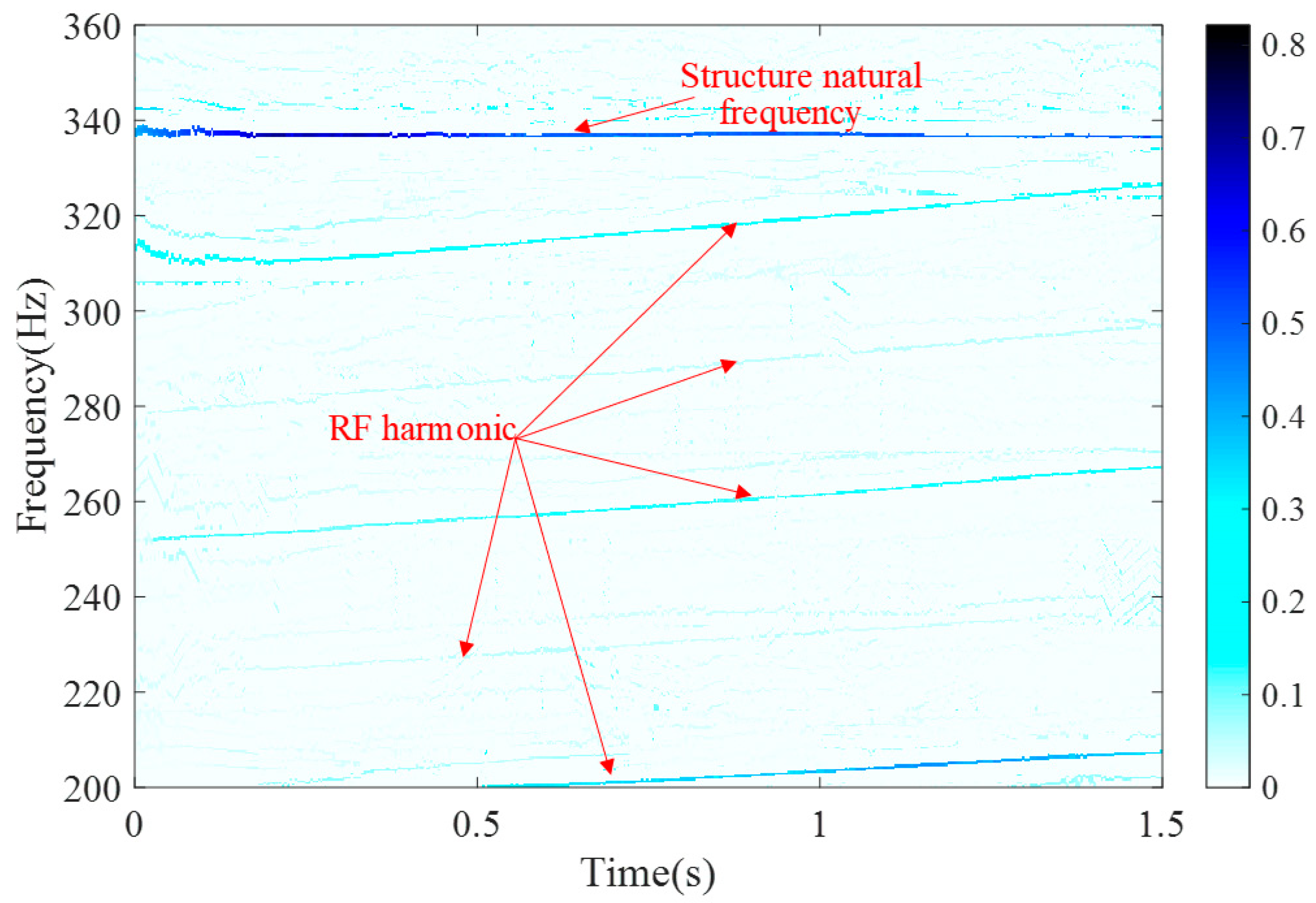
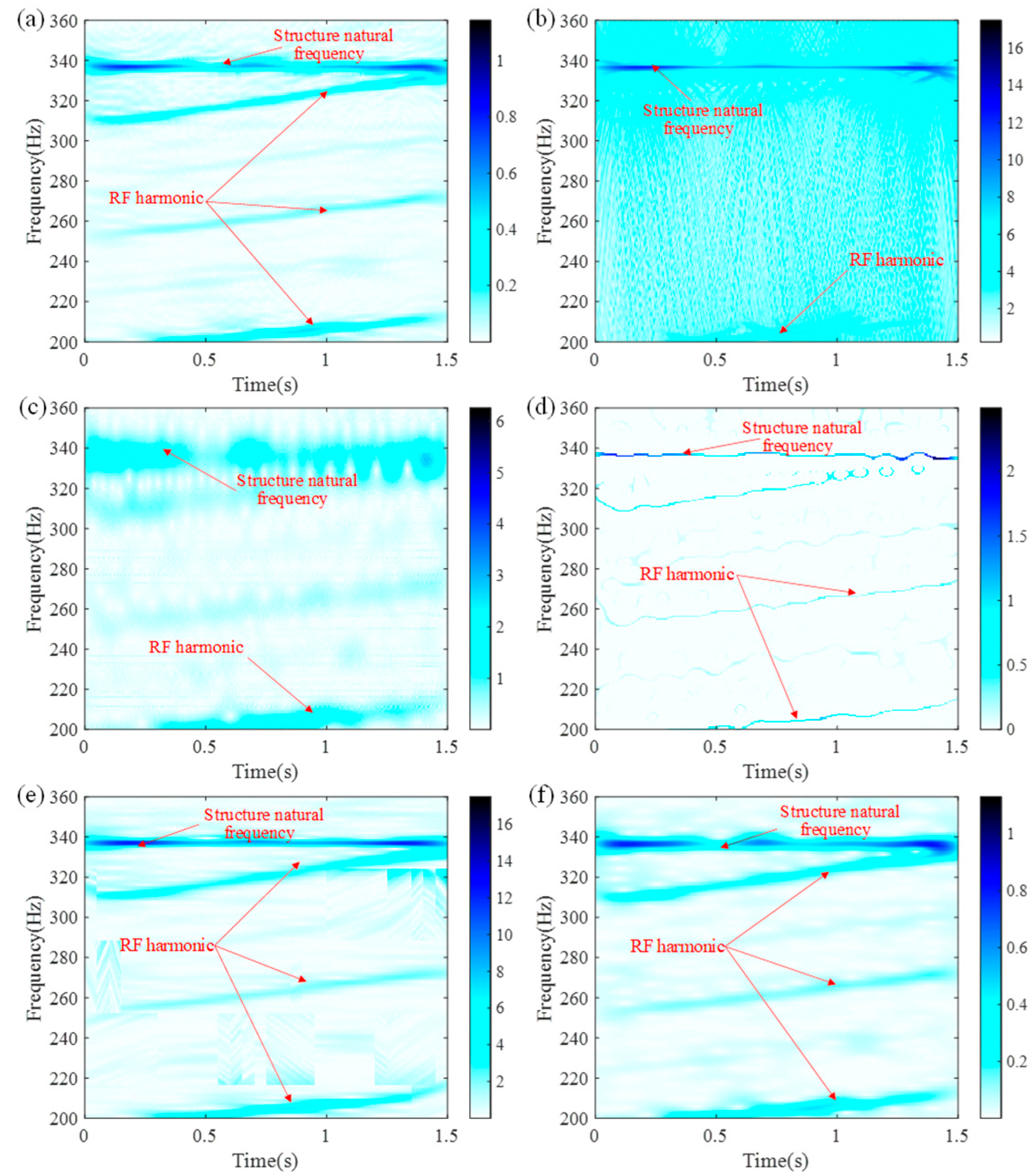

| Method | SBCT | GLCT | CWT | SET | EMCT | STFT | LESSRCT |
| Rényi entropy | 16.0713 | 18.3627 | 16.8712 | 14.7565 | 16.8717 | 16.9143 | 13.5316 |
| Fault Type | Pitch Diameter | Number of Balls | Ball Diameter | FCF |
|---|---|---|---|---|
| inner race fault | 38.52 mm | 9 | 7.94 mm | 5.43 fr |
| Method | SBCT | GLCT | CWT | SET | EMCT | STFT | LESSRCT |
| Rényi entropy | 18.1515 | 20.7281 | 18.4348 | 15.1607 | 19.0051 | 19.3523 | 16.6139 |
| Method | SBCT | GLCT | CWT | SET | EMCT | STFT | LESSRCT |
| Computation Time (s) | 0.2345 | 1.5701 | 0.1192 | 0.1444 | 1.0459 | 0.0938 | 1.3119 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quan, D.; Niu, Y.; Zhao, Z.; He, C.; Yang, X.; Li, M.; Wang, T.; Zhang, L.; Ma, L.; Zhao, Y.; et al. Resolving Non-Proportional Frequency Components in Rotating Machinery Signals Using Local Entropy Selection Scaling–Reassigning Chirplet Transform. Aerospace 2025, 12, 616. https://doi.org/10.3390/aerospace12070616
Quan D, Niu Y, Zhao Z, He C, Yang X, Li M, Wang T, Zhang L, Ma L, Zhao Y, et al. Resolving Non-Proportional Frequency Components in Rotating Machinery Signals Using Local Entropy Selection Scaling–Reassigning Chirplet Transform. Aerospace. 2025; 12(7):616. https://doi.org/10.3390/aerospace12070616
Chicago/Turabian StyleQuan, Dapeng, Yuli Niu, Zeming Zhao, Caiting He, Xiaoze Yang, Mingyang Li, Tianyang Wang, Lili Zhang, Limei Ma, Yong Zhao, and et al. 2025. "Resolving Non-Proportional Frequency Components in Rotating Machinery Signals Using Local Entropy Selection Scaling–Reassigning Chirplet Transform" Aerospace 12, no. 7: 616. https://doi.org/10.3390/aerospace12070616
APA StyleQuan, D., Niu, Y., Zhao, Z., He, C., Yang, X., Li, M., Wang, T., Zhang, L., Ma, L., Zhao, Y., & Wu, H. (2025). Resolving Non-Proportional Frequency Components in Rotating Machinery Signals Using Local Entropy Selection Scaling–Reassigning Chirplet Transform. Aerospace, 12(7), 616. https://doi.org/10.3390/aerospace12070616






