Independence Requirement Analysis for Common-Mode Analysis of Aircraft System Safety Based on AADL
Abstract
1. Introduction
2. AADL Modeling Method for Typical Aircraft Systems
2.1. Construction of System Nominal Model
2.2. Construction of System Extended Model
- Error propagation indicates the conditions under which a component emits an error;
- Error event represents the event that occurs in the component;
- Error transition defines how the state machine moves from one state to another, including the initial state, transition conditions, and termination state;
- Error source indicates that an error propagates out of the component;
- Error path describes how an error that originates outside a component, passes through the component;
- Error sink indicates that an error that enters a component, is handled inside the component;
- Error state defines the specific error states of the state-machine error-behavior models.
2.3. AADL Modeling: A Case Study of the Primary Flight Computer
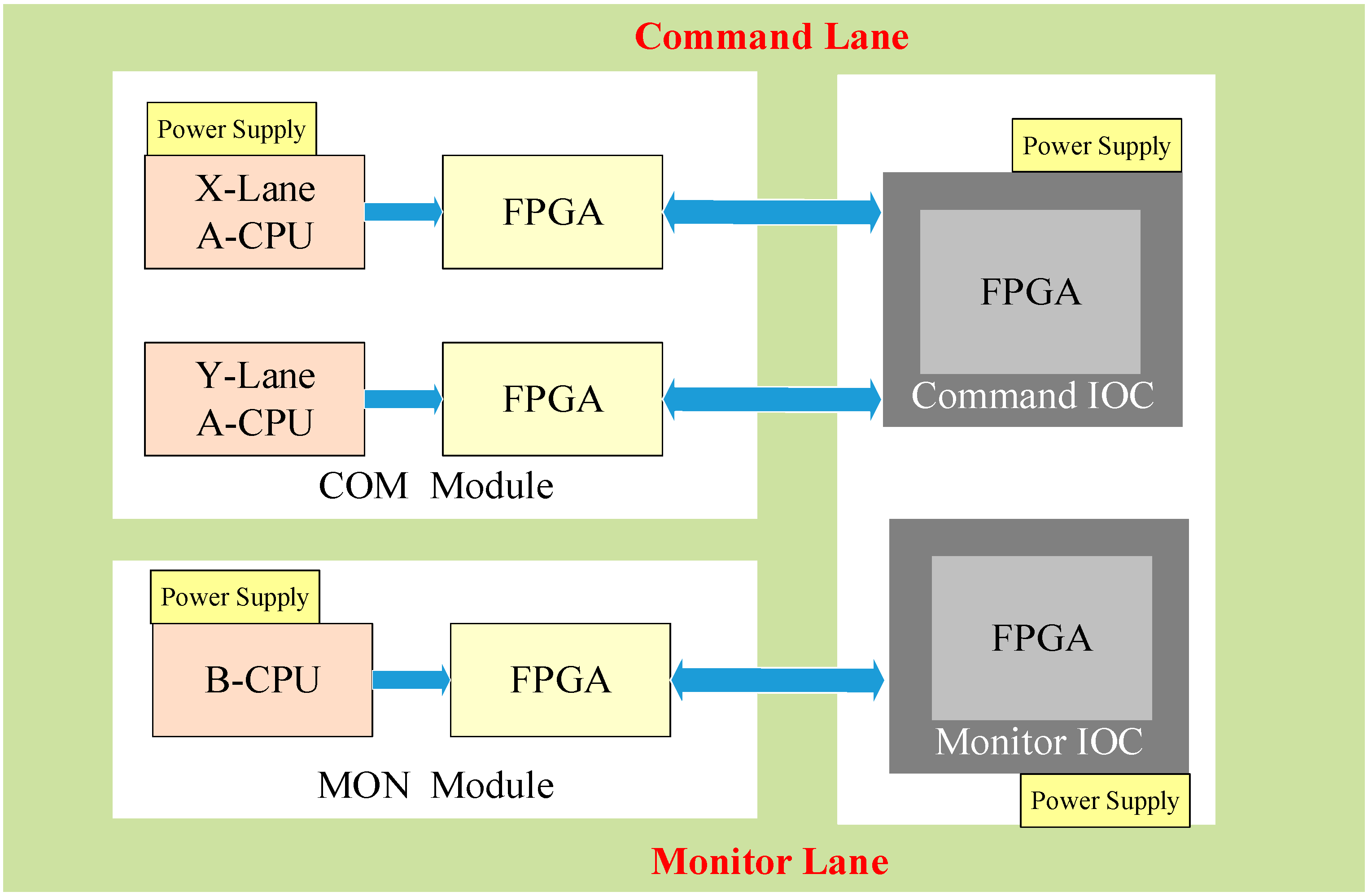
2.3.1. Description of the PFC
2.3.2. Nominal Model of the PFC
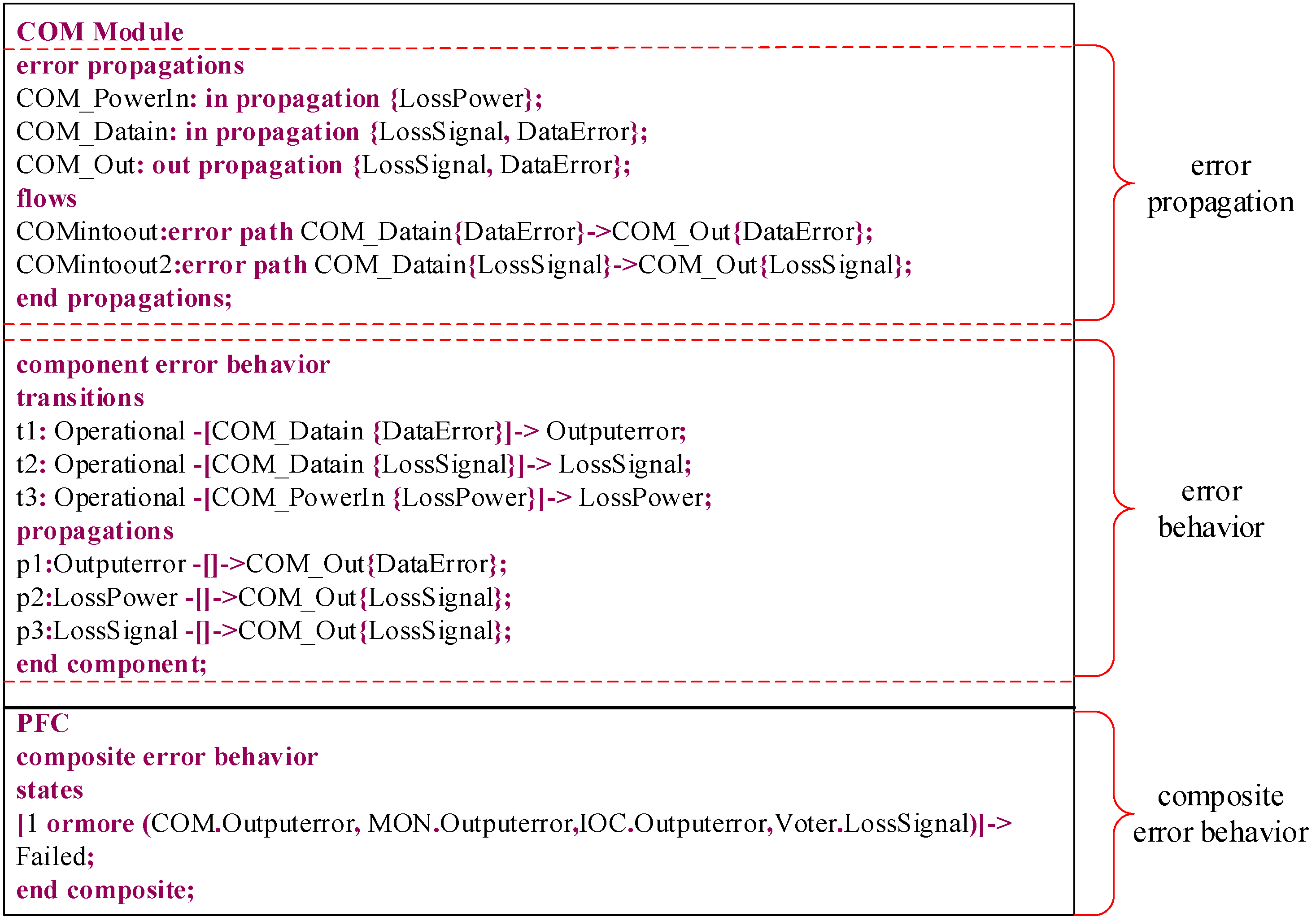
2.3.3. Extended Model of the PFC
3. Identification of Independence Requirements Using Fault Propagation
3.1. Common-Mode Analysis Process
3.2. Fault Propagation Model Construction Based on the AADL Model
3.3. Common-Mode Independence Requirements Identification
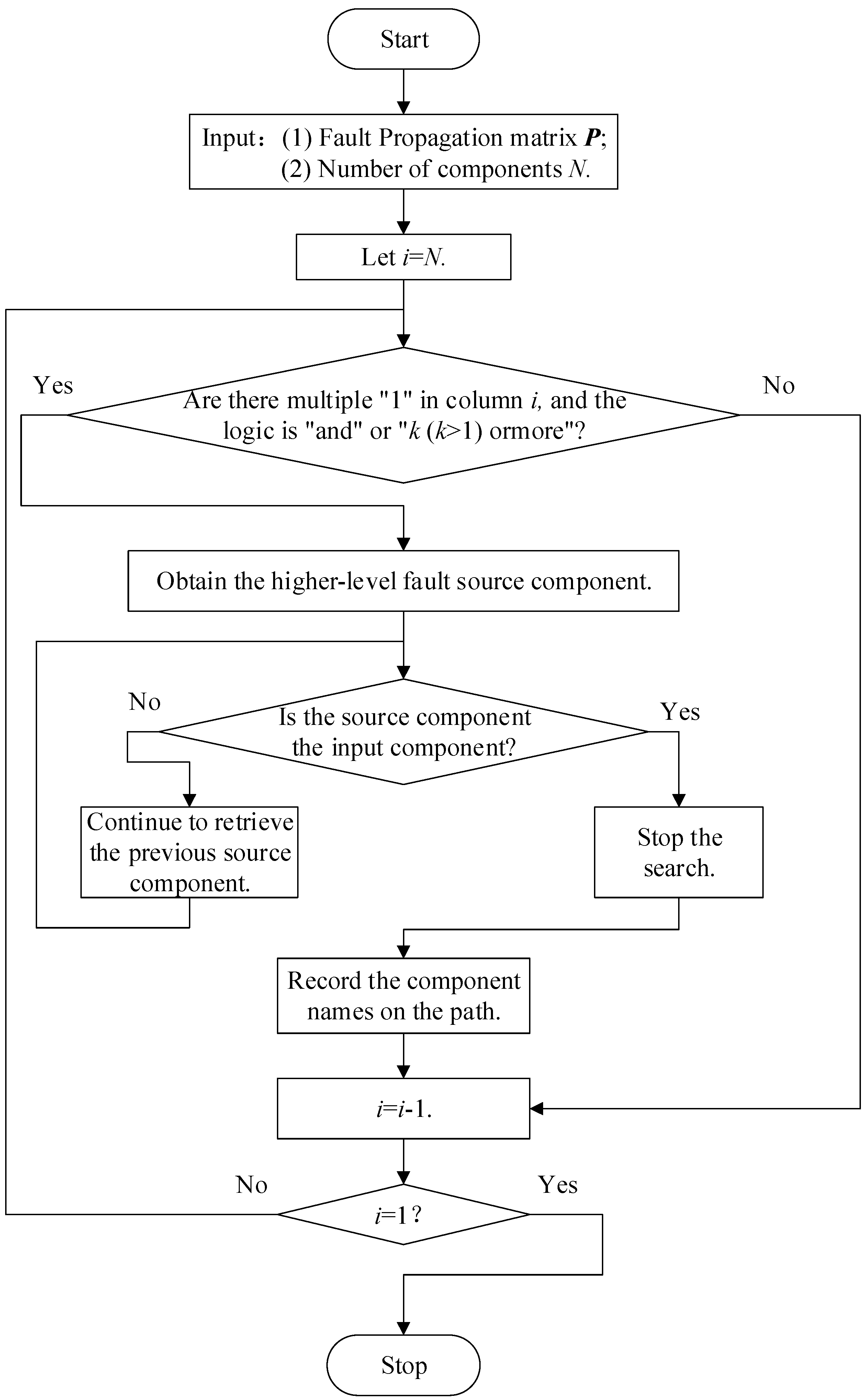
| Algorithm 1 The algorithm of Error propagation path determination |
| Extract Error propagation path: Extract_CP( ) INPUT: the error propagation model OUTPUT: component path |
|
3.4. Independence Requirement Identification: A Case Study of the PFC
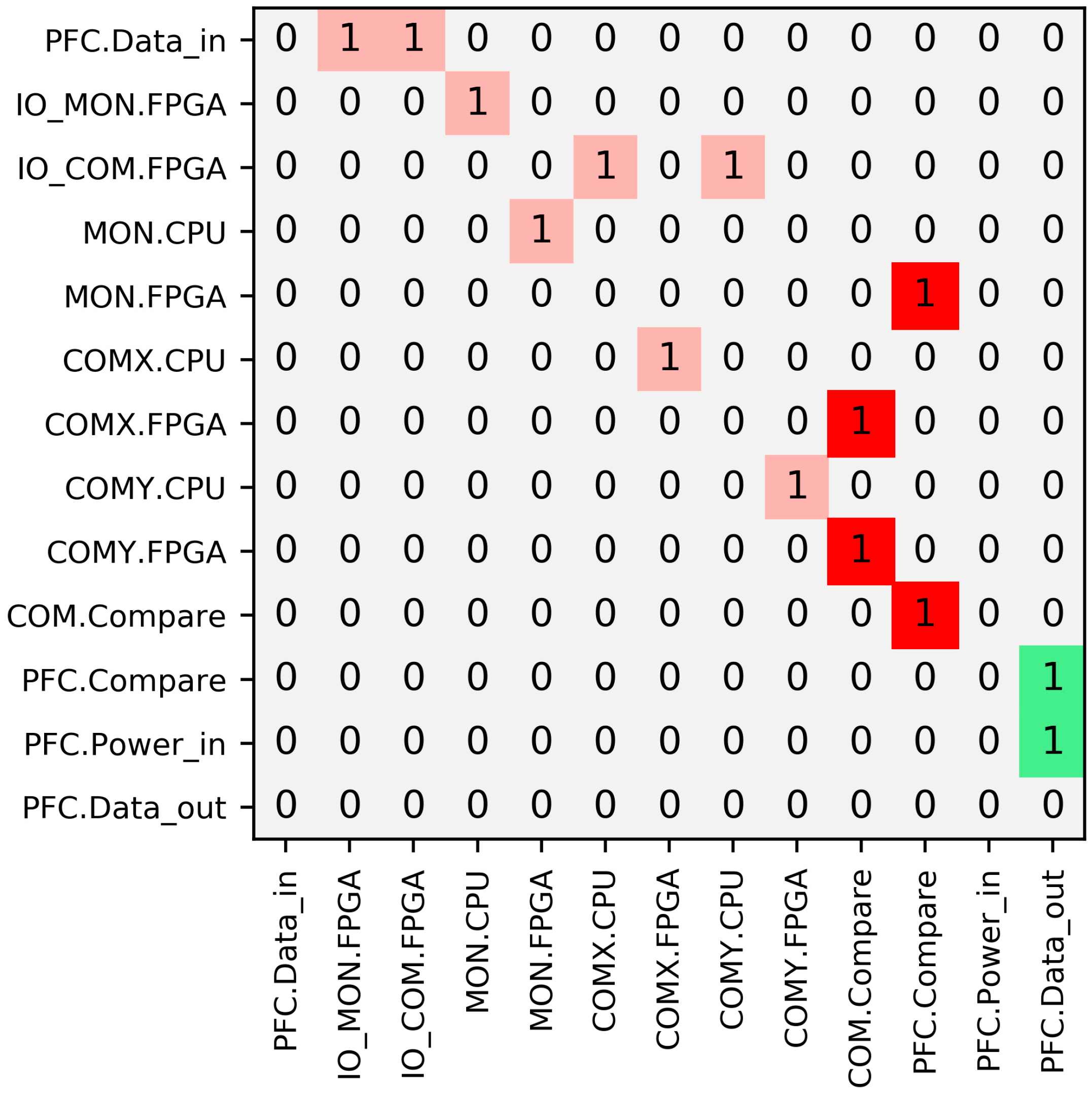
3.4.1. Fault Propagation Model of the PFC
3.4.2. Common-Mode Independence Requirements Identification of the PFC
4. Discussion and Comparison Analysis
4.1. Common-Mode Independence Requirements Analysis
4.2. Comparison with FTA-Based Method
5. Conclusions
- AADL is used to establish nominal and extended models of redundant systems. CMA is conducted based on these models, ensuring consistency between the aircraft analysis and the design models.
- A fault propagation model is established based on the AADL model. It can identify factors that may cause aircraft system CMF and propose independence requirements. The analysis results can be dynamically updated in response to architecture modification.
- The effectiveness of the proposed method is verified by comparing the CMA method based on the fault propagation model with the traditional FTA method. The proposed method can avoid the cumbersome process of constructing fault trees in traditional CMA.
- AADL-based automation for independence requirements: We introduce a novel, automated method to derive common-mode independence requirements directly from AADL models. By constructing a fault propagation model and analyzing its logic (e.g., “AND” gates), the method systematically identifies potential CMF component combinations, significantly reducing manual effort and subjectivity compared to traditional FTA-based CMA.
- Ensured consistency and dynamic update capability: The approach maintains consistency between the AADL design model and safety analysis (fault propagation model, requirements). Crucially, both the model and derived requirements can be dynamically updated as the architecture evolves, enabling efficient iterative design and assessment.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CMF | Common-mode failures |
| CMA | Common-mode analysis |
| FTA | Fault tree analysis |
| MBSA | Model-based safety analysis |
| AADL | Architecture analysis and design language |
| PFC | Primary flight computer |
| CPU | Central processing unit |
| FPGA | Field programmable gate array |
| OSATE | Open source AADL tool environment |
| IOC | Input and Output Controller |
| COM | Command Module |
| MON | Monitor Module |
References
- ARP4761A; Guidelines for Conducting the Safety Assessment Process on Civil Aircraft, Systems, and Equipment. SAE International: Warrendale, PA, USA, 2023.
- Peng, C.; Sun, Y.C.; Guo, Y.Y. Assessment of safety risk in airline operations based on constant-sum game. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2024, 238, 157–168. [Google Scholar] [CrossRef]
- Huang, M.Y.; Jie, Y.W.; Song, Z.T. Common mode airworthiness requirements and certification considerations for fly-by-wire. Civ. Aircr. Des. Res. 2023, 2, 1–7. [Google Scholar]
- Hana, M.; Dominique, B.; Etienne, B. A benchmark of incremental model transformation tools based on an industrial case study with AADL. Softw. Syst. Model. 2022, 22, 175–201. [Google Scholar]
- Zhang, X.S.; Leng, K.; Luo, S.M.; Zeng, Q.H. Research on the safety analysis of multi-purpose civil engine. Qual. Reliab. 2023, 5, 35–40. [Google Scholar]
- ARP4754A; Guidelines for Development of Civil Aircraft and Systems. SAE International: Warrendale, PA, USA, 2010.
- Gao, S.; Wang, J.T.; Zhang, J. Reliability analysis of a redundant series system with common cause failures and delayed vacation. Reliab. Eng. Syst. Saf. 2023, 239, 109467. [Google Scholar] [CrossRef]
- Sun, M.; Gautham, S.; Ge, Q. Defining and characterizing model-based safety assessment: A review. Saf. Sci. 2024, 172, 106425. [Google Scholar] [CrossRef]
- Chen, L.; Jiao, J.; Zhao, T.D. Review for model-based safety analysis of complex safety-critical system. Syst. Eng. Electron. 2017, 39, 1287–1291. [Google Scholar]
- Rauzy, A. Mode automata and their compilation into fault trees. Reliab. Eng. Syst. Saf. 2002, 78, 1–12. [Google Scholar] [CrossRef]
- Joshi, A.; Miller, S.P.; Whalen, M.; Heimdahl, M.P.E. A proposal for model-based safety analysis. In Proceedings of the 24th Digital Avionics Systems Conference, Washington, DC, USA, 30 October–3 November 2005; Volume 2, p. 13. [Google Scholar]
- Akerlund, O.; Bieber, P.; Boede, E.; Bozzano, M.; Bretschneider, M.; Castel, C.; Cavallo, A.; Cifaldi, M.; Gauthier, J.; Griffault, A.; et al. ISAAC, a framework for integrated safety analysis of functional, geometrical and human aspects. In Proceedings of the Embedded Real Time Software and Systems Conference, Toulouse, France, 25–27 January 2006. [Google Scholar]
- Lanzani, L.; Uliano, L.; Scattolini, R. Integration of commonalities in the paradigm of model-based safety analysis in aerospace. In Proceedings of the 17th International Conference on Probabilistic Safety Assessment and Management and Asian Symposium on Risk Assessment and Management, Kyoto, Japan, 7–11 October 2024. [Google Scholar]
- Magdalena, P.; Wojciech, S. Assessment of the Potential of Electric Propulsion for General Aviation Using Model-Based System Engineering (MBSE) Methodology. Aerospace. 2022, 9, 74. [Google Scholar]
- Qi, J.; Hu, J.; Gu, Q.F. Class flattening method for Altarica 3.0 model. Comput. Sci. 2021, 48, 51–59. [Google Scholar]
- Arnold, A.; Point, G.; Griffault, A.; Rauzy, A. The AltaRica formalism for describing concurrent systems. Fundam. Inform. 1999, 40, 109–124. [Google Scholar] [CrossRef]
- Feiler, P.; Gluch, D.; Hudak, J. The Architecture Analysis & Design Language (AADL): An Introduction; Carnegie Mellon University, Software Engineering Institute’s Digital Library, Software Engineering Institute: Pittsburgh, PA, USA, 2006. [Google Scholar]
- AS5506/1; SAE Architecture Analysis and Design Language (AADL) Annex Volume 1: Annex E: Error Model Annex. SAE International Technical Standard: Warrendale, PA, USA, 2006.
- Jiang, Z.Y.; Zhao, T.D.; Wang, S.H. New Model-Based Analysis Method with Multiple Constraints for Integrated Modular Avionics Dynamic Reconfiguration Process. Processes 2020, 8, 574. [Google Scholar] [CrossRef]
- Ling, S.X.; Yang, Z.B.; Guo, P.; Zhou, Y. An approach for IMA software code generation on domestic airborne operating system. Aeronaut. Comput. Tech. 2024, 54, 84–88. [Google Scholar]
- Hou, Z.G.; Xiong, M.L.; Wang, H.W. Civil aviation safety risk intelligent early warning model based on text mining and multi-model fusion. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2023, 237, 2402–2427. [Google Scholar] [CrossRef]
- Pop, P.; Zarrin, B.; Barzegaran, M. The FORA fog computing platform for industrial IoT. Inf. Syst. 2021, 98, 101727. [Google Scholar] [CrossRef]
- Sannes, P.S.; Apvrille, L.; Vingerhoeds, R. Checking SysML models against safety and security properties. J. Aerosp. Inf. Syst. 2021, 18, 906–918. [Google Scholar]
- Li, D.M.; Li, J.; Lin, H.F. Reliability Analysis method of Embedded System AADL Model Based on Fault Tree Analysis. Comput. Sci. 2017, 44, 182–188. [Google Scholar]
- Maruf, A.M.; Azim, A. Requirements-preserving design automation for multiprocessor embedded system applications. J. Ambient Intell. Humaniz. Comput. 2020, 12, 821–833. [Google Scholar] [CrossRef]
- Liu, L.; Lei, L.; Zhao, W. A Safety Evaluation Method of IMA Dynamic Reconfiguration Process Based on CPN. J. Phys. Conf. Ser. 2020, 1646, 012053. [Google Scholar] [CrossRef]
- Belt, J.; Hatcliff, J.; Shackleton, J. Model-driven development for the seL4 microkernel using the HAMR framework. J. Syst. Archit. 2023, 134, 102789. [Google Scholar] [CrossRef]
- Li, Z.; Cao, Z.N.; Fang, F.J. A Modeling and Verification Method of Cyber-Physical Systems Based on AADL and Process Algebra. Int. J. Softw. Eng. Knowl. Eng. 2024, 34, 49–89. [Google Scholar] [CrossRef]
- Hamdane, M.E.; Harous, S.; Kerkouche, E. Improving consistency of AADL models: A composition approach. Syst. Eng. 2023, 26, 257–270. [Google Scholar] [CrossRef]
- Lu, Y.; Qin, S.D.; Guo, P. Hardware-software Integrated Reliability Modeling and Analysis Using AADL. J. Softw. 2022, 33, 2995–3014. [Google Scholar]
- Yang, H.Y.; Sun, Y.C. A combination method for integrated modular avionics safety analysis. Aircr. Eng. Aerosp. Technol. 2023, 95, 345–357. [Google Scholar] [CrossRef]
- Zhang, R.; Geng, L.; Liu, W. Research on static fault tree analysis method for inerting system safety based on random number generation. Aircr. Eng. Aerosp. Technol. 2023, 95, 649–657. [Google Scholar] [CrossRef]
- Liu, W.; Guo, Q.; Wang, M. Research on Airborne Electronic Equipment Common Mode Analysis Method. Aeronaut. Comput. Tech. 2022, 52, 126–129. [Google Scholar]
- Luo, J.G. Quantitative safety analysis of train control system considering common cause failure. Control Inf. Technol. 2024, 1, 116–120. [Google Scholar]
- Luo, J.W.; Ge, J.Z.; Chen, K.P. Review of reliability assessment methods for complex systems. Electron. Prod. Reliab. Environ. Test. 2024, 41, 122–130. [Google Scholar]
- Tao, J.; Ye, Y.; Jiang, Z.Q.; Tang, B.; Liu, Q. Research on reliability model of power synchronous network based on Beidou system. Electron. Des. Eng. 2024, 32, 150–154. [Google Scholar]

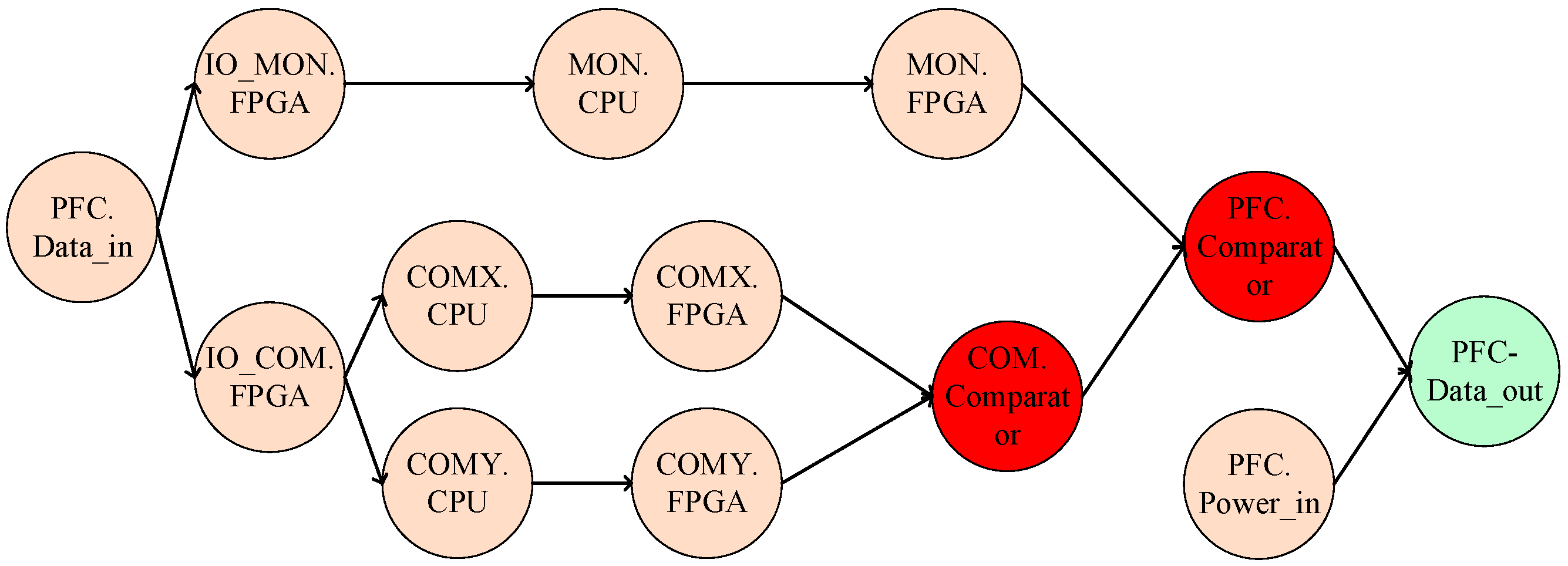
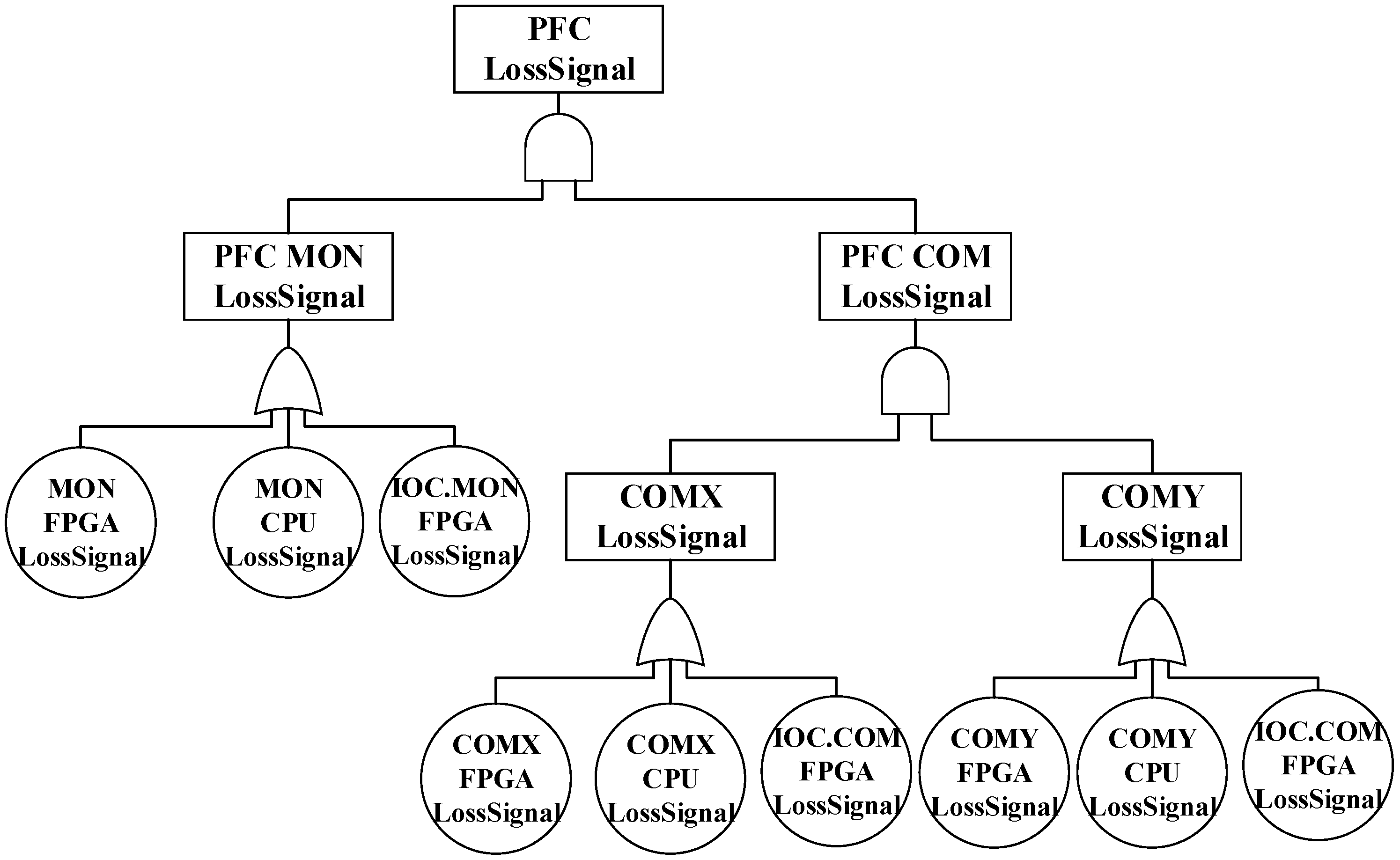
| Category | Component | Detailed Explanations |
|---|---|---|
| Software | Data | Different types of data |
| Thread | Schedulable units for parallel execution | |
| Process | Virtual processor for scheduling and executing threads | |
| Hardware | Processor | Scheduling and executing threads |
| Memory | Store code and data | |
| Bus | Connect processors, memory, and devices | |
| Device | Components such as sensors and actuators that represent external interfaces | |
| System | Abstract | Represent any other component |
| System | Integrate software, hardware, and other components |
| Common-Mode Types | Common-Mode Sub-Types | Common-Mode Sources |
|---|---|---|
| Concept and Design | Design Architecture | Electrical power, hydraulic, ventilation, etc. |
| Technology, Materials, Equipment | Size, hardware, software, material, etc. | |
| Manufacturing | Manufacturer | Common manufacturer, procedure, etc. |
| Operation | Staff, procedures | Common staff, same procedure |
| Environment | Electrical and radiation | Electromagnetic, radiation, etc. |
| Mechanical and thermal | Temperature, grit, vibration, etc. |
| Component Name | Design Architecture | Technology, Materials, Equipment | Manufacturer |
|---|---|---|---|
| IO_COM. FPGA | IOC_Power | IOC | FPGA manufacturer |
| IO_MON. FPGA | IOC_Power | IOC | FPGA manufacturer |
| COMX. CPU | COM_Power | COM | CPU_A manufacturer |
| COMX. FPGA | COM_Power | COM | FPGA manufacturer |
| COMY. CPU | COM_Power | COM | CPU_A manufacturer |
| COMY. FPGA | COM_Power | COM | FPGA manufacturer |
| COM. Comparator | COM_Power | COM | Comparator manufacturer |
| MON. CPU | MON_Power | MON | CPU_B manufacturer |
| MON. FPGA | MON_Power | MON | FPGA manufacturer |
| PFC. Comparator | PFC_Power | PFC | Comparator manufacturer |
| Code | Component Pair | Independence Requirement Description | |
|---|---|---|---|
| 1 | COMX. CPU | COMY. CPU | CPU in COM X-lane and Y-lane should be independent |
| 2 | COMX. CPU | MON. CPU | CPU in COM and MON module should be independent |
| 3 | COMX. FPGA | COMY. FPGA | FPGA in COM X-lane and Y-lane should be independent |
| 4 | COMX. FPGA | MON. FPGA | FPGA in COM and MON module should be independent |
| 5 | IO_COM. FPGA | IO_MON. FPGA | FPGA in IOC module COM and MON should be independent |
| 6 | COMX. CPU | COMY. FPGA | CPU in X lane and FPGA in Y lane should be independent |
| 7 | COMY. CPU | COMX. FPGA | CPU in Y lane and FPGA in X lane should be independent |
| 8 | COMX. FPGA | IO_MON. FPGA | CPU in COM and IOC module should be independent |
| 9 | COMY. FPGA | IO_MON. FPGA | N/A |
| 10 | MON. FPGA | IO_MON. FPGA | N/A |
| ID | Independence Requirement |
|---|---|
| 1 | CPU in COM X-lane and Y-lane should be independent |
| 2 | CPU in COM and MON module should be independent |
| 3 | FPGA in COM X-lane and Y-lane should be independent |
| 4 | CPU in COM and IOC module should be independent |
| 5 | FPGA in COM and MON module should be independent |
| 6 | FPGA in IOC module COM and MON should be independent |
| 7 | CPU in X lane and FPGA in Y lane should be independent |
| 8 | CPU in Y lane and FPGA in X lane should be independent |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruan, H.; Qi, F.; Wei, X.; Zhou, Y.; Lu, Z. Independence Requirement Analysis for Common-Mode Analysis of Aircraft System Safety Based on AADL. Aerospace 2025, 12, 603. https://doi.org/10.3390/aerospace12070603
Ruan H, Qi F, Wei X, Zhou Y, Lu Z. Independence Requirement Analysis for Common-Mode Analysis of Aircraft System Safety Based on AADL. Aerospace. 2025; 12(7):603. https://doi.org/10.3390/aerospace12070603
Chicago/Turabian StyleRuan, Hongze, Fan Qi, Xiaohui Wei, Yadong Zhou, and Zhong Lu. 2025. "Independence Requirement Analysis for Common-Mode Analysis of Aircraft System Safety Based on AADL" Aerospace 12, no. 7: 603. https://doi.org/10.3390/aerospace12070603
APA StyleRuan, H., Qi, F., Wei, X., Zhou, Y., & Lu, Z. (2025). Independence Requirement Analysis for Common-Mode Analysis of Aircraft System Safety Based on AADL. Aerospace, 12(7), 603. https://doi.org/10.3390/aerospace12070603









