Advancing Aviation Safety Through Predictive Maintenance: A Machine Learning Approach for Carbon Brake Wear Severity Classification
Abstract
1. Introduction
2. Literature Review
2.1. A Lack of Consideration for the Operational and Environmental Contexts
2.2. A Lack of Representation of the Operational Variability in Vehicle Dynamics
2.3. A Shift from Traditional Models to ML Approaches
2.4. Need for ML Model Interpretability and Uncertainty Quantification
2.5. Balancing Trial-And-Error with Computational Constraints for Hyperparameter Tuning
2.6. Observations from the Literature and Statement of Research Contributions
- Insufficient integration of operational and environmental context: Most prior studies rely on sparse datasets, often overlooking important variables such as aircraft-specific metrics, operational factors, weather conditions, and airport characteristics. This highlights the need for a comprehensive and representative dataset that captures the interactions among these factors.
- Limited representation of real-world operational variability: Many studies rely on simulations or controlled experiments that hold certain variables (e.g., speed, pressure) constant, failing to capture the dynamic and unpredictable nature of real-world vehicle operations. This limits model generalizability and applicability and underscores the need for data that reflects true operational variability in aircraft dynamics.
- Incomplete adoption of robust ML techniques due to limited data: While ML models show promise in capturing complex wear patterns, their performance is often constrained by limited, non-representative training data. This highlights the need for broader data collection and integration.
- Lack of interpretability and uncertainty quantification in ML models: Deep learning models used in prior studies are often opaque and computationally intensive, hindering their deployment in real-time systems. Moreover, few studies quantify predictive uncertainty, which is essential for safety-critical applications like brake wear prediction.
- Lack of systematic hyperparameter optimization: Many studies rely on trial-and-error methods for model selection and tuning, often constrained by computational resources and lacking transparency in the optimization process.
- Comprehensive data utilization: Real-world flight operations data from a commercial airline is integrated with environmental and airport context from FlightAware®, resulting in a rich and multidimensional dataset suitable for ML model training.
- Rigorous benchmarking of classification approaches: A supervised learning pipeline is developed to systematically evaluate and compare a wide range of classifiers, including interpretable models such as Logistic Regression and Decision Trees, and high-performance ensemble methods such as XGBoost and Categorical Boosting (CatBoost).
- Structured hyperparameter optimization: Grid search with cross-validation is employed to systematically tune model parameters and enhance predictive accuracy across all algorithms.
- Influential factor analysis: The most significant features driving brake wear severity are identified to guide actionable insights for airline operations and maintenance planning.
- Uncertainty measurement: Uncertainty quantification is incorporated to reflect the stochastic nature of operational data, thereby improving the reliability of maintenance recommendations.
3. Methodology
4. Implementation
4.1. Step 1: Feature Engineering and Data Fusion
4.2. Step 1: Data Preprocessing
4.2.1. Feature Exclusion Based on Correlation
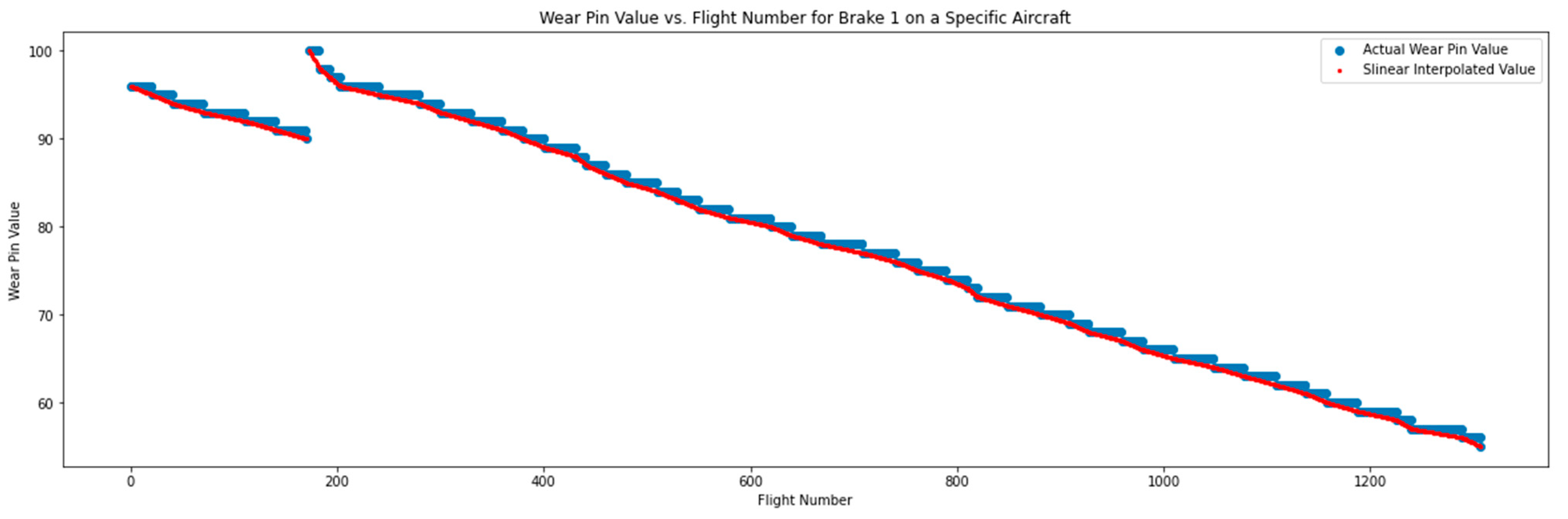
4.2.2. Wear Pin Value Correction and Interpolation
4.2.3. Averaging Feature Values over Constant Wear Pin Segments
4.2.4. Data Labeling and Outlier Identification
4.2.5. Handling Missing Data and Scaling Numerical Features
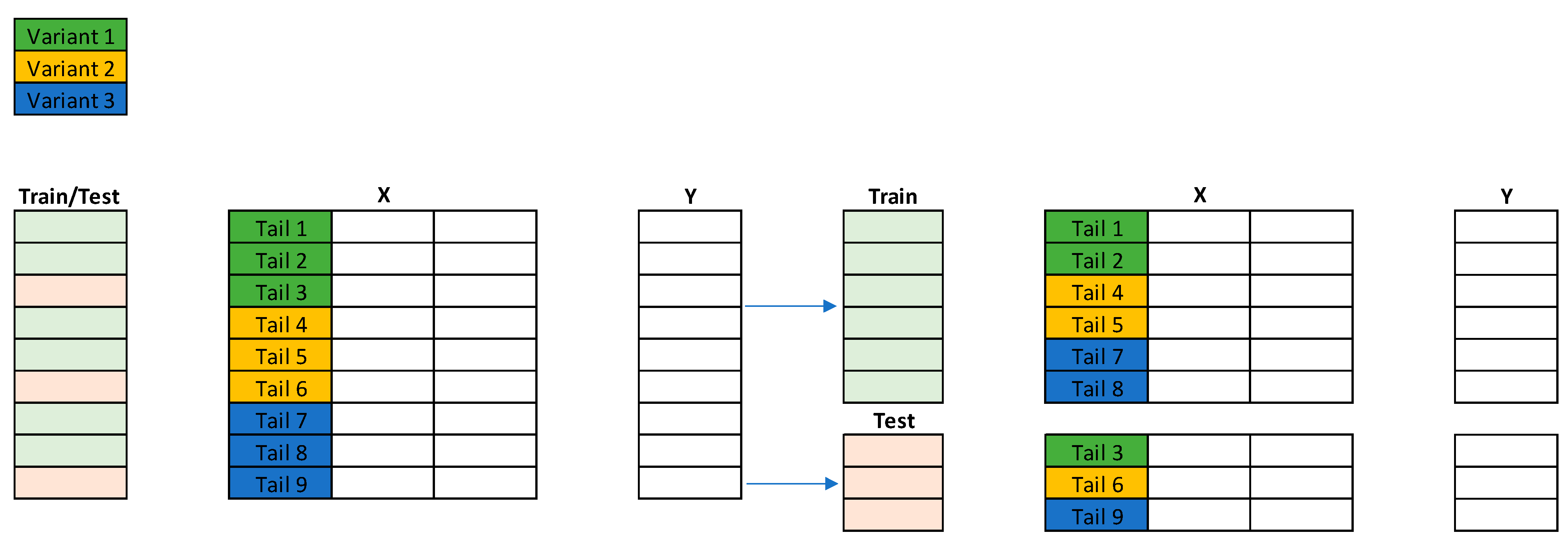
4.3. Step 3: Data Splitting
4.4. Step 4: Model Training and Hyperparameter Tuning
- Approach 2: Simplifying the task to a binary classification problem by excluding data points labeled as ‘Medium’ and focusing solely on distinguishing between ‘High’ and ‘Low’ wear. This simplification is particularly appealing for models where clear differentiation between extreme wear conditions is more relevant than the nuanced distinction of ‘Medium’ wear.
- Approach 3: Merging the ‘Medium’ and ‘Low’ wear labels based on the observation that these two categories share similar feature distributions, as revealed in prior analyses [51]. This approach also treats the problem as a binary classification task to predict wear being either ‘High’ or the combined category of ‘Low/Medium.’
4.4.1. Hyperparameter Tuning
4.4.2. Algorithms Benchmarked with Varying Hyperparameters
4.5. Step 5: Model Testing and Evaluation
4.6. Step 6: Results Analysis and Model Selection
- Performance Metrics Assessment: Key performance metrics, such as those mentioned in Step 5, are reviewed to assess the performance of the models across the different wear categories. These metrics help understand the models’ abilities to correctly predict high and low wear conditions and their robustness against false predictions.
- Model Selection Based on Practical Implications: The top model is selected based on its performance and practicality in deployment. The latter considers several factors, including the model’s ability to minimize both FN and FP rates, the impact of these rates on maintenance operations and safety, and the overall cost-effectiveness of implementing the model. In this context, an FN occurs when the model predicts a ‘Low’ wear condition when the actual label is ‘High.’ This case is particularly concerning because failing to identify a high-wear condition could lead to undetected brake wear, potentially compromising safety. Therefore, minimizing the FN rate is key to detecting and promptly addressing all significant wear instances. An FP, on the other hand, happens when the model predicts a ‘High’ wear condition when the actual label is ‘Low.’ While this does not pose a direct safety risk, it can lead to unnecessary inspections and maintenance work, increasing operational costs and causing potential downtime. Minimizing the FP rate is important to maintain cost-effectiveness and operational efficiency. This analysis helps select the model that best balances accuracy with practical deployment considerations, ensuring that it can be effectively leveraged by existing aircraft maintenance systems.
4.7. Step 7: Model Interpretability and Explainability
4.8. Step 8: Uncertainty Quantification
5. Results and Discussion
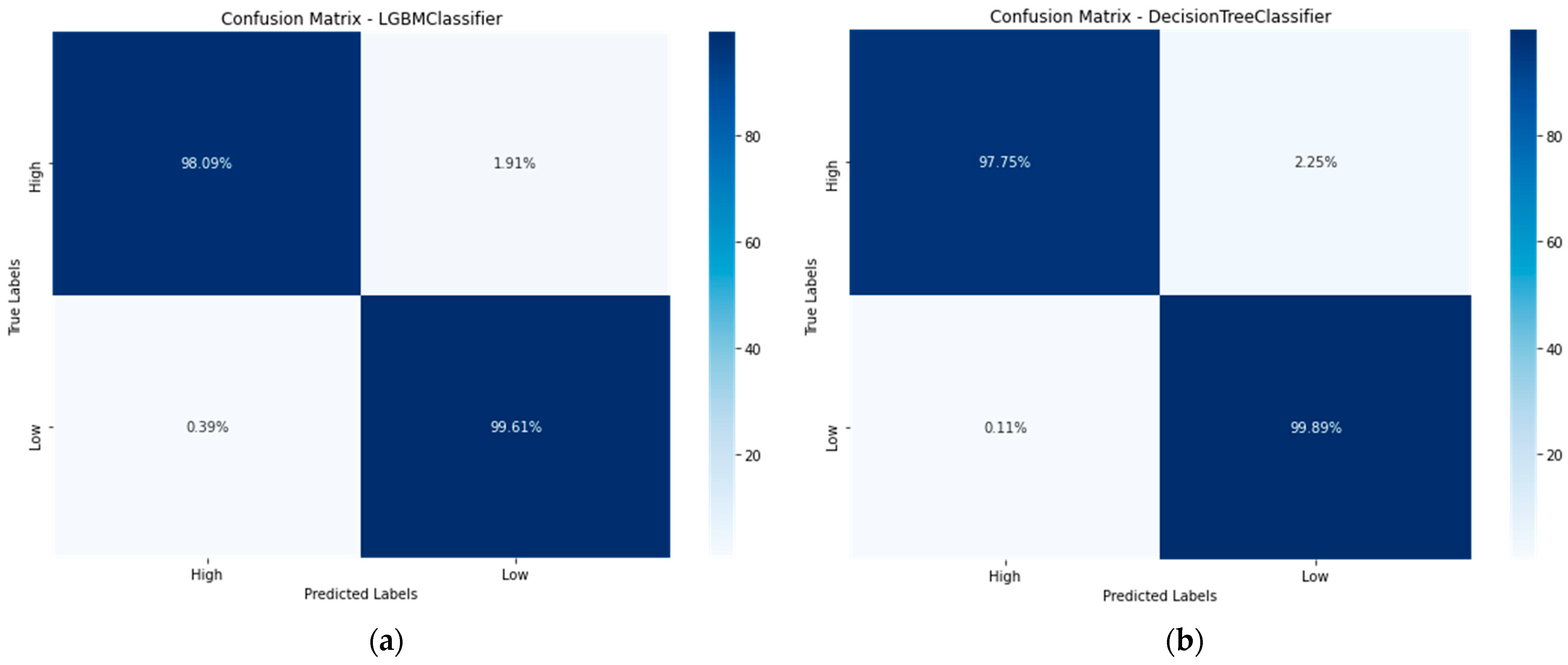
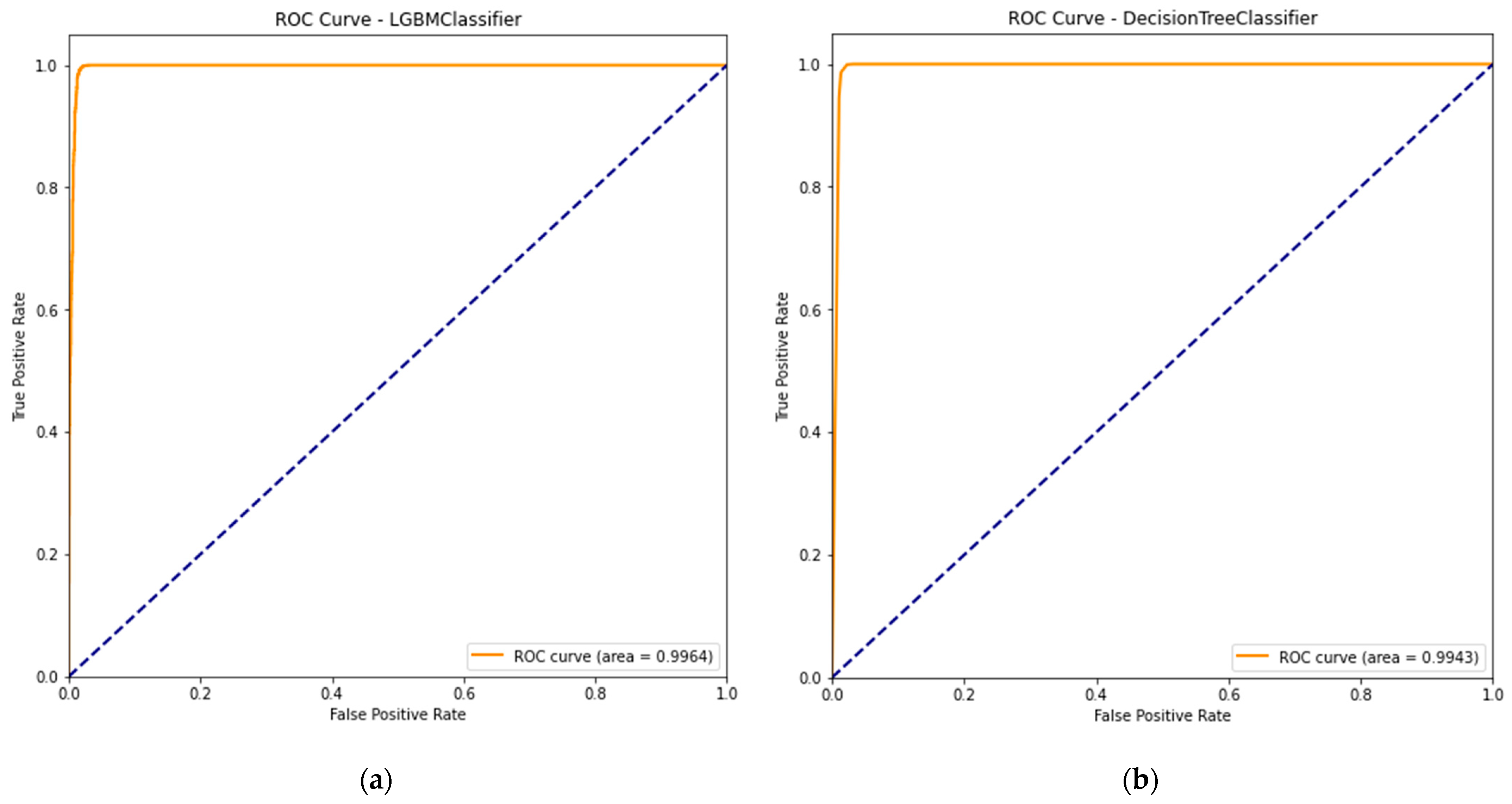
5.1. Model Performance Evaluation and Selection
5.2. Model Explainability/Interpretability
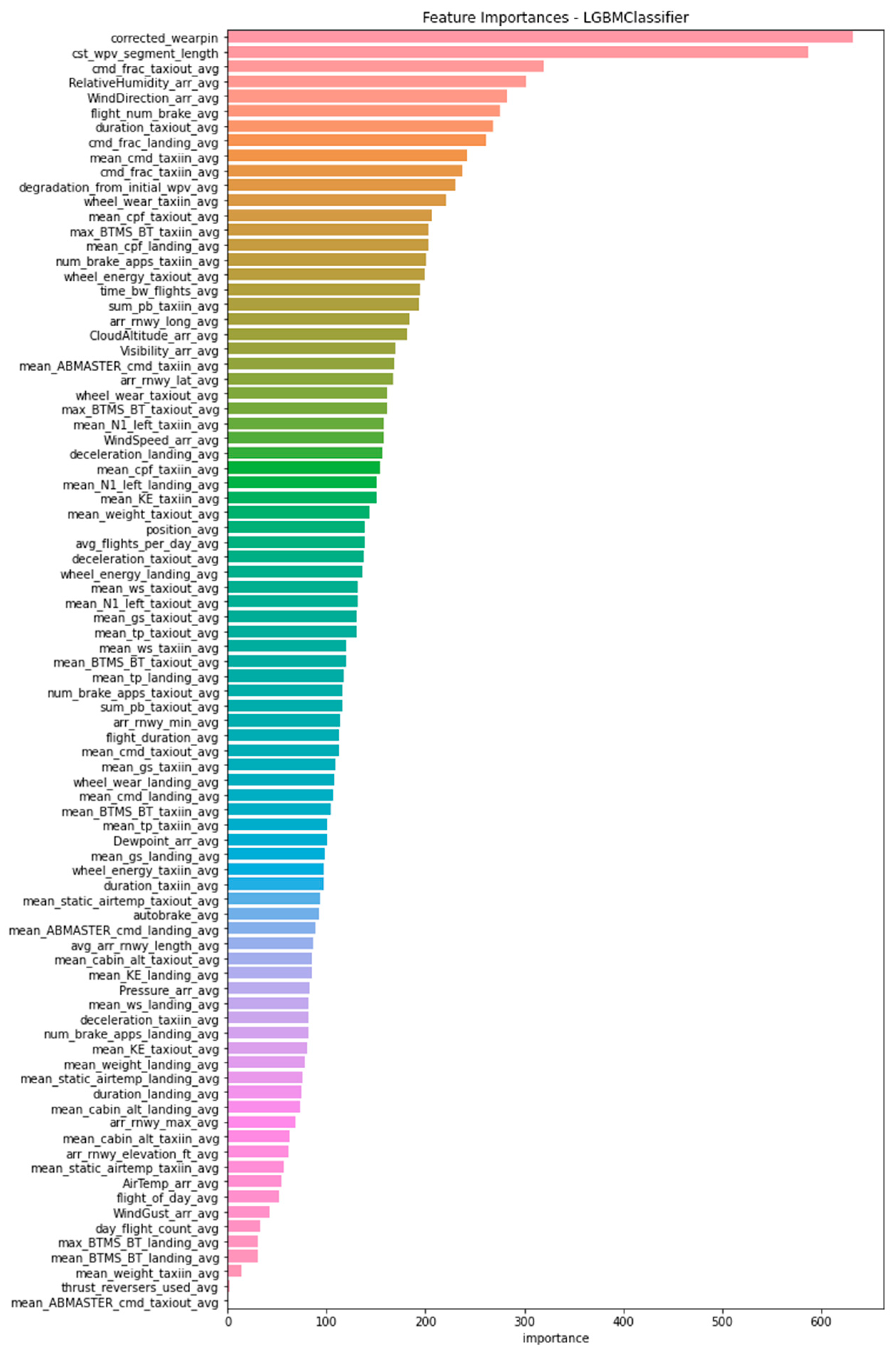
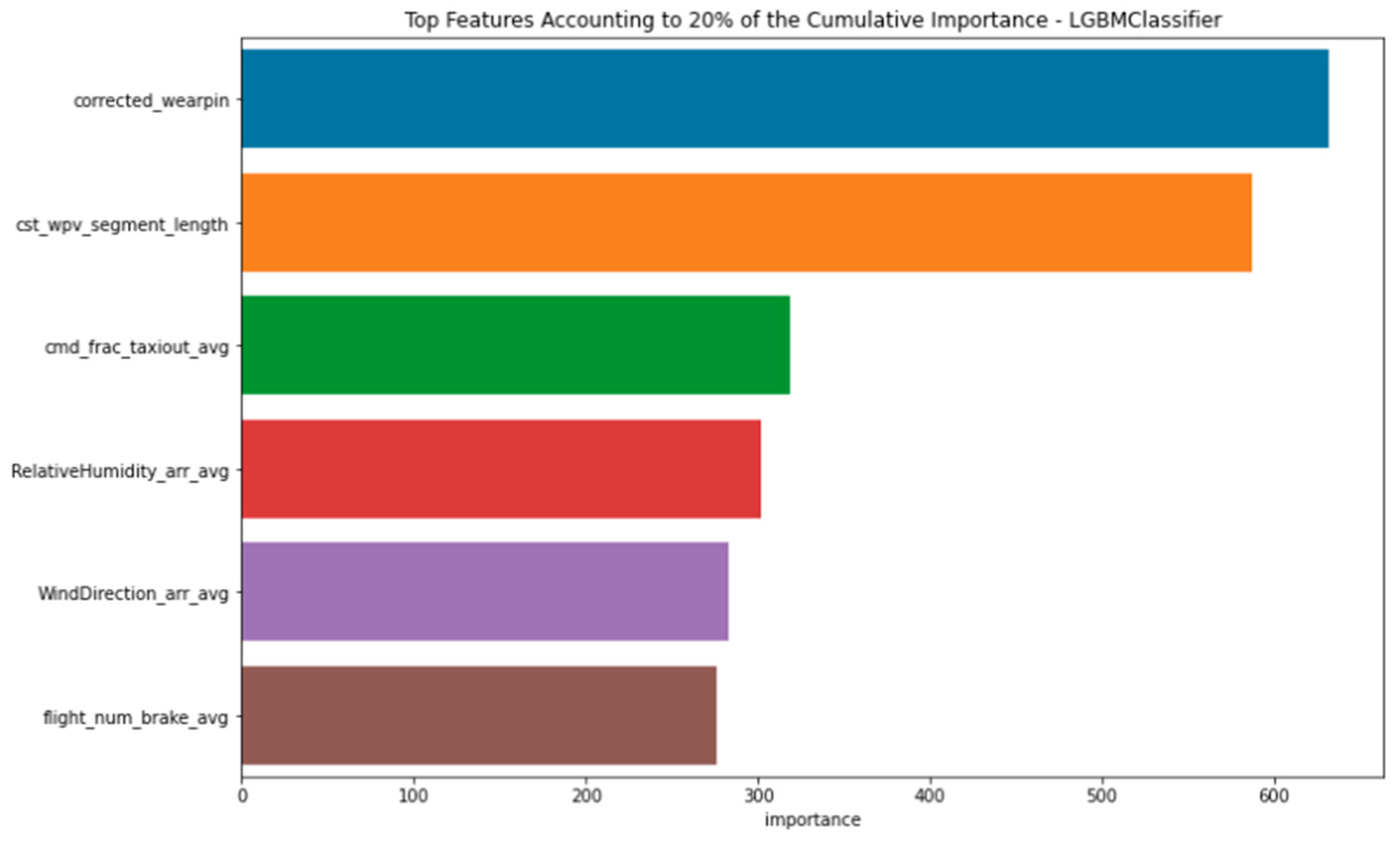
5.2.1. Feature Importance
- ‘corrected_wearpin’: This feature corresponds to the original wear pin measurement, corrected during data preprocessing to account for any errors. It is a direct measure of carbon pad thickness and is key to accurately predicting the brake’s remaining life. Additionally, by analyzing changes in the wear pin value over time, it is possible to determine whether the brake wears more, shortly after installation or progressively over time, providing insights into underlying wear patterns and potential issues related to initial installation or long-term usage.
- ‘cst_wvp_segment_length’: This feature captures the number of consecutive flights during which the wear pin value remains constant. An extended period without change may suggest reduced brake wear or efficient brake usage, indicating that the brakes are being applied effectively without excessive or unnecessary engagement. Such patterns are valuable for assessing brake durability across varying operational conditions.
- ‘cmd_frac_taxiout_avg’: This feature represents the average fraction of brake command that the specific brake (out of the eight brakes on the wide-body aircraft) contributes to during the taxi-out phase. This measurement is significant because it reflects the operational load and stress on the brake as the aircraft taxis out of the gate, influencing brake wear rate.
- ‘RelativeHumidity_arr_avg’: This parameter captures the average relative humidity at the arrival airports across the analyzed flights, underscoring the potential influence of environmental conditions on brake performance and the rate at which they degrade.
- ‘WindDirection_arr_avg’: This feature indicates the average wind direction at the airports where the flights arrive, which can also influence aircraft dynamics and braking requirements upon landing. For instance, headwinds or crosswinds might require different braking intensities, thus affecting brake wear.
- ‘flight_num_brake_avg’: This feature captures the average number of flights a specific brake has experienced since its installation. Frequent brake use may lead to faster wear, making this an important factor in predicting when the brake might need maintenance or replacement.
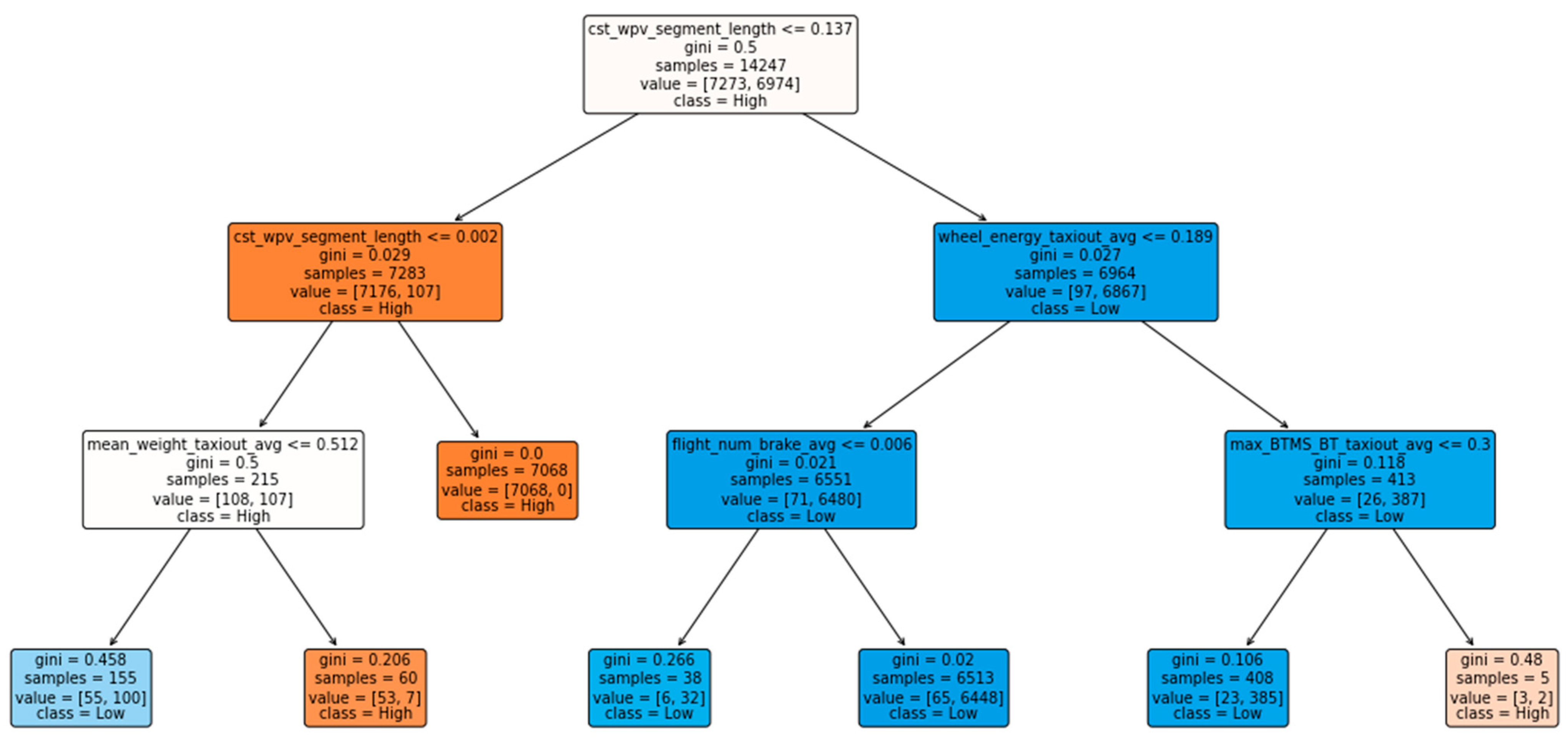
5.2.2. Decision Rules
- Root Node: This is the starting point of the decision tree; the first split in the data is made based on whether the value of ‘cst_wvp_segment_length’ (i.e., the number of flights over which the wear pin value remains constant) is less than or equal to 0.137. Note that all the features were scaled before model training using MinMaxScaler.
- Splitting Nodes: These are the nodes where the branches split off. Each split is based on a condition, with the variables used as conditions for splits in the tree being
- ○
- ‘mean_weight_taxiout_avg’: This variable represents the average aircraft weight during the taxi-out phase. A higher weight during taxi out suggests more significant stress on the braking system due to the increased force required to slow down or stop the heavier aircraft. Therefore, values higher than 0.512 lead to a high-wear classification, which aligns with the intuitive understanding that heavier aircraft exert more wear on the brakes.
- ○
- ‘wheel_energy_taxiout_avg’: This variable measures the average energy at the wheels during taxi out. Lower values of wheel energy, below 0.189 and leading to a low wear classification, indicate less kinetic energy that needs to be dissipated by the brakes. Consequently, less energy at the wheels means the brakes are subjected to lower stress and wear during operations, which correlates with a lower likelihood of significant wear.
- ‘max_BTMS_BT_taxiout_avg’: This variable captures the average maximum brake temperature during taxi out, as measured by the Brake Temperature Monitoring System (BTMS). Lower temperatures, values explicitly less than 0.3, and resulting in a low wear classification imply that the brakes are not overheating, which could cause accelerated wear or lead to carbon oxidation. Cooler brake temperatures may suggest that the braking system is not overused and operates within safe thermal limits, reducing the risk of excessive wear.These features used in splits also highlight the significant impact of the taxi-out phase on carbon brake wear, and the selected configuration (max_depth = 3, min_samples_leaf = 4, min_samples_split = 2) constrains the tree’s complexity to improve generalization.
- Gini Index: Each node lists a Gini impurity, which measures how often a random sample would be incorrectly classified according to the label distribution in the subset. A Gini index of 0 indicates perfect purity, meaning all elements in the node belong to a single class.
- Samples: This shows the number of samples sorted into that node after applying the test condition.
- Value: This indicates the distribution of the samples in the classes. For example, value = [7176, 107] means there are 7176 samples of class ‘High’ and 107 samples of class ‘Low’ in this particular node.
- Class: Each node has a class label representing the majority class within that node (i.e., either ‘High’ or ‘Low’ carbon brake wear).
5.3. Uncertainty Quantification
5.3.1. LGBM
5.3.2. Decision Tree
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| AUC | Area Under ROC Curve |
| BLR | Bayesian Linear Regression |
| BTMS | Brake Temperature Monitoring System |
| CatBoost | Categorical Boosting |
| CMD | Command |
| CPL | Continuous Parameter Logging |
| DT | Decision Tree |
| FN | False Negative |
| FP | False Positive |
| KNN | K-Nearest Neighbors |
| LBFGS | Limited-memory Broyden–Fletcher–Goldfarb–Shanno |
| LGBM | Light Gradient Boosting Machine |
| LIBLINEAR | A Library for Large Linear Classification |
| MAE | Mean Absolute Error |
| METAR | Meteorological Aerodrome Report |
| ML | Machine Learning |
| MSE | Mean Squared Error |
| NEWTON-CG | Newton-Conjugate Gradient |
| NHHSMM | Non-Homogeneous Hidden Semi-Markov Model |
| PCHIP | Piecewise Cubic Hermite Interpolating Polynomial |
| RBF | Radial Basis Function |
| RMSE | Root Mean Squared Error |
| RNN | Recurrent Neural Network |
| ROC | Receiver Operating Characteristic |
| RUL | Remaining Useful Life |
| SAG | Stochastic Average Gradient |
| SAGA | Stochastic Average Gradient Accelerated |
| SVC | Support Vector Classifier |
| SVM | Support Vector Machine |
| TL | Transfer Learning |
| TN | True Negative |
| TP | True Positive |
| XGBoost | eXtreme Gradient Boosting |
Appendix A
| Interpolation Method | Model | Best Parameters | Accuracy | Recall | Precision | F1 Score | AUC Score |
|---|---|---|---|---|---|---|---|
| Slinear | LGBM | {‘learning_rate’: 0.03, ‘max_depth’: 20, ‘n_estimators’: 200, ‘num_leaves’: 62, ‘random_state’: 0} | 0.9892 | 0.9885 | 0.9898 | 0.9891 | 0.9964 |
| Decision Tree | {‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.9892 | 0.9882 | 0.9902 | 0.9891 | 0.9943 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9891 | 0.9880 | 0.9900 | 0.9890 | 0.9960 | |
| CatBoost | {‘depth’: 10, ‘iterations’: 1000, ‘learning_rate’: 0.1, ‘random_state’: 0} | 0.9886 | 0.9882 | 0.9889 | 0.9885 | 0.9963 | |
| Random Forest | {‘criterion’: ‘gini’, ‘max_depth’: 30, ‘min_samples_leaf’: 1, ‘min_samples_split’: 4, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9871 | 0.9868 | 0.9871 | 0.9870 | 0.9945 | |
| SVC | {‘C’: 1, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.9837 | 0.9833 | 0.9838 | 0.9835 | 0.9815 | |
| Logistic Regression | {‘C’: 100, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.9805 | 0.9802 | 0.9804 | 0.9803 | 0.9829 | |
| KNN | {‘metric’: ‘manhattan’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.8218 | 0.8091 | 0.8411 | 0.8136 | 0.9041 | |
| PCHP | CatBoost | {‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9883 | 0.9876 | 0.9888 | 0.9882 | 0.9961 |
| Decision Tree | {‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.9875 | 0.9867 | 0.9882 | 0.9874 | 0.9943 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9872 | 0.9864 | 0.9879 | 0.9871 | 0.9957 | |
| LGBM | {‘learning_rate’: 0.03, ‘max_depth’: -1, ‘n_estimators’: 200, ‘num_leaves’: 62, ‘random_state’: 0} | 0.9870 | 0.9862 | 0.9878 | 0.9869 | 0.9965 | |
| Random Forest | {‘criterion’: ‘entropy’, ‘max_depth’: None, ‘min_samples_leaf’: 2, ‘min_samples_split’: 6, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9863 | 0.9861 | 0.9863 | 0.9862 | 0.9944 | |
| SVC | {‘C’: 1, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.9837 | 0.9833 | 0.9838 | 0.9835 | 0.9814 | |
| Logistic Regression | {‘C’: 100, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘saga’} | 0.9818 | 0.9816 | 0.9817 | 0.9817 | 0.9822 | |
| KNN | {‘metric’: ‘manhattan’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.7846 | 0.7709 | 0.8108 | 0.7730 | 0.8804 | |
| Spline Order 1 | CatBoost | {‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9349 | 0.9356 | 0.9338 | 0.9345 | 0.9770 |
| LGBM | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 15, ‘random_state’: 0} | 0.9341 | 0.9348 | 0.9330 | 0.9337 | 0.9610 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9341 | 0.9348 | 0.9330 | 0.9337 | 0.9609 | |
| Decision Tree | {‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.9301 | 0.9311 | 0.9290 | 0.9298 | 0.9517 | |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.9256 | 0.9271 | 0.9246 | 0.9253 | 0.9588 | |
| Random Forest | {‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘n_estimators’: 500, ‘random_state’: 0} | 0.9156 | 0.9188 | 0.9157 | 0.9155 | 0.9664 | |
| Logistic Regression | {‘C’: 0.01, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘liblinear’} | 0.9142 | 0.9175 | 0.9144 | 0.9140 | 0.9480 | |
| SVC | {‘C’: 0.01, ‘gamma’: ‘auto’, ‘kernel’: ‘rbf’, ‘probability’: True, ‘random_state’: 0} | 0.9134 | 0.9169 | 0.9138 | 0.9132 | 0.9266 | |
| Spline Order 3 | CatBoost | {‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9064 | 0.9040 | 0.9062 | 0.9050 | 0.9653 |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.8993 | 0.8975 | 0.8984 | 0.8979 | 0.9508 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0} | 0.8944 | 0.8918 | 0.8939 | 0.8928 | 0.9515 | |
| LGBM | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 15, ‘random_state’: 0} | 0.8933 | 0.8907 | 0.8929 | 0.8917 | 0.9515 | |
| Decision Tree | {‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.8854 | 0.8824 | 0.8850 | 0.8836 | 0.9299 | |
| Random Forest | {‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 4, ‘n_estimators’: 200, ‘random_state’: 0} | 0.8702 | 0.8721 | 0.8684 | 0.8694 | 0.9492 | |
| Logistic Regression | {‘C’: 0.001, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.8678 | 0.8701 | 0.8661 | 0.8670 | 0.9147 | |
| SVC | {‘C’: 0.01, ‘gamma’: ‘auto’, ‘kernel’: ‘rbf’, ‘probability’: True, ‘random_state’: 0} | 0.8675 | 0.8697 | 0.8658 | 0.8667 | 0.9006 | |
| Spline Order 5 | CatBoost | {‘depth’: 4, ‘iterations’: 1000, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9182 | 0.9175 | 0.9171 | 0.9173 | 0.9710 |
| XGBoost | {‘learning_rate’: 0.03, ‘max_depth’: 3, ‘n_estimators’: 400, ‘random_state’: 0} | 0.9176 | 0.9172 | 0.9163 | 0.9167 | 0.9720 | |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.9001 | 0.8988 | 0.8991 | 0.8989 | 0.9481 | |
| LGBM | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 15, ‘random_state’: 0} | 0.8882 | 0.8894 | 0.8864 | 0.8874 | 0.9517 | |
| Decision Tree | {‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.8773 | 0.8782 | 0.8754 | 0.8764 | 0.9286 | |
| Random Forest | {‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘n_estimators’: 200, ‘random_state’: 0} | 0.8510 | 0.8509 | 0.8489 | 0.8497 | 0.9414 | |
| SVC | {‘C’: 0.1, ‘gamma’: ‘scale’, ‘kernel’: ‘sigmoid’, ‘probability’: True, ‘random_state’: 0} | 0.8427 | 0.8428 | 0.8407 | 0.8415 | 0.8482 | |
| Logistic Regression | {‘C’: 0.001, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘liblinear’} | 0.8426 | 0.8426 | 0.8405 | 0.8413 | 0.9131 |
| Interpolation Method | Model | Best Parameters | Accuracy | Recall | Precision | F1 Score | AUC Score |
|---|---|---|---|---|---|---|---|
| Slinear | Random Forest | {‘class_weight’: ‘balanced_subsample’, ‘criterion’: ‘gini’, ‘max_depth’: None, ‘min_samples_leaf’: 2, ‘min_samples_split’: 6, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9305 | 0.9172 | 0.9164 | 0.9168 | 0.9742 |
| CatBoost | {‘auto_class_weights’: ‘Balanced’, ‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9258 | 0.9291 | 0.9028 | 0.9141 | 0.9797 | |
| Decision Tree | {‘class_weight’: ‘balanced’, ‘criterion’: ‘entropy’, ‘max_depth’: 5, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.9255 | 0.9237 | 0.9042 | 0.9130 | 0.9778 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_delta_step’: 1, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0, ‘scale_pos_weight’: 1} | 0.9243 | 0.8896 | 0.9266 | 0.9054 | 0.9725 | |
| LGBM | {‘class_weight’: ‘balanced’, ‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 300, ‘num_leaves’: 15, ‘random_state’: 0} | 0.9017 | 0.9222 | 0.8744 | 0.8901 | 0.9790 | |
| Logistic Regression | {‘C’: 100, ‘class_weight’: ‘balanced’, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.9004 | 0.9136 | 0.8727 | 0.8875 | 0.9603 | |
| SVC | {‘C’: 10, ‘class_weight’: ‘balanced’, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.8846 | 0.9115 | 0.8581 | 0.8728 | 0.9622 | |
| KNN | {‘metric’: ‘euclidean’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.7529 | 0.7210 | 0.7081 | 0.7133 | 0.7896 | |
| PCHIP | CatBoost | {‘auto_class_weights’: ‘Balanced’, ‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9078 | 0.9260 | 0.8817 | 0.8970 | 0.9740 |
| Random Forest | {‘class_weight’: ‘balanced_subsample’, ‘criterion’: ‘gini’, ‘max_depth’: 10, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9072 | 0.9260 | 0.8811 | 0.8964 | 0.9645 | |
| LGBM | {‘class_weight’: ‘balanced’, ‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 300, ‘num_leaves’: 15, ‘random_state’: 0} | 0.9069 | 0.9267 | 0.8808 | 0.8962 | 0.9737 | |
| Decision Tree | {‘class_weight’: ‘balanced’, ‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.9069 | 0.9267 | 0.8808 | 0.8962 | 0.9700 | |
| Logistic Regression | {‘C’: 100, ‘class_weight’: ‘balanced’, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.8921 | 0.9150 | 0.8660 | 0.8808 | 0.9558 | |
| SVC | {‘C’: 1, ‘class_weight’: ‘balanced’, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.8866 | 0.9130 | 0.8612 | 0.8755 | 0.9578 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_delta_step’: 1, ‘max_depth’: 4, ‘n_estimators’: 100, ‘random_state’: 0, ‘scale_pos_weight’: 2.03} | 0.8957 | 0.8280 | 0.9312 | 0.8609 | 0.9691 | |
| Spline Order 1 | XGBoost | {‘learning_rate’: 0.01, ‘max_delta_step’: 1, ‘max_depth’: 3, ‘n_estimators’: 200, ‘random_state’: 0, ‘scale_pos_weight’: 1} | 0.9024 | 0.9104 | 0.8719 | 0.8868 | 0.9509 |
| CatBoost | {‘auto_class_weights’: ‘Balanced’, ‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.9013 | 0.9138 | 0.8704 | 0.8864 | 0.9581 | |
| LGBM | {‘class_weight’: ‘balanced’, ‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 15, ‘random_state’: 0} | 0.8894 | 0.9060 | 0.8578 | 0.8741 | 0.9476 | |
| Decision Tree | {‘class_weight’: ‘balanced’, ‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.8874 | 0.9041 | 0.8557 | 0.8720 | 0.9334 | |
| Random Forest | {‘class_weight’: ‘balanced_subsample’, ‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 4, ‘n_estimators’: 100, ‘random_state’: 0} | 0.8770 | 0.9008 | 0.8461 | 0.8621 | 0.9453 | |
| Logistic Regression | {‘C’: 0.001, ‘class_weight’: ‘balanced’, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.8762 | 0.9005 | 0.8454 | 0.8613 | 0.9133 | |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.8782 | 0.8862 | 0.8452 | 0.8601 | 0.9349 | |
| SVC | {‘C’: 0.01, ‘class_weight’: ‘balanced’, ‘gamma’: ‘auto’, ‘kernel’: ‘sigmoid’, ‘probability’: True, ‘random_state’: 0} | 0.8740 | 0.8990 | 0.8433 | 0.8590 | 0.9068 | |
| Spline Order 3 | XGBoost | {‘learning_rate’: 0.03, ‘max_delta_step’: 0, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0, ‘scale_pos_weight’: 1} | 0.8859 | 0.8578 | 0.8589 | 0.8584 | 0.9348 |
| CatBoost | {‘auto_class_weights’: ‘Balanced’, ‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.8763 | 0.8677 | 0.8416 | 0.8526 | 0.9400 | |
| LGBM | {‘class_weight’: ‘balanced’, ‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 15, ‘random_state’: 0} | 0.8628 | 0.8619 | 0.8258 | 0.8395 | 0.9245 | |
| Decision Tree | {‘class_weight’: ‘balanced’, ‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.8653 | 0.8495 | 0.8293 | 0.8382 | 0.9076 | |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.8416 | 0.8422 | 0.8030 | 0.8167 | 0.9081 | |
| Random Forest | {‘class_weight’: ‘balanced’, ‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘n_estimators’: 100, ‘random_state’: 0} | 0.8328 | 0.8499 | 0.7980 | 0.8117 | 0.9205 | |
| SVC | {‘C’: 0.01, ‘class_weight’: ‘balanced’, ‘gamma’: ‘auto’, ‘kernel’: ‘sigmoid’, ‘probability’: True, ‘random_state’: 0} | 0.8321 | 0.8497 | 0.7975 | 0.8111 | 0.8672 | |
| Logistic Regression | {‘C’: 0.001, ‘class_weight’: ‘balanced’, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘liblinear’} | 0.8321 | 0.8492 | 0.7973 | 0.8109 | 0.8836 | |
| Spline Order 5 | CatBoost | {‘auto_class_weights’: ‘Balanced’, ‘depth’: 4, ‘iterations’: 500, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.8649 | 0.8590 | 0.8284 | 0.8407 | 0.9323 |
| XGBoost | {‘learning_rate’: 0.01, ‘max_delta_step’: 1, ‘max_depth’: 3, ‘n_estimators’: 200, ‘random_state’: 0, ‘scale_pos_weight’: 1} | 0.8670 | 0.8334 | 0.8362 | 0.8348 | 0.9213 | |
| LGBM | {‘class_weight’: ‘balanced’, ‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 15, ‘random_state’: 0} | 0.8544 | 0.8446 | 0.8166 | 0.8280 | 0.9164 | |
| Decision Tree | {‘class_weight’: ‘balanced’, ‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.8503 | 0.8384 | 0.8119 | 0.8228 | 0.8966 | |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.8286 | 0.8284 | 0.7895 | 0.8026 | 0.8978 | |
| Random Forest | {‘class_weight’: ‘balanced_subsample’, ‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘n_estimators’: 100, ‘random_state’: 0} | 0.8080 | 0.8184 | 0.7720 | 0.7838 | 0.9034 | |
| Logistic Regression | {‘C’: 0.001, ‘class_weight’: ‘balanced’, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘liblinear’} | 0.8060 | 0.8167 | 0.7701 | 0.7818 | 0.8698 | |
| SVC | {‘C’: 0.01, ‘class_weight’: ‘balanced’, ‘gamma’: ‘auto’, ‘kernel’: ‘rbf’, ‘probability’: True, ‘random_state’: 0} | 0.8051 | 0.8171 | 0.7697 | 0.7813 | 0.8434 |
| Model | Best Parameters | Accuracy | Recall | Precision | F1 Score | AUC Score |
|---|---|---|---|---|---|---|
| CatBoost | {‘depth’: 4, ‘iterations’: 1000, ‘learning_rate’: 0.01, ‘random_state’: 0} | 0.8634 | 0.8619 | 0.8651 | 0.8630 | 0.9684 |
| Random Forest | {‘criterion’: ‘entropy’, ‘max_depth’: 10, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘n_estimators’: 100, ‘random_state’: 0} | 0.8455 | 0.8444 | 0.8478 | 0.8458 | 0.9500 |
| LGMB | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_class’: 3, ‘num_leaves’: 15, ‘objective’: ‘multiclass’, ‘random_state’: 0} | 0.8434 | 0.8394 | 0.8519 | 0.8406 | 0.9625 |
| XGBoost | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_class’: 3, ‘objective’: ‘multi:softmax’, ‘random_state’: 0} | 0.8434 | 0.8394 | 0.8518 | 0.8406 | 0.9605 |
| Decision Tree | {‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 1, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.8030 | 0.8106 | 0.8042 | 0.8012 | 0.9503 |
| Logistic Regression | {‘C’: 100, ‘max_iter’: 300, ‘multi_class’: ‘multinomial’, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.7925 | 0.7928 | 0.7958 | 0.7942 | 0.9300 |
| SVC | {‘C’: 100, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.7840 | 0.7866 | 0.7887 | 0.7871 | 0.9280 |
| KNN | {‘metric’: ‘euclidean’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.5466 | 0.5375 | 0.5681 | 0.5386 | 0.7339 |
| Model | Best Parameters | Accuracy | Recall | Precision | F1 Score | AUC Score |
|---|---|---|---|---|---|---|
| LGBM | {‘learning_rate’: 0.0454, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 32, ‘random_state’: 0} | 0.7342 | 0.7302 | 0.7312 | 0.7306 | 0.7965 |
| CatBoost | {‘depth’: 6, ‘iterations’: 100, ‘learning_rate’: 0.0198, ‘random_state’: 0, ‘verbose’: 0} | 0.7334 | 0.7293 | 0.7303 | 0.7298 | 0.7950 |
| XGBoost | {‘learning_rate’: 0.0373, ‘max_depth’: 3, ‘n_estimators’: 101, ‘random_state’: 0} | 0.7330 | 0.7289 | 0.7299 | 0.7293 | 0.7949 |
| SVC * | {‘C’: 90.9715, ‘gamma’: ‘scale’, ‘kernel’: ‘rbf’, ‘probability’: True, ‘random_state’: 0} | 0.7277 | 0.7223 | 0.7247 | 0.7232 | 0.7858 |
| Random Forest | {‘criterion’: ‘gini’, ‘max_depth’: 6, ‘min_samples_leaf’: 5, ‘min_samples_split’: 3, ‘n_estimators’: 134, ‘random_state’: 0} | 0.7172 | 0.7129 | 0.7138 | 0.7133 | 0.7802 |
| Logistic Regression | {‘C’: 0.0080, ‘max_iter’: 940, ‘random_state’: 0, ‘solver’: ‘saga’} | 0.7107 | 0.7050 | 0.7074 | 0.7059 | 0.7699 |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 14, ‘weights’: ‘uniform’} | 0.7092 | 0.7053 | 0.7057 | 0.7055 | 0.7635 |
| Decision Tree | {‘criterion’: ‘entropy’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 7, ‘random_state’: 0} | 0.7075 | 0.6914 | 0.7145 | 0.6919 | 0.7488 |
| Hyperparameter Optimization Method | Model | Best Parameters | Accuracy | Recall | Precision | F1 Score | AUC Score |
| Grid Search (5-fold cross-validation) | LGBM | {‘learning_rate’: 0.03, ‘max_depth’: 20, ‘n_estimators’: 200, ‘num_leaves’: 62, ‘random_state’: 0} | 0.9892 | 0.9885 | 0.9898 | 0.9891 | 0.9964 |
| Decision Tree | {‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘random_state’: 0} | 0.9892 | 0.9882 | 0.9902 | 0.9891 | 0.9943 | |
| XGBoost | {‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9891 | 0.9880 | 0.9900 | 0.9890 | 0.9960 | |
| CatBoost | {‘depth’: 10, ‘iterations’: 1000, ‘learning_rate’: 0.1, ‘random_state’: 0} | 0.9886 | 0.9882 | 0.9889 | 0.9885 | 0.9963 | |
| Random Forest | {‘criterion’: ‘gini’, ‘max_depth’: 30, ‘min_samples_leaf’: 1, ‘min_samples_split’: 4, ‘n_estimators’: 100, ‘random_state’: 0} | 0.9871 | 0.9868 | 0.9871 | 0.9870 | 0.9945 | |
| SVC | {‘C’: 1, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.9837 | 0.9833 | 0.9838 | 0.9835 | 0.9815 | |
| Logistic Regression | {‘C’: 100, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’} | 0.9805 | 0.9802 | 0.9804 | 0.9803 | 0.9829 | |
| KNN | {‘metric’: ‘manhattan’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’} | 0.8218 | 0.8091 | 0.8411 | 0.8136 | 0.9041 | |
| HyperOpt (200 iterations) | Decision Tree | {‘criterion’: ‘entropy’, ‘max_depth’: 6, ‘min_samples_leaf’: 3, ‘min_samples_split’: 3, ‘random_state’: 0} | 0.9892 | 0.9884 | 0.9899 | 0.9891 | 0.9945 |
| LGBM | {‘learning_rate’: 0.0427, ‘max_depth’: 3, ‘n_estimators’: 100, ‘num_leaves’: 76, ‘random_state’: 0} | 0.9891 | 0.9881 | 0.9900 | 0.9890 | 0.9965 | |
| CatBoost | {‘depth’: 9, ‘iterations’: 900, ‘learning_rate’: 0.2651, ‘random_state’: 0, ‘verbose’: 0} | 0.9886 | 0.9881 | 0.9889 | 0.9885 | 0.9959 | |
| XGBoost | {‘learning_rate’: 0.2280, ‘max_depth’: 6, ‘n_estimators’: 396, ‘random_state’: 0} | 0.9885 | 0.9878 | 0.9890 | 0.9883 | 0.9958 | |
| Random Forest | {‘criterion’: ‘entropy’, ‘max_depth’: 5, ‘min_samples_leaf’: 2, ‘min_samples_split’: 6, ‘n_estimators’: 135, ‘random_state’: 0} | 0.9860 | 0.9859 | 0.9858 | 0.9859 | 0.9935 | |
| SVC | {‘C’: 0.8624, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0} | 0.9837 | 0.9833 | 0.9838 | 0.9835 | 0.9816 | |
| Logistic Regression | {‘C’: 63.7954, ‘max_iter’: 140, ‘random_state’: 0, ‘solver’: ‘saga’} | 0.9803 | 0.9800 | 0.9803 | 0.9801 | 0.9826 | |
| KNN | {‘metric’: ‘minkowski’, ‘n_neighbors’: 14, ‘weights’: ‘uniform’} | 0.8052 | 0.7924 | 0.8222 | 0.7964 | 0.8871 |
References
- Liu, Z.; Li, Z.; Qin, C.; Shang, Y.; Liu, X. The Review and Development of the Brake System for Civil Aircrafts. In Proceedings of the 2016 IEEE International Conference on Aircraft Utility Systems (AUS), Beijing, China, 10–12 October 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Allen, T.; Miller, T.; Preston, E. Operational Advantages of Carbon Brakes. Aeromagazine 2009, 3, 35. Available online: https://code7700.com/pdfs/operational_advantages_carbon_brakes.pdf (accessed on 5 June 2025).
- Wang, H. A Survey of Maintenance Policies of Deteriorating Systems. Eur. J. Oper. Res. 2002, 139, 469–489. [Google Scholar] [CrossRef]
- Zhu, T.; Ran, Y.; Zhou, X.; Wen, Y. A Survey of Predictive Maintenance: Systems, Purposes and Approaches. arXiv 2019, arXiv:1912.07383. [Google Scholar]
- Kotsiantis, S.B. Supervised Machine Learning: A Review of Classification Techniques. In Emerging Artificial Intelligence Applications in Computer Engineering; Maglogiannis, I.G., Ed.; IOS Press: Amsterdam, The Netherlands, 2007; Volume 160, pp. 3–24. [Google Scholar]
- Singh, A.; Thakur, N.; Sharma, A. A Review of Supervised Machine Learning Algorithms. In Proceedings of the 2016 3rd International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 16–18 March 2016; IEEE: New York, NY, USA, 2016. [Google Scholar]
- Phillips, P.; Diston, D.; Starr, A.; Payne, J.; Pandya, S. A review on the optimisation of aircraft maintenance with application to landing gears. In Engineering Asset Lifecycle Management; Kiritsis, D., Emmanouilidis, C., Koronios, A., Mathew, J., Eds.; Springer: London, UK, 2010; pp. 89–106. [Google Scholar] [CrossRef]
- Oikonomou, A.; Loutas, T.; Eleftheroglou, N.; Freeman, F.; Zarouchas, D. Remaining Useful Life Prognosis of Aircraft Brakes. Int. J. Progn. Health Manag. 2022, 13, 3072. [Google Scholar] [CrossRef]
- Hsu, T.-H.; Chang, Y.-J.; Hsu, H.-K.; Chen, T.-T.; Hwang, P.-W. Predicting the Remaining Useful Life of Landing Gear with Prognostics and Health Management (PHM). Aerospace 2022, 9, 462. [Google Scholar] [CrossRef]
- Travnik, M.; Hansman, R.J. A Data Driven Approach for Predicting Friction-Limited Aircraft Landings. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022. [Google Scholar] [CrossRef]
- Steffan, J.J.; Jebadurai, I.J.; Asirvatham, L.G.; Manova, S.; Larkins, J.P. Prediction of Brake Pad Wear Using Various Machine Learning Algorithms. In Recent Trends in Design, Materials and Manufacturing; Singh, M.K., Gautam, R.K., Eds.; Lecture Notes in Mechanical Engineering; Springer: Singapore, 2022; pp. 529–543. [Google Scholar] [CrossRef]
- Magargle, R.; Johnson, L.; Mandloi, P.; Davoudabadi, P.; Kesarkar, O.; Krishnaswamy, S.; Batteh, J.; Pitchaikani, A. A Simulation-Based Digital Twin for Model-Driven Health Monitoring and Predictive Maintenance of an Automotive Braking System. In Proceedings of the 12th International Modelica Conference, Prague, Czech Republic, 15–17 May 2017; Linköping University Electronic Press: Linköping, Sweden, 2017; pp. 235–244. [Google Scholar] [CrossRef]
- Küfner, T.; Döpper, F.; Müller, D.; Trenz, A.G. Predictive Maintenance: Using Recurrent Neural Networks for Wear Prognosis in Current Signatures of Production Plants. Int. J. Mech. Eng. Robot. Res. 2021, 10, 583–591. [Google Scholar] [CrossRef]
- De Martin, A.; Jacazio, G.; Sorli, M. Simulation of Runway Irregularities in a Novel Test Rig for Fully Electrical Landing Gear Systems. Aerospace 2022, 9, 114. [Google Scholar] [CrossRef]
- Cao, J.; Bao, J.; Yin, Y.; Yao, W.; Liu, T.; Cao, T. Intelligent prediction of wear life of automobile brake pad based on braking conditions. Ind. Lubr. Tribol. 2023, 75, 157–165. [Google Scholar] [CrossRef]
- Harlapur, C.C.; Kadiyala, P.; Ramakrishna, S. Brake pad wear detection using machine learning. Int. J. Adv. Res. Ideas Innov. Technol. 2019, 5, 498–501. [Google Scholar]
- Burnaev, E. Time-series classification for industrial applications: A brake pad wear prediction use case. In IOP Conference Series: Materials Science and Engineering, Proceedings of the 4th International Conference on Mechanical, System and Control Engineering, Moscow, Russian, 20–23 June 2020; IOP Publishing: Bristol, UK, 2020; Volume 904, p. 012012. [Google Scholar] [CrossRef]
- Choudhuri, K.; Shekhar, A. Predicting Brake Pad Wear Using Machine Learning. Engineering Briefs 2020. Available online: https://assets-global.website-files.com/5e73648af0a7112f91aff9af/5f0c473ff3f009253a3c38a9_EB2020-STP-015.pdf (accessed on 5 June 2025).
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Charbuty, B.T.; Abdulazeez, A.M. Classification Based on Decision Tree Algorithm for Machine Learning. J. Appl. Sci. Technol. Trends 2021, 2, 20–28. [Google Scholar] [CrossRef]
- Song, Y.-Y.; Lu, Y. Decision tree methods: Applications for classification and prediction. Shanghai Arch. Psychiatry 2015, 27, 130–135. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Gunn, S.R. Support Vector Machines for Classification and Regression; Technical Report; Citeseer: Princeton, NJ, USA, 1997; pp. 5–16. [Google Scholar]
- FlightAware®. About FlightAware®. Available online: https://flightaware.com/about/ (accessed on 5 June 2025).
- Boeing. Boeing 787 Dreamliner. Available online: https://www.boeing.com/commercial/787/#/family (accessed on 5 June 2025).
- Zhou, L.; Pan, S.; Wang, J.; Vasilakos, A.V. Machine learning on big data: Opportunities and challenges. Neurocomputing 2017, 237, 350–361. [Google Scholar] [CrossRef]
- Drone Pilot Ground School. How to Read An Aviation Routine Weather (METAR) Report. Available online: https://www.dronepilotgroundschool.com/reading-aviation-routine-weather-metar-report/ (accessed on 5 June 2025).
- Gultepe, I.; Sharman, R.; Williams, P.D.; Zhou, B.; Ellrod, G.; Minnis, P.; Trier, S.; Griffin, S. A Review of High Impact Weather for Aviation Meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
- Horne, W.B.; McCarty, J.L.; Tanner, J.A. Some Effects of Adverse Weather Conditions on Performance of Airplane Antiskid Braking Systems. In NASA Technical Note; NASA: Washington, DC, USA, 1976; ISBN NASA TN D-8202. [Google Scholar]
- FlightAware®. FlightAware® APIs. Available online: https://flightaware.com/commercial/data/ (accessed on 5 June 2025).
- García, S.; Luengo, J.; Herrera, F. Data Preprocessing in Data Mining, 1st ed.; Springer: Cham, Switzerland, 2015; Volume 72. [Google Scholar] [CrossRef]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised learning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Bennett, D.A. How can I deal with missing data in my study? Aust. N. Z. J. Public Health 2001, 25, 464–469. [Google Scholar] [CrossRef]
- Enders, C.K. Applied Missing Data Analysis, 2nd ed.; Guilford Publications: New York, NY, USA, 2022. [Google Scholar]
- Birkhoff, G.; Schultz, M.H.; Varga, R.S. Piecewise Hermite interpolation in one and two variables with applications to partial differential equations. Numer. Math. 1968, 11, 232–256. [Google Scholar] [CrossRef]
- Rabbath, C.A.; Corriveau, D. A comparison of piecewise cubic Hermite interpolating polynomials, cubic splines and piecewise linear functions for the approximation of projectile aerodynamics. Def. Technol. 2019, 15, 741–757. [Google Scholar] [CrossRef]
- Davis, P.J. Interpolation and Approximation, 1st ed.; Courier Corporation: North Chelmsford, MA, USA, 1975. [Google Scholar]
- McKinley, S.; Levine, M. Cubic spline interpolation. Coll. Redwoods 1998, 45, 1049–1060. [Google Scholar]
- Späth, H. One Dimensional Spline Interpolation Algorithms, 1st ed.; A K Peters/CRC Press: New York, NY, USA, 1995. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- Blu, T.; Thévenaz, P.; Unser, M. Linear interpolation revitalized. IEEE Trans. Image Process. 2004, 13, 710–719. [Google Scholar] [CrossRef]
- Hodge, V.; Austin, J. A Survey of Outlier Detection Methodologies. Artif. Intell. Rev. 2004, 22, 85–126. [Google Scholar] [CrossRef]
- Lee, D.K.; In, J.; Lee, S. Standard deviation and standard error of the mean. Korean J. Anesthesiol. 2015, 68, 220–223. [Google Scholar] [CrossRef] [PubMed]
- Kwak, S.K.; Kim, J.H. Statistical data preparation: Management of missing values and outliers. Korean J. Anesthesiol. 2017, 70, 407–411. [Google Scholar] [CrossRef] [PubMed]
- Raju, V.G.; Lakshmi, K.P.; Jain, V.M.; Kalidindi, A.; Padma, V. Study the Influence of Normalization/Transformation Process on the Accuracy of Supervised Classification. In Proceedings of the 2020 Third International Conference on Smart Systems and Inventive Technology (ICSSIT), Tirunelveli, India, 20–22 August 2020; IEEE: Piscataway, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Aly, M. Survey on multiclass classification methods. Neural Netw. 2005, 19, 2. [Google Scholar]
- Kolo, B. Binary and Multiclass Classification; Lulu.com: Morrisville, NC, USA, 2011. [Google Scholar]
- Lorena, A.C.; de Carvalho, A.C.P.L.F.; Gama, J.M.P. A review on the combination of binary classifiers in multiclass problems. Artif. Intell. Rev. 2008, 30, 19–37. [Google Scholar] [CrossRef]
- Jammal, P.; Pinon Fischer, O.J.; Mavris, D.N.; Wagner, G. Predictive Maintenance of Aircraft Braking Systems: A Machine Learning Approach to Clustering Brake Wear Patterns. In Proceedings of the AIAA SciTech 2025 Forum, Orlando, FL, USA, 6–10 January 2025; AIAA: Reston, VA, USA, 2025. [Google Scholar] [CrossRef]
- Longadge, R.; Dongre, S. Class Imbalance Problem in Data Mining Review. arXiv 2013, arXiv:1305.1707. [Google Scholar] [CrossRef]
- Dreiseitl, S.; Ohno-Machado, L. Logistic regression and artificial neural network classification models: A methodology review. J. Biomed. Inform. 2002, 35, 352–359. [Google Scholar] [CrossRef] [PubMed]
- Peterson, L.E. K-nearest neighbor. Scholarpedia 2009, 4, 1883. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. LightGBM: A Highly Efficient Gradient Boosting Decision Tree. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., Von Luxburg, U., Bengio, S., Wallach, H., Fergus, R., Vishwanathan, S., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2017; Volume 30. Available online: https://proceedings.neurips.cc/paper_files/paper/2017/file/6449f44a102fde848669bdd9eb6b76fa-Paper.pdf (accessed on 5 June 2025).
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; Bengio, S., Wallach, H., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2018; Volume 31. Available online: https://proceedings.neurips.cc/paper_files/paper/2018/file/14491b756b3a51daac41c24863285549-Paper.pdf (accessed on 5 June 2025).
- Bergstra, J.; Bardenet, R.; Bengio, Y.; Kégl, B. Algorithms for Hyper-Parameter Optimization. In Proceedings of the Advances in Neural Information Processing Systems 24, Granada, Spain, 12–14 December 2011; Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F., Weinberger, K.Q., Eds.; Curran Associates, Inc.: Red Hook, NY, USA, 2011; Volume 24. Available online: https://proceedings.neurips.cc/paper_files/paper/2011/file/86e8f7ab32cfd12577bc2619bc635690-Paper.pdf (accessed on 5 June 2025).
- Krstajic, D.; Buturovic, L.J.; Leahy, D.E.; Thomas, S. Cross-validation pitfalls when selecting and assessing regression and classification models. J. Cheminform. 2014, 6, 10. [Google Scholar] [CrossRef] [PubMed]
- Hossin, M.; Sulaiman, M.N. A Review on Evaluation Metrics for Data Classification Evaluations. Int. J. Data Min. Knowl. Manag. Process 2015, 5, 1–11. [Google Scholar] [CrossRef]
- Lever, J. Classification evaluation: It is important to understand both what a classification metric expresses and what it hides. Nat. Methods 2016, 13, 603–605. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble Methods in Machine Learning. In Multiple Classifier Systems. MCS 2000. Lecture Notes in Computer Science; Sharkey, A.J.C., Ed.; Springer: Berlin/Heidelberg, Germany, 2000; Volume 1857, pp. 1–15. [Google Scholar] [CrossRef]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar]
- Opitz, D.; Maclin, R. Popular ensemble methods: An empirical study. J. Artif. Intell. Res. 1999, 11, 169–198. [Google Scholar] [CrossRef]
- Komer, B.; Bergstra, J.; Eliasmith, C. Hyperopt-Sklearn: Automatic Hyperparameter Configuration for Scikit-Learn. In Proceedings of the 13th Python in Science Conference (SciPy 2014), Austin, TX, USA, 6–12 July 2014; pp. 1–7. [Google Scholar]

| Operational and Utilization Metrics | Aircraft, Technical, and Environmental Metrics | Wheels and Brakes Metrics | Pilot Inputs and Engine Metrics | |
|---|---|---|---|---|
| Airport ICAO Codes | Aircraft ID/Tail Number | Brake Position | Mean Wheel Speed * | Autobrake Setting |
| Flight Start/End Timestamps | Aircraft Class | Wear Pin Value | Wheel Energy * | Thrust Reverser Usage |
| Tail Flight Number | Mean Ground Speed * | Brake Command (CMD) Fraction * | Mean Brake CMD * | Mean Captain or First Officer Pedal Force * |
| Flight Duration | Deceleration * | Number of Brake Applications * | Mean and Max Brake Temperature Monitoring System (BTMS) Brake Temperature * | Mean Engine N1 Left/Right * |
| Tail Flight Count Per Day | Aircraft Weight * | Mean Autobrake Master CMD * | ||
| Rolling Average Flights/Day (Window: 100 Flights) | Mean Kinetic Energy * | Mean Tire Pressure * | ||
| Time Between Flights | Mean Cabin Altitude * | Wheel Wear * | ||
| Time Duration * | Static Air Temperature * | Mean Electronic Brake Actuator Force * | ||
| Tail Flight Number of the Day | Parking Brake Sum * | |||
| Interpolation Method | MAE | MSE | RMSE | RMSE/Range | % Positive Degradation Introduced |
|---|---|---|---|---|---|
| linear | 0.4895 | 0.3324 | 0.5765 | 0.0058 | 0 |
| slinear | 0.4895 | 0.3324 | 0.5765 | 0.0058 | 0 |
| quadratic | 0.5021 | 0.3696 | 0.608 | 0.0061 | 1.7298 |
| cubic | 0.5039 | 0.3772 | 0.6141 | 0.0062 | 1.5278 |
| pchip | 0.4914 | 0.3338 | 0.5778 | 0.0058 | 0 |
| akima | 0.4913 | 0.3331 | 0.5771 | 0.0058 | 0.2711 |
| Interpolation Method | Lower Bound—High Wear | Upper Bound—High Wear | Lower Bound—Low Wear | Upper Bound—Low Wear |
|---|---|---|---|---|
| linear | −1.0000 | −0.0492 | −0.0335 | −0.0051 |
| slinear | −1.0000 | −0.0492 | −0.0335 | −0.0051 |
| quadratic | −1.7749 | −0.0499 | −0.0334 | 0.0612 |
| cubic | −1.7621 | −0.0499 | −0.0334 | 0.0707 |
| pchip | −1.0000 | −0.0499 | −0.0334 | −0.0001 |
| akima | −1.0000 | −0.0500 | −0.0334 | 0.0000 |
| Column * | Missing % |
|---|---|
| Average Wheel Speed (Taxi Out) * | 8.207 |
| Average Wheel Speed (Landing) * | 8.207 |
| Average Wheel Speed (Taxi In) * | 8.207 |
| Average Cloud Altitude Upon Arrival ** | 1.931 |
| Average Air Temperature Upon Arrival ** | 1.078 |
| Average Pressure Upon Arrival ** | 1.078 |
| Average Dew Point Upon Arrival ** | 1.078 |
| Average Relative Humidity Upon Arrival ** | 1.078 |
| Average Wind Gust Upon Arrival ** | 1.078 |
| Average Wind Speed Upon Arrival ** | 1.078 |
| Average Wind Direction Upon Arrival ** | 1.078 |
| Model | Hyperparameters | Range of Values |
|---|---|---|
| Logistic Regression | C | [0.001, 0.01, 0.1, 1, 10, 100] |
| solver | [‘lbfgs’, ‘liblinear’, ‘newton-cg’, ‘sag’, ‘saga’] | |
| max_iter | [100, 300, 500] | |
| SVC | kernel | [‘linear’, ‘rbf’, ‘poly’, ‘sigmoid’] |
| C | [0.001, 0.01, 0.1, 1, 10, 100] | |
| gamma | [‘scale’, ‘auto’] | |
| probability | [True] | |
| KNN | n_neighbors | [3, 5, 7, 10] |
| weights | [‘uniform’, ‘distance’] | |
| metric | [‘euclidean’, ‘manhattan’] | |
| Decision Tree | max_depth | [3, 5, 8, 10, 20, 30, None] |
| criterion | [‘gini’, ‘entropy’, ‘log_loss’] | |
| min_samples_split | [2, 4, 6] | |
| min_samples_leaf | [1, 2, 4] | |
| Random Forest | n_estimators | [100, 200, 300, 400, 500] |
| max_depth | [3, 5, 8, 10, 20, 30, None] | |
| min_samples_split | [2, 4, 6] | |
| min_samples_leaf | [1, 2, 4] | |
| criterion | [‘gini’, ‘entropy’, ‘log_loss’] | |
| XGBoost | learning_rate | [0.01, 0.03, 0.05, 0.1, 0.2, 0.3] |
| n_estimators | [100, 200, 300, 400, 500] | |
| max_depth | [3, 5, 8, 10, 20, 30, None] | |
| LGBM | num_leaves | [15, 31, 62] |
| max_depth | [3, 5, 8, 10, 20, 30, None] | |
| n_estimators | [100, 200, 300, 400, 500] | |
| learning_rate | [0.01, 0.03, 0.05, 0.1, 0.2, 0.3] | |
| CatBoost | iterations | [500, 1000, 1500] |
| learning_rate | [0.01, 0.03, 0.05, 0.1, 0.2, 0.3] | |
| depth | [4, 6, 8, 10] |
| Model | Best Parameters | Accuracy | Recall | Precision | F1 Score | AUC Score |
|---|---|---|---|---|---|---|
| LGBM | ‘learning_rate’: 0.03, ‘max_depth’: 20, ‘n_estimators’: 200, ‘num_leaves’: 62, ‘random_state’: 0 | 0.9892 | 0.9885 | 0.9898 | 0.9891 | 0.9964 |
| Decision Tree | ‘criterion’: ‘gini’, ‘max_depth’: 3, ‘min_samples_leaf’: 4, ‘min_samples_split’: 2, ‘random_state’: 0 | 0.9892 | 0.9882 | 0.9902 | 0.9891 | 0.9943 |
| XGBoost | ‘learning_rate’: 0.01, ‘max_depth’: 3, ‘n_estimators’: 100, ‘random_state’: 0 | 0.9891 | 0.9880 | 0.9900 | 0.9890 | 0.9960 |
| CatBoost | ‘depth’: 10, ‘iterations’: 1000, ‘learning_rate’: 0.1, ‘random_state’: 0 | 0.9886 | 0.9882 | 0.9889 | 0.9885 | 0.9963 |
| Random Forest | ‘criterion’: ‘gini’, ‘max_depth’: 30, ‘min_samples_leaf’: 1, ‘min_samples_split’: 4, ‘n_estimators’: 100, ‘random_state’: 0 | 0.9871 | 0.9868 | 0.9871 | 0.9870 | 0.9945 |
| SVC | ‘C’: 1, ‘gamma’: ‘scale’, ‘kernel’: ‘linear’, ‘probability’: True, ‘random_state’: 0 | 0.9837 | 0.9833 | 0.9838 | 0.9835 | 0.9815 |
| Logistic Regression | ‘C’: 100, ‘max_iter’: 100, ‘random_state’: 0, ‘solver’: ‘lbfgs’ | 0.9805 | 0.9802 | 0.9804 | 0.9803 | 0.9829 |
| KNN | ‘metric’: ‘manhattan’, ‘n_neighbors’: 10, ‘weights’: ‘uniform’ | 0.8218 | 0.8091 | 0.8411 | 0.8136 | 0.9041 |
| Sample Index | True Label | Predicted Label | Probability of High Wear | Probability of Low Wear |
|---|---|---|---|---|
| 5529 | 0 | 0 | 0.9988 | 0.0012 |
| 4770 | 0 | 0 | 0.9988 | 0.0012 |
| 4718 | 1 | 1 | 0.0013 | 0.9987 |
| 3813 | 0 | 0 | 0.9988 | 0.0012 |
| 1252 | 1 | 1 | 0.0016 | 0.9984 |
| Sample Index | True Label | Predicted Label | Probability of High Wear | Probability of Low Wear |
|---|---|---|---|---|
| 4348 | 0 | 0 | 1.0000 | 0.0000 |
| 4080 | 1 | 1 | 0.0100 | 0.9900 |
| 1391 | 1 | 1 | 0.0100 | 0.9900 |
| 5380 | 1 | 1 | 0.1579 | 0.8421 |
| 2795 | 1 | 1 | 0.0100 | 0.9900 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jammal, P.; Pinon Fischer, O.; Mavris, D.N.; Wagner, G. Advancing Aviation Safety Through Predictive Maintenance: A Machine Learning Approach for Carbon Brake Wear Severity Classification. Aerospace 2025, 12, 602. https://doi.org/10.3390/aerospace12070602
Jammal P, Pinon Fischer O, Mavris DN, Wagner G. Advancing Aviation Safety Through Predictive Maintenance: A Machine Learning Approach for Carbon Brake Wear Severity Classification. Aerospace. 2025; 12(7):602. https://doi.org/10.3390/aerospace12070602
Chicago/Turabian StyleJammal, Patsy, Olivia Pinon Fischer, Dimitri N. Mavris, and Gregory Wagner. 2025. "Advancing Aviation Safety Through Predictive Maintenance: A Machine Learning Approach for Carbon Brake Wear Severity Classification" Aerospace 12, no. 7: 602. https://doi.org/10.3390/aerospace12070602
APA StyleJammal, P., Pinon Fischer, O., Mavris, D. N., & Wagner, G. (2025). Advancing Aviation Safety Through Predictive Maintenance: A Machine Learning Approach for Carbon Brake Wear Severity Classification. Aerospace, 12(7), 602. https://doi.org/10.3390/aerospace12070602








