Intelligent 5G-Aided UAV Positioning in High-Density Environments Using Neural Networks for NLOS Mitigation

Abstract

The accurate and reliable positioning of unmanned aerial vehicles (UAVs) in urban environments is crucial for urban air mobility (UAM) application, such as logistics, surveillance, and disaster management. However, global navigation satellite systems (GNSSs) often fail in densely populated areas due to signal reflections (multipath propagation) and obstructions non-line-of-sight (NLOS), causing significant positioning errors. To address this, we propose a machine learning (ML) framework that integrates 5G position reference signals (PRSs) to correct UAV position estimates. A dataset was generated using MATLAB’s UAV simulation environment, including estimated coordinates derived from 5G time of arrival (TOA) measurements and corresponding actual positions (ground truth). This dataset was used to train a fully connected feedforward neural network (FNN), which improves the positioning accuracy by learning patterns between predicted and actual coordinates. The model achieved significant accuracy improvements, with a mean absolute error (MAE) of 1.3 m in line-of-sight (LOS) conditions and 1.7 m in NLOS conditions, and a root mean squared error (RMSE) of approximately 2.3 m. The proposed framework enables real-time correction capabilities for dynamic UAV tracking systems, highlighting the potential of combining 5G positioning data with deep learning to enhance UAV navigation in urban settings. This study addresses the limitations of traditional GNSS-based methods in dense urban environments and offers a robust solution for future UAV advancements.

1. Introduction

The rapid evolution of unmanned aerial vehicles (UAVs) has initiated a new era of applications in many sectors, including logistics, surveillance, agriculture, and disaster management. Figure 1 illustrates representative examples of UAV applications in these sectors. UAM represents a transformative solution to address transportation and logistics challenges in densely populated areas. Using UAVs and electric vertical take-off and landing (eVTOL) aircraft, the UAM aims to reduce travel times, alleviate traffic congestion, and reduce greenhouse gas emissions, making it a promising alternative to traditional land-based transportation systems [1]. However, a critical challenge for UAVs in urban environments is accurate positioning and navigation through complex urban structures. This challenge directly impacts safety, operational efficiency, and regulatory compliance for all urban UAV applications. Global navigation satellite systems (GNSSs) often struggle in cities due to signal reflections, multipath propagation, and obstructions of non-line-of-sight (NLOS) conditions [2]. These limitations are intensified in dense urban environments where GNSS signals reflect off buildings and other structures before reaching the UAV receiver, causing positioning errors that can exceed several meters [3,4]. Moreover, any requirement for clear line of sight (LOS) to multiple satellites is often challenging in urban canyons, tunnels, and areas with dense foliage, further reducing the accuracy and reliability of GNSS-based navigation systems [5]. These positioning inaccuracies pose significant risks for UAV operations, including potential collisions with buildings, infrastructure, or other aircraft, making reliable positioning a fundamental prerequisite for the widespread adoption of UAV technologies in urban settings. To address these challenges, 5G positioning reference signals (PRSs) have emerged as a promising approach to improve UAV positioning accuracy. The deployment of 5G networks offers unique advantages, such as higher-frequency carriers, wider bandwidths, and improved infrastructure, enabling precise positioning, navigation, and timing services in urban areas [4,6,7]. Unlike the GNSS, which is highly susceptible to multipath errors and environmental obstructions, 5G PRS can even utilize reflected signals to enhance accuracy, achieving meter-level precision in urban scenarios [8,9,10]. This makes 5G PRS a strong candidate technology for improving UAV navigation, particularly in areas where GNSS performance is compromised [11].

Despite these advancements, current UAV positioning systems in urban environments face significant limitations. Hybrid approaches that integrate GNSS, 5G, and additional sensors such as LiDAR and inertial measurement units (IMUs) have demonstrated improved robustness. However, they often fail to adapt dynamically to challenging conditions such as severe multipath interference and dynamic NLOS scenarios, especially in real-time applications [12]. Furthermore, traditional model-based GNSS methods remain computationally demanding and less effective in dynamically noisy environments, limiting their usability in critical applications such as disaster management and last-mile delivery [13,14]. These challenges underscore the urgent need for innovative frameworks that combine high-precision 5G PRS with adaptive deep learning methods to achieve reliable real-time UAV positioning in complex urban environments. Our objective in this study is to address these challenges by introducing a novel approach that integrates 5G PRS data with deep learning techniques to improve the accuracy of UAV positioning. Unlike previous methods that rely solely on signal processing or traditional filtering techniques, our approach leverages the pattern recognition capabilities of neural networks to correct positioning errors in real time, particularly in challenging NLOS conditions where conventional methods struggle. The key contributions of this study are as follows:

• Neural network-based position correction: We design and implement a fully connected feedforward neural network (FNN) to correct 3D position estimates derived from 5G Time of Arrival (TOA) measurements. This approach differs from existing methods by learning the complex relationship between estimated and actual positions, rather than relying on predetermined error models that often fail in dynamic urban environments.
• Comprehensive simulation framework: We develop a simulation environment that incorporates both LOS and NLOS conditions, ensuring robustness and practical applicability in real-world urban environments. Unlike previous studies that focus primarily on ideal or simplified conditions, our framework accounts for the complex signal propagation characteristics encountered in dense urban settings.
• Real-time correction mechanism: We implement a real-time correction system that demonstrates significant improvements in positioning accuracy, outperforming traditional GNSS-based and hybrid methods. Our approach achieves a mean absolute error (MAE) of 1.3 m in LOS conditions and 1.7 m in NLOS conditions, representing substantial improvements over conventional techniques.
• Extensive performance evaluation: We conduct a thorough evaluation of the proposed framework using MAE and root mean squared error (RMSE) metrics, demonstrating the potential of this approach for scalable and resilient UAV navigation across various urban scenarios and conditions.

• This research uses the unique characteristics of 5G signals and combines them with advanced neural network architectures to provide a scalable solution to the limitations of existing UAV positioning systems. These innovations enable the wider adoption of UAM technologies by supporting precise and reliable navigation in densely populated urban environments. Our approach combines 5G positioning techniques with machine learning to create a robust UAV positioning system. The implementation follows a three stage process:

• Data generation and simulation: We use MATLAB’s UAV simulation environment to generate a comprehensive dataset that includes estimated coordinates derived from 5G TOA measurements and the corresponding actual positions (ground truth). The simulation incorporates realistic urban scenarios with varying degrees of signal obstruction, multipath propagation, and NLOS conditions to ensure the robustness of the model in real-world environments.
• Neural network architecture and training: A fully connected feedforward neural network (FNN) is implemented to learn the complex mapping between estimated and actual UAV positions. The architecture includes multiple hidden layers with appropriate non-linear activation functions to effectively capture spatial relationships within the data. The network is trained using supervised learning, with estimated coordinates as inputs and true positions as target outputs.
• Performance evaluation framework: We evaluate the model performance using standard evaluation metrics, including MAE and RMSE, in a variety of scenarios. Our method is benchmarked against traditional approaches, such as 5G TOA combined with Kalman filtering, to quantify improvements in accuracy and reliability, particularly under challenging NLOS conditions.

• The results indicate that our neural network-based correction mechanism significantly improves positioning accuracy in both LOS and NLOS conditions, with MAE values of 1.3 m and 1.7 m, respectively, and an RMSE of approximately 2.3 m. These findings highlight the potential of combining 5G positioning data with deep learning to enhance UAV navigation in urban settings, addressing the limitations of traditional GNSS-based methods in dense urban environments and offering a robust solution for future UAV advancements.

2. Related Work

The integration of ML and DL into 5G-based positioning systems has been extensively studied due to the increasing demand for high-precision localization in urban and indoor environments. These environments pose significant challenges due to NLOS conditions, multipath propagation, and signal degradation. The following sections provide an overview of recent advancements in ML and DL for 5G positioning. The adoption of 5G PRS for UAV positioning has gained significant attention due to their high accuracy and robustness in various environments. Several studies have highlighted the potential of 5G PRS to achieve precision at the centimeter level through advanced carrier phase measurements and time-based techniques [15]. Using 5G double-difference carrier phase measurements combined with a roadside unit, the impact of clock offset errors in UAV positioning has been mitigated. These experiments [16] achieved an RMSE of approximately 0.79 m using four 5G gNodeBs in an LOS environment, highlighting the potential of achieving submeter accuracy with minimal base stations. Similarly, carrier phase positioning has been investigated using 5G New Radio (NR) signals based on orthogonal frequency division multiplexing, where a multi-frequency carrier phase ranging method was proposed to mitigate the impact of antenna reference point position errors, demonstrating that centimeter- to millimeter-level accuracy can be achieved under simulated [17].

NLOS detection is another critical aspect to improve positioning accuracy, particularly for UAV applications operating in urban or obstructed environments. An NLOS detection method has been introduced that uses the discrepancy between received signal strength indicator (RSSI)-based and time-based measurements [18]. This approach effectively filters out erroneous signals that cause high positioning errors, significantly improving positioning accuracy and achieving submeter accuracy 95% of the time when integrated with a Kalman filter (EK)-based estimator. Recent studies have also evaluated the performance of PRS under different network configurations and propagation conditions. Detailed evaluation of the PRS-based Time Difference Of Arrival (TDOA) method has shown that the PRS design supports flexible resource allocation and beam scanning. This flexibility helps balance positioning accuracy and resource efficiency, with satisfactory performance even with limited PRS bandwidth, which is significant for UAV deployments in indoor and outdoor environments [19]. Another relevant approach is the use of location fingerprinting methods [20]. When combined with a weighted K-nearest neighbor algorithm, RSSI-based fingerprinting was employed to achieve substantial localization accuracy. Although this work primarily focused on wildlife tracking, such techniques could be adapted for UAV positioning in scenarios where precise signal propagation models are challenging to establish. Overall, 5G PRS has shown great promise in UAV positioning, with key advances in carrier phase measurements, error mitigation through multi-frequency and NLOS detection techniques, and adaptability to different positioning methods such as TDOA and fingerprinting. However, challenges remain, such as the need for extensive infrastructure, potential weaknesses to interference, and the complexity of integrating these techniques into existing UAV systems. Despite the advancements made, several limitations and challenges have been identified in using 5G PRS for UAV positioning.

• High positioning accuracy often requires a dense network of 5G base stations, which may only be available in some areas, and not available in, for example, rural or less-developed regions.
• 5G PRS is less susceptible to multipath errors than GNSS, but urban environments can still introduce significant signal reflections and obstructions that affect positioning accuracy.
• Techniques like carrier phase measurements and multi-frequency ranging require sophisticated hardware and signal processing capabilities, increasing the complexity and cost of UAV systems.
• Advanced signal processing and communication with multiple base stations can increase the energy consumption of UAVs, which is a critical consideration given their limited battery capacity [21].

• The advent of 5G has enabled the development of novel positioning techniques using ML algorithms. ML-based methods for 5G positioning were explored, including neural networks and random forest regression, demonstrating their effectiveness in handling NLOS conditions using the measurement of the signal beam power [22]. This work highlights the potential of ML to achieve sub-10 m accuracy in urban environments. Similarly, a software-defined receiver has been proposed, incorporating ML for TOA estimation in indoor environments, achieving high pseudorange measurement accuracy even under multipath conditions [23]. These studies lay the foundation for the incorporation of ML to better cope with NLOS conditions. Our work extends this by utilizing 5G PRS data to enhance UAV positioning accuracy in dense urban environments. In another approach, DL architectures have shown significant promise in improving positioning accuracy. A temporal convolutional network was proposed for millimeter-wave positioning, achieving sub-2 m accuracy in outdoor NLOS scenarios. The method uses beam-formed fingerprints to extract spatial information from received signals, outperforming traditional geometry-based methods [24]. The application of RF fingerprinting combined with DL-assisted positioning in 5G has achieved mean positioning errors of 1 to 1.5 m in urban scenarios [25]. These DL-based methods illustrate the potential to extract complex features for positioning. This work builds on this by utilizing fully connected neural networks trained on 5G PRS data to improve UAV positioning accuracy in urban settings. In recent research, hybrid positioning methods that combine 5G signals with other technologies such as GNSS have gained attention for their improved accuracy. A hybrid approach supervised by ML that fuses GNSS and 5G signals has been proposed [12]. By classifying LOS and NLOS links using features extracted from both signal types, sub-30 cm accuracy was achieved indoors and sub-2 m accuracy for 90% of positioning fixes in urban scenarios [26].

However, while hybrid positioning approaches combining GNSS and 5G have shown promise, they still need to overcome challenges due to GNSS dependency in areas with limited satellite visibility. The integration of 5G position reference signals (PRSs) offers a promising solution to the limitations of global navigation satellite systems (GNSSs) in urban environments. By focusing on 5G PRS, systems can achieve improved robustness and accuracy in positioning, particularly in urban scenarios where GNSS signals are often unreliable due to multipath effects and signal blockages. This approach uses the advanced capabilities of 5G networks, such as low latency and high bandwidth, to provide precise and reliable positioning, reducing the dependency on GNSS and improving performance in challenging environments. Kalman filters have been widely used in UAV navigation and positioning because of their effectiveness in estimating the state of a dynamic system in the presence of noise. The Extended Kalman Filter (EKF) and Unscented Kalman Filter (UKF) are particularly popular variants that can cope with non-linear models. A filtered neural network framework has been introduced that integrates an Entropy-Adaptive KF with a recurrent neural network for UAV localization [27]. This framework was able to cope with non-Gaussian noise in GPS data, achieving robust position estimates with minimal delays. The use of Extended KF was highlighted in 5G networks, as it improved mobile robot localization accuracy and showed benefits when used with UAVs in complex environments [28]. Although KFs are effective in smoothing and predicting state estimates, they rely on accurate system models and may struggle with highly non-linear dynamics or changing noise characteristics. Our approach builds upon these methods by using neural networks to handle complex, non-linear signal conditions more effectively, especially in urban environments where traditional filtering techniques may be insufficient. Long Short-Term Memory (LSTM) networks, a type of recurrent neural network, are capable of learning temporal dependencies in sequential data. This makes them suitable for modeling time series data in UAV navigation and positioning. An LSTM-based approach has been proposed for UAV trajectory prediction and position estimation [29]. By capturing the temporal correlations in the UAV motion data, this model improved accuracy over traditional methods. Similarly, LSTM networks were used to improve the accuracy of GNSS positioning by learning from historical positioning errors and correcting them in real time [30]. Integrating LSTM networks with 5G PRS data provides an opportunity to model temporal patterns in signal measurements, potentially improving positioning robustness in dynamic urban environments. However, LSTMs require large training datasets and can be computationally intensive, which may limit their applicability for real-time UAV systems. A comprehensive survey on advances in positioning techniques highlighted the transition from 5G to 6G [31], emphasizing the role of ML and DL in addressing future networks’ requirements for stringent accuracy and latency. The findings also highlighted applications in industrial automation and vehicular systems. Our research aims to address some of these challenges despite considerable advancements in integrating 5G PRS and ML/DL for positioning. Prior works typically fall into two limitations: dependence on hybrid sensor systems (e.g., GNSS/5G/IMU), and performance degradation in dynamic NLOS urban environments. Our work addresses both challenges with the following innovations:

• We propose a lightweight, fully connected neural network that corrects 5G TDOA-based positions without relying on additional sensors, making the system more scalable and energy efficient for UAVs.
• Our dataset includes systematically simulated LOS and NLOS urban flight scenarios based on 3GPP TR 38.901 models—most studies focus on static or ideal LOS settings.
• Unlike earlier models, which generalize poorly under fluctuating noise, our architecture integrates statistical outlier filtering, NLOS labeling, and adaptive neural corrections for robust, real-time performance.

• Although 5G PRS signal patterns were modeled under standard 3GPP conditions, practical issues such as synchronization delays, cell handovers, and RF interference were not explicitly simulated. These factors could degrade TOA reliability and will be explored in future experiments with hardware-in-the-loop setups or field tests. These contributions differentiate our framework as a scalable, simulation-validated solution suitable for real-time UAV tracking solely based on the 5G positioning inputs.

3. System Design and Implementation

This section outlines the complete workflow of our 5G-aided UAV positioning framework, structured into cohesive stages for clarity. A summary diagram is provided in Figure 2 to illustrate the end-to-end system. We begin with the simulation setup, which replicates realistic urban environments using MATLAB R2024b, incorporating UAV trajectories and 5G base station (gNodeB) deployment. Next, PRSs are generated, and TOA data are collected and converted TDOA for initial position estimation. A Kalman filter is then applied to refine these estimates. The dataset creation stage logs both the estimated and actual UAV positions along with contextual parameters such as signal strength and NLOS/LOS conditions. This structured dataset supports the training of a fully connected FNN to learn and correct for systematic positioning errors. Finally, we describe the training process, including preprocessing, optimization, and evaluation. Metrics such as MAE, RMSE, and R-squared (R²) are used to assess model performance under various signal conditions.

3.1. Urban Environment and Simulation Setup

This study utilizes a MATLAB-based simulation environment (Figure 3) to generate a synthetic dataset for UAV positioning in urban environments. The simulation framework builds on the 3GPP TR 38.901 Urban Macro (UMa) and 5G positioning reference signal (PRS) specifications, which are widely adopted for modeling 5G channel behavior. Our contribution is in extending and integrating these models into a fully developed machine learning system, including scenario generation, signal simulation, TOA estimation, and position tracking. TOA estimation is central to 5G-based positioning and serves as the input to the geometric localization stage. TOA is calculated by measuring the time delay between the known transmission time of PRS and their reception at the UAV. Since 5G PRS signals are highly structured and orthogonal across cells, cross-correlation can be used to estimate this delay with high precision. The resulting propagation time is then converted into a range estimate between the UAV and each gNodeB. These range estimates are later fused through multilateration or TDOA techniques to compute the UAV position.

The data generation process included several critical steps:

• Simulation parameters such as building density, PRS configuration, and urban propagation models were chosen to reflect realistic 5G deployments, as summarized in

  Table 1. Simulation parameters for data generation.

  Parameter	Value/Range
  Urban channel model	3GPP TR 38.901 UMa
  Carrier frequency	3 GHz
  Number of UAVs	3
  UAV altitude range	50–120 m
  UAV speed range	5–15 m/s
  Number of gNodeBs	6
  gNB placement	Rooftop (height: 10–75 m)
  Building density	20/50 buildings/km2
  PRS configuration	Orthogonal, unique per gNB/UAV
  LOS/NLOS labeling	Explicit per link
  TOA estimation method	Cross-correlation with PRS
  Positioning method	TDOA + Kalman filter
  Dataset output	$\left(X_e,Y_e,Z_e\right)$ and $\left(X_t,Y_t,Z_t\right)$ per timestep

  .
• While the simulation includes LOS/NLOS-dependent path loss, multipath fading, and receiver noise, it excludes some advanced physical-layer effects such as log-normal shadowing, inter-cell interference, and Doppler spread. These factors have been shown to introduce localization errors even at low UAV speeds (5–15 m/s) in prior studies [32,33,34]. Their impact is moderate under controlled conditions, which supports our phased approach: starting with an idealized environment to validate algorithm performance. Future work will incorporate these effects through extended simulations and hardware-in-the-loop testing.
• To ensure the relevance of the results to real-world scenarios, we adopted parameters in line with regulatory standards and industry practices. For instance, the UAV altitude range (50–120 m) and speed (5–15 m/s) align with urban air mobility guidelines, while the use of 3 GHz carrier frequency and rooftop-mounted gNodeBs (10–75 m height) mirrors common 5G infrastructure deployments. The use of orthogonal PRS with unique resource allocations for each cell replicates standard network configurations aimed at minimizing interference and enabling high-accuracy positioning.
• Three UAVs fly semi-randomized trajectories through a 3D urban environment. Each trajectory consists of straight-line segments, turning points, and vertical movements, simulating realistic missions such as aerial delivery or surveillance. UAV altitudes vary between 50 and 120 m, and horizontal speeds range from 5 to 15 m/s. These trajectories are designed to expose the UAVs to both LOS and NLOS conditions.
• To test generalization under diverse urban conditions, we define two distinct environments:

  –

  LOS-Dominant: Low building density (∼20 buildings/km²) representing open urban or suburban areas.

  –

  NLOS-Dominant: Dense urban layout (∼50 buildings/km²) mimicking signal blockages and multipath effects in city centers.

• Each UAV receives 5G PRS signals from six rooftop-mounted ground gNodeBs (gNBs). All gNBs operate at the same carrier frequency (3 GHz), with unique cell identities and non-overlapping PRS resource allocations. This ensures orthogonality across signals, enabling time-synchronized TOA measurement without inter-cell interference.
• PRS signals propagate through the 3D urban environment based on LOS/NLOS-dependent path loss models. UAVs record the received PRS waveforms at each time step and estimate the TOA via cross-correlation. The LOS/NLOS status for each UAV-gNB link is explicitly labeled. These TOA values are converted to time difference of arrival (TDOA) measurements, which are used for geometric position estimation via a spherical intersection algorithm.
• A Kalman filter smooths the TDOA-based position estimates, reducing random noise and improving temporal consistency. The filtered trajectories provide high-fidelity position estimates for each UAV.
• At each time step, for every UAV, the dataset records the following:

  –

  Estimated 3D position: $(X_e,Y_e,Z_e)$.

  –

  True ground-truth position: $(X_t,Y_t,Z_t)$.

  –

  Metadata: LOS/NLOS label, UAV ID, scenario ID, time index, visible gNBs.

  The final dataset contains approximately 9000 labeled samples. These are used to train and evaluate supervised ML models for UAV localization.

3.2. Dataset Description

We created a comprehensive dataset of 9000 samples using MATLAB’s UAV simulation, capturing a wide range of 285 urban navigation scenarios. The input matrix has shape (N, 3), where N = number of samples (500), and each row corresponds to the estimated (Xe, Ye, Ze) coordinates. The target matrix also has shape (N, 3), representing the true positions (Xt, Yt, Zt). Auxiliary parameters like RSS and path loss were evaluated but not used in the final model to reduce complexity. To ensure transparency, we simulated semi-random UAV trajectories at altitudes ranging from 50 to 120 m and horizontal speeds of 5 to 15 m/s, including straight runs, turns, and altitude changes. The different trajectories provided a mix of LOS and NLOS situations near virtual buildings, generating varied signal propagation conditions. For each time step, the dataset records the PRS-based position estimate, the true location of the UAV, and the estimation error in X, Y, and Z, allowing the post-analysis of error trends. While this dataset provides a controlled and reproducible environment for model training, we acknowledge that it does not include real-world imperfections such as hardware-related delays, environmental interference, or dynamic changes in 5G propagation. To address this, future extensions will incorporate real measurement data from aerial 5G testbeds (e.g., NSF AERPAW) to calibrate our simulation parameters.

Additionally, we plan to apply domain randomization techniques such as varying base station densities, signal fading models, and environmental layouts to improve the model’s generalizability beyond fixed simulated scenes. We also log contextual data such as received signal strength, path loss, and a binary label for LOS/NLOS conditions at that time. Each sample of the dataset includes a timestamp indicating when the measurement was taken for the temporal analysis of the movements of the UAV, the estimated position of the UAV in (X, Y, Z) from TDOA measurements refined by a KF, the ground truth position (X, Y, Z) for the accuracy assessment, and the estimation error for the difference between the estimated and ground truth positions. It also contains signal parameters such as signal strength, path loss, and LOS/NLOS conditions to show how environmental factors affect the positioning accuracy, along with unique identifiers for each UAV and gNodeB to support multi-object tracking. Furthermore, the dataset provides time series error data for all three UAVs in three dimensions, plus binary NLOS labels that mark signal obstruction conditions at each time step, making it possible to assess how these obstructions impact estimation errors and the overall robustness of the tracking algorithm. Our simulation framework is grounded in the 3GPP TR 38.901 model, offering a representative approximation of urban signal behavior. However, additional enhancements, as described above, are necessary to bridge the gap between simulation and deployment fully. To account for this, Gaussian noise is injected into TOA readings to simulate practical conditions. Future work will extend the simulator to model frequency fading, Doppler effects, and pedestrian-induced fluctuations for deeper realism.

3.3. Robust Handling of Real-Time Noisy Data

Figure 4 illustrates a sequential flowchart representing a signal processing pipeline used for refining and improving the accuracy of location estimation, likely in applications such as UAV positioning, wireless localization, and navigation systems.

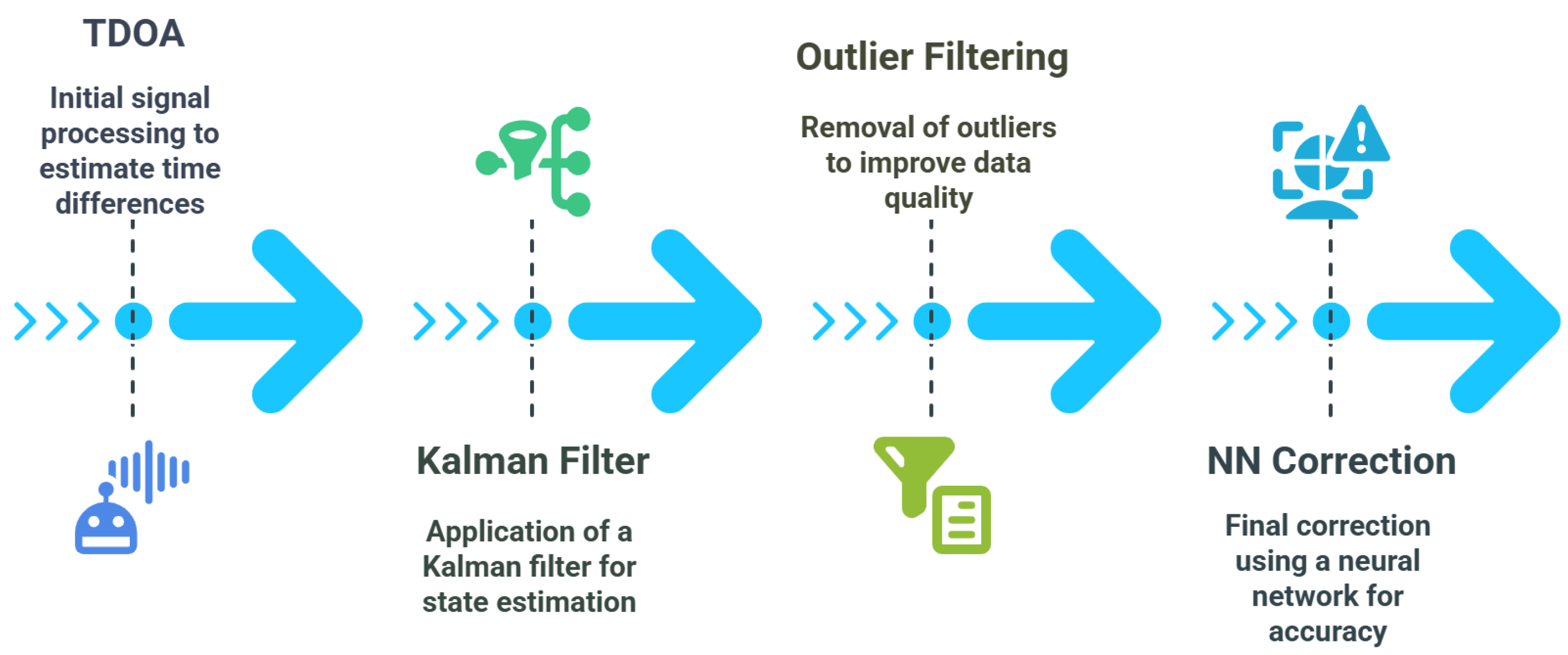
• Input: TDOA (Time Difference of Arrival)
  • Function: TDOA measures the time difference at which a signal arrives at multiple receivers or sensors. This initial measurement helps estimate the position of a source (e.g., a UAV or mobile device) based on signal propagation delays.
  • Purpose: Provides the raw location data used as the starting point for position estimation. However, these readings are often noisy and require further processing.
• Kalman Filter
  • Function: A Kalman filter is an optimal recursive data processing algorithm. It estimates the state of a system from noisy measurements.
  • Purpose: Smoothens the TDOA data by predicting and updating position estimates based on both measurement and motion models. It helps to reduce random noise but may still leave some irregular outliers.
• Outlier Filtering
  • Function: This step involves detecting and removing abnormal or highly deviated data points that can distort the position estimation. Common techniques include statistical methods, median filters, or robust thresholding.
  • Purpose: Enhances the robustness of the system by eliminating errors introduced by multipath propagation, interference, or sensor faults.
• NN Correction (Neural Network Correction)
  • Function: A trained neural network model is applied to fine-tune the filtered data. The network learns from historical or labeled data and can capture non-linear patterns or biases that traditional filters might miss.
  • Purpose: Provides a final, highly accurate position correction, making the system intelligent and adaptive to complex environments like NLOS conditions.

• To address the inherent noise in real-world 5G data, the proposed system integrates statistical outlier rejection (using ±3$\mathrm{\sigma }$ limits), Kalman filtering, and neural network-based error correction. These layers dynamically adjust signal trust levels and discard unreliable data flagged as NLOS. First, we apply the statistical outlier rejection Algorithm 1, continuously monitoring incoming measurements and filtering outliers that deviate beyond a trusted range, ensuring that sudden interference-based glitches do not corrupt the position solution. Next, a KF combined with sensor fusion smooths out noise by optimally weighing the UAV motion model against incoming observations. If the 5G data is momentarily too noisy, the filter trusts the predicted state more. Additional onboard sensors, such as IMUs, provide short-term stability when signals degrade, preventing the position estimate from drifting. We also implement real-time NLOS mitigation in dense urban environments: the system uses a neural network to detect and correct NLOS-induced errors and can lower or discard measurements flagged as NLOS when enough of the other signals are available. A neural network further enables adaptive error correction, learning from recurring biases, e.g., systematic underestimates near certain buildings, and outputting a data-driven correction. Robust estimation techniques such as RANSAC allow us to exclude inconsistent base stations in the multilateration step, and the entire process is computationally light, avoiding the need for heavy batch computations or excessive smoothing that would introduce lag.

By combining predictive filtering, outlier detection, sensor fusion, learned corrections, and robust estimation techniques, the trajectory of the UAV remains stable and accurate despite momentary disturbances, which is crucial for real-time navigation and tracking. The dataset is structured to support multiple analytical tasks, including performance evaluation of the UAV tracking system in dense high-rise areas, open spaces, and various LOS/NLOS scenarios; algorithm development by training and testing new tracking algorithms through the analysis of estimation errors and their correlation with signal parameters; and statistical analysis to study how environmental factors such as NLOS conditions or gNodeB density affect tracking performance. By simulating realistic urban flight scenarios and incorporating detailed 5G signal propagation models, the dataset provides a solid foundation for evaluating and enhancing UAV tracking algorithms in UAM applications.

Algorithm 1 Simplified UAV position estimation enhancement.

Require:  Simulation parameters, 5G PRS settings, UAV trajectories, gNodeB positions Ensure:  Trained neural network model for position correction 1: Simulate Urban Environment and 5G Signal Propagation     1.1 Simulate UAV flights and gNodeB placements     1.2 Model 5G PRS transmission and propagation effects 2: Estimate UAV Positions     2.1 Receive PRS signals and estimate TOA     2.2 Calculate TDOA and estimate positions     2.3 Refine estimates using a KF     2.4 Perform real-time outlier detection by comparing incoming TDOA values against predicted ones.     2.5 Temporarily exclude or down-weight measurements flagged as NLOS or persistently unreliable, ensuring they do not corrupt the position estimate. 3: Prepare Dataset for Training     3.1 Collect estimated and ground truth positions     3.2 Normalize data and split into training and test sets     3.3 Include NLOS labels and cleaned measurements to train the model under realistic signal conditions. 4: Train Neural Network     4.1 Define network architecture     4.2 Train model using MSE loss and Adam optimizer     4.3 Incorporate systematic error patterns. 5: Evaluate and Deploy Model     5.1 Evaluate model performance (RMSE)     5.2 Deploy model for real-time UAV position correction     5.3 Continuously monitor performance in flight and retrain or update thresholds if error metrics exceed acceptable levels.

3.4. Neural Network Architecture

For simplicity and deployability, the neural network is trained on only the 3D estimated coordinates (X, Y, Z). Auxiliary features such as RSS and LOS/NLOS flags are evaluated during feature selection but are excluded from the final model to maintain low complexity and avoid overfitting, given the relatively small sample size. We designed a fully connected FNN to map the estimated UAV coordinates (derived from 5G PRS measurements) to the actual UAV coordinates as illustrated in Figure 5.

Architecture Overview: The model follows a structured design:

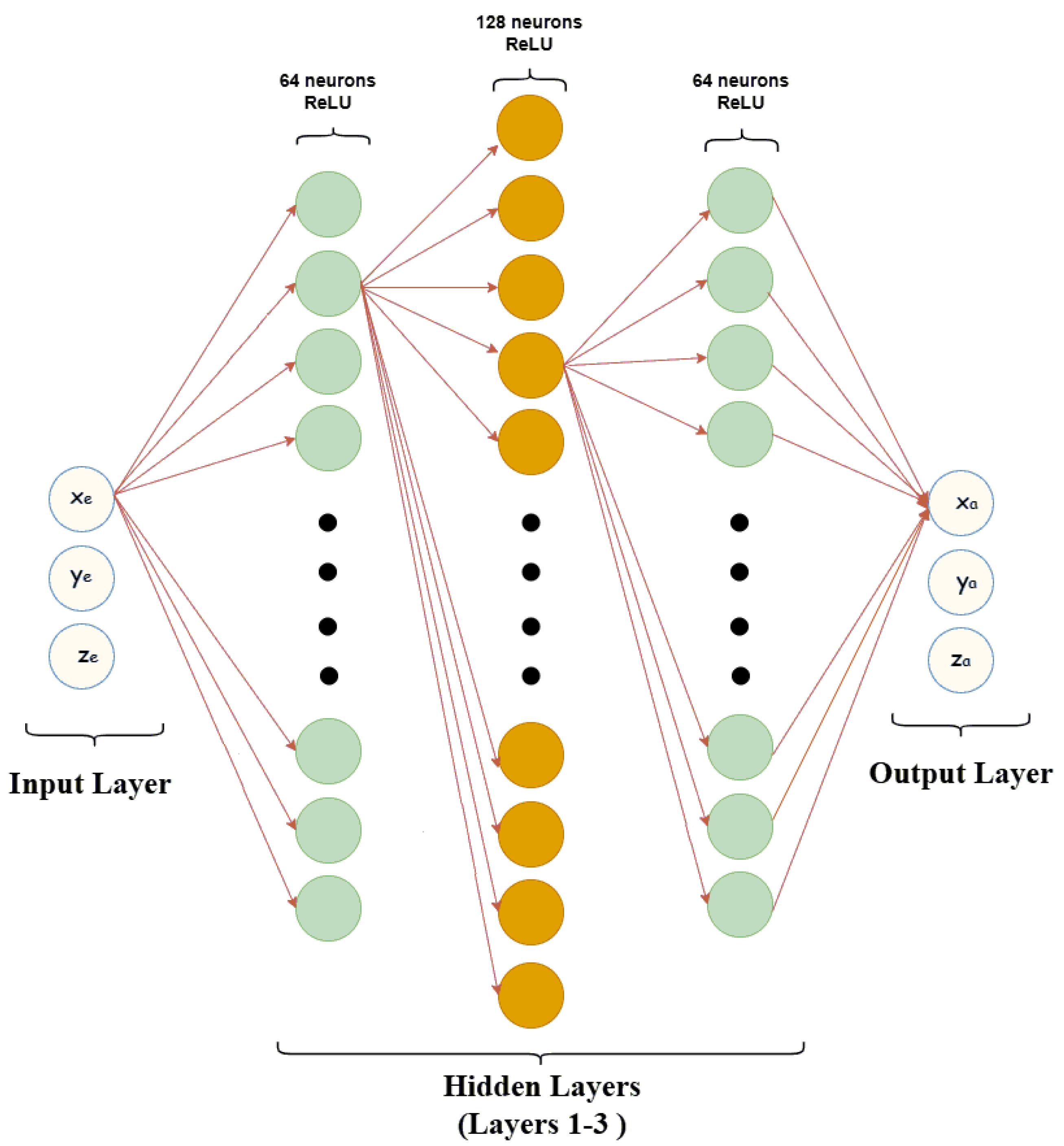
• Input Layer: Accepts three input features representing the estimated UAV coordinates. Layers: The network includes three intermediate layers:

  –

  First Hidden Layer: Expands the input to 64 neurons, applying the ReLU activation function.

  –

  Second Hidden Layer: Increases the complexity with 128 neurons, capturing deeper relationships.

  –

  Third Hidden Layer: Reduces the feature space to 64 neurons to refine the representation before prediction.

• Layer: Produces three output values representing the actual UAV coordinates. No activation function is applied to allow unrestricted predictions.

Figure 5 shows a simplified block diagram of the correction process. The input consists of TDOA-based estimated positions; corrections are applied using learned neural mappings, without relying on auxiliary features such as RSS.

• Activation Function:

• The ReLU (Rectified Linear Unit) activation function introduces non-linearity in the hidden layers. It ensures the network can learn complex patterns by allowing positive values to pass through unchanged while setting negative values to zero which is defined in Equation (1):

  $$\mathrm{ReLU}\left(x\right)=max(0,x).$$

  (1)

Justification for Architectural Choices

• The structure (64–128–64 neurons) balances the learning capacity and computational efficiency. Expanding first helps capture detailed patterns, while reducing later prevents overfitting.
• This design also ensures feasibility for deployment on UAVs with limited compute and memory.
• ReLU helps the network learn complex relationships without suffering from vanishing gradients.
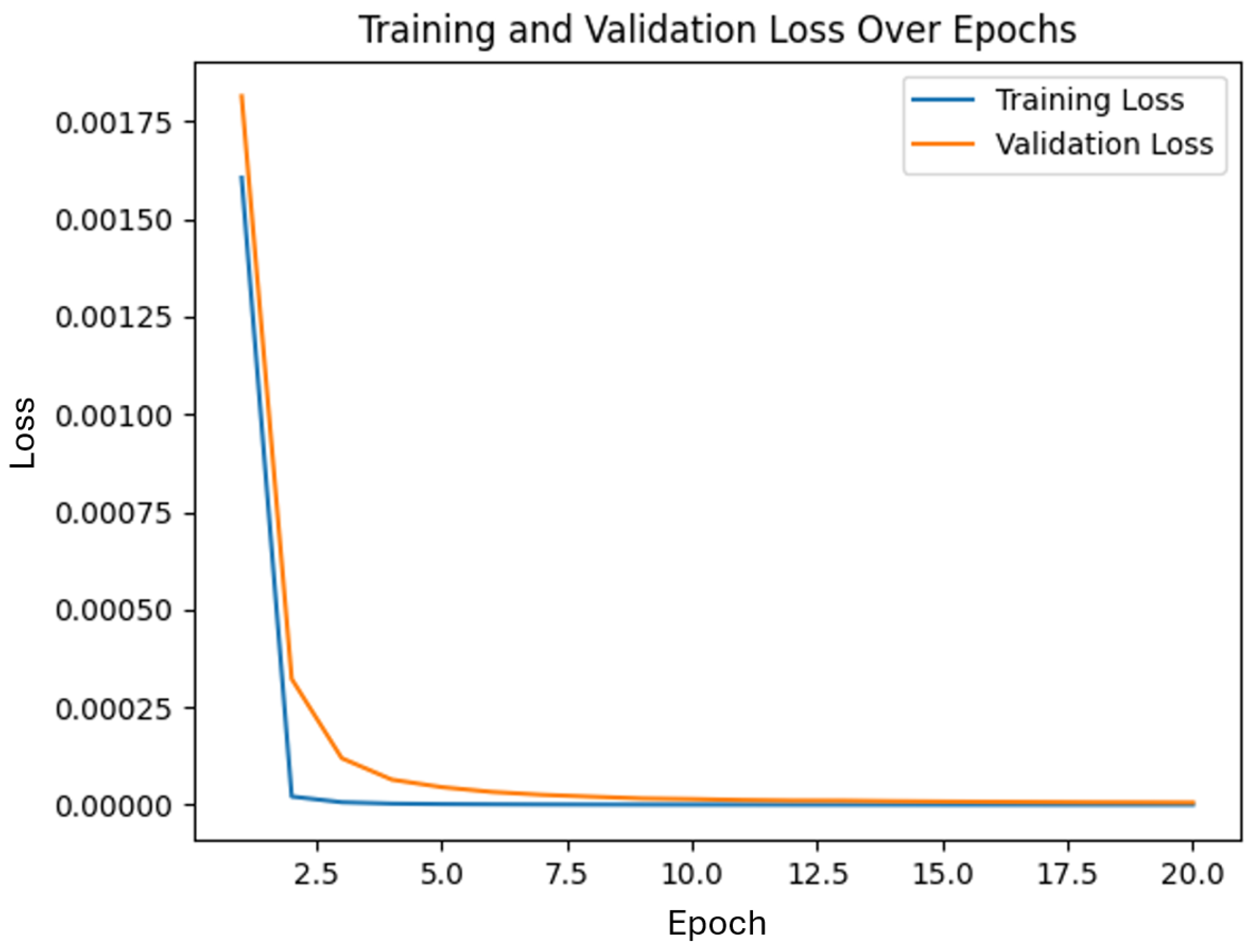
• Our three-layer neural network architecture proved to be the optimal configuration for our specific requirements. When we explored a five-layer architecture, the marginal improvements in accuracy were practically negligible, falling within our measurement uncertainty range, making the results essentially almost identical to the three-layer model. The three-layer architecture stood out because it perfectly balanced our key priorities: it delivered the accuracy that we needed without overcomplicating the model, maintained strong performance under various test conditions, and kept computational costs reasonable. The network was empirically optimized using validation loss. Starting from a single hidden layer, we incrementally increased the number of layers and neurons (from 16 to 128 per layer). Beyond three layers, validation loss plateaued and overfitting was observed as monitored by a rise in the validation error despite continued training accuracy improvements. Thus, the three-layer architecture with 64 neurons each was chosen for optimal generalization. The deeper architectures we tested did not justify the additional computational overhead, especially when the three-layer design effectively met our accuracy targets. The choice of three layers was not just about raw performance numbers—it represented the most pragmatic solution for our real-world constraints and objectives. It provided everything we needed: robust accuracy, efficient processing, and sustainable computational demands. Sometimes, simpler is better; in this case, the three-layer architecture proved precisely what we needed.
• Fully connected layers were chosen because the input features (5G PRS-derived coordinates) do not have spatial or sequential dependencies, making convolutional or recurrent networks unnecessary.

3.5. Training Procedure

Before training, the full dataset of 9000 samples was split into 70% training, 15% validation, and 15% test. Splits were performed randomly while ensuring a balanced mix of LOS and NLOS samples across all sets to preserve statistical representativeness. Each sample includes estimated 3D coordinates from 5G TOA → TDOA conversion (input), ground-truth coordinates (target), path loss, signal strength (RSS), and LOS/NLOS flag (auxiliary features). The researchers used the training set to train the model, the validation set to fine-tune and stop early, and the test set for final evaluation. For data cleaning, outliers were removed using the three-sigma rule (|error| > 3$\sigma$), where $\mathrm{\sigma }$ denotes the standard deviation of the error distribution. This statistical filtering removes extreme anomalies in positioning errors that may result from multipath signal spikes or simulation artifacts [35]. We normalized input features, such as estimated coordinates, using min-max scaling to maintain numerical stability, applying the same parameters across all data splits for consistency. We also created additional features, such as received signal strength (RSS), path loss, and LOS/NLOS labels to help the model understand the environmental conditions. These steps ensured a clean, consistent, and realistic dataset, allowing the model to generalize well to new data. The primary input to the neural network consists of 3D coordinates (X, Y, Z) estimated from TDOA measurements refined with a Kalman filter. Optional auxiliary inputs (e.g., RSS and LOS/NLOS flags) were evaluated, but in the final model, only the estimated coordinates were used for regression to simplify deployment. Feature normalization was applied using min-max scaling based on the training set.

The model was trained using the MSE loss function, which is defined in Equation (2):

$$L={\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2$$

(2)

Equation (2) defines the MSE loss function, where L represents the loss, $y_i$ is the ground truth value, ${\widehat{y}}_i$ is the predicted value, and n is the total number of samples. The MSE penalizes significant errors more heavily, making it a suitable choice for regression tasks in neural network training. MSE was chosen because it strongly penalizes significant errors, which is critical in the accuracy of UAV positioning. Although MSE can be sensitive to outliers, the data cleaning, normalization, and additional metrics monitoring (such as MAE) mitigated its potential drawbacks.

We used Adam Optimizer with a learning rate of 0.001. This adaptive optimization method efficiently handles noisy data and sparse gradients. We used default hyperparameters (${\beta }_1=0.9,{\beta }_2=0.999,ϵ={10}^{-8}$) as recommended in [36,37].

The model was trained for 20 epochs with a batch size of 32. The training loop followed these key steps:

• Forward Pass:Compute the predictions for the input batch.
• Loss Computation: Calculate the MSE loss.
• Backward Pass: Compute gradients via backpropagation.
• Parameter Update: Update model weights using the Adam Optimizer.

The validation loss was monitored at the end of each epoch. Although early stopping was not explicitly implemented in the provided code, this mechanism can be easily integrated by halting training when the validation loss does not improve after a predefined number of epochs.

3.6. Model Evaluation, Testing, and Deployment

The model was evaluated using a held-out test set comprising 15% of the total dataset, which was not used during training or validation. The data were split into 70% for training, 15% for validation, and 15% for testing. This approach ensures an unbiased assessment of the model’s generalization capability. To maintain fairness in comparative evaluation, all internally developed models and baseline methods were tested under identical simulation conditions. These included consistent UAV trajectories, signal propagation characteristics based on the 3GPP TR 38.901 standard, and matching LOS/NLOS distributions. This uniform setup ensures that observed differences in performance are attributable solely to model behavior rather than variations in the data or environment. For real-time operation, the trained model is integrated into an inference pipeline suitable for onboard deployment. Input features are normalized prior to prediction and are inverse transformed post-inference to restore physical coordinate outputs compatible with UAV navigation systems.

3.7. Implementation Details

The methodology was implemented using PyTorch version 1.13.1 for deep learning, along with pandas and scikit-learn for data preprocessing and normalization. Visualization was conducted using matplotlib. All experiments were executed on an NVIDIA GPU to accelerate both training and inference. These methodological enhancements effectively integrate machine learning techniques with 5G Positioning Reference Signal (PRS) data, resulting in a robust and scalable solution for enhancing UAV positioning accuracy in urban environments under both LOS and NLOS conditions.

4. Results and Discussion

4.1. Overview of Results

The proposed ML-based UAV positioning system significantly improves accuracy and robustness in urban environments. The key evaluation metrics, mean absolute error (MAE), mean squared error (MSE), and R-squared, demonstrate that the model effectively refines position estimates based on 5G Positioning Reference Signal (PRS) data. The clear distinction between LOS and NLOS performance highlights the system’s ability to manage signal degradation. These results confirm the system’s potential for deployment in urban delivery, disaster response, and surveillance, where reliable navigation is essential.

4.2. Training and Validation Loss Convergence

As illustrated in Figure 6, the training and validation losses show smooth convergence over 20 epochs, stabilizing by the third epoch. This indicates that the model quickly learns most patterns in the data early in training. The final loss values are as follows:

Training Loss: 0.000009

Validation Loss: 0.000156

These results confirm that the model achieves generalization without overfitting. The small gap between training and validation loss indicates robust model performance on unseen data, a critical factor for real-world deployment. The rapid convergence observed in training and validation indicates that the model is computationally efficient, reducing the time and resources needed for model training and fine-tuning in real-world applications.

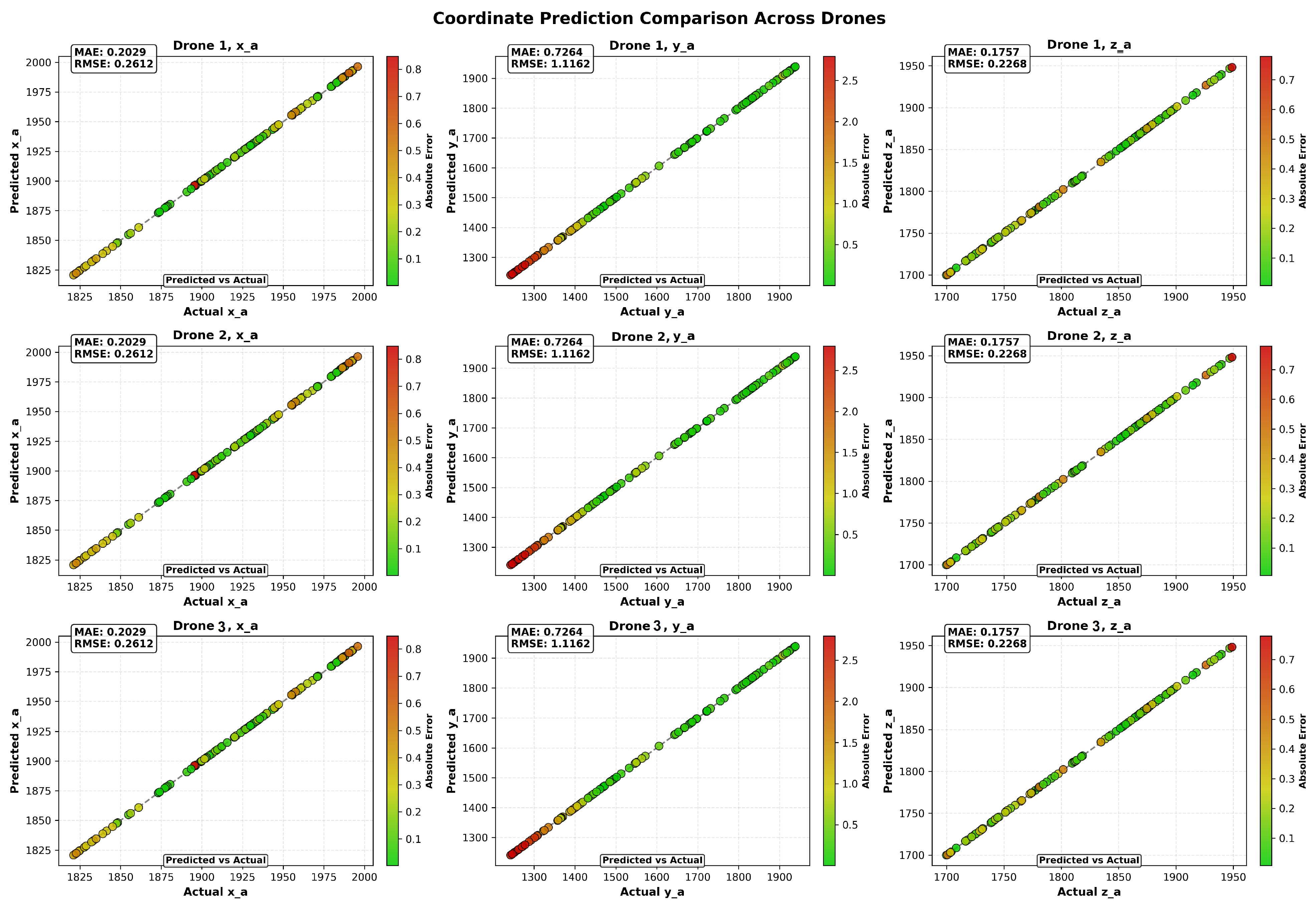
4.3. Quantitative Analysis of Position Estimation

This subsection presents the core performance metrics used to assess the accuracy of the proposed positioning model. The evaluation quantifies the differences between predicted and actual UAV positions under both LOS and NLOS conditions.

The primary metrics used are mean absolute error (MAE) and root mean squared error (RMSE), which capture the average and variance-sensitive components of the localization error, respectively. These are defined as follows:

$$\mathrm{MAE}={\displaystyle \frac{1}{n}}\sum _{i=1}^n|y_i-{\widehat{y}}_i|$$

(3)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{(y_i-{\widehat{y}}_i)}^2}$$

(4)

Here, $y_i$ denotes the ground truth position, ${\widehat{y}}_i$ is the model’s predicted position, and n is the total number of test samples. In addition to MAE and RMSE, the coefficient of determination ($R^2$) was used to assess the proportion of variance in the actual positions that is explained by the model’s predictions.

Table 2. Overall performance metrics for position estimation.

Metric	Value
MSE	0.000012
MAE	2.63 m
RMSE	3.12 m
R-Squared ($R^2$)	0.666549

summarizes the overall performance of the model on the full test set. The average MAE across all samples is approximately 2.63 m, with an RMSE of 3.12 m and $R^2=0.666$. These results confirm the model’s ability to significantly reduce positioning error, even in dense urban environments.

These results demonstrate that the model effectively refines raw position estimates. While the average error is acceptable for general navigation tasks such as delivery and surveillance, further optimization may be necessary for high-precision use cases. A breakdown of the performance under LOS and NLOS conditions is presented in Section 4.4.

4.4. LOS vs. NLOS Performance

To evaluate the model’s robustness under varying signal propagation conditions, performance is assessed separately for line-of-sight (LOS) and non-line-of-sight (NLOS) scenarios. As expected, the localization accuracy declines in NLOS settings due to signal obstruction, multipath propagation, and attenuation. Nevertheless, the model demonstrates consistent and reliable performance across both environments.

Table 3. Positioning accuracy under LOS and NLOS conditions.

Condition	MAE (m)	RMSE (m)	MSE (m2)
LOS	1.30	1.60	2.56
NLOS	1.70	2.05	4.20

summarizes the key performance metrics under each condition. The mean absolute error (MAE) under LOS is 1.30 m, increasing to 1.70 m in NLOS. Similarly, the RMSE increases from 1.60 m to 2.05 m. Despite this degradation, the model maintains sub-2 m accuracy under NLOS and significantly outperforms traditional baseline methods.

These results confirm the model’s ability to maintain high positioning accuracy in both ideal and obstructed urban environments, supporting its suitability for real-world UAV applications such as navigation, surveillance, and delivery in complex cityscapes.

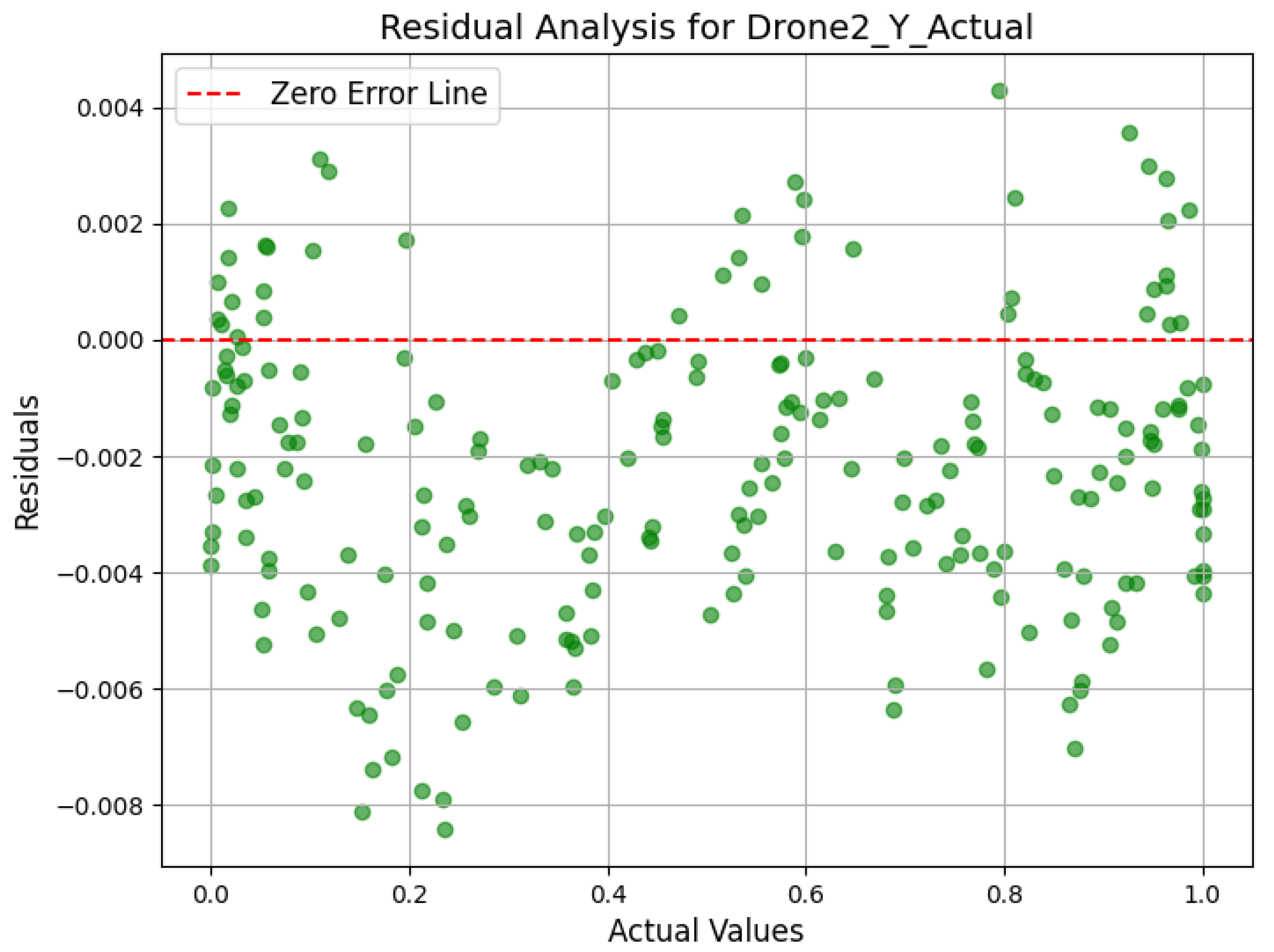
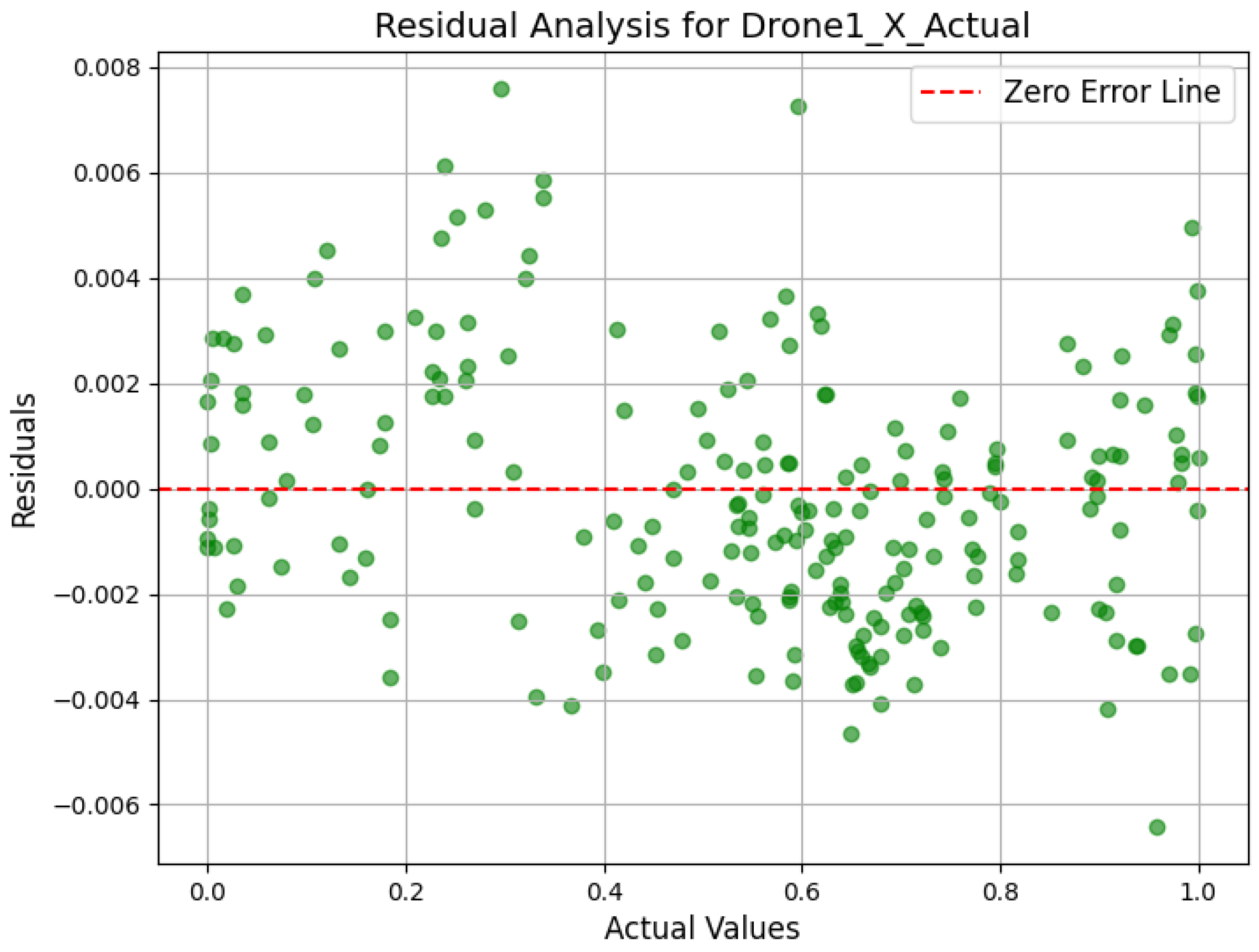
4.5. Scatter Plot and Residual Analysis

To visually assess the alignment between the predicted and actual UAV positions, scatter plots were generated for the X, Y, and Z axes across three UAVs. As shown in Figure 7, the predicted coordinates exhibit strong alignment with the ground truth, clustering tightly around the identity line ($y=x$). This indicates high predictive accuracy, particularly along the horizontal (X, Y) axes. Each subplot includes color-coded markers representing the absolute error for each sample, with green indicating low error and red indicating higher deviation. These plots confirm that the model achieves sub-2 m precision under both LOS and NLOS conditions. Residual analysis, shown in Figure 8 and Figure 9, further supports these findings. Errors are symmetrically distributed around zero in all spatial dimensions, indicating no systematic bias. However, the residuals in the Z-axis show a slightly wider spread, especially under NLOS conditions, highlighting the challenge of vertical localization in obstructed environments.

These visual results complement the quantitative findings in Table 3, reinforcing the model’s strong lateral accuracy and robust performance across varying urban scenarios.

4.6. Spatial Error Distribution

An analysis of prediction errors along the X, Y, and Z dimensions reveals that the model performs more accurately in the horizontal plane (X and Y) than in the vertical (Z) dimension. Specifically, errors in the Z-axis are more pronounced, particularly under NLOS conditions. This reflects an anisotropic error distribution, where lateral estimates are more stable than vertical ones. This degradation in vertical accuracy is likely due to increased multipath propagation and reduced signal quality when direct paths are obstructed. Additionally, the geometry of terrestrial 5G base station antennas is optimized for horizontal coverage, limiting vertical angular resolution for UAVs operating above rooftop level. Residual analysis (Section 4.5) confirms a wider spread in Z-axis residuals under NLOS conditions, consistent with increased signal dispersion and elevation uncertainty in obstructed urban environments. While the model effectively handles horizontal localization, vertical positioning requires further refinement. This is particularly important for applications involving complex 3D flight paths, such as rooftop landings, multilevel navigation, and autonomous inspections in urban canyons.

Future work may address this limitation by incorporating altitude-aware neural architectures or fusing radio-based predictions with complementary modalities such as barometric sensors, LiDAR altimetry, or inertial navigation systems. These enhancements could mitigate Z-axis ambiguity and improve vertical accuracy under challenging propagation conditions.

4.7. Comparison of Raw vs. Corrected Position Estimates

To quantify the benefit of the proposed learning-based approach, we compare the final corrected position estimates with the raw outputs derived from 5G TDOA-based multilateration refined using a Kalman filter. Here, “raw” refers to traditional estimates computed without any neural correction.

Table 4. Comparison of raw vs. corrected positioning error.

Condition	MAE (Raw)	MAE (Corrected)	RMSE (Raw)	RMSE (Corrected)
LOS	3.8 m	1.3 m	4.7 m	1.6 m
NLOS	5.1 m	1.7 m	6.3 m	2.05 m

presents the MAE and RMSE under both LOS and NLOS conditions. The raw MAE under LOS and NLOS is 3.8 m and 5.1 m, respectively, compared to 1.3 m and 1.7 m after correction—a reduction of over 60%. Figure 10 illustrates the improvement in positioning error achieved by the proposed method under both LOS and NLOS conditions.

These results demonstrate that the proposed model substantially improves positioning performance under both propagation conditions. Even under NLOS, where multipath and signal degradation are most pronounced, the corrected error remains below 2 m, confirming the model’s robustness and effectiveness in real-world urban environments.

5. Conclusions and Future Work

This study addressed the critical challenge of accurate UAV positioning in complex urban environments, where traditional GNSS methods often fail due to signal reflections and obstructions. Reliable positioning is fundamental for the safety, efficiency, and regulatory compliance of urban UAV operations, including package delivery, infrastructure inspection, and emergency response. The limitations of traditional positioning systems in dense urban areas remain a significant barrier to the widespread adoption of UAV technologies for urban air mobility and related applications. Our findings show that combining 5G positioning reference signals with neural network-based corrections can significantly reduce the challenges of positioning in NLOS environments. Its accuracy and reliability across different signal conditions make the system well-suited for urban UAV operations, where navigating through dense, complex environments is critical to both safety and mission success. This paper proposed a 5G PRS-aided UAV positioning system enhanced with a neural network-based correction module. The proposed approach achieved significant improvements in positioning accuracy, with a mean absolute error of 1.3 m under LOS conditions and 1.7 m under NLOS conditions, and a root mean squared error (RMSE) of approximately 2.3 m. These results represent a significant improvement over traditional methods, particularly in challenging urban non-line-of-sight (NLOS) scenarios where traditional approaches often fail. The main contributions of this work are as follows:

• A hybrid positioning framework that integrates 5G positioning reference signals (PRS) with a neural network-based correction module, specifically designed to address the challenges of UAV navigation in urban environments.
• A lightweight neural network architecture tailored for real-time deployment on resource-constrained UAV platforms, enabling accurate positioning without significant computational overhead.
• A realistic simulation environment that captures key urban signal propagation effects, including LOS/NLOS variability, multipath fading, and other critical impairments.
• Quantitative performance evaluation, showing mean absolute errors of 1.3 m under LOS and 1.7 m under NLOS conditions, with a RMSE of approximately 2.3 m representing a substantial improvement over traditional methods, especially in urban NLOS scenarios.
• A discussion of practical deployment challenges, such as regulatory restrictions on BVLOS operations, and second-order real-world effects like log-normal shadowing, inter-cell interference, synchronization issues, and Doppler spread.

• As shown in Table 5, our approach offers advantages in both accuracy and computational efficiency compared to conventional multilateration, neural network fingerprinting, hybrid GNSS/5G fusion, and graph-based optimization methods. The real-time capabilities and adaptability to NLOS environments support integration into intelligent airspace systems and autonomous navigation platforms. The system combines detailed signal modeling with practical design choices, aiming to improve both the algorithm and its real-world usability. The neural network correction module is built for embedded use, with a lightweight design that supports fast onboard processing and low latency. This allows for real-time position updates, even in dynamic urban environments with changing signal conditions.

Table 5. Comparison of positioning techniques for urban UAV applications (under consistent simulation conditions where applicable).

Approach	Accuracy	Computational Efficiency	Remarks	Ref
Proposed 5G PRS + Neural Network Correction (5G TDOA + Kalman + FNN)	∼1.3 m MAE (LOS), ∼1.7 m MAE (NLOS), ∼2.3 m RMSE. Significantly reduces baseline error.	High—Designed for urban NLOS; ML model compensates for multipath and removes outliers in real time.	Moderate—Real-time feasible. Lightweight FNN inference with Kalman filtering. Suitable for onboard UAV use.	Our approach
Baseline 5G TDOA + Kalman Filter (Conventional Multilateration)	3.8 m (LOS), 5.1 m (NLOS) MAE. Performance degrades in dense urban areas.	Medium—Effective in LOS; poor in NLOS due to lack of multipath mitigation.	High—Very efficient. Suitable for real-time but lacks advanced error correction.	[38]
Neural Network Fingerprinting (Deep Learning + GNSS)	Few-meter-level accuracy in mapped urban areas. Performance declines with environmental changes.	High in mapped areas. Requires large training datasets; less adaptive to online changes.	Medium—Heavy offline training; fast inference. Needs storage for fingerprint database.	[39]
Hybrid GNSS/ 5G EKF Fusion (EKF + 5G + GNSS)	∼1–3 m static urban, ∼1–4 m dynamic. Better than GNSS- or 5G-only.	High—Dual-system robustness. Effective fallback if one signal is degraded.	Medium—EKF is real-time friendly, but processing 5G + GNSS increases complexity.	[40]
Graph-Based 5G + IMU Fusion (Graph Optimization)	∼0.15–0.3 m error in indoor LOS. Centimeter-level accuracy in ideal setups.	High—Robust in structured environments. Still being evaluated outdoors with multipath.	Moderate—Real-time capable but computationally heavier than EKF.	[41]

Table 5. Comparison of positioning techniques for urban UAV applications (under consistent simulation conditions where applicable).

Approach	Accuracy	Computational Efficiency	Remarks	Ref
Proposed 5G PRS + Neural Network Correction (5G TDOA + Kalman + FNN)	∼1.3 m MAE (LOS), ∼1.7 m MAE (NLOS), ∼2.3 m RMSE. Significantly reduces baseline error.	High—Designed for urban NLOS; ML model compensates for multipath and removes outliers in real time.	Moderate—Real-time feasible. Lightweight FNN inference with Kalman filtering. Suitable for onboard UAV use.	Our approach
Baseline 5G TDOA + Kalman Filter (Conventional Multilateration)	3.8 m (LOS), 5.1 m (NLOS) MAE. Performance degrades in dense urban areas.	Medium—Effective in LOS; poor in NLOS due to lack of multipath mitigation.	High—Very efficient. Suitable for real-time but lacks advanced error correction.	[38]
Neural Network Fingerprinting (Deep Learning + GNSS)	Few-meter-level accuracy in mapped urban areas. Performance declines with environmental changes.	High in mapped areas. Requires large training datasets; less adaptive to online changes.	Medium—Heavy offline training; fast inference. Needs storage for fingerprint database.	[39]
Hybrid GNSS/ 5G EKF Fusion (EKF + 5G + GNSS)	∼1–3 m static urban, ∼1–4 m dynamic. Better than GNSS- or 5G-only.	High—Dual-system robustness. Effective fallback if one signal is degraded.	Medium—EKF is real-time friendly, but processing 5G + GNSS increases complexity.	[40]
Graph-Based 5G + IMU Fusion (Graph Optimization)	∼0.15–0.3 m error in indoor LOS. Centimeter-level accuracy in ideal setups.	High—Robust in structured environments. Still being evaluated outdoors with multipath.	Moderate—Real-time capable but computationally heavier than EKF.	[41]

Additional efficiency can be achieved using quantization and pruning [42], while low-power hardware solutions, such as nanoscale sensors and energy-efficient logic circuits [43,44], can help support deployment in power-constrained UAV platforms. These include log-normal shadowing, inter-cell interference, imperfect synchronization, and Doppler spread, all of which can introduce significant localization errors even at modest UAV speeds [32,33,34]. Regulatory constraints also present practical challenges: large-scale field trials for Beyond Visual Line of Sight (BVLOS) operations remain restricted by national aviation authorities, such as the FAA and EASA, and are further limited by public concerns over privacy and noise pollution [45,46].

Future work will aim to bridge the gap between simulation and real-world deployment through the following directions:

• Implementing real-time inference pipelines optimized for embedded UAV systems with limited computational resources.
• Integrating multi-sensor data sources such as GNSS, IMUs, and LiDAR to enable more robust and resilient hybrid localization.
• Scaling the framework for fleet-level deployment, including support for distributed localization and coordination across UAV swarms.
• Improving simulation fidelity by incorporating Doppler spread, shadowing, synchronization errors, and other signal distortion effects.

• The proposed system is compatible with real-world 5G/UAV testbeds such as AERPAW and 5GRAIL, which provide access to live network signals, mobile UAV operations, and timing synchronization effects [47,48,49]. These platforms offer a foundation for end-to-end testing and hardware-in-the-loop validation under realistic conditions. This study demonstrates that accurate, real-time UAV localization in complex urban environments is achievable by integrating 5G positioning reference signals with lightweight neural network-based correction. The results highlight the potential for deployment in autonomous UAV fleets operating within next-generation urban airspace frameworks, supporting the advancement of urban air mobility and enabling new applications that demand precise positioning in challenging conditions.