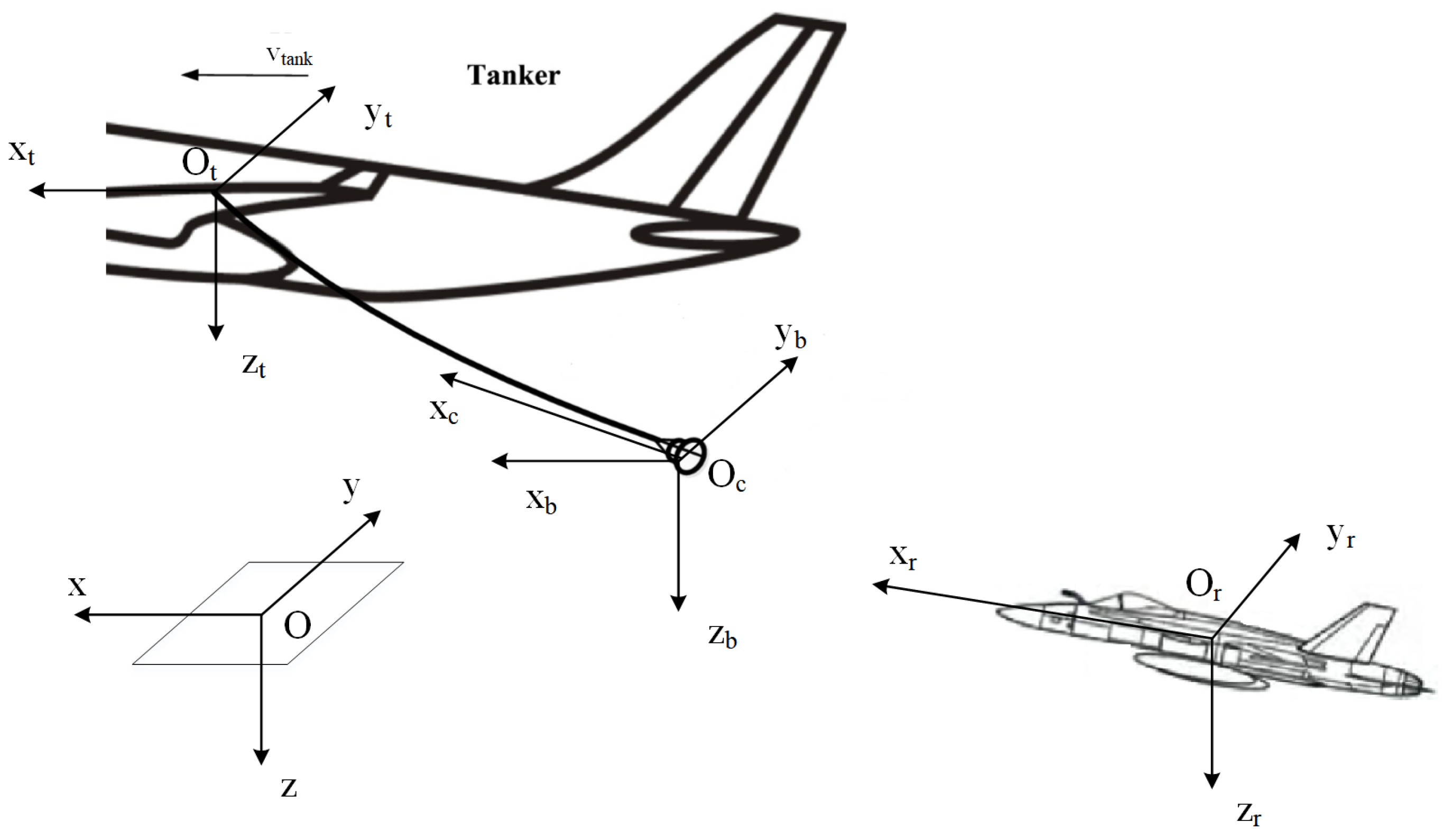
1. Introduction
In the modern aviation field, aerial refueling technology, as a key factor in enhancing the combat effectiveness of aircraft, is receiving widespread attention [
1]. In military scenarios, with the continuous evolution of the warfare, higher requirements are placed on the long-range, persistent and rapid response capabilities of combat aircraft. Aerial refueling technology enables fighter jets to continuously perform missions far from their bases, greatly enhancing the flexibility and strategic deterrence of military operations [
2,
3]. Given its simplicity, flexibility, and versatility in structure, the hose and drogue aerial refueling method remains one of the main approaches. With the development of aerial refueling technology and the ever increasing requirements of modern flight missions for this technology, there is an urgent need for autonomy in aerial refueling to expand its application scope and ensure its high-precision, high-safety, and high-efficiency implementation [
4]. For manned aircraft, autonomous aerial refueling (AAR) technology aims to reduce the risks and complexity of the pilot’s operation and improve the efficiency and safety of refueling docking; for unmanned aerial vehicles, it has become an essential technology for enhancing the combat radius and endurance [
5,
6].
However, achieving AAR faces numerous challenges. Among them, the accurate prediction of the drogue position is the core challenge for safe and efficient refueling [
7]. During the refueling process, the drogue is affected by complex aerodynamics, the relative motion between the tanker and the receiver aircraft, and environmental factors, resulting in a highly uncertain and dynamically changing position [
8,
9]. Turbulence, gusts, etc., in the air can cause irregular swings and displacements of the drogue, and changes in the speed, acceleration, and attitude of the tanker and receiver aircraft will further exacerbate the complexity of the drogue position [
10,
11]. These factors make it difficult for the receiver aircraft to accurately predict the future position of the drogue, posing great difficulties for the refueling operation. If the drogue position cannot be accurately predicted, deviations may occur during the docking process between the receiver aircraft and the drogue, and even collision accidents may happen, seriously threatening flight safety [
12].
A large number of studies have been carried out on position prediction methods [
13,
14]. Conventional drogue position prediction methods are mainly based on empirical models or simple physical models [
15,
16]. These methods may have some accuracy in relatively stable environments, but their limitations gradually emerge in actual complex aerial refueling scenarios. Empirical models often rely on a large amount of historical data and specific flight conditions and lack adaptability to complex dynamic environments; simple physical models have difficulty fully considering the interactions of various complex factors, resulting in large deviations between prediction results and actual situations.
In recent years, with the rapid development of artificial intelligence and machine learning technologies, using data-driven methods for drogue position prediction has become a new research direction [
17,
18]. These methods can mine the hidden patterns and features in data by learning and analyzing a large amount of flight data, thus establishing more accurate prediction models. However, pure data-driven methods often ignore the constraints of physical principles, which may lead to physically unreasonable prediction results. Moreover, the generalization ability of the models may be affected when data are limited [
19].
The emergence of physics-informed neural networks (PINNs) provides a new idea for solving the above problems [
20]. PINNs combine physical knowledge with neural networks. While leveraging the powerful nonlinear fitting ability of neural networks, physical equations are introduced as constraint conditions, causing the prediction results of the model to conform to both data characteristics and physical laws [
21,
22]. This method has unique advantages in dealing with problems with complex physical processes and dynamic changes, and is expected to provide a more accurate and reliable solution for the prediction of the AAR drogue position.
This paper aims to conduct in-depth research on the prediction method of the AAR drogue position based on PINNs. First, a detailed analysis of the motion characteristics and influencing factors of the drogue during the AAR process is carried out. Second, a neural network model integrating physical information is constructed, and the model is trained and optimized using simulated data. Finally, the effectiveness and accuracy of the model are verified through experiments, providing theoretical support and technical guarantee for the development of AAR technology.
The main contributions of this paper are as follows. For the first time, a prediction model that deeply integrates physical information with an attention-augmented long short-term memory (AALSTM) is proposed. It makes full use of the interpretability of physical models and the powerful nonlinear fitting ability of data-driven models, significantly improving the prediction accuracy and stability of the drogue position.
A comprehensive and detailed physical model of the refueling drogue is established. The calculation formulas for gravity, aerodynamic force, and hose tension, as well as the decomposition formulas of each force on the coordinate axes, are presented. The ordinary differential equation of Newton’s second law is established based on the inertial system, making the dynamic model more in line with actual working conditions and providing accurate physical constraints for model integration.
The PINN is designed and comprehensively verified through simulation experiments. The parameter values of the dynamic equations are presented. The data collection and processing methods for AALSTM are detailed. The design of each dimension of the neural network, the division of training data, and the model training method are also discussed. A comparison with conventional methods is made to demonstrate the advantages of the method proposed in this paper in key indicators, providing a strong basis for practical applications.
The rest of the paper is organized as follows. The related work is elaborated in
Section 2. The physical model is introduced in
Section 3. The design process of PINN based on the AALSTM is presented in detail in
Section 4. The simulation test examples and the result analysis are provided in
Section 5. Finally, the conclusions are summarized in
Section 6.
2. Related Work
In the field of drogue position prediction, previous research has achieved certain results, but there is still room for improvement. Refs. [
23,
24] conducted an in-depth analysis of the force conditions of the drogue under different flight conditions based on a conventional physical model and predicted the position by establishing accurate kinematic equations. In this study, the analysis of various forces is relatively detailed. For example, corresponding calculation formulas are given for gravity, aerodynamic force, and hose tension. However, the actual aerial refueling environment is extremely complex, and there are many interference factors that are difficult to model accurately, such as unstable airflows and random changes in the atmospheric environment. These factors limit the prediction accuracy of this method in practical applications.
Refs. [
25,
26,
27] used an conventional neural network for drogue position prediction, making full use of the powerful nonlinear fitting ability of the neural network to capture some features in the data. During the data processing stage, the model can model complex nonlinear relationships to a certain extent through learning a large amount of historical data. However, due to the lack of in-depth integration of physical laws, the model cannot reasonably constrain and correct the prediction results according to physical principles when facing complex working conditions, resulting in poor prediction performance. For example, when encountering special flight attitudes or extreme weather conditions, the prediction results often deviate from the actual values.
In the research of AALSTM, refs. [
28,
29,
30] proposed an innovative model that combines an attention mechanism with LSTM for natural language processing tasks. By dynamically adjusting the weights of inputs at different time steps, this method enables the model to focus more on key information, thus effectively improving the accuracy of text classification and sentiment analysis. In text classification tasks, through the attention mechanism, the model can quickly locate keywords and key sentences related to the text category, improving the classification accuracy. This idea provides important reference for applying AALSTM in the prediction of the AAR drogue position. In time-series data processing, the attention mechanism can help the model better capture important features of the data at different time points, which has potential application value for drogue position prediction tasks that need to handle complex time-series data.
In the application of PINNs, refs. [
31,
32] used PINNs to solve nonlinear dynamic problems. By ingeniously using the constraint conditions of physical models to improve neural network training, they significantly enhanced the generalization ability and prediction accuracy of the model. When solving nonlinear dynamic problems, PINNs integrate conservation laws, boundary conditions, etc. Incorporatingphysical models as constraints into the neural network training process enables the model to not only learn data features but also to follow physical laws.
In the AAR scenario, integrating physical information into neural networks is expected to solve the problem of the lack of physical basis in data-driven methods. Through the constraints of the physical model, the model can reasonably predict the motion state of the drogue according to physical principles under different flight conditions, thereby improving the reliability of drogue position prediction.
Existing prediction methods for the AAR drogue position have their own advantages and disadvantages. The methods based on physical models have a theoretical basis but lack adaptability to complex environments; data-driven methods rely on a large amount of high-quality data and have limited generalization ability. PINNs provide a new direction for solving these problems, but further exploration and improvement are still needed. Therefore, in-depth research on the prediction method of the AAR drogue position based on PINNs has theoretical and practical significance.
4. Design of PINN Based on Attention-Augmented LSTM
4.1. Architecture of PINN
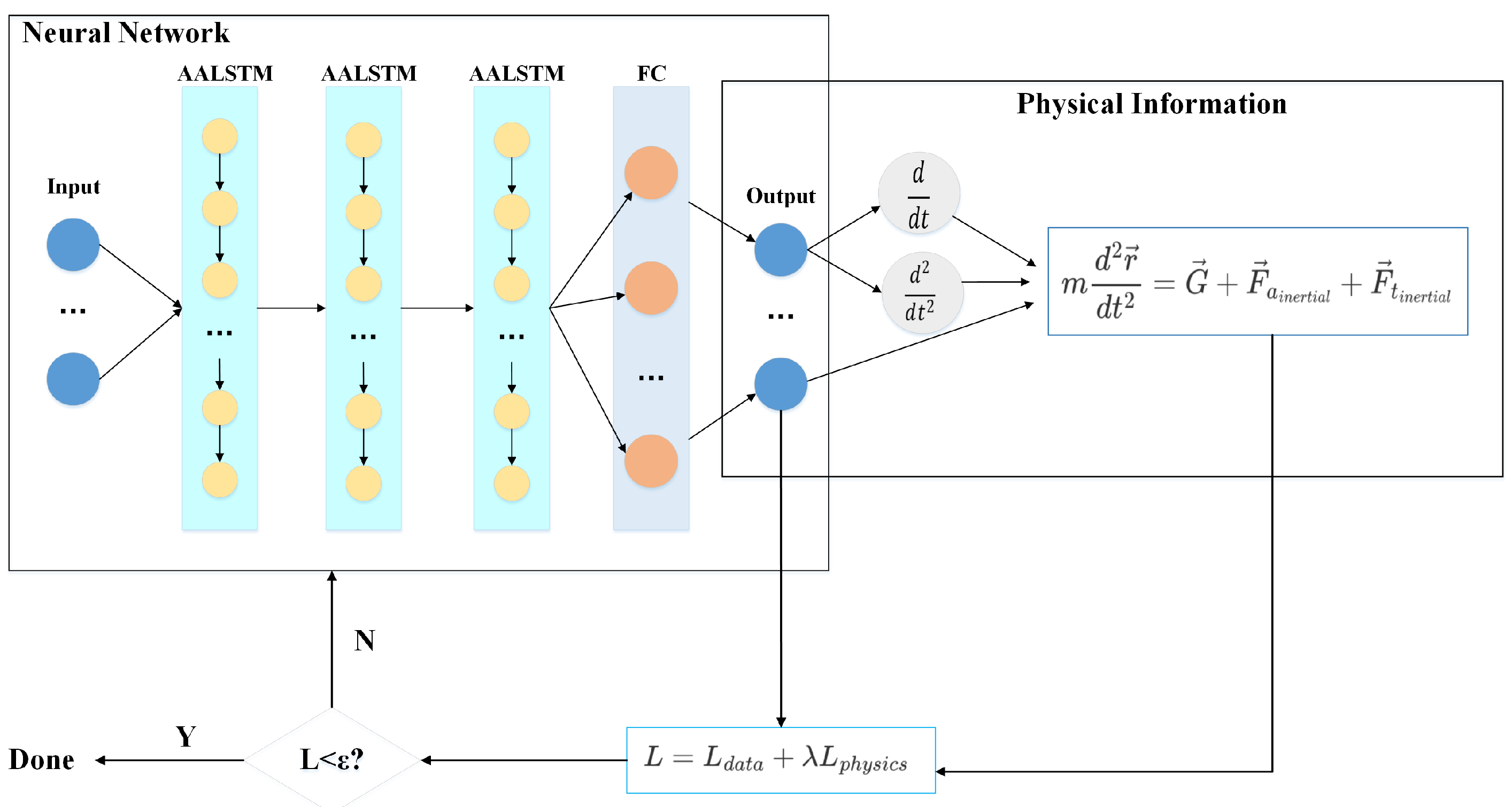
The PINN is a neural network framework that combines deep learning and physical modeling. On the basis of conventional neural networks, it integrates physical laws and prior knowledge, enabling the network’s training and prediction processes to better follow physical laws, thereby improving the model’s generalization ability and prediction accuracy. In the research on the position prediction of the drogue in AAR, this architecture shows unique advantages and adaptability.
The PINN consists of three parts: a data-driven neural network, physical information constraints, and a loss function.
The data-driven neural network usually adopts the structure of a multi-layer perceptron (MLP), which consists of an input layer, several hidden layers, and an output layer. In the scenario of predicting the position of the drogue in AAR, the input layer receives the raw data related to the refueling process. The hidden layers perform feature extraction and representation learning on the input data through a series of nonlinear transformations, mining the complex relationships among these data. The output layer outputs the prediction results, providing an important reference for the aerial refueling process. The neurons in each layer are connected through weights and biases, and these parameters are continuously adjusted during the training process to minimize the loss function.
Physical information constraints are the core part of the PINN, which integrates prior knowledge such as physical laws, conservation laws, and boundary conditions into the network. In this study, the physical model established in
Section 3 is used as the physical information constraint and integrated into the network.
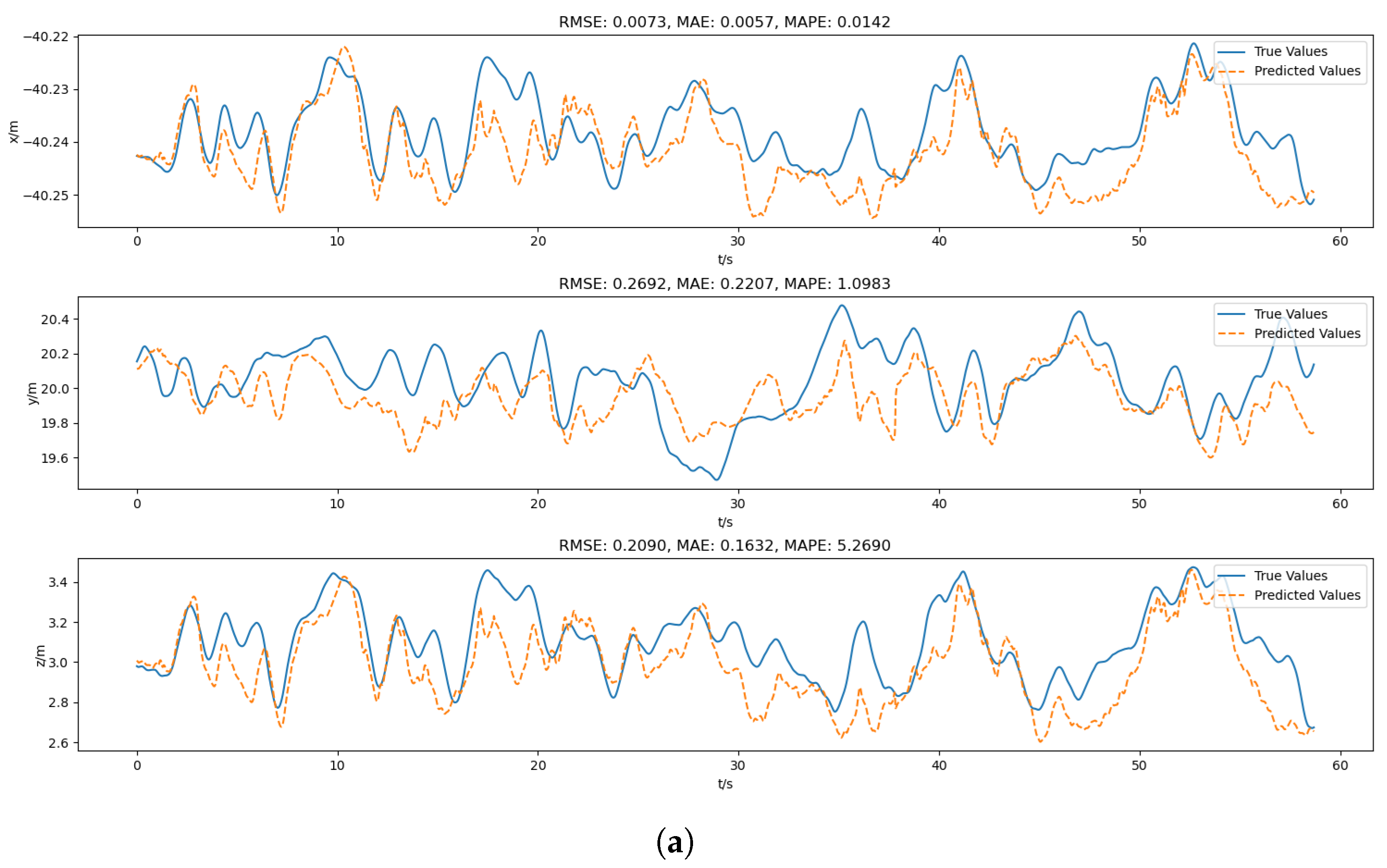
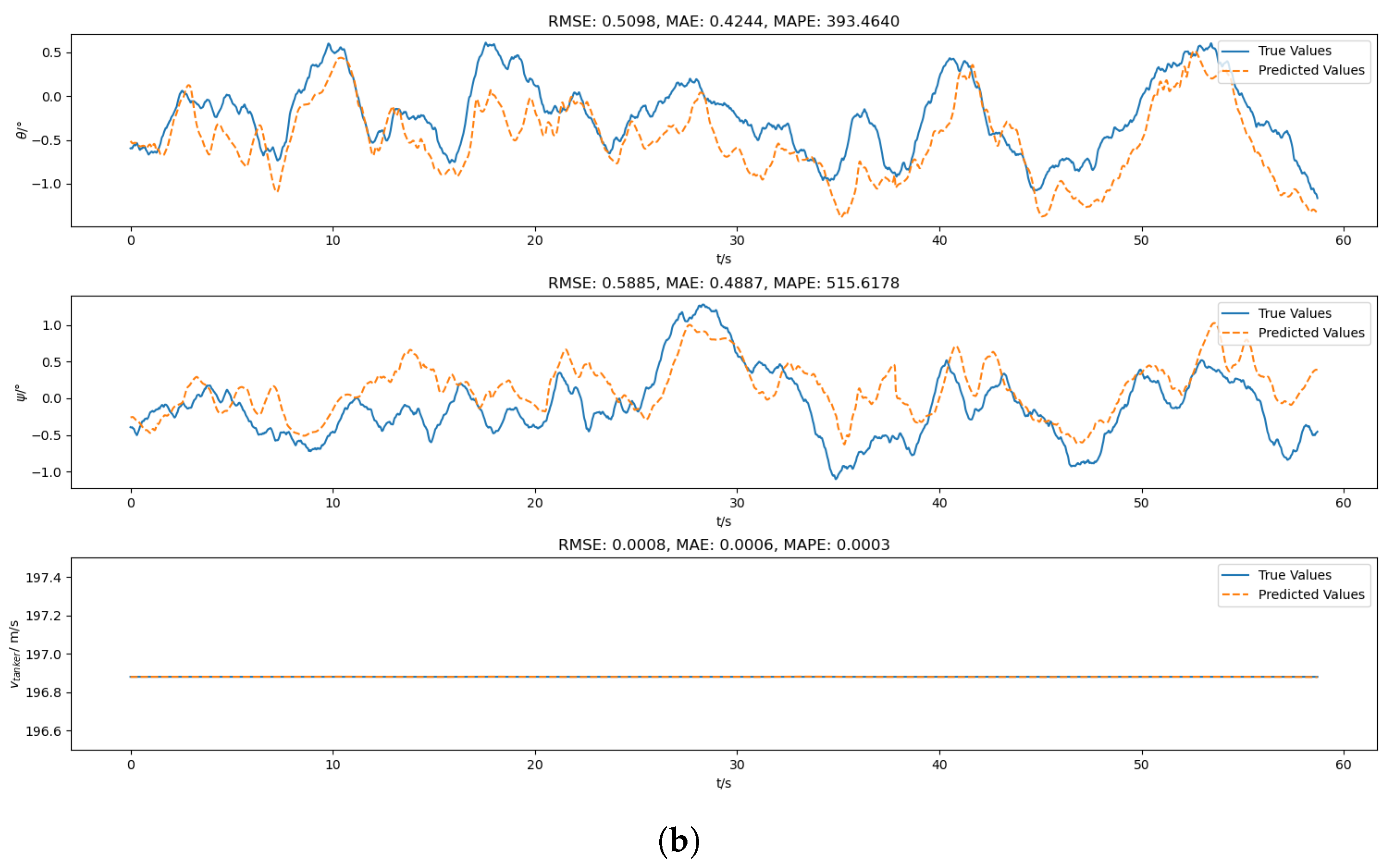
The loss function of the PINN consists of two parts: data fitting loss and physical information loss. The data fitting loss measures the difference between the network’s prediction results and the observed data, and usually uses common loss function forms such as mean-squared error (MSE). In the design of the data fitting loss in this study, considering that the output signal contains multiple dimensions, such as the drogue’s position, pitch angle, yaw angle, and tanker’s speed, the mean-squared error is used to calculate the error of each dimension, and the errors of all dimensions are accumulated. This can quantify the prediction error of each dimension and prompt the model to fit the actual data as accurately as possible in each dimension. The physical information loss measures the deviation between the network’s prediction results and the physical information constraints. In this study, the physical constraint loss is designed based on the drogue dynamic equations established according to Newton’s second law. The physical information loss is determined by calculating the sum of the squared residuals between the resultant external force and acceleration obtained from the model’s prediction information at each time step and both sides of the physical model equation. This allows the model to continuously adjust its parameters during the training process to ensure the consistency between the prediction results and the physical model. These two parts of the loss are combined through weighted summation to obtain the final loss function L, which is used to balance the relative importance of the data fitting loss and the physical constraint loss. The value of the weight needs to be determined through experiments to find the optimal balance.
The PINN is a fusion of supervised learning and unsupervised learning. Its architecture is shown in
Figure 2.
The present state of the physics-informed system is the three coordinate values of the drogue in the refueling pod coordinate system,
, with auxiliary parameters being the drogue pitch angle
and yaw angle
. The next state is the solution for the state
at time
based on the present state and physical Equation (
11). The sizes of the LSTM input layer, hidden layer, and output layer are denoted by
n,
h, and
o, respectively.
4.2. Description of the Attention-Augmented LSTM
In the complex task of predicting the position of the drogue in AAR, the Attention-Augmented LSTM (AALSTM) is introduced. This network architecture skillfully combines the advantages of conventional LSTM with the unique functions of the attention mechanism, demonstrating excellent performance in processing time-series data, especially in adapting to the requirements of drogue position prediction. Compared with the conventional LSTM, the AALSTM algorithm has the following advantages.
Effective capture of long-term dependencies: LSTM effectively solves this problem by introducing key components such as memory cells, input gates, forget gates, and output gates. This advantage is inherited in AALSTM. In the scenario of AAR, the position change of the drogue is comprehensively affected by multiple factors, and its motion trajectory shows complex time-series characteristics. For example, factors such as the adjustment of the tanker’s flight attitude and the continuous action of the air current will affect the drogue’s position at different time scales. AALSTM can store and transmit this long-term influence information through its memory cells, thus accurately capturing the patterns of change in the drogue’s position over a long time span and providing strong support for accurate prediction.
Attention mechanism highlighting key information: The attention mechanism is a key feature of AALSTM. When processing time-series data related to the drogue’s position, the importance of data at different moments for predicting the current position of the drogue is not the same. For example, the data around the moment when the drogue is disturbed by a sudden air current have a higher reference value for understanding and predicting the subsequent position change of the drogue. The attention mechanism can automatically learn and assign different weights to data at different moments, thus highlighting the role of key information. By calculating the attention weights, AALSTM can focus more on the historical data that are most crucial for the current prediction, enhancing the model’s attention to important features and thus improving the prediction accuracy. This ability to accurately capture key information enables the model to quickly screen valuable information and make more reliable predictions when facing the complex and changeable aerial refueling environment.
Dynamic adaptation to complex environment changes: The environmental factors in the process of AAR are complex and changeable. For example, the instability of the air current and the change in the relative motion state between the tanker and the receiver aircraft will lead to dynamic adjustments in the change law of the drogue’s position. The attention mechanism of AALSTM has dynamic adaptability. It can continuously adjust the distribution of attention weights according to the real-time changes in the input data. When the environment changes, the model can quickly refocus on new key information and timely adapt to the changes in the change law of the drogue’s position. This dynamic adaptability enables AALSTM to maintain good prediction performance in different aerial refueling scenarios, enhancing the model’s robustness and generalization ability.
Overall, AALSTM can significantly improve the prediction accuracy in the prediction of the drogue’s position in AAR. By accurately capturing long-term dependencies, highlighting key information, and dynamically adapting to environmental changes, the model can more precisely grasp the change trend of the drogue’s position. At the same time, since the attention mechanism can focus on key information and reduce the processing of irrelevant data, it improves the model’s computational efficiency to a certain extent.
Below is a description of the AALSTM algorithm. Suppose there is an input sequence
, where
represents the input vector at the
i-th time step and
N is the total number of time steps. Then, calculate the attention weights. First, calculate the score
for each time step:
where
is a weight matrix used to map the input vector
to a new feature space;
is a weight vector used to perform a weighted sum of the mapped features; and
is the bias vector. The attention weight
is calculated through the softmax function:
The attention weight
represents the relative importance of the input at the
i-th time step in the entire input sequence, and
. Perform a weighted sum of the input sequence through the attention weights to obtain the input representation
with the attention mechanism:
Use the input representation with the attention mechanism as the input of LSTM, and interact with the hidden state and cell state of the conventional LSTM. The description of LSTM is as follows:
Candidate cell state
:
Update hidden state
:
where
is the sigmoid activation function, ⊙ represents element-wise multiplication, and
and
are the weight matrices and bias vectors of LSTM.
In the entire process, the attention mechanism provides more targeted input for LSTM, enabling LSTM to better process time-series data and improving the performance of the model.
4.3. Input and Output Signals of AALSTM and Sliding Window Design
Feature signals are defined as follows: (1) drogue position , which is defined in the refueling pod coordinate system; (2) drogue pitch angle and yaw angle ; and (3) tanker speed .
Label signals, which are the real values of the model’s output signals corresponding to the inputs, are defined as follows: (1) predicted drogue position ; (2) predicted pitch angle and yaw angle ; (3) and predicted tanker speed .
Other output signals of the model, which are used for physical information calculation and belong to the type of unsupervised learning, are defined as follows: (1) predicted elongation of the hose , which reflects the degree of hose stretching and is related to relative motion; and (2) predicted aerodynamic coefficients of the drogue , which are used to predict the aerodynamic forces of the refueling drogue.
The sliding window is designed as follows. The input signal is sampled at a time interval of . The time-series is converted into the supervised learning form of “input sequence → output label”. Here, the input sequence represents the observations of the past time steps, and the output label represents the real values of the next N time steps.
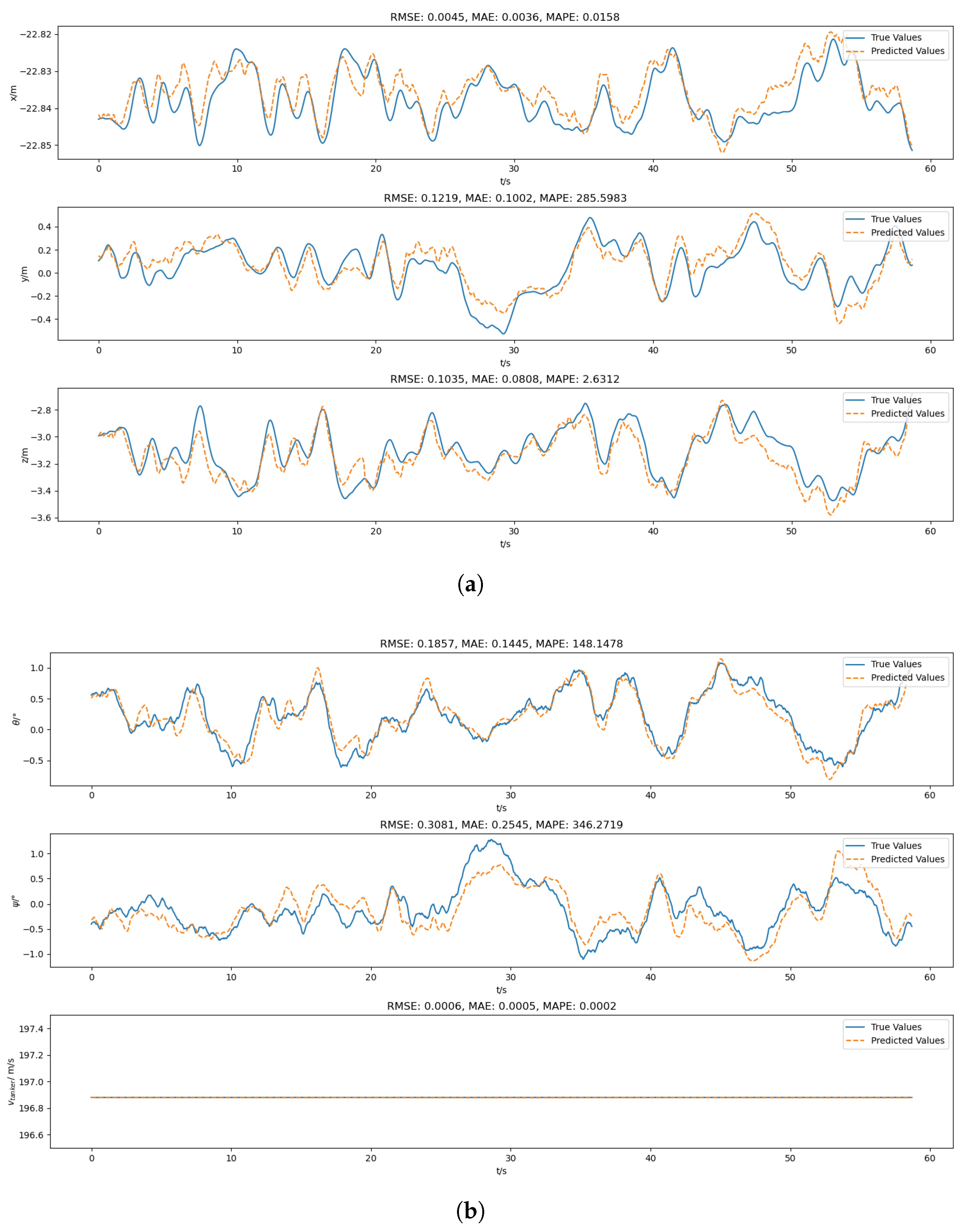
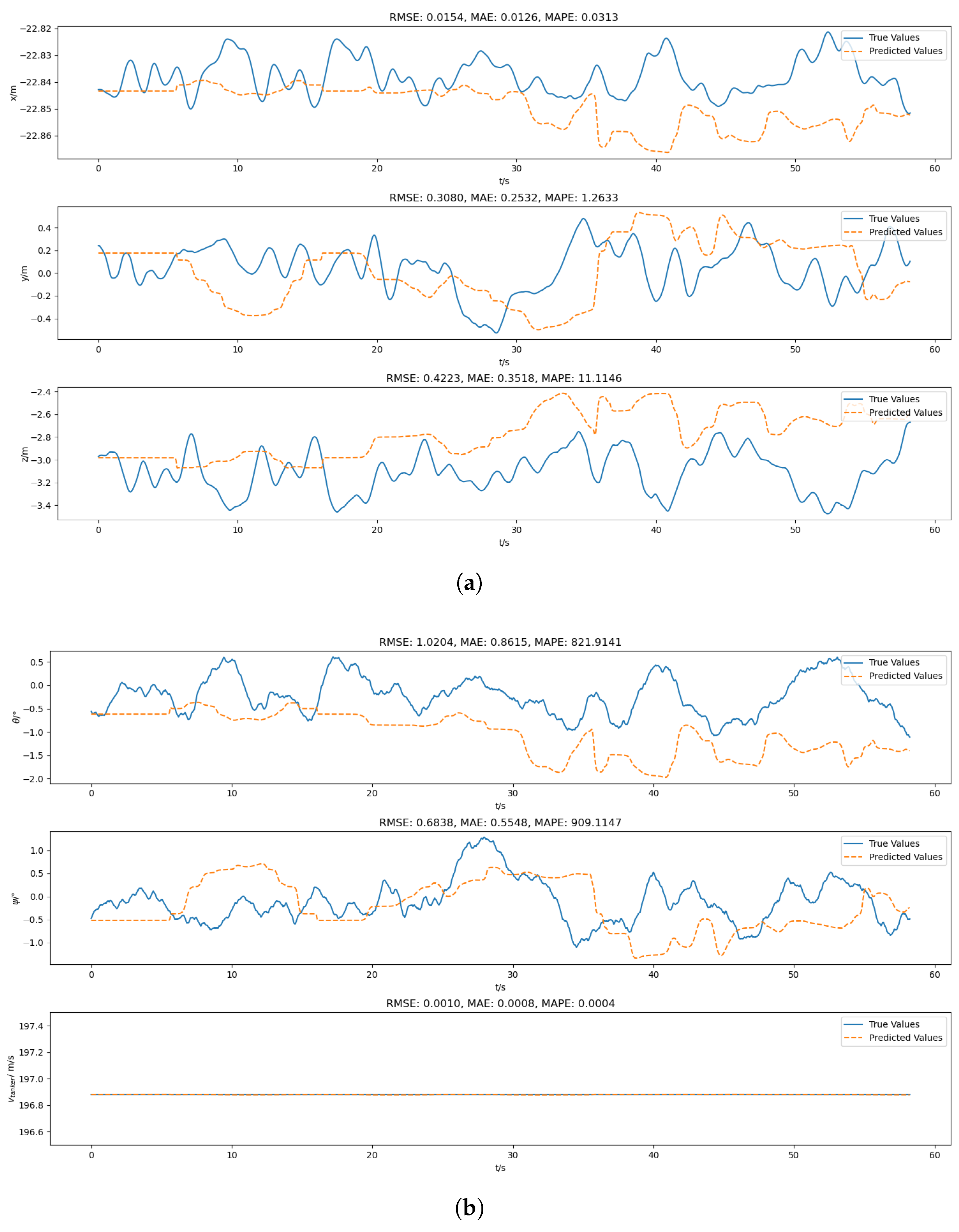
In the scenario of drogue position prediction, the selection of sliding window parameters needs to be combined with physical characteristics and control decision-making requirements. The choice of the prediction sliding window size is constrained by the physical characteristics of the drogue, and the value of needs to cover the key cycles of drogue movement (such as airflow disturbance cycles and system response delays). According to historical data, the movement cycle of the drogue is generally 1 to 3 s, and the duration of historical data corresponding to is 2 to 4 times the movement cycle of the drogue, which can capture the typical swinging cycle. If is too small, key dynamics (such as airflow fluctuations) will be missed, leading to prediction oscillations; if is too large, historical noise will be introduced, reducing the model’s sensitivity to recent changes.
The prediction step size N needs to match the time scale of control decisions. A too large N may increase the learning difficulty of the model because it needs to capture dependency relationships over a longer time span; a too small N has no obvious effect on control decisions. The prediction results in this study are mainly used in the scenario of AAR docking control, and a 0.5 s advance prediction plays an important role in improving the success rate of AAR docking.
4.4. Loss Function Design
In the AAR drogue position prediction model based on AALSTM, the design of the loss function is crucial for the training and performance improvement of the model. It needs to comprehensively consider the differences between the predicted values and the true values, as well as the constraints of the physical model, to ensure that the model can not only accurately fit the data but also satisfy the physical laws.
4.4.1. Data Fitting Loss
The data fitting loss mainly measures the difference between the model’s predicted values and the true values. Considering that the output signals contain multiple dimensions, such as the drogue position, pitch angle, yaw angle, tanker speed, etc., the mean-squared error (MSE) is used to calculate the error of each dimension, and the errors of all dimensions are accumulated.
Suppose there are a total of
M samples. For the
k-th sample, the output signal has
D dimensions (corresponding to various prediction parameters), the predicted value is
, and the real value is
(
). Then, the calculation formula for the data fitting loss
is given by
This design can quantify the prediction error of each dimension and give higher weights to larger errors, prompting the model to fit the actual data as accurately as possible in each dimension.
4.4.2. Physical Constraint Loss
The physical constraint loss is used to ensure that the model’s prediction results conform to the physical model of the refueling drogue established previously. The dynamic equation of the drogue established based on Newton’s second law is the core of the physical model. Therefore, the physical constraint loss can be designed based on this equation.
At each time step, according to the information of the drogue’s position predicted by the model, combined with known physical parameters (such as mass, elastic coefficient, etc.), the resultant external force and acceleration are calculated.
The differential equation of Newton’s second law established based on the inertial system is
. The differential equations expanded in the three axes are expressed as follows:
Taking the
x-axis direction as an example, the residual
is calculated as follows:
Similarly, the residuals
and
in the
y-axis and
z-axis directions can be obtained. The physical constraint loss
is given by
where
M is the total number of time steps. In this way, the model continuously adjusts its parameters during the training process to ensure the consistency between the prediction results and the physical model.
4.4.3. Total Loss Function
The data fitting loss and the physical constraint loss are combined by weighted summation to obtain the total loss function
L:
where
is a hyperparameter used to balance the relative importance of the data fitting loss and the physical constraint loss. The value of
needs to be determined through experiments to find the optimal balance between data fitting and physical constraints. If the value of
is too large, the model may focus too much on physical constraints and ignore data fitting; if the value of
is too small, the role of physical constraints may not be obvious, and the model cannot fully utilize physical information to improve the prediction accuracy.
During the model training process, by minimizing the total loss function L, the model can fit the data while following physical laws, thereby improving the accuracy and stability of the AAR drogue position prediction.