Wide-Range Variable Cycle Engine Control Based on Deep Reinforcement Learning
Abstract
1. Introduction
- A methodology for the design of controllers is proposed. This methodology is based on deep reinforcement learning. The objective of this methodology is to address the complex control problem associated with a wide-area variable-cycle engine that features an interstage turbine mixed architecture.
- The Deep Deterministic Policy Gradient (DDPG) algorithm is employed to effectively address the nonlinearity, multi-variable coupling, and high-dimensional dynamic characteristics of variable cycle engines.
- Combined with the action space pruning technique, the performance of the controller is optimized and the convergence speed of training is improved. The efficacy of the method in addressing multi-variate coupling problems is substantiated by simulation verification.
2. Preliminary Knowledge and Problem Description
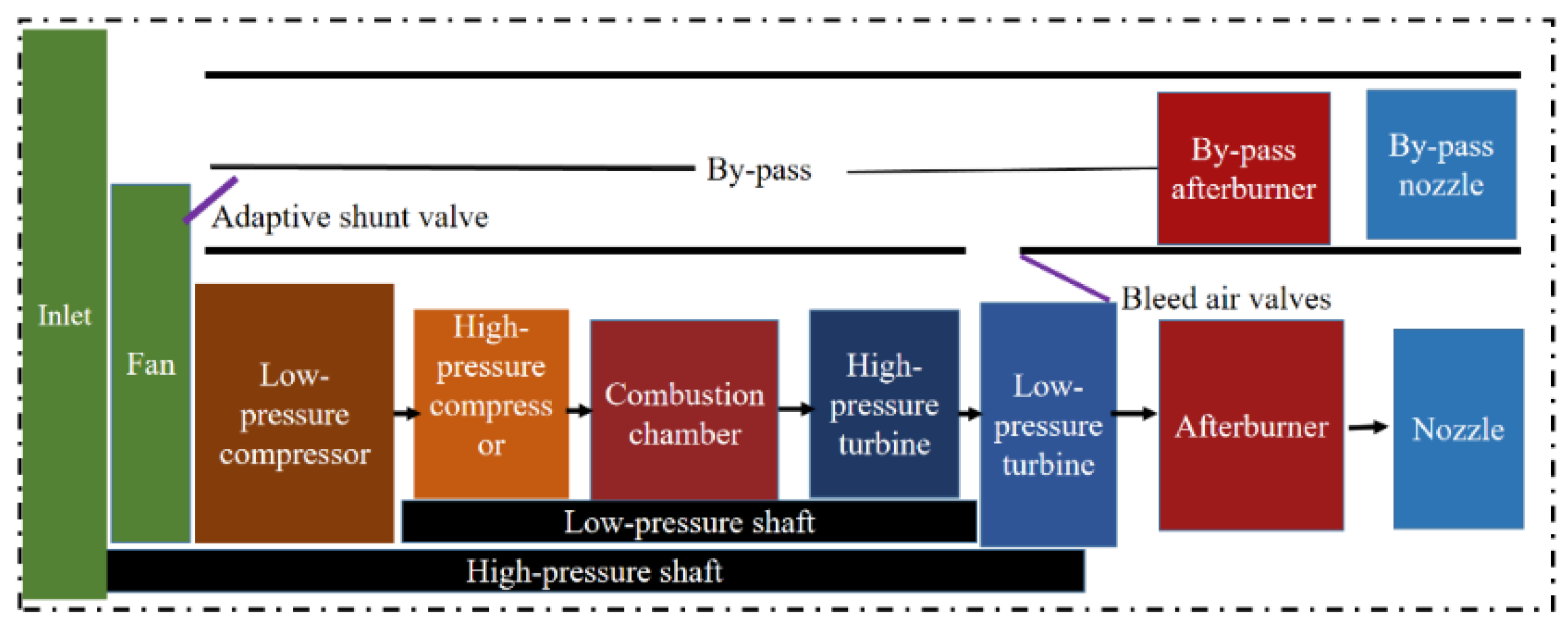
2.1. Study Objects
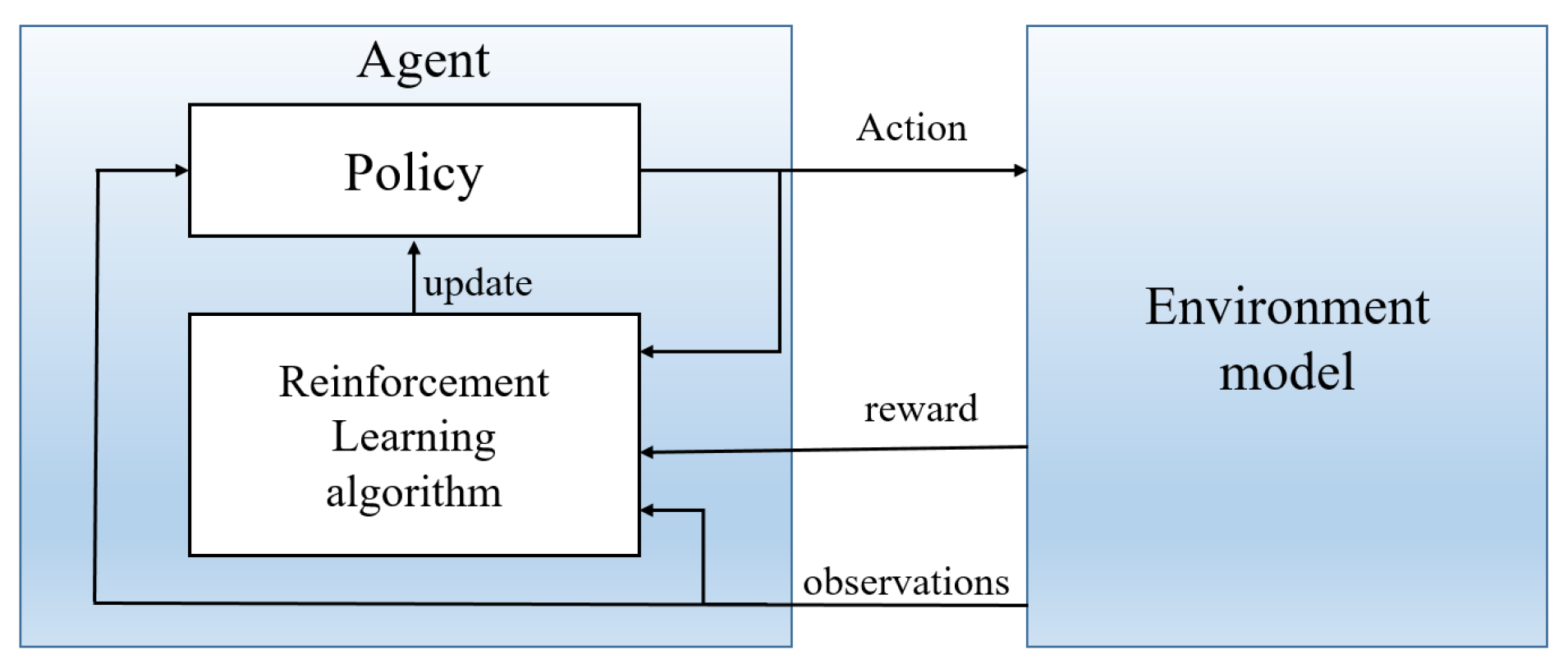
2.2. Overview of Deep Reinforcement Learning
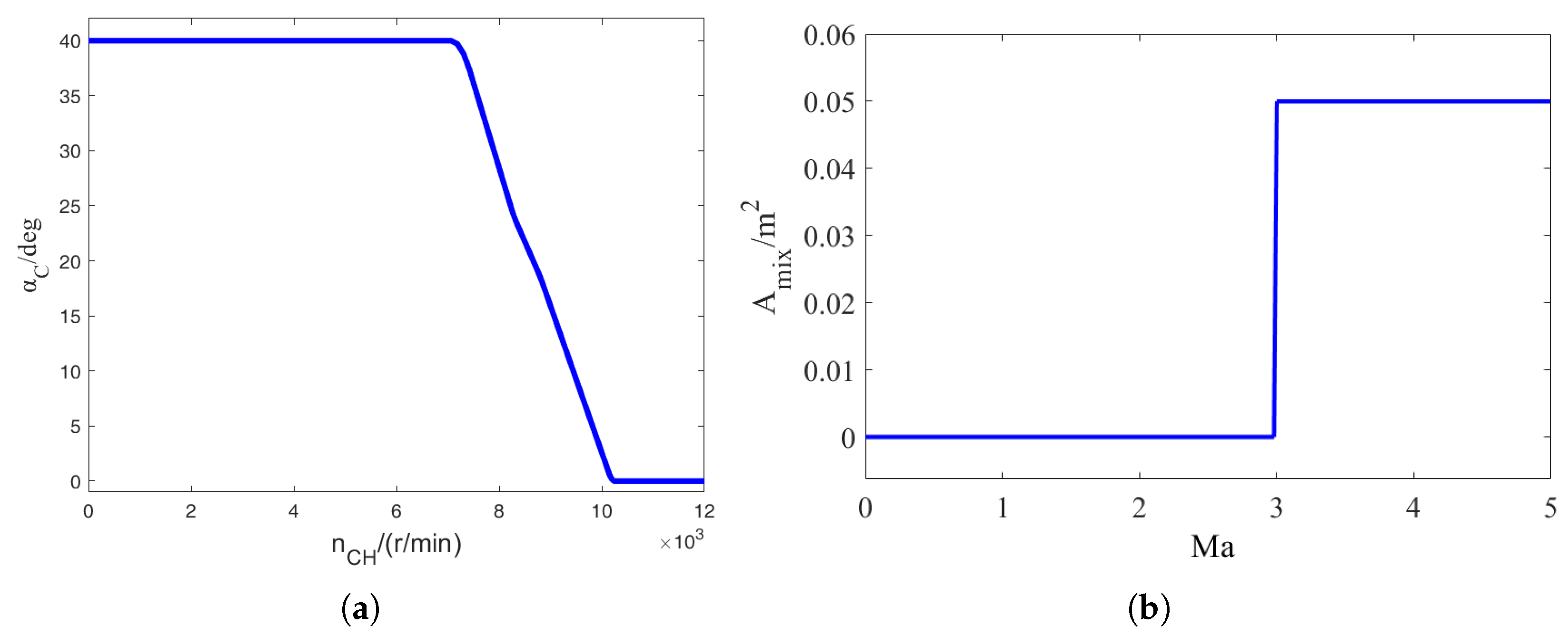
2.3. Description of the Problem
- (2.3a) Speed tracking control: Ensure that the tracking error of the the low-pressure relative speed eventually converges to zero.
- (2.3b) Connotation drop ratio tracking control: Ensure that the tracking error of the connotation drop ratio eventually converges to zero.
- (2.3c) Outer culvert boost ratio tracking control: Ensure that the tracking error of the outer culvert boost ratio eventually converges to zero.
- (2.3d) Limiting protection control: No over-temperature, over-rotation, or surge occur under any flight condition.
3. Design of the Deep Reinforcement Learning Controller
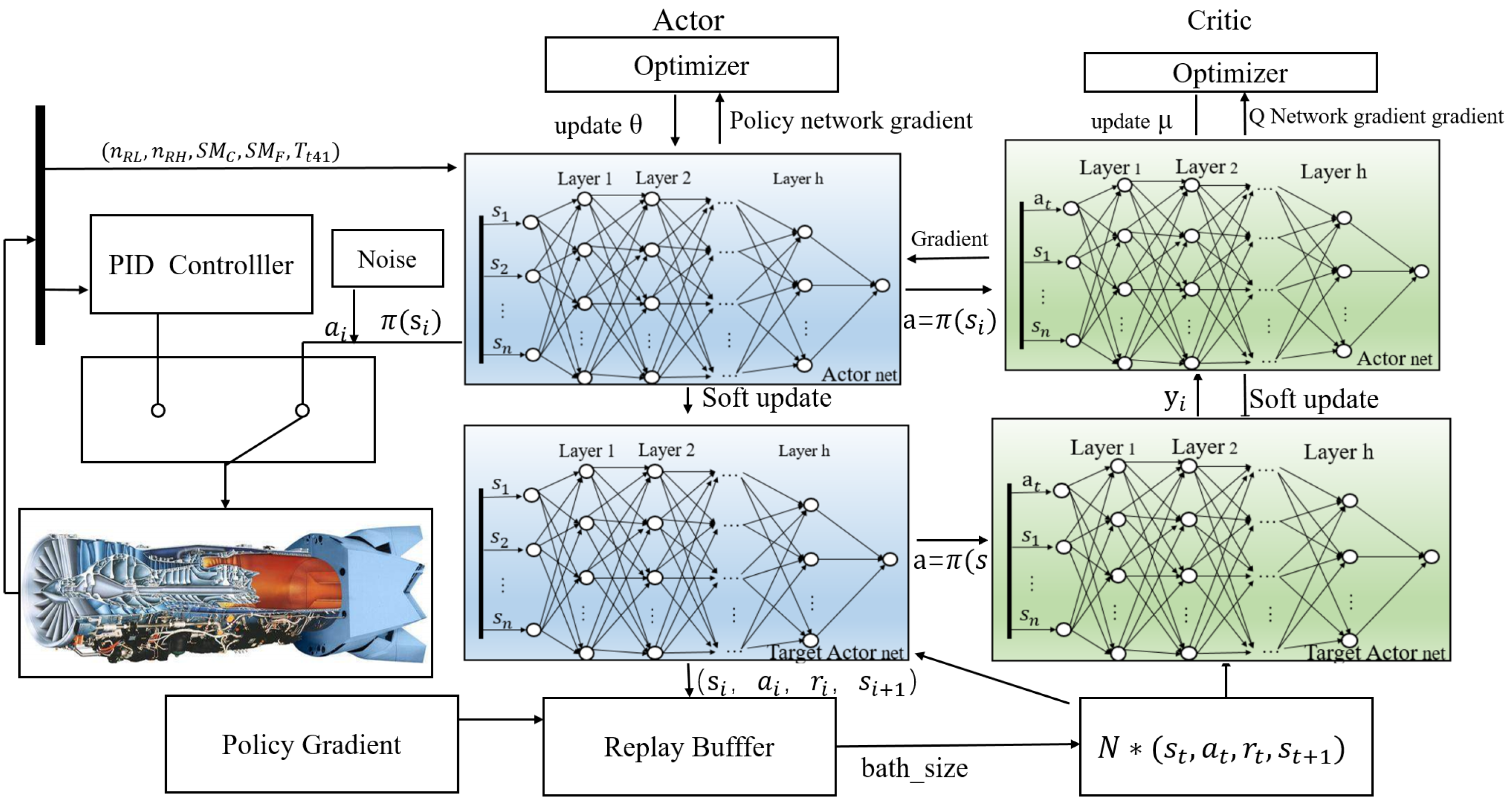
3.1. Control System Structure
3.2. Designing the Agent
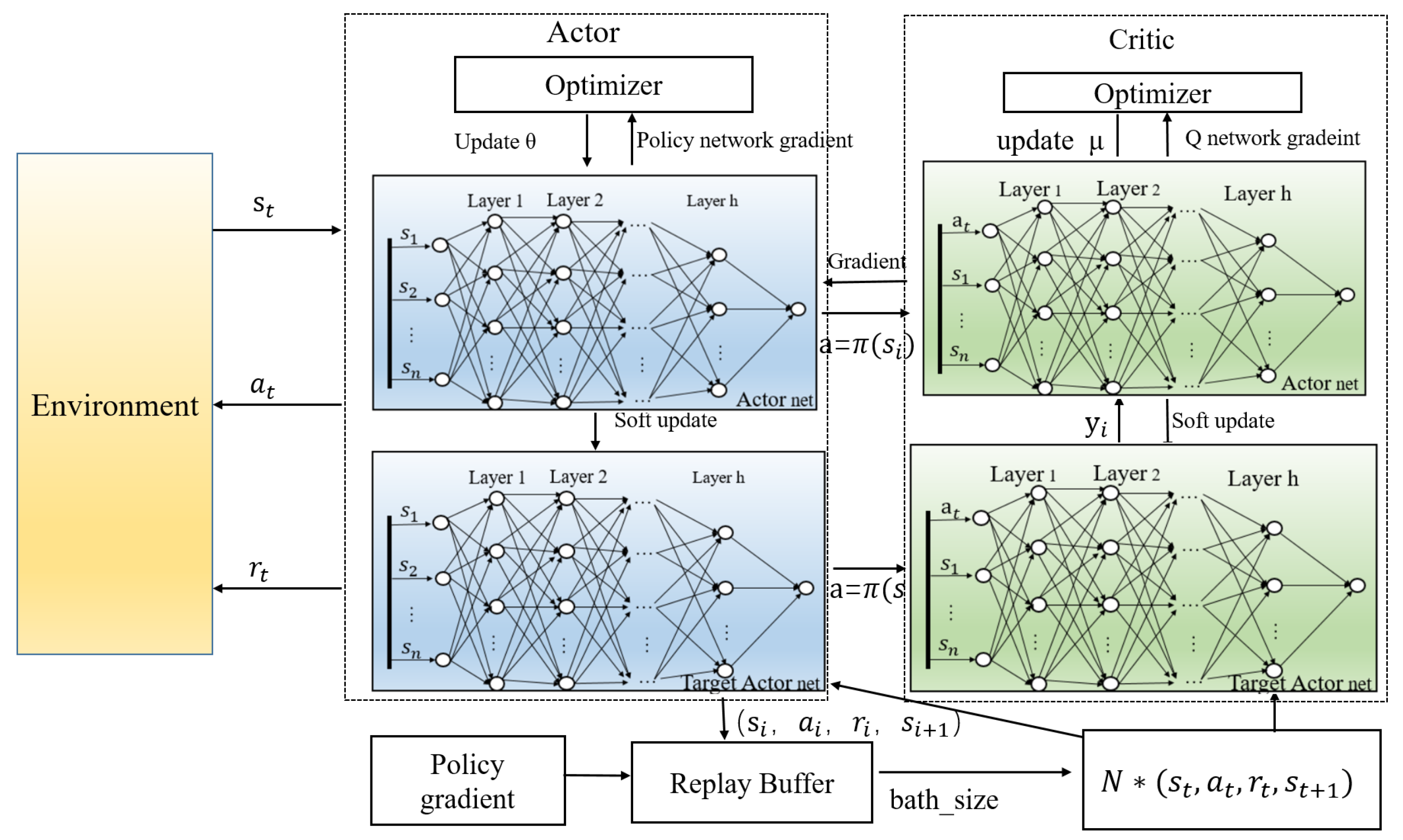
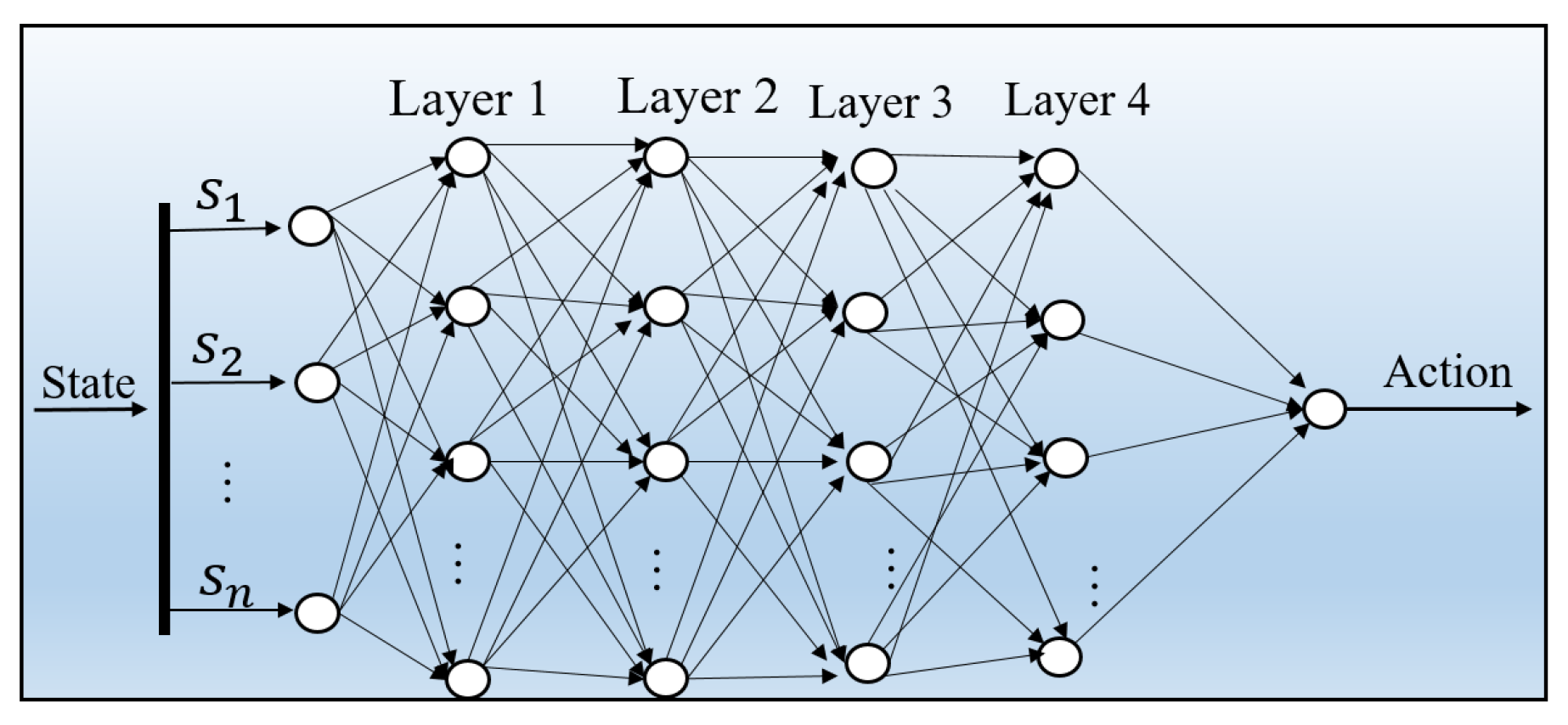
3.2.1. Agent Structure
3.2.2. Principles of Policy Optimization
| Algorithm 1: DDPG pseudocode |
 |
3.3. Algorithm Setup
3.4. Network Training
3.4.1. Overall Training Framework and Data Interaction
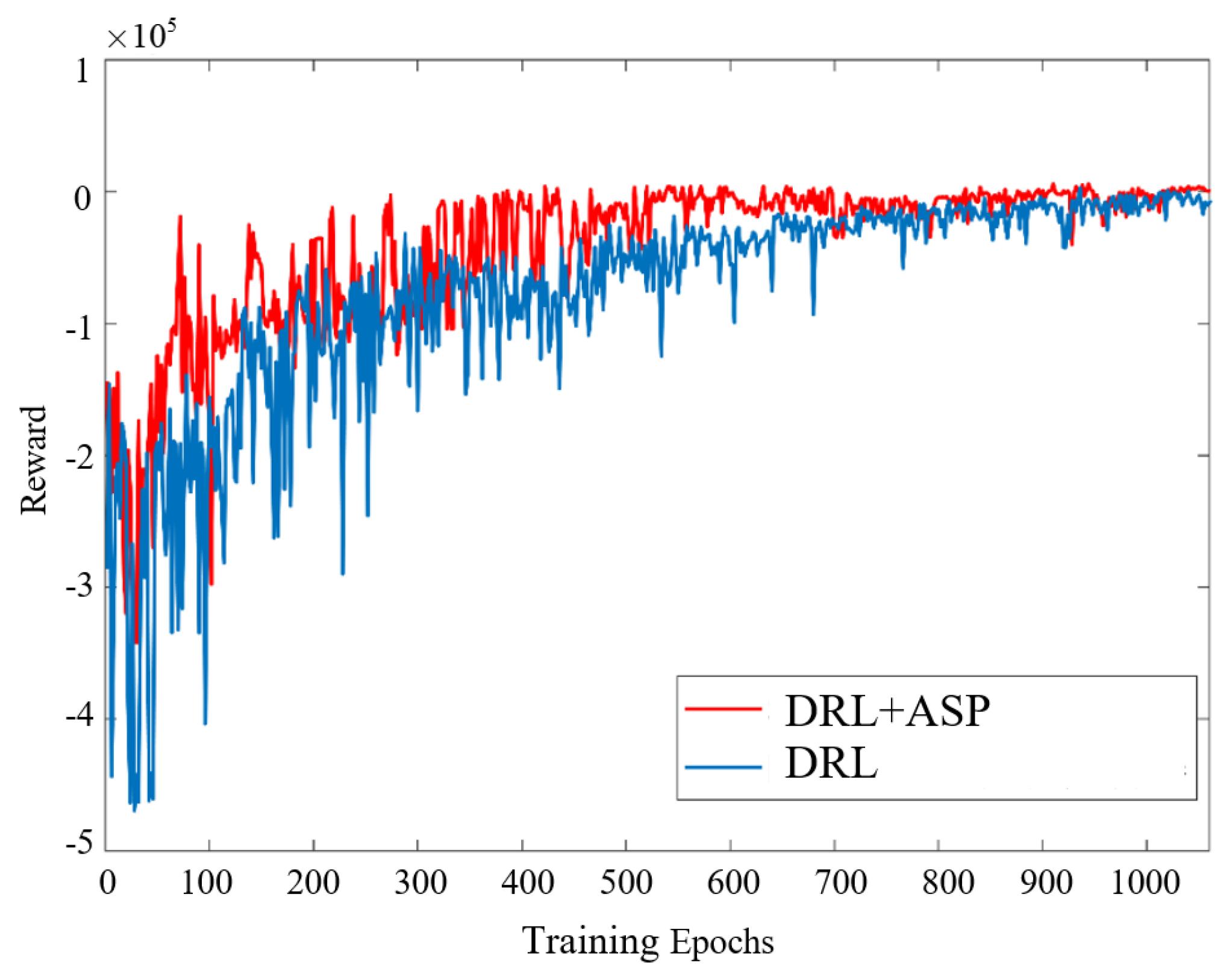
3.4.2. Training Results and Analysis
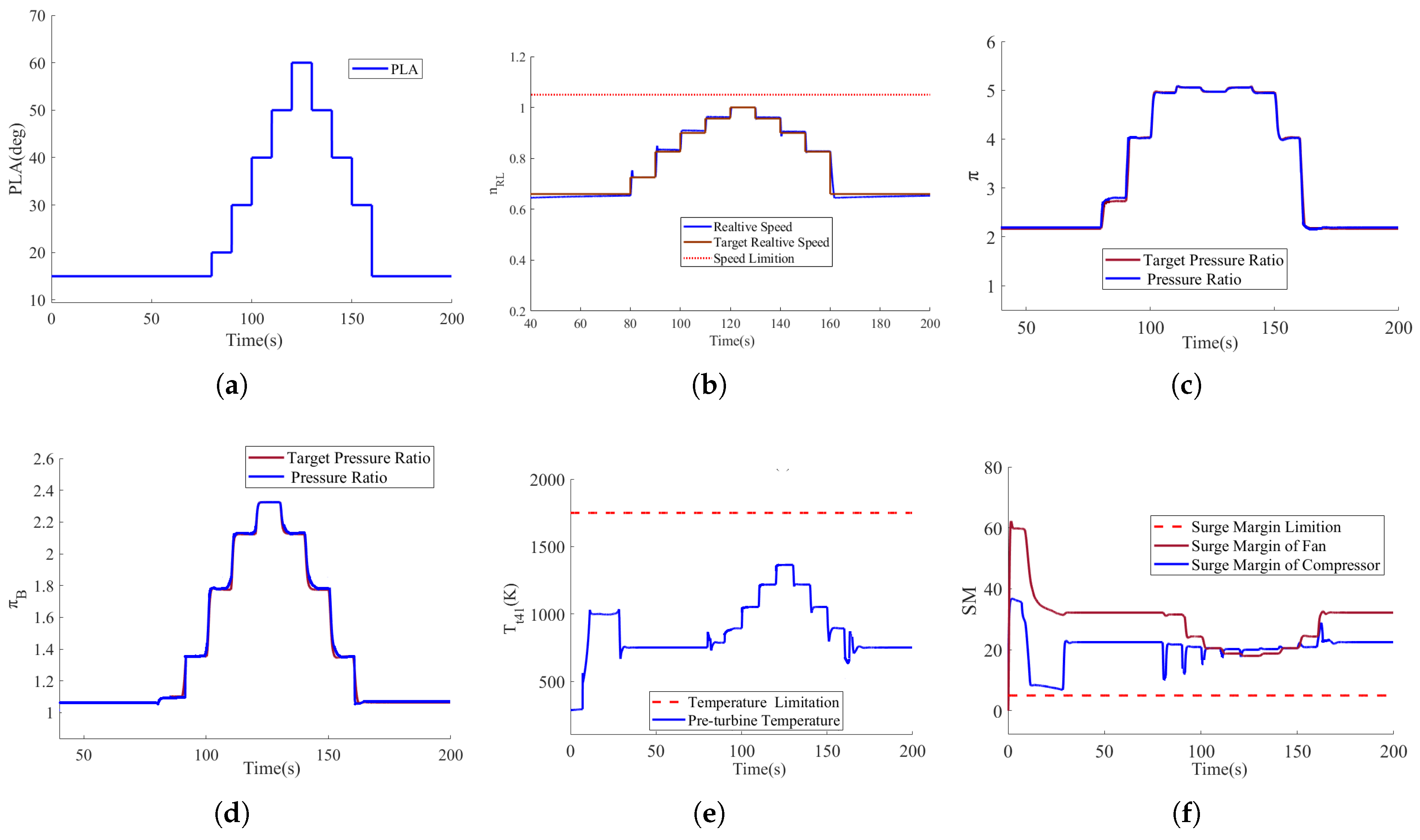
4. Simulation Results and Analysis
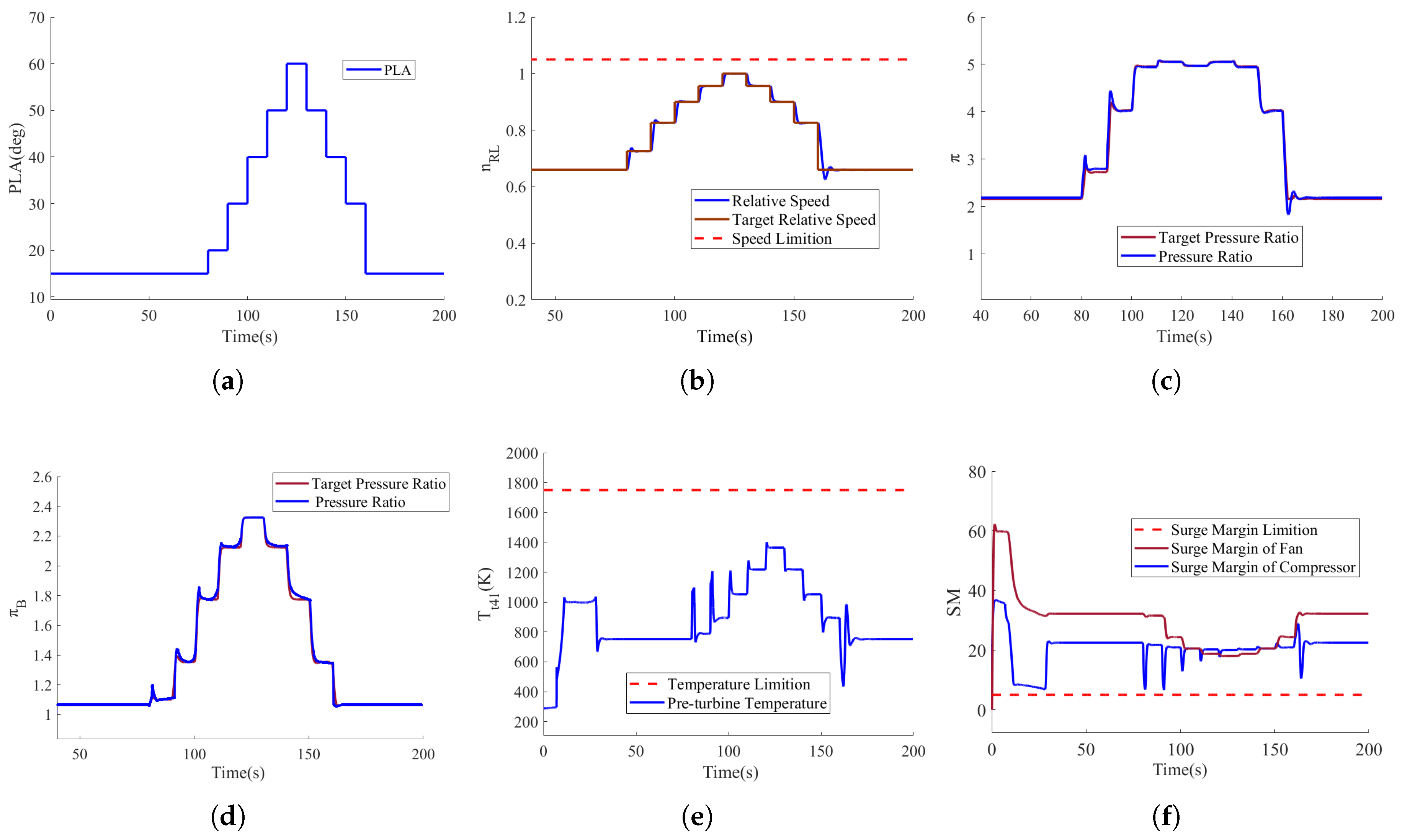
4.1. Simulation Results and Analysis for H = 0 km, Ma = 0
4.2. Simulation Results and Analysis for H = 10 km, Ma = 0.9
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| VCE | Variable Cycle Engine |
| ITMA | Interstage Turbine Mixed Architecture |
| DDPG | Deep Deterministic Policy Gradient |
| DRL | Deep Reinforcement Learning |
Appendix A
| Symbol | Adjustable Variable Name | Unit |
|---|---|---|
| Nozzle throat area (inner) | ||
| Nozzle throat area (outer) | ||
| Internal and external bleed air intake area | ||
| Fan physical speed | r/min | |
| High-pressure corrected speed | r/min | |
| Low-pressure relative speed | \ | |
| High-pressure relative speed | \ | |
| Atmospheric static pressure | Pa | |
| Engine intake pressure | Pa | |
| Pressure after high-pressure compressor | Pa | |
| Post-turbine pressure | Pa | |
| Pre-combustor pressure (outer bypass) | Pa | |
| PLA | Throttle lever angle | deg |
| Surge margin of high-pressure compressor | \ | |
| Surge margin of fan | \ | |
| Atmospheric static temperature | K | |
| Temperature after fan | K | |
| Pre-turbine temperature | K | |
| Main combustion chamber fuel flow | kg/s | |
| Afterburner fuel flow | kg/s | |
| Guide vane angle of the high-pressure compressor | deg | |
| Pressure ratio | \ | |
| B | Bypass ratio | \ |
| cmd | Target value | \ |
References
- Huang, X.; Chen, Y.; Zhou, H. Analysis on development trend of global hypersonic technology. Bull. Chin. Acad. Sci. 2024, 39, 1106–1120. [Google Scholar]
- Zhong, S.; Kang, Y.; Li, X. Technology Development of Wide-Range Gas Turbine Engine. Aerosp. Power 2023, 4, 19–23. [Google Scholar]
- Johnson, L. Variable Cycle Engine Developments at General Electric-1955-1995; AIAA: Reston, VA, USA, 1995; pp. 105–143. [Google Scholar]
- Mu, Y.; Wang, F.; Zhu, D. Simulation of variable geometry characteristics of single bypass variable cycle engine. Aeroengine 2024, 50, 52–57. [Google Scholar]
- Brown, R. Integration of a variable cycle engine concept in a supersonic cruise aircraft. In Proceedings of the AIAA/SAE/ASME 14th Joint Propulsion Conference, Las Vegas, NV, USA, 18–20 June 1978. [Google Scholar]
- Allan, R. General Electric Company variable cycle engine technology demonstrator p-rogram. In Proceedings of the AIAA/SAE/ASME 15th Joint Propulsion Conference, Las Vegas, NV, USA, 18–20 June 1979. [Google Scholar]
- Feng, Z.; Mao, J.; Hu, D. Review on the development of adjusting mechanism invariable cycle engine and key technologies. Aeroengine 2023, 49, 18–26. [Google Scholar]
- Zhang, Y.; Yuan, W.; Zou, T. Modeling technology of high-flow triple-bypass variable cycle engine. J. Propuls. Technol. 2024, 45, 35–43. [Google Scholar]
- Liu, B.; Nie, L.; Liao, Z. Overall performance of interstage turbine mixed architecture variable cycle engine. J. Propuls. Technol. 2023, 44, 27–37. [Google Scholar]
- Zeng, X.; Gou, L.; Shen, Y. Analysis and modeling of variable cycle engine control system. In Proceedings of the 11th International Conference on Mechanical and Aerospace Engineering (ICMAE), Athens, Greece, 18–21 July 2020. [Google Scholar]
- Wu, Y.; Yu, Z.; Li, C.; He, M. Reinforcement learning in dualarm trajectory planning for a free-floating space robot. Aerosp. Sci. Technol. 2020, 98, 105657. [Google Scholar] [CrossRef]
- Gu, S.; Holly, E.; Lillicrap, T. Deep reinforcement learning for robotic manipulation with asynchronous off-policy updates. In Proceedings of the IEEE International Conference on Robotics & Automation, Singapore, 29 May–3 June 2017. [Google Scholar]
- Wada, D.; AraujoEstrada, S.A.; Windsor, S. Unmanned aerial vehicle pitch control under delay using deep reinforcement learning with continuous action in wind tunnel test. Aerospace 2021, 8, 258. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, H.; Tian, Y. Reinforcement learning based two-level control framework of UAV swarm for cooperative persistent surveillance in an unknown urban area. Aerosp. Sci. Technol. 2020, 98, 261–281. [Google Scholar] [CrossRef]
- Sallab, A.; Abdou, M.; Perot, E. End-to-End deep reinforcement learning for lane keeping assist. In Proceedings of the 30th Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- Kiran, B.; Sobh, I.; Talpaert, V. Deep reinforcement learning for autonomous driving: A survey. IEEE Trans. Intell. Transp. Syst. 2021, 28, 4909–4926. [Google Scholar] [CrossRef]
- Mehryar, M.; Afshin, R.; Talwalkar, A. Reinforcement learning. In Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2018; pp. 379–405. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D. Playing Atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar]
- Qiu, X. Deep Reinforcement Learning. In Foundations of Machine Learning; China Machine Press: Beijing, China, 2020; pp. 339–360. [Google Scholar]
- Francois-Lavet, V.; Henderson, P.; Islam, R. An introduction to deep reinforcement learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Zheng, Q.; Jin, C.; Hu, Z. A study of aero-engine control method based on deep reinforcement learning. IEEE Access 2018, 6, 67884–67893. [Google Scholar] [CrossRef]
- Liu, C.; Dong, C.; Zhou, Z. Barrier Lyapunov function based reinforcement learning control for air-breathing hypersonic vehicle with variable geometry inlet. Aerosp. Sci. Technol. 2020, 96, 105537–105557. [Google Scholar] [CrossRef]
- Fang, J.; Zheng, Q.; Cai, C. Deep reinforcement learning method for turbofan engine acceleration optimization problem within full flight envelope. Aerosp. Sci. Technol. 2023, 136, 108228–108242. [Google Scholar] [CrossRef]
- Tao, B.; Yang, L.; Wu, D. Deep reinforcement learning-based optimal control of variable cycle engine performance. In Proceedings of the 2022 International Conference on Advanced Robotics and Mechatronics (ICARM), Guilin, China, 7–9 November 2022. [Google Scholar]
- Gao, W.; Zhou, X.; Pan, M. Acceleration control strategy for aero-engines based on model-free deep reinforcement learning method. Aerosp. Sci. Technol. 2022, 120, 107248–107260. [Google Scholar] [CrossRef]
- Silver, D.; Lever, G.; Heess, N. Deterministic Policy Gradient Algorithms. Proc. Mach. Learn. Res. 2014, 32, 387–395. [Google Scholar]
- Hahnloser, R.; Sarpeshkar, R.; Mahowald, M. Digital selection and analogue amplification coexist in a cortex-inspired silicon circuit. Nature 2000, 405, 947–951. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Kanervisto, A.; Scheller, C.; Hautamäki, V. Action space shaping in deep reinforcement learning. In Proceedings of the 2020 IEEE Conference on Games (CoG), Osaka, Japan, 24–27 August 2020. [Google Scholar]




| Notation | Definition | Range |
|---|---|---|
| Main combustion chamber fuel flow | 0–1.4 (kg/s) | |
| Afterburner fuel flow | 0–6 (kg/s) | |
| Guide vane angle of the high-pressure compressor | 0–40 (deg) | |
| Nozzle throat area | 0–0.45 () | |
| Bypass nozzle throat area | 0–0.3 () | |
| Internal and external bleed air intake area | 0–0.05 () |
| Parameter | Value |
|---|---|
| Number of hidden layers in the Actor network | 4 |
| Number of hidden layers in the Critic network | State: 2, Action: 3 |
| Number of nodes in the Actor network | 30, 30, 20, 20 |
| Number of nodes in the Critic network | State: 30, 20, Action: 20, 20, 20 |
| Learning rate of the Actor | 0.0001 |
| Learning rate of the Critic | 0.001 |
| Soft update rate | 0.001 |
| Replay Buffer | 1,000,000 |
| Number of samples in the replay Buffer N | 512 |
| Discount factor | 0.99 |
| Notation | Parameter Name | Unit | Input/Output |
|---|---|---|---|
| H | Flight altitude | km | Input |
| Ma | Flight Mach number | \ | |
| Low-pressure relative rotational speed command | \ | ||
| Connotation drop ratio command | \ | ||
| Outer culvert boost ratio command | \ | ||
| Main combustion chamber fuel flow | kg/s | Output | |
| Nozzle throat area | |||
| Bypass nozzle throat area |
| Notation | Instructions | Data |
|---|---|---|
| Open-loop control strategy | ||
| DRL control strategy | ||
| Open-loop control strategy | ||
| DRL control strategy | ||
| DRL control strategy | ||
| Open-loop control strategy | ||
| Calculate pressure ratio | ||
| Calculate pressure ratio and safety constraints | ||
| For safety constraints | ||
| For safety constraints | ||
| For safety constraints |
| Parameter Name | Parameter Value |
|---|---|
| Dimensionality of observations | 8 |
| Dimensionality of actions | 3 |
| Training step | 0.02 s |
| Number of training epochs | 1000 |
| Control Type | PLA | t/s (PID) | Overshoot (PID) | t/s (DRL) | Overshoot (DRL) | (%) |
|---|---|---|---|---|---|---|
| 20–30 | 3.164 | 1.422 | 1.374 | 1.74 | 56.57 | |
| 30–40 | 3.260 | 0.532 | 1.439 | 0 | 55.86 | |
| 40–50 | 2.589 | 0 | 1.145 | 0 | 55.77 | |
| 50–60 | 2.205 | 0 | 1.068 | 0 | 51.56 | |
| 60–50 | 2.109 | 0 | 1.314 | 0.8 | 37.70 | |
| 50–40 | 2.205 | 0 | 1.232 | 0.2 | 44.13 | |
| 40–30 | 1.918 | 0 | 1.232 | 0 | 35.77 | |
| 30–20 | 8.245 | 4.25 | 5.139 | 2.25 | 37.67 | |
| 20–30 | 3.147 | 9.19 | 1.746 | 9.76 | 44.64 | |
| 30–40 | 2.493 | 0 | 1.234 | 0 | 50.54 | |
| 40–50 | 2.301 | 0 | 1.204 | 0 | 47.87 | |
| 50–60 | 2.205 | 0 | 1.001 | 0 | 54.58 | |
| 60–50 | 2.589 | 0 | 1.356 | 0 | 47.72 | |
| 50–40 | 2.685 | 0 | 1.247 | 0 | 53.66 | |
| 40–30 | 2.876 | 0 | 1.332 | 0 | 53.75 | |
| 30–20 | 3.875 | 0 | 1.562 | 0 | 59.67 | |
| 20–30 | 3.931 | 0.2623 | 2.336 | 0.3016 | 40.56 | |
| 30–40 | 4.027 | 0.614 | 2.598 | 0.678 | 35.43 | |
| 40–50 | 3.452 | 0 | 2.356 | 0 | 31.8 | |
| 50–60 | 2.589 | 0 | 2.331 | 0 | 9.97 | |
| 60–50 | 3.356 | 0 | 2.547 | 0 | 24.1 | |
| 50–40 | 3.26 | 0 | 2.368 | 0 | 27.39 | |
| 40–30 | 5.465 | 0 | 2.896 | 0 | 47.13 | |
| 30–20 | 6.136 | 0.348 | 3.019 | 0.256 | 50.76 |
| Control Type | PLA | t/s (PID) | Overshoot (PID) | t/s (DRL) | Overshoot (DRL) | (%) |
|---|---|---|---|---|---|---|
| 60–75 | 3.164 | 0.344 | 1.515 | 0.2225 | 52.04 | |
| 75–60 | 4.044 | 0.207 | 1.693 | 0.1563 | 58.19 | |
| 60–90 | 2.869 | 1.429 | 1.837 | 0 | 35.97 | |
| 90–115 | 3.45 | 1.225 | 2.872 | 0 | 16.75 | |
| 60–75 | 2.876 | 4.801 | 0.842 | 2.205 | 35.96 | |
| 75–60 | 2.780 | 4.845 | 1.304 | 2.106 | 53.03 | |
| 60–90 | 3.931 | 8.252 | 1.868 | 5.874 | 52.43 | |
| 90–115 | 3.547 | 5.667 | 1.658 | 3.265 | 53.22 | |
| 60–75 | 2.301 | 4.6709 | 1.056 | 3.356 | 54.06 | |
| 75–60 | 3.132 | 5.2516 | 1.754 | 3.386 | 43.99 | |
| 60–90 | 3.068 | 11.77 | 1.398 | 8.93 | 54.41 | |
| 90–115 | 3.356 | 4.15 | 2.209 | 2.25 | 34.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Y.; Wang, F.; Mu, Y.; Sun, H. Wide-Range Variable Cycle Engine Control Based on Deep Reinforcement Learning. Aerospace 2025, 12, 424. https://doi.org/10.3390/aerospace12050424
Ding Y, Wang F, Mu Y, Sun H. Wide-Range Variable Cycle Engine Control Based on Deep Reinforcement Learning. Aerospace. 2025; 12(5):424. https://doi.org/10.3390/aerospace12050424
Chicago/Turabian StyleDing, Yaoyao, Fengming Wang, Yuanwei Mu, and Hongfei Sun. 2025. "Wide-Range Variable Cycle Engine Control Based on Deep Reinforcement Learning" Aerospace 12, no. 5: 424. https://doi.org/10.3390/aerospace12050424
APA StyleDing, Y., Wang, F., Mu, Y., & Sun, H. (2025). Wide-Range Variable Cycle Engine Control Based on Deep Reinforcement Learning. Aerospace, 12(5), 424. https://doi.org/10.3390/aerospace12050424





