A Deep Reinforcement Learning-Based Cooperative Guidance Strategy Under Uncontrollable Velocity Conditions
Abstract
1. Introduction
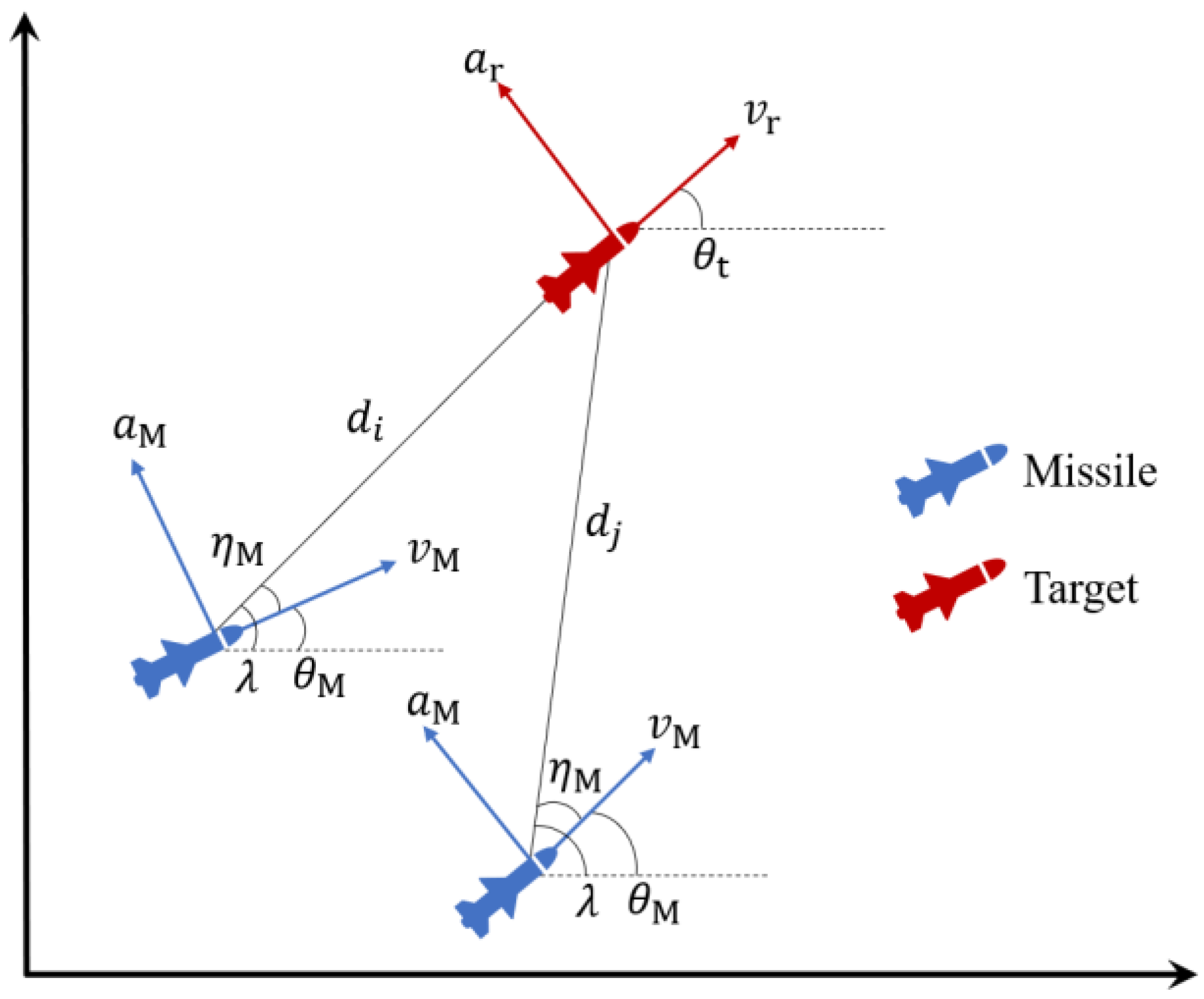
2. Problem Statement
3. Design Procedure for Planar Guidance Strategies
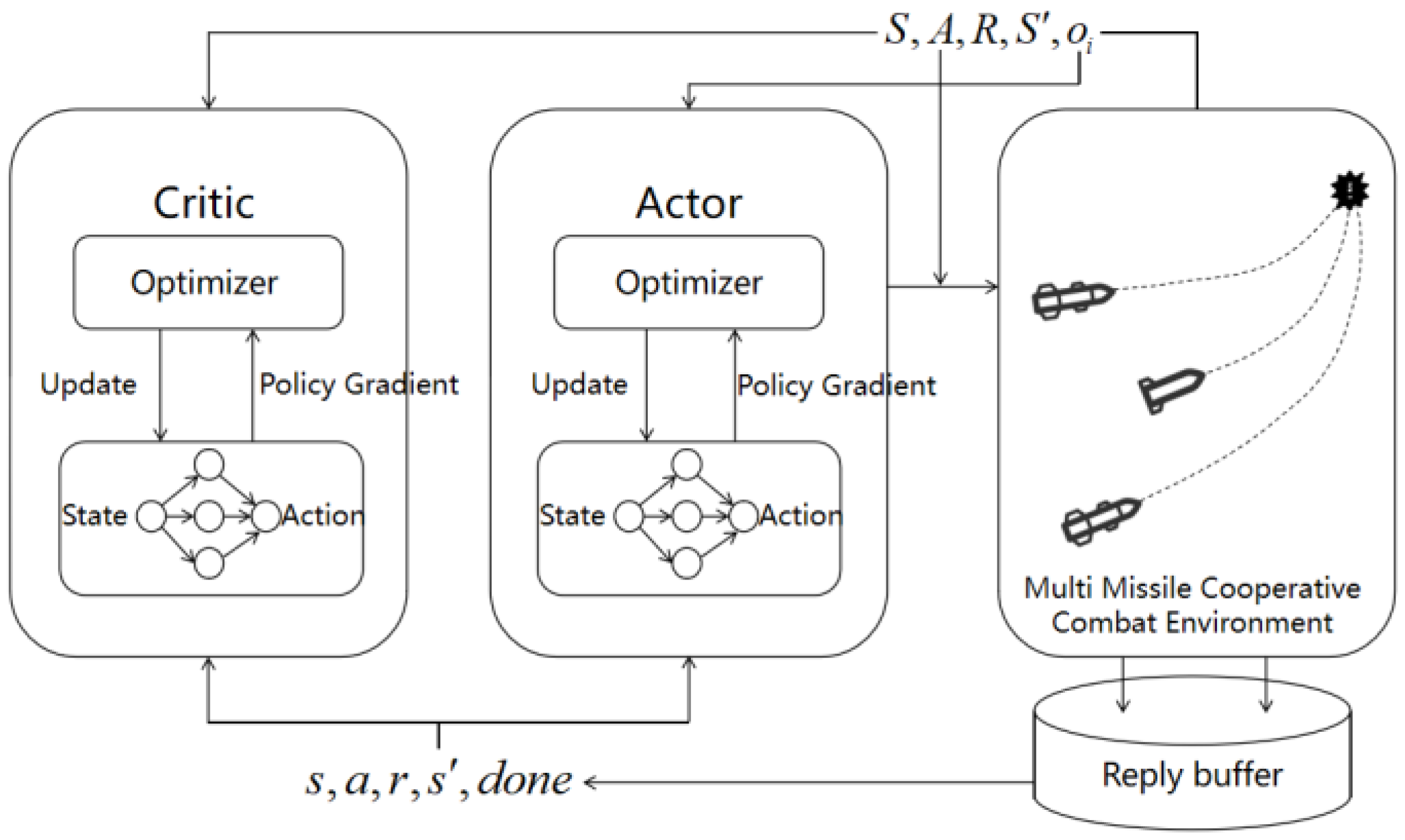
3.1. Multi-Agent Proximal Policy Optimization
3.2. Training Procedure of MAPPO Cooperative Guidance Strategy
3.2.1. Distance-Based Heuristic Reward Reshaping Method
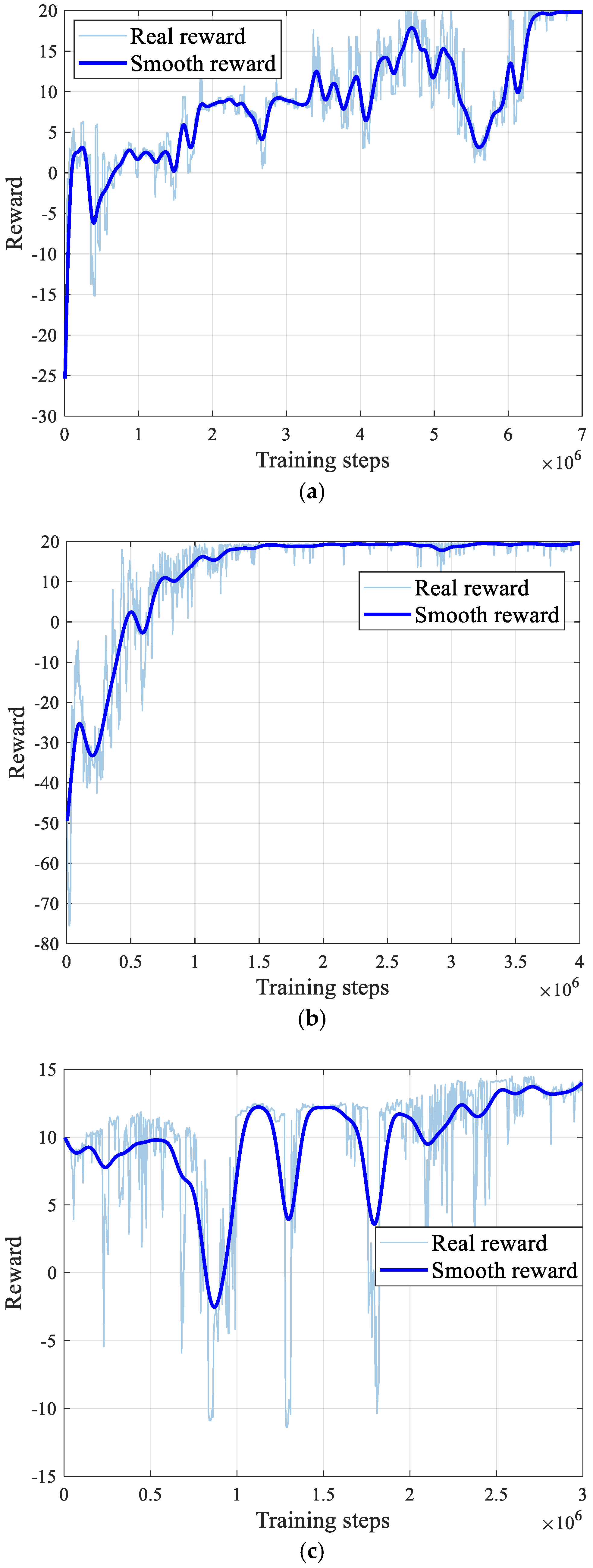
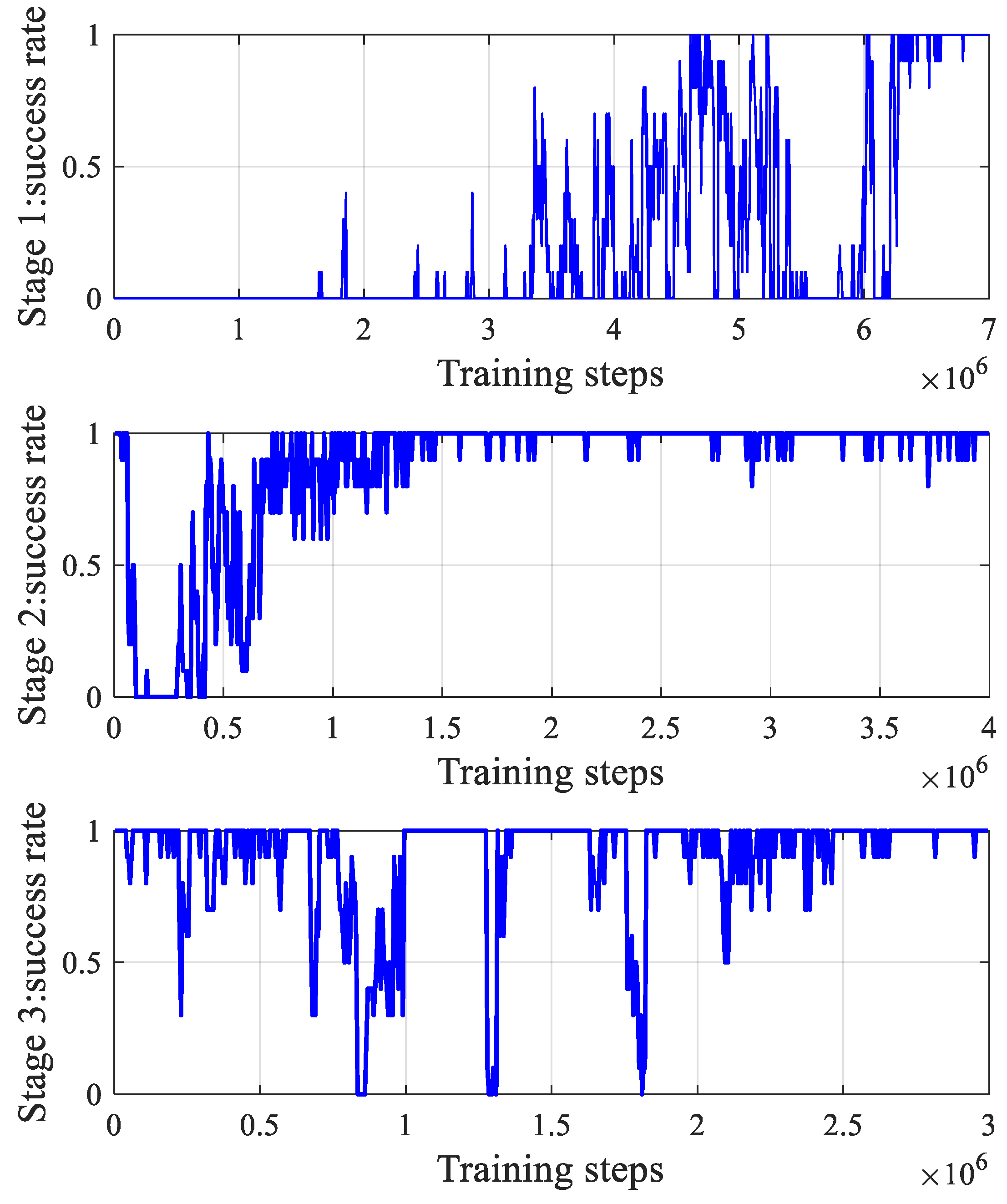
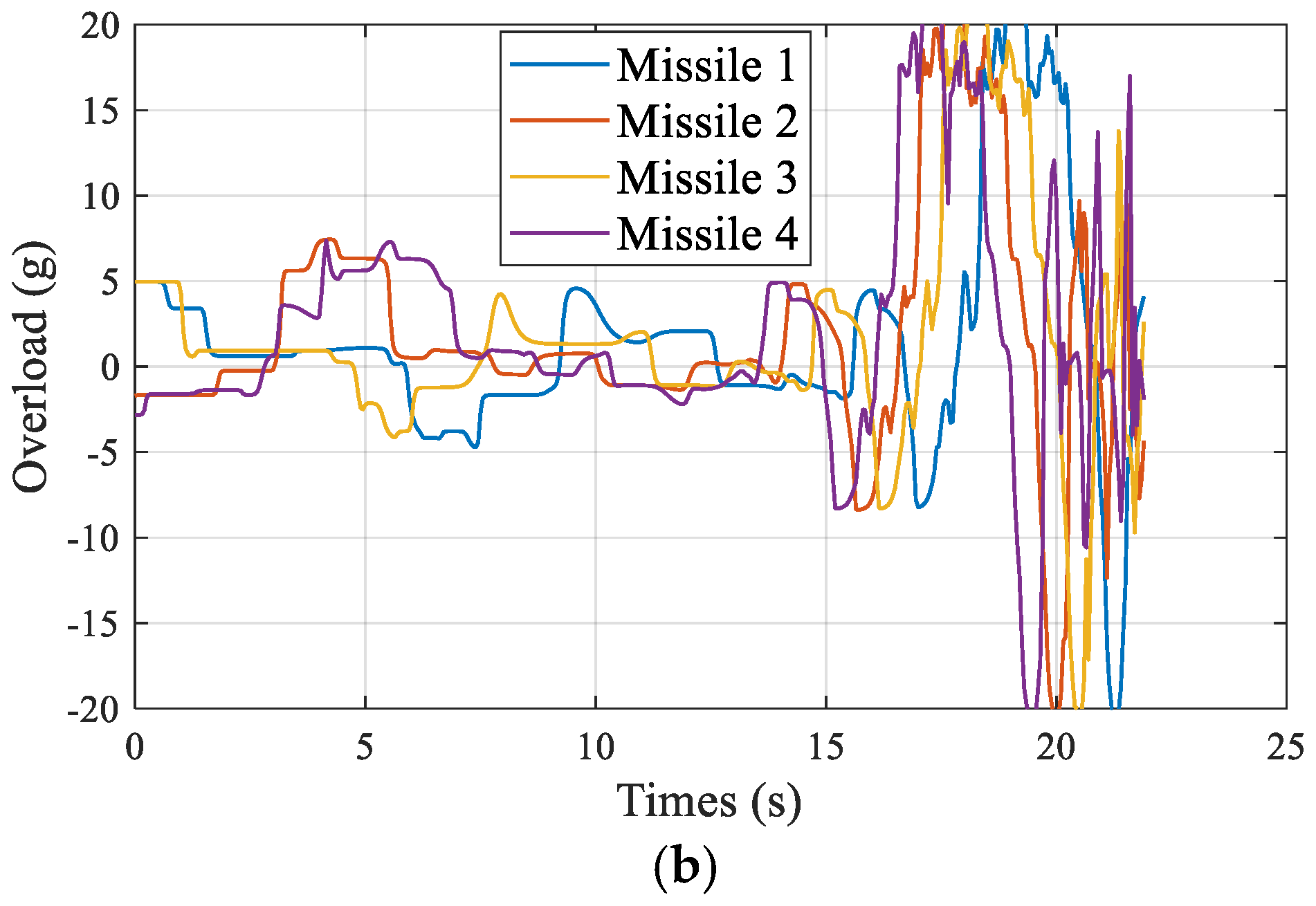
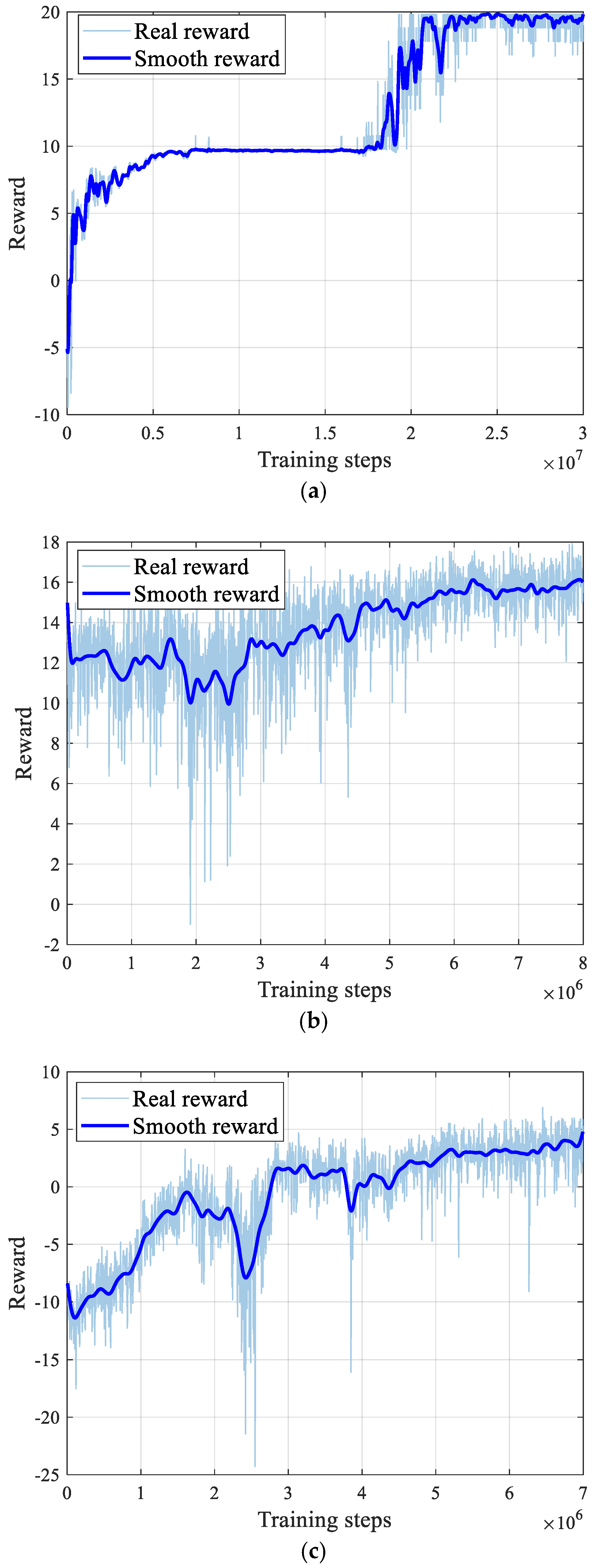
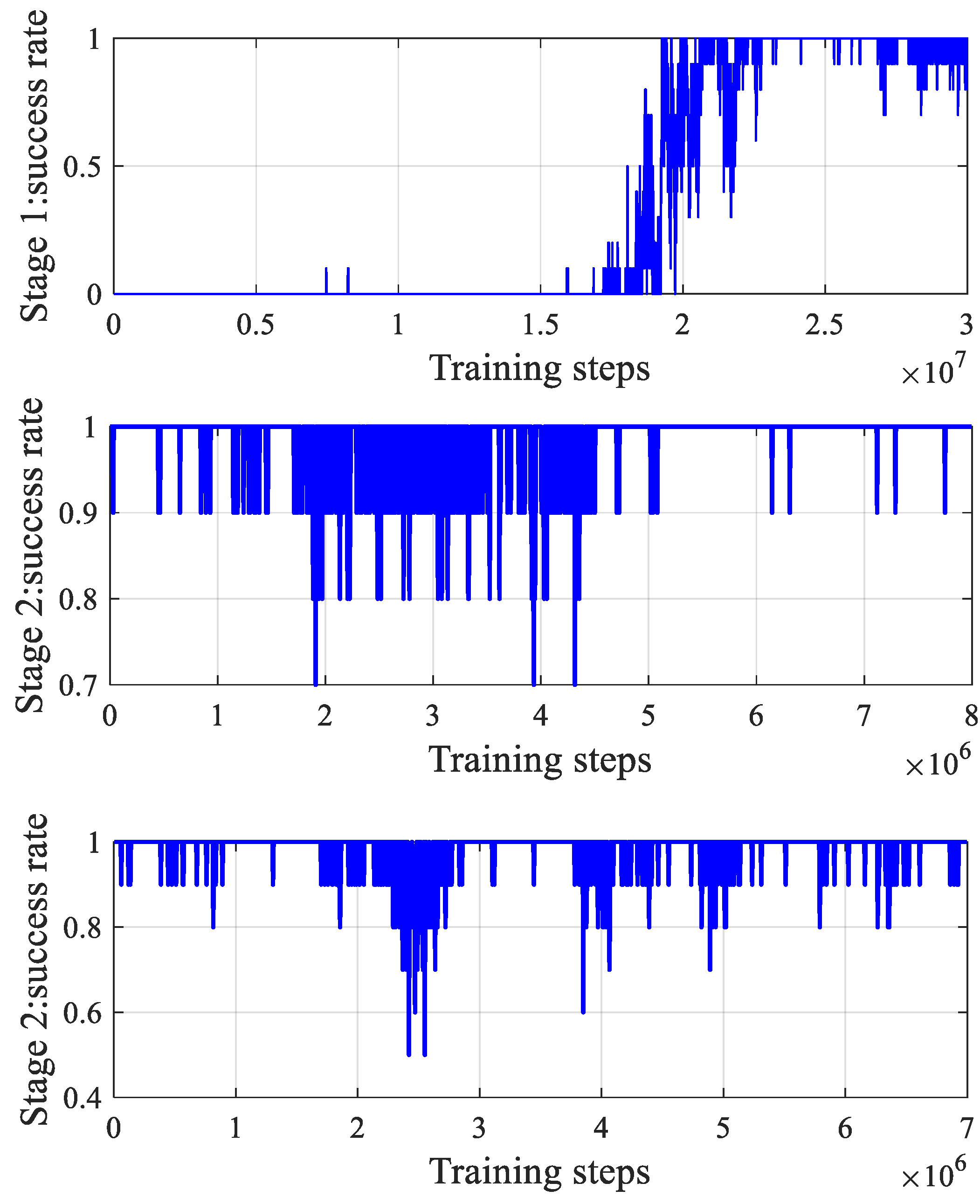
3.2.2. Multi-Stage Curriculum Training Framework
- Stage 1: The focus is on obtaining a cooperative confrontation strategy for the agents, without considering energy consumption or action jitter.
- Stage 2: An overload constraint reward mechanism is introduced to ensure smooth agent actions during the cooperative attack, preventing jitter.
- Stage 3: This stage incorporates the agent energy consumption during the cooperative confrontation, preventing excessive energy use and optimizing the overall operational efficiency.
3.2.3. Planar Multi-Agent Cooperative Guidance Law Design
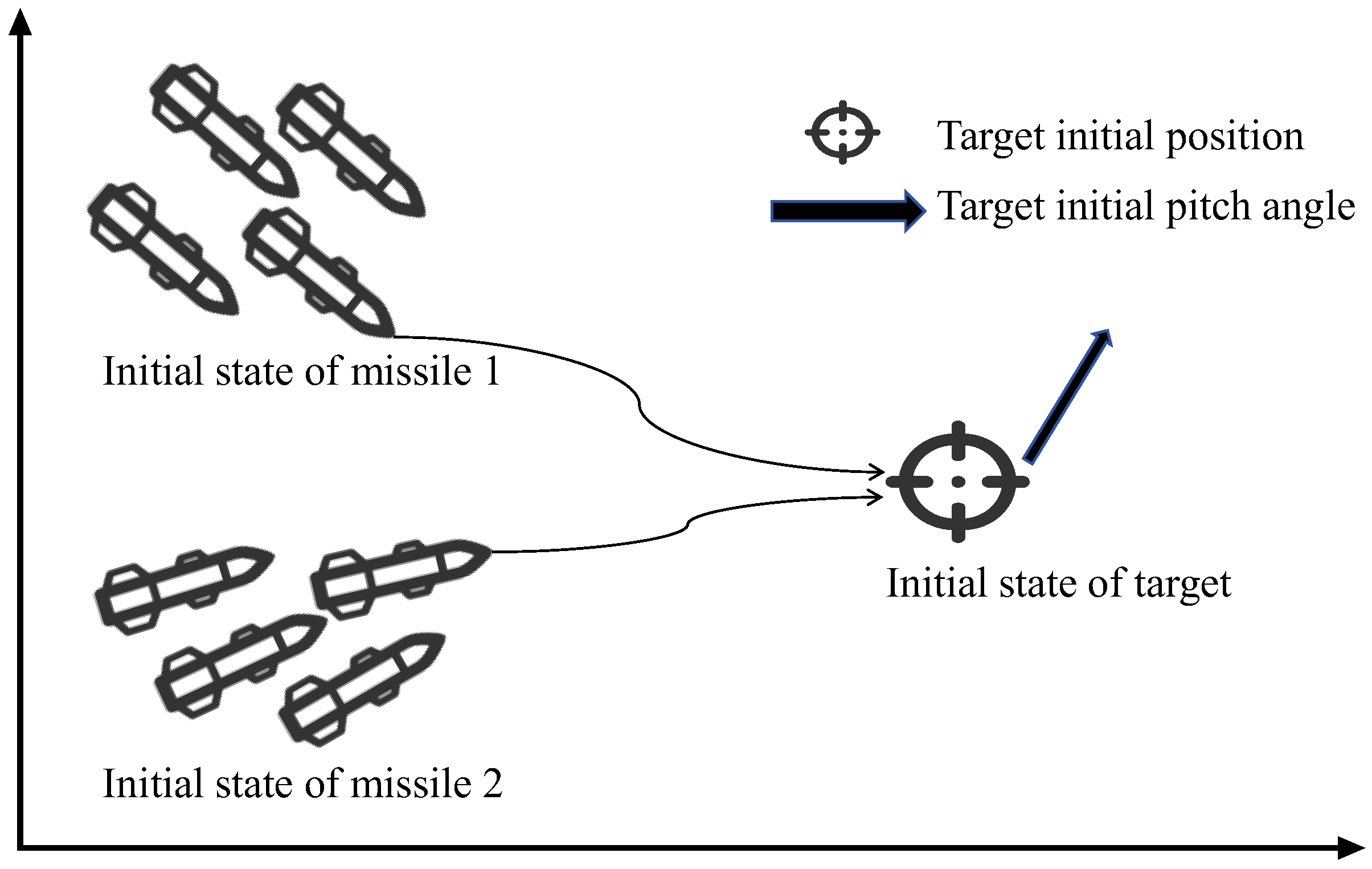
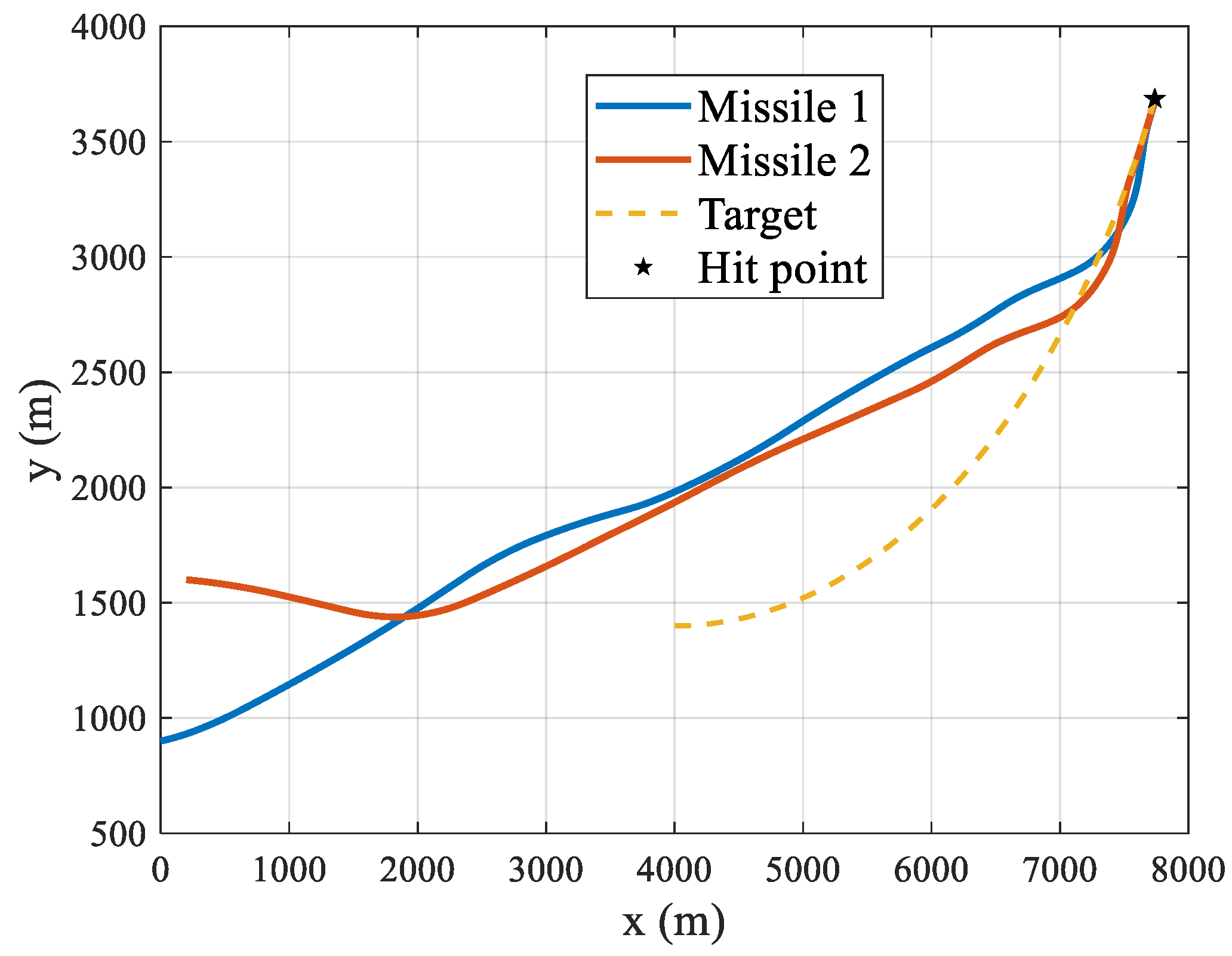
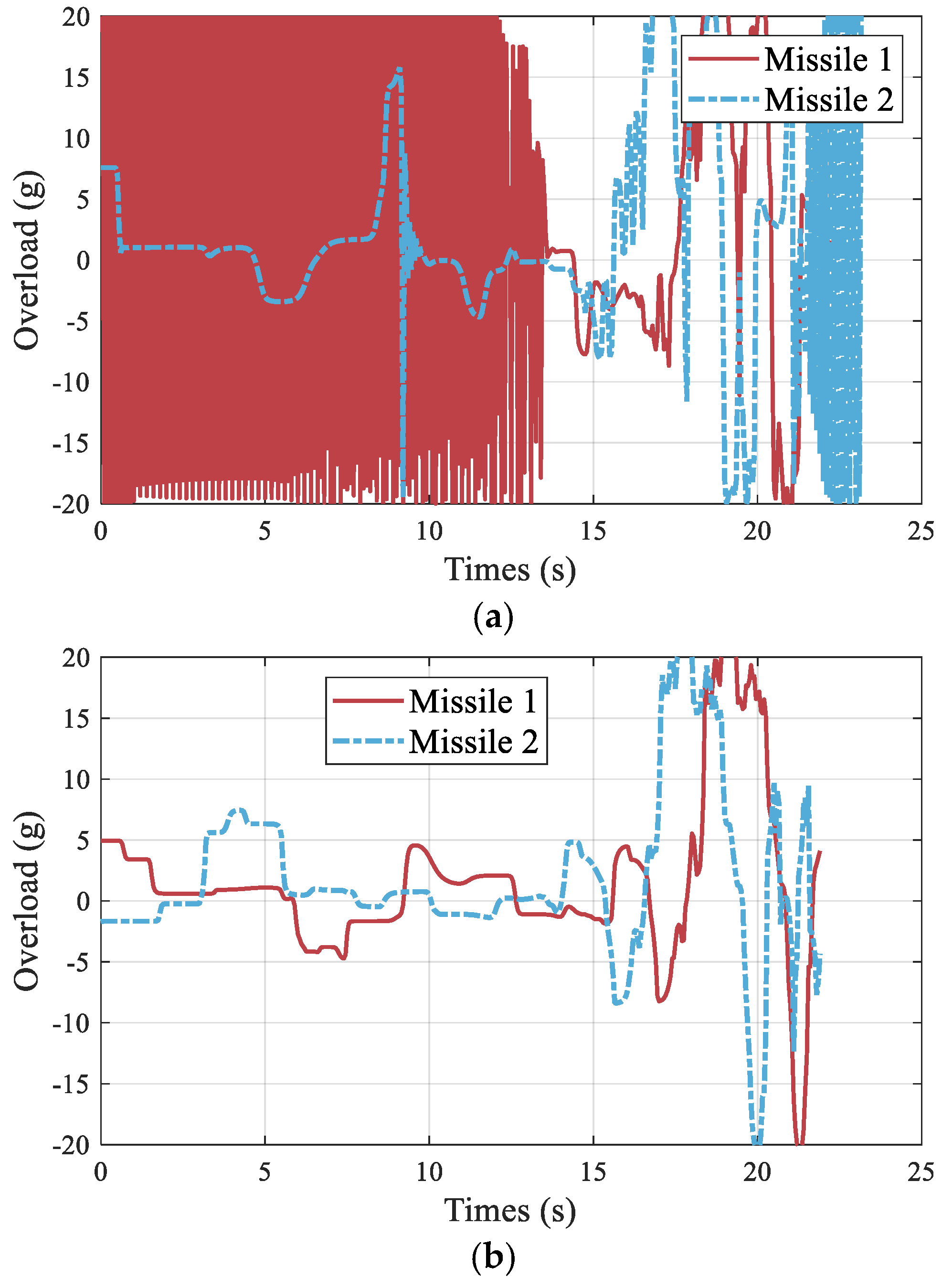
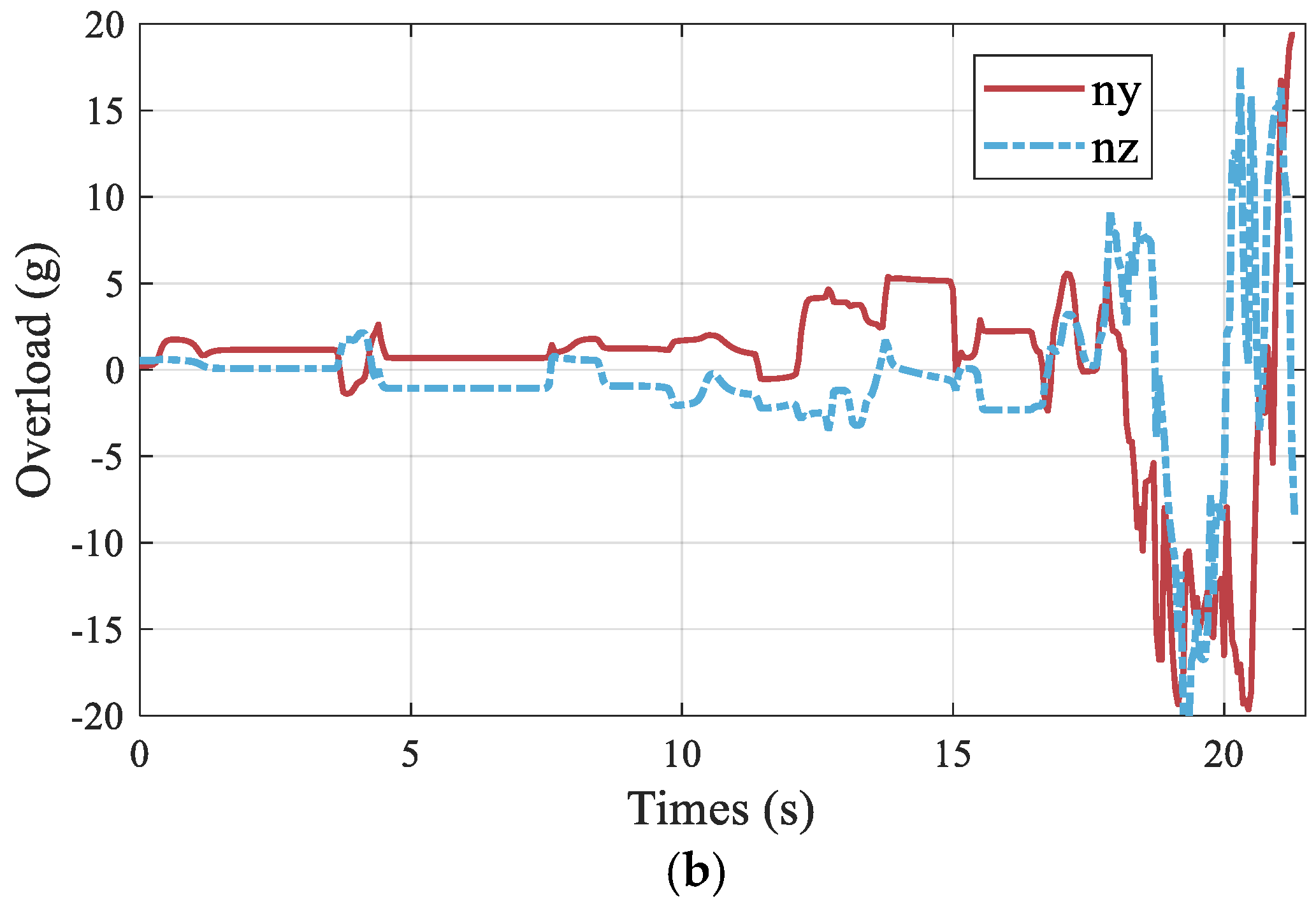
4. Numerical Results and Analysis
4.1. Verification of the Multi-Stage Curriculum Training Method
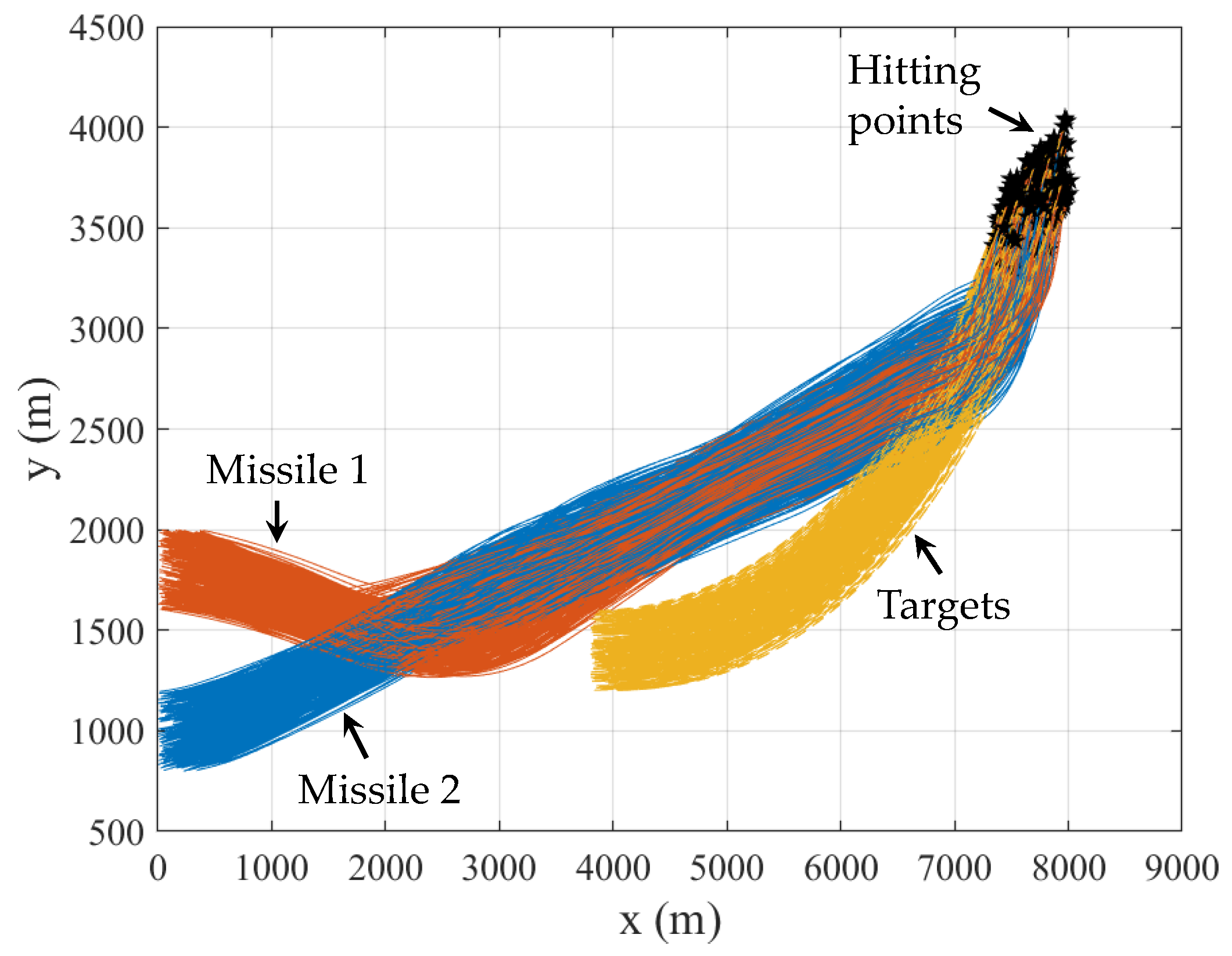
4.2. Generalization Analysis of RLCG
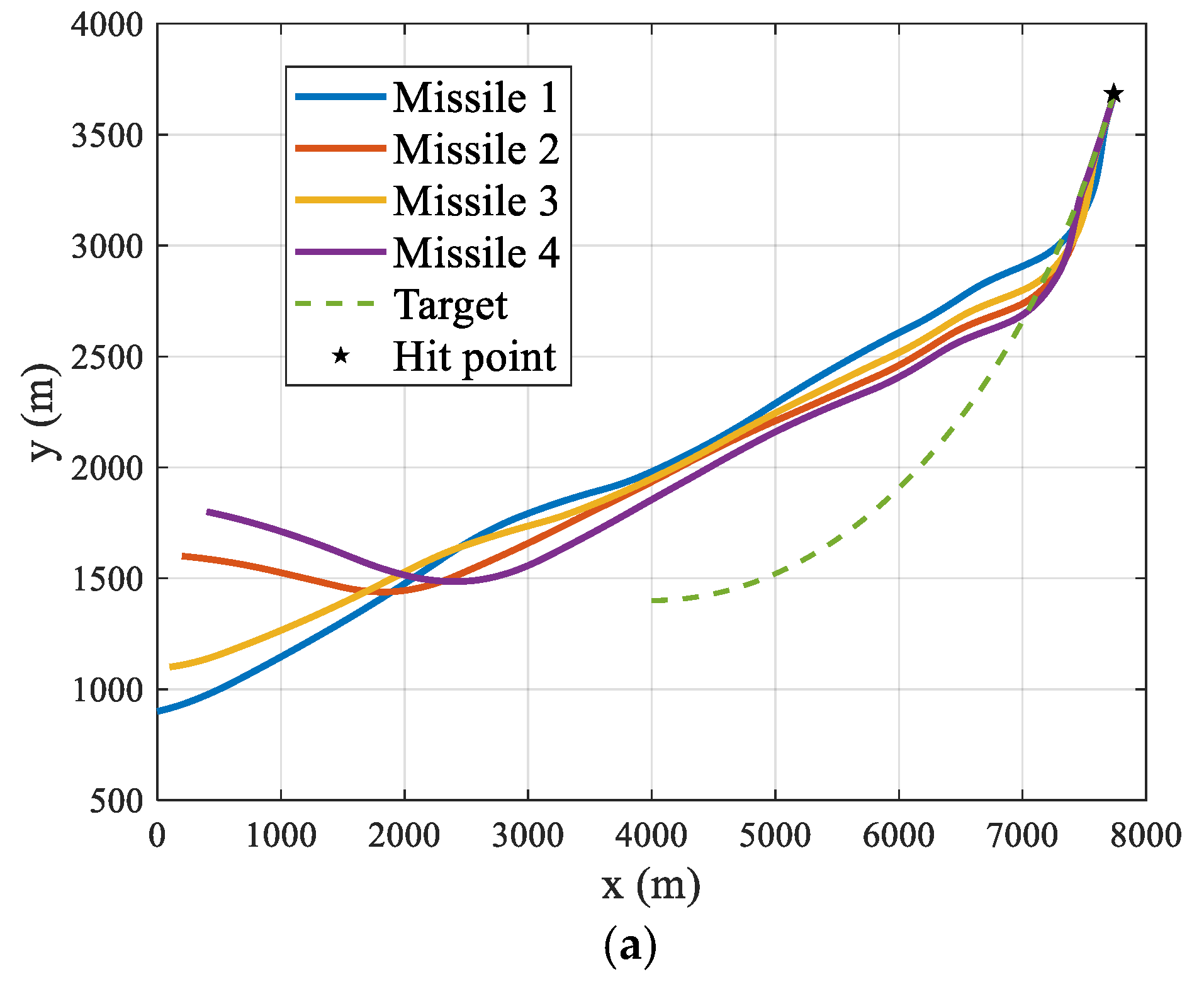
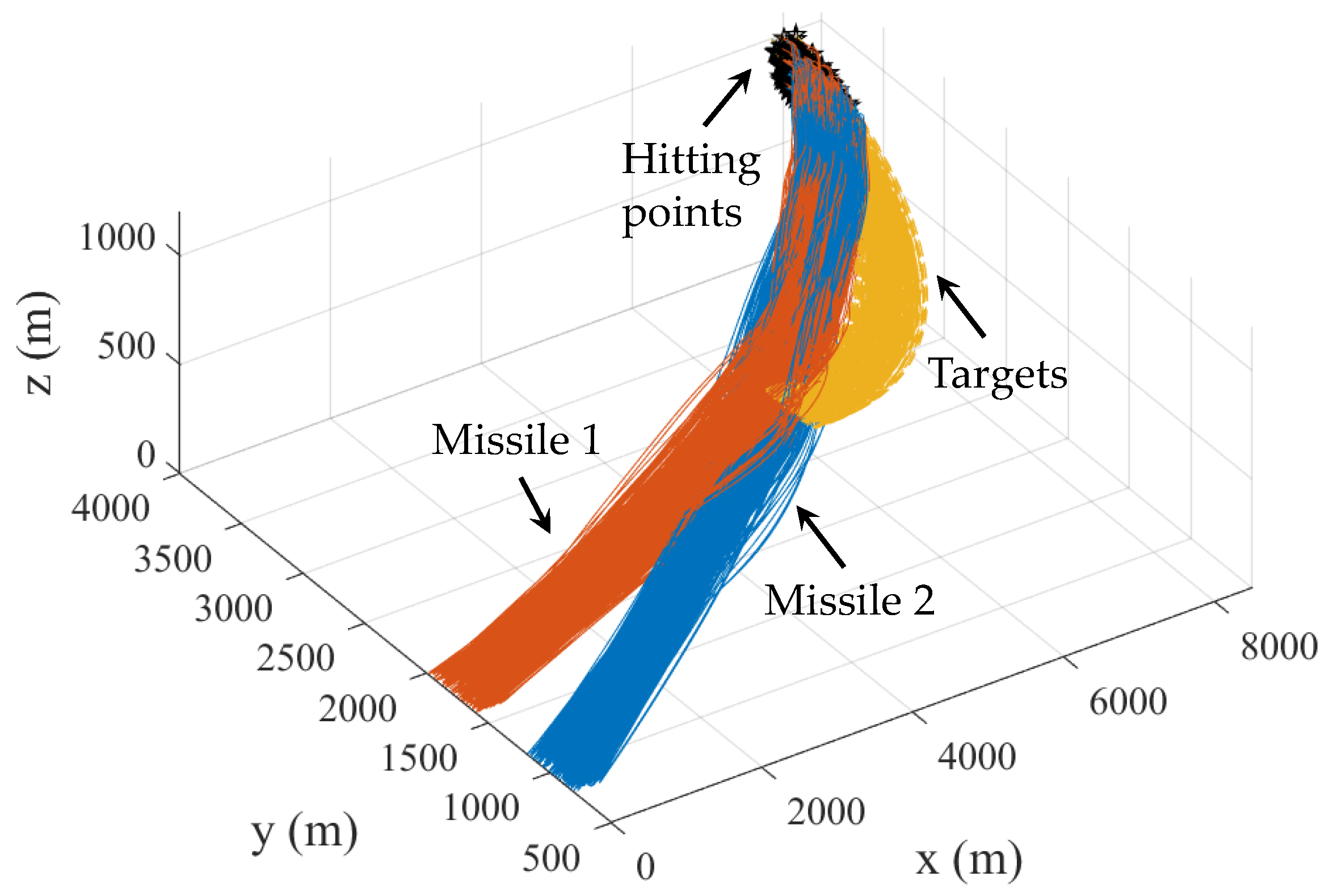
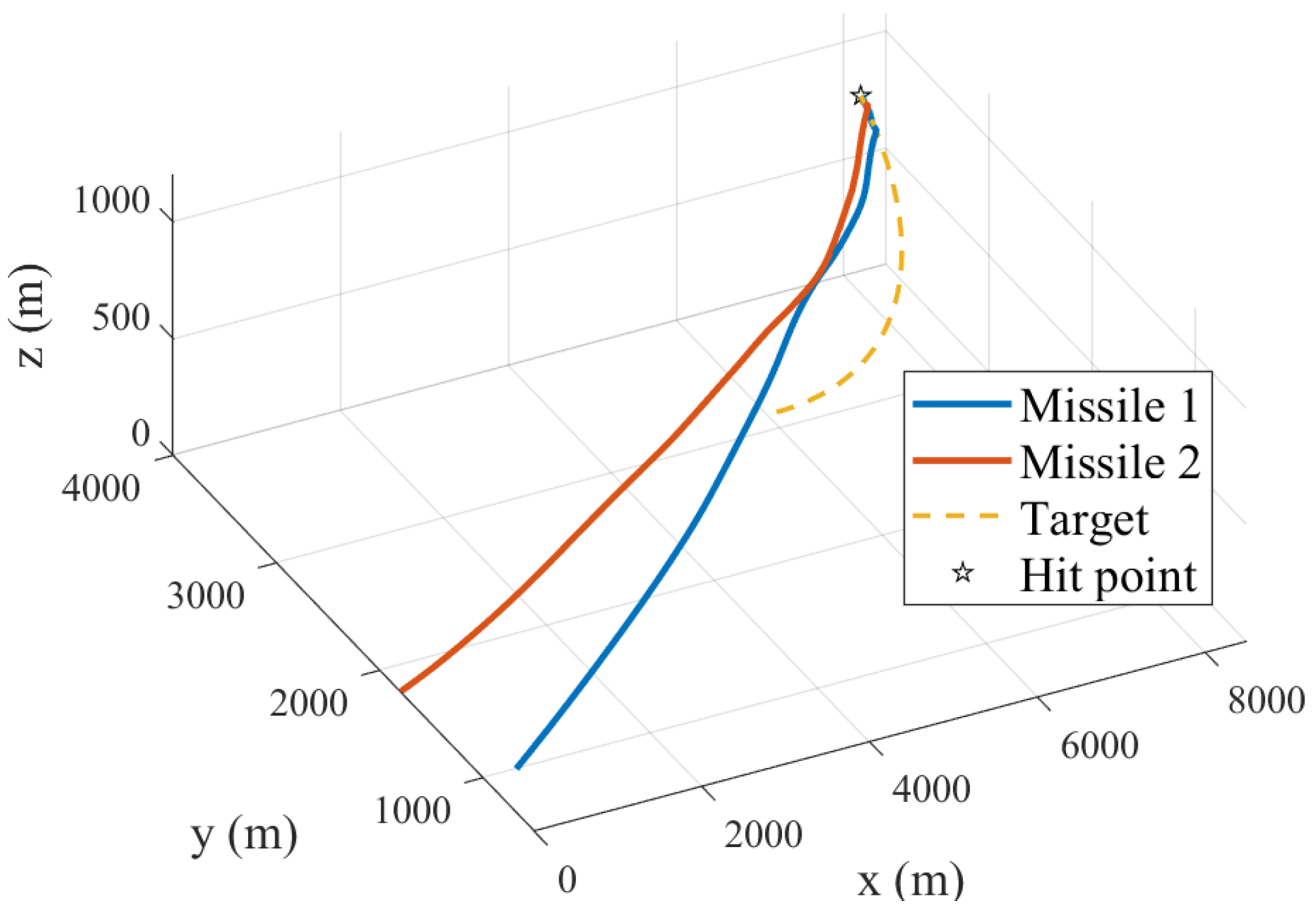
5. Extension to Three-Dimensional Engagements
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Ma, G.; Liu, A. Guidance law with impact time and impact angle constraints. Chin. J. Aeronaut. 2013, 26, 4960–4966. [Google Scholar] [CrossRef]
- Zhao, J.; Zhou, R.; Jin, X. Progress in reentry trajectory planning for hypersonic vehicle. J. Syst. Eng. Electron. 2014, 25, 627–639. [Google Scholar] [CrossRef]
- Wang, J.Q.; Li, F.; Zhao, J.H.; Wang, C.M. Summary of guidance law based on cooperative attack of multi-missile method. Flight Dyn. 2011, 29, 6–10. [Google Scholar]
- Jeon, I.-S.; Lee, J.-I.; Tahk, M.-J. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Guo, Y.; Li, X.; Zhang, H.; Cai, M.; He, F. Data-driven method for impact time control based on proportional navigation guidance. J. Guid. Control Dyn. 2020, 43, 955–966. [Google Scholar] [CrossRef]
- Hu, Q.; Han, T.; Xin, M. New impact time and angle guidance strategy via virtual target approach. J. Guid. Control Dyn. 2018, 41, 1755–1765. [Google Scholar] [CrossRef]
- Sinha, A.; Kumar, S.R.; Mukherjee, D. Three-dimensional guidance with terminal time constraints for wide launch envelops. J. Guid. Control Dyn. 2021, 44, 343–359. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S.; Holzapfel, F. Polynomial shaping of the look angle for impact-time control. J. Guid. Control Dyn. 2017, 40, 2668–2673. [Google Scholar] [CrossRef]
- Dong, W.; Wang, C.; Wang, J.; Xin, M. Varying-gain proportional navigation guidance for precise impact time control. J. Guid. Control Dyn. 2023, 46, 535–552. [Google Scholar] [CrossRef]
- Cho, N.; Kim, Y. Modified pure proportional navigation guidance law for impact time control. J. Guid. Control Dyn. 2016, 39, 852–872. [Google Scholar] [CrossRef]
- Tekin, R.; Erer, K.S.; Holzapfel, F. Impact time control with generalized-polynomial range formulation. J. Guid. Control Dyn. 2018, 41, 1190–1195. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, K.; Zhang, G.; Yan, L. Virtual target approach-based optimal guidance law with both impact time and terminal angle constraints. Nonlinear Dyn. 2022, 107, 3521–3541. [Google Scholar] [CrossRef]
- Chen, X.; Wang, J. Two-stage guidance law with impact time and angle constraints. Nonlinear Dyn. 2019, 95, 2575–2590. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, W.; Li, J.; Yu, W. Guidance algorithm for impact time, angle, and acceleration control under varying velocity condition. Aerosp. Sci. Technol. 2022, 123, 107462. [Google Scholar] [CrossRef]
- Wang, P.; Guo, Y.; Ma, G.; Lee, C.-H.; Wie, B. New look-angle tracking guidance strategy for impact time and angle control. J. Guid. Control Dyn. 2022, 45, 545–557. [Google Scholar] [CrossRef]
- Surve, P.; Maity, A.; Kumar, S.R. Polynomial based impact time and impact angle constrained guidance. IFAC-PapersOnLine 2022, 55, 486–491. [Google Scholar] [CrossRef]
- Chen, Y.; Shan, J.; Liu, J.; Wang, J.; Xin, M. Impact time and angle constrained guidance via range-based line-of-sight shaping. Int. J. Robust. Nonlinear Control 2022, 32, 3606–3624. [Google Scholar] [CrossRef]
- Shiyu, Z.; Rui, Z. Cooperative guidance for multimissile salvo attack. Chin. J. Aeronaut. 2008, 21, 533–539. [Google Scholar] [CrossRef]
- Jiang, Z.; Ge, J.; Xu, Q.; Yang, T. Impact time control cooperative guidance law design based on modified proportional navigation. Aerospace 2021, 8, 231. [Google Scholar] [CrossRef]
- Li, Q.; Yan, T.; Gao, M.; Fan, Y.; Yan, J. Optimal Cooperative Guidance Strategies for Aircraft Defense with Impact Angle Constraints. Aerospace 2022, 9, 710. [Google Scholar] [CrossRef]
- Qilun, Z.; Xiwang, D.; Liang, Z.; Chen, B.; Jian, C.; Zhang, R. Distributed cooperative guidance for multiple missiles with fixed and switching communication topologies. Chin. J. Aeronaut. 2017, 30, 1570–1581. [Google Scholar]
- Kumar, S.R.; Mukherjee, D. Cooperative salvo guidance using finite-time consensus over directed cycles. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 1504–1514. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Huang, P. Optimal cooperative line-of-sight guidance for defending a guided missile. Aerospace 2022, 9, 232. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, J. Distributed guidance law design for cooperative simultaneous attacks with multiple missiles. J. Guid. Control Dyn. 2016, 39, 2439–2447. [Google Scholar] [CrossRef]
- Lyu, T.; Guo, Y.; Li, C.; Ma, G.; Zhang, H. Multiple missiles cooperative guidance with simultaneous attack requirement under directed topologies. Aerosp. Sci. Technol. 2019, 89, 100–110. [Google Scholar] [CrossRef]
- Yu, H.; Dai, K.; Li, H.; Zou, Y.; Ma, X.; Ma, S.; Zhang, H. Distributed cooperative guidance law for multiple missiles with input delay and topology switching. J. Frankl. Inst. 2021, 358, 9061–9085. [Google Scholar] [CrossRef]
- Zadka, B.; Tripathy, T.; Tsalik, R.; Shima, T. Consensus-based cooperative geometrical rules for simultaneous target interception. J. Guid. Control Dyn. 2020, 43, 2425–2432. [Google Scholar] [CrossRef]
- Cevher, F.Y.; Leblebicioğlu, M.K. Cooperative Guidance Law for High-Speed and High-Maneuverability Air Targets. Aerospace 2023, 10, 155. [Google Scholar] [CrossRef]
- Shakya, A.K.; Pillai, G.; Chakrabarty, S. Reinforcement learning algorithms: A brief survey. Expert. Syst. Appl. 2023, 231, 23541. [Google Scholar] [CrossRef]
- Zhang, R.; Zong, Q.; Zhang, X.; Dou, L.; Tian, B. Game of drones: Multi-UAV pursuit-evasion game with online motion planning by deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 7900–7909. [Google Scholar] [CrossRef]
- Wu, M.-Y.; He, X.-J.; Qiu, Z.-M.; Chen, Z.-H. Guidance law of interceptors against a high-speed maneuvering target based on deep Q-Network. Trans. Inst. Meas. Control 2022, 44, 1373–1387. [Google Scholar] [CrossRef]
- Li, W.; Zhu, Y.; Zhao, D. Missile guidance with assisted deep reinforcement learning for head-on interception of maneuvering target. Complex. Intell. Syst. 2022, 8, 1205–1216. [Google Scholar] [CrossRef]
- Qinhao, Z.; Baiqiang, A.; Qinxue, Z. Reinforcement learning guidance law of Q-learning. Syst. Eng. Electron. 2020, 42, 414–419. [Google Scholar]
- Guo, J.; Hu, G.; Guo, Z.; Zhou, M. Evaluation Model, Intelligent Assignment, and Cooperative Interception in multimissile and multitarget engagement. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 3104–3115. [Google Scholar] [CrossRef]
- Ni, W.; Liu, J.; Li, Z.; Liu, P.; Liang, H. Cooperative guidance strategy for active spacecraft protection from a homing interceptor via deep reinforcement learning. Mathematics 2023, 11, 4211. [Google Scholar] [CrossRef]
- Zhou, W.; Li, J.; Liu, Z.; Shen, L. Improving multi-target cooperative tracking guidance for UAV swarms using multi-agent reinforcement learning. Chin. J. Aeronaut. 2022, 35, 100–112. [Google Scholar] [CrossRef]
- Xi, A.; Cai, Y. Deep Reinforcement Learning-Based Differential Game Guidance Law against Maneuvering Evaders. Aerospace 2024, 11. [Google Scholar] [CrossRef]
- Ha, I.-J.; Hur, J.-S.; Ko, M.-S.; Song, T.-L. Performance analysis of PNG laws for randomly maneuvering targets. IEEE Trans. Aerosp. Electron. Syst. 1990, 26, 713–721. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, Y. The surprising effectiveness of ppo in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Li, X.; Vasile, C.I.; Belta, C. Reinforcement learning with temporal logic rewards. In Proceedings of the International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; pp. 3834–3839. [Google Scholar]
- Ma, M.; Song, S. Multi-missile cooperative guidance law for intercepting maneuvering target. Aero Weapon. 2021, 28, 19–27. [Google Scholar]



| Stage | Reward Function Parameters |
|---|---|
| Stage 1 | |
| Stage 2 | |
| Stage 3 |
| Parameter | Missile 1 | Missile 2 | Target |
|---|---|---|---|
| Initial x-axis coordinate (m) | 0~400 | 0~400 | 3800~4200 |
| Initial y-axis coordinate (m) | 800~1200 | 1600~2000 | 1200~1600 |
| Initial velocity (m/s) | 400 | 400 | 210 |
| Initial pitch angle (°) | 0 | 0 | / |
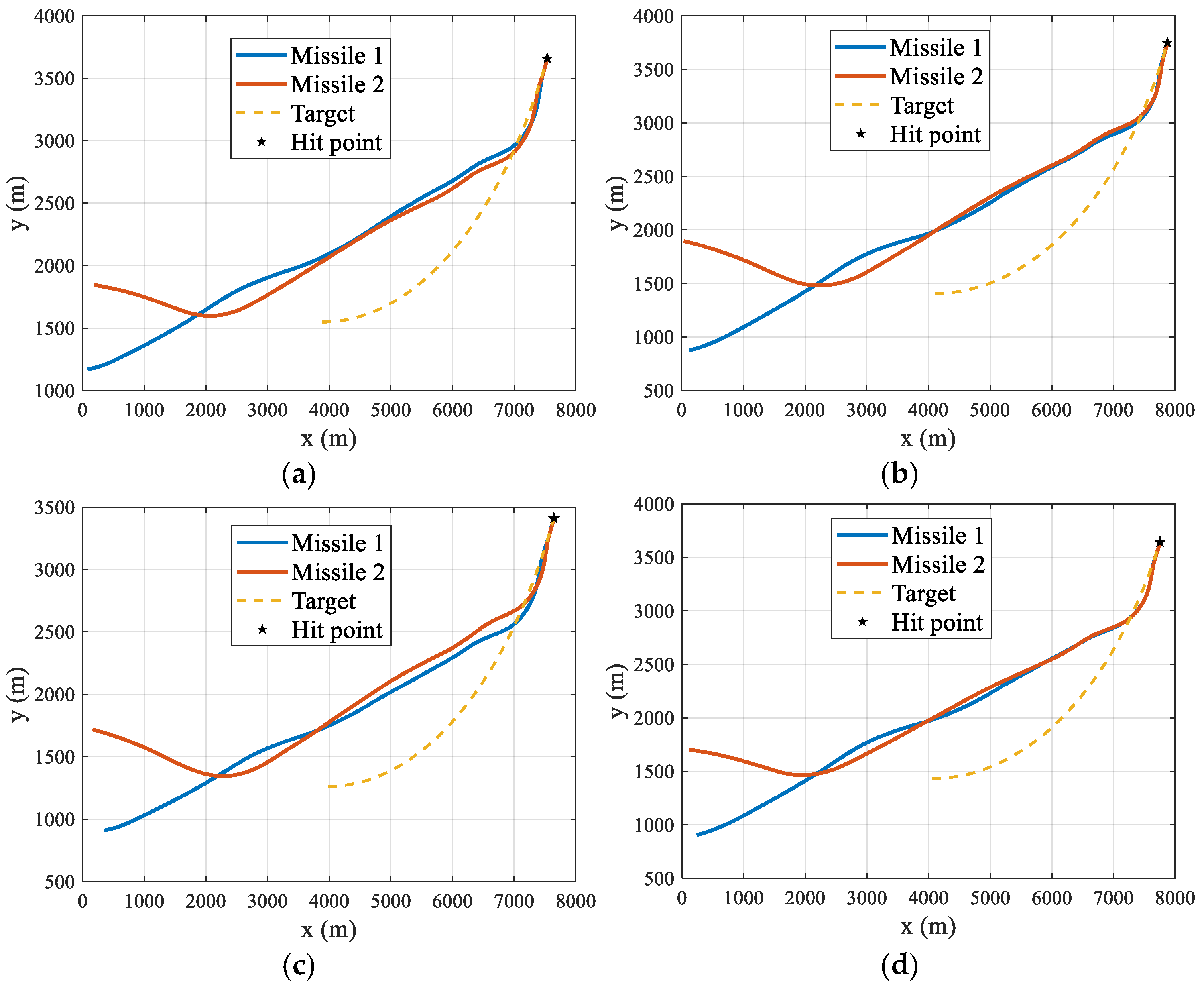
| Figure | Initial Position of Missile 1 | Initial Position of Missile 2 | Initial Position of Target | Attack Time (s) |
|---|---|---|---|---|
| Figure 10a | (82.68, 1167.44) | (195.36, 1844.69) | (3888.79, 1548.29) | 21.05 |
| Figure 10b | (118.72, 875.08) | (32.29, 1895.37) | (4106.36, 1407.36) | 23.00 |
| Figure 10c | (351.97, 909.63) | (165.69, 1718.43) | (3976.52, 1263.32) | 21.25 |
| Figure 10d | (239.97, 906.32) | (113.87, 1701.43) | (4051.51, 1431.93) | 21.60 |
| Parameter | Missile 1 | Missile 2 | Target |
|---|---|---|---|
| Initial x-axis coordinate (m) | 0~600 | 0~600 | 3700~4300 |
| Initial y-axis coordinate (m) | 700~1300 | 1500~2100 | 1100~1700 |
| Parameter | Missile 1 | Missile 2 | Target |
|---|---|---|---|
| Initial x-axis coordinate (m) | 0~400 | 0~400 | 3800~4200 |
| Initial y-axis coordinate (m) | 800~1200 | 1600~2000 | 1200~1600 |
| Initial z-axis coordinate (m) | 0 | 0 | 1000 |
| Initial velocity (m/s) | 400 | 400 | 210 |
| Initial pitch angle (°) | 0 | 0 | / |
| Initial yaw angle (°) | 0 | 0 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, H.; Zhang, K.; Tan, M.; Wang, J. A Deep Reinforcement Learning-Based Cooperative Guidance Strategy Under Uncontrollable Velocity Conditions. Aerospace 2025, 12, 411. https://doi.org/10.3390/aerospace12050411
Cui H, Zhang K, Tan M, Wang J. A Deep Reinforcement Learning-Based Cooperative Guidance Strategy Under Uncontrollable Velocity Conditions. Aerospace. 2025; 12(5):411. https://doi.org/10.3390/aerospace12050411
Chicago/Turabian StyleCui, Hao, Ke Zhang, Minghu Tan, and Jingyu Wang. 2025. "A Deep Reinforcement Learning-Based Cooperative Guidance Strategy Under Uncontrollable Velocity Conditions" Aerospace 12, no. 5: 411. https://doi.org/10.3390/aerospace12050411
APA StyleCui, H., Zhang, K., Tan, M., & Wang, J. (2025). A Deep Reinforcement Learning-Based Cooperative Guidance Strategy Under Uncontrollable Velocity Conditions. Aerospace, 12(5), 411. https://doi.org/10.3390/aerospace12050411






