Abstract
Lattice structures, with their unique design, offer properties like a programmable elastic modulus, an adjustable Poisson’s ratio, high specific strength, and a large specific surface area, making them the key to achieving structural lightweighting, improving impact resistance, vibration suppression, and maintaining high thermal efficiency in the aerospace field. However, functional prediction and inverse design remain challenging due to cross-scale effects, extensive spatial freedom, and high computational costs. Recent advancements in AI have driven progress in predicting lattice structure functionality. This paper begins with an introduction to the lattice types, their properties, and applications. Then the development process for the performance-prediction methods of lattice structures is summarized. The current applications of performance-prediction methods, which are data-driven and related to material properties, structural properties, and performance under conditions of coupled multi-physical fields, are analyzed, and this analysis further extends to the data-driven methods in relation to their prediction of lattice structure functionality. This paper summarizes the application of data-driven methods in the prediction of the mechanical, energy absorption, acoustic, and thermal properties of lattice structures; elaborates on the application of these methods in the optimization design of lattice structures in the aerospace field; and details the relevant theory and references for the field of lattice structure performance analysis. Finally, the progress and problems in the functional prediction of lattice structures under the current research is demonstrated, and the future development direction of this field is envisioned.
1. Introduction
With advancements in manufacturing technology, the aerospace field is transitioning from traditional design frameworks to more sophisticated approaches that incorporate multiple functional requirements, including being lightweight, being load-bearing, providing vibration suppression, and having high thermal efficiency capabilities. Lattice structures effectively meet these functional requirements [1,2,3,4,5]. As shown in Figure 1, lattice structures are artificially designed materials whose properties and characteristics are primarily dictated by their structure, rather than material composition [6]; these structures often exhibit unique properties that are difficult to realize with natural materials, such as a negative Poisson’s ratio [7] and a high stiffness-to-weight ratio [8].

Figure 1.
Applications of lattice structures in the aerospace field. (a) Lattice-filled airfoil structures [1]; (b) a Kagome lattice structure reducing the vibration amplitude of the wing [2]; (c) a TPMS lattice structure heat exchanger [3].
Traditional design approaches for lattice structures primarily encompass forward design methods and topology optimization techniques. The forward design process involves iterative adjustments of structural parameters (e.g., unit cell dimensions, wall thickness) until the measured or simulated properties satisfy predetermined design criteria. This methodology typically demands substantial domain expertise from designers and follows a conventional “design–fabricate–test” cycle, which often leads to prolonged development timelines, elevated experimental costs, and significant challenges in structural optimization [9]. These limitations make it increasingly inadequate for contemporary optimization requirements.
Topology optimization, while offering design flexibility, presents its own set of challenges, including non-unique response–design relationships and an expansive design space that complicates the accurate prediction of mechanical behavior [10]. This approach relies heavily on high-fidelity numerical simulations to provide precise performance predictions. By leveraging computational modeling and analyses, it eliminates the necessity for physical prototyping and testing, thereby achieving considerable reductions in both the development time and costs. This computational paradigm enables designers to perform optimization and design improvements during the early stages of product development.
In modern engineering practice, simulation analysis has become an essential component of the design process. However, lattice structures present unique computational challenges due to their cross-scale effects and enormous topology design space. These simulations typically require numerous parameter iterations, resulting in substantial computational time investments. Furthermore, the accurate performance evaluation of lattice structures demands significant computational resources, particularly when dealing with complex operational scenarios involving multi-physics coupling simulations. These requirements lead to prohibitive computational expenses and create substantial obstacles in meeting real-time simulation demands [11,12].
To overcome these challenges, researchers have developed several innovative approaches, including surrogate modeling, homogenization techniques, and data-driven performance-prediction methods. Among these, artificial intelligence (AI) technologies—like machine learning (ML) and deep learning (DL)—have revolutionized data-driven prediction methodologies due to their exceptional computational capabilities. Unlike traditional programming, ML and DL systems autonomously learn patterns from data to make accurate decisions or predictions. These technologies are increasingly being leveraged across diverse research domains, including material property prediction [13], intelligent manufacturing systems [14], and defect detection in materials [15].
AI-driven approaches employ advanced techniques, such as random forests and neural networks, to establish direct input–output mappings, enabling the development of highly efficient, deep learning-based surrogate models. These models facilitate precise predictions of structural performance while significantly reducing computational costs [16]. Recent advancements in computer hardware, particularly the enhanced processing power of modern CPUs and GPUs, coupled with substantial improvements in algorithmic feature extraction, have further accelerated AI adoption. Modern AI systems excel at identifying complex nonlinear relationships between input parameters (e.g., geometric configurations and material properties) and output responses (e.g., displacement and stress distributions), leading to substantial gains in both prediction accuracy and computational efficiency.
In recent years, more and more research has focused on the application of machine learning and deep learning in additive manufacturing processes and structural design. Zhu et al. [17] explored the use of ML to enhance the mechanical properties of materials, specifically targeting the modulus of magnesium-based materials. Wang et al. [18] focused on the application of machine learning in optimizing process parameters and process monitoring to improve the stability and efficiency of additive manufacturing processes. Khan et al. [19] introduced the relevant applications of machine learning methods in defect prediction, detection, and optimization. These reviews elaborate on the enormous potential of machine learning in the field of additive manufacturing, but there is a lack of information on how to achieve the active design of structural functionality while the process of structural design is the most important link in the additive manufacturing process.
This paper focuses on the application of functional lattice structures and AI technologies in related fields, providing a review and summary of the existing literature. It first describes typical lattice structures and their functional properties, then introduces existing methods for lattice functionality prediction, and finally reviews research on AI in structural performance prediction and optimization. Applications of data-driven methods in lattice functionality prediction are discussed, and the achievements and applications of multifunctional lattice structure design in aerospace field are introduced. Finally current issues are proposed and future directions in the relevant research areas are explored.
2. Lattice Structures and Functional Properties
For centuries, researchers have mimicked natural cellular structures with hollow designs, such as bones, honeycomb structures, and Voronoi structures [20], to create porous structures with high specific strength and stiffness, as shown in Figure 2, which have been applied in some engineering applications [21,22,23]. However, the design of these complex structures with potentially superior performance has been limited by traditional manufacturing technology. With the development of additive manufacturing, the design approach for cellular structures has gradually shifted from traditional process design to function-driven design. These structures, composed of orderly repeating units, are called lattice structures. Due to their non-random characteristics, lattice structures perform better than random cellular structures, offering advantages such as a negative Poisson’s ratio, large surface area, high internal porosity, and low thermal expansion coefficient [24,25,26,27,28,29,30,31,32]. Additionally, the performance of lattice structures is highly adjustable, and different designs of lattice structure can meet multifunctional requirements. These superior properties have enabled the use of lattice structures in the aerospace field, such as structural lightweighting, energy absorption, vibration suppression, and high thermal efficiency [33]. This chapter will introduce typical types of lattice structures and their functional properties.
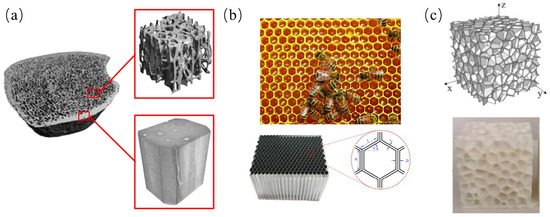
Figure 2.
Cellular structures: (a) porous structure of human bone [21]; (b) honeycomb structure [20]; (c) Voronoi structure [22].
2.1. Types of Lattice Structures
2.1.1. Strut-Based Lattice Structures
Strut-based lattice structures are formed by the periodic arrangement of basic units consisting of struts and nodes in space [34]. The most common structures in current research are body-centered cubic (BCC) structures and face-centered cubic (FCC) structures, named after their analogous crystal structures. Other Strut-based topologies include cubic, octet truss, and diamond structures, as shown in Figure 3a. Strut-based lattice structures can be characterized by the number of struts (s) and nodes (n), which together determine the Maxwell number (M) of the unit cell. The relationship between s, n, and M is as follows [35]:

Figure 3.
Typical lattice structures: (a) support-based lattice structures; (b) triply periodic minimal surface lattice structures; (c) shell lattice structures.
If M < 0, the number of struts is insufficient to balance the external forces caused by the nodes, resulting in structural bending primarily due to the bending stress of the struts. When M ≥ 0, no bending occurs at the nodes, and the structure is tension-dominated [36]. Under the same mass, tension-dominated structures have greater stiffness, while bending-dominated structures exhibit greater flexibility.
2.1.2. Triply Periodic Minimal Surface Lattice Structures
Lattice structures based on triply periodic minimal surfaces (TPMSs) are composed of minimal surfaces that form infinite, non-intersecting periodic lattices in three principal directions. A TPMS is defined by an implicit equation that defines a set of zeros for the function F(x, y, z) = 0, identifying a set of points located on the surface of a unit cell, creating a lattice structure based on the triply periodic minimal surface [37]. Examples of such structures include Gyroid, Schwarz diamond, and Lidinoid, as shown in Figure 3b.
2.1.3. Shell Lattice Structures
Shell lattice structures are unit cell structures composed of plates rather than struts or continuous surfaces [38]. Unlike the lattice structures mentioned above, the plates within the unit cell of a shell lattice structure form enclosed pores. While this provides a high elastic performance and load-bearing capacity [39,40], it also results in disadvantages such as a poor heat exchange performance and high manufacturing difficulty [41]. Figure 3c shows typical shell lattice structures.
2.2. Lattice Structure Functionality
Lattice structures, due to their unique spatial configuration, exhibit properties such as being light weight and having high specific strength and high energy absorption [42]. The applications of lattice structures can be broadly categorized into two main types: structural applications and functional applications. Structural applications include energy-absorbing structures, while functional applications often involve vibration damping materials and heat exchangers design [33].
Lattice structures, as periodic porous structures, exhibit excellent energy absorption performance. In Figure 4a, Zhao et al. [43] compared the mechanical properties of BCC lattice structures with and without TPMSs made from Ti-6Al-4V using SLM, showing that BCC lattices with TPMSs have higher energy absorption capabilities. Harris et al. [44] created a metal hybrid lattice structure with square honeycomb lattice walls from 316L stainless steel, as shown in Figure 4b. The sample demonstrated high strength and a high energy absorption per unit volume. Wen et al. [45] developed a new layered honeycomb structure using a porous grapefruit peel, with the schematic shown in Figure 4c. Compared to standard honeycombs, the specific energy absorption (SEA) of the layered honeycomb increased 1.5 times during both out-of-plane and in-plane crushing processes. Du Plessis et al. [46] experimentally studied a lattice structure inspired by the exoskeleton of an extinct mammal, as shown in Figure 4d. The experiment indicated that the presence of a dense layer in the structure enhanced its energy absorption performance.
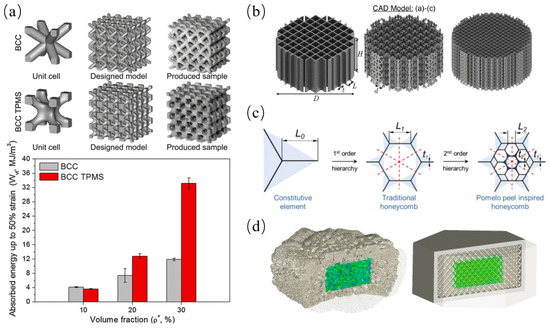
Figure 4.
Applications of lattice structures in energy absorption: (a) comparison of energy absorption performance between BCC and BCC TPMS lattice structures [43]; (b) metal hybrid lattice structure with square honeycomb lattice walls [44]; (c) layered lattice with grapefruit-peel-like porous structure [45]; (d) lattice structure inspired by animal exoskeletons [46].
Topology acoustics indicate that lattice structures have superior sound insulation properties [47]. Sun et al. [48] used 316L stainless steel to create acoustic lattice structure samples with different size parameters using SLM, as shown in Figure 5a. Within the frequency range of 1 to 6.3 kHz, both lattice structure samples demonstrated better sound absorption performance compared to bulk material samples. Metamaterials with characteristics such as negative stiffness, bistability, high energy dissipation, and high damping ratios can effectively reduce vibration and sound wave propagation. For example, thin film acoustic metamaterials made from elastic membranes and asymmetric rigid plates can absorb low-frequency air noise at selected resonance frequencies [49]. Spadoni et al. [50] proposed lattice structures incorporating chiral resonator elements with integrated frequency-selective characteristics to achieve a high damping performance, leveraging the potential noise reduction and vibration isolation features of chiral honeycombs.
In heat exchange systems, such as heat exchangers, radiators, and heat pipes, efficient heat transfer media are required. The interconnected voids within lattice structures allow fluid flow through the material, making lattice-based heat exchangers more efficient in thermal conductivity compared to other structures [51]. Do et al. [52] conducted experimental studies to determine the pressure drop and heat transfer performance of water flowing through microscale lattice structures. The experiment shows that the increase of the ratio of unit cell size to the strut diameter leads to a stronger influence of the offset on the pressure drop. Sélo et al. [53] manufactured a microscale cross-flow heat exchanger using nickel-based micro-lattice structures. The experimental data showed that the thermal conductivity of the lattice structure increased by 30% after heat treatment. Ho et al. [54] used SLM to create a novel heat exchanger with a rhombic dodecahedron lattice structure, with the schematic and specific printed parts shown in Figure 5b. Compared to traditional finned-tube heat exchangers, this new heat exchanger demonstrated a 45% increase in thermal conductivity, while the pressure drop was higher than in finned-tube heat exchangers. At the same mass flow rate of air, the heat transfer coefficient values of the porous lattice heat exchangers were more than two times those of the finned-tube heat exchangers.
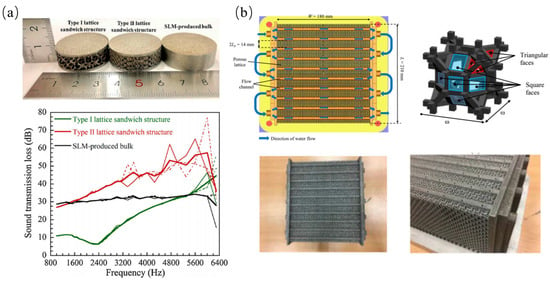
Figure 5.
Applications of lattice structures in acoustics and heat exchangers systems: (a) 316L stainless steel acoustic material and sound insulation performance [48]; (b) novel heat exchanger with rhombic dodecahedron lattice structure [54].
Due to the unique properties of the lattice structure, it has a wide range of applications in biomedical, automotive, aerospace, and other fields as shown in Figure 6. Garner et al. [55] developed a type of lattice structure for topologically optimized medical implants with gradient unit cells with a bone implant featuring discrete density distribution. Feng et al. [56] used an anisotropic control strategy to regulate the elastic modulus and isotropy of a lattice structure to design the structure of the acetabular cup implant. The three-dimensional lattice structure of non-inflatable tires can effectively prevent tire blowouts [57]. NTopology Introduced the simulation-driven design for additive manufacturing with a shell-and-lattice infill to create more stiff aerospace components with a weight reduction of up to 50% [58].
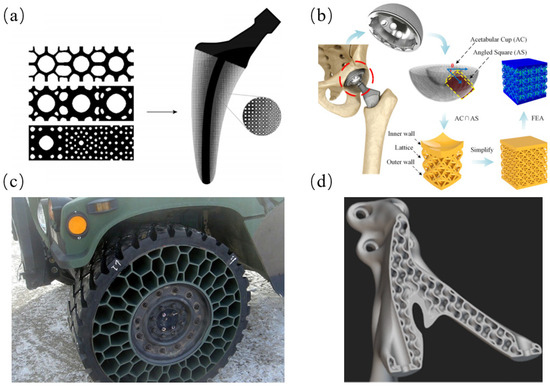
Figure 6.
Applications of lattice structures in biomedical, automotive, and aerospace fields: (a) gradient lattice medical implant [55]; (b) lattice structure orthopedic implants [56]; (c) elastic honeycomb lattice tires [57]; (d) NASA EXCITE bracket [58].
2.3. Lattice Structure Applications in Aerospace Field
The lattice structure plays a crucial role in lightweight design in the aerospace industry due to its high specific strength, excellent energy absorption capacity, vibration suppression, and high thermal efficiency. Compared to traditional solid structures, lattice structures can significantly reduce the overall weight while maintaining or improving mechanical properties through topology optimization and material distribution optimization. This is crucial for improving the fuel efficiency of aircraft, enhancing the payload capacity, and improving structural durability. In key components such as satellite components, aircraft skins, rocket fairings, wing supports, and landing buffer systems, lattice structures can not only reduce structural weight, but also optimize heat dissipation performance and improve impact resistance, thus meeting the stringent requirements of aerospace vehicles for lightweight and high-strength materials. Li et al. [59] presented a topology optimization strategy for the design of AM-based, functionally graded cellular structures. As shown in Figure 7a, compared to traditional truss structures, it significantly increases stiffness while reducing the structural mass. Cheng et al. [60] proposed a lattice structure topology optimization framework for the design of aero-brackets manufactured by SLM, as shown in Figure 7b. Daniel et al. [61] introduced a novel resistojet thruster concept that uses an entirely new heat exchanger, manufactured as a highly miniaturized single piece with a geometrically complex triply periodic minimal surface (TPMS) lattice structure. The prototype thruster weighed only 22 g and demonstrated a 67% reduction in the power required to achieve the same specific impulse. Zhang et al. [62] proposed a collaborative optimization technology with a structural topology lattice biomimetic configuration for a satellite antenna structure. Compared with the original structural configuration, the dynamic response is reduced by more than 25% and the weight is reduced by more than 17%.

Figure 7.
Applications of lattice structures in aerospace: (a) quadrotor cantilever filled with lattice [59]; (b) lattice pillow bracket filled with lattice [60]; (c) CubeSat TPMS heat exchanger [61]; (d) satellite bracket structure filled with lattice [62].
3. Data-Driven Prediction of Lattice Structure Functionality
3.1. The Development Process of Lattice Structure Research and Performance-Prediction Methods
The geometric design flexibility of lattice structures enables them to achieve functionalities that traditional materials cannot. By adjusting the design parameters of lattice structures, such as the unit cell topology or geometric parameters, the functional responses of these structures can change significantly. However, understanding the performance of different lattice structures is challenging due to their unique geometries, volume fractions, and compositional properties. Accurately predicting the performance of any designed lattice structure is a key issue in current lattice structure research.
Research on lattice structure performance began in the 1970s, with the American Society of Civil Engineers reporting on lattice structure performance. The design model for lattice materials proposed by Ashby and Gibson in 1997, known as the Gibson–Ashby model [63], marked a peak in early research into lattice structures. Due to time and cost constraints, experimenting with a large number of lattice structure samples with different geometries and functionalities is almost impossible. Additionally, the complexity of lattice structures makes performance prediction through simulation methods costly in terms of computation and memory, which does not meet the requirements for predicting the performance of numerous lattice structures.
To address the issue of lattice functionality prediction, researchers have used beam theory and homogenization theory for performance analyses over the past few decades. Beam theory research dates back to 1750, with the Euler–Bernoulli beam theory, proposed by Leonhard Euler and Daniel Bernoulli, serving as the foundation for subsequent research. In the 1920s, Timoshenko developed the Timoshenko beam theory model based on previous research. As lattice structure research advanced, researchers found that lattice structures with large aspect ratios could simplify lattice models using beam theory, allowing for the prediction of mechanical performance. Although beam theory analysis methods can quickly solve mechanical performance [64], they have limitations due to the requirement for beam aspect ratios, and they neglect the impact of beam intersections on the overall structure performance, leading to discrepancies between the predicted and the actual performance [65].
Homogenization theory, initially developed to address partial differential equations [66], estimates the macroscopic properties of homogenized materials based on the response of their underlying microscopic structure, allowing heterogeneous materials to be replaced with equivalent homogeneous materials [67]. The application of homogenization methods to lattice performance prediction dates back to 1988, when Bendsøe and Kikuchi [68] used progressive homogenization methods to calculate the effective material properties of anisotropic materials, obtaining the effective elastic modulus of unit lattice materials. Weeger et al. [69] introduced a numerical homogenization method for computing the constitutive model of cubic lattice structures, deriving the relationships between effective macroscopic strain, stress, and microscopic boundary deformations and rotations. Li et al. [70] developed a homogenization model based on 3D RVE calculations to study the impact of corrugated core height and angle on the natural frequency. Huang et al. [71] proposed a finite-element-method-based homogenization approach within the framework of anisotropic micropolar continua, providing a universal method for the homogenization of orthogonal lattices and conformal metamaterials. Li et al. [72] applied homogenization methods to compute the mechanical performance of anisotropic lattice structures and integrated this into topology optimization processes. The optimized structures not only improved stiffness but also exhibited robustness in damage resistance and buckling capacity. However, the frequent use of numerical homogenization methods makes simulations and optimizations time-consuming. To reduce the computational cost of lattice functionality prediction, many methods have been developed in recent years, with machine learning and deep learning technologies in AI becoming a focus of research.
In recent years, with the rise of AI, machine learning and deep learning technologies have been applied to various scientific and engineering fields, including materials science, chemistry, particle physics, computational mechanics, and quantum mechanics [73]. The unique advantage of machine learning and deep learning lies in their data-driven approach, allowing models to automatically discover and map meaningful information from large amounts of generated data, unlike physics-based or rule-based methods. In recent research, data-driven methods for predicting structural performance and conducting structural design have become revolutionary new technologies. In 2024, Ansys combined simulation accuracy with the high speed of generative AI to introduce SimAI technology, which rapidly predicts simulation results based on AI. This chapter will introduce the development of data-driven performance prediction models and their applications for lattice structure performance prediction, and the development process of research on lattice structure performance is shown in Figure 8.
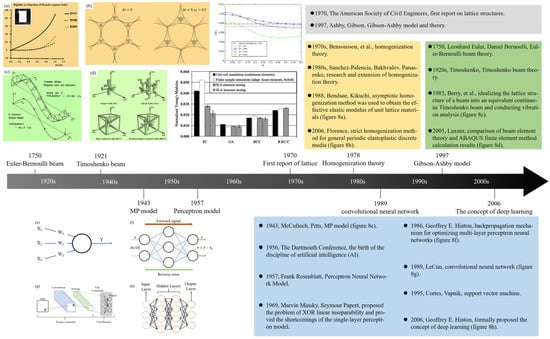
Figure 8.
The progress of lattice functional research and AI technology development [63,66,74,75,76,77,78,79,80,81,82,83,84]: (a) asymptotic homogenization method for the effective elastic modulus of unit lattice materials [68] (b) strict homogenization method for general periodic elastoplastic discrete media [76] (c) simple beam finite element analysis models for a flexible lattice beam [78] (d) comparison of beam element theory and ABAQUS finite element method [79] (e) MP model [80] (f) backpropagation algorithm [82] (g) convolutional neural network [83] (h) concept of deep learning [83].
3.2. Data-Driven Performance Prediction Models
Since the concept of AI was introduced in 1956, various machine learning models have been continuously developed and applied. With advancements in artificial neural networks and significant increases in computational power, the concepts and models of deep learning have emerged. Driven by today’s big data era, these models can help designers rapidly and accurately predict various performances, such as material properties [85], structural behaviors, and multi-physics coupling, which traditionally require substantial time and research costs. This section focuses on data-driven machine learning and deep learning models used for performance prediction and the summary of the prediction model is shown in Table 1.

Table 1.
Data-driven performance prediction models.
3.2.1. Machine Learning Prediction Models
In material performance prediction, using machine learning models for numerically driven material performance forecasting has become an effective method in complex design domains. Pan et al. [86] utilized machine learning methods, such as random forest regression models, to develop models correlating small punch test (SPT) load displacement and uniaxial tensile test true stress-strain curves, as shown in Figure 9a. Hou et al. [90] employed machine learning models, including ridge regression, support vector machine regression, and gradient-boosting regression trees, for model integration to predict the ultimate tensile strength and the yield strength of magnesium alloys. The results, shown in Figure 9b, indicate that the integrated model’s predicted mechanical properties are very close to the experimental values. Li et al. [91] first developed a genetic algorithm-optimized BP neural network model to predict the transverse mechanical properties of unidirectional carbon-fiber-reinforced polymer composites with micropores, as illustrated in Figure 9c. This method demonstrated good consistency between the predicted results and the test dataset. Elizabeth et al. [87] used machine learning methods, such as decision trees and random forests, to predict the mechanical properties of multi-scale hybrid polymer nanocomposites. The results showed strong correlations, low prediction errors, and high model prediction accuracy.
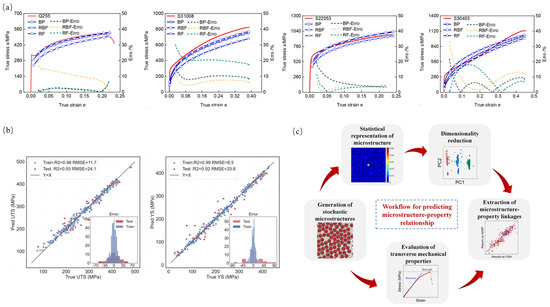
Figure 9.
Data-driven machine learning performance prediction models: (a) prediction of true stress-strain curves and errors using machine learning models [86]; (b) performance prediction of magnesium alloys using an integrated model [90]; (c) workflow for performance prediction of composite material microstructures [91].
In terms of structural performance prediction, Alok Warey et al. [113] combined high-fidelity computational fluid dynamic (CFD) simulations with machine learning algorithms to predict vehicle occupant thermal comfort. The trained machine learning model was tested on unseen CFD-generated data, with an error of less than 5%. Saboori et al. [92] developed a new computational method based on artificial neural networks (ANNs) for predicting flow behavior and thermal patterns at the microscale using the data of pore-scale porous media (PSPM) walls and high-fidelity numerical simulations. Fan et al. [89] used a secondary development of the ABAQUS plugin to generate datasets and built a gradient-boosted regression model to quickly predict local stresses at the nozzle junctions of pressure vessels, achieving an accuracy level greater than 0.999. Zhang et al. [88] proposed a method combining a finite element analysis (FEA) with a random forest model to accurately predict the mechanical properties of laminated composite plates, analyzing failure factors under random stress states, failure factors of open-hole laminates, and critical buckling eigenvalues based on Puck’s theory. Cui et al. [93] developed a method using fluid–structure interaction (FSI) simulations and ANN models to predict airflow fields. The ANN model was trained using extensive simulation and test datasets, significantly reducing the time and computational costs. Qu et al. [95] combined FSI theory with finite element methods to create a physics-guided database containing 1000 input combinations. They used a categorical feature-boosting model to establish a metamodel for predicting internal forces in tunnel linings and maximum surface deformation, effectively replacing FEA for performance predictions. Zhu et al. [94] developed a multi-physics model coupling biomass syngas with Ni particle coarsening in a solid oxide fuel cell (SOFC), generating sufficient training data for ANN models to predict the SOFC’s performance degradation due to Ni coarsening. The absolute relative error of the predicted decay rates and the average current density was 0.767% and 0.248%, respectively, demonstrating the reliability of the ANN predictions. Francesco et al. [96] used an ANN-based, multilayer perceptron model to simulate the deformation of carbon-fiber-reinforced polymer (CFRP) structures, predicting and compensating for thermodynamic behavior. The predicted tool-tip-point displacement matched the experimental results, with the residuals in the y-direction being smaller than 7.0 μm.
3.2.2. Deep Learning Prediction Models
Deep learning models, unlike traditional machine learning models, were developed based on neural networks and have the ability to automatically learn feature representations, significantly reducing the need for manual intervention. This makes deep learning models more adaptable and flexible in performance prediction for complex scenarios. Additionally, deep learning models typically contain a large number of parameters, allowing them to effectively utilize big data and fully leverage their performance advantages.
Wang et al. [100] used a deep neural network model to quickly and accurately predict the thermomechanical properties of liquid cooling on flat surfaces. As shown in Figure 10a, compared to the CFD results, the deep neural network model predicted the solid temperature and stress with an average absolute error of 0.5% and 0.08%. Ma et al. [97] employed a deep learning model based on an improved convolutional neural network (CNN) and loss function formation method to study the mixing characteristics of film cooling in rocket engines. The trained CNN model was embedded in both baseline and test cases of film cooling to predict the film cooling flow field, as shown in Figure 10b, with a global error of less than 5.5 × 10−3. Liu et al. [101] trained a deep neural network to create a surrogate model for predicting airfoil aerodynamic coefficients, providing results within one second. The optimized airfoil achieved a peak drag coefficient and moment coefficient reduction of 82.5% and 88.6%, respectively, compared to the baseline wing. Guo et al. [98] proposed a flexible and general approximation model based on convolutional neural networks for the real-time prediction of 2D or 3D non-uniform, steady laminar flows, achieving prediction speeds four orders of magnitude faster than CPU-based CFD solvers, with low error rates. Wu et al. [103] used conditional Wasserstein Gan-GP (CWGAN-GP), CNN, and multi-gate mixture-of-Experts-3D (MMoE-3D) models to learn designers’ expertise in shape modification and geometric optimization, proposing an innovative deep-generative-model-based optimization solution for missile aerodynamic shape optimization. Zhang et al. [104] developed a graphical U-net model to predict the quasi-static physical properties of generated designs using finite element analysis results, as shown in Figure 10c. In benchmark tests, the prediction error for nonlinear deformation behavior ranged from 8–20%, and the evaluation time was reduced from 200 s to less than 0.5 s.
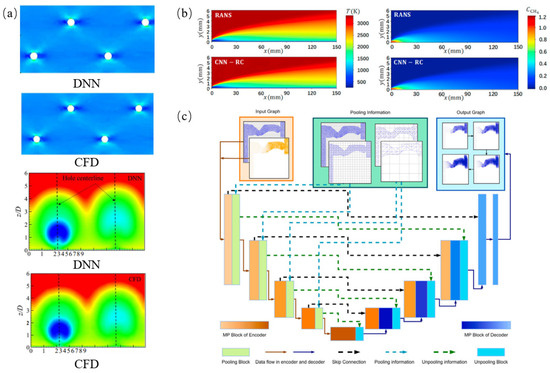
Figure 10.
Applications of data-driven fluid performance prediction: (a) prediction of thermal–mechanical performance of liquid cooling [100]; (b) prediction of rocket engine film cooling flow field [97]; (c) the proposed graph. U-net takes the input graph and the linear FEA result under a small strain to predict the following nonlinear response under a large strain [104].
Shao et al. [107] used finite element analysis software to obtain a large number of training cases and employed fully connected neural networks and long short-term memory (LSTM) neural networks as surrogate models. These models predicted the stress distribution and stress sequences during bullet impacts on different target materials. As shown in Figure 11a, the computational accuracies of these models were 92.19% and 92.41%, respectively, similar to the results from the finite element analysis. Ding et al. [102] established a multilayer deep neural network (DNN) regression model with backpropagation, based on the discrete element method (DEM) model, to predict the initial crack positions and related stresses in the defect layers of fiber-reinforced polymer (FRP) composites with rectangular and hexagonal fiber distributions. This is illustrated in Figure 11b. Li et al. [109] proposed a prediction model based on graph neural networks (GNNs), which used discrete representations of structures and iterative methods to accurately predict related field variables, such as displacement, strain, and stress. This is depicted in Figure 11c.
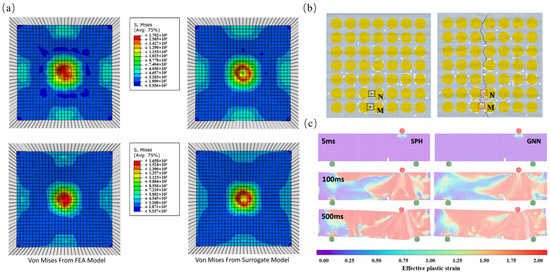
Figure 11.
Data-driven prediction of static physical properties: (a) U-net predicting nonlinear deformation behavior [107]; (b) DNN model predicting initial crack locations and stresses in composite defect layers [102]; (c) graph neural network predicting field variables [109].
Li et al. [110] proposed a real-time and accurate prediction method for three-dimensional flow–thermal–structural coupling fields based on a deep convolutional conditional generative adversarial network (DCCGAN) architecture, called the 3D field solution generative adversarial network (fsGAN). The experimental results indicate that this method is a promising tool for the real-time prediction of detailed coupling field parameters in hypersonic flight vehicles. Wang et al. [99] employed a CNN to predict fluid forces and used the finite element method (FEM) to solve solid structure responses. They established a new CNN-FEM framework and iterative scheme for solving fluid–structure interaction (FSI) problems to achieve a balance between fluid forces and structural forces, as shown in Figure 12a. The average equivalent stress prediction results of this method are close to those from commercial software, with an accuracy exceeding 92%, and the computational efficiency is 100 times that of commercial software. Zhou et al. [106] proposed a real-time hybrid simulation (RTHS) method for FSI under seismic loads, using LSTM neural networks to build models for the real-time computation of complex numerical substructures and data exchange for complex physical–numerical boundaries, exploring complex coupling effects between fluids and structures in deep-water environments.
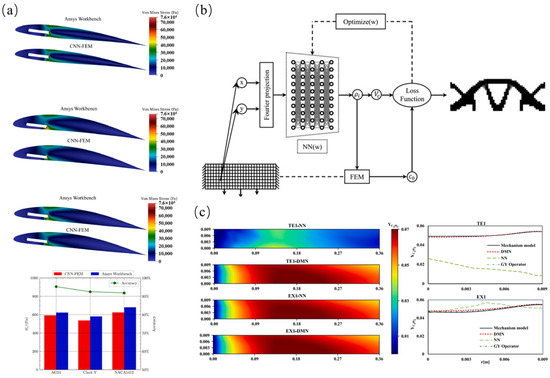
Figure 12.
Data-driven fluid–structure interaction performance prediction: (a) comparison of prediction results and simulation results using CNN-FEM framework [99]; (b) boundary smoothing in topology optimization based on neural networks [105]; (c) comparison of concentration field profiles predicted by different networks [112].
Mudhsh et al. [111] used a random vector functional link network model to model the thermal–hydraulic behavior of a helical plate heat exchanger (HPHE), accurately predicting the outlet temperatures of hot and cold fluids. Kou et al. [112] proposed a deep multi-field network (DMN) that trains a set of operator networks using a small amount of data generated by mechanism models and then combines it with a multi-hidden layer neural network (NN) to form an improved physics-informed neural network. Using the proposed DMN, multiple fields were accurately predicted under various particle distributions, and the optimal initial distribution was quickly identified, as shown in Figure 12c. Michal et al. [108] proposed a machine learning prediction method that combines sequence learning models (LSTM networks or gated recurrent units) with shallow neural networks. The good correlation between the experiments and the predictions indicates that the proposed machine learning-based damage model can reasonably predict the lifespan under complex thermal–mechanical loads. Shishir et al. [105] used a fully connected feedforward NN as an optimizer for thermal–mechanical coupling topology optimization by minimizing the network’s loss function, as shown in Figure 12b. The effectiveness of this method was validated through case studies.
3.3. Functional Prediction of Lattice Structures and Applications
Compared to traditional structures, lattice structures offer greater design freedom, and their functionality changes with different topologies. With the development of machine learning and deep learning technologies, researchers have discovered that AI has significant potential for tuning the performance of lattice structures. This section will introduce recent research applications where data-driven prediction methods have been used for functional design of lattice structures.
3.3.1. Mechanical Performance
For lattice structures’ mechanical performance, Mohammad et al. [114] utilized a physics-guided neural network (PGNN) to predict truss structures with customized anisotropic stiffness. They trained on an extensive dataset containing millions of cells to generate three-dimensional lattice metamaterials with target mechanical properties, achieving higher computational efficiency and prediction accuracy compared to traditional methods. Jia et al. [115] introduced a new data-driven approach for designing three-dimensional lattice structures with desired properties. They created a mechanical performance dataset using a combination of homogenization methods and finite element methods to train artificial neural networks, generating three-dimensional lattice unit structures with accurately predicted mechanical properties. Li et al. [116] proposed a new deep learning method, Balance-CGAN, which effectively designs TPMS structures meeting target performance standards, achieving a design error as low as 4.6%. Peng et al. [117] developed a 3D U-Net-based, three-dimensional CNN for the rapid homogenization of parallelepiped microstructures. This method is hundreds of times faster than numerical homogenization and can accurately predict local displacements and the microscopic mechanical properties of parallelepiped microstructures. Zhang et al. [118] used a deep neural network method based on smoothed Gabor spectra (SGS) to predict the basic mechanical properties of three-dimensional woven lattice structures, such as the in-plane compressive strength and the out-of-plane elastic modulus. The predictions achieved over 90% accuracy compared to the experimental data for most test sets. Paul et al. [119] introduced an effective graph model representation for lattice unit cell shells and used an improved crystal graph convolutional neural network (mCGCNN) to accurately describe the structure–property relationship for an entire new shell lattice topology family. Jain et al. [120] introduced LatticeGraphNet (LGN), which harnesses two GNNs (LGN-i for learning the reduced responses of the lattices in metamaterials and LGN-ii for learning the three-dimensional responses) for predicting the response of lattices and structures. This model can predict nonlinear behavior, such as buckling.
Data-driven methods for lattice mechanical performance prediction have also advanced reverse design research. Chan Soo Ha et al. [121] proposed a rapid reverse design process based on deep learning, using a generative machine learning strategy to simulate nearly all possible uniaxial compression stress-strain curves for lattice materials. Wu et al. [122] developed a new optimization framework using derivative-aware neural networks (DANN), creating a novel multi-scale topology optimization method for the additive manufacturing of lattices, as shown in Figure 13a. Brown et al. [123] applied deep reinforcement learning to mechanical metamaterial design, creating metamaterials based on designer-specified target stress-strain curves and minimizing or maximizing hysteresis in cyclic compression. Wang et al. [124] proposed a scalable multi-scale metamaterial data-driven design integration framework using the continuous and highly structured latent space of a Variational Autoencoder (VAE) model, as shown in Figure 13b. This framework organizes complex microstructures into a continuous, highly structured latent space for microstructure mapping and structural design. Wang et al. [125] introduced a new lattice-generation strategy with the aid of machine learning, designing gradient lattice structures. Their NN-based inverse lattice generator takes target mechanical properties as input and outputs lattice cells, as shown in Figure 13c. Zheng et al. [126] developed a deep learning-based, growth-type metamaterial reverse-design method. This approach, using conditional generative adversarial networks (CGANs), generates a batch of growth-type metamaterials with custom Poisson’s ratios and Young’s moduli without prior knowledge, as shown in Figure 13d.
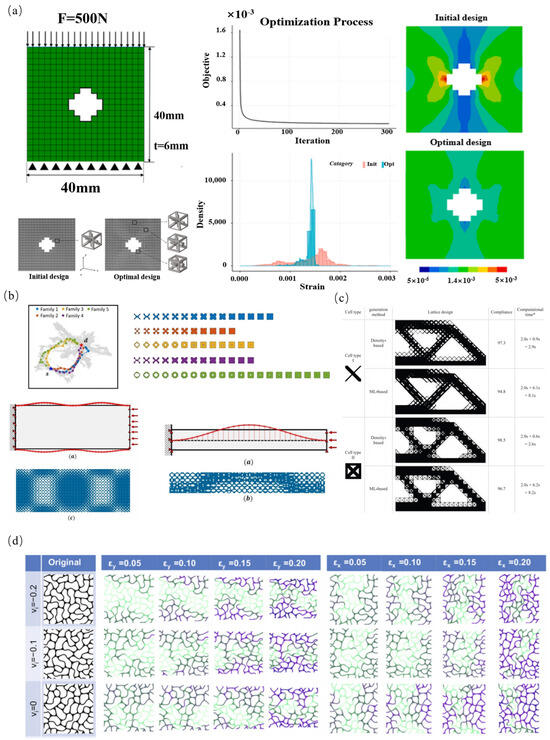
Figure 13.
Data-driven lattice structure mechanical performance prediction: (a) derivative-aware neural network for multi-scale topology optimization [122]; (b) multi-scale metamaterial data-driven design space and design cases, while star s and d represent the relevant parameters between the design source point and the design target point [124]; (c) neural network output of lattice cells based on target mechanical properties input [125], * Computational time = Low resolution topology optimization time + lattice mapping time; (d) growth-type metamaterials with customized Poisson’s ratios [126].
The data-driven lattice mechanical-performance-prediction methods enable designers to control lattice mechanical properties at the early design stages. This enhances design efficiency and reduces costs, with significant application prospects in aerospace and other fields. As shown in Figure 14, by designing lattice structures and controlling lattice mechanical properties, lightweight and functional integration can be achieved for critical components, such as nose cones [62], landing gear [127], engines [128] and rudder wing [129].

Figure 14.
Applications of lattices with different mechanical properties in aircraft: (a) lattice-filled nose cone [62]; (b) lattice-filled landing gear [130]; (c) lattice-filled engine cylinder [131]; (d) lattice-filled rudder wing [127].
3.3.2. Absorption Performance
Wu et al. [128] used a deep neural network method based on D2 distribution to predict lattice energy-absorption effects, as shown in Figure 15a. The results indicate that this method can effectively predict energy absorption with an error of approximately 13%. Isanaka et al. [129] proposed a design method for lattice structures that locally enhances them by identifying structural failure modes through machine learning. By improving the plasticity and reducing the Young’s modulus of the constitutive material for local enhancement, as shown in Figure 15b, the energy absorption of the lattice structure increased by 32.12%.
Yu et al. [132] used the backpropagation neural network (BPNN) algorithm to build a machine learning model that establishes the underlying mapping relationship between the thickness parameters of hyperbolic beam structures and their mechanical properties, resulting in optimal structural design parameters and a 57% improvement in energy absorption performance. Chan Soo Ha et al. [121] achieved customizable mechanical behavior by reverse designing non-uniform lattice structures composed of design parameters from different locations. The designed lattice structure exhibited excellent energy absorption performance. Eren et al. [133] used a deep learning-based 3D generative adversarial network (3DGAN) model to generate lattice configurations with better energy-absorption performance. Compared to the original configuration, energy absorption increased by 57%, with the configurations and energy absorption data shown in Figure 15c.
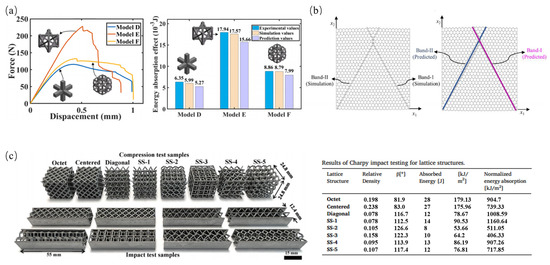
Figure 15.
Data-driven prediction of lattice structures’ energy-absorption performances: (a) deep neural networks for predicting lattice energy-absorption performance [128]; (b) machine learning for identifying structural failure regions and enhancing lattice structures’ energy-absorption performances [129]; (c) 3D generative adversarial networks for generating models and impact energy absorption [133].
The lattice structure energy-absorption performance-prediction methods enable the design of lattice structures with varying energy-absorption properties. Currently, as shown in Figure 16, energy-absorbing lattices are applied in various fields, including spacecraft re-entry capsules [134], landing gear for space vehicles [135], rocket skins [136], automotive engine hoods [137], and landing buffer structures [138]. By designing energy-absorbing lattice structures, components achieve better impact resistance and vibration reduction effects.

Figure 16.
Applications of lattice structures’ energy-absorption performance: (a) lattice-filled landing gear to improve impact absorption [135]; (b) lattice-filled rocket skin to absorb vibrations [136]; (c) lattice-filled automotive engine hoods to absorb impacts [137]; (d) landing buffer structure for the return capsule with lattice structure [138].
3.3.3. Acoustic Performance
To predict the acoustic performance of lattice structures, Chatterjee et al. [139] quantified the influence of random parameters in acoustic metamaterials on hyperdamping using machine learning. The study showed that hyperdamping allows the structure to dissipate energy more quickly, increasing the total dissipation and attenuation rate by approximately five times. Jain et al. [140] proposed a machine learning-based, multi-band metamaterial absorber for terahertz applications, significantly reducing simulation time while ensuring accuracy, cutting resource costs by 70% compared to the original absorber. Shendy et al. [141] presented a parallel, feedforward, multilayer, artificial neural network using a double-walled hexagonal lattice, where sinusoidal periodic perturbations were applied to the lattice walls to increase the number and width of bandgaps, enhancing the bandgap characteristics. The results demonstrated that the proposed neural network could predict bandgap characteristics with an average accuracy of over 80%.
Liu et al. [142] trained deep backpropagation neural networks and radial basis function neural networks to predict the dispersion relations of one-dimensional acoustic metamaterials. The results indicated that both types of neural networks performed well and could accurately predict the band structure of unit cells. Li et al. [143] trained an autoencoder to extract the topological features from sample images, and a finite element analysis was employed to study the band gaps of samples. The trained models were ultimately employed to design phononic crystals with anticipated band gaps, as shown in Figure 17. Liu et al. [144] reviewed machine learning models for phononic metamaterials, introducing mainstream machine learning models applied to acoustic metamaterials, discussing their capabilities and limitations, and exploring potential directions for future research. Figure 18 illustrates different types of acoustic lattice structures, showing that the efficient design of various acoustic lattice structures can be achieved through performance-prediction methods.
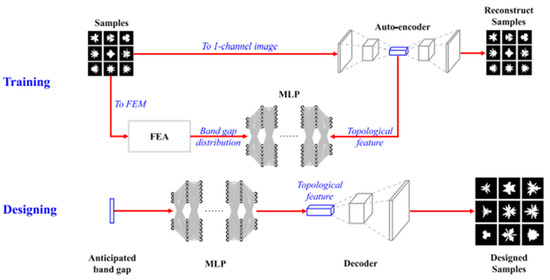
Figure 17.
The workflow of designing phononic crystals with anticipated band gaps based on data-driven neural network [143].
Figure 18.
Types of acoustic lattice structures: (a) acoustic black hole vibration-isolation lattice structure [145]; (b) coupling-inspired vibration-isolation lattice structure [146]; (c) body-centered cubic vibration-isolation lattice structure [147]; (d) cylindrical shell vibration-isolation lattice structure [148].
3.3.4. Thermal Performance
To predict the thermal performance of lattice structures, Asuka et al. [149] proposed a NN-based performance-prediction surrogate model using the area, hydraulic diameter, and effective flow channel structure as input parameters. This model can accurately and quickly predict the heat transfer characteristics and the pressure loss of fluids under different lattice structures, as shown in Figure 19a. Shen et al. [150] proposed using an artificial neural network trained with a Bayesian regularization algorithm to predict the thermal behavior and heat transfer characteristics of phase change materials (PCMs) with three lattice structures during melting and solidification processes, as shown in Figure 19b. The prediction achieved a minimum mean square error of 0.00003601 and a maximum correlation coefficient of 0.9998. Aksoy et al. [151] used an ensemble artificial neural network algorithm to predict the thermal performance of lightweight lattice structure heat sinks, with the structural diagram and ensemble model prediction regression shown in Figure 19c, achieving an accuracy of 99.8%. Huang et al. [152] proposed an interpretable deep learning method with feedback for predicting the thermal conductivity of porous structures. The prediction results demonstrated high accuracy, and the error distribution followed a normal distribution, indicating the model’s high stability.
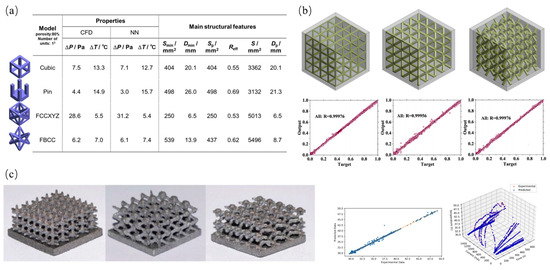
Figure 19.
Data-driven prediction of thermal performance of lattice structures: (a) neural network prediction of fluid heat transfer characteristics and pressure loss in lattice structures [149]; (b) artificial neural network prediction of thermal behavior and heat transfer characteristics of lattice phase change materials [150]; (c) heat dissipation lattice structure and prediction regression diagram [151].
Figure 20 shows lattice structures with different thermal performance characteristics, demonstrating that performance-prediction methods can quickly identify lattice structures with thermal properties that meet the design requirements within the design domain.

Figure 20.
Lattice structures with different thermal performances: (a) Tetrahedral lattice heat sink [153]. (b) Kagome lattice heat sink [154]. (c) Hexagonal lattice heat sink [155]. (d) Tetrahedral lattice heat sink [156].
4. Challenges, Limitations, and Prospects
4.1. Costs of Additive Manufacturing and AI
Although data-driven AI can quickly predict and design lattice structure performance for use in the aerospace industry, its cost factors, including additive manufacturing costs and AI computing costs, significantly constrain its widespread application. For the production process, the cost of the powder or silk required for additive manufacturing is higher than that of traditional materials, and the manufacturing process limits the types of materials. Due to defects in additive manufacturing processes, post-processing is essential, which also increases manufacturing costs.
Regarding the cost of AI, both hardware and software need to be considered. When dealing with a large-scale dataset and complex AI models, the performance of the hardware, such as the GPU, CPU, and RAM, must meet certain conditions. To ensure accuracy, integrating data-driven AI predictions with practical application scenarios also requires a significant amount of prior work. Designers need to evaluate costs before using this technology to ensure economic benefits.
4.2. Quality of AI Dataset
For AI, especially in relation to data-driven prediction, a high-quality dataset is crucial. Although the cases mentioned in Section 3.3 have demonstrated the ability of data-driven AI to predict and design lattice structure functionality, models established for predicting different functionalities often rely on specific datasets established by designers. A large-scale and diverse dataset is pivotal in enabling a predictive model to possess generalization capabilities and achieve high accuracy. To ensure the authenticity of the predicted results, the errors between simulation experiments and physical experiments should also be taken into account when establishing the dataset.
4.3. Performance of AI Models
A suitable AI model is beneficial for the accuracy, robustness, and interpretability of prediction results. Unlike popular applications of AI, such as text, audio, images, and other one-dimensional and two-dimensional problems, the performance prediction of lattice structures is a highly complex, three-dimensional, nonlinear mapping problem. The accuracy of data-driven AI is considerable, but due to its spatial complexity, it still lacks interpretability, and its low robustness is also a current research issue. This means that high accuracy can be achieved for predicting specific lattice structures, but it is difficult to generalize to any lattice structure for use, which limits its application in the aerospace. Identifying how to improve the interpretability of models is one of the current research focuses.
4.4. Modeling of Heterogeneous Lattice Structure
The current research on lattice structures mainly focuses on predicting and designing the properties of regular hexahedral cell structures, while the actual structures for engineering purposes, like wings, cabins, and jet tailpipes, are often composed of a mixture of heterogeneous lattice cells filled with conformal lattice cells and incomplete cells. As mentioned in Section 3.1, many theoretical models and methods have been established for the performance analysis of regular hexahedral lattice structures, such as the beam element method and the homogenization method. For heterogeneous lattices with more complex spatial structures, these theories actually need to be updated and expanded accordingly, which has led to challenges in calculating the performance of heterogeneous lattice structures in current research. Obtaining accurate heterogeneous lattice properties is a prerequisite for constructing a performance-prediction dataset for conformal lattice structures.
4.5. Reverse Design Based on Lattice Structure Manufacturing Errors
For lattice structures, additive manufacturing processes greatly enhance their manufacturability, enabling them to achieve the functionality required by designers. In recent years, powder bed fusion (PBF), fused deposition modeling (FDM), and directed energy deposition (DED) technologies have become the main manufacturing technologies for lattice structure manufacturing [33,42]. There are still many problems in the manufacturing process, such as material limitations, molding size limitations, low surface roughness, low accuracy, and the presence of molding defects, which have led to significant deviations between the predicted and actual performance of lattice structures. At present, researchers have used machine learning methods to predict process errors in lattice structures and improve the product quality by adjusting the process parameters [19,157]. However, achieving the real-time monitoring of manufacturing defects, interpreting the analyses of error causes, and reverse designing lattice structures and processes remain challenges in current research.
5. Conclusions
Lattice structures are an effective means of achieving extreme lightweighting, high performance, and the multifunctional integration of key functional components in the aerospace field. In this paper, lattice structures based on supports, triply periodic minimal surface structures, and shell lattice structures are introduced, the additive manufacturing processes of lattice structures are presented, and the unique superior performance of lattice structures and their related applications in aerospace field are discussed. Additionally, the development of performance-prediction methods for lattice structures over the past few decades is explored, including beam element theory analysis methods and homogenization theory analysis methods. A detailed introduction to the recently emerging, AI-based, data-driven methods is provided. Firstly, different data-driven AI models and their respective application scenarios are reviewed. Then, the application of data-driven methods in predicting the various functionalities of lattice structures is discussed. Finally, the challenges, limitations, and prospects in current research on data-driven lattice structure performance prediction are discussed. This article aims to reveal the significance of data-driven AI methods in predicting lattice structure performance and proposes the application prospects of the methods in aerospace and other fields.
Author Contributions
Conceptualization, N.D. and S.Y.; methodology, N.D. and S.Y.; software, S.Y. and Q.C.; validation, N.D. and S.Y.; formal analysis, S.Y.; investigation, S.Y. and Q.C.; resources, N.D. and S.Y.; data curation, S.Y. and Q.C.; writing—original draft preparation, S.Y.; writing—review and editing, N.D. and S.Y.; visualization, S.Y.; supervision, N.D.; project administration, N.D.; funding acquisition, N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Key Research and Development Program [grant numbers 2023YFB4603901, 2023YFB4603900]; the National Natural Science Foundation of China [grant number 52275255]; and the Natural Science Foundation of Jiangsu Province [grant number BK20220896].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cramer, N.B.; Kim, J.; Gregg, C.; Cheung, K.C.; Swei, S.S.-M. Modeling of tunable elastic ultralight aircraft. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. AIAA 2019-3159. [Google Scholar]
- Wang, R.; Shang, J.; Li, X.; Luo, Z.; Wu, W. Vibration and damping characteristics of 3D printed mKagome lattice with viscoelastic material filling. Sci. Rep. 2018, 8, 9604. [Google Scholar]
- Zhang, Y.; Yan, Z.; Shen, M.; Jiang, Q.; Wang, W.; Sang, Y.; Hao, B. Study on the thermal control performance of lightweight minimal surface lattice structures for aerospace applications. Appl. Therm. Eng. 2025, 261, 125110. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, X.; Guo, C.; Dai, N. Toughness-improving design of lattice sandwich structures. Mater. Des. 2023, 226, 111600. [Google Scholar] [CrossRef]
- Jia, M.; Dai, N.; Wang, T.; Cao, Q.; Yan, L.; Dai, H. A compact quasi-zero stiffness metamaterial for energy absorption and impact protection. Thin-Walled Struct. 2024, 205, 112360. [Google Scholar] [CrossRef]
- Oliveri, G.; Overvelde, J.T. Inverse design of mechanical metamaterials that undergo buckling. Adv. Funct. Mater. 2020, 30, 1909033. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Challapalli, A.; Patel, D.; Li, G. Inverse machine learning framework for optimizing lightweight metamaterials. Mater. Des. 2021, 208, 109937. [Google Scholar] [CrossRef]
- Mohanavel, V.; Ali, K.A.; Prasath, S.; Sathish, T.; Ravichandran, M. Microstructural and tribological characteristics of AA6351/Si3N4 composites manufactured by stir casting. J. Mater. Res. Technol. 2020, 9, 14662–14672. [Google Scholar] [CrossRef]
- Zargham, S.; Ward, T.A.; Ramli, R.; Badruddin, I.A. Topology optimization: A review for structural designs under vibration problems. Struct. Multidiscipl. Optim. 2016, 53, 1157–1177. [Google Scholar] [CrossRef]
- Pattnaik, P.; Sharma, A.; Choudhary, M.; Singh, V.; Agarwal, P.; Kukshal, V. Role of machine learning in the field of Fiber reinforced polymer composites: A preliminary discussion. Mater. Today Proc. 2021, 44, 4703–4708. [Google Scholar] [CrossRef]
- Sigmund, O.; Maute, K. Topology optimization approaches. Struct. Multidiscip. Optim. 2013, 48, 1031–1055. [Google Scholar] [CrossRef]
- Wang, Z.-L.; Adachi, Y. Property prediction and properties-to-microstructure inverse analysis of steels by a machine-learning approach. Mater. Sci. Eng. A 2019, 744, 661–670. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Y.; Zhang, L.; Gao, R.; Wu, D. Deep learning for smart manufacturing: Methods and applications. Int. J. Ind. Manuf. Syst. Eng. 2018, 48, 144–156. [Google Scholar] [CrossRef]
- Hu, E.; Seetoh, I.P.; Lai, C.Q. Machine learning assisted investigation of defect influence on the mechanical properties of additively manufactured architected materials. Int. J. Mech. Sci. 2022, 221, 107190. [Google Scholar] [CrossRef]
- Bird, G.D.; Gorrell, S.E.; Salmon, J.L. Dimensionality-reduction-based surrogate models for real-time design space exploration of a jet engine compressor blade. Aerosp. Sci. Technol. 2021, 118, 107077. [Google Scholar] [CrossRef]
- Zhu, Z.; Ning, W.; Niu, X.; Wang, Q.; Shi, R.; Zhao, Y. Designing high elastic modulus magnesium-based composite materials via machine learning approach. Mater. Today Commun. 2023, 37, 107249. [Google Scholar] [CrossRef]
- Wang, C.; Tan, X.P.; Tor, S.B.; Lim, C.S. Machine learning in additive manufacturing: State-of-the-art and perspectives. Addit. Manuf. 2020, 36, 101538. [Google Scholar] [CrossRef]
- Khan, N.; Asad, H.; Khan, S.; Riccio, A. Towards defect-free lattice structures in additive manufacturing: A holistic review of machine learning advancements. J. Manuf. Process. 2025, 144, 1–53. [Google Scholar] [CrossRef]
- Korkmaz, M.E.; Gupta, M.K.; Robak, G.; Moj, K.; Krolczyk, G.M.; Kuntoğlu, M. Development of lattice structure with selective laser melting process: A state of the art on properties, future trends and challenges. J. Manuf. Process. 2022, 81, 1040–1063. [Google Scholar] [CrossRef]
- McGregor, M.; Patel, S.; McLachlin, S.; Vlasea, M. Architectural bone parameters and the relationship to titanium lattice design for powder bed fusion additive manufacturing. Addit. Manuf. 2021, 47, 102273. [Google Scholar] [CrossRef]
- Yuan, Y.; Zhang, Y.; Ruan, D.; Zhang, A.; Liang, Y.; Tan, P.J.; Chen, P. Deformation and failure of additively manufactured Voronoi foams under dynamic compressive loadings. Eng. Struct. 2023, 284, 115954. [Google Scholar] [CrossRef]
- Nazir, A.; Abate, K.M.; Kumar, A.; Jeng, J.-Y. A state-of-the-art review on types, design, optimization, and additive manufacturing of cellular structures. Int. J. Adv. Manuf. Technol. 2019, 104, 3489–3510. [Google Scholar] [CrossRef]
- Liu, Y.J.; Wang, H.L.; Li, S.J.; Wang, S.G.; Wang, W.J.; Hou, W.T.; Hao, Y.L.; Yang, R.; Zhang, L.C. Compressive and fatigue behavior of beta-type titanium porous structures fabricated by electron beam melting. Acta Mater. 2017, 126, 58–66. [Google Scholar] [CrossRef]
- Liu, Y.J.; Li, S.J.; Wang, H.L.; Hou, W.T.; Hao, Y.L.; Yang, R.; Sercombe, T.B.; Zhang, L.C. Microstructure, defects and mechanical behavior of beta-type titanium porous structures manufactured by electron beam melting and selective laser melting. Acta Mater. 2016, 113, 56–67. [Google Scholar] [CrossRef]
- Rueger, Z.; Ha, C.S.; Lakes, R.S. Flexible Cube Tilt Lattice with Anisotropic Cosserat Effects and Negative Poisson’s Ratio. Phys. Status Solidi (B) Basic Res. 2019, 256, 1800512. [Google Scholar] [CrossRef]
- Großmann, A.; Gosmann, J.; Mittelstedt, C. Lightweight lattice structures in selective laser melting: Design, fabrication and mechanical properties. Mater. Sci. Eng. A 2019, 766, 138356. [Google Scholar] [CrossRef]
- Boccarusso, L.; Durante, M.; Langella, A. Lightweight hemp/bio-epoxy grid structure manufactured by a new continuous process. Compos. Part B Eng. 2018, 146, 165–175. [Google Scholar] [CrossRef]
- Liang, S.-X.; Wang, X.; Zhang, W.; Liu, Y.-J.; Wang, W.; Zhang, L.-C. Selective laser melting manufactured porous Fe-based metallic glass matrix composite with remarkable catalytic activity and reusability. Appl. Mater. Today 2020, 19, 100543. [Google Scholar] [CrossRef]
- Parra-Cabrera, C.; Achille, C.; Kuhn, S.; Ameloot, R. 3D printing in chemical engineering and catalytic technology: Structured catalysts, mixers and reactors. Chem. Soc. Rev. 2018, 47, 209–230. [Google Scholar] [CrossRef]
- Ni, X.; Li, M.; Weiner, M.; Alù, A.; Khanikaev, A.B. Demonstration of a quantized acoustic octupole topological insulator. Nat. Commun. 2020, 11, 2108. [Google Scholar] [CrossRef]
- Iandiorio, C.; Mattei, G.; Marotta, E.; Costanza, G.; Tata, M.E.; Salvini, P. The Beneficial Effect of a TPMS-Based Fillet Shape on the Mechanical Strength of Metal Cubic Lattice Structures. Materials 2024, 17, 1553. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.-Y.; Liang, S.-X.; Liu, Y.; Zhang, L.-C. Additive manufacturing of metallic lattice structures: Unconstrained design, accurate fabrication, fascinated performances, and challenges. Mater. Sci. Eng. R 2021, 146, 100648. [Google Scholar] [CrossRef]
- Syam, W.P.; Jianwei, W.; Zhao, B.; Maskery, I.; Elmadih, W.; Leach, R. Design and analysis of strut-based lattice structures for vibration isolation. Precis. Eng. 2018, 52, 494–506. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Leary, M.; Mazur, M.; Williams, H.; Yang, E.; Alghamdi, A.; Lozanovski, B.; Zhang, X.; Shidid, D.; Sternahl, L.; Witt, G.; et al. Inconel 625 lattice structures manufactured by selective laser melting (SLM): Mechanical properties, deformation and failure modes. Mater. Des. 2018, 157, 179–199. [Google Scholar] [CrossRef]
- Maskery, I.; Sturm, L.; Aremu, A.O.; Panesar, A.; Williams, C.B.; Tuck, C.J.; Wildman, R.D.; Ashcroft, I.A.; Hague, R.J.M. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer 2018, 152, 62–71. [Google Scholar] [CrossRef]
- Berger, J.B.; Wadley, H.N.G.; McMeeking, R.M. Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness. Nature 2017, 543, 533–537. [Google Scholar] [CrossRef]
- Tancogne-Dejean, T.; Diamantopoulou, M.; Gorji, M.; Bonatti, C.; Mohr, D. 3D Plate-Lattices: An Emerging Class of Low-Density Metamaterial Exhibiting Optimal Isotropic Stiffness. Adv. Mater. 2018, 30, 1803334. [Google Scholar] [CrossRef]
- Friedrich, M.; Kružík, M. Derivation of von Kármán Plate Theory in the Framework of Three-Dimensional Viscoelasticity. Arch. Ration. Mech. Anal. 2020, 238, 489–540. [Google Scholar] [CrossRef]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Dallago, M.; Raghavendra, S.; Luchin, V.; Zappini, G.; Pasini, D.; Benedetti, M. The role of node fillet, unit-cell size and strut orientation on the fatigue strength of Ti-6Al-4V lattice materials additively manufactured via laser powder bed fusion. Int. J. Fatigue 2021, 142, 105946. [Google Scholar] [CrossRef]
- Zhao, M.; Liu, F.; Fu, G.; Zhang, D.; Zhang, T.; Zhou, H. Improved Mechanical Properties and Energy Absorption of BCC Lattice Structures with Triply Periodic Minimal Surfaces Fabricated by SLM. Materials 2018, 11, 2411. [Google Scholar] [CrossRef] [PubMed]
- Harris, J.A.; Winter, R.E.; McShane, G.J. Impact response of additively manufactured metallic hybrid lattice materials. Int. J. Impact Eng. 2017, 104, 177–191. [Google Scholar] [CrossRef]
- Wen, Z.; Sha, Y.; Yu, T.X. Crushing resistance and energy absorption of pomelo peel inspired hierarchical honeycomb. Int. J. Impact Eng. 2019, 125, 163–172. [Google Scholar]
- Plessis, A.D.; Broeckhoven, C.; Yadroitsev, I.; Yadroitsava, I.; Roux, S.G. Analyzing nature’s protective design: The glyptodont body armor. J. Mech. Behav. Biomed. Mater. 2018, 82, 218–223. [Google Scholar] [CrossRef]
- Weiner, M.; Ni, X.; Li, M.; Alù, A.; Khanikaev, A.B. Demonstration of a third-order hierarchy of topological states in a three-dimensional acoustic metamaterial. Sci. Adv. 2020, 6, 4166. [Google Scholar] [CrossRef]
- Sun, X.; Jiang, F.; Wang, J. Acoustic properties of 316l stainless steel lattice structures fabricated via selective laser melting. Metals 2020, 10, 111. [Google Scholar] [CrossRef]
- Ji, J.C.; Luo, Q.; Ye, K. Vibration control based metamaterials and origami structures: A state-of-the-art review. Mech. Syst. Signal Process. 2021, 161, 107945. [Google Scholar] [CrossRef]
- Spadoni, A.; Ruzzene, M. Structural and acoustic behavior of chiral truss-core beams. World Acad. Sci. Eng. Technol. 2006, 128, 616–626. [Google Scholar] [CrossRef]
- Bai, X.; Zheng, Z.; Nakayama, A. Heat transfer performance analysis on lattice core sandwich panel structures. Int. J. Heat Mass Transf. 2019, 143, 118525. [Google Scholar] [CrossRef]
- Do, G.; Geißelbrecht, M.; Schwieger, W.; Freund, H. Additive manufacturing of interpenetrating periodic open cellular structures (interPOCS) with in operando adjustable flow characteristics. Chem. Eng. Process. Process Intensif. 2020, 148, 107786. [Google Scholar] [CrossRef]
- Sélo, R.R.J.; Catchpole-Smith, S.; Maskery, I.; Ashcroft, I.; Tuck, C. On the thermal conductivity of AlSi10Mg and lattice structures made by laser powder bed fusion. Addit. Manuf. 2020, 34, 101214. [Google Scholar] [CrossRef]
- Ho, J.Y.; Leong, K.C.; Wong, T.N. Additively-manufactured metallic porous lattice heat exchangers for air-side heat transfer enhancement. Int. J. Heat Mass Transf. 2020, 150, 119262. [Google Scholar] [CrossRef]
- Garner, E.; Kolken, H.M.A.; Wang, C.C.L.; Zadpoor, A.A.; Wu, J. Compatibility in microstructural optimization for additive manufacturing. Addit. Manuf. 2019, 26, 65–75. [Google Scholar] [CrossRef]
- Feng, J.; Liu, B.; Lin, Z.; Fu, J. Isotropic octet-truss lattice structure design and anisotropy control strategies for implant application. Mater. Des. 2021, 203, 109595. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, W.; Zhu, L.; Meng, F.; Liu, J.; Wen, G. Review on lattice structures for energy absorption properties. Compos. Struct. 2023, 304, 116397. [Google Scholar] [CrossRef]
- NTop. Next-Gen Engineering Design Software: nTop. Available online: https://www.ntop.com/resources/blog/introducing-ntop-4/ (accessed on 14 April 2023).
- Li, D.; Liao, W.; Dai, N.; Dong, G.; Tang, Y.; Xie, Y.M. Optimal design and modeling of gyroid-based functionally graded cellular structures for additive manufacturing. Comput.-Aided Des. 2018, 104, 87–99. [Google Scholar] [CrossRef]
- Cheng, L.; Bai, J.; To, A.C. Functionally graded lattice structure topology optimization for the design of additive manufactured components with stress constraints. Comput. Methods Appl. Mech. Eng. 2019, 344, 334–359. [Google Scholar] [CrossRef]
- Turner, D.; Howie, R.; Bland, P. The Development of a Next-Generation Latticed Resistojet Thruster for CubeSats. Aerospace 2024, 11, 714. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, H.; Li, S.; Zhu, J.; Zhou, L. Material-structure integrated design for high-performance aerospace thin-walled component. Acta Aeronaut. Astronaut. Sin. 2023, 44, 627428. [Google Scholar]
- Ashby, M.F.; Gibson, L.J. Cellular Solids: Structure and Properties; Press Syndicate of the University of Cambridge: Cambridge, UK, 1997. [Google Scholar]
- Iandiorio, C.; Milani, D.; Salvini, P. Optimal Uniform Strength Design of Frame and Lattice Structures. Comput. Struct. 2024, 301, 107430. [Google Scholar] [CrossRef]
- Sai, G.; Ning, D.; Xiaosheng, C.; Ren, L.; Zhang, W. Prediction of mechanical properties of lattice based on multi-resolution beam element model. Mach. Des. Manuf. Eng. 2020, 51, 52–58. [Google Scholar]
- Bensousson, A.; Lions, J.-L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; AMS CHELSEA PUBLISHING: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Rao, C.; Liu, Y. Three-dimensional convolutional neural network (3D-CNN) for heterogeneous material homogenization. Comput. Mater. Sci. 2020, 184, 109850. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Kikuchi, N. Generating optimal topologies in structural design using a homogenization method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Weeger, O. Numerical homogenization of second gradient, linear elastic constitutive models for cubic 3D beam-lattice metamaterials. Int. J. Solids Struct. 2021, 224, 111037. [Google Scholar] [CrossRef]
- Li, H.; Ge, L.; Liu, B.; Su, H.; Feng, T.; Fang, D. An equivalent model for sandwich panel with double-directional trapezoidal corrugated core. J. Sandw. Struct. Mater. 2020, 22, 2445–2465. [Google Scholar] [CrossRef]
- Huang, L.; Yuan, H.; Zhao, H. An FEM-based homogenization method for orthogonal lattice metamaterials within micropolar elasticity. Int. J. Mech. Sci. 2023, 238, 107836. [Google Scholar] [CrossRef]
- Li, D.; Liao, W.; Dai, N.; Xie, Y.M. Anisotropic design and optimization of conformal gradient lattice structures. Comput.-Aided Des. 2020, 119, 102787. [Google Scholar] [CrossRef]
- Muhammad; Kennedy, J.; Lim, C.W. Machine learning and deep learning in phononic crystals and metamaterials—A review. Mater. Today Commun. 2022, 33, 104606. [Google Scholar] [CrossRef]
- Sanchez-Palencia, E. Non-Homogeneous Media and Vibration Theory; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Timoshenko, S. History of Strength of Materials; McGraw-Hill: New York, NY, USA, 1953. [Google Scholar]
- Florence, C.; Sab, K. A rigorous homogenization method for the determination of the overall ultimate strength of periodic discrete media and an application to general hexagonal lattices of beams. Eur. J. Mech. A/Solids 2006, 25, 72–97. [Google Scholar] [CrossRef]
- Timoshenko, S.P. LXVI. On the correction for shear of the differential equation for transverse vibrations of prismatic bars. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1921, 41, 744–746. [Google Scholar] [CrossRef]
- Berry, D.T.; Yang, T.Y.; Skelton, R.E. Dynamics and control of lattice beams using simplified finite element models. J. Guid. 1985, 8, 5. [Google Scholar] [CrossRef]
- Luxner, M.H.; Stampfl, J.; Pettermann, H.E. Finite element modeling concepts and linear analyses of 3D regular open cell structures. Mech. Behav. Cell. Solids 2005, 40, 5859–5866. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Miller, G. The cognitive revolution: A historical perspective. Trends Cogn. Sci. 2003, 7, 141–144. [Google Scholar] [CrossRef]
- Crevier, D. AI: The Tumultuous Search for Artificial Intelligence; BasicBooks: New York, NY, USA, 1993. [Google Scholar]
- Christian, B. The Alignment Problem: Machine Learning and Human Values; W. W. Norton & Company: New York, NY, USA, 2020. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Okafor, C.E.; Iweriolor, S.; Ani, O.I.; Ahmad, S.; Mehfuz, S.; Ekwueme, G.O.; Chukwumuanya, O.E.; Abonyi, S.E.; Ekengwu, I.E.; Chikelu, O.P. Advances in machine learning-aided design of reinforced polymer composite and hybrid material systems. Hybrid Adv. 2023, 2, 100026. [Google Scholar] [CrossRef]
- Pan, H.; Peng, J.; Geng, X.; Gao, M.; Miao, X. Prediction of mechanical properties for typical pressure vessel steels by small punch test combined with machine learning. Int. J. Press. Vessel. Pip. 2023, 206, 105060. [Google Scholar] [CrossRef]
- Champa-Bujaico, E.; Díez-Pascual, A.M.; Redondo, A.L.; Garcia-Diaz, P. Optimization of mechanical properties of multiscale hybrid polymer nanocomposites: A combination of experimental and machine learning techniques. Compos. Part B 2024, 269, 111099. [Google Scholar] [CrossRef]
- Zhang, C.; Li, Y.; Jiang, B.; Wang, R.; Liu, Y.; Jia, L. Mechanical properties prediction of composite laminate with FEA and machine learning coupled method. Compos. Struct. 2022, 299, 116086. [Google Scholar] [CrossRef]
- Fan, H.; Hu, L. Pressure vessel nozzle local stress prediction software based on ABAQUS machine learning. SoftwareX 2023, 24, 101550. [Google Scholar] [CrossRef]
- Hou, H.; Wang, J.; Ye, L.; Zhu, S.; Wang, L.; Guan, S. Prediction of mechanical properties of biomedical magnesium alloys based on ensemble machine learning. Mater. Lett. 2023, 348, 134605. [Google Scholar] [CrossRef]
- Li, M.; Zhang, H.; Li, S.; Zhu, W.; Ke, Y. Machine learning and materials informatics approaches for predicting transverse mechanical properties of unidirectional CFRP composites with microvoids. Mater. Des. 2022, 224, 111340. [Google Scholar] [CrossRef]
- Saboori, T.; Zhao, L.; Mesgarpour, M.; Wongwises, S.; Mahian, O. A novel macro-scale machine learning prediction based on high-fidelity CFD simulations: A case study on the pore-scale porous Trombe wall with phase change material capsulation. J. Build. Eng. 2022, 54, 104505. [Google Scholar] [CrossRef]
- Cui, H.; Wang, C.; Liu, X.; Liu, X.; Yuan, J.; Liu, Y. Prediction of the distribution of airflow within the cotton canopy using fluidestructure interaction simulation and machine-learning methods. Biosyst. Eng. 2023, 232, 51–66. [Google Scholar] [CrossRef]
- Zhu, P.; Wu, Z.; Wang, H.; Yan, H.; Li, B.; Yang, F.; Zhang, Z. Ni coarsening and performance attenuation prediction of biomass syngas fueled SOFC by combining multi-physics field modeling and artificial neural network. Appl. Energy 2022, 322, 119508. [Google Scholar] [CrossRef]
- Qu, P.; Zhang, L.; Zhu, Q.; Wu, M. Probabilistic reliability assessment of twin tunnels considering fluid–solid coupling with physics-guided machine learning. Reliab. Eng. Syst. Saf. 2023, 231, 109028. [Google Scholar] [CrossRef]
- Aggogeri, F.; Merlo, A.; Pellegrini, N. Modeling the thermo-mechanical deformations of machine tool structures in CFRP material adopting data-driven prediction schemes. Mechatronics 2020, 71, 102436. [Google Scholar] [CrossRef]
- Ma, H.; Zhang, Y.-X.; Haidn, O.J.; Thuerey, N.; Hu, X.-Y. Supervised learning mixing characteristics of film cooling in a rocket combustor using convolutional neural networks. Acta Astronaut. 2020, 175, 11–18. [Google Scholar] [CrossRef]
- Guo, X.; Li, W.; Iorio, F. Convolutional neural networks for steady flow approximation. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 481–490. [Google Scholar]
- Wang, L.; Xu, J.; Wang, Z.; Zhang, B.; Luo, Z.; Yuan, J.; Tan, A.C.C. A novel cost-efficient deep learning framework for static fluid–structure interaction analysis of hydrofoil in tidal turbine morphing blade. Renew. Energy 2023, 208, 367–384. [Google Scholar] [CrossRef]
- Wang, C.; Liu, Y.; Zhang, J. Prediction of thermo-mechanical performance for effusion cooling by machine learning method. Int. J. Heat Mass Transf. 2023, 207, 123969. [Google Scholar] [CrossRef]
- Liu, J.; Chen, R.; Lou, J.; Hu, Y.; You, Y. Deep-learning-based aerodynamic shape optimization of rotor airfoils to suppress dynamic stall. Aerosp. Sci. Technol. 2023, 133, 108089. [Google Scholar] [CrossRef]
- Ding, X.; Gu, Z.; Hou, X.; Xia, M.; Ismail, Y.; Ye, J. Effects of defects on the transverse mechanical response of unidirectional fibre-reinforced polymers: DEM simulation and deep learning prediction. Compos. Struct. 2023, 321, 117301. [Google Scholar] [CrossRef]
- Wu, P.; Yuan, W.; Ji, L.; Zhou, L.; Zhou, Z.; Feng, W.; Guo, Y. Missile aerodynamic shape optimization design using deep neural networks. Aerosp. Sci. Technol. 2022, 126, 107640. [Google Scholar] [CrossRef]
- Zhang, C.; Ridard, A.; Kibsey, M.; Zhao, Y.F. Variant design generation and machine learning aided deformation prediction for auxetic metamaterials. Mech. Mater. 2023, 181, 104642. [Google Scholar] [CrossRef]
- Shishir, M.I.R.; Tabarraei, A. Multi–materials topology optimization using deep neural network for coupled thermo–mechanical problems. Comput. Struct. 2024, 291, 107218. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, D.; Zhang, Y.; Li, N.; Gao, S.; Yue, Y. Real-time hybrid simulation incorporating machine learning for deep-water bridges subjected to seismic ground motion with fluid-structure dynamic interaction. Soil Dyn. Earthq. Eng. 2023, 175, 108263. [Google Scholar] [CrossRef]
- Shao, M.; Chen, J.; Wang, T. Accelerating Analysis for Structure Design via Deep Learning Surrogate Models. Adv. Intell. Syst. 2023, 5, 2200099. [Google Scholar] [CrossRef]
- Bartošák, M. Using machine learning to predict lifetime under isothermal low-cycle fatigue and thermo-mechanical fatigue loading. Int. J. Fatigue 2022, 163, 107067. [Google Scholar] [CrossRef]
- Li, Q.; Wang, Z.; Li, L.; Hao, H.; Chen, W.; Shao, Y. Machine learning prediction of structural dynamic responses using graph neural networks. Comput. Struct. 2023, 289, 107188. [Google Scholar] [CrossRef]
- Li, N.; Liu, Y.; Gong, G.; Zhao, L.; Yuan, H. A generative deep learning approach for real-time prediction of hypersonic vehicles in fluid-thermo-structural coupling fields. Aerosp. Sci. Technol. 2023, 139, 108398. [Google Scholar] [CrossRef]
- Mudhsh, M.; El-Said, E.M.S.; Aseeri, A.O.; Almodfer, R.; Elaziz, M.A.; Elshamy, S.M.; Elsheikh, A.H. Modelling of thermo-hydraulic behavior of a helical heat exchanger using machine learning model and fire hawk optimizer. Case Stud. Therm. Eng. 2023, 49, 103294. [Google Scholar] [CrossRef]
- Kou, C.; Jia, S.; Yuan, X.; Luo, Y. Deep multi-field network for physical and concentration field prediction of TDM reactor under different carbon particle distributions. Chem. Eng. Sci. 2023, 280, 118944. [Google Scholar] [CrossRef]
- Warey, A.; Kaushik, S.; Khalighi, B.; Cruse, M.; Venkatesan, G. Data-driven prediction of vehicle cabin thermal comfort: Using machine learning and high-fidelity simulation results. Int. J. Heat Mass Transf. 2020, 148, 119083. [Google Scholar] [CrossRef]
- Abu-Mualla, M.; Huang, J. Inverse design of 3D cellular materials with physics-guided machine learning. Mater. Des. 2023, 232, 112103. [Google Scholar] [CrossRef]
- Jia, Z.; Gong, H.; Liu, S.; Zhang, J.; Zhang, Q. Designing three-dimensional lattice structures with anticipated properties through a deep learning method. Mater. Des. 2024, 244, 113139. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Tian, J.; Ning, K.; Li, K.; Xia, S.; Zhou, L.; Lu, Y. Performance-based inverse structural design of complex gradient triply periodic minimal surface structures based on a deep learning approach. Mater. Today Commun. 2024, 40, 109424. [Google Scholar] [CrossRef]
- Peng, H.; Liu, A.; Huang, J.; Cao, L.; Liu, J.; Lu, L. PH-Net: Parallelepiped microstructure homogenization via 3D Convolutional Neural Networks. Addit. Manuf. 2022, 60, 103237. [Google Scholar]
- Zhang, C.; Wang, B.; Zhu, H.; Fan, H. Structure genome based machine learning method for woven lattice structures. Int. J. Mech. Sci. 2023, 245, 108134. [Google Scholar] [CrossRef]
- Meyer, P.P.; Bonatti, C.; Tancogne-Dejean, T.; Mohr, D. Graph-based metamaterials: Deep learning of structure-property relations. Mater. Des. 2022, 223, 111175. [Google Scholar] [CrossRef]
- Jain, A.; Haghighat, E.; Nelaturi, S. LatticeGraphNet: A two-scale graph neural operator for simulating lattice structures. Eng. Comput. 2024. [Google Scholar] [CrossRef]
- Ha, C.S.; Yao, D.; Xu, Z.; Liu, C.; Liu, H.; Elkins, D.; Kile, M.; Deshpande, V.; Kong, Z.; Bauchy, M.; et al. Rapid inverse design of metamaterials based on prescribed mechanical behavior through machine learning. Nat. Commun. 2023, 14, 5765. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Luo, J.; Zhong, J.; Xu, Y.; Wan, B.; Huang, W.; Fang, J.; Steven, G.P.; Sun, G.; Li, Q. Topology optimization for design and additive manufacturing of functionally graded lattice structures using derivative-aware machine learning algorithms. Addit. Manuf. 2023, 78, 103833. [Google Scholar]
- Brown, N.K.; Deshpande, A.; Garland, A.; Pradeep, S.A.; Fadel, G.; Pilla, S.; Li, G. Deep reinforcement learning for the design of mechanical metamaterials with tunable deformation and hysteretic characteristics. Mater. Des. 2023, 235, 112428. [Google Scholar] [CrossRef]
- Wang, L.; Chan, Y.-C.; Ahmed, F.; Liu, Z.; Zhu, P.; Chen, W. Deep generative modeling for mechanistic-based learning and design of metamaterial systems. Comput. Method Appl. Mech. Eng. 2020, 372, 113377. [Google Scholar] [CrossRef]
- Wang, J.; Panesar, A. Machine learning based lattice generation method derived from topology optimization. Addit. Manuf. 2022, 60, 103238. [Google Scholar]
- Zheng, X.; Chen, T.-T.; Guo, X.; Samitsu, S.; Watannabe, I. Controllable inverse design of auxetic metamaterials using deep learning. Mater. Des. 2021, 211, 110178. [Google Scholar] [CrossRef]
- Wang, C.; Zhu, J.; Wu, M.; Hou, J.; Zhou, H.; Meng, L.; Li, C. Multi-scale design and optimization for solid-lattice hybrid structures and their application to aerospace vehicle components. Chin. J. Aeronaut. 2021, 34, 386–398. [Google Scholar] [CrossRef]
- Wu, Y.; Mao, Z.; Feng, Y. Energy absorption prediction for lattice structure based on D2 shape distribution and machine learning. Compos. Struct. 2023, 319, 117136. [Google Scholar] [CrossRef]
- Isanaka, B.R.; Mukhopadhyay, T.; Varma, R.K.; Kushvaha, V. On exploiting machine learning for failure pattern driven strength enhancement of honeycomb lattices. Acta Mater. 2022, 239, 118226. [Google Scholar] [CrossRef]
- Tae-Wook, K. KARI Optimizes and Converts 3D Lattice Design with DfAM Process and Materialise 3-Matic. Available online: https://www.materialise.com/en/inspiration/cases/kari-3d-modeling-lattice-design-metal-3d-printing (accessed on 14 April 2023).
- Cobra Aero Reduced Air-Cooled Cylinder Weight by 50% with nTop. Available online: https://www.ntop.com/resources/case-studies/cobra-aero-multiphysics-simulation-drone-engine/ (accessed on 14 April 2023).
- Yu, J.; Shi, X.; Feng, Y.; Chang, J.; Liu, J.; Xi, H.; Huang, S.; Zhang, W. Machine learning-based design and optimization of double curved beams for multi-stable honeycomb structures. Extrem. Mech. Lett. 2023, 65, 102109. [Google Scholar] [CrossRef]
- Eren, O.; Yüksel, N.; Borklü, H.R.; Sezer, H.K.; Canyurt, O.E. Deep learning-enabled design for tailored mechanical properties of SLM-manufactured metallic lattice structures. Eng. Appl. Artif. Intell. 2024, 130, 107685. [Google Scholar] [CrossRef]
- Wang, G.; Ma, S.; Wang, C.; Ma, B.; Zeng, F. Design and Optimization of Lattice Infilled Landing Impact Absorbing Structure for a Reentry Capsule. IET Conf. Proc. 2022, 2022, 1427–1431. [Google Scholar] [CrossRef]
- TeamIndus Moonshot. Structural Evolution of the TeamIndus Spacecraft That Will Land on the Moon. Available online: https://medium.com/teamindus/structural-evolution-of-the-teamindus-spacecraft-that-will-land-on-the-moon-b5aa6bc73ccc (accessed on 15 December 2017).
- Eureka. 3D-Printed Lattice Structure Absorbs Vibrations and Provides Support. Available online: https://www.eurekamagazine.co.uk/content/news/3d-printed-lattice-structure-absorbs-vibrations-and-provides-support/ (accessed on 1 August 2016).
- Yin, S.; Chen, H.; Wu, Y.; Li, Y.; Xu, J. Introducing composite lattice core sandwich structure as an alternative proposal for engine hood. Compos. Struct. 2018, 201, 131–140. [Google Scholar] [CrossRef]
- Parva, M. Thermal Protection System. Available online: http://svarka-24.info/3d-pechat-teper-i-v-svarke/ (accessed on 5 July 2020).
- Chatterjee, T.; Bera, K.K.; Banerjee, A. Machine learning enabled quantification of stochastic active metadamping in acoustic metamaterials. J. Sound Vib. 2023, 567, 117938. [Google Scholar] [CrossRef]
- Jain, P.; Chhabra, H.; Chauhan, U.; Singh, D.K.; Anwer, T.M.K.; Ahammad, S.H.; Hossain, M.A.; Rashed, A.N.Z. Multiband Metamaterial absorber with absorption prediction by assisted machine learning. Mater. Chem. Phys. 2023, 307, 128180. [Google Scholar] [CrossRef]
- Shendy, M.; Alkhader, M.; Abu-Nabah, B.A.; Jaradat, M.A.; Venkatesh, T.A. Machine learning assisted approach to design lattice materials with prescribed band gap characteristics. Eur. J. Mech./A Solids 2023, 102, 105125. [Google Scholar] [CrossRef]
- Liu, C.; Yu, G. Predicting the Dispersion Relations of One-Dimensional Phononic Crystals by Neural Networks. Sci. Rep. 2019, 9, 15322. [Google Scholar] [CrossRef]
- Li, X.; Ning, S.; Liu, Z.; Yan, Z.; Luo, C.; Zhuang, Z. Designing phononic crystal with anticipated band gap through a deep learning based data-driven method. Comput. Methods Appl. Mech. Eng. 2020, 361, 112737. [Google Scholar] [CrossRef]
- Liu, C.; Yu, G.; Liu, Z. Machine learning models in phononic metamaterials. Curr. Opin. Solid State Mater. Sci. 2024, 28, 101133. [Google Scholar] [CrossRef]
- Sheng, H.; He, M.-X.; Zhao, J.; Kam, C.T.; Ding, Q.; Lee, H.P. The ABH-based lattice structure for load bearing and vibration suppression. Int. J. Mech. Sci. 2023, 252, 108378. [Google Scholar] [CrossRef]
- Pham, D.-B.; Huang, S.-C. A novel bio-inspired lattice metamaterial for energy absorption and vibration mitigation. J. Mech. Sci. Technol. 2024, 38, 2725–2739. [Google Scholar] [CrossRef]
- An, X.; Lai, C.; He, W.; Fan, H. Three-dimensional meta-truss lattice composite structures with vibration isolation performance. Extrem. Mech. Lett. 2019, 33, 100577. [Google Scholar] [CrossRef]
- An, X.; Yuan, X.; Sun, G.; Hou, X.; Fan, H. Design of lattice cylindrical shell meta-structures for broadband vibration reduction and high load-bearing capacity. Thin-Walled Struct. 2024, 197, 111647. [Google Scholar] [CrossRef]
- Suzuki, A.; Nakatani, H.; Kobashi, M. Machine learning surrogate modeling toward the design of lattice-structured heat sinks fabricated by additive manufacturing. Mater. Des. 2023, 230, 111969. [Google Scholar] [CrossRef]
- Shen, S. Numerical simulation and ANN prediction of phase change material embedded within 3D printing lattice structures. Case Stud. Therm. Eng. 2024, 53, 103818. [Google Scholar] [CrossRef]
- Aksoy, B.; Salman, O.K.M.; Özsoy, K. The estimation of the thermal performance of heat sinks manufactured by direct metal laser sintering based on machine learning. Measurement 2023, 225, 113625. [Google Scholar] [CrossRef]
- Huang, Q.; Hong, D.; Niu, B.; Long, D.; Zhang, Y. An interpretable deep learning strategy for effective thermal conductivity prediction of porous materials. Int. J. Heat Mass Transf. 2024, 221, 125064. [Google Scholar] [CrossRef]
- Wang, N.; Kaur, I.; Singh, P.; Li, L. Prediction of effective thermal conductivity of porous lattice structures and validation with additively manufactured metal foams. Appl. Therm. Eng. 2021, 187, 116558. [Google Scholar] [CrossRef]
- Jiayu, L.; Wenyang, Z.; Wei, L.; BingQing, C. Laser Additive Manufacturing and Heat Transfer Performance Measurement of Lattice Structure Heat Exchanger. Chin. J. Lasers 2023, 50, 4. [Google Scholar]
- Ferrari, L.; Barbato, M.; Esser, B.; Petkov, I.; Kuhn, M.; Gianella, S.; Barcena, J.; Jimenez, C.; Francesconi, D.; Liedtke, V.; et al. Sandwich structured ceramic matrix composites with periodic cellular ceramic cores: An active cooled thermal protection for space vehicles. Compos. Struct. 2016, 154, 61–68. [Google Scholar] [CrossRef]
- Son, K.N.; Weibel, J.A.; Kumaresan, V.; Garimella, S.V. Design of multifunctional lattice-frame materials for compact heat exchangers. Int. J. Heat Mass Transf. 2017, 115, 619–629. [Google Scholar] [CrossRef]
- Reddy, B.V.S.; Shaik, A.M.; Sastry, C.C.; Krishnaiah, J.; Patil, S.; Nikhare, C.P. Performance evaluation of machine learning techniques in surface roughness prediction for 3D printed micro-lattice structures. J. Manuf. Process. 2025, 137, 320–341. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).