Experimental Study on the Icing of Rotating Intake Cones in Wind Tunnels Under Supercooled Large-Droplet Conditions
Abstract
1. Introduction
2. Experimental Equipment
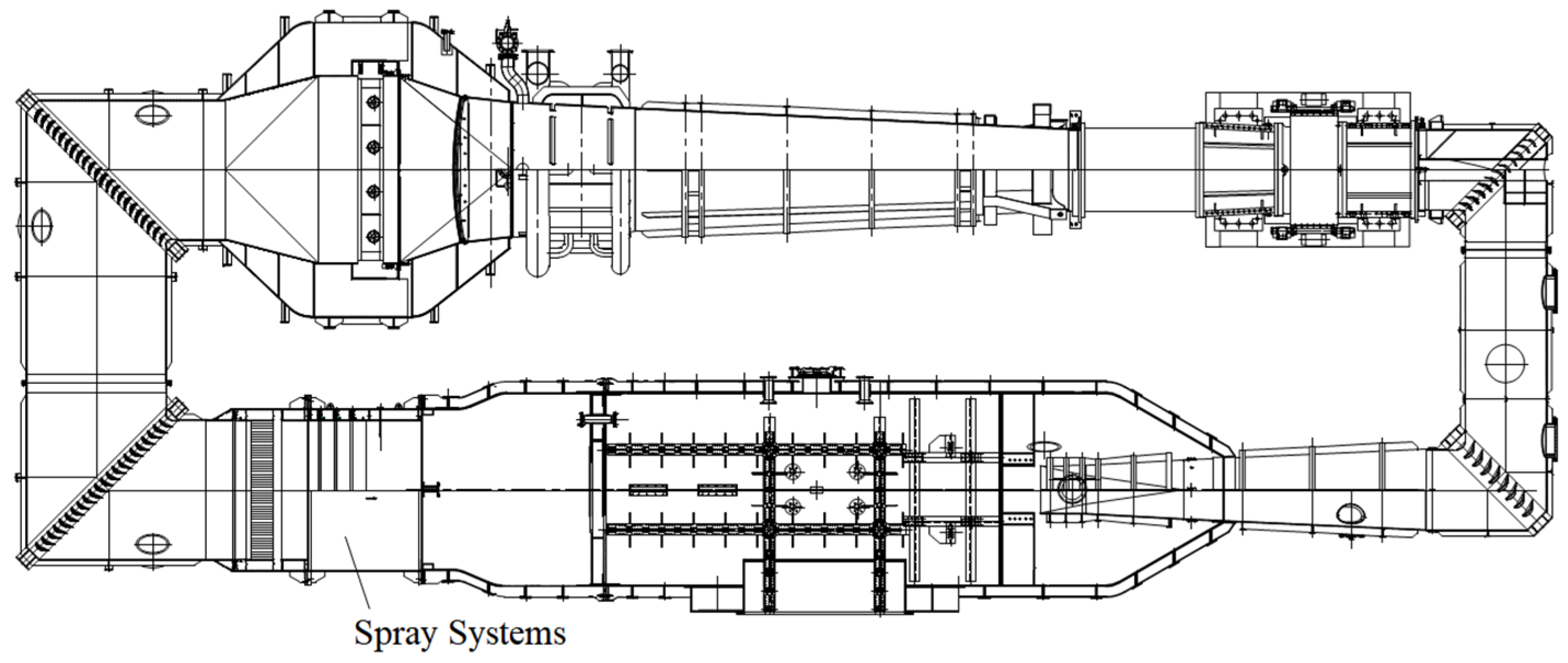
2.1. Icing Wind Tunnel
2.2. Experimental Model
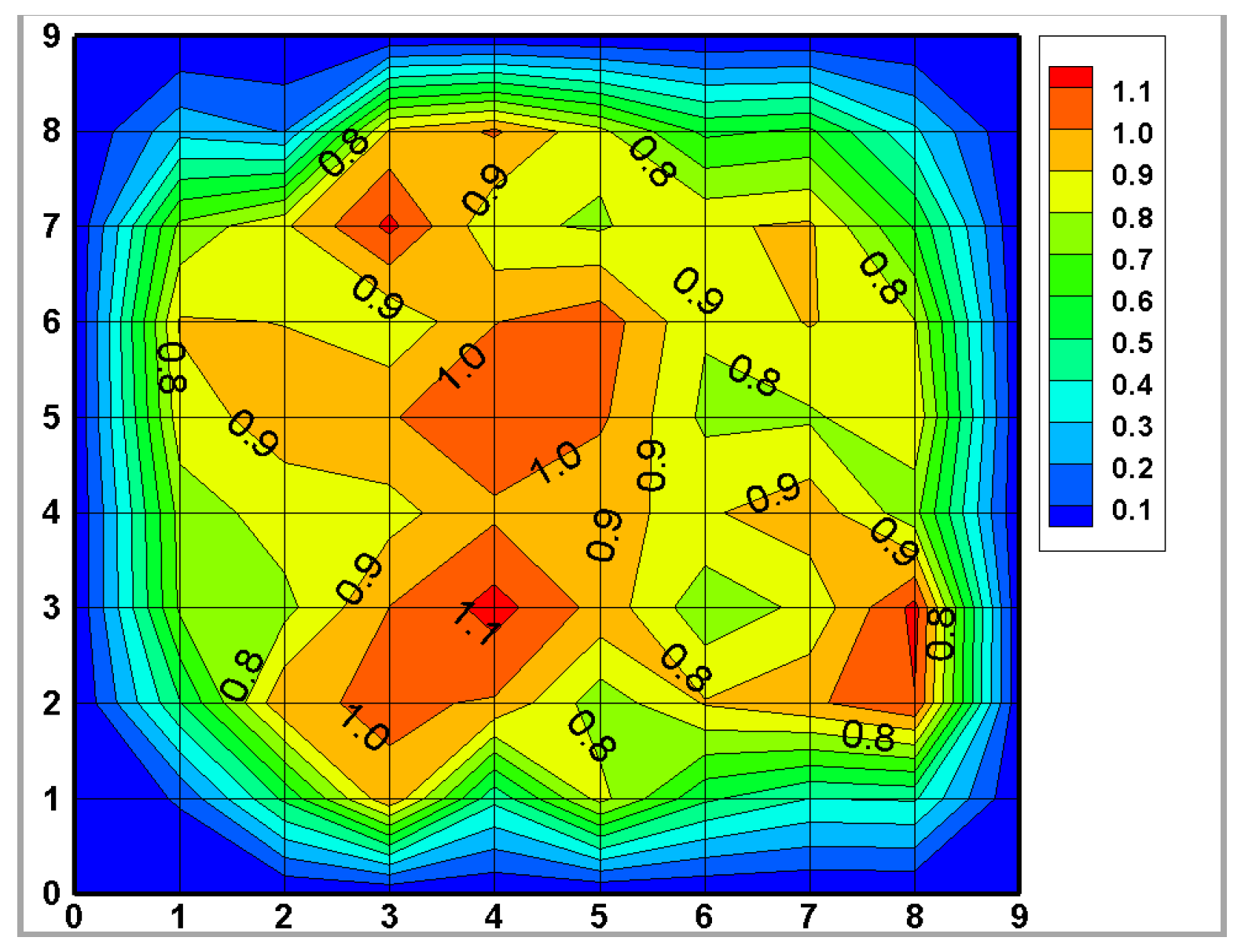
2.3. Experimental Methods
3. Experimental Results and Discussion
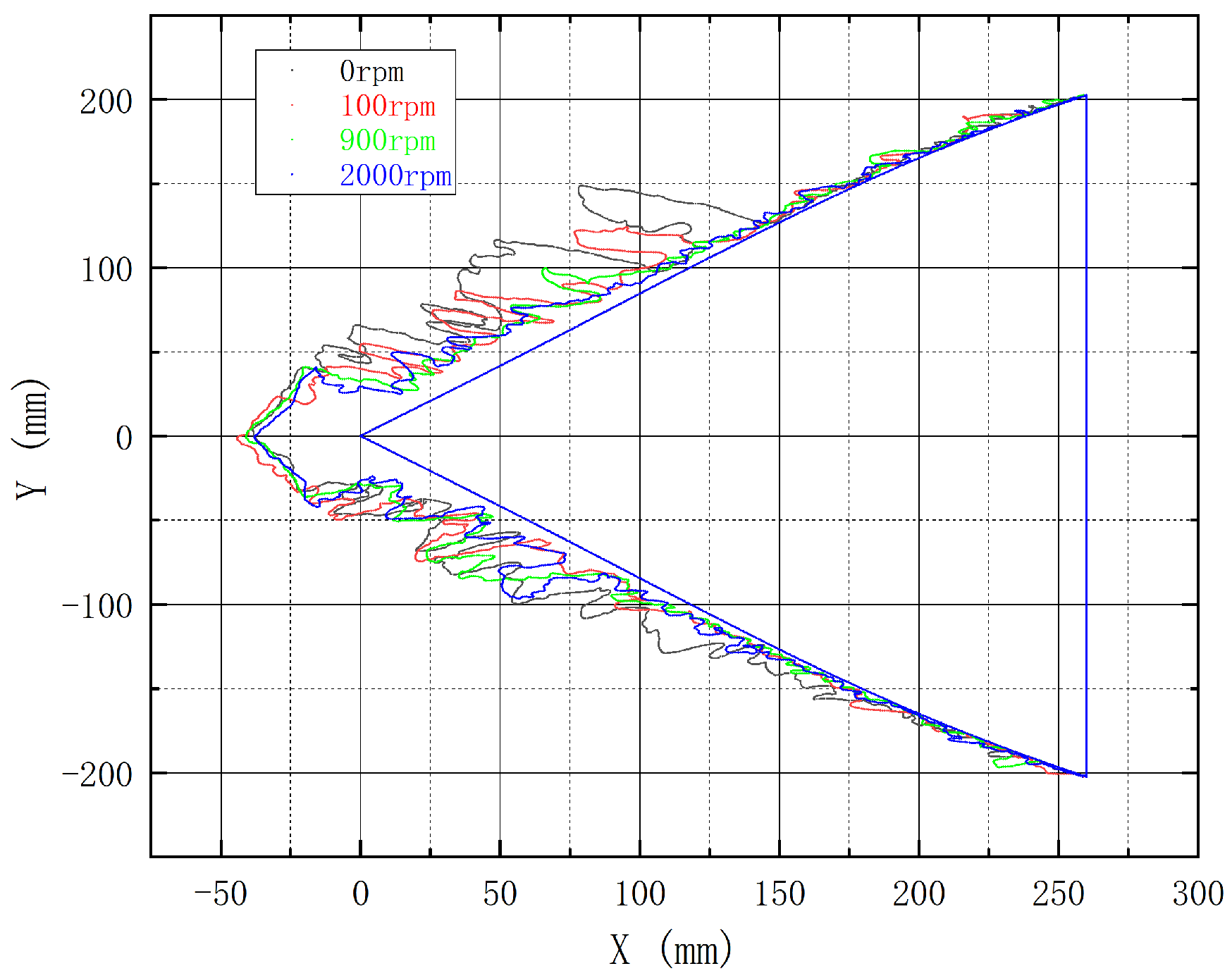
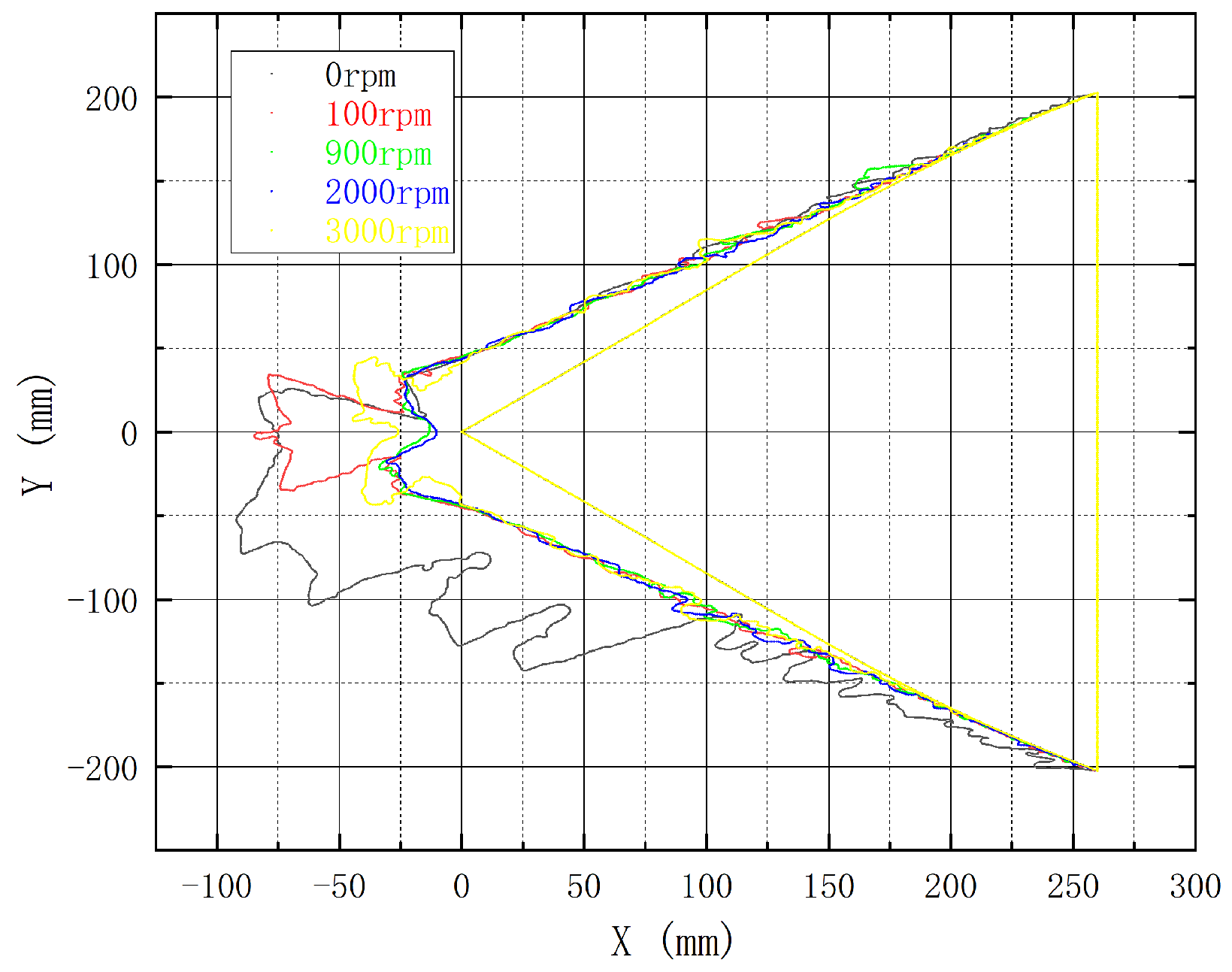
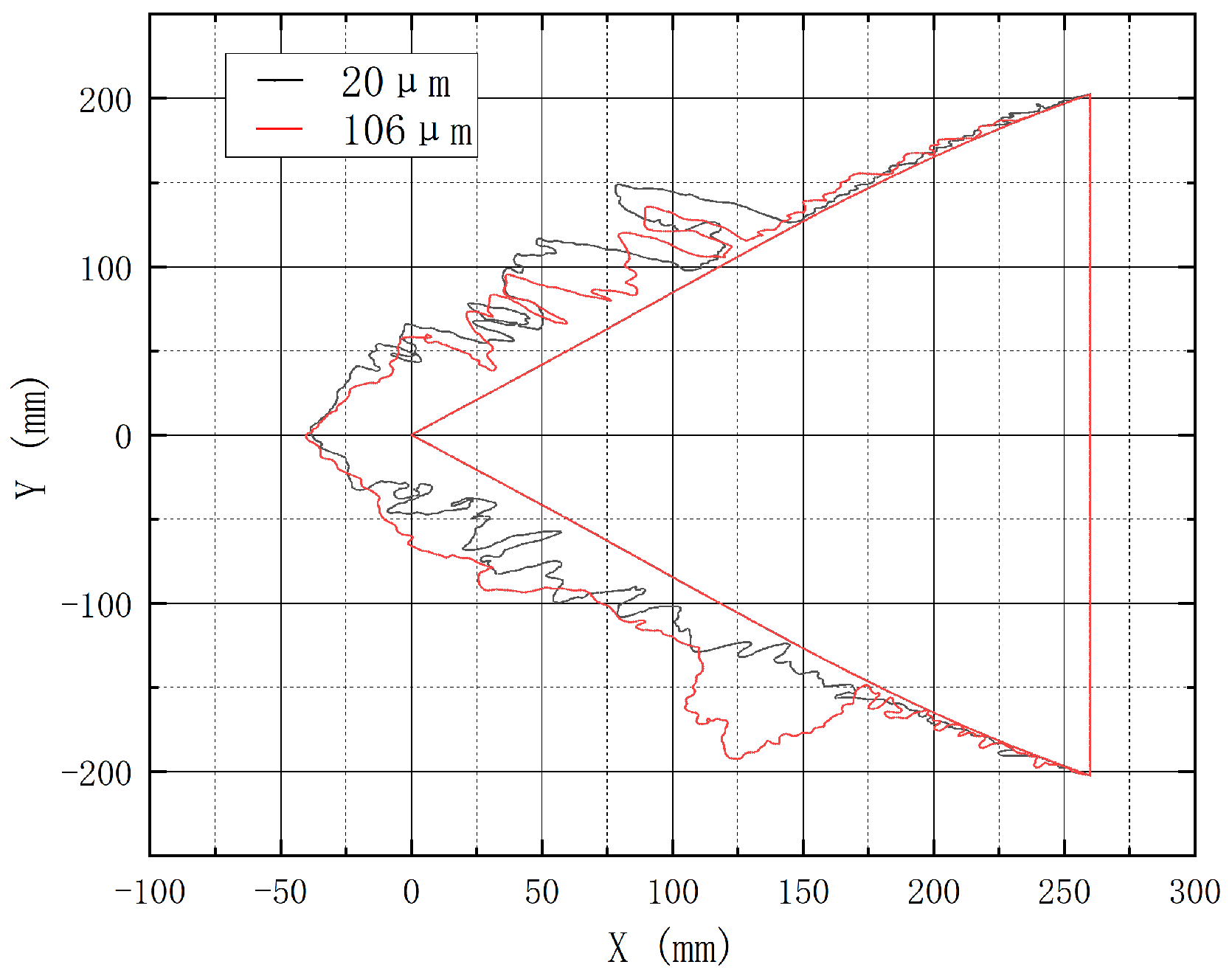
3.1. Influence of Rotational Speed on Icing
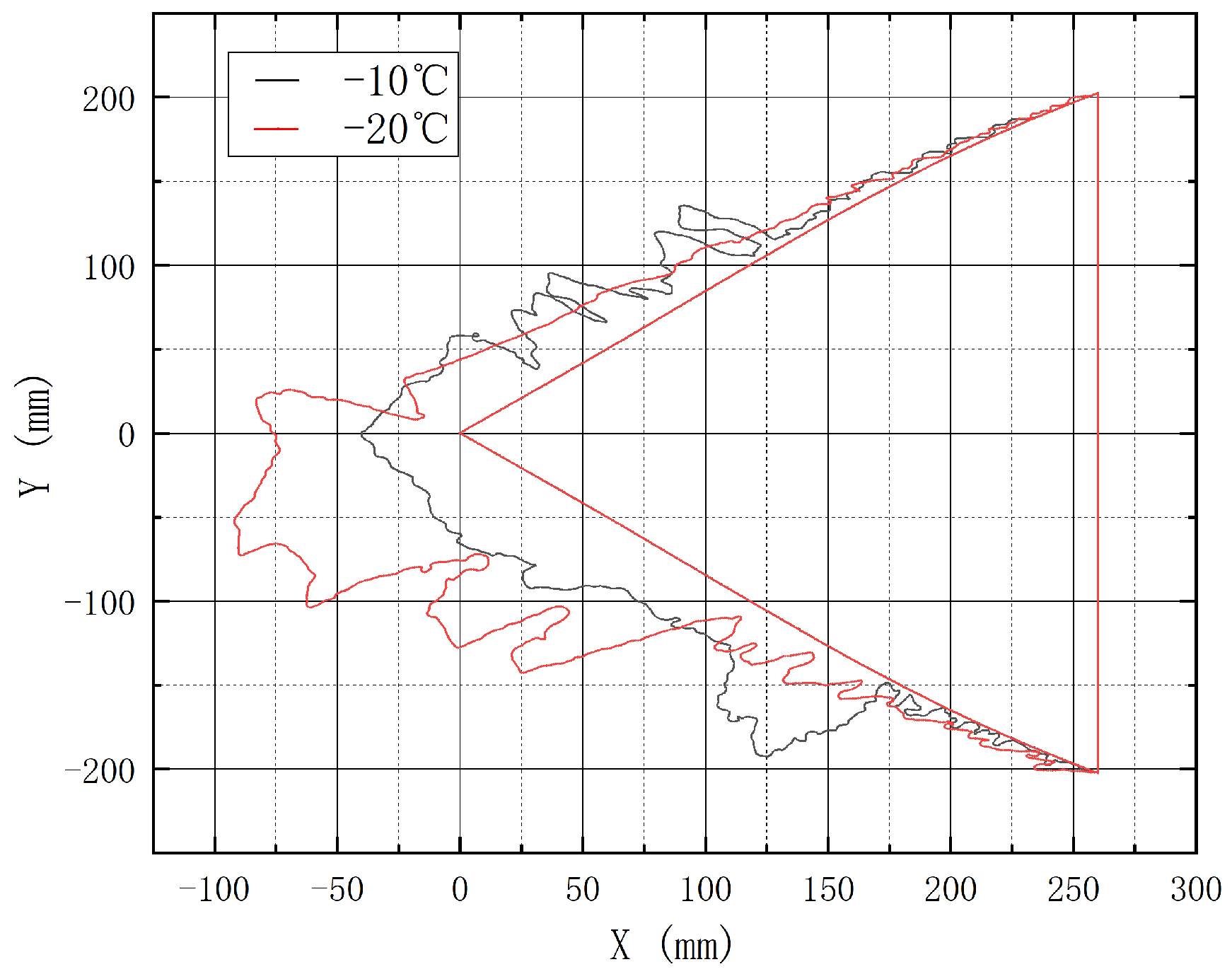
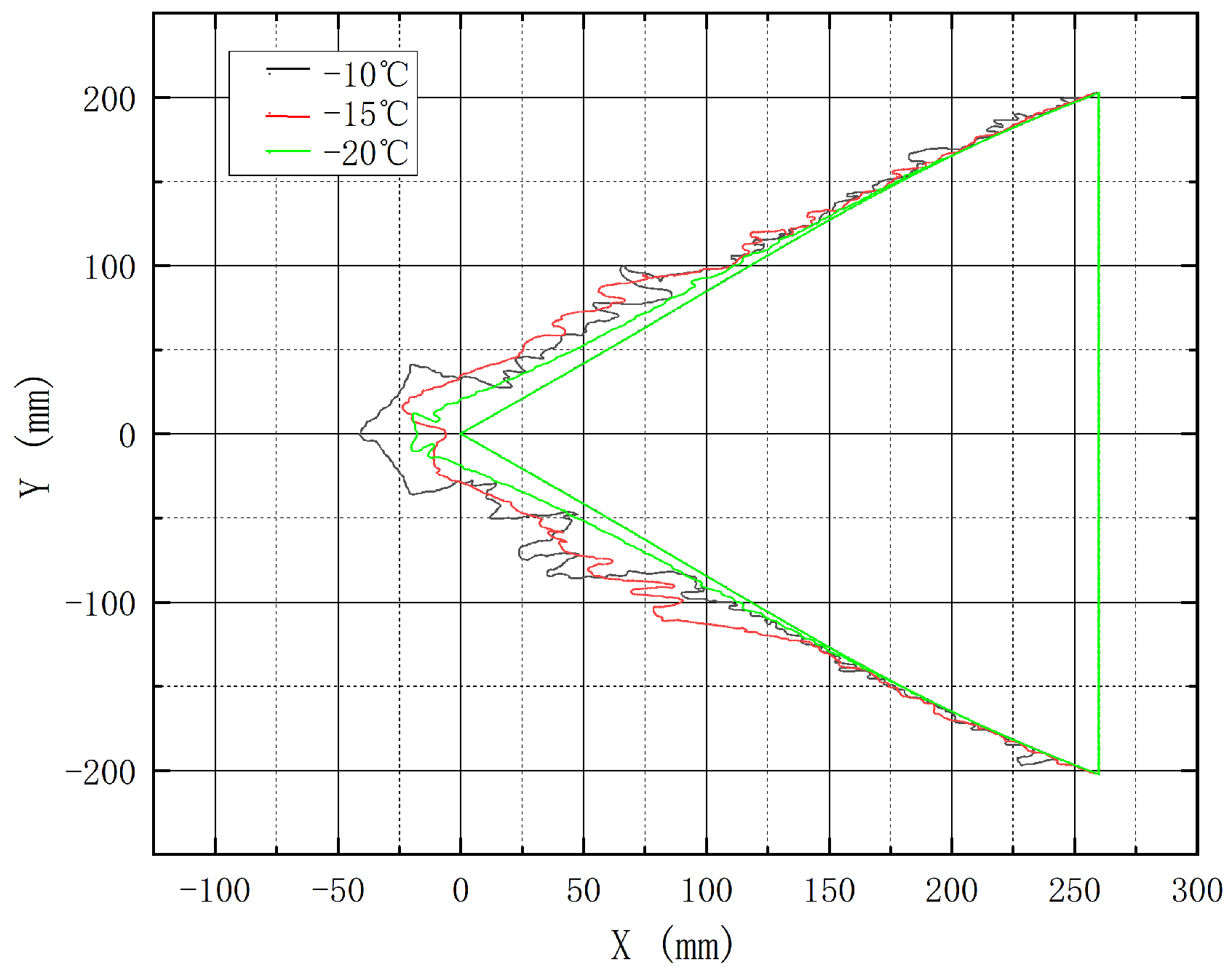
3.2. Influence of Temperature on Icing
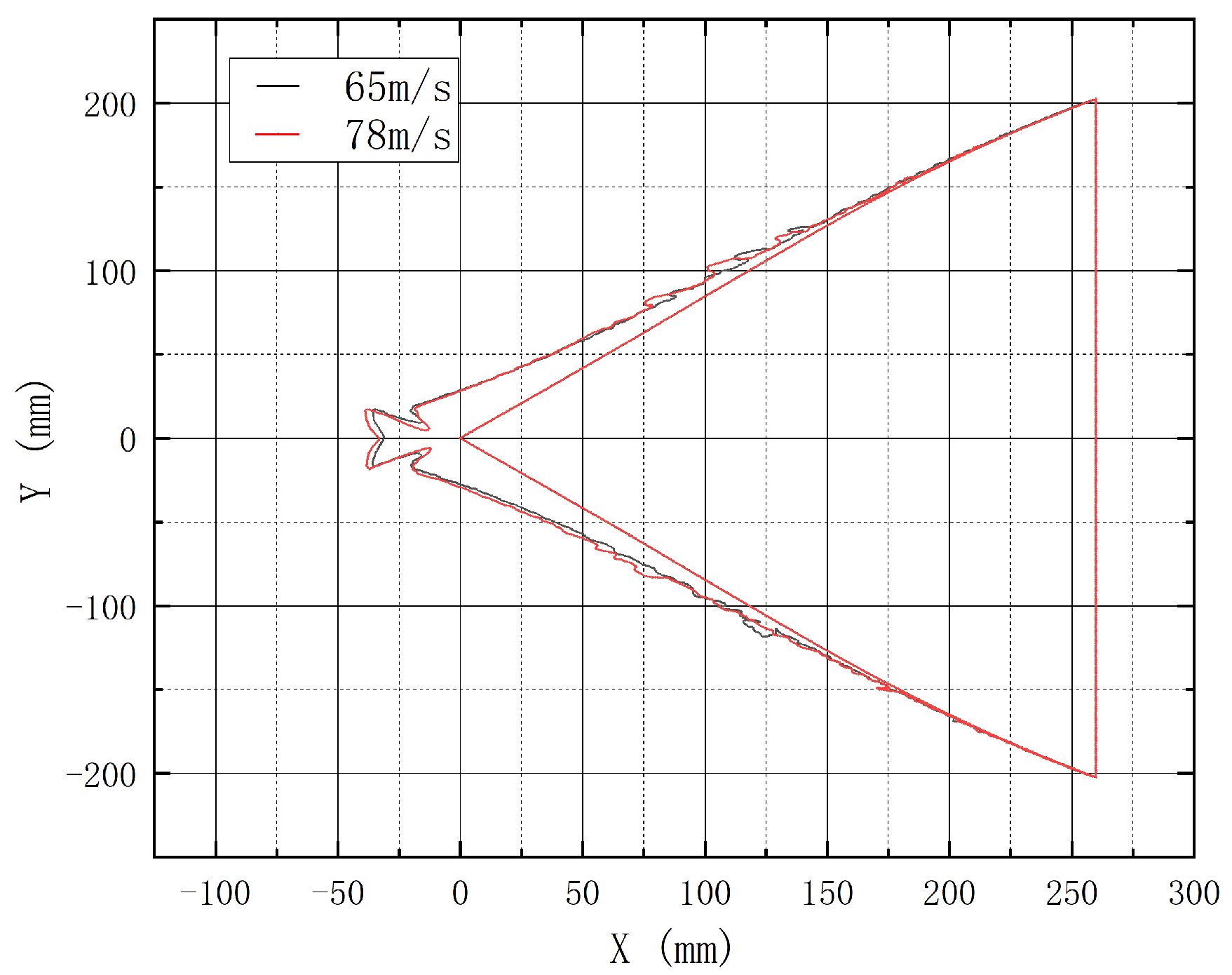
3.3. Influence of Wind Speed on Icing
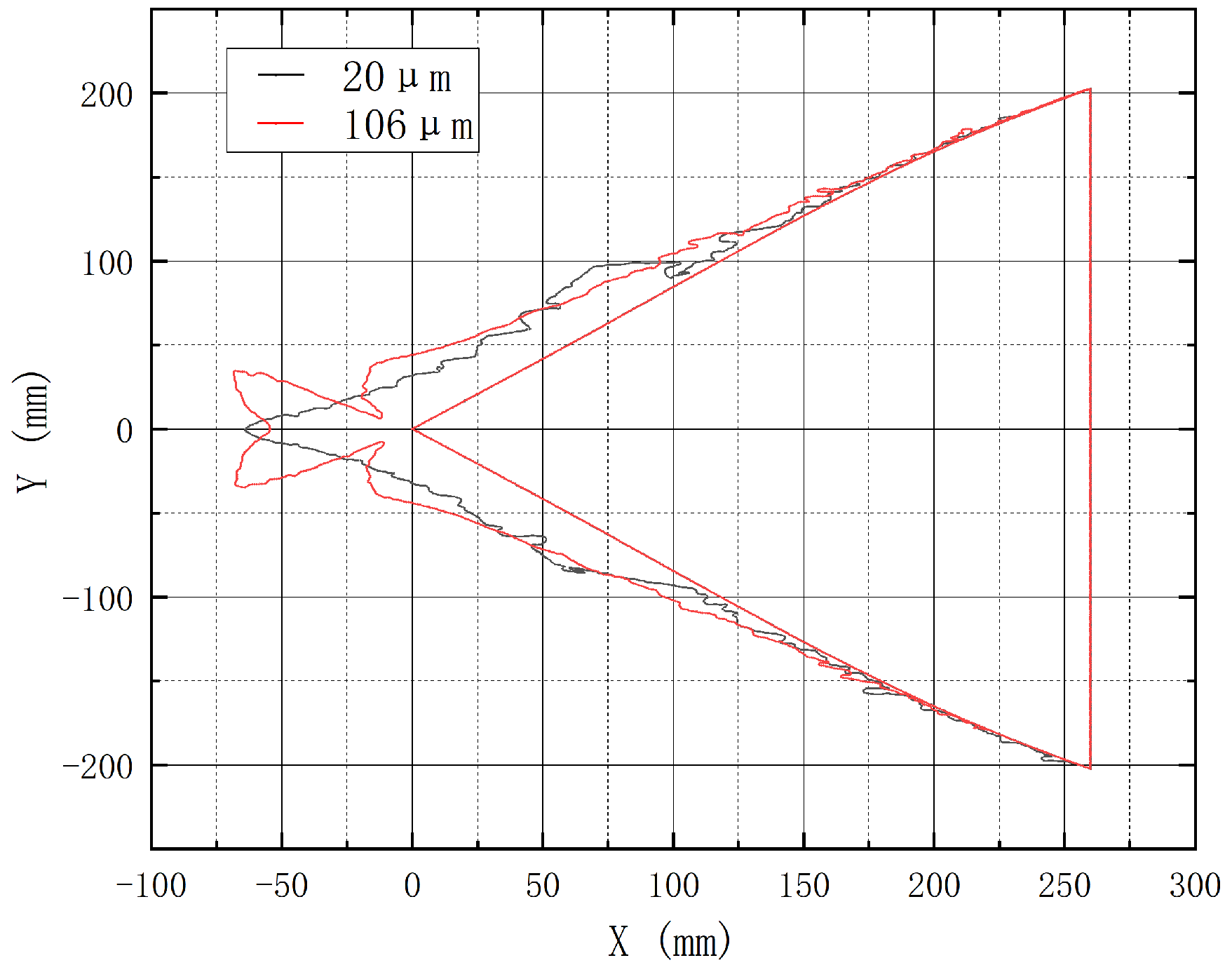
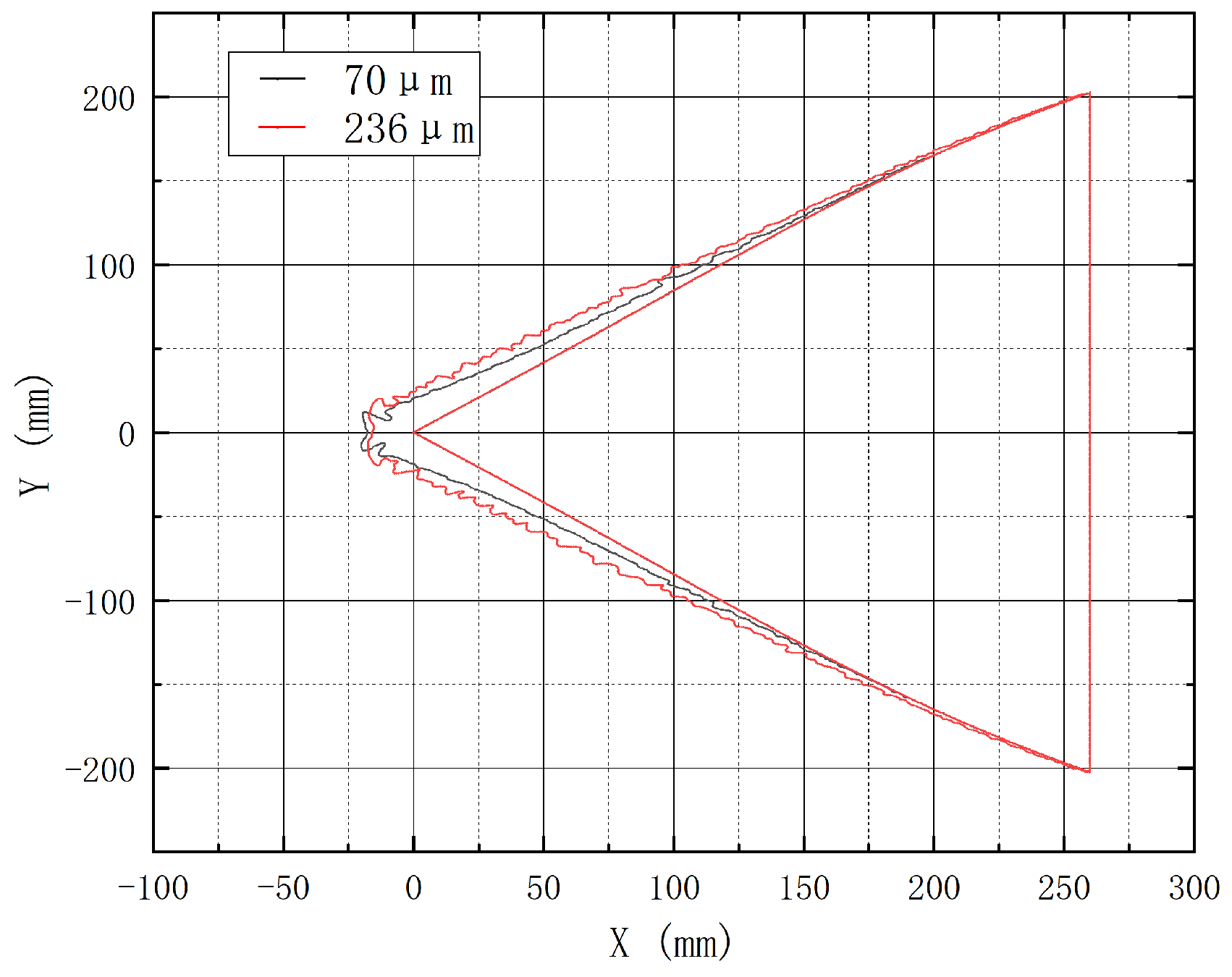
3.4. Influence of MVD on Icing
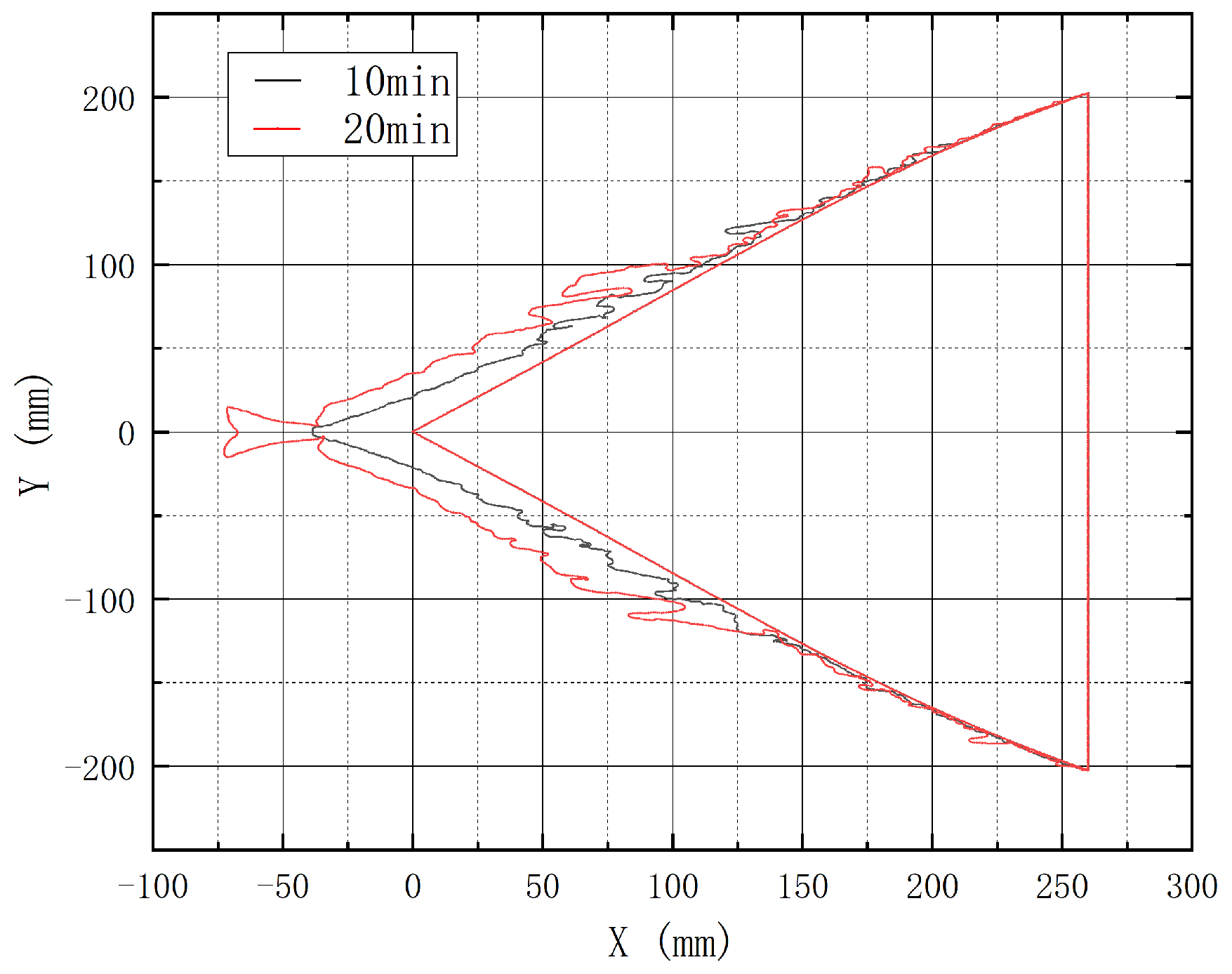
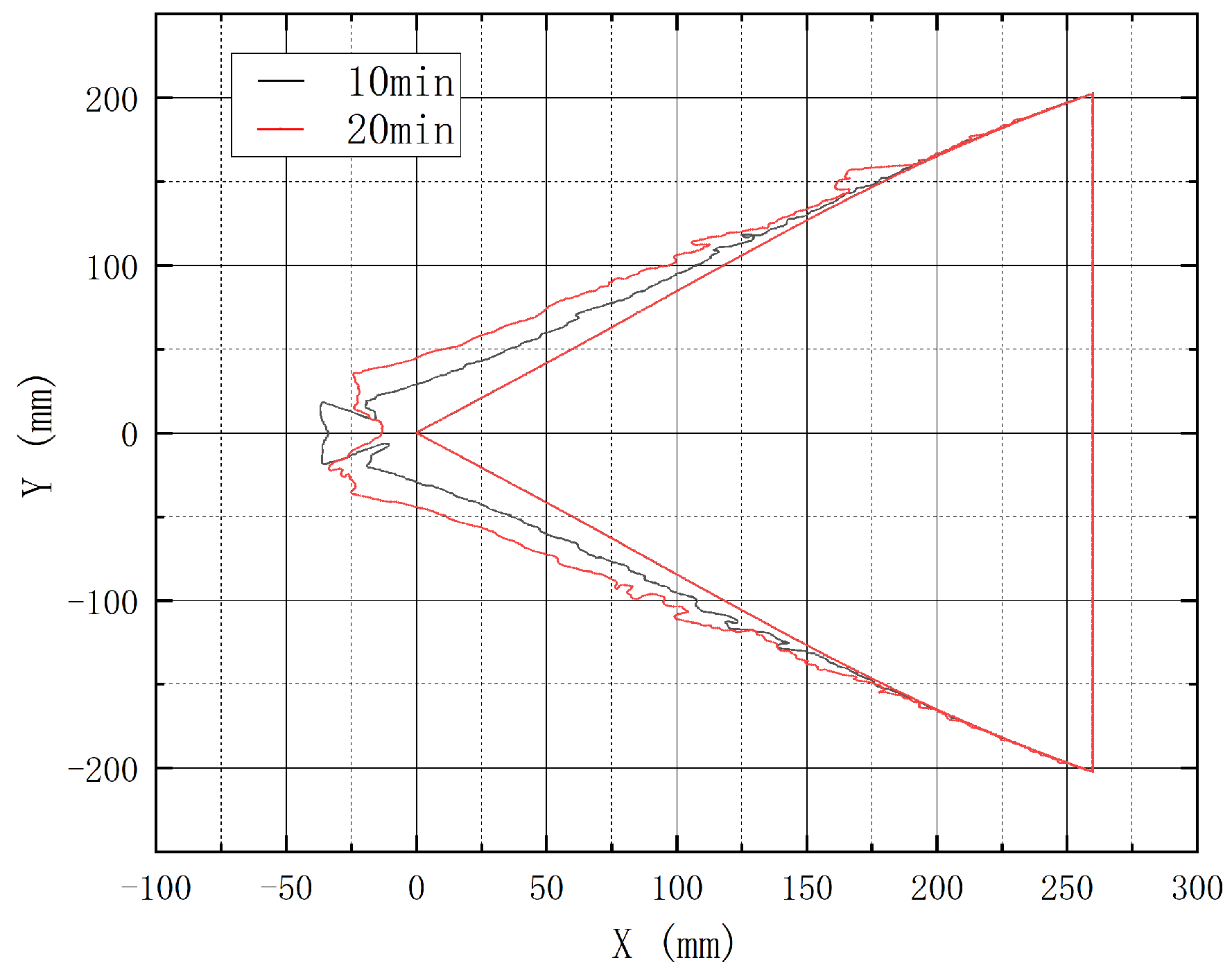
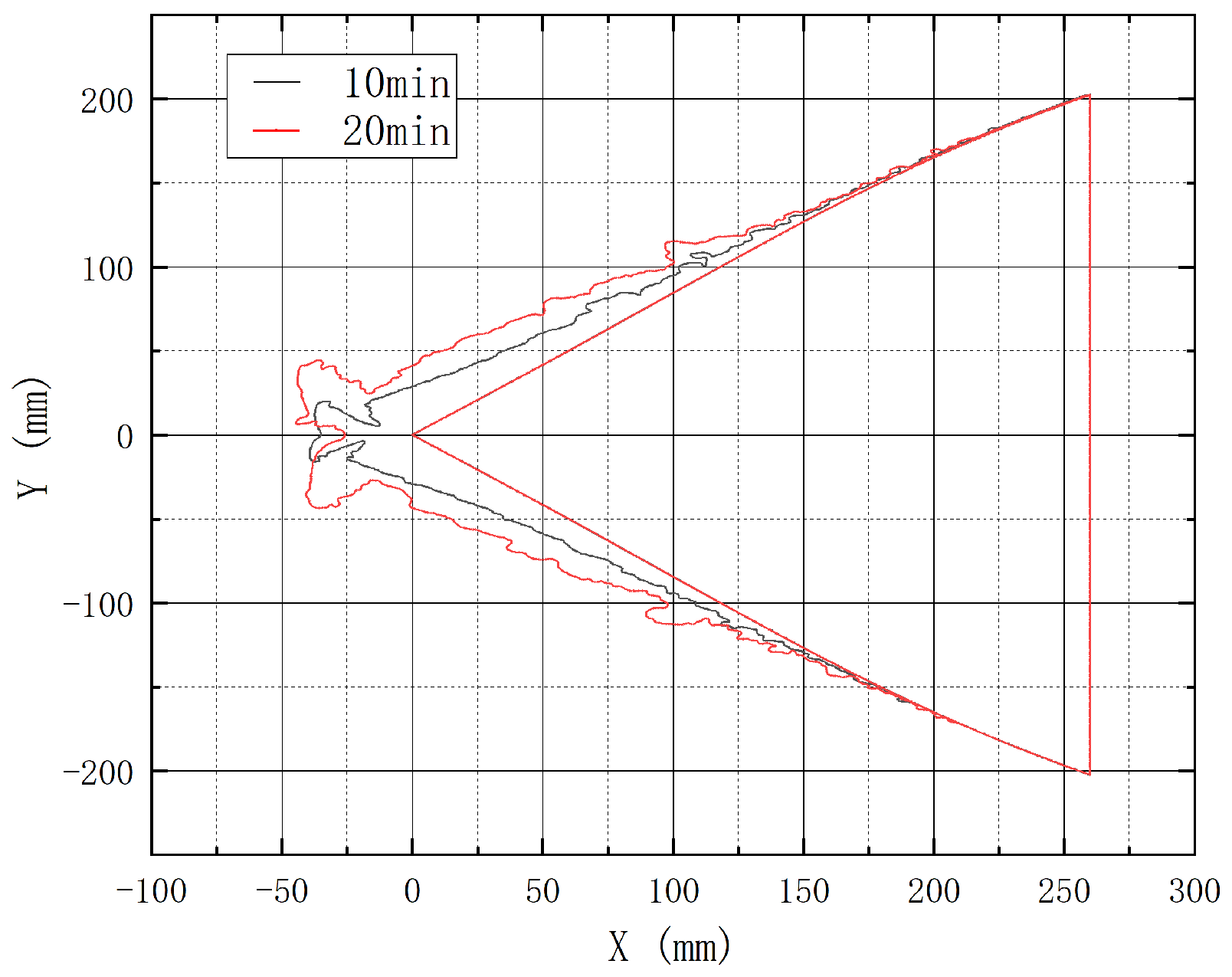
3.5. Influence of Time on Icing
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SLD | Supercooled Large Droplet |
| LWC | Liquid Water Content |
| MVD | Mean Volume Diameter |
| AVIC | Aviation Industry Corporation of China |
| SAE | Society of Automotive Engineers |
| ARP | Aerospace Recommended Practice |
| FARs | Federal Aviation Regulations |
References
- Yamazaki, M.; Jemcov, A.; Sakaue, H. A review on the current status of icing physics and mitigation in aviation. Aerospace 2021, 8, 188. [Google Scholar] [CrossRef]
- Zhou, L.; Yi, X.; Liu, Q. A review of icing research and development of icing mitigation techniques for fixed-wing UAVs. Drones 2023, 7, 709. [Google Scholar] [CrossRef]
- Dong, W.; Zhu, J.; Lei, G.; Zheng, M. Numerical Simulation of Hot Air Anti-Icing Characteristics of an Aero-Engine Strut. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, AIAA-2015-0537, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Lian, W.; Xuan, Y. Experimental investigation on a novel aero-engine nose cone anti-icing system. Appl. Therm. Eng. 2017, 121, 1011–1021. [Google Scholar] [CrossRef]
- Mason, J.; Strapp, W.; Chow, P. The ice particle threat to engines in flight. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, AIAA-2006-0206, Reno, Nevada, 9–12 January 2006. [Google Scholar]
- Shi, L.; Feng, F.; Guo, W.; Li, Y. Research and Development of a Small-Scale Icing Wind Tunnel Test System for Blade Airfoil Icing Characteristics. Int. J. Rotating Mach. 2021, 2021, 5598859. [Google Scholar] [CrossRef]
- Li, Y.; Tagawa, K.; Feng, F.; Li, Q.; He, Q. A wind tunnel experimental study of icing on wind turbine blade airfoil. Energy Convers. Manag. 2014, 85, 591–595. [Google Scholar] [CrossRef]
- Li, L.; Hu, H. An experimental study of dynamic ice accretion process on aero-engine spinners. In Proceedings of the 55th AIAA Aerospace Sciences Meeting, AIAA-2017-0551, Grapevine, TX, USA, 9–13 January 2017. [Google Scholar]
- Wang, J.; Hu, Y.P.; Ji, H.H.; Chen, N.-L.; Cao, G.Z. Experiment of ice accretion and shedding on rotating spinner. J. Aerosp. Power 2014, 29, 1352–1357. [Google Scholar]
- Chen, N.L.; Ji, H.H.; Hu, Y.P.; Wang, J.; Cao, G. Experimental study of icing accretion on a rotating conical spinner. Heat Mass Transf. 2015, 51, 1717–1729. [Google Scholar] [CrossRef]
- Hu, Y.P.; Ji, H.H.; Wang, J.; Chen, N.L.; Cao, G.Z.; Tong, H.; Pang, L. Experiment on effect of cone angle on ice accretion of rotating spinner. J. Aerosp. Power 2014, 29, 495–503. [Google Scholar]
- Mu, Z.D.; Shen, X.B.; Lin, G.P.; Bu, X. Numerical simulation for ice accretion on rotating cowling considering water film shedding. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, AIAA 2016-2187, San Diego, CA, USA, 4–8 January 2016. [Google Scholar]
- Zhao, Q.Y.; Dong, W.; Zhu, J.J. Droplets impinging characteristic analysis of the rotating fairing of aero-engine. Gas Turbine Exp. Res. 2011, 24, 32–35. [Google Scholar]
- Wu, M.L.; Chang, S.N.; Leng, M.Y.; Wang, C. Simulation of droplet impingement characteristics of spinner based on Eulerian method. J. Beijing Univ. Aeronaut. Astronaut. 2014, 40, 1263–1267. [Google Scholar]
- Zhang, L.F.; Zhang, M.H.; Liu, Z.X. Collection efficiency of rotating spin in jet engine. In Proceedings of the 22nd International Symposium on Air Breathing Engines Conference, Phoenix, AZ, USA, 25–30 October 2015. [Google Scholar]
- Zhang, L.F.; Zhang, M.H.; Zhang, X.X.; Liu, Z. Modeling of ice accretion on rotating cone in aero-engine. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, AIAA 2016-5059, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Hu, Y.; Xu, C.; Li, S.; Li, P.; Liu, L. Experimental study on icing and anti-icing of a rotating conical spinner. Appl. Therm. Eng. 2023, 219, 119373. [Google Scholar] [CrossRef]
- He, H.; Peng, H.; Li, G.; Zhang, W.; Zhao, Z. Ice accretion and ice shedding on an aero-engine rotating cone. Phys. Fluids 2025, 37, 037169. [Google Scholar] [CrossRef]
- Qi, H.; Chang, S.; Yang, Y. Numerical study of mixed phase ice accumulation in aero-engine inlet system. Appl. Therm. Eng. 2023, 231, 120909. [Google Scholar] [CrossRef]
- Mahmoudi, F.Y.; Farhadi, M.; Darzi, A.R. Investigating effects of different anti-icing parameters on gas turbine air intake ice formation. J. Therm. Anal. Calorim. 2023, 148, 3793–3804. [Google Scholar] [CrossRef]
- Guo, Q.; Du, J.; Qian, F.; Ding, N. Numerical Study of Particle Implementation on Aeroengine under Mixed-Phase Conditions. Mechanics 2024, 30, 415–422. [Google Scholar] [CrossRef]
- Honsek, R.; Habashi, W.G.; Aube, M.S. Eulerian modeling of in-flight icing due to supercooled large droplets. J. Aircraft. 2008, 45, 1290–1296. [Google Scholar] [CrossRef]
- Zhang, C.; Liu, H. Effect of drop size on the impact thermodynamics for supercooled large droplet in aircraft icing. Phys. Fluids 2016, 28, 062107. [Google Scholar] [CrossRef]
- Zhu, D.; Pei, R.; Yang, Q.; Bu, X.; Zhu, Y.; Lin, G. Experimental researches on a hot air anti-icing system in FL-61 icing wind tunnel. Aerodyn. Res. Exp. 2020, 32, 144. [Google Scholar]
- Jia, W.; Zhang, F.; Zhang, Z. Numerical and experimental investigation of the supercooled large droplets icing of rotating spinner. Appl. Therm. Eng. 2024, 257, 124159. [Google Scholar] [CrossRef]


















| Item | Design Indicator |
|---|---|
| Mach number control accuracy | <0.001 |
| Mach number distribution accuracy | <0.002 |
| Average airflow deviation angle | ≤0.1° |
| Total temperature control accuracy | ±1 K |
| Total pressure control accuracy | ≤0.2% |
| Turbulence degree | ≤0.2% |
| LWC | 0.3~3 g/m3 |
| MVD | 15~500 μm |
| Uniformity of LWC | ±20% |
| Continuous icing time | 60 min |
| Condition | Wind Speed (V) m/s | Static Temperature (Ts) °C | MVD μm | LWC g/m3 | Rotational Speed (Rev) rpm | Icing Time (t) min |
|---|---|---|---|---|---|---|
| 1 | 78 | −10 | 20 | 1.0 | 0 | 20 |
| 2 | 78 | −10 | 20 | 1.0 | 100 | 20 |
| 3 | 78 | −10 | 20 | 1.0 | 900 | 20 |
| 4 | 78 | −10 | 20 | 1.0 | 2000 | 20 |
| 5 | 78 | −10 | 50 | 1.5 | 100 | 10 |
| 6 | 78 | −10 | 50 | 1.5 | 1500 | 10 |
| 7 | 78 | −20 | 106 | 1.0 | 0 | 20 |
| 8 | 78 | −20 | 106 | 1.0 | 100 | 20 |
| 9 | 78 | −20 | 106 | 1.0 | 900 | 20 |
| 10 | 78 | −20 | 106 | 1.0 | 2000 | 20 |
| 11 | 78 | −20 | 106 | 1.0 | 3000 | 20 |
| 12 | 78 | −10 | 106 | 1.0 | 0 | 20 |
| 13 | 78 | −15 | 20 | 1.0 | 900 | 20 |
| 14 | 78 | −20 | 20 | 1.0 | 900 | 20 |
| 15 | 78 | −20 | 106 | 1.0 | 1500 | 10 |
| 16 | 65 | −20 | 106 | 1.0 | 1500 | 10 |
| 17 | 78 | −20 | 70 | 1.0 | 2500 | 6 |
| 18 | 78 | −20 | 236 | 1.0 | 2500 | 6 |
| 19 | 78 | −20 | 20 | 1.0 | 900 | 10 |
| 20 | 78 | −20 | 106 | 1.0 | 900 | 10 |
| 21 | 78 | −20 | 106 | 1.0 | 3000 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Zhao, H.; Zhu, D.; Dai, H.; Wang, Z. Experimental Study on the Icing of Rotating Intake Cones in Wind Tunnels Under Supercooled Large-Droplet Conditions. Aerospace 2025, 12, 384. https://doi.org/10.3390/aerospace12050384
Zhang Z, Zhao H, Zhu D, Dai H, Wang Z. Experimental Study on the Icing of Rotating Intake Cones in Wind Tunnels Under Supercooled Large-Droplet Conditions. Aerospace. 2025; 12(5):384. https://doi.org/10.3390/aerospace12050384
Chicago/Turabian StyleZhang, Zhiqiang, Huanyu Zhao, Dongyu Zhu, Hao Dai, and Zhengzhi Wang. 2025. "Experimental Study on the Icing of Rotating Intake Cones in Wind Tunnels Under Supercooled Large-Droplet Conditions" Aerospace 12, no. 5: 384. https://doi.org/10.3390/aerospace12050384
APA StyleZhang, Z., Zhao, H., Zhu, D., Dai, H., & Wang, Z. (2025). Experimental Study on the Icing of Rotating Intake Cones in Wind Tunnels Under Supercooled Large-Droplet Conditions. Aerospace, 12(5), 384. https://doi.org/10.3390/aerospace12050384







