The Influence of Ice Accretion on the Thermodynamic Performance of a Scientific Balloon: A Simulation Study
Abstract
1. Introduction
2. Theoretical Model
2.1. Cloud Radiation Properties
- 1.
- Optical thickness of clouds
- 2.
- Transmittance of the cloud
- 3.
- Cloud reflectance
- 4.
- Cloud emittance
2.2. Ice Accretion Model
2.3. Thermodynamic Model with Cloud Modification
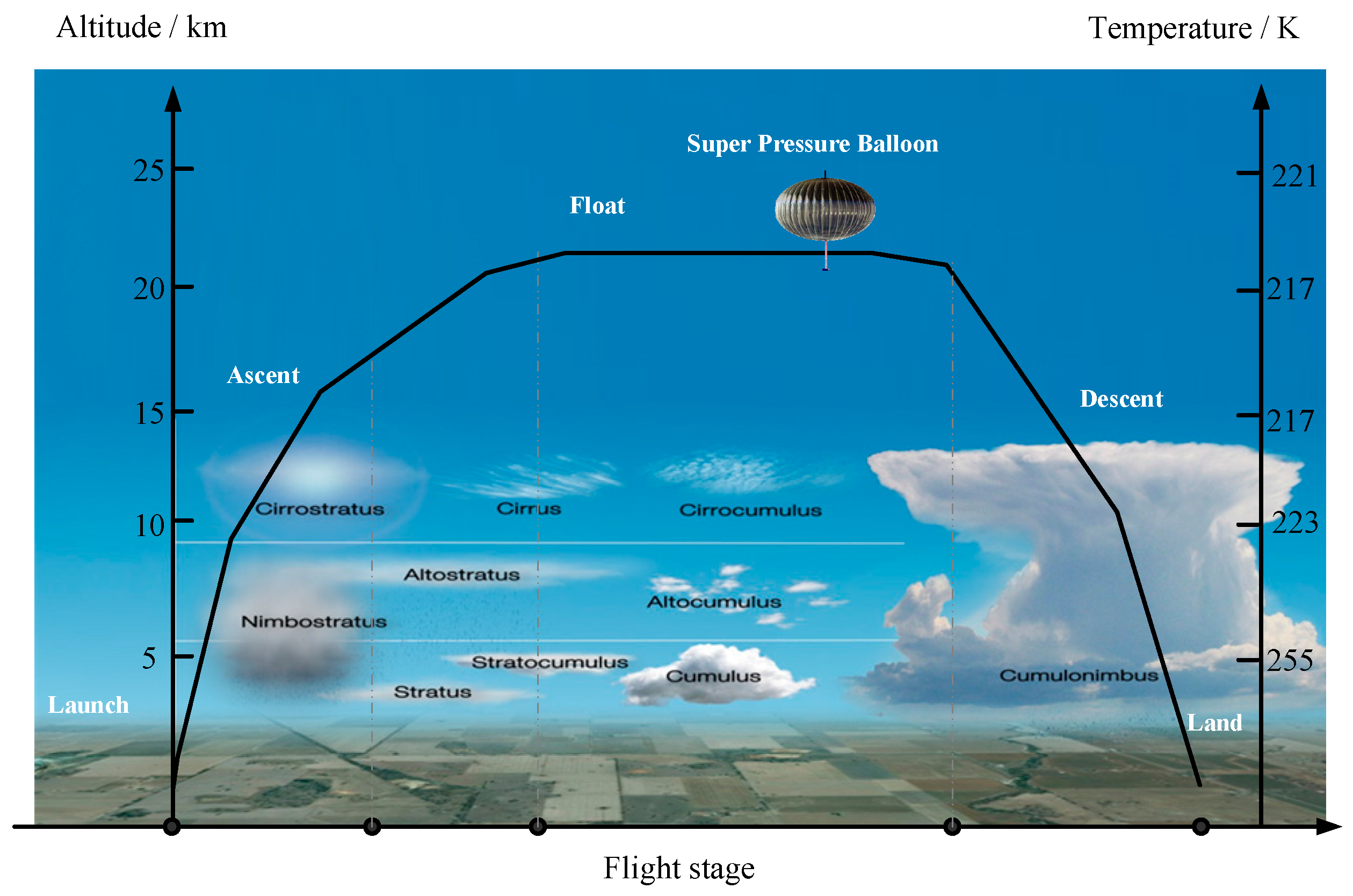
2.3.1. Geometry of the Balloon
2.3.2. Thermal Environment of the Balloon
- 1.
- Balloon film thermal model
- (1)
- Absorbed solar direct radiation flux
- (2)
- Absorbed solar scatter radiation flux [5]
- (3)
- Absorbed solar albedo radiation flux
- (4)
- Absorbed cloud reflected solar radiation flux
- (5)
- Absorbed atmosphere infrared radiation flux
- (6)
- Absorbed cloud infrared radiation flux
- (7)
- Absorbed Earth-surface infrared radiation flux
- (8)
- Emitted infrared radiation flux of the external balloon film
- (9)
- Absorbed infrared radiation flux of the internal balloon film
- (10)
- Net gain of external convective heat transfer flux
- (11)
- Net gain of internal convective heat transfer flux
- 2.
- Helium thermal model [4]
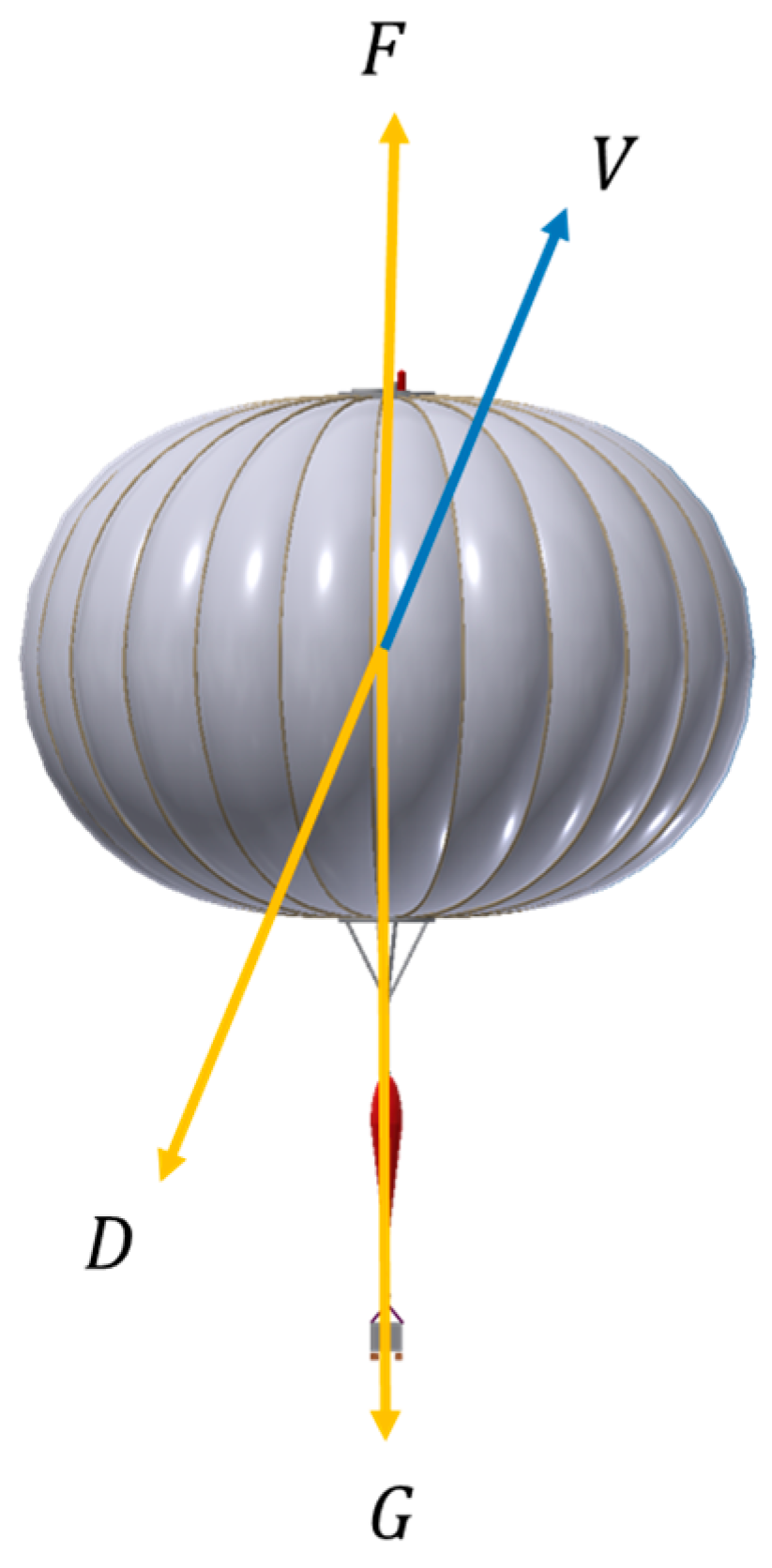
2.3.3. Dynamic Model of the Balloon
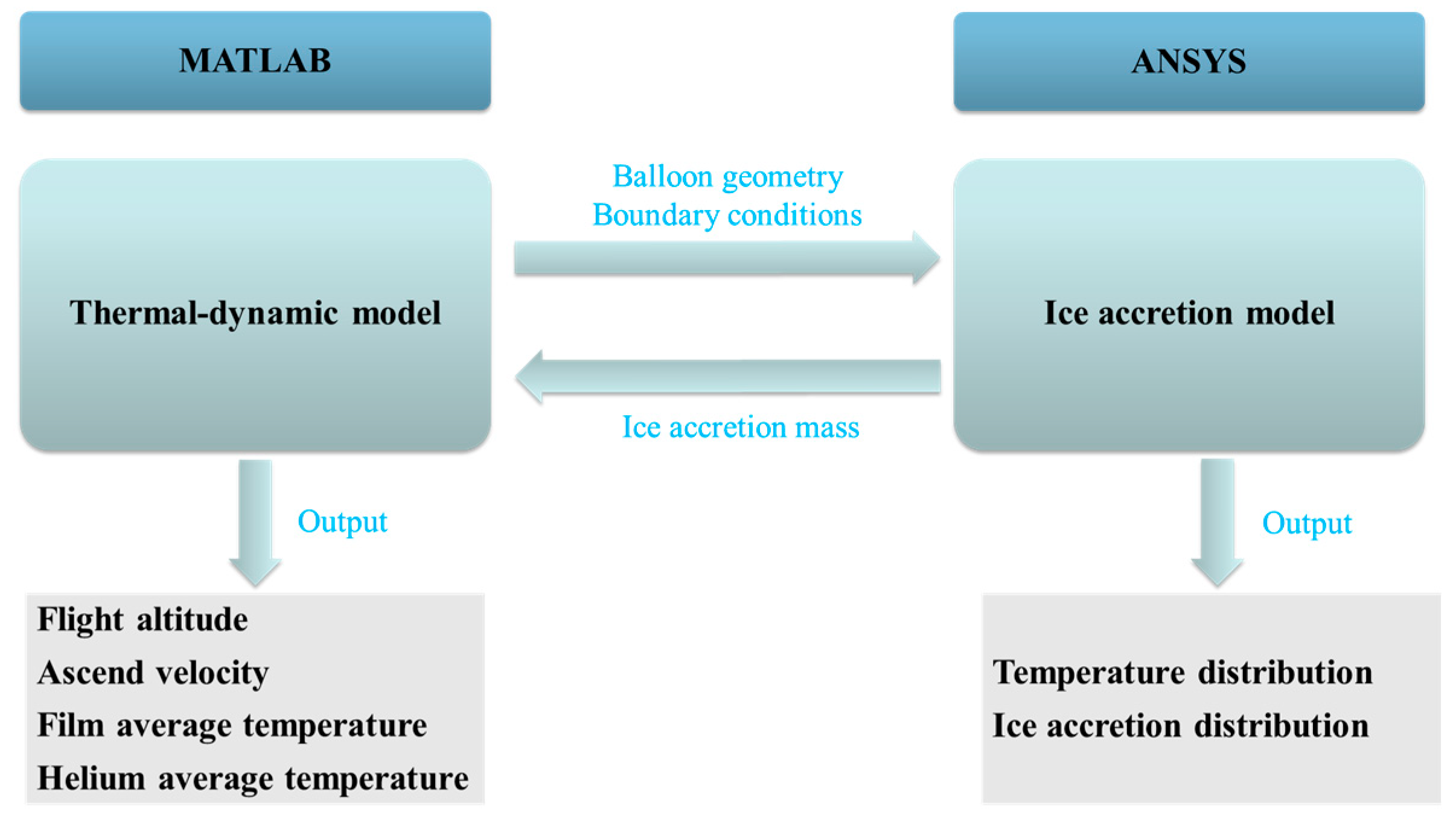
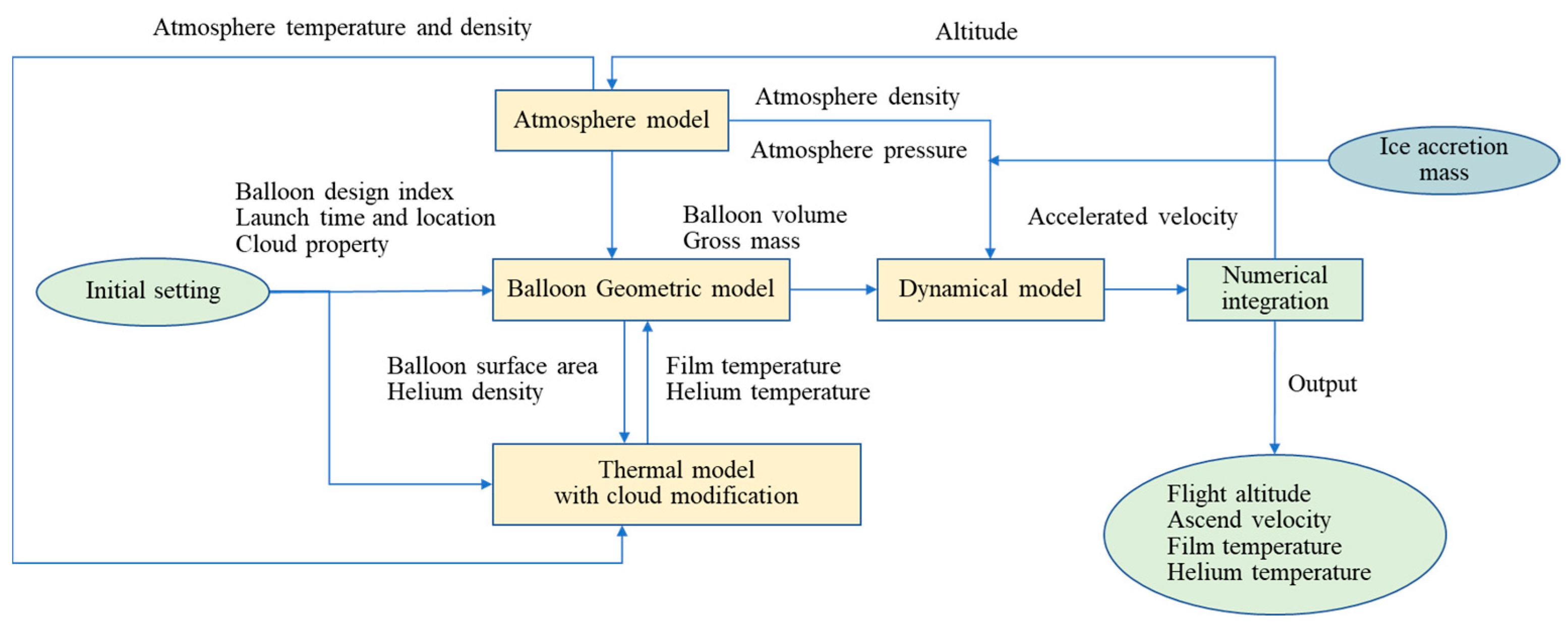
3. Analysis Method
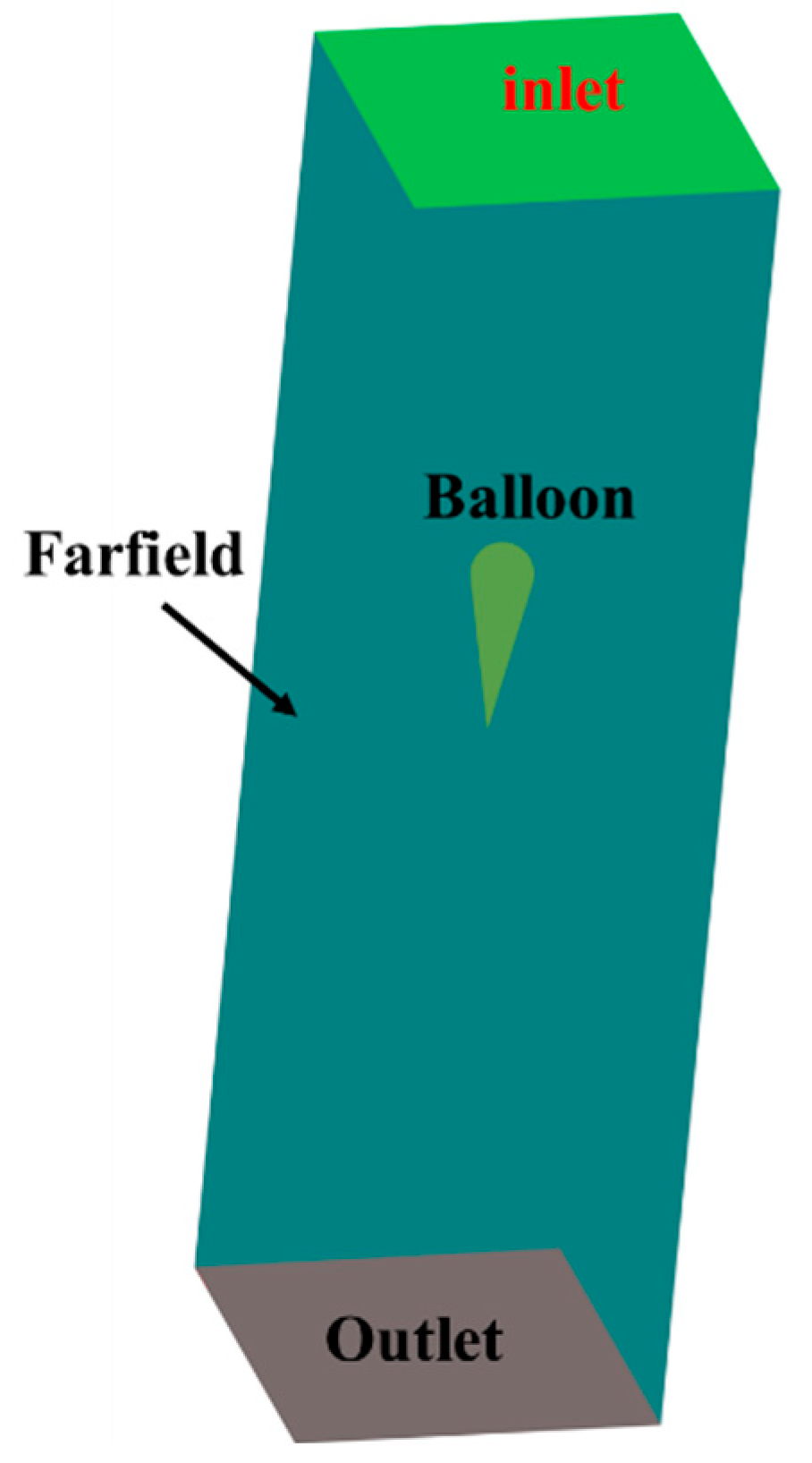
3.1. Ice Accretion Analysis Method
3.2. Thermodynamic Analysis Method
4. Model Validation
4.1. Ice Accretion Model Validation
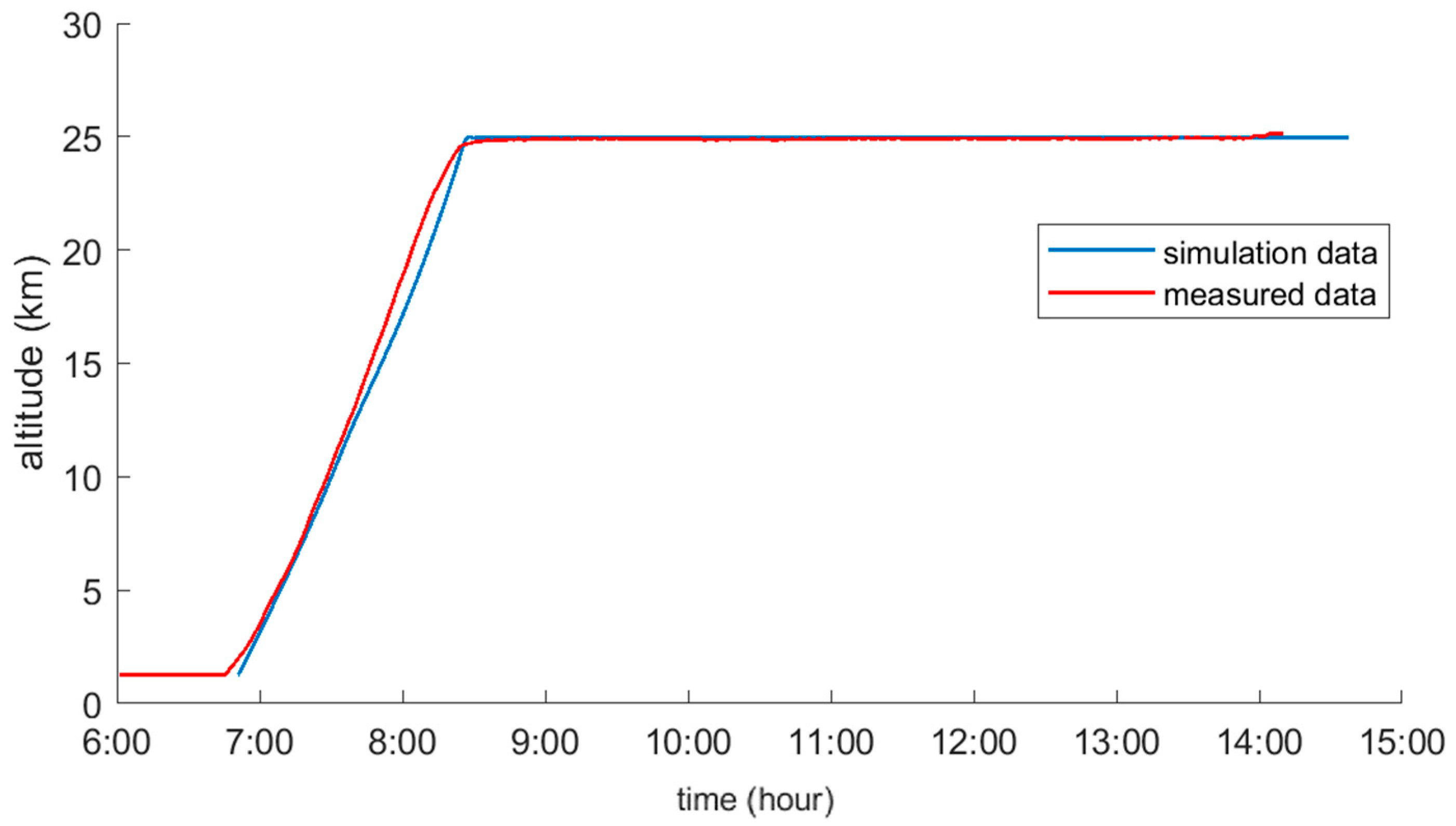
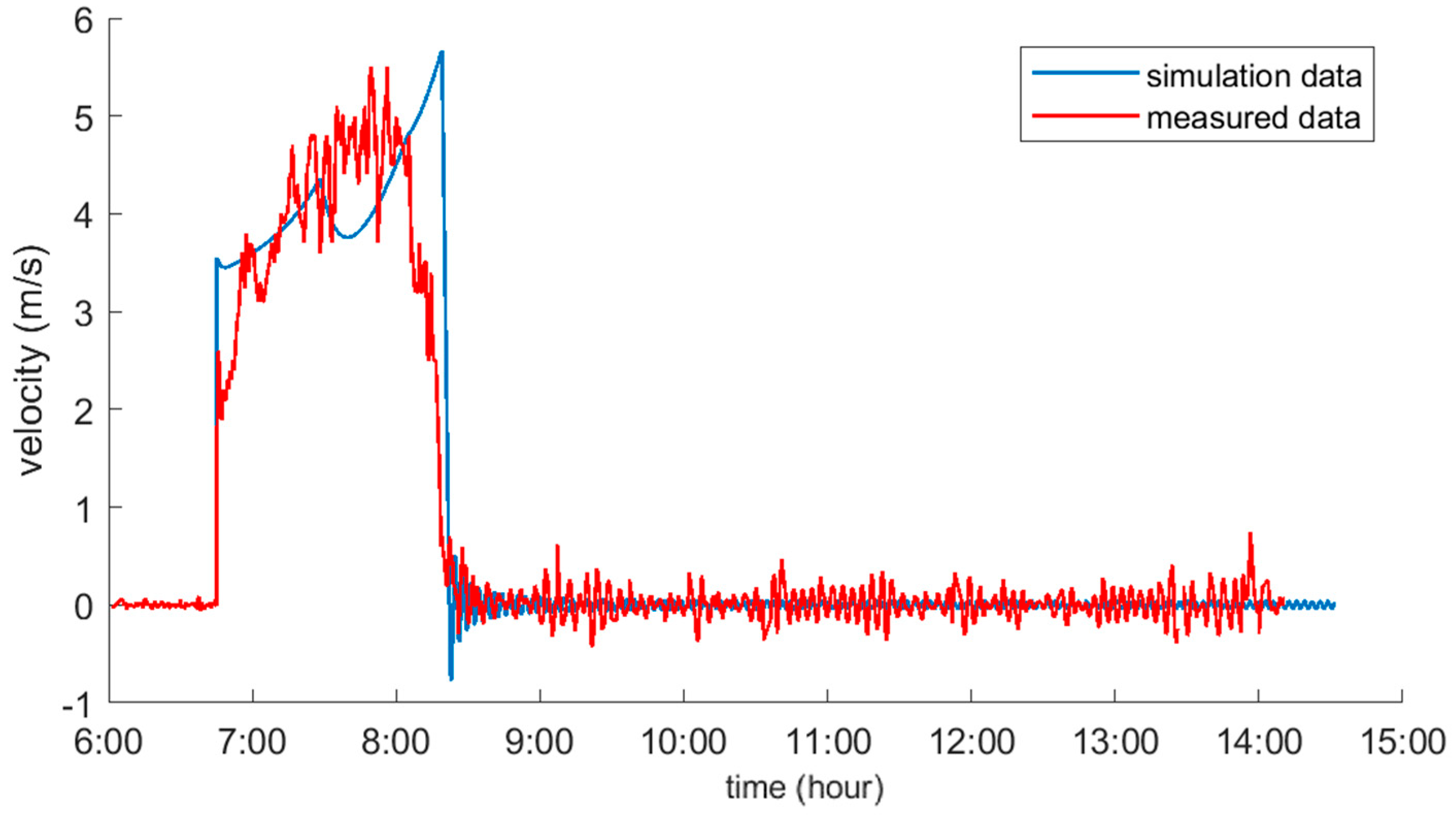
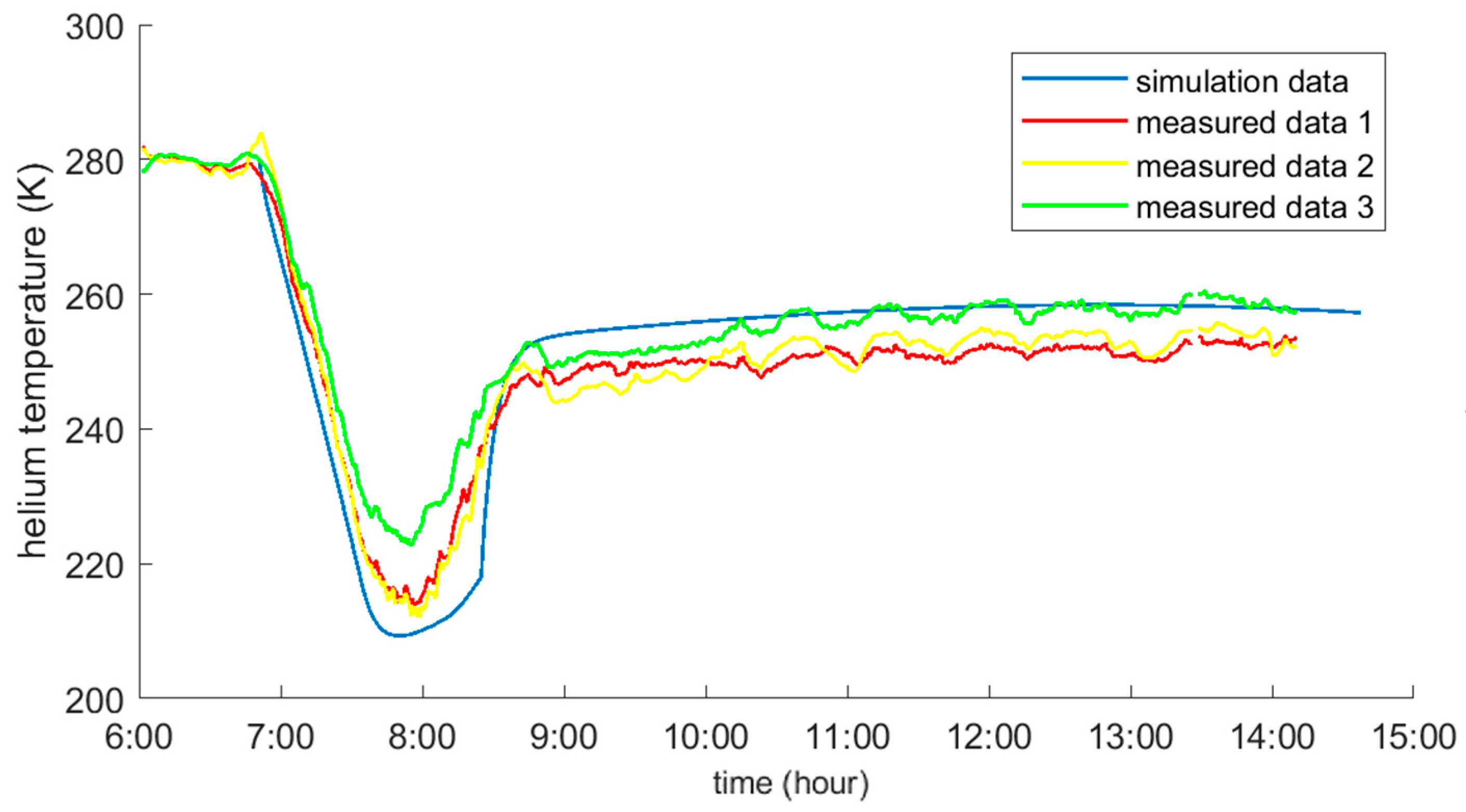
4.2. Thermodynamic Model Validation
5. Results and Discussion
5.1. Ice Accretion Performance
5.1.1. Temperature and Flow Distribution
5.1.2. Droplet Collection Efficiency Distribution
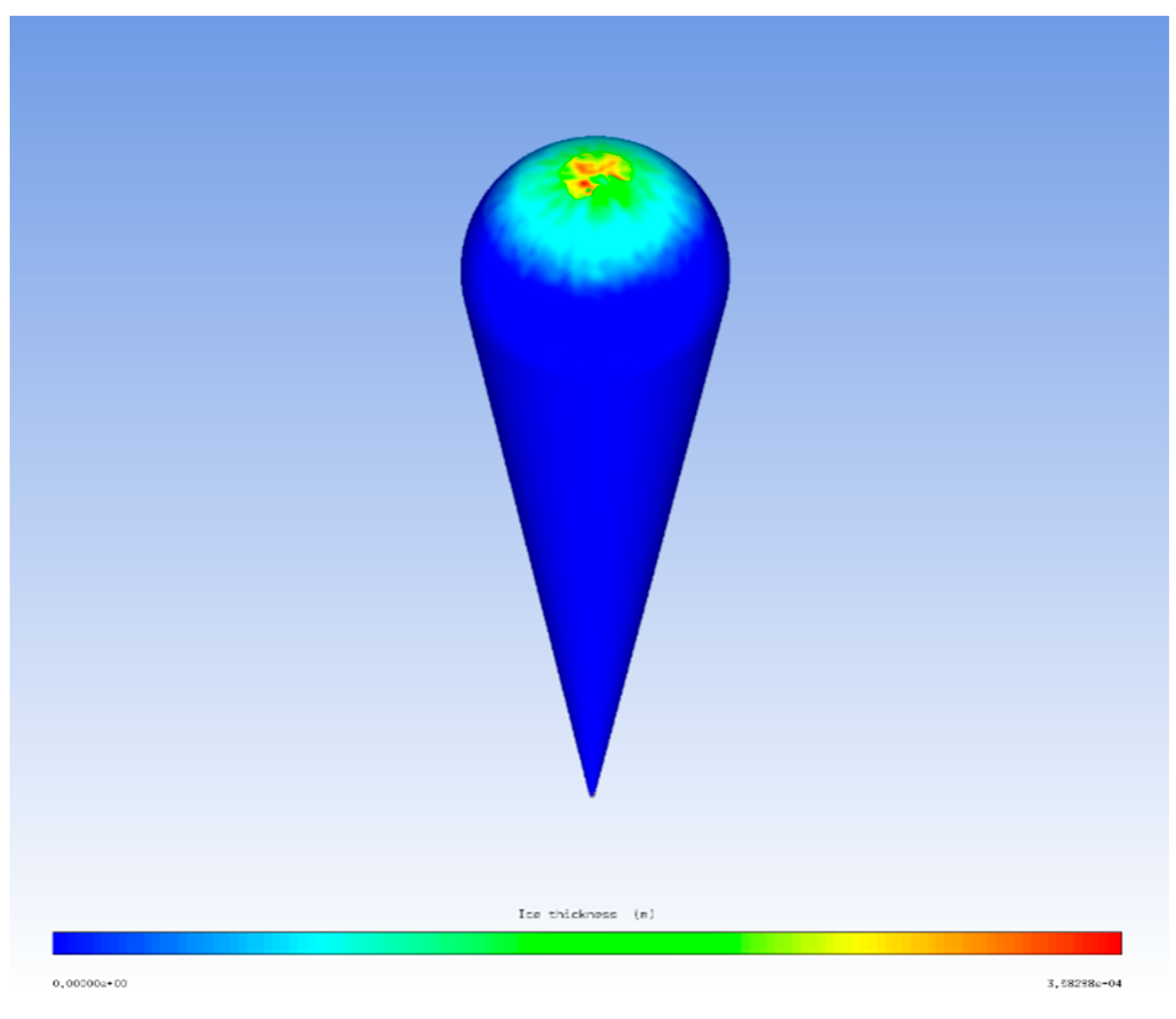
5.1.3. Ice Accretion Distribution
5.2. Influence of Ice Accretion
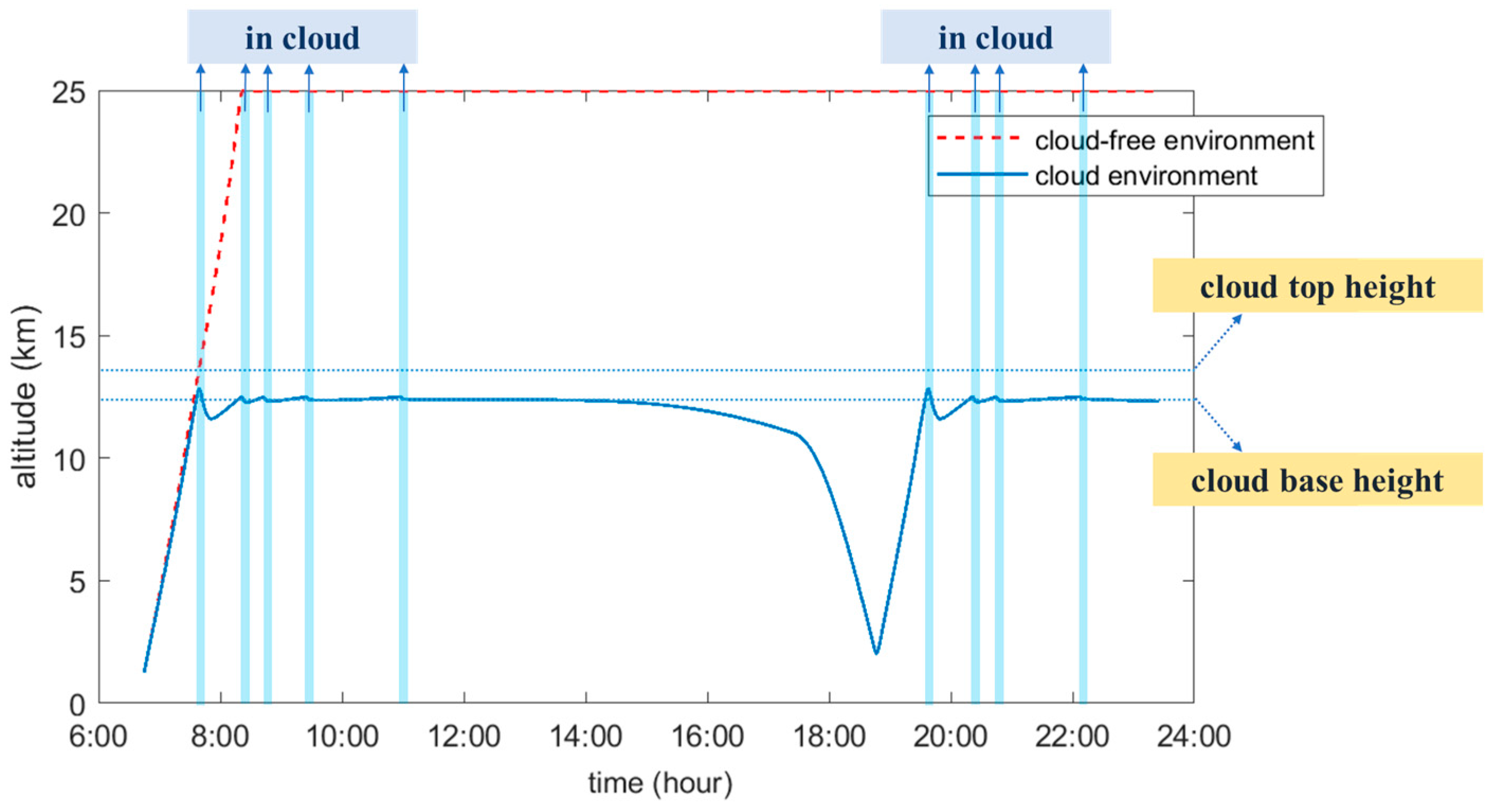
5.2.1. Flight Altitude
5.2.2. Ascent Velocity
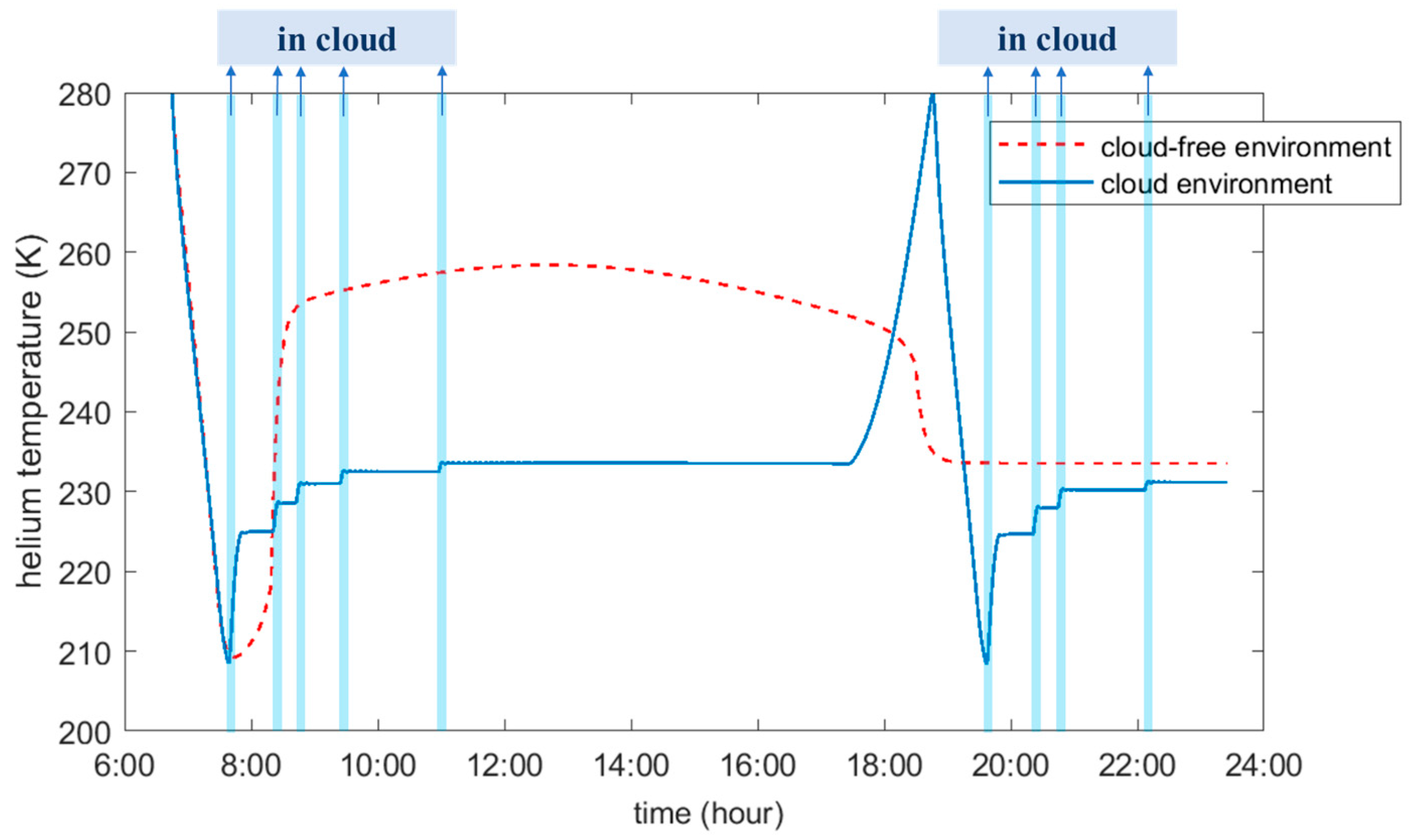
5.2.3. Helium Temperature
5.2.4. Helium Super Pressure
6. Conclusions
- (1)
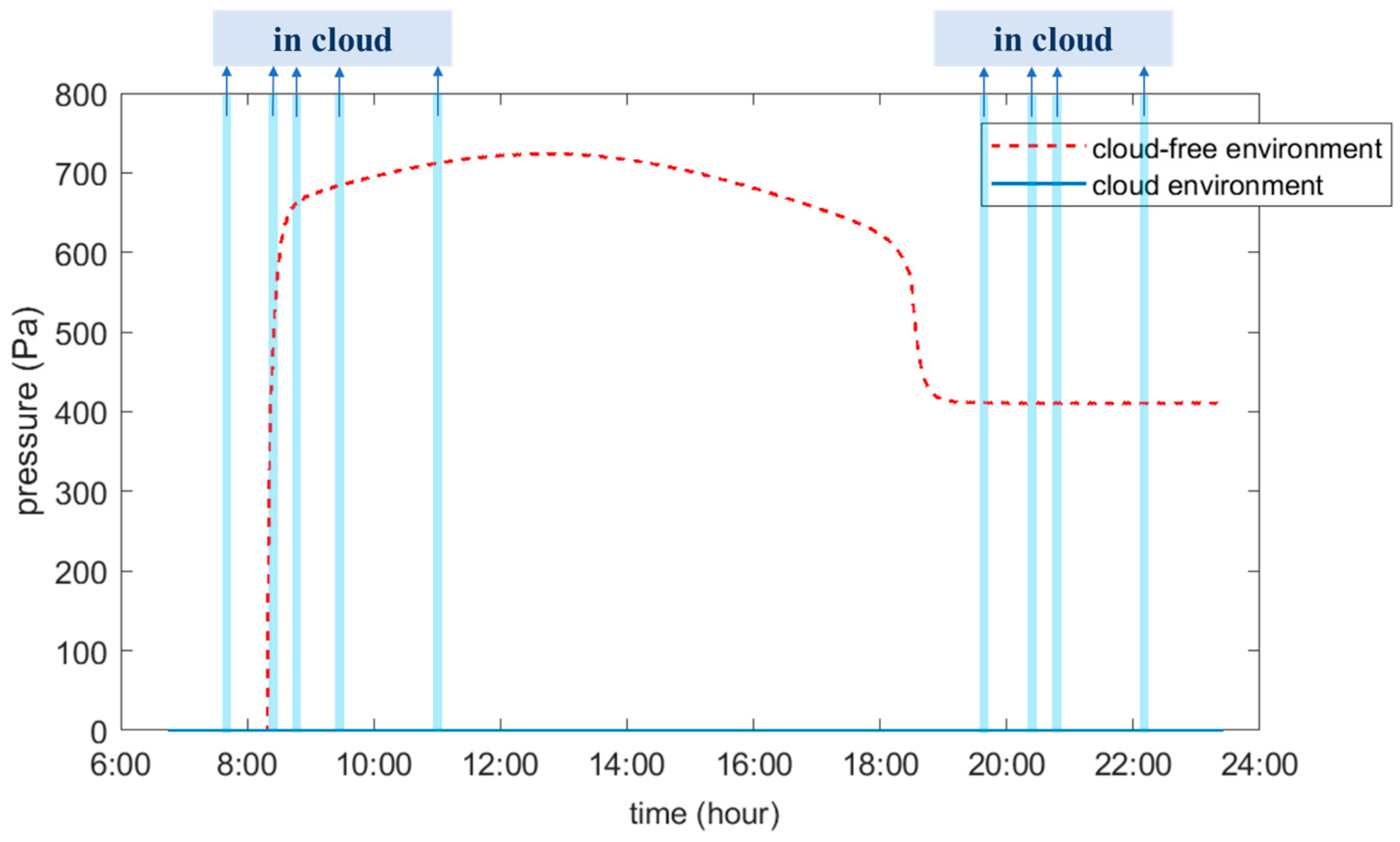
- When a scientific balloon ascends through clouds, the clouds influence its thermal environment. When the balloon’s surface temperature is below the icing point of 273.15 K, and it encounters ice droplets in clouds, there is a risk of ice accretion on the surface;
- (2)
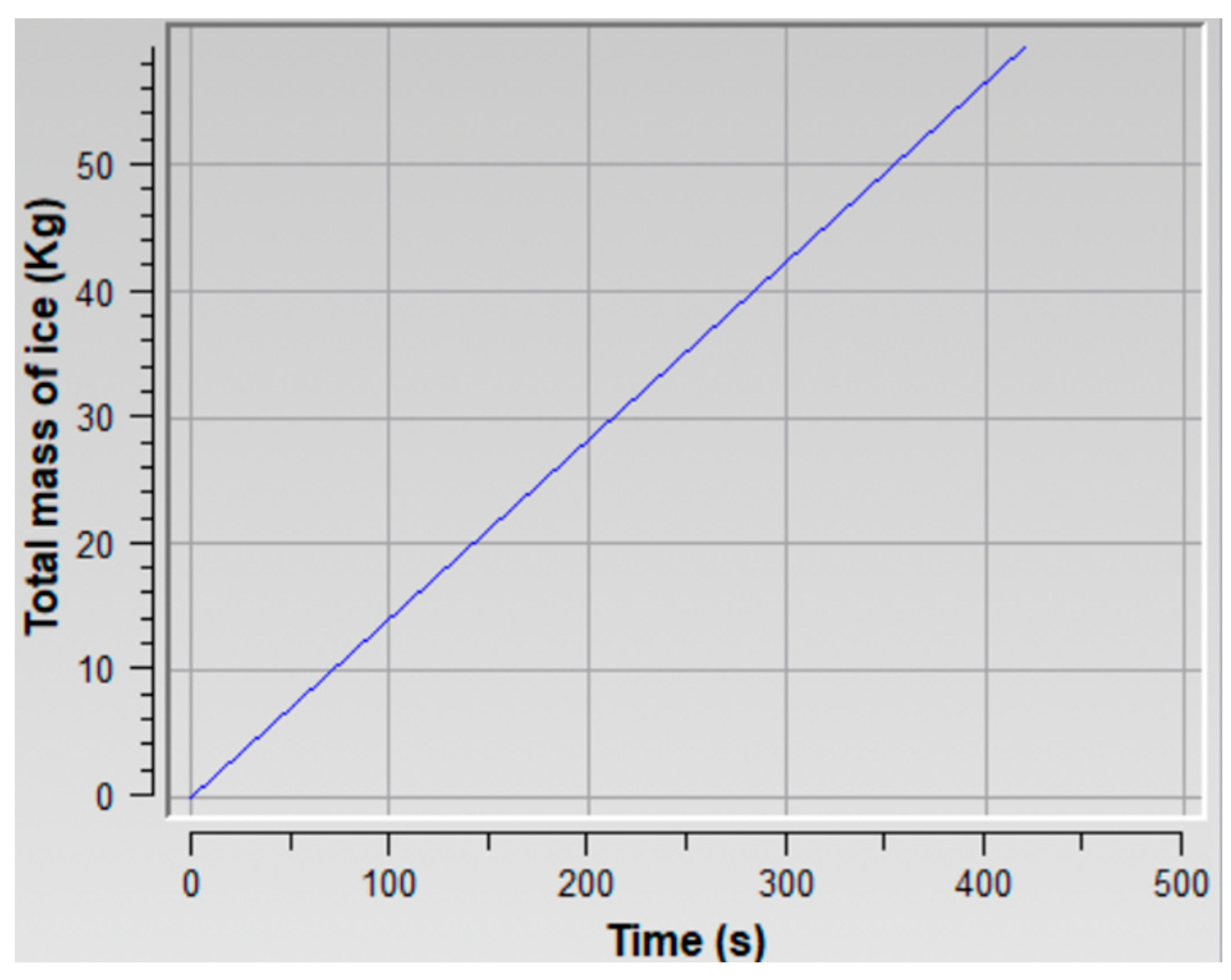
- In an icing situation, thicker ice is distributed on the windward part of the balloon’s surface, and thinner ice is distributed on the rest of the balloon. Under certain conditions, the maximum ice thickness can be 0.000358 m after 420 s of ice accretion. In this study, the total ice accretion mass was 59.5 kg, and the mass rate of ice accretion was about 0.14 kg/s;
- (3)
- Ice accretion on the balloon’s surface influences its thermodynamic performance. When the mass rate of ice accretion is about 0.14 kg/s, ice accretion prevents the balloon from ascending through the clouds and causes it to remain floating at the base of the clouds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Colozza, A. High-Altitude, Long-Endurance Balloons for Coastal Surveillance; NASA TM-2005-213427; NASA: Washington, DC, USA, 2005. [Google Scholar]
- Kreith, F.; Kreider, J.F. Numerical Prediction of the Performance of High Altitude Balloons; NCAR Technical Note NCAR-IN/STR-65; Atmospheric Technology Division, National Center for Atmospheric Research: Boulder, CO, USA, 1974. [Google Scholar]
- Carlson, L.A.; Horn, W.J. A New Thermal and Trajectory Model for High Altitude Balloons. In Proceedings of the 7th AIAA Aerodynamic Decelerator and Balloon Technology Conference, San Diego, CA, USA, 21–23 October 1981. [Google Scholar]
- Farley, R.E. BalloonAscent: 3-D simulation tool for the ascent and float of High-Altitude Balloons. In Proceedings of the AIAA 5th Aviation, Technology, Integration, and Operations Conference, AIAA 2005-7412, Arlington, VA, USA, 26–28 September 2005. [Google Scholar]
- Dai, Q.M.; Fang, X.D.; Li, X.; Tian, L. Performance simulation of high altitude scientific balloons. Adv. Space Res. 2012, 49, 1045–1052. [Google Scholar] [CrossRef]
- Louchev, O.A. Steady state model for the thermal regimes of shells of airships and hot air balloons. Int. Heat Mass Transf. 1992, 35, 2683–2693. [Google Scholar] [CrossRef]
- Xia, X.L.; Li, D.F.; Sun, C.; Ruan, L.-M. Transient behavior of stratospheric balloons at float conditions. Adv. Space Res. 2010, 46, 1184–1190. [Google Scholar] [CrossRef]
- Wang, Y.W.; Yang, C.X. A comprehensive numerical model examining the thermal performance of airships. Adv. Space Res. 2011, 48, 1515–1522. [Google Scholar] [CrossRef]
- Liu, Q.; Wu, Z.; Zhu, M.; Xu, W. A comprehensive numerical model investigating the thermal-dynamic performance of scientific balloon. Adv. Space Res. 2014, 53, 325–338. [Google Scholar] [CrossRef]
- Messinger, B.L. Equilibrium temperature of an unheated icing surface as a function of air speed. Aeronaut. Sci. 1953, 20, 29–42. [Google Scholar] [CrossRef]
- Shen, X.B.; Lin, G.P.; Yu, J.; Bu, X.Q.; Du, C.H. Three-Dimensional Numerical Simulation of Ice Accretion at the Engine Inlet. J. Aircraft. 2013, 50, 635–642. [Google Scholar] [CrossRef]
- Cao, Y.; Huang, J.; Yin, J. Numerical simulation of three-dimensional ice accretion on an aircraft wing. Int. J. Heat Mass Transf. 2016, 92, 34–54. [Google Scholar] [CrossRef]
- Liu, Q.; Yang, Y.; Wang, Q.; Cui, Y.; Cai, J. Icing performance of stratospheric airship in ascending process. Adv. Space Res. 2019, 64, 2405–2416. [Google Scholar] [CrossRef]
- Muhammed, M.; Virk, M.S. Ice Accretion on Fixed-Wing Unmanned Aerial Vehicle—A Review Study. Drones 2022, 6, 86. [Google Scholar] [CrossRef]
- Muhammed, M.; Virk, M.S. Ice Accretion on Rotary-Wing Unmanned Aerial Vehicles—A Review Study. Aerospace 2023, 10, 261. [Google Scholar] [CrossRef]
- Slingo, A. A GCM parameterization for the shortwave radiative properties of water clouds. J. Atmos. Sci. 1989, 46, 1419–1427. [Google Scholar] [CrossRef]
- Lindner, T.H.; Li, J. Parameterization of the optical properties for water clouds in the infrared. J. Clim. 2000, 13, 1797–1805. [Google Scholar] [CrossRef]
- Stephens, G.L.; Ackerman, S.; Smith, E.A. A shortwave parameterization revised to improve cloud absorption. J. Atmos. Sci. 1984, 41, 687–690. [Google Scholar] [CrossRef]
- Sun, Z.; Liu, J.; Zeng, X.N.; Liang, H. Estimation of global and net solar radiation at the Earth surface under cloudy-sky condition. J. Meteorol. Environ. 2014, 30, 1–9. [Google Scholar]
- Chylek, P.; Ramaswamy, V. Simple approximation for infrared emissivity of water clouds. J. Atmos. Sci. 1982, 39, 171–177. [Google Scholar] [CrossRef]
- Bourgault, Y.; Boutanios, Z.; Habashi, W.G. Three-Dimensional Eulerian Approach to Droplet Impingement Simulation Using FENSAP-ICE Part 1 Model, Algorithm, and Validation. J. Aircr. 2000, 37, 95–103. [Google Scholar] [CrossRef]
- Beaugendre, H.; Morency, F.; Habashi, W.G. FENSAP-ICEs Three-Dimensional In-Flight Ice Accretion Module ICE3D. J. Aircr. 2003, 40, 239–247. [Google Scholar] [CrossRef]
- Satellite Weather Application Platform v2.0. Available online: http://rsapp.nsmc.org.cn/geofy (accessed on 28 May 2023).



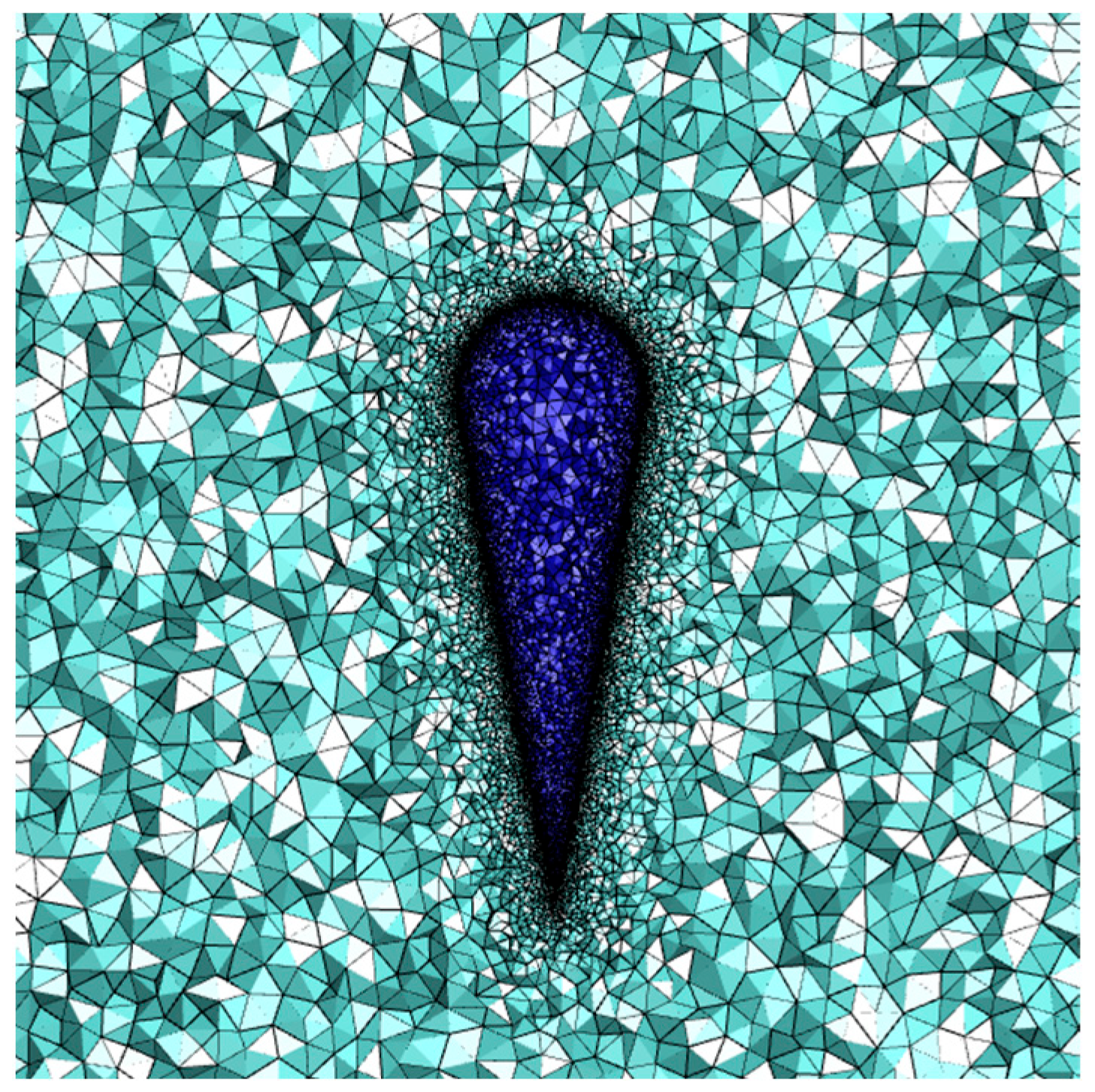



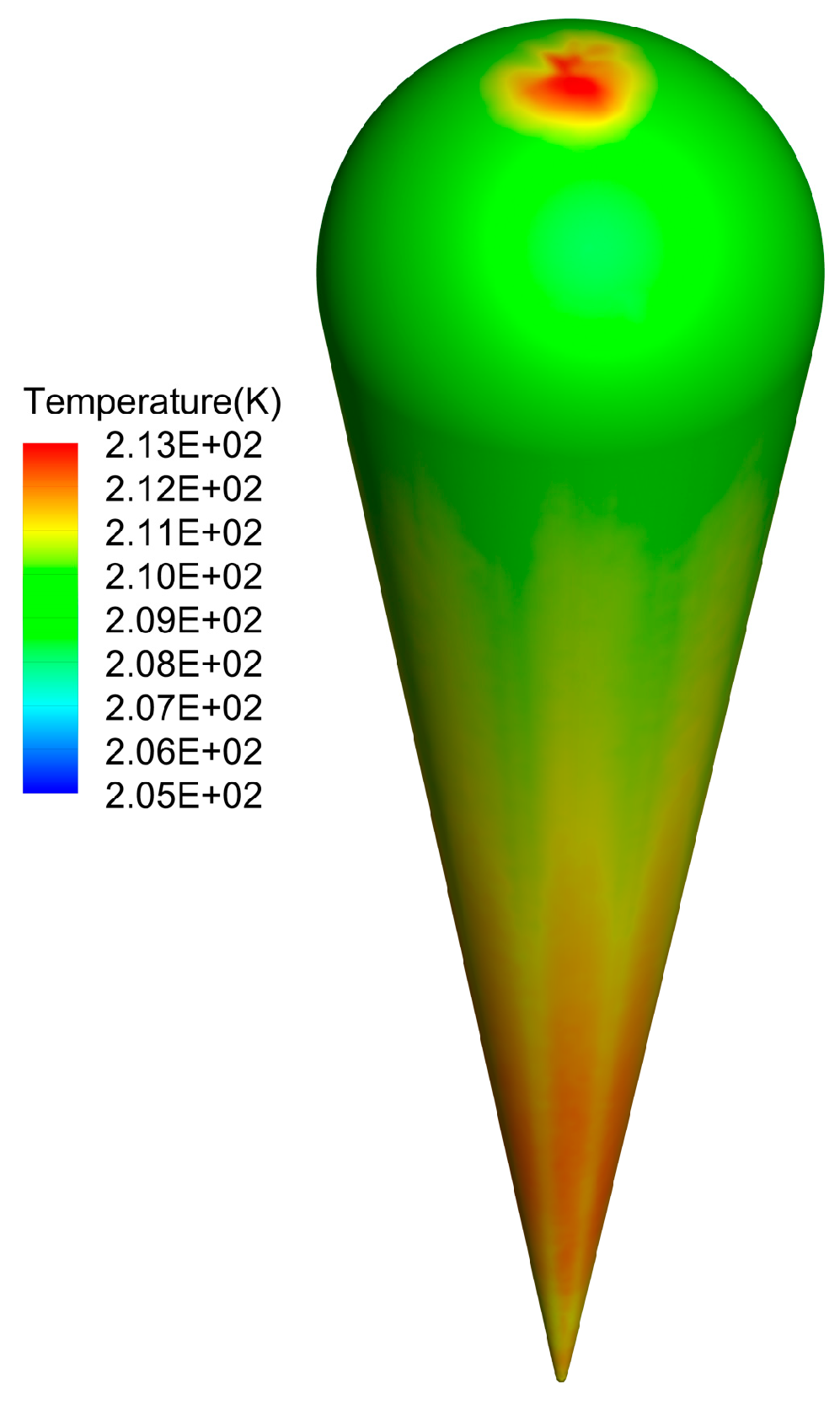
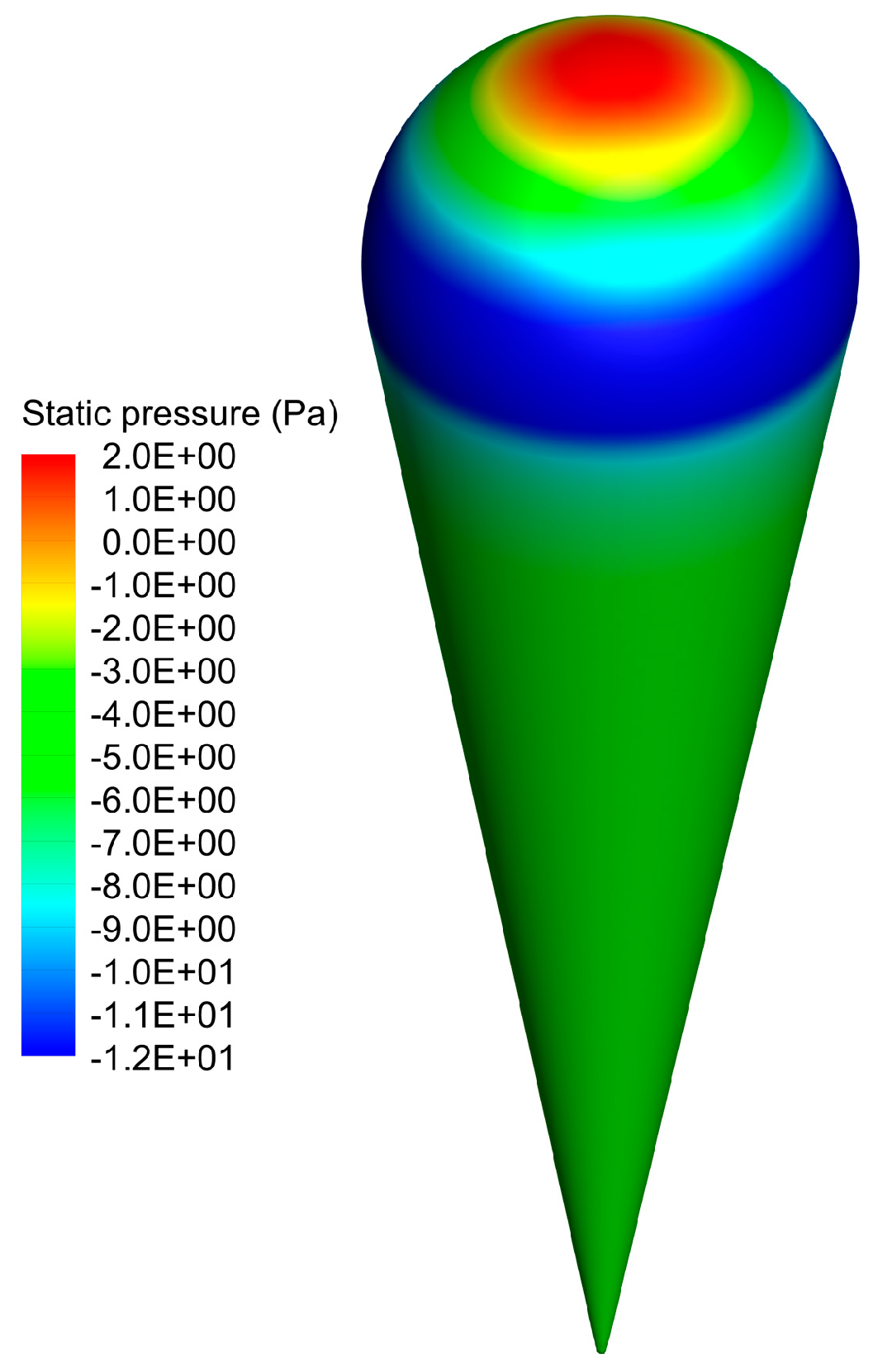
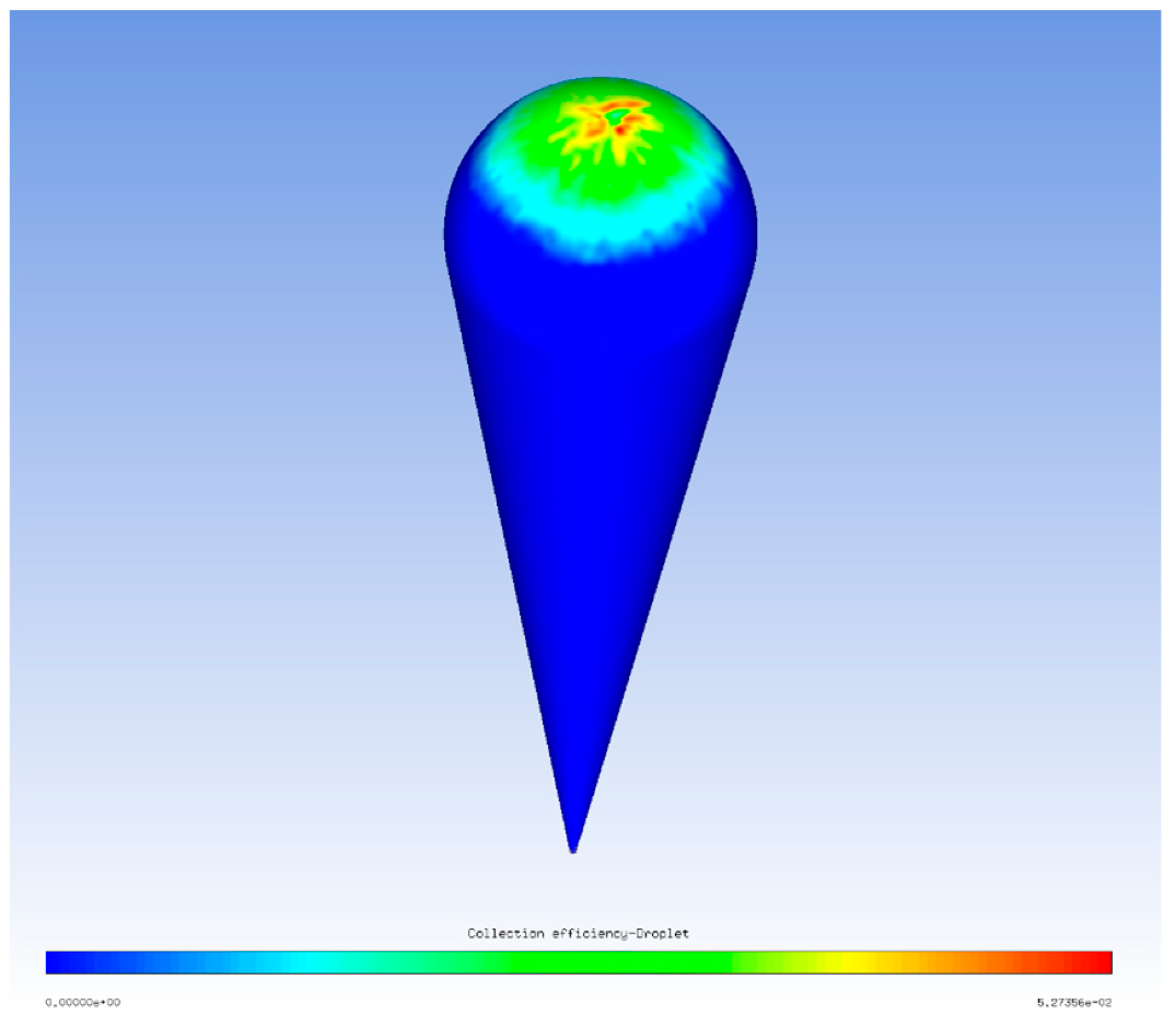

| Mesh ID | No. of Grid Cells (Millions) | Surface Mean Temperature (K) | Surface Maximum Temperature (K) | Surface Minimum Temperature (K) |
|---|---|---|---|---|
| 1 | 2.834 | 210.9 | 215 | 205 |
| 2 | 5.443 | 210.3 | 213 | 205 |
| 3 | 7.046 | 209.8 | 212 | 205 |
| Design Index | Value |
|---|---|
| Floating altitude | 25 km |
| Volume | 7240 m3 |
| Total mass | 280 kg |
| Balloon film mass | 120 kg |
| Payload mass | 124 kg |
| 2302.7 | 0.02 | 0.9 | 0.078 | 0.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Q.; He, L.; Yang, Y.; Zhao, K.; Li, T.; Zhu, R.; Wang, Y. The Influence of Ice Accretion on the Thermodynamic Performance of a Scientific Balloon: A Simulation Study. Aerospace 2024, 11, 899. https://doi.org/10.3390/aerospace11110899
Liu Q, He L, Yang Y, Zhao K, Li T, Zhu R, Wang Y. The Influence of Ice Accretion on the Thermodynamic Performance of a Scientific Balloon: A Simulation Study. Aerospace. 2024; 11(11):899. https://doi.org/10.3390/aerospace11110899
Chicago/Turabian StyleLiu, Qiang, Lan He, Yanchu Yang, Kaibin Zhao, Tao Li, Rongchen Zhu, and Yanqing Wang. 2024. "The Influence of Ice Accretion on the Thermodynamic Performance of a Scientific Balloon: A Simulation Study" Aerospace 11, no. 11: 899. https://doi.org/10.3390/aerospace11110899
APA StyleLiu, Q., He, L., Yang, Y., Zhao, K., Li, T., Zhu, R., & Wang, Y. (2024). The Influence of Ice Accretion on the Thermodynamic Performance of a Scientific Balloon: A Simulation Study. Aerospace, 11(11), 899. https://doi.org/10.3390/aerospace11110899






