Abstract
Space trajectory planning is a complex combinatorial problem that requires selecting discrete sequences of celestial bodies while simultaneously optimizing continuous transfer parameters. Traditional optimization methods struggle with the increasing computational complexity as the number of possible targets grows. This paper presents a novel reinforcement-learning algorithm, inspired by AlphaZero, designed to handle hybrid discrete–continuous action spaces without relying on discretization. The proposed framework integrates Monte Carlo Tree Search with a neural network to efficiently explore and optimize space trajectories. While developed for space trajectory planning, the algorithm is broadly applicable to any problem involving hybrid action spaces. Applied to the Global Trajectory Optimization Competition XI problem, the method achieves competitive performance, surpassing state-of-the-art results despite limited computational resources. These results highlight the potential of reinforcement learning for autonomous space mission planning, offering a scalable and cost-effective alternative to traditional trajectory optimization techniques. Notably, all experiments were conducted on a single workstation, demonstrating the feasibility of reinforcement learning for practical mission planning. Moreover, the self-play approach used in training suggests that even stronger solutions could be achieved with increased computational resources.
1. Introduction
Space trajectory planning falls under the category of hybrid optimal control problems, as it involves both discrete and continuous variables. It typically requires determining the best sequence of celestial bodies to visit while simultaneously optimizing transfer durations or costs. These celestial bodies can include planets, asteroids, or even other spacecraft.
The challenge of optimizing transfer sequences in space missions shares conceptual similarities with time-dependent vehicle routing problems [1], particularly in managing dynamic constraints and optimizing travel paths. These problems are categorized as NP-hard due to the rapid exponential increase in complexity as the number of variables grows.
To address this challenge, researchers have increasingly focused on automating the search process, as both the discrete sequence selection and continuous variables optimization demand significant computational resources. Various methodologies have been explored, including tree search algorithms [2,3,4,5], evolutionary algorithms [6,7,8,9,10,11,12,13,14], and hybrid approaches [15] that integrate both techniques to balance exploration and efficiency. These approaches have demonstrated the effectiveness of metaheuristics in exploring complex complex solution spaces.
In recent years, deep learning has shown great potential in addressing challenges related to space mission design, especially in local trajectory optimization [16,17,18,19,20]. Meanwhile, reinforcement learning has become increasingly popular for autonomous navigation and control. Its ability to make decisions under uncertainty makes it particularly useful for real-time guidance, allowing spacecraft to adapt dynamically to unexpected conditions during mission operations. Numerous studies have demonstrated outstanding performance across various problems, such as rendezvous and docking [21,22], planetary landing [23,24], and orbit transfer [25,26,27,28].
Outside the field of space engineering, the integration of Monte Carlo Tree Search (MCTS) with deep learning has become increasingly influential in reinforcement learning, especially following the success of DeepMind’s AlphaGo [29], the first self-play system to beat human world champions in Go. This system integrated MCTS with neural networks, utilizing the search framework to guide exploration and execute strategic decision-making at crucial branching points. The neural networks supplied both policy and value estimations, allowing AlphaGo to assess board positions with a level of sophistication that had previously been unattainable.
Earlier versions of AlphaGo depended on large datasets of human-played games. However, later iterations, such as AlphaGo Zero [30], introduced a groundbreaking approach by removing human supervision entirely. Instead of learning from expert gameplay, AlphaGo Zero started with random play and progressively improved through self-play and reinforcement learning. It employed an MCTS procedure guided by a neural network architecture capable of simultaneously estimating both policy and value functions. This novel approach not only resulted in superior performance but also underscored the efficacy of MCTS as a reinforcement-learning component in high-dimensional decision spaces. Building on these advancements, DeepMind subsequently unveiled AlphaZero [31], a generalization of the AlphaGo Zero paradigm. AlphaZero demonstrated the ability to master multiple complex board games, including chess, shogi, and Go, using an identical reinforcement-learning framework. Without any reliance on domain-specific knowledge, AlphaZero relied exclusively on self-play and MCTS-guided exploration, showcasing the generalizability of the method.
These approaches have proven highly effective in board games, with later algorithms like MuZero [32] showing that the simultaneous learning of a model of the environment, a value function, and a policy also results in achieving superhuman performance, even in playing computer games. However, their application to other domains remains relatively new and not yet fully explored. As far as the authors are aware, the only documented attempt at applying an AlphaZero-like algorithm to space trajectory planning is found in [33]. While this study presents encouraging results, it also reveals several limitations. The authors observe that the original Predictor Upper Confidence Trees (PUCT) algorithm tends to get stuck in suboptimal solutions. A key issue is the early reliance on the neural network for evaluation, which misguides the search and prevents it from finding optimal solutions. To address this issue, they incorporate rollouts for node evaluation, as in standard MCTS, before allowing the network to provide value estimates. Additionally, the experiments are limited to small target sets (with a maximum of 30 objects), whereas real-world missions may involve thousands of targets. The study does not explore how well the method scales to such larger problems, making scalability a significant concern. Lastly, by discretizing time, the authors effectively transform the action space into a fully discrete set, bypassing the inherent hybrid nature of space trajectory planning and potentially hindering the quality of solutions.
Board games and space trajectory planning differ significantly in their fundamental characteristics, unsurprisingly making the direct application of AlphaZero problematic. As noted by the authors of [34] in their review study, researchers from diverse fields have tailored the original algorithm to suit their specific needs, leading to a wide range of algorithmic variations. However, while new variants continue to emerge in individual studies, there has been little focus on developing a broader understanding of why certain adaptations work particularly well for specific problem settings.
This work presents AstroZero, a novel algorithm inspired by AlphaZero, specifically designed to handle hybrid discrete–continuous action spaces. A strong emphasis is placed on providing a clear, low-level understanding of its effectiveness in the context of space trajectory planning. In addressing these challenges, AstroZero not only resolves the problems identified in [33] but also explains why these types of issue arise in the first place. Moreover, the proposed algorithm is capable of dealing with tens of thousands of targets without any kind of time discretization. The outcome is a general self-play reinforcement-learning algorithm that can be applied seamlessly to any problem involving hybrid action spaces, extending beyond the domain of space trajectory planning.
The remainder of this article is organized as follows. Section 2 provides a thorough description of AstroZero, detailing the integration of reinforcement learning and MCTS to optimize space trajectories. It explains the reinforcement-learning pipeline, the self-play mechanism, a novel tree policy formulation, and the modified MCTS search procedure designed to handle hybrid discrete–continuous action spaces efficiently.
Section 3 presents the experimental setup and results. It describes the application of AstroZero to the eleventh Global Trajectory Optimization Competition (GTOC XI) problem, outlining the environment model, training procedure, and key performance metrics. The section also compares AstroZero’s performance against previous state-of-the-art solutions, demonstrating its effectiveness in optimizing interplanetary transfers.
Section 4 discusses the broader implications of AstroZero’s approach, highlighting its advantages over traditional trajectory optimization methods and its potential applicability to other complex planning problems. It also addresses the challenges encountered during training and optimization, providing insights into future research directions.
Finally, Section 5 summarizes the key findings of this study, emphasizing the contributions of reinforcement learning in autonomous space mission planning and outlining potential areas for further improvement and exploration.
2. Methods
AstroZero integrates reinforcement learning and MCTS to handle the complexities of space trajectory planning. Unlike traditional approaches that separately address discrete decision-making and continuous optimization, AstroZero unifies them within a structured learning framework. This section presents the key components of the proposed algorithm, including the description of the reinforcement-learning pipeline, self-play and training mechanisms, a novel tree policy formulation, and a modified MCTS search procedure. Through these methods, AstroZero is tailored to work with hybrid global planning problems.
2.1. Reinforcement Learning in AstroZero
As in AlphaZero, the proposed algorithm relies on a single neural network, , with parameters . Given a state s, the network produces two outputs: a probability distribution over possible actions and an estimated state-value, expressed as . The network architecture splits into two distinct heads in its final layers. One head is dedicated to generating the policy vector , which assigns probabilities to each action a given state s, and another head responsible for approximating the scalar state-value v, which predicts the expected return from the current state.
AstroZero’s neural network is trained through self-play, although in this case the term does not refer to competition between different parameters for the same neural network, as seen in AlphaZero. Instead, it describes an iterative learning process where the agent refines its policy by continuously interacting with its own generated experiences. In self-play, an MCTS search is performed from each states s using . The search produces a probability distribution over available actions, where the probability of selecting a particular action is proportional to the exponentiated visit count of its corresponding state–action pair:
Here, is the number of times the state–action pair has been visited and is a temperature parameter, influencing the degree of exploration versus exploitation. Rather than selecting the most visited action, this mechanism ensures a dynamic balance between trying new options and leveraging prior knowledge.
During training, the model’s parameters are continuously adjusted so that the policy prediction closely matches the action probabilities generated by MCTS, while the estimated state-value v aligns with the actual returns G observed from self-play. AstroZero, like AlphaZero, follows a policy iteration approach: MCTS serves as the mechanism for refining the policy, while state-values obtained through self-play are used for policy evaluation.
At the start of training, the policy-value network is initialized with random weights, meaning its decision-making is initially no better than standard MCTS (arguably worse, since state values given by rollouts are replaced with random predicted values). To encourage exploration and prevent the algorithm from prematurely converging to suboptimal policies, Dirichlet noise is added to action prior probabilities of the root node before each MCTS search. These prior probabilities are derived from the network’s policy output vector , which assigns a probability to every possible action. However, not all actions are necessarily valid in a given state, and some may be illegal according to the rules of the environment. These illegal actions are masked out: their probabilities are set to zero, and the remaining values are renormalized to ensure they form a valid probability distribution over only the legal moves. This masking process is not part of the learning algorithm itself but depends on the environment’s rules. It simply ensures that the agent considers only feasible actions.
Following the same strategy used in AlphaZero, the prior probabilities of each state–action pair are updated according to:
where the noise term is sampled from a Dirichlet distribution. The exploration parameter controls the balance between these two components. A commonly used value is adopted in this work, without specific adjustments.
A fundamental difference between AlphaZero and AstroZero is the way rewards are distributed. In AlphaZero, rewards are delayed until the end of an episode, only being assigned upon reaching a terminal state. AstroZero, however, operates in a deterministic space trajectory planning environment, where rewards can be allocated at each state transition. This shift in reward structure significantly impacts how MCTS computes, stores, and updates state-values throughout the search process.
To formalize this, consider an objective function J that represents the optimization goal. The reward at a given time step t is defined as the change in J from one step to the next, . The cumulative return over multiple steps can then be written as:
By allowing rewards to be assigned at each state transition, this approach enables the algorithm to obtain useful signals at each level of the tree. This continuous feedback mechanism helps MCTS steer the search process more efficiently. Consequently, the estimated action-value of a given state–action pair is given by:
where denotes the estimated value of the state that results from applying action to state .
In traditional reinforcement learning, when the agent–environment interaction may continue indefinitely with no predefined final time, a positive discount factor is typically used. The return is usually defined as:
This discount factor is necessary to ensure that the return remains bounded in infinite-horizon settings. This property is fundamental: the goal of the agent is to maximize G, and provides a consistent and practical way to define the optimality of actions at any given time.
However, for problems where the interaction is guaranteed to terminate, the return is inherently finite, even without discounting (as long as the sequence of rewards is bounded). In such settings, all rewards are equally important, regardless of when they occur during the interaction.
The planning task in space trajectories always has a time horizon; even if the ending time is unknown, the interaction is guaranteed to eventually end. AstroZero leverages this characteristic by treating rewards uniformly throughout the trajectory, eliminating the need for discounting and ensuring that decisions account for long-term outcomes as much as short-term gains. Setting yields a finite, bounded return and ensures that all rewards are equally weighted in the optimization process.
2.2. Self-Play and Training
AstroZero’s training process follows an asynchronous setup where multiple worker processes run independently, generating self-play data. These workers store their results in a shared replay buffer. Meanwhile, a dedicated training process continuously samples from this buffer, refining the neural network’s parameters before saving the updated model in a shared storage.
Rather than operating on outdated policies, each worker fetches the most recent network parameters from shared storage at the start of a new episode. This ensures that every self-play simulation is run with the latest training updates.
The relationship between self-play and training is illustrated in Figure 1, where an episode unfolds step by step. At every state in the sequence (where T denotes the terminal time step), MCTS conducts a search to determine the next move, following the selection rule defined in Equation (1).
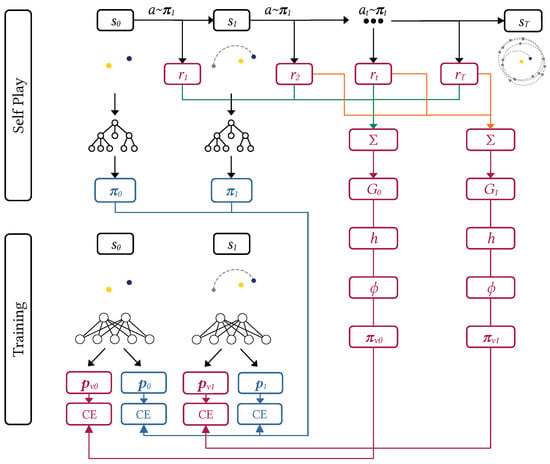
Figure 1.
AstroZero self-play and training pipeline.
Once an episode concludes, all visited states are paired with their respective returns G and the updated policy distributions , forming a dataset of training tuples that is added to the replay buffer. Notably, while different temperature parameters may have influenced action selection during self-play, the training process always assumes . This ensures that the neural network learns to reproduce the MCTS visit distribution without the added stochasticity from exploration.
The training objective is to align the network’s outputs with these targets. The policy head of the network is trained to predict a distribution over actions, which is optimized to match the MCTS distribution using Cross-Entropy (CE) loss. Simultaneously, the value head is tasked with predicting the expected return from each state. However, since the returns G can span a wide and potentially unbounded range, directly regressing on them can lead to unstable optimization due to large gradients from the value head overwhelming those from the policy head.
To address this issue, the network’s value head is redesigned to output value logits, as shown in the lower part of Figure 1. Following the approach in [32], returns sampled from the replay buffer undergo an invertible transformation before being fed into the network:
This transformation compresses extreme values, improving numerical stability. The transformed value is then mapped to a discrete categorical representation using a function , such that any transformed return can be reconstructed as a weighted combination of two adjacent discrete supports, and :
Instead of producing a single scalar, the network now outputs a probability distribution over these discrete support values.
During training, once a return has been transformed using h, the next step is to distribute it across the closest discrete support values. Instead of assigning a single numerical value, the function represents it as a weighted sum of its two nearest supports. For example, a return of 649.7729 is transformed by h into 25.16, which falls between the discrete supports at 25 and 26. The function then assigns to and to . Any other entries in the probability vector remain zero and the objective of training is for and to match and . This transformation does not alter the algorithm behavior (the aim is always matching the network predictions to the MCTS results) but facilitates training, because all the terms in the CE have similar magnitude and dominating gradients for the value head, that would arise for large return values, are avoided.
When the trained network is later used for inference in self-play, it produces a probability distribution over the predefined support set. The inverse mapping reconstructs the continuous value by combining the weighted contributions of the two closest supports. To return this value to its original scale, the final step involves applying the inverse of h, effectively undoing the earlier transformation. For instance, if the network predicts a probability of for the support value and for , outputs the value . Applying then rescales it, yielding 156.3438 as the estimated value for that state.
Crucially, all of these transformations happen internally during training and do not affect the search algorithm. Their sole purpose is to stabilize training by enforcing similar output magnitudes between the policy and value heads, ensuring balanced gradient updates.
Rather than sampling training examples uniformly from the replay buffer, AstroZero employs Prioritized Experience Replay (PER) [35], giving greater importance to examples where the Monte Carlo estimates differ significantly from the observed returns (indicating that the search is weak in that region). The priority assigned to each example i is determined by the absolute error between its MCTS value and actual return:
where represents the total number of stored examples and is a hyperparameter that controls the degree of prioritization. By emphasizing samples with higher errors, this method ensures that the network focuses more on difficult examples, improving its ability to correct inaccurate value estimates.
The network is trained using a weighted loss function that accounts for these sampling priorities:
Here, the sum runs over all examples in the minibatch , where is its size. The term serves as an importance-sampling correction factor, counteracting the bias introduced by PER. The two terms inside the brackets are the CE loss components represented in Figure 1; the target distributions and are the categorical encoding of the target value and the MCTS policy, respectively, and and are the network’s categorical value output and predicted policy distribution. L2 regularization is applied by the last term of the equation, adding a penalty term to the loss function proportional to the sum of the squares of the network’s weights, preventing overfitting.
Since high-priority examples are sampled more frequently, a weighting mechanism prevents them from dominating the training process. Each selected example is downscaled based on its priority:
where is a hyperparameter that controls how strongly this correction is applied. Again, a standard value is used for this hyperparameter, without optimization. This prevents the model from overfitting to a small subset of high-error experiences while still allowing important examples to be revisited frequently.
2.3. Tree Policy
During MCTS, a simulated trajectory descends through the search tree by following a tree policy, eventually reaching a leaf node. This policy is typically based on an upper confidence bound formula, which balances exploration and exploitation. In AlphaZero, DeepMind’s standard PUCT formula governs this process:
At any given point in the search, this equation evaluates each state–action pair using two key components. The first term, (see Equation (4)), represents the estimated return for taking action a from state s, favoring actions with high estimated returns. The second term introduces an exploration factor, weighted by the prior probability from Equation (2) (where for non-root states) and scaled by the exploration constant . This term encourages selecting actions that either have strong prior probabilities or have been explored less frequently, preventing the algorithm from prematurely converging on suboptimal decisions. By combining these two effects, PUCT ensures that MCTS systematically revisits uncertain state–action pairs, allowing the search to refine its value estimates over time.
In zero-sum games, the return of each episode is either 1 for winning, 0 for a draw, and −1 for losing the game. Therefore, action-values are constrained within the interval . In contrast, space trajectory planning deals with returns that can be arbitrarily large, as they depend on the performance index. Direct use of these unbounded values would lead to unbalanced terms in the PUCT formula. To address this, AstroZero normalizes action-values within the search tree to ensure stability and compatibility with MCTS.
Normalization is performed dynamically by referencing the highest and lowest observed values within the tree. Each action-value is rescaled based on the range of values encountered so far:
where the minimum and maximum are taken over all state–action pairs within the tree. This transformation ensures that all values fall within the range , making them numerically stable for use in the search process. The normalized value replaces in the PUCT formula.
When no visits have been made from a particular state, AstroZero defaults to the standard AlphaZero initialization, setting all unvisited normalized action-values to zero. Thus, the first choice at each level of subtrees is the action that has the highest prior probability. However, once at least one action has been explored, unvisited actions are assigned temporary estimates based on their prior probabilities relative to the most promising action:
where represents the (visited) action with the highest estimated value. This prevents the search from being overly influenced by already visited actions while allowing unexplored options to be considered in a more informed way.
During the initial phase of training, the neural network produces state-value estimates close to zero due to its uniformly initialized weights. At this stage, the prior probabilities are roughly uniform. In this setting, during each MCTS search, the state–action pair from the root node corresponding to the first trajectory to apply two simulated actions may generally assume a disproportionately high PUCT score. As a matter of fact, if the two rewards of such trajectory are significantly greater than zero, the corresponding action-value for the edge connecting the root to that trajectory becomes excessively large compared to others. The action-values of other visited edges, being determined by their respective rewards and the network’s initial baseline estimate, create a strong bias within the PUCT formula. This bias skews the search process toward longer trajectories, amplifying the effect.
This creates exactly the effect encountered by the authors of [33]. Without incorporating rollouts, they struggled to shift the tree policy away from focusing on specific subtrees. Although they did not normalize action-values, their maximum return was still somewhat comparable to the confidence bound, yet the problem persisted. Beyond this, we argue that another issue arises: during training, the network begins assigning excessively high prior probabilities to such overly-visited edges. As a result, the bias becomes self-reinforcing, further restricting exploration and preventing the discovery of potentially more optimal paths.
Another significant flaw emerges when applying the AlphaZero PUCT formula to space trajectory planning. The formula can be rewritten as:
where is given by
This reformulation sheds light on an important dynamic: the term acts as an adjustment factor that accounts for the difference between the policy prior and the empirical selection probability emerging from MCTS. If a particular action is chosen less frequently than expected, this ratio increases, raising its PUCT value and promoting further exploration. Conversely, when an action is selected more often than its prior would suggest, the ratio shrinks, lowering the PUCT value and discouraging additional visits. However, the impact of this adjustment is moderated by the square root of the sum-of-visit-counts in the denominator. As more iterations are performed, this correction diminishes in strength, meaning MCTS initially follows the prior closely but gradually shifts toward the observed action-values.
This characteristic of the formula leads to a tendency for MCTS to converge on highly skewed final policies. Even slight initial differences in action-values can cause large disparities in visit counts. As the total number of simulations increases, the influence of weakens, and actions with marginally better values receive a growing share of visits. This imbalance is then reinforced over time, creating a cycle in which certain actions are disproportionately favored while others remain underexplored, even if their estimated action-value is just slightly worse.
Such a dynamic is advantageous in decision-making environments with a large number of poor choices, such as board games, where early commitment to strong moves helps refine the search. However, in space trajectory planning, where transfer opportunities often come with similar costs, this behavior becomes problematic. If MCTS locks onto a particular trajectory too early, alternative paths, some of which may lead to better outcomes, are prematurely pruned.
To address this issue, AstroZero introduces a modified version of the PUCT formula:
where the factor r is defined as:
with being a scalar hyperparameter.
This revision improves exploration by ensuring a more balanced allocation of visits among competing actions with similar values. The first key change is in the denominator of the confidence bound, where replaces . This adjustment makes the exploration term decrease more directly with increments in the visit counts of specific pairs. Additionally, the factor r dynamically adapts based on the ratio , amplifying the confidence bound when a node is visited less frequently than expected and reducing it when a node is overvisited. As the visit count grows, r approaches unity, ensuring that the influence of the prior diminishes once a reliable action-value estimate is established. This prevents the model from disproportionately favoring high-prior but suboptimal actions while overlooking low-prior actions that may be valuable.
Together, these modifications prevent MCTS from collapsing into overly narrow policies, instead maintaining a more even search distribution across similarly valued actions. Moreover, the revised formula addresses issues related to uniform network initialization. In the original formulation, when priors are nearly uniform, the confidence bounds scale similarly across actions, allowing action-values to dominate and biasing the search toward longer trajectories. AstroZero’s version counteracts this effect by more aggressively penalizing overvisited state–action pairs with uniform priors while preserving the confidence scale for other pairs. As a result, the search process remains more balanced and avoids premature convergence on suboptimal paths.
2.4. Policy Iteration
Adapting AlphaZero to space trajectory planning introduces a major challenge: handling the hybrid nature of action spaces. Traditional MCTS only works when decisions are selected from a finite set. However, space trajectory optimization involves parameters like transfer durations that exist on a continuous spectrum. Prior research [36,37,38,39] has attempted to extend MCTS to continuous spaces using progressive widening, a technique designed to manage infinite action spaces by gradually expanding the set of considered actions as a node accumulates more visits.
The essence of progressive widening is to control the exploration process in continuous domains. Instead of evaluating an unmanageable number of actions at every step, the algorithm begins with a small set of sampled options and introduces more choices as the search revisits the node. This approach allows early exploration to remain broad while directing computational resources toward refining high-potential regions of the action space over time. In discrete MCTS, where the action space is inherently limited, this issue does not arise. However, applying progressive widening to hybrid discrete–continuous spaces introduces complications, particularly because it lacks a natural way to separate the discrete and continuous decision-making processes. One potential workaround is to apply progressive widening selectively to the continuous component of hybrid actions. However, this approach still suffers from the risk of excessive node expansion, which is impractical in environments with high branching factors.
AstroZero takes a fundamentally different approach by reinterpreting the problem within a fully discrete framework. Instead of treating continuous parameters as part of the action space, it restructures MCTS to operate entirely within a discrete Markov Decision Process (MDP). Under this paradigm, continuous parameters such as transfer durations are not sampled as part of the main search tree. Instead, they are optimized locally within each discrete decision after the action has been selected. This avoids the need for direct discretization while preserving the ability to fine-tune continuous variables where necessary.
This approach is particularly well-suited to space trajectory planning, where the number of discrete choices may be extremely large. A typical trajectory optimization scenario may involve thousands of potential targets, making a naive joint handling of discrete and continuous variables computationally infeasible. Explicitly modeling continuous parameters within the search tree would lead to uncontrolled growth, and a neural network responsible for evaluating all possible state–action pairs would require an intractably large architecture.
AstroZero circumvents this issue by integrating local optimization results into global decision-making. Rather than constructing an explicitly continuous search tree, it estimates action-values based on the best locally optimized outcomes. This allows MCTS to retain its efficiency while indirectly accounting for continuous variables. By separating broad trajectory exploration from fine-grained continuous adjustments, AstroZero ensures that the search remains computationally feasible without sacrificing accuracy in trajectory optimization.
In AstroZero, the MCTS algorithm perceives a fully discrete action space, where each action corresponds to selecting a specific celestial body as the next destination. The total number of available actions at any given step matches the number of celestial bodies under consideration. Figure 2 illustrates how this process unfolds within the search tree. At each step t in the MDP, the neural network processes the current state s to generate a prior policy and a scalar value estimate v. These outputs inform the MCTS procedure, which refines the prior into an improved policy while updating the state-value estimate through iterative simulations. Each node in the search tree corresponds to a state s, while edges connecting nodes represent actions a. These edges store key information, including the prior probability , the reward , and the visit count .
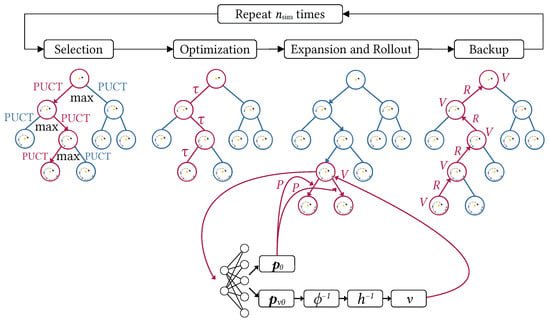
Figure 2.
MCTS in AstroZero.
To choose an action from a given state , the algorithm runs MCTS simulations, each consisting of four sequential steps:
- Selection.The search tree is traversed using the tree policy, prioritizing promising actions based on prior information and visit statistics.
- Optimization.When a leaf node is reached, the algorithm optimizes the transfer durations for all actions along the trajectory leading up to this state. This process maximizes the cumulative reward and produces a set of optimized rewards:Each value in this set represents the optimized reward for a specific transfer.
- Expansion and Rollout.The neural network evaluates the newly expanded leaf node, computing its policy vector and state-value estimate . The algorithm initializes new edges corresponding to each possible action from this node with:A new node is added to the search tree for each available action.
- Backup.The updated value estimates propagate back through the tree along the trajectory from the leaf to the root. The state-value of the leaf node is set as:The visit count and reward of the edge leading to the leaf are updated:For each preceding node in the trajectory (moving backward from to ), the algorithm updates the reward and state-value estimates using:
Before expanding a new leaf node, the neural network must first compute prior probabilities for all possible actions. To accomplish this task, the environment model must provide a list of legal actions from the current state. The priors generated by the network are masked to exclude illegal moves and renormalized to form a valid probability distribution, as mentioned in Section 2.1.
AstroZero avoids the computational challenges of explicitly expanding continuous decision spaces by integrating local optimization within discrete search. Instead of treating transfer durations as separate decision variables that require independent tree expansion, AstroZero embeds their optimization directly within the MCTS process. When an action is selected, the corresponding reward is not a fixed value but is determined by solving a local continuous optimization problem over the transfer durations .
The algorithm refines the estimated reward associated with each edge dynamically as more simulations are conducted. Each time an edge is traversed in the search tree, its estimated reward is updated based on the current local optimization of the trajectory that goes from root to leaf. Formally, the reward emerges as an expectation over optimal transfer durations determined during MCTS simulations:
This creates a feedback loop where the reward functions as a Monte Carlo estimate, converging toward an optimal value as the search progresses.
By structuring the problem in this way, AstroZero maintains a purely discrete search tree while still capturing the influence of continuous variables. This approach ensures that MCTS remains computationally manageable without sacrificing precision in trajectory planning. The refined action-value estimates that emerge from this process not only improve policy learning but also lead to more effective exploration, as high-value trajectories are prioritized without prematurely discarding alternatives due to suboptimal initial transfer durations.
The interaction between discrete action selection and continuous trajectory optimization introduces a limitation: the state assigned to a node in the search tree is determined by the transfer durations computed at the time of expansion. However, these durations are subject to refinement as additional simulations improve their values. This means that the state originally assigned to a node may no longer be an accurate representation of the actual state reached later in the search process. This discrepancy becomes particularly problematic in scenarios where the feasibility of future actions depends on arrival time. Even if the destination celestial body remains unchanged, slight variations in arrival time can shift the set of possible next actions due to time-sensitive constraints on available transfers. If the search tree were strictly tied to the initial transfer durations, it could prematurely exclude valid options associated with different time windows and those discovered in later simulations.
To address this issue, AstroZero does not treat the state at a given node as a fixed outcome of past decisions. Instead, during node expansion, the set of legal actions is defined over a time window rather than a single deterministic arrival time. This ensures that the search process remains robust to future refinements, preventing the tree from restricting viable paths.
Another critical design choice in AstroZero is the timing of action execution in the environment model. Unlike standard MCTS applications, where actions are applied sequentially at each decision step, AstroZero delays execution until an entire trajectory is optimized. This is because transfer durations influence the cumulative reward over the full trajectory, and committing to a duration before all subsequent decisions have been refined could lead to suboptimal results.
Instead of applying the selected action immediately, AstroZero stores only the discrete choice along with the improved policy distribution. At the end of each MCTS search, unselected actions at the decision node are discarded, but the root node remains unchanged to retain information relevant to the optimization process. Once a terminal state is reached, the algorithm optimizes all transfer durations one final time and executes the full sequence of actions in the environment. At this stage, the trajectory yields the final returns, ensuring that optimization occurs over the complete path.
2.5. Optimization Step
The choice of local optimization technique is independent of the proposed algorithm, and a wide variety of methods may be used for refining trajectory parameters. In this work, a subsimplex variant [40] of the Nelder–Mead method is applied, leveraging its ability to optimize without requiring gradient information. The optimizer is implemented with the open-source NLOPT library [41]. Since MCTS requires repeated evaluations of different trajectories, this derivative-free approach ensures computational efficiency while effectively adjusting transfer durations. The standard Nelder–Mead method, however, is prone to instability and slow convergence in high-dimensional settings, which is why the subsimplex variant is preferred, as it introduces adaptive simplex updates to improve robustness.
Mathematically, this optimization refines a trajectory by adjusting the transfer duration vector for a sequence of discrete actions leading from the root state to a leaf state . The objective function maximized during this step is the cumulative reward:
where is computed based on the mission environment model.
Crucially, the role of this optimization within the MDP is not to alter the state transitions directly but to refine the reward estimates that guide policy learning. Since the transition function remains discrete in the MCTS tree, the influence of continuous optimization is reflected in the action-value updates, rather than in the expansion of the tree itself. This interplay between discrete exploration and continuous refinement allows AstroZero to balance exploration and exploitation more effectively. The policy distribution is shaped not just by visit counts and prior probabilities but also by the improved rewards obtained from optimizing transfer durations. This integration ensures that, as the search progresses, it focuses on increasingly promising paths.
3. Results
AstroZero’s performance is tested on the GTOC XI problem [42]. This edition of the competition is an ideal testbed since it was the most competitive in the event’s history, with numerous teams later publishing their methodologies and findings [43,44,45,46,47,48].
The problem scenario envisions a futuristic mission in which humanity is constructing a Dyson ring, an early step toward a full Dyson sphere. The ring consists of twelve stations evenly placed along a circular orbit around the Sun. To supply these stations with construction materials, ten motherships are launched from Earth, each assigned a set of asteroid targets to be transferred to the designated orbit. The transport of asteroids is made possible through Asteroid Transfer Devices (ATDs), which generate thrust by using asteroid material as propellant.
What makes this optimization problem particularly challenging is the need to coordinate multiple interdependent mission phases. These include selecting target asteroids, planning flyby sequences, and optimizing how to allocate resources among the stations. Each decision influences the overall outcome, requiring advanced combinatorial optimization techniques to balance trade-offs across the mission’s various phases.
3.1. Problem Description
The competition organizers [42] outline a mission centered around designing a Dyson ring orbit with 12 construction stations and optimizing the transfer of asteroids to this orbit. The primary objective is to maximize the minimum total mass delivered to any station while minimizing propellant consumption. A conceptual diagram in Figure 3 illustrates a mothership performing asteroid flybys and the subsequent material transfer to the designated stations.
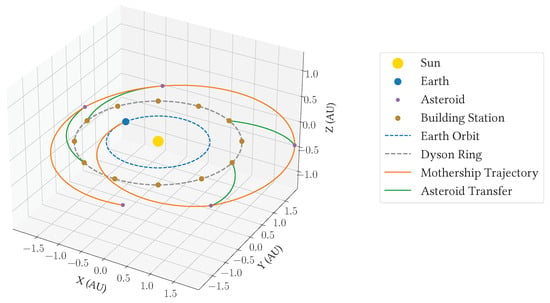
Figure 3.
Representation of the building process of the Dyson ring.
The mission unfolds over a 20-year period, running from 1 January 2121 to 1 January 2141, corresponding to Modified Julian Date (MJD) 95,739.0 to 103,044.0. The mission is considered complete when the last asteroid successfully reaches its assigned station.
The mission allows for the deployment of up to 10 motherships, each launching from Earth without directional constraints. Their departure hyperbolic excess velocity can vary between 0 and . Once in space, these motherships operate concurrently, executing sequences of impulsive maneuvers and asteroid flybys to optimize their trajectories.
During each asteroid flyby, an ATD is deployed, imparting an instantaneous impulse for rendezvous. In order for an ATD to be released, each mothership must approach an asteroid with a relative velocity not exceeding . After activation, the ATD remains operational, continuously providing thrust to redirect the asteroid toward its assigned construction station.
The Dyson ring stations are positioned at equal angular intervals along a circular orbit. Mission planners have flexibility in defining four critical orbital parameters of the ring: the semimajor axis (a), inclination (i), right ascension of the ascending node (), and the phase of the first station () at the starting epoch. While asteroids can be transported to any station, scheduling constraints must be respected. To prevent simultaneous asteroid arrivals at multiple stations, a minimum interval of 90 days must separate each station construction.
The trajectories of both motherships and asteroids evolve according to Keplerian motion in the J2000 heliocentric ecliptic reference frame, as imposed by the GTOC XI rules. Their position and velocity, represented as and , evolve according to the following equations of motion:
where is the gravitational parameter of the Sun. It is worth noting that a different dynamical model (e.g., including perturbations) would only affect the performance index value and how it is calculated, without influencing how the algorithm searches for optimal solutions. From the algorithm’s perspective, only the resulting transitions between states and their associated rewards matter, not the physical model that governs how those transitions occur.
The motherships execute impulsive maneuvers: velocity changes occur instantaneously at discrete points along their trajectories. In contrast, asteroid transfers rely on ATDs, which provide continuous thrust with a constant acceleration of .
Since ATDs use asteroid material as propellant, the mass of the asteroid gradually decreases over time. The loss rate is proportional to the asteroid’s initial mass :
with . As a result, the asteroid’s remaining mass upon reaching its construction station is determined by:
where represents the duration of the asteroid’s transfer under ATD propulsion.
Once an asteroid is assigned to a construction station, it cannot be redirected or transferred again. Similarly, each ATD is dedicated to a single asteroid and remains active only until the asteroid reaches its designated station, at which point the device ceases operation. Throughout the mission, gravity-assisted maneuvers are not permitted for either the motherships or the asteroids, requiring all trajectory adjustments to rely solely on propulsion. Additionally, to prevent excessive proximity to the Sun, both motherships and asteroids must maintain a minimum heliocentric distance of at all times. Motherships are also subject to maneuvering constraints, as they are allowed no more than four impulsive maneuvers between launch and their first asteroid encounter, as well as between any two successive asteroid flybys.
The competition required participants to develop an optimal asteroid selection and transfer strategy. With a dataset of 83,453 candidate asteroids, each characterized by specific orbital parameters and an initial mass, competitors had to determine the best way to allocate these resources among the 12 construction stations.
Success in the competition hinged on balancing multiple objectives. The goal was to maximize the minimum mass delivered to any single station, ensuring an even distribution of materials. If represents the residual mass of asteroid i upon arrival at station j, then the total mass collected at station j is given by:
where is the number of asteroids transferred to station j. The station receiving the smallest total mass determines the minimum collected mass across all stations:
In addition to maximizing , teams had to simultaneously minimize two other factors: the total velocity change executed by the fleet of motherships and the semimajor axis of the Dyson ring orbit. The competition’s performance index was defined as:
where is measured in and (measured in ) and (measured ) are the dyson ring radius and the total velocity increment of the k-th mothership, respectively.
To encourage early submissions in the competition timeframe, a bonus factor B scales the formula. Initially set at , this incentive decreased rapidly in the early stages of the competition and approached by the competition’s conclusion. Since the most competitive solutions were submitted in the later phases [42], this work sets .
3.2. Reinforcement-Learning Approach
The proposed algorithm is applied to a specific aspect of the GTOC XI problem. The focus is on optimizing the mothership’s trajectory rather than on tackling the entire mission design, including station configuration and material distribution. By assuming a predefined Dyson ring at , the arrival mass of each asteroid to the ring can be easily estimated. Although this constraint limits solution optimality, it enables a focused approach to trajectory planning by reducing the complexity of the problem.
This value of the Dyson ring’s semimajor axis is not the result of any optimization. During the actual competition, only a few teams attempted to optimize . Increasing its value results in larger masses at the ring. However, appears quadratically in the denominator of the performance index, suggesting that the impact of variations in on the final performance is relatively modest. Therefore, while an optimal value must exist, its effect on the solution sequences generated by the algorithm is expected to be minimal. This allows us to focus on optimizing the trajectory and other factors without the added complexity of tuning .
Reinforcement learning offers an effective method for solving this problem. The challenge is inherently combinatorial, requiring sequential asteroid selections that influence fuel efficiency and collected mass. Each decision constrains future choices, as favorable trajectories depend on the relative positions of the celestial bodies, which evolve throughout the mission. Traditional heuristics have proven useful in trajectory optimization, but a key advantage of the proposed approach is its heuristic-free nature. The learning agent autonomously explores the solution space, adapting its strategy through experience and potentially discovering novel, non-intuitive paths that conventional methods might overlook.
Although the problem is framed in a multi-agent setting, AstroZero is applied to select the asteroid sequence of a single mothership. The various trajectories found can then be combined to maximize the overall performance index. Let denote the total estimated mass (at the ring) collected by all motherships; an upper bound on is given by . If M denotes the estimated mass contribution of a single mothership to the Dyson ring and denotes its total velocity increment, the corresponding J contribution to the performance index is then given by:
This formula represents an approximate upper bound on the competition’s performance index. As a matter of fact, if all motherships have identical velocity increments and collect equal masses, and . To estimate M, a set of precomputed optimal low-thrust trajectories is used to derive an interpolation formula based on the orbital elements of the asteroids.
3.3. Environment Model
To reduce the size of the network’s policy head, only a subset of asteroids is included in the action space. Asteroids contributing less than to the Dyson ring are excluded from optimization, limiting the candidate set to 16,713 and significantly improving computational efficiency.
A key challenge in modeling the environment is that the state of the mothership, defined by its current epoch, position, and velocity, is not fully Markovian. In a true Markov process, future decisions depend only on the present state. In this problem, the set of viable asteroid rendezvous options is shaped by the mothership’s trajectory history. Previously visited asteroids influence the remaining available targets and the amount of collected mass, while the efficiency of the trajectory up to that point directly affects the estimated return.
To account for the dependencies introduced by past decisions, the state representation is defined as:
where and are the position and velocity vectors of the mothership, t is the epoch, is the total velocity increment expended up to this state, and M denotes the total mass of asteroids collected up to this state.
The term is an eight-dimensional embedding that encodes information about the set of visited asteroids in compact form. To construct , each asteroid ID is mapped to a fixed eight-dimensional vector using an embedding layer. Given an asteroid ID i, this layer returns the i-th row of a predefined embedding matrix of shape , where N is the total number of distinct asteroid IDs considered. These vectors serve only as identifiers in a continuous space and are not updated during training. The final embedding is then obtained by averaging the embedding vectors of all visited asteroids. This averaging produces a fixed-size, permutation-invariant representation that compactly reflects the visit history, enabling the agent to track which asteroids have been visited without increasing the state dimensionality with each new visit. This enables the reinforcement-learning agent to track visited asteroids while keeping the input representation compact.
An explicit tuning of the embedding dimensionality was not performed. The choice of eight dimensions was based on a practical trade-off: it provides enough capacity to yield a sufficiently expressive representation of the visit history, while keeping the overall state vector compact. Notably, the state vector without the embedding already has nine dimensions. Using an embedding much larger than this would have unbalanced the state representation, potentially complicating the learning process and increasing computational cost. An embedding size of eight was therefore considered a reasonable choice to capture historical information while keeping the overall state dimensionality within a manageable range.
Competition results [48] show that two-impulse maneuvers consistently yield near-optimal performance. This is largely because the relatively short mission duration favors direct transfers, and many asteroids share similar orbits, allowing for low-cost maneuvers that complete in under one full revolution. Therefore, transfer legs are direct Lambert arcs between the asteroids’ positions.
The environment model governs the state transitions, yielding a new state and a scalar reward after each applied action. Each action leads to a new trajectory segment, determined by solving Lambert’s problem, with the updated state reflecting the mothership’s position, velocity, time, expended , collected mass, and asteroid visit history at the end of the transfer. The reward measures the change in the performance index.
A crucial aspect of this process is computing the velocity adjustments needed at each asteroid encounter. While the primary trajectory follows a sequence of Lambert arcs, additional velocity corrections may be required to satisfy rendezvous constraints. In cases where the mothership’s velocity is not within the limit with respect to the asteroid’s velocity, an extra impulse is applied, following the approach described by the problem organizers [42].
At the start of the mission, the mothership can depart Earth in any direction, with an initial hyperbolic excess velocity ranging from 0 to . The first transfer is determined by solving Lambert’s problem for the departure trajectory. If the velocity increment required to transition from Earth’s velocity to the initial velocity of the Lambert arc is more than , an additional impulse is applied; otherwise, the velocity is directly set to the initial velocity on the transfer trajectory. To allocate enough time for final transfers to the Dyson ring, the mothership sequence is limited to a timeframe ending on 1 January 2137, allowing 3 years for final transfers.
At each step, the environment determines the set of legal actions by filtering out previously visited asteroids. While any asteroid with a feasible Lambert transfer could theoretically be a valid destination, considering all possibilities is computationally impractical. Unlike in board games, where some moves might yield unexpected results, space trajectory planning inherently favors low-cost transfers, and very expensive maneuvers are never part of optimal solutions. Therefore, Lambert arcs between asteroid pairs are precomputed at monthly intervals, starting from the initial mission date. Transfer durations are restricted to between 2 and 8 months, with steps of 1 month. The following constraints define the legal action space: asteroid-to-asteroid transfers are only allowed if both departure and arrival velocities relative to their respective asteroids remain below . For Earth departures, the relative velocity must be below , while the arrival relative velocity at the first asteroid is permitted up to , as the first flyby is the most expensive. The subsequent transfers are performed between bodies with similar orbits, making maneuvers less demanding. However, the first intercept requires a significant trajectory adjustment, resulting in a higher velocity increment.
These precomputed transfers are only used to mask actions at each expansion step in MCTS. To mitigate the risk of pruning promising actions due to small deviations in time during AstroZero’s optimization step, the environment considers transfers occurring within a two-month window around the precomputed Lambert solutions.
3.4. Performance
AstroZero was trained on the GTOC XI environment, running for 1 million minibatches on a single machine equipped with a 13th Gen Intel Core i9-13900 processor and two NVIDIA GeForce RTX 3070 Ti GPUs. To generate training data, 24 asynchronous threads played in self-play episodes, each starting at a randomly selected time within the first two years of the mission. Move selection was based on 200 MCTS iterations, a relatively low number imposed by the high computational cost of the modified MCTS, due to the optimization step. To manage this constraint effectively, two modifications are introduced. Instead of optimizing all transfer times from root to leaf during each MCTS simulation, the model only optimizes the last three transfers within each path. A complete optimization is performed only at the end of an episode, reducing computational overhead while still refining transfer durations.
To enhance search efficiency, progressive widening is implemented, allowing the tree to grow gradually instead of expanding all possible actions from a node immediately. As the search progresses, additional nodes are introduced only when the number of visits of state–action pairs from a node satisfies the condition:
where k and are two scalar values and is the visit count of each action from state s. When this condition is satisfied, a new child node from state s is added. The expansion follows a priority-based strategy, selecting the action with the highest prior probability among those not yet explored. By dynamically adjusting the branching factor, this method allows deeper exploration in promising regions while still keeping MCTS simulations computationally manageable. The parameters and governed the progressive widening dynamics, while upon expansion each node was assigned a maximum of 20 children. This was purely an efficiency trade-off: if sufficient computational resources were available, a larger number of MCTS simulations could replace the need for progressive widening altogether.
The temperature parameter for action selection started at 1 and gradually decreased to 0.1 over 500,000 training steps, encouraging greater exploitation as training progressed. Exploration was enhanced by Dirichlet noise, with an exploration fraction of . Action probabilities were sampled from a Dirichlet distribution, according to , where represents the number of legal actions at a given node. The exploration constant was , and the parameter in Equation (17) was set to 0.01.
The neural network architecture consisted of a fully connected feedforward network. The input vector passed through two hidden layers of 512 units each, followed by a larger layer containing 1024 units. The value head had two additional hidden layers with 256 units each, and its output mapped to a 201-unit categorical support, covering integer values from −100 to 100 (so that passing through and , scores approximately from −10,000 to 10,000 are represented). The policy head featured two hidden layers of 1024 units and an output layer containing one unit per discrete action, amounting to 16,713 output units.
The network was initialized with random parameters and trained using stochastic gradient descent with momentum. Training samples were drawn using PER with parameters and from the most recent 400 games. The learning rate followed an exponential decay schedule, starting at 0.1 and gradually decreasing to 0.001 over 750,000 steps. A momentum factor of 0.9 was used, and the weight decay coefficient of Equation (9) for L2 regularization was set to . A new network checkpoint was generated every 1000 steps. The self-play workers always used the most recent checkpoint, allowing the model to progressively refine the latest policy and value estimates as training advanced.
Most of the hyperparameters, such as , , , , and , were set to commonly used default values. This choice reflects the focus of this work, which is to evaluate the effectiveness of the proposed algorithm (even with non-optimized hyperparameters) rather than to optimize hyperparameter settings. Nonetheless, a sensitivity analysis of these parameters could provide valuable insights into the robustness of the algorithm and is left for future work. Similarly, the impact of the neural network architecture on solution quality was not explored in depth. The chosen architecture was designed to provide sufficient capacity for the two output heads while also adhering to memory constraints imposed by the available hardware. Investigating architectural variations remains an interesting direction for future research.
AstroZero’s training proceeded for eight days, during which it played around 4000 games and collected over 700,000 samples. With a limited number of self-play workers, maintaining balance between training updates, data collection, and replay buffer size is critical. Training was paused whenever network parameters updates outpaced episode steps by a factor of 10. The efficiency of training depends on the careful tuning of dataset size and update frequency. If training progresses too quickly relative to data collection, the model is prone to overfitting. In addition, if data collection is slow and the replay buffer is too big, the model risks relying on outdated policies. The computational constraints of our setup led to extended training times, a challenge that could be mitigated by increasing the number of self-play workers.
As shown in Figure 4, AstroZero’s performance steadily improved throughout training. Even in early iterations, when the neural network was initialized with random parameters, the model demonstrated promising results. By the midpoint of training, self-play scores were comparable with the top-ranked competition entries. By the end of training, the algorithm discovered trajectories close to the winning solutions. The highest recorded score reached 8144.
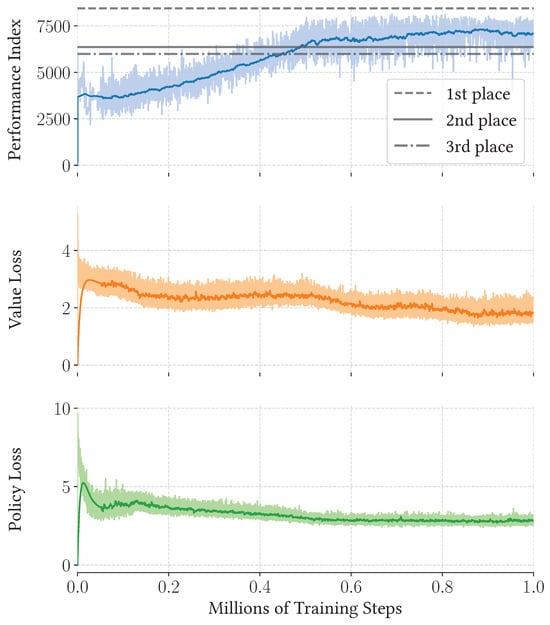
Figure 4.
Peformance index, value loss, and policy loss over the course of training.
A revised leaderboard in Table 1 compares AstroZero’s performance with the original competition results, providing a clearer perspective on its strengths. In the table, represents the average total velocity increment of the motherships. AstroZero strikes a competitive balance between fuel efficiency and mass collection. While the ESA-ACT Joint Team achieves a higher minimum station mass due to their larger Dyson ring radius, this comes at the expense of a lower overall score.

Table 1.
Revised GTOC XI leaderboard.
AstroZero’s trajectory planning closely matches the efficiency and mass collection of the competition’s winner, though it falls slightly short in both aspects. However, an important distinction is that AstroZero operated with a smaller candidate asteroid pool, whereas the winning team later refined their trajectory by considering a broader set of asteroids. Additionally, AstroZero imposed an upper bound on , meaning it did not explicitly optimize the subdivision and distribution of asteroids among the building stations. That said, most teams improved their performance post-search by incorporating additional asteroids not initially considered, leading to further improvements.
Since AstroZero’s algorithms worked with a limited subset of asteroids, its reported scores likely provide a reliable approximation of its final performance, assuming that similar post-processing refinements were applied. Future research could expand the asteroid pool and explicitly address the dispatching to building stations for a more precise evaluation. By broadening the search to include more asteroids, better trajectories may emerge, particularly in cases where no efficient transfer exists between massive asteroids. In such scenarios, finding an inexpensive transfer to a smaller asteroid that serves as a bridge to promising chains could yield superior results.
4. Discussion
AstroZero showcases the potential of reinforcement learning in space trajectory planning, even with limited computing power. Traditional methods depend on expert knowledge and carefully designed rules, but AstroZero learns to improve its performance on its own, without needing human guidance. This marks a major shift in how trajectory optimization is done, replacing manual fine-tuning with an automated, goal-driven approach. By avoiding reliance on preset rules, AstroZero proves that reinforcement learning can effectively tackle complex space mission challenges.
While AstroZero is inspired by large-scale reinforcement-learning programs like AlphaGo Zero and AlphaZero, it operates with far fewer resources. DeepMind’s models were trained on thousands of high-performance processors, while this study was conducted on a custom-built workstation assembled and operated in Turin, Italy. The system is equipped with a 13th Gen Intel Core i9-13900 CPU (made in China for Intel Corporation, Santa Clara, CA, USA) and two NVIDIA GeForce RTX 3070 Ti GPUs (made in China for NVIDIA Corporation, Santa Clara, CA, USA), using only 24 self-play workers. Despite this difference in computing power, AstroZero delivers results that rival the winning team from GTOC XI, demonstrating the efficiency of its approach.
Beyond its direct application to the GTOC XI problem, AstroZero represents a compelling direction for future research in interplanetary mission design. It successfully handles tens of thousands of potential targets without relying on time discretization, a capability that sets it apart from many conventional trajectory optimization methods. In doing so, AstroZero not only advances the field of space trajectory optimization but also provides a foundation for tackling a wide range of scientific and engineering problems characterized by hybrid action spaces.
While prior research has introduced adaptations of AlphaZero for various domains, there has been little focus on understanding why specific modifications work well for certain problem settings. This work bridges this gap in hybrid action spaces by providing a low-level analysis of the reinforcement-learning dynamics. Future research could refine and extend this framework to more complex mission architectures.
5. Conclusions
A new general reinforcement-learning algorithm is benchmarked against the GTOC XI problem for global trajectory optimization, illustrating how reinforcement learning can effectively discover interplanetary transfer strategies. The novel hybrid method for handling continuous variables within a discrete Markov Decision Process delivers outstanding results, securing second place in the final leaderboard and coming close to first place. These achievements are realized using a single workstation, underscoring the potential of the algorithm in a more computationally efficient setting.
Beyond its immediate application, this work highlights the scalability and adaptability of reinforcement learning in autonomous space mission planning. AstroZero’s ability to efficiently navigate large-scale hybrid optimization problems suggests that reinforcement learning could become a viable alternative to traditional methods, particularly as computational resources continue to advance. Moreover, its success in handling vast search spaces without time discretization indicates that similar approaches could be extended to other domains where discrete and continuous decision-making must be seamlessly integrated.
Future research could explore wider search spaces, incorporate additional mission constraints, or apply the approach to broader space exploration challenges. With continuous advancements in machine learning, reinforcement-learning-based trajectory optimization could play a crucial role for future autonomous mission planning, paving the way for more adaptive and scalable space exploration strategies.
Author Contributions
Conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, A.F.; project administration, resources, supervision, L.C.; writing—original draft, review & editing, A.F. and L.C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the arcticle.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Malandraki, C.; Daskin, M.S. Time Dependent Vehicle Routing Problems: Formulations, Properties and Heuristic Algorithms. Transp. Sci. 1992, 26, 185–200. [Google Scholar] [CrossRef]
- Armellin, R.; Bellome, A.; Fu, X.; Holt, H.; Parigini, C.; Wijayatunga, M.; Yarndley, J. GTOC12: Results from TheAntipodes. Astrodynamics 2025, 9, 55–75. [Google Scholar] [CrossRef]
- Daniel Hennes, D.I. Interplanetary Trajectory Planning with Monte Carlo Tree Search. In Proceedings of the Twenty-Fourth International Joint Conference on Artificial Intelligence (IJCAI 2015), Buenos Aires, Argentina, 25–31 July 2015. [Google Scholar]
- Federici, L.; Zavoli, A.; Colasurdo, G. On the use of A* search for active debris removal mission planning. J. Space Saf. Eng. 2021, 8, 245–255. [Google Scholar] [CrossRef]
- Viavattene, G.; Devereux, E.; Snelling, D.; Payne, N.; Wokes, S.; Ceriotti, M. Design of multiple space debris removal missions using machine learning. Acta Astronaut. 2022, 193, 277–286. [Google Scholar] [CrossRef]
- Acciarini, G.; Izzo, D.; Mooij, E. MHACO: A Multi-Objective Hypervolume-Based Ant Colony Optimizer for Space Trajectory Optimization. In Proceedings of the 2020 IEEE Congress on Evolutionary Computation (CEC), Glasgow, UK, 19–24 July 2020; pp. 1–8. [Google Scholar] [CrossRef]
- Ceriotti, M.; Vasile, M. MGA trajectory planning with an ACO-inspired algorithm. Acta Astronaut. 2010, 67, 1202–1217. [Google Scholar] [CrossRef]
- Englander, J.A.; Conway, B.A. Automated Solution of the Low-Thrust Interplanetary Trajectory Problem. J. Guid. Control. Dyn. 2017, 40, 15–27. [Google Scholar] [CrossRef]
- Gad, A.; Abdelkhalik, O. Hidden Genes Genetic Algorithm for Multi-Gravity-Assist Trajectories Optimization. J. Spacecr. Rocket. 2011, 48, 629–641. [Google Scholar] [CrossRef]
- Masi, L.; Vasile, M. A multidirectional Physarum solver for the automated design of space trajectories. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation (CEC), Beijing, China, 6–11 July 2014; pp. 2992–2999. [Google Scholar] [CrossRef]
- Olds, A.D.; Kluever, C.A.; Cupples, M.L. Interplanetary Mission Design Using Differential Evolution. J. Spacecr. Rocket. 2007, 44, 1060–1070. [Google Scholar] [CrossRef]
- Simões, L.F.; Izzo, D.; Haasdijk, E.; Eiben, A.E. Multi-rendezvous Spacecraft Trajectory Optimization with Beam P-ACO. In Proceedings of the Evolutionary Computation in Combinatorial Optimization, Amsterdam, The Netherlands, 19–21 April 2017; Hu, B., López-Ibáñez, M., Eds.; Springer: Cham, Switzerland, 2017; pp. 141–156. [Google Scholar]
- Zhang, Y.; Zhu, Y.; Zhang, J.; Wang, H.; Jin, K.; Fu, L. GTOC12: Methods and results from the National University of Defense Technology. Astrodynamics 2025, 9, 129–141. [Google Scholar] [CrossRef]
- Zuo, M.; Dai, G.; Peng, L.; Wang, M.; Liu, Z.; Chen, C. A case learning-based differential evolution algorithm for global optimization of interplanetary trajectory design. Appl. Soft Comput. 2020, 94, 106451. [Google Scholar] [CrossRef]
- Vasile, M.; De Pascale, P. Preliminary Design of Multiple Gravity-Assist Trajectories. J. Spacecr. Rocket. 2006, 43, 794–805. [Google Scholar] [CrossRef]
- D’Ambrosio, A.; Schiassi, E.; Curti, F.; Furfaro, R. Pontryagin Neural Networks with Functional Interpolation for Optimal Intercept Problems. Mathematics 2021, 9, 996. [Google Scholar] [CrossRef]
- Izzo, D.; Öztürk, E. Real-Time Guidance for Low-Thrust Transfers Using Deep Neural Networks. J. Guid. Control. Dyn. 2021, 44, 315–327. [Google Scholar] [CrossRef]
- Li, H.; Baoyin, H.; Topputo, F. Neural Networks in Time-Optimal Low-Thrust Interplanetary Transfers. IEEE Access 2019, 7, 156413–156419. [Google Scholar] [CrossRef]
- Mughal, A.H.; Chadalavada, P.; Munir, A.; Dutta, A.; Qureshi, M.A. Design of deep neural networks for transfer time prediction of spacecraft electric orbit-raising. Intell. Syst. Appl. 2022, 15, 200092. [Google Scholar] [CrossRef]
- Rubinsztejn, A.; Sood, R.; Laipert, F.E. Neural network optimal control in astrodynamics: Application to the missed thrust problem. Acta Astronaut. 2020, 176, 192–203. [Google Scholar] [CrossRef]
- Federici, L.; Benedikter, B.; Zavoli, A. Deep Learning Techniques for Autonomous Spacecraft Guidance During Proximity Operations. J. Spacecr. Rocket. 2021, 58, 1774–1785. [Google Scholar] [CrossRef]
- Hovell, K.; Ulrich, S. Deep Reinforcement Learning for Spacecraft Proximity Operations Guidance. J. Spacecr. Rocket. 2021, 58, 254–264. [Google Scholar] [CrossRef]
- Gaudet, B.; Linares, R.; Furfaro, R. Terminal adaptive guidance via reinforcement meta-learning: Applications to autonomous asteroid close-proximity operations. Acta Astronaut. 2020, 171, 1–13. [Google Scholar] [CrossRef]
- Furfaro, R.; Scorsoglio, A.; Linares, R.; Massari, M. Adaptive generalized ZEM-ZEV feedback guidance for planetary landing via a deep reinforcement learning approach. Acta Astronaut. 2020, 171, 156–171. [Google Scholar] [CrossRef]
- Federici, L.; Zavoli, A. Robust interplanetary trajectory design under multiple uncertainties via meta-reinforcement learning. Acta Astronaut. 2024, 214, 147–158. [Google Scholar] [CrossRef]
- Holt, H.; Armellin, R.; Baresi, N.; Hashida, Y.; Turconi, A.; Scorsoglio, A.; Furfaro, R. Optimal Q-laws via reinforcement learning with guaranteed stability. Acta Astronaut. 2021, 187, 511–528. [Google Scholar] [CrossRef]
- LaFarge, N.B.; Miller, D.; Howell, K.C.; Linares, R. Autonomous closed-loop guidance using reinforcement learning in a low-thrust, multi-body dynamical environment. Acta Astronaut. 2021, 186, 1–23. [Google Scholar] [CrossRef]
- Zavoli, A.; Federici, L. Reinforcement Learning for Robust Trajectory Design of Interplanetary Missions. J. Guid. Control. Dyn. 2021, 44, 1440–1453. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef] [PubMed]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Silver, D.; Hubert, T.; Schrittwieser, J.; Antonoglou, I.; Lai, M.; Guez, A.; Lanctot, M.; Sifre, L.; Kumaran, D.; Graepel, T.; et al. A general reinforcement learning algorithm that masters chess, shogi, and Go through self-play. Science 2018, 362, 1140–1144. [Google Scholar] [CrossRef]
- Schrittwieser, J.; Antonoglou, I.; Hubert, T.; Simonyan, K.; Sifre, L.; Schmitt, S.; Guez, A.; Lockhart, E.; Hassabis, D.; Graepel, T.; et al. Mastering Atari, Go, chess and shogi by planning with a learned model. Nature 2020, 588, 604–609. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Hou, X.; Hu, Y.H.; Liu, Y.; Pan, Q. A Reinforcement Learning Scheme for Active Multi-Debris Removal Mission Planning With Modified Upper Confidence Bound Tree Search. IEEE Access 2020, 8, 108461–108473. [Google Scholar] [CrossRef]
- Kemmerling, M.; Lütticke, D.; Schmitt, R.H. Beyond games: A systematic review of neural Monte Carlo tree search applications. Appl. Intell. 2024, 54, 1020–1046. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized Experience Replay. arXiv 2016, arXiv:1511.05952. [Google Scholar]
- Couëtoux, A.; Milone, M.; Brendel, M.; Doghmen, H.; Sebag, M.; Teytaud, O. Continuous Rapid Action Value Estimates. In Proceedings of the Asian Conference on Machine Learning, Taoyuan, Taiwain, 14–15 November 2011; Hsu, C.N., Lee, W.S., Eds.; South Garden Hotels and Resorts; Proceedings of Machine Learning Research. Volume 20, pp. 19–31. [Google Scholar]
- Kim, B.; Lee, K.; Lim, S.; Kaelbling, L.; Lozano-Perez, T. Monte Carlo Tree Search in Continuous Spaces Using Voronoi Optimistic Optimization with Regret Bounds. Proc. AAAI Conf. Artif. Intell. 2020, 34, 9916–9924. [Google Scholar] [CrossRef]
- Lee, J.; Jeon, W.; Kim, G.H.; Kim, K.E. Monte-Carlo Tree Search in Continuous Action Spaces with Value Gradients. Proc. AAAI Conf. Artif. Intell. 2020, 34, 4561–4568. [Google Scholar] [CrossRef]
- Timothy, Y.; Viliam Lisý, M.B. Monte Carlo Tree Search in ContinuousAction Spaces with Execution Uncertainty. In Proceedings of the Twenty-Fifth International Joint Conference on Artificial Intelligence (IJCAI-16), New York City, NY, USA, 9–15 July 2016. [Google Scholar]
- Rowan, T.H. Functional Stability Analysis of Numerical Algorithms. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 1990. UMI Order No. GAX90-31702. [Google Scholar]
- Johnson, S.G. The NLopt Nonlinear-Optimization Package. 2007. Available online: https://github.com/stevengj/nlopt (accessed on 14 March 2025).
- Shen, H.X.; Luo, Y.Z.; Zhu, Y.H.; Huang, A.Y. Dyson sphere building: On the design of the GTOC11 problem and summary of the results. Acta Astronaut. 2023, 202, 889–898. [Google Scholar] [CrossRef]
- Liu, X.; Zeng, X.; Shao, C.; Xu, Y.; Hu, J.; Liu, P.; Yang, H.; Li, S. A greedy-based hybrid trajectory optimization method for the “Dyson Ring” building problem. Acta Astronaut. 2023, 202, 829–840. [Google Scholar] [CrossRef]
- Lu, S.; Zhang, Y.; Zhang, J.; Cai, H.; Qi, R.; Li, X.; Qi, Y.; Xiao, Q.; Shen, A.; Zhang, T.; et al. GTOC 11: Results found at Beijing Institute of Technology and China Academy of Space Technology. Acta Astronaut. 2023, 202, 876–888. [Google Scholar] [CrossRef]
- Russell, R.P.; McArdle, S.; Ottesen, D.; Zucchelli, E.M.; Brandenburg, W.E. Global trajectory optimization, pathfinding, and scheduling for a multi-flyby, multi-spacecraft mission. Acta Astronaut. 2023, 202, 863–875. [Google Scholar] [CrossRef]
- Sikes, J.D.; Pezent, J.B.; Sandel, C.G.; Rubinsztejn, A.; Sood, R. GTOC-11: Results from the University of Alabama. Acta Astronaut. 2023, 202, 841–852. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, N.; Guo, X.; Wu, D.; Xie, X.; Li, J.; Yang, J.; Chen, S.; Jiang, F.; Baoyin, H.; et al. GTOC 11: Results from Tsinghua University and Shanghai Institute of Satellite Engineering. Acta Astronaut. 2023, 202, 819–828. [Google Scholar] [CrossRef]
- Zhang, H.; Ma, H.; Yang, L.; Lin, X.; Xu, L.; Xia, C.; Li, J.; Li, D.; Huo, M.; Zhang, G. GTOC11: Methods and results from the team of Harbin Institute of Technology. Acta Astronaut. 2023, 202, 853–862. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).