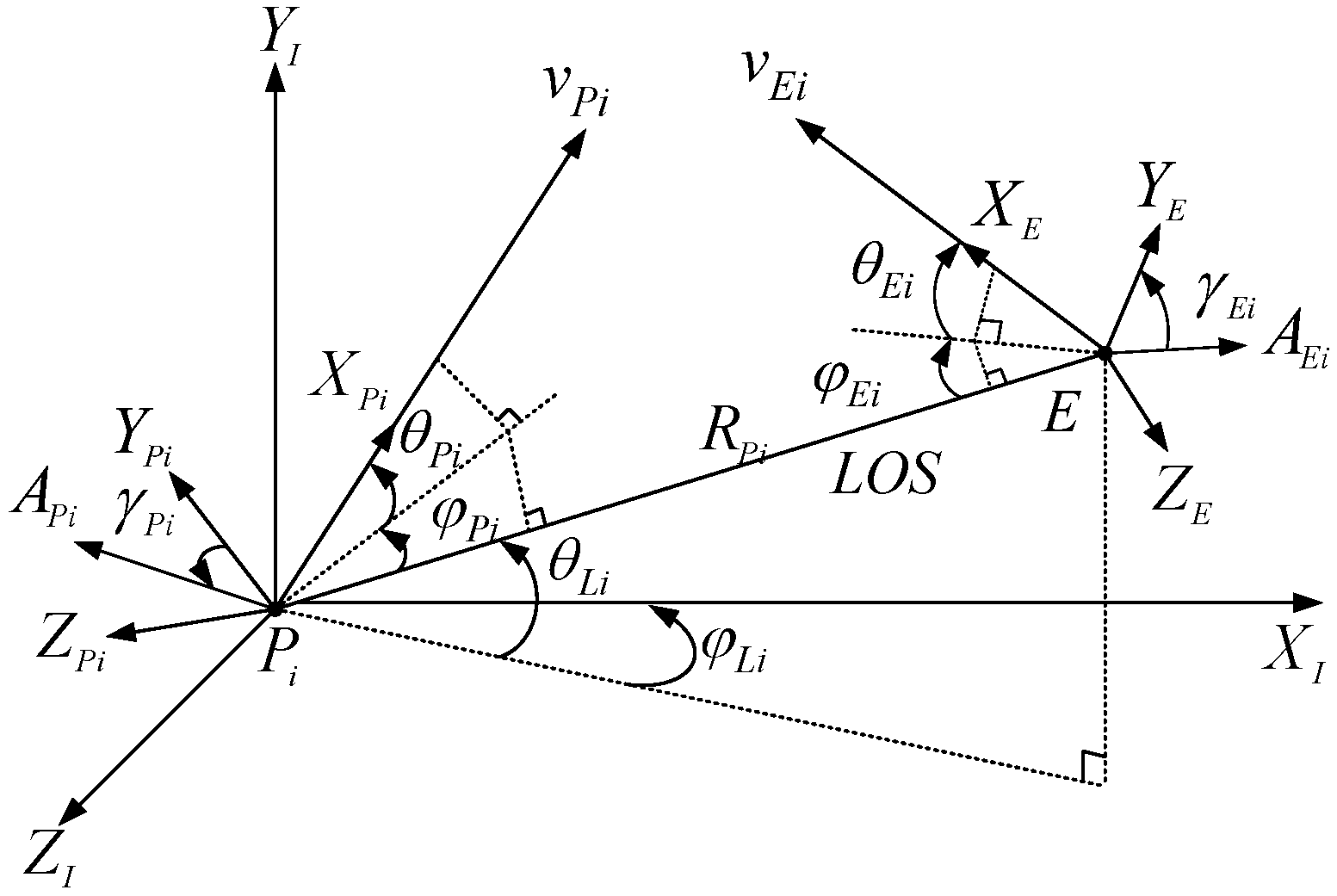
1. Introduction
Motivation: With the increasingly complex global security situation, missile interception technology has become an indispensable part of modern air defense and missile defense operations. Traditional missile interception problems often focus on the interactions between a few missiles and targets. However, as the number of missiles increases and the battlefield environment becomes more complex, the limitations of traditional methods have become more apparent. To address this challenge, the Mean Field Game method provides a new solution approach. The introduction of MFG theory allows for the effective resolution of control and optimization problems in large-scale, multi-target environments, avoiding the computational explosion caused by high-dimensional problems found in traditional methods [
1,
2]. Previous studies on the missile multi-to-multi interception problem mostly expanded from one-to-one or many-to-one situations to many-to-many. However, this process often leads to dimensional explosion, and as the number of individuals increases, the communication burden intensifies, often causing communication blockage. Therefore, this paper employs the MFG method to solve the missile multi-to-multi interception problem. As
, the coupling effects between individuals are minimized. By deriving the optimal solution of the mean field for both parties in the game, this paper proves the consistency between the Nash equilibrium of finite individuals and the mean field Nash equilibrium.
The application of MFG has covered multiple fields, especially in military decision-making, resource allocation, and multi-agent systems, showing broad potential. In missile interception problems, the MFG method models the behavior of each missile, assuming that the behavior of participants is influenced solely by the statistical distribution of the group. This avoids complex mutual computations between individuals [
3]. This makes MFG an effective tool for handling large-scale missile interception systems, providing near-optimal control strategies, without relying on the state of each missile [
4,
5]. In recent years, researchers have conducted extensive theoretical studies on MFG methods, covering topics from the derivation of the Hamilton–Jacobi–Bellman (HJB) equations to Nash equilibrium analysis in mean field games [
6]. The HJB equations provide a mathematical framework for solving optimal control strategies, considering the control constraints, state variables, and optimality conditions of dynamic systems, thus leading to the optimal solution [
7]. However, the difficulty of solving the HJB equations increases significantly as the number of participants grows [
8]. Therefore, the introduction of MFG effectively simplifies this problem, allowing for reasonable solutions in large-scale systems [
9,
10]. In the specific application of missile interception problems, the MFG framework not only focuses on the interaction between missiles and targets but also considers the cooperation and competition among multiple missiles [
11]. This is especially important because modern missile defense systems typically contain multiple interceptors. When facing multiple enemy targets, optimizing the strategy of each missile to achieve optimal performance for the overall system is a critical issue. By using MFG-based modeling, researchers are able to derive the optimal interception strategy for each missile, while ensuring computational efficiency [
12]. With the continuous development of MFG theory, more and more research has begun to focus on how to effectively solve HJB equations in high-dimensional spaces and handle complex boundary conditions. For example, Bensoussan et al. [
4] proposed a numerical solution method based on MFG theory that can handle complex problems involving large numbers of participants, while Fathi et al. [
5] explored the optimization of control strategies in multi-agent collaboration and competition. These studies provide theoretical support for the design of multi-missile interception control strategies. Furthermore, the advantages of the MFG method lie in its ability to simplify computational complexity using the statistical distribution of group behavior, rather than directly calculating the interactions between individuals [
13]. This characteristic makes the MFG method highly applicable in real-time defense systems, especially in complex battlefield environments with multiple targets and interceptors. Researchers have successfully solved many challenges that traditional methods find difficult to address by continuously improving the MFG framework [
9].
In this study, we assume that the number of targets is sufficiently large to apply the Mean Field Game (MFG) approach. However, in practical applications, the number of targets is typically finite, which may affect the applicability of this method. While the MFG approach effectively handles large-scale systems and provides equilibrium solutions, its validity might be limited when the number of targets is small. We will discuss how a limited number of targets can influence the applicability and effectiveness of the MFG method.
The goal of this paper is to explore the optimal control strategy in missile interception problems based on the MFG theory, and to analyze the existence and uniqueness of the
-Nash equilibrium [
14] in mean field games. Through an in-depth study of this problem, this paper not only promotes the application of multi-agent systems in missile defense but also provides theoretical support for optimal control problems in large-scale complex systems [
15]. The main innovations of this paper are as follows:
Application of MFG to missile interception problems in three-dimensional space: This paper is the first to apply the Mean Field Game method to multi-missile interception target problems in three-dimensional space, particularly focusing on nonlinear interception systems. This innovation supplants traditional one-to-one and many-to-one interception models, extending them to a many-to-many interception problem. By fully utilizing the distributed nature of the MFG method, missile strategies are optimized in complex environments, avoiding the issue of dimensional explosion, while not requiring individuals to perceive the behavior of all other participants. Compared to existing studies that mainly considered two-dimensional cases, this paper starts from three-dimensional space, where both state and control information are constrained, making it more aligned with practical application scenarios.
Consideration of complex interactions between missiles and targets: When multiple missiles simultaneously attack adjacent and closely located targets, interference between missiles may occur. To address this challenge, this paper proposes a dynamic adjustment mechanism based on the distribution of adjacent groups in three-dimensional space. Each missile adjusts its strategy according to the distribution of nearby groups, both its own and the target’s, thus minimizing interference. Furthermore, when approaching a target group, the missile updates its strategy based on the target group’s distribution to increase the interception probability. To reduce the risk of being intercepted, the target adopts a decentralized evasion strategy by perceiving changes in the missile distribution and the nearby target distribution, thus determining the optimal escape path. The optimal strategies for missiles and targets are inherently adversarial.
-Nash equilibrium study in a two-group MFG model: This paper investigates a two-group MFG problem, where individuals within the same group cooperate with each other, and cooperation is realized through distribution, while individuals from different groups compete. Each player does not need to perceive the behavior of all individuals, but only needs to understand the distribution of both groups and the distribution of the adjacent group. As the number of players increases, the
-Nash equilibrium can be approximated as a global Nash equilibrium [
16], greatly simplifying the problem-solving process and improving the computational efficiency of the model. This approach is inspired by the multi-population MFG model described in Section 7.1.1 of Probabilistic Theory of Mean Field Games with Application [
17].
This paper proposes a method for calculating the distribution of nearby groups in three-dimensional space. By considering the distribution of nearby groups around the missile, it reduces the interference from surrounding missiles, as well as from groups nearby the target. Compared to traditional methods, which require calculating interactions between all individuals, this paper only considers the effects brought by nearby groups, making the computation more efficient and practically applicable. These innovations highlight the unique contribution of this paper in the existing literature.
In comparison with the approach proposed by Toumi et al. (2024) [
18] in their study on large-scale multi-agent systems, which also considered interactions between agents in a distributed manner, our model extends the concept into a three-dimensional space, where both missile and target distributions become more complex, due to input constraints rather than spatial constraints. While Toumi et al. focused on congestion avoidance in crowd scenarios with agent rewards based on their distance from other agents, our model specifically incorporates missile–target dynamics in a three-dimensional combat scenario, optimizing strategies to minimize interference and improve interception success, despite the input limitations in such a constrained control environment.
Compared to the study by [
17], in the field of missile interception, when the number of missiles is sufficiently large, the difference between the individual state and the group mean under the
-equilibrium will gradually decrease, indicating that the individual state will progressively follow the changes in the group state.
The rest of the paper is organized as follows: In
Section 2, we first present the missile interception model, based on which we derive the spatial equations and the cost functions for both the pursuers and the evaders. We also describe the basic form of the
-Nash equilibrium. In
Section 3, we derive the distribution functions for both the pursuers and the evaders. By manipulating the terminal function, we introduce a new cost function. In
Section 4, we apply the principles of dynamic programming to obtain the Hamilton–Jacobi–Bellman (HJB) equations for both the pursuers and the evaders, from which we derive the optimal strategies. In
Section 5, we present the unique solution form of the forward–backward stochastic differential equations. We then prove the boundedness of the states, and finally show the difference between individuals and the mean field in the
-Nash equilibrium. In
Section 6, we provide the experimental results. Finally, in
Section 7, we present the concluding remarks.
3. The Distribution Functions for the Pursuers and Evaders
For convenience, in the subsequent derivations, we first introduce the distribution functions for the pursuer and evaders. Let
be a smooth function that is compactly supported and possesses at least second-order continuous derivatives. According to Itô’s lemma,
where
is a function of
s,
x, and
m, representing the dynamics of the system. We assume the difference in distribution of the pursuers and evaders is given by
where
and
are the distribution functions for the pursuer and the evaders, respectively. Substituting this into the equation, we obtain The following equations describe the evolution of the distribution of the system. We first start by writing down the change in the function
over the domain
:
This equation shows the rate of change in the integral of
with respect to
, involving both the Laplacian of
and the interaction term
, which represents the influence of the pursuers on the system’s evolution.
Next, we use the duality product to express the change in the system in terms of the inner product:
where
denotes the inner product. This equation expresses the rate of change in the inner product of
h and
, which corresponds to the evolution of the system in the dual space.
Further, we can write the next expression for the system dynamics:
This equation shows the rate of change in the inner product of
h with the distribution
, where the evolution of
is described in terms of its Laplacian and the divergence of the interaction term.
Finally, based on the above derivation, we obtain the following partial differential equation for
:
This equation is the key partial differential equation that governs the dynamics of the pursuer and evader system. It describes how the distribution
evolves over time.
The term
represents the relative information between the pursuer and the evaders, given by the following equation:
This expression measures the relative information between the pursuer’s and evader’s distributions.
Finally, we can express the time evolution of the difference between the pursuer’s and evader’s distributions as
This final equation describes the evolution of the difference between the pursuer’s and evader’s distributions. The term
represents any external influence on the system.
The continuity equation for the pursuer is defined as
The continuity equation for the evaders is defined similarly, but with the opposite direction of change:
where
and
are random processes with zero mean and finite variance. The following definitions are used throughout the derivations:
is the distribution function of the pursuer at time
s.
is the distribution function of the evaders at time
s, which may be a Gaussian distribution or other distribution that describes the dynamics of the target.
is a positive constant that controls the speed at which the missile distribution
converges to the target distribution
.
is the Laplace operator, which represents the spatial diffusion of the missile distribution.
is the perturbation term, which represents random noise in the system, typically modeled as white noise or a stochastic process. Finally, we have the normalization condition:
where
represents the support of the distribution, and the integral ensures that the total probability is normalized to 1.
4. The Optimal Feedback Strategies
For convenience, in the subsequent calculations, we simplify the cost function. The pursuer’s cost function is redefined as
where This equation is a simplification of Equation (15), designed to facilitate subsequent calculations and proofs. We have divided Equation (15) into two parts: the first part represents the running cost, and the second part corresponds to the terminal cost.
The running cost includes the state during motion, the sum of the probability measures of the neighboring group distributions, and the functional changes between the neighboring groups of the pursuers and evaders. The terminal cost function incorporates the state at the terminal time and the distribution difference between pursuers and evaders at the terminal time.
is the terminal cost, which depends on the state
and distribution
at the final time
T,
is the running cost at each time
s, with control strategies
and distribution
. The terminal cost
is defined as
The running cost
is given by
Assumption 2. For the convenience of the subsequent calculations of the cost function , it is assumed that [30]: There exist positive constants , , and such that To process the terminal value
using the Itô–Wentzell formula, we consider the auxiliary process
, which represents the terminal condition. The dynamics of
are given by
with the terminal condition as follows:
By substituting the above formula and applying the Itô–Wentzell formula, we have
Derivative with respect to time
t. Using the chain rule,
Substituting the evolution equations for the pursuer and evaders,
According to the Equation (34), the following is the distribution change of the evader:
Substituting the above equations, we obtain
Therefore, we can obtain
Taking the Derivative with Respect to
x:
This is the derivative of
. Taking the Second Derivative with Respect to
x:
This is the second derivative of
. Variational Derivative with Respect to
m:
Substituting Derivative Terms into the Formula. Substituting all the terms, we obtain
Pursuer’s Dynamic Equation:
Evader’s Dynamic Equation:
To incorporate the terminal condition into the optimization process, we introduce an auxiliary process
, with the dynamics as shown above. The terminal condition is now processed dynamically using the formula:
where
represents the discount factor, accounting for the accumulated cost over time [
31]. Next, we apply Ito’s Lemma to expand
:
We then compute the expectation:
Substituting this into the dynamic programming equation,
Simplifying yields the Hamilton–Jacobi–Bellman (HJB) equation:
Substituting
into the equation,
where
is the discount factor affecting all terms.
represents the instantaneous cost, while
handles the terminal condition.
is the value function of the pursuer’s strategy at time
t and state
. The term
represents the time derivative of the value function, indicating the rate of change in
with respect to time.
is the spatial derivative, showing how
changes with respect to the state variable
.
is the second-order spatial derivative, describing the curvature of
in space. The term
captures the interaction between the state process dynamics and the spatial gradient of the value function.
represents the diffusion term, accounting for uncertainty or noise in the process. We first simplify and obtain the following HJB equation for the pursuer:
Similarly, the HJB equation for the evaders is obtained as
Assumption 3. Initial Conditions: We assume that there exists a constant K such that, for all (the number of players), the initial state of each player i lies within a closed ball centered on the initial mean with radius K. In other words, the initial states of all players are constrained within a finite region.
This assumption ensures that, when analyzing and solving the game, the initial states of the players are not excessively large, thereby avoiding issues of instability or intractability due to extreme initial conditions. This is crucial for ensuring the existence and solvability of the solution. Based on Theorem 4.12 in [
32], we assume that the population distribution
is absolutely continuous and satisfies the following partial differential equation as its distributional solution:
where
is the population distribution at time
t, and
is the Borel vector field associated with individual decisions. This condition ensures that the evolution of the population follows the distributional solution of the above equation, which directly influences the strategies of individuals in the game. In the game model, we assume that a player’s behavior is not only driven by their own state but also influenced by the distribution of the entire population. This influence is reflected in the second term of the HJB equation, through the distributional solution [
33]. In this case, individuals respond to the distribution of the population in their decision-making process, ensuring that each player’s behavior is consistent with the distribution of the overall population. We assume that the value functions for the pursuer and the evaders are given by the following expressions:
Equation (50) represents the value function for the
i-th pursuer. The terms
,
, and
are parameters that determine the quadratic, linear, and constant contributions to the value function, respectively, while
is the position of the
i-th pursuer.
Equation (51) represents the value function for the
i-th evader. Similarly,
,
, and
are parameters that define the quadratic, linear, and constant terms, while
is the position of the
i-th evader.
Next, we compute the partial derivatives of the value functions with respect to
s and
x:
Substituting these derivatives into the equation, we obtain the following HJB equation for the pursuer:
Next, we compute the time derivatives of the parameters
,
, and
:
We assume the boundary conditions at time
T are
The optimal strategy for the pursuer can be derived as follows:
The optimal strategy for the evaders is derived as follows:
6. Numerical Analysis
In this study, we assume that there are differences in the flight dynamics between the pursuers and the evaders. Specifically, the pursuers typically have higher speeds and a greater normal acceleration, which enables them to more quickly approach the target and perform the interception task. In contrast, the evaders have lower speeds and a smaller normal acceleration, which results in weaker maneuverability, thus affecting their evasion ability.
The differences in flight dynamics between the pursuers and evaders directly influence the success rate of the interception task. Under otherwise similar conditions, the higher speed and greater maneuverability of the pursuers allow them to track the evaders more effectively and reduce the interception time. On the other hand, the lower maneuverability of the evaders makes them more likely to be caught, unless specific strategies are employed to increase the probability of successful evasion. We will further analyze the specific impact of differences in flight dynamics on interception strategies and explore the effects of optimization of these differences on system performance in the subsequent sections.
In this study, the control strategies for both the pursuers and evaders are calculated using the optimal state feedback strategy. Despite the differences in flight dynamics, the strategies for both parties are designed to maximize their individual performance. However, the differences in flight dynamics lead to adjustments in the strategies, so that the pursuers can approach the target more quickly, while the evaders must employ strategies to delay capture, despite their limited maneuverability.
Example 1. The initial conditions for this simulation are as follows:
Initial positions: The initial positions of both the pursuer and the evaders follow a normal distribution. The mean position of the pursuer is , with the covariance matrix: The mean position of the evaders are , with the covariance matrix: Initial velocities: The pursuers’ velocities are set to 4000 m/s, respectively, while the evaders’ velocity is 3500 m/s.
Acceleration limits: The maximum normal accelerations are 30 g for the pursuers and 20 g for the evaders (g = 9.81 m/s2).
Flight path angles: The initial flight path angles for both the pursuers are set to (elevation and azimuth). The initial flight path angles for both the evaders are set to (elevation and azimuth). The covariance matrix for these angles is given by: Time step: A time interval of 0.1 s was used for numerical integration.
In the first experiment, five pursuers and five evaders each employed the optimal strategy during the simulation. The simulation environment is summarized in
Table 2. During the simulation, the Runge–-Kutta method was applied in each iteration.
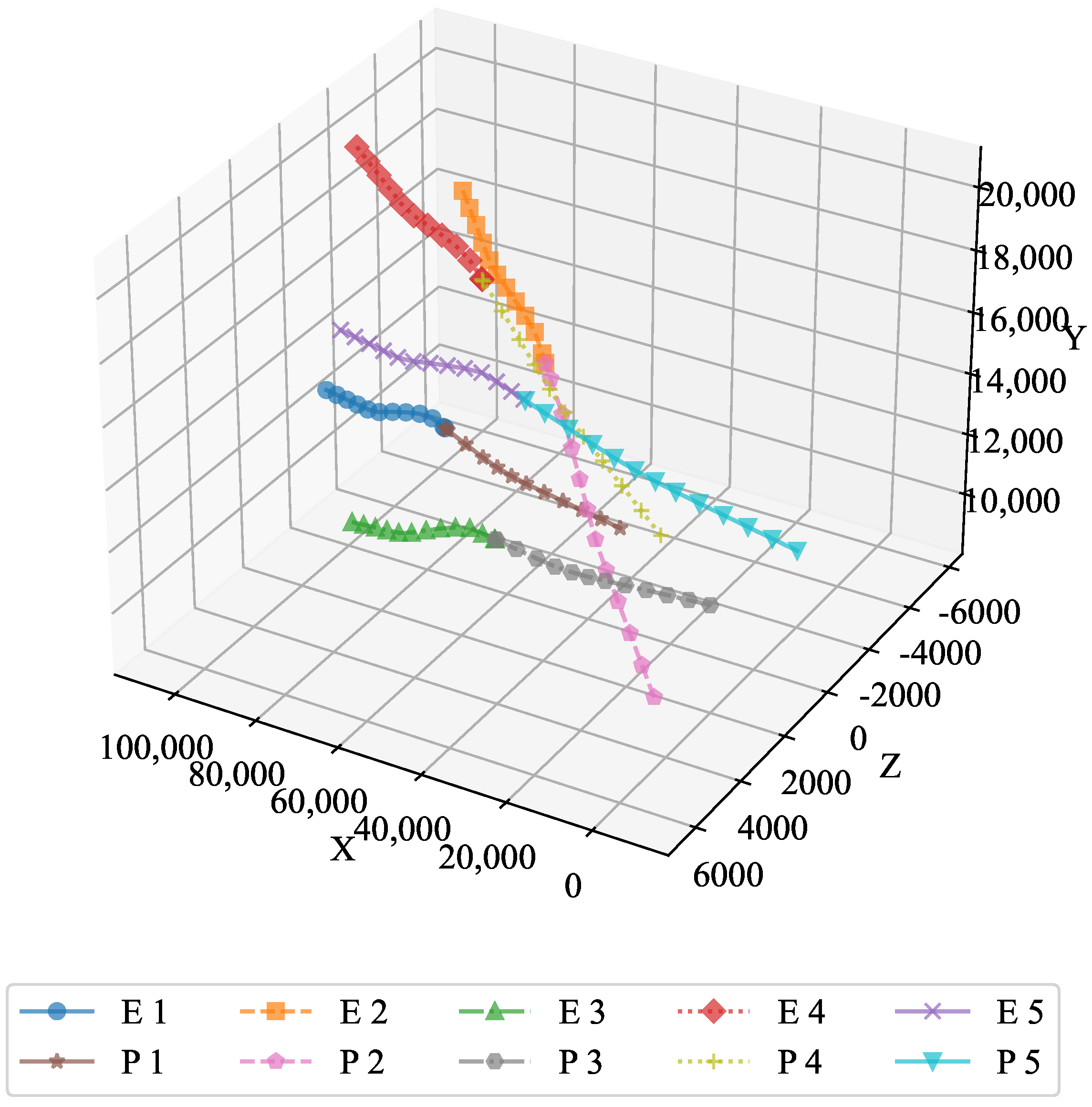
The optimal trajectory is depicted in
Figure 2, which illustrates the efficiency and effectiveness of the optimal feedback strategy. The strategy ensured that both the pursuers and the evaders followed paths that minimized or maximized their respective objectives, demonstrating the capability of the algorithm to handle dynamic environments.
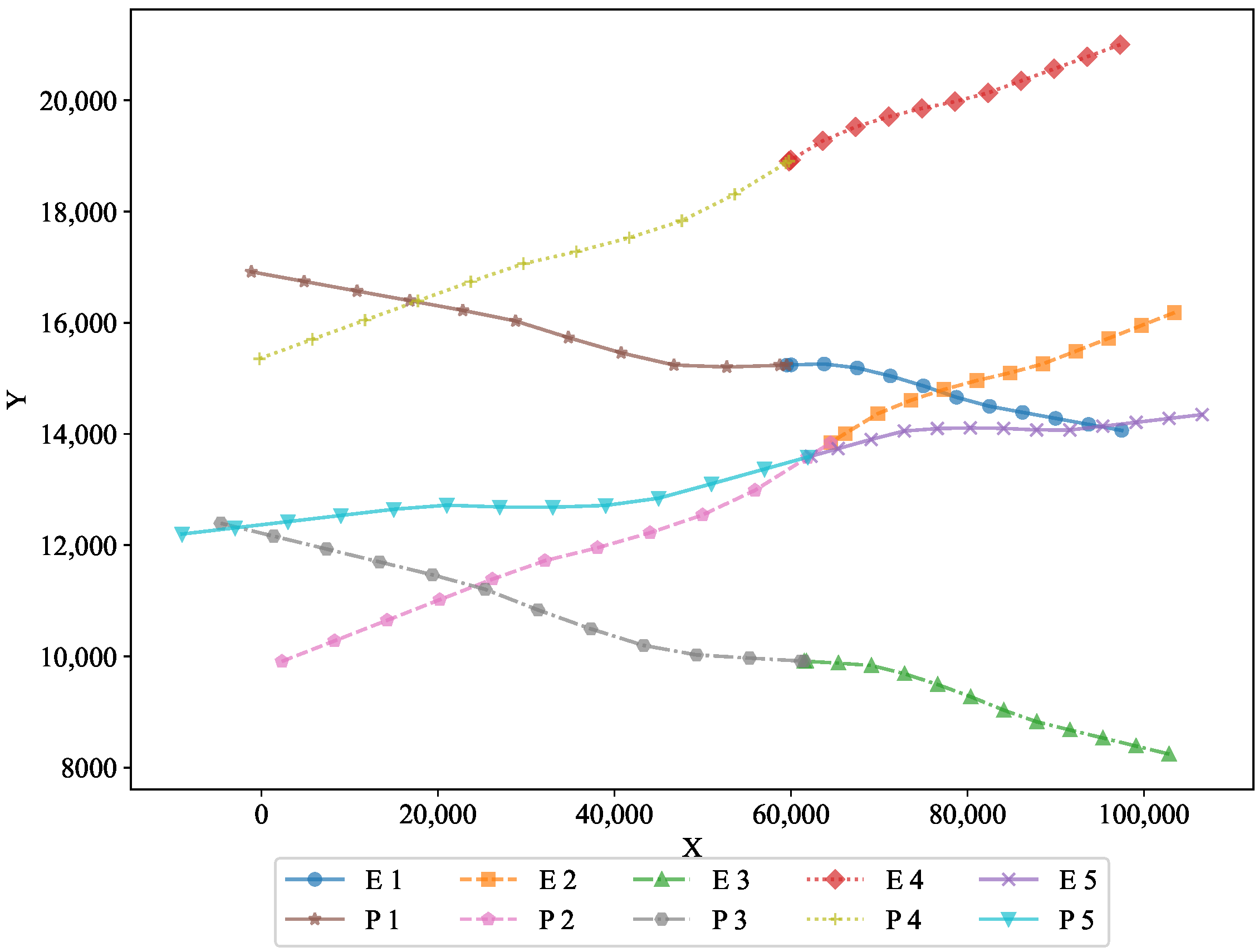
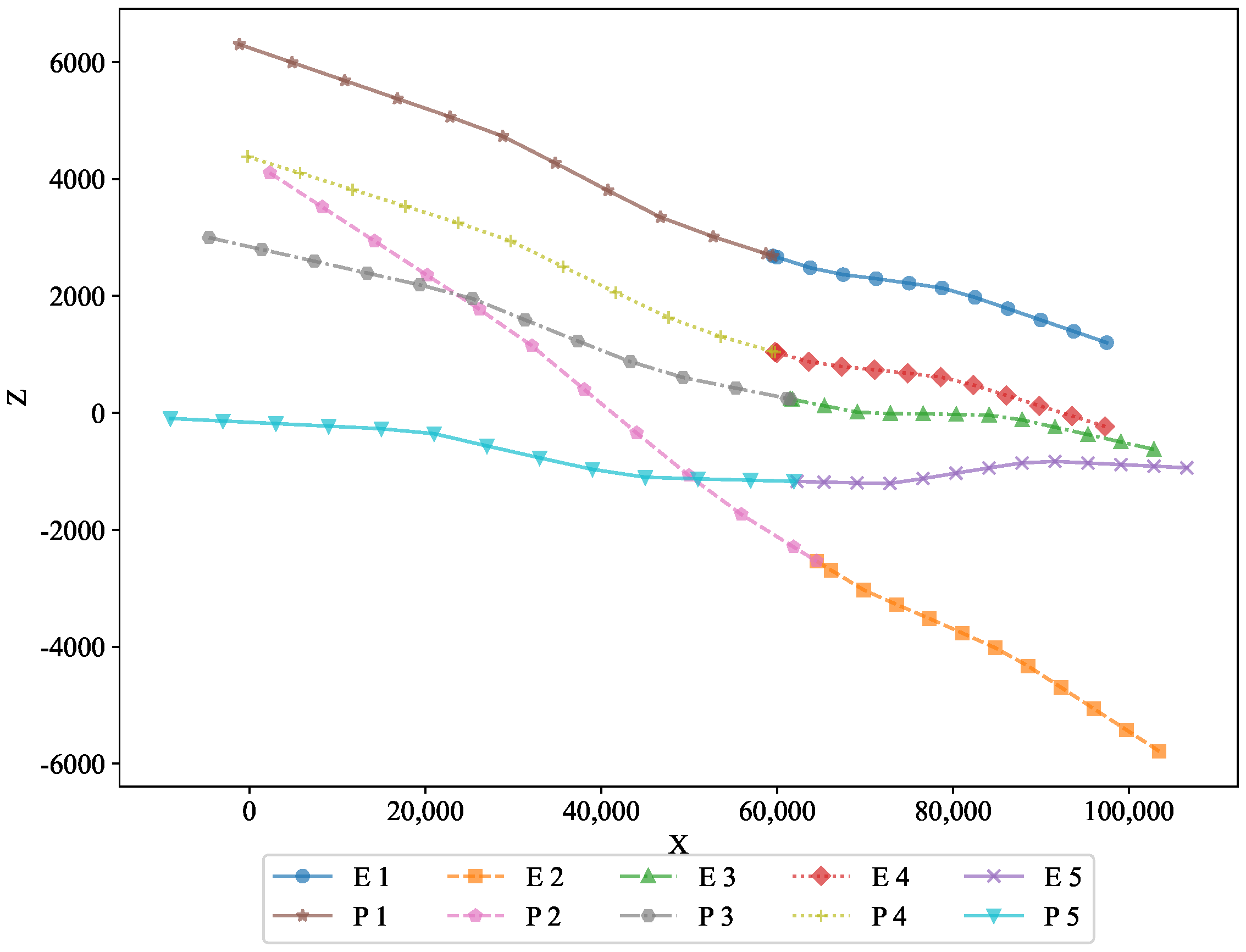
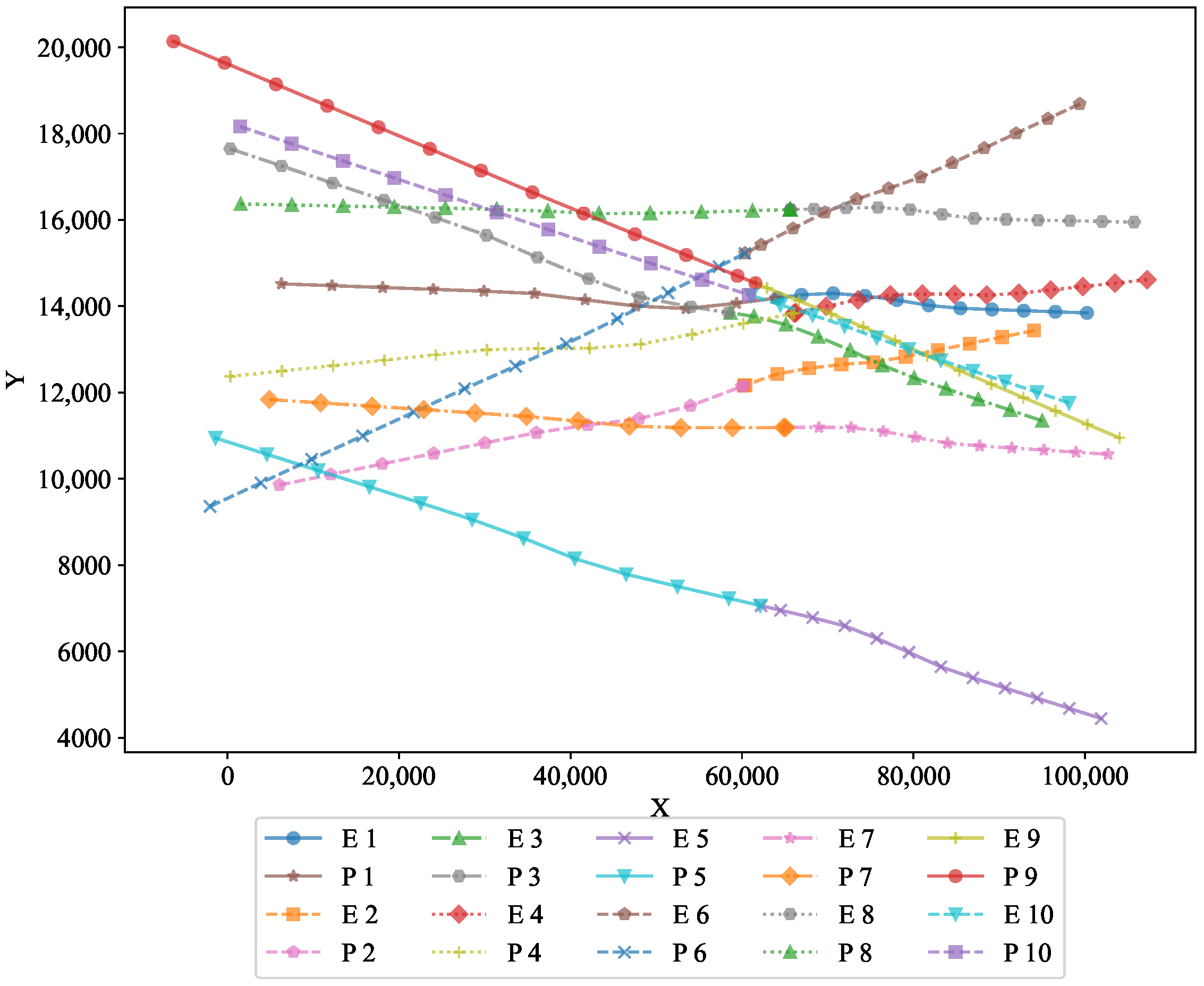
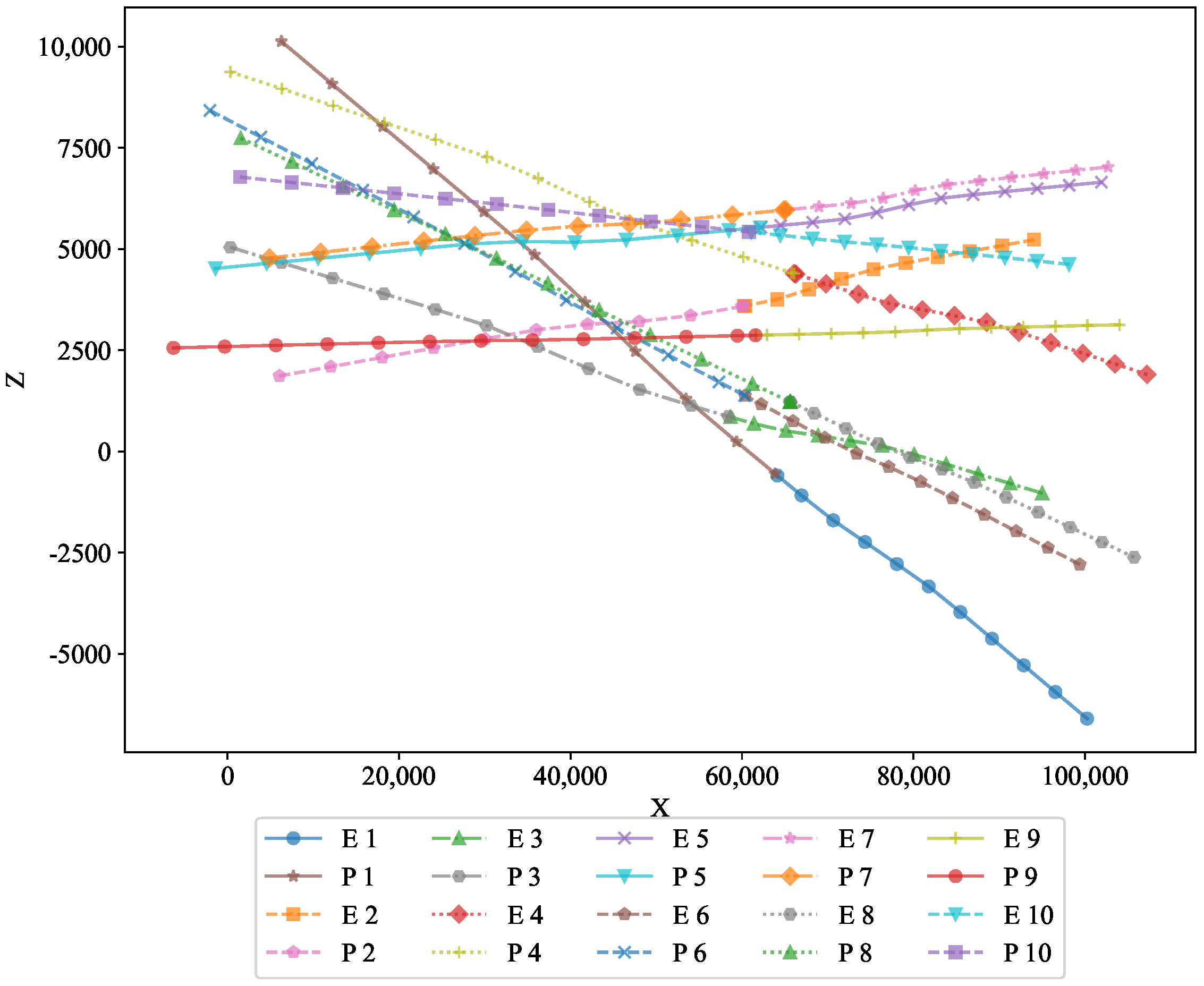
To further analyze the performance, two-dimensional projections in the X–Y and X–Z planes are shown in
Figure 3 and
Figure 4, respectively. These projections offer a clearer view of the trajectories in different planes, revealing how the optimal state feedback strategy successfully adapted to the spatial constraints. The figures demonstrate the feasibility of the optimal state feedback strategy algorithm proposed in this paper, highlighting its ability to maintain precise control over the motion of the pursuers and evaders, even under varying conditions.
These results show that the strategy not only guided the system toward the desired outcomes, but also did so in a manner that was robust to changes in the initial conditions and perturbations. The efficiency of the strategy is reflected in the smooth and predictable nature of the trajectories, making it an effective solution for real-time applications in pursuit–evasion problems.
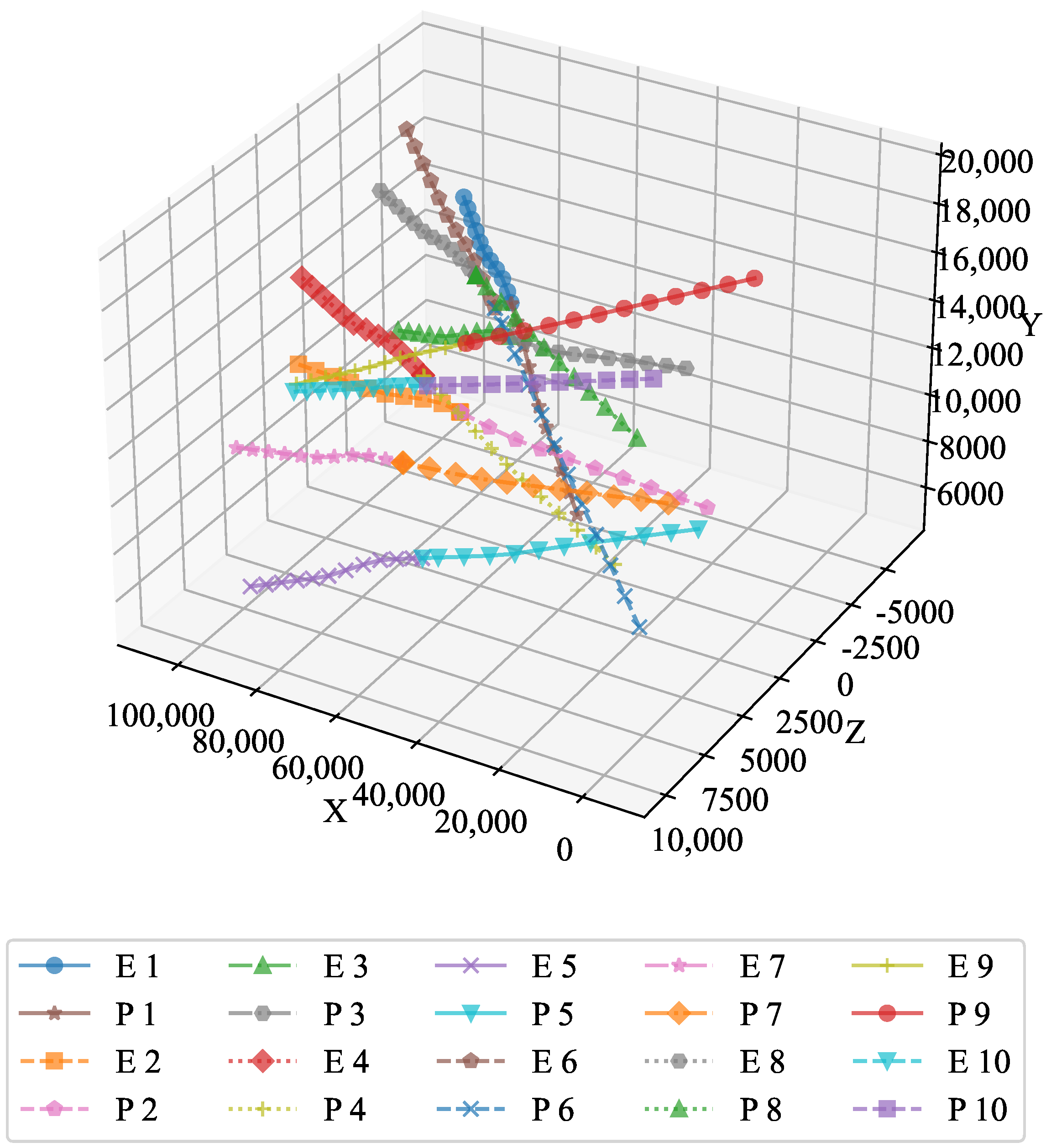
The 3D plot illustrates the overall trajectory of the pursuers and evaders. The paths taken by both entities followed smooth, well-defined curves, which highlights the efficacy of the optimal feedback strategy in controlling their movement across three-dimensional space. The optimal feedback strategy is clearly visible, as both the pursuers and the evaders followed well-defined paths. This demonstrates the robustness of the strategy in guiding the system to its desired outcome.
The XY projection highlights the movement of both pursuers and evaders along the horizontal plane. It visually demonstrates how the optimal strategy governed their trajectories, ensuring effective pursuit and evasion on the two-dimensional surface. This projection shows the horizontal movement of the pursuers and evaders, illustrating the optimality of the feedback strategy in maintaining a controlled pursuit−evasion scenario.
In the XZ projection, we can observe the vertical motion of both the pursuers and the evaders. This visualization confirms the optimal feedback strategy’s ability to manage the 3D movement dynamics and maintain the desired behavior in the vertical direction. This view highlights the vertical movement of both the pursuers and evaders, further validating the strategy’s ability to effectively handle 3D motion dynamics.
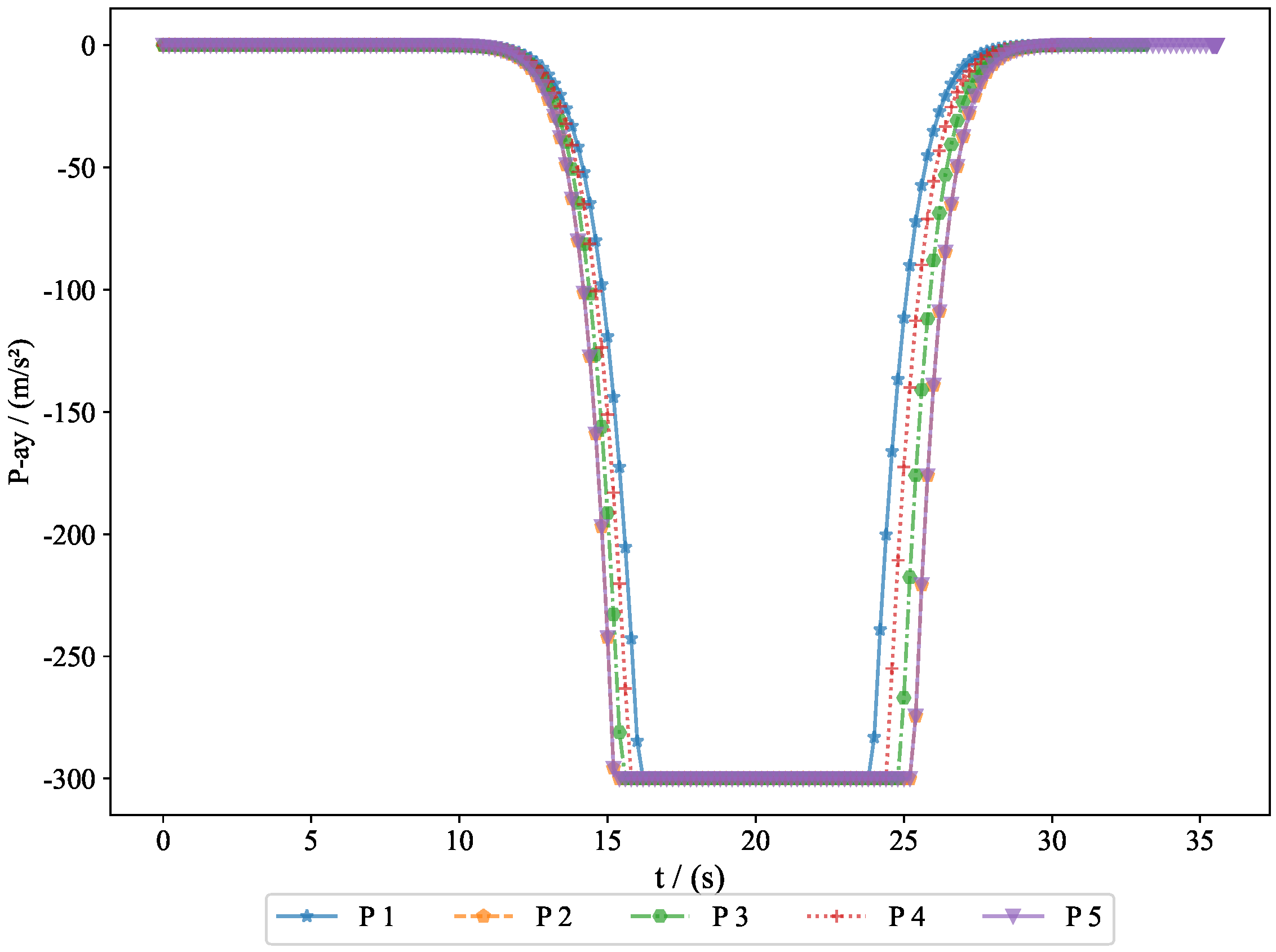
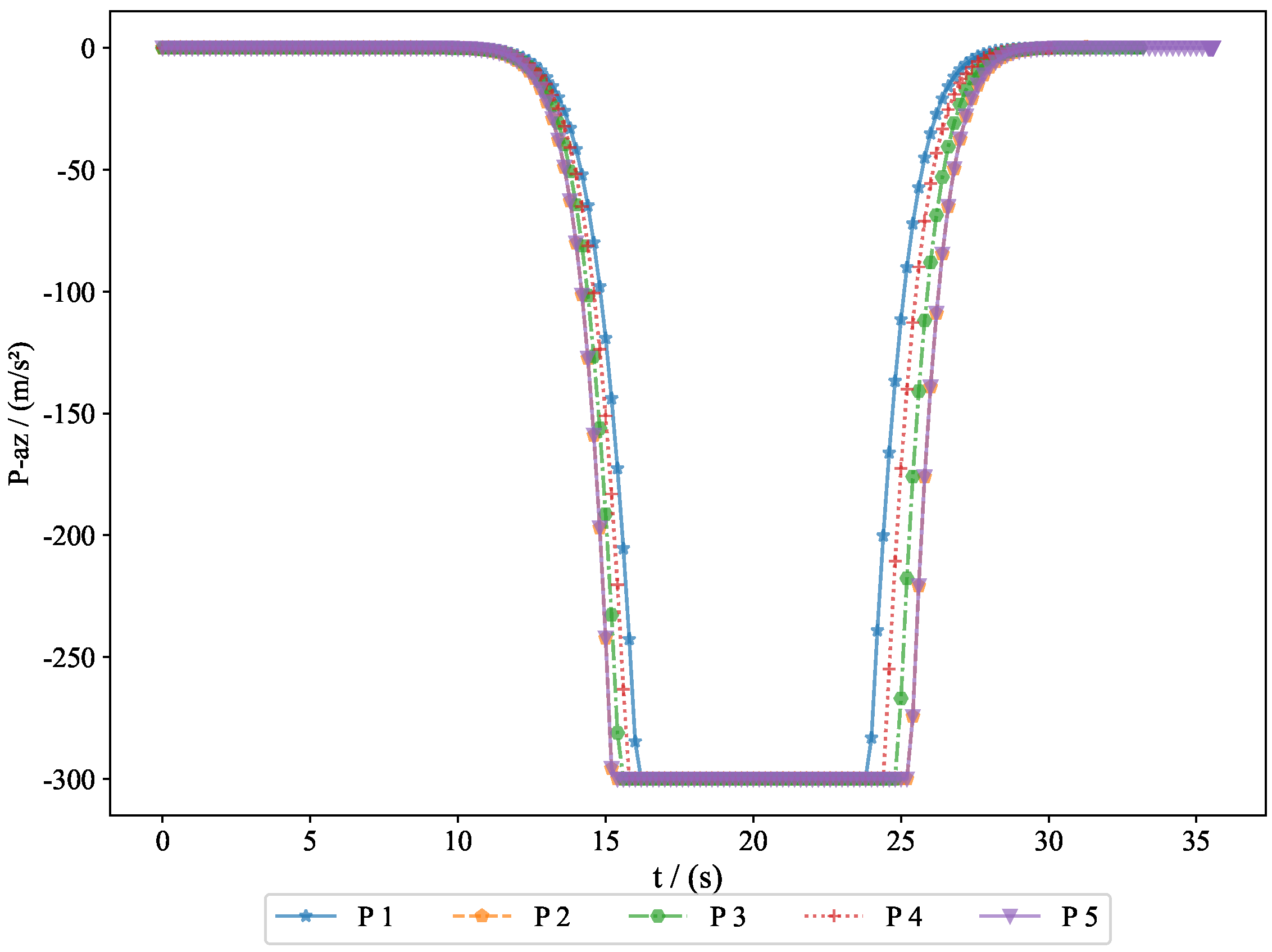
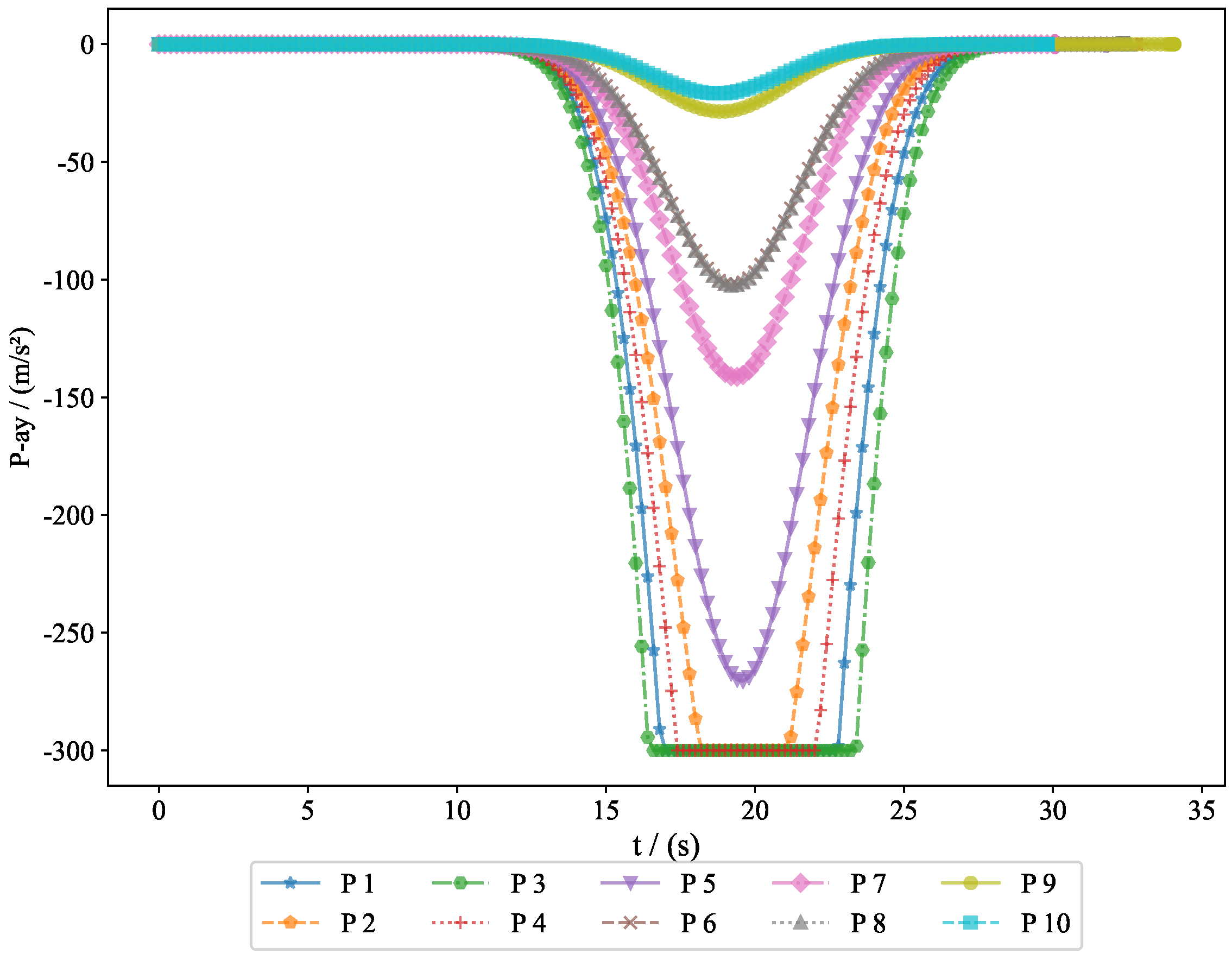
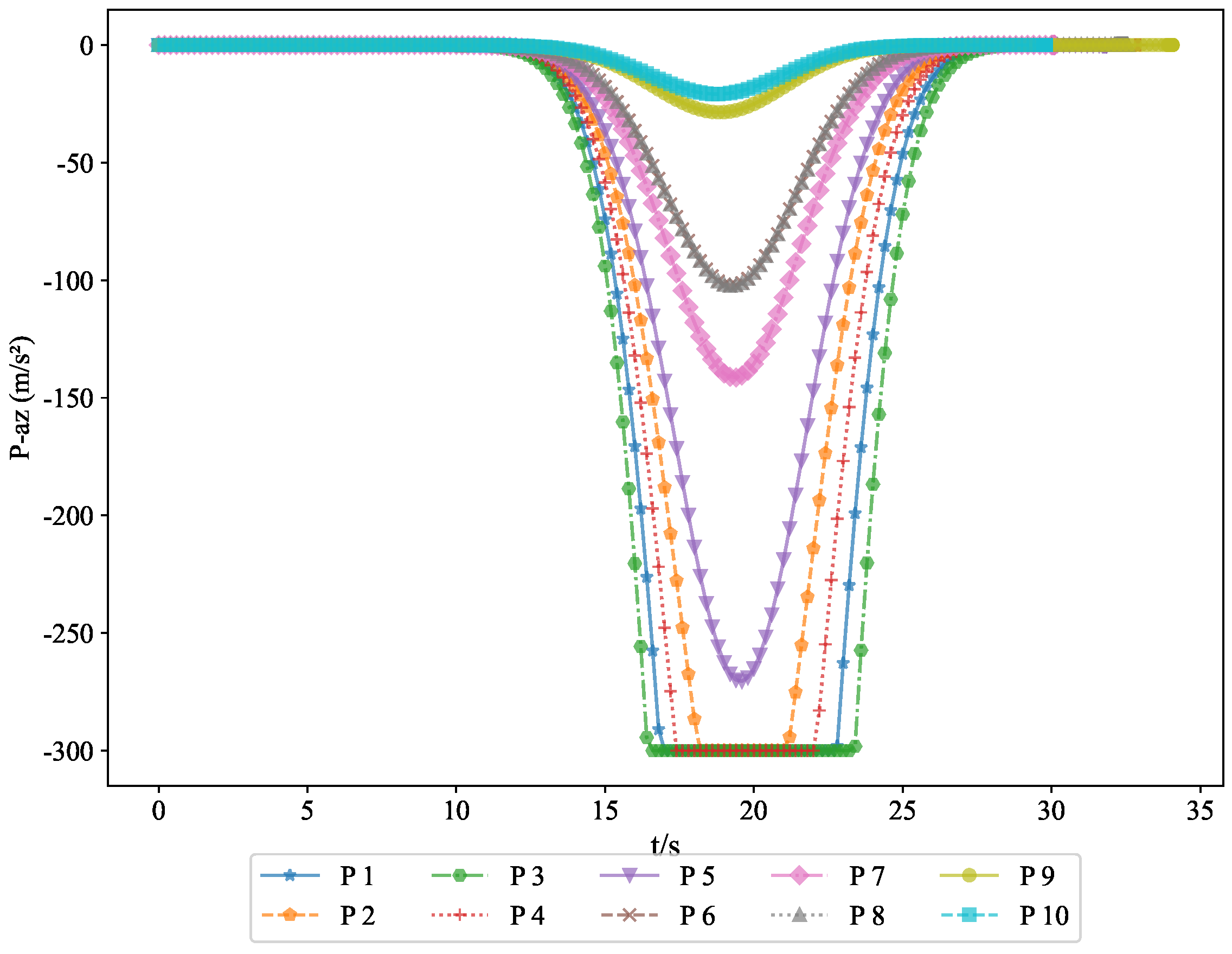
The acceleration variations of the pursuers are shown in
Figure 5 and
Figure 6, while the acceleration variations of the evaders are shown in
Figure 7 and
Figure 8. Since the simulation model was based on a missile interception scenario, we introduced a constraint on the normal acceleration to better reflect real-world conditions. The sign of the normal acceleration only indicates direction, with the acceleration starting from zero and eventually returning to zero. This represents the convergence of the line-of-sight angle, achieving a head-on interception. Here, the normal acceleration refers to the acceleration in the velocity frame, where the acceleration directions of the pursuers and evaders are opposite. However, due to the nature of the game theory problem, the optimal strategies of both parties evolve simultaneously.
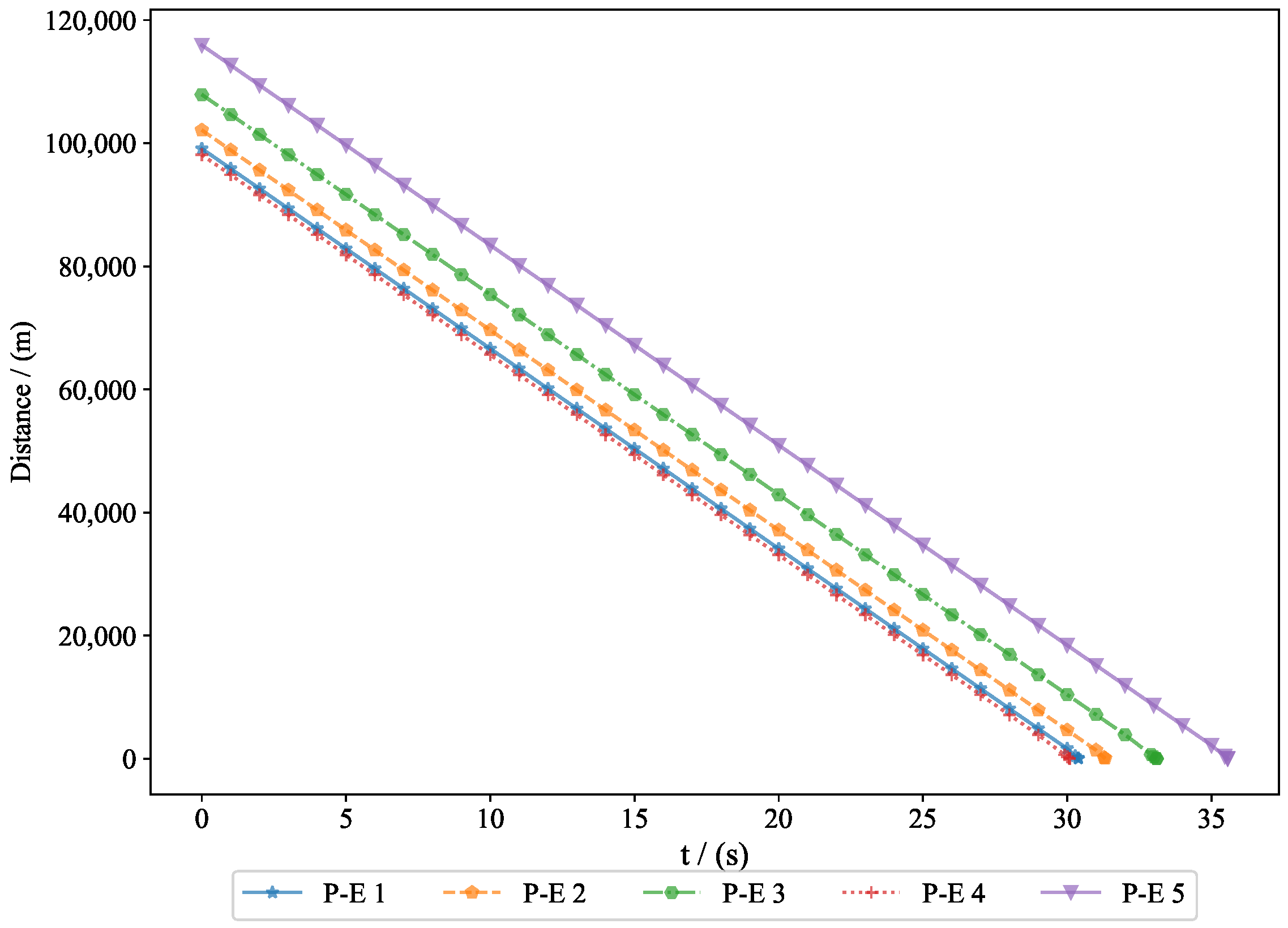
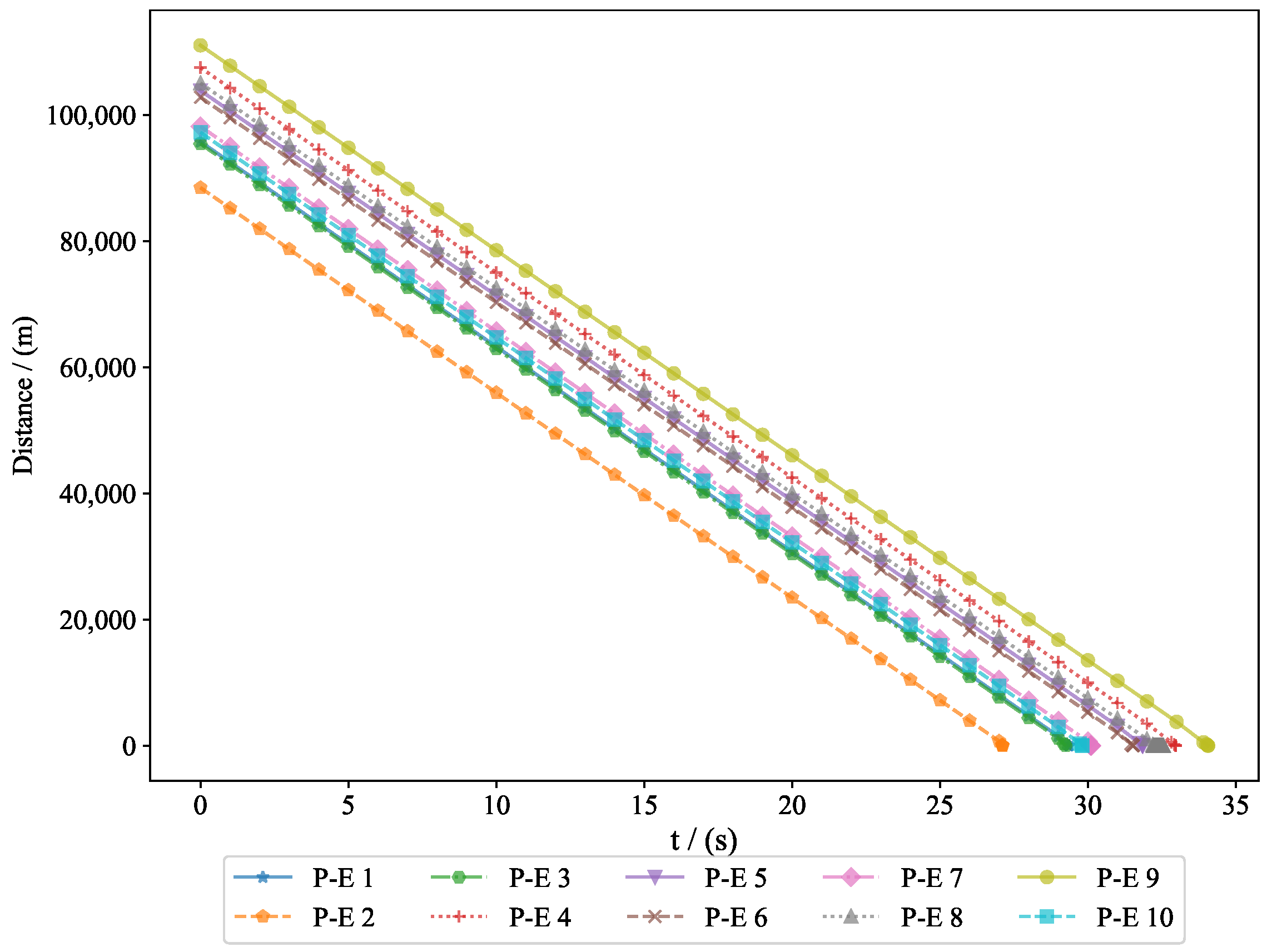
The distance between the evaders and the pursuers is shown in
Figure 9, where the final miss distances were
,
,
,
, and
. In missile interception problems, an interception is typically considered successful when the distance is less than one meter. In this paper, interception is defined by the condition
or
, where
R represents the distance between the pursuers and the evaders. The evaders is captured by the pursuers between
and
. Generally, the terminal guidance phase in missile interception lasts between 20 and 40 s, and the results from Experiment 1 fell within this range. The convergence of the final distance and acceleration led to the convergence of the system state. Given that the initial state was bounded and ultimately converged, this demonstrates the bounded nature of the system state. The successful interception of five evaders by the pursuers proves the feasibility of the proposed approach.
Example 2. To verify the feasibility of the algorithm, we increased the number of pursuers and evaders. In Experiment 2, we used 10 pursuers and 10 evaders. Figure 10 shows a 3D interception diagram for the 10VS10 scenario. From this, it can be observed that the double-population game strategy based on MFG is effective in practical situations. This experiment demonstrated the feasibility of the proposed strategy in addressing the evasion problem of nearby populations. Figure 11 shows the projection in the vertical direction, clearly presenting the positional relationships between the groups.
Figure 12 shows the projection in the horizontal direction, further enhancing the understanding of the interactions between the two groups.
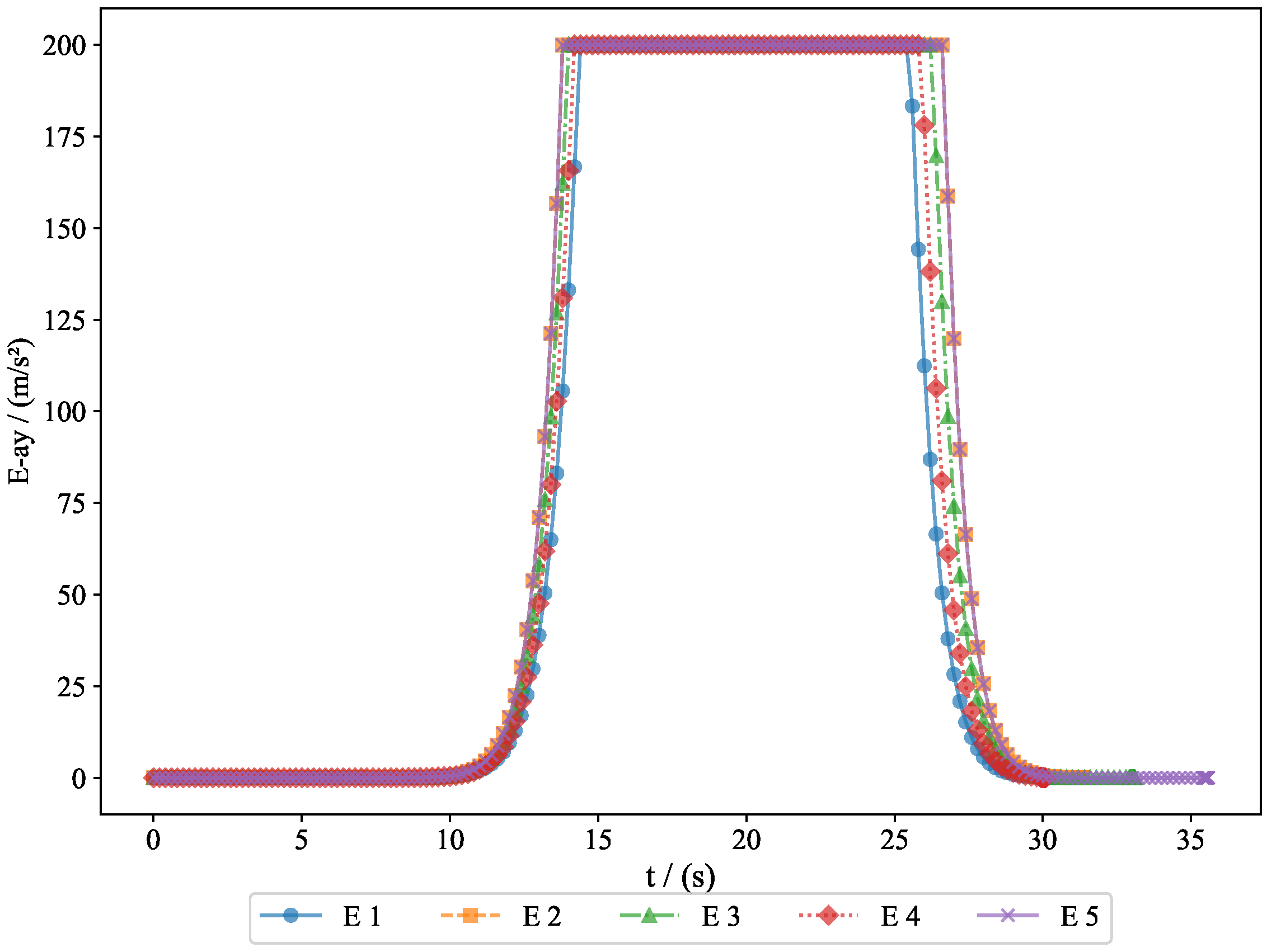
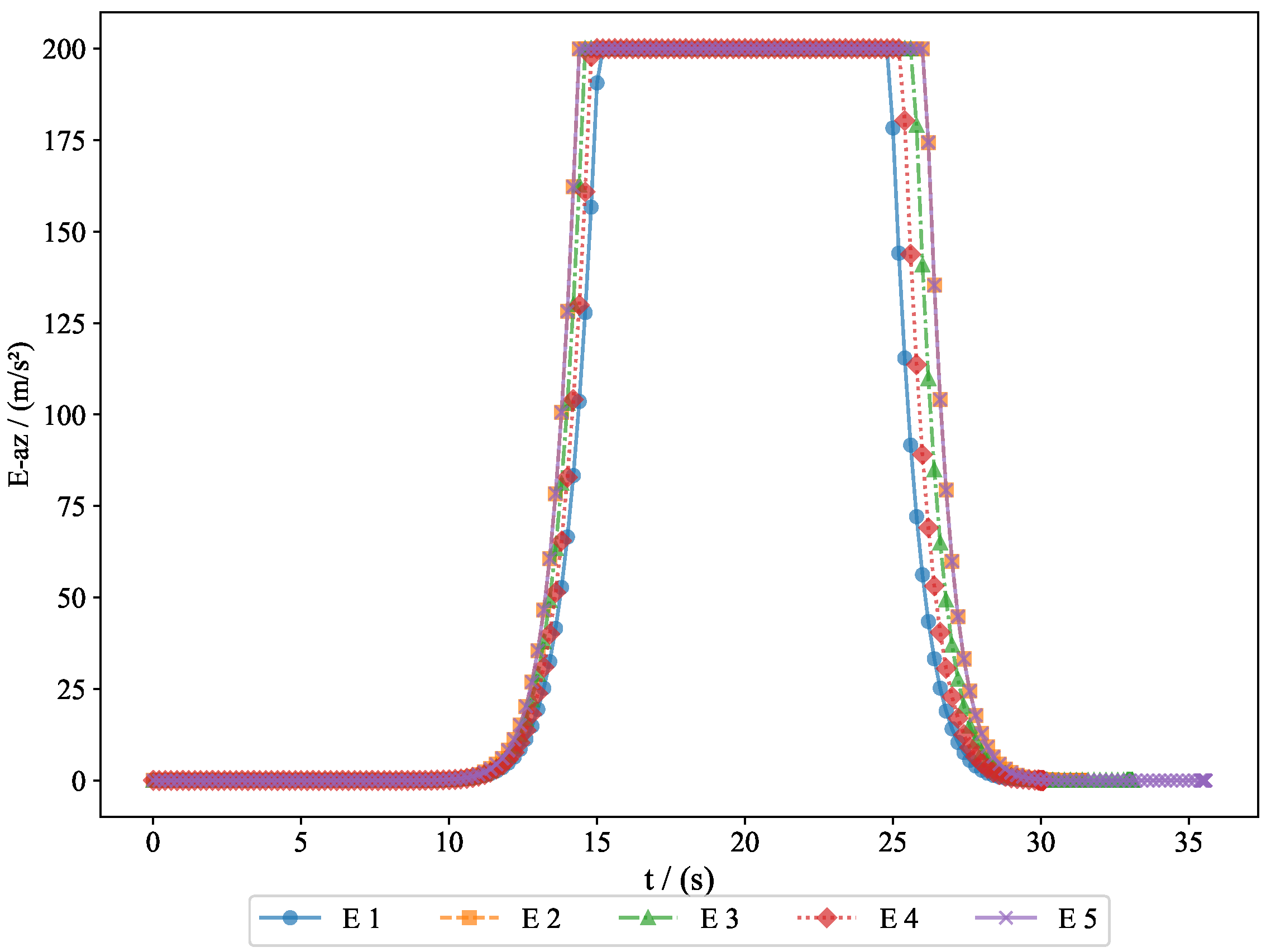
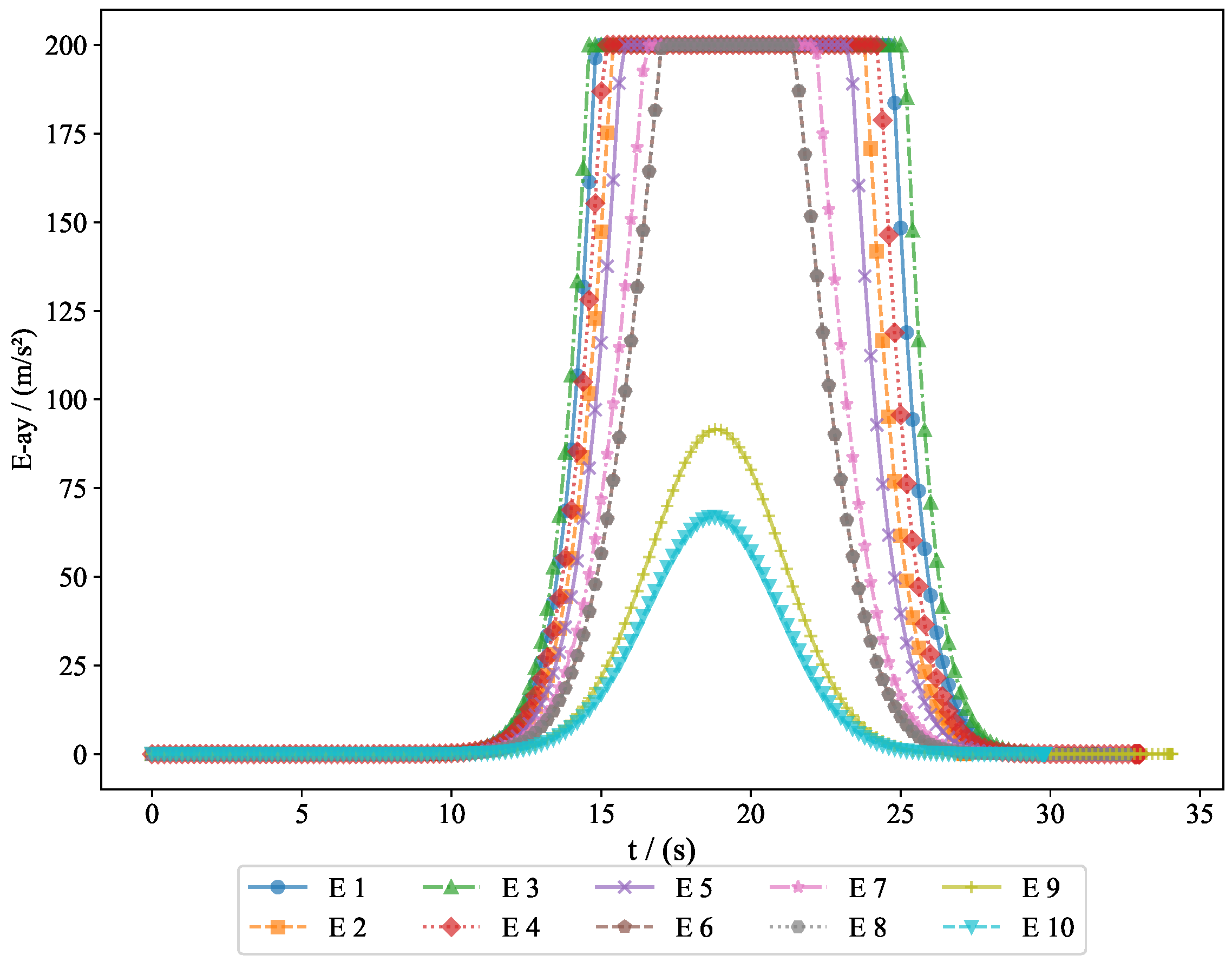
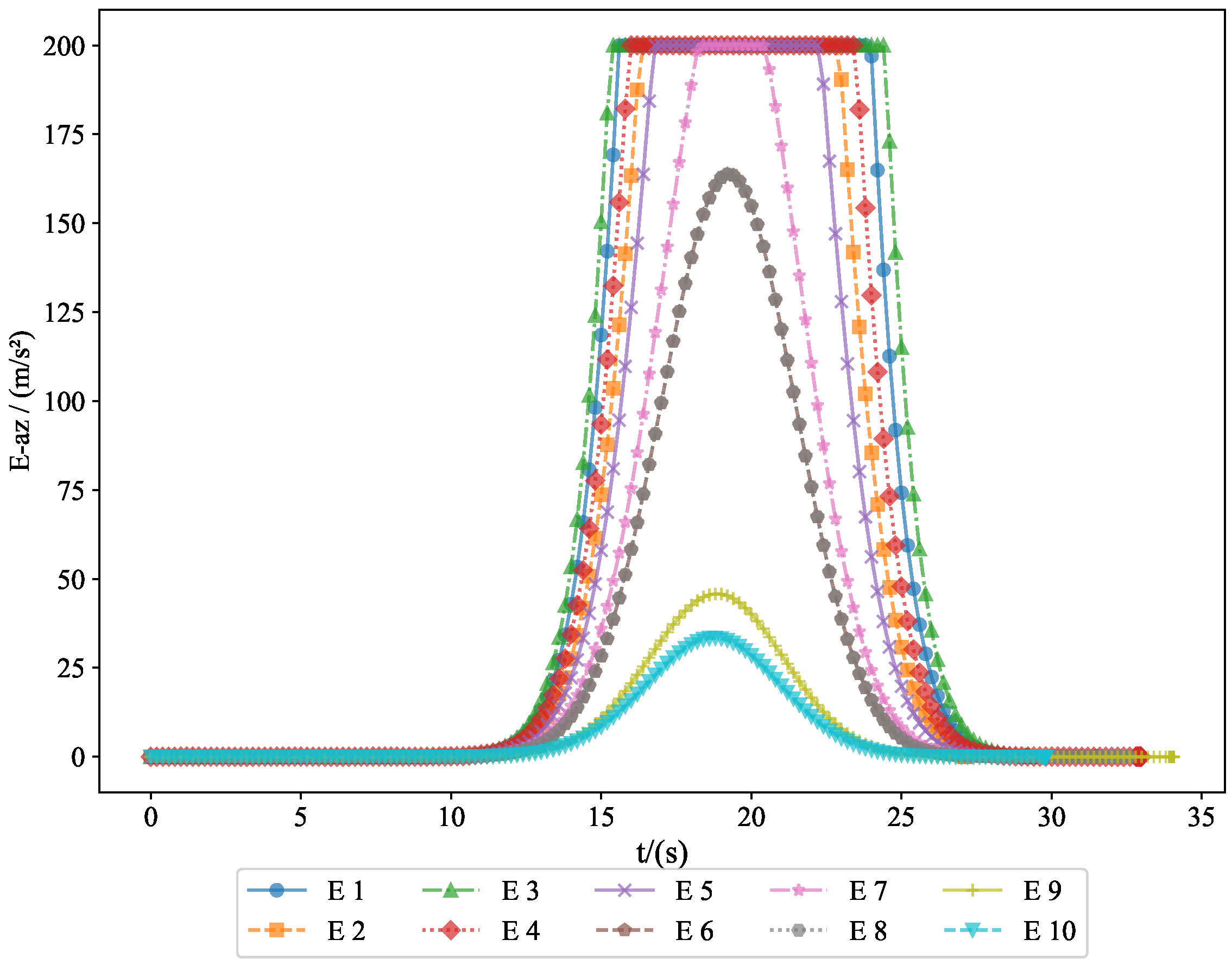
To further analyze the movement patterns of the pursuers and evaders, we present the acceleration changes of both the pursuers and evaders along the
y-axis and
z-axis.
Figure 13 shows the acceleration changes of the pursuers along the
y-axis, illustrating how the pursuers adjusted their vertical acceleration to respond to the movement of the evaders.
Figure 14 displays the acceleration changes of the pursuers along the
z-axis, providing further insight into their vertical adjustments.
Similarly,
Figure 15 shows the acceleration changes of the evaders along the
y-axis, revealing how the evaders modified their vertical acceleration to increase the likelihood of a successful escape.
Figure 16 demonstrates the acceleration changes of the evaders along the
z-axis, helping us understand how they adjusted their movement strategy to avoid capture by the pursuers. These figures provide important information regarding the acceleration changes of both the pursuers and evaders in three-dimensional space, serving as a basis for subsequent behavioral analysis and strategy optimization.
Figure 17 shows the variation in distance between 10 pursuers and 10 evaders, where the final miss distances were
,
,
,
,
,
,
,
,
, and
. As the experiment progressed, the relative positions of the pursuers and evaders continuously changed in three-dimensional space, resulting in fluctuations in the distance between them. By observing this figure, we can clearly see how the pursuers gradually shortened the distance to the evaders, while at certain moments, the evaders successfully increased the distance through effective evasion strategies. These data provided important insights for further analyzing the behavior patterns of chasing and evading, helping to optimize the dynamic interaction strategies between pursuers and evaders.
Based on the many-to-many strategy presented in this article, the experimental results demonstrate that the pursuers successfully captured the evaders, with the system’s state converging to zero and the mean value of the state being finite. At the termination time, the values of the value functions equaled zero. The proposed many-to-one and many-to-many pursuit algorithms effectively enabled the interception of multiple targets.
To test the robustness of the model, we conducted 100 independent experiments with varying initial conditions. The initial positions of the pursuers and evaders were randomly selected, with the constraint that the initial distance between them was always greater than 100,000 m. The initial angles were chosen within a predefined permissible range, to ensure consistency across all trials. The experimental parameters and results are presented in
Table 3.
Numerical Stability: To further evaluate the stability of the solution, we varied key system parameters, including control input constraints, system dynamics, and the distribution functions of both the pursuers and evaders, using different distributions—such as exponential, chi-square, Weibull, and normal distributions—for comparison. The results showed that, despite variations in these parameters, the system consistently performed well, with the pursuers successfully intercepting the evaders in most trials. This indicates that the solution to the FBSDEs remained stable and robust, even when small perturbations were introduced into the system parameters.
To provide a more comprehensive view of the advantages and limitations of the MFG approach, we will include a detailed comparison with traditional methods in this paper. Specifically, we compare the performance of the MFG approach and traditional methods in solving the same missile interception problem, particularly in the case of a limited number of targets. Traditional methods typically use proportional guidance laws to intercept targets and assume a smaller number of targets, calculating the behavior of each target individually. In contrast, the MFG approach handles the behavior of large-scale target populations using the mean field assumption. This comparison will help us better demonstrate the advantages of the MFG approach in various scenarios, as well as its potential limitations when the number of targets is limited.
Traditional methods use proportional guidance laws to intercept targets. In comparison, the MFG approach proposed in this paper was tested with 100 targets in 100 experiments, and the results were compared in terms of average miss distance and interception success rate. The experimental results are shown in
Table 4.
The primary reason for the failure of traditional methods is that, as the number of targets increases, there is mutual interference between the individuals, making the system dynamics complex and difficult to control. Additionally, the proximity of target groups can significantly affect the interception results, as interactions between targets may lead to misjudgments or deviations in the pursuers’ actions, thereby reducing the success rate of interception. In this case, the density and relative positions of the target group become key factors influencing interception performance.
To overcome these issues, this paper adopts the Mean Field Game (MFG) strategy, which effectively simplifies the behavior model of large-scale target populations using the mean field assumption. Through this approach, we are able to reduce interference between individuals, particularly mitigating the negative impact of groups in proximity on the interception results. The experimental results show that the MFG strategy significantly improved the interception success rate, while reducing the miss distance, demonstrating the effectiveness and advantages of this method in complex environments.