Reliability Evaluation of Landing Gear Retraction/Extension Accuracy Based on Bayesian Theory
Abstract
1. Introduction
2. Main Landing Gear Retraction/Extension Test
2.1. Test Design
2.2. Normality Testing
- (1)
- First, the obtained data were arranged in ascending order to determine the relative location of each data point within the entire dataset;
- (2)
- Next, the corresponding cumulative probability value was calculated for each data point as , where i is the rank of the data point after sorting and n is the total number of data points;
- (3)
- Each data point and its corresponding cumulative probability value were plotted on normal probability paper, a special type of graph paper with the horizontal axis scaled according to the cumulative distribution function for the normal distribution and the vertical axis representing the values of the data points;
- (4)
- Finally, the sample was considered to exhibit a normal distribution if the plotted points fell along or near a straight line;
2.3. Hypothesis Testing
3. Iterative Reliability Model Based on Bayesian Theory
3.1. Reliability Model
3.2. Bayesian-Updated Iterative Model for the Reliability of Landing Gear Retraction/Extension Angle
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anderson, J.D. Aircraft Performance and Design; McGraw-Hill: New York, NY, USA, 1999; pp. 245–268. [Google Scholar]
- Cook, M.V. Flight Dynamics Principles, 3rd ed.; Elsevier: Oxford, UK, 2013; Chapter 7. [Google Scholar]
- Federal Aviation Administration. “Airworthiness Standards: Transport Category Airplanes” 14 CFR Part 25, §25.729, 2021. Available online: https://www.ecfr.gov/current/title-14/chapter-I/subchapter-C/part-25 (accessed on 15 March 2025).
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics, 2nd ed.; Wiley: Hoboken, NJ, USA, 1995; pp. 173–190. [Google Scholar]
- Yin, Y.; Hong, N.; Huajin, N.; Ming, Z. Reliability Analysis of Landing Gear Retraction System Influenced by Multifactors. J. Beijing Univ. Aeronaut. Astronaut. 2016, 53, 953–960. [Google Scholar]
- Hongxian, W.; Caijun, X.; Hong, N. Design and Application of Aircraft Landing Gear Retraction—Extension Fatigue Test System. J. Exp. Mech. 2010, 25, 175–177. [Google Scholar]
- National Transportation Safety Board. Analysis of Landing Gear-Related Accidents; NTSB/SS-17/01; National Transportation Safety Board: Washington, DC, USA, 2017. [Google Scholar]
- Lincoln, J.W. Case Studies in Aircraft Structural Integrity. In Contemporary Research in Engineering Science; Batra, R.C., Ed.; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar] [CrossRef]
- Jinhui, W.; Dequan, Z.; Jie, L.; Xinyu, J.; Xu, H. A computational framework of kinematic accuracy reliability analysis for industrial robots. Appl. Math. Model. 2020, 82, 189–216. [Google Scholar]
- Hong, W. Reliability Analysis of Landing Gear Structure and Reliability Test of Lock Mechanism; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2010. [Google Scholar]
- Wei, X. Reliability Analysis of Optimized Landing Gear Retraction and Retraction Structure for Type X Military Aircraft; Xi’an University of Electronic Science and Technology: Xi’an, China, 2014. [Google Scholar]
- SAE International. Aircraft Landing Gear Systems Testing and Evaluation; AIR5426; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Qiang, L.; Yuansheng, F. Study on evaluation method of small sample reliability test for failure life. China Mech. Eng. 1996, 7, 93–94. [Google Scholar]
- Zhou, C.; Ji, M.; Zhang, Y.; Liu, F.; Zhao, H. Mechanism reliability and sensitivity analysis of landing gear under multiple failure modes. J. Northwestern Polytech. Univ. 2021, 39, 46–54. [Google Scholar] [CrossRef]
- Chhajer, H.; Roy, R. Rationalised experiment design for parameter estimation with sensitivity clustering. Sci. Rep. 2024, 14, 25864. [Google Scholar]
- Gao, Z.T.; Xiong, J. Fatigue Reliability; Beijing University of Aeronautics and Astronautics Press: Beijing, China, 2000. [Google Scholar]
- Cheng, C.; Zhang, J.F. Analysis of Motion Reliability for Planar Trajectory Mechanisms. Mech. Sci. Technol. Aerosp. Eng. 2014, 33, 1635–1636. [Google Scholar]
- Zhang, F.; Qiao, Z.; Tian, Y.; Wu, M.; Xu, X. Reliability Analysis of Complex Structures Under Multi-Failure Mode Utilizing an Adaptive AdaBoost Algorithm. Appl. Sci. 2024, 14, 10098. [Google Scholar] [CrossRef]
- Shiming, D. The Reliability Analysis of a Trainer’s Landing Gear Retracting-Extending Mechanism; Xidian University: Xi’an, China, 2012; pp. 15–16. [Google Scholar]
- Johnson, R.; Lee, H. Data scarcity challenges in aviation maintenance. AIAA J. 2020, 58, 45–59. [Google Scholar]
- Wu, X.; Zhang, Y.; Yin, J.; Yao, Z. A finite element model updating method for aqueduct structures based on Bayesian theory. Hydro-Sci. Eng. 2024, 6, 148–156. [Google Scholar]
- Gholamizadeh, K.; Zarei, E.; Yazdi, M.; Amin, M.T. Applying Bayesian Networks to Safety Causation Analysis and Modeling in Socio-technical Systems: Bridging Theory and Practice. In Safety Causation Analysis in Sociotechnical Systems: Advanced Models and Techniques; Studies in Systems, Decision and Control; Springer: Cham, Switzerland, 2024; Volume 541. [Google Scholar]
- Shi’an, W. Mathematical Statistic; Beijing University of Technology Press: Beijing, China, 2000. [Google Scholar]
- Yuan, X.; Wang, S.; Valdebenito, M.A.; Faes, M.G.; Beer, M. Sample regeneration algorithm for structural failure probability function estimation. Probab. Eng. Mech. 2023, 71, 103387. [Google Scholar] [CrossRef]









| Retraction and Extension Angle θ (°) | Rotating Shaft Angle | Retraction/Extension Actuator Displacement(mm) | Retraction/Extension Torque (N·m) | Applied Load (N) | Servo Loading Mechanism Vertical Displacement (mm) |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1666 | 1410.8 | 0 |
| 10 | 11.4 | −20.4 | 1589 | 1300.3 | 48.6 |
| 20 | 22.8 | −44.3 | 1415 | 1183.3 | 141.6 |
| 30 | 34.3 | −70.9 | 1176 | 1057.8 | 275.9 |
| 40 | 45.9 | −99.7 | 913 | 932.6 | 447.4 |
| 50 | 57.6 | −129.7 | 660 | 817.9 | 650.5 |
| 60 | 69.5 | −160 | 443 | 732.6 | 878.8 |
| 70 | 81.7 | −189.1 | 265 | 695.2 | 1125 |
| 80 | 94.3 | −215.6 | 114.8 | 788.6 | 1381.1 |
| 89.536 | 106.8 | −236.5 | 0 | 0 | 1626.7 |
| Unloaded Angle θU (°) | Loaded Angle θL (°) | ||
|---|---|---|---|
| Angle range | Mean | Angle range | Mean |
| 11.2~11.7 | 11.4 | 11.0~11.9 | 11.5 |
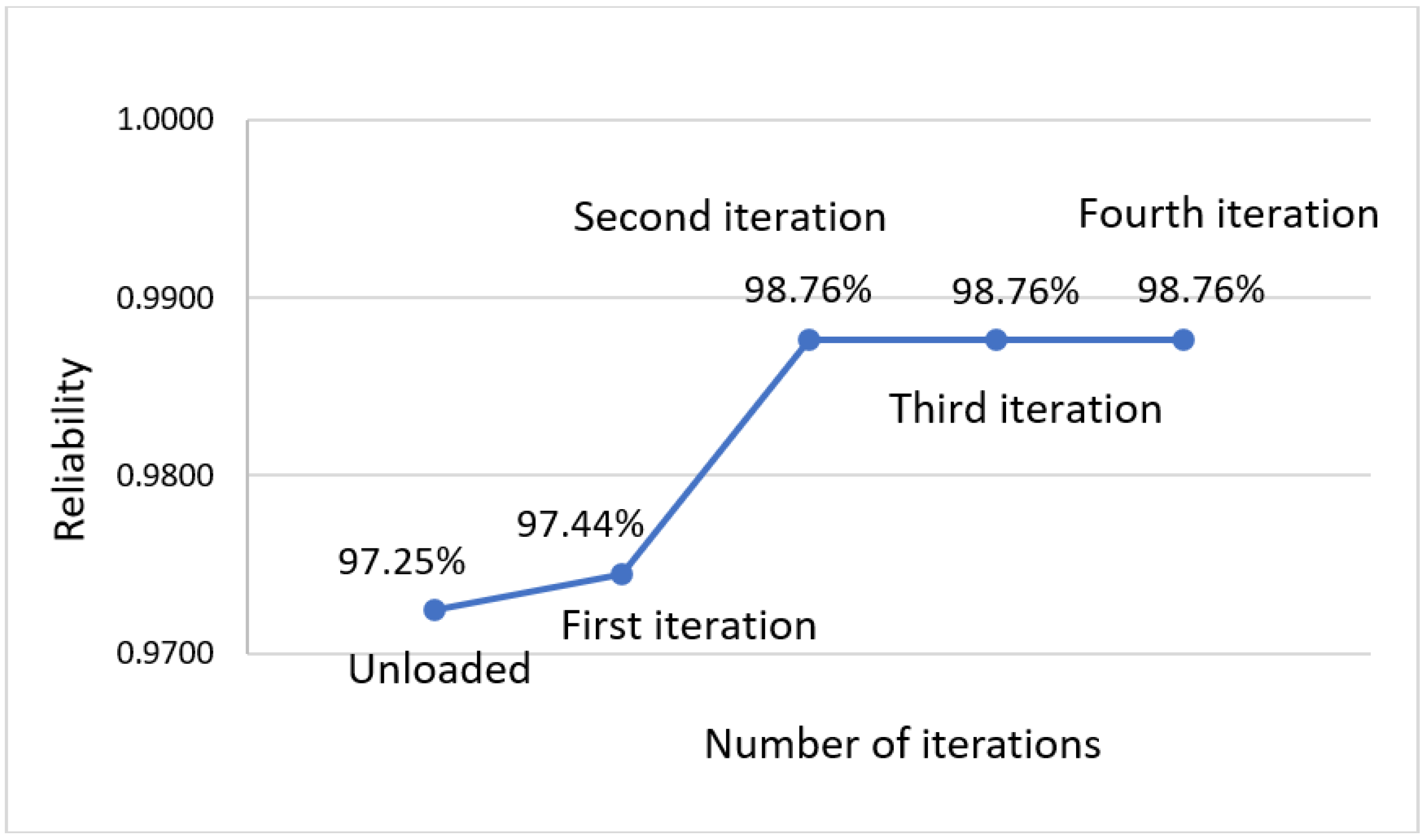
| Measurements Used as Prior Information | Mean Angle (°) | Standard Deviation | Reliability (%) |
|---|---|---|---|
| Unloaded data points (80) | 11.513 | 0.194 | 0.9725 |
| First iteration: loaded data points 1–20 | 11.467 | 0.079 | 0.9744 |
| Second iteration: loaded data points 21–40 | 11.482 | 0.112 | 0.9876 |
| Third iteration: loaded data points 41–60 | 11.483 | 0.078 | 0.9876 |
| Fourth iteration: loaded data points 61–80 | 11.501 | 0.066 | 0.9876 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lv, Y.; Chen, X.; Li, Y.; Tian, Y.; Zhang, F. Reliability Evaluation of Landing Gear Retraction/Extension Accuracy Based on Bayesian Theory. Aerospace 2025, 12, 300. https://doi.org/10.3390/aerospace12040300
Lv Y, Chen X, Li Y, Tian Y, Zhang F. Reliability Evaluation of Landing Gear Retraction/Extension Accuracy Based on Bayesian Theory. Aerospace. 2025; 12(4):300. https://doi.org/10.3390/aerospace12040300
Chicago/Turabian StyleLv, Yuanbo, Xianmin Chen, Yao Li, Yuxiang Tian, and Feng Zhang. 2025. "Reliability Evaluation of Landing Gear Retraction/Extension Accuracy Based on Bayesian Theory" Aerospace 12, no. 4: 300. https://doi.org/10.3390/aerospace12040300
APA StyleLv, Y., Chen, X., Li, Y., Tian, Y., & Zhang, F. (2025). Reliability Evaluation of Landing Gear Retraction/Extension Accuracy Based on Bayesian Theory. Aerospace, 12(4), 300. https://doi.org/10.3390/aerospace12040300







