Numerical Investigation of Stage Separation Control of Tandem Hypersonic Vehicles Based on Lateral Jet
Abstract
1. Introduction
2. Numerical Method for Multi-Body Separation
2.1. Governing Equations and Numerical Methods
2.2. Rigid Body Dynamics Motion Model
2.3. Dynamic Grid Method for Moving Boundaries
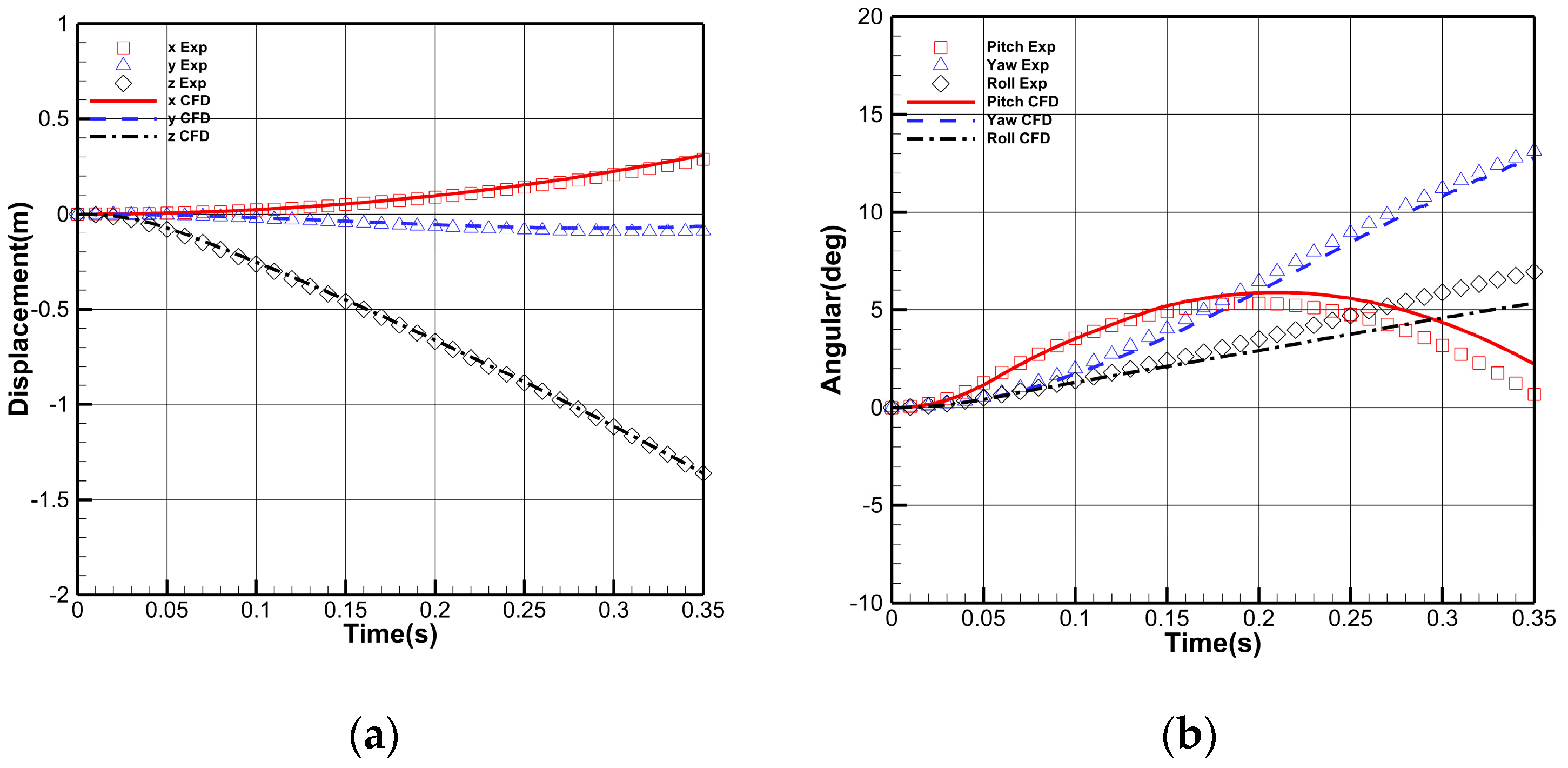
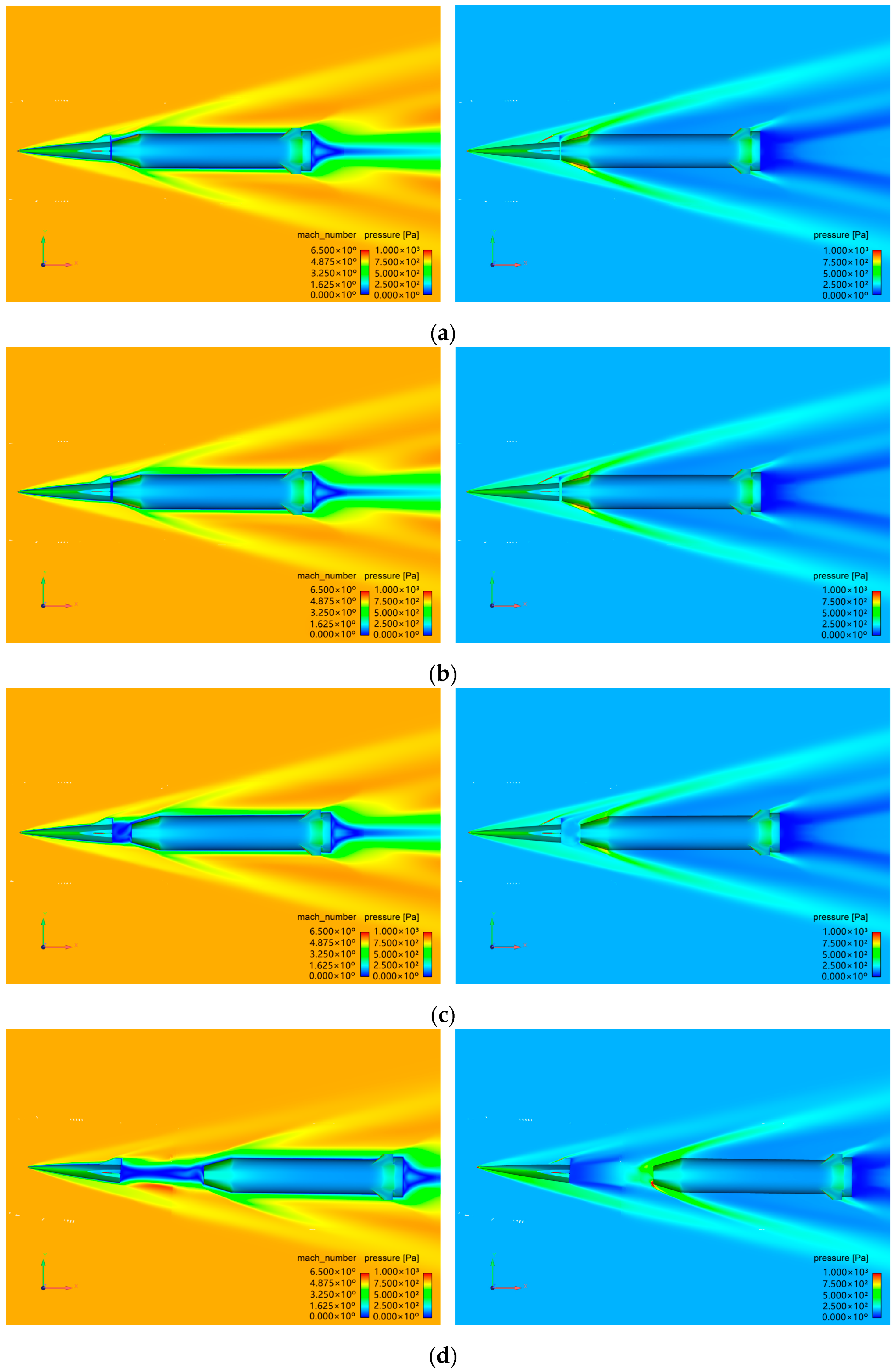
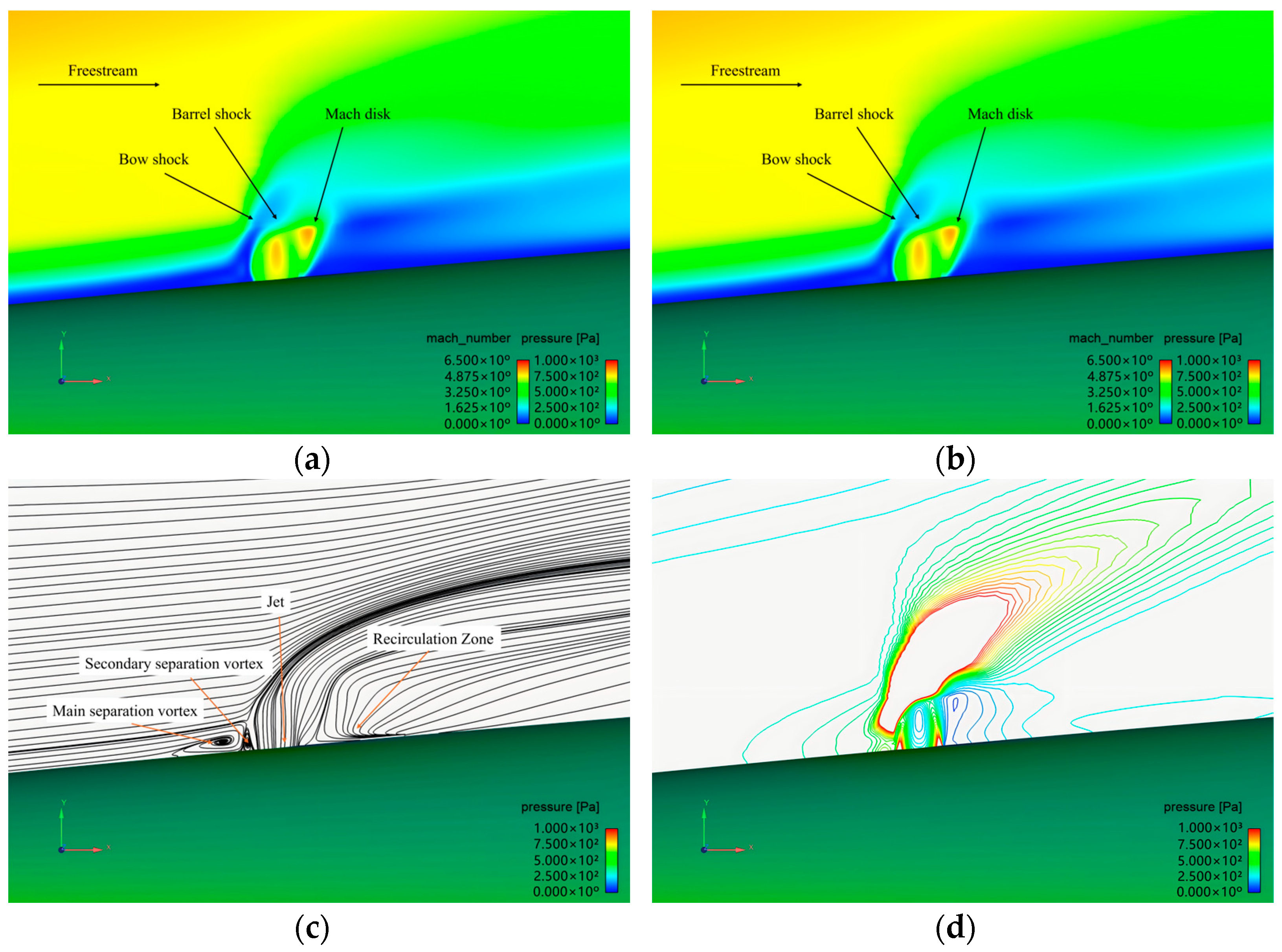
2.4. Validation of Numerical Methods
3. Numerical Simulation of Stage Separation Control Based on Lateral Jet
3.1. Computational Models and Conditions
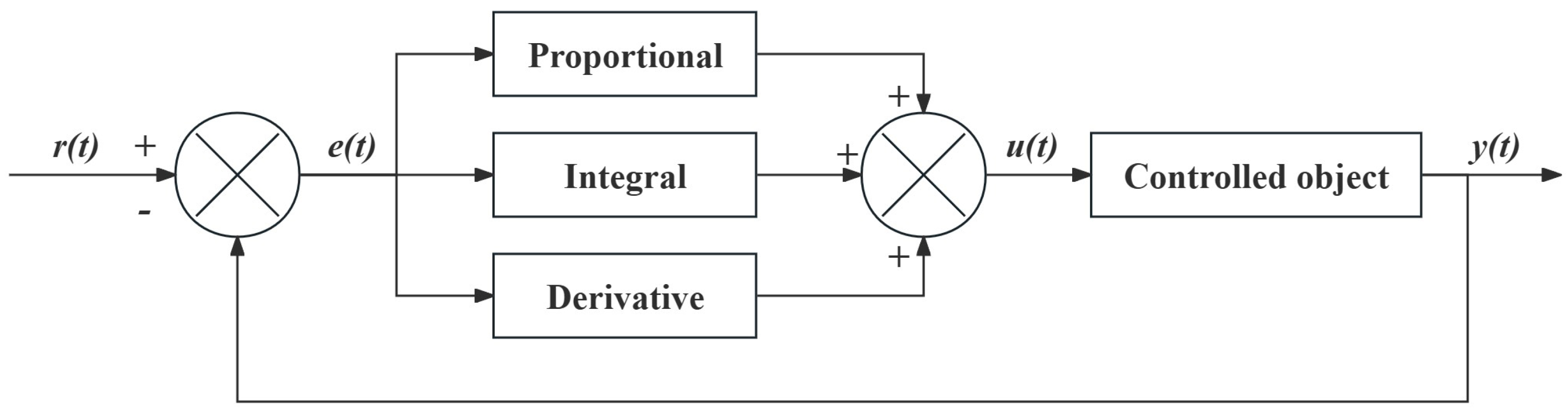
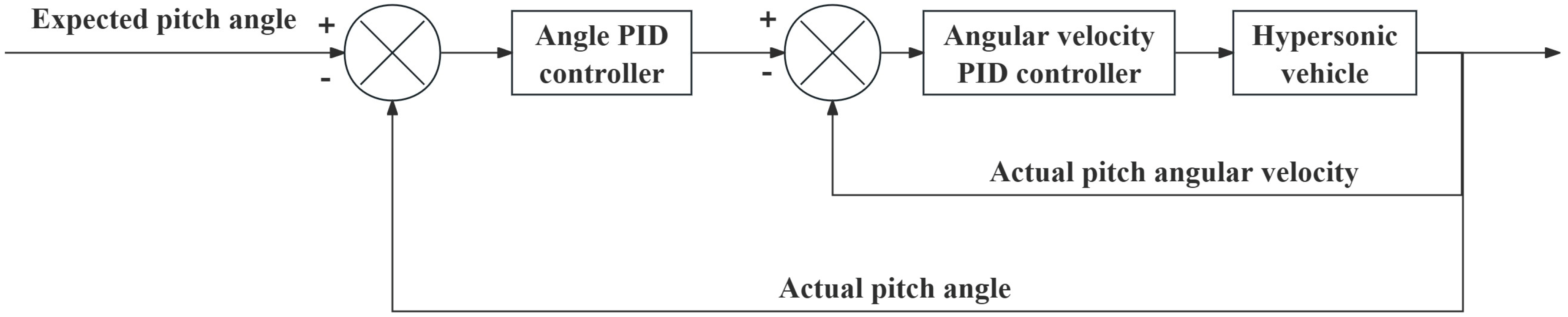
3.2. Principle of Cascade PID Controller
3.3. Numerical Simulation of Stage Separation
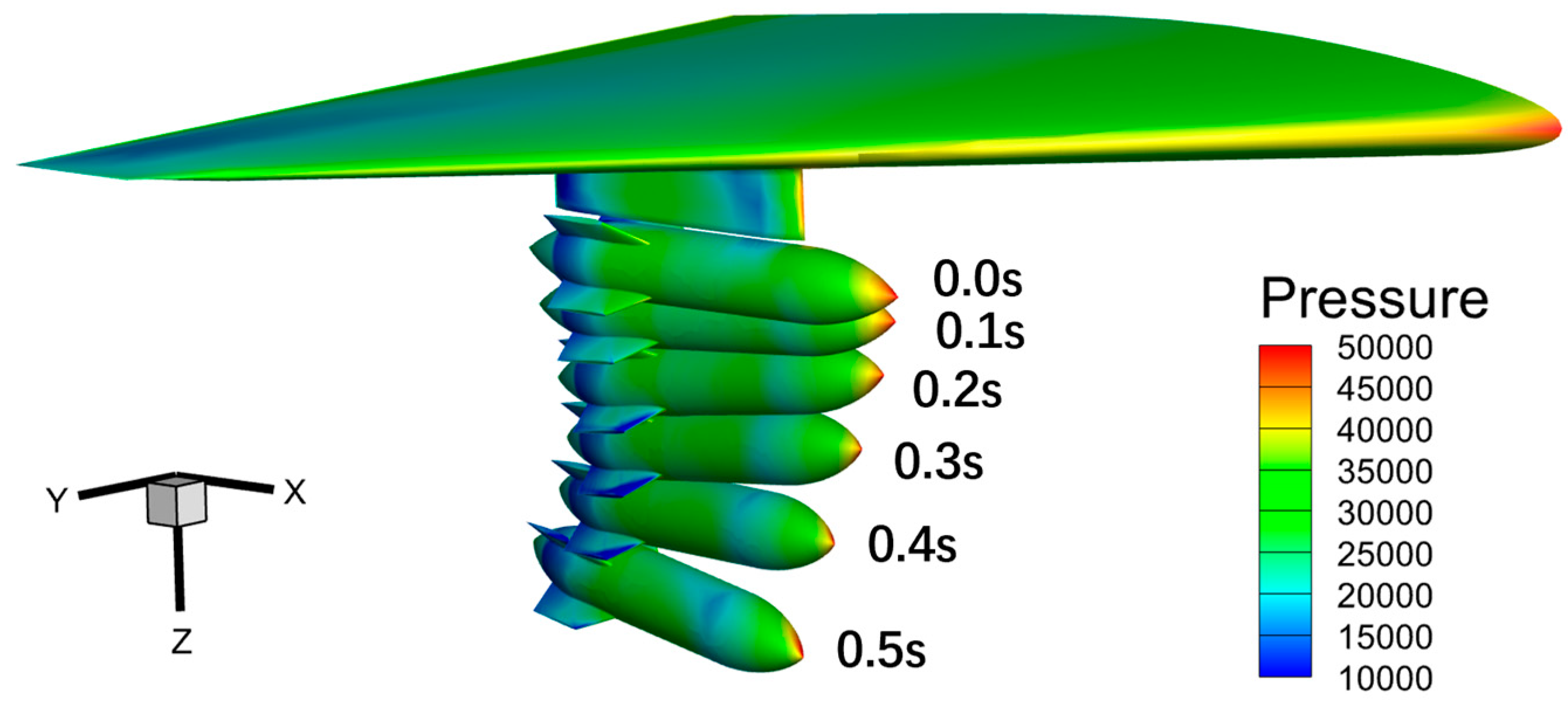
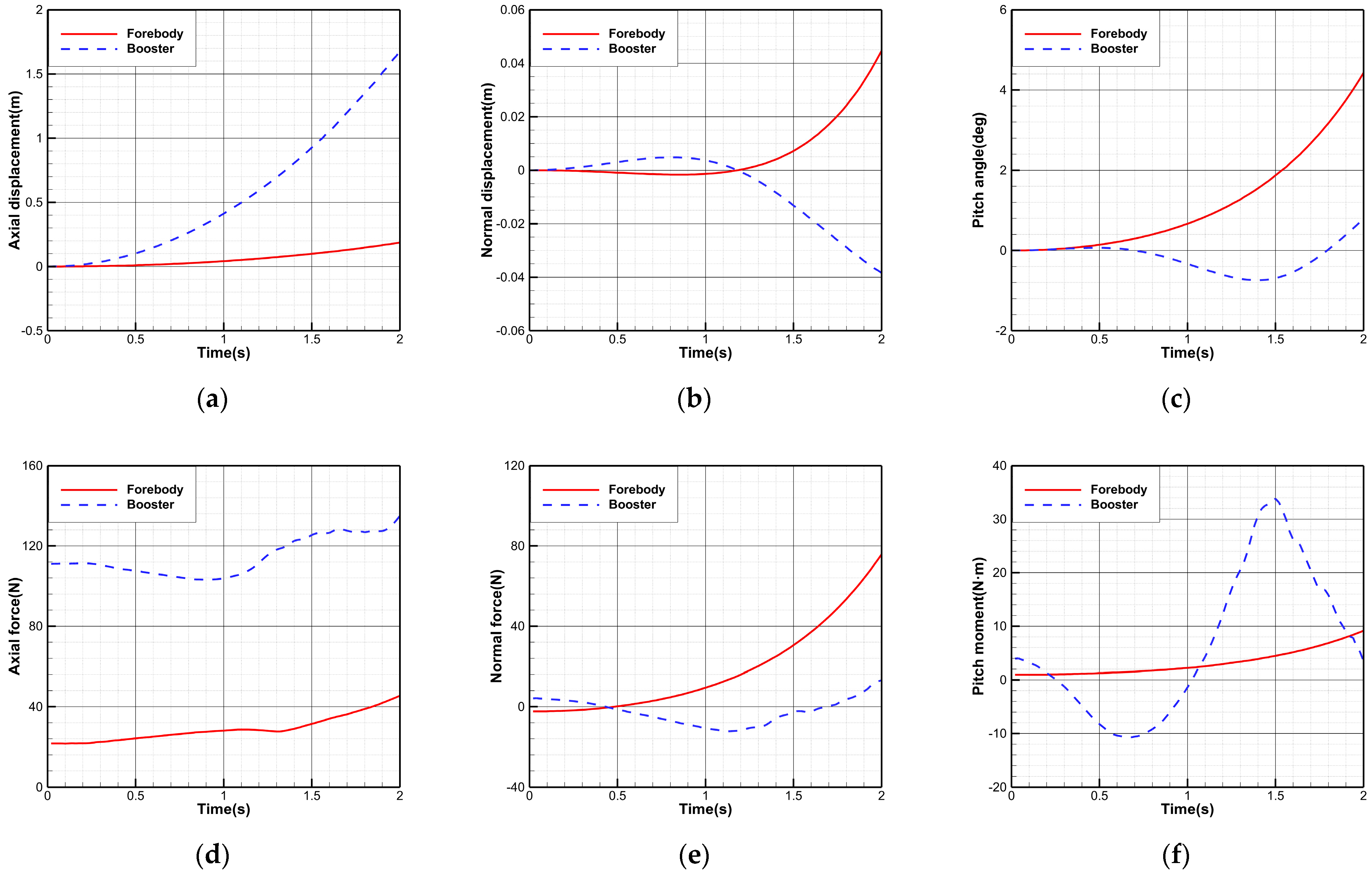
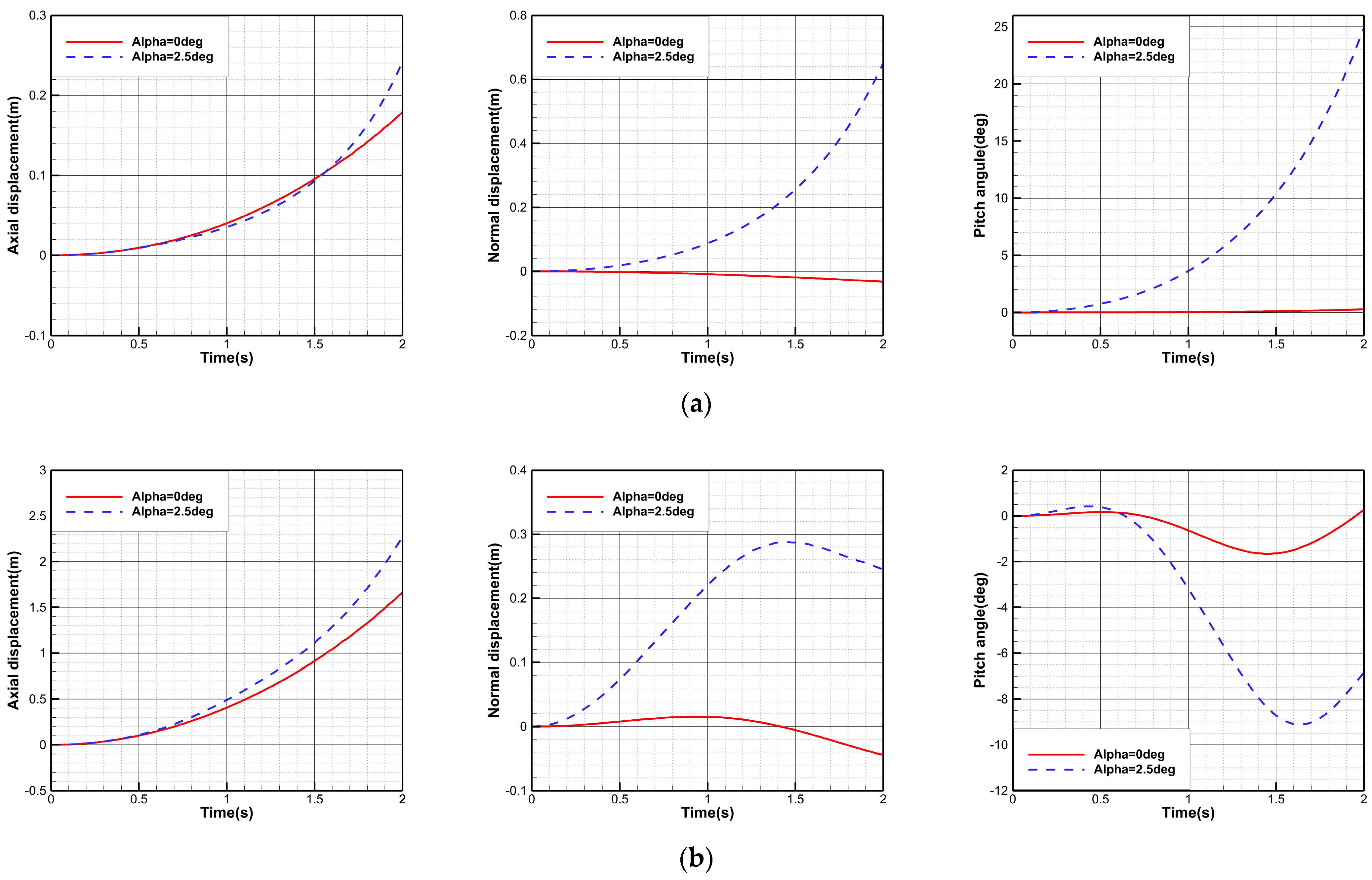
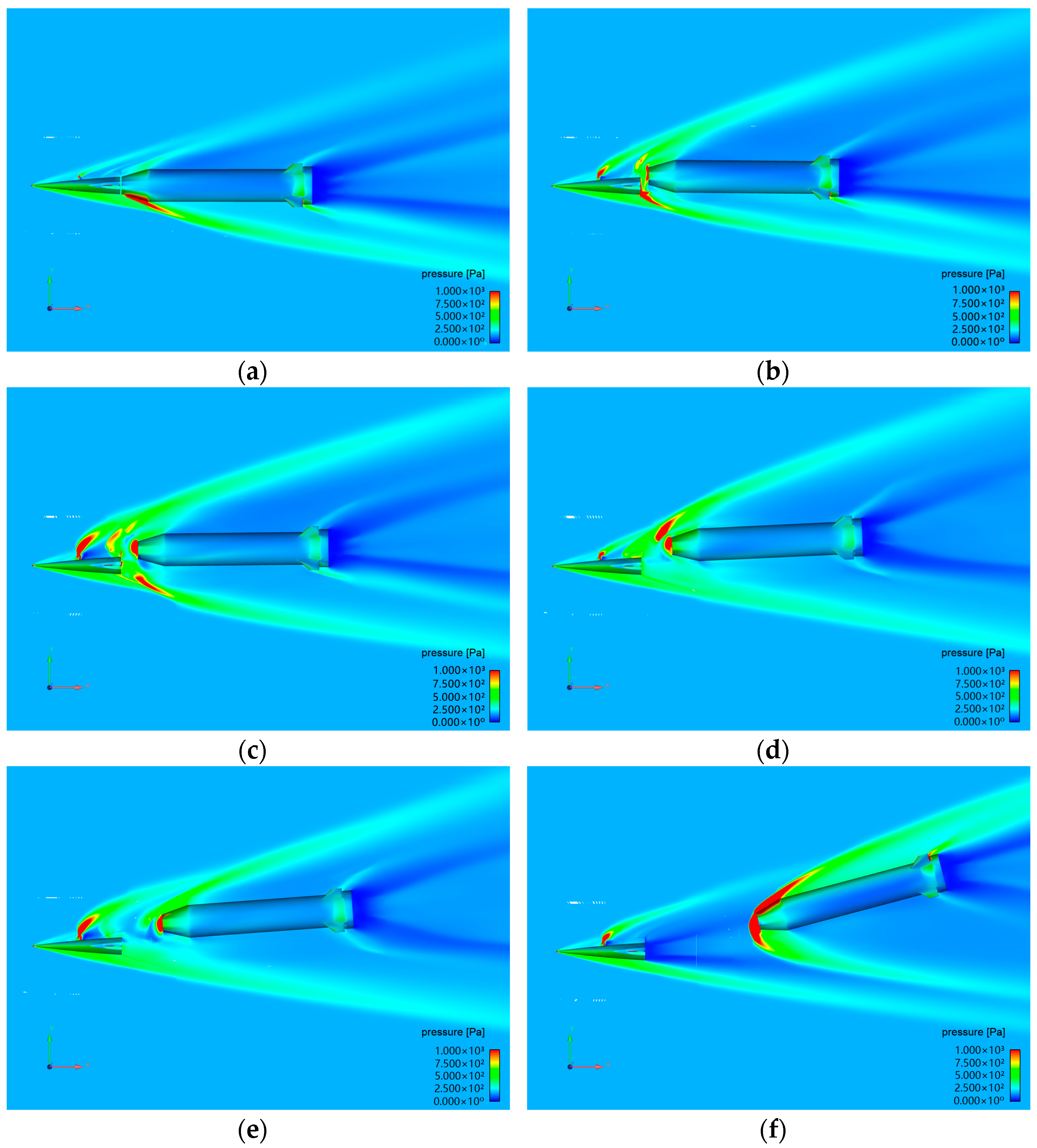
3.3.1. Free Stage Separation
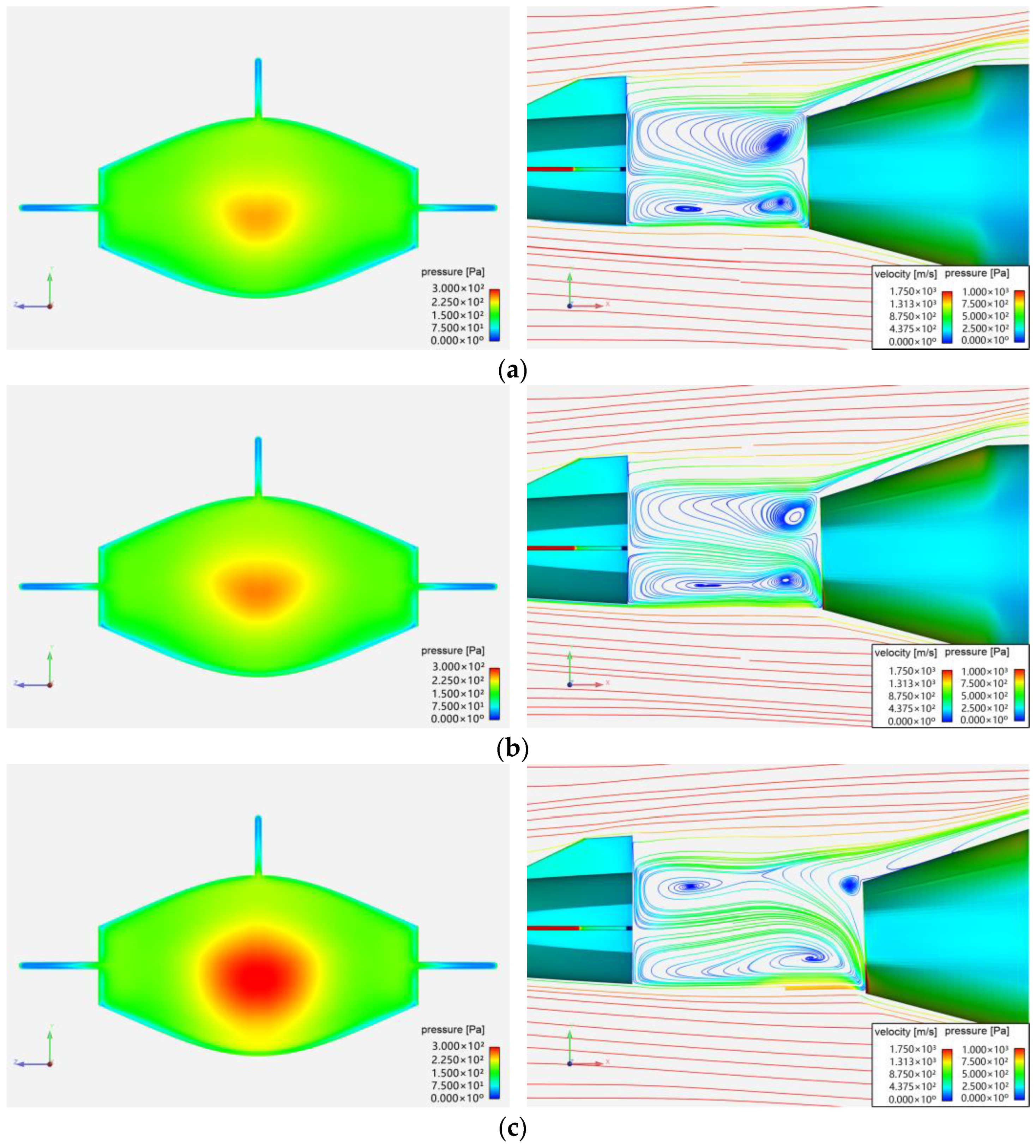
3.3.2. Open-Loop Attitude Control Based on Lateral Jet
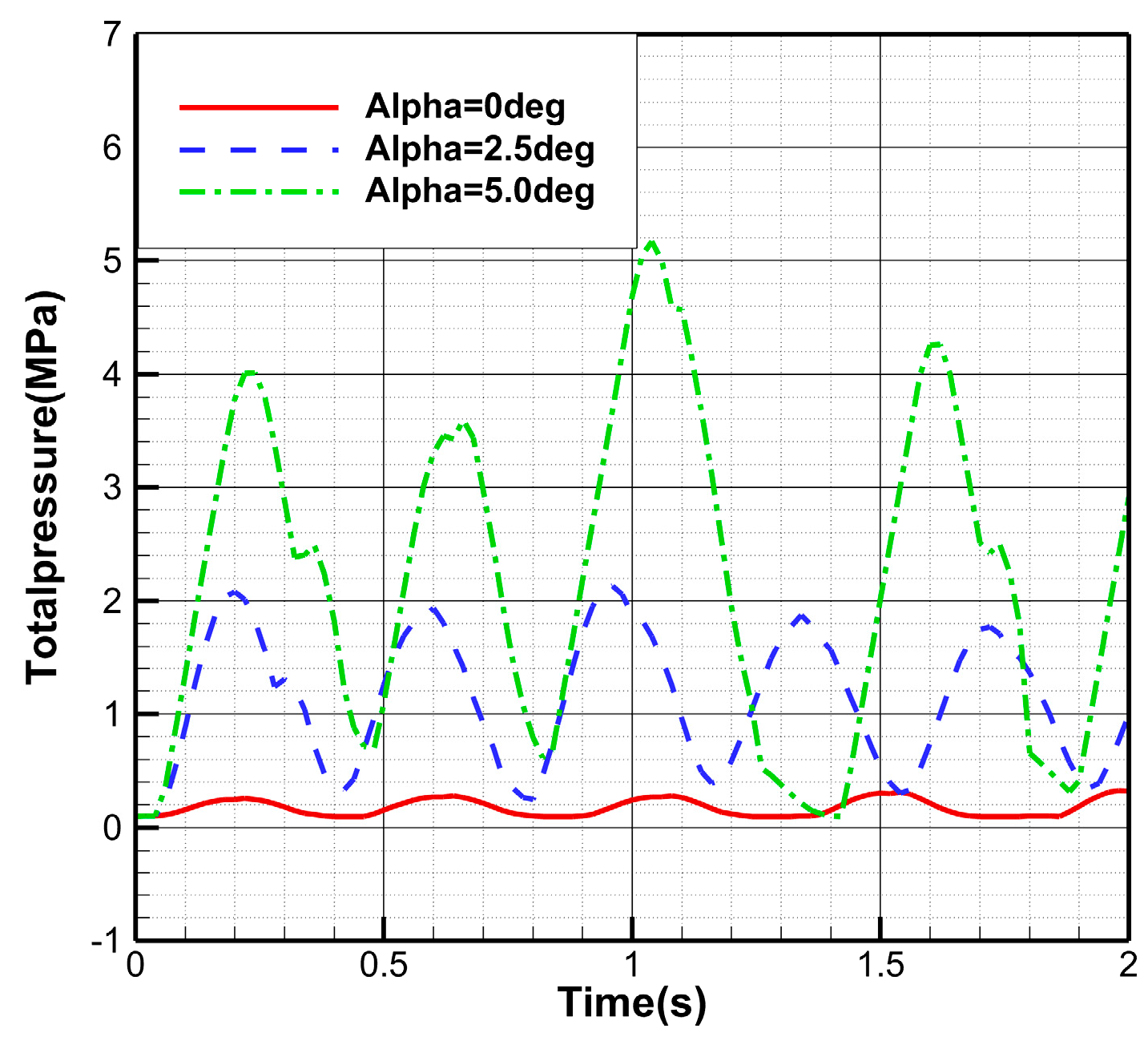
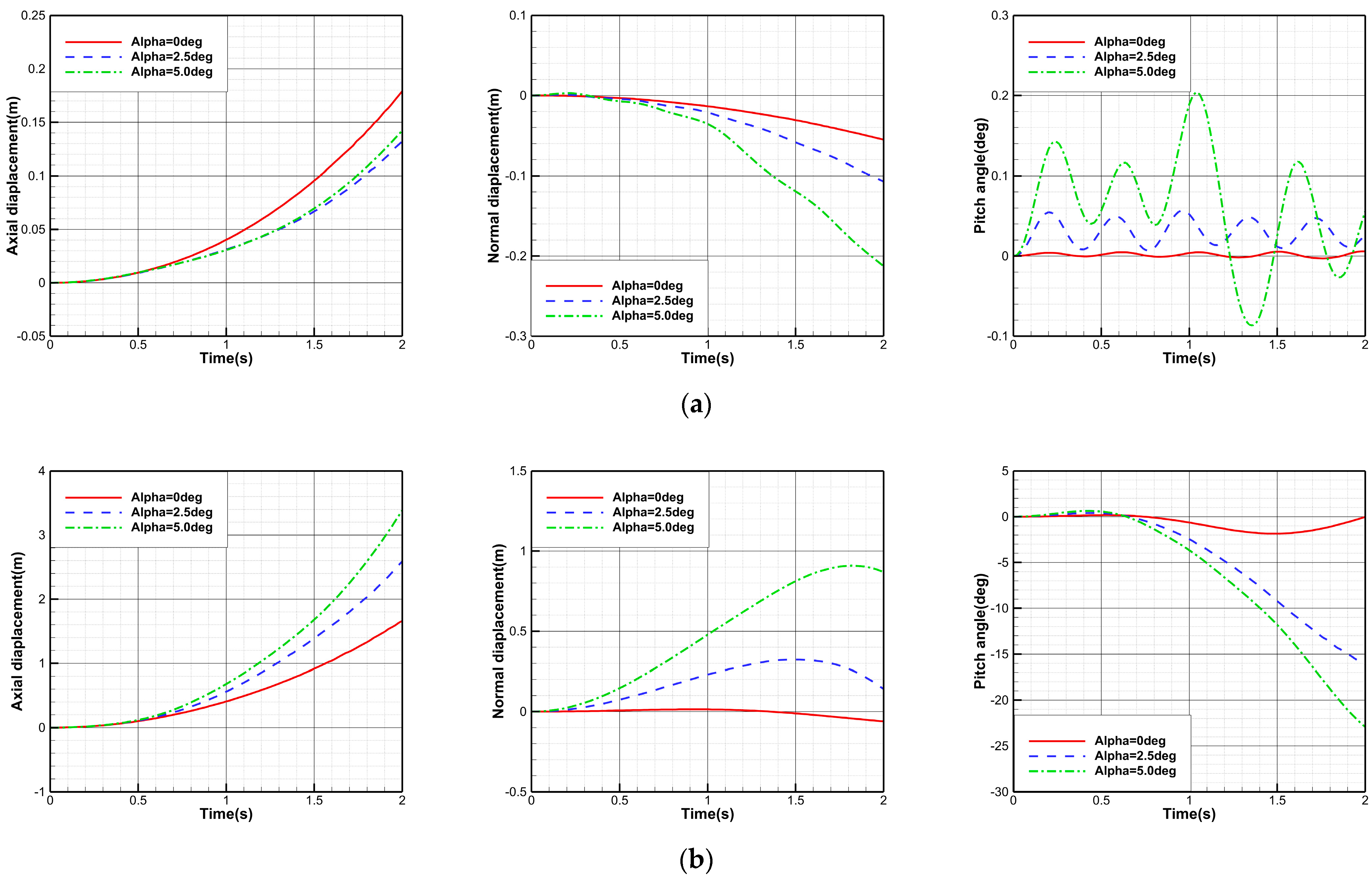
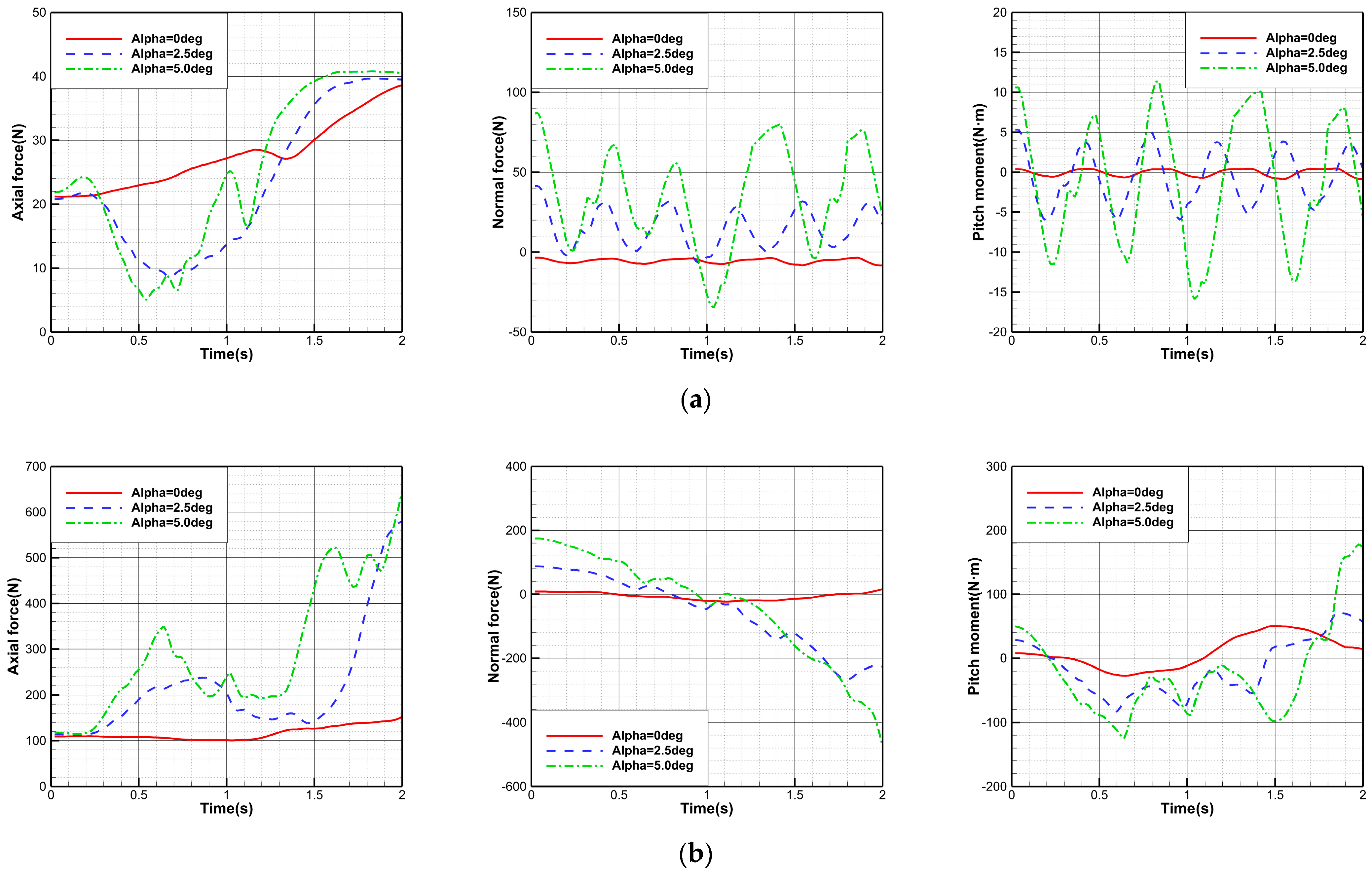
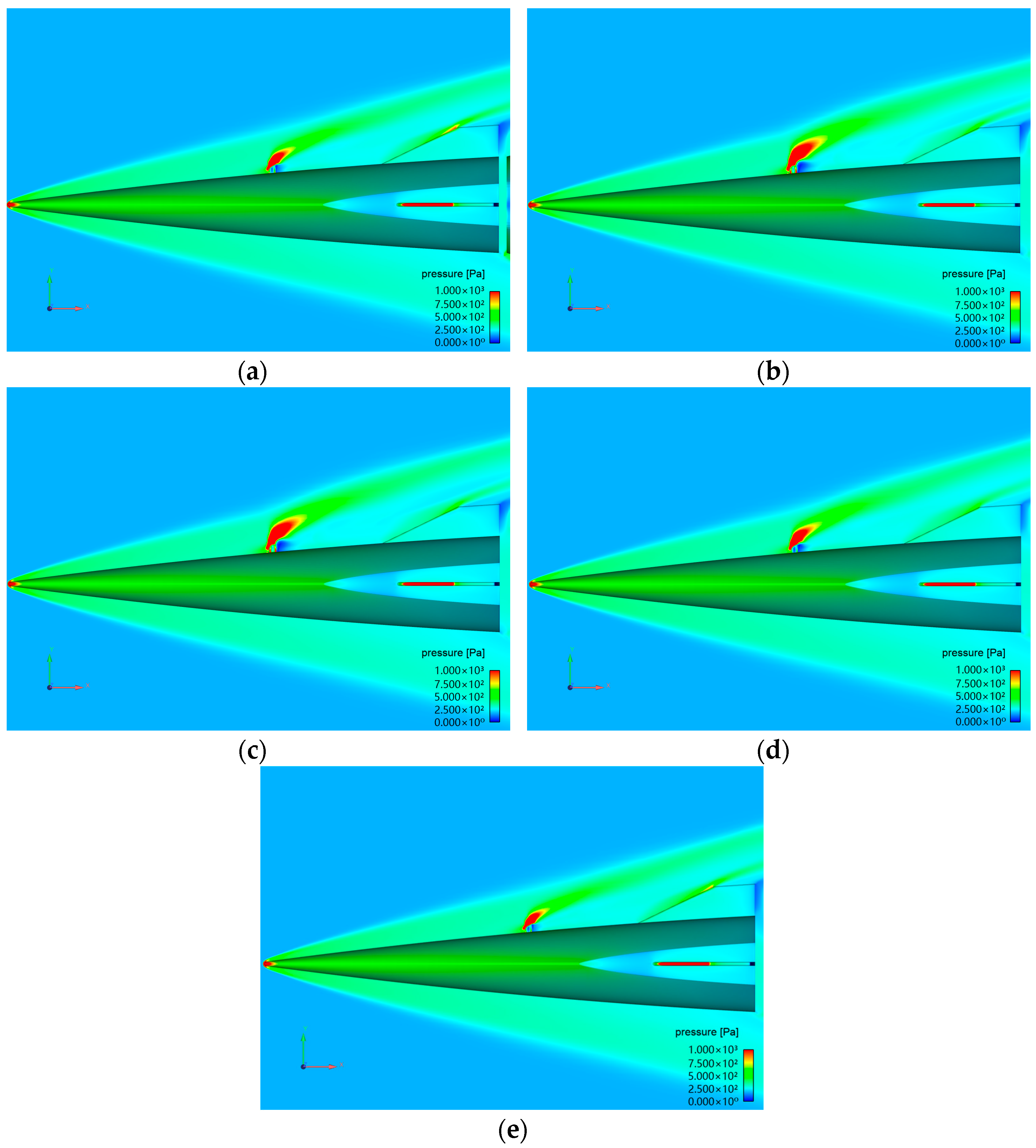
3.3.3. Closed-Loop Attitude Control Based on Lateral Jet
4. Conclusions
- (1)
- During free stage separation, the forebody’s pitch angle still reached 4.43° at an angle of attack , which could adversely affect its subsequent flight missions.
- (2)
- The open-loop attitude control method based on lateral jet can effectively control the pitch angle of the forebody only when the angle of attack is 0°. However, since the angle of attack may change during actual flight, the applicability of the open-loop control method is limited.
- (3)
- Under the control of the closed-loop attitude control algorithm, the total pressure of the lateral jet exhibits a wave-like variation, and the amplitude of the total pressure increases with the angle of attack. Consequently, the overshoot of the forebody pitch angle and the pitch angle after separation also increases, leading to a decline in the control effectiveness of the closed-loop algorithm. However, when the angle of attack is 5.0°, the forebody pitch angle after separation is only 0.06°, indicating that the closed-loop attitude control method based on lateral jet outperforms the open-loop method in both control effectiveness and applicability.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xiang, G.X.; Wang, C.; Teng, H.H.; Jiang, Z.L. Shock/shock interactions between bodies and wings. Chin. J. Aeronaut. 2018, 31, 255–261. [Google Scholar] [CrossRef]
- Lungu, C.; Ramasamy, S.; Scarborough, D.; Jagoda, J.; Menon, S. Experimental studies of stage separation in a Mach 2.5 free stream. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Oriando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef]
- McQuellin, L.P.; Kennell, C.M.; Sytsma, J.M.; Choudhury, R.; Neely, A.; Buttsworth, D.R.; Slivester, T. Investigating endo-atmospheric separation of a hypersonic flyer-sustainer using wind tunnel based free-flight. In Proceedings of the 23rd AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Montreal, QC, Canada, 10–12 March 2020. [Google Scholar] [CrossRef]
- Qian, F.X.; Guo, P.; Gao, P.; Liu, Q.; Wang, Y.J.; Yi, G.Q. Stage separation trajectory simulation test technique in high speed wind tunnel. J. Exp. Fluid Mech. 2021, 35, 90–98. [Google Scholar]
- Li, J.P.; Chen, S.S.; Cai, F.J.; Yan, C. Numerical investigation of vented plume into a supersonic flow in the early stage of rocket hot separation. Aerosp. Sci. Technol. 2020, 107, 106249. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.P.; Xue, X.P.; Jiang, Z.L. Numerical investigation on safe stage separation problem of a TSTO model at Mach 7. Chin. J. Theor. Appl. Mech. 2022, 54, 526–542. [Google Scholar]
- Jia, J.H.; Fu, D.B.; He, Z.P.; Yang, J.F.; Hu, L.J. Hypersonic aerodynamic interference investigation for a two-stage-to-orbit model. Acta Astronaut. 2020, 168, 138–145. [Google Scholar] [CrossRef]
- Bahm, C.; Baumann, E.; Martin, J.; Bose, D.; Beck, R.; Strovers, B. The X-43A Hyper-X Mach 7 flight 2 guidance, navigation, and control overview and flight test results. In Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonics Systems and Technologies Conference, Capua, Italy, 16–20 May 2005. [Google Scholar] [CrossRef]
- Pinier, J.T.; Niskey, C.J. Ares I and Ares I-X stage separation aerodynamic testing. J. Spacecr. Rocket. 2012, 49, 842–852. [Google Scholar] [CrossRef][Green Version]
- Bordelon, W.; Frost, A.; Reed, D. Stage separation wind tunnel tests of a generic TSTO launch vehicle. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Oriando, FL, USA, 23–26 June 2003. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Jiang, Z. Experimental study of longitudinal stage separation of two-body configuration in shock tunnel. AIAA J. 2022, 60, 6940–6946. [Google Scholar] [CrossRef]
- Hohn, O.M.; Gülhan, A. Impact of retrorocket plumes on upper-stage aerothermodynamics during stage separation. J. Spacecr. Rocket. 2017, 54, 640–651. [Google Scholar] [CrossRef]
- Moelyadi, M.A.; Breitsamter, C.; Laschka, B. Stage-separation aerodynamics of two-stage space transport systems. Part 1: Steady-state simulations. J. Spacecr. Rocket. 2008, 45, 1230–1239. [Google Scholar] [CrossRef]
- Moelyadi, M.A.; Breitsamter, C.; Laschka, B. Stage-separation aerodynamics of two-stage space transport systems part 2: Unsteady simulation. J. Spacecr. Rocket. 2008, 45, 1240–1250. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.P.; Jiang, Z.L. Unsteady interaction mechanism of transverse stage separation in hypersonic flow for a two-stage-to-orbit vehicle. Phys. Fluids 2023, 35, 488–503. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, Z.S.; Lu, W.B.; He, S. Numerical investigation on the safe stage-separation mode for a TSTO vehicle. Aerosp. Sci. Technol. 2020, 107, 106349. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Jiang, Z. Numerical investigation of aerodynamic separation schemes for two-stage-to-orbit-like two-body system. Aerosp. Sci. Technol. 2022, 131, 107995. [Google Scholar] [CrossRef]
- Li, Y.; Reimann, B.; Eggers, T. Coupled Simulation of CFD and Flight Mechanics with a Two-Species-Gas-Model for the Hot Staging of a Multistage Rocket. In Proceedings of the 19th AIAA International Space Planes and Hypersonic Systems and Technologies Conference, Atlanta, GA, USA, 16–20 June 2014. [Google Scholar]
- Erdem, E.; Kontis, K. Numerical and experimental investigation of transverse injection flows. Shock. Waves 2010, 20, 103–118. [Google Scholar]
- Ukai, T.; Zare-Behtash, H.; Erdem, E.; Lo, K.H.; Kontis, K.; Obayashi, S. Effectiveness of jet location on mixing characteristics inside a cavity in supersonic flow. Exp. Therm. Fluid Sci. 2014, 52, 59–67. [Google Scholar] [CrossRef]
- Erdem, E.; Kontis, K. Experimental investigation of sonic transverse jets in Mach 5 crossflow. Aerosp. Sci. Technol. 2021, 110, 106419. [Google Scholar] [CrossRef]
- Erdem, E.; Kontis, K.; Saravanan, S. Penetration characteristics of air, carbon dioxide and helium transverse sonic jets in Mach 5 cross flow. Sensors 2014, 14, 23462–23489. [Google Scholar] [CrossRef]
- Zhang, J.M.; Cai, J.; Cui, Y. Effect of nozzle shapes on lateral jets in supersonic cross-flows. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar]
- Kontis, K.; Stollery, J.L. Control effectiveness of a jet-slender body combination at hypersonic speeds. J. Spacecr. Rocket. 1997, 34, 762–768. [Google Scholar]
- Min, B.Y.; Lee, J.W.; Byun, Y.H. Numerical investigation of the shock interaction effect on the lateral jet controlled missile. Aerosp. Sci. Technol. 2006, 10, 385–393. [Google Scholar] [CrossRef]
- Graham, M.J.; Weinacht, P.; Brandeis, J. Numerical investigation of supersonic jet interaction for finned bodies. J. Spacecr. Rocket. 2002, 39, 376–383. [Google Scholar] [CrossRef]
- Liang, W.; Zhang, X.; Zhao, W.L.; Li, X.; Duan, X. Research on the interference of side jet plume to a slenderbody in a subsonic or transonic freestream condition at large angle of attack. Air Space Def. 2022, 5, 38–43. [Google Scholar]
- Jia, M.L.; Chen, S.S.; Li, J.P.; Yuan, W.; Lin, B.X.; Gao, Z.H. Uncertainty and sensitivity study on lateral jet interaction for hypersonic missile. J. Spacecr. Rocket. 2024, 61, 458–472. [Google Scholar] [CrossRef]
- Gao, Y.; Lei, J.M. Numerical investigation on transient effect of jet interference characteristics of lateral-jet-controlled spinning missile. Aerospace 2022, 9, 430. [Google Scholar] [CrossRef]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications, 3rd ed.; Butterworth-Heinemann: Oxford, UK, 2001; pp. 15–25. [Google Scholar]
- Tian, S.L.; Xu, K.; Xia, J.; Chen, L. Efficient parallel dynamic overset unstructured grid for flow simulation with moving bodies. AIAA J. 2023, 61, 2135–2166. [Google Scholar]
- Li, X.F.; Liu, Y.; Qian, Z.S. Applications of overset grid technique to CFD simulation of high Mach number multi-body interaction/separation flow. Procedia Eng. 2015, 99, 458–476. [Google Scholar] [CrossRef][Green Version]
- Benek, J.; Buning, P.; Steger, J. A 3-D chimera grid embedding technique. In Proceedings of the 7th Computational Physics Conference, Cincinnati, OH, USA, 15–17 July 1985. [Google Scholar]
- Snyder, D.; Koutsavdis, E.; Anttonen, J. Transonic store separation using unstructured CFD with dynamic meshing. In Proceedings of the 33rd AIAA Fluid Dynamics Conference and Exhibit, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Tian, S.; Fu, J.; Chen, J. A numerical method for multi-body separation with collisions. Aerosp. Sci. Technol. 2021, 109, 106426. [Google Scholar] [CrossRef]
- Huang, Z.H. Aerospace Aerodynamics; Astronautic Publishing House: Beijing, China, 1994. [Google Scholar]



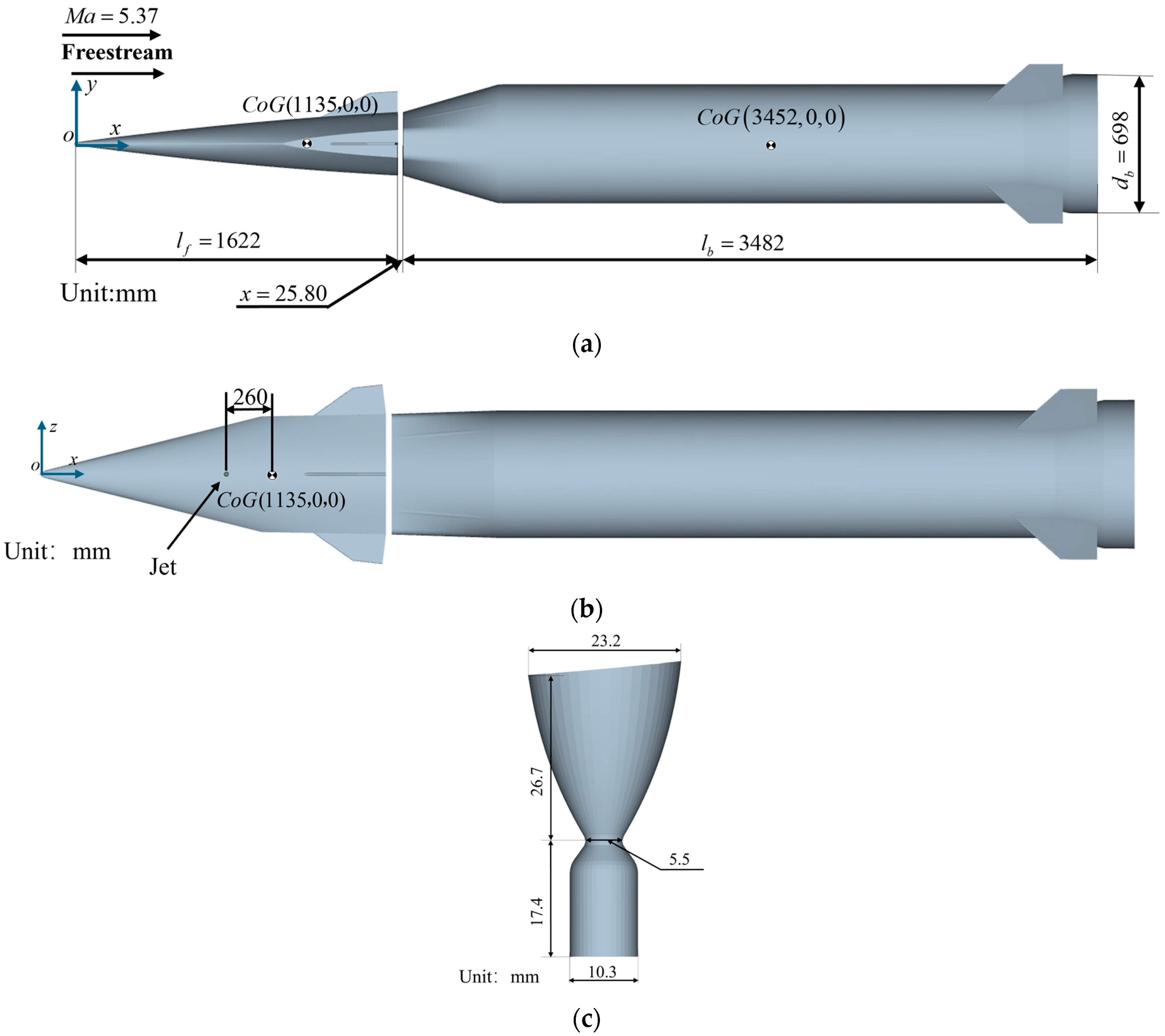
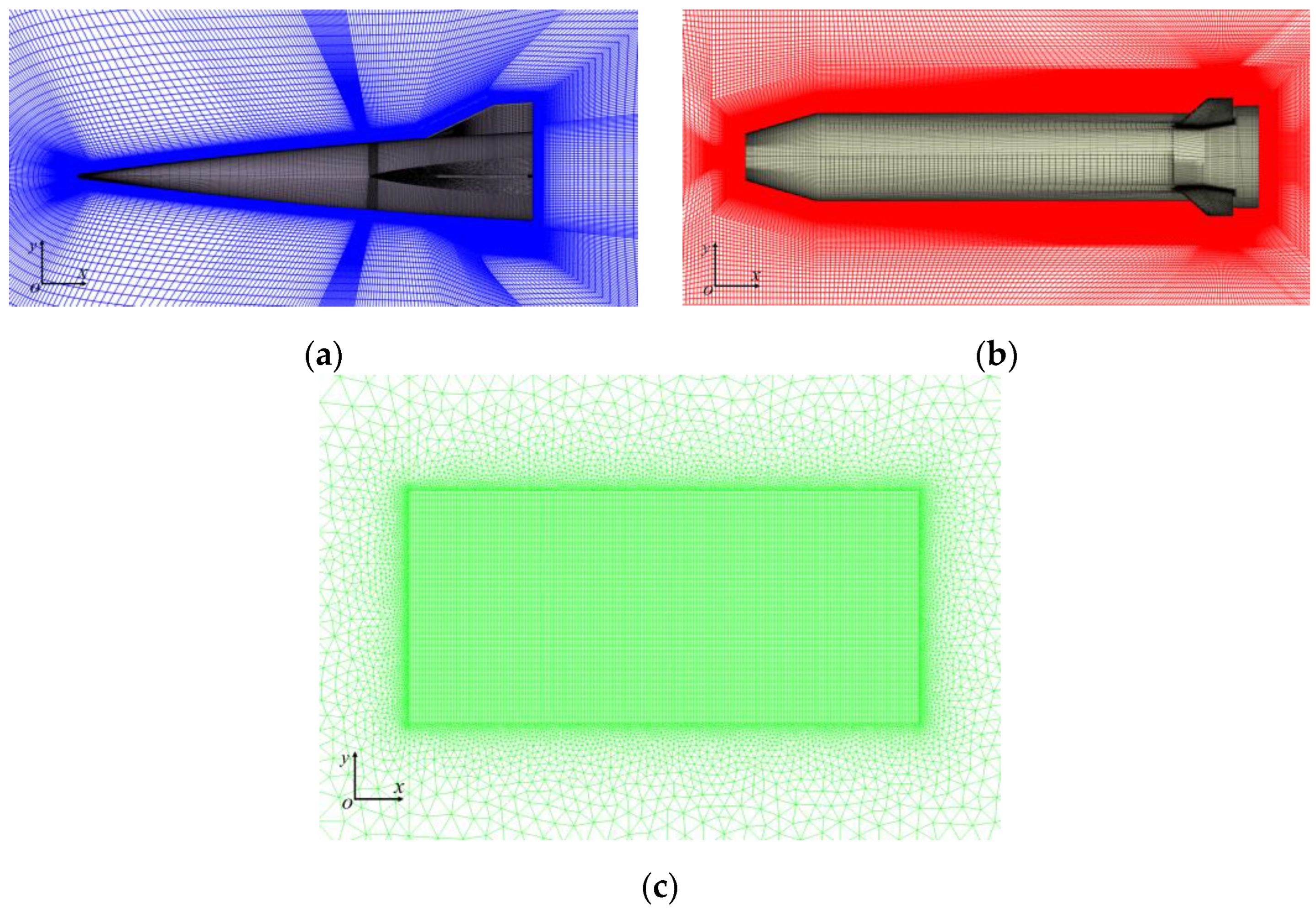
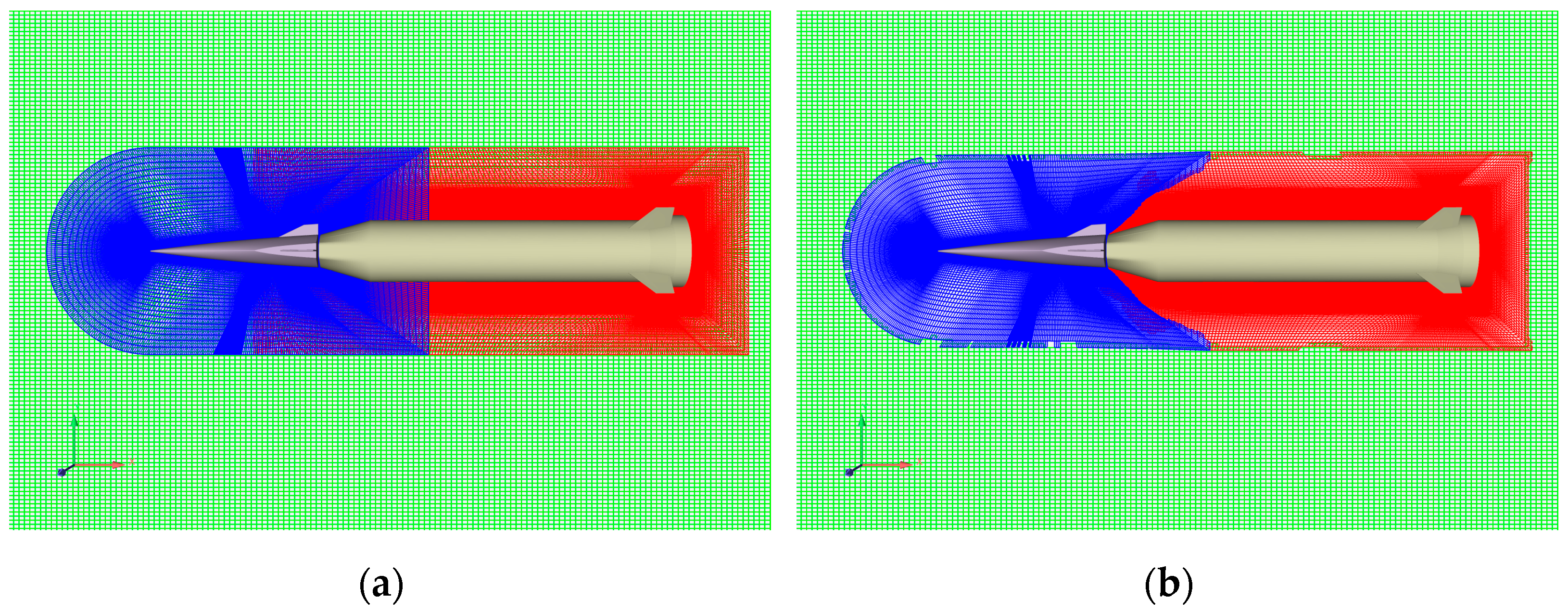



| Parameters | Forebody | Booster |
|---|---|---|
| Length (mm) | 1622 | 3482 |
| Center of gravity (mm) | (1135, 0, 0) | (3452, 0, 0) |
| Mass (kg) | 270 | 130 |
| (kg·m2) | 10.1 | 11.9 |
| (kg·m2) | 53.6 | 180.5 |
| (kg·m2) | 47.7 | 180.5 |
| Parameters | Out Loop | Inner Loop |
|---|---|---|
| 20 | 500 | |
| 0.1 | 1 | |
| 0.1 | 0.5 |
| Boundary Conditions | Free Separation | Open-Loop | Closed-Loop |
|---|---|---|---|
| Freestream | Pressure farfield | Pressure farfield | Pressure farfield |
| Surface of aircraft | Wall | Wall | Wall |
| Plane of symmetry | Symmetry | Symmetry | Symmetry |
| Jet inlet. | None | Pressure inlet | Pressure inlet |
| Parameters | Lateral Jet |
|---|---|
| Total pressure (Pa) | 155,000 |
| Static pressure (Pa) | 100,000 |
| Total temperature (K) | 800 |
| Gas constant (J/(kg·K)) | 287 |
| Specific heat ratio | 1.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, W.; Fu, J.; He, P.; Tian, S. Numerical Investigation of Stage Separation Control of Tandem Hypersonic Vehicles Based on Lateral Jet. Aerospace 2025, 12, 286. https://doi.org/10.3390/aerospace12040286
Guo W, Fu J, He P, Tian S. Numerical Investigation of Stage Separation Control of Tandem Hypersonic Vehicles Based on Lateral Jet. Aerospace. 2025; 12(4):286. https://doi.org/10.3390/aerospace12040286
Chicago/Turabian StyleGuo, Wenhua, Jiawei Fu, Pengzhen He, and Shuling Tian. 2025. "Numerical Investigation of Stage Separation Control of Tandem Hypersonic Vehicles Based on Lateral Jet" Aerospace 12, no. 4: 286. https://doi.org/10.3390/aerospace12040286
APA StyleGuo, W., Fu, J., He, P., & Tian, S. (2025). Numerical Investigation of Stage Separation Control of Tandem Hypersonic Vehicles Based on Lateral Jet. Aerospace, 12(4), 286. https://doi.org/10.3390/aerospace12040286






