Effect of Dynamic Flexural Strength on Impact Response Analysis of AlN Substrates for Aerospace Applications
Abstract
1. Introduction
2. Experimental Tests
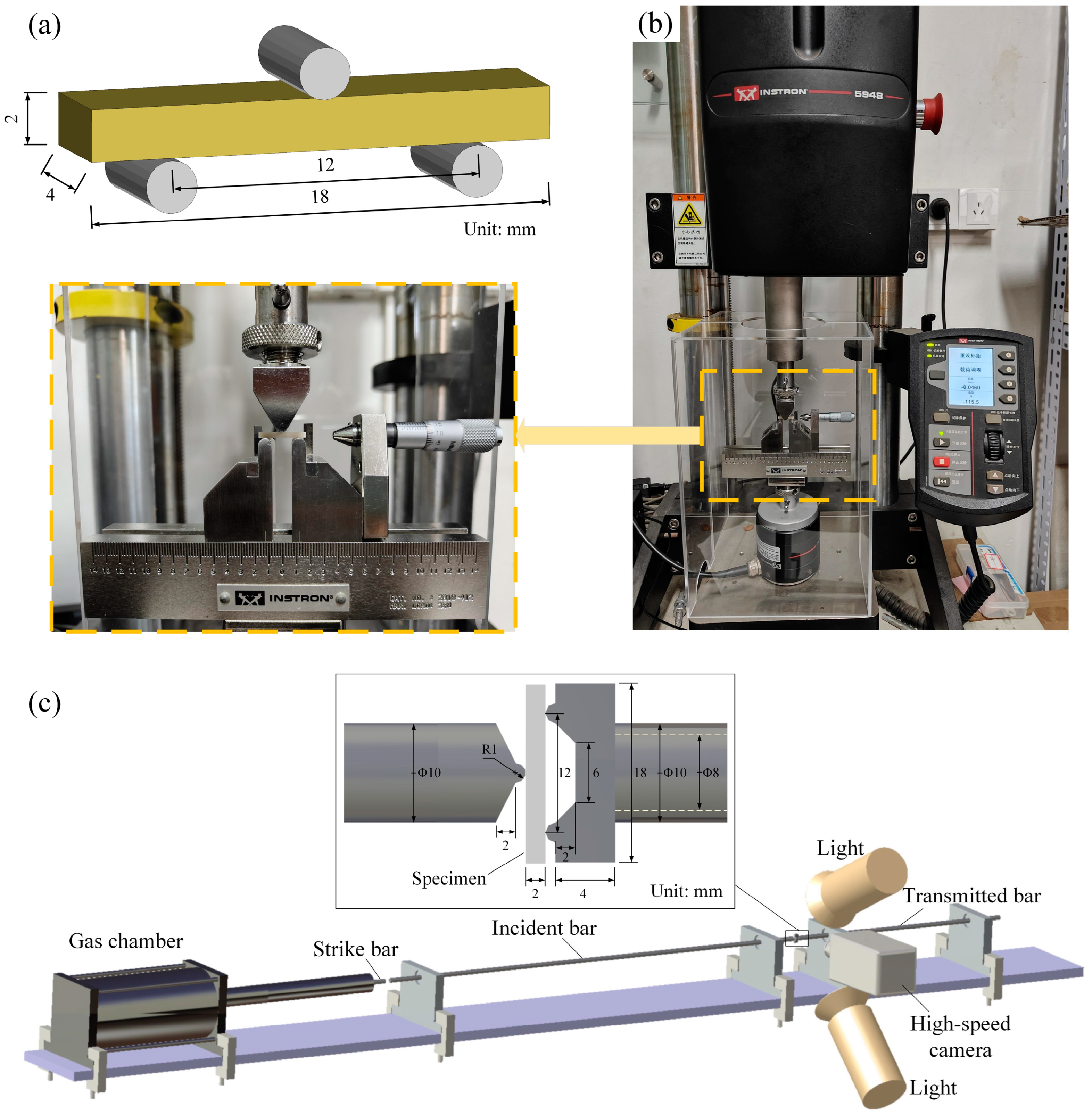
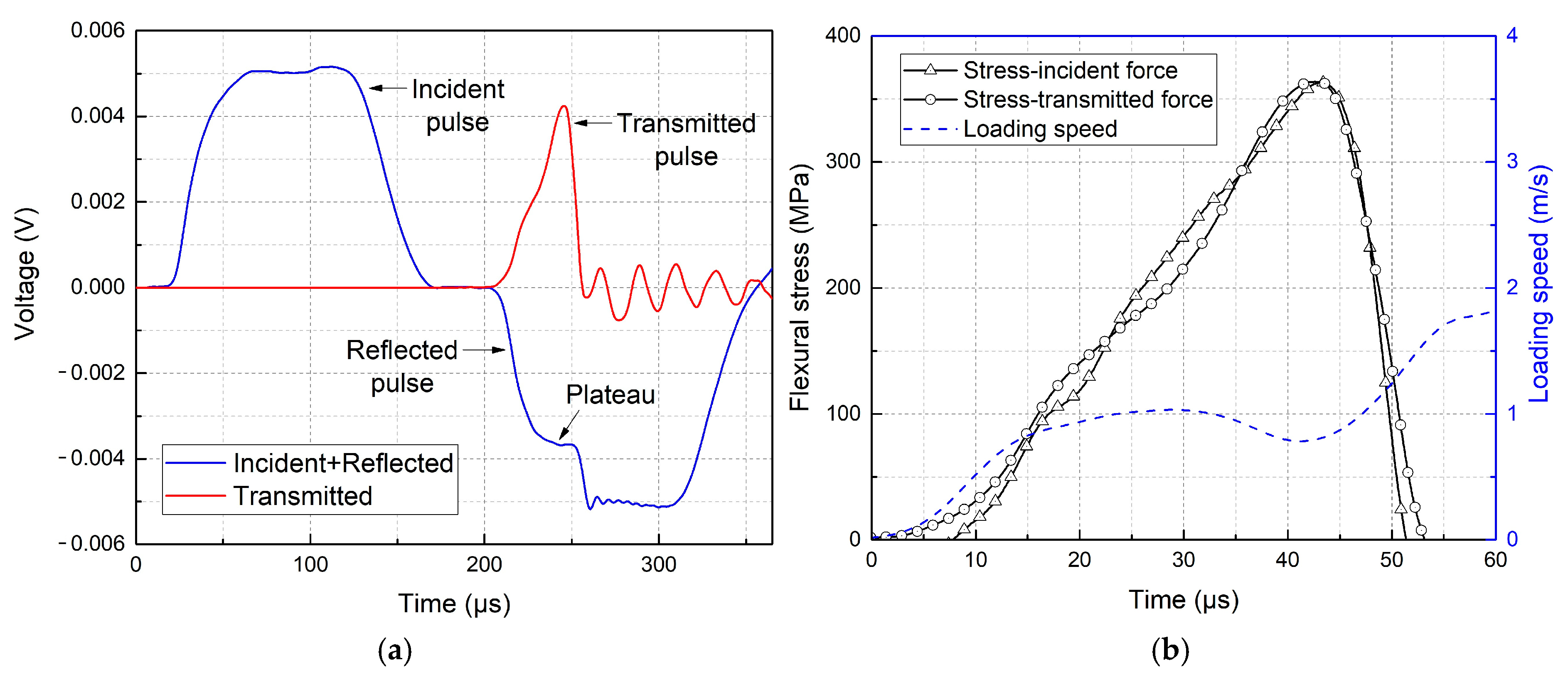
2.1. Quasi-Static and Dynamic Flexural Tests
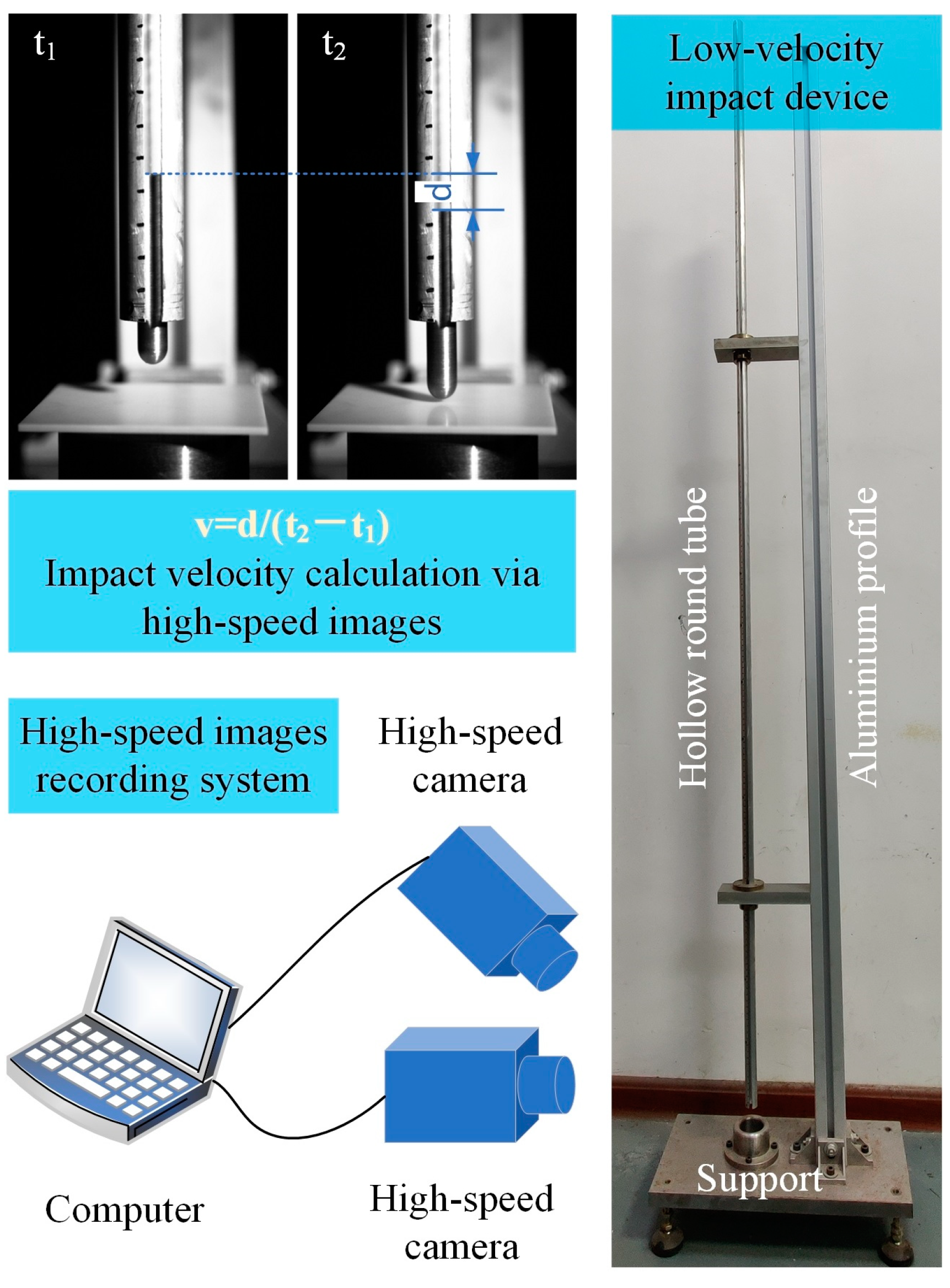
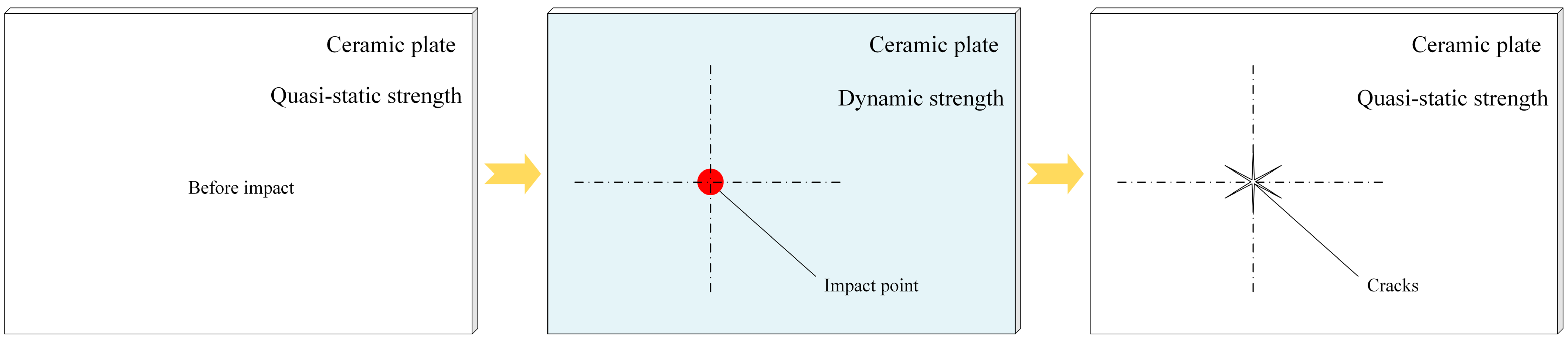
2.2. Drop-Impact Test
3. Numerical Analysis and Validation
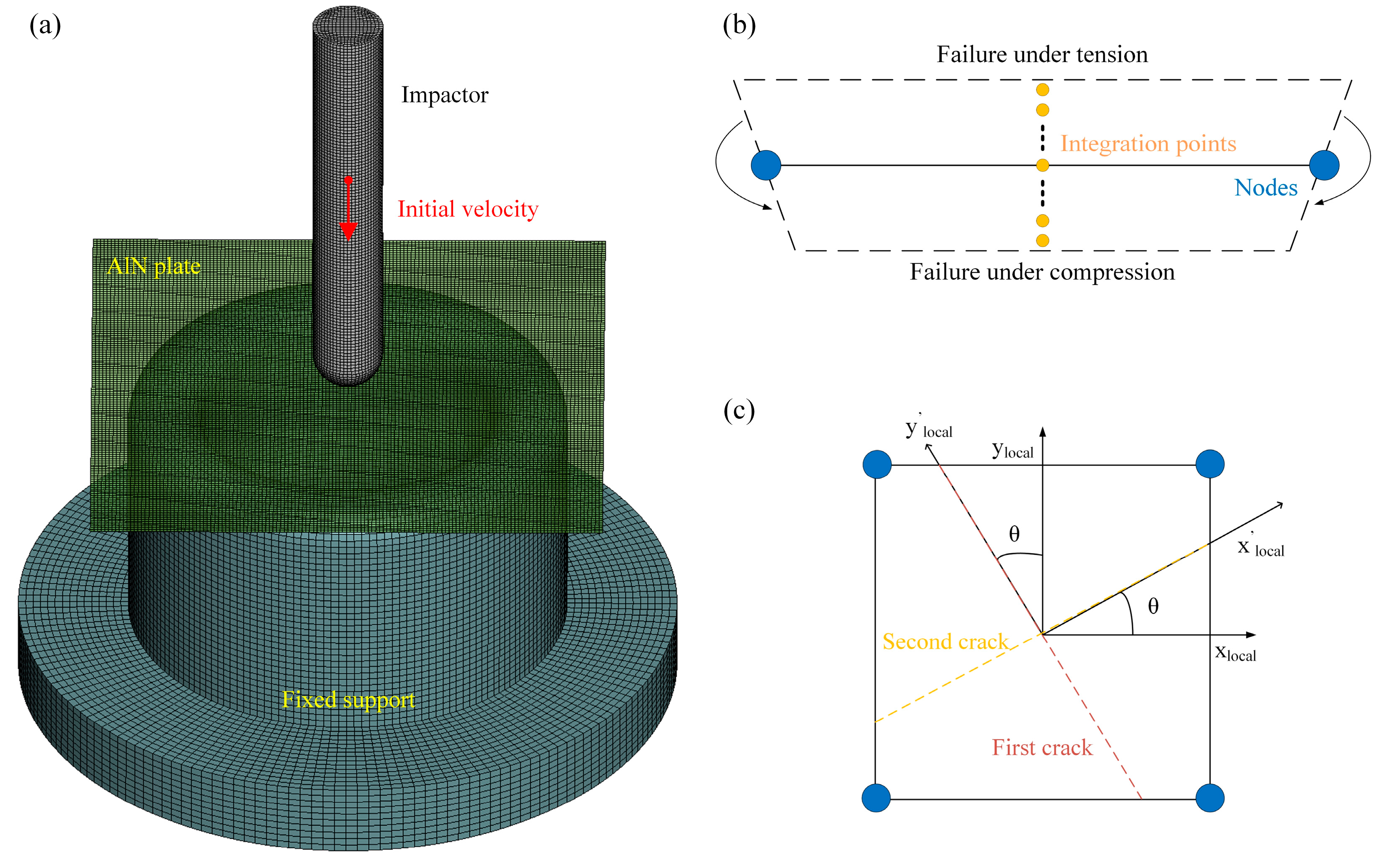
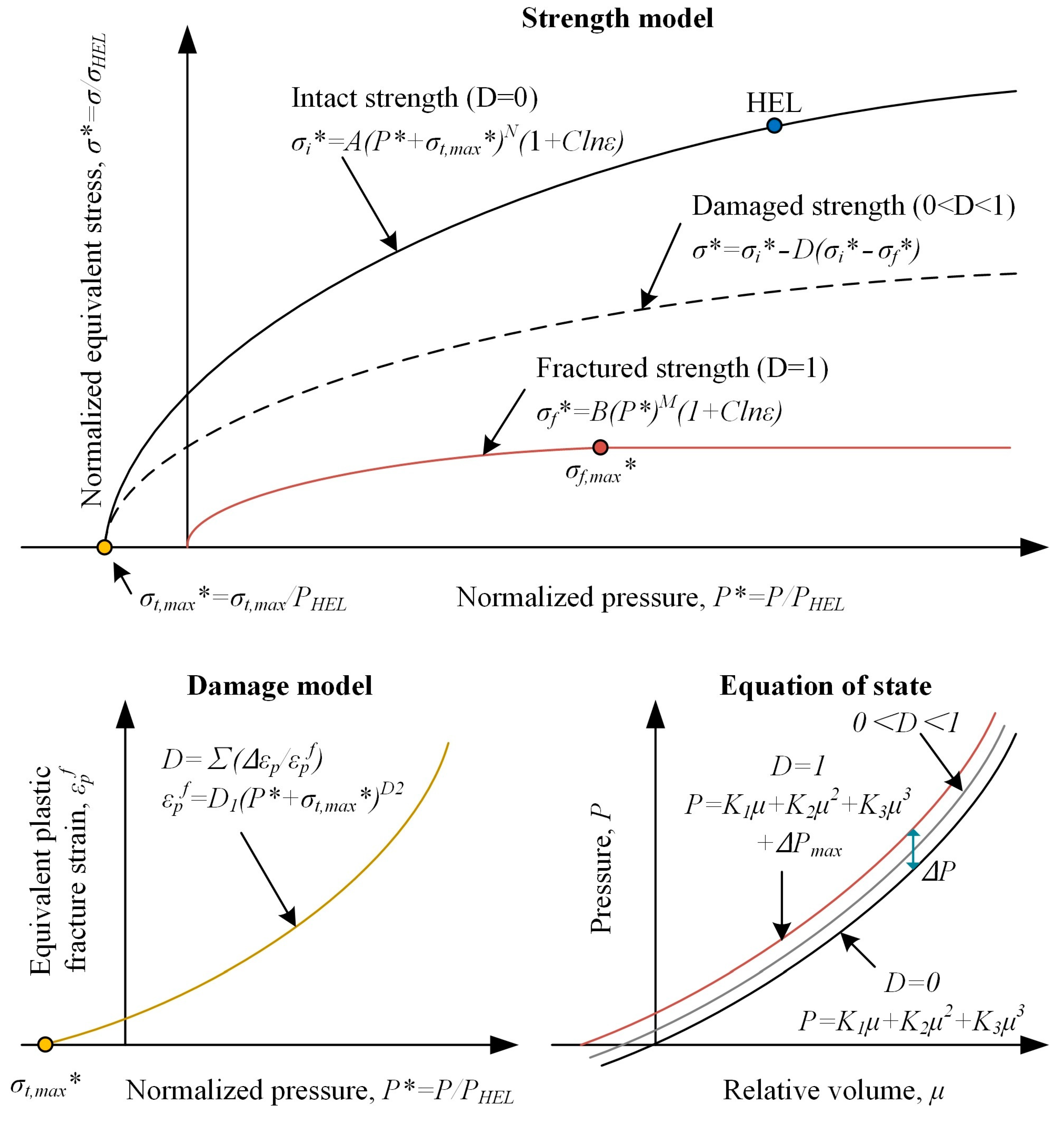
3.1. Smeared Fixed-Crack Model
3.2. Failure Prediction of AlN Substrates Under Low-Velocity Impact Loads
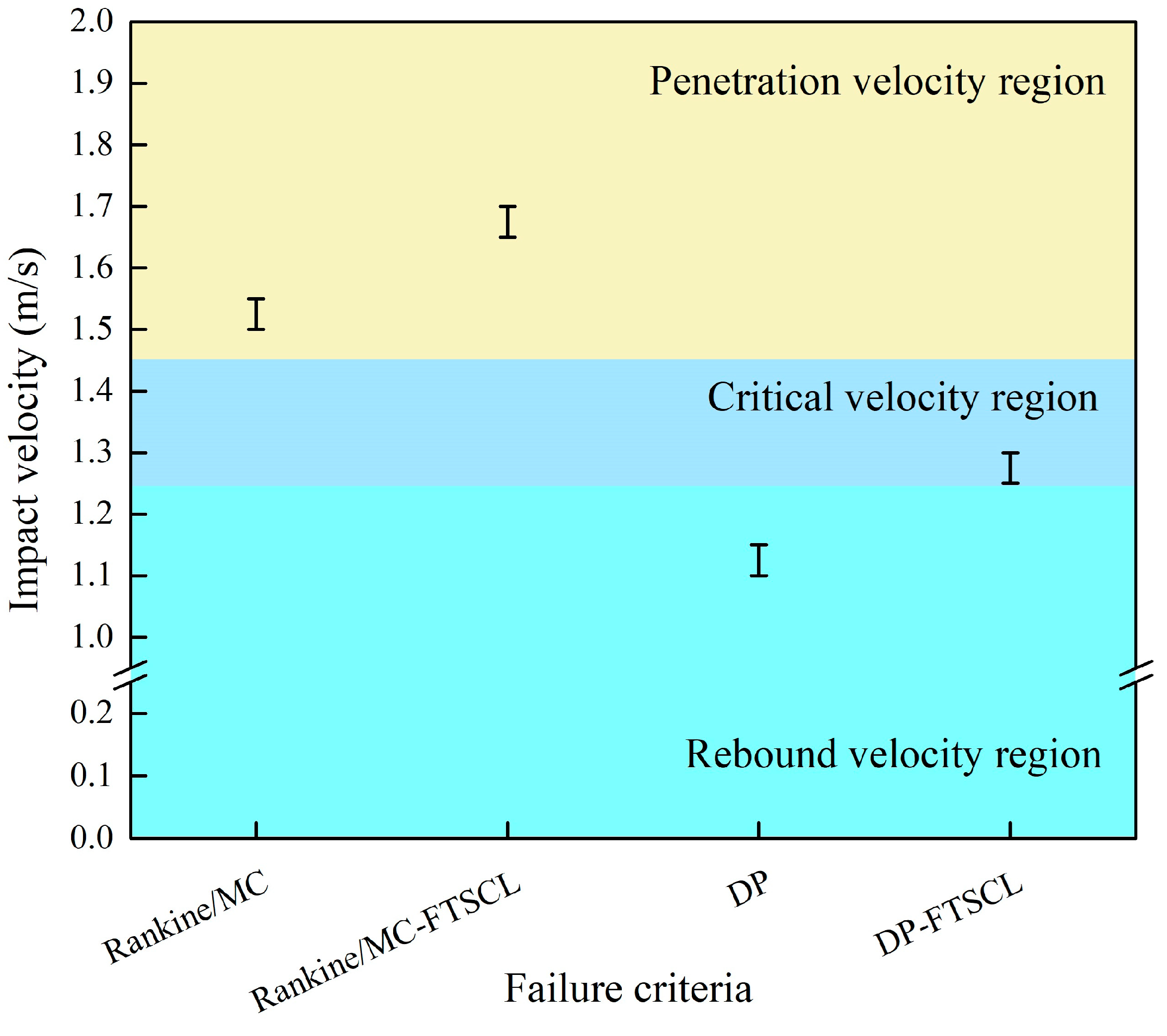
3.3. Comparison and Discussions
4. Parametric Study
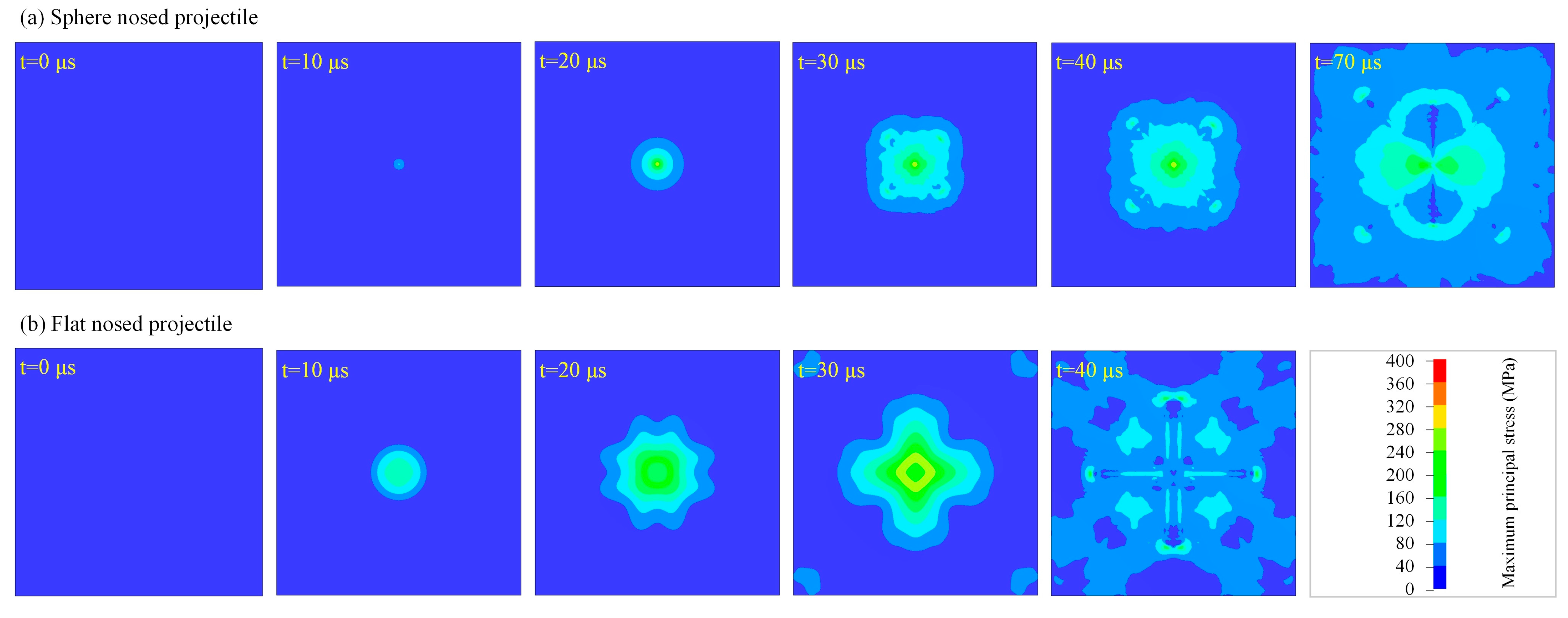
4.1. Effect of the Impactor Nose Shape
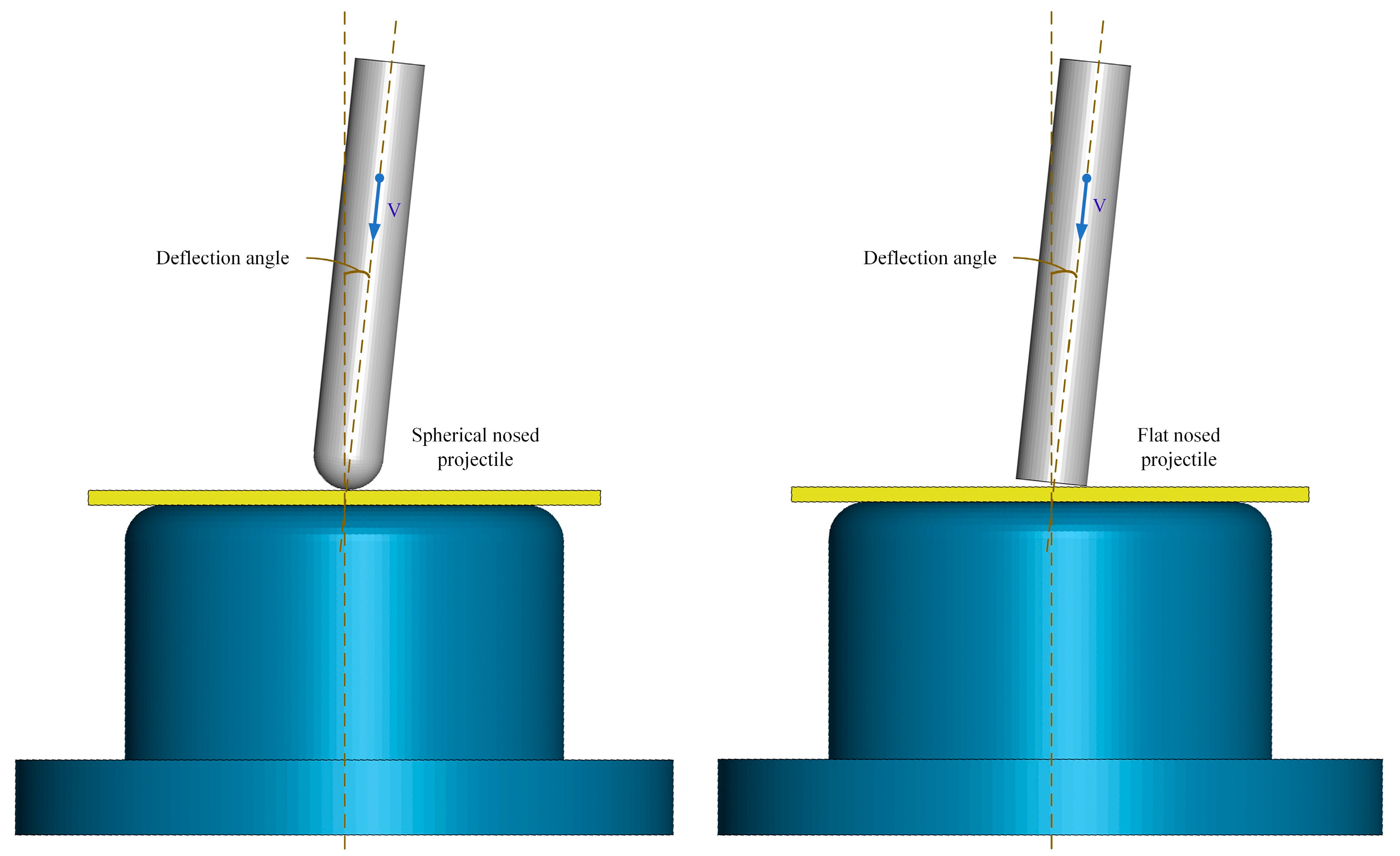
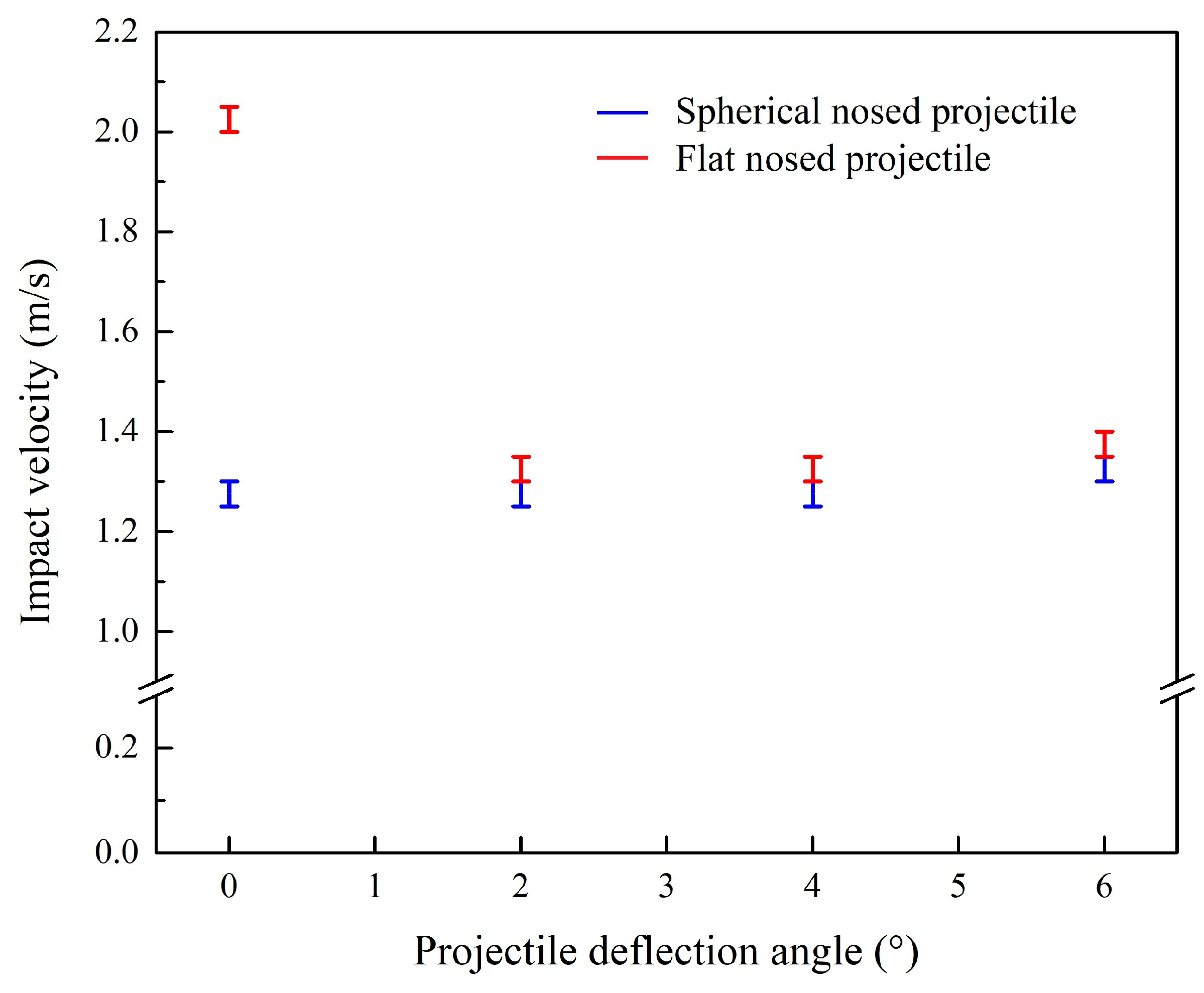
4.2. Effect of the Impactor Deflection Angles
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Flexural strength; | |
| Failure load; | |
| L, b, h | Span length, width and thickness of the sample; |
| Incident, reflection and transmission strain signal; | |
| u(t), V(t) | Loading displacement and loading speed; |
| C0 | Longitudinal elastic wave velocity of the loading bar; |
| E, A | Young’s modulus and cross-section area of the bars; |
| PI, PT | Force history from loading side and supporting side; |
| σ1, σ2 | Principal stresses in the shell elements; |
| ν | Poisson’s ratio; |
| FC | Compressive strength; |
| FT | Quasi-static tensile strength; |
| FTmod | Modified dynamic tensile strength; |
| FTSCL | Scale factor for dynamic tensile strength; |
| AlN | Aluminum nitride; |
| MEMS | Micro-electro mechanical systems; |
| FEM | Finite-element method; |
| SHPB | Split Hopkinson pressure bar; |
| JH-2 | Johnson–Holmquist II; |
| MC | Mohr–Coulomb; |
| DP | Drucker–Prager. |
References
- Zagorac, D.; Zagorac, J.; Djukic, M.B.; Jordanov, D.; Matović, B. Theoretical study of AlN mechanical behaviour under high pressure regime. Theor. Appl. Fract. Mech. 2019, 103, 102289. [Google Scholar] [CrossRef]
- Baek, S.-H.; Jeong, H.; Ryu, S.-S. AlN with high strength and high thermal conductivity based on an MCAS-Y2O3-YSZ multi-additive system. J. Eur. Ceram. Soc. 2022, 42, 898–904. [Google Scholar] [CrossRef]
- Fattahi, M.; Vaferi, K.; Vajdi, M.; Moghanlou, F.S.; Namini, A.S.; Asl, M.S. Aluminum nitride as an alternative ceramic for fabrication of microchannel heat exchangers: A numerical study. Ceram. Int. 2020, 46, 11647–11657. [Google Scholar] [CrossRef]
- Chen, G.-R.; Lin, K.-L.; Lin, C.-C. Aging effect on high heat dissipation DBA and DBAC substrates for high power electronics. Ceram. Int. 2022, 48, 28889–28897. [Google Scholar] [CrossRef]
- Hung, S.-W.; Chen, T.-K. Disclosing AlN ceramic substrate process failure mode and effect analysis. Microelectron. Reliab. 2019, 103, 113508. [Google Scholar] [CrossRef]
- Luo, H.; Li, Y.; Fan, C.; Wu, X.; Liu, G. Design and experimental research on buffer protection of high-g penetrator for deep space exploration. Acta Astronaut. 2021, 189, 63–78. [Google Scholar] [CrossRef]
- Zhang, X.-H.; Li, J.-Z.; Qin, F.; Wang, L. Experiments and numerical simulations of microelectronic devices subjected to multipoint impact loading. Microelectron. Reliab. 2021, 127, 114408. [Google Scholar] [CrossRef]
- Ji, M.; Li, H.; Zheng, J.; Yang, S.; Zaiemyekeh, Z.; Hogan, J.D. An experimental study on the strain-rate-dependent compressive and tensile response of an alumina ceramic. Ceram. Int. 2022, 48, 28121–28134. [Google Scholar] [CrossRef]
- Jia, X.-T.; Zhang, Z.-H.; Li, X.-Y.; Liu, L.-J.; Wang, Q.; He, Y.-Y.; Feng, X.-X.; Liu, Y.; Sun, Y.-H.; Cheng, X.-W. Compressive properties and failure mechanisms of AlON ceramics under different strain rates. Ceram. Int. 2024, 50, 12787–12801. [Google Scholar] [CrossRef]
- Venkatesan, J.; Iqbal, M.A.; Madhu, V. Experimental and numerical study of the dynamic response of B4C ceramic under uniaxial compression. Thin Walled Struct. 2020, 154, 106785. [Google Scholar] [CrossRef]
- Song, Q.; Cheng, Z. Dynamic response of the TiB2–SiC/B4C composite ceramic under dynamic loading. Int. J. Appl. Ceram. Technol. 2023, 20, 2511–2521. [Google Scholar] [CrossRef]
- Iqbal, M.A.; Khan, M.K. Failure pattern in ceramic metallic target under ballistic impact. Def. Technol. 2024, 40, 173–190. [Google Scholar] [CrossRef]
- An, R.; Wang, Y.; Bao, J.; Jiang, B.; Cheng, H.; Cheng, X.; Wang, F. Predicting ballistic resistance based on the mechanical properties of armored ceramics. J. Mater. Res. Technol. 2024, 32, 2370–2385. [Google Scholar] [CrossRef]
- Bresciani, L.M.; Manes, A.; Giglio, M. An analytical model for ballistic impacts against ceramic tiles. Ceram. Int. 2018, 44, 21249–21261. [Google Scholar] [CrossRef]
- Wang, X.-E.; Yang, J.; Liu, Q.-F.; Zhang, Y.-M.; Zhao, C. A comparative study of numerical modelling techniques for the fracture of brittle materials with specific reference to glass. Eng. Struct. 2017, 152, 493–505. [Google Scholar] [CrossRef]
- Fan, Y.; You, H.; Tian, X.; Yang, X.; Li, X.; Prakash, N.; Yu, Y. A meshfree peridynamic model for brittle fracture in randomly heterogeneous materials. Comput. Methods Appl. Mech. Eng. 2022, 399, 115340. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, D.; Suo, T.; Li, Y.; Manes, A. Investigation into different numerical methods in predicting the response of aluminosilicate glass under quasi-static and impact loading conditions. Int. J. Mech. Sci. 2021, 196, 106286. [Google Scholar] [CrossRef]
- Kim, H.-S.; Ha, B.-K.; Yoo, B.-Y.; Jeong, H.-S.; Park, S.-H. Numerical prediction of dynamic fracture strength of edge-mounted non-symmetric tempered glass panels under steel ball drop impact. J. Mater. Res. Technol. 2022, 17, 270–281. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, D.; Qin, F. Smeared fixed crack model for quasi-static and dynamic biaxial flexural response analysis of aluminosilicate glass plates. Thin Walled Struct. 2024, 205, 112533. [Google Scholar] [CrossRef]
- Zemanová, A.; Hála, P.; Konrád, P.; Sovják, R.; Šejnoha, M. Gradual fracture of layers in laminated glass plates under low-velocity impact. Comput. Struct. 2023, 283, 107053. [Google Scholar] [CrossRef]
- Zemanová, A.; Hála, P.; Konrád, P.; Šejnoha, M. Smeared Fixed Crack Model for Numerical Modelling of Glass Fracture in LS-DYNA. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2023. [Google Scholar] [CrossRef]
- Hála, P.; Zemanová, A.; Zeman, J.; Šejnoha, M. Numerical study on failure of laminated glass subjected to low-velocity impact. Glas. Struct. Eng. 2023, 8, 99–117. [Google Scholar] [CrossRef]
- Hogan, J.D.; Farbaniec, L.; Sano, T.; Shaeffer, M.; Ramesh, K.T. The effects of defects on the uniaxial compressive strength and failure of an advanced ceramic. Acta Mater. 2016, 102, 263–272. [Google Scholar] [CrossRef]
- Huang, J.Y.; Lin, C.K.; Bian, Y.L.; Xie, H.L.; Chai, H.W.; Ding, Y.Y.; Luo, S.N. Strain rate effects on fragment morphology of ceramic alumina: A synchrotron-based study. Int. J. Mech. Sci. 2024, 280, 109506. [Google Scholar] [CrossRef]
- Zhang, X.; Zou, Y.; Hao, H.; Li, X.; Ma, G.; Liu, K. Laboratory test on dynamic material properties of annealed float glass. Int. J. Prot. Struct. 2012, 3, 407–430. [Google Scholar] [CrossRef]
- Holmquist, T.J.; Templeton, D.W.; Bishnoi, K.D. Constitutive modeling of aluminum nitride for large strain, high-strain rate, and high-pressure applications. Int. J. Impact Eng. 2001, 25, 211–231. [Google Scholar] [CrossRef]
- Islam, M.R.I.; Zheng, J.Q.; Batra, R.C. Ballistic performance of ceramic and ceramic-metal composite plates with JH1, JH2 and JHB material model. Int. J. Impact Eng. 2020, 137, 103469. [Google Scholar] [CrossRef]
- Baranowski, P.; Kucewicz, M.; Gieleta, R.; Stankiewicz, M.; Konarzewski, M.; Bogusz, P.; Pytlik, M.; Małachowski, J. Fracture and fragmentation of dolomite rock using the JH-2 constitutive model: Parameter determination, experiments and simulations. Int. J. Impact Eng. 2020, 140, 103543. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Ma, G. Dynamic material model of annealed soda-lime glass. Int. J. Impact Eng. 2015, 77, 108–119. [Google Scholar] [CrossRef]
- Meyland, M.J.; Bønding, C.K.T.; Eriksen, R.N.W.; Nielsen, J.H. An experimental investigation of the flexural strength of soda–lime–silica glass at high loading rates. Glas. Struct. Eng. 2019, 4, 175–183. [Google Scholar] [CrossRef]
- Cheng, M.; Chen, W.; Sridhar, K.R. Experimental method for a dynamic biaxial flexural strength test of thin ceramic substrates. J. Am. Ceram. Soc. 2002, 85, 1203–1209. [Google Scholar] [CrossRef]
- Nie, X.; Chen, W.W.; Wereszczak, A.A.; Templeton, D.W. Effect of loading rate and surface conditions on the flexural strength of borosilicate glass. J. Am. Ceram. Soc. 2009, 92, 1287–1295. [Google Scholar] [CrossRef]
- Quinn, G.D.; Morrell, R. Design Data for Engineering Ceramics: A Review of the Flexure Test. J. Am. Ceram. Soc. 1991, 74, 2037–2066. [Google Scholar] [CrossRef]
- Wang, Z.; Suo, T.; Sheikh, M.Z.; Li, Y.; Wang, X.; Wang, Y. Quasi-static and dynamic flexural behavior of annealed and chemically strengthened aluminosilicate glass with notch defects. J. Non Cryst. Solids 2019, 521, 119479. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, T.; Sang, S.; Qin, F.; Zhang, C. Experimental and numerical investigation on the discrete fracture property and dynamic flexural response of aluminum nitride ceramics. Eng. Fract. Mech. 2024, 308, 110384. [Google Scholar] [CrossRef]
- Wang, Z.; Manes, A. Stress analysis and fracture simulation of aluminosilicate glass plates under Ring-On-Ring loading. Forces Mech. 2021, 5, 100047. [Google Scholar] [CrossRef]
- Pelfrene, J.; Kuntsche, J.; Van Dam, S.; Van Paepegem, W.; Schneider, J. Critical assessment of the post-breakage performance of blast loaded laminated glazing: Experiments and simulations. Int. J. Impact Eng. 2016, 88, 61–71. [Google Scholar] [CrossRef]
- Chen, W.; Ravichandran, G. Static and dynamic compressive behavior of aluminum nitride under moderate confinement. J. Am. Ceram. Soc. 1996, 79, 579–584. [Google Scholar] [CrossRef]
- Subhash, G.; Ravichandran, G. Mechanical behaviour of a hot pressed aluminum nitride under uniaxial compression. J. Mater. Sci. 1998, 33, 1933–1939. [Google Scholar] [CrossRef]
- Hu, G.; Ramesh, K.T.; Cao, B.; McCauley, J.W. The compressive failure of aluminum nitride considered as a model advanced ceramic. J. Mech. Phys. Solids 2011, 59, 1076–1093. [Google Scholar] [CrossRef]
- Osnes, K.; Hopperstad, O.S.; Børvik, T. Rate dependent fracture of monolithic and laminated glass: Experiments and simulations. Eng. Struct. 2020, 212, 110516. [Google Scholar] [CrossRef]
- Zaiemyekeh, Z.; Li, H.; Sayahlatifi, S.; Ji, M.; Zheng, J.; Romanyk, D.L.; Hogan, J.D. Computational finite element modeling of stress-state- and strain-rate-dependent failure behavior of ceramics with experimental validation. Ceram. Int. 2023, 49, 13878–13895. [Google Scholar] [CrossRef]
- Tan, S.; Long, S.; Yao, X.; Zhang, X. An improved material model for loading-path and strain-rate dependent strength of impacted soda-lime glass plate. J. Mater. Res. Technol. 2021, 15, 1905–1919. [Google Scholar] [CrossRef]
- Ma, D.; Wang, Z.; Giglio, M.; Amico, S.C.; Manes, A. Influence of strain-rate related parameters on the simulation of ballistic impact in woven composites. Compos. Struct. 2022, 300, 116142. [Google Scholar] [CrossRef]
- Simons, E.C.; Weerheijm, J.; Toussaint, G.; Sluys, L.J. An experimental and numerical investigation of sphere impact on alumina ceramic. Int. J. Impact Eng. 2020, 145, 103670. [Google Scholar] [CrossRef]
- Bresciani, L.M.; Manes, A.; Romano, T.A.; Iavarone, P.; Giglio, M. Numerical modelling to reproduce fragmentation of a tungsten heavy alloy projectile impacting a ceramic tile: Adaptive solid mesh to the SPH technique and the cohesive law. Int. J. Impact Eng. 2016, 87, 3–13. [Google Scholar] [CrossRef]
- Wang, Z.; Ren, T.; Suo, T.; Manes, A. Quasi-static and low-velocity impact biaxial flexural fracture of aluminosilicate glass—An experimental and numerical study. Thin Walled Struct. 2021, 165, 107939. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Ma, D.; Wang, X.; Li, Y.; Suo, T.; Manes, A. Experimental and numerical investigation on the ballistic performance of aluminosilicate glass with different nosed projectiles. Ceram. Int. 2023, 49, 17729–17745. [Google Scholar] [CrossRef]
- Johnson, G.R.; Holmquist, T.J. An improved computational constitutive model for brittle materials. In AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 1994; Volume 309, pp. 981–984. [Google Scholar]
- Simons, E.C.; Weerheijm, J.; Sluys, L.J. A viscosity regularized plasticity model for ceramics. Eur. J. Mech. A Solids 2018, 72, 310–328. [Google Scholar] [CrossRef]
- Baranowski, P.; Kucewicz, M.; Janiszewski, J. JH-2 constitutive model of sandstone for dynamic problems. Sci. Rep. 2024, 14, 3339. [Google Scholar] [CrossRef]
- Fadhil, B.M. Ballistic impact on ceramic armour with different nosed projectiles: Numerical study. Int. J. Mech. Mater. Eng. 2012, 7, 69–77. [Google Scholar]
- Zhu, Q.; Zhang, C.; Curiel-Sosa, J.L.; Bui, T.Q.; Xu, X. Finite element simulation of damage in fiber metal laminates under high velocity impact by projectiles with different shapes. Compos. Struct. 2019, 214, 73–82. [Google Scholar] [CrossRef]
- Ansari, M.M.; Chakrabarti, A. Influence of projectile nose shape and incidence angle on the ballistic perforation of laminated glass fiber composite plate. Compos. Sci. Technol. 2017, 142, 107–116. [Google Scholar] [CrossRef]
- Gupta, N.K.; Iqbal, M.A.; Sekhon, G.S. Effect of projectile nose shape, impact velocity and target thickness on deformation behavior of aluminum plates. Int. J. Solids Struct. 2007, 44, 3411–3439. [Google Scholar] [CrossRef]
- Walker, J.D.; Anderson, C.E., Jr. The influence of initial nose shape in eroding penetration. Int. J. Impact Eng. 1994, 15, 139–148. [Google Scholar] [CrossRef]







| Flexural Strength (MPa) | Loading Velocity (m/s) | ||
|---|---|---|---|
| 3.33 × 10−7 | 3.33 × 10−6 | 1 | |
| No. 1 | 353.6 | 343.1 | 433.3 |
| No. 2 | 349.6 | 362.1 | 395.7 |
| No. 3 | 342.2 | 332.6 | 382.3 |
| No. 4 | 367.2 | 348.2 | 396.7 |
| No. 5 | 355.1 | 351.6 | 365.2 |
| No. 6 | 329.6 | 338.2 | 403.6 |
| No. 7 | 370.3 | 332.6 | 362.2 |
| No. 8 | 319.8 | 370.3 | 433.5 |
| No. 9 | 335.8 | 364.6 | 378.3 |
| No. 10 | 363.8 | 348.8 | 388.8 |
| Average | 348.7 | 349.2 | 394.0 |
| 349.0 | |||
| Impact Velocity (m/s) | Sample Status |
|---|---|
| 1.05 | Did not fail |
| 1.24 | Did not fail |
| 1.46 | Failed |
| 1.67 | Failed |
| 1.94 | Failed |
| 3.02 | Failed |
| 4.29 | Failed |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (kg·m−3) | 3226 | (MPa) | 349 |
| E (GPa) | 320 | (MPa) | 3000 |
| ν | 0.25 | FTSCL | 1.13 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (kg·m−3) | 3226 | B | 0.31 |
| G (GPa) | 127 | M | 0.21 |
| HEL (GPa) | 9 | K1 (GPa) | 201 |
| (GPa) | 6 | K2 (GPa) | 260 |
| (GPa) | 5 | K3 (GPa) | 0 |
| (MPa) | 320 | β | 1 |
| A | 0.85 | D1 | 0.02 |
| N | 0.29 | D2 | 1.85 |
| C | 0.013 |
| Items | Experimental Tests | Numerical Simulation—Smeared Fixed-Crack Model | Numerical Simulation—JH-2 Model |
|---|---|---|---|
| Critical velocity range | 1.24–1.46 m/s | 1.25–1.30 m/s | 2.85–2.90 m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Liu, Y. Effect of Dynamic Flexural Strength on Impact Response Analysis of AlN Substrates for Aerospace Applications. Aerospace 2025, 12, 221. https://doi.org/10.3390/aerospace12030221
Wang Z, Liu Y. Effect of Dynamic Flexural Strength on Impact Response Analysis of AlN Substrates for Aerospace Applications. Aerospace. 2025; 12(3):221. https://doi.org/10.3390/aerospace12030221
Chicago/Turabian StyleWang, Zhen, and Yan Liu. 2025. "Effect of Dynamic Flexural Strength on Impact Response Analysis of AlN Substrates for Aerospace Applications" Aerospace 12, no. 3: 221. https://doi.org/10.3390/aerospace12030221
APA StyleWang, Z., & Liu, Y. (2025). Effect of Dynamic Flexural Strength on Impact Response Analysis of AlN Substrates for Aerospace Applications. Aerospace, 12(3), 221. https://doi.org/10.3390/aerospace12030221







