A Distributed Cooperative Guidance Law with Prescribed-Time Consensus Performance
Abstract
1. Introduction
- The aircraft achieves cooperation within a prescribed time. Unlike traditional laws that only provide an upper time limit, this law enables preset cooperation time, allowing for precise consensus control.
- Unlike general methods, this law directly handles flight time under the communication topology, enhancing accuracy without requiring arrival time estimation.
- The proposed law imposes no restrictions on the number of cooperating aircraft and has been validated in single-node failure scenarios, ensuring high applicability to complex missions.
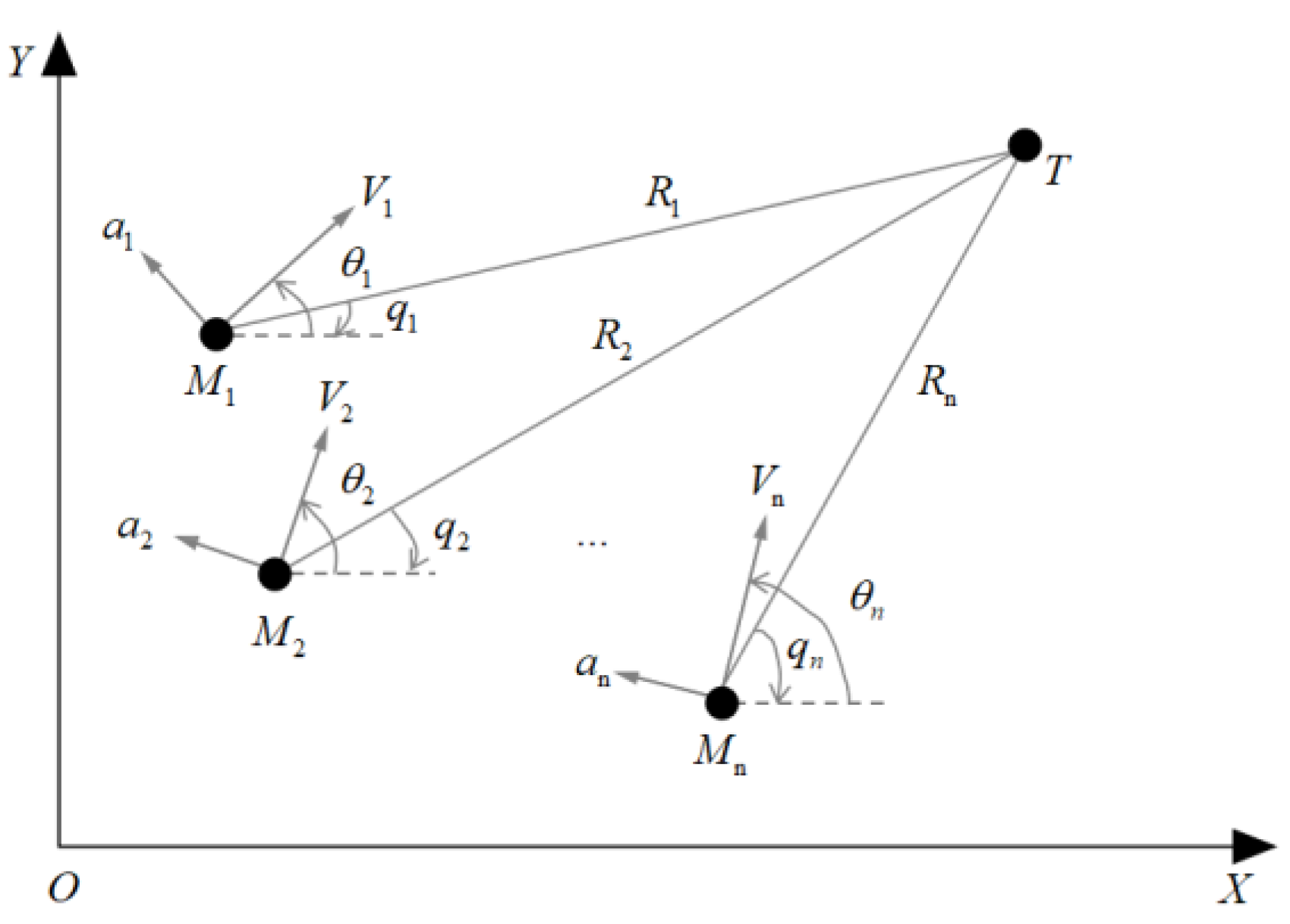
2. Basic Theory and Motion Model
2.1. Basic Theory
2.2. Motion Model
3. Main Result
3.1. Design Strategy
3.2. Undirected Topology Cooperative Guidance Law
- 1.
- is twice continuously differentiable on the interval .
- 2.
- is monotonically increasing from to , where represents the prescribed time.
- 3.
- .
- 4.
- and when .
3.3. Directed Topology Cooperative Guidance Law
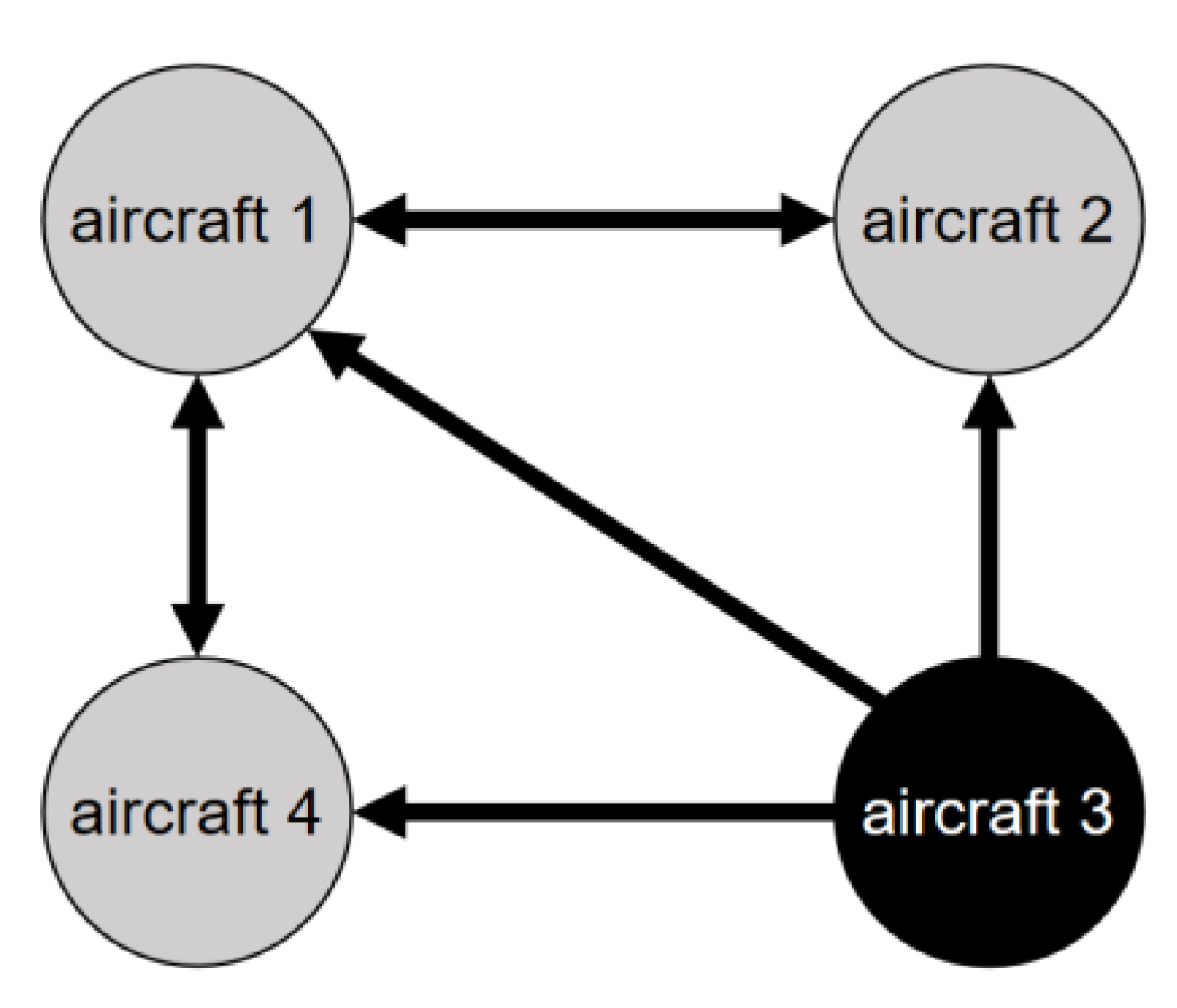
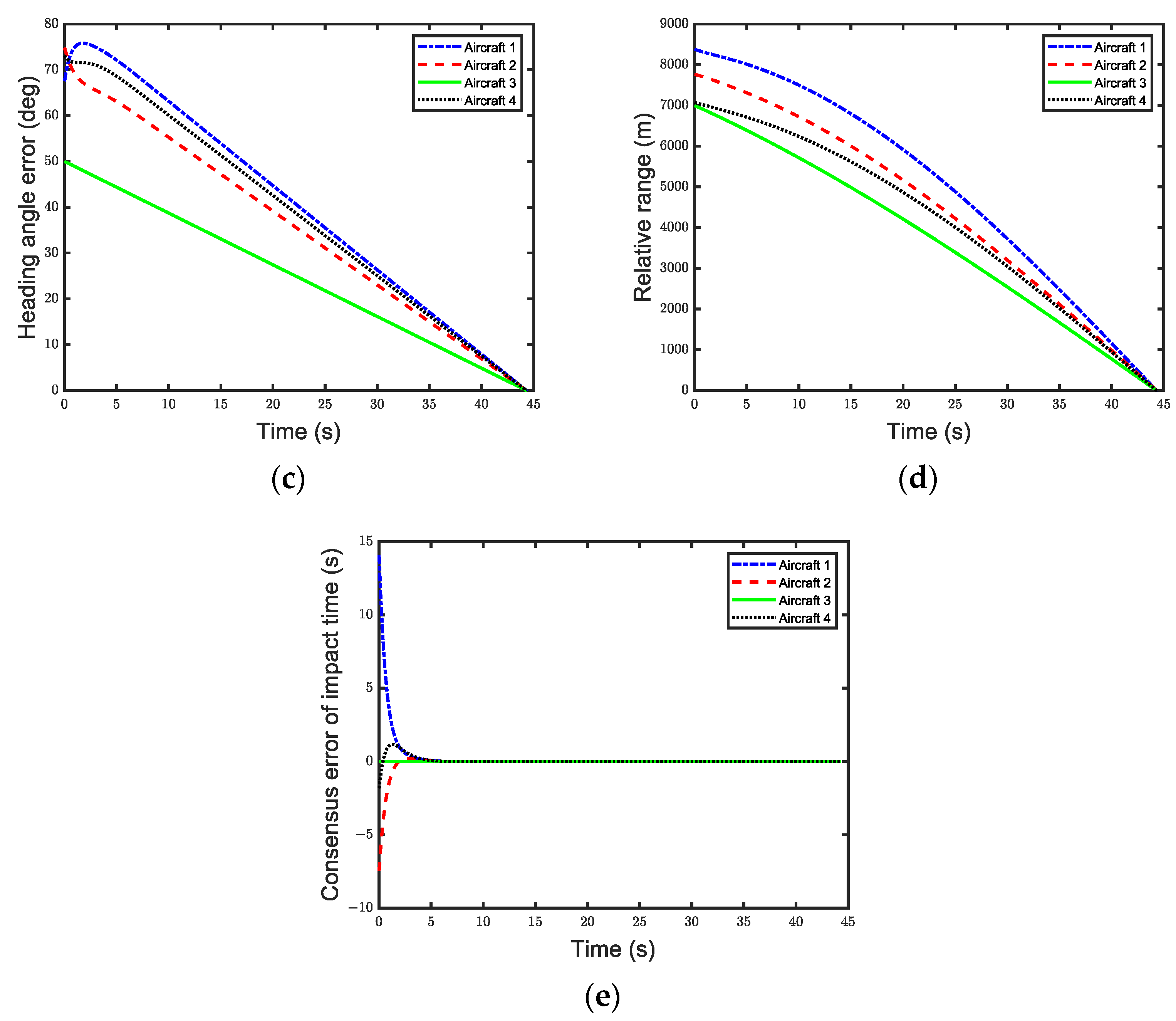
4. Numerical Simulations
4.1. Undirected Topology
4.2. Directed Topology
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tuncer, O.; Cirpan, H.A. Adaptive fuzzy based threat evaluation method for air and missile defense systems. Inf. Sci. 2023, 643, 119191. [Google Scholar] [CrossRef]
- Zeng, J.; Dou, L.; Xin, B. A joint mid-course and terminal course cooperative guidance law for multi-missile salvo attack. Chin. J. Aeronaut. 2018, 31, 1311–1326. [Google Scholar] [CrossRef]
- Lyu, T.; Guo, Y.; Li, C.; Ma, G.; Zhang, H. Multiple missiles cooperative guidance with simultaneous attack requirement under directed topologies. Aerosp. Sci. Technol. 2019, 89, 100–110. [Google Scholar] [CrossRef]
- In-Soo, J.; Jin-Ik, L.; Min-Jea, T. Impact-time-control guidance law for anti-ship missiles. IEEE Trans. Control Syst. Technol. 2006, 14, 260–266. [Google Scholar] [CrossRef]
- Jeon, I.-S.; Lee, J.-I.; Tahk, M.-J. Impact-Time-Control Guidance with Generalized Proportional Navigation Based on Nonlinear Formulation. J. Guid. Control Dyn. 2016, 39, 1885–1890. [Google Scholar] [CrossRef]
- Liu, S.; Liu, W.; Yan, B.; Liu, S.; Yin, Y. Impact Time Control Guidance Law for Large Initial Lead Angles Based on Sliding Mode Control. J. Phys. Conf. Ser. 2021, 2031, 012050. [Google Scholar] [CrossRef]
- Kim, H.-G.; Shin, J. Lyapunov-Based Impact Time Control Guidance Law with Performance Prediction. Aerospace 2023, 10, 308. [Google Scholar] [CrossRef]
- He, S.; Lee, C.-H.; Shin, H.-S.; Tsourdos, A. Optimal three-dimensional impact time guidance with seeker’s field-of-view constraint. Chin. J. Aeronaut. 2021, 34, 240–251. [Google Scholar] [CrossRef]
- Zhu, C.; Xu, G.; Wei, C.; Cai, D.; Yu, Y. Impact-Time-Control Guidance Law for Hypersonic Missiles in Terminal Phase. IEEE Access 2020, 8, 44611–44621. [Google Scholar] [CrossRef]
- Wang, N.; Wang, X.; Cui, N.; Li, Y.; Liu, B. Deep reinforcement learning-based impact time control guidance law with constraints on the field-of-view. Aerosp. Sci. Technol. 2022, 128, 107765. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, J.; He, S.; Shin, H.-S.; Tsourdos, A. Learning prediction-correction guidance for impact time control. Aerosp. Sci. Technol. 2021, 119, 107187. [Google Scholar] [CrossRef]
- You, H.; Chang, X.; Zhao, J.; Wang, S.; Zhang, Y. Three-dimensional impact-angle-constrained fixed-time cooperative guidance algorithm with adjustable impact time. Aerosp. Sci. Technol. 2023, 141, 108574. [Google Scholar] [CrossRef]
- Zhang, W.; Yan, J.; Yan, B. Finite-Time Distributed Cooperative Guidance Law with Impact Angle Constraint. Int. J. Aerosp. Eng. 2023, 2023, 5568394. [Google Scholar] [CrossRef]
- Ye, T.; Yuan-li, C. A Cooperative Guidance Law for Multiple Missiles with Impact Time and Terminal Angle Constraints. In Proceedings of the 2019 Chinese Control and Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1504–1510. [Google Scholar]
- Chen, Z.; Chen, W.; Liu, X.; Cheng, J. Three-dimensional fixed-time robust cooperative guidance law for simultaneous attack with impact angle constraint. Aerosp. Sci. Technol. 2021, 110, 106523. [Google Scholar] [CrossRef]
- Gu, Z.; Wang, X.; Wang, Z. Fixed-Time Distributed Event-Triggered Cooperative Guidance Methods for Multiple Vehicles with Limited Communications to Achieve Simultaneous Arrival. Aerospace 2024, 11, 709. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, J.; Dong, X.; Ren, Z. Three-dimensional cooperative guidance strategy and guidance law for intercepting highly maneuvering target. Chin. J. Aeronaut. 2021, 34, 485–495. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, X. Multiple missiles fixed-time cooperative guidance without measuring radial velocity for maneuvering targets interception. ISA Trans. 2022, 126, 388–397. [Google Scholar] [CrossRef]
- Ma, X.; Dai, K.; Zou, Y.; Yu, H.; Zhang, H.; Wang, X. Fixed-time anti-saturation grouped cooperative guidance law with state estimations of multiple maneuvering targets. J. Frankl. Inst. 2023, 360, 5524–5547. [Google Scholar] [CrossRef]
- Gao, J.; Li, X.; Zang, S.; Ma, J.; Zhang, J.; Yan, B. Adaptive Distributed Fixed-Time Cooperative Three-Dimensional Guidance Law for Multimissiles against Manoeuvring Target. Int. J. Aerosp. Eng. 2023, 2023, 4692840. [Google Scholar] [CrossRef]
- Chen, C.; Han, Y.; Zhu, S.; Zeng, Z. Prescribed-Time Cooperative Output Regulation of Heterogeneous Multiagent Systems. IEEE Trans. Ind. Inform. 2024, 20, 2432–2443. [Google Scholar] [CrossRef]
- Song, Y.; Ye, H.; Lewis, F.L. Prescribed-Time Control and Its Latest Developments. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4102–4116. [Google Scholar] [CrossRef]
- Shakouri, A.; Assadian, N. A Framework for Prescribed-Time Control Design via Time-Scale Transformation. IEEE Control Syst. Lett. 2022, 6, 1976–1981. [Google Scholar] [CrossRef]
- Xu, C.; Wu, B.; Zhang, Y. Distributed prescribed-time attitude cooperative control for multiple spacecraft. Aerosp. Sci. Technol. 2021, 113, 106699. [Google Scholar] [CrossRef]
- Bai, H.; Mei, S.; Dong, J. Hierarchical temporal sequence convergence in prescribed-time control for quadrotor UAVs under unknown dynamic disturbances. Aerosp. Sci. Technol. 2024, 148, 109094. [Google Scholar] [CrossRef]
- Miao, Q.; Zhang, K.; Jiang, B. Incremental fully actuated system approach-based prescribed-time fault-tolerant formation control of helicopters under multiple faults. Aerosp. Sci. Technol. 2024, 151, 109334. [Google Scholar] [CrossRef]

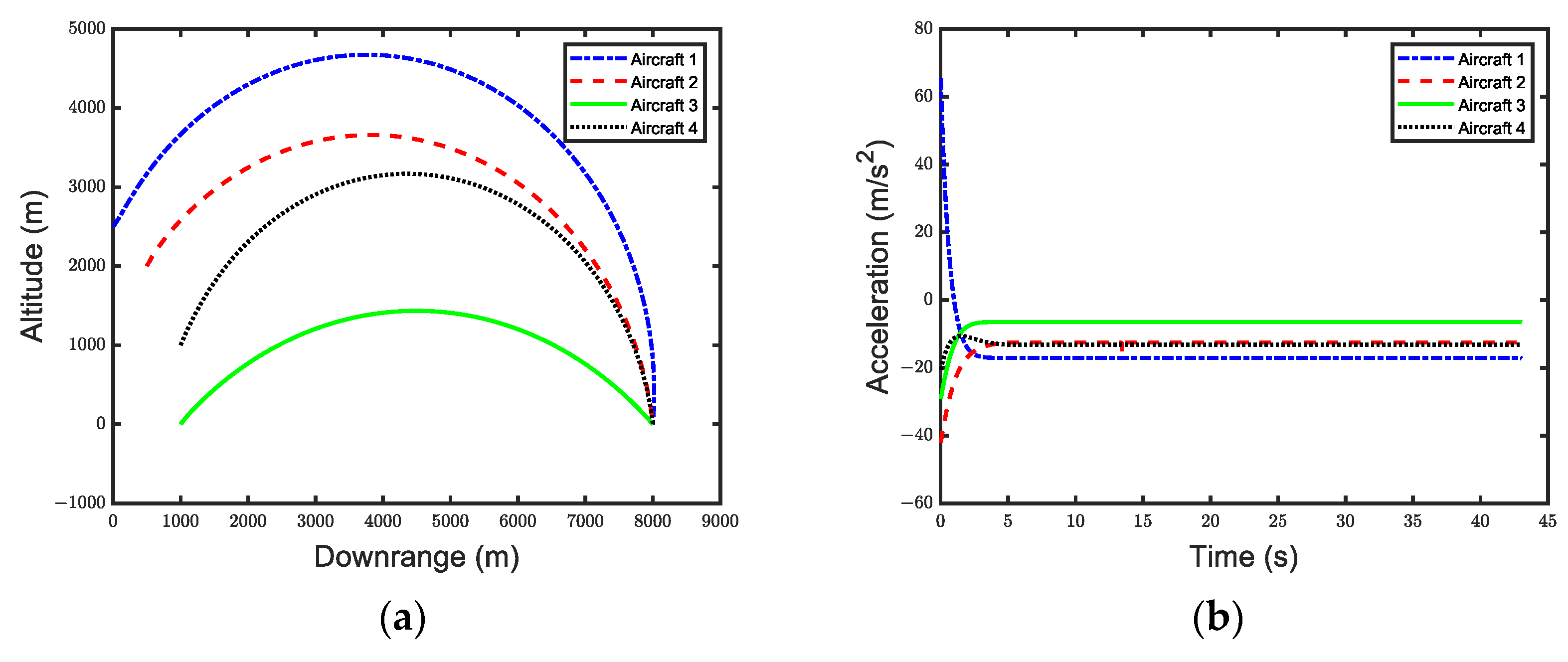
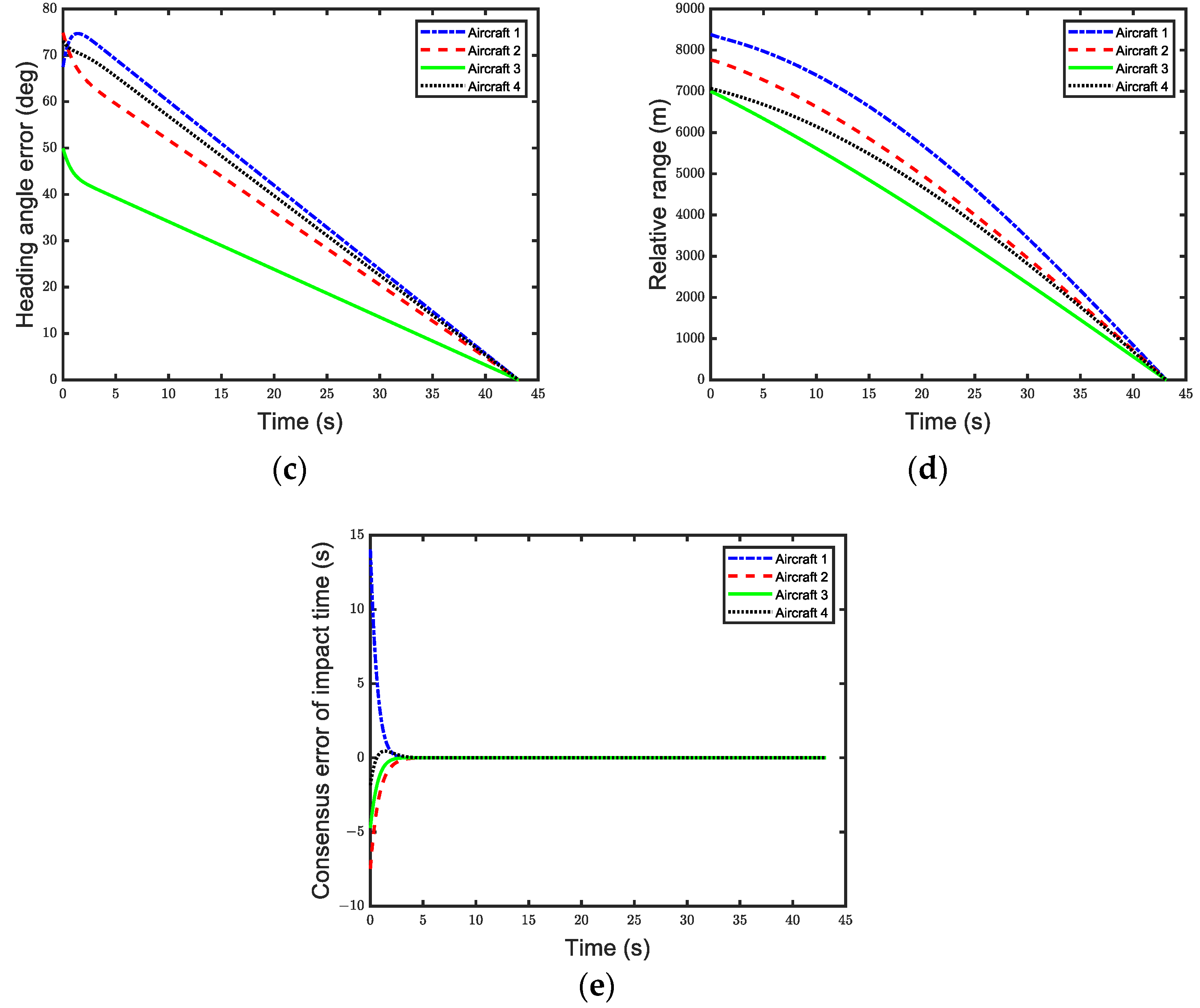

| Initial Relative Range (m) | Velocity (m/s) | Initial Heading Angle (deg) | Initial LOS Angle (deg) | |
|---|---|---|---|---|
| 1 | 8320 | 270 | 50 | −17.37 |
| 2 | 7760 | 230 | 60 | −14.95 |
| 3 | 7000 | 180 | 50 | 0 |
| 4 | 7070 | 220 | 65 | −8.15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ou, C.; Shen, A.; Cheng, Z.; Long, Y. A Distributed Cooperative Guidance Law with Prescribed-Time Consensus Performance. Aerospace 2025, 12, 169. https://doi.org/10.3390/aerospace12030169
Ou C, Shen A, Cheng Z, Long Y. A Distributed Cooperative Guidance Law with Prescribed-Time Consensus Performance. Aerospace. 2025; 12(3):169. https://doi.org/10.3390/aerospace12030169
Chicago/Turabian StyleOu, Chao, Ao Shen, Zhongtao Cheng, and Yaosong Long. 2025. "A Distributed Cooperative Guidance Law with Prescribed-Time Consensus Performance" Aerospace 12, no. 3: 169. https://doi.org/10.3390/aerospace12030169
APA StyleOu, C., Shen, A., Cheng, Z., & Long, Y. (2025). A Distributed Cooperative Guidance Law with Prescribed-Time Consensus Performance. Aerospace, 12(3), 169. https://doi.org/10.3390/aerospace12030169





