The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing
Abstract
1. Introduction
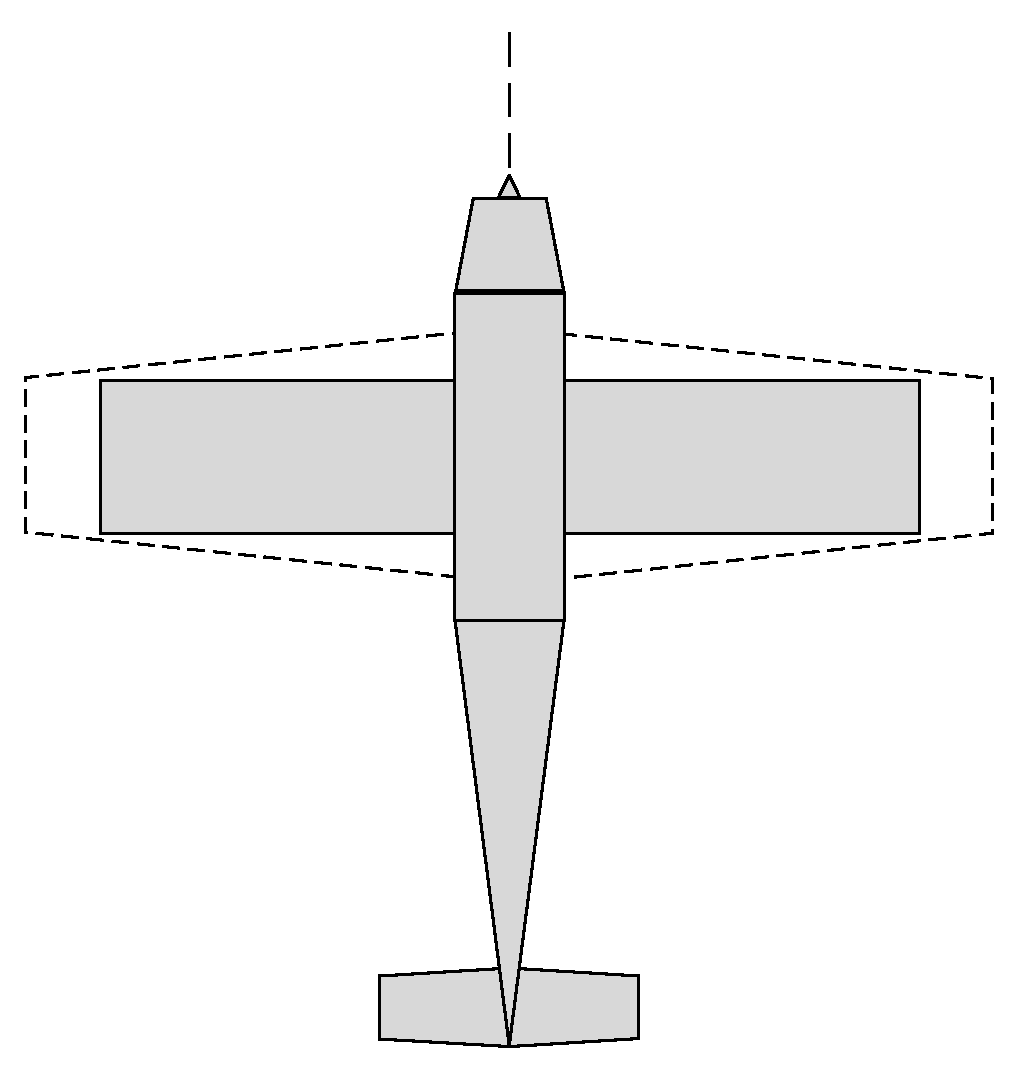
2. Variable Area Wing Design
2.1. Strategy of Morphing Wing in Planform
2.1.1. Demand Analysis of Metamaterial Properties in Morphing Mechanism
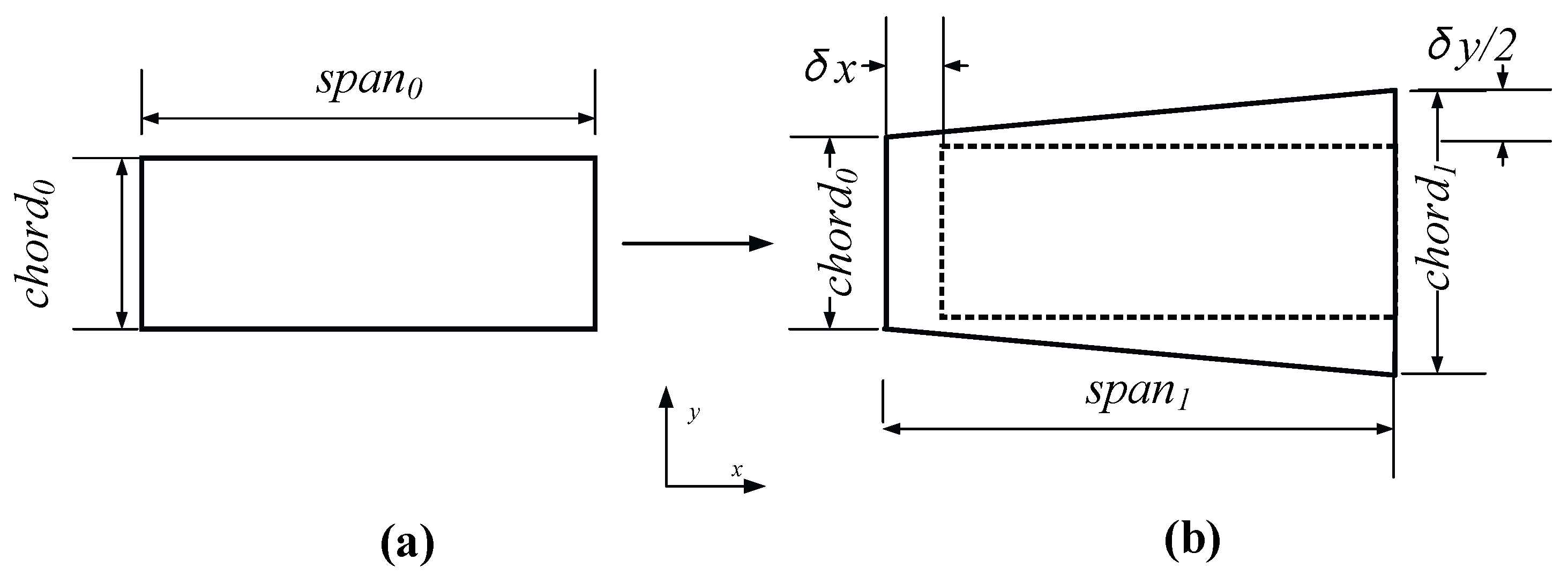
2.1.2. Morphing Ability Analysis of NPR Metamaterial in Wing Planform
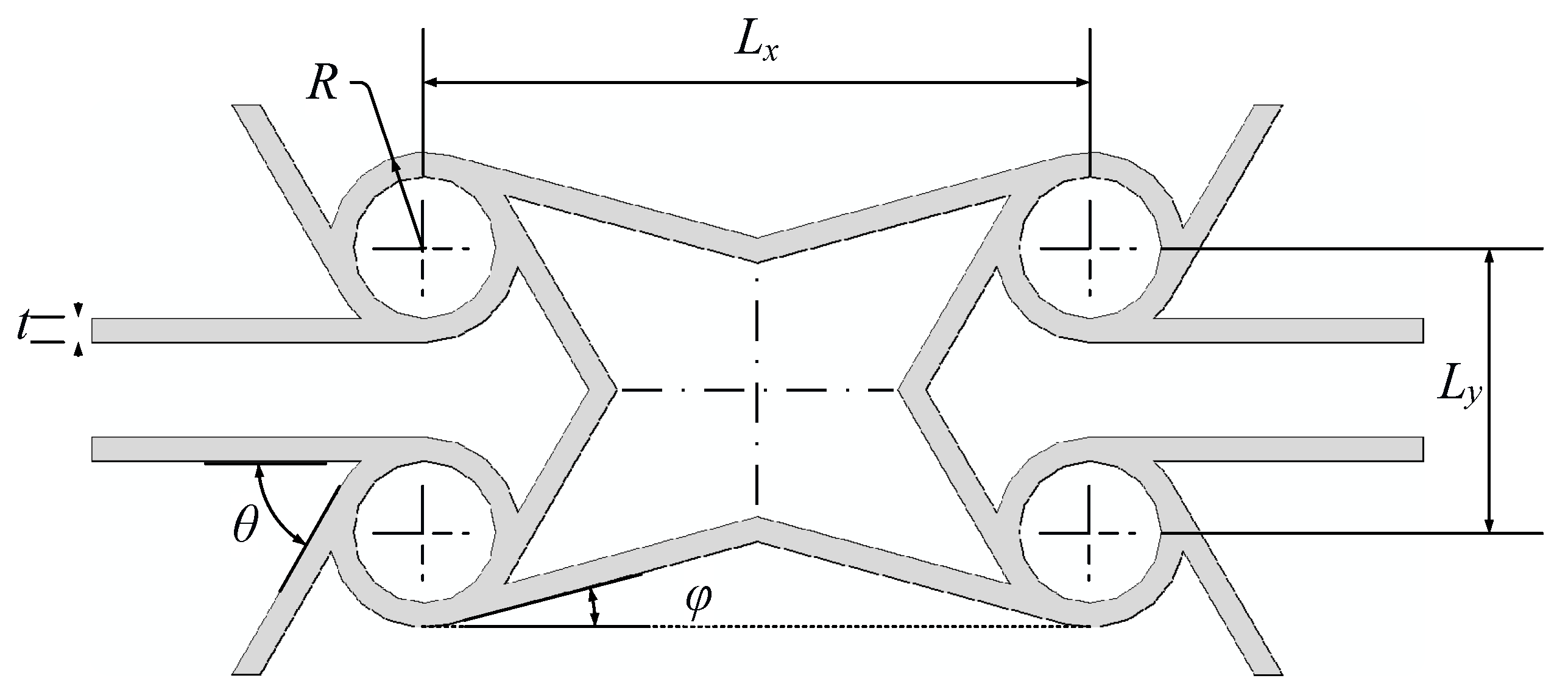
2.2. Method of Morphing Wing Based on BRATC Metamaterial Cell
2.2.1. Deformation Analysis Scheme Based on BRATC Metamaterial Cell
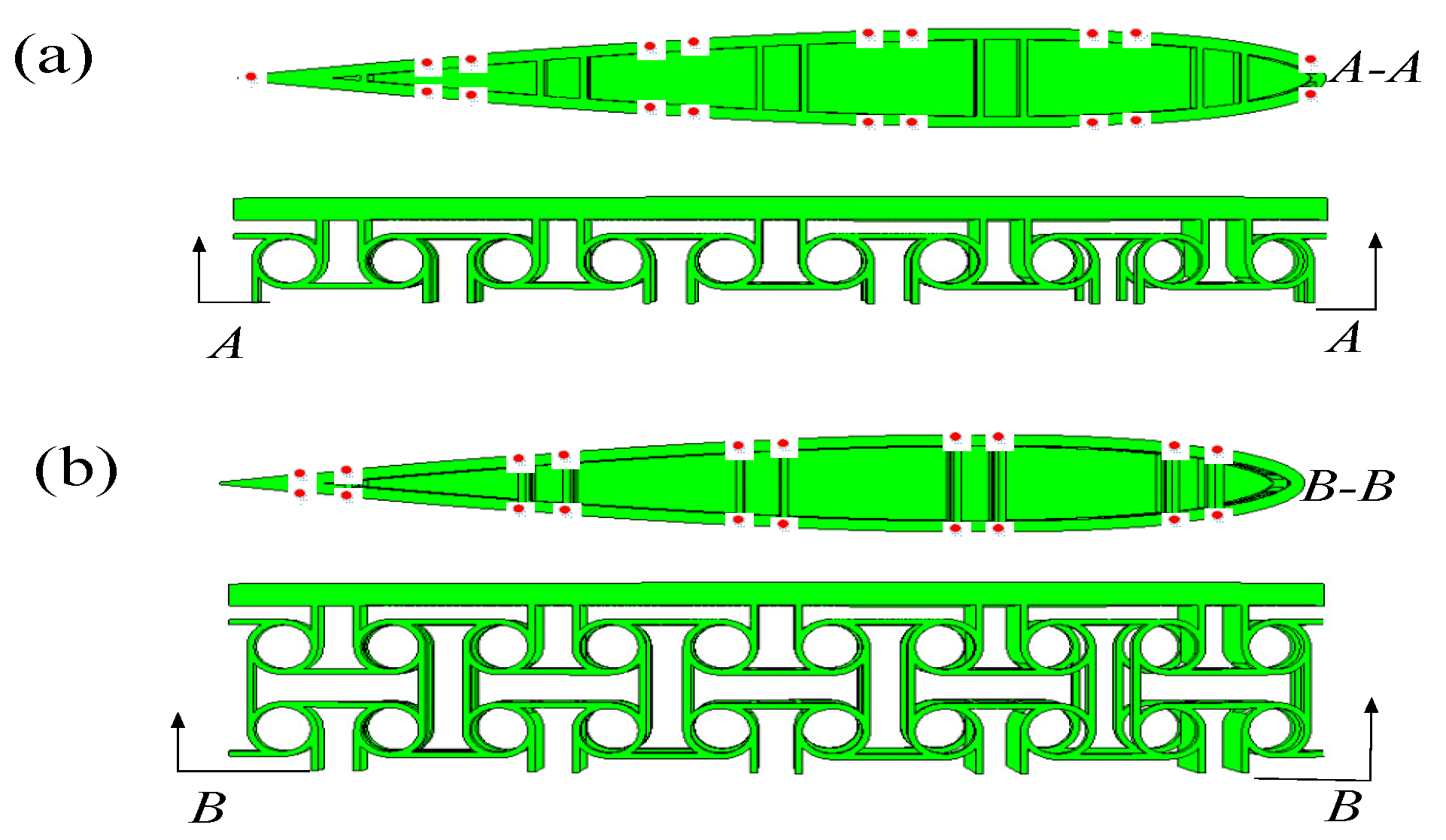
2.2.2. Morphing-Wing Model Based on BRATC Cell
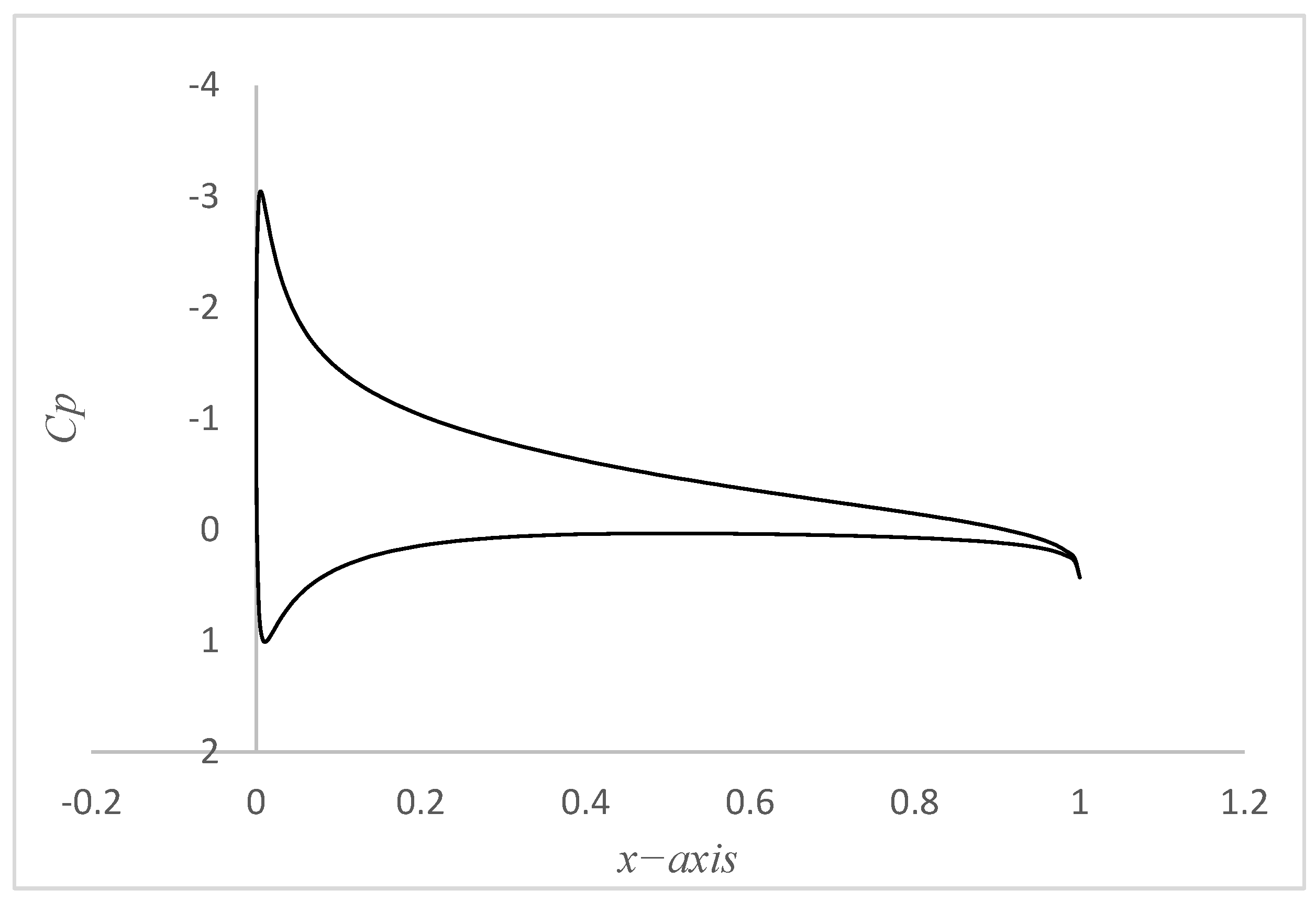
2.2.3. Loads and Boundary Conditions in Wing Model
- 1.
- Boundary conditions: BC1
- 2.
- Displacement load: Load 1
- 3.
- Air load: Load 2
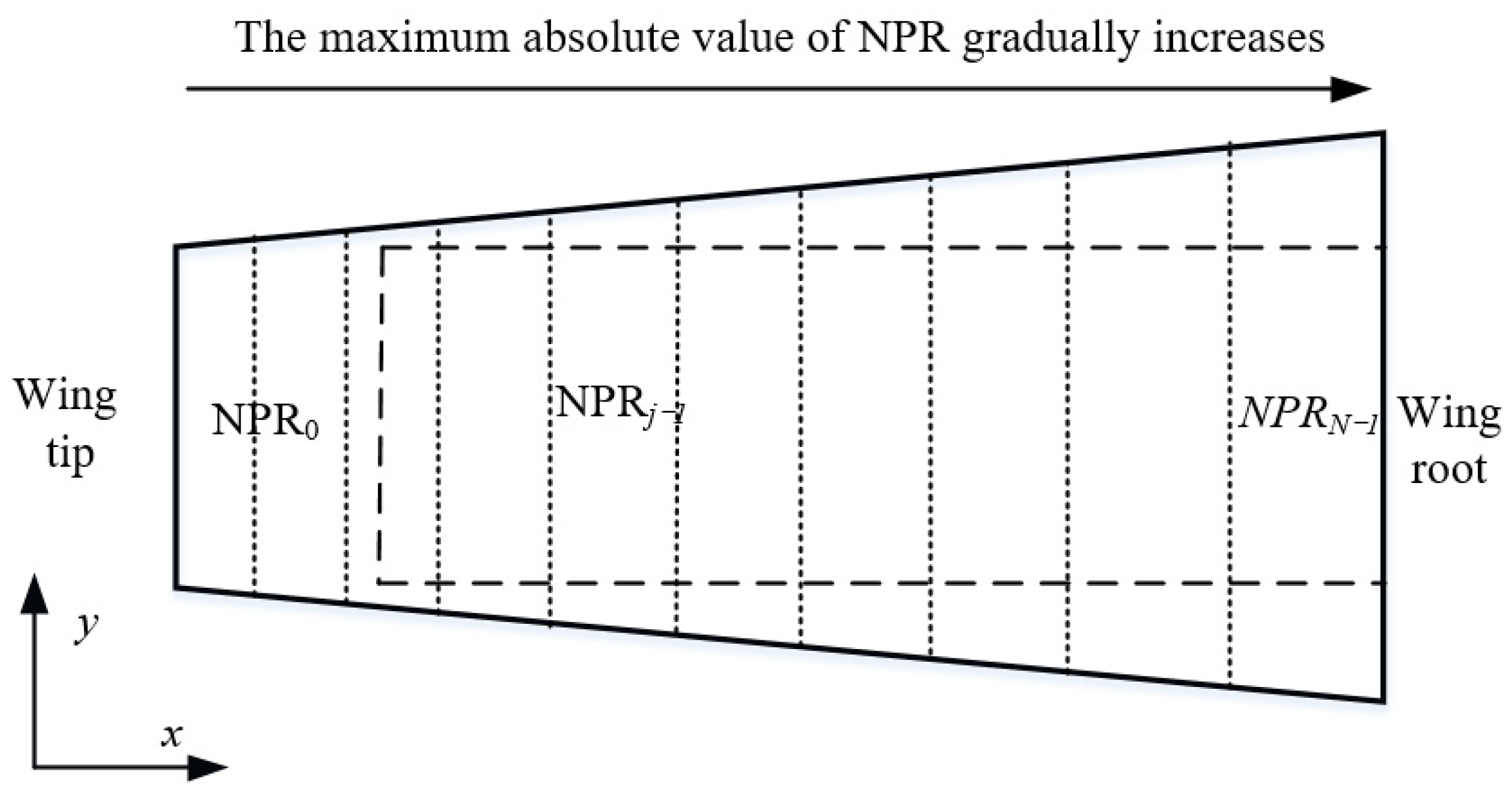
2.2.4. Optimization of Morphing-Wing Contour Based on BRATC Cell
3. Optimization Results and Analysis
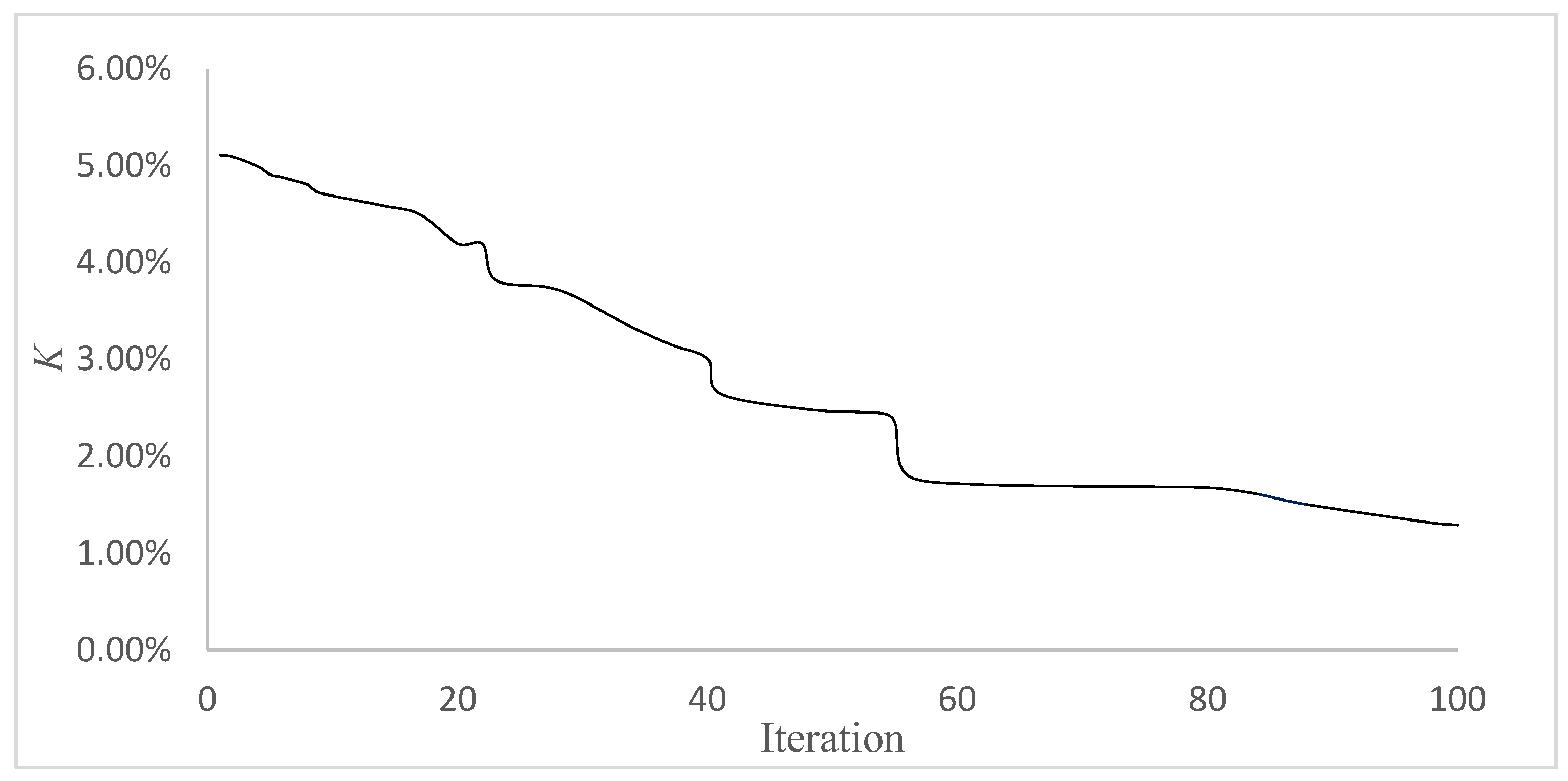
3.1. Morphing-Wing Contour Error
3.2. Nephogram of Stress and Displacement
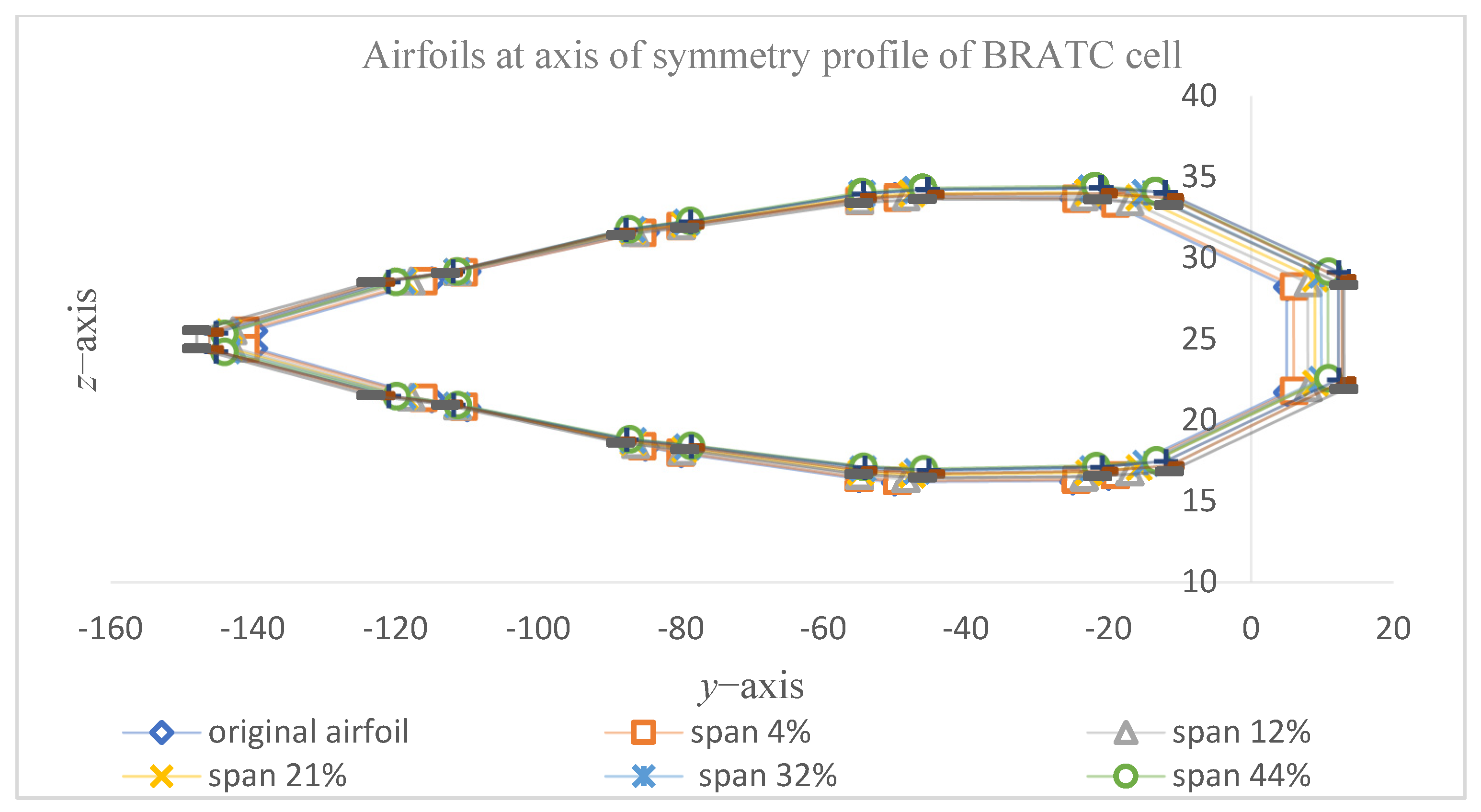
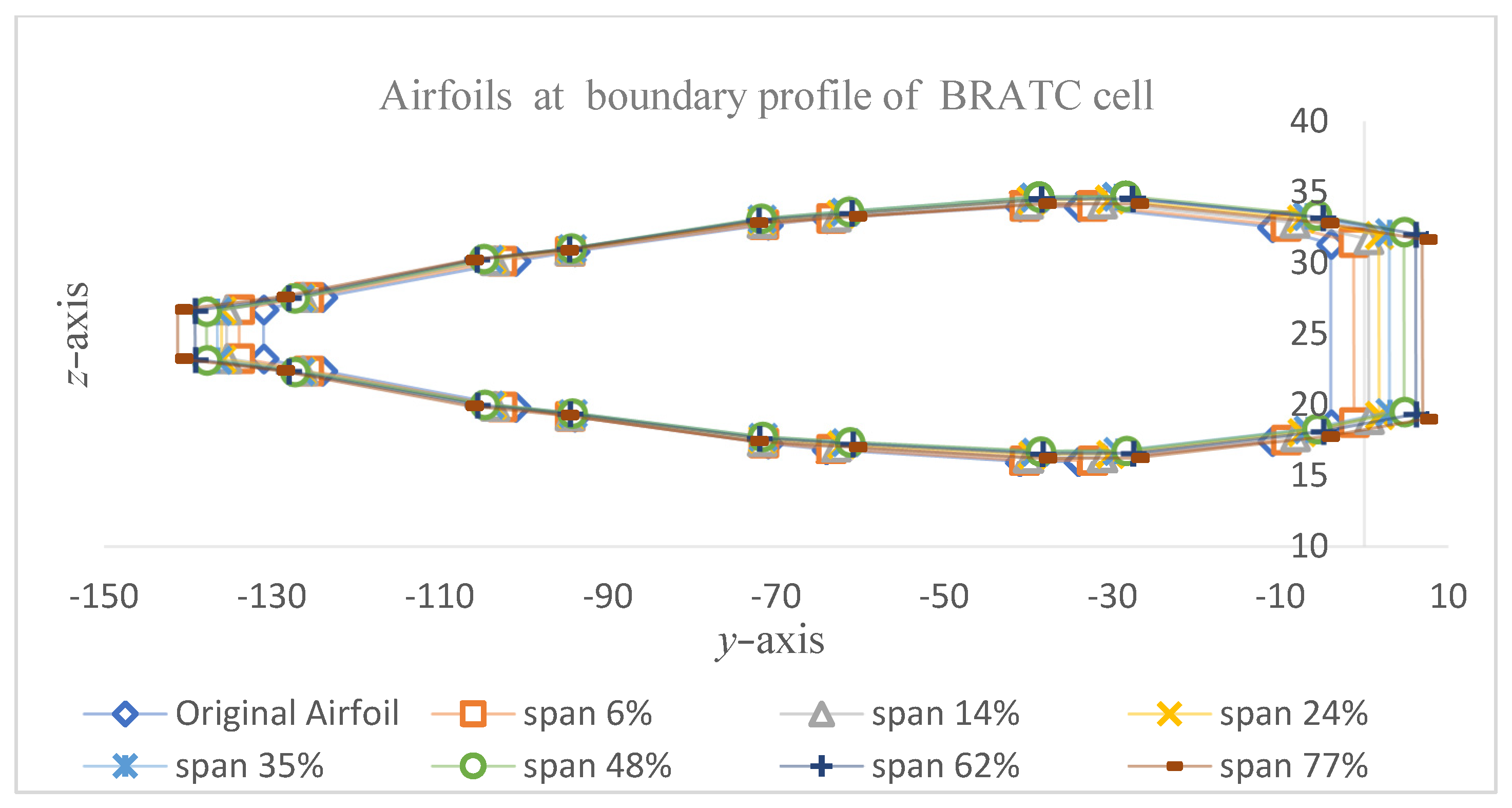
3.3. The Airfoil Along Spanwise Direction
3.4. Comparison of Object Contours with Different Taper Ratios
4. Validation Experiment
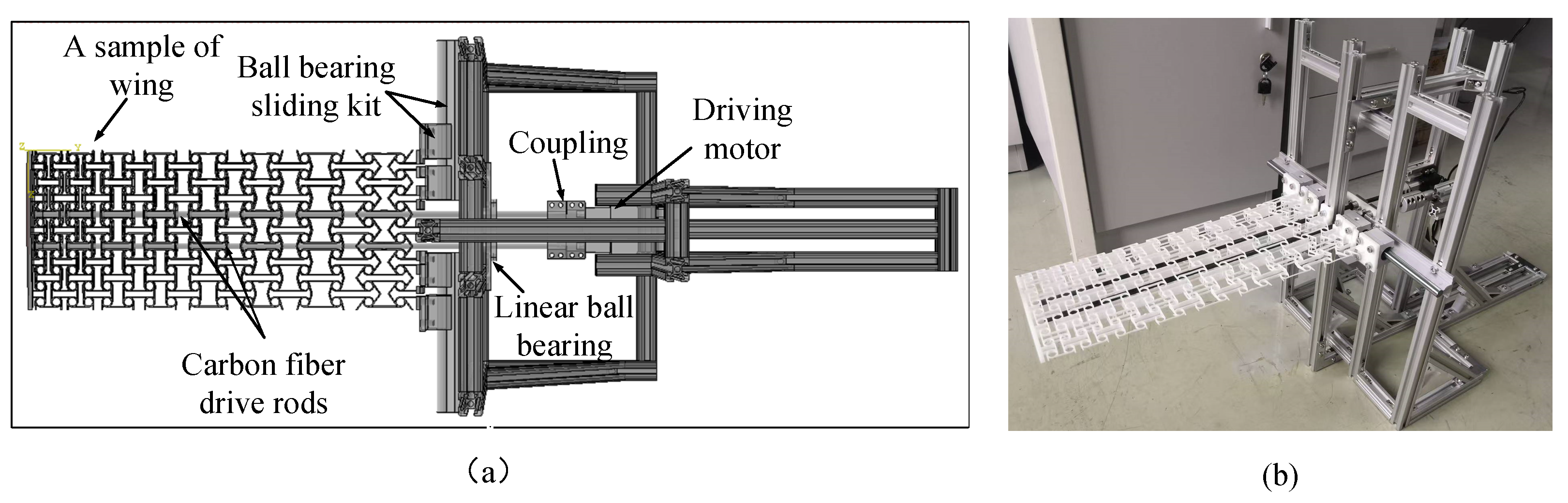
4.1. Experimental Equipment
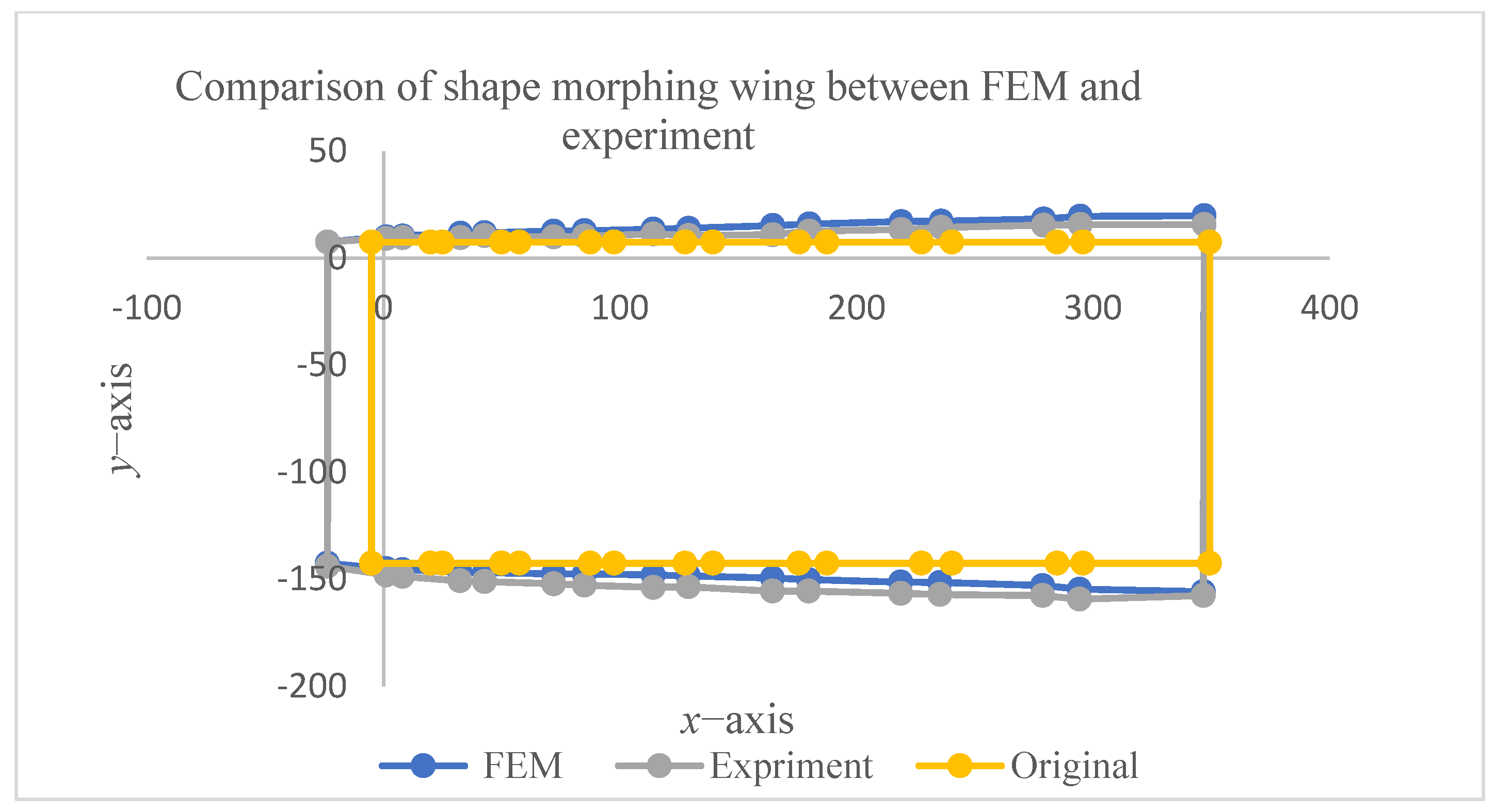
4.2. Results of Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| NPR | negative Poisson’s ratio |
| BRATC | bi-directional re-entrant anti-tetrachiral |
| Nomenclature | |
| span0 | Span of undeformed wing |
| chord0 | Chord of undeformed wing |
| chord1 | Chord of deformed wing at wing root |
| span1 | Span of deformed wing |
| δx | The increase in spanwise |
| δy | The increase in chordwise (wing root) |
| Δspan | Relative variations in spanwise |
| Δchord | Relative variations in chordwise at wing root |
| εx | Strain of a metamaterial cell |
| Δy | Deformation in y-axis direction of a metamaterial cell |
| y0 | Original length of the metamaterial cell along y-axis |
| νxy | Poisson’s ratio of the metamaterial cell. |
| ax | Nondimensionalized length of a BRATC cell |
| ay | Nondimensionalized width of a BRATC cell |
| b | Nondimensionalized height of a BRATC cell |
| θ | An angle in a BRATC cell |
| φ | An angle in a BRATC cell |
| Dis_load | Displacement load |
| V | Cruising speed |
| ρ | Air density |
| v | Air kinematic viscosity |
| Re | Reynolds number |
| Cp | Pressure coefficient |
| CL | Lift coefficient |
| S | Reference wing surface area in xy plane |
| L | Lift |
| K | Shape error |
| Ar | Relative change rate of wing area |
References
- Bae, J.S.; Seigler, T.M.; Inman, D.J. Aerodynamic and Static Aeroelastic Characteristics of a Variable-Span Morphing Wing. J. Aircr. 2005, 42, 528–534. [Google Scholar] [CrossRef]
- Chu, L.; Qi, L.I.; Feng, G.U.; Xintian, D.U.; Yuqing, H.E.; Deng, Y. Design, modeling, and control of morphing aircraft: A review. Chin. J. Aeronaut. 2022, 35, 220–246. [Google Scholar] [CrossRef]
- Jha, A.K.; Kudva, J.N. Morphing aircraft concepts, classifications, and challenges. In Smart Structures and Materials 2004: Industrial and Commercial Applications of Smart Structures Technologies; SPIE: San Diego, CA, USA, 2004; Volume 5388, pp. 213–224. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M.; Friswell, M.I.; Cantwell, W.J. Recent developments in the aeroelasticity of morphing aircraft. Prog. Aerosp. Sci. 2021, 120, 100682. [Google Scholar] [CrossRef]
- Yuzhu, L.I.; Wenjie, G.E.; Zhou, J.; Zhang, Y.; Zhao, D.; Wang, Z.; Dong, D. Design and experiment of concentrated flexibility-based variable camber morphing wing. Chin. J. Aeronaut. 2022, 35, 455–469. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Z.; Song, C.; Yang, C. A morphing wing with cellular structure of non-uniform density. Smart Mater. Struct. 2021, 30, 105005. [Google Scholar] [CrossRef]
- Li, D.; Guo, S.; Aburass, T.O.; Yang, D.; Xiang, J. Active control design for an unmanned air vehicle with a morphing wing. Aircr. Eng. Aerosp. Technol. Int. J. 2016, 88, 168–177. [Google Scholar] [CrossRef]
- Ozbek, E.; Ekici, S.; Karakoç, T.H. A comprehensive review of state-of-art FishBAC—Fishbone active camber morphing wing surfaces–: A promising morphing method. Aircr. Eng. Aerosp. Technol. 2024, 96, 983–993. [Google Scholar] [CrossRef]
- Kim, Y.; Jo, Y. Development of two types of in-plane motion actuators with modular design and application to morphing wings. Mech. Adv. Mater. Struct. 2024, 31, 12183–12199. [Google Scholar] [CrossRef]
- Karagiannis, D.; Stamatelos, D.; Kappatos, V.; Spathopoulos, T. An investigation of shape memory alloys as actuating elements in aerospace morphing applications. Mech. Adv. Mater. Struct. 2017, 24, 647–657. [Google Scholar] [CrossRef]
- Geva, A.; Abramovich, H.; Arieli, R. Investigation of a Morphing Wing Capable of Airfoil and Span Adjustment Using a Retractable Folding Mechanism. Aerospace 2019, 6, 85. [Google Scholar] [CrossRef]
- Ajaj, R.; Friswell, M.; Flores, E.S.; Little, O.; Isikveren, A. Span Morphing: A Conceptual Design Study. In Proceedings of the 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, Honolulu, HI, USA, 23–26 April 2012; Volume 2012, p. 1510. [Google Scholar]
- Ajaj, R.M.; Friswell, M.I.; Bourchak, M.; Harasani, W. Span morphing using the GNATSpar wing. Aerosp. Sci. Technol. 2016, 53, 38–46. [Google Scholar] [CrossRef]
- Elelwi, M.; Calvet, T.; Botez, R.M.; Dao, T.M. Wing component allocation for a morphing variable span of tapered wing using finite element method and topology optimisation—Application to the UAS-S4. Aeronaut. J. 2021, 125, 1313–1336. [Google Scholar] [CrossRef]
- Elelwi, M.; Kuitche, M.A.; Botez, R.M.; Dao, T.M. Comparison and analyses of a variable span-morphing of the tapered wing with a varying sweep angle. Aeronaut. J. 2020, 124, 1146–1169. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Friswell, M.I.; Flores, E.I.S.; Keane, A.; Isikveren, A.T.; Allegri, G.; Adhikari, S. An integrated conceptual design study using span morphing technology. J. Intell. Mater. Syst. Struct. 2014, 25, 989–1008. [Google Scholar] [CrossRef]
- Alulema, V.H.; Valencia, E.A.; Toapanta, E.; Guailla, C.; Pazmio, M. Performance Assessment of a Variable-Span Morphing Wing Small UAV for High Altitude Surveillance Missions. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–28 August 2020; Volume 2020, p. 3962. [Google Scholar] [CrossRef]
- Huang, C.; Yang, C.; Wu, Z.; Tang, C. Variations of flutter mechanism of a span-morphing wing involving rigid-body motions. Chin. J. Aeronaut. 2018, 31, 490–497. [Google Scholar] [CrossRef]
- Ajaj, R.M.; Parancheerivilakkathil, M.S.; Amoozgar, M. ASAPP: A polymorphing wing capable of Active Span extension And Passive Pitch. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021; Volume 2021, p. 0621. [Google Scholar] [CrossRef]
- Haider, Z.; Ajaj, R.M.; Seneviratne, L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: Effect of Morphing Rate. Aerospace 2023, 10, 57. [Google Scholar] [CrossRef]
- Haider, Z.; Ajaj, R.M.; Seneviratne, L. On the Aeroelasticity of the Active Span and Passive Pitching Polymorphing Wing: A Parametric Study. Aerospace 2022, 9, 483. [Google Scholar] [CrossRef]
- Beaverstock, C.S.; Woods, B.K.S.; Fincham, J.H.S.-M.; Friswell, M.I. Performance Comparison between Optimised Camber and Span for a Morphing Wing. Aerospace 2015, 2, 524–554. [Google Scholar] [CrossRef]
- Parancheerivilakkathil, M.S.; Haider, Z.; Ajaj, R.M.; Amoozgar, M. A Polymorphing Wing Capable of Span Extension and Variable Pitch. Aerospace 2022, 9, 205. [Google Scholar] [CrossRef]
- Sun, J.; Du, L.; Scarpa, F.; Liu, Y.; Leng, J. Morphing wingtip structure based on active inflatable honeycomb and shape memory polymer composite skin: A conceptual work. Aerosp. Sci. Technol. 2021, 111, 106541. [Google Scholar] [CrossRef]
- Tarnowski, A. Morphing wing with skin discontinuity—Kinematic concept. Aircr. Eng. Aerosp. Technol. 2017, 89, 535–546. [Google Scholar] [CrossRef]
- Avila, A.; Avila, J.; Chaves, F. A Morphological Study on Cellular Composites with Negative Poisson Ratio. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003; p. 1951. [Google Scholar]
- Boston, D.M.; Arrieta, A.F. Multistable Honeycomb Architecture for Spanwise Wing Morphing. In Proceedings of the AIAA Scitech 2021 Forum, Virtual Event, 11–15 & 19–21 January 2021; p. 0479. [Google Scholar]
- Boston, D.M.; Phillips, F.R.; Henry, T.; Arrieta, A.F. Aeroelastic analysis of spanwise morphing wing with multistable honeycomb. In Proceedings of the AIAA SCITECH 2022 Forum, San Diego, CA, USA, 3–7 January 2022; p. 0319. [Google Scholar]
- Boston, D.M.; Phillips, F.R.; Henry, T.C.; Arrieta, A.F. Spanwise wing morphing using multistable cellular metastructures. Extrem. Mech. Lett. 2022, 53, 101706. [Google Scholar] [CrossRef]
- Han, Z.; Wang, Z.; Wei, K. Shape morphing structures inspired by multi-material topology optimized bi-functional metamaterials. Compos. Struct. 2022, 300, 116135. [Google Scholar] [CrossRef]
- Yokota, K.; Barthelat, F. Design guidelines for the morphing of stiff lattice materials. Mech. Adv. Mater. Struct. 2023, 31, 10070–10080. [Google Scholar] [CrossRef]
- Olympio, K.; Gandhi, F. Zero-v Cellular Honeycomb Flexible Skins for One-Dimensional Wing Morphing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Honolulu, HI, USA, 23–26 April 2007; Volume 2007, p. 1735. [Google Scholar]
- Zadeh, M.N.; Dayyani, I.; Yasaee, M. Fish Cells, a new zero Poisson’s ratio metamaterial—Part I: Design and experiment. J. Intell. Mater. Syst. Struct. 2020, 31, 1617–1637. [Google Scholar] [CrossRef]
- Zadeh, M.N.; Dayyani, I.; Yasaee, M. Fish Cells, a new zero Poisson’s ratio metamaterial—Part II: Elastic properties. J. Intell. Mater. Syst. Struct. 2020, 31, 2196–2210. [Google Scholar] [CrossRef]
- Chen, X.; Fu, M.-H.; Li, W.-H.; Sheshenin, S.V. An Unusual 3D Metamaterial with Zero Poisson’s Ratio in Partial Directions. Adv. Eng. Mater. 2021, 23, 2001491. [Google Scholar] [CrossRef]
- Castillo-Acero, M.A.; Cuerno-Rejado, C.; Gómez-Tierno, M.A. Morphing structure for a rudder. Aeronaut. J. 2016, 120, 1291–1314. [Google Scholar] [CrossRef][Green Version]
- Phillips, F.R.; Henry, T.; Hrynuk, J.T.; Haynes, R.; Bain, E.; Westrich, J. Towards the Development of a Span-wise Extending Unmanned Aerial System. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; Volume 2020, p. 2006. [Google Scholar]
- Jha, A.; Dayyani, I. Shape optimisation and buckling analysis of large strain zero Poisson’s ratio fish-cells metamaterial for morphing structures. Compos. Struct. 2021, 268, 113995. [Google Scholar] [CrossRef]
- Budarapu, P.R.; Y B, S.S.; Natarajan, R. Design concepts of an aircraft wing: Composite and morphing airfoil with auxetic structures. Front. Struct. Civ. Eng. 2016, 10, 394–408. [Google Scholar] [CrossRef]
- Gong, M.; Tao, C.; Zhang, C.; Ji, H.; Qiu, J. A method for regulating negative Poisson’s ratio by a reentrant anti-tetrachiral structure. Mech. Adv. Mater. Struct. 2022, 29, 7399–7414. [Google Scholar] [CrossRef]
- Wang, H.; Nie, R.; Zhang, C.; Ji, H.; Qiu, J. Investigation of bi-directional re-entrant anti-tetrachiral structure for regulating negative Poisson’s ratio. Mech. Adv. Mater. Struct. 2024, 31, 6282–6297. [Google Scholar] [CrossRef]
- Chen, Y.J.; Scarpa, F.; Liu, Y.J.; Leng, J.S. Elasticity of anti-tetrachiral anisotropic lattices. Int. J. Solids Struct. 2013, 50, 996–1004. [Google Scholar] [CrossRef]
- Beyer, H.-G.; Schwefel, H.-P. Evolution strategies—A comprehensive introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
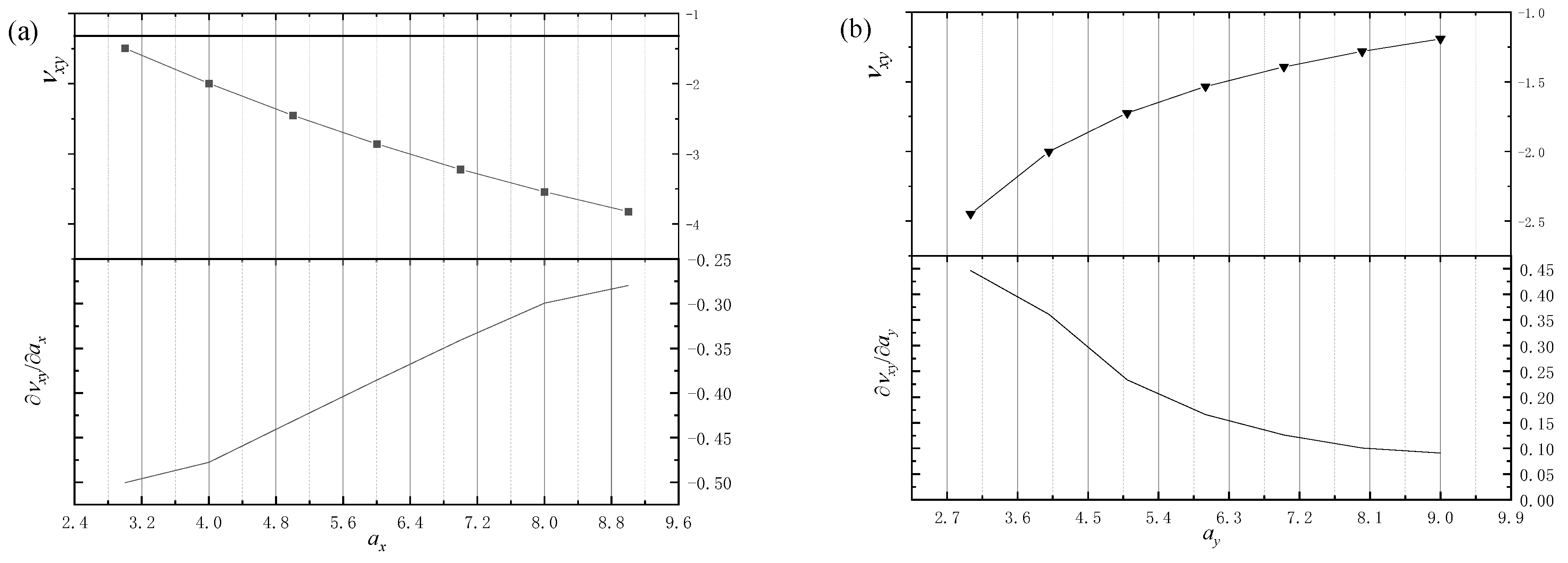
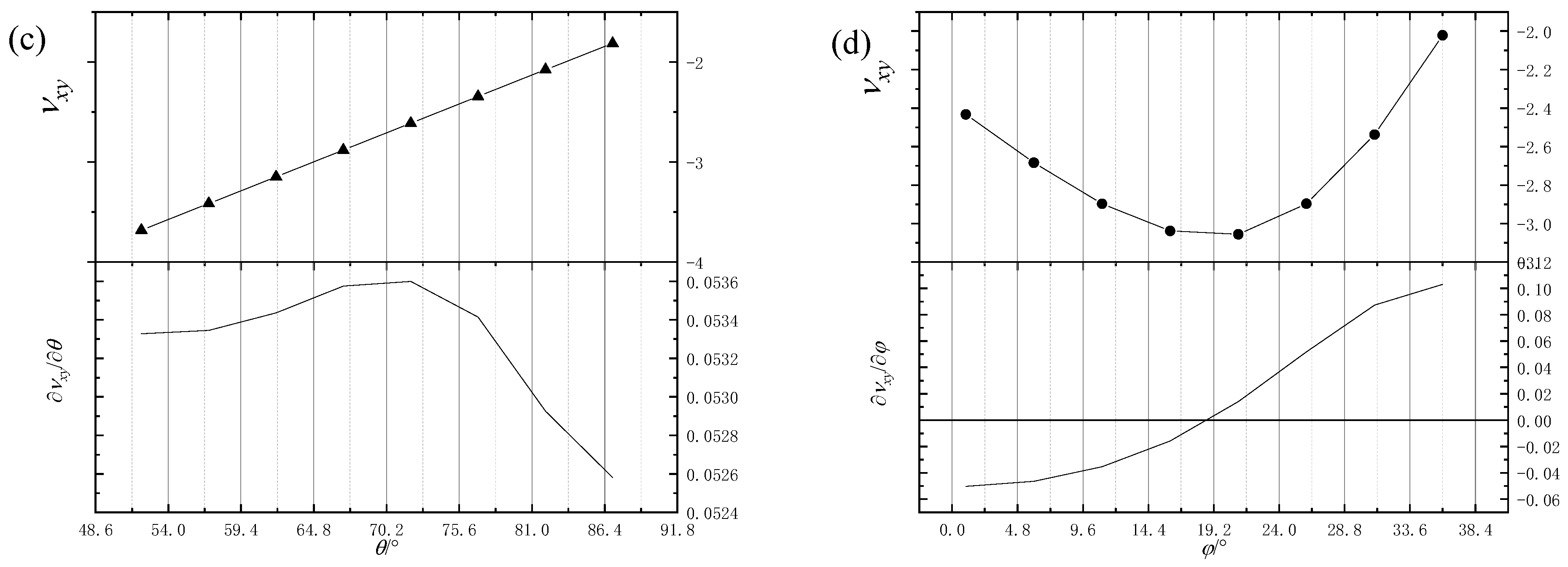
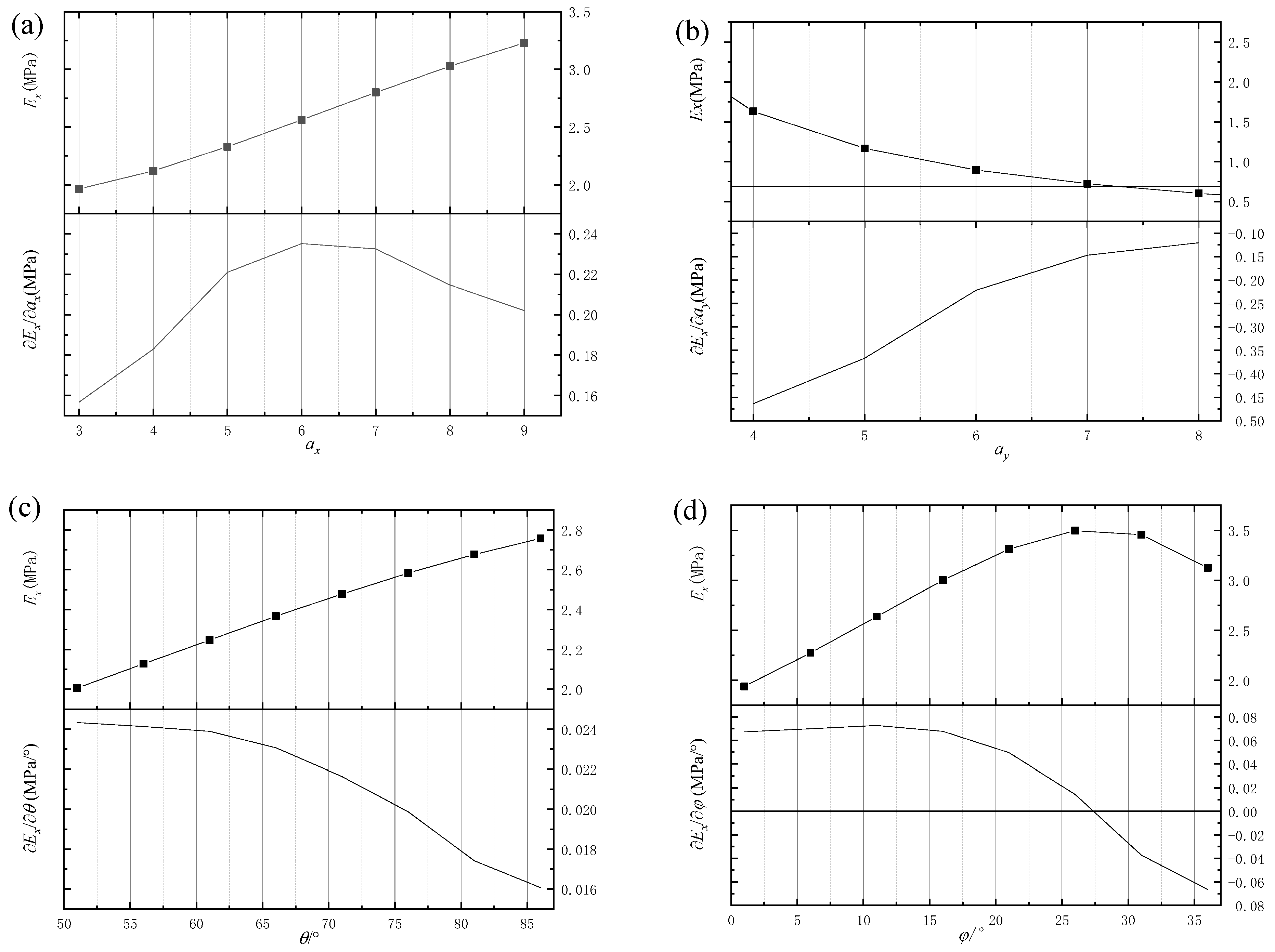

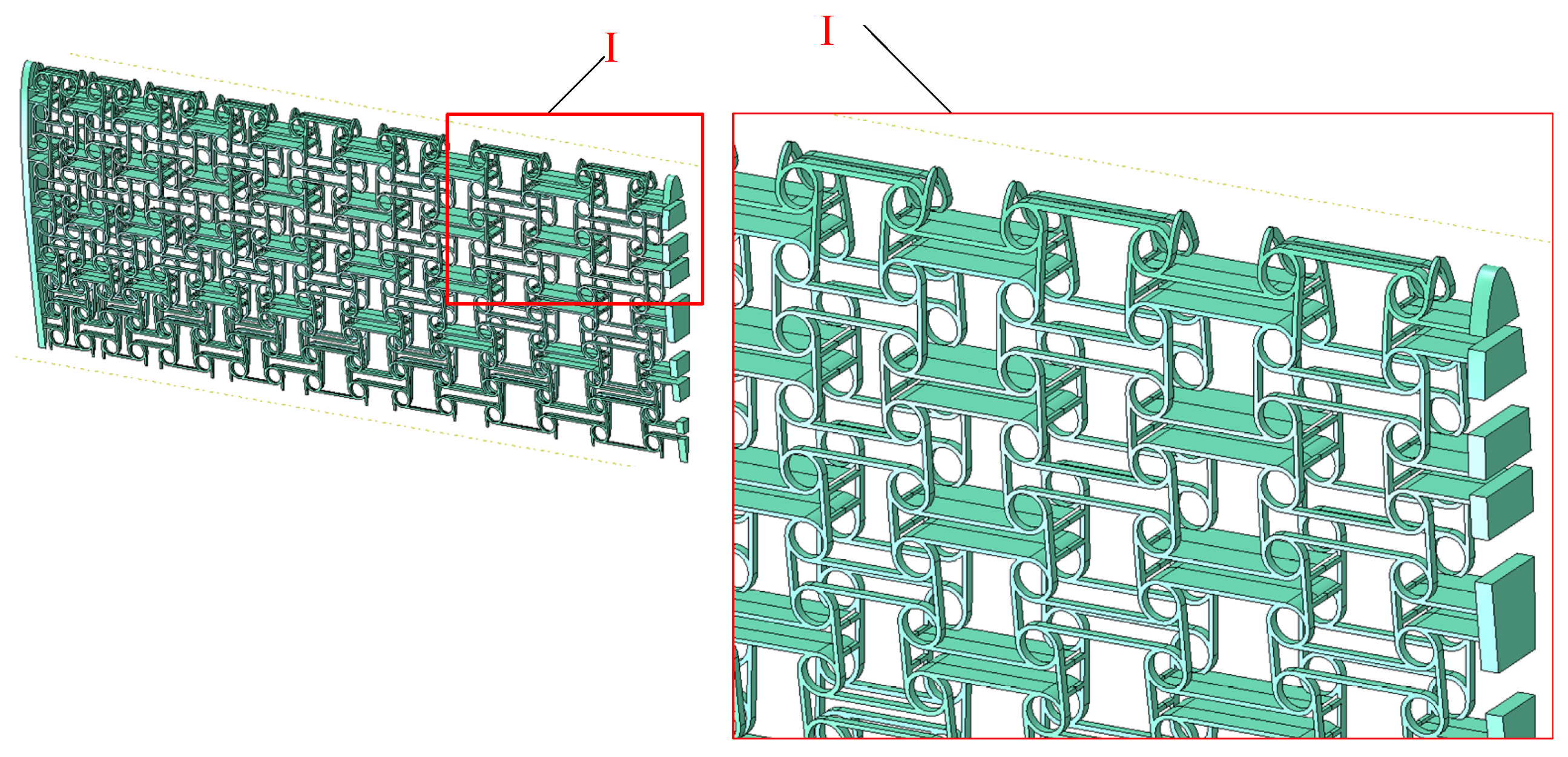





| NO. | b | ax | ay | θ/° | φ/° |
|---|---|---|---|---|---|
| 0 | 0.2 | 3 | 3 | 90 | 0 |
| 1 | 0.2 | 3 | 3 | 90 | 0 |
| 2 | 0.2 | 4 | 3 | 90 | 0 |
| 3 | 0.2 | 4 | 3 | 90 | 0 |
| 4 | 0.2 | 5 | 3 | 80 | 4 |
| 5 | 0.2 | 5 | 3 | 75 | 4 |
| 6 | 0.2 | 6 | 3 | 70 | 0 |
| 7 | 0.2 | 6 | 3 | 60 | 0 |
| Degree of Freedom | Face A | Face B | Face C |
|---|---|---|---|
| Ux | Dis_load | 0 | 0 |
| Uy | 0 | 0 | Free |
| Uz | Free | 0 | 0 |
| URx | Free | 0 | 0 |
| URy | Free | 0 | 0 |
| URz | Free | 0 | 0 |
| NO. | b | ax | ay | θ/° | φ/° |
|---|---|---|---|---|---|
| 0 | 0.2 | 3 | 3 | 90 | 0 |
| 1 | 0.2 | 3 | 3 | 90 | 0 |
| 2 | 0.2 | 4 | 3 | 90 | 0 |
| 3 | 0.2 | 4 | 3 | 90 | 0 |
| 4 | 0.2 | 5 | 3 | 58 | 4.5 |
| 5 | 0.2 | 5 | 3 | 52 | 13.8 |
| 6 | 0.2 | 6 | 3 | 49.8 | 7 |
| 7 | 0.2 | 6 | 3 | 44 | 0.1 |
| Δspan | Δchord | Ar | K |
|---|---|---|---|
| 5% | 20% | 15.50% | 1.29% |
| 5% | 25% | 18.13% | 1.40% |
| 5% | 30% | 20.75% | 2.02% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Zhang, C.; Wang, C.; Qiu, J. The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing. Aerospace 2025, 12, 125. https://doi.org/10.3390/aerospace12020125
Wang H, Zhang C, Wang C, Qiu J. The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing. Aerospace. 2025; 12(2):125. https://doi.org/10.3390/aerospace12020125
Chicago/Turabian StyleWang, Haifeng, Chao Zhang, Chen Wang, and Jinhao Qiu. 2025. "The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing" Aerospace 12, no. 2: 125. https://doi.org/10.3390/aerospace12020125
APA StyleWang, H., Zhang, C., Wang, C., & Qiu, J. (2025). The Application of Negative Poisson’s Ratio Metamaterials in the Optimization of a Variable Area Wing. Aerospace, 12(2), 125. https://doi.org/10.3390/aerospace12020125






