Divergence Evaluation Criteria for Lunar Departure Trajectories Under Bi-Circular Restricted Four-Body Problem
Abstract
1. Introduction
2. Fundamental of Multi-Body Dynamics
2.1. Circular Restricted Three-Body Problem
2.2. Bi-Circular Restricted Four-Body Problem
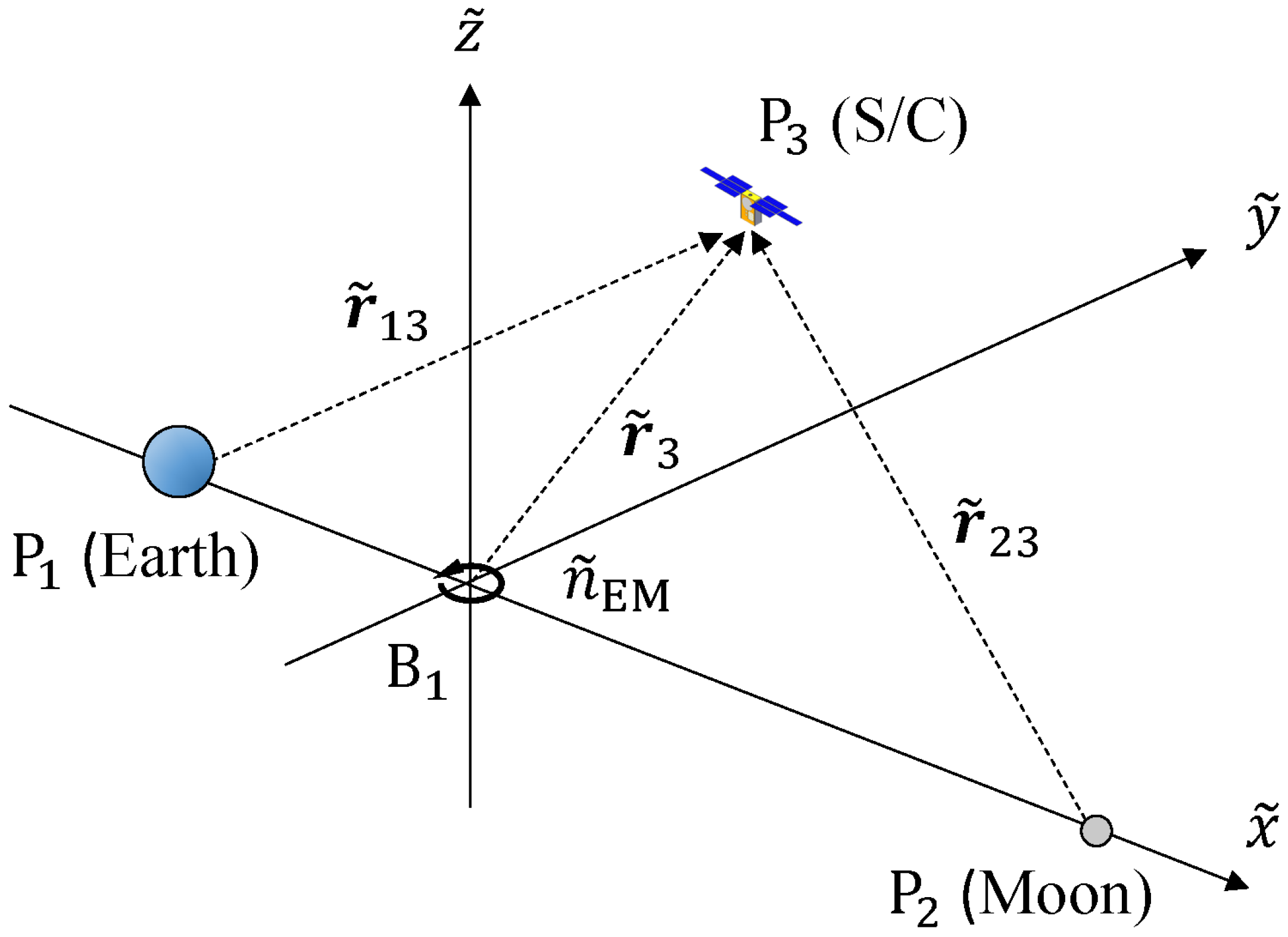
2.2.1. Earth–Moon Rotating Frame
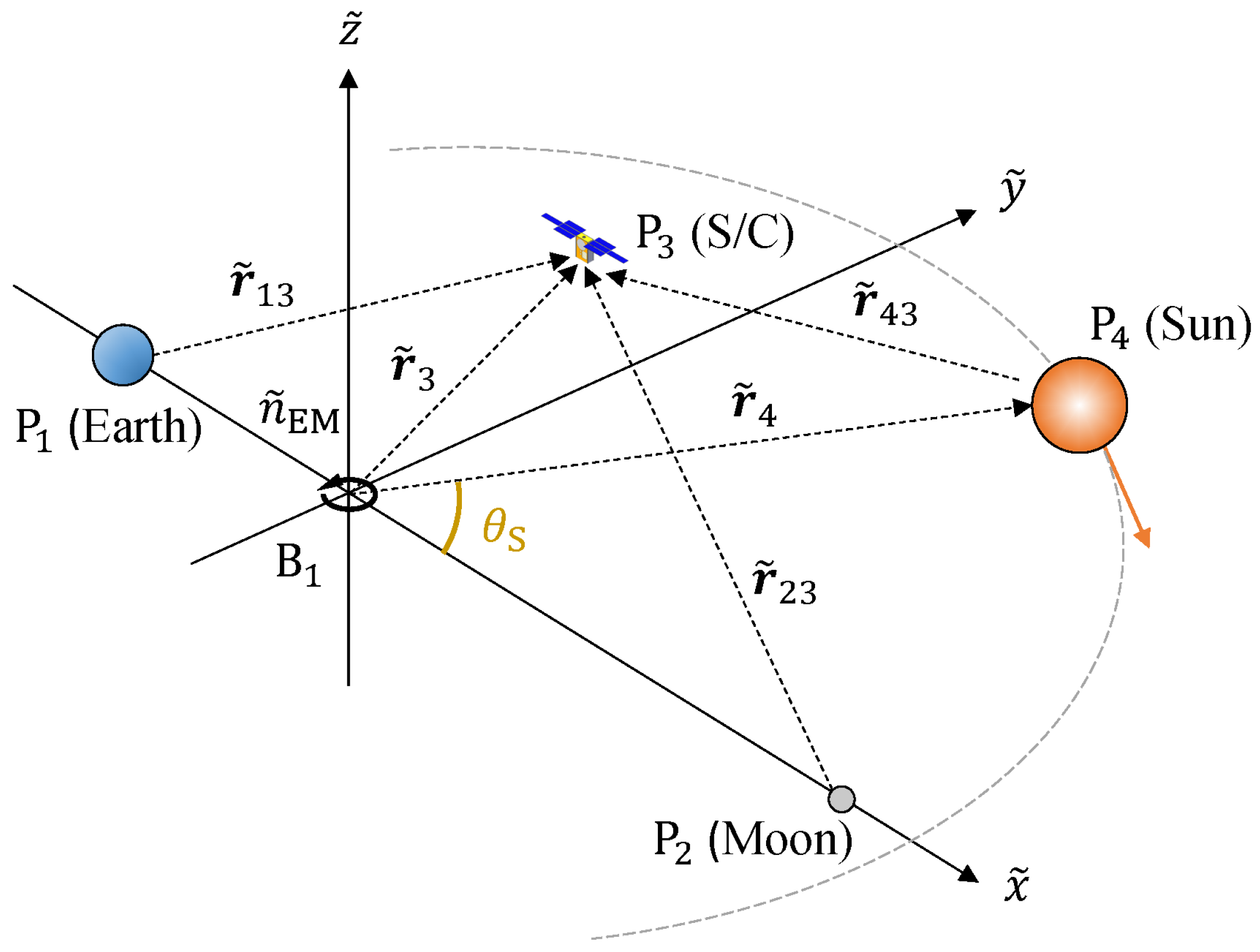
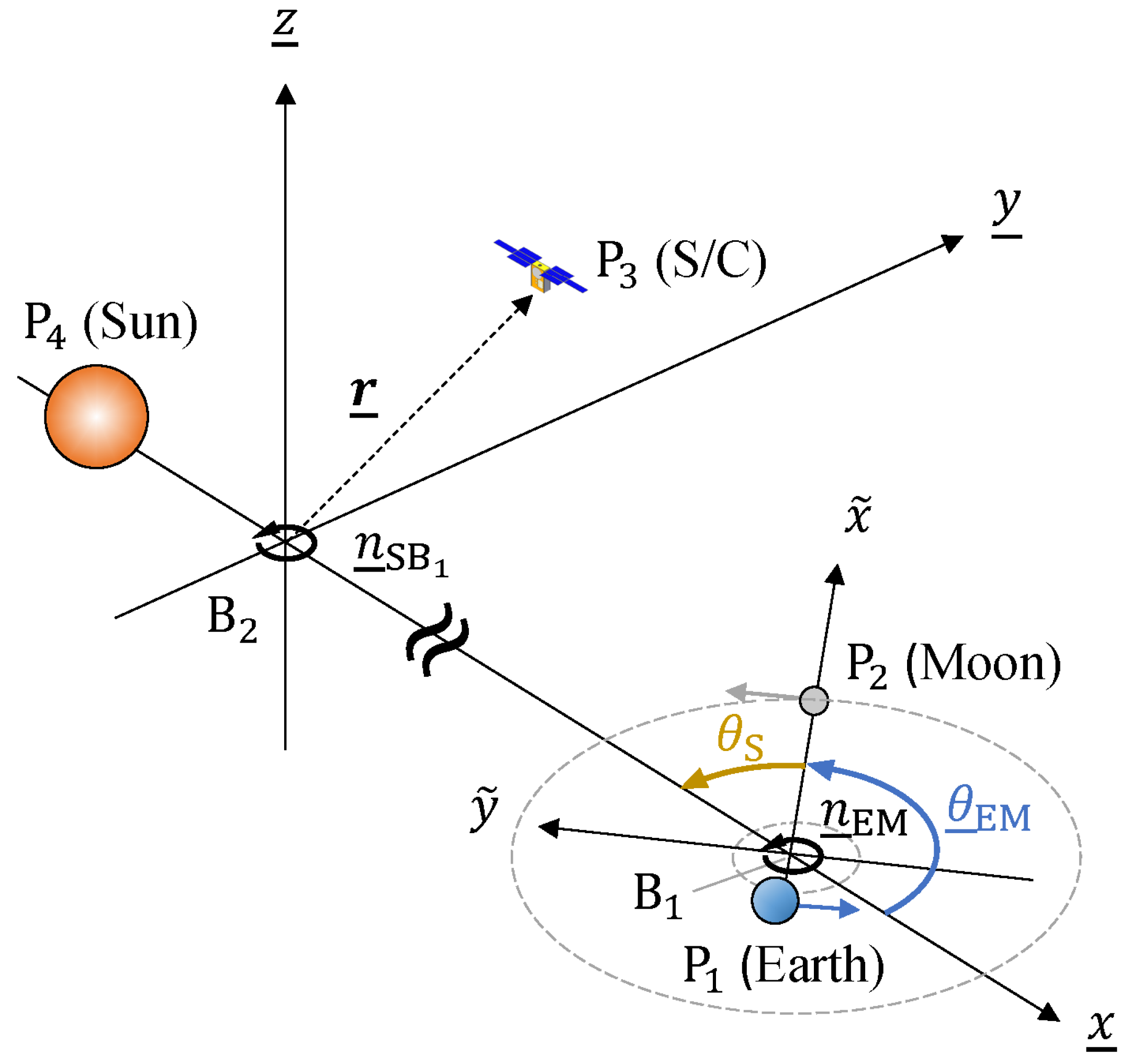
2.2.2. Sun- Rotating Frame
2.3. Jacobi Integral, Hamiltonian and
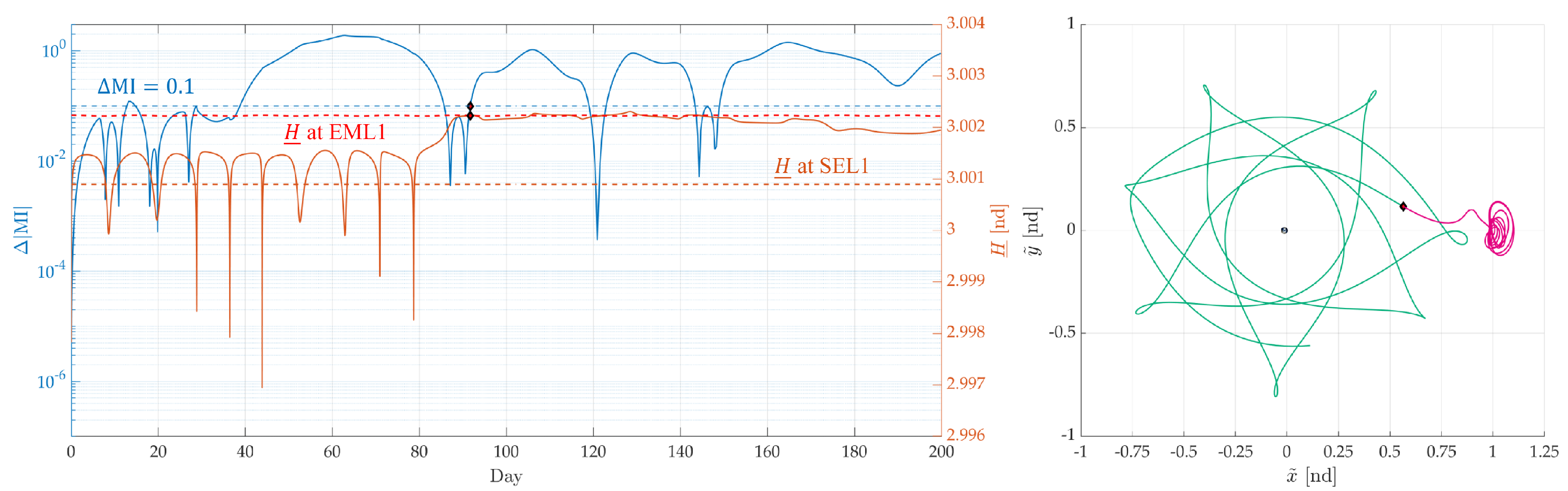
2.3.1. Jacobi Integral
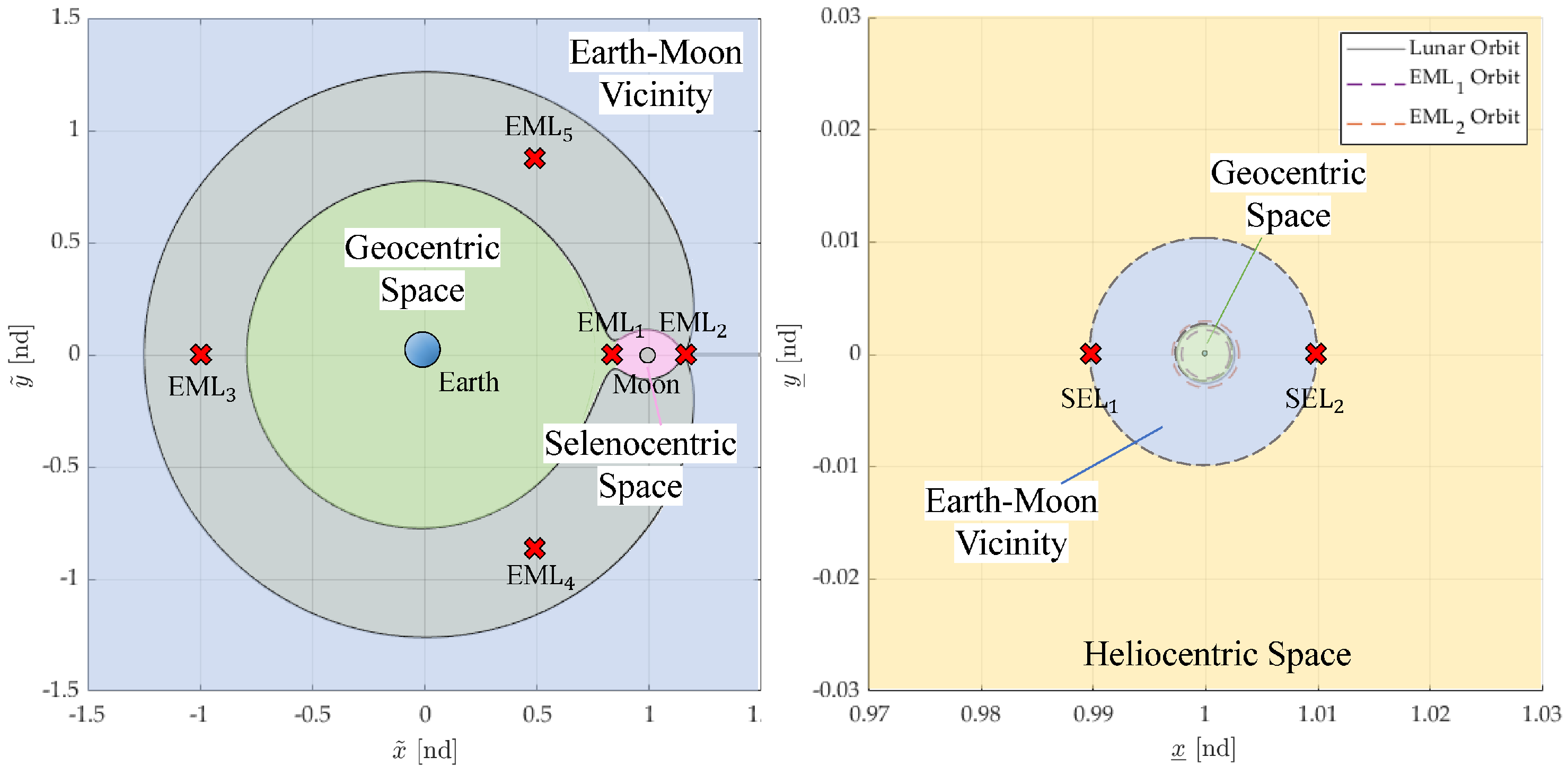
- The space around the center of each celestial body (geocentric, selenocentric).
- The space inside the Earth–Moon fusion region (E–M inner space).
- The space outside the Earth–Moon fusion region (E–M outer space).
2.3.2. Hamiltonian
2.3.3.
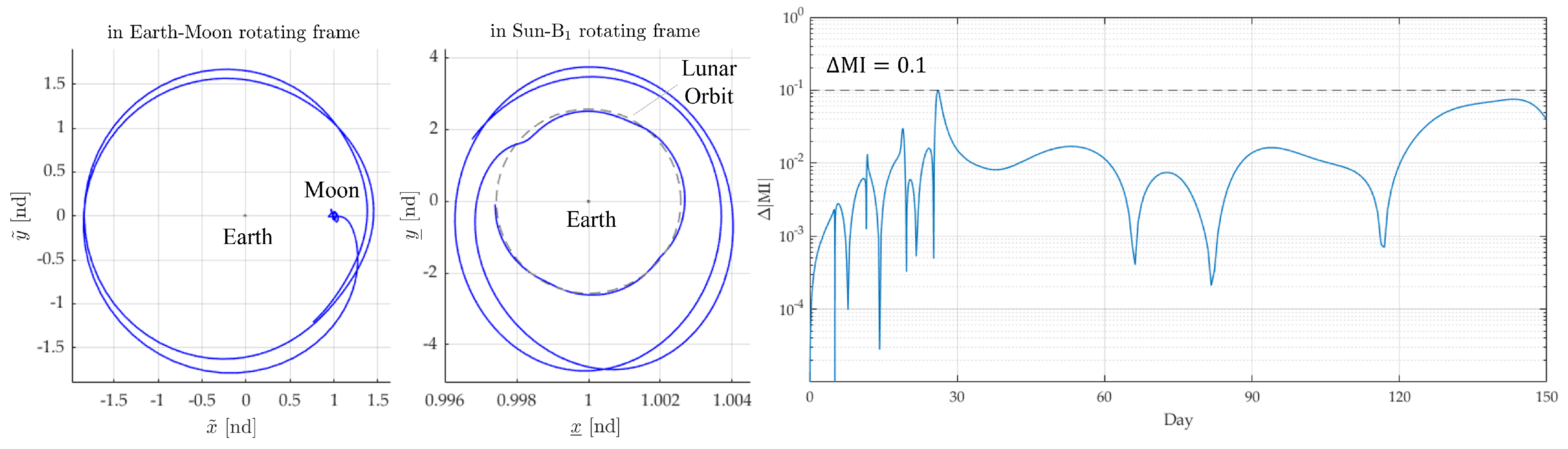
2.4. Momentum Integral
3. Algorithms of Departure Evaluation
3.1. Classification of Cislunar Space
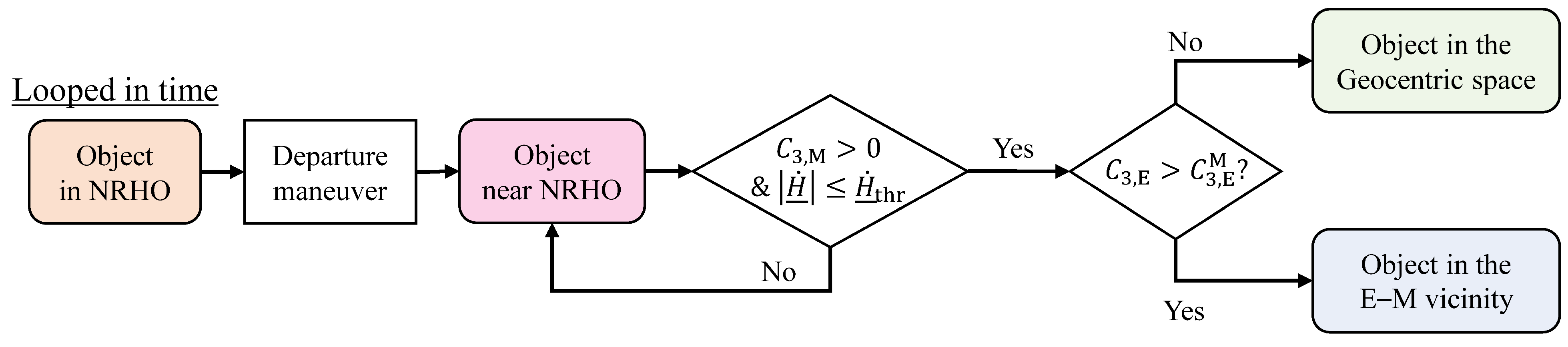
3.2. Criteria of Divergence Instance
3.2.1. Departure to Geocentric Space
3.2.2. Departure to Earth–Moon Vicinity
3.2.3. Departure to Heliocentric Space
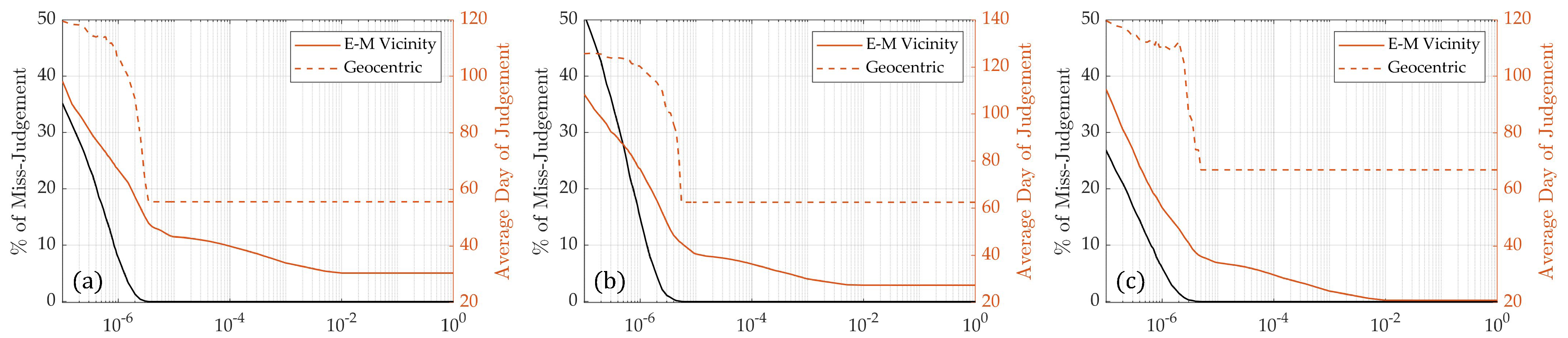
4. Result: Time to Depart from NRHOs
4.1. Calculation Environment
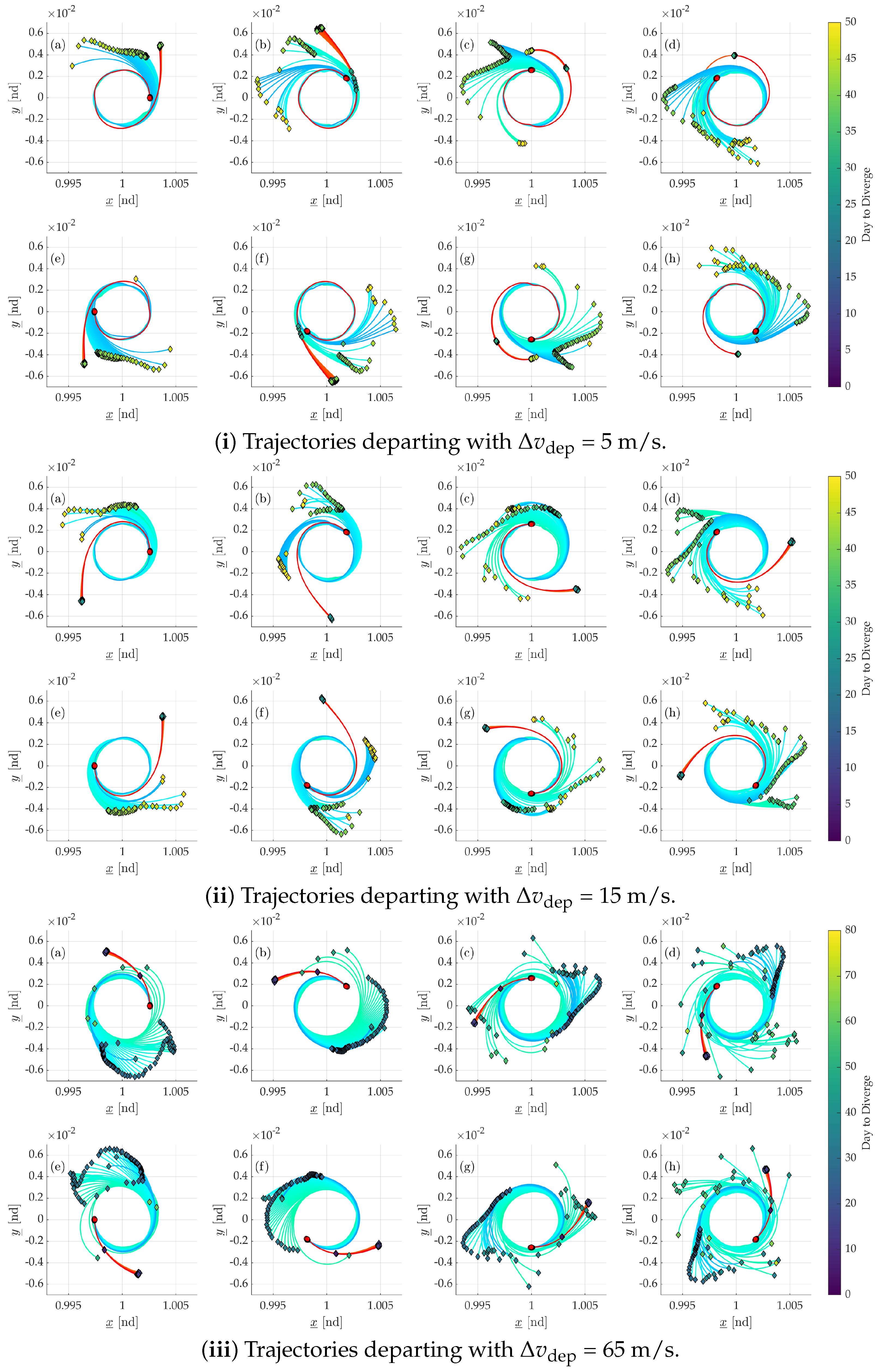
4.2. Analysis 1: Empirical Validation of the Algorithm
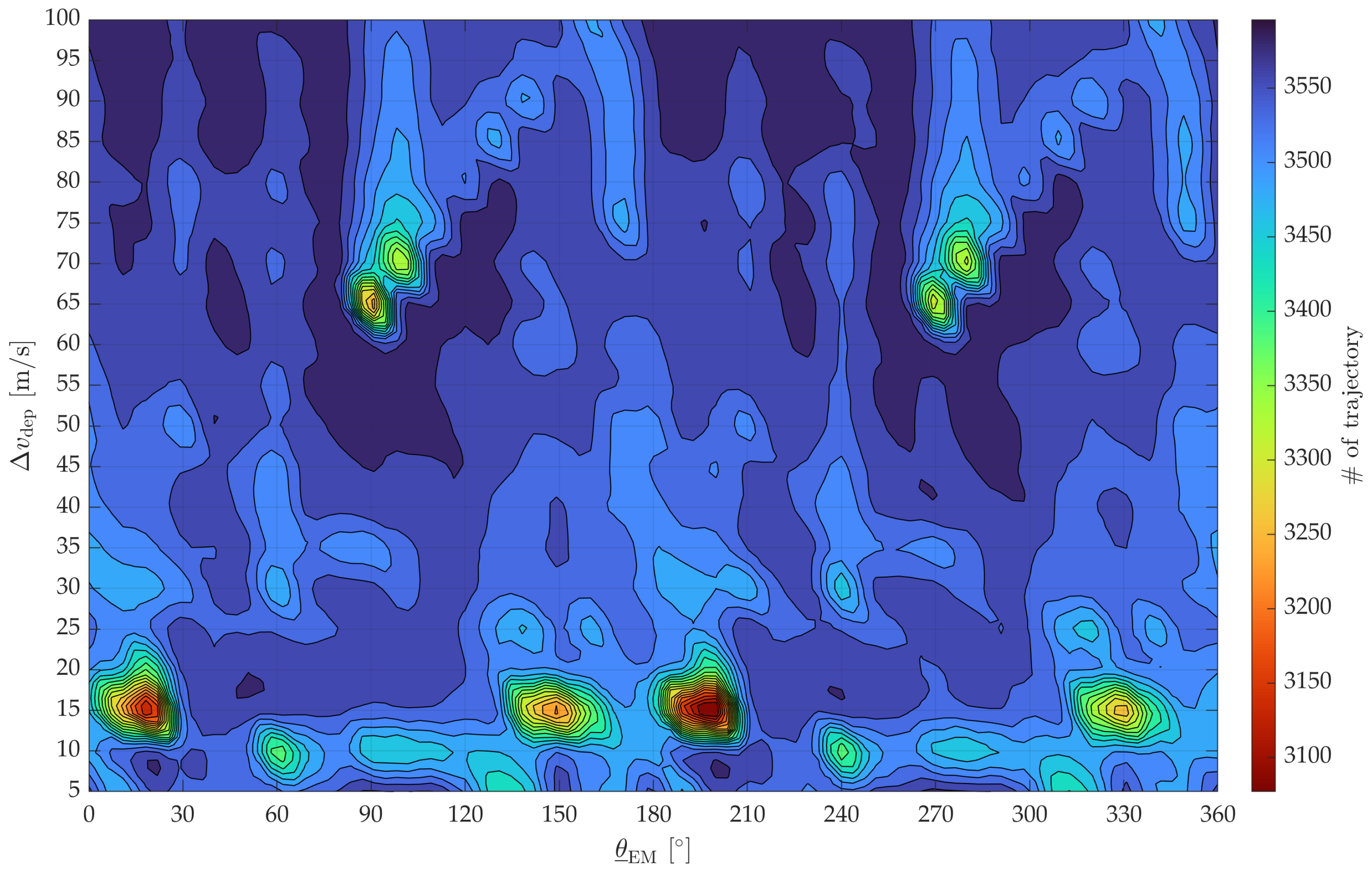
4.3. Analysis 2: Changes in Divergence Behavior Due to the Sun’s Phase Angle
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Fuller, S.; Lehnhardt, E.; Zaid, C.; Halloran, K. Gateway program status and overview. J. Space Saf. Eng. 2022, 9, 625–628. [Google Scholar] [CrossRef]
- Williams, J.; Lee, D.E.; Whitley, R.J.; Bokelmann, K.A.; Davis, D.C.; Berry, C.F. Targeting Cislunar Near Rectilinear Halo Orbits for Human Space Exploration. In Proceedings of the AAS/AIAA Space Flight Mechanics Meeting, San Antonio, TX, USA, 5–9 February 2017. [Google Scholar]
- Boudad, K.K.; Howell, K.C.; Davis, D.C. Dynamics of synodic resonant near rectilinear halo orbits in the bicircular four-body problem. Adv. Space Res. 2020, 66, 2194–2214. [Google Scholar] [CrossRef]
- Howell, K.C.; Breakwell, J.V. Almost rectilinear halo orbits. Celest. Mech. 1984, 32, 29–52. [Google Scholar] [CrossRef]
- Boudad, K.K.; Howell, K.C.; Davis, D.C. Departure and Escape Dynamics from the Near Rectilinear Halo Orbits in the Earth-Moon-Sun System. J. Astronaut. Sci. 2022, 69, 1076–1114. [Google Scholar] [CrossRef]
- Annat, P.; Beal, C.; Verniere, J.; Felin, A.; Pinede, R.; Jaubeat, J.; Moussi, A. Hera Cubesats Trajectory Design and ConOps for Didymos Binary Asteroid Characterization. In Proceedings of the Small Satellite Conference, Utah State University, Logan, UT, USA, 1–3 August 2024. [Google Scholar]
- Tanaka, K.; Kawaguchi, J. Small-amplitude Periodic Orbit around Sun-Earth L1/L2 Controlled by Solar Radiation Pressure. Trans. JSASS Aerosp. Technol. Japan 2016, 59, 33–42. [Google Scholar] [CrossRef]
- Sánchez, J.P.; Morante, D.; Hermosin, P.; Ranuschio, D.; Eatalella, A.; Viera, D.; Centuori, S.; Jones, G.; Snodgrass, C.; Levasseur-Regourd, A.C.; et al. ESA F-Class Comet Interceptor: Trajectory design to intercept a yet-to-be-discovered comet. Acta Astronaut. 2021, 188, 265–277. [Google Scholar] [CrossRef]
- Saito, Y.; Kameyama, S.; Kuwahara, T. Simplified Data-Reduction Method for Hybrid Propulsion. J. Propuls. Power 2024, 40, 490–496. [Google Scholar] [CrossRef]
- Saito, T.; Kuwahara, T.; Saito, Y.; Sato, Y. Guidance strategies for controlled Earth reentry of small spacecraft in low Earth orbit. Acta Astronaut. 2025, 229, 684–697. [Google Scholar] [CrossRef]
- Komachi, S.; Fujita, S.; Takeda, K.; Nakaoka, H.; Kuwahara, T.; Yoshida, K.; Kawaguchi, J. Safe Attitude and Orbit Control for ISS-Deployed CubeSat HOKUSHIN-1 with Cold-Gas Propulsion System. In Proceedings of the 2024 IEEE/SICE International Symposium on System Integration (SII), Ha Long, Vietnam, 8–11 January 2024. [Google Scholar] [CrossRef]
- Kawaguchi, J.; Nada, Y.; Ishigooka, Y.; Kuwahara, T.; Yoshida, K. Asynchronous One-Way Range Measurement Applied to Microspace Probes. J. Spacecr. Rocket. 2022, 59, 1602–1612. [Google Scholar] [CrossRef]
- Kawaguchi, J.; Fujita, M.; Fujita, S.; Sakamoto, Y.; Kuwahara, T.; Yoshida, K.; Nishimoto, S.; Takeda, K.; Komachi, S.; Hayato, K. On the low-cost asynchronous one-way range measurement method and the device for micro to nano deep space probes. Acta Astronaut. 2024, 214, 457–465. [Google Scholar] [CrossRef]
- Oguri, K.; Oshima, K.; Campagnola, S.; Kakihara, K.; Ozaki, N.; Baresi, N.; Kawakatsu, Y.; Funase, R. EQUULEUS Trajectory Design. J. Astronaut. Sci. 2020, 67, 950–976. [Google Scholar] [CrossRef]
- Vaquero, M.; Howell, K.C. Leveraging Resonant-Orbit Manifolds to Design Transfers Between Libration-Point Orbits. J. Guid. Control. Dyn. 2014, 37, 1143–1157. [Google Scholar] [CrossRef]
- Nakazawa, K.; Takeda, K.; Komachi, S.; Fujita, S.; Kuwahara, T. Constructing Earth-Moon Data Relay System: Trajectory Design of Ballistic Lunar Transfer for Nano Spacecraft. In Proceedings of the 2023 IEEE/SICE International Symposium on System Integration (SII), Atlanta, GA, USA, 17–20 January 2023. [Google Scholar] [CrossRef]
- Farquhar, R.W. Utilization of Multi-Body Trajectories in the Sun-Earth-Moon System; NASA Technical Memorandum 80740; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1980. Available online: https://ntrs.nasa.gov/citations/19800022786 (accessed on 24 January 2025).
- Farquhar, R.W.; Dunham, D.W.; Hsu, S.C. Orbital acrobatics in the Sun-Earth-Moon system. In Proceedings of the International Symposium on Spacecraft Flight Dynamics, Toulouse, France, 20–23 December 1986. [Google Scholar]
- Short, C.R.; Blazevski, D.; Howell, K.C.; Haller, G.H. Stretching in phase space and applications in general nonautonomous multi-body problems. Celest. Mech. Dyn. Astron. 2015, 122, 213–238. [Google Scholar] [CrossRef]
- Guzzetti, D.; Zimovan, E.M.; Howell, K.C.; Davis, D.C. Stationkeeping Analysis for Spacecraft in Lunar Near Rectilinear Halo Orbits. In Proceedings of the Space Flight Mechanics Meeting, San Antonio, TX, USA, 5–9 February 2017. [Google Scholar]
- Muralidharan, V.; Howell, K.C. Stretching directions in cislunar space: Applications for departures and transfer design. Astrodynamics 2023, 7, 153–178. [Google Scholar] [CrossRef]
- Oshima, K. Retrograde co-orbital orbits in the Earth-Moon system: Planar stability region under solar gravitational perturbation. Astrophys. Space Sci. 2021, 366, 88. [Google Scholar] [CrossRef]
- Oshima, K. Extended analysis on stability, capture, and escape for planar retrograde periodic orbit around Earth. Astrophys. Space Sci. 2025, 370, 48. [Google Scholar] [CrossRef]
- Zimovan-Spreen, E.M.; Howell, K.C.; Davis, D.C. Near rectilinear halo orbits and nearby higher-period dynamical structures: Orbital stability and resonance properties. Celest. Mech. Dyn. Astron. 2020, 132, 28. [Google Scholar] [CrossRef]
- Fu, S.; Liang, Y.; Wu, D.; Gong, S. Low-energy Earth-Moon transfers with lunar ballistic capture based on Lagrangian coherent structures in a four-body model. Adv. Space Res. 2025, 75, 4993–5013. [Google Scholar] [CrossRef]
- Szebehely, V.; Grebenikov, E. Theory of Orbits, the Restricted Problem of Three Bodies; Academic Press: New York, NY, USA, 1967. [Google Scholar] [CrossRef]
- Howell, K.C. Three-dimensional, periodic, ‘halo’ orbits. Celest. Mech. 1984, 32, 53–71. [Google Scholar] [CrossRef]
- Koon, W.S.; Lo, M.W.; Marsden, J.E.; Ross, S.D. Dynamical Systems, the Three-Body Problem and Space Mission Design, 3rd ed.; Marsden Books: Wellington, New Zealand, 2011; pp. 24–41. [Google Scholar] [CrossRef]
- Meyer, K.R.; Offin, D.C. Introduction to Hamiltonian Dynamical Systems and the N-Body Problem, 3rd ed.; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Yamakawa, H. On Earth-Moon Transfer Trajectory with Gravitational Capture. Ph.D. Dissertation, University of Tokyo, Tokyo, Japan, 1992; pp. 175–188. [Google Scholar]
- Curtis, H.D. Orbital Mechanics for Engineering Students, 4th ed.; Butterworth-Heinemann: Oxford, UK, 2020; pp. 93–98. [Google Scholar] [CrossRef]
- Boudad, K.K.; Davis, D.C.; Howell, K.C. Disposal Trajectories from Near Rectilinear Halo Orbits. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Snowbird, UT, USA, 19–23 August 2018. [Google Scholar]
- Belbruno, E.; Carrico, J. Calculation of weak stability boundary ballistic lunar transfer trajectories. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar] [CrossRef]
- Scheuerle, S.T.; Howell, K.C.; Davis, D.C. Energy-informed pathways: A fundamental approach to designing ballistic lunar transfers. Adv. Space Res. 2024, 75, 1096–1117. [Google Scholar] [CrossRef]
- Scheuerle, S.T. Low-Energy Lunar Transfers in the Bicircular Restricted Four-Body Problem. Ph.D. Dissertation, Purdue University, West Lafayette, IN, USA, 2024. [Google Scholar]
- Castelli, R. Regions of Prevalence in the Coupled Restricted Three-Body Problems Approximation. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 804–816. [Google Scholar] [CrossRef]
- Boost C++ Libraries. Boost 1.85.0 Library Documentation. Available online: https://www.boost.org/doc/libs/1_85_0 (accessed on 24 January 2025).
- Boost C++ Libraries. Class Template Runge Kutta fehlberg78. Available online: https://beta.boost.org/doc/libs/1_74_0/libs/numeric/odeint/doc/html/boost/numeric/odeint/runge_kutta_fehlberg78.html (accessed on 24 January 2025).
- The MathWorks, Inc. MATLAB Version: 24.1.0.2628055 (R2024a). Available online: https://www.mathworks.com/ (accessed on 24 January 2025).
- The MathWorks, Inc. MATLAB MEX File Functions. Available online: https://jp.mathworks.com/help/matlab/ref/mex.html (accessed on 24 January 2025).
- Takubo, Y.; Shimane, Y.; Ho, K. Optimization of Earth-Moon Low-Thrust-Enhanced Low-Energy Transfer. In Proceedings of the AAS/AIAA Astrodynamics Specialist Conference, Big Sky, MT, USA, 13–17 August 2023. [Google Scholar]
- Capuzzo-Dolcetta, R.; Giancotti, M. A study of low-energy transfer orbits to the Moon: Towards an operational optimization technique. Celest. Mech. Dyn. Astron. 2013, 115, 215–232. [Google Scholar] [CrossRef]
- Folkner, W.M.; Williams, J.G.; Boggs, D.H.; Park, R.S.; Kuchynka, P. The Planetary and Lunar Ephemerides DE430 and DE431. Interplanet. Netw. Prog. Rep. 2014, 42–196, 1–81. Available online: https://ipnpr.jpl.nasa.gov/progress_report/42-196/196C.pdf (accessed on 24 January 2025).
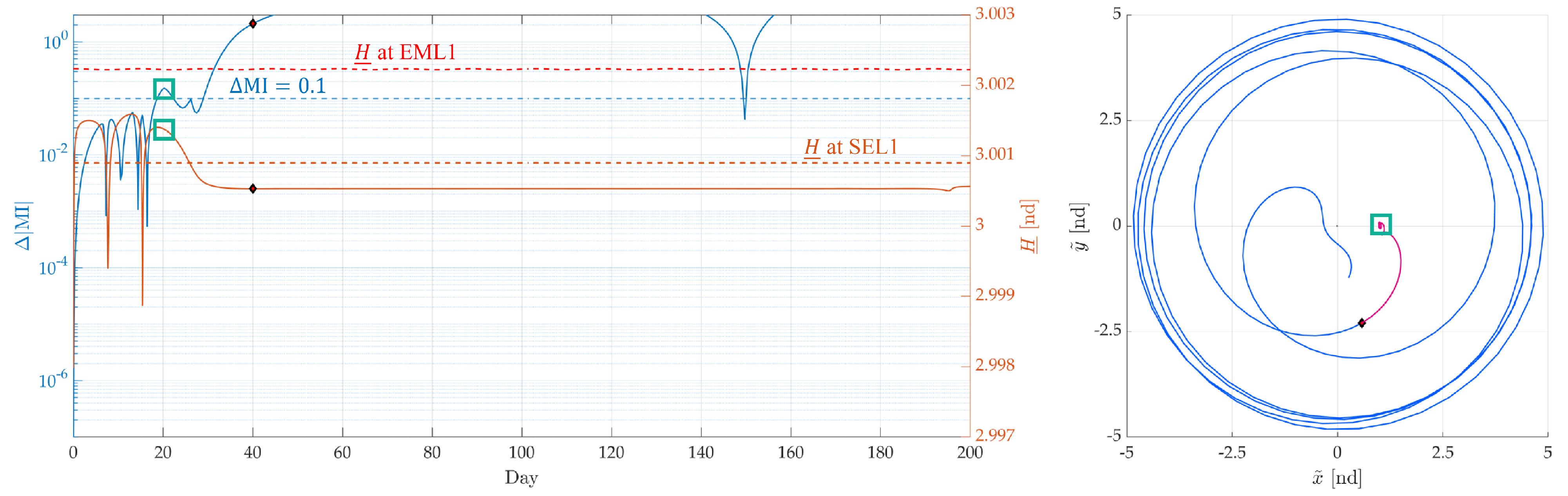
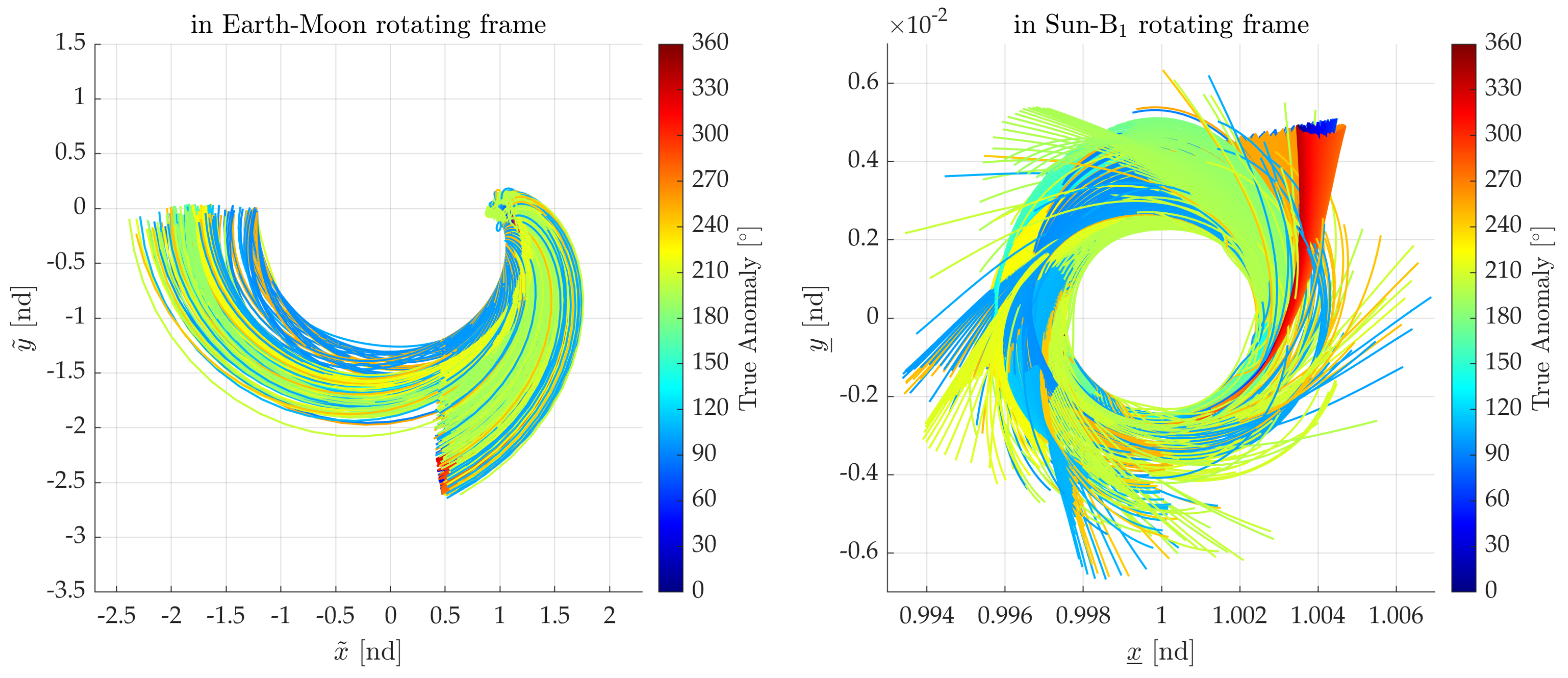
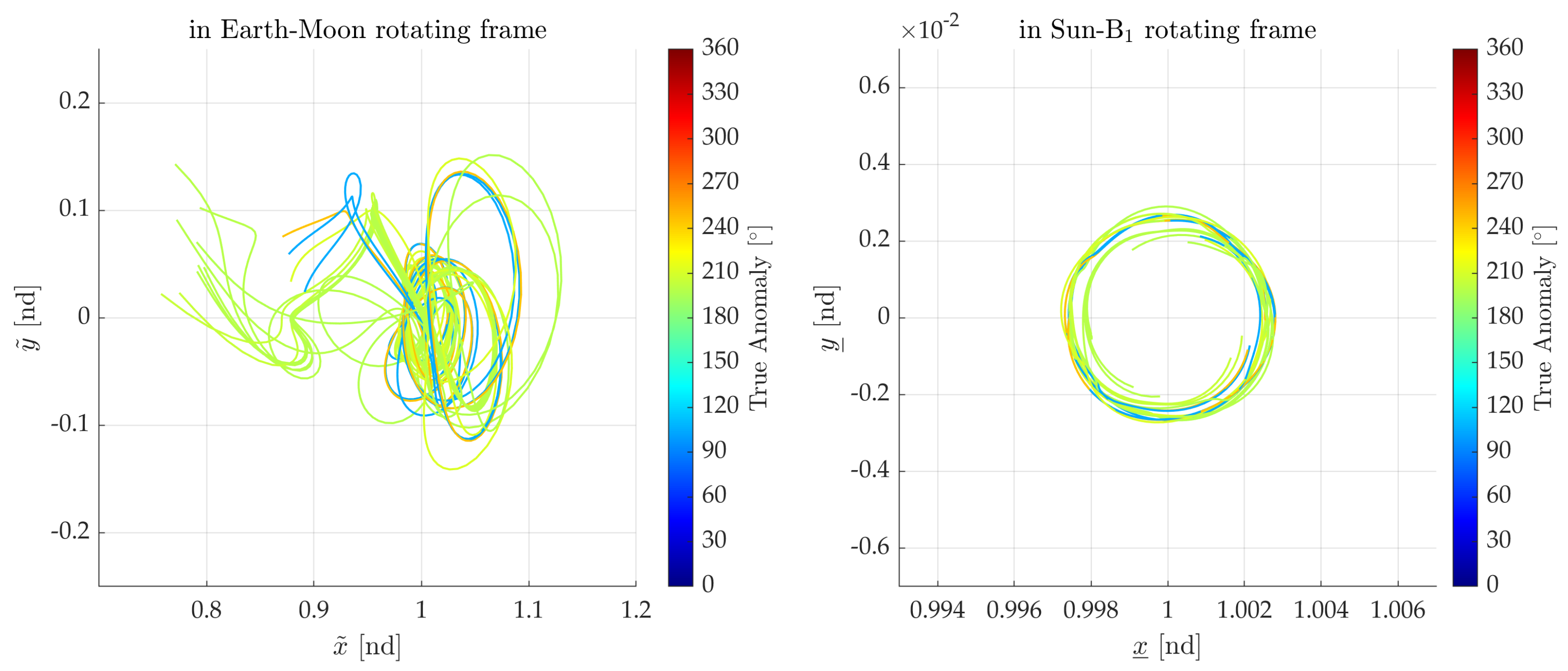
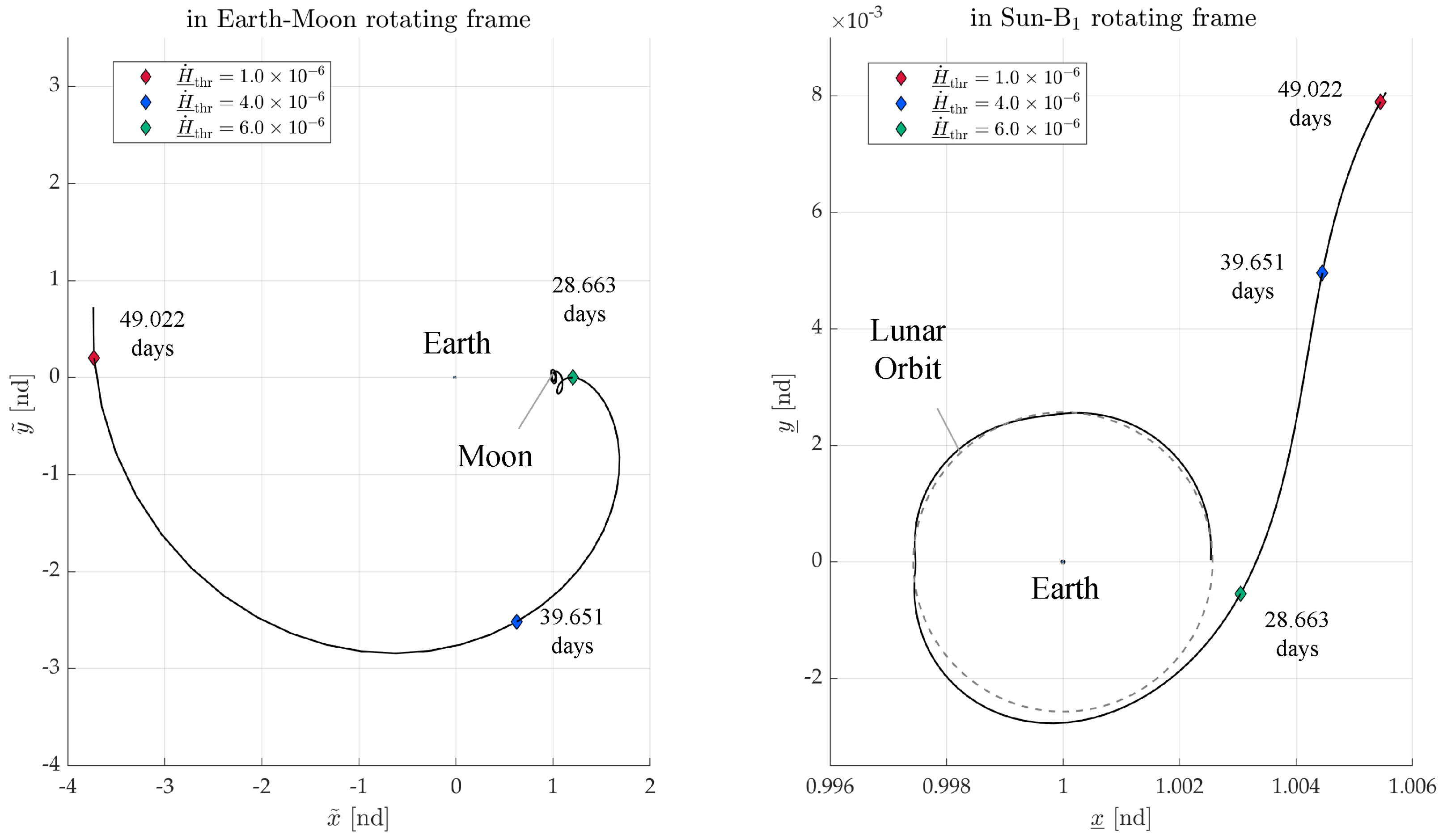
| Lagrange Point | Value |
|---|---|
| EML1 | 3.002236 |
| EML2 | 3.000834 |
| SEL1 | 3.000898 |
| SEL2 | 3.000895 |
| Analysis 1 | Analysis 2 | ||||
|---|---|---|---|---|---|
| Preference | Value | # of Grid | Value | # of Grid | Unit |
| TA | 0.0 to 359.9 | 3600 | 0.0 to 359.9 | 3600 | |
| 5.0 to 100.0 | 7 | 5.0 to 100.0 | 20 | m/s | |
| 0.0 (fixed) | 1 | 0.0 to 360.0 | 37 | ||
| # of Trajectories | Average Day to Diverge | |||||
|---|---|---|---|---|---|---|
| [m/s] | E–M Vic. | Heliocentric | Geocentric | E–M Vic. | Heliocentric | Geocentric |
| 5.0 | 3566 | 2590 | 13 | 45.348 | 58.557 | 55.669 |
| 10.0 | 3498 | 2101 | 6 | 44.471 | 78.095 | 62.582 |
| 15.0 | 3483 | 2833 | 7 | 35.753 | 43.286 | 66.975 |
| 20.0 | 3508 | 2571 | 3 | 34.174 | 49.863 | 59.159 |
| 25.0 | 3536 | 2305 | 2 | 33.296 | 72.915 | 74.202 |
| 50.0 | 3526 | 2173 | 1 | 25.523 | 91.116 | 51.392 |
| 100.0 | 2976 | 2590 | 0 | 17.761 | 33.969 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takeda, K.; Kuwahara, T. Divergence Evaluation Criteria for Lunar Departure Trajectories Under Bi-Circular Restricted Four-Body Problem. Aerospace 2025, 12, 918. https://doi.org/10.3390/aerospace12100918
Takeda K, Kuwahara T. Divergence Evaluation Criteria for Lunar Departure Trajectories Under Bi-Circular Restricted Four-Body Problem. Aerospace. 2025; 12(10):918. https://doi.org/10.3390/aerospace12100918
Chicago/Turabian StyleTakeda, Kohei, and Toshinori Kuwahara. 2025. "Divergence Evaluation Criteria for Lunar Departure Trajectories Under Bi-Circular Restricted Four-Body Problem" Aerospace 12, no. 10: 918. https://doi.org/10.3390/aerospace12100918
APA StyleTakeda, K., & Kuwahara, T. (2025). Divergence Evaluation Criteria for Lunar Departure Trajectories Under Bi-Circular Restricted Four-Body Problem. Aerospace, 12(10), 918. https://doi.org/10.3390/aerospace12100918






