SynthATDelays: A Minimalist Python Package for the Generation of Synthetic Air Transport Delay Data
Abstract
1. Introduction
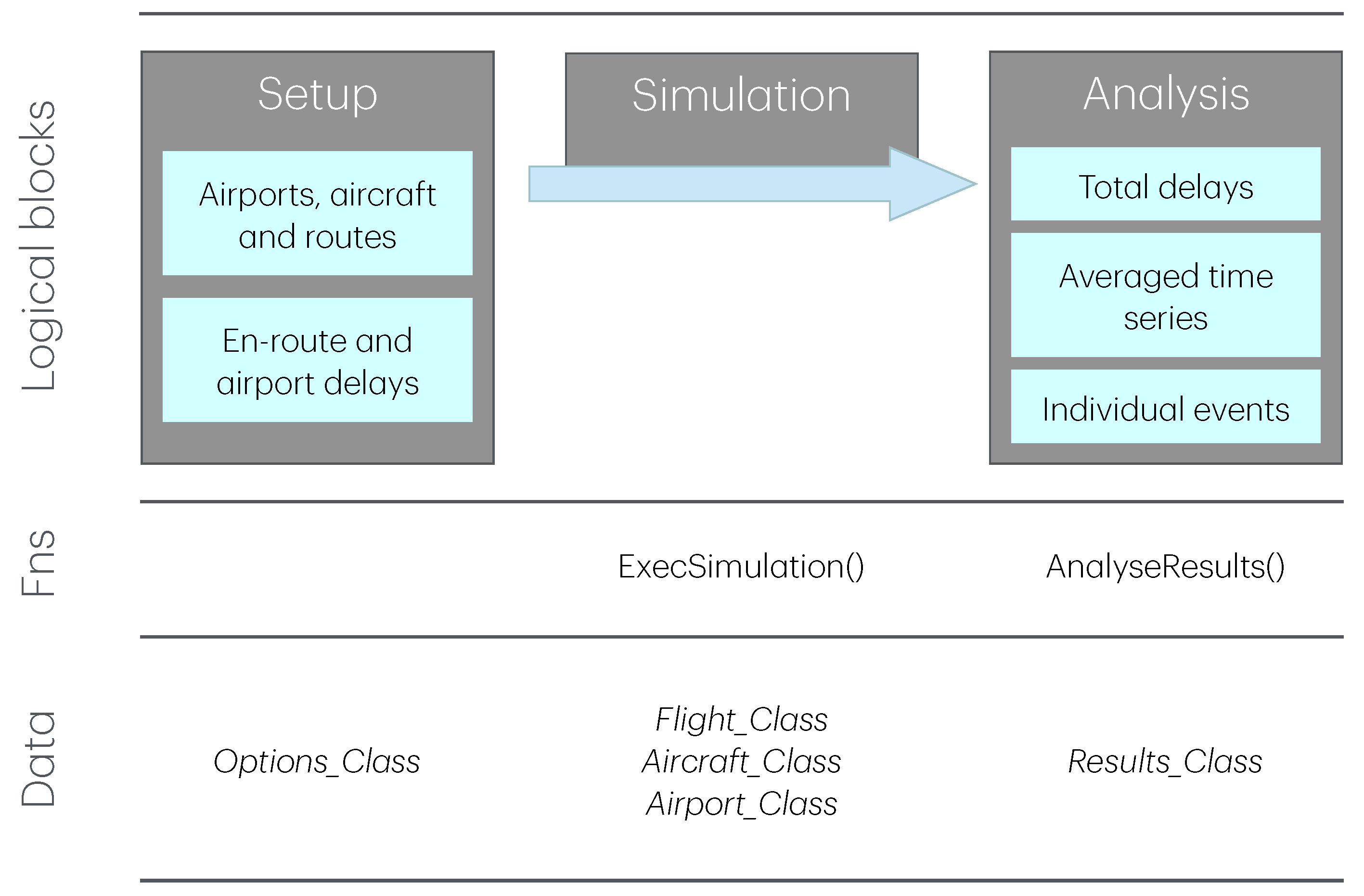
2. The Structure and Internal Logic of the Package
2.1. Setting Up the Simulation
- Airports, including their number, their capacity (in operations per hour), and the flight time required to travel between them. Note that geographical information is not modelled; it is therefore possible to model non-Euclidean networks of flights.
- Aircraft, including their number, the minimum turnaround time between subsequent operations, and the buffer time left to recover delays.
- The route operated by each aircraft, defined as a list of airports that are visited sequentially. This allows, for instance, to define simple hub-and-spoke operations (e.g., ), more complex variations of the same (e.g., ), or triangular routes (e.g., ).
- Delay generation. Delays can be defined to either affect flights on specific routes or all flights landing at specific airports. The package provides several predefined functions to calculate their magnitude, including the use of delay profiles synthesised from real operations at major European airports; alternatively, the user can define custom ones—see the documentation for details and examples [36].
- Dependencies between routes. These model situations in which two flights operate different routes with one airport in common (e.g., and ), such that the latter cannot take off until the former has landed. They can thus be used to simulate the presence of connecting passengers, or the crew having to change aircraft. This further allows for modelling the propagation of delays between airports that are not directly connected by a flight.
- Additional options, including, e.g., the duration of nights, i.e., of a period in which flights cannot operate; or the number of days to be simulated.
2.2. The Simulation
- If the aircraft is idle, find its first scheduled flight not already executed; if its scheduled departure time is less than or equal to t, the aircraft is added to the airport queue, which is used to account for its limited capacity. The program also checks for dependencies, and the flight is activated only if the preceding one has already landed. The actual landing time is calculated by adding the distance between the departure and arrival airports and any other en-route or airport delays defined in the options of the scenario. Finally, the status of the aircraft is updated to airborne.
- If the aircraft is airborne and the current time t is equal or greater than the landing time, the status of the aircraft is changed to that corresponding to the turnaround process.
- Finally, if the aircraft is performing the turnaround and the time passed is greater than the minimum turnaround time, the status of the aircraft is changed back to idle, and the whole process repeats.
2.3. Analysis of the Results
3. Examples
3.1. Step-by-Step Tutorial
| Listing 1: Basic initialisation code, using one of the predefined scenarios. |
 |
| Listing 2: Call to the function to execute the simulation, taking as input the options created in Listing 1. |
 |
| Listing 3: Code to define enroute delays, execute the simulation, and finally extracting high-level results about the delay evolution. |
 |
| Listing 4: Definition of airport-based delays. |
 |
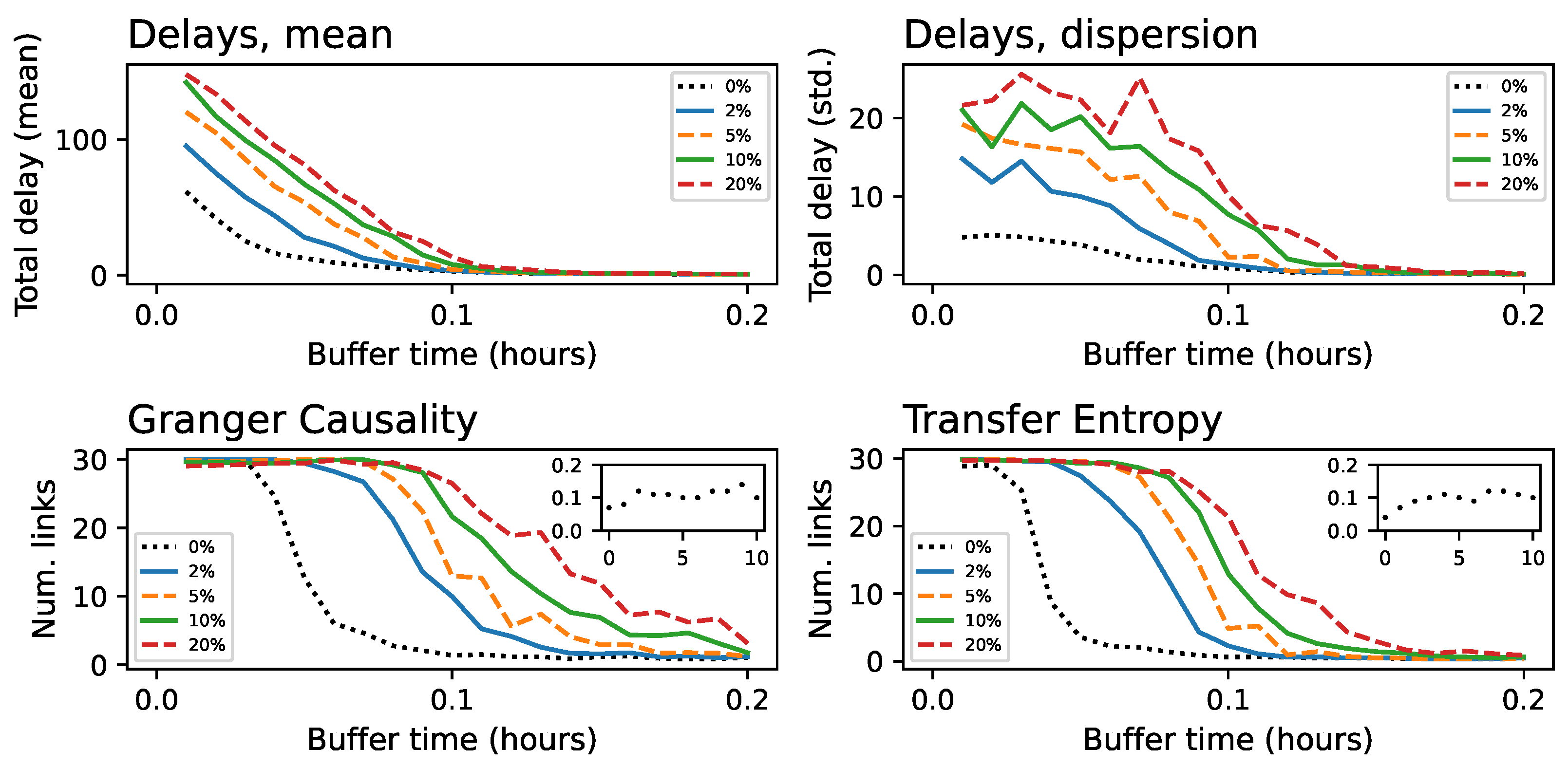
3.2. What Is the Impact of the Buffer Time and of Links Between Flights?
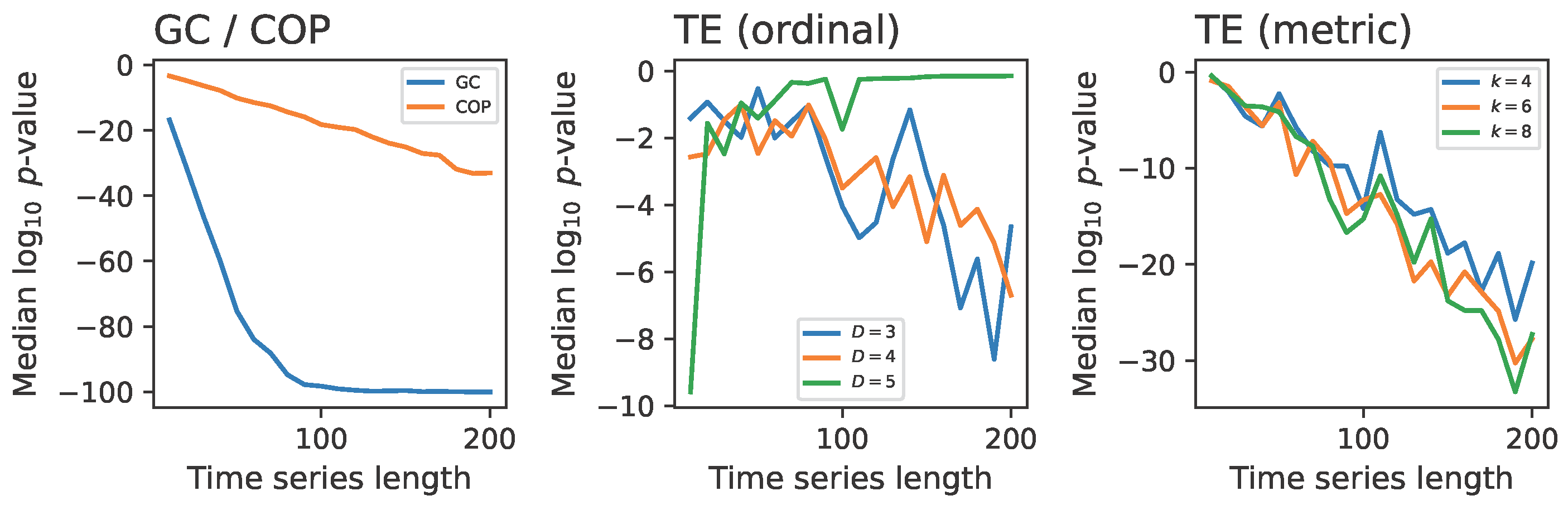
3.3. Which Functional Metric Ought to Be Used?
- Granger Causality (GC). The GC test was initially proposed to test for causal relations in economic time series, but has since found wide-ranging applications in various scientific and technical fields [37,38]. It is based on the idea of “predictive causality” [39], i.e., situations in which past values of one time series provide statistically significant information about future values of another time series beyond what is explained by the past values of the latter. The test compares two linear models: a restricted model that predicts future values using only its own past delays and an unrestricted model that incorporates past values from the second time series. Whenever the latter has a higher prediction accuracy, it is said that the latter time series “Granger-causes” the former one. Note that, in spite of its popularity, it is strictly not a test for causality, as highlighted by Granger himself [40]; or, to use the words of Ref. [41], “Granger causality is designed to measure effect, not mechanism”.
- Continuous Ordinal Patterns (COPs). This is a method based on pre-processing the time series under analysis using Continuous Ordinal Patterns (COPs) [42] to then apply the same GC test as described above [43]. COPs are patterns (here of length 4) that are compared against sub-windows of the original time series; they thus quantify the presence of specific non-linear structures, making these explicit for the GC test, and hence overcoming the linear nature of the latter.
- Transfer Entropy (TE). The TE from X to Y is defined as the amount of uncertainty reduced in the future values of Y by knowing the past values of X, after considering the past values of Y [44]. Such uncertainty is calculated as an entropy, which is in turn calculated using two estimators of the underlying probability distributions.
- Ordinal estimator: the probability distribution is obtained by mapping the time series into an ordinal space, created by “permutation patterns”—i.e., the rank order of values inside small sub-windows of the original series [45]. We here consider pattern lengths (also called embedding dimensions) of , 4, and 5.
- Metric estimator: this approach, also called the Kozachenko–Leonenko estimator [46], uses a nearest-neighbours approach to estimate the entropy of a continuous random variable as the expectation of the logarithm of the density. We here use , 6, and 8 nearest neighbours.
The implementation of this metric corresponds to the one included in the infomeasure Python package [47].
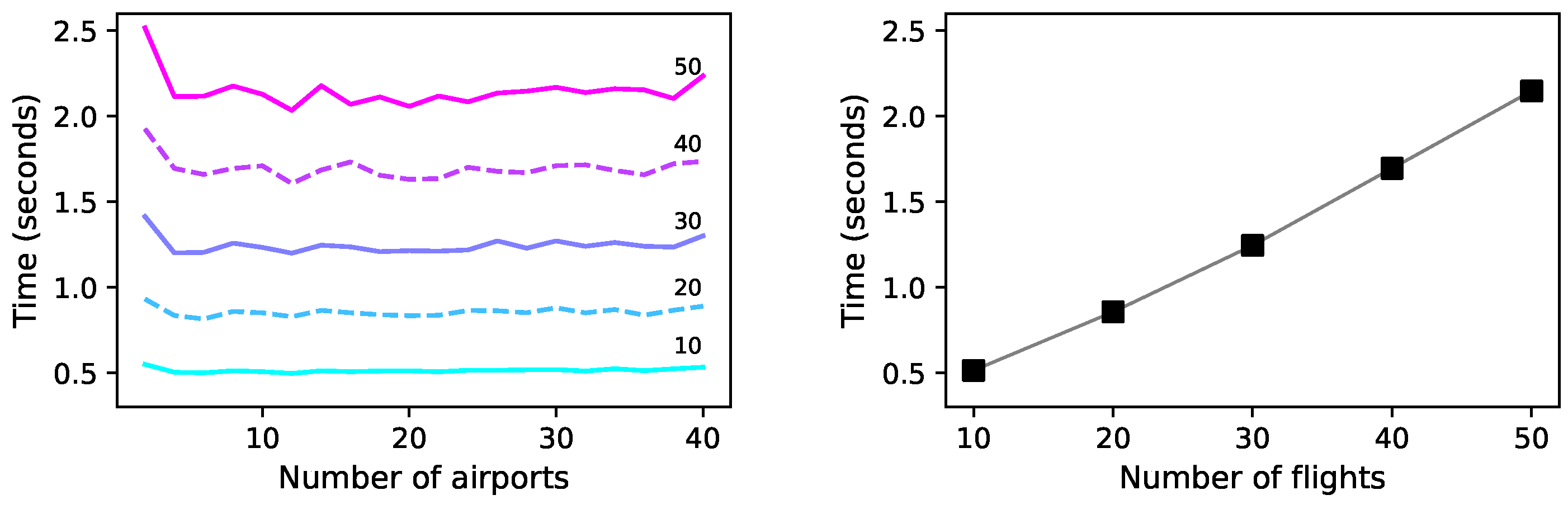
4. Additional Technical Considerations
5. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Carlier, S.; De Lépinay, I.; Hustache, J.C.; Jelinek, F. Environmental impact of air traffic flow management delays. In Proceedings of the 7th USA/Europe Air Traffic Management Research and Development Seminar (ATM2007), Barcelona, Spain, 2–5 July 2007; Volume 2, p. 16. [Google Scholar]
- Peterson, E.B.; Neels, K.; Barczi, N.; Graham, T. The economic cost of airline flight delay. J. Transp. Econ. Policy 2013, 47, 107–121. [Google Scholar]
- Cao, Y.; Zhu, C.; Wang, Y.; Li, Q. A method of reducing flight delay by exploring internal mechanism of flight delays. J. Adv. Transp. 2019, 2019, 7069380. [Google Scholar] [CrossRef]
- Wang, Y.; Cao, Y.; Zhu, C.; Wu, F.; Hu, M.; Duong, V.; Watkins, M.; Barzel, B.; Stanley, H.E. Universal patterns in passenger flight departure delays. Sci. Rep. 2020, 10, 6890. [Google Scholar] [CrossRef]
- Mitsokapas, E.; Schäfer, B.; Harris, R.J.; Beck, C. Statistical characterization of airplane delays. Sci. Rep. 2021, 11, 7855. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Liao, C.; Hang, X.; Li, L.; Delahaye, D.; Hansen, M. Distribution prediction of strategic flight delays via machine learning methods. Sustainability 2022, 14, 15180. [Google Scholar] [CrossRef]
- Olivares, F.; Zanin, M. Quantifying Deviations from Gaussianity with Application to Flight Delay Distributions. Entropy 2025, 27, 354. [Google Scholar] [CrossRef]
- Schultz, M.; Lorenz, S.; Schmitz, R.; Delgado, L. Weather impact on airport performance. Aerospace 2018, 5, 109. [Google Scholar] [CrossRef]
- Zanin, M.; Zhu, Y.; Yan, R.; Dong, P.; Sun, X.; Wandelt, S. Characterization and prediction of air transport delays in China. Appl. Sci. 2020, 10, 6165. [Google Scholar] [CrossRef]
- de Oliveira, M.; Eufrásio, A.B.R.; Guterres, M.X.; Murça, M.C.R.; de Arantes Gomes, R. Analysis of airport weather impact on on-time performance of arrival flights for the Brazilian domestic air transportation system. J. Air Transp. Manag. 2021, 91, 101974. [Google Scholar] [CrossRef]
- Rodríguez-Sanz, Á.; Cano, J.; Rubio Fernandez, B. Impact of weather conditions on airport arrival delay and throughput. Aircr. Eng. Aerosp. Technol. 2022, 94, 60–78. [Google Scholar] [CrossRef]
- Zanin, M. Can we neglect the multi-layer structure of functional networks? Phys. A Stat. Mech. Its Appl. 2015, 430, 184–192. [Google Scholar] [CrossRef]
- Pastorino, L.; Zanin, M. Air delay propagation patterns in Europe from 2015 to 2018: An information processing perspective. J. Phys. Complex. 2021, 3, 015001. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, S.; Mei, H. Analysis of airport risk propagation in Chinese air transport network. J. Adv. Transp. 2022, 2022, 9958810. [Google Scholar] [CrossRef]
- Pastorino, L.; Zanin, M. Local and Network-Wide Time Scales of Delay Propagation in Air Transport: A Granger Causality Approach. Aerospace 2023, 10, 36. [Google Scholar] [CrossRef]
- Chen, S.; Du, W.; Liu, R.; Cao, X. Finding spatial and temporal features of delay propagation via multi-layer networks. Phys. A Stat. Mech. Its Appl. 2023, 614, 128526. [Google Scholar] [CrossRef]
- Rebollo, J.J.; Balakrishnan, H. Characterization and prediction of air traffic delays. Transp. Res. Part C Emerg. Technol. 2014, 44, 231–241. [Google Scholar] [CrossRef]
- Monmousseau, P.; Delahaye, D.; Marzuoli, A.; Féron, E. Predicting and analyzing US air traffic delays using passenger-centric data-sources. In Proceedings of the ATM 2019, 13th USA/Europe Air Traffic Management Research and Development Seminar, Vienna, Austria, 17–21 June 2019. [Google Scholar]
- Liu, Y.; Liu, Y.; Hansen, M.; Pozdnukhov, A.; Zhang, D. Using machine learning to analyze air traffic management actions: Ground delay program case study. Transp. Res. Part E Logist. Transp. Rev. 2019, 131, 80–95. [Google Scholar] [CrossRef]
- Huynh, T.K.; Cheung, T.; Chua, C. A systematic review of flight delay forecasting models. In Proceedings of the 2024 7th International Conference on Green Technology and Sustainable Development (GTSD), Ho Chi Minh City, Vietnam, 25–26 July 2024; pp. 533–540. [Google Scholar]
- Grether, D.; Fürbas, S.; Nagel, K. Agent-based modelling and simulation of air transport technology. Procedia Comput. Sci. 2013, 19, 821–828. [Google Scholar] [CrossRef][Green Version]
- Delgado, L.; Gurtner, G.; Weiszer, M.; Bolic, T.; Cook, A. Mercury: An open source platform for the evaluation of air transport mobility. In Proceedings of the 13th SESAR Innovation Days, Seville, Spain, 27–30 November 2023. [Google Scholar][Green Version]
- Hoekstra, J.M.; Ellerbroek, J. Bluesky ATC simulator project: An open data and open source approach. In Proceedings of the 7th International Conference on Research in Air Transportation, Philadelphia, PA, USA, 20–24 June 2016; Volume 131, p. 132. [Google Scholar][Green Version]
- Hui, K.Y.; Nguyen, C.H.; Lui, G.N.; Liem, R.P. AirTrafficSim: An open-source web-based air traffic simulation platform. J. Open Source Softw. 2023, 8, 4916. [Google Scholar] [CrossRef]
- Lin, Y.; Zhang, J.W.; Liu, H. Deep learning based short-term air traffic flow prediction considering temporal—Spatial correlation. Aerosp. Sci. Technol. 2019, 93, 105113. [Google Scholar] [CrossRef]
- Yan, Z.; Yang, H.; Li, F.; Lin, Y. A deep learning approach for short-term airport traffic flow prediction. Aerospace 2021, 9, 11. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Lü, J.; Liu, K.; Zhu, A.; Snoussi, H.; Zhang, B. Synchronous spatiotemporal graph transformer: A new framework for traffic data prediction. IEEE Trans. Neural Netw. Learn. Syst. 2022, 34, 10589–10599. [Google Scholar] [CrossRef]
- Xu, Q.; Pang, Y.; Liu, Y. Air traffic density prediction using Bayesian ensemble graph attention network (BEGAN). Transp. Res. Part C Emerg. Technol. 2023, 153, 104225. [Google Scholar] [CrossRef]
- Chen, X.; Yu, H.; Cao, K.; Zhou, J.; Wei, T.; Hu, S. Uncertainty-aware flight scheduling for airport throughput and flight delay optimization. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 853–862. [Google Scholar] [CrossRef]
- Wei, M.; Yang, S.; Wu, W.; Sun, B. A multi-objective fuzzy optimization model for multi-type aircraft flight scheduling problem. Transport 2024, 39, 313–322. [Google Scholar] [CrossRef]
- Xu, Y.; Wandelt, S.; Sun, X. Airline scheduling optimization: Literature review and a discussion of modelling methodologies. Intell. Transp. Infrastruct. 2024, 3, liad026. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, P.; Chen, X.; Wang, Y.; Zhang, Y.; Du, Y. Optimization of relative parameters in transfer entropy estimation and application to corticomuscular coupling in humans. J. Neurosci. Methods 2018, 308, 276–285. [Google Scholar] [CrossRef] [PubMed]
- Sipahi, R.; Porfiri, M. Improving on transfer entropy-based network reconstruction using time-delays: Approach and validation. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 023125. [Google Scholar] [CrossRef] [PubMed]
- Ursino, M.; Ricci, G.; Magosso, E. Transfer entropy as a measure of brain connectivity: A critical analysis with the help of neural mass models. Front. Comput. Neurosci. 2020, 14, 45. [Google Scholar] [CrossRef] [PubMed]
- Novelli, L.; Lizier, J.T. Inferring network properties from time series using transfer entropy and mutual information: Validation of multivariate versus bivariate approaches. Netw. Neurosci. 2021, 5, 373–404. [Google Scholar] [CrossRef] [PubMed]
- SynthATDelays Documentation. Available online: https://gitlab.com/MZanin/synth-at-delays/-/wikis/Home/ (accessed on 15 August 2025).
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Shojaie, A.; Fox, E.B. Granger causality: A review and recent advances. Annu. Rev. Stat. Its Appl. 2022, 9, 289–319. [Google Scholar] [CrossRef]
- Diebold, F.X. Elements of Forecasting; South-Western College Pub.: Cincinnati, OH, USA, 1998. [Google Scholar]
- Granger, C.W. Causality, cointegration, and control. J. Econ. Dyn. Control 1988, 12, 551–559. [Google Scholar] [CrossRef]
- Barrett, A.B.; Barnett, L. Granger causality is designed to measure effect, not mechanism. Front. Neuroinform. 2013, 7, 6. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M. Continuous ordinal patterns: Creating a bridge between ordinal analysis and deep learning. Chaos Interdiscip. J. Nonlinear Sci. 2023, 33, 033114. [Google Scholar] [CrossRef] [PubMed]
- Zanin, M. Augmenting granger causality through continuous ordinal patterns. Commun. Nonlinear Sci. Numer. Simul. 2024, 128, 107606. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Kozachenko, L. Sample estimate of the entropy of a random vector. Probl. Pered. Inform. 1987, 23, 9. [Google Scholar]
- Büth, C.M.; Acharya, K.; Zanin, M. Infomeasure: A Comprehensive Python Package for Information Theory Measures and Estimators. Sci. Rep. 2025, 15, 29323. [Google Scholar] [CrossRef]
- Acharya, K.; Olivares, F.; Zanin, M. How representative are air transport functional complex networks? A quantitative validation. Chaos Interdiscip. J. Nonlinear Sci. 2024, 34, 043133. [Google Scholar] [CrossRef] [PubMed]
- Harris, C.R.; Millman, K.J.; Van Der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef] [PubMed]
- Seabold, S.; Perktold, J. Statsmodels: Econometric and statistical modeling with python. SciPy 2010, 7, 92–96. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Büth, C.M.; Zanin, M. SynthATDelays: A Minimalist Python Package for the Generation of Synthetic Air Transport Delay Data. Aerospace 2025, 12, 900. https://doi.org/10.3390/aerospace12100900
Büth CM, Zanin M. SynthATDelays: A Minimalist Python Package for the Generation of Synthetic Air Transport Delay Data. Aerospace. 2025; 12(10):900. https://doi.org/10.3390/aerospace12100900
Chicago/Turabian StyleBüth, Carlson Moses, and Massimiliano Zanin. 2025. "SynthATDelays: A Minimalist Python Package for the Generation of Synthetic Air Transport Delay Data" Aerospace 12, no. 10: 900. https://doi.org/10.3390/aerospace12100900
APA StyleBüth, C. M., & Zanin, M. (2025). SynthATDelays: A Minimalist Python Package for the Generation of Synthetic Air Transport Delay Data. Aerospace, 12(10), 900. https://doi.org/10.3390/aerospace12100900






