Abstract
Global Navigation Satellite Systems (GNSSs) are widely used in many applications but can be out of use in some critical conditions. Hybrid pseudolite systems utilize ground and aero stations as pseudolites to provide positioning signals for users within the covered area. The positioning accuracy is an important performance parameter for the pseudolite system and is decided by the layout of the pseudolites. This paper proposes a layout optimization method based on an Incremental Geometric Dilution of Precision (IGDOP) model. The IGDOP considers the GDOP value into two parts. One is the fixed part corresponding to the ground stations, and the other is the varying part related to the movable aero pseudolite stations. Thus, when the aero pseudolites’ position changes, the new GDOP value could be obtained only by calculating the varying part. Then, a Monte-Carlo Genetic Algorithm (MC-GA) is proposed for the IGDOP calculation for a minimum value. This algorithm comprises two main components: first, it leverages the random sampling capability of the Monte-Carlo Algorithm to provide sample points that satisfy the sample space for the subsequent Genetic Algorithm, which serve as individuals of the initial population; subsequently, it searches for the minimum value of IGDOP via the Genetic Algorithm and determines the optimized layout of the hybrid pseudolite system. Simulations are carried out using a hybrid pseudolite system with four fixed stations and n movable stations. The results validate the developed IGDOP model and show that the approach enables scalable optimization of n − 1 movable stations via four fixed stations, providing an efficient, low-complexity solution to the system layout optimization.
1. Introduction
In the modern era, Global Navigation Satellite Systems (GNSSs) have been deeply integrated into nearly every aspect of contemporary life, playing an indispensable role in civilian applications such as smartphone navigation, autonomous driving, and emergency response, as well as in critical military operations [1,2,3]. However, GNSS signals are highly susceptible to interference, attenuation, or even complete blockage in complex environments such as urban canyons, indoor spaces, and densely vegetated areas [4,5]. To overcome these limitations and enhance the reliability and accuracy of positioning services, pseudolite systems have emerged as a promising solution [6,7].
A pseudolite is a ground- or space-based signal transmitter that emits signals analogous to those of GNSS satellites. These signals can augment existing navigation systems or provide independent positioning and timing services in environments where GNSS signals are weak or unavailable [8,9,10]. Due to their strong anti-interference capabilities, relatively low cost, and high positioning accuracy, pseudolite systems have been widely explored and applied in areas such as indoor positioning [11,12], navigation in complex terrain [13], and military operations [14].
Extensive research has been conducted by scholars worldwide on the optimization of pseudolite system deployment. In the field of space-based pseudolite system layout optimization, international researchers have made notable progress. For example, a centralized and distributed autonomous reconfiguration method combining convex optimization and genetic algorithms is proposed, enabling distributed spacecraft formations to achieve target geometry transitions with low propellant consumption while ensuring safety [15]. Simulation results demonstrated that the optimized network could achieve wide-area coverage while maintaining acceptable Position Dilution of Precision (PDOP) throughout the service region [16]. Regarding optimization algorithms, methods have been developed based on minimizing the Geometric Dilution of Precision (GDOP) at the center of the target area. Compared with empirical approaches and the Non-dominated Sorting Genetic Algorithm II (NSGA-II), these methods produced lower average GDOP values, enhanced robustness, and higher positioning accuracy, enabling rapid determination of optimal pseudolite deployment schemes [17].
In the domain of ground-based pseudolite system optimization, Chinese researchers have also made significant advancements. By constructing mathematical models for pseudolite base station deployment and incorporating real terrain data extracted from Digital Elevation Models (DEM), a deployment method based on NSGA-II was proposed. This method employs viewshed analysis to determine signal coverage, with coverage and weighted precision factor as objective functions. A case study conducted in a mountainous area in Zhangjiajie, Hunan Province, validated the effectiveness of the proposed algorithm through simulation results [18]. To address the ill-posed nature of certain ground-based pseudolite systems, Tikhonov regularization was applied. Furthermore, positioning performance was significantly improved by increasing receiver observations through a dual-frequency, dual-antenna, single-station configuration transmitting four signals. Positioning was computed using single-differenced carrier phase observations, and integer ambiguity was resolved with the LAMBDA method [19].
Despite the substantial progress made in optimizing both space-based and ground-based pseudolite systems, research on integrated regional pseudolite systems that combine both types remains relatively underdeveloped. Such integrated systems offer the potential to synergize the wide-area coverage of space-based pseudolites with the high-accuracy positioning of ground-based systems, providing more reliable and precise positioning services for specific regions [20,21]. However, existing studies have yet to sufficiently address how to optimize the collaborative deployment of space-based and ground-based pseudolites to achieve optimal positioning performance, indicating considerable room for exploration.
To this end, this paper focuses on research regarding the optimization of a hybrid deployment algorithm for space-based and ground-based pseudolites. Specifically, it aims to optimize the layout of movable pseudolites and fixed pseudolites by constructing a reasonable mathematical model that fully accounts for the characteristics of the two types of platforms (i.e., space-based and ground-based ones). Herein, fixed base stations (fixed pseudolites) refer to a type of pseudolites that remain stationary either in the air or on the ground, while movable base stations (movable pseudolites) refer to a type of pseudolites that possess mobility, whether located in the air or on the ground. For the research objective of this paper, ground-based fixed base stations are selected as the initial fixed pseudolites, and movable base stations with mobility—such as stratospheric airships, unmanned aerial vehicles (UAVs), and other unmanned systems—are used as movable pseudolites. By applying innovative optimization techniques, this paper addresses key challenges in the deployment of regional pseudolite systems, thereby providing new insights and methodologies for the development of this field as well as for enhancing the quality and reliability of regional positioning services.
2. Principles of the Developed GDOP Model
To develop a pseudolite layout optimization algorithm based on a novel Geometric Dilution of Precision (GDOP) relationship, this study first transformed the conventional GDOP calculation model. Utilizing matrix theory and geometric derivations, a novel GDOP calculation model based on geometric structure was established. This model evaluates the positioning accuracy of navigation systems within a given area by calculating the solid geometry (such as polyhedral volumes) and planar geometry (triangular areas) formed between pseudolites, then incorporating these into a novel GDOP model based on geometric structures.
Building upon this novel GDOP model, a mathematical relationship between the GDOP values and configurations of n and n − 1 pseudolites was derived. This relationship demonstrates that, given the known layout configuration and GDOP value of any n − 1 pseudolites, it is possible not only to deduce the optimal layout configuration of the n-th pseudolite to enhance regional positioning accuracy but, more significantly, to enable an iterative optimization mechanism. Specifically, starting from the minimum positioning requirement (i.e., knowledge of at least 4 pseudolites), the algorithm can iteratively optimize the layout of the subsequent n − 1pseudolites. This iterative approach ultimately achieves the global optimization of the cooperative layout between stationary base stations and movable pseudolites within the target region.
2.1. Conventional GDOP Model
In satellite navigation systems, the Geometric Dilution of Precision (GDOP) [3] serves as a critical metric for quantifying the impact of spatial satellite distribution on positioning accuracy. Key types of Dilution of Precision (DOP) include:
- GDOP (Geometric DOP, evaluating 3D position and time solution accuracy);
- PDOP (Position DOP);
- HDOP (Horizontal DOP);
- VDOP (Vertical DOP);
With PDOP and GDOP being the most extensively adopted.
GDOP characterizes the geometry strength of satellite constellations, reflecting the amplification effect of spatial geometric configurations on positioning errors. As a rule of thumb, more uniform satellite distribution yields lower GDOP values, thereby enhancing positioning accuracy. Notably, the DOP evaluation framework is equally applicable to pseudolite systems for assessing their geometric configurations’ impact on positioning performance.
Let denote the user’s 3D coordinates and the receiver clock bias. The pseudorange observation from the j-th pseudolite to the user is given by:
where is the 3D position of the -th pseudolite; is the speed of light; denotes the receiver’s clock offset.
Taylor expansion of Equation (1) at the user’s approximate location and approximate clock difference and neglecting the higher order terms gives:
where denotes the difference between the user’s true position and the approximate position; and denotes the cosine of the direction of the unit vector pointing to the -th pseudolite from the receiver’s approximate position .
For a pseudolite system with n pseudolites, Equation (2) can be expressed in matrix form as:
Matrix Form:
where denotes the pseudorange residual for the j-th pseudolite, , , represent the direction cosines between the pseudolite and the receiver, respectively, c denotes the speed of light (2.998 × 108 m/s).
The precision dilution matrix is derived from Equation (3):
The geometric dilution of precision (GDOP) evaluation metric is defined as:
where represents the diagonal element in the precision Dilution matrix, denotes the trace of the matrix.
Geometric Dilution of Precision (GDOP), which quantifies the combined impact of receiver 3D coordinates (x,y,z) and clock bias () positioning errors, serves as the primary criterion for evaluating positioning accuracy in airborne pseudolite systems. Building upon the classical DOP computational model.
2.2. Geometric GDOP Model
Based on the conventional GDOP model, this study employs matrix algebraic transformation and geometric interpretation of determinants to convert into . By expanding the diagonal elements of the adjugate matrix and the determinant , their relationship with the spatial geometry of pseudolite constellations is established. The new GDOP model for a given configuration is derived by computing planar triangular areas and spatial pyramidal volumes of the pseudolite group. The complete derivation is presented below.
A matrix transformation of the precision dilution matrix results in: .
where , , , represent the diagonal elements of the matrix , denotes the Adjugate Matrix of the matrix.
The following can be obtained:
For the precision factor:
To further establish the relationship between GDOP and geometric structures, geometric transformations are applied to , , .
where denote the indices of any three pseudolites among the n pseudolites; (, ,) represent the direction cosines of the unit vector from the receiver to the j-th pseudolite:
where, denotes the vertical elevation angle of the space-based pseudolite relative to the receiver, and denotes the horizontal azimuth angle of the space-based pseudolite relative to the receiver.
- Determinant corresponds to the sum of the squared areas of the triangles formed by the pseudolite projection points , , and onto the YOZ-plane of the Cartesian coordinate system established at the receiver position O.
- Determinant corresponds to the sum of the squared areas of the triangles formed by the pseudolite projection points , , and onto the XOZ-plane of the Cartesian coordinate system established at the receiver position O.
- Determinant corresponds to the sum of the squared areas of the triangles formed by the pseudolite projection points , , and onto the XOY-plane of the Cartesian coordinate system established at the receiver position O.
- Determinant denotes the product of the volume of the parallelepiped formed by the user and any three pseudolites among the n pseudolites, and the coordinate points.
- The determinant denotes the sum of the scaled volumes (i.e., each multiplied by a coefficient) of the tetrahedrons formed by any combination of four pseudolite projection points on the YOZ-plane of the Cartesian coordinate system established at the user position O.
Thus, a novel GDOP calculation model based on geometric structures can be derived:
where, parameters in the aforementioned formula are specifically explained as follows:
- , , and correspond to the sums of squared areas of the projection triangles onto the XOY-plane, YOZ-plane, and XOZ-plane, respectively.
- and denote the scaled hexahedron volume and the scaled tetrahedron volume, respectively
2.3. The Incremental GDOP Model
As given in Equation (7), assume that g11, g22, g33, g44 represent the diagonal elements of matrix A corresponding to n − 1 pseudolites, as specified in Equation (15); and q11, q22, q33, q44 represent the diagonal elements of matrix B corresponding to n pseudolites, as specified in Equation (16).
Derived from the derivation of Equations (8)–(12), the result of the matrix transformation is:
where , , , , represent the determinant expansion difference components between the corresponding diagonal elements for n pseudolites and n − 1 pseudolites, respectively. , , , , , , represent the difference components in the expansion of the observation matrix determinant for n pseudolites compared to that for n − 1 pseudolites, respectively.
Assume that , , , , represent the sums of the difference terms for:
- and ;
- the determinant expansion terms between n pseudolites and n − 1 pseudolites, respectively;
Based on the mathematical derivation above, the following can be obtained:
Further simplification of the above formulas yields the expressions for parameters B and C as follows:
Equation (22) reveals the correlation between the pseudolite navigation system composed of n pseudolites and the one composed of n − 1 pseudolites: Given the actual layout configuration and GDOP values of the n − 1-pseudolite navigation system, by combining the Incremental GDOP (IGDOP)algorithm model with optimization algorithms, the optimal layout configuration of the n-pseudolite navigation system—formed by adding the n-th pseudolite to the aforementioned n − 1-pseudolite navigation system—can be derived, thereby improving the overall positioning accuracy. Furthermore, when fixed base stations (which serve as fixed pseudolites) are insufficient in precision, regional positioning accuracy can be enhanced by introducing movable base stations (movable pseudolites), and this model provides a theoretical basis for this approach. Finally, given the GDOP values and distribution of four pseudolites, the optimal layout scheme of the n-pseudolite system can be obtained through iterative computation using this model.
3. Design of Monte-Carlo Genetic Algorithm
This section begins by introducing the Monte Carlo algorithm and the genetic algorithm. Building upon these two algorithms, the Monte Carlo algorithm provides the initial population individuals required for the sample space sampling points to the genetic algorithm. After obtaining the population through random sampling via the Monte Carlo algorithm, a novel optimization algorithm—the Monte Carlo-Genetic Algorithm (MC-GA)-is formed by combining it with the genetic algorithm based on gene mutation and crossover. To determine the optimal deployment position of the n-th pseudolite that minimizes the average Increment-based Geometric Dilution of Precision (IGDOP) for users in the target area, this study employs the Monte Carlo-Genetic Algorithm (MC-GA) for optimization. The complete workflow of this optimization algorithm is illustrated in Figure 1, primarily comprising parameter initialization, modeling of user and candidate pseudolite positions, iterative optimization based on the genetic algorithm (including fitness evaluation, selection, crossover, and mutation), and final determination of the optimal solution.
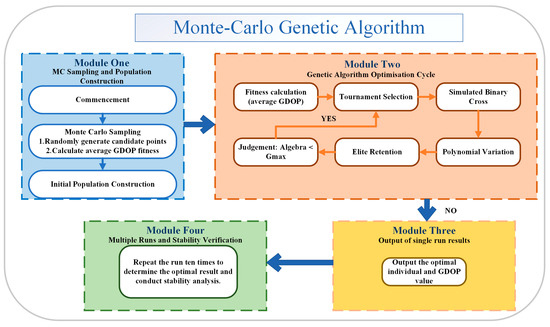
Figure 1.
Schematic flow of the overall steps of the optimization algorithm.
3.1. Monte Carlo Algorithm
The Monte Carlo method, originating from Buffon’s 18th-century needle experiment for π estimation [22], employs random sampling and statistical experiments to derive numerical solutions through computed averages or probabilities [23]. Compared to alternative approaches, it features fewer application constraints, simpler algorithmic structures, easier computer implementation, and particular suitability for complex probability distributions, system simulations, and optimization problems.
3.2. Genetic Algorithm
The genetic algorithm operates by encoding problem solutions into chromosomal representations, where each chromosome a string of genes-constitutes a potential solution. An initial population consisting of multiple chromosomes is generated. A fitness function is designed to evaluate each chromosome’s performance according to the survival-of-the-fittest principle. Based on fitness values, genetic operations are applied to iteratively improve solution quality across generations.
3.3. Monte-Carlo Genetic Algorithm (MC-GA)
This paper addresses the simultaneous optimization of multiple constraints (e.g., sampling space boundaries) and multi-objective functions (denoted as B and C in Equation (22)) in a novel incremental GDOP computation model. A genetic algorithm integrated with Monte Carlo stochastic simulation is proposed to enhance global exploration capabilities through random sampling while complementing the iterative optimization process of the genetic algorithm. The specific implementation steps are as follows:
- Spatial Definition and Sampling Area Initialization
- Sampling and Candidate Point Evaluation
- Genetic Algorithm Population Initialization
- GDOP Calculation for Known Nodes and Iterative Optimization
- Algorithm Validation and Visualization
In this optimization algorithm, the method is applied to solve for the maximum value. However, for GDOP, a lower GDOP value indicates higher positioning accuracy; hence, the fitness function employed herein is designed to solve for the minimum value.
The core idea of the Monte Carlo Genetic Algorithm (MC-GA) proposed in this paper lies in leveraging the Monte Carlo (MC) method to efficiently explore the vast solution space and provide a high-quality initial population for the Genetic Algorithm (GA). Subsequently, the iterative evolutionary mechanism of GA is employed for local refinement to ultimately identify the optimal deployment locations that minimize the regional average Geometric Dilution of Precision (GDOP). The integration of MC and GA is not merely sequential but represents a deep fusion:
- Monte Carlo Phase (Global Exploration):First, large-scale uniform random sampling is conducted within the candidate sampling space for movable pseudolites (a cylinder with a height of 50 km). Each sampling point represents a candidate pseudolite position. The improvement in GDOP resulting from the inclusion of each sampling point into the system is computed (rapidly evaluated using the incremental GDOP model derived in Section 2). This phase aims to prevent GA from converging to local optima due to poor initial population quality while quickly identifying promising regions of the solution space.
- Genetic Algorithm Phase (Local Exploitation):From the MC sampling results, the top P points (where P is the population size) with the best performance (i.e., the smallest GDOP values) are selected to form the initial population of GA. Subsequently, GA performs iterative evolution through selection, crossover, and mutation operations to further refine these high-quality initial solutions and conduct a detailed search for the global optimum.
This hybrid approach fully leverages the global random search capability of MC and the directed optimization ability of GA, ensuring both global convergence and significantly improving the convergence speed of the algorithm.
4. Simulations and Results
This study aims to address the issue of insufficient communication and navigation positioning accuracy for fixed base stations (such as signal towers or transmission stations that can serve as ground-based pseudolites) established in remote areas, particularly those with significant terrain relief like mountains and valleys. By integrating airborne mobile base stations (e.g., airships, UAVs) with ground-based pseudolites to form an air-ground pseudolite integrated communication and navigation system, we seek to enhance the communication and navigation precision within such regions. To validate the effectiveness of the proposed GDOP (Geometric Dilution of Precision) relational model for pseudolite layout optimization under practical regional conditions, we simulated a system with four ground-based pseudolites located at different mountain altitudes. The Monte Carlo-Genetic Algorithm (MC-GA) was employed to iteratively optimize the position of a fifth pseudolite (an airborne pseudolite). Simulation results demonstrate the accuracy metrics of the new system. Subsequently, using a system of five air-ground pseudolites as the known condition, the optimal position for a sixth airborne pseudolite was iteratively determined.
Through the aforementioned simulation experiments, we aim to demonstrate the correctness of the IGDOP model and the feasibility of implementing the layout optimization algorithm. Furthermore, to illustrate the superior efficiency of the IGDOP computational model compared to the traditional GDOP model, and the advantage of the MC-GA algorithm being more suitable for this computational model, this section conducts comparative experiments: one comparing the efficiency of the two different computational models under the same MC-GA algorithm, and another comparing the convergence performance of the same IGDOP model under different algorithms (Genetic Algorithm—GA).
In the experiments, the simulation area’s altitude was stratified. Uniform sampling across these layers was achieved using the Monte Carlo-Genetic Algorithm, and genetic algorithm iterations were performed based on parameters B and C from the model. The following sections detail the parameter settings, algorithm workflow, and simulation results.
4.1. Key Steps and Parameter Details of the Algorithm
To investigate the feasibility and reproducibility of the pseudolite placement optimization algorithm based on the GDOP relational model, the key steps and parameters of the MC-GA are detailed as follows.
- (1)
- Parameter Initialisation and Sampling Space Definition
The relevant parameters of the Monte Carlo Genetic Algorithm and the definitions of sampling are presented in Table 1 to ensure reproducibility and readability for readers.

Table 1.
Optimization algorithm parameter setting.
The transformed coordinates are defined by the following expressions:
In the expression, , , and denote the components of the transformed coordinate point; (, , ) represents the user position; and (, , ) represents the actual position of the i-th pseudolite. The transformed coordinates are calculated from the aforementioned , , and .
- (2)
- Monte Carlo Sampling and Initial Population Construction
- A total of NMC candidate points are generated uniformly at random within the three-dimensional sampling space.
- For each candidate point (, , ), it is treated as the n-th pseudolite. The incremental GDOP model (Equation (20)) is utilized to rapidly compute the average GDOP value across the entire target region, which serves as the fitness value for this point.
- From these NMC points, the top P (As shown in Table 1) points with the optimal fitness values (i.e., the smallest average GDOP) are selected to form the initial population for the genetic algorithm (GA).
- (3)
- Iterative Optimisation Using Genetic Algorithms
- Fitness Evaluation: For each individual in the population (representing a pseudolite position), its fitness (regional average GDOP) is computed using the incremental GDOP (IGDOP) model.
- Selection: Tournament selection is employed to select parent individuals from the current population.
- Crossover: Selected parent individuals undergo SBX (Simulated Binary Cross) with a probability of Pc (As shown in Table 1) to generate offspring individuals. SBX effectively maintains population diversity and facilitates exploration.
- Mutation: Polynomial mutation is applied to offspring individuals with a probability of Pm (As shown in Table 1) to introduce random perturbations, thereby preventing premature convergence.
- Elitism Strategy: The two best individuals from the current generation are unconditionally preserved in the next generation’s population to ensure non-degradation of algorithmic performance.
The above steps are repeated until the maximum generation number Gmax is reached.
- (4)
- Validation of Results and Stability Analysis
Finally, the results were validated through simulation and stability analysis.
- Record the position of the best individual in the final generation and its corresponding GDOP value (IGDOP Minimum Value).
- To mitigate the effects of GA randomness, the entire MC-GA process is independently repeated for 10 runs (each using a different random seed). The best result from these 10 runs is ultimately reported, and a statistical analysis of all results is conducted to verify the algorithm’s stability (as shown in Table 2, Table 3, Table 4 and Table 5).
 Table 2. GDOP values and optimal position results for 10 repetitions of the experiment for the fifth pseudolite.
Table 2. GDOP values and optimal position results for 10 repetitions of the experiment for the fifth pseudolite. Table 3. Numerical results corresponding to the optimal GDOP for parameter B and parameter C for 10 repeated experiments for the fifth pseudolite.
Table 3. Numerical results corresponding to the optimal GDOP for parameter B and parameter C for 10 repeated experiments for the fifth pseudolite. Table 4. GDOP values and optimal position results for 10 repetitions of the experiment for the sixth pseudolite.
Table 4. GDOP values and optimal position results for 10 repetitions of the experiment for the sixth pseudolite. Table 5. Numerical results corresponding to the optimal GDOP for parameter B and parameter C for 10 repeated experiments for the sixth pseudolite.
Table 5. Numerical results corresponding to the optimal GDOP for parameter B and parameter C for 10 repeated experiments for the sixth pseudolite.
The novelty of the proposed MC-GA algorithm in this paper lies in the following aspects: (1) By replacing traditional random initialization with Monte Carlo (MC) sampling, the algorithm provides directional guidance for the GA, significantly reducing the number of iterations required. (2) The entire optimization process is tightly coupled with the incremental GDOP (IGDOP) model proposed in Section 2. When evaluating each candidate position, there is no need to recalculate the entire matrix and its inverse. Instead, only the incremental components (parameters B and C) are computed, making fitness evaluations at the scale of tens of thousands feasible. This approach notably lowers computational complexity compared to traditional methods. (3) The complete algorithmic steps, operator selection, and parameter settings are provided above. Other researchers can fully reproduce the simulations and results presented in Section 4 of this paper, given the known positions of the four fixed pseudolites (Table 1).
4.2. Simulation Results
Building upon the content of Section 3.1 and Section 3.2, this chapter presents experimental simulations. A Monte Carlo Genetic Optimization Algorithm (MC-GA) based on the GDOP relationship model is constructed, with a circular area of 10 km radius serving as the simulation scope. The aim is to evaluate the advantages and feasibility of the layout optimization algorithm through GDOP coverage values within this area. Specifically, when the number of pseudolites fixed base stations with known positions is four, the GDOP relationship model is studied and validated, and the optimal position of the fifth movable pseudolite is iteratively optimized using the MC-GA, thereby obtaining the optimal layout configuration of the pseudolite system that minimizes the GDOP values within the area. Subsequently, after obtaining the position of the fifth movable pseudolite, and based on these five pseudolites with known positions, the optimal position of the sixth movable pseudolite is determined using the same layout optimization algorithm based on the GDOP relationship model, and the GDOP values within the area are evaluated. The specific simulation results are presented in the following figures and tables.
First, using the GDOP-based calculation model, regional GDOP simulation and visualization were performed for the fixed pseudolites listed in Table 1, resulting in Figure 2. This figure intuitively reflects the regional positioning accuracy provided by the four pseudolites through the Geometric Dilution of Precision (GDOP).
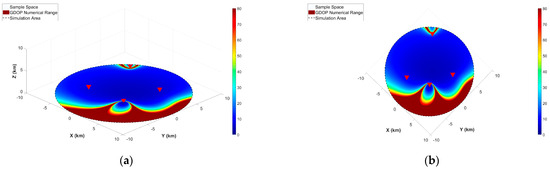
Figure 2.
Schematic of the layout of the fixed pseudolites, in which (a,b) show the side and top views of the fixed four pseudolites, respectively.
Next, based on Equation (20), a Monte Carlo Genetic Algorithm (MC-GA) is used to iteratively optimize parameters B and C C over 10 repeated trials based on the known geometric accuracy factors (GDOP) of the four fixed pseudolites. Subsequently, the layout of the fifth pseudolite is visualised and the regional GDOP values of the five pseudolite system at this point are given. The visualisation results reflect the trend of the optimal GDOP values over the 10 iterations with the results of each experiment (Figure 3).
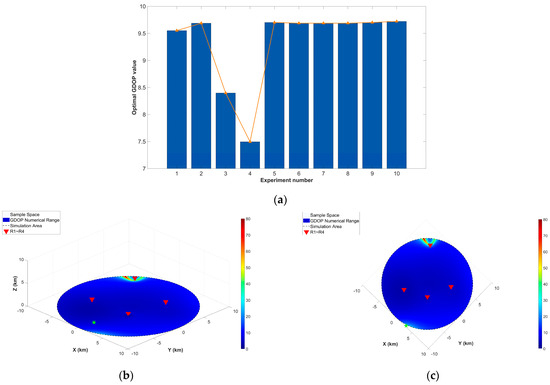
Figure 3.
Schematic diagram of the layout of the fifth pseudolite, where (a) shows the iterative process of 10 repeated experiments, and (b,c) represent the elevation view and plan view of the layout, respectively.
The optimal layout position of the fifth pseudolite and its corresponding GDOP value are obtained by repeatedly optimizing the iterative algorithm 10 times, and the optimal results of parameter B and parameter C iteration in each experiment are obtained, as shown in the following tables.
The specific position of the fifth pseudolite obtained via the optimized layout algorithm is R5: (3.02, −9.77, 2.44). By comparing the four-pseudolite system and the newly formed five-pseudolite system, as shown in Figure 2 and Figure 3, it can be seen that optimizing the layout of the added pseudolite using the MC-GA layout optimization model based on the GDOP relationship model can significantly improve the regional positioning accuracy.
To demonstrate the advantages of the IGDOP computational model and the MC-GA algorithm, this study takes the iterative optimization of the fifth pseudolite position within a four-pseudolite system as an example. Firstly, independent iterative simulation comparisons were conducted between the IGDOP and traditional GDOP models using the MC-GA algorithm. Subsequently, the convergence performance of the MC-GA algorithm was compared with that of the standard Genetic Algorithm (GA) when applied to the IGDOP model, as illustrated in Figure 4.
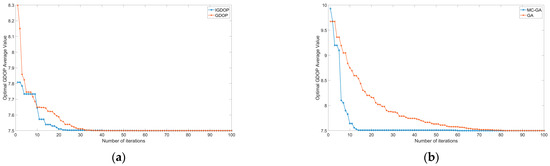
Figure 4.
Comparative schematic diagram where: (a) compares the performance of the IGDOP model versus the traditional GDOP model under the MC-GA algorithm, and (b) compares the performance of the MC-GA algorithm versus the standard Genetic Algorithm (GA) using the IGDOP computational model.
As shown in Figure 4a, under the MC-GA algorithm with 100 iterations, the IGDOP model demonstrates faster convergence speed compared to the traditional GDOP model. This improved efficiency stems from the reduced computational load of IGDOP, as indicated by Equations (23)–(25), leading to accelerated convergence. Figure 4b illustrates the convergence rates of the IGDOP model when optimized using the MC-GA algorithm versus the standard Genetic Algorithm (GA). The results indicate that the MC-GA algorithm achieves significantly faster convergence compared to the GA.
According to Equations (5) and (22), the following equations are determined:
Since the GDOP relational model proposed in this paper is obtained by transforming on the traditional GDOP model, the following equation exists:
As can be seen from Equation (25), the four terms on the right side of the equation all contain specific parameters of n − 1 pseudolites, and if the calculation is required, the part of n − 1 pseudolites needs to be repeated constantly, and for the left side of the equation, since is known, the algorithm only needs to use the algorithm to iteratively optimize the parameter B and the parameter C, and the amount of computation is significantly smaller than that of the traditional GDOP model.
Based on the fifth movable pseudolite obtained through optimization iterations in the preceding content, together with the remaining four fixed pseudolites, a new fixed pseudolite system was formed. Using the GDOP relationship model and the Monte Carlo Genetic Algorithm (MC-GA), the layout optimization result of the sixth movable pseudolite was visualized. The following figure presents a comparison of the layout of the five-pseudolite system and the optimized six-pseudolite system. This figure also illustrates the occurrence frequency of the optimal average GDOP and the variation trend of the optimal GDOP in each trial after 10 repeated experimental iterations (Figure 5).
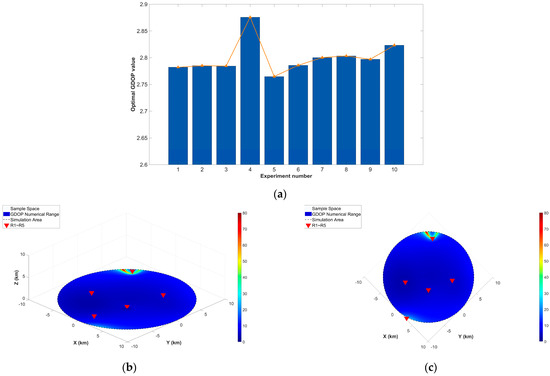
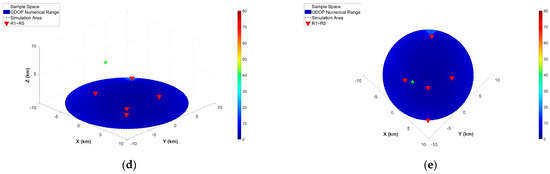
Figure 5.
Schematic diagram of the layout of the sixth pseudolite, where (a) presents the iterative process of the 10 replicate experiments, (b,c) depict the configuration scheme of the five fixed pseudolites, and (d,e) represent the elevation view and plan view of the layout, respectively.
The optimal layout position of the sixth pseudolite and its corresponding GDOP value are obtained by repeating the optimization iteration algorithm for 10 times, and the optimal results of the parameter B and parameter C iterations in each experiment are also obtained, as shown in Table 4 and Table 5.
Multiple repetitions of the experiment effectively alleviate the randomness brought by the crossover and mutation operations of the genetic algorithm, thus improving the reliability of the experimental results. As shown in Table 4, the optimal results are obtained in the third iteration of the experiment, in which the optimal position of the sixth pseudolite is R6 = (−1.35, −3.52, 7.98), corresponding to a GDOP value of 2.764852. Through Table 5, we can obtain the values of parameter B and parameter C obtained in each optimization iteration.
5. Discussion
In this study, we first propose a novel GDOP calculation model based on a geometric structure to solve for GDOP. This model calculates GDOP by solving geometric structure parameters formed by pseudolites, such as the area of triangles and the volume of pyramids formed between pseudolites, providing a new perspective for researching and solving GDOP. Compared with traditional GDOP calculation models, it can more clearly reflect the correlation between the Geometric Dilution of Precision (GDOP) and the geometric structure from the formula structure. Secondly, building upon this geometric structure-based GDOP model, we further propose a GDOP relationship model. This relationship model reflects the GDOP relationship between an (n − 1)-pseudolite system and an n pseudolite system and offers the following advantages: (1) With the known positions of n − 1 pseudolites, the optimal layout of the n-th pseudolite can be obtained by combining this formula with a layout optimization algorithm, such as the Monte Carlo Genetic Algorithm (MC-GA) used in this paper. This pseudolite, together with the original pseudolite system, forms a new regional navigation system, thereby improving regional positioning accuracy. (2) The relationship model offers the advantage of iterative optimization. Since a pseudolite positioning system requires at least four pseudolites, for scenarios where four or more fixed pseudolite base stations (i.e., non-movable constellation base stations) have been deployed in a region but the regional positioning accuracy is still insufficient, the layout of the fifth pseudolite can be iteratively optimized using the four pseudolites. Based on the known five-pseudolite system, the layout of the sixth pseudolite can then be iteratively derived using this formula, and so on. Therefore, the layout of the next pseudolite can be obtained from the preceding pseudolite system, enabling the iterative optimization of the layout of n pseudolites based on four pseudolites, thus achieving the selection and layout optimization of the pseudolite constellation. This is particularly important for areas with poor signal coverage, such as mountainous regions, where fixed base stations may be unable to provide sufficiently accurate communication and positioning services due to layout constraints. In such cases, it is necessary to deploy movable pseudolites to form a new regional communication and navigation system together with fixed pseudolite base stations. (3) The GDOP relational model proposed in this paper has a smaller computational volume compared with the traditional GDOP model, and the iteration speed can be significantly improved by combining with other optimization algorithms, which can reflect its advantages when multiple pseudolites are required to be optimized as targets.
Figure 6 demonstrates the complete process of pseudolite layout optimization: (a,b) show four fixed pseudolites with known positions; (d) display the optimal layout position of the fifth pseudolite obtained through the layout optimization algorithm; based on the five-pseudolite base station configuration, (e,f) present the optimized layout result of the sixth pseudolite. This set of schematic diagrams clearly illustrates the advantages of the proposed layout optimization algorithm model: the model can determine the optimal layout of the n-th pseudolite when the positions of n − 1 pseudolites are known by incorporating optimization methods such as the Monte Carlo Genetic Algorithm (MCGA), thereby forming a new regional navigation system with the original system to significantly improve positioning accuracy. More importantly, the model features iterative optimization capability, enabling sequential optimization of the fifth, sixth, and more pseudolites based on an initial four-pseudolite configuration. This effectively addresses the issue of insufficient positioning accuracy in regions with fixed pseudolite base stations, ultimately achieving optimal selection and layout of an n-pseudolite constellation.
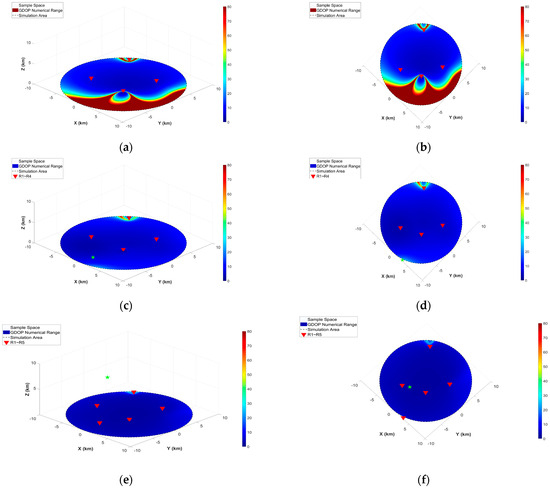
Figure 6.
Schematic layout of 4, 5 and 6 pseudolites, where (a,b) indicate the schematic layout of 4-pseudolite systems, (c,d) are the side and top views of 5-pseudolite systems, respectively, and (e,f) are the side and top views of 6-pseudolite systems, respectively.
This study systematically validates the feasibility of the proposed GDOP relationship model through comprehensive simulation experiments. Notably, taking a four-pseudolite configuration as the initial setup, the Monte Carlo Genetic Algorithm (MC-GA) was employed for layout optimization, which fully demonstrates the significant advantages of this algorithmic model in pseudolite deployment optimization. The proposed method is not only applicable to hybrid “fixed-movable pseudolite” deployment optimization, but also provides an innovative solution for improving positioning accuracy in UAV-assisted emergency rescue missions and urban communication and positioning, as well as weak signal environments such as mountainous areas.
Another advantage of the proposed GDOP model is its reduced computational load compared to the traditional model. Furthermore, when integrated with optimization algorithms, it requires fewer iterations. Specific conclusions are provided in Section 4 with detailed analysis and discussion.
6. Conclusions
In recent research, many scholars have focused on aspects related to pseudolite layout optimization and constellation selection for space-based pseudolite systems, as well as the selection and layout design of ground-based pseudolites. However, less research has been conducted on the layout optimization of the combination of space-based and ground-based pseudolite systems, especially in remote areas such as mountainous areas, canyons and urban high-rise environments, where the fixed base station often encounters technical challenges such as limited communication and positioning capabilities and insufficient mobility. Aiming at the problems of insufficient positioning accuracy and inability to improve communication performance through position adjustment in these areas, an optimal deployment optimization algorithm based on the GDOP relational model is proposed. By combining movable pseudolites such as stratospheric blimps and unmanned aerial vehicles (UAVs), the air-based + ground-based pseudolites to build a complete air-earth-earth pseudolite system, this method effectively solves the challenge of fixed base stations being unable to meet the communication and positioning requirements in complex environments. By taking four pseudolites as an example, based on the initial four-pseudolite configuration, this study verifies the feasibility and superiority of the proposed method by optimising five pseudolites and six pseudolites in multiple repetitive experiments. The method provides a space-based + ground-based solution idea for when a single space-based or single ground-based pseudolite system is unable to achieve accuracy, which significantly improves the accuracy of regional communication and navigation signals. In terms of the GDOP model, the proposed GDOP relational model has less computational effort compared with the traditional GDOP model, and combined with specific optimization algorithms, it can effectively improve the convergence and reduce the number of iterations for multiple-pseudolite systems.
Author Contributions
Conceptualization, Z.G. and B.L.; methodology, Z.G.; software, Z.G.; validation, Z.G. and B.L.; formal analysis, B.L.; investigation, Z.G. and B.L.; writing—original draft preparation, Z.G.; writing—review and editing, Z.G. and Y.W.; visualization, Z.G.; supervision, Z.G. and Y.W.; project administration, Z.G. and Y.W.; funding acquisition, B.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in this article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Xu, S.; Zhao, K.; Sun, Y.; Fu, X.; Luo, K. Visual Point Cloud Map Construction and Matching Localization for Autonomous Vehicle. Drones 2025, 9, 511. [Google Scholar] [CrossRef]
- Sam-Odusina, T.; Perkasa, P.; Chalmers, C.; Fergus, P.; Longmore, S.N.; Wich, S.A. Detection and Geolocation of Peat Fires Using Thermal Infrared Cameras on Drones. Drones 2025, 9, 459. [Google Scholar] [CrossRef]
- Jiang, P.; Geng, X.; Pan, G.; Li, B.; Ning, Z.; Guo, Y.; Wei, H. GNSS Anti-Interference Technologies for Unmanned Systems: A Brief Review. Drones 2025, 9, 349. [Google Scholar] [CrossRef]
- Zhao, X.; Tang, P.; Song, Q.; Jiang, T.; Wang, Y.; Tian, L.; Li, W.; Zhang, J. Experimental Analysis of Multipath Effects on GNSS Positioning in Urban Canyon. In Proceedings of the 2021 IEEE 4th International Conference on Electronic Information and Communication Technology (ICEICT), Xi’an, China, 18–20 August 2021; pp. 557–562. [Google Scholar]
- Hussain, A.; Akhtar, F.; Khand, Z.H.; Rajput, A.; Shaukat, Z. Complexity and Limitations of GNSS Signal Reception in Highly Obstructed Enviroments. Eng. Technol. Appl. Sci. Res. 2021, 11, 6864–6868. [Google Scholar] [CrossRef]
- Dai, L.; Rizos, C.; Wang, J. The Role of Pseudo-Satellite Signals in Precise GPS-Based Positioning. J. Geospat. Eng. 2001, 3, 33–44. [Google Scholar]
- Stone, J.M.; LeMaster, E.A.; Powell, J.D.; Rock, S. GPS pseudolite transceivers and their applications. In Proceedings of the 1999 National Technical Meeting of The Institute of Navigation, San Diego, CA, USA, 25–27 January 1999; pp. 415–424. [Google Scholar]
- Jiang, Q.; Wang, T.; Zhong, Y.; Qu, Y. Research on pseudo satellite positioning system based on closed environment. Sci. J. Econ. Manag. Res. Vol. 2023, 5, 3. [Google Scholar]
- Puengnim, A.; Patino-Studencka, L.; Thielecke, J.; Rohmer, G. Precise positioning for virtually synchronized pseudolite system. In Proceedings of the International Conference on Indoor Positioning and Indoor Navigation, Montbéliard, France, 28–31 October 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–8. [Google Scholar]
- Guo, X.; Liu, K.; Meng, Z.; Li, X.; Yang, J. Pseudolite-Based Lane-Level Vehicle Positioning in Highway Tunnel. IEEE Trans. Intell. Transp. Syst. 2024, 25, 1612–1624. [Google Scholar] [CrossRef]
- Wan, X.; Zhan, X. The research of indoor navigation system using pseudolites. Procedia Eng. 2011, 15, 1446–1450. [Google Scholar] [CrossRef][Green Version]
- Rizos, C.; Barnes, J.; Small, D.; Voigt, G.; Gambale, N. A new pseudolite-based positioning technology for high precision indoor and outdoor positioning. In Proceedings of the International Symposium and Exhibition on Geoinformation, Shah Alam, Malaysia, 13–14 October 2003; pp. 13–14. [Google Scholar][Green Version]
- Yu, B.; Fan, G.; Luo, Y.; Sheng, C.; Gan, X.; Huang, L.; Rong, Q. Multi-source fusion positioning algorithm based on pseudo-satellite for indoor narrow and long areas. Adv. Space Res. 2021, 68, 4456–4469. [Google Scholar] [CrossRef]
- Vitto, V.; Burton, D.; Carter, W.; Corder, J.; Crawford, N.; Morefield, C.; Nielson, D.; Sorenson, H.; Stear, E.; Stewart, J. Vision of Aerospace Command and Control for the 21st Century. 1996. Available online: https://apps.dtic.mil/sti/html/tr/ADB217170/ (accessed on 27 September 2025).
- Sarno, S.; Guo, J.; D’Errico, M.; Gill, E. A guidance approach to satellite formation reconfiguration based on convex optimization and genetic algorithms. Adv. Space Res. 2020, 65, 2003–2017. [Google Scholar] [CrossRef]
- Lyon, H.M.; Inalhan, G.; Bourne, D.; Tsourdos, A. High-Altitude UAS Pseudo-Satellites: Architecture for End-to-End Military Communications. In AIAA Scitech 2021 Forum; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2021. [Google Scholar]
- Yang, X.; Liu, W.; Ye, X.; Li, X.; Wei, S.; Wang, F. A geometry-based method for the rapid deployment of a UAV pseudolite navigation system in a target area. J. Geod. 2023, 97, 90. [Google Scholar] [CrossRef]
- Yang, L.; Yang, K.; Sun, D. Research on the Station Layout Method of Ground-Based Pseudolite Positioning System Based on NSGA-II Algorithm. Wirel. Commun. Mob. Comput. 2021, 2021, 1520859. [Google Scholar] [CrossRef]
- Teunissen, P.; De Jonge, P.J.; Tiberius, C. The LAMBDA method for fast GPS surveying. In Proceedings of the International Symposium “GPS Technology Applications”, Bucharest, Romania, 26–29 September 1995. [Google Scholar]
- Novakovic, G.; Dapo, A.; Kodzic, D. Pseudolite applications in positioning and navigation. Int. Multidiscip. Sci. Geo Conf. SGEM 2010, 1, 829. [Google Scholar]
- Liu, T.; Liu, J.; Wang, J.; Zhang, H.; Zhang, B.; Ma, Y.; Sun, M.; Lv, Z.; Xu, G. Pseudolites to support location services in smart cities: Review and prospects. Smart Cities 2023, 6, 2081–2105. [Google Scholar] [CrossRef]
- Xie, G. Probability Theory and Mathematical Statistics; Higher Education Press: Beijing, China, 2002. [Google Scholar]
- Wu, H.; Liu, L. Monte Carlo method and applica-tions in solving special problems. J. Taiyuan Norm. Univ. 2009, 8, 76–79. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).