UQ4CFD: An Uncertainty Quantification Platform for CFD Simulation
Abstract
1. Introduction
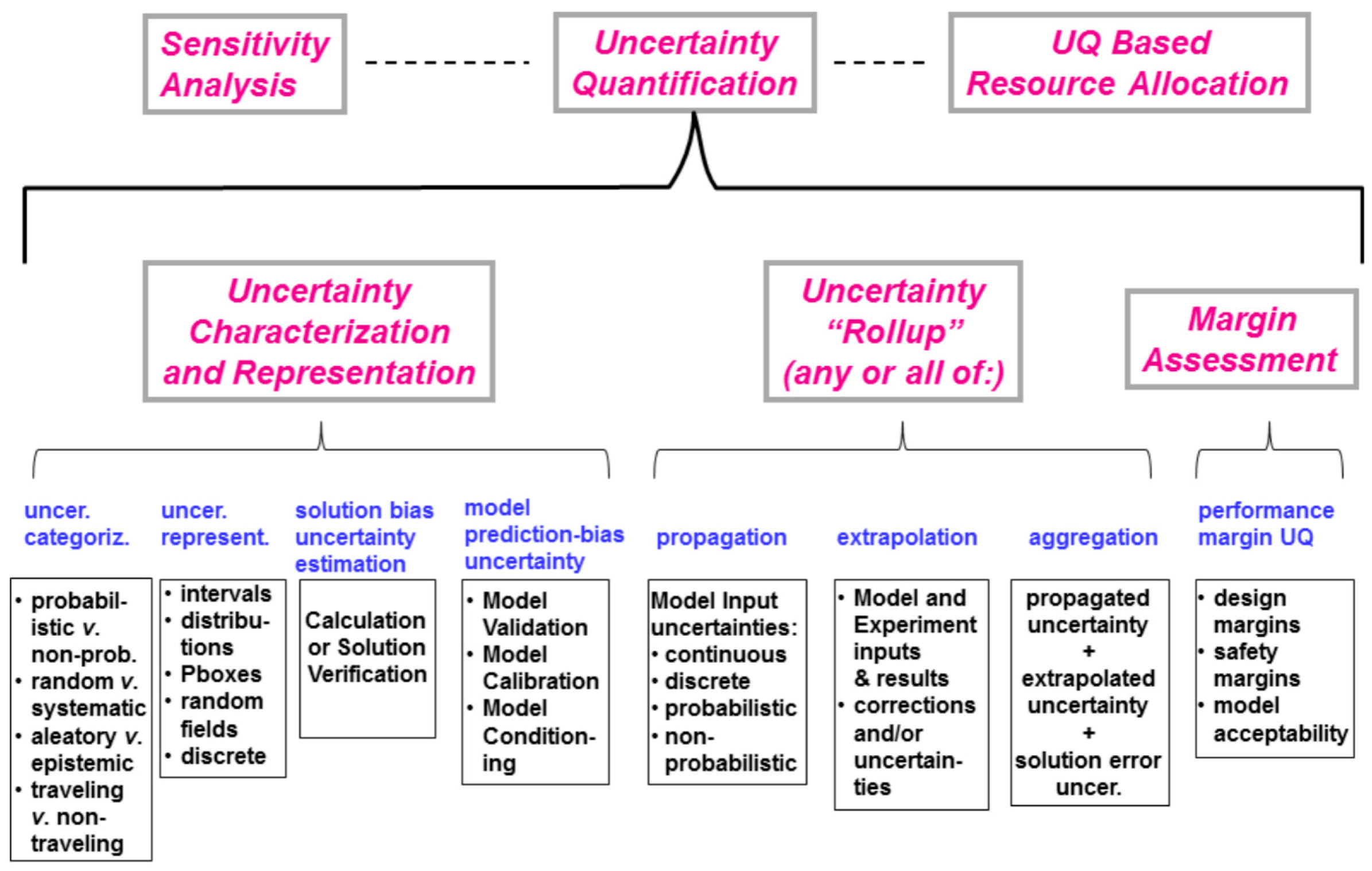
2. CFD Uncertainty Quantification Framework
2.1. Input Uncertainty Characterization
2.2. Uncertainty Propagation
2.2.1. DoE
2.2.2. Propagation with CFD Solver or Surrogate Model
2.2.3. Uncertainty Analysis
2.3. Sensitivity Analysis
2.4. Model Calibration
2.5. Model Validation
2.6. Numerical Discretization Uncertainty Analysis
3. The UQ4CFD Platform
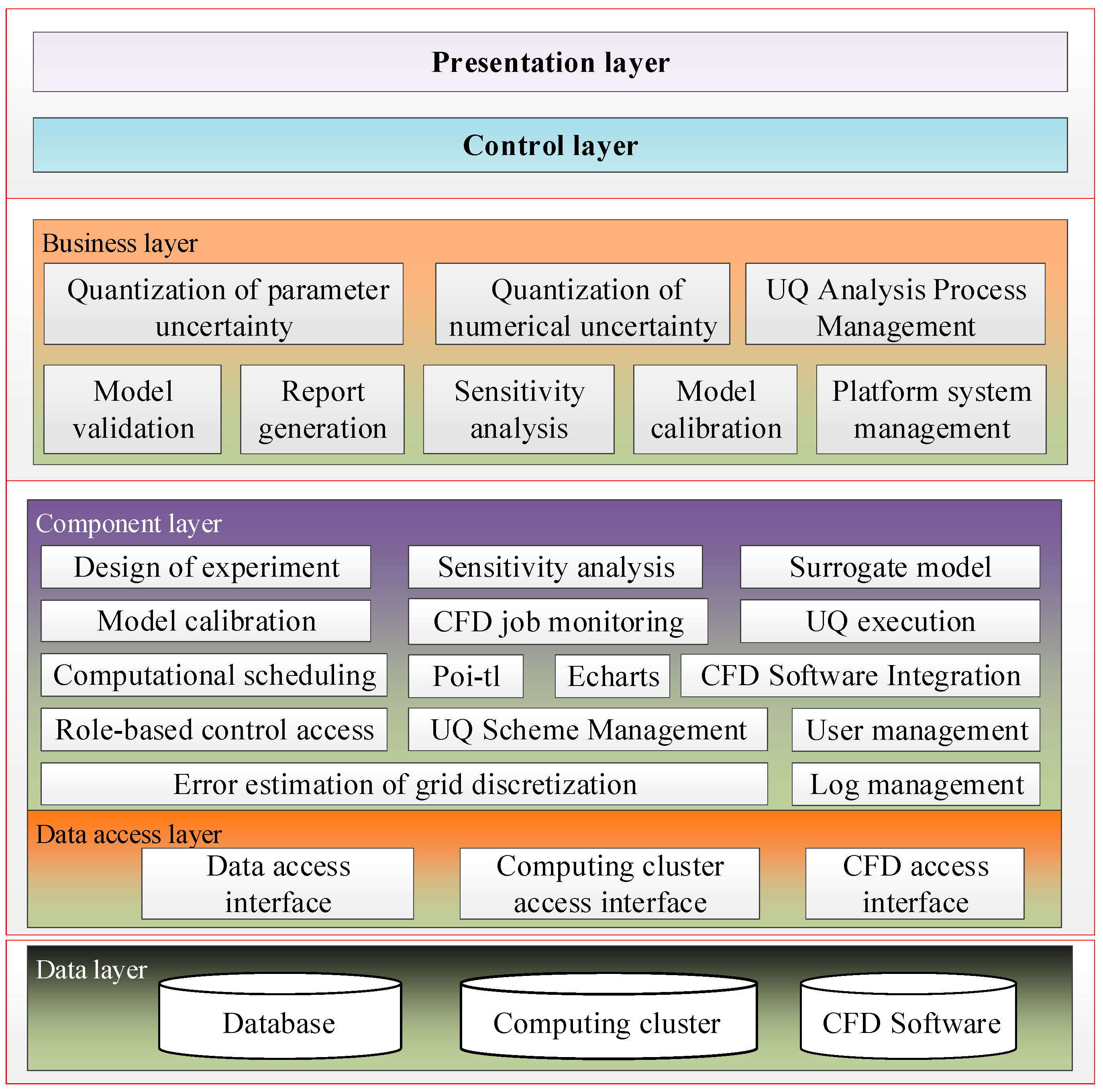
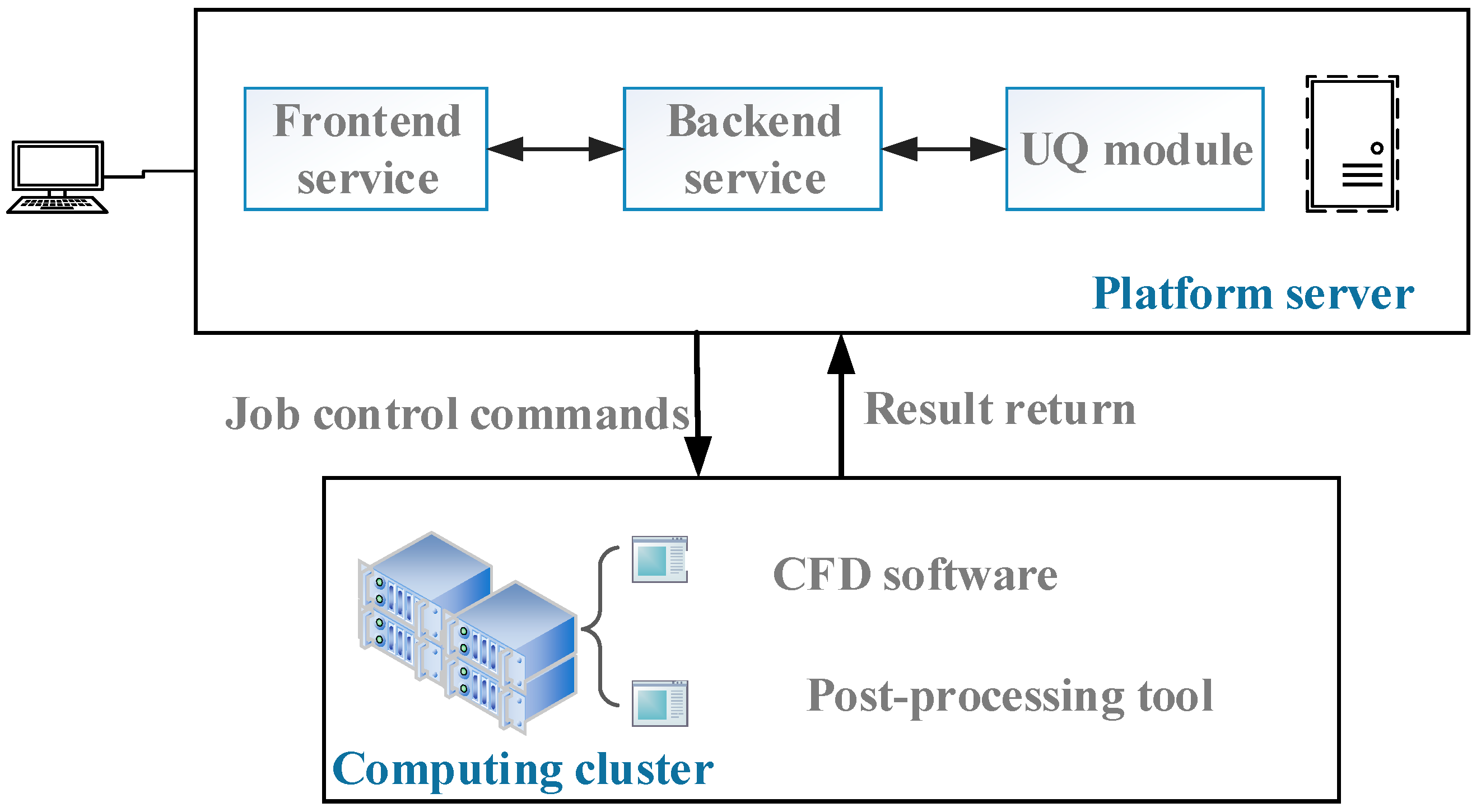
3.1. Software Architecture
3.2. Software Module
3.2.1. UQ Algorithm Module
3.2.2. CFD Software Integration Module
3.2.3. CFD Job Management Module
3.2.4. UQ Workflow Customization Module
3.2.5. Chart and Report Generation Module
3.2.6. System Management Module
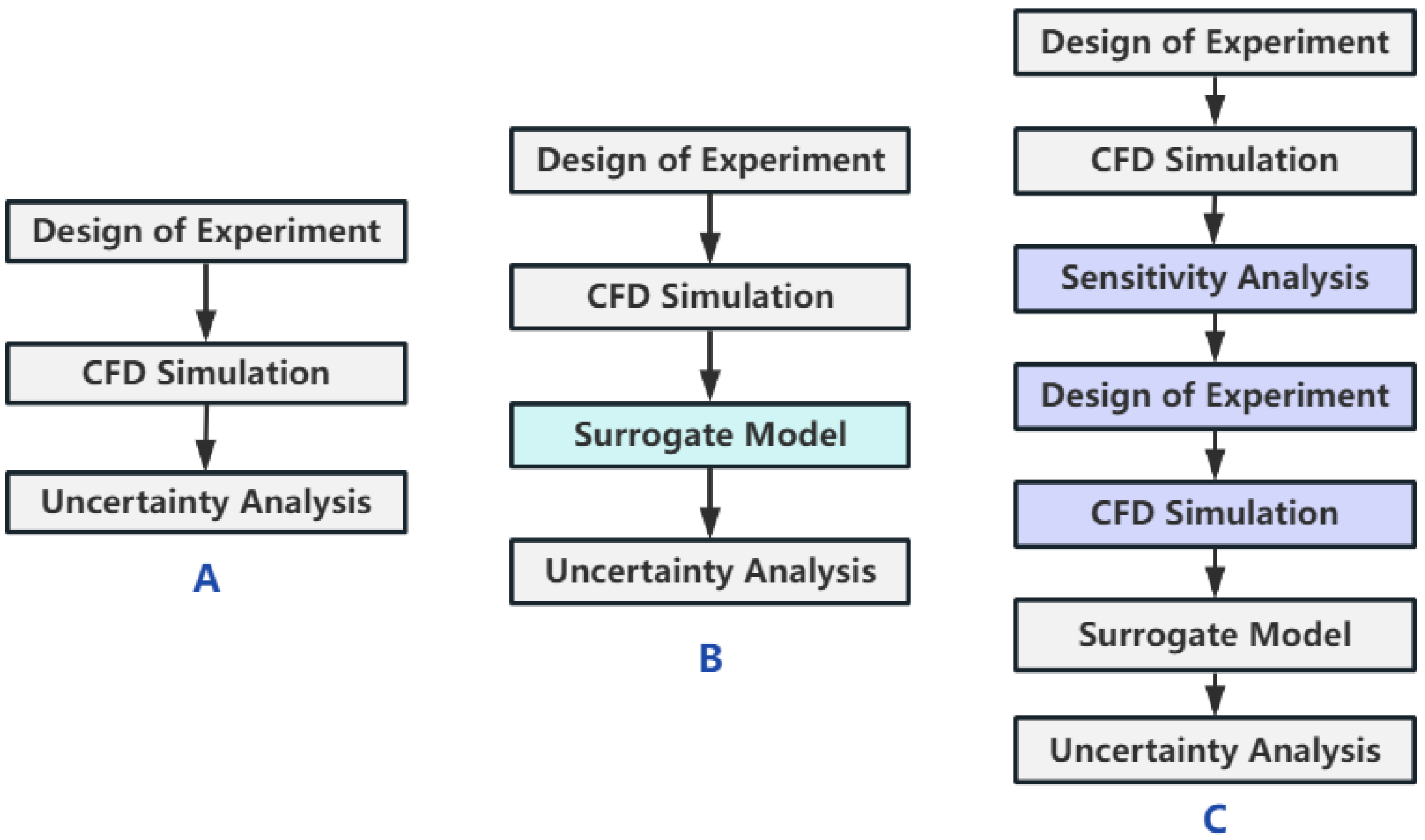
3.3. Software Features
3.3.1. Automation
3.3.2. Flexibility
3.3.3. User-Friendly
4. Test and Application
4.1. Algorithm Test
4.1.1. Sensitivity Analysis Algorithms Test
4.1.2. Model Calibration Algorithms Test
4.2. Numerical Discretization Uncertainty Quantification
4.3. Parametric Uncertainty Quantification
4.3.1. Problem Definition
4.3.2. Uncertainty Propagation
4.3.3. Sensitivity Analysis
4.3.4. Model Calibration
4.4. Application Beyond CFD
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hirsch, C. Non-deterministic simulation for CFD-based design methodologies. In Proceedings of the NATO RTO-AVT-147 Symposium on Computational Uncertainty in Military Vehicle Design, Athens, Greece, 2–6 December 2007. [Google Scholar]
- Obarc, J.; Lamar, J.E. Overview of the cranked-arrow wing aerodynamics project international. J. Aircr. 2009, 46, 355–368. [Google Scholar] [CrossRef]
- Slotnick, J.; Khodadoust, A.; Alonso, J.; Darmofal, D.; Gropp, W.; Lurie, E.; Mavriplis, D. CFD Vision 2030 Study: A Path to Revolutionary Computational Aerosciences; NASA/CR-2014-218178; NASA Langley Research Center: Hampton, VA, USA, 2014.
- Mangeant, F. Current Engineering Practices in UQ&M in Aeronautics and Associated Challenges. 2015. Available online: https://docs.google.com/viewer?a=v&pid=sites&srcid=ZGVmYXVsdGRvbWFpbnx1cTIwMTVwYXJpc2ZyfGd4Ojc5MjFlZGVjNmNlM2UxMDQ (accessed on 19 May 2020).
- Lu, J.; Li, J.; Song, Z.; Zhang, W.; Yan, C. Uncertainty and sensitivity analysis of heat transfer in hypersonic three-dimensional shock waves/turbulent boundary layer interaction flows. Aerosp. Sci. Technol. 2022, 123, 107447. [Google Scholar]
- Carter, N.; Aiken, T.T.; Boyd, I.D. Sensitivity Analysis and Uncertainty Quantification of Plasma Formation in Nonequilibrium Hypersonic Airflows. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025; p. 0950. [Google Scholar]
- Gao, L.; Tu, P.; Yang, G.; Yang, S. Uncertainty Modeling of Fouling Thickness and Morphology on Compressor Blade. Aerospace 2025, 12, 547. [Google Scholar] [CrossRef]
- Tang, P.; Sun, J.; Nian, J.; Lu, J.; Liu, Q. Uncertainty Quantification of the Impact of High-Pressure Compressor Blade Geometric Deviations on Aero Engine Performance. Aerospace 2025, 12, 767. [Google Scholar] [CrossRef]
- Schaefer, J.A.; Hosder, S.; Mani, M.; Cary, A.W.; Krakos, J. The effect of grid topology and flow solver on turbulence model closure coefficient uncertainties for a transonic airfoil. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 4400. [Google Scholar]
- Chen, J.; Zhao, J.; Xiao, W.; Lv, L.; Zhao, W.; Wu, X. A Multi-Fidelity Uncertainty Propagation Model for Multi-Dimensional Correlated Flow Field Responses. Aerospace 2024, 11, 263. [Google Scholar] [CrossRef]
- García-Gutiérrez, A.; Domínguez, D.; Delgado, A.; Rubio, C. Uncertainty Quantification in CFD Aerodynamics: Methods, Applications, and Future Directions. Preprints 2024, 2024120650. Available online: https://doi.org/10.20944/preprints202412.0650.v1 (accessed on 19 May 2020).
- Chen, X.; Wang, G.; Ye, Z.Y.; Wu, X. A review of uncertainty quantification methods for Computational Fluid Dynamics. Acta Aerodyn. Sin. 2021, 39, 1–13. [Google Scholar] [CrossRef]
- Adams, B.M.; Bohnhoff, W.J.; Dalbey, K.R.; Ebeida, M.S.; Eddy, J.P.; Eldred, M.S.; Hooper, R.W.; Hough, P.D.; Hu, K.T.; Jakeman, J.D.; et al. Dakota, A Multilevel Parallel Object-Oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 6.12 User’s Manual; SAND2020-5001 Unlimited Release; Sandia National Lab.(SNL-NM): Albuquerque, NM, USA, 2020.
- Tong, C. PSUADE Reference Manual, Version 1.7; Lawrence Livermore National Laboratory: Livermore, CA, USA, 2015.
- Marelli, S.; Sudret, B. UQLab: A framework for uncertainty quantification in MATLAB. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management; ETH-Zürich: Zürich, Switzerland, 2015. [Google Scholar]
- Wang, C.; Duan, Q.Y.; Charles, H.T.; Di, Z.; Gong, W. A GUI platform for uncertainty quantification of complex dynamical models. Environ. Model. Softw. 2016, 76, 1–12. [Google Scholar] [CrossRef]
- Riha, D.S.; Thacker, B.H.; Pleminhg, J.B.; Walker, J.D.; Mullin, S.A.; Weiss, C.E.; Rodriguez, E.A.; Leslie, P.O. Verification and validation for a penetration model using a deterministic and probabilistic design tool. Int. J. Impact Eng. 2006, 33, 681–690. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practise: A Guide to Assessing Scientific Models; John Wiley & Sons, Ltd.: Chichester, UK, 2004. [Google Scholar]
- Andrianov, G.; Burriel, S.; Cambier, S.; Dutfoy, A.; Dutka-Malen, I.; de Rocquigny, E.; Sudret, B. Open TURNS, an open source initiative to treat uncertainties, Risks’N statistics in a structured industrial approach. In Proceedings of the ESREL’ 2007 Safety and Reliability Conference, Stavenger, Norway, 25–27 June 2007. [Google Scholar]
- Poeter, E.P.; Hill, M.C. UCODE, a computer code for universal inverse modeling. Comput. Geosci. 1999, 25, 457–462. [Google Scholar] [CrossRef]
- Blanchard, J.-B.; Damblin, G.; Martinez, J.-M.; Arnaud, G.; Gaudier, F. The Uranie platform: An Open-source software for optimisation, meta-modelling and uncertainty analysis. EPJ Nucl. Sci. Technol. 2019, 5, 4. [Google Scholar]
- Mehta, U.B.; Eklund, D.R.; Romero, V.J.; Pearce, J.A.; Keim, N.S. Simulation Credibility: Advances in Verification, Validation and Uncertainty Quantification; NASA/TP-2016-219422; NASA Ames Research Center: Moffett Field, CA, USA, 2016.
- Xiu, D.B.; Karniadakis, G.E. The Wiener-Askey polynomial chaos for stochastic differential equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Faes, M.; Imholz, M.; Vandepitte, D.; Moens, D. A review of interval field approaches for uncertainty quantification in numerical models. In Modern Trends in Structural and Solid Mechanics 3: Non-deterministic Mechanics; ISTE Ltd.: London, UK; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2021; pp. 95–110. [Google Scholar]
- Sentz, K.; Ferson, S. Combination of Evidence in Dempster-Shafer Theory; Contemporary Pacific: Honolulu, HI, USA, 2002. [Google Scholar]
- Swiler, L.P.; Mayes, R.L.; Eldred, M.S. Epistemic uncertainty in the calculation of margins. In Proceedings of the 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2009. AIAA Paper AIAA 2009-2249. [Google Scholar]
- Myers, R.H. Response Surface Methodology; Allyn and Bacon, Inc.: Boston, MA, USA, 1971. [Google Scholar]
- Box, G.E.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters: Design, Innovation, and Discovery, 2nd ed.; Wiley: Hoboken, NJ, USA, 2005; ISBN 0-471-71813-0. [Google Scholar]
- Fishman, G.S. Monte Carlo: Concepts, Algorithms, and Applications; Springer: New York, NY, USA, 1996. [Google Scholar]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code. Technometrics 1979, 21, 239–245. [Google Scholar]
- Sobol’, I.M. Distribution of points in a cube and the approximate evaluation of integrals. USSR Comput. Math. Math. Phys. 1967, 7, 86–112. [Google Scholar] [CrossRef]
- Krishnamurthy, T. Response surface approximation with augmented and compactly supported radial basis functions. In Proceedings of the 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Norfolk, VA, USA, 7–10 April 2003. [Google Scholar]
- Krige, D.G. A statistical approach to some basic mine valuations problems on the witwatersrand. J. S. Afr. Inst. Min. Metall. 1951, 52, 119–139. [Google Scholar]
- Park, J.; Sandberg, I.W. Universal approximation using radial-basis-function networks. Neural Comput. 1991, 3, 246–257. [Google Scholar] [CrossRef]
- Shang, X.; Su, L.; Fang, H.; Zeng, B.; Zhang, Z. An efficient multi-fidelity Kriging surrogate model-based method for global sensitivity analysis. Reliab. Eng. Syst. Saf. 2023, 229, 108858. [Google Scholar] [CrossRef]
- Kawai, S.; Shimoyama, K. Kriging-model-based uncertainty quantification in computational fluid dynamics. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; p. 2737. [Google Scholar]
- Chen, J.; Xiao, W.; Lv, L.; Zhao, J.; Zhao, W.; Wu, X. An Adaptive Meta-Modelling Approach for Multi-Dimensional Correlated Flow Field Responses. Int. J. Comput. Fluid Dyn. 2023, 37, 791–801. [Google Scholar] [CrossRef]
- Tripathy, R.K.; Bilionis, I. UQ Deep, Learning deep neural network surrogate models for high dimensional uncertainty quantification. J. Comput. Phys. 2018, 375, 565–588. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.-S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Shustin, P.F.; Ubaru, S.; Kalantzis, V.; Horesh, L.; Avron, H. PCENet: High dimensional surrogate modeling for learning uncertainty. arXiv 2022, arXiv:2202.05063. [Google Scholar] [CrossRef]
- Azarhoosh, Z.; Ghazaan, M.I. A review of recent advances in surrogate models for uncertainty quantification of high-dimensional engineering applications. Comput. Methods Appl. Mech. Eng. 2025, 433, 117508. [Google Scholar] [CrossRef]
- Morris, M.D. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Sobol’, I.M.; Kucherenko, S. Derivative based global sensitivity measures and their link with global sensitivity indices. Math. Comput. Simul. 2009, 79, 3009–3017. [Google Scholar] [CrossRef]
- Sobol’, I.M. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Borgonovo, E. A new uncertainty importance measure. Reliab. Eng. Syst. Saf. 2007, 92, 771–784. [Google Scholar] [CrossRef]
- Dennis, J.E., Jr.; Moré, J.J. Quasi-Newton methods, motivation and theory. SIAM Rev. 1977, 19, 46–89. [Google Scholar] [CrossRef]
- Nazareth, J.L. Conjugate gradient method. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 348–353. [Google Scholar] [CrossRef]
- Katoch, S.; Chauhan, S.S.; Kumar, V. A review on genetic algorithm: Past, present, and future. Multimed. Tools Appl. 2021, 80, 8091–8126. [Google Scholar] [CrossRef] [PubMed]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and efficient global optimization for conceptual rainfall-runoff models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, A. Optimization by simulated annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Wang, C.; Duan, Q.Y.; Gong, W.; Ye, A.; Di, Z.; Miao, C. An evaluation of adaptive surrogate modeling based optimization with two benchmark problems. Environ. Model. Softw. 2014, 60, 167–179. [Google Scholar] [CrossRef]
- Neal, R.M. Probabilistic Inference Using Markov Chain Monte Carlo Methods; Technical Report CRG-TR-93-1; Department of Computer Science: Amsterdam, The Netherlands; University of Toronto: Toronto, ON, Canada, 1993. [Google Scholar]
- Wang, N.; Yao, W.; Zhao, Y.; Chen, X.; Zhang, X.; Li, L. A new interval area metric for model validation with limited experimental data. ASME J. Mech. Des. 2018, 140, 061403. [Google Scholar]
- Ferson, S.; Kreinovich, V.; Grinzburg, L.; Myers, D.S.; Sentz, K. Constructing Probability Boxes and Dempster-Shafer Structures; Sandia National Lab.: Albuquerque, NM, USA, 2015.
- Li, W.; Chen, W.; Jiang, Z.; Lu, Z.; Liu, Y. New validation metrics for models with multiple correlated responses. Reliab. Eng. Syst. Saf. 2014, 127, 1–11. [Google Scholar] [CrossRef]
- Tinoco, E. Summary data from the seventh AIAA CFD drag prediction workshop. In Proceedings of the AIAA Aviation 2023 Forum, San Diego, CA, USA, 12–16 June 2023. [Google Scholar]
- Rumsey, C.L.; Slotnick, J.P.; Woeber, C.D. Fourth High-Lift Prediction/Third Geometry and Mesh Generation Workshops: Overview and Summary. J. Aircr. 2023, 60, 1160–1177. [Google Scholar]
- Celik, I.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef]
- Eça, L.; Hoekstra, M. A procedure for the estimation of the numerical uncertainty of CFD calculations based on grid refinement studies. J. Comput. Phys. 2014, 262, 104–130. [Google Scholar] [CrossRef]
- Cortesi, A.F.; Constantine, P.G.; Magin, T.E.; Congedo, P.M. Forward and backward uncertainty quantification with active subspaces: Application to hypersonic flows around a cylinder. J. Comput. Phys. 2020, 407, 109079. [Google Scholar] [CrossRef]
- Peyvan, A.; Kumar, V.; Karniadakis, G.E. Fusion DeepONet: A Data-Efficient Neural Operator for Geometry-Dependent Hypersonic Flows on Arbitrary Grids. arXiv 2025, arXiv:2501.01934. [Google Scholar]
- Iwanaga, T.; Usher, W.; Herman, J. Toward SALib 2.0: Advancing the accessibility and interpretability of global sensitivity analyses. Socio-Environ. Syst. Model. 2022, 4, 18155. [Google Scholar]
- Chen, J.; Wu, X.; Zhang, J.; Li, B.; Jia, H.; Zhou, N. FlowStar: General unstructured-grid CFD software for National Numerical Wind tunnel (NNW) Project. ACTA Aeronaut. Astronaut. Sin. 2021, 42, 625739. [Google Scholar]
- Cui, P.; Li, H.; Jia, H.; Li, L.; Qin, F.; Wu, X.; Zhang, Y. An improved Harten–Lax–Leer–Einfeldt plus plus scheme for unstructured grid and cell-centred finite-volume method. Phys. Fluids 2025, 37, 076130. [Google Scholar] [CrossRef]
- Spalart, P.R.; Allmaras, S.R. A One-Equation Turbulence Model for Aerodynamic Flows. AIAA J. 1992, 30, 5–12. [Google Scholar]
- Chen, J.; Zhang, C.; Liu, X.; Zhao, H.; Hu, X.; Wu, X. Uncertainty quantification analysis with sparse polynomial chaos method. ACTA Aeronaut. Astronaut. Sin. 2020, 41, 169–177. [Google Scholar]
- Lachaud, J.R.; Martin, A.; Cozmuta, I.; Laub, B. Test Case Series 1 (2011). Ablation Workshop: Code Comparison. 1. Available online: https://uknowledge.uky.edu/ablation_code/1 (accessed on 3 March 2025).
- Liu, X.; Guo, Y.J.; Liu, W.; Zeng, L. Finite element computation of three-dimensional ablation thermal response for carbonaceous materials. J. Astronaut. 2016, 37, 1150–1156. [Google Scholar]
- Ghoreyshi, M.; Badcock, K.J.; Da Ronch, A.; Marques, S.; Swift, A.; Ames, N. Framework for establishing limits of tabular aerodynamic models for flight dynamics analysis. J. Aircr. 2011, 48, 42–55. [Google Scholar] [CrossRef]
- Mohammadi-Amin, M.; Entezari, M.M.; Alikhani, A. An efficient surrogate-based framework for aerodynamic database development of manned reentry vehicles. Adv. Space Res. 2018, 62, 997–1014. [Google Scholar] [CrossRef]





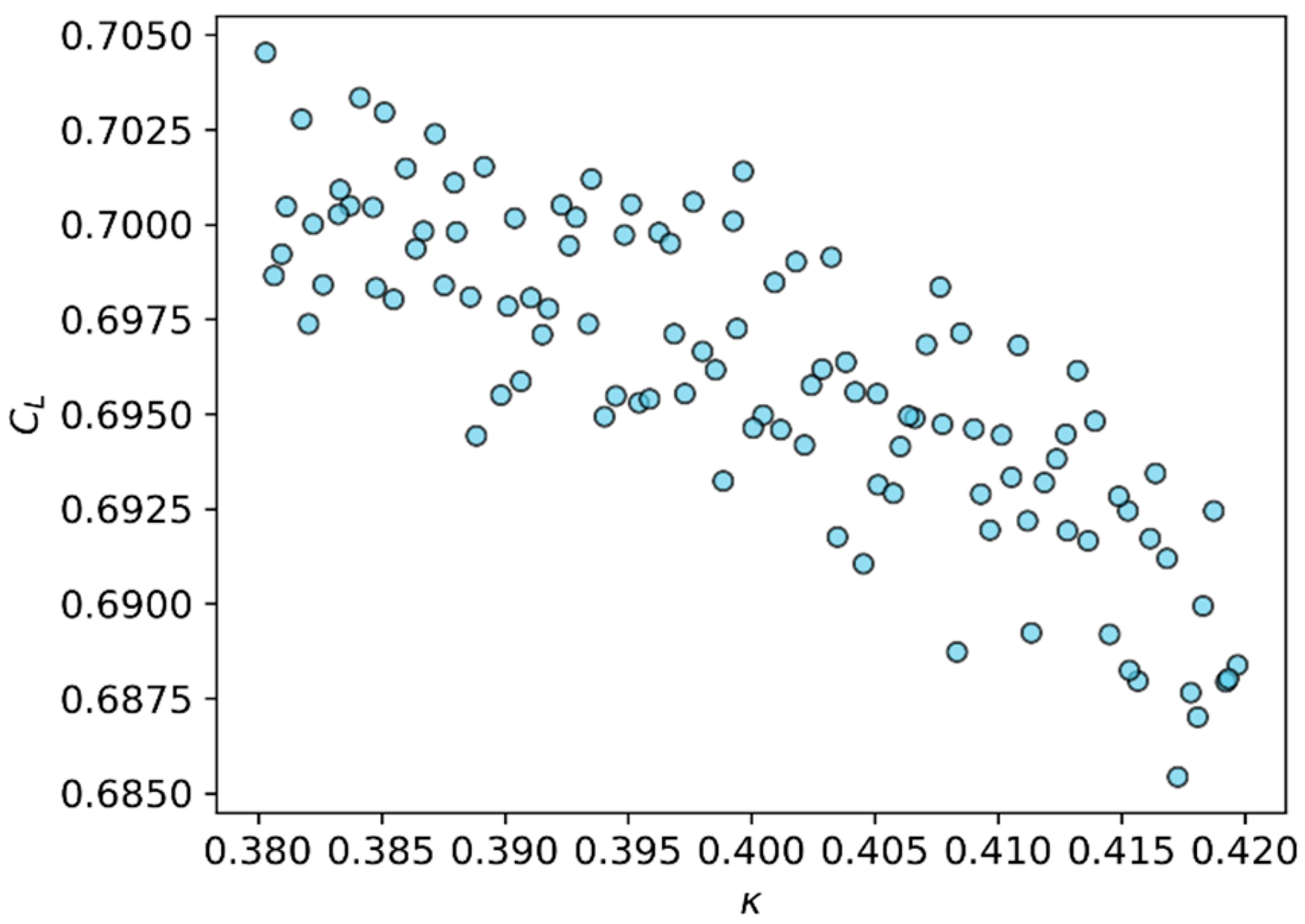
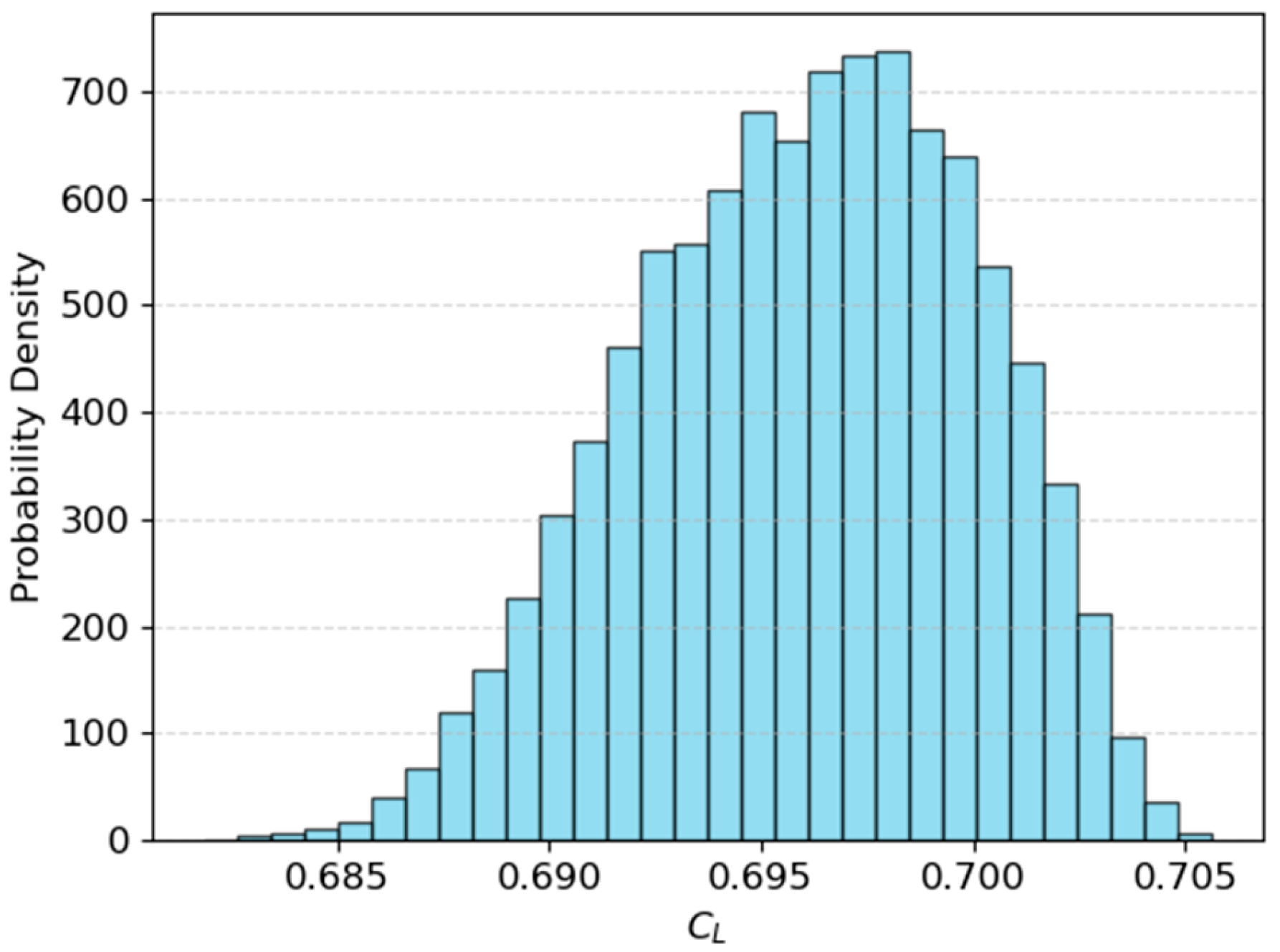
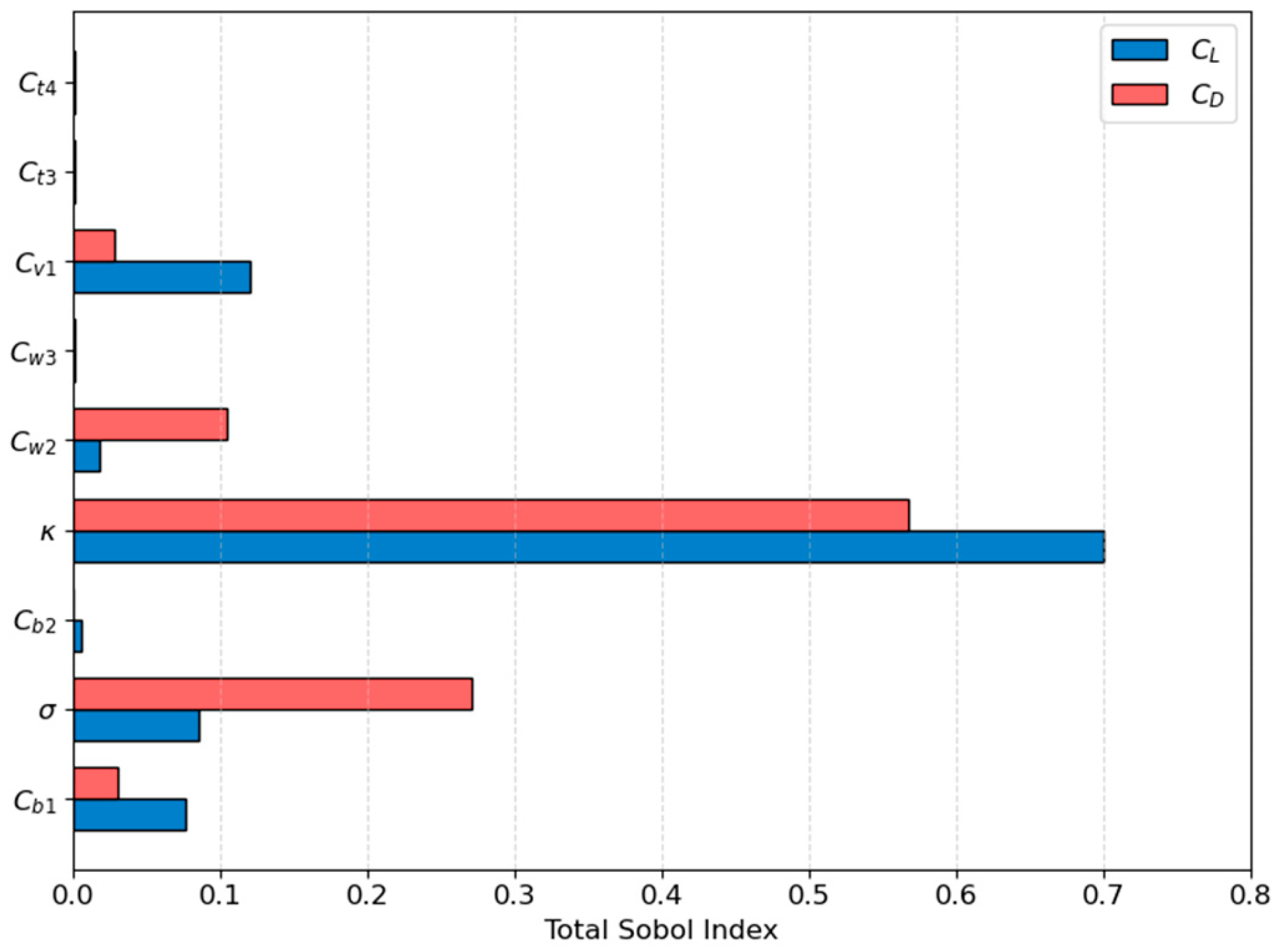
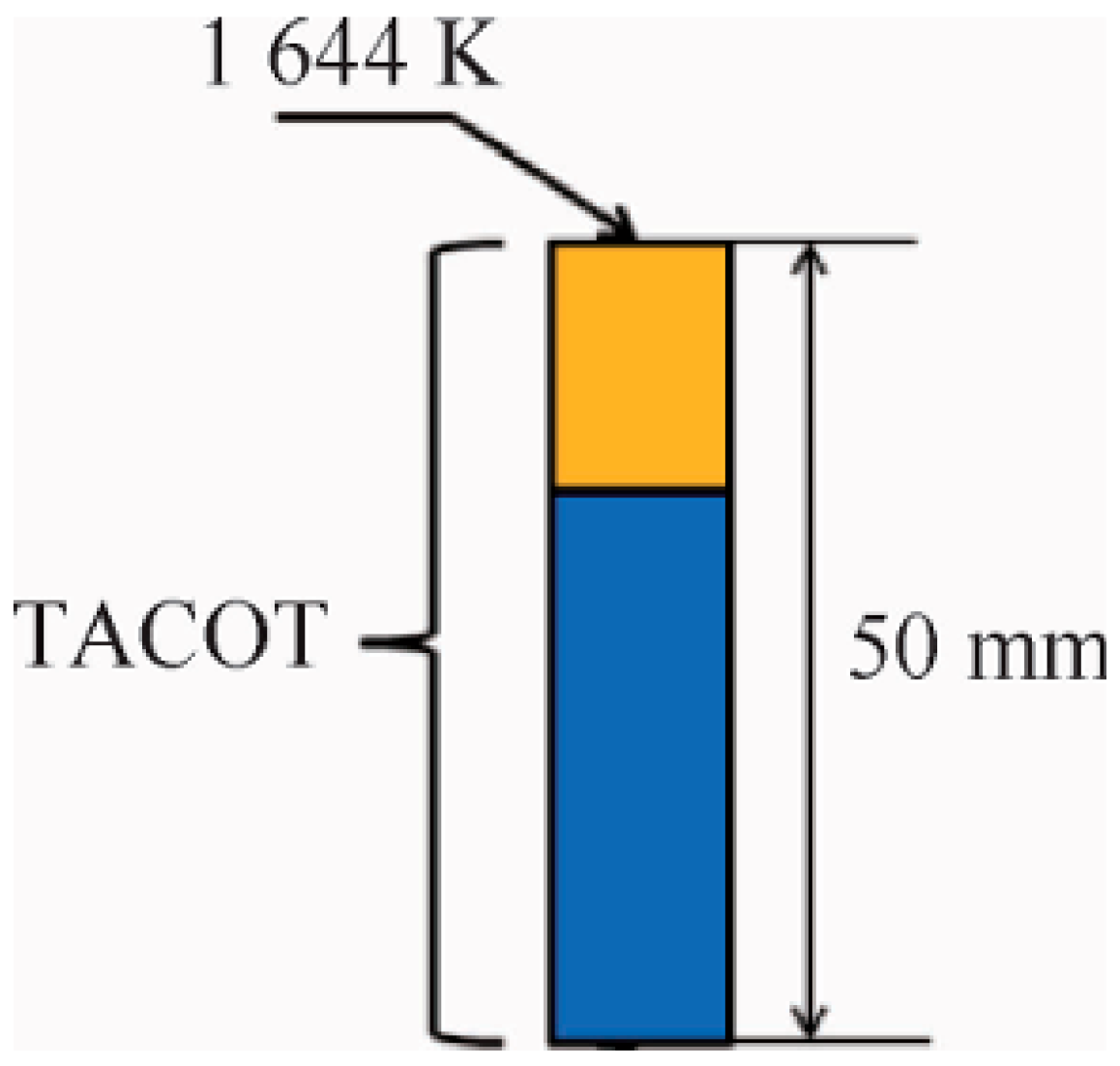

| Sub-Module | Function | Algorithms |
|---|---|---|
| Design of experiment | Generate input sample data which can accurately reflect the characteristics of the model in the design space | Central-Composite [27], Full-Factorial [28], Monte Carlo [29], Latin Hypercube Sampling [30], Sobol [31], MOAT [42] |
| Uncertainty analysis | Quantify the uncertainty of model outputs | Statistical Analysis, Interval Analysis [24], Probability Box [26] |
| Sensitivity analysis | Qualitative or quantitative analysis of the influence of uncertain input factors on model outputs | Morris [42], Sobol [44], PCE-Sobol |
| Surrogate model | Construct a high-precision surrogate model to replace CFD solver for uncertainty analysis | Polynomial Chaos Expansion [23], Radial Basis Function [32], Kriging [33], Neural Network [34] |
| Model calibration | Calibrate model parameters to reduce the deviation between the simulation and experimental results | Quasi-Newton [46], Conjugate Gradient [47], Genetic Algorithm [48], MCMC [52] |
| Model validation metric | Quantitatively evaluate the coincidence degree between simulation results and experimental results | Area Metric [53], Interval Area Metric [53], Probability Box Metric [54], U-pooling [55] |
| Numerical discretization uncertainty analysis | Evaluate the influence of grid discretization on model outputs | GCI [58], Richardson Extrapolation [59] |
| Method | S1 | S2 | S3 | ST1 | ST2 | ST3 |
|---|---|---|---|---|---|---|
| Theoretical solutions | 0.3138 | 0.4424 | 0.0000 | 0.5574 | 0.4424 | 0.2436 |
| Sobol (SALib software) | 0.3168 | 0.4437 | 0.0122 | 0.5558 | 0.4418 | 0.2446 |
| Sobol (UQ4CFD) | 0.3185 | 0.4432 | 0.0013 | 0.5513 | 0.4327 | 0.2360 |
| PCE-Sobol (UQ4CFD) | 0.3147 | 0.4414 | 0.0000 | 0.5586 | 0.4414 | 0.2439 |
| Parameters | Probability Distribution | Min | Max |
|---|---|---|---|
| M | Uniform | 7 | 13 |
| D | Uniform | 0.02 | 0.12 |
| L | Uniform | 0.01 | 3 |
| Parameters | Exact Value | MAP | Posterior Mean |
|---|---|---|---|
| M | 10.000 | 10.000 | 10.041 |
| D | 0.070 | 0.070 | 0.071 |
| L | 1.505 | 1.505 | 1.505 |
| Observed Order | Richardson Extrapolation Solution | GCI |
|---|---|---|
| 2.00002 | 0.02570 | 0.00042 |
| Parameter | Minimum Value | Maximum Value | Standard Value |
|---|---|---|---|
| cb1 | 0.12893 | 0.137 | 0.1355 |
| σ | 0.6 | 1.0 | 2/3 |
| cb2 | 0.60983 | 0.6875 | 0.622 |
| κ | 0.38 | 0.42 | 0.41 |
| cw2 | 0.055 | 0.3525 | 0.3 |
| cw3 | 1.75 | 2.5 | 2.0 |
| cv1 | 6.9 | 7.3 | 7.1 |
| ct3 | 1.0 | 2.0 | 1.2 |
| ct4 | 0.3 | 0.7 | 0.5 |
| Parameter | Standard Value | Calibrated Value | Relative Error |
|---|---|---|---|
| κ | 0.41 | 0.406 | 0.976% |
| cv1 | 7.1 | 7.102 | −0.028% |
| Radial Basis Function | Kriging | Neural Network |
|---|---|---|
| 4.039 | 1.484 | 4.040 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, W.; Zhao, J.; Lv, L.; Chen, J.; Zhang, P.; Wu, X. UQ4CFD: An Uncertainty Quantification Platform for CFD Simulation. Aerospace 2025, 12, 886. https://doi.org/10.3390/aerospace12100886
Xiao W, Zhao J, Lv L, Chen J, Zhang P, Wu X. UQ4CFD: An Uncertainty Quantification Platform for CFD Simulation. Aerospace. 2025; 12(10):886. https://doi.org/10.3390/aerospace12100886
Chicago/Turabian StyleXiao, Wei, Jiao Zhao, Luogeng Lv, Jiangtao Chen, Peihong Zhang, and Xiaojun Wu. 2025. "UQ4CFD: An Uncertainty Quantification Platform for CFD Simulation" Aerospace 12, no. 10: 886. https://doi.org/10.3390/aerospace12100886
APA StyleXiao, W., Zhao, J., Lv, L., Chen, J., Zhang, P., & Wu, X. (2025). UQ4CFD: An Uncertainty Quantification Platform for CFD Simulation. Aerospace, 12(10), 886. https://doi.org/10.3390/aerospace12100886





