Analysis of Electro-Thermal De-Icing on a NACA0012 Airfoil Under Harsh SLD Conditions and Different Angles of Attack
Abstract
1. Introduction
2. Methodology
2.1. Governing Equations for the Icing/De-Icing Model
2.2. Numerical Model Setup and Validation
3. Results and Discussion
3.1. Simulation of Ice Accretion Without De-Icing
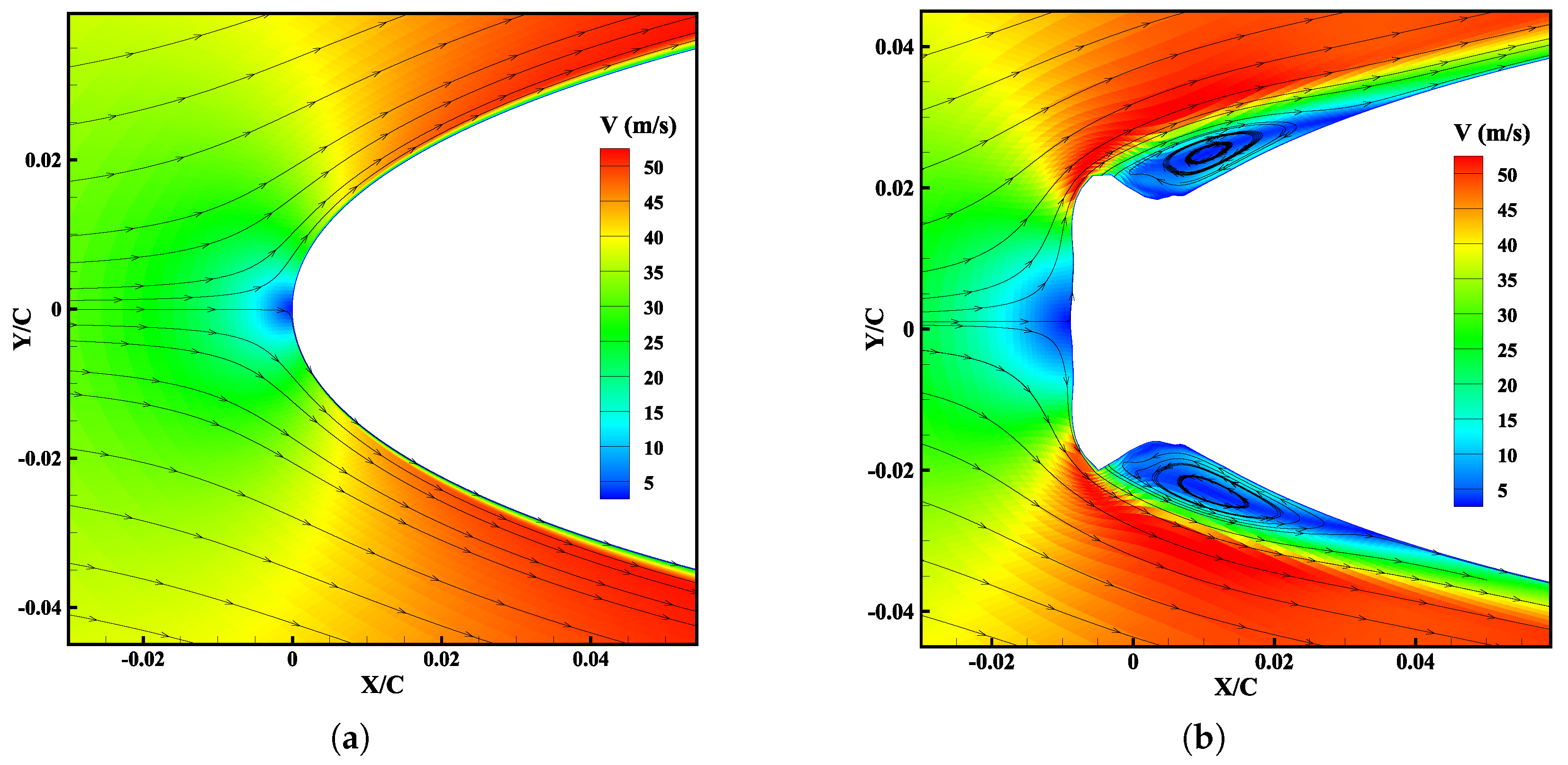
3.2. Aerodynamics Degradation
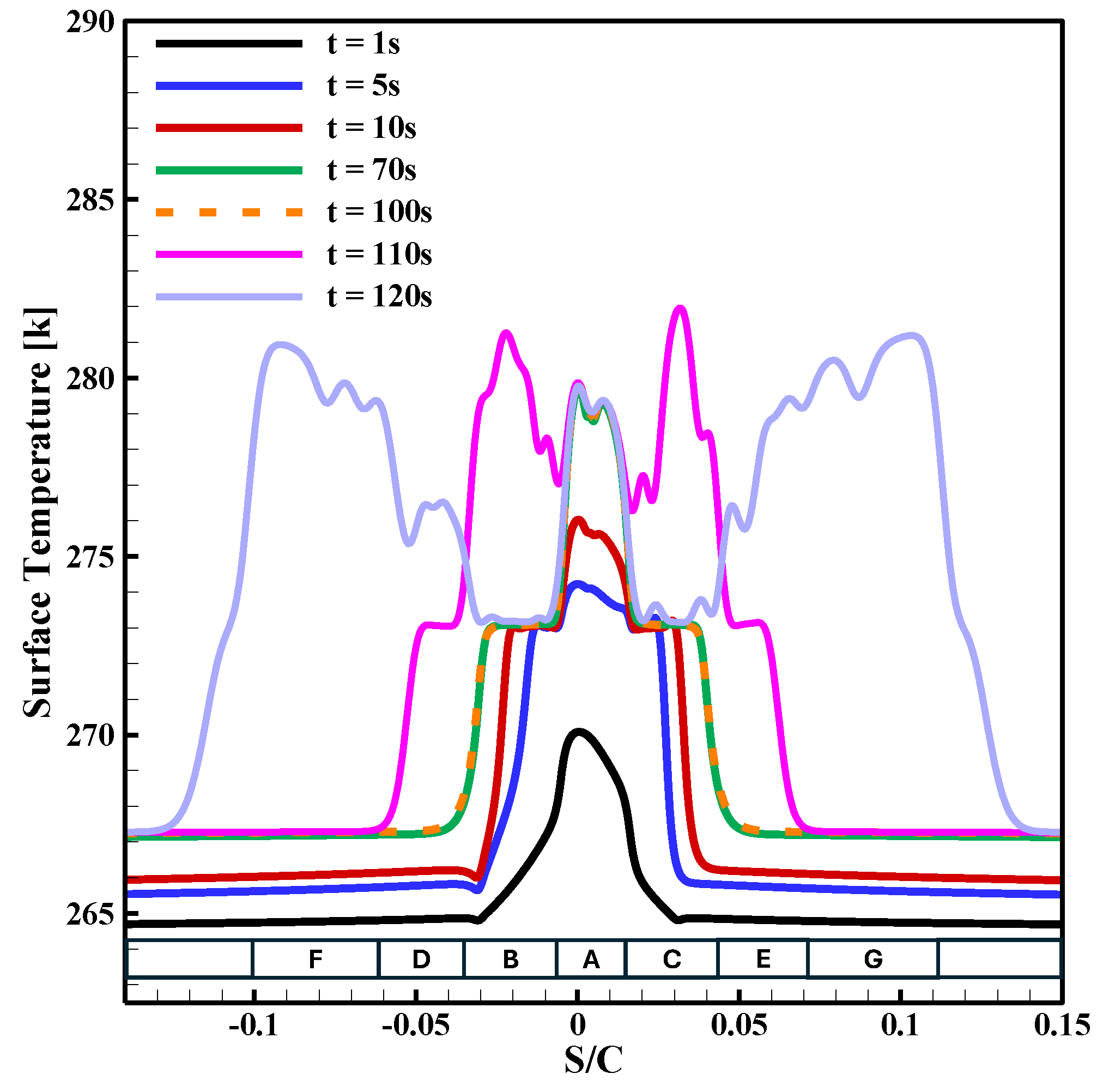
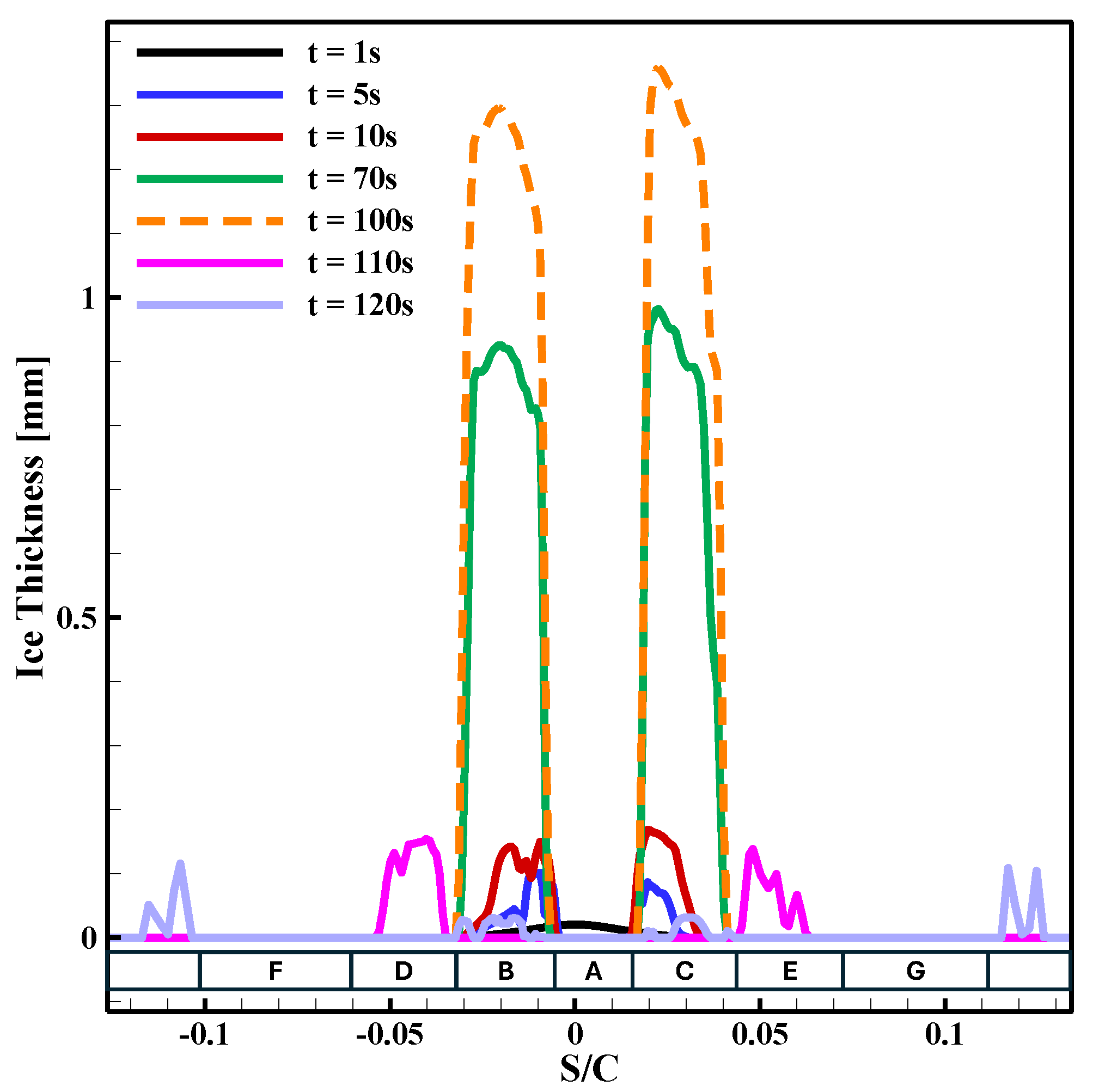
3.3. Analysis of Electro-Thermal De-Icing System in Normal Icing Conditions
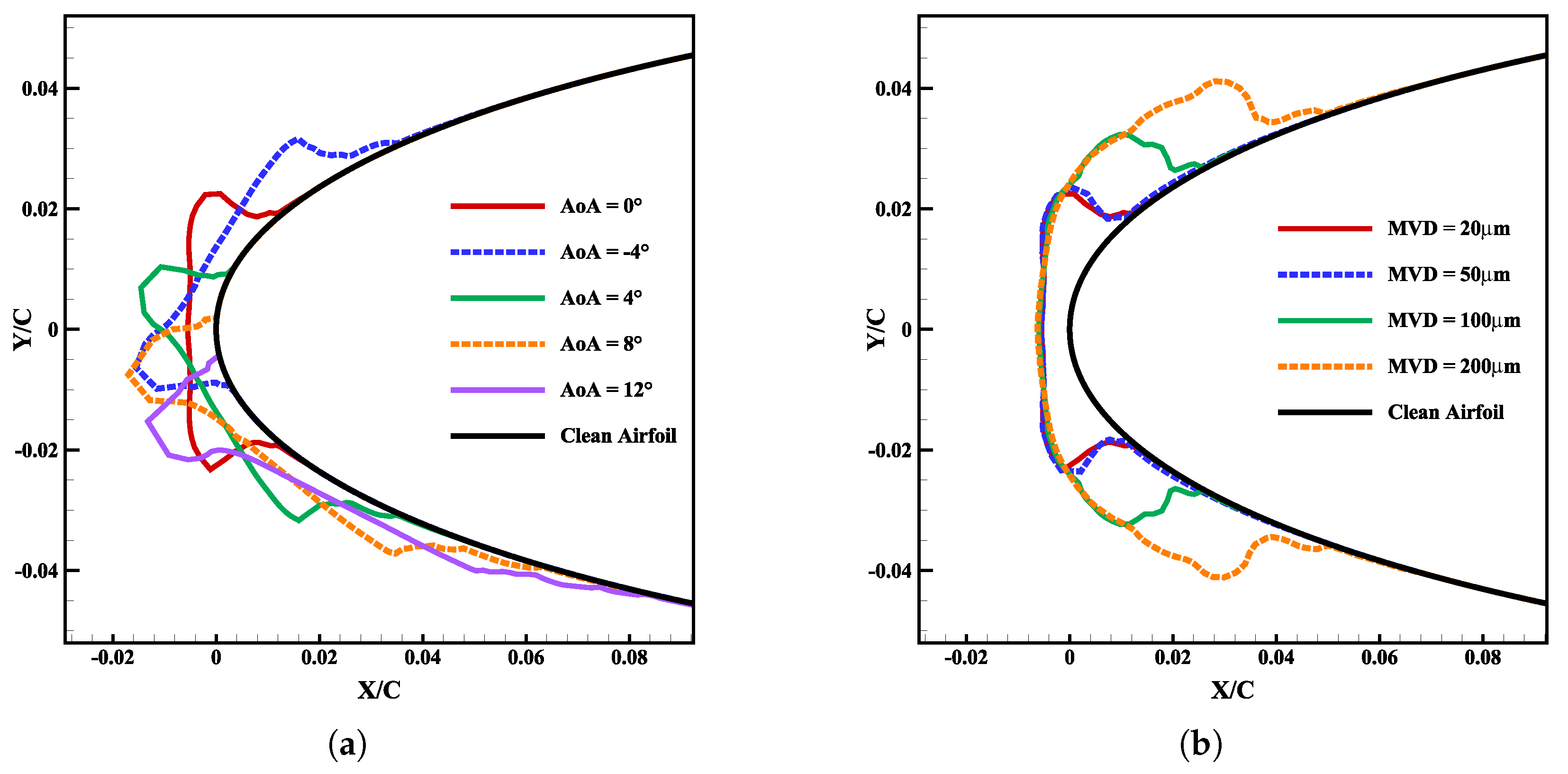
3.4. Analysis of Electro-Thermal De-Icing System at Various Angles of Attack
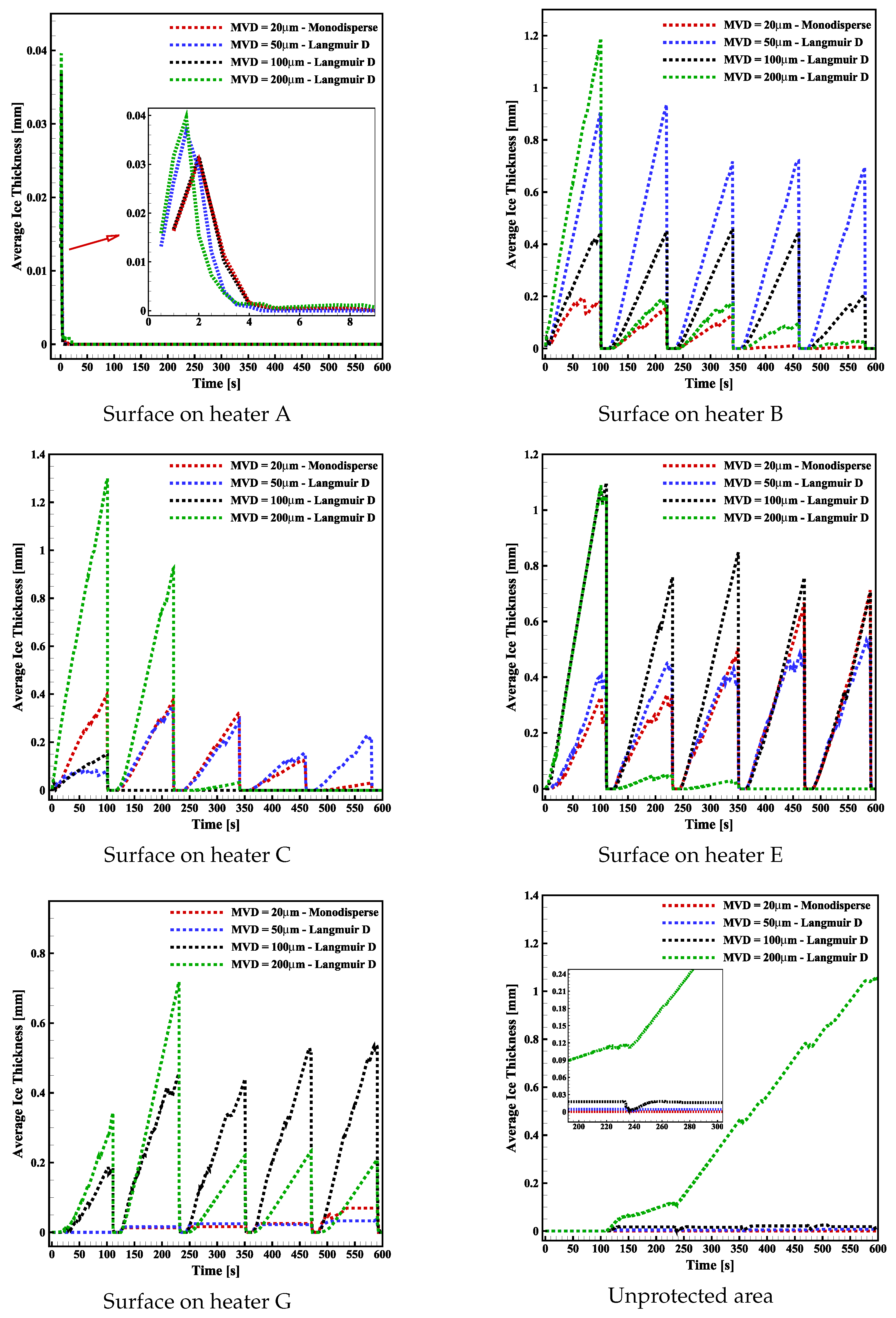
3.5. Analysis of Electro-Thermal De-Icing System in Harsh SLD Condition
3.6. Broader Implications and Outlook
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameters | |
| Convective heat-transfer coefficient [W ] | |
| Specific heat [J ] | |
| Energy of droplet [J] | |
| h | Thickness [m] |
| L | Latent heat [J ] |
| LWC | Liquid water content [kg ] |
| Mass transfer rate [kg ] | |
| Q | Heat flux [W ] |
| T | Temperature [K] |
| Mean velocity [m ] | |
| Velocity vector [m ] | |
| Water volume fraction | |
| Weber number | |
| Ohnesorge number | |
| Droplet’s surface tension | |
| Mundo parameter | |
| Cossali parameter | |
| Boltzmann constant [W ] | |
| Solid emissivity | |
| Collection efficiency | |
| Froude Number | |
| Drag coefficient | |
| Droplet Reynolds number | |
| K | Inertial parameter |
| Dynamic viscosity [Pa s] | |
| Wall shear stress [Pa] | |
| Enthalpy change [J] | |
| S | Curvilinear arc length along the airfoil surface from the leading-edge [m] |
| C | Chord length (leading edge to trailing edge) [m] |
| Subscripts | |
| a | Air |
| d | Droplet |
| evap | Evaporation |
| f | Water film |
| rec | Recovery |
| ∞ | Reference (freestream) |
References
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Kong, W.; Liu, H. Unified icing theory based on phase transition of supercooled water on a substrate. Int. J. Heat Mass Transf. 2018, 123, 896–910. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, Q.; Lin, T.; Cheng, P. A review of recent literature on icing phenomena: Transport mechanisms, their modulations and controls. Int. J. Heat Mass Transf. 2020, 159, 120074. [Google Scholar] [CrossRef]
- Bourgault, Y.; Beaugendre, H.; Habashi, W.G. Development of a shallow-water icing model in FENSAP-ICE. J. Aircr. 2000, 37, 640–646. [Google Scholar] [CrossRef]
- Nath, P.; Lokanathan, N.; Wang, J.; Benmeddour, A.; Nichman, L.; Ranjbar, K.; Hickey, J.P. Parametric investigation of aerodynamic performance degradation due to icing on a symmetrical airfoil. Phys. Fluids 2024, 36, 075117. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Y.; Li, H.; Zhao, W. Numerical study on glaze ice accretion characteristics over time for a NACA 0012 airfoil. Coatings 2023, 14, 55. [Google Scholar] [CrossRef]
- Esmaeilifar, E.; Raj, L.P.; Myong, R. Computational simulation of aircraft electrothermal de-icing using an unsteady formulation of phase change and runback water in a unified framework. Aerosp. Sci. Technol. 2022, 130, 107936. [Google Scholar] [CrossRef]
- Rausa, A.; Guardone, A. Multi-physics simulation of in-flight ice shedding. In Proceedings of the Journal of Physics: Conference Series; IOP Publishing: Bristol, UK, 2021; Volume 1730, p. 012024. [Google Scholar]
- Sengupta, B.; Raj, L.P.; Cho, M.; Son, C.; Yoon, T.; Yee, K.; Myong, R. Computational simulation of ice accretion and shedding trajectory of a rotorcraft in forward flight with strong rotor wakes. Aerosp. Sci. Technol. 2021, 119, 107140. [Google Scholar] [CrossRef]
- Farabello, L.; Scarabino, A.; Bacchi, F. Numerical analysis of ice accretion on an airfoil: A case study. Rev. Fac. Ing. Univ. Antioq. 2025, 116, 100–109. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Sotoudeh, F.; Chun, B.; Lee, B.J.; Karimi, N.; Faroughi, S.A. The potential for anti-icing wing and aircraft applications of mixed-wettability surfaces-A comprehensive review. Cold Reg. Sci. Technol. 2024, 217, 104042. [Google Scholar] [CrossRef]
- Janjua, Z.A.; Turnbull, B.; Hibberd, S.; Choi, K.S. Mixed ice accretion on aircraft wings. Phys. Fluids 2018, 30, 027101. [Google Scholar] [CrossRef]
- Bodoc, V.; Berthoumieu, P.; Déjean, B. Experimental investigation of large droplet impact with application to SLD icing. Microgravity Sci. Technol. 2021, 33, 59. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, F.; Kong, W.; Liu, H. The Characteristics of SLD icing accretions and aerodynamic effects on high-lift configurations. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 3385. [Google Scholar]
- Yamazaki, M.; Jemcov, A.; Sakaue, H. A review on the current status of icing physics and mitigation in aviation. Aerospace 2021, 8, 188. [Google Scholar] [CrossRef]
- Lee, J.W.; Cho, M.Y.; Kim, Y.H.; Yee, K.; Myong, R.S. Current status and prospect of aircraft ice protection systems. J. Korean Soc. Aeronaut. Space Sci. 2020, 48, 911–925. [Google Scholar] [CrossRef]
- Gallia, M.; Carnemolla, A.; Premazzi, M.; Guardone, A. Optimisation of a Nacelle Electro-Thermal Ice Protection System for Icing Wind Tunnel Testing. Trans. Aerosp. Res. 2023, 2023, 32–44. [Google Scholar] [CrossRef]
- Tormen, D.; Zanon, A.; De Gennaro, M. Ice Protection System Design for the Next Generation Civil Tiltrotor Engine Intake; Technical Report; SAE Technical Paper: Warrendale, PA, USA, 2023. [Google Scholar]
- Hann, R.; Enache, A.; Nielsen, M.C.; Stovner, B.N.; van Beeck, J.; Johansen, T.A.; Borup, K.T. Experimental heat loads for electrothermal anti-icing and de-icing on UAVs. Aerospace 2021, 8, 83. [Google Scholar] [CrossRef]
- Shi, K.; Duan, X. A review of ice protection techniques for structures in the Arctic and offshore harsh environments. J. Offshore Mech. Arct. Eng. 2021, 143, 064502. [Google Scholar] [CrossRef]
- Pourbagian, M.; Habashi, W. On Optimal Design of Electro-Thermal In-Flight Ice Protection Systems. In Proceedings of the 5th AIAA Atmospheric and Space Environments Conference, San Diego, CA, USA, 24–27 June 2013; p. 2937. [Google Scholar]
- Gallia, M.; Rausa, A.; Martuffo, A.; Guardone, A. A Comprehensive Numerical Model for Numerical Simulation of Ice Accretion and Electro-Thermal Ice Protection System in Anti-icing and De-icing Mode, with an Ice Shedding Analysis; SAE International: Warrendale, PA, USA, 2023; pp. 2688–3627. ISSN 0148-7191. [Google Scholar] [CrossRef]
- He, Z.; Wang, J. Anti-icing strategies are on the way. Innovation 2022, 3, 100278. [Google Scholar] [CrossRef]
- He, Z.; Xie, H.; Jamil, M.I.; Li, T.; Zhang, Q. Electro-/Photo-Thermal Promoted Anti-Icing Materials: A New Strategy Combined with Passive Anti-Icing and Active De-Icing. Adv. Mater. Interfaces 2022, 9, 2200275. [Google Scholar] [CrossRef]
- Mauery, T.; Alonso, J.; Cary, A.; Lee, V.; Malecki, R.; Mavriplis, D.; Medic, G.; Schaefer, J.; Slotnick, J. A Guide for Aircraft Certification by Analysis; Technical Report; National Aeronautics and Space Administrat: Hampton, VA, USA, 2021.
- Gutiérrez, B.A.; Della Noce, A.; Gallia, M.; Bellosta, T.; Guardone, A. Numerical simulation of a thermal Ice Protection System including state-of-the-art liquid film model. J. Comput. Appl. Math. 2021, 391, 113454. [Google Scholar] [CrossRef]
- Bennani, L.; Trontin, P.; Radenac, E. Numerical simulation of an electrothermal ice protection system in anti-icing and deicing mode. Aerospace 2023, 10, 75. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, Z.; Su, J.; Yao, J.; Wang, H. Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations. Aerospace 2025, 12, 492. [Google Scholar] [CrossRef]
- Stewart, E.A.; Bartkus, T.P. Computational Icing Analysis on NASA’s SIDRM Geometry to Investigate Collection Efficiency. In Proceedings of the International Conference on Icing of Aircraft, Engines, and Structures, Vienna, Austria, 20–22 June 2023. [Google Scholar]
- Uranai, S.; Fukudome, K.; Mamori, H.; Fukushima, N.; Yamamoto, M. Numerical simulation of the anti-icing performance of electric heaters for icing on the NACA 0012 airfoil. Aerospace 2020, 7, 123. [Google Scholar] [CrossRef]
- Milani, Z.R.; Matida, E.; Razavi, F.; Ronak Sultana, K.; Timothy Patterson, R.; Nichman, L.; Benmeddour, A.; Bala, K. Numerical Icing Simulations of Cylindrical Geometry and Comparisons to Flight Test Results. J. Aircr. 2024, 61, 1272–1282. [Google Scholar] [CrossRef]
- Martini, F.; Ibrahim, H.; Contreras Montoya, L.; Rizk, P.; Ilinca, A. Turbulence modeling of iced wind turbine airfoils. Energies 2022, 15, 8325. [Google Scholar] [CrossRef]
- Esmaeilifar, E.; Sengupta, B.; Raj, L.P.; Myong, R. In-flight anti-icing simulation of electrothermal ice protection systems with inhomogeneous thermal boundary condition. Aerosp. Sci. Technol. 2024, 150, 109210. [Google Scholar] [CrossRef]
- Papadakis, M.; Yeong, H.W.; Wong, S.C.; Vargas, M.; Potapczuk, M. Experimental Investigation of Ice Accretion Effects on a Swept Wing: Final Report; FAA Technical Report DOT/FAA/AR-05/39; Federal Aviation Administration: Washington, DC, USA, 2005. [Google Scholar]
- Langmuir, I.; Blodgett, K. A Mathematical Investigation of Water Droplet Trajectories; Number 5418, Army Air Forces Headquarters, Air Technical Service Command: Washington, DC, USA, 1946. [Google Scholar]
- Ansys. Ansys FENSAP-ICE User Manual, Release 2022 R2; Ansys: Canonsburg, PA, USA, 2022. [Google Scholar]
- Aupoix, B.; Spalart, P. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness. Int. J. Heat Fluid Flow 2003, 24, 454–462. [Google Scholar] [CrossRef]
- Wright, W.B.; Al-Khalil, K.; Miller, D. Validation of NASA thermal ice protection computer codes. II–LEWICE/Thermal. In Proceedings of the 35th Aerospace Sciences Meeting and Exhibit, AIAA, Reno, NV, USA, 6–9 January 1997. [Google Scholar] [CrossRef]
- Zhou, Z.; Li, F.; Li, G.; Sang, W. Icing numerical simulation for single and multi-element airfoils. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4232. [Google Scholar]
- Costes, M.; Moens, F.; Brunet, V. Prediction of iced airfoil aerodynamic characteristics. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016; p. 1547. [Google Scholar]
- Shen, X.; Wang, H.; Lin, G.; Bu, X.; Wen, D. Unsteady simulation of aircraft electro-thermal deicing process with temperature-based method. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2020, 234, 388–400. [Google Scholar] [CrossRef]
- Federal Aviation Administration. CFR Part 25 Appendix C. In Federal Register Rules and Regulations; Federal Aviation Administration: Washington, DC, USA, 2011. [Google Scholar]
- Federal Aviation Administration. Airplane and Engine Certification Requirements in Supercooled Large Drop, Mixed Phase, and Ice Crystal Icing Conditions. In Federal Register Rules and Regulations; Federal Aviation Administration: Washington, DC, USA, 2014. [Google Scholar]
- Yang, X.; Bai, X.; Cao, H. Influence analysis of rime icing on aerodynamic performance and output power of offshore floating wind turbine. Ocean. Eng. 2022, 258, 111725. [Google Scholar] [CrossRef]
- Suzzi, N.; Croce, G. Numerical simulation of film instability over low wettability surfaces through lubrication theory. Phys. Fluids 2019, 31, 122106. [Google Scholar] [CrossRef]
- Raj, L.P.; Lee, J.; Myong, R. Ice accretion and aerodynamic effects on a multi-element airfoil under SLD icing conditions. Aerosp. Sci. Technol. 2019, 85, 320–333. [Google Scholar] [CrossRef]
- Papadakis, M.; Federal Aviation Administration, Office of Aviation Research; Wichita State University, Department of Aerospace Engineering; NASA Glenn Research Center. Experimental Investigation of Ice Accretion Effects on a Swept Wing: Final Report; DOT/FAA/AR, U.S. Department of Transportation, Federal Aviation Administration, Office of Aviation Research: Wichita, KS, USA, 2005.
- Zumwalt, G.W.; Schrag, R.L.; Bernhart, W.D.; Friedberg, R.A. Electro-Impulse De-Icing Testing, Analysis and Design; Technical Report NASA-CR-4175; NASA Lewis Research Center: Cleveland, OH, USA, 1988.
- Venna, S.V.; Lin, Y.; Botura, G. Piezoelectric Transducer Actuated Leading Edge De-Icing with Simultaneous Shear and Impulse Forces. J. Aircr. 2007, 44, 509–515. [Google Scholar] [CrossRef]
- Kolbakir, C.; Hu, H.; Liu, Y.; Hu, H. An experimental study on different plasma actuator layouts for aircraft icing mitigation. Aerosp. Sci. Technol. 2020, 107, 106325. [Google Scholar] [CrossRef]
- Federal Aviation Administration. 14 CFR Part 25, Appendix O—Supercooled Large Drop (SLD) Icing Conditions. In Code of Federal Regulations, Title 14, Aeronautics and Space; Federal Aviation Administration: Washington, DC, USA, 2014. [Google Scholar]
- Federal Aviation Administration. 14 CFR Part 25, §25.1420—Supercooled Large Drop Icing Conditions. In Code of Federal Regulations, Title 14, Aeronautics and Space; Federal Aviation Administration: Washington, DC, USA, 2014. [Google Scholar]

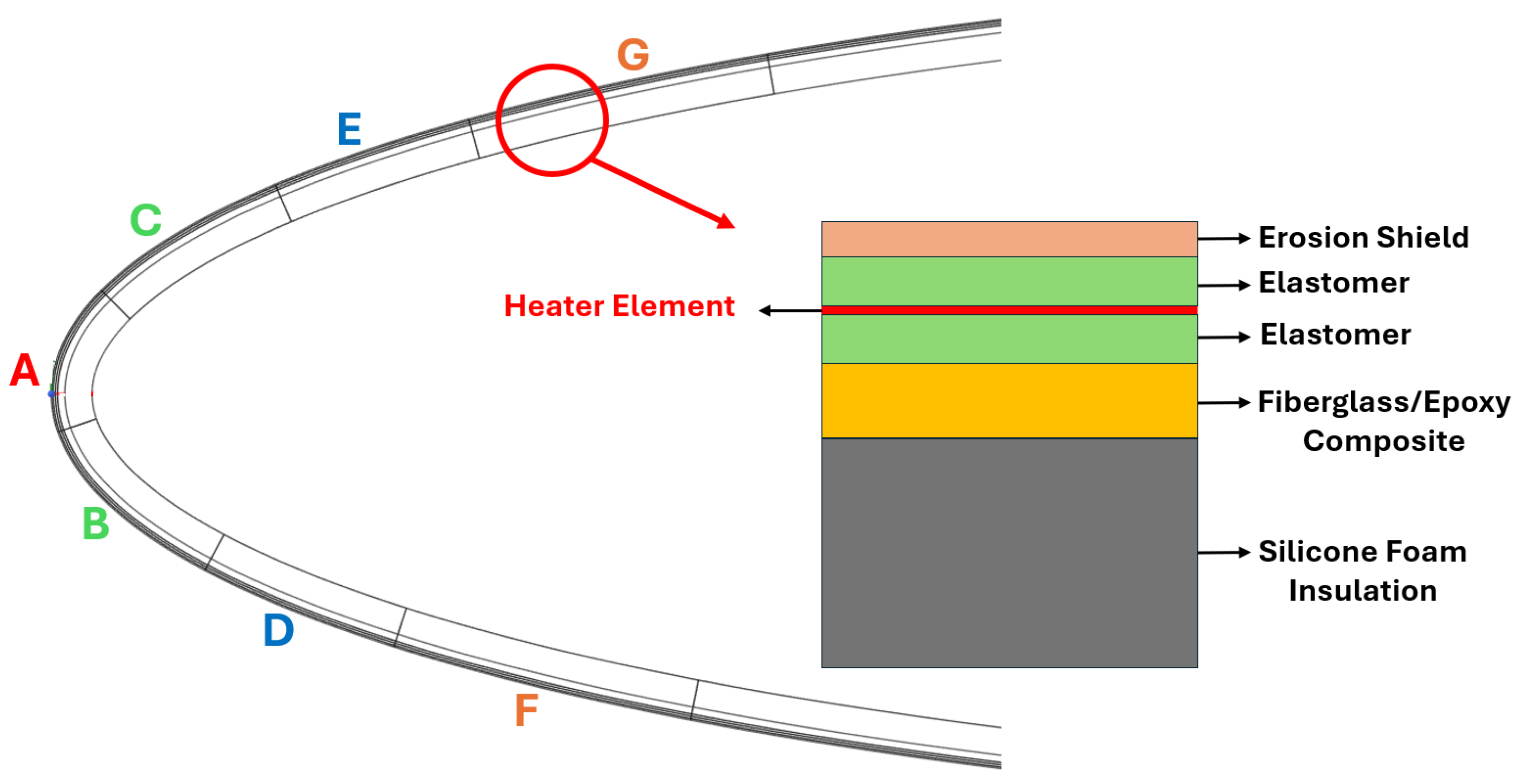
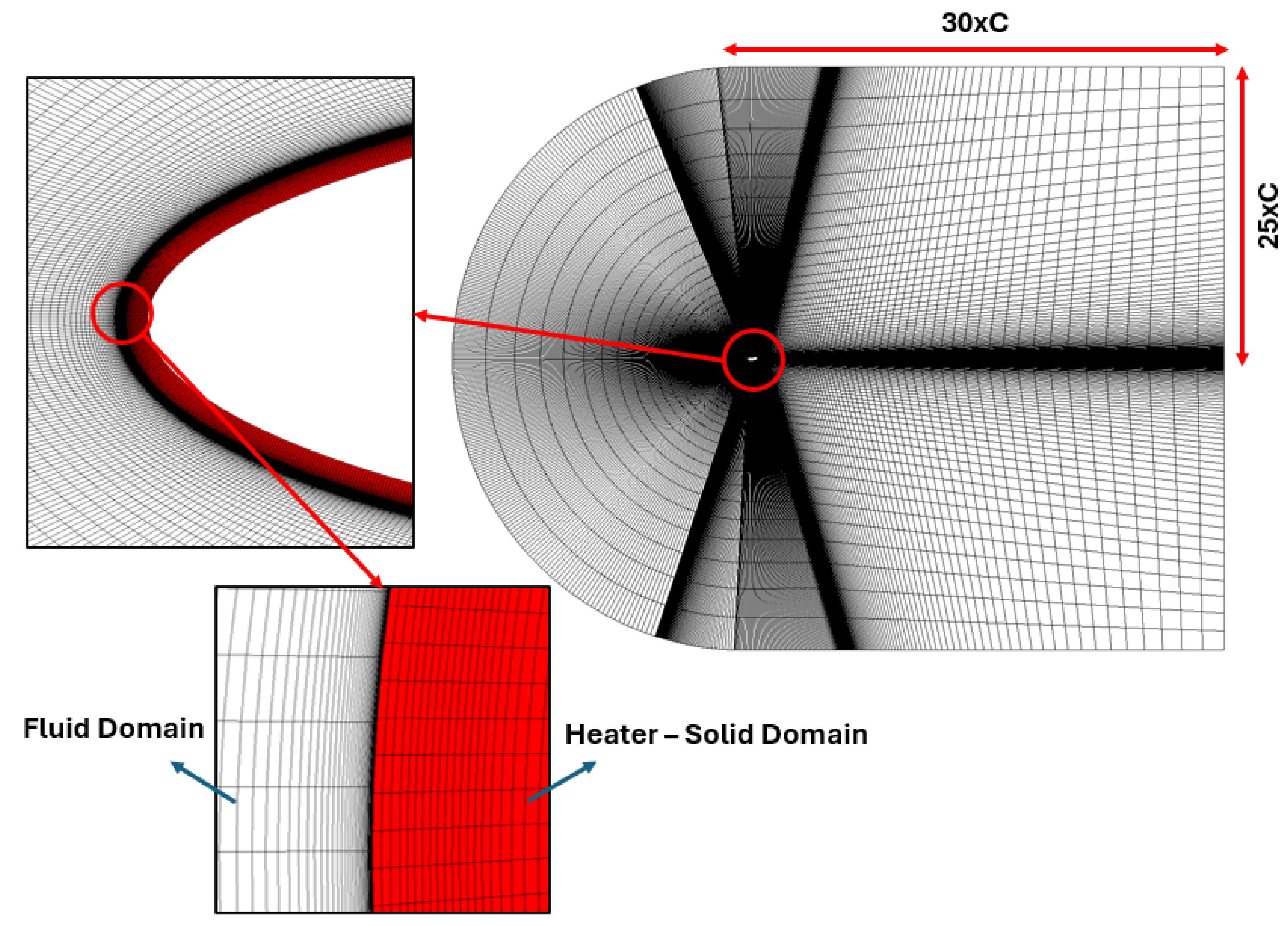
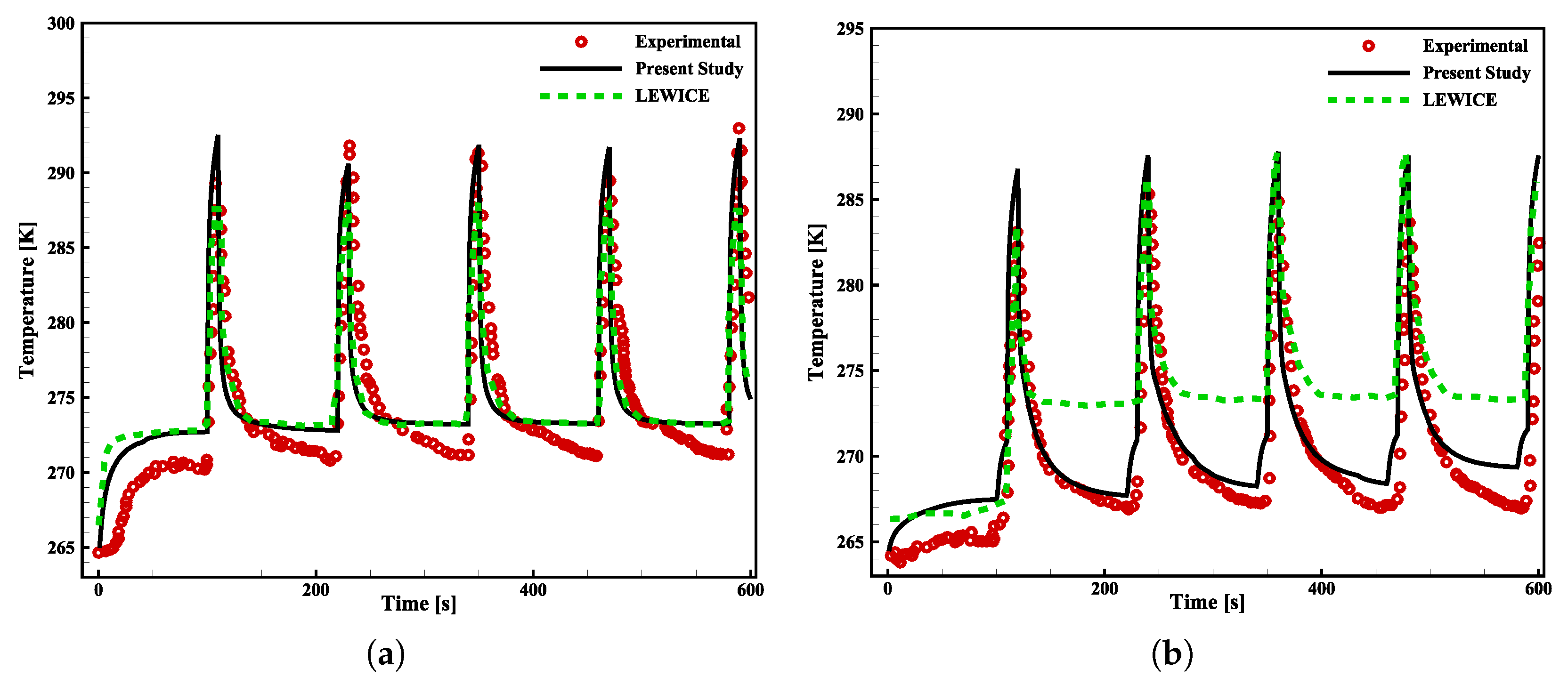
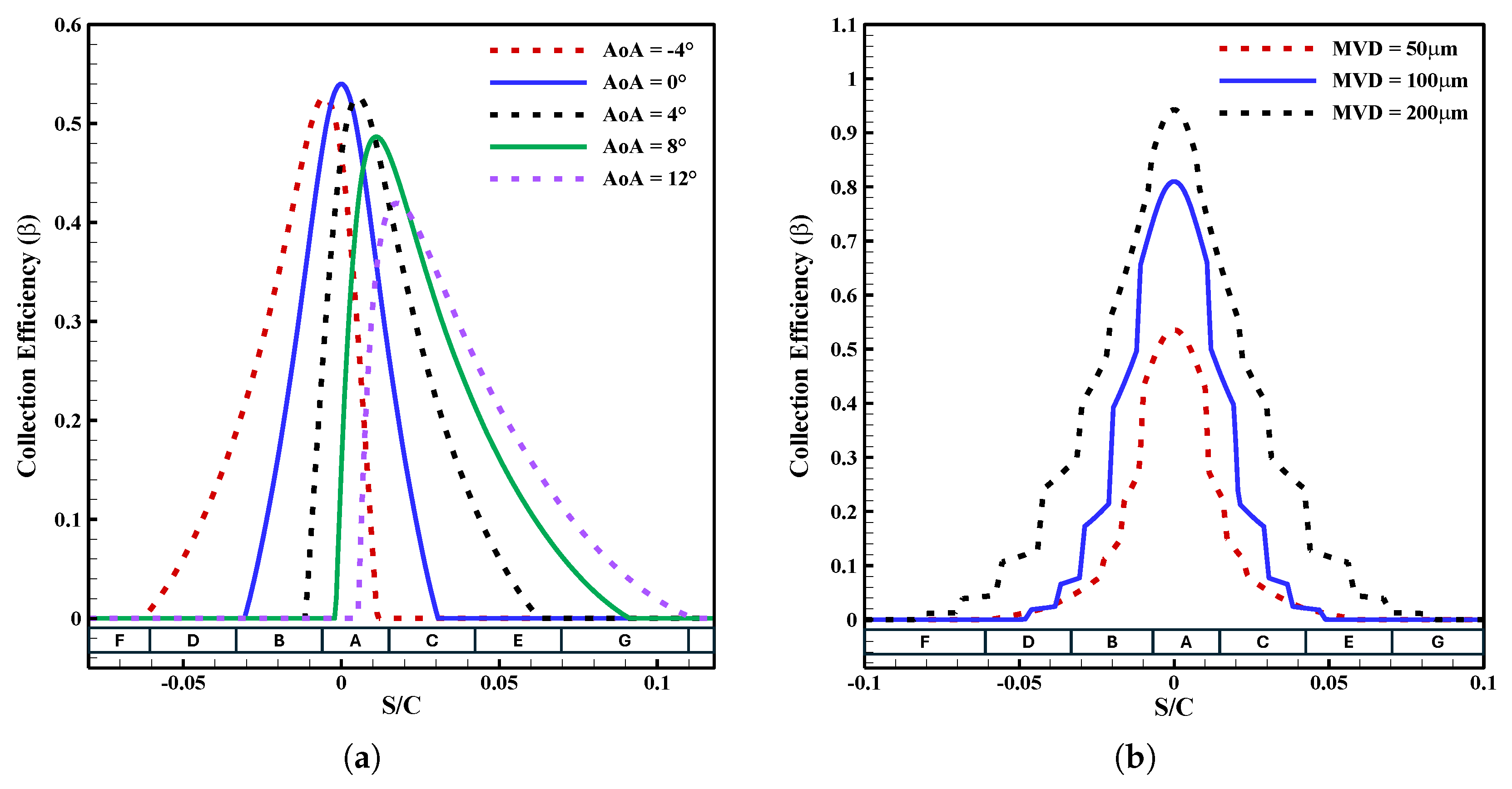
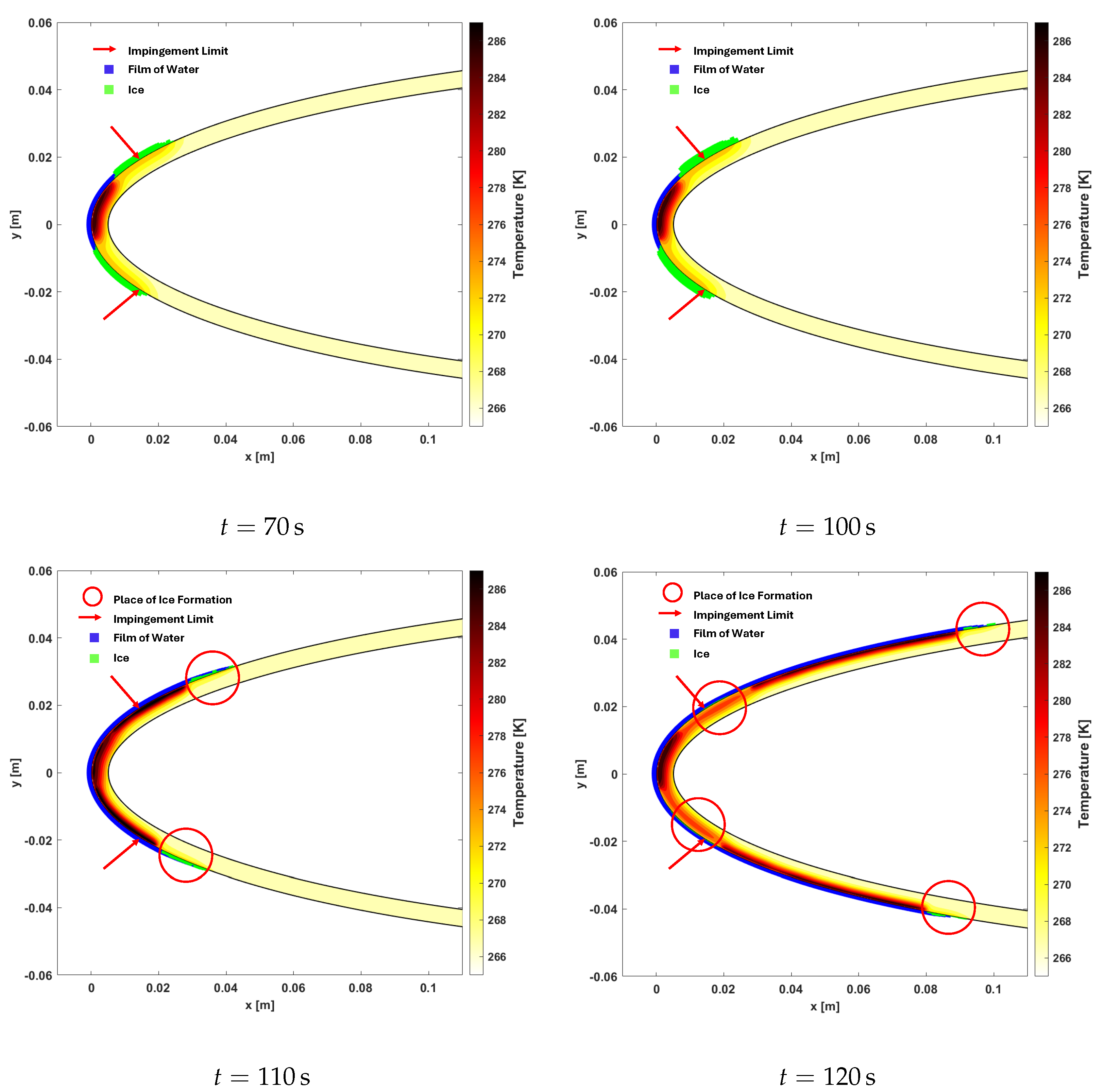
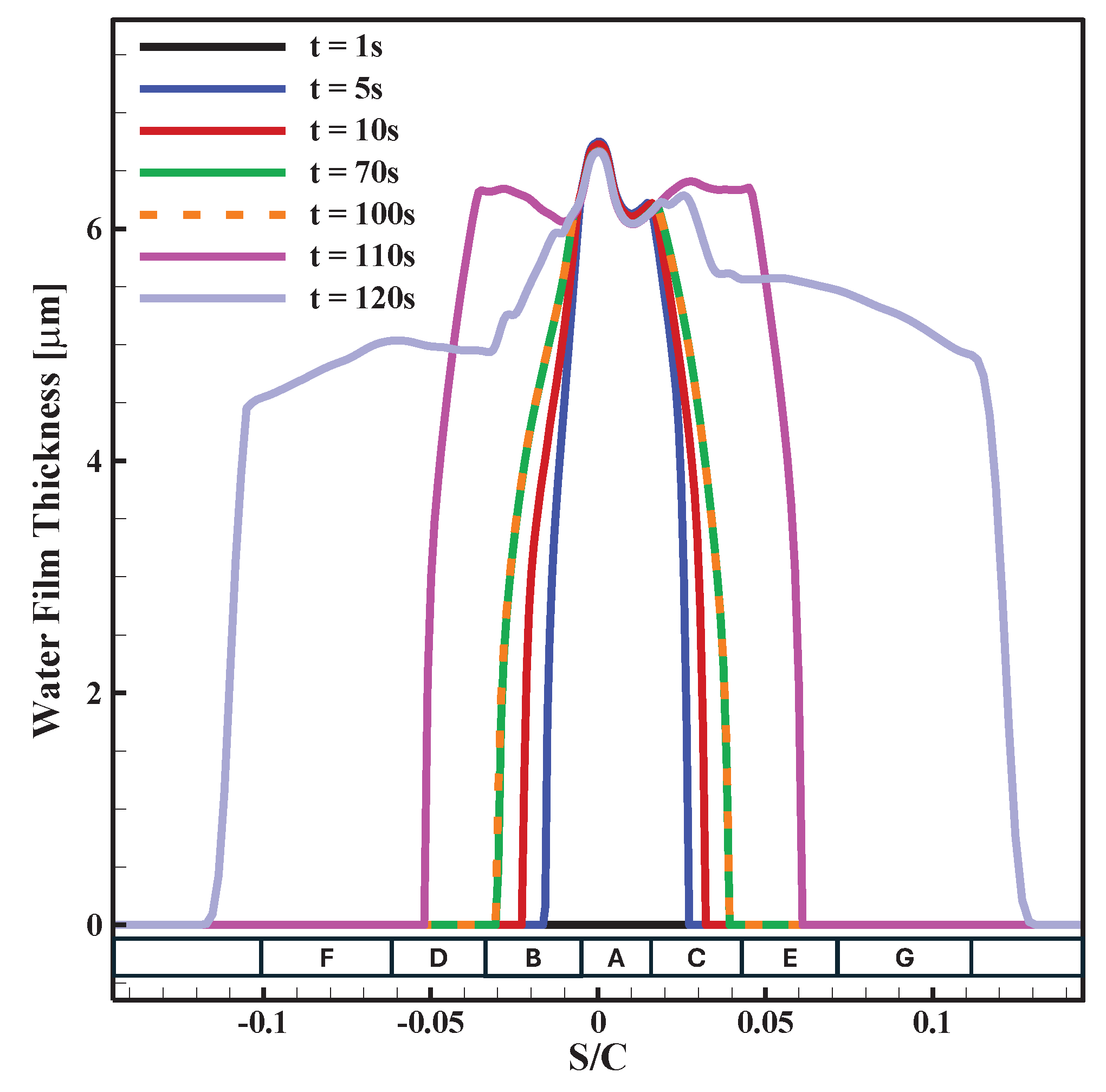
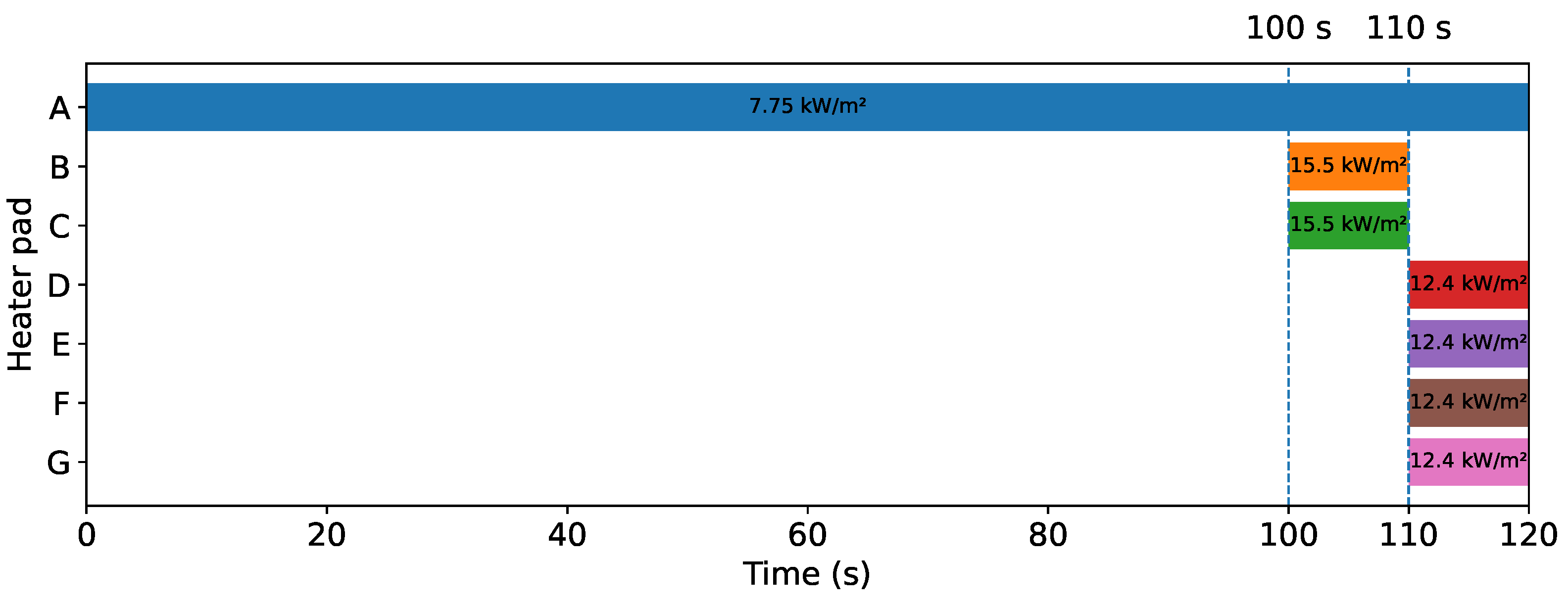
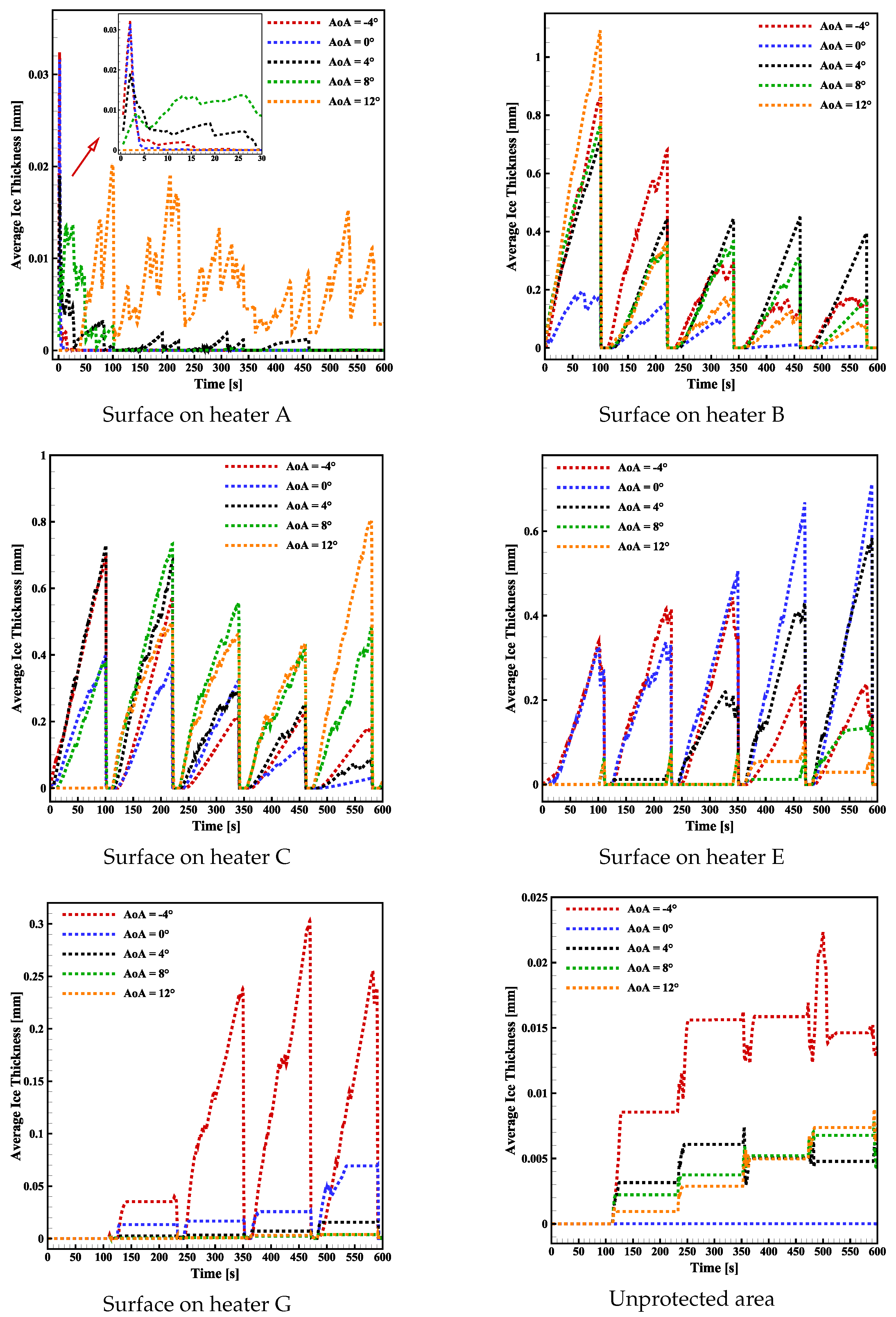
| Computational Grid | Total Number of Cells | First Cell Height [m] | Drag Coefficient (CD) | Percentage Change Compared to Previous Mesh |
|---|---|---|---|---|
| Coarse | 38,500 | 2.00 × | 0.01463 | - |
| Medium | 82,400 | 2.00 × | 0.01546 | 5.67% |
| Fine | 161,800 | 2.00 × | 0.01587 | 2.48% |
| Very Fine | 310,600 | 2.00 × | 0.01598 | 0.69% |
| Material | k [W/m.K] | [kg/] | [J/kg.K] | Thickness [mm] |
|---|---|---|---|---|
| Heating element (alloy 90) | 41.018 | 8906.26 | 385.112 | 0.0127 |
| Erosion shield (SS 301 HH) | 16.269 | 8025.25 | 502.32 | 0.2032 |
| Elastomer (COX 4300) | 0.256 | 1383.99 | 1255.8 | 0.2794 |
| Fiberglass/epoxy composite | 0.294 | 1794.07 | 1569.75 | 0.889 |
| Silicone foam insulation | 0.121 | 648.75 | 1130.22 | 3.429 |
| Heater | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Start (S/C) | −0.0051 | −0.0329 | 0.0157 | −0.0607 | 0.0435 | −0.1024 | 0.0713 |
| End (S/C) | 0.0157 | −0.0051 | 0.0435 | −0.0329 | 0.0713 | −0.0607 | 0.1129 |
| Heating Element | Power Density [W/] | Duration [s] |
|---|---|---|
| A | 7750 | 0 to 120 |
| B-C | 15500 | 100 to 110 |
| D-E-F-G | 12400 | 110 to 120 |
| Case | LWC | MVD | AOA | Roughness Height | Icing Time | ||
|---|---|---|---|---|---|---|---|
| [K] | [m/s] | [g/m3] | [m] | [deg] | [m] | [min] | |
| Normal Flight Condition | |||||||
| Case 1 | 266.483 | 44.704 | 0.78 | 20 | 0 | 500 | 10 |
| Case 2 | 266.483 | 44.704 | 0.78 | 20 | −4 | 500 | 10 |
| Case 3 | 266.483 | 44.704 | 0.78 | 20 | 4 | 500 | 10 |
| Case 4 | 266.483 | 44.704 | 0.78 | 20 | 8 | 500 | 10 |
| Case 5 | 266.483 | 44.704 | 0.78 | 20 | 12 | 500 | 10 |
| Harsh Flight Condition | |||||||
| Case 6 | 266.483 | 44.704 | 0.78 | 50 | 0 | 500 | 10 |
| Case 7 | 266.483 | 44.704 | 0.78 | 100 | 0 | 500 | 10 |
| Case 8 | 266.483 | 44.704 | 0.78 | 200 | 0 | 500 | 10 |
| Class i | Ratio /MVD | Weight Fraction [] (%) |
|---|---|---|
| 1 | 0.31 | 5 |
| 2 | 0.52 | 10 |
| 3 | 0.71 | 20 |
| 4 | 1.00 | 30 |
| 5 | 1.37 | 20 |
| 6 | 1.74 | 10 |
| 7 | 2.22 | 5 |
| Case | Change in | Change in | ||||
|---|---|---|---|---|---|---|
| Case 1 | 0 | 0 | - | 0.01587 | 0.01901 | 19.8% |
| Case 2 | −0.4109 | −0.3993 | −2.8% | 0.01706 | 0.02062 | 20.9% |
| Case 3 | 0.4108 | 0.4036 | −1.8% | 0.01705 | 0.02031 | 19.1% |
| Case 4 | 0.797 | 0.7837 | −1.7% | 0.02233 | 0.02558 | 14.6% |
| Case 5 | 1.104 | 0.9813 | −11.1% | 0.03656 | 0.05420 | 48.2% |
| Case 6 | 0 | 0 | - | 0.01587 | 0.01874 | 18.1% |
| Case 7 | 0 | 0 | - | 0.01587 | 0.02088 | 31.6% |
| Case 8 | 0 | 0 | - | 0.01587 | 0.02166 | 36.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nohooji, S.G.; Tembely, M. Analysis of Electro-Thermal De-Icing on a NACA0012 Airfoil Under Harsh SLD Conditions and Different Angles of Attack. Aerospace 2025, 12, 883. https://doi.org/10.3390/aerospace12100883
Nohooji SG, Tembely M. Analysis of Electro-Thermal De-Icing on a NACA0012 Airfoil Under Harsh SLD Conditions and Different Angles of Attack. Aerospace. 2025; 12(10):883. https://doi.org/10.3390/aerospace12100883
Chicago/Turabian StyleNohooji, Sobhan Ghorbani, and Moussa Tembely. 2025. "Analysis of Electro-Thermal De-Icing on a NACA0012 Airfoil Under Harsh SLD Conditions and Different Angles of Attack" Aerospace 12, no. 10: 883. https://doi.org/10.3390/aerospace12100883
APA StyleNohooji, S. G., & Tembely, M. (2025). Analysis of Electro-Thermal De-Icing on a NACA0012 Airfoil Under Harsh SLD Conditions and Different Angles of Attack. Aerospace, 12(10), 883. https://doi.org/10.3390/aerospace12100883






