Abstract
This paper investigates the fixed-time tracking control problem for agile missiles with multiple heterogeneous actuators in the presence of saturation constraints and external disturbances. To reduce the turning radius and promote maneuvering envelope, a novel combination scheme for blended actuators is introduced in this paper, consisting of a flexible mechanism control system (FCS), reaction-jet control system (RCS), and aerodynamic control. Based on the proposed nonsingular terminal sliding mode surface, a fixed-time anti-saturation controller with an auxiliary system is presented first to ensure global fixed-time stability and to compensate for the adverse effects of input saturation. Subsequently, a fixed-time disturbance observer is constructed to estimate uncertainties and lumped disturbances, and to address the chattering problem. To assign the total virtual control command to different actuators, a control allocation based on dynamic programming considering actuator dynamics is established. Finally, detailed numerical simulations and comparisons are provided to verify the effectiveness and superiority of the proposed control scheme.
1. Introduction
Agile missiles are significantly more effective at intercepting highly maneuverable targets than conventional missiles and are extensively used in modern warfare. During a large-angle maneuver known as the agile turn, the missile inevitably enters the high angle of attack state, resulting in the loss of aerodynamic control. The multi-actuator scheme, such as reaction-jet control system (RCS) and aerodynamic control, is the most prevalent method for providing maneuverability under the given conditions [1,2,3]. The RCS system comprises an array of small and radially positioned lateral thrusters designed to generate thrust perpendicular to the missile’s centerline, thereby improving the maneuverability of the agile missile. However, the control scheme mentioned above is incapable of ensuring a small turning radius at high velocities, thus limiting the applicability of agile missiles in space-constrained environments.
The use of flexible mechanisms as an auxiliary actuator has garnered considerable interest. The affordable guided airdrop system (AGAS) in the United States is the first to use a flexible control surface to adjust its trajectory [4,5]. Subsequently, the flexible mechanism has found widespread application in the fields of spacecraft recovery [6], intelligent airdrop [7], and parafoil systems [8]. However, a similar flexible mechanism has never been utilized for precise attitude control in high-speed systems, such as agile missiles. Considering the advantages of a flexible mechanism that can generate a large quantity of aerodynamic force instantaneously, this paper proposes a flexible mechanism control system for agile missiles to regulate attitude and velocity simultaneously, with the goal of minimizing the turning radius as much as possible. The details of FCS are described in Section 2.
Over the past few decades, various control system designs for agile missiles have been proposed [9,10,11]. In order to satisfy the requirements of fast convergence rate and high control accuracy, many control methods based on finite-time control theory have been developed [12,13,14]. However, finite-time control methods have the disadvantage that the convergence time of the system is dependent on the initial state [15]. To overcome this drawback, the fixed-time stability property was proposed as a further extension of the finite-time stability by Cruz-Zavala [16] and has been applied to several scenarios due to its attractive features. A fixed-time nonsingular terminal sliding-mode control (NTSMC) method was designed for high-order nonlinear systems in Ref. [17] to guarantee global fixed-time stability, which can alleviate the impact of matched and mismatched disturbances. To address the attitude tracking problem for hypersonic morphing vehicles, Ref. [18] developed a multi-variable fixed-time sliding mode controller to ensure the convergence of system errors within a fixed time, despite multisource uncertainty and strong external disturbances. Ref. [19] proposed a fixed-time adaptive control allocation technique to distribute the desired virtual control torque to each actuator for the rest-to-rest attitude maneuver of an over-actuated spacecraft subject to actuator output constraints. Based on a faster terminal sliding mode surface, a novel fixed-time prescribed performance control for robot manipulators was designed in Ref. [20], and the chattering problem was alleviated by incorporating a neural network that approximates the robot dynamics model. Although the aforementioned research has made some achievements, few studies have examined intricate control system design, such as agile missiles with blended control actuators.
Another problem encountered in practice is that missile control actuators are susceptible to magnitude constraints [21,22]. Physical input saturation in control systems will drastically limit performance and contribute to instability [23,24]. To mitigate the impact of input and rate saturation, a fixed-time coordinated tracking controller combined with an anti-windup saturation compensator and an auxiliary system was developed in Ref. [25]. Ref. [26] introduced an auxiliary system with a smooth and nonsingular switching function to overcome the effect of input saturation on unmanned aerial vehicles. In Ref. [27], actuator saturation was considered in the attitude coordinated control problem for multiple spacecraft, and an adaptive compensation law was implemented to alleviate the adverse effects. Ref. [28] developed an attitude-tracking controller for trans-medium aircraft with constrained actuators, where an auxiliary system based on a double power function was employed to compensate for the actuator saturation. Although the input saturation problem has been extensively studied, no fixed-time results have considered the autopilot design for agile turning subject to input saturation.
The efficient disturbance observer is critical in improving control performance due to frequent strong external disturbances and aerodynamic uncertainties during an agile turn [29,30]. Motivated by the benefits of fixed-time theory, disturbance observers with fixed-time convergence have been a recent research hotspot [31,32,33]. To estimate unmeasurable velocities and unknown disturbances, a fixed-time extended state observer based on a bi-limit homogeneous technique was proposed for the trajectory tracking problem of unmanned surface vehicles [34]. A fixed-time disturbance observer combined with fixed-time technology and a linear algorithm was developed for high-order integrator chains subject to matched disturbances and time delays, which can compensate for unknowns and disturbances [35]. In addition, to enhance control efficiency and decrease energy consumption for agile missiles equipped with multiple actuators, it is essential to employ suitable control allocation methods in the control scheme. There are various valid allocation methods, such as the direct allocation method, dynamic programming method, and closed-loop control allocation. This paper proposes a control allocation method to assign the total virtual control demand among different actuators.
Up to now, the problem of designing fixed-time controllers for agile missiles with multiple heterogeneous actuators in the presence of input saturation has not been systematically addressed. Motivated by this, an anti-saturation fixed-time NTSMC combined with a fixed-time disturbance observer and a control allocator is proposed in this paper. The major contributions of this study are as follows.
- (1)
- A new combination scheme of multiple heterogeneous actuators, including FCS, RCS, and aerodynamic control, for agile missiles is introduced in this paper. FCS is responsible for decelerating and supplying lateral aerodynamic control force, while RCS is utilized for precision attitude control. The coordination of different actuators can significantly reduce the turning radius, thereby expanding the application space for agile missiles;
- (2)
- A novel fixed-time anti-saturation controller with an auxiliary system based on NTSMC is proposed for the first time to ensure that errors of the control system converge to zero within a fixed time and to counteract the detrimental effect of input saturation;
- (3)
- The control accuracy is improved by designing a fixed-time disturbance observer to handle uncertainties and external disturbances in the agile turn, effectively alleviating the chattering problem.
The remainder of this paper is organized as follows. The preliminaries and mathematical modeling of the agile missile with FCS are presented in Section 2. Section 3 introduces the fixed-time disturbance observer and provides details of the proposed fixed-time tracking control in conjunction with the constructed auxiliary system. Additionally, the control allocation with the consideration of actuator dynamics is presented. In Section 4, simulation results and comparisons are performed, followed by conclusions in Section 5.
2. Mathematical Model and Preliminaries
In this section, the mathematical model of the agile missile with multiple heterogeneous actuators is formulated. In particular, some definitions and lemmas are recalled simultaneously.
2.1. Notations
The notations in this paper are defined as follows: denotes the absolute value of a scalar. We define a function as and . Moreover, is the saturation function satisfying
where is the known bound of .
2.2. Relative Lemmas
The following lemmas will be employed in deriving the main conclusions of this paper.
Lemma 1.
([36]). Consider the following system:
where
and
are the scalar state variables;
and
are appropriate positive constants, satisfying
and ;
and
meet
and , respectively;
is the amplification factor to be designed, which satisfies
; and the perturbation term
is finite and unknown. Then, the system will converge to a neighborhood of the origin in fixed time.
Lemma 2.
([34]). For any positive scalers , Equation (5) always holds:
Lemma 3.
([25]). For the Lyapunov function , if the time derivative
satisfies the inequality
, where ,
,
, and are positive constants, the value converges to zero in fixed time, and the temporal boundary is .
Lemma 4.
([37]). Considering a nonsingular terminal sliding surface
where ,
,
, and
. Then, the equilibrium of (4) is fixed-time stable and the settling time
is bounded by
2.3. Problem Statement
2.3.1. Agile Missile Dynamics
A specific illustration of the agile missile with multiple heterogeneous actuators, including RCS, FCS, and aerodynamic surfaces, is shown in Figure 1. FCS is installed at the tail of the missile, and the primary component of FCS is an asymmetrical brake parachute that generates aerodynamic drag and lateral control force to alter the missile’s attitude rapidly. is the joint point. The RCS system is installed in front of the centroid of the missile. and are the body coordinate systems of the agile missile and FCS.
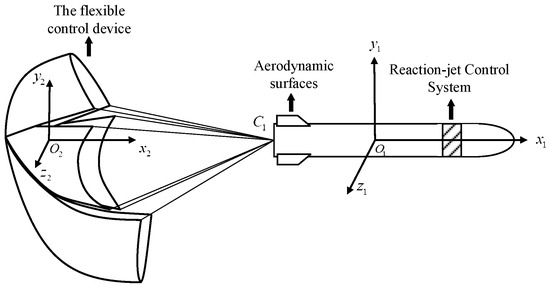
Figure 1.
Schematic diagram of the agile missile.
Assumption 1.
The agile missile and FCS are modeled as rigid bodies, while the connecting ropes between them are considered flexible bodies.
DATCOM can help to acquire the aerodynamic data of the agile missile, while the aerodynamic coefficients of the flexible control mechanism can be obtained using LS-DYNA 971. Hence, with Assumption 1, the rigid–flexible coupling dynamics model of the agile missile with FCS can be established.
Assumption 2.
To enhance the focus on the controller algorithm, this study primarily investigates the flat maneuver of the missile.
The longitudinal dynamics of the agile missile with FCS can be given as follows:
The control force and control moment, including , , and , can be determined by the geometry relationships and the internal forces of the connecting ropes [38]. The internal force on each connecting rope can be expressed as
where is the original length of each connecting rope, and are the elastic coefficient and damping coefficient of each connecting rope, and is the total number of the connecting ropes.
The specific expression of the aerodynamic pitching moment and the control moment is shown as
Assumption 3.
The external disturbances are assumed to be continuous and differentiable, which satisfy and
. and
are positive constants.
2.3.2. Effect of FCS
In this subsection, a numerical simulation of the agile missile with FCS is performed to demonstrate the effectiveness of FCS tentatively. For the sake of clarity, the angle units throughout the remainder of this paper are expressed in degrees. The initial parameters of the agile missile are set as follows: , , , and . The aerodynamic coefficients of FCS are shown in Figure 2. The gravity is ignored in the simulation conditions.
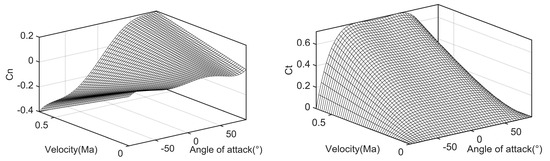
Figure 2.
Aerodynamic coefficients of FCS.
The response curves of the missile are shown in Figure 3. It can be seen from Figure 3a that, in the absence of control, the angle of attack can decrease to −25° rapidly in 0.4 s, while the pitch angle reduces to −19°. The missile velocity is plotted in Figure 3b, which proves that the missile will decelerate sharply due to the influence of FCS. The above results illustrate that FCS possesses the capability to quickly alter both the attitude and velocity of the missile concurrently. It is essential to acknowledge that the prolonged opening of FCS will lead to an excessive decrease in speed, thereby necessitating the selection of an appropriate time to abandon the device.
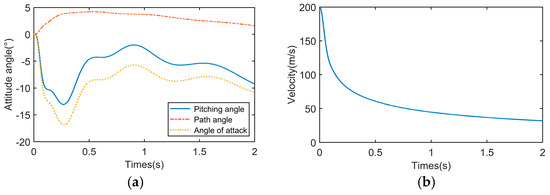
Figure 3.
Response curves of the agile missile. (a) Attitude angle; (b) velocity.
2.4. Control Scheme and Design Objectives
This paper aims to design a fixed-time attitude control scheme for agile missiles with multiple heterogeneous actuators to achieve fast and small-radius agile turning despite actuator saturation. The coordination of different actuators, including FCS, RCS, and aerodynamic control, is arranged as follows: FCS is in charge of decelerating and providing lateral aerodynamic control force in the initial phase of agile turning and will be disengaged once the control moment affects the pitch angle rate; and RCS and aerodynamic surfaces operate continuously and are used for precise attitude control. The specific control objectives can be obtained as follows:
- (a)
- The closed-loop control system exhibits global fixed-time stability, and system errors converge to zero within a fixed time;
- (b)
- The turning radius of the missile with multiple heterogeneous actuators decreases significantly during agile turning;
- (c)
- The designed scheme must be robust in the presence of unknown lumped disturbances.
3. Anti-Saturation Fixed-Time NTSMC
This section introduces a NTSMS-based auxiliary system and the corresponding command-tracking error system. A fixed-time disturbance observer is first improved to compensate for uncertainties and external disturbances in agile turn. Then, the anti-saturation fixed-time NTSMS combined with the proposed observer is synthesized and its stability is proven.
3.1. Anti-Saturation Error System
Due to the physical limitations of missile actuators, the magnitude constraints on and are considered in this paper. Therefore, the missile attitude dynamics are rewritten as
where
represents the known information, is the external disturbance, , , and is the difference between the designed input and the actual input.
To mitigate the adverse effects of input saturation, an auxiliary sliding surface is designed as
where and are system states for compensating the input saturation, , , , and . And the auxiliary system is implemented as
where
and , , , , , and is the upper bound of .
Considering the missile dynamics (9) and the auxiliary system (12), we define the command tracking error as and , where is the pitch angle command. Hence, the system error dynamics can be described as
The command tracking problem will be solved once the errors system (15) and the auxiliary system (12) converge to zero.
3.2. Fixed-Time Disturbance Observer Design
Inspired by the differentiator in Ref. [39], a bi-limit-weighted homogeneity fixed-time disturbance observer is designed, wherein the objective is to estimate the uncertainties and external disturbances in agile turn. The fixed-time observer is designed as follows:
where and are the states of the observer, and , , , , and represent the observer coefficients satisfying , , , , , and .
Theorem 1.
Consider the system (15), the fixed-time disturbance observer given in Equation (16) with the appropriate observer gains can transform the estimation of external disturbances into the form of system (4). Then, the error of the system converges to a neighborhood of zero in a fixed time.
Proof.
First, the errors between the estimated external disturbances and the real external disturbances are designed as follows:
Taking the derivative of Equation (17) and substituting Equation (16) results in
To summarize, the estimation errors can be formed as
It follows from Assumption 3 and Lemma 1 that the error of the system can converge to a neighborhood of the origin in a fixed time. The proof is complete. □
3.3. Fixed-Time Anti-Saturation Controller Design
A nonsingular terminal sliding mode surface with respect to command tracking errors is proposed as
where , , , and .
Taking the derivative of Equation (21) yields
Based on the proposed sliding mode surface Equation (21) and disturbance estimation from the fixed-time observer, a fixed-time control law is designed as
where
and , , and , where is the maximum disturbance estimation error.
Theorem 2.
Considering the error system Equation (15) with Assumption 3, if given the controller in Equation (23) and the fixed-time disturbance observer in Equation (16) with proper control parameters, the error system can converge to zero in fixed time.
Proof.
To verify the stability of the error system, considering the Lyapunov function and taking the time derivative of yield
Combining Equations (11) and (14), we can obtain
Similarly, we also get
It follows from Equations (25)–(27) that
As mentioned, and always exist; hence Equation (28) can be simplified as
According to Lemma 2, we can obtain
where and .
Following the treatment in [39], the state space is divided into two different areas:
When the system states are in the area , we obtain
It follows from Lemma 3 that the sliding surface and will converge to zero within a fixed time, or the system states will enter the area .
In the area , if , we can infer from Equation (32) that the sliding surface is still an attractor. If , assume that and . We can acquire , and taking the time derivative of yields
In view of , it can be concluded that if , then , while , there is . As a result, system states will monotonically transgress the area into . Similarly, if and , it can be concluded that system states will monotonically transgress the area into . Hence, the sliding surface and can be reached from anywhere within fixed time. According to Lemma 4, the error system states and will reach the origin within a fixed time when the sliding mode surface is satisfied. The proof is complete. □
Remark 1.
The incorporation of the proposed fixed-time disturbance observer facilitates the fulfillment of , thereby effectively diminishing the coefficient value of the switching item and alleviating the chattering phenomenon.
Remark 2.
To achieve a further decline in the chattering problem, it is recommended that the function be replaced with a continuous or smooth function, exemplified by the sigmoid function
where
is the coefficient to be designed.
3.4. Control Allocation
For the missile with multiple actuators, the control scheme necessitates an allocator to distribute the virtual control command to each actuator dynamically. Considering actuator dynamics, a control allocator based on the sequential quadratic programming method is introduced in this subsection.
Considering the practical performance of actuators and the sampling time of the digital control system, we first define the allocation constraints as
where
and are the upper and lower constraints of actuator magnitudes, and are the minimal and maximal constraints of actuator rates, and is the sampling time.
Then, based on the sequential quadratic programming, we can consider the dynamic control allocation as an optimization problem
where and are the weight factors matrices, is the control effectiveness matrix, can indicate aerodynamic control loss during the high attack of angle flight, is the maximum available angle of attack of aerodynamic control, and is a scaling factor.
By solving the above sequential quadratic programming problem, we can acquire the optimal control command of each actuator.
4. Results and Discussion
In this section, numerical simulations are performed to demonstrate the effectiveness of the proposed control scheme. The action of the agile turn is assumed to take place within the vertical plane; thus, the pitch angle command is set to a constant value of . Two cases are performed to respectively verify the availability of coordination of multiple heterogeneous actuators and the superiority of the designed controller.
The initial parameters of the agile missile are set as follows: , , , , , , , , the maximum thrust of RCS , the maximum elevator deflection angle , the thrust force of the main engine , , and . The external disturbance is expressed as . The main engine starts and lasts for one second when the pitch angle is greater than . The parameters of the control scheme are given in Table 1 and Table 2.

Table 1.
Design parameters of the disturbance observer.

Table 2.
Design parameters of the controller.
Case 1: To show the effectiveness of coordination of multiple heterogeneous actuators, a comparison between the proposed actuator combination and the traditional RCS/aerodynamic control combination is conducted. The proposed anti-saturation fixed-time controller is used in both simulations, with all initial conditions and controller parameters being the same. The results of the simulation are shown in Figure 4, Figure 5 and Figure 6.
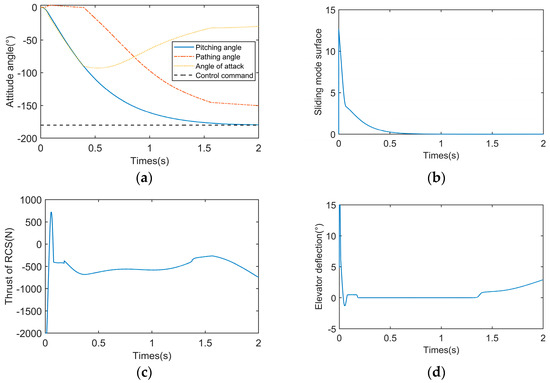
Figure 4.
Response curves of the agile missile with multiple heterogeneous actuators. (a) Attitude angle; (b) sliding mode surface; (c) thrust of RCS; (d) elevator deflection.
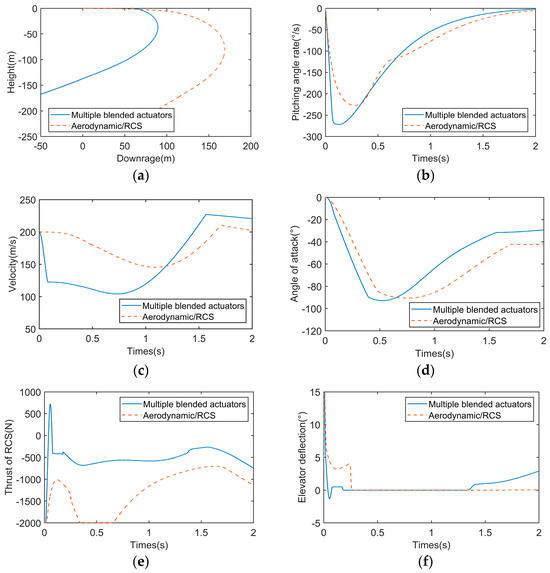
Figure 5.
Contrast curves between two actuator combinations. (a) Trajectory; (b) pitch angle rate; (c) velocity; (d) angle of attack; (e) trust of RCS; (f) elevator deflection.
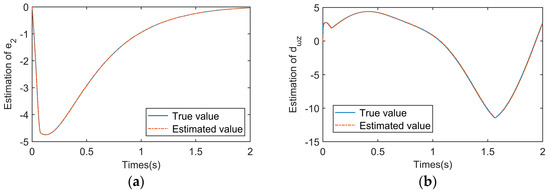
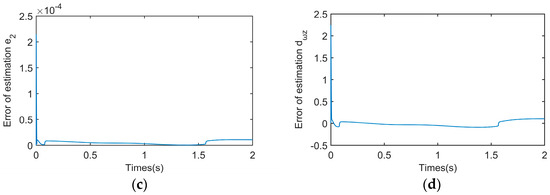
Figure 6.
Estimation results. (a) Estimation of ; (b) estimation of ; (c) estimation error of ; (d) estimation error of .
Figure 4 depicts the command tracking curves of the agile missile with multiple heterogeneous actuators. The curves of the attitude angle are shown in Figure 4a. It can be seen that the pitch angle decreases to −180.05°, showing that the missile can precisely track the command . Additionally, the pathing angle decreases below −150°, indicating the missile can execute a rapid turn within two seconds. The designed control input and actual control input are illustrated in Figure 4c,d, which can prove the validity of the proposed anti-saturation controller with an auxiliary system. Significantly, the substantial control input during the initial period emphasizes the necessity of saturation compensation.
The comparisons of two actuator combinations are illustrated in Figure 5. It can be clearly seen from the maneuver trajectories in Figure 5a that the missile equipped with multiple heterogeneous actuators can perform an agile turn with a significantly smaller turning radius. The curves in Figure 5b show that the missile with multiple heterogeneous actuators initially has a larger pitch angle rate, which is caused mainly by the control moment . It is worth noting that, as shown in Figure 5c, the missile equipped with multiple heterogeneous actuators initially experiences a sharp decrease in speed and eventually reaches a higher terminal velocity compared with the traditional RCS/aerodynamic control combination, which is beneficial to subsequent attack missions. The simulation results show that the terminal velocity of the missile with multiple heterogeneous actuators is 213.92 m/s, while the terminal velocity of the traditional missile is only 202.15 m/s. The key reason for this phenomenon is that the angle of attack of the low-speed missile can recover faster during the main engine operation, thus reducing the missile’s drag coefficient and increasing the thrust force component of the main engine in the speed coordinate system. The curves plotted in Figure 5d indicate that the angle of attack of the missile with multiple heterogeneous actuators is always relatively small after starting the main engine. Figure 5e,f illustrate the actual input, from which we can deduce that the missile with multiple heterogeneous actuators requires less control energy.
Remark 3.
Figure 5c depicts that the missile experiences a significant deceleration due to the influence of FCS. Therefore, the control strategy involving multiple heterogeneous actuators imposes significant demands on the time to abandon FCS.
To verify the validity of the proposed fixed-time disturbances observer, the estimation results are shown in Figure 6. Therein, the actual state variables and , and the estimated states and are respectively illustrated in the same subfigures. Figure 6c,d depicts the error curves between the actual state variables and the observed value. It can be seen that the proposed disturbance observer accurately estimates the external disturbance, and the significantly slight estimation error shows the excellent performance of the proposed observer.
Case 2: A comparison between the proposed method (we call it AFNTSMC), a fixed-time integral TSMC method (FITSMC) in [20], and an adaptive dynamic surface control with input saturation based on the barrier Lyapunov function (BLF-ADSC) in [27] is carried out. The parameters of the proposed anti-saturation fixed-time control laws are set as: , , , , , , , , , , , , , , and .
The responses under the three methods are illustrated in Figure 7. As seen in Figure 7a, the proposed approach enables the missile to achieve an agile turn with an evidently smaller radius compared with the other methods. Figure 7b,c depict the pitch angle and pitch angle rate curves under different conditions, showing that the missile effectively tracks the pitch angle command with all controllers. The terminal pitch angles of the missile under the proposed controller is −180.27°, while the terminal pitch angles of the missile under FITSMC and BLF-ADSC are −177.95° and −181.38°, respectively. Static control errors under different controllers are depicted in Table 3. Remarkably, the proposed controller has higher control accuracy and a faster convergence rate throughout the entire control process. The angle of attack curves plotted in Figure 7d illustrate that the missile with the proposed controller can build up a large angle of attack more quickly and then converge to a smaller value.
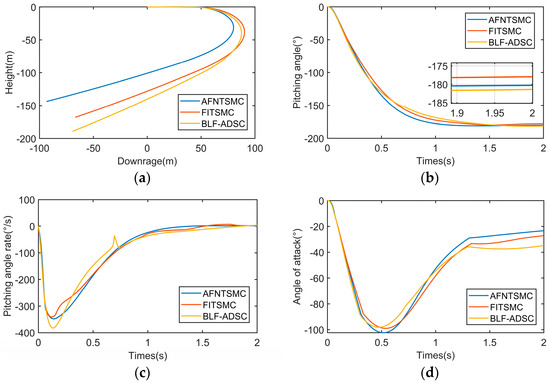
Figure 7.
Comparison results under the different controllers. (a) Trajectories; (b) pitch angle; (c) pitch angle rate; (d) angle of attack.

Table 3.
Static control error under different controllers.
The above simulation results show that the proposed actuator combination offers notable advantages compared with the traditional RCS/aerodynamic control combination for agile missiles, particularly in terms of terminal velocity, turning radius, and energy consumption. Furthermore, the designed anti-saturation controller can guarantee that the tracking error converges to a satisfactory control accuracy within a fixed time and outperforms other methods.
5. Conclusions
A new combination scheme of blended actuators and the corresponding fixed-time anti-saturation controller was developed for agile missiles to address the attitude tracking problem. The combination of multiple heterogeneous actuators, including FCS, RCS, and aerodynamic surfaces, can achieve rough velocity control and precise attitude control of the missile. Furthermore, with the appropriate control parameters, a missile equipped with multiple heterogeneous actuators can execute agile turns with a significantly smaller turning radius and achieve a higher terminal velocity compared with the traditional RCS/aerodynamic control combination. By combining an auxiliary system with a nonsingular terminal sliding mode surface, an anti-saturation controller was introduced to guarantee the fixed-time convergence of control system errors, even in the presence of input saturation. Moreover, a fixed-time disturbance observer and a control allocator were proposed to address external disturbances and enhance control accuracy. Comparative numerical simulations were conducted to verify the effectiveness and superiority of the proposed scheme.
The main contribution of this study is that it provides a new reference for missile control modes and the design of fixed-time controllers, further expanding the application scenarios for agile missiles. However, the current work lacks accurate dynamic modeling of the flexible mechanism control system. Further work will focus on the dynamic characteristic analysis of FCS and the practical application of agile missiles with FCS.
Author Contributions
Writing—original draft preparation, J.L.; writing—review and editing, J.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
Nomenclature
| Missile velocity | Pitching moment of inertia | ||
| Angle of attack | Reference length of the missile | ||
| Pitch angle | Distance between RCS and the mass center | ||
| Pitch rate | Distance between the mass center and the aerodynamic pressure center | ||
| Dynamic pressure | Thrust force of the main engine | ||
| Aerodynamic drag coefficient | Reference area of the missile | ||
| Aerodynamic lift coefficient | Elevator deflection angle | ||
| Control moment from FCS | Lateral force | ||
| Control moment from RCS | Aerodynamic control moment | ||
| , , | Partial derivative of the pitching moment coefficient | , | Control force from FCS on the body coordinate system |
References
- Guo, Y.; Guo, J.; Liu, X.; Li, A.; Wang, C. Finite-time blended control for air-to-air missile with lateral thrusters and aerodynamic surfaces. Aerosp. Sci. Technol. 2020, 97, 105638. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, J.; Liu, C.; Coombes, M.; Li, S.; Chen, W.H. On the Actuator Dynamics of Dynamic Control Allocation for a Small Fixed-Wing UAV with Direct Lift Control. IEEE Trans. Control. Syst. Technol. 2020, 28, 984–991. [Google Scholar] [CrossRef]
- Hou, Y.; Lv, M.; Liang, X.; Yang, A. Fuzzy adaptive fixed-time fault-tolerant attitude tracking control for tailless flying wing aircrafts. Aerosp. Sci. Technol. 2022, 130, 107950. [Google Scholar] [CrossRef]
- Dellicker, S.; Benney, R.; Patel, S.; Williams, T.; Hewgley, C.; Yakimenko, O.; Howard, R.; Kaminer, I. Performance, control, and simulation of the Affordable Guided Airdrop System. In Proceedings of the Modeling & Simulation Technologies Conference, Denver, CO, USA, 14–17 August 2000. [Google Scholar]
- Yakimenko, O.; Dobrokhodov, V.; Johnson, J.; Kaminer, I.; Delliker, S.; Benney, R. Guidance and control of affordable guided airdrop system-science direct. IFAC Proc. Vol. 2002, 35, 13–18. [Google Scholar] [CrossRef]
- Wei, H.; Xu, C.; Zhang, Z. The Development of Inflatable Entry Decelerator Technology. Spacecr. Recovery Remote Sens. 2019, 40, 14–24. [Google Scholar]
- Favini, E.; Niezrecki, C.; Chen, J.; Willis, D.; Niemi, E.; Desabrais, K. Review of smart material technologies for active parachute applications. Act. Passiv. Smart Struct. Integr. Syst. 2010, 7643, 764310. [Google Scholar]
- Zhu, H.; Sun, Q.; Tao, J.; Chen, Z.; Dehmer, M.; Xie, G. Flexible modeling of parafoil delivery system in wind environments. Commun. Nonlinear Sci. Numer. Simul. 2021, 108, 106210. [Google Scholar] [CrossRef]
- Lee, C.H.; Kim, T.H.; Tahk, M.J. Agile Missile Autopilot Design using Nonlinear Backstepping Control with Time-Delay Adaptation. Trans. Jpn. Soc. Aeronaut. Space Sci. 2014, 57, 9–20. [Google Scholar] [CrossRef]
- Gong, X.; Chen, W.; Chen, Z. All-aspect attack guidance law for agile missiles based on deep reinforcement learning. Aerosp. Sci. Technol. 2022, 127, 107677. [Google Scholar] [CrossRef]
- Han, S.; Bai, J.H.; Hong, S.M.; Roh, H.; Tahk, M.J.; Yun, J.; Park, S. Guidance Law for Agile Turn of Air-to-Air Missile during Boost Phase. Int. J. Aeronaut. Space Sci. 2017, 18, 709–718. [Google Scholar] [CrossRef]
- Zheng, Z.; Xie, L. Finite-time path following control for a stratospheric airship with input saturation and error constraint. Int. J. Control. 2019, 92, 368–393. [Google Scholar] [CrossRef]
- Li, G.; Xin, M.; Miao, C. Finite-Time Input-to-State Stability Guidance Law. J. Guid. Control. Dyn. 2018, 41, 2199–2213. [Google Scholar] [CrossRef]
- Sun, S.; Zhou, D.; Hou, W.T. A guidance law with finite time convergence accounting for autopilot lag. Aerosp. Sci. Technol. 2013, 25, 132–137. [Google Scholar] [CrossRef]
- Ni, J.; Liu, L.; Liu, C.; Liu, J. Fixed-Time Leader-Following Consensus for Second-Order Multiagent Systems with Input Delay. IEEE Trans. Ind. Electron. 2017, 64, 8635–8646. [Google Scholar] [CrossRef]
- ECruz-Zavala, J.A.; Moreno, L.M. Fridman, Uniform robust exact differentiator. IEEE Trans. Autom. Control 2011, 56, 2727–2733. [Google Scholar] [CrossRef]
- Fang, X.; Zhong, Q.; Liu, F.; Ding, Z.; Yang, T. Fixed-time nonsingular terminal sliding mode control for a class of nonlinear systems with mismatched disturbances and its applications. Nonlinear Dyn. 2023, 111, 21065–21077. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, P.; Tang, G.; Bao, W. Fixed-time sliding mode control for hypersonic morphing vehicles via event-triggering mechanism. Aerosp. Sci. Technol. 2023, 140, 108458. [Google Scholar] [CrossRef]
- Kang, Z.; Shen, Q.; Wu, S.; Damaren, C.J. Prescribed Performance-Based Fixed-Time Adaptive Control Allocation for Overactuated Spacecraft. J. Guid. Control Dyn. 2023, 46, 390–400. [Google Scholar] [CrossRef]
- Truong, T.N.; Vo, A.T.; Kang, H.J. A model-free terminal sliding mode control for robots: Achieving fixed-time prescribed performance and convergence. ISA Trans. 2024, 144, 330–341. [Google Scholar] [CrossRef]
- Liang, X.; Hou, M. Adaptive Dynamic Surface Control for Integrated Missile Guidance and Autopilot in the Presence of Input Saturation. J. Aerosp. Eng. 2015, 28, 04014121. [Google Scholar] [CrossRef]
- Guo, J.; Peng, Q.; Guo, Z. SMC-based Integrated Guidance and Control for Beam Riding Missiles with Limited LBPU. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2969–2978. [Google Scholar] [CrossRef]
- Zhou, Q.; Wang, L.; Wu, C.; Li, H.; Du, H. Adaptive fuzzy control for nonstrict-feedback systems with input saturation and output constraint. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1–12. [Google Scholar] [CrossRef]
- Sun, L.; Zheng, Z. Disturbance-observer-based robust backstepping attitude stabilization of spacecraft under input saturation and measurement uncertainty. IEEE Trans. Ind. Electron. 2017, 64, 7994–8002. [Google Scholar] [CrossRef]
- Gong, X.P.; Chen, W.C.; Chen, Z.Y. Fixed-time formation control for spacecraft with prescribed performance guarantee under input saturation. Aerosp. Sci. Technol. 2021, 119, 107176. [Google Scholar]
- Liu, K.; Yang, P.; Jiao, L.; Wang, R.; Yuan, Z.; Dong, S. Antisaturation fixed-time attitude tracking control based low-computation learning for uncertain quadrotor UAVs with external disturbances. Aerosp. Sci. Technol. 2023, 142, 108668. [Google Scholar] [CrossRef]
- Gao, H.; Xia, Y.Q.; Zhang, X.P.; Zhang, G. Distributed fixed-time attitude coordinated control for multiple spacecraft with actuator saturation. Chin. J. Aeronaut. 2022, 35, 292–302. [Google Scholar] [CrossRef]
- Liu, Z.J.; Meng, Z.J. Fixed-time attitude control for aircraft with strongly constrained actuators. Aerosp. Sci. Technol. 2023, 141, 108532. [Google Scholar] [CrossRef]
- Ma, Y.; Guo, J.; Tang, S. High angle of attack command generation technique and tracking control for agile missiles. Aerosp. Sci. Technol. 2015, 45, 324–334. [Google Scholar] [CrossRef]
- Gómez-Peñate, S.; López-Estrada, F.R.; Valencia-Palomo, G.; Rotondo, D.; Guerrero-Sánchez, M.E. Actuator and sensor fault estimation based on a proportional multiple-integral sliding mode observer for linear parameter varying systems with inexact scheduling parameters. Int. J. Robust Nonlinear Control 2021, 31, 8420–8441. [Google Scholar] [CrossRef]
- Zhang, L.J.; Xia, Y.Q.; Shen, G.H.; Cui, B. Fixed-time attitude tracking control for spacecraft based on a fixed-time extended state observer. Sci. China-Inf. Sci. 2021, 064, 150–166. [Google Scholar] [CrossRef]
- Ai, X.; Yu, J. Fixed-time trajectory tracking for a quadrotor with external disturbances: A flatness-based sliding mode control approach. Aerosp. Sci. Technol. 2019, 89, 58–76. [Google Scholar] [CrossRef]
- Wang, T.; Liu, Y.; Zhang, X. Extended state observer-based fixed-time trajectory tracking control of autonomous surface vessels with uncertainties and output constraints. ISA Trans. 2022, 128, 174–183. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.S.; Qiu, B.B.; Liu, L.; Yang, Y. Global fixed-time trajectory tracking control of underactuated USV based on fixed-time extended state observer. ISA Trans. 2023, 132, 267–277. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Wang, Y.; Yin, L.A. Practical fixed-time observer-based generalized cascade predictor design for synchronization of integrator systems with delays and complex unknowns. ISA Trans. 2023, 135, 159–172. [Google Scholar] [CrossRef] [PubMed]
- Wu, R.; Wei, C.; Yan, F.; Cui, N.; Zhang, L. FxTDO-Based Non-Singular Terminal Sliding Mode Control for Second-Order Uncertain Systems. IET Control Theory Appl. 2018, 12, 2459–2467. [Google Scholar] [CrossRef]
- Li, H.; Cai, Y. On SFTSM control with fixed-time convergence. IET Control Theory Appl. 2017, 11, 766–773. [Google Scholar] [CrossRef]
- Shen, G.H.; Xia, Y.Q.; Sun, H.R. A 6DOF mathematical model of parachute in Mars EDL. Adv. Space Res. 2015, 55, 1823–1831. [Google Scholar] [CrossRef]
- Sun, R.; Shan, A.; Zhang, C.; Wu, J.; Jia, Q. Quantized Fault-Tolerant Control for Attitude Stabilization with Fixed-Time Disturbance Observer. J. Guid. Control Dyn. 2021, 44, 229–255. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).