A Zonal Detached Eddy Simulation of the Trailing Edge Stall Process of a LS0417 Airfoil
Abstract
1. Introduction
2. The Formulation of ZDES
2.1. The Definition of the Background Turbulence Model
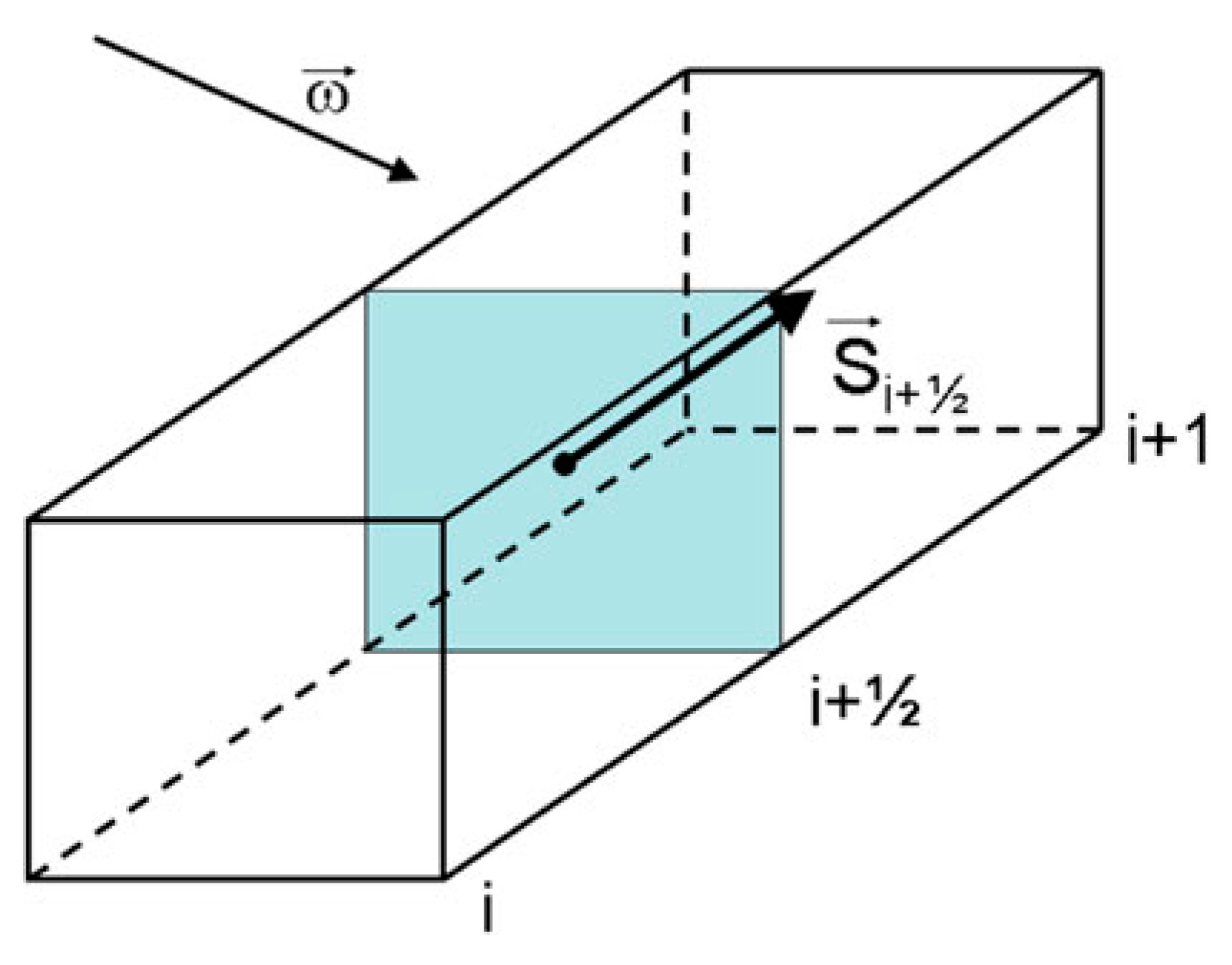
2.2. The Definition of the Hybrid Length Scale
2.3. The Definition of the Subgrid Scale
3. The Prediction of Stall
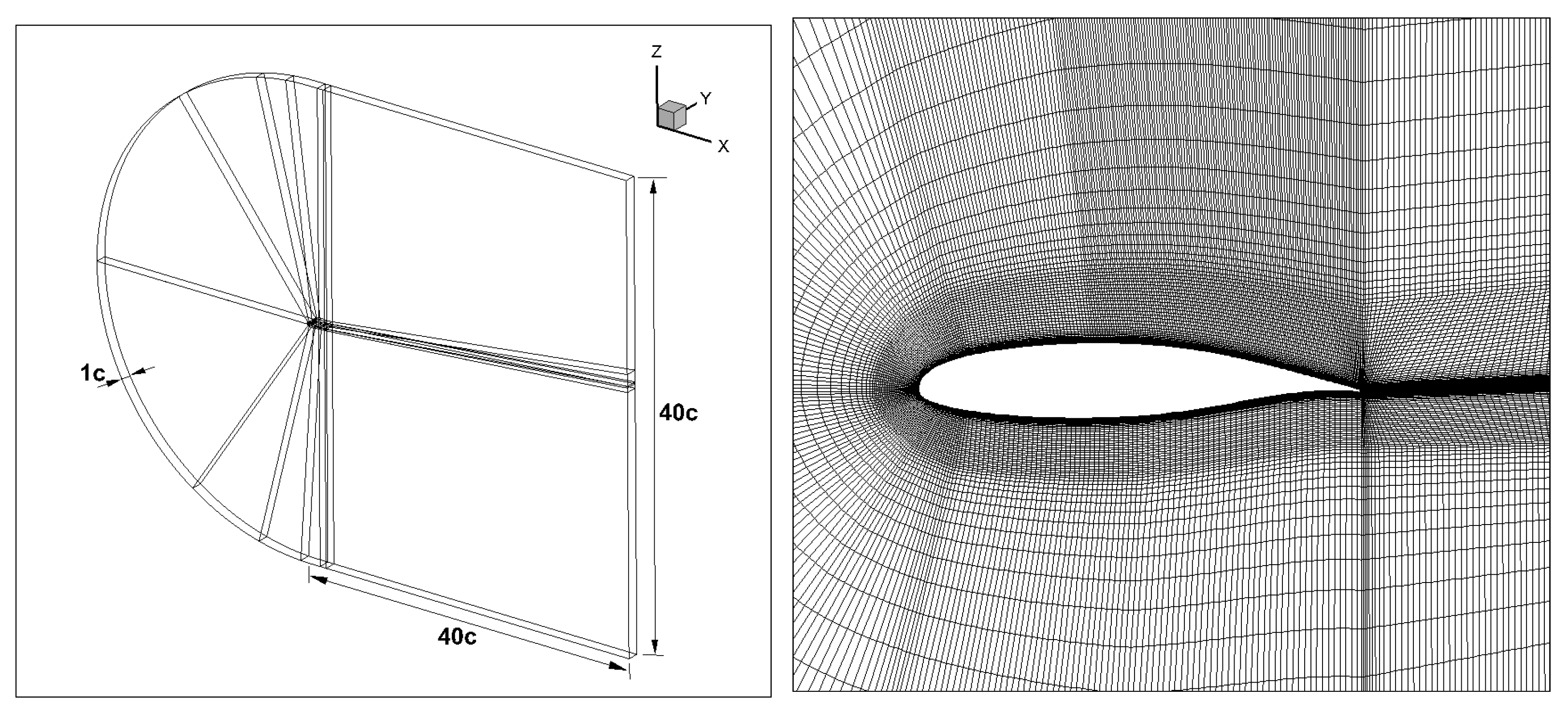
3.1. The Introduction of the Airfoil and the Experiment
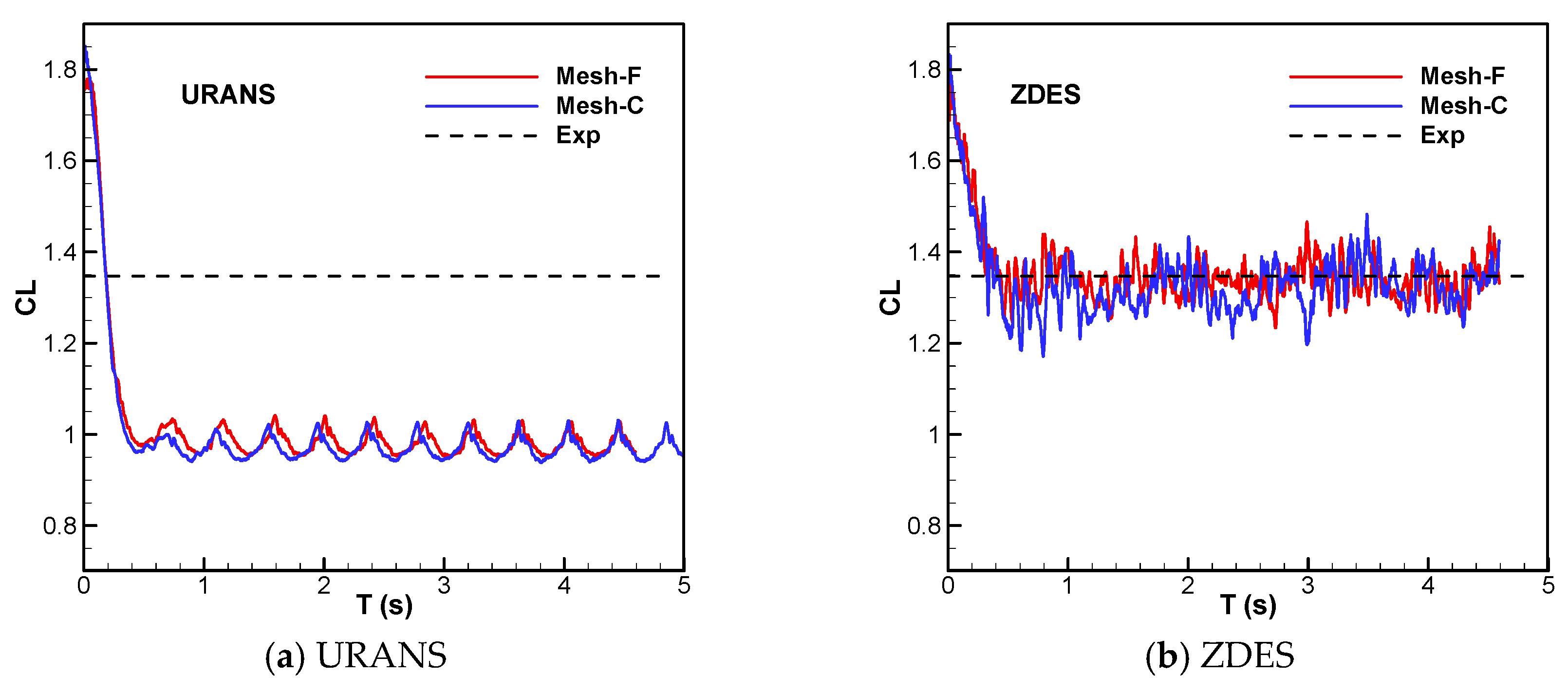
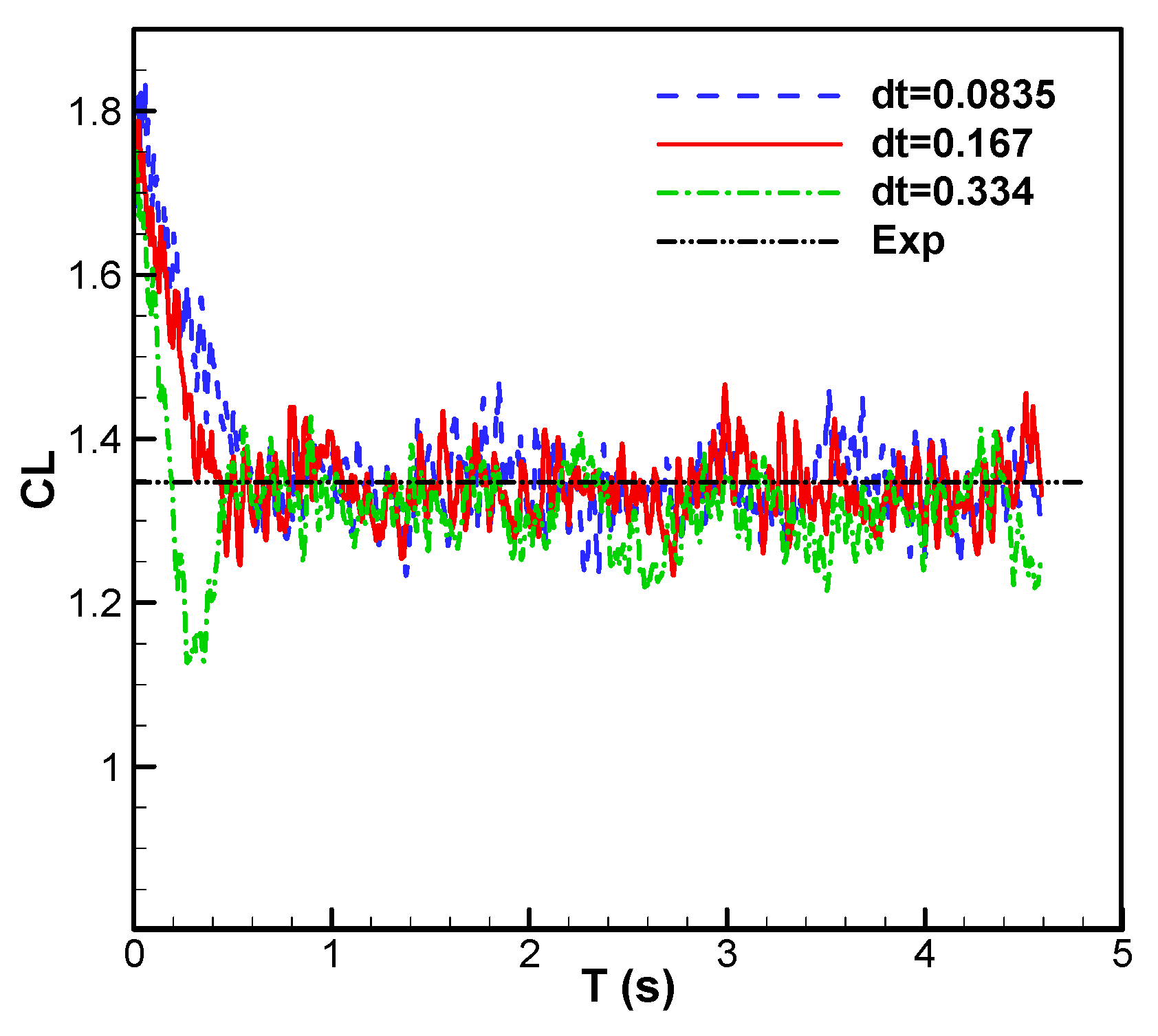
3.2. The Grid Density and the Time Step Validation
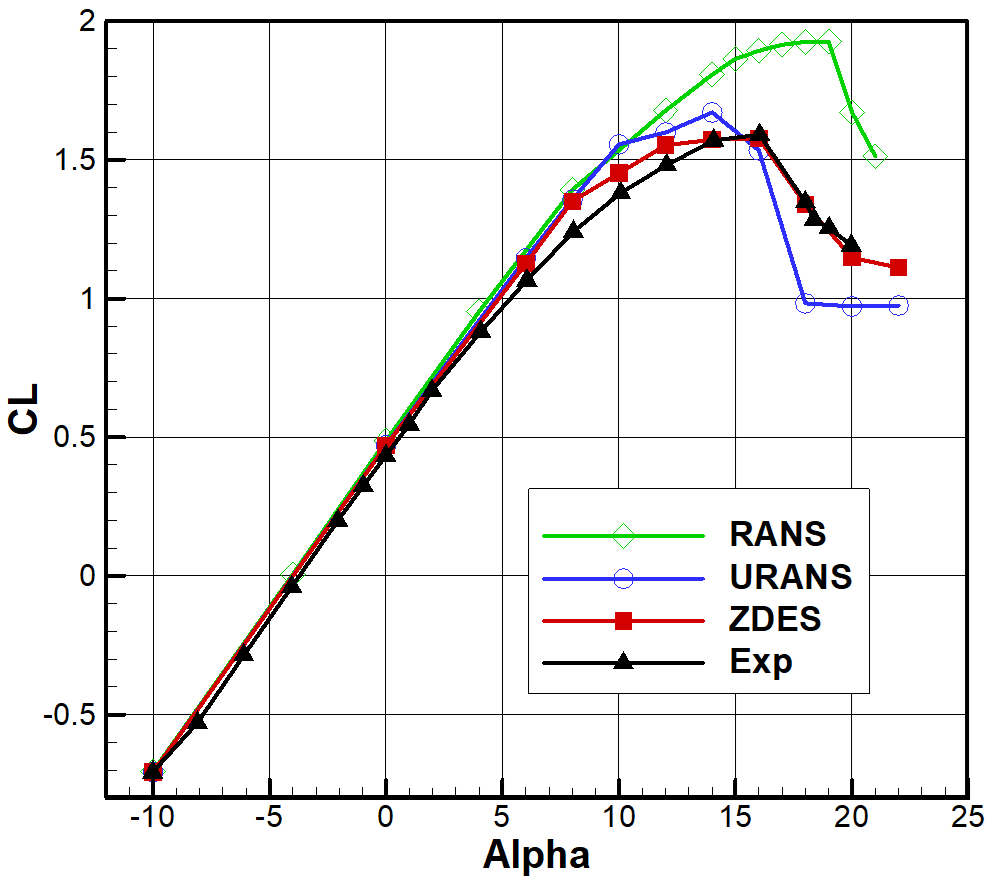
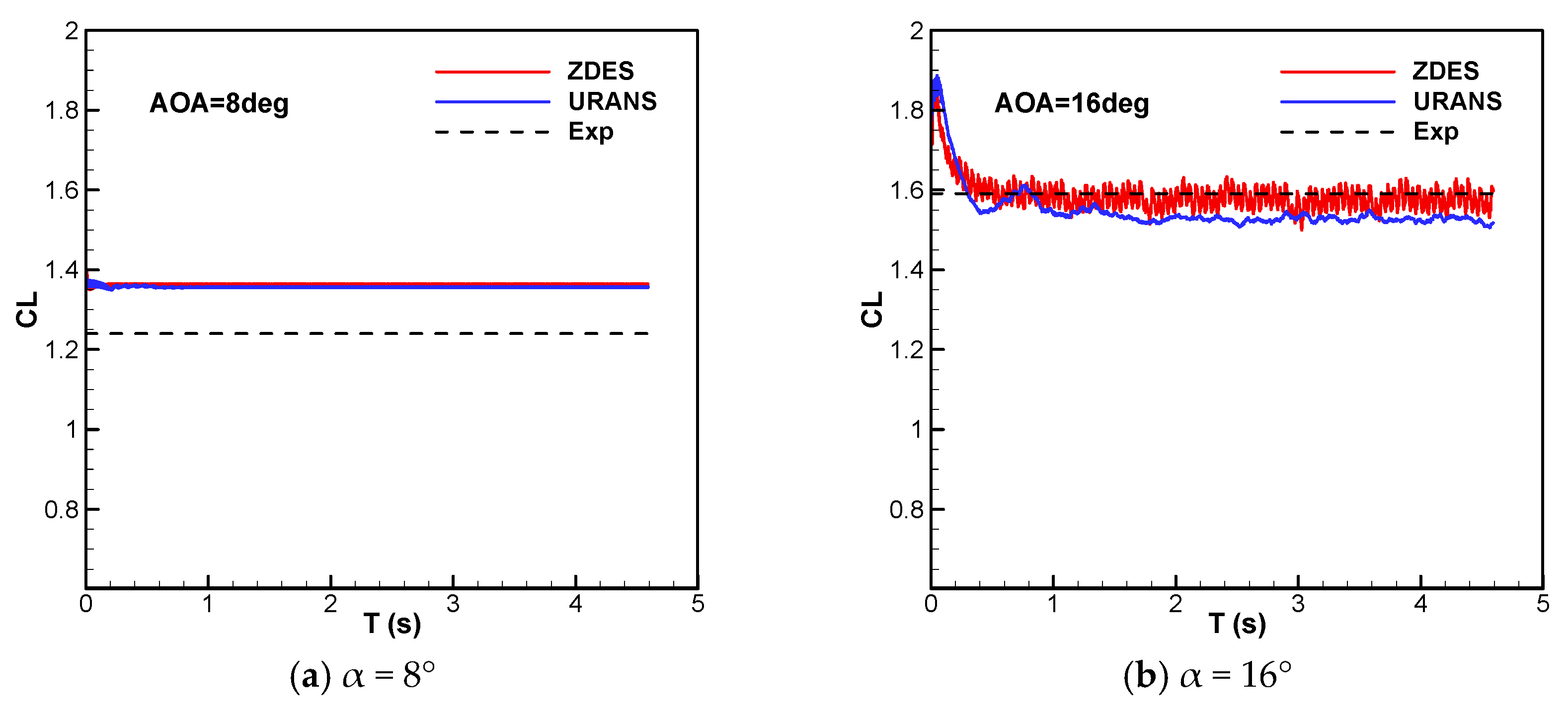
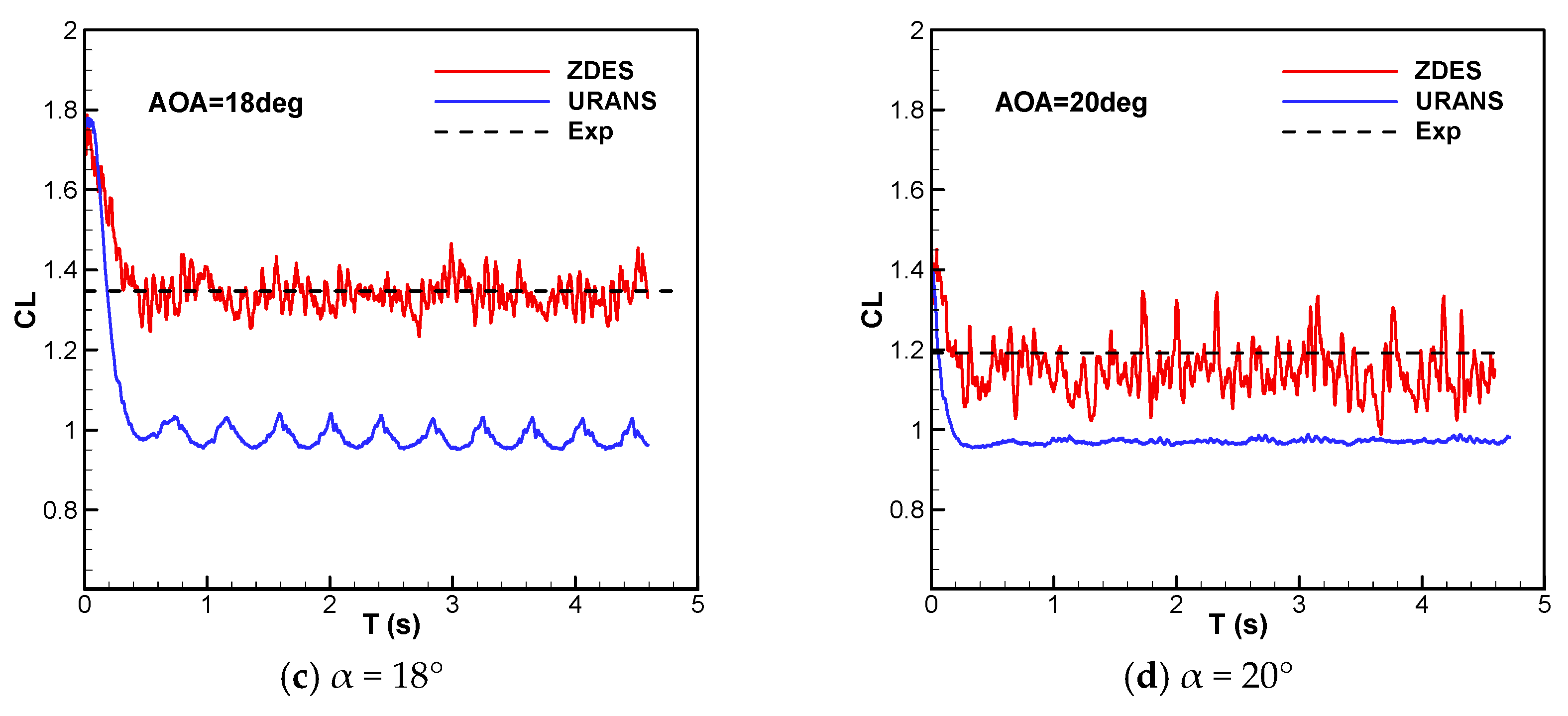
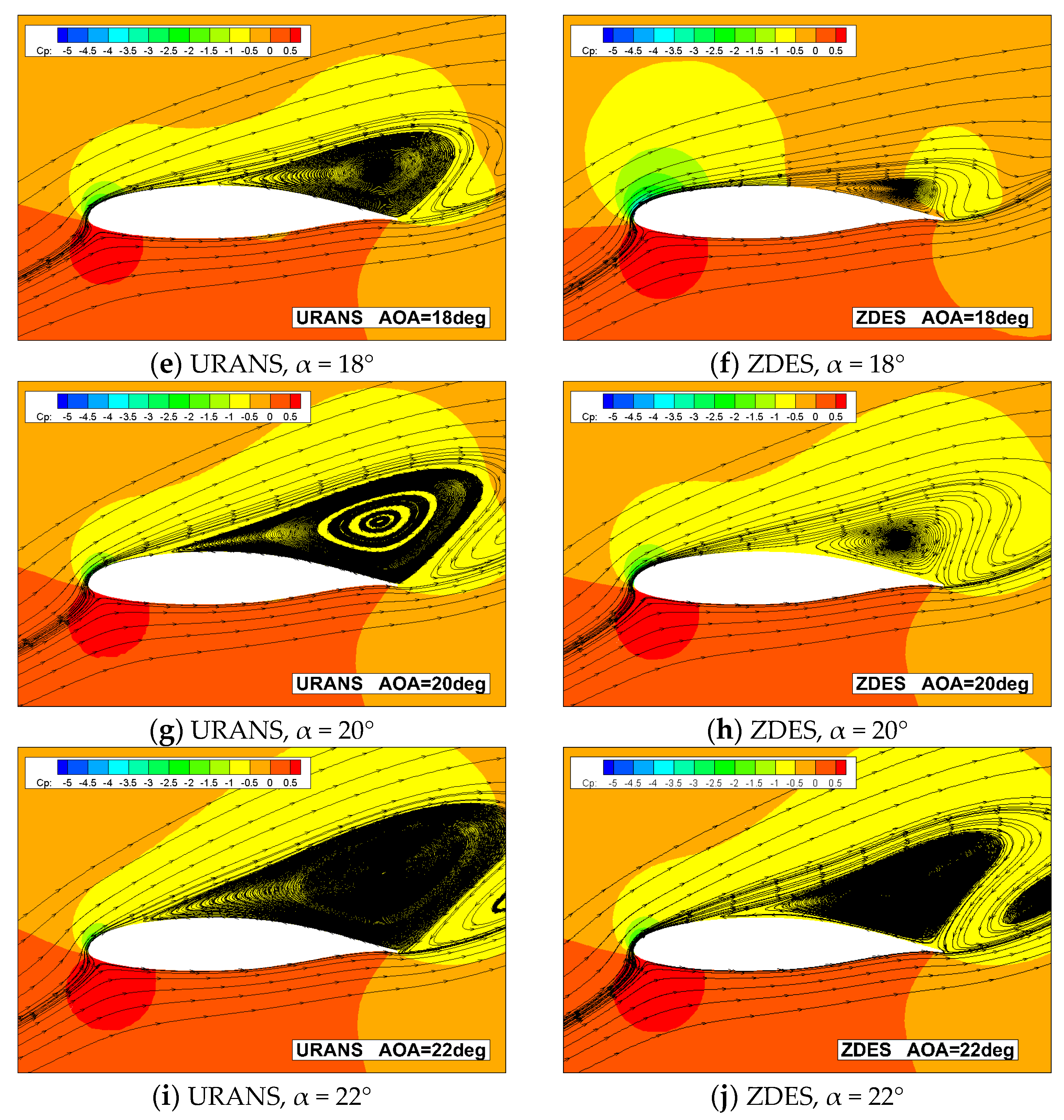
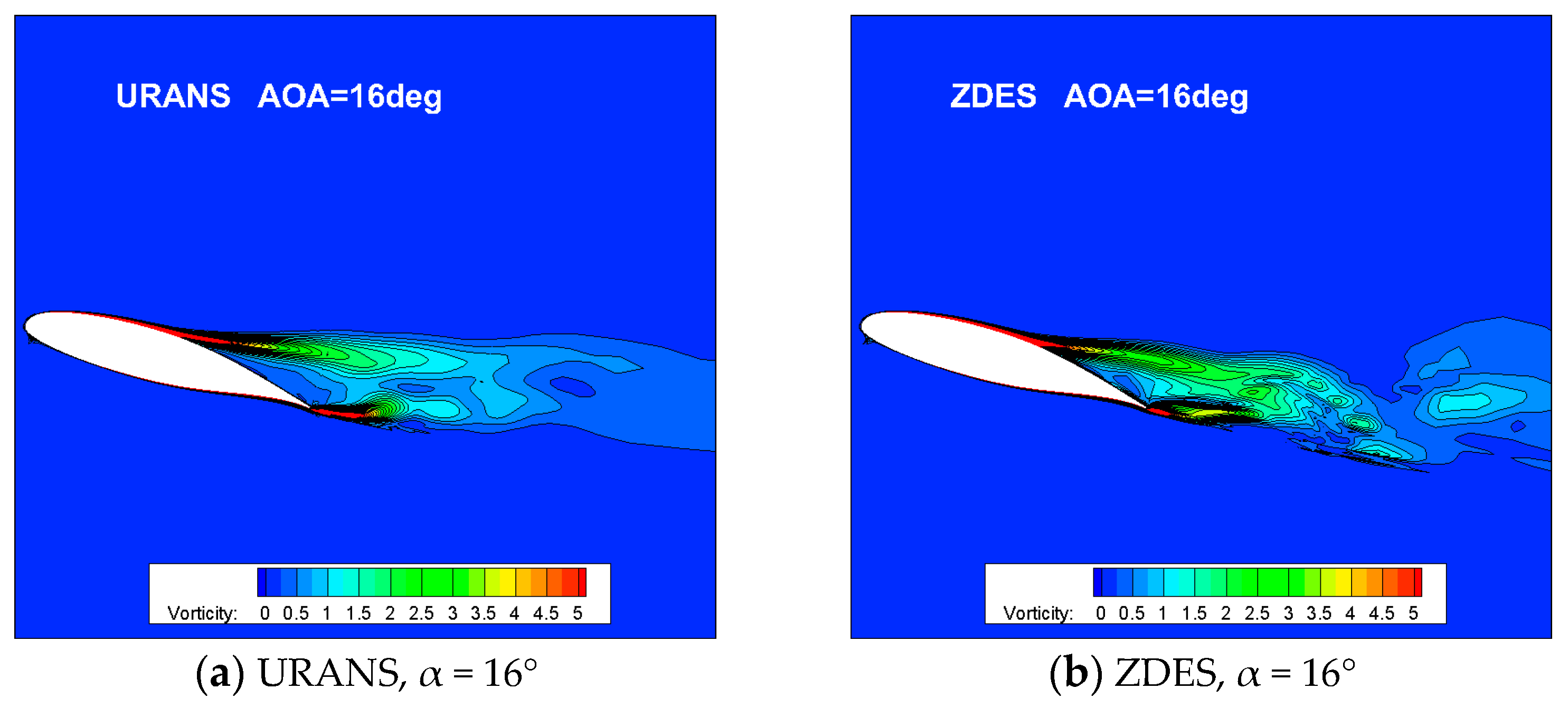
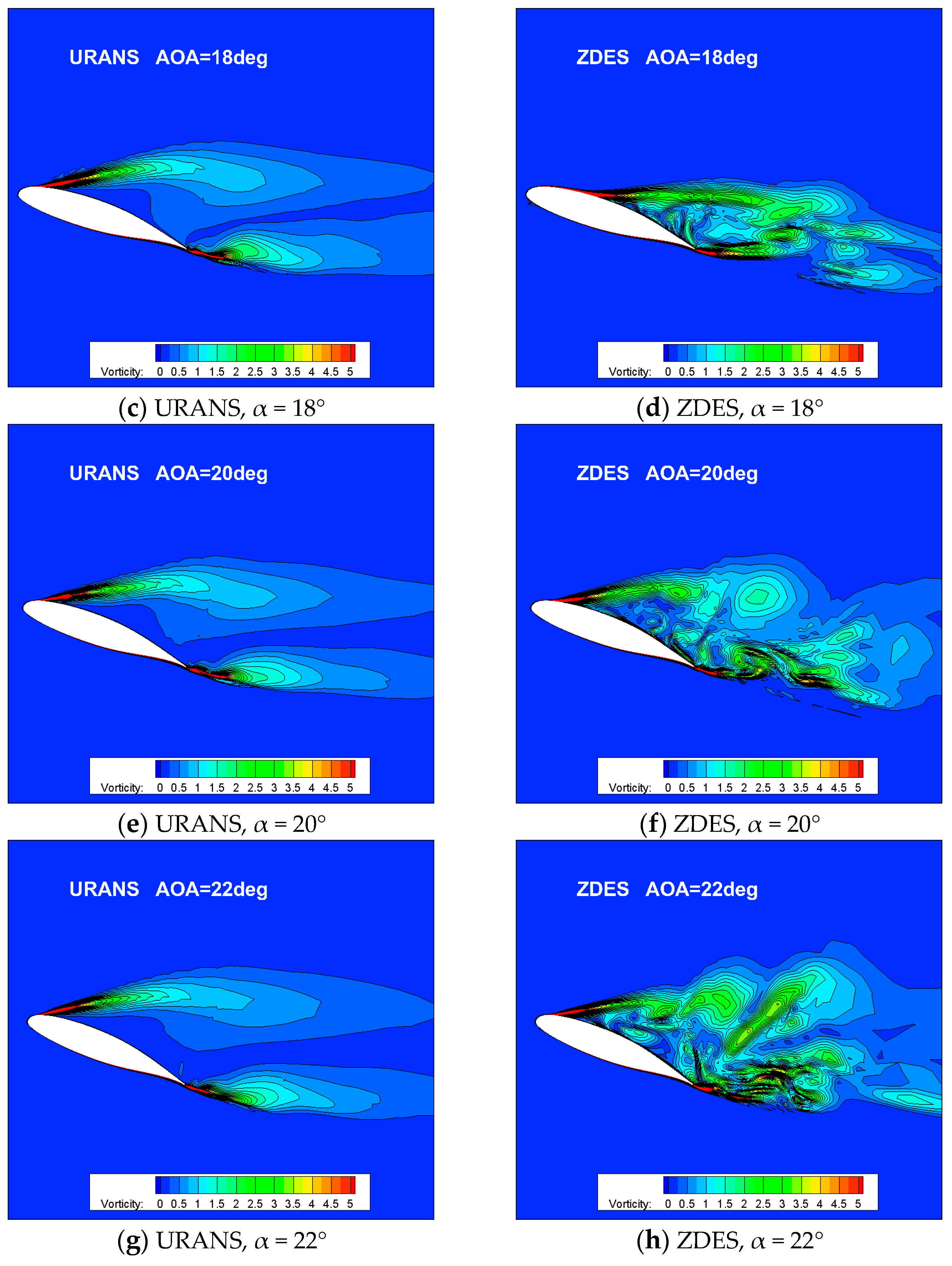
3.3. The Prediction of Stall Process
4. Conclusions
- (1)
- The stall AOA and maximum lift coefficient of the airfoil are overpredicted notably by RANS. The accuracy of the prediction of the stall AOA is improved with the application of URANS; however, the excessively sharp decreases in lift are both obtained using RANS and URANS under post-stall conditions.
- (2)
- The stall point predicted by ZDES is consistent with the experiment value; the gradual drop of lift is also obtained under the post-stall condition. The unsteady characteristics of lift during the stall process in the ZDES result are more pronounced than those in the URANS result.
- (3)
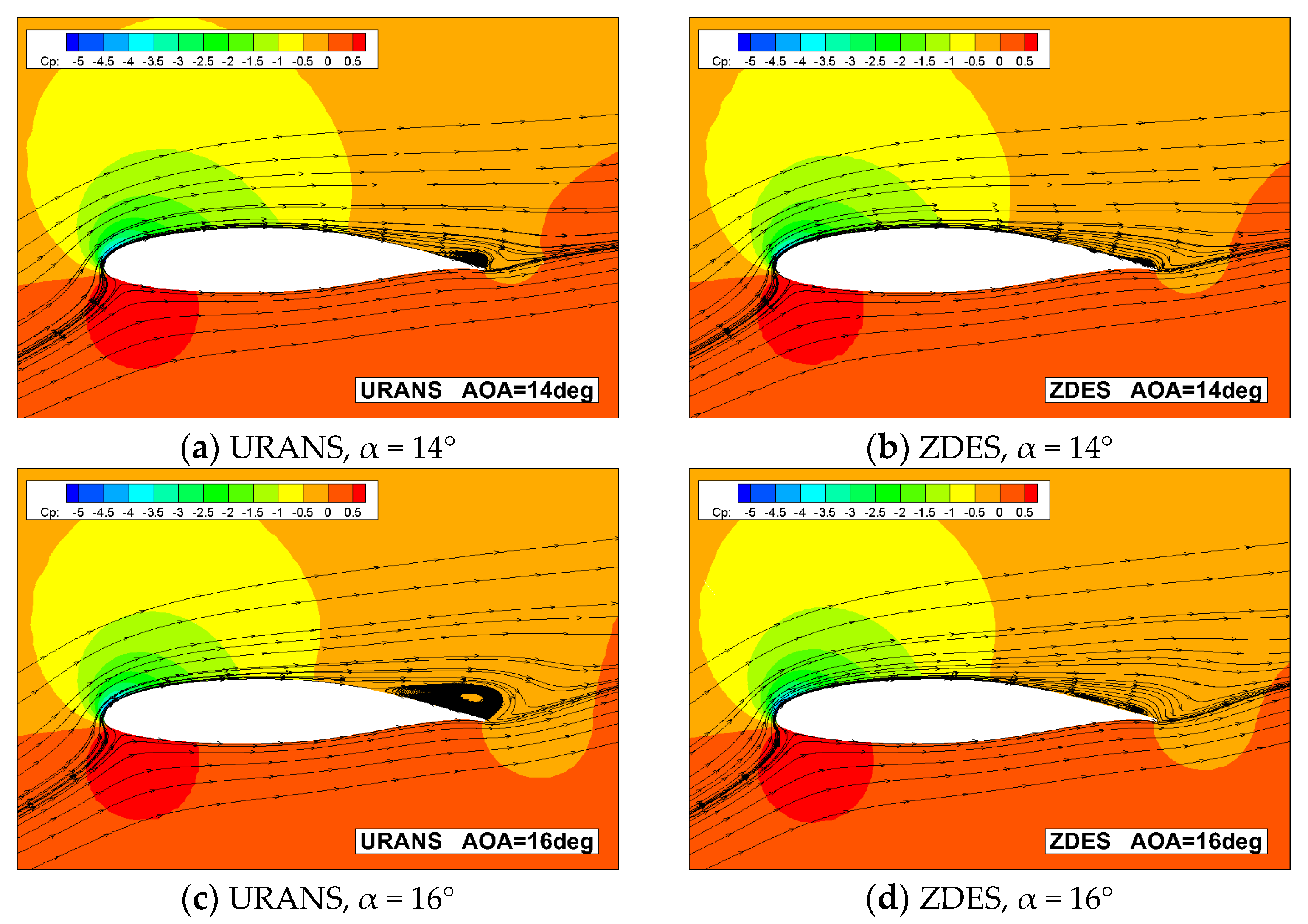
- With the increase in the AOA, the expanding of the separation region at the trailing edge during the stall process are both predicted via URANS and ZDES, but a milder development of separation and decrease in leading edge peak suction are manifested in the ZDES result, which corresponds to a more reasonable stall prediction.
- (4)
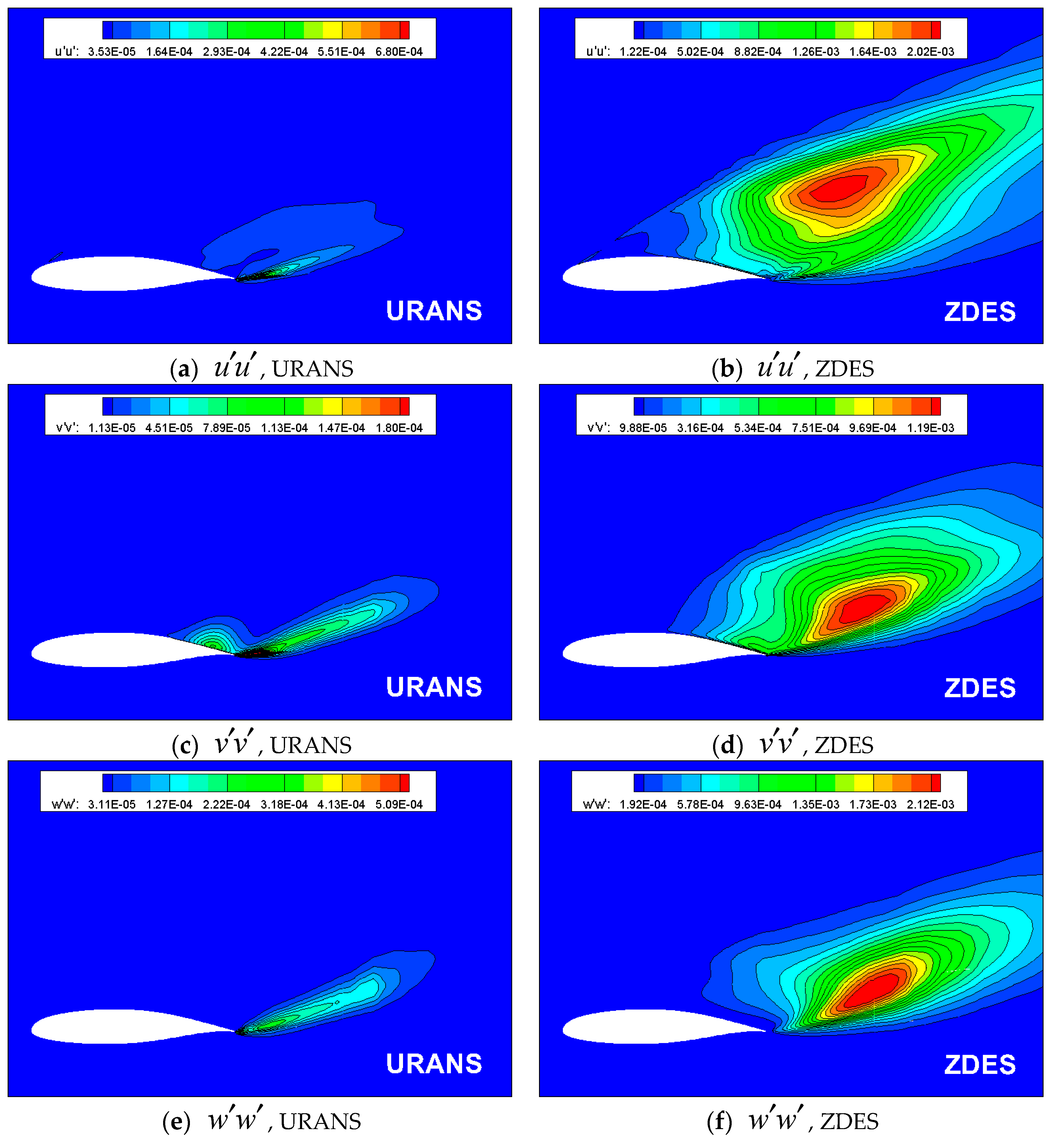
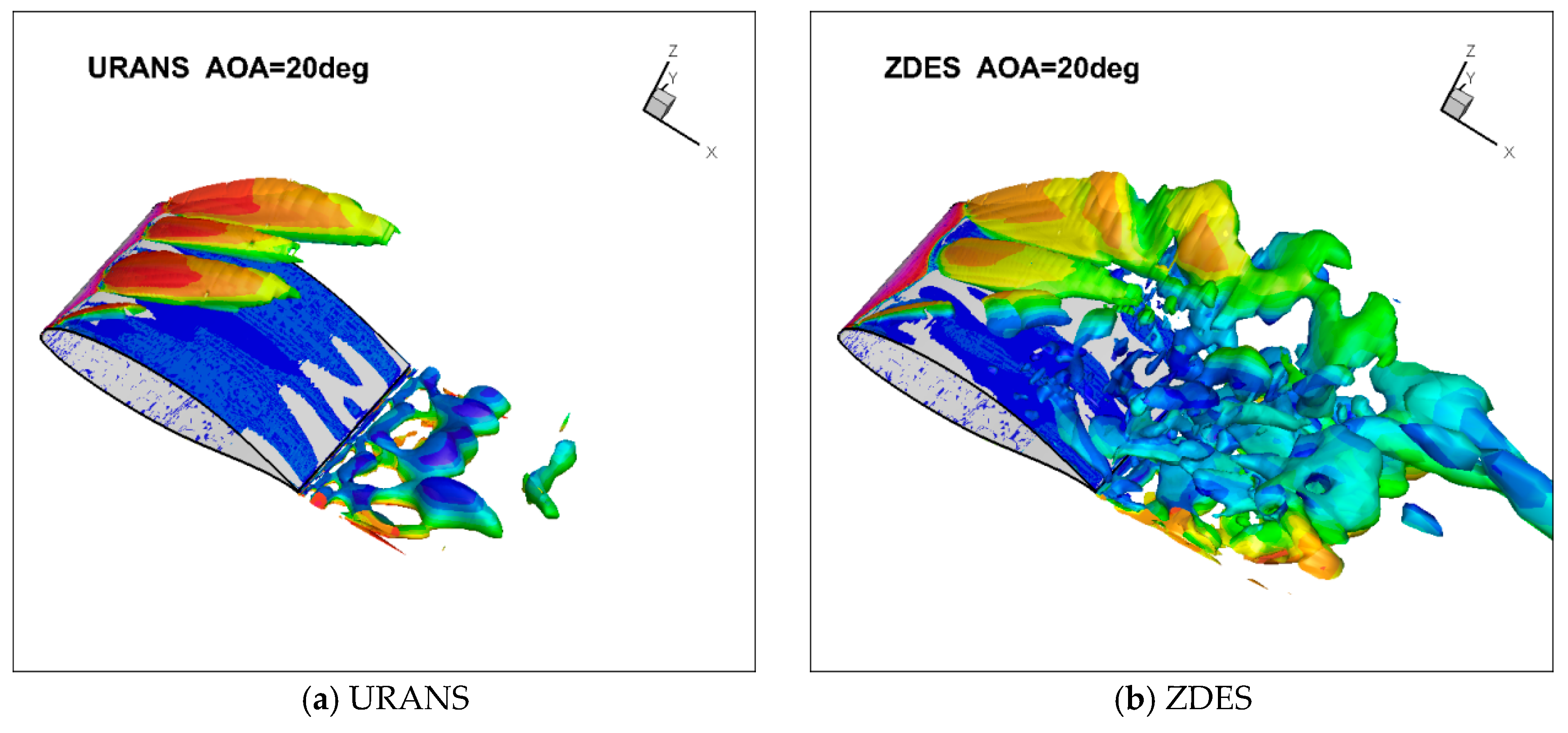
- The alternate shedding and the interference of the leading edge and the trailing edge vortices are illustrated by ZDES near the stall point, while the core region of turbulent fluctuation is captured, which indicates the essential difference in the predicted stall result between URANS and ZDES.
- (5)
- From the result of ZDES, it is indicated that the core region of turbulent fluctuation is at the location far from the wall, where the interference of the leading edge and trailing edge vortices occurs. The phenomenon reveals the dominated flow behaviors under the post-stall condition of the trailing edge stall.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mccullough, G.B.; Gault, D.E. Examples of Three Representative Types of Airfoil-Section Stall at Low Speed; NASA: Greenbelt, MD, USA, 1951; NACA-TN-2502. [Google Scholar]
- Rhie, C.M.; Chow, W.L. Numerical study of the turbulent flow past an airfoil with trailing edge separation. AIAA J. 1983, 21, 1525–1532. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-eddy simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Shur, M.; Spalart, P.R.; Strelets, M.; Travin, A. Detached-eddy simulation of an airfoil at high angle of attack. In Engineering Turbulence Modelling and Experiments; Elsevier Science Ltd.: London, UK, 1999; pp. 669–678. [Google Scholar]
- Im, H.S.; Zha, G.C. Delayed detached eddy simulation of airfoil stall flows using high-order schemes. J. Fluids Eng. 2014, 136, 111104. [Google Scholar] [CrossRef]
- Menter, F.R.; Kuntz, M. Adaptation of eddy-viscosity turbulence models to unsteady separated flow behind vehicles. In The Aerodynamics of Heavy Vehicles: Trucks, Buses, and Trains; Springer: Berlin/Heidelberg, 2004; pp. 339–352. [Google Scholar]
- Yang, Y.; Zha, G.C. Simulation of airfoil stall flows using IDDES with high order schemes. In Proceedings of the 46th AIAA Fluid Dynamics Conference, Washington, DC, USA, 13–17 June 2016; p. 3185. [Google Scholar]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. A hybrid RANS-LES approach with delayed-DES and wall-modelled LES capabilities. Int. J. Heat Fluid Flow 2008, 29, 1638–1649. [Google Scholar] [CrossRef]
- Wang, G.; Wang, S.; Li, H.; Fu, X.; Liu, W. Comparative assessment of SAS, IDDES and hybrid filtering RANS/LES models based on second-moment closure. Adv. Mech. Eng. 2021, 13, 16878140211028447. [Google Scholar] [CrossRef]
- Gilling, L.; Sørensen, N.; Davidson, L. Detached eddy simulations of an airfoil in turbulent inflow. In Proceedings of the 47th AIAA Aerospace Sciences Meeting Including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; p. 270. [Google Scholar]
- Wang, L.; Li, L.; Fu, S. A comparative study of DES type methods for mild flow separation prediction on a NACA0015 airfoil. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2528–2543. [Google Scholar] [CrossRef]
- Guo, H.; Li, G.; Zou, Z. Numerical simulation of the flow around NACA0018 airfoil at high incidences by using RANS and DES methods. J. Mar. Sci. Eng. 2022, 10, 847. [Google Scholar] [CrossRef]
- Li, D.; Men’shov, I.; Nakamura, Y. Detached-eddy simulation of three airfoils with different stall onset mechanisms. J. Aircr. 2006, 43, 1014–1021. [Google Scholar] [CrossRef]
- Cokljat, D.; Liu, F. DES of turbulent flow over an airfoil at high incidence. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002; p. 590. [Google Scholar]
- Durrani, N.; Qin, N. Behavior of detached-eddy simulations for mild airfoil trailing-edge separation. J. Aircr. 2011, 48, 193–202. [Google Scholar] [CrossRef]
- Shur, M.L.; Spalart, P.R.; Strelets, M.K.; Travin, A.K. An enhanced version of DES with rapid transition from RANS to LES in separated flows. Flow Turbul. Combust. 2015, 95, 709–737. [Google Scholar] [CrossRef]
- Yalçın, Ö.; Cengiz, K.; Özyörük, Y. High-order detached eddy simulation of unsteady flow around NREL S826 airfoil. J. Wind. Eng. Ind. Aerodyn. 2018, 179, 125–134. [Google Scholar] [CrossRef]
- Deck, S. Recent improvements in the zonal detached eddy simulation (ZDES) formulation. Theor. Comput. Fluid Dyn. 2012, 26, 523–550. [Google Scholar] [CrossRef]
- Le Pape, A.; Richez, F.; Deck, S. Zonal detached-eddy simulation of an airfoil in poststall condition. AIAA J. 2013, 51, 1919–1931. [Google Scholar] [CrossRef]
- Richez, F.; Le Pape, A.; Costes, M. Zonal detached-eddy simulation of separated flow around a finite-span wing. AIAA J. 2015, 53, 3157–3166. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Chauvet, N.; Deck, S.; Jacquin, L. Zonal detached eddy simulation of a controlled propulsive jet. AIAA J. 2007, 45, 2458–2473. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Li, J. Numerical Investigation of Stall Characteristics of Common Research Model Configuration Based on Zonal Detached Eddy Simulation Method. Aerospace 2023, 10, 817. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, H.; Li, Y. Enhancing the Resolution of Blade Tip Vortices in Hover with High-Order WENO Scheme and Hybrid RANS–LES Methods. Aerospace 2023, 10, 262. [Google Scholar] [CrossRef]
- Zhang, H.; Li, J.; Jiang, Y.; Shi, W.; Jin, J. Analysis of the expanding process of turbulent separation bubble on an iced airfoil under stall conditions. Aerosp. Sci. Technol. 2021, 114, 106755. [Google Scholar] [CrossRef]
- Shu, C.W. High order ENO and WENO schemes for computational fluid dynamics. In High-Order Methods for Computational Physics; Springer: Berlin/Heidelberg, Germany, 1999; pp. 439–582. [Google Scholar]
- Whitcomb, R.T.; Clark, L.R. An Airfoil Shape for Efficient Flight at Supercritical Mach Numbers; NASA: Greenbelt, MD, USA, 1965; No. L-4517. [Google Scholar]
- McGhee, R.J.; Bingham, G.J. Low-Speed Aerodynamic Characteristics of a 17-Percent-Thick Supercritical Airfoil Section, Including a Comparison between Wind-Tunnel and Flight Data; NASA: Greenbelt, MD, USA, 1972; No. L-8290. [Google Scholar]
- Palmer, W.E.; Elliott, D.W.; White, J.E. Flight and Wind Tunnel Evaluation of a 17% Thick Supercritical Airfoil on a T-2C Airplane. In Vol. II-Flight Measured Wing Wake Profiles and Surface Pressures; North American Rockwell: Barberton, OH, USA, 1971; NR71H-150. [Google Scholar]
- Xu, H.Y.; Qiao, C.L.; Yang, H.Q.; Ye, Z.Y. Delayed detached eddy simulation of the wind turbine airfoil S809 for angles of attack up to 90 degrees. Energy 2017, 118, 1090–1109. [Google Scholar] [CrossRef]


| Chordwise | Normal | Spanwise | ||||
|---|---|---|---|---|---|---|
| Mesh-C | 281 | 400 | 87 | 0.8 | 29 | 3000 |
| Mech-F | 332 | 300 | 121 | 0.8 | 41 | 2000 |
| Airfoil | DES-Type Methods | Re | AOA | Grid Size |
|---|---|---|---|---|
| NACA0012 [4] | DES | 1 × 105 | 45° | 2.0 × 105 |
| NACA0012 [5] | DES and DDES | 1.3 × 106 | 17°/25°/ 45°/60° | 6.0 × 105 |
| NACA0012 [7] | IDDES | 1.3 × 106 | 5°/17°/ 45°/60° | 8.64 × 105 |
| NACA0012 [9] | IDDES | 1.3 × 106 | 45° | 5.87 × 105 |
| NACA0015 [10] | DES | 1.6 × 106 | 12°~20° | 2.0 × 107 |
| NACA0015 [11] | DDES and IDDES | 1.0 × 106 | 11° | 1.35 × 107 |
| NACA0018 [12] | DDES | 1.0 × 106 | 5°~40° | 2.07 × 106 |
| NACA633-018 [13] | DES | 5.8 × 106 | 0°~18° | 4.07 × 105 |
| A-airfoil [14] | DES | 2.1 × 106 | 13.3° | 3.78 × 105 |
| A-airfoil [15] | DES and DDES | 2.0 × 106 | 13.3° | 2.00 × 106 |
| NREL S826 [17] | SLA-IDDES | 1.0 × 106 and 1.45 × 106 | 4°~12° | 9.47 × 105 |
| URANS | ZDES | Exp | |
|---|---|---|---|
| Mesh-C | 0.9684 | 1.3197 | 1.35 |
| Mech-F | 0.9826 | 1.3398 |
| dt | 0.334 | 0.167 | 0.0835 | Exp |
| CL | 1.3121 | 1.3398 | 1.3418 | 1.35 |
| AOA | CL of EXP | URANS | ZDES | ||
|---|---|---|---|---|---|
| CAL | ERR | CAL | ERR | ||
| 12 | 1.48 | 1.5987 | 8.02% | 1.5527 | 4.91% |
| 14 | 1.57 | 1.671 | 6.43% | 1.5726 | 0.17% |
| 16 | 1.59 | 1.5345 | −3.49% | 1.5773 | −0.80% |
| 18 | 1.35 | 0.9826 | −27.21% | 1.3398 | −0.76% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, W.; Zhang, H.; Li, Y. A Zonal Detached Eddy Simulation of the Trailing Edge Stall Process of a LS0417 Airfoil. Aerospace 2024, 11, 731. https://doi.org/10.3390/aerospace11090731
Shi W, Zhang H, Li Y. A Zonal Detached Eddy Simulation of the Trailing Edge Stall Process of a LS0417 Airfoil. Aerospace. 2024; 11(9):731. https://doi.org/10.3390/aerospace11090731
Chicago/Turabian StyleShi, Wenbo, Heng Zhang, and Yuanxiang Li. 2024. "A Zonal Detached Eddy Simulation of the Trailing Edge Stall Process of a LS0417 Airfoil" Aerospace 11, no. 9: 731. https://doi.org/10.3390/aerospace11090731
APA StyleShi, W., Zhang, H., & Li, Y. (2024). A Zonal Detached Eddy Simulation of the Trailing Edge Stall Process of a LS0417 Airfoil. Aerospace, 11(9), 731. https://doi.org/10.3390/aerospace11090731





