Abstract
Trajectory prediction serves as a prerequisite for future trajectory-based operation, significantly reducing the uncertainty of aircraft movement information within airspace by scientifically forecasting the three-dimensional positions of aircraft over a certain period. As convergence points in the aviation network, airport terminal airspace exhibits the most complex traffic conditions in the entire air route network. It has stronger mutual influences and interactions among aircraft compared to the en-route phase. Current research typically uses the trajectory time series information of a single aircraft as input for subsequent predictions. However, it often lacks consideration of the close-range spatial interactions between multiple aircraft in the terminal airspace. This results in a gap in the study of aircraft trajectory prediction that couples spatiotemporal features. This paper aims to predict the four-dimensional trajectories of aircraft in terminal airspace, constructing a Spatio-Temporal Transformer (ST-Transformer) prediction model based on temporal and spatial attention mechanisms. Using radar aircraft trajectory data from the Guangzhou Baiyun Airport terminal airspace, the results indicate that the proposed ST-Transformer model has a smaller prediction error compared to mainstream deep learning prediction models. This demonstrates that the model can better integrate the temporal sequence correlation of trajectory features and the potential spatial interaction information among trajectories for accurate prediction.
1. Introduction
In the foreseeable future, the global air traffic business volume will continue to maintain a rapid growth trend. According to Eurocontrol’s prediction, without bold actions, European Union airports will be unable to accommodate approximately 1.5 million flights by 2040, equivalent to approximately 160 million passengers unable to fly [1]. Compared to ground transportation, aerial operations have more degrees of freedom and are more susceptible to various weather conditions. This necessitates quicker decisions and adjustments within short timeframes. To ensure safe operations and avoid collisions, aircraft cannot autonomously choose their flight paths. Instead, they must communicate in real-time with ground-based air traffic management (ATM) systems and follow the instructions of air traffic controllers. This mode of operation leads to a series of issues as traffic volume increases, including flight delays, airspace congestion, and increased workload for controllers. The main conflict now is between the capability of civil air traffic management and the rapidly growing demand for flights. This situation poses new requirements for the automation level of the current human-centric, machine-assisted ATM system. There is an urgent need for innovation in both operational concepts and technologies [2].
The transition from controller-centric, airspace sector-based operations to trajectory-based operations (TBOs) is a system-level solution proposed by the international civil aviation community in recent years. By introducing the concept of four-dimensional trajectory (4DT), the management of airspace resources has shifted from traditional single dimensions such as airways, altitude levels, or time to a comprehensive four-dimensional (4D) spatiotemporal resource, enabling coordinated air traffic operations. In the sixth edition of the Global Air Navigation Plan (GANP) issued by the International Civil Aviation Organization (ICAO), the Aviation System Block Upgrade (ASBU) plan explicitly identifies TBO as one of the ultimate goals to be globally promoted and applied after 2031 [3]. The United States and Europe have also proposed the next-generation air traffic management system (NextGen) [4] and Single European Sky ATM Research (SESAR) [5] to address the increase in traffic and emerging challenges.
By enabling real-time sharing and dynamic maintenance of trajectory information among relevant parties such as air traffic controllers, airlines, airports, and aircraft, TBO facilitates collaborative decision-making among multiple parties. It can be effectively applied in high-traffic, high-density, and short-interval operational environments, enhancing airspace safety and improving the utilization of airspace resources. TBO provides a more precise, safe, and efficient air traffic management model for the future [6]. TBO primarily consists of three components: trajectory prediction system, conflict detection and resolution system, and trajectory surveillance system [7]. In a high-density aviation network, the cooperation of these three systems promotes the automated generation and implementation of controller instructions, allowing aircraft to assume a portion of the air traffic control tasks autonomously. Among them, trajectory prediction, as a prerequisite for the successful implementation of TBO, plays a crucial role [8]. FAA defines an aircraft trajectory as a description of an aircraft’s motion in the air and on the ground. This includes information on four dimensions-latitude, longitude, altitude, and time [9]. Through scientific prediction of an aircraft’s three-dimensional position (longitude, latitude, altitude) for a specific period in the future, it provides accurate future flight trajectories and estimated times of passing critical waypoints. This enhances the ability of the air traffic management system to perceive and assess the operational situation in the airspace, improving its situational awareness [10].
In recent years, with the support of big data, high-performance computing, and machine learning algorithms, artificial intelligence technology has achieved rapid development and application in various industries. Thanks to this, compared to traditional mathematical model-based prediction methods, trajectory prediction methods based on intelligent algorithms have achieved significant improvements in prediction accuracy [11]. Since trajectory data are multi-dimensional with rich sequential characteristics, these methods transform the trajectory prediction problem into a multi-dimensional time series prediction problem. They achieve future trajectory prediction by mining complex patterns and nonlinear relationships among vast amounts of data. Compared to other neural network models, the attention mechanism does not rely on sequential processing and can handle the entire input sequence in parallel. It dynamically focuses on the parts most relevant to the current task. This allows it to better capture long-distance dependencies and achieve information transmission and modeling over longer distances [12].
The airport terminal airspace, as the most complex subsystem within the entire air traffic management system, also imposes the highest workload on air traffic controllers. In this airspace, aircraft must transition from approach and departure phases to en-route flight phases, leading to high aircraft density, significant differences in flight performance, and complex and variable tactical commands [13]. Compared to the cruising phase, aircraft in the terminal airspace are more affected by the close-range interactions with other aircraft. They adjust their movements based on the status of nearby aircraft to avoid conflicts. Therefore, trajectory prediction in this airspace is particularly complex and important, as it can reduce operational uncertainty. However, most current trajectory prediction methods rarely consider the close proximity of aircraft, focusing only on the nonlinear relationships in individual aircraft’s spatiotemporal features. This independence in prediction results may lead to potential collisions between aircraft [14]. In previous research, our Transformer-based long-term trajectory prediction model did not consider the close-range interactions between aircraft [15]. Based on this, we discard the recurrent neural network’s sequence modeling approach and use the attention mechanism to build a terminal airspace trajectory prediction model. This model considers the time series features of an aircraft’s own trajectory and incorporates close spatial interactions between multiple aircraft. By coupling spatiotemporal features, the model can better capture and reflect the complexity of dynamic interactions between aircraft. This improves the accuracy and reliability of trajectory prediction in the airport terminal airspace.
In summary, this paper contributes to the prediction of aircraft trajectories in the terminal airspace in the following ways:
- Based on aircraft trajectory data and air traffic control spacing regulations, an aircraft spatial structure graph is constructed. A vectorized representation method is defined for spatial interaction information between aircraft to characterize the close-range spatial positional relationship between them;
- To delve deeply into the multi-faceted trajectory characteristics, time series features and spatial position features of aircraft are targeted separately. Based on the attention mechanism, a temporal attention module and a spatial attention module are constructed to achieve an in-depth exploration of trajectory features from various aspects;
- Considering the terminal airspace aircraft operation scenario, a Spatio-Temporal Transformer (ST-Transformer) model is constructed by stacking temporal attention and spatial attention modules. This achieves high-precision short-term trajectory prediction with spatiotemporal feature coupling.
The rest of the paper is organized as follows. First, Section 2 reviews the studies performed in the field of aircraft trajectory prediction. Section 3 introduces the problem setup and the proposed trajectory prediction framework. In Section 4, the specific implementation process and results of the experiment will be discussed. A discussion of limitations and future directions of the proposed work is described in Section 5.
2. Literature Review
This section reviews the current research methods in the field of aircraft trajectory prediction, which can be categorized into non-data-driven methods based on mathematical modeling and deep learning models based on big data mining. Considering the close spatial interactions between aircraft, Section 2.2 will specifically analyze the literature related to this aspect. Finally, the section summarizes the shortcomings of the current research.
2.1. Aircraft Trajectory Prediction Method
In recent years, numerous scholars have conducted extensive research on the topic of aircraft trajectory prediction. Experts from Europe and the United States collaborated to formulate the FAA/Eurocontrol Action Plan 16 (AP16), which focuses on all issues related to airborne or ground-based trajectory predictor (TP) [16]. Although different decision support tools (DST) and automation systems have vastly varying requirements for TP in terms of accuracy, uncertainty, response time, and input data, the design and implementation of all TPs are similar. Based on this, AP16 proposed a general TP model that divides the prediction process into four modules: preparation, prediction, update, and output. Among them, the prediction process is the core of the TP, which calculates trajectory data through a set of methods and algorithms.
Aircraft trajectory prediction methods can be categorized into dynamic models and state estimation models. In this paper, these methods are collectively referred to as non-data-driven methods, and they will be reviewed in Section 2.1.1. Additionally, the currently popular data-driven models based on deep learning will be discussed in detail in Section 2.1.2.
2.1.1. Non-Data-Driven Method
As early as the 1990s, some scholars in Western countries had already begun research on trajectory prediction methods. Among them, the trajectory prediction method based on kinetic models is the earliest studied and oriented towards practical applications [17]. This method primarily investigates the relationship between the forces acting on an aircraft and its motion. By utilizing performance parameters such as aircraft mass, speed, descent or climb rate, engine type, and power, combined with weather data and aircraft intentions, it predicts the continuous points of future aircraft trajectories. This is achieved by integrating differential equations over a time interval. Among these, the Point Mass Model (PMM) is the most widely used model for constructing aircraft motion. This model approximates the aircraft as a mass point influenced by aerodynamic forces, drag, gravity, and engine performance while ignoring its rolling motion [18,19,20]. Due to the high computational complexity and need for numerous parameters, kinetic methods often rely on ideal assumptions to simplify the model. However, the aircraft operating environment is highly uncertain, and many parameters are difficult to measure accurately, making this method unstable when tested on real data. Alligier et al. [21] demonstrated through experiments on the same dataset that regression prediction methods achieve higher accuracy than PMM.
Furthermore, the essence of trajectory prediction lies in estimating the future trajectory of aircraft. This is achieved by analyzing the relationship between their future positions and historical states, such as position, speed, acceleration, and heading angle. Constructing a model of aircraft motion using state estimation theory is also a key prediction approach. In the initial research, to simplify the model, the state estimation was conducted under the assumption of a single mode, for example, using the Kalman Filter (KF) algorithm and Hidden Markov Models (HMM) [22,23,24,25]. Although single-model estimation has been widely used and achieved certain effectiveness, aircraft in actual operation exhibit multiple flight mode characteristics, and their three-dimensional state features in space need to be considered. Therefore, the problem of trajectory prediction can be viewed as an estimation problem of Stochastic Linear Hybrid Systems (SLHS). Since a single model cannot effectively estimate mixed systems with different modes, the multi-model estimation can achieve more accurate predictions by using different state estimators matching the aircraft motion, thereby attracting more attention. However, multi-model methods have the drawback of exponential growth in computational complexity with the number of models. To address this, the Interacting Multiple Model (IMM) algorithm was proposed. This algorithm has relatively low computational complexity and superior prediction performance [26,27].
2.1.2. Deep Learning Method
The widespread adoption of radar navigation surveillance equipment has enabled efficient acquisition of large amounts of aircraft trajectory data. Trajectory data generally fluctuate within a controllable range and show high temporal and spatial autocorrelation. With the development of computer technology, utilizing machine learning algorithms to extract the spatiotemporal variation patterns of aircraft trajectories from large-scale, multidimensional, and nonlinear historical data and using these patterns to predict trajectories has gradually become the mainstream approach [11]. In this section, we will review the evolution of prediction methods, detailing the transition from traditional machine learning algorithms to deep learning algorithms. We will also explore the currently popular methods that incorporate attention mechanisms.
Alligier et al. [28] utilized machine learning algorithms to train the calculation of engine thrust from historical radar data to improve the accuracy of PMM. De Leege et al. [29] constructed a generalized linear model using actual flight trajectory and weather data to predict aircraft trajectories in terminal airspace, addressing the shortcomings of kinetic models in weather perception.
Due to the sequential nature of trajectory data, trajectory prediction can be regarded as a time series prediction task. Among the various machine learning algorithms, deep learning algorithms have achieved superior performance in time series prediction. The core idea is to mimic the workings of the human brain’s neural networks, using multiple layers of neural networks to learn and recognize patterns in complex data. Deep learning algorithms do not require assumptions of mathematical models or manual intervention. By using large-scale trajectory datasets, they can learn nonlinear mapping relationships of spatiotemporal influences, significantly improving the accuracy of trajectory prediction. Common deep learning-based prediction methods include Recurrent Neural Network (RNN), Long Short-Term Memory (LSTM) network, and Gated Recurrent Unit (GRU) [30]. This type of model typically takes aircraft positions and related information as input features and outputs the three-dimensional positions at multiple future time points, estimated flight time, or probability distribution of the trajectory. Shi et al. [31] proposed a trajectory prediction model based on LSTM, considering the dynamic dependency between adjacent points in the trajectory sequence, which helped to improve prediction accuracy. Pang et al. [32] combined flight plans and historical flight trajectories to construct a trajectory prediction framework under convective weather conditions and utilized LSTM for solving. Han et al. [33] used GRU to establish a model for short-term real-time trajectory prediction, where the main idea was to divide training and prediction into historical and real-time models. Wu et al. [34] researched a 4DT prediction model based on a Back Propagation (BP) neural network. Ma and Tian [35] combined Convolutional Neural Network (CNN) and LSTM, resulting in superior prediction accuracy of this hybrid model compared to single models. Zeng et al. [36] proposed a Sequence-to-sequence LSTM (SS-DLSTM) based on the encoder-decoder structure to enhance the accuracy and robustness of terminal airspace trajectory prediction, effectively capturing the dependencies and repetitions between trajectories. Cheng et al. [37] demonstrated that compared to CNN and Least Square (LS), LSTM-based trajectory prediction models could achieve better prediction performance, especially in long-term trajectory prediction. Shi et al. [38] established three physical constraints for different phases of aircraft operation—climb, cruise, and approach—and further proposed a constrained LSTM network-based model. Tran et al. [39] modeled aircraft intent as the relative relationship between the current position and the planned waypoints. They further utilize convolutional layers and GRU to integrate this intent for trajectory prediction. Wu et al. [40] combined LSTM and Generative Adversarial Network (GAN), using the discriminator network to obtain scores representing the difference between predicted and actual trajectories. Although LSTM and various combinations of deep learning algorithms can, to some extent, alleviate issues such as gradient explosion and vanishing gradients when processing long-term data, LSTM still suffers from limitations in memory capacity when dealing with excessively long sequences.
The attention mechanism is currently a commonly used optimization technique in deep learning models, which was first applied in the fields of computer vision [41] and machine translation [42], achieving significant performance improvements. It imitates an important mechanism of human information processing, i.e., selectively focusing on certain information based on different contextual relationships and importance while ignoring other irrelevant information. When processing sequence data, different parts are assigned different weights, realizing the pairwise correlation between each unit in the input time series [12]. Schimpf et al. [43] considered the addition of an independent self-attention mechanism layer based on the existing convolutional-recurrent neural network design, and experiments showed that the attention mechanism significantly improved the performance of the convolutional layers. Wu et al. [44] employed the K-medoids clustering algorithm to cluster trajectories and then incorporated an attention mechanism to capture the important features of trajectory points, constructing a trajectory feature extraction network based on CNN and bidirectional LSTM (Bi-LSTM). Jia et al. [45] integrated attention mechanisms into LSTM, focusing more on the influencing factors between data in time series prediction. Ding et al. [46] introduced a dual attention mechanism into the CNN-BiLSTM model and employed a genetic algorithm (GA) to optimize the model’s hyperparameters, ensuring the model’s optimal learning capability and overcoming the drawbacks of manual parameter adjustment.
In 2017, the Google team proposed the Transformer model [47] to address machine translation problems. Given its astonishing performance in the field of Natural Language Processing (NLP), it also offered a new approach to handling sequence data. The Transformer model is built upon the multi-head attention and self-attention. This model abandons the traditional recurrent structures of RNN and instead relies entirely on the attention mechanism. By learning from input sequences, the model can establish correlations across different positions within the sequences. Additionally, the parallelism of the attention mechanism allows the model to perform computations efficiently on GPU. Guo et al. [48] proposed FlightBERT, a new trajectory prediction model based on binary encoding, using a stacked Transformer as the backbone network. In 2023, they further improved this model by addressing the limitations of binary encoding representation, resulting in FlightBERT++ [49]. Tong et al. [50] introduced a long-term trajectory prediction model based on the Transformer to handle long-term sequence information. Dong et al. [51] combined the Temporal Convolutional Network (TCN) and the Informer model to achieve accurate trajectory prediction during the approach phase.
2.2. Trajectory Prediction Model Considering Spatiotemporal Feature Coupling
Research into trajectory prediction that considers the interaction between spatial and temporal information was first applied to pedestrian trajectory prediction on the ground. For pedestrians, avoiding obstacles and other people is a significant factor in determining their path. Alahi et al. [52] proposed Social-LSTM, which constructs an LSTM for each individual independently and then connects them with a social pooling layer to share information. Gupta et al. [53] also simulated interactions between people with a pooling layer and built a GAN prediction model based on an encoder-decoder architecture. Zhang et al. [54] developed a state refinement module for the LSTM network, introducing SR-LSTM. This model arranges pedestrians together and updates their current states to utilize the current intentions of their neighbors. Liu et al. [55] proposed a two-stage method for pedestrian trajectory interaction modeling: “mode extraction” and “mode aggregation”. They developed a long-term trajectory prediction model based on LSTM. Building on this research, some scholars have gradually extended these methods to aircraft trajectory prediction. Xu et al. [56] applied Social-LSTM to terminal airspace trajectory prediction to achieve collaborative trajectory prediction for multiple aircraft. Shafienya et al. [57] combined CNN-GRU and 3D-CNN models for spatiotemporal feature extraction and prediction, respectively, to generate high-level accurate spatiotemporal feature mappings. Xu et al. [58] proposed a 4DT prediction model of a social spatiotemporal graph convolutional neural network (S-STGCNN) based on pattern matching, treating each aircraft as a node in a graph and using spatiotemporal graph convolution to extract graph features, achieving the fusion of spatiotemporal features. Sudarsanan et al. [59] used a Graph Neural Network (GNN) for terminal trajectory prediction. They represented the traffic state of aircraft in the airspace at a given time using a graph, transforming the trajectory prediction framework into a node feature prediction problem.
2.3. Summary
Data-driven aircraft trajectory prediction methods learn complex features from historical data. Particularly, deep learning-based methods can overcome the limitations of traditional non-data-driven methods, where some parameters are difficult to obtain accurately. These methods are easy to operate and understand, with high prediction accuracy and stable performance, making them a research hotspot in recent years. Many scholars have conducted extensive research to further improve aircraft trajectory prediction accuracy by constructing models using combined algorithms. However, the improvement in accuracy with excessive combinations of algorithms is limited and can lead to a waste of computational resources. The attention mechanism, which abandons the sequential data processing approach of traditional neural networks, focuses on the weighted processing of input data. Thus, applying the attention mechanism to aircraft trajectory prediction to enhance prediction accuracy has become a significant research topic.
In the complex operating environment of airport terminal airspace, aircraft significantly adjust their trajectories based on the influence of surrounding aircraft. However, current research mainly focuses on using individual aircraft trajectory information as input for prediction, with each aircraft’s trajectory prediction being relatively independent. There is a lack of studies that integrate the temporal sequence features of aircraft with their spatial position features for trajectory prediction. Therefore, it is necessary to further explore the hidden non-model behaviors in historical flight trajectory data and the close spatial interactions among multiple aircraft in terminal airspace. This can lead to the development of trajectory prediction models that couple spatiotemporal features, aiming to improve the efficiency and accuracy of trajectory predictions in airport terminal airspace.
3. Methodologies
This section will focus on the detailed construction process of the terminal airspace aircraft trajectory prediction model used in this paper. First, Section 3.1 will elaborate on the mathematical formulation of the prediction problem. Then, Section 3.2 will provide a detailed description of the specific structure of the model.
3.1. Problem Setup
This article focuses on the 4DT prediction problem in the terminal airspace. The trained prediction model aims to predict aircraft positions for multiple future time steps, given the state information from the preceding time period. This work lays the foundation for future free flight implementation. Within a specific time frame, assume that there are N aircraft operating within the terminal airspace. We define as the set of trajectories for N aircraft. Further, each aircraft’s trajectory set is composed of trajectory points corresponding to each moment within the time frame, and each trajectory point is made up of multidimensional time series feature data. When the time step is , the input sequence for the i-th aircraft consists of trajectory features corresponding to each moment, denoted as . When the time step is , the predicted trajectory features at each moment are represented as . The prediction process can be represented by Equation (1):
where is a function that maps a sequence of trajectory states over a certain time step to a future sequence. The Overall framework for terminal airspace aircraft trajectory prediction is shown in Figure 1.
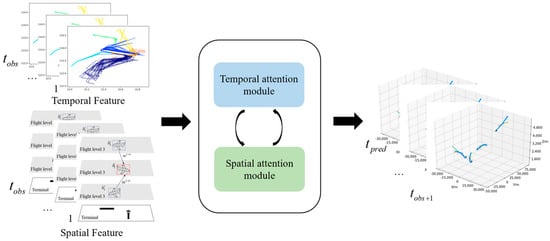
Figure 1.
Flowchart of the terminal airspace aircraft trajectory prediction model. On the left side of the figure is the model’s input, which is divided into the temporal feature dataset and the spatial feature dataset. Through the interaction of the temporal attention module and the spatial attention module, the model can excavate hidden patterns within the historical data, thereby generating the final predicted trajectory output.
3.2. The Structure of ST-Transformer
This section will provide a detailed overview of the components of the ST-Transformer model. First, we will explain the structure and function of the temporal attention module and the spatial attention module. Next, we will describe the encoder-decoder architecture of the ST-Transformer model in detail, aiding readers in understanding the data processing within the model.
3.2.1. Temporal Attention Module
The structure of the temporal attention module is inspired by the Transformer network architecture [48]. This module independently processes the time series features of each aircraft, focusing on extracting temporal dependencies. Previous studies have shown that this model outperforms RNN and LSTM in the field of trajectory prediction, demonstrating superior predictive capabilities [15,50].
- (1)
- Temporal feature dataset
The temporal feature dataset consists of individual aircraft trajectory data . We define as the set of trajectory point features for the i-th aircraft at time t, which can be expressed as Equation (2). represents the set of trajectory features of the i-th aircraft from time 1 to j.
where represents the timestamp at time . denotes the flight number. , and are the three-dimensional position of the trajectory point after coordinate transformation, which will be described in detail in Section 4.1. To facilitate model data reading, the timestamp is calculated as the difference between the current time and a reference time (1 January 1970). The flight number is processed using label encoding.
- (2)
- Temporal attention mechanism
For each aircraft, the trajectory time series feature set is first passed through an embedding layer to perform an embedding operation, including positional encoding and high-dimensional mapping. The resulting embedded features, denoted as , , …, , serve as the input to the temporal attention module. Within the module, linear transformations are applied to compute the query matrix , key matrix , and value matrix as shown in Equations (3)–(5):
where , , represent the query function, key function, and value function, respectively, which are shared among all aircraft.
For each aircraft, based on , and , the multi-head attention mechanism is used to calculate the correlation scores between trajectory points. The calculation formula is shown in Equations (6) and (7):
where is the distribution function. represents the dimension of the vectors, and it serves to scale the dot-product between and . is a fully connected layer merging the output from k heads. is the output of self-attention for the m-th head in multi-head attention. is the concatenated output of k independent self-attention heads, with each self-attention head having different attention weights. The final embedding output is produced by two add and norm layers and a feed-forward layer. The overall structure of the temporal attention module is shown in Figure 2.
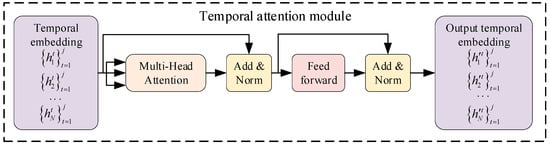
Figure 2.
The structure of the temporal attention module. The temporal attention module takes an individual trajectory as input, embeds the feature data, and uses a multi-head attention mechanism to thoroughly extract the temporal features of the trajectory data. The final embedding is output through two add and norm layers and a feed-forward layer.
3.2.2. Spatial Attention Module
The spatial attention module is designed to learn the interactive spatial position features among aircraft. Its main structure involves the introduction of attention mechanisms into graph structures, enabling the transmission of positional information between neighboring aircraft. Similar to Graph Attention Networks (GAT), the spatial attention module adaptively assigns weights to each aircraft based on its relevance to neighboring aircraft. This allows for the integration of neighboring aircraft features to update the node features, effectively modeling the spatial positional interactions between aircraft.
- (1)
- Spatial feature dataset
The spatial feature dataset takes the constructed aircraft spatial structure graph at time t as a unit, as shown in Figure 3, where represents the set of all nodes in the graph at time t, that is, the set of N aircraft trajectory features in the graph. represents the set of undirected edges between all aircraft pairs in the graph at a time t. The construction method of the undirected edge set between aircraft pairs is based on the spatial position relationship of the aircraft in the terminal airspace at time t. The formula for the Euclidean distance between aircraft pair (i, j) is shown in Equation (8):
where , are the three-dimensional position coordinates of aircraft i and j at time , respectively. Given that the spatial influence between aircraft in the terminal airspace diminishes with distance, calculating the attention scores between every pair of aircraft would result in excessive computational complexity. Therefore, we introduce a neighboring distance threshold ζ to filter and select nearby aircraft for attention score computation. If the distance is less than ζ, an undirected edge is established between the aircraft pair (i, j). ζ is defined in combination with the actual control work regulations and is set to 10 km in this case.
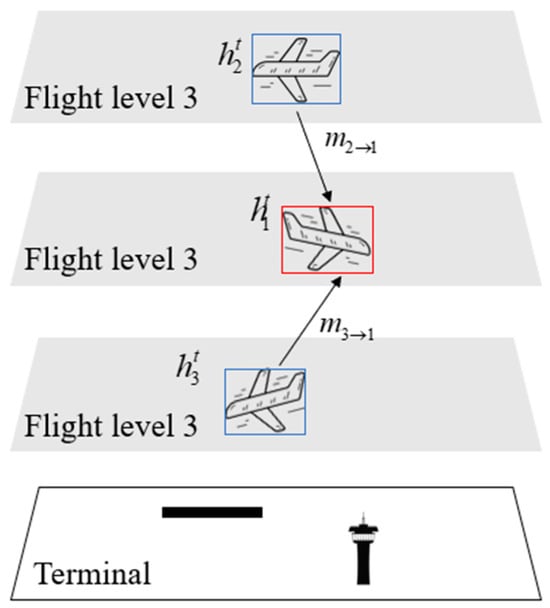
Figure 3.
Aircraft spatial structure graph. The spatial attention module takes the modeled aircraft spatial structure graph as input and uses the attention mechanism to model the spatial interaction relationships between aircraft.
- (2)
- Node feature update rule
Based on the constructed aircraft spatial structure graph shown in Figure 3, the vectorized representation of spatial interaction information between aircraft pair (i, j) can be defined as the dot product of the query vector of aircraft i and the key vector of aircraft j, as shown in Equation (9):
where , , and . Then, the attention function in Equation (5) can be rewritten as Equation (10):
Assume the neighbor node set of the aircraft at node is , and its own embedding trajectory feature is . Based on the aforementioned attention calculation formula, the value matrixes are weighted and summed according to the attention scores of each neighboring node of node i in the graph, in order to obtain the output of the spatial attention mechanism, as shown in Formula (11):
Based on the above calculation of the attention mechanism, we can update the feature of node at time through Equation (12). This updated feature is denoted as which considers the positional relationship between the aircraft and its surrounding aircraft.
where represents the attention convolution result of aircraft at time t; is a fully connected layer. is the feature of aircraft at time after updated. The spatial attention module can better capture the important neighboring node information of aircraft within the graph structure, thereby more effectively representing the features of aircraft .
3.2.3. ST-Transformer
The modules described in the previous two sections are capable of modeling the temporal sequence features and spatial interaction features of aircraft, respectively. To further model the coupling of temporal and spatial features, we constructed the ST-Transformer model for terminal airspace aircraft trajectory prediction. This model employs a sequence-to-sequence architecture, which is composed of two encoders and a decoder, as illustrated in Figure 4.
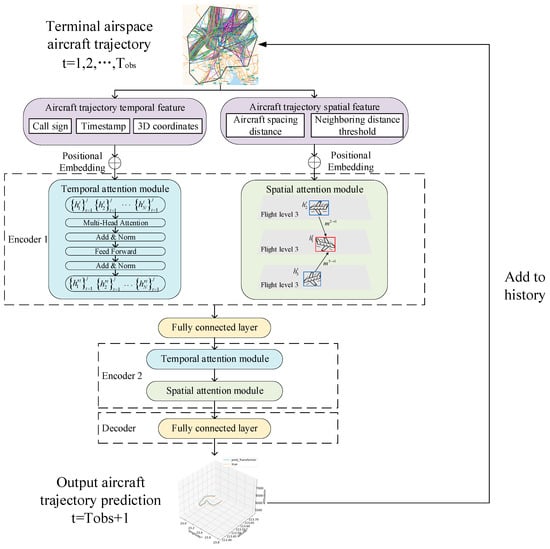
Figure 4.
The structure of aircraft trajectory prediction model. ST-Transformer is divided into three parts. Encoder 1 is used to separately encode the time series features and spatial position features. Encoder 2 is used to fuse and further delve into both parts of the information. Finally, the decoder is used to output the prediction results.
Encoder 1 is designed with a temporal attention module and a spatial attention module working in parallel. This configuration allows the model to independently process two separate datasets: the temporal feature dataset and the spatial feature dataset, both of which are first embedded through a fully connected layer. The temporal attention module focuses on capturing the sequential patterns and trends over time, while the spatial attention module targets the spatial relationships and interactions. After processing these features, the outputs from the parallel modules are combined using an additional fully connected layer. This fusion generates a new set of features that integrate both temporal and spatial information, providing a more comprehensive representation of the trajectory data.
To delve deeper into the spatiotemporal interactions, Encoder 2 is structured with a temporal attention module and a spatial attention module arranged in series. The temporal attention module models time series characteristics with spatial information, while the spatial attention module enhances the output temporal embedding with spatial attention.
Finally, the decoder, which consists of fully connected layers, is responsible for generating predictions for based on the processed features. These predictions are then integrated into the historical data, enabling consistent and recursive time forecasting.
4. Experiments
This section will utilize real radar aircraft trajectory data for the experiment. Section 4.1 introduces the dataset and the data preprocessing steps. Section 4.2 explains the evaluation metrics used in this case. Section 4.3 details the model’s hyperparameter selection and training process. Finally, Section 4.4 discusses the experimental results. In the experiment, we analyzed the prediction errors for different prediction intervals and compared the prediction performance of our model with various deep learning models. Furthermore, we visualized the prediction results of aircraft with adjacent relationships to verify the effectiveness of our model in improving prediction accuracy by considering spatiotemporal feature coupling.
4.1. Datasets
The historical trajectory data used in this paper originate from secondary surveillance radar (SSR) monitoring data. SSR periodically sends inquiry signals to aircraft in the sky, each containing a unique identification code to distinguish different aircraft. When an aircraft’s transponder receives the inquiry signal, it responds with a distinctive reply signal. This signal includes not only the identification code but also other flight-related information, such as latitude, longitude, altitude, and speed. Compared to the automatic dependent surveillance-broadcast (ADS-B) data commonly used for trajectory prediction, the radar data employed in this study have advantages such as higher update frequency and less missing data, resulting in better data quality. This enhances the preparation for subsequent predictive tasks.
After decompressing the raw radar trajectory data and selecting relevant features, the initial aircraft trajectory points are represented in three-dimensional coordinates using latitude and longitude . Using latitude and longitude to record the positions of aircraft does not provide an intuitive depiction of their movement within the terminal area and complicates spatial distance calculations. To obtain the Cartesian coordinates used in Equation (2), a coordinate transformation is required. Given that this study focuses on trajectory prediction within the terminal area, the Mercator projection is employed. The Mercator projection maintains relative accuracy for distances and angles at medium and small scales. The latitude and longitude data are projected and converted into Cartesian coordinates using Equation (13):
where represents the projected Cartesian coordinates, denotes the original latitude and longitude coordinates, and is the projection reference point, typically at the intersection of the prime meridian and equator. The Earth’s semi-major axis () is set to 6,378,137 m, and the semi-minor axis () is 6,356,752 m. The first eccentricity () is 0.0818, and the second eccentricity () is 0.0821.
In this case, we use the real trajectory data from the Guangzhou terminal airspace. Therefore, using the center coordinates of runway 20R/02L at Guangzhou Baiyun Airport as the origin, the projected coordinates of the origin point are obtained as by Equation (13). After converting any trajectory point’s longitude and latitude coordinates to projected coordinates , the relative position coordinates of the aircraft with respect to the airport center-point can be obtained, as shown in Equation (14).
Based on Equations (13) and (14), the latitude and longitude coordinates of the boundary points of the Guangzhou terminal airspace are also converted to determine the physical spatial range of the terminal airspace, as shown in Figure 5. After filtering data for a typical operational day, we obtained 1211 trajectory data entries.
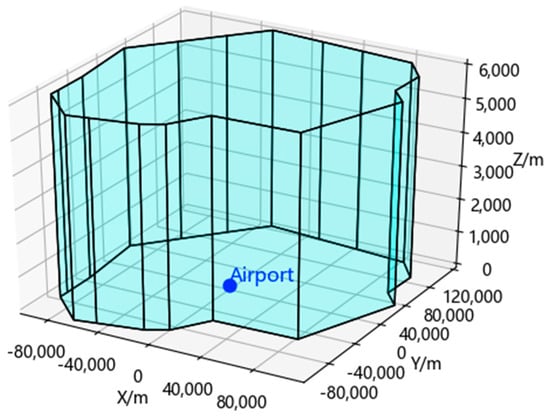
Figure 5.
Terminal airspace physical configuration. The coordinate origin is set at the center of the airport runway.
Due to radar signal fluctuations, recorded data may contain missing or abnormal key fields, affecting the accuracy of subsequent trajectory predictions. Initial analysis of the dataset revealed that duplicate records are infrequent and can be directly deleted. In this study, data are resampled at 5 s intervals, defining each time step as 5 s. Missing trajectory data are completed using linear interpolation. If is missing, it is filled by selecting the two adjacent time points. The principle is as Equation (15):
4.2. Evaluation Metrics
In this case, longitude and latitude were transformed into a Cartesian coordinate system with the airport center as the origin during data preprocessing. Mean Absolute Displacement Error (), Mean Absolute Displacement Horizontal Error (), and Mean Absolute Displacement Vertical Error () are used as metrics to evaluate trajectory prediction errors, measured in meters. The calculation method is shown in Equations (16)–(18). DE denotes the three-dimensional distance between each predicted point and its corresponding true value. DHE represents the distance between the two-dimensional coordinates of each predicted point and the true point. DVE indicates the distance between each predicted point’s altitude and the true altitude. Smaller values of these error metrics indicate better predictive performance on the given dataset.
We also selected commonly used metrics for evaluating the performance of the deep learning prediction model, including Mean Absolute Percentage Error (MAPE) and R-squared (R2). The closer the R2 value is to 1, the more accurate the model’s predictions are. The formulas for these metrics are shown in Equations (18) and (19).
where represents the three-dimensional coordinates of the aircraft i’s actual trajectory at time t. represents the predicted trajectory coordinates of aircraft i at time t. represents the mean actual trajectory for aircraft i. N denotes the number of aircraft and denotes the length of the trajectory prediction sequence.
4.3. Model Training
In predictive modeling, the setting of hyperparameters is crucial for the model’s performance. By finely tuning these hyperparameters, one can effectively balance the model’s fitting capability and generalization performance, thereby enhancing the accuracy and stability of trajectory prediction. The parameters of the ST-Transformer prediction model include network weight parameters and hyperparameters. Network weight parameters refer to the connection weights and biases between neurons. The initial values of network weights are randomly initialized, and their updating and final determination primarily involve autonomous learning through the process of minimizing the loss function using stochastic gradient descent. Hyperparameters encompass structural and training parameters. By specifying the range of each hyperparameter, various combinations of these parameters are generated to identify the combination that minimizes the loss function, as shown in Table 1 with specific values.

Table 1.
Parameter setting.
The trajectory prediction model based on the ST-Transformer proposed in this paper is built using the Python PyTorch 1.12.1. It takes trajectory temporal feature datasets and spatial feature datasets as inputs and outputs predictions of subsequent step-length aircraft three-dimensional coordinates. The specific training process is as follows:
- (1)
- The dataset is split into training and testing sets in a 7:3 ratio;
- (2)
- Structural parameters of the network are defined, including the number of encoding layers, the number of heads in the multi-head attention mechanism, and the number of training epochs;
- (3)
- Hyperparameters used during training are set, including the network learning rate and dropout rate in hidden layers. The Adam optimization strategy is employed, using Mean Squared Error (MSE) between predicted and historical trajectories as the loss function. Training begins with one epoch to minimize the loss function and obtain optimal network weight parameters;
- (4)
- The training process in (3) is repeated until the maximum specified number of training epochs is reached. The trained model is then saved for potential finetuning in subsequent stages.
4.4. Experimental Analysis
In this section, the trained ST-Transformer prediction model’s performance on the test set was analyzed using evaluation metrics. In the experiments, the model was tasked with predicting trajectory data for the subsequent 60 s, given the aircraft’s preceding 40 s. With each trajectory point spaced 5 s apart, the observation sequence length was 8, and the prediction sequence length was 12. The training process was monitored for changes in the loss values across training epochs. As shown in Figure 6, it can be observed that as the number of training epochs increases, the training loss gradually stabilizes, indicating that the model converges toward optimal parameters.
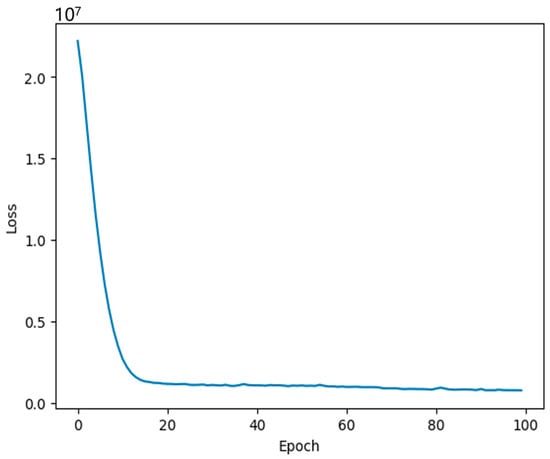
Figure 6.
Training loss value.
To quantitatively evaluate the accuracy of the terminal airspace trajectory prediction model over different prediction intervals, three error metrics, DE, DHE, and DVE, were computed between each pair of predicted and actual trajectory points across all test samples within specified prediction durations. Since these three metrics are all measured in meters, they are convenient for direct comparison. The results were visualized using box plots. As shown in Figure 7, the prediction model achieves higher accuracy in altitude compared to the horizontal plane across all prediction times. This is because aircraft have smaller altitude variations compared to horizontal position changes within the terminal airspace. As the prediction time increases, the median of the error box plots remains relatively stable. However, the range of the three error distributions expands significantly. This indicates an increase in the number and dispersion of extreme values and outliers, leading to greater data distribution inconsistency. Thus, as prediction time grows, the model’s performance at certain points deteriorates. For instance, abrupt trajectory changes due to low-altitude turbulence can cause larger deviations.
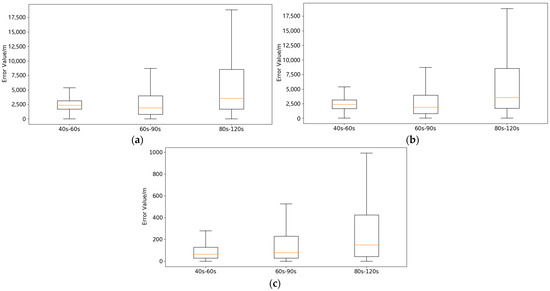
Figure 7.
Box plots of different prediction length error metrics. (a) DE box plot; (b) DHE box plot; (c) DVE box plot.
For DE, we further tracked the prediction time windows corresponding to the upper and lower error limits identified in the box plot. The results show that the maximum errors typically occur during aircraft turns, indicating a significant increase in prediction error during these maneuvers. In contrast, the minimum errors are usually observed during straight flight periods, suggesting that the prediction model performs more stably and with lower errors during straight flights. This phenomenon indicates that turning may involve more complex factors or dynamic changes, leading to less accurate predictions. In contrast, the model’s prediction accuracy is higher during steady, straight flight. A representative three-dimensional comparison is shown in Figure 8.
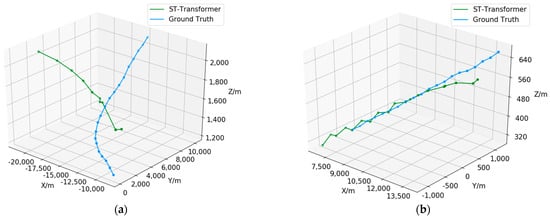
Figure 8.
Example of prediction time windows corresponding to DE extremes. (a) Upper limit of DE; (b) lower limit of DE.
To comprehensively evaluate the prediction performance of the proposed model, a series of widely used aircraft trajectory prediction models were selected as comparison algorithms. For all models, the batch size is set to 7, with each batch containing around 128 aircraft from different time windows. The activation function used is ReLU, and the Adam optimizer is employed. The comparison model and its parameter settings are as follows:
- (1)
- Back Propagation (BP) Neural Network: A multilayer feedforward neural network trained using the error backpropagation algorithm, it is one of the most classic and widely used models in neural networks;
- (2)
- Recurrent Neural Network (RNN): A type of neural network model used for processing sequential data. It captures temporal dependencies in sequences through its recurrent structure and shared parameters;
- (3)
- Long Short-Term Memory (LSTM): A special type of RNN that effectively captures long-term dependencies by introducing gating mechanisms;
- (4)
- State Refined LSTM (SR-LSTM): SR-LSTM is based on the research results by Zhang et al. in pedestrian trajectory prediction [54]. The model introduces a state refinement module to model the interaction behaviors between pedestrians;
- (5)
- S-Transformer: S-Transformer model does not include the spatial attention module and is a vanilla Transformer model with individual trajectory data as the input unit [47].
For the BP model, the embedding size is set to 32, the number of neurons per hidden layer is 64, the dropout rate is 0.1, the learning rate is 0.0019, and the number of training epochs is 200. For the RNN, LSTM, and SR-LSTM models, the loss function converged within 100 training epochs, so the number of epochs is set to 100. For the RNN and LSTM models, the parameters are set as follows: embedding size is 32, number of hidden layers is 2, number of neurons per hidden layer is 64, dropout rate is 0.1, and learning rate is 0.0015. Additionally, in the SR-LSTM model, the number of refinement layers is set to 2. The parameters of the S-Transformer model are consistent with those of the ST-Transformer model, with 100 training epochs.
All models were trained using the same trajectory dataset and the same training and testing split ratio. The aim is to analyze the strengths and weaknesses of each model in trajectory prediction through horizontal comparison. The results of evaluation metrics are shown in Table 2.

Table 2.
Results of the prediction evaluation metrics.
According to the table above, ST-Transformer performs the best in all five evaluation metrics. Given that MADE, MADHE, and MADVE are all measured in meters, to provide a more intuitive understanding, we have plotted a line graph of the evaluation metrics, as illustrated in Figure 9.
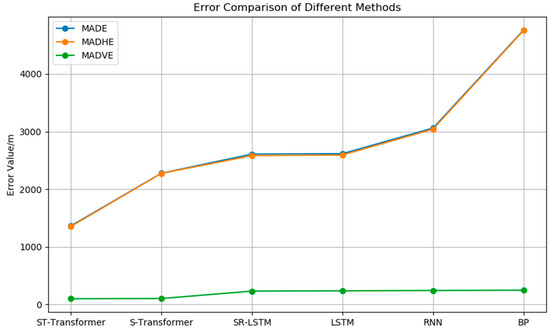
Figure 9.
Comparison of errors (MADE, MADHE, MADVE) for different methods.
From the figure above, it is evident that compared to RNN and BP, LSTM reduces the MADE error by approximately 45% and 14%, respectively, highlighting the advantages of LSTM in solving time-series prediction problems. SR-LSTM constructs an LSTM prediction module for each aircraft and adds a state refinement module to align and update the current state of the aircraft, leading to improved prediction accuracy over LSTM. The S-Transformer, which abandons the traditional sequence structure and adopts an attention mechanism, achieves the lowest prediction errors in both two-dimensional space and altitude compared to the above four models. This indicates that the attention mechanism can better capture aircraft operational patterns and improve prediction accuracy. The ST-Transformer model, designed for terminal airspace trajectory prediction, incorporates spatial attention alongside temporal attention. This enhances the model’s ability to capture close-range spatial interactions among aircraft, enabling trajectory prediction with coupled spatiotemporal features. Compared to the S-Transformer, the ST-Transformer reduces the three error metrics by 40.1%, 40.5%, and 3.4%, respectively.
To further understand the positional influence among aircraft, we can output the neighboring aircraft for each one. Figure 10 shows an example of several batches in the test set. The black squares indicate the presence of an undirected edge between two aircraft, forming a spatial structure graph.
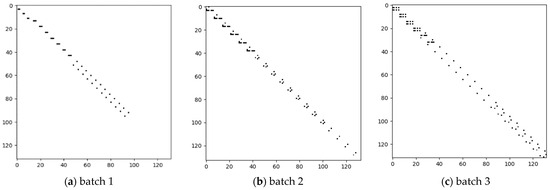
Figure 10.
Aircraft adjacency.
To verify whether the ST-Transformer model considers the mutual influence among multiple aircraft during prediction, we examined the positional changes of interacting aircraft over time from a microscopic perspective. We selected the historical and future predicted trajectories of neighboring aircraft within different time windows for three-dimensional visualization, as shown in Figure 11. The origin coordinates represent the airport runway midpoint, as shown below. Although there are some deviations between the predicted and actual trajectories, the ST-Transformer model effectively captures and simulates the operational trends of aircraft compared to other models, resulting in more accurate trajectory predictions. Notably, Aircraft 2 and Aircraft 3 are in closer proximity. Controllers may pay extra attention to these aircraft to avoid potential conflicts, causing both to adjust their trajectories in response to each other. We can clearly see that in time windows 5 and 6, the model accurately predicts the right turn trend of Aircraft 3. Compared to other models that do not consider close-range spatial interactions between aircraft, ST-Transformer can achieve more accurate terminal trajectory predictions.
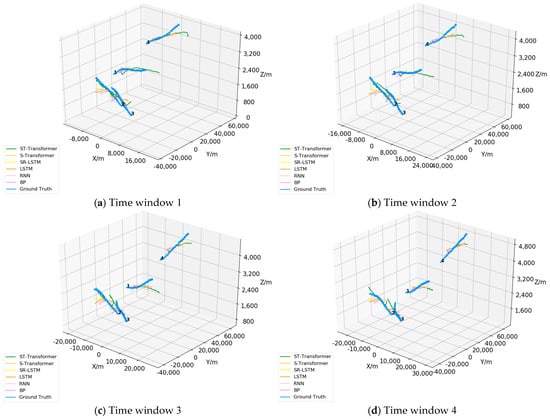
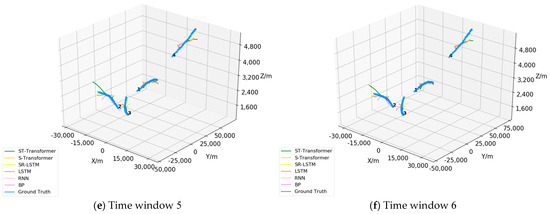
Figure 11.
Trajectory prediction results under different time windows.
Further, we compare the impact of different aircraft adjacent distance threshold ζ on prediction accuracy. Figure 12 shows the error values when changing the graph proximity threshold (in units of 10, 20, and 30 km). We observe no significant change in the error metrics. This indicates that setting ζ = 10 km nearly covers all aircraft close-range interactions in the airspace at a given time, and the constructed spatial structure graph effectively reflects positional relationships among the aircraft.
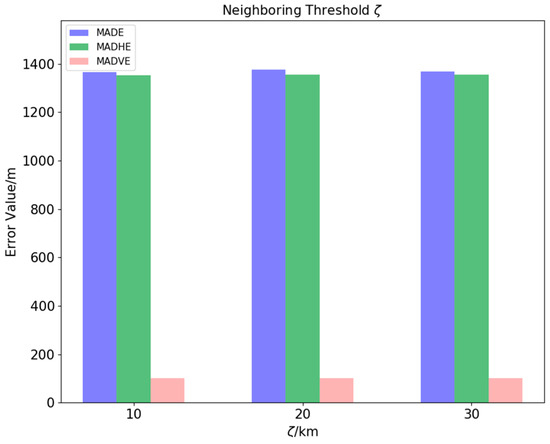
Figure 12.
Error values for different ζ.
The case study compares the prediction evaluation metrics of the ST-Transformer with five other trajectory prediction models through instance validation using real datasets. The result demonstrates that the model constructed in this paper addresses certain shortcomings in the current state of research. First, the model builds temporal and spatial attention modules based on the attention mechanism. Compared to traditional recurrent neural networks, attention mechanisms offer superior performance when handling sequential data. Features are encoded with rich contextual information through an encoder and then fed into a decoder to generate the final prediction. Moreover, unlike other models, this model considers close-range spatial interactions between aircraft and couples of spatiotemporal features, overcoming the limitation of predicting based on an individual trajectory input.
5. Conclusions
Considering the significant close-range spatial interaction between aircraft operating in terminal airspace, this paper constructs a trajectory prediction model based on temporal and spatial attention mechanisms. This model forms the ST-Transformer model by stacking temporal attention modules and spatial attention modules. It effectively captures individual trajectory’s deep temporal features and the complex close-range spatial relationships between aircraft, thereby achieving more accurate and reliable trajectory predictions.
In the future TBO mode, the aircraft trajectory prediction system can provide pilots, controllers, and other relevant parties with accurate future trajectory information. This will help to better manage aircraft spacing, improve management efficiency under busy traffic conditions, and reduce safety risks. Additionally, the prediction results can further support the development of terminal intelligent decision support tools (DST) for aircraft conflict detection, airspace flow management, abnormal behavior detection, and flight sequencing. This will achieve refined airspace management and improve airspace utilization.
Since the output trajectories are deterministic trajectories in this paper, future research should focus not only on improving trajectory prediction accuracy but also on maintaining effective integration between the trajectory prediction system and the conflict management system. To construct a probabilistic aircraft conflict alert model, it is necessary to introduce an uncertainty perception module based on the model proposed in this paper to achieve probabilistic trajectory prediction. Monte Carlo sampling techniques can be used to calculate the probability of conflicts between aircraft. This will benefit the future application and development of intelligent air traffic management systems and promote the concept of free flight for aircraft.
Author Contributions
Conceptualization, X.D., Y.T., J.L. and L.W.; methodology, X.D. and Y.T.; software, X.D.; validation, X.D. and L.D.; formal analysis, X.D. and J.L.; investigation, X.D. and L.D.; resources, Y.T. and L.W.; data curation, X.D.; writing—original draft preparation, X.D.; writing—review and editing, X.D. and J.L.; visualization, X.D.; supervision, Y.T. and L.W.; project administration, Y.T.; funding acquisition, Y.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the China Postdoctoral Science Foundation Funded Project, grant number 2024M752347; the Jiangyin-Tsinghua Innovation Leadership Action Project, grant number 1108; the Natural Science Foundation of Jiangsu Province, grant number BK20230892; the Jiangsu High Level “Shuang-Chuang” Project, grant number JSSCBS20220212 and Nanjing University of Aeronautics and Astronautics Graduate Research and Practice Innovation Program Project, grant number xcxjh20230730.
Data Availability Statement
Data are contained within the article.
Acknowledgments
We would like to thank the Green Civil Aviation Technology Laboratory of the College of Civil Aviation for providing the data used in the model tests described in this paper. And we would like to thank all reviewers for their valuable reviews.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- European Aviation in 2040—Challenges of Growth 2018. Available online: https://www.eurocontrol.int/publication/challenges-growth-2018 (accessed on 2 October 2018).
- Jiang, C. Recent advances for smart air traffic management: An overview. In Proceedings of the International Conference on Artificial Intelligence in China, Zhuhai, China, 11–13 December 2020; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Global Air Navigation Plan Strategy. Available online: https://www4.icao.int/ganpportal/ganpdocument#/ (accessed on 1 October 2018).
- Joint Planning and Development Office. Concept of Operations for the Next Generation Air Transportation System; Joint Planning and Development Office: Washington, DC, USA, 2007. [Google Scholar]
- European ATM Master Plan 2020. Available online: https://www.sesarju.eu/masterplan2020 (accessed on 17 December 2019).
- Mondoloni, S.; Rozen, N. Aircraft Trajectory Prediction and Synchronization for Air Traffic Management Applications. Prog. Aerosp. Sci. 2020, 119, 100640. [Google Scholar] [CrossRef]
- EUROCONTROL Specification for Trajectory Prediction. Available online: https://www.eurocontrol.int/publication/eurocontrol-specification-trajectory-prediction (accessed on 3 March 2017).
- Schuster, W.; Ochieng, W. Performance Requirements of Future Trajectory Prediction and Conflict Detection and Resolution Tools within SESAR and NextGen: Framework for the Derivation and Discussion. J. Air Transp. Manag. 2014, 35, 92–101. [Google Scholar] [CrossRef]
- Trajectory Based Operations (TBO). Available online: https://www.faa.gov/air_traffic/technology/tbo#:~:text=Aircraft%20trajectory%20is%20the%20core%20tenant%20of%20TBO.,when%20-%20at%20key%20points%20along%20its%20route (accessed on 9 February 2022).
- Song, Y.; Cheng, P.; Mu, C. An Improved Trajectory Prediction Algorithm Based on Trajectory Data Mining for Air Traffic Management. In Proceedings of the 2012 IEEE International Conference on Information and Automation, Shenyang, China, 6–8 June 2012. [Google Scholar] [CrossRef]
- Zeng, W.; Chu, X.; Xu, Z.; Liu, Y.; Quan, Z. Aircraft 4D Trajectory Prediction in Civil Aviation: A Review. Aerospace 2022, 9, 91. [Google Scholar] [CrossRef]
- Niu, Z.; Zhong, G.; Yu, H. A Review on the Attention Mechanism of Deep Learning. Neurocomputing 2021, 452, 48–62. [Google Scholar] [CrossRef]
- Liu, W.; Hwang, I. Probabilistic Trajectory Prediction and Conflict Detection for Air Traffic Control. J. Guid. Control Dyn. 2011, 34, 1779–1789. [Google Scholar] [CrossRef]
- Wang, Z.; Liang, M.; Delahaye, D. A Hybrid Machine Learning Model for Short-Term Estimated Time of Arrival Prediction in Terminal Manoeuvring Area. Transp. Res. Part C Emerg. Technol. 2018, 95, 280–294. [Google Scholar] [CrossRef]
- Dong, X.; Tian, Y.; Niu, K.; Sun, M.; Li, J. Research on Flight Trajectory Prediction Method Based on Transformer. In Proceedings of the International Conference on Smart Transportation and City Engineering (STCE 2023), Chongqing, China, 16–18 December 2023. [Google Scholar] [CrossRef]
- FAA/EUROCONTROL. Common TP Structure and Terminology in Support of SESAR & NextGen; Techincal Report FAA/EUROCONTROL: Brussels, Belgium, 2010. [Google Scholar]
- Sturdy, J.; Andrews, J.; Welch, J. Aircraft Trajectory Prediction for Terminal Automation. In Proceedings of the Guidance, Navigation and Control Conference, Boston, MA, USA, 14–16 August 1989. [Google Scholar] [CrossRef]
- Lymperopoulos, I.; Lygeros, J.; Lecchini, A. Model Based Aircraft Trajectory Prediction During Takeoff. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Thipphavong, D.P.; Schultz, C.A.; Lee, A.G.; Chan, S.H. Adaptive Algorithm to Improve Trajectory Prediction Accuracy of Climbing Aircraft. J. Guid. Control Dyn. 2013, 36, 15–24. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, J.; Hu, R.; Zhu, H. Online Four Dimensional Trajectory Prediction Method Based on Aircraft Intent Updating. Aerosp. Sci. Technol. 2018, 77, 774–787. [Google Scholar] [CrossRef]
- Alligier, R.; Hamed, M.G.; Gianazza, D.; Serrurier, M. Ground-Based Prediction of Aircraft Climb: Point-Mass Model vs. Regression Methods. In Proceedings of the 1st Annual Complex World Conference, Seville, Spain, 11–15 July 2011. [Google Scholar]
- Chatterji, G. Short-Term Trajectory Prediction Methods. In Proceedings of the Guidance, Navigation, and Control Conference and Exhibit, Portland, OR, USA, 9–11 August 1999. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, G.; Xiao, G. Dynamic Trajectory Prediction for Continuous Descend Operations Based on Unscented Kalman Filter. In Proceedings of the 2020 Chinese Intelligent Systems Conference, Shenzheng, China, 24–25 October 2020. [Google Scholar] [CrossRef]
- Ayhan, S.; Samet, H. Aircraft Trajectory Prediction Made Easy with Predictive Analytics. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016. [Google Scholar] [CrossRef]
- Lin, Y.; Yang, B.; Zhang, J.; Liu, H. Approach for 4-d trajectory management based on HMM and trajectory similarity. J. Mar. Sci. Technol. 2019, 27, 7. [Google Scholar] [CrossRef]
- Baek, K.Y.; Bang, H.C. ADS-B Based Trajectory Prediction and Conflict Detection for Air Traffic Management. Int. J. Aeronaut. Space Sci. 2012, 13, 377–385. [Google Scholar] [CrossRef][Green Version]
- Zhang, J.; Wu, X.; Wang, F. Aircraft Trajectory Prediction Based on Modified Interacting Multiple Model Algorithm. J. Donghua Univ. (Engl. Ed.) 2015, 32, 180–184. [Google Scholar] [CrossRef]
- Alligier, R.; Gianazza, D.; Durand, N. Learning the Aircraft Mass and Thrust to Improve the Ground-Based Trajectory Prediction of Climbing Flights. Transp. Res. Part C Emerg. Technol. 2013, 36, 45–60. [Google Scholar] [CrossRef]
- De Leege, A.; Van Paassen, M.; Mulder, M. A Machine Learning Approach to Trajectory Prediction. In Proceedings of the AIAA Guidance, Navigation, and Control (GNC) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar] [CrossRef]
- Hashemi, S.M.; Botez, R.M.; Grigorie, T.L. New Reliability Studies of Data-Driven Aircraft Trajectory Prediction. Aerospace 2020, 7, 145. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q.; Yan, B.; Zhang, H. LSTM-Based Flight Trajectory Prediction. In Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Pang, Y.; Yao, H.; Hu, J.; Liu, Y. A Recurrent Neural Network Approach for Aircraft Trajectory Prediction with Weather Features from Sherlock. In Proceedings of the AIAA Aviation 2019 Forum, Dallas, TX, USA, 17–21 June 2019. [Google Scholar] [CrossRef]
- Han, P.; Wang, W.; Shi, Q.; Yang, J. Real-Time Short- Term Trajectory Prediction Based on GRU Neural Network. In Proceedings of the 2019 IEEE/AIAA 38th Digital Avionics Systems Conference (DASC), San Diego, CA, USA, 8–12 September 2019. [Google Scholar] [CrossRef]
- Wu, Z.-J.; Tian, S.; Ma, L. A 4D Trajectory Prediction Model Based on the BP Neural Network. J. Intell. Syst. 2020, 29, 1545–1557. [Google Scholar] [CrossRef]
- Ma, L.; Tian, S. A Hybrid CNN-LSTM Model for Aircraft 4D Trajectory Prediction. IEEE Access 2020, 8, 134668–134680. [Google Scholar] [CrossRef]
- Zeng, W.; Quan, Z.; Zhao, Z.; Xie, C.; Lu, X. A Deep Learning Approach for Aircraft Trajectory Prediction in Terminal Airspace. IEEE Access 2020, 8, 151250–151266. [Google Scholar] [CrossRef]
- Cheng, C.; Guo, L.; Wu, T.; Sun, J.; Gui, G.; Adebisi, B.; Gacanin, H.; Sari, H. Machine-Learning-Aided Trajectory Prediction and Conflict Detection for Internet of Aerial Vehicles. IEEE Internet Things J. 2022, 9, 5882–5894. [Google Scholar] [CrossRef]
- Shi, Z.; Xu, M.; Pan, Q. 4-D Flight Trajectory Prediction with Constrained LSTM Network. IEEE Trans. Intell. Transp. Syst. 2021, 22, 7242–7255. [Google Scholar] [CrossRef]
- Tran, P.N.; Nguyen, H.Q.V.; Pham, D.-T.; Alam, S. Aircraft Trajectory Prediction with Enriched Intent Using Encoder-Decoder Architecture. IEEE Access 2022, 10, 17881–17896. [Google Scholar] [CrossRef]
- Wu, X.; Yang, H.; Chen, H.; Hu, Q.; Hu, H. Long-Term 4D Trajectory Prediction Using Generative Adversarial Networks. Transp. Res. Part C Emerg. Technol. 2022, 136, 103554. [Google Scholar] [CrossRef]
- Guo, M.H.; Xu, T.X.; Liu, J.J.; Liu, Z.N.; Jiang, P.T.; Mu, T.J.; Zhang, S.H.; Martin, R.R.; Cheng, M.M.; Hu, S.M. Attention Mechanisms in Computer Vision: A Survey. Comp. Vis. Media 2022, 8, 331–368. [Google Scholar] [CrossRef]
- Luong, M.T.; Pham, H.; Manning, C.D. Effective Approaches to Attention-Based Neural Machine Translation. arXiv 2015, arXiv:1508.04025. [Google Scholar]
- Schimpf, N.; Knoblock, E.J.; Wang, Z.; Apaza, R.D.; Li, H. Flight Trajectory Prediction Based on Hybrid- Recurrent Networks. In Proceedings of the 2021 IEEE Cognitive Communications for Aerospace Applications Workshop (CCAAW), Cleveland, OH, USA, 21–23 June 2021. [Google Scholar] [CrossRef]
- Wu, Y.; Yu, H.; Du, J.; Liu, B.; Yu, W. An Aircraft Trajectory Prediction Method Based on Trajectory Clustering and a Spatiotemporal Feature Network. Electronics 2022, 11, 3453. [Google Scholar] [CrossRef]
- Jia, P.; Chen, H.; Zhang, L.; Han, D. Attention-LSTM Based Prediction Model for Aircraft 4-D Trajectory. Sci. Rep. 2022, 12, 15533. [Google Scholar] [CrossRef] [PubMed]
- Ding, W.; Huang, J.; Shang, G.; Wang, X.; Li, B.; Li, Y.; Liu, H. Short-Term Trajectory Prediction Based on Hyperparametric Optimisation and a Dual Attention Mechanism. Aerospace 2022, 9, 464. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Guo, D.; Wu, E.Q.; Wu, Y.; Zhang, J.; Law, R.; Lin, Y. FlightBERT: Binary Encoding Representation for Flight Trajectory Prediction. IEEE Trans. Intell. Transp. Syst. 2023, 24, 1828–1842. [Google Scholar] [CrossRef]
- Guo, D.; Zhang, Z.; Yan, Z.; Zhang, J.; Lin, Y. FlightBERT++: A Non-Autoregressive Multi-Horizon Flight Trajectory Prediction Framework. In Proceedings of the 38th AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 20–27 February 2024. [Google Scholar] [CrossRef]
- Tong, Q.; Hu, J.; Chen, Y.; Guo, D.; Liu, X. Long-Term Trajectory Prediction Model Based on Transformer. IEEE Access 2023, 11, 143695–143703. [Google Scholar] [CrossRef]
- Dong, Z.; Fan, B.; Li, F.; Xu, X.; Sun, H.; Cao, W. TCN-Informer-Based Flight Trajectory Prediction for Aircraft in the Approach Phase. Sustainability 2023, 15, 16344. [Google Scholar] [CrossRef]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social LSTM: Human Trajectory Prediction in Crowded Spaces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social GAN: Socially Acceptable Trajectories with Generative Adversarial Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–22 June 2018. [Google Scholar]
- Zhang, P.; Ouyang, W.; Zhang, P.; Xue, J.; Zheng, N. SR-LSTM: State Refinement for LSTM Towards Pedestrian Trajectory Prediction. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 16–20 June 2019. [Google Scholar] [CrossRef]
- Liu, Q.; Shi, X.; Jiang, R.; Zhang, H.; Lu, L.; Shibasaki, R. Modeling Interpretable Social Interactions for Pedestrian Trajectory. Transp. Res. Part C Emerg. Technol. 2024, 162, 104617. [Google Scholar] [CrossRef]
- Xu, Z.; Zeng, W.; Chu, X.; Cao, P. Multi-Aircraft Trajectory Collaborative Prediction Based on Social Long Short-Term Memory Network. Aerospace 2021, 8, 115. [Google Scholar] [CrossRef]
- Shafienya, H.; Regan, A.C. 4D Flight Trajectory Prediction Using a Hybrid Deep Learning Prediction Method Based on ADS-B Technology: A Case Study of Hartsfield–Jackson Atlanta International Airport (ATL). Transp. Res. Part C Emerg. Technol. 2022, 144, 103878. [Google Scholar] [CrossRef]
- Xu, Z.; Liu, Y.; Chu, X.; Tan, X.; Zeng, W. Aircraft Trajectory Prediction for Terminal Airspace Employing Social Spatiotemporal Graph Convolutional Network. J. Aerosp. Inf. Syst. 2023, 20, 319–333. [Google Scholar] [CrossRef]
- Sudarsanan, V.S.; Kostiuk, P.F. Deep-Learning Framework for Terminal Airspace Trajectory Prediction and In-Time Prognostics. J. Aerosp. Inf. Syst. 2024, 21, 1–13. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).