1. Introduction
In the aerospace and defense industries, pyroshock tests are crucial to ensuring the structural integrity of electronic and optical components. When pyrotechnic explosives detonate during separation events, antenna activations, or solar panel deployments, they generate intense shock waves known as pyroshocks. These shocks differ significantly from ordinary vibration events. While large components and structures with lower resonance frequencies often sustain minimal damage due to the short wavelength of pyroshocks, sensitive electronic and optical components can be seriously affected. Such damage poses a significant risk to the success of missions.
The objectives of pyroshock tests are outlined in multiple standards, which include procedures for evaluation of the durability and reliability of components that have to endure external shocks. These standards ensure consistency in testing through standardized techniques [
1,
2,
3,
4,
5]. The impact forces range from 1000 to 10,000 g, classified as near-field, mid-field, and far-field shocks. Each shock type requires specific testing techniques, protocols, and apparatus to accurately reproduce these forces in a consistent manner [
6,
7,
8,
9,
10,
11,
12,
13].
The Shock Response Spectrum (SRS) is crucial for the analysis of shock environments in aerospace components. SRS offers a frequency-based depiction of a shock’s impact on structures, enabling engineers to predict how different spacecraft components will respond to such shocks. This insight is crucial for designing more resilient systems and devising effective mitigation strategies. Various experimental and numerical methods have been developed to accurately predict pyroshock responses in spacecraft structures. Ding [
14] introduced a new methodology, validated through light-gas gun tests using a virtual mode synthesis method and an acceleration frequency response function. Choi [
15] proposed an innovative experimental technique that combined in-line filtering with laser pulse stimulation, achieving high accuracy and cost-effectiveness in predicting pyroshock responses. Wang et al. [
16] explored the application of stress wave theory to model and predict pyroshock responses at the spacecraft-rocket interface, providing valuable insights into mitigation strategies. Yalçinkaya and Gürsoy [
17] compared experimental results from metal-to-metal impact tests with finite element (FE) simulations. The comparison demonstrated high agreement for the study of the numerical validation of pyroshock test systems using explicit FE simulations.
Moreover, the study by Gour et al. on the tear and fracture of elastomeric skins in morphing wings underscores the broader relevance of stress and shock management in aerospace applications. Their research on mechanical stresses, including tear and fracture in morphing wings, parallels the challenges encountered in pyroshock testing, where accurate testing and modeling are crucial for ensuring the reliability and performance of aerospace components under extreme conditions [
18].
This research aims to identify optimal test conditions that meet specific requirements while minimizing the stress on test specimens caused by repeated incorrect test executions. Conventional test methods require extensive trial and error to find conditions that satisfy the requirements, leading to significant time and resource losses. To minimize this trial and error, this study investigates the changes in the shock response spectrum (SRS) using a numerical approach to structural vibration analysis and employs a genetic algorithm to quickly and accurately determine the optimal test conditions. In a pendulum-based testing apparatus, the weights of the steel ball, the angles of the pendulum, and the installation positions of the test specimen on the table structure result in approximately 2000 possible combinations. The genetic algorithm quickly and accurately identifies the optimal test conditions. An automated pyroshock test system is designed to enhance repeatability and reduce human errors, ensuring precise test execution.
2. Experimental Study of the Pyroshock Tests
2.1. Quantification of Vibration Damage
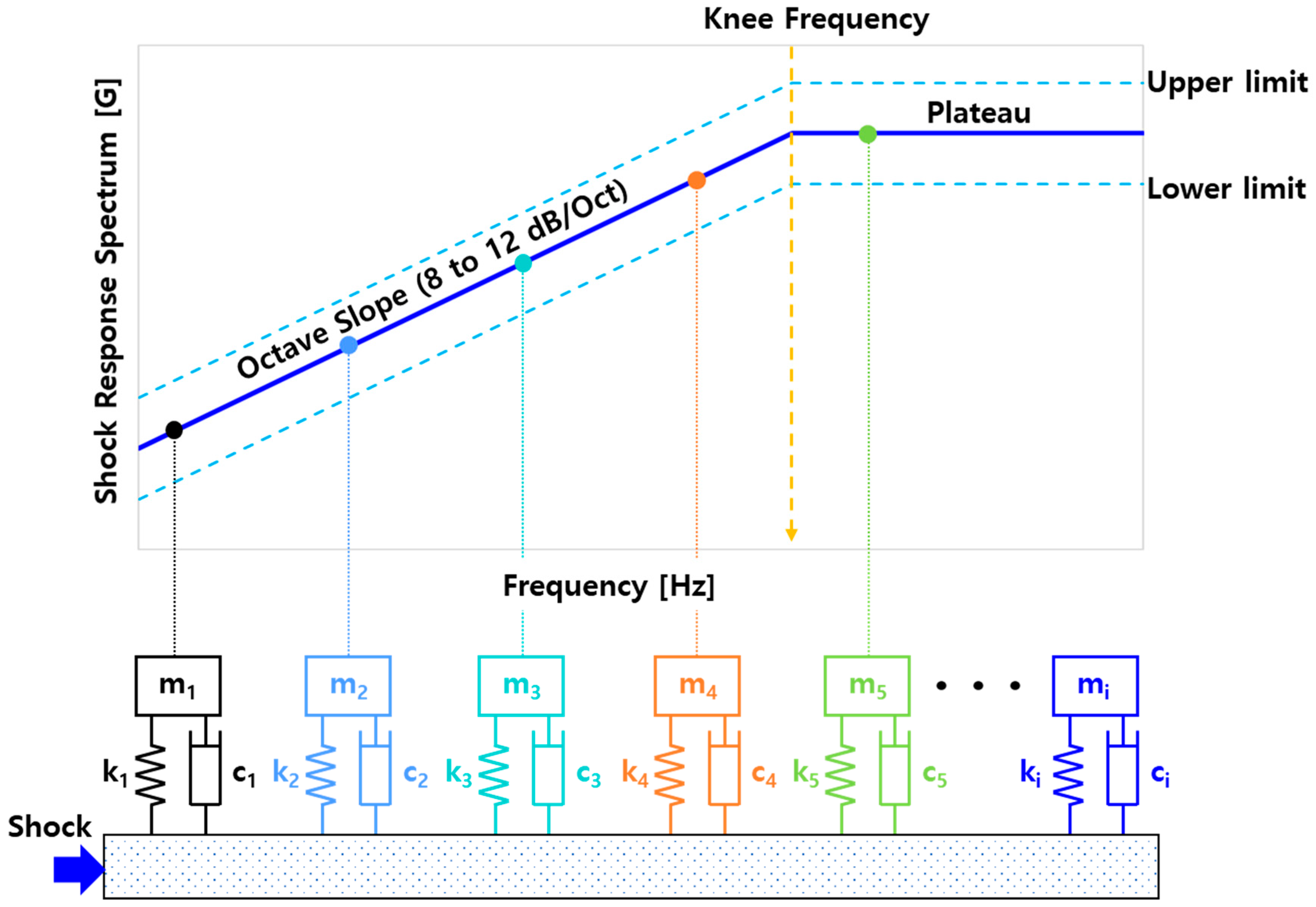
The SRS is a crucial tool in estimation of vibration damage for analyzing and quantifying shock environments. It describes the relationship between the maximum response and the natural frequency of a series of single-degree-of-freedom (SDOF) oscillators subjected to a given table structure excitation. The SRS transforms time-domain shock excitations into a frequency-domain representation. The transformed magnitude is expressed in terms of displacement, velocity, or acceleration. This method is particularly valuable in the aerospace, electronics, and mechanics industries for specifying shock test parameters and design for environmental adaptability.
The SRS was introduced by Biot in the 1930s during his studies on the impact of earthquakes on buildings. By the 1940s, SRS plots were being generated using analog computers, significantly reducing the complexity and volume of data required to describe a shock event [
7,
19,
20]. The SRS represents a transient shock acceleration response in the frequency domain, defined as the relationship between the peak absolute magnitude and the natural frequency of a series of SDOF oscillators, each with different frequencies but subjected to the same shock transient load. The calculation process involves conversion of a time-domain impulse excitation into the SRS representation in the frequency domain [
9].
To calculate the SRS, the time-domain shock response is transformed into the frequency-domain representation to understand how different frequency components of a shock impact a system. The process begins with an acceleration input, typically an acceleration-time history of the shock event. A series of SDOF systems, each with a different natural frequency but the same damping ratio, is used to analyze the response. The response of each SDOF system to the input acceleration is computed using numerical methods such as the Newmark-beta method, Runge–Kutta, or digital filters. The peak response of each system is then plotted against the natural frequency to form the SRS. The ramp-invariant method is commonly employed for its computational efficiency and accuracy. This method approximates the continuous transfer function with a discrete transfer function using digital filters, allowing the calculation of the acceleration response in the time domain. The resulting SRS curve provides a comprehensive view of the maximum responses across various frequencies, which is crucial for the design of systems capable of withstanding shock environments [
21].
A typical SRS graph is shown in
Figure 1, and several factors affect the SRS. The duration of the shock has the most significant impact on the shape and trend of the SRS, especially at low frequencies. Longer durations result in higher amplitudes due to the greater energy transferred to the system. While the amplitude of the shock affects the overall amplitude of the SRS, it does not change its trend; the SRS amplitude is proportional to the shock input signal amplitude. Different waveforms can influence the frequency point of peak acceleration but have a minor effect on the overall envelope of the SRS [
7,
19].
2.2. Pyroshock Test Standard
The pyroshock testing standards which are most often referred to are summarized in
Table 1 and
Table 2 [
1,
2,
3,
4]. Impact forces are grouped by intensity into three categories, namely near-field, mid-field, and far-field. Each category requires unique testing methods, processes, and equipment to correctly reproduce the corresponding impact forces.
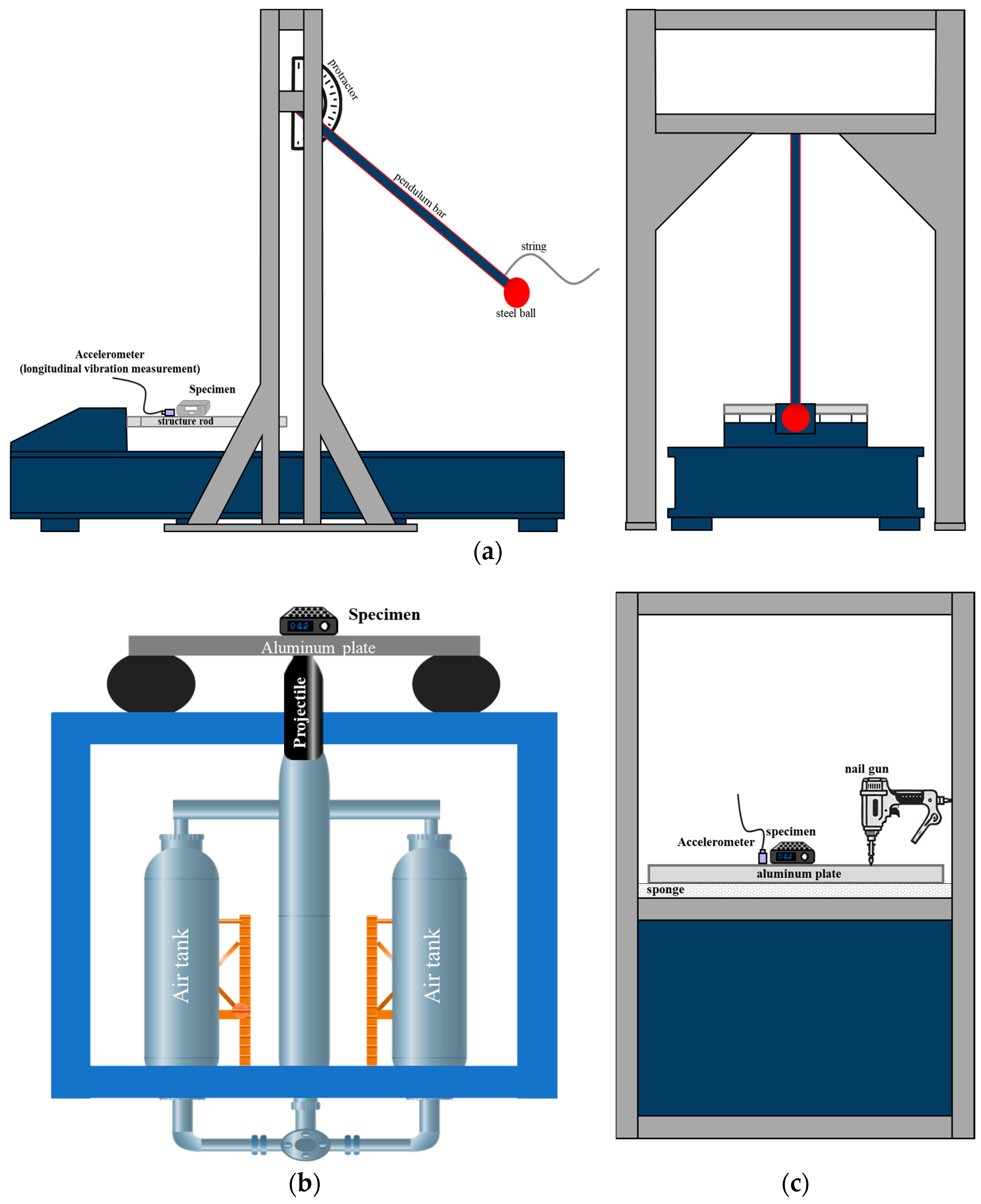
This research details the execution of a pyroshock test using a pendulum-based mechanical device. In this system, a steel ball mounted on a pendulum arm impacts a structure to generate pyroshock loads. The electronic components are installed on the structure to assess their response to the shock. The kinetic energy transferred from the pendulum to the structure creates the pyroshock loads. The shock energy level can be adjusted by varying the weight of the steel ball and the angle of the pendulum. Similar procedures are applicable to the other test methods.
2.3. Various Pyroshock Test Equipments
Many testing procedures conduct pyroshock tests using various impact sources. The test equipment used by each procedure is classified according to its specific testing methods.
2.3.1. Pendulum Method
The pendulum method is one of the most commonly used techniques among pyroshock test methods. To implement test conditions that meet specific requirements, various combinations of hammer weights, shapes, and boundary conditions are employed. While the shapes of the pendulums may vary, they share a common principle of controlling the hammer’s potential energy by adjusting the length and angle of the pendulum. To prevent multiple impacts due to rebound, the string connected to the pendulum is held securely [
22,
23,
24,
25,
26,
27,
28,
29].
2.3.2. Pneumatic Projectile Method
In this configuration, the movement of the hammer along the guide is regulated by pressurized air, analogous to the trajectory of a bullet through a gun barrel. To meet the specified requirements, various parameters are adjusted, including the thickness of the resonant plate, the boundary conditions, and the impact load. The impact load is controlled by the type of hammer and the air pressure. This method ensures that multiple impacts due to rebound do not occur [
30,
31,
32,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46].
2.3.3. Nail Gun Method
The nail gun method represents a cost-effective and practical approach for performing the pyroshock tests. By utilizing the kinetic energy of commercial nail guns, this method eliminates the need to manufacture separate equipment such as pendulum or pneumatic hammer guides. Compared with the previously mentioned methods, the nail gun approach also offers excellent repeatability [
47,
48,
49,
50].
2.4. Experimental Setup to Implement Pyroshock
This study performs a pyroshock test based on the pendulum method, as illustrated in
Figure 2a. To conduct the pyroshock test, a pendulum weight ranging from 12 to 30 kg is used to impact a rectangular table structure. The pendulum angle can be adjusted from 10 to 90 degrees. The test operator uses a protractor to visually set the pendulum angle, aiming to establish a test arrangement that meets the specifications. However, due to the reliance on the operator’s visual estimate, the applied load varies depending on the operator. The operator holds an additional string, which is released to deliver the impact. To prevent secondary impacts, the string is recaptured immediately after the initial impact. Determining the suitable test configuration is often a trial-and-error process that can take one to two days. The accelerometer (352B70, PCB Piezotronics, New York, NY, USA) is used for the longitudinal vibration measurements. The measured accelerations are digitized using the Simcenter SCADAS Mobile 05 module (SIEMENS, Munich, Germany) and subsequently stored and analyzed with Simcenter Testlab (Version 18).
2.5. Application of Genetic Algorithm (GA) for Test Parameter Optimizations
The GA is a class of optimization algorithms inspired by the principles of natural selection and genetics. Introduced in 1975, GAs belong to the broader family of evolutionary algorithms (EAs), which include Evolutionary Programming (EP), Evolution Strategies (ES), and Genetic Programming (GP). The key components of GAs include a population of potential solutions (chromosomes), a fitness function to evaluate the suitability of these solutions, and genetic operators such as selection, crossover, and mutation that guide the evolution of the population towards optimal solutions. The process begins with the initialization of a random population, followed by iterative cycles of evaluation, selection, reproduction, and replacement until a termination criterion is met [
51].
The main strength of GAs lies in their ability to perform global optimization in complex landscapes, making them highly suitable for problems where traditional methods, such as non-linear, multi-modal, or high-dimensional spaces, struggle. They are widely applied in fields of engineering design, machine learning, scheduling, and evolutionary robotics. GAs excel in finding global optima, avoiding the pitfalls of local optima that often trap gradient-based methods. Their robustness allows them to perform well even when the objective function is noisy or discontinuous, and their flexibility enables them to handle various types of variables and constraints effectively [
52].
The GA is a well-established optimization technique widely used across various applications. Sun et al. [
53] introduced an adaptive genetic algorithm (AGA) to optimize the synthesis of pyroshock acceleration profiles. The AGA dynamically adjusted its parameters to enhance convergence and performance, aiming to minimize the error between the synthesized and target shock response spectrum (SRS). This adaptive mechanism significantly improved the algorithm’s accuracy and computational efficiency by avoiding local optima and identifying a global solution. Viale et al. [
54] applied a GA to optimize the shape and size of a resonant plate for pyroshock testing. The GA determined geometric parameters and utilized a CAD modeler and finite element (FE) solver to predict the plate’s behavior. By adjusting parameters to minimize the SRS error, the GA ensured that the plate met shock test requirements while avoiding local minima. Additionally, Viale et al. [
55] used a GA to optimize parameters of a pyroshock test simulation model, iterating through a population of potential solutions and applying genetic operators to minimize discrepancies between simulated and experimental SRS. This iterative process evolved solutions toward the optimal parameter set, enhancing the simulation model’s accuracy. Monti et al. [
56] employed a GA in a two-level optimization strategy to determine optimal parameters for simulating dynamic loads in space structures. The GA conducted a global search to identify a satisfactory parameter set, which was further refined using a heuristic algorithm. This approach helped avoid local optima and iteratively improved parameters through selection, crossover, and mutation operations. Chen et al. [
57] investigated optimized actuator positions for active vibration control in a GARTEUR aircraft model. He employed a genetic algorithm, integrating controllability, observability criteria, and system energy criteria. The method involved encoded actuator positions as chromosomes and using selection, crossover, and mutation to identify positions that greatly improved vibration control performance.
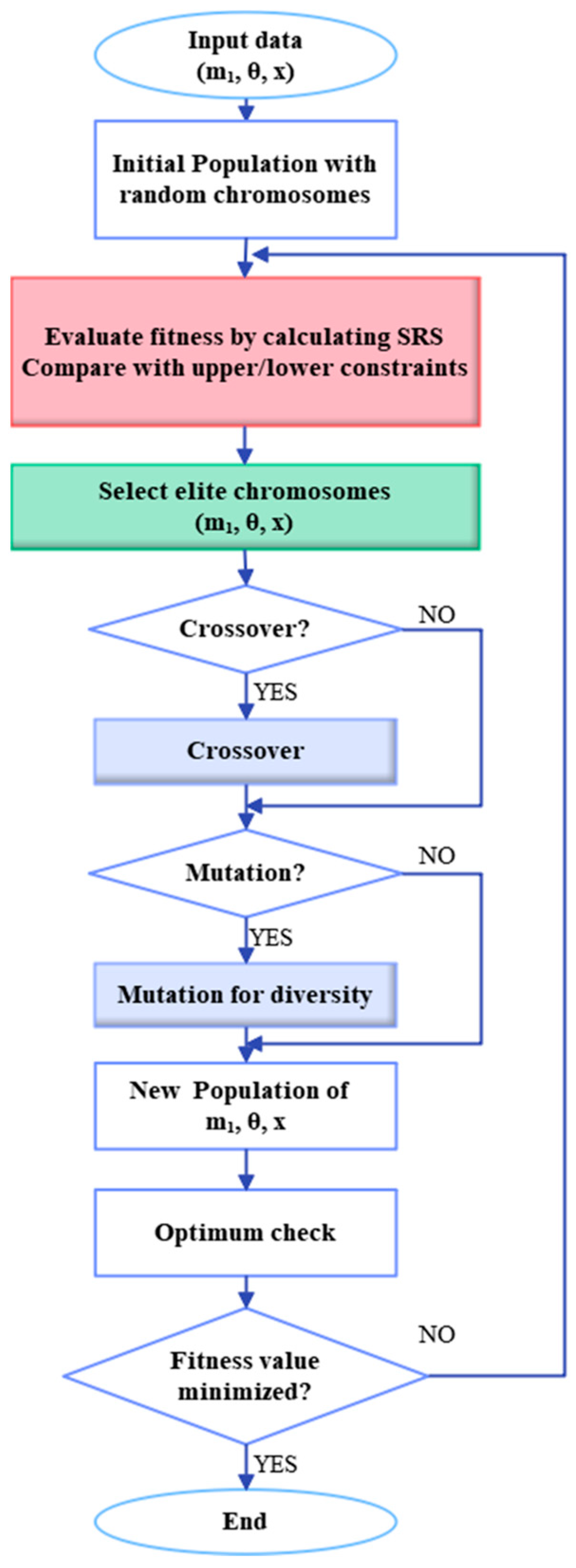
As illustrated in
Figure 3, this paper presents a study that utilized GA to iteratively optimize the combination of the weight mass, the pendulum angle, and the specimen location. The objective was to identify conditions that satisfy SRS requirements in the formulation of longitudinal vibration. The control variables, objective function, constraints, and parameters used in the genetic algorithm are summarized in
Table 3. Four types of mass were considered: 12, 18, 24, and 30 kg. The angle varied from 10 to 90 degrees, resulting in 81 discrete values. The specimen position on the pyroshock test equipment ranged from 0.2 to 0.7 m in six increments. Consequently, 2 bits were used for the mass, 7 bits for the angle, and 3 bits for the position, resulting in a total of 12 bits per chromosome to represent these values in the GA. For example, encoding a mass of 18 kg, an angle of 45 degrees, and a position of 0.5 m yielded [01] for the mass, [0101101] for the angle, and [011] for the position. Thus, the chromosome was represented as [010101101011].
3. Prediction of Impacted Wave Propagation
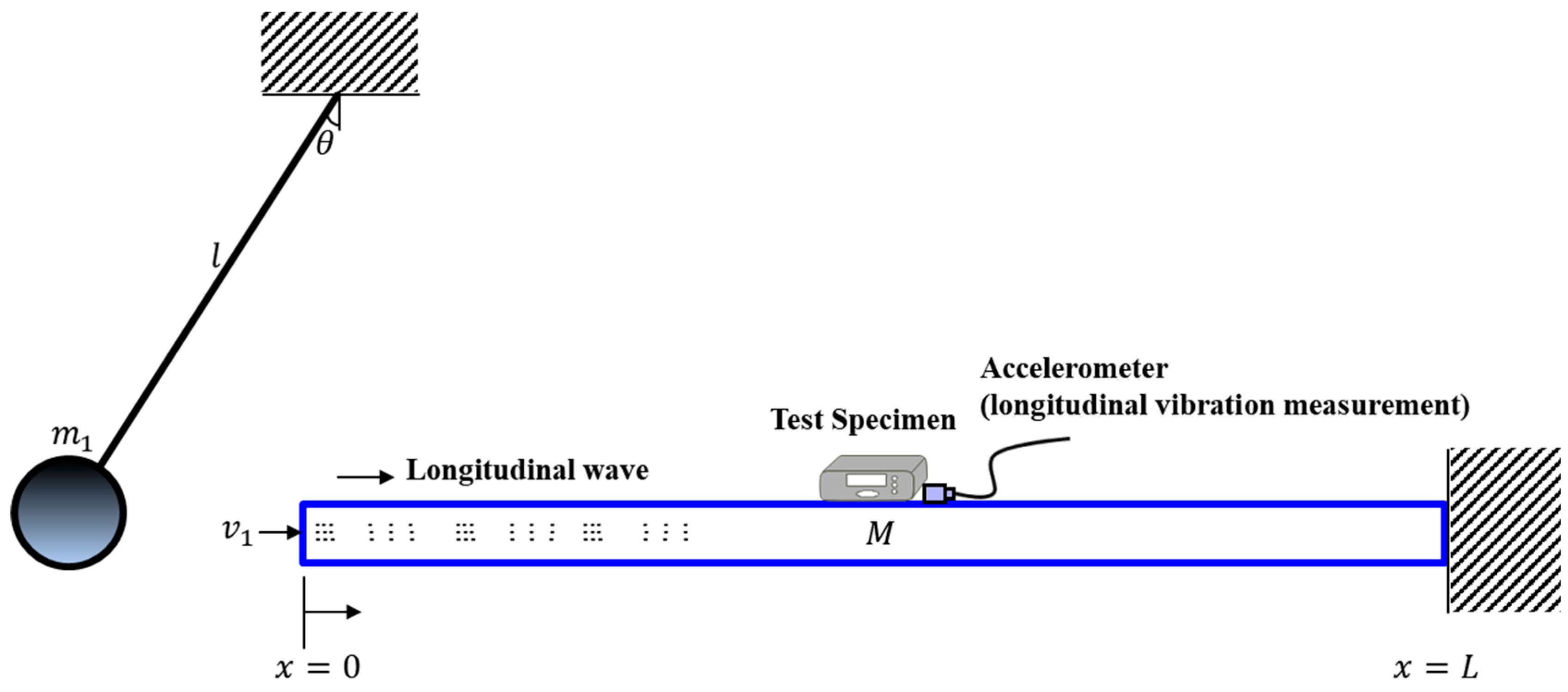
3.1. Modeling of Structure Vibration Undergoing Pyroshocks
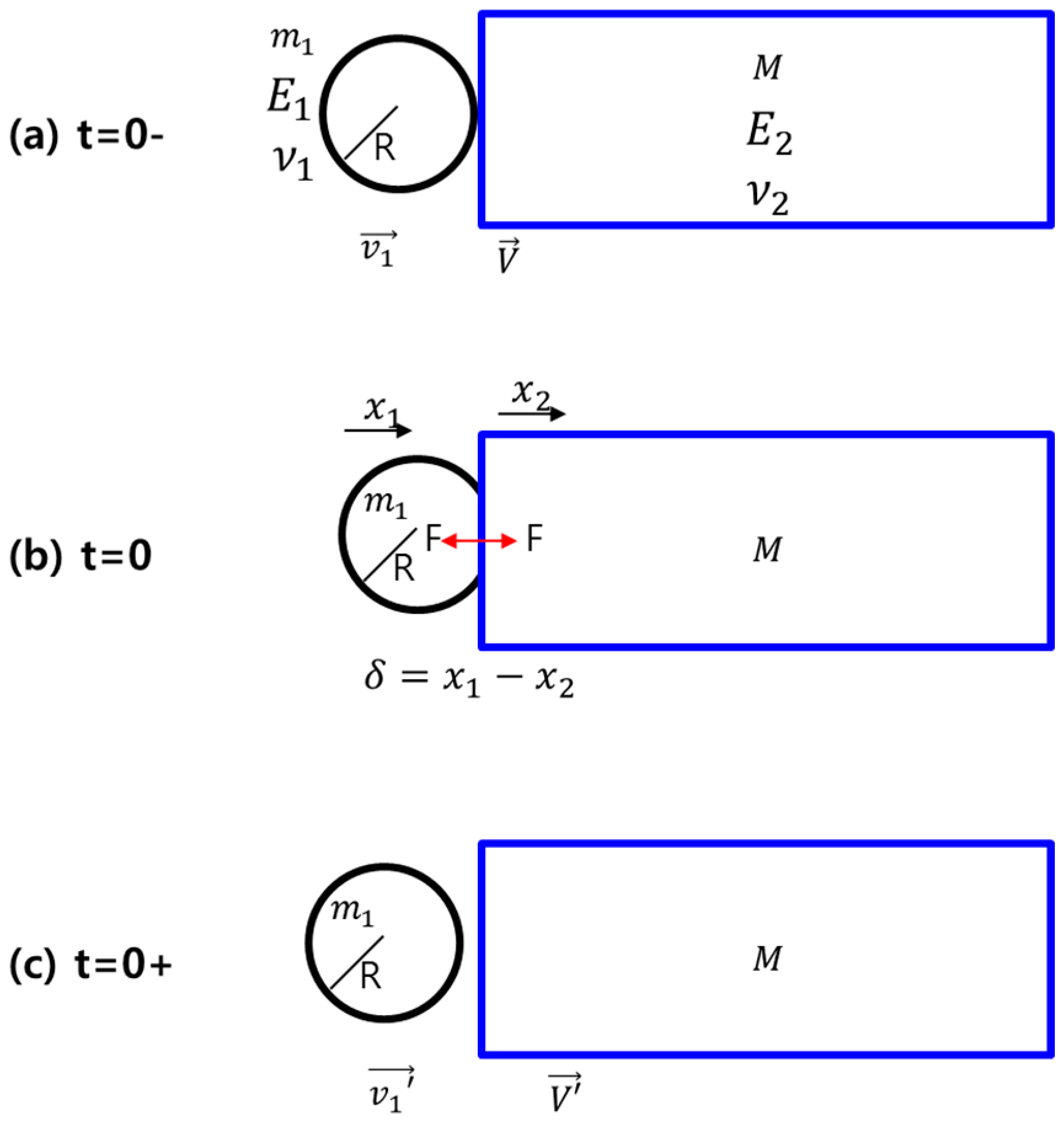
The pendulum method is used in this study to investigate the dynamics of an aluminum rectangular structure impacted by a steel ball. The system, shown in
Figure 4, consists of an aluminum structure with length
and mass
M, and a pendulum with length
and mass
, inclined at an angle θ. The pendulum impacts the structure, resulting in dynamic behavior. When the structure is subjected to a longitudinal impact, the resulting excitation primarily induces longitudinal vibrations. Since transverse modes receive negligible energy input from such an impact, they contribute minimally to the overall vibrational response. Also, most SRS requirements specify a knee frequency in the range of 1000 to 3000 Hz. The first natural frequency of transverse vibrations that directly influences the knee frequency is approximately 200 Hz and can therefore be considered negligible. Consequently, the transverse vibration components were excluded from this analysis.
3.2. Governing Equation of the Structure Vibration
The longitudinal vibration of the structure induced by the pendulum’s impact was expressed as
Applying the boundary conditions of a fixed-free table structure,
By simplifying the coefficients, the above vibration response was rewritten as follows.
By applying the initial conditions
,
, the displacement and acceleration are expressed as follows.
The interaction between the steel ball and the beam before and after the shock is explained by the Hertzian contact theory and is shown in
Figure 5. It can be written as the Equation (8).
where
and
.
The following established relationship
,
and
is used to simplify the equation. The relative acceleration between the steel ball and the structure can be described as
. Utilizing Equation (8), the above equation is rewritten as
. Applying the initial condition at
t = 0−, where
and
, and performing integration, we get:
Because the maximum relative displacement
is obtained at
= 0,
and
are written as
,
. Applying the law of energy conservation,
the Equations (11) and (12) are equivalent.
Also, by Impulse-momentum principle,
and it is written as
By substituting Equation (14) into Equation (13) and simplifying the expression, the following result is obtained.
where
.
Here,
was derived from the relationship between the pendulum length and the angle. The longitudinal vibration of the table structure is formulated as follows:
4. Improvement of Test Repeatability
4.1. Overview of the Test
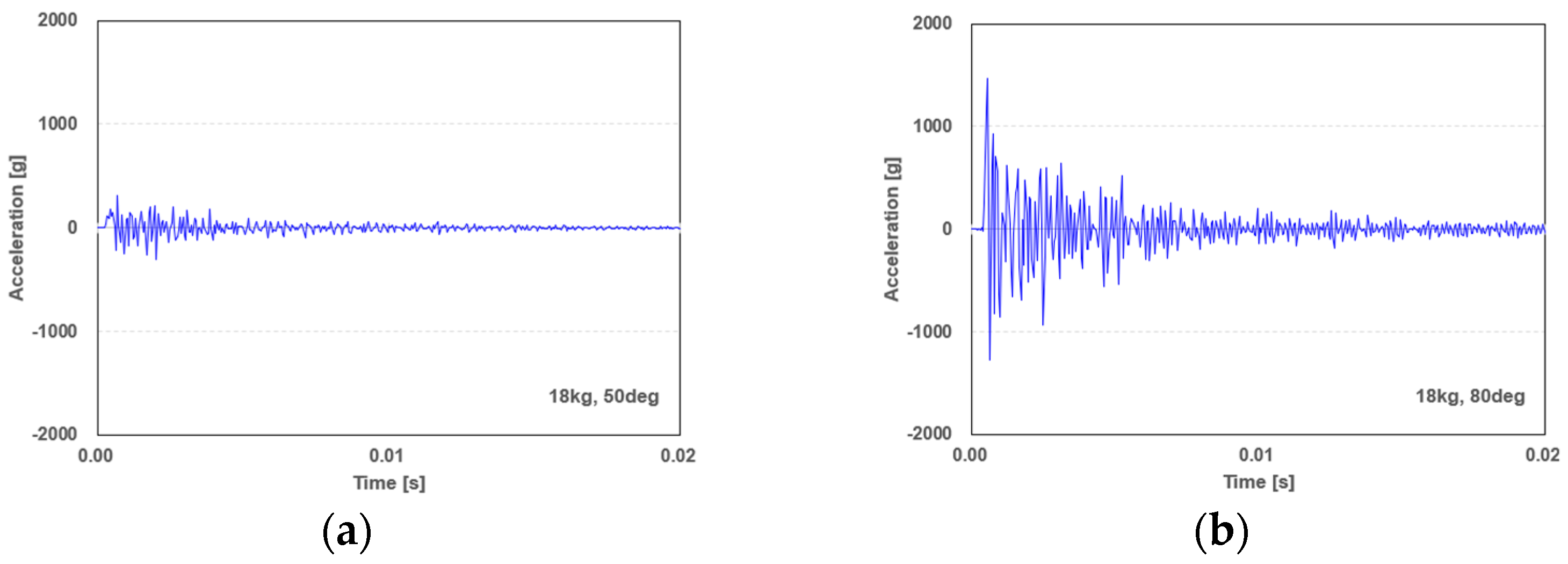
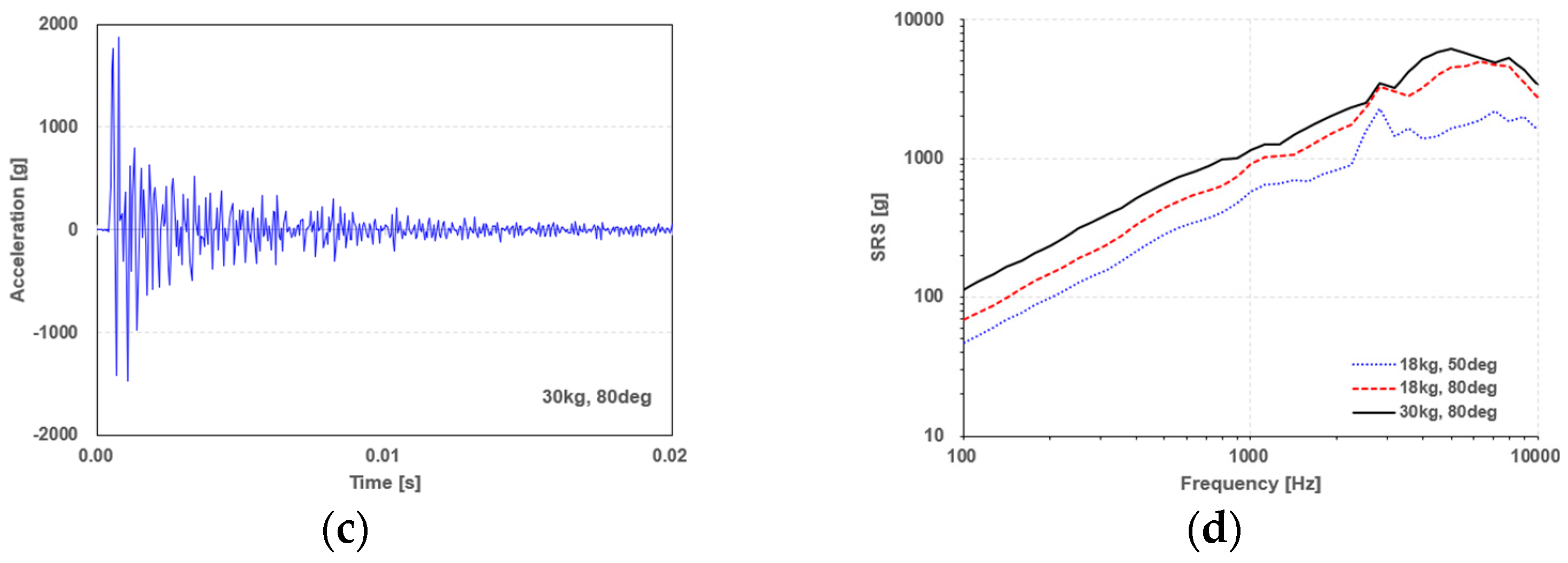
MIL-STD-7003A and ECSS-E-ST-10-03C provide detailed descriptions of the procedures and requirements for the pyroshock tests. These standards specifically address the shock level and tolerance of the SRS and stipulate that the shock duration in the time domain should not exceed 20 ms. In the pendulum-based pyroshock test equipment discussed in this paper, the conditions such as impact energy and impact time are determined by the angle of the pendulum and the mass of the weight. As illustrated in
Figure 6, an increase in the angle and mass of the weight leads to a corresponding increase in transient acceleration responses, resulting in a higher amplitude in the SRS. The increased vibration amplitude affects the impact duration. By precisely controlling the impact parameters, it is possible to achieve the desired SRS with improved repeatability.
4.2. The Need to Improve Test Repeatability
In this test, the precise motion of the pendulum is crucial. However, manually initiating the pendulum’s motion leads to discrepancies in release timing and method, reducing the reliability and repeatability of the measured data. Use of a release aid device, similar to those used in archery, enhances the consistency of the tests.
To maintain consistent pendulum motion, all experimental conditions should be identical for each trial. Manual release introduces various issues, including timing variability, procedural inconsistency, and human error. Archery release aids prevent micro-movements of the fingers, ensuring a uniform release of the bowstring. Application of this concept to the pendulum improves the repeatability of the experiments involving a pendulum and steel ball.
Several studies have demonstrated the efficacy of automated release mechanisms in pendulum tests. Brüggemann et al. [
58] described the development of an automated modal pendulum for experimental modal analysis that provides consistent force application and reduces errors compared with manual methods. This automated method enhances data quality and reliability, making it a valuable tool for assessing the dynamic behavior of milling machines. According to Wikipedia, a release aid in archery allows archers to achieve more consistent and accurate releases by mechanically releasing the bowstring, thereby eliminating human error and finger strain. By emulating this approach, an automated pyroshock equipment was designed, significantly enhancing the reproducibility and repeatability of pendulum-based tests, resulting in more accurate and consistent test outcomes.
4.3. Design of an Automated Testing Device
An automated testing device was developed to address the issues associated with manual pendulum release. This system consistently positioned the steel ball at a predetermined height and discharged it evenly. Precision motors and reducers controlled the motion of the pendulum and ensured precise drop placements. To prevent re-impact from rebound after the initial impact, a stopper device was included. This system ensured the accuracy and repeatability of the tests by preventing multiple impacts due to rebound.
The automated testing equipment improved three critical factors: the uniform timing of the pendulum’s release, the accurate alignment of the pendulum’s initial position, and the prevention of re-impact. By maintaining consistent release conditions and minimizing multiple impacts, the automated test system effectively compensated for the drawbacks of manual tests.
4.4. Application to the Test Specimen
The developed automated test equipment was used to conduct pyroshock tests on the circuit board. A circuit board is an essential tool for verifying the accuracy and quality of electronic circuit designs and assembly processes, particularly for space applications. This board includes various surface mount technology components, such as a ball grid array and a quad flat package. According to the SRS requirements, electronic components are more significantly affected by high-frequency shocks than low-frequency ones, leading to critical issues from an electrical perspective rather than structural damage. To assess the integrity of the test specimens, visual inspections and simple electrical characteristic tests were performed before and after the pyroshock tests.
5. Results and Discussion
5.1. Comparison of Results between Analysis and Experiment
The estimated accelerations in a fixed-free beam impacted by a steel ball were compared with measured responses. The SRS was calculated using a Tom Irvine algorithm [
6]. The following procedures were used to determine the test settings. Conditions that satisfied the requirements were identified using analytical data. These conditions were applied during the test. After the test, the results were compared with the analytical predictions and assessed for compliance with the requirements.
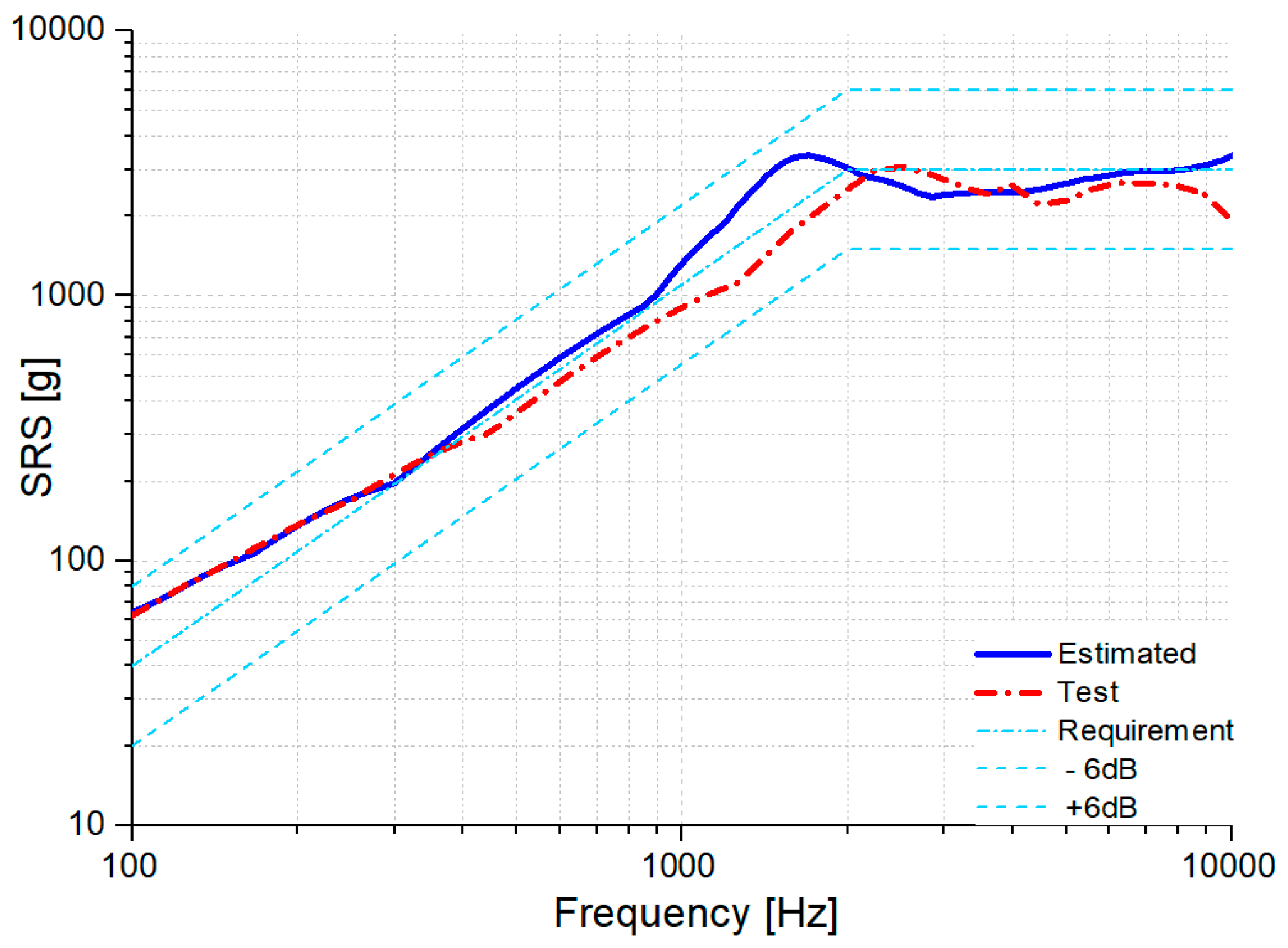
Figure 7 confirms the comparability and fulfillment of these conditions.
The experiments utilized a 24 kg steel ball with the pendulum set at a 50-degree angle. The results under these constant conditions were compared, revealing similar patterns across all frequency regions, with each result meeting the necessary requirements. This consistency indicated that the operating conditions could be efficiently anticipated using the analytical model, thereby reducing trial and error.
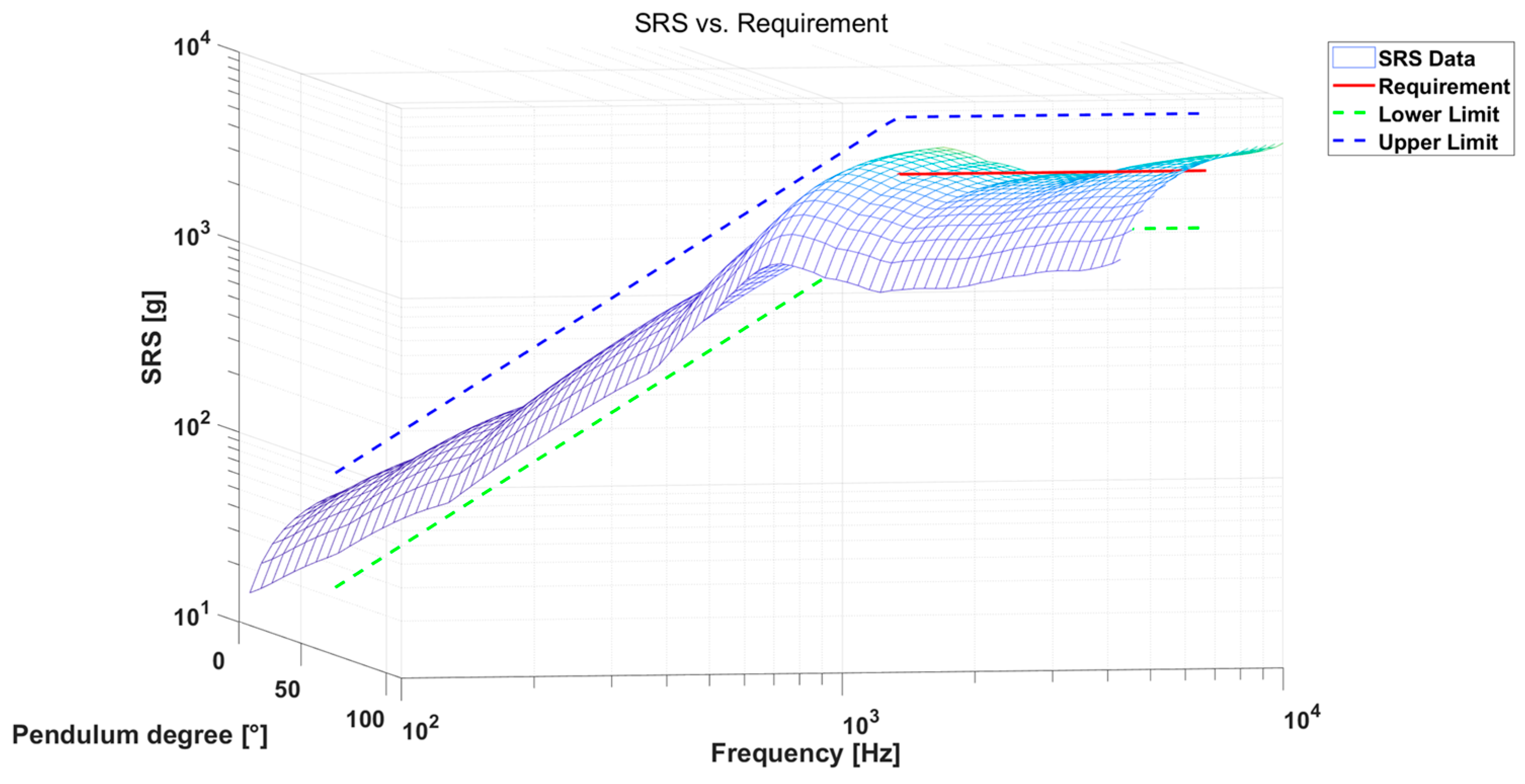
The pendulum angle was adjusted within a range of 10 to 90 degrees, and the resulting SRS was displayed on a three-dimensional graph shown in
Figure 8. As expected, SRS levels increased with rising pendulum angles. Furthermore, by overlaying the requirements and upper/lower limits onto the three-dimensional graph, a direct comparison was made to determine conformity with the requirements. The SRS exhibits an increasing trend with the increase in the mass of the weight. By adjusting the combination of angle and mass, it is possible to determine a test condition that satisfies the requirements.
5.2. Optimal Test Parameter Combinations via GA
The flowchart illustrating the process of obtaining the optimal combination of the mass (
) of the weight, the angle (θ) of the pendulum, and the location (
) of the specimen through a Genetic Algorithm is shown in
Figure 3. The process begins with an arbitrary initial population, where the specified chromosome encoding for
, θ, and
is substituted into Equation (17) for the longitudinal vibration of the table structure to calculate vibration response and the SRS. These calculated SRS values are then compared with the requirements and constraints of the objective function. The elite chromosomes are retained, while the non-elite ones undergo mutation and crossover to generate a new population.
The objective function calculates the difference between the computed SRS results and the requirements, using the sum of the squares of these differences to determine the cost. Additionally, a penalty is applied if the computed SRS results exceed the upper or lower constraints. The fitness value is then calculated as the sum of the cost and penalty, with more weight potentially added to more critical factors. In this study, however, both cost and penalty are considered equally significant and are weighted equally. The goal of the GA is to minimize the fitness value, thereby determining the optimal values for
, θ, and
. The GA parameters used for the optimization process in this paper are listed in
Table 4.
Enhancing optimization capability and decision speed requires precise adjustment of genetic algorithm parameters tailored to the specific problem. This study considered four types of mass (
) at 12, 18, 24, and 30 kg, 81 angles (θ) ranging from 10 to 90 degrees, and six positions (
x) ranging from 0.2 to 0.7 m on the pyroshock test equipment’s pattern hole, resulting in a total of 1944 possible combinations (4 × 81 × 6). To select the appropriate parameters for this study, several examples were referenced, and a trial-and-error process was conducted. The GA parameters used are presented in
Table 5. As illustrated in
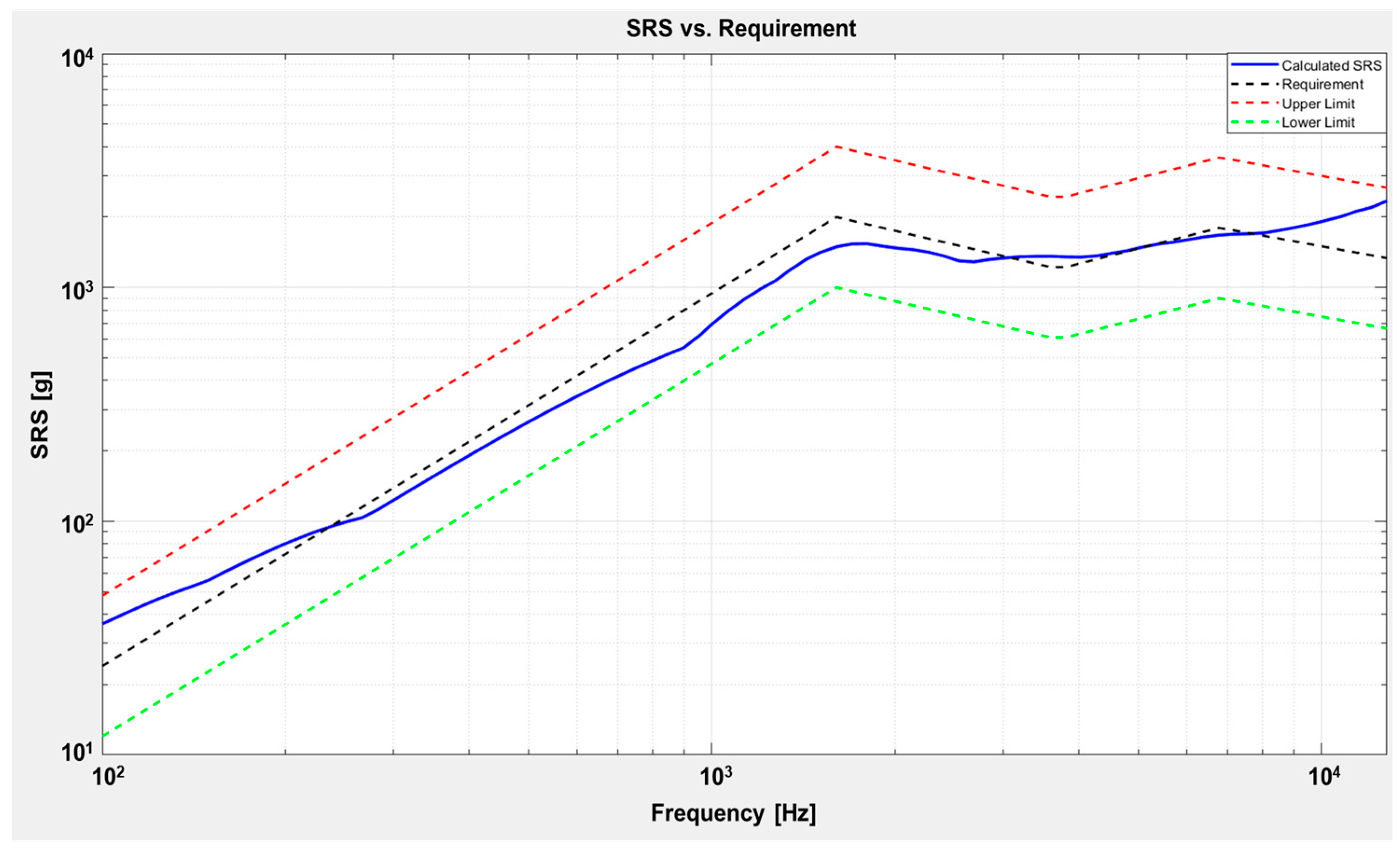
Figure 9, the SRS resulting from this parameter combination satisfies the specified requirements. Thee population size and generation size were set to 200, the elite count to 10, the crossover fraction to 70%, and the mutation rate to 20%. Although the generation size was set to 200, as shown in
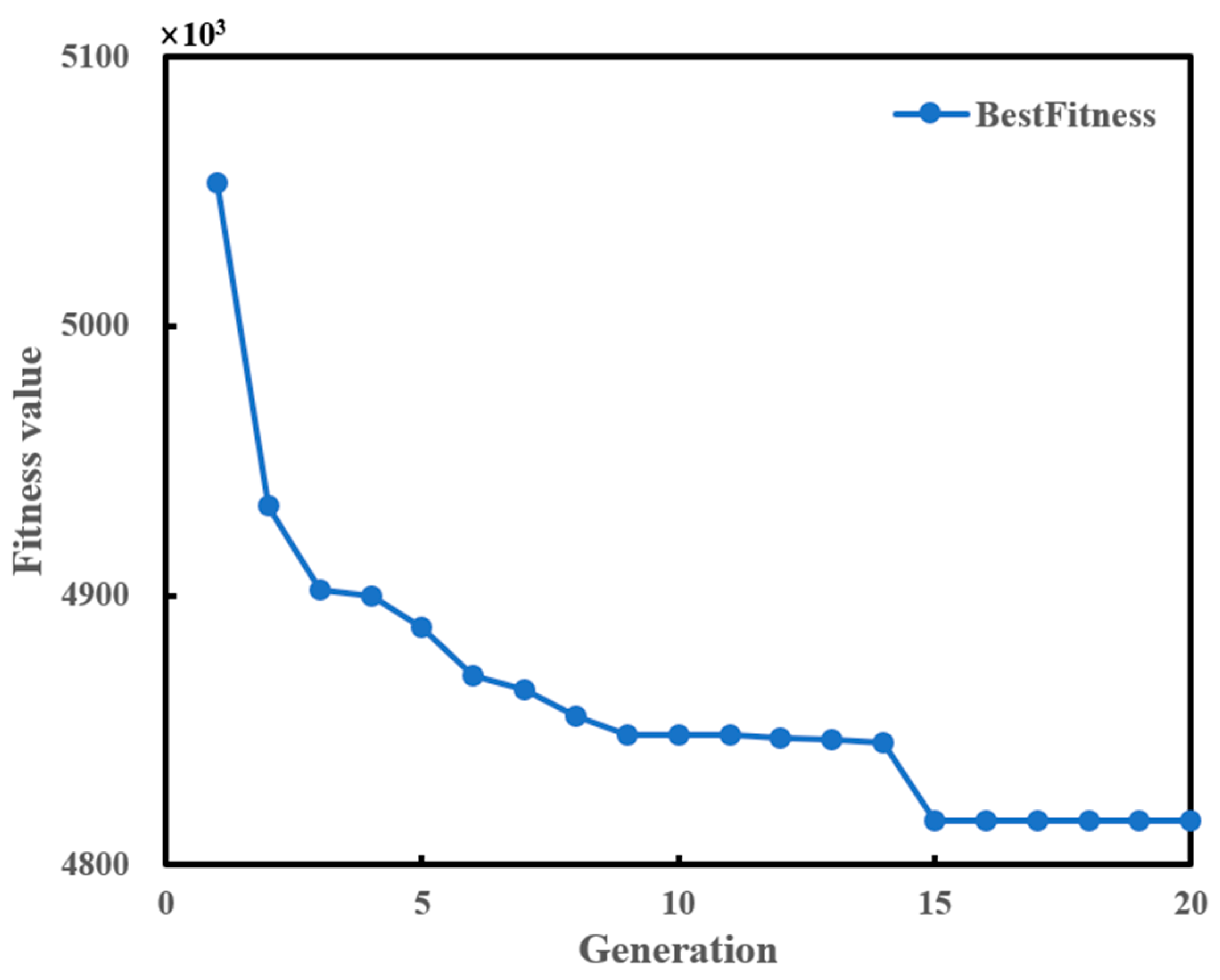
Figure 10, the best fitness value converged between 15 and 20 generations.
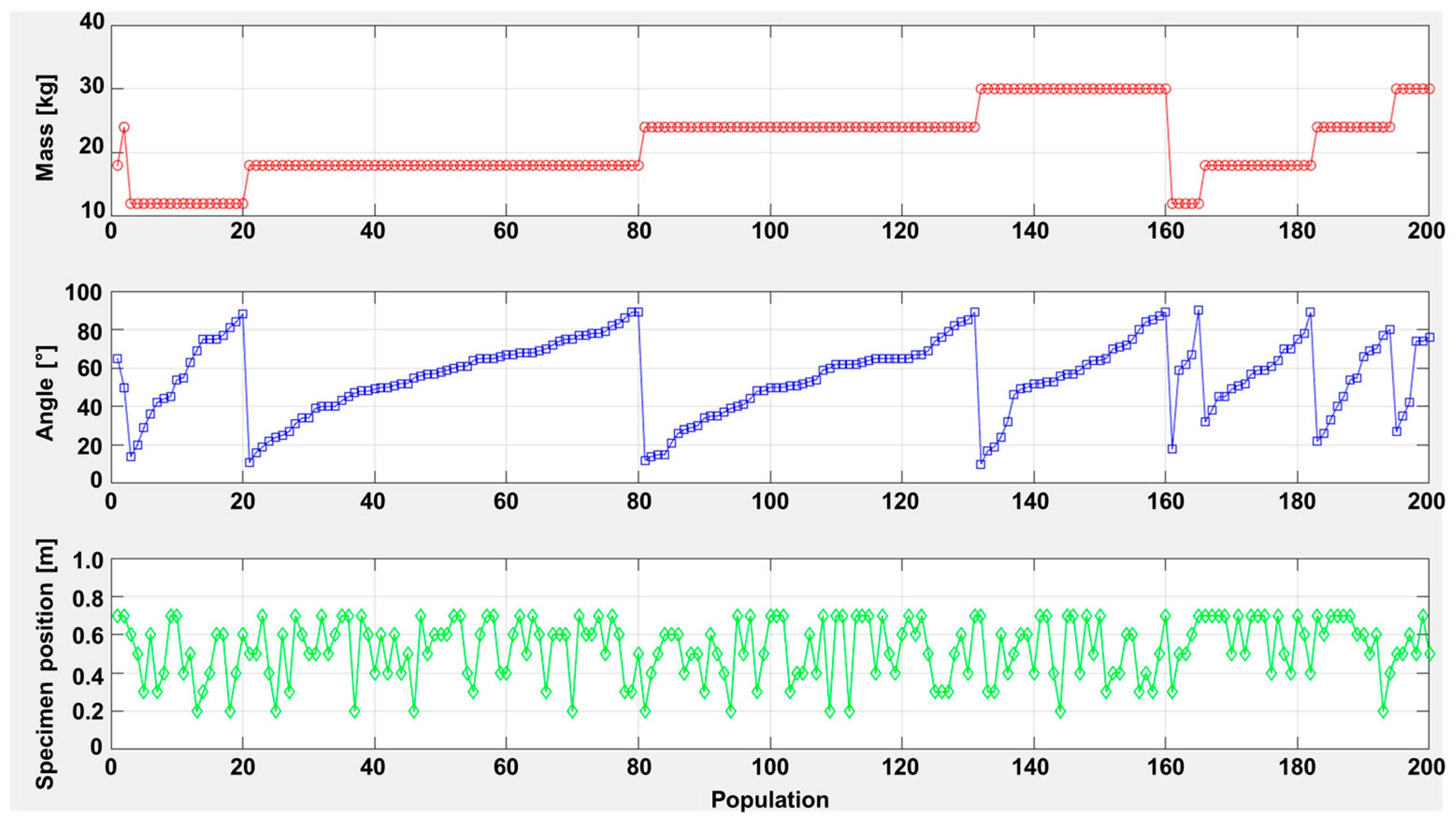
Figure 11 illustrates how the combinations of a generation population vary throughout the optimization process.
5.3. Improvement of Repeatability through Automated Testing
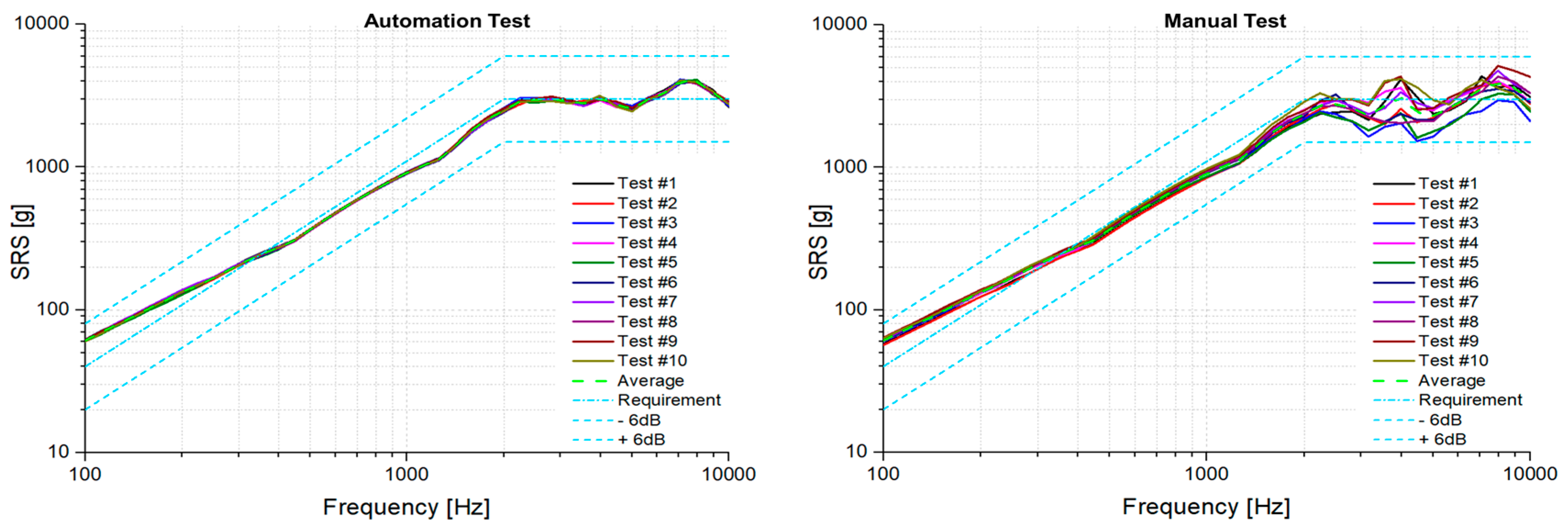
The results of the automated and manual tests are compared in
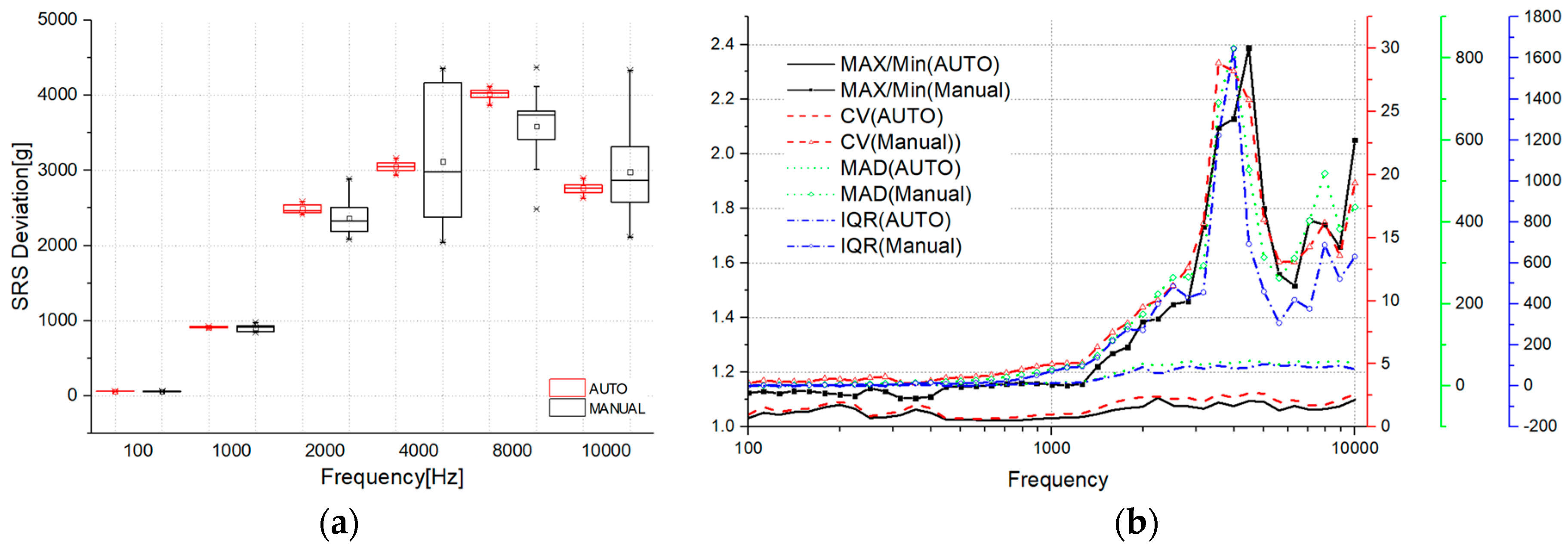
Figure 12. The solid line represents the results of ten repeated tests, while the light blue dotted line indicates the requirement, upper limit, and lower limit, respectively. The automated test results demonstrated consistent performance across all frequencies, whereas the manual test results showed limited repeatability, particularly at 4000 Hz. A box plot in
Figure 13 clearly illustrates the variance between the two tests, highlighting the greater reliability of the automated method. To examine the repeatability variance between the automated and manual tests, four indicators were used: max/min ratio, coefficient of variation (CV), mean absolute deviation (MAD), and interquartile range (IQR). The results revealed comparable trends across all four indicators, with automated tests showing greater consistency across all frequencies.
Furthermore, the automated test resulted in considerable advantages in repeatability and productivity. The manual test required at least two people and took 238 s to complete, for a total of 476 person-seconds (TPS). In contrast, the automated system enabled one person to complete the identical test in 85 s. This resulted in a significant time-saving ratio, which represented an 82.14% improvement. In addition, the productivity increase rate which measured how much productivity per person increased as a result of automation was calculated as 5.6. This substantial increase emphasized the significant improvement in workload capacity and employee efficiency achieved through the use of the automated testing methods. This not only accelerates the testing process, but also frees up human resources for other critical tasks, further enhancing overall operational efficiency.
5.4. Determination of Abnormalities after the Pyroshock Test
The pyroshock test results for the circuit boards were subjected to comprehensive analysis. Circuit boards are essential tools for validating the accuracy and quality of the underlying circuit designs and assembly processes, especially in the context of space applications. These boards incorporate various surface mount technology (SMT) components, such as ball grid arrays (BGA), quad flat packages (QFP), and small outline integrated circuits (SOIC). These components play a critical role in evaluating soldering techniques, alignment precision, and electrical continuity, thereby ensuring the reliability and performance of the final electronic product. This validation process is vital for maintaining the high standards required for electronic components in space, where reliability is paramount.
It was observed that electrical devices are prone to resonant vibrations at high frequencies, which can potentially lead to failure. To investigate this, two identical circuit boards were subjected to pyroshock testing: one using automated pyroshock equipment and the other using a manual pyroshock test method. Visual inspections were conducted both before and after the pyroshock tests. Additionally, resistance measurements were taken at several pads on the circuit boards for comparison. The test conditions included a 24 kg weight, a pendulum inclination of 50 degrees, and the specimen mounted at a height of 0.6 m, with each sample being impacted ten times.
The results indicated that the test board (Sample #2) subjected to the automated pyroshock equipment showed no anomalies upon visual inspection and exhibited only minimal changes in resistance measurements. In contrast, the test board (Sample #1) subjected to the manual pyroshock test method displayed no significant changes in resistance; however, it did exhibit detachment in a soldered section of the QFP. This detachment is attributed to the high-frequency impact of around 4000 Hz induced by the inconsistencies inherent in the manual method. Notably, several pads on both test boards had cables soldered to them, and these solder joints remained intact. The flexible cables likely absorbed most of the shock energy. The summarized test results are presented in
Table 6 and
Table 7.
6. Conclusions
The similarity between the pyroshock tests and the analytical predictions were verified by the vibration wave analysis. By considering variables, including the pendulum weight, the pendulum angle, and the specimen installation position, the pyroshock analysis model effectively determined the necessary variables to meet given test requirements, thereby significantly reducing the trial-and-error process during actual tests. This pyroshock test prediction process enhanced the reliability and consistency of the test results. Additionally, by using the derived wave approach and the genetic algorithm, the process to satisfy the test requirements from approximately 2000 variable combinations was optimized. To address the issue of poor test repeatability, often affected by variations in pendulum angle, steel ball release method, and timing, the automated test equipment was designed and verified. Inspired by release assist devices, the automated test system incorporated a stopper to prevent rebound impact from the ball. This design ensured a consistent release process of the steel ball, minimized human error, and improved the repeatability of test results.
Comparison with the manual test methods demonstrated a significant improvement in the repeatability of the automated test method. The automated test method not only enhanced the accuracy and repeatability of the tests, but also reduced the workload and time required for each test. Tests were conducted on the same circuit boards using both manual and automated methods, confirming the impact of excessive high-frequency components.
Future research aims to further enhance the automated system by application of real-time feedback. Precision sensors and actuators may monitor and adjust the pendulum’s motion, significantly improving accuracy and consistency. Various optimization techniques need to be explored to derive test conditions that meet test requirements. Through multiple trials, the developed automated test methods and condition predictions may be refined to identify and improve any shortcomings.
In conclusion, the accurate prediction of test conditions and the development of an automated testing system represent significant advancements in the field of pyroshock testing. Aerospace electronic components require considerable time for development and manufacturing. This research significantly contributes to preventing unnecessary delays and damage during the test process. These improvements, including the verification of the similarity between pyroshock tests and predictions, the effective determination and GA optimization of necessary test variables to meet test requirements, and the development of an automated test system capable of consistently implementing test conditions, collectively enhance the reliability and repeatability of test procedures. Moreover, the automated test method not only improves accuracy and repeatability but also reduces the workload required for each test, thereby providing crucial benefits for mechanical durability validation of aerospace components.
Author Contributions
Conception and design, W.B. and J.P.; Data Collection, W.B.; Analysis and interpretation, W.B. and J.P.; Writing the article, W.B. and J.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (RS-2022-0014-3396).
Data Availability Statement
The data presented in this study are available in article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- ECSS-E-ST-10-03C; Space Engineering—Testing. ECSS: Nice, France, 2022.
- NASA-STS-7003A; Pyroshock Test Criteria. NASA: Washington, DC, USA, 2011.
- MIL-STD-810H; Environmental Engineering considerations and Laboratory Tests. U.S. Department of Defense: Arlington, VA, USA, 2019.
- MIL-STD-1540D; Product Verification Requirements for Launch, Upper-Stage, and Space Vehicles. U.S. Department of Defense: Arlington, VA, USA, 1999.
- ECSS-E-HB-32-25A; Mechanical Shock Design and Verification Handbook. European Cooperation for Space Standardization: Noordwijk, The Netherlands, 2015.
- Irvine, T. SRS Matlab Script (Kelly-Richman & Smallwood). Available online: https://www.vibrationdata.com/matlab.htm (accessed on 1 August 2023).
- Sisemore, C. Shock Response Spectrum Primer. In Proceedings of the 91st Shock and Vibration Symposium, Orlando, FL, USA, 19–23 September 2021. [Google Scholar]
- Lee, J.-R.; Chia, C.C.; Kong, C.-W. Review of Pyroshock Wave Measurement and Simulation for Space Systems. Measurement 2012, 45, 631–642. [Google Scholar] [CrossRef]
- Irvine, T. An Introduction to the Shock Response Spectrum, Revision S; 2012. Available online: https://www.vibrationdata.com/tutorials2/srs_intr.pdf (accessed on 1 March 2023).
- Davie, N.T.; Bateman, V.I. Pyroshock testing, chapter 26, part 2. In Harris’ Shock and Vibration Handbook; Sandia National Laboratories: Albuquerque, NM, USA, 1996. [Google Scholar]
- Davie, N.T.; Bateman, V.I. Pyroshock Simulation for Satellite Components Using a Tunable Resonant Fixture-Phase 1; SAND 92-2135; 1992. Available online: https://www.osti.gov/biblio/6897405 (accessed on 15 July 2022).
- Davie, N.T. Simulation of Pyroshock Environments Using a Tunable Resonant Fixture. U.S. Patent 5,565,626, 15 October 1993. [Google Scholar]
- Kolaini, A.R.; Nayeri, R.; Kerm, D.L. Pyroshock Simulation Systems: Are We Correctly Qualifying Flight Hardware for Pyroshock Environments? In Proceedings of the 25th Aerospace Testing Seminar, Pasadena, CA, USA, 12–15 October 2009. [Google Scholar]
- Ding, J.; Sun, Y.; Dang, Y. Pyroshock Response Prediction of Spacecraft Structure in Wide Frequency Domain Based on Acceleration FRF. Aerospace 2022, 9, 54. [Google Scholar] [CrossRef]
- Choi, M. Experimental Prediction of Shock Response Spectra of Point-Wise Explosive Pyroshock in a Space Launcher Composite Structure Using Laser Pulse Excitation and In-line Filtering. SAE Int. J. Aerosp. 2013, 6, 65–69. [Google Scholar] [CrossRef]
- Wang, X.; Yu, T.; Yan, H.; Ding, J.; Li, Z.; Qin, Z. Application of Stress Wave Theory for Pyroshock Isolation at Spacecraft-Rocket Interface. Initiat. Pyrotech. 2007, 5, 5–8. [Google Scholar] [CrossRef]
- Yalçinkaya, T.; Gürsoy, B. Numerical Validation of a Pyroshock Test System and Application to Qualification Tests. Aerospace 2022, 9, 400. [Google Scholar] [CrossRef]
- Gour, S.; Ahmad, D.; Kumar, D.; Ajaj, R.M.; Zweiri, Y. Investigating the Tear Fracture of Elastomeric Skins in Morphing Wings: An Experimental and Computational Study. Int. J. Appl. Mech. 2023, 15, 2350096. [Google Scholar] [CrossRef]
- Sun, W.; Su, Q.; Yuan, H.; Chen, S. Performance Analysis of Absolute Acceleration Shock Response Spectrum. J. Phys. Conf. Ser. 2020, 1676, 012131. [Google Scholar] [CrossRef]
- Sun, W.; Su, Q.; Yuan, H.; Liu, L. Calculation and Characteristic Analysis on Different Types of Shock Response Spectrum. J. Phys. Conf. Ser. 2020, 1676, 012236. [Google Scholar] [CrossRef]
- Tuma, J.; Koci, P. Calculation of a Shock Response Spectrum. In Proceedings of the International Carpathian Control Conference (ICCC), Prague, Czech Republic, 3–4 February 2011. [Google Scholar]
- Almesmari, A.; Jarrar, F.; Almaskari, F.; Marpu, P.R.; Abdul Shukoor, N.; Govindan, J.K. Development of a Metal-to-Metal Mid-Field Shock Test Procedure for Nanosatellites. IEEE J. Miniaturization Air Space Syst. 2020, 1, 103–109. [Google Scholar] [CrossRef]
- Kiryenko, S.; Piret, G.; Kasper, J. ESA ESTEC Shock Bench Presentation; European Space Agency: Paris, France, 2005. [Google Scholar]
- Binder, J.; McCarty, M.; Rasmussen, C. Development of a Pyrotechnic Shock Simulation Apparatus for Spacecraft Applications; California Polytechnic State University: San Luis Obispo, CA, USA, 2012. [Google Scholar]
- Lacher, A.; Jüngel, N.; von Wagner, U.; Bäcker, A. Analytical Calculation of In-Plane Response of Plates with Concentrated Masses to Impact and Application to Pyroshock Simulation. J. Sound Vib. 2012, 331, 3358–3370. [Google Scholar] [CrossRef]
- Smith, J.; Brown, A. Analysis of the Shock Response Spectrum and Resonant Plate Testing Methods. J. Aerosp. Test. 2019, 45, 631–645. [Google Scholar]
- Jung, J.R.; Kim, I.G.; Lee, S.J.; Kang, C.H. Characteristics of the shock response spectrum for structures subjected to pyroshock. In Proceedings of the Korean Society for Aeronautical & Space Sciences Spring Conference, Gyeongju, Republic of Korea, 13–15 April 2011. [Google Scholar]
- Jeon, H.; Kim, M.; Kim, M.; Kwon, Y.; Yu, Y.; Kim, I. The Parametric Study of the Design Variables on the SRS of Pyroshock Resonant Bar. J. Korea Inst. Mil. Sci. Technol. 2018, 21, 413–421. [Google Scholar]
- Jonsson, M. Development of a Shock Test Facility for Qualification of Space Equipment. Master’s Thesis, Chalmers University of Technology, Department of Applied Mechanics, Division of Dynamics, Göteborg, Sweden, 2012; pp. 1–96. [Google Scholar]
- Charvet, B.; Dilhan, D.; Palladino, M. Shock Bench Enhancements. In Proceedings of the 13th European Conference on Spacecraft Structures, Materials & Environmental Testing, Braunschweig, Germany, 1–4 April 2014. [Google Scholar]
- Küçükbayram, A.İ. Analysis and Verification of a Pyroshock Test System. Master’s Thesis, Department of Mechanical Engineering, Middle East Technical University, Ankara, Turkey, 2021; pp. 1–12. [Google Scholar]
- Adebolu, I.O.; Masui, H.; Cho, M. Quantitative Evaluation of SRS Similarity for Aerospace Testing Applications. J. Aerosp. Test. 2021, 29, 123–136. [Google Scholar] [CrossRef]
- Davie, N.T.; Bateman, V.I. Recent Developments in Pyroshock Simulation Using Fixtures with Tunable Resonant Frequencies. Proc. Inst. Environ. Sci. 2020, 46, 77–89. [Google Scholar]
- Zhang, L.; Wang, J. Research on Impact Reduction of Flexible Boundary Particle Damping Honeycomb Plate Based on Discrete Element Multi-Body Dynamics Coupling. J. Aerosp. Eng. 2019, 32, 405–418. [Google Scholar]
- Kolaini, A.R.; Fernandez, J.P. JPL Tunable Beam Pyroshock Simulation System. In Proceedings of the Spacecraft & Launch Vehicle Dynamic Environments Workshop, El Segundo, CA, USA, 26–28 June 2007; pp. 1–12. [Google Scholar]
- Lee, S.-J.; Hwang, D.-H.; Han, J.-H. Development of Pyroshock Simulator for Shock Propagation Test. Shock. Vib. 2018, 9753793. [Google Scholar] [CrossRef]
- Garnier, J.; De Fruytier, C. Experimental Shock Damage Risk Assessment for New Generation TAS-B Plasmic Propulsion Unit. In Proceedings of the 13th European Conference on Spacecraft Structures, Materials & Environmental Testing, Braunschweig, Germany, 1–4 April 2014. [Google Scholar]
- Spletzer, M.; Sisemore, C. Design of a Resonant Plate Shock Fixture to Attenuate Excessive High-Frequency Energy Inputs. In Proceedings of the 87th Shock and Vibration Symposium, New Orleans, LA, USA, 17–20 October 2016. [Google Scholar]
- Titulaer, J.J.; Allen, B.R.; Maly, J.R. An Alternative to Pyrotechnic Testing for Shock Identification; CSA Engineering, Inc.: Mountain View, CA, USA, 2008. [Google Scholar]
- Gambler, F.; Conti, C.; Dehombreux, P.; Filippi, E. Development of a Test Facility to Simulate Pyroshock Environments in a Laboratory. Trans. Built Environ. 1998, 32, 274–282. [Google Scholar]
- Hwang, D.-H.; Park, H.-S.; Han, J.-H. Development of a Miniature Point Source Pyroshock Simulator. J. Sound Vib. 2020, 481, 115438. [Google Scholar] [CrossRef]
- Jeong, J.-W.; Lim, J.-H.; Kim, K.-W.; Lee, J.-J. Development of a Point Pyroshock Source Simulator. Shock. Vib. 2017. [Google Scholar] [CrossRef]
- Kim, B.-S.; Lee, J. Development of Impact Test Device for Pyroshock Simulation Using Impact Analysis. Aerospace 2022, 9, 407. [Google Scholar] [CrossRef]
- Adebolu, I.O. Evaluation of Shock Response Spectrum Similarity and Repeatability in the Qualification Testing of Space Components. Ph.D. Thesis, Kyushu Institute of Technology, Fukuoka, Japan, 2021. [Google Scholar]
- RAL Space. First Pyroshock Tests Completed at RAL Space. RAL Space. 2020. Available online: https://www.ralspace.stfc.ac.uk/Pages/First-pyroshock-tests-completed-at-RAL-Space.aspx (accessed on 3 May 2024).
- MTES Pyroshock Test. MTES. Available online: http://mtes.co.kr/sub/sub2_2_2.php (accessed on 3 May 2024).
- Beyond Gravity Switzerland Pyroshock Test. Available online: https://triasrnd.com/l/93-pyroshock-test (accessed on 3 May 2024).
- DLR—Institute of Space Systems. Mechanical-Dynamical Test Facilities: Pyroshock. Laboratories Brochure. Available online: https://www.dlr.de/en/irs/media/publications/institute-brochures (accessed on 3 May 2024).
- Astrofein. Environmental Simulation. Astrofein. Available online: https://www.astrofein.com/en/environmental-simulation/ (accessed on 3 May 2024).
- von Wagner, U.; Jüngel, N.; Ritzmann, S.; Bäger, A. Simulation of Pyroshocks. In Proceedings of the 1st CEAS European Air and Space Conference, Berlin, Germany, 10–13 September 2007. [Google Scholar]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization, and Machine Learning; Addison-Wesley: Boston, MA, USA, 1989. [Google Scholar]
- Gen, M.; Cheng, R. Genetic Algorithms and Engineering Design; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Sun, W.; Huang, Y.; Chen, H. An Improved Adaptive Genetic Algorithm for Optimizing Pyroshock Acceleration Synthesis. IEEE Access 2019, 7, 132682–132692. [Google Scholar] [CrossRef]
- Viale, L.; Daga, A.P.; Garibaldi, L. Design of a Resonant Plate for Pyroshock Testing Based on Shape and Size Heuristic Optimization. 2023. Available online: https://hal.science/hal-04179596/document (accessed on 1 May 2024).
- Viale, L.; Daga, A.P.; Fasana, A.; Garibaldi, L. On pyroshock tests for aerospace equipment qualification: A comprehensive parametric model for the simulation and the design of pyroshock test facilities. Int. J. Impact Eng. 2023, 180, 104697. [Google Scholar] [CrossRef]
- Monti, R.; Gasbarri, P. Dynamic load synthesis for shock numerical simulation in space structure design. Acta Astronaut. 2017, 137, 222–231. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, J.; Wang, K.; Zhang, F. Optimal Placement of Actuators for Active Vibration Control Using EER and Genetic Algorithm. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering (ICMAE), Brussels, Belgium, 22–25 July 2019; pp. 449–453. [Google Scholar]
- Brüggemann, T.; Biermann, D.; Zabel, A. Development of an Automatic Modal Pendulum for the Measurement of Frequency Responses for the Calculation of Stability Charts. Procedia CIRP 2015, 33, 587–592. [Google Scholar] [CrossRef]
Figure 1.
SRS predictions in the frequency domain.
Figure 1.
SRS predictions in the frequency domain.
Figure 2.
Various pyroshock test methods. (a) Pendulum method; (b) Pneumatic projectile method; (c) Nail gun method.
Figure 2.
Various pyroshock test methods. (a) Pendulum method; (b) Pneumatic projectile method; (c) Nail gun method.
Figure 3.
Flow chart of the genetic algorithm used for shock test parameters.
Figure 3.
Flow chart of the genetic algorithm used for shock test parameters.
Figure 4.
Analytical model of pyroshock test system using longitudinal wave propagation.
Figure 4.
Analytical model of pyroshock test system using longitudinal wave propagation.
Figure 5.
Hertzian contact model when hitting the structure.
Figure 5.
Hertzian contact model when hitting the structure.
Figure 6.
Comparison of transient acceleration response and SRS with the varying mass and angle. Vibration responses for (a) mass 18 kg, angle 50°, (b) mass 18 kg, angle 80°, and (c) mass 30 kg, angle 80°. (d) The resulting SRS obtained with different test conditions.
Figure 6.
Comparison of transient acceleration response and SRS with the varying mass and angle. Vibration responses for (a) mass 18 kg, angle 50°, (b) mass 18 kg, angle 80°, and (c) mass 30 kg, angle 80°. (d) The resulting SRS obtained with different test conditions.
Figure 7.
Comparisons of measured and predicted vibration responses.
Figure 7.
Comparisons of measured and predicted vibration responses.
Figure 8.
Effects of the pendulum angle and frequency on the estimated SRS.
Figure 8.
Effects of the pendulum angle and frequency on the estimated SRS.
Figure 9.
Comparison between the optimal SRS obtained through GA and the test requirements.
Figure 9.
Comparison between the optimal SRS obtained through GA and the test requirements.
Figure 10.
Convergence of objective functions to minimize the fitness value.
Figure 10.
Convergence of objective functions to minimize the fitness value.
Figure 11.
Combinations of a generation population.
Figure 11.
Combinations of a generation population.
Figure 12.
Test repeatability comparisons between automation and manual tests.
Figure 12.
Test repeatability comparisons between automation and manual tests.
Figure 13.
(a) Box plot and (b) four indicators comparison between automated and manual tests.
Figure 13.
(a) Box plot and (b) four indicators comparison between automated and manual tests.
Table 1.
Summary of pyroshock test standards.
Table 1.
Summary of pyroshock test standards.
| Standard | Title | Purpose | Features |
|---|
| NASA-STD-7003A | Pyroshock Test Criteria | To establish guidelines for simulating and measuring the impact of pyroshocks on aerospace vehicles | - -
Establishes pyroshock levels for equipment and components used in space missions - -
Provides detailed instructions for the measurement, evaluation, and testing of pyroshock
|
| ECSS-E-ST-10-03C | Space Engineering–Testing | To describe testing procedures and principles for evaluating space hardware and systems | - -
Delivers an extensive overview of the environmental testing required for space missions - -
Presents a broad approach to multiple environmental tests, including pyroshock
|
| MIL-STD-810H | Environmental Engineering Considerations and Laboratory Tests | To outline test methods and procedures for replicating environmental conditions affecting military equipment | - -
Provides test methods for a broad spectrum of environmental conditions - -
Includes pyroshock as one of the environmental tests covered
|
| MIL-STD-1540D | Test Requirements for Space Vehicles | To establish test requirements for space vehicles | - -
Provides detailed guidelines on test requirements for space vehicles and their subsystems - -
Encompasses pyroshock testing procedures, criteria, and methods for data analysis
|
Table 2.
Classification of Pyroshock.
Table 2.
Classification of Pyroshock.
| Standard | Intensity | Max. Acceleration (g) | Max. Frequency
(kHz) | Test Method |
|---|
| MIL-STD-810H | Near-field | 10,000 or more | 10 or more | - -
Explosives explosion
|
| Mid-field | 10,000 or less | 3~10 | - -
Mechanical test devices
|
| Far-field | 1000 or less | 3 or less | - -
Mechanical test devices - -
Electric exciters
|
| NASA-STD-7003A | Near-field | 5000 or more | 100 or more | - -
Explosives explosion
|
| Mid-field | 1000~5000 | 10 or more | - -
Mechanical test devices
|
| Far-field | 1000 or less | 10 or less | - -
Mechanical test devices - -
Electric exciters
|
Table 3.
Genetic algorithm optimization parameters.
Table 3.
Genetic algorithm optimization parameters.
| Aspect | Details |
|---|
| Control Variables | - -
Mass (m1): Discrete values, {12, 18, 24, 30} kg - -
Angle (θ): Range from 10° to 90° - -
Position (x): Discrete positions: {0.2~0.7} m
|
| Objective Function | Minimize the sum of squared differences between the calculated SRS and the required SRS, plus penalties for violating upper and lower
SRS limits
Cost = Σ(max(0,|SRScalc,i − SRSreq,i|))2 + λ·Σ(max(0,SRScalc,i − SRSupper,i) + max(0, SRSlower,i−SRScalc,i))
where
- -
SRScalc,i: the calculated SRS - -
SRSreq,i: the required SRS - -
SRSlower,i, SRSupper,i: lower and upper allowable SRS limits - -
λ: a weighting factor
|
| Constraints | - -
Mass constraint: m ∈ {12, 18, 24, 30} - -
Angle constraint: 10° ≤ θ ≤ 90° - -
Position constraint: x ∈ {0.2~0.7} - -
SRS values must not exceed the defined upper limit or fall below the defined lower limit
|
| GA Parameters | - -
Population size, Max generations - -
Crossover fraction, Mutation - -
Gaussian with a rate of 0.01 - -
Selection: Tournament selection - -
Elitism: Top 10 individuals preserved from each generation
|
Table 4.
GA parameters for optimization process.
Table 4.
GA parameters for optimization process.
| Algorithm Type | Population Size | Generation Size | Elite
Count | Crossover Fraction | Mutation Function | Mutation Rate | Selection Function |
|---|
| Continuous | 200 | 200 | 10 | 70% | Gaussian | 20% | Tournament |
Table 5.
Optimal value of the parameters through GA.
Table 5.
Optimal value of the parameters through GA.
| Parameter | Value |
|---|
| Mass () [kg] | 24 |
| Angle (θ) [°] | 29 |
| Specimen location () [m] | 0.6 |
Table 6.
Resistance Value Variations Resulting from Manual Pyroshock Tests (Sample #1).
Table 6.
Resistance Value Variations Resulting from Manual Pyroshock Tests (Sample #1).
| Terminal | Pristine
[mΩ] | After the Test
[mΩ] | Change
[mΩ] | Rate of Change
[%] |
|---|
| T1 | 237.05 | 236.48 | 0.57 | 0.24 |
| T3 | 329.95 | 328.13 | 1.82 | 0.55 |
| T5 | 255.69 | 253.84 | 1.85 | 0.72 |
Table 7.
Resistance Value Variations Resulting from Automated Pyroshock Tests (Sample #2).
Table 7.
Resistance Value Variations Resulting from Automated Pyroshock Tests (Sample #2).
| Terminal | Pristine
[mΩ] | After the Test
[mΩ] | Change
[mΩ] | Rate of Change
[%] |
|---|
| T1 | 236.49 | 235.79 | 0.70 | 0.30 |
| T3 | 334.23 | 333.77 | 0.46 | 0.14 |
| T5 | 257.21 | 256.33 | 0.88 | 0.34 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).